Abstract
Taking into account the motional induction effect, in which the Earth crust that has finite electrical conductivity vibrates in the ambient geomagnetic field resulting in motionally induced electric current, we derive semi-analytical solutions of seismo-electromagnetic signals generated by an earthquake source in 3-D multi-layered media, which consists of an air half-space and multiple solid layers. First, both the elastic and electromagnetic (EM) wave-fields involved in the governing equations, which have the form of Maxwell’s equations coupled with elastodynamic equations, are expanded by a set of vector basis functions in cylindrical coordinate system. Then, we reorganize the transformed governing equations expressed by expansion coefficients and obtain corresponding first-order ordinary differential equations for the wave-fields in air and solid media. The expansion of the motionally induced electric current and the reorganization of Maxwell’s equations are the most important part, and also the most complicated and tedious part of this work. Thereafter, we solve the first-order ordinary differential equations through the Luco–Apsel–Chen generalized reflection and transmission method gaining solutions of the expansion coefficients. Finally, we obtain the frequency–space-domain semi-analytical solutions written as integrations of corresponding expansion coefficients over wavenumber domain, which can be numerically calculated by the discrete wavenumber method. The time-domain solutions can be achieved by further applying the discrete inverse Fourier transform. To have a numerical stability at any high frequency, we adopt the analytical regularization approach in the derivation process by introducing two artificial interfaces with infinitely small distance from the source. On the basis of the semi-analytical solutions, we can tell that only EM fields of TM mode (in which magnetic fields are transversely polarized) will be induced by SH waves, whereas EM fields of both TE mode (in which magnetic fields are transversely polarized) and TM mode will be induced by P and SV waves. The derived semi-analytical solutions can be used to calculate seismo-electromagnetic signals either below or above the free surface.

Similar content being viewed by others
Introduction
Temporal variation of electromagnetic (EM) fields observed before and during earthquake events has been reported by many researchers (e.g., Belov et al. 1974; Gokhberg et al. 1989; Farser-Smith et al. 1990; Takeuchi et al. 1997; Honkura et al. 2000, 2004; Nagao et al. 2000; Karakelian et al. 2002; Matsushima et al. 2002; Tang et al. 2010; Fujinawa et al. 2011; Han et al. 2011, 2014, 2015, 2016, 2017; Huang 2011a, b; Hattori et al. 2013; Xu et al. 2013; Fujinawa and Noda 2015). These EM signals have attracted many attentions from geophysical scientists, because they are obviously connected to earthquake and provide a new perspective to detect and study development of earthquake and occurrence processes, as well as the precursory anomaly of earthquake. Hence, many theoretical and experimental efforts have been made to reveal the physical mechanism of the earthquake-related EM signals. After decades of research, geophysical scientists have come up with several possible physical models that consider different seismo-electromagnetic coupling mechanisms to explain the earthquake-related EM signals. Nowadays, four kinds of mechanisms, i.e., electrokinetic effect (e.g., Mizutani et al. 1976; Pride 1994), piezoelectric effect (Ogawa and Utada 2000; Huang 2002), piezomagnetic effect (e.g., Okubo et al. 2011; Yamazaki 2016), and the motional induction effect (e.g., Gershenzon et al. 1993; Honkura et al. 2000, 2004), are widely accepted and frequently used for analyzing the earthquake-related EM signals. These four mechanisms are based on relatively independent physical hypothesises, and in fact, it is hard to explain all observed EM signals by just one of the mechanisms. The realistic earthquake-related EM signals may be governed by part or all of the four mechanisms, and hence, it is worthwhile to conduct extensive investigations to figure out the seismo-electromagnetic conversion characteristics of the four different mechanisms. For example, a technique extending the Luco–Apsel–Chen (LAC) generalized reflection and transmission (GRT) method (Luco and Apsel 1983; Chen 1993), which is a well-known and very useful method for the study of synthetic seismogram (Martin and Thompson 1997; Chen 2007; Ge and Chen 2008), was introduced to simulate seismic waves and EM signals by considering the electrokinetic effect (Ren et al. 2007, 2010a, b). Later, this technique was adopted to study the EM signals generated by earthquake sources (Ren 2009; Ren et al. 2012, 2015, 2016a, b, 2020; Zhang et al. 2013; Huang et al. 2015; Sun et al. 2019).
Motional induction effect is also known as seismo-dynamo effect (Honkura et al. 2000, 2009) or crustal dynamo effect (Iyemori et al. 1996). It is based on the physical idea that the seismic ground motion of Earth’s conducting crust immersed in the ambient geomagnetic field can yield an electromotive force and a motional induction current, which causes temporal variations in EM fields. Gershenzon et al. (1993) investigated several seismo-electromagnetic coupling effects using a dipole model for the source of the earthquake-related EM signals to estimate the EM signals caused by motional induction, piezomagmetic and electrokinetic effects. Iyemori et al. (1996) adopted the motional induction effect to discuss coseismic EM signals of the 1995 Hyogoken-Nanbu M7.2 earthquake by considering an electrically conducting slab moving in geomagnetic field. Matsushima et al. (2002) recorded the coseismic EM signals of the 1999 M7.4 İzmit earthquake and its aftershock, and claimed that the seismo-dynamo effect is a plausible mechanism for the recorded EM signals. Ujihara et al. (2004) conducted magnetotelluric observations to record EM data for the aftershock of the 26 May 2003 M7.1 off Miyagi Perfecture earthquake, and they concluded that the seismo-dynamo effect is responsible for the EM signals associated with seismic waves. Tang et al. (2010) also proposed that the coseismic EM signals of the aftershocks of 2008 Wenchuan Ms8.0 earthquake were possibly caused by motional induction effect.
To get a fundamental insight into the motional induction effect, quantitative investigations were also conducted by researchers. Yamazaki (2012) developed a solution for motional induction effect in 3-D horizontally layered model with seismic waves approximated as plane waves. He showed that the amplitudes of magnetic field arising from a Rayleigh wave with displacement of 10 cm and a period of 30 s were as large as 0.1 nT. Gao et al. (2014) provided analytical solutions for motional induction effect in a homogeneous full-space model. Their analytical solutions also showed that the coseismic electric and magnetic signals corresponding to the seismic waves with the acceleration of 0.1 m/s2 can be as large as 1 mV/km and 0.1 nT, respectively. Later, Gao et al. (2019) studied the EM responses to an earthquake source due to the motional induction effect in a 2-D horizontally layered model. These quantitative studies suggested that the motional induction effect possibly plays an important role in generated EM signals during earthquake. However, these studies have some limitations. The solutions of Yamazaki (2012) cannot apply for the near-field case, since the approximation of seismic plane wave was used. The analytical solutions (Gao et al. 2014) are only for a homogeneous full-space. The 2-D solutions of Gao et al. (2019) only account for a special situation, in which the fault plane is perpendicular to the plane of seismic wave propagation. Besides, Gao et al. (2019) claimed that it was difficult to derive the 3-D solutions by methods like the LAC GRT method, and that double space-to-wavenumber Fourier transforms must be applied to derive the 3-D solutions. However, they were wrong about this point.
In this study, we consider a 3-D multi-layered model, which is widely used in the study of seismology, and use the LAC GRT method to derive the semi-analytical solutions of seismo-electromagnetic signals generated by an earthquake source due to the motional induction effect. The mathematical derivations are shown step by step to assure the credibility. The remainder of this paper is organized as follows. First, we summarize the governing equations that have the form of Maxwell’s equations coupled with elastodynamic equations, as well as boundary conditions for seismic waves and EM signals in a multi-layered model. Second, we give a brief introduction to a set of vector basis functions, which is expressed in cylindrical coordinates, and use it to obtain transformed governing equations. In this process, deriving the expansion coefficients of the cross product of seismic displacement to ambient geomagnetic field is complicated but a key step. Later, we show the mathematical derivation process for obtaining the general solutions of the transformed governing equations in the frequency domain. Finally, we utilize the LAC GRT method to determine the source terms and wave–amplitude vectors, and insert them into the general solutions obtaining the semi-analytical solutions in frequency–space domain. The time–space-domain solutions can be achieved by further applying the discrete inverse Fourier transform.
Governing equations and boundary conditions for multi-layered media
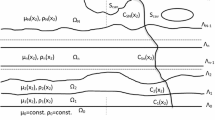
The multi-layered media concerned in the study are illustrated in Fig. 1. There are N homogeneous solid layers below an air half-space, and each solid layer is bounded by horizontally flat interfaces, \(z = z^{(j)}\) and \(z = z^{(j + 1)}\). The interface with the depth of \(z = z^{(1)}\) is a free surface. The bottom layer (N-th solid layer) is a half-space and thus has a lower interface \(z = z^{(N + 1)} = + \infty\). A double couple point source is embedded in the sth solid layer and located at \((0,0,z_{s} )\). To eliminate the exponential growth factors in the source term (see Source term section), the analytical regularization approach (Chen 1999; Ren et al. 2010b) is applied by inserting two artificial interfaces \(z = z^{(s - )} = z_{s} - \vartriangle z\) and \(z = z^{(s + )} = z_{s} + \vartriangle z\), where \(\vartriangle z\) is positive and infinitely small quantity. When \(\vartriangle z\) approaches to zero (i.e., \(\vartriangle z \to 0\)), the sth solid layer actually will be divided into two layers, \(z^{(s)} \le z \le z^{(s - )}\) and \(z^{(s + )} \le z \le z^{(s + 1)}\).
The elastic and electrical properties of each solid layer are described by Lamé constant \(\lambda^{(j)}\), shear modulus \(G^{(j)}\), density \(\rho^{(j)}\), magnetic permeability \(\mu^{(j)}\), electrical permittivity \(\varepsilon^{(j)}\), and conductivity \(\sigma^{(j)}\). The two parameters \(\mu^{(j)}\) and \(\varepsilon^{(j)}\) can be related to \(\mu_{0}\) (the vacuum magnetic permeability) and \(\varepsilon_{0}\) (the vacuum electrical permittivity) by \(\mu^{(j)} = \mu_{r}^{(j)} \mu_{0}\) and \(\varepsilon^{(j)} = \varepsilon_{r}^{(j)} \varepsilon_{0}\), where \(\mu_{r}^{(j)}\) and \(\varepsilon_{r}^{(j)}\) represent the relative magnetic permeability and relative electrical permittivity, respectively. We will also derive the semi-analytical solutions of EM fields in the near-free-surface air (e.g., with altitude less than several kilometers), which is far away from ionosphere, and therefore presumably can be treated as non-conductive, i.e., \(\sigma^{(0)} = 0\). For the air medium, we assume \(\mu^{(0)} = \mu_{0}\) and \(\varepsilon^{(0)} = \varepsilon_{0}\).
Assuming a time dependence of \(e^{ - i\omega t}\), one can find the governing equations of seismo-electromagnetic signals in the jth solid layer can be written as the following frequency-domain expressions:
where \(j = 1,2, \ldots ,N\); \(\tilde{\varepsilon }^{(j)} = \varepsilon^{(j)} + \frac{i}{\omega }\sigma^{(j)}\); \(\omega\) represents the circular frequency; u is the seismic displacement (meaning \(- i\omega {\mathbf{u}}\) represents the seismic vibration velocity); F indicates the body force density; \(\delta_{j,s}\) is Kronecker delta function; \({{\varvec{\uptau}}}\) is the traction acting on a horizontal plane below the air half-space; \({\mathbf{e}}_{z}\) represents the unit vector along z-direction; E and H are the electric and magnetic fields, respectively; \({\mathbf{B}}^{{\text{a}}}\) indicates the ambient geomagnetic field. The seismic waves are independent of EM signals. The second term in the right side of Eq. (3) represents the induction electric current generated by the vibration of conductive media in geomagnetic field. It acts as the source of EM fields. This study considers time and spatial scales up to several minutes and several hundred kilometers, respectively. Although the ambient geomagnetic field \({\mathbf{B}}^{{\text{a}}}\) varies over these scales, the amplitudes of these temporal–spatial variations are significantly smaller than the temporal–spatial average. Therefore, temporal–spatial variations in \({\mathbf{B}}^{{\text{a}}}\) should cause only minor changes on the resultant EM variations. For this reason, \({\mathbf{B}}^{{\text{a}}}\) is considered as a uniform vector over the area and period of interest (Yamazaki 2012).
Equation (2) is derived from \({{\varvec{\uptau}}}^{(j)} = {{\varvec{\Gamma}}}^{(j)} \cdot {\mathbf{e}}_{z}\), where \({{\varvec{\Gamma}}}^{(j)}\) is the stress tensor given by:
where \({\mathbf{I}}\) is the identity matrix and the superscript ‘T’ represents the transpose of the matrix. The boundary conditions that should be taken into consideration in deriving the semi-analytical solutions are the reason of using \({{\varvec{\uptau}}}\) instead of \({{\varvec{\Gamma}}}^{(j)}\).
The detailed boundary conditions are as follows
-
i.
Traction free on the free surface, that is:
$$\left. {{{\varvec{\uptau}}}^{(1)} } \right|_{{z = z^{(1)} }} = {\mathbf{0}};$$(6) -
ii.
Continuities of seismic displacement and traction fields at subsurface interfaces, that is:
$$\left. {\left[ {\begin{array}{*{20}c} {{\mathbf{u}}^{(j - 1)} } \\ {{{\varvec{\uptau}}}^{(j - 1)} } \\ \end{array} } \right]} \right|_{{z = z^{(j)} }} = \left. {\left[ {\begin{array}{*{20}c} {{\mathbf{u}}^{(j)} } \\ {{{\varvec{\uptau}}}^{(j)} } \\ \end{array} } \right]} \right|_{{z = z^{(j)} }} ,\quad (j = 2,3, \ldots ,N);$$(7) -
iiii.
Continuities of horizontal components of EM fields at each interface, that is:
$$\left. {\left[ {\begin{array}{*{20}c} {{\mathbf{e}}_{z} \times {\mathbf{H}}^{(j - 1)} } \\ {{\mathbf{e}}_{z} \times {\mathbf{E}}^{(j - 1)} } \\ \end{array} } \right]} \right|_{{z = z^{(j)} }} = \left. {\left[ {\begin{array}{*{20}c} {{\mathbf{e}}_{z} \times {\mathbf{H}}^{(j)} } \\ {{\mathbf{e}}_{z} \times {\mathbf{E}}^{(j)} } \\ \end{array} } \right]} \right|_{{z = z^{(j)} }} ,\quad (j = 1,2, \ldots ,N);$$(8) -
iv.
Radiation condition at infinity (\(z = \pm \infty\)), that is:
$$\left. {\left[ {\begin{array}{*{20}c} {{\mathbf{u}}^{(N)} } \\ {{{\varvec{\uptau}}}^{(N)} } \\ {{\mathbf{H}}^{(N)} } \\ {{\mathbf{E}}^{(N)} } \\ \end{array} } \right]} \right|_{{z = z^{(N + 1)} }} = {\mathbf{0}},$$(9)$$\left. {\left[ {\begin{array}{ll} {{\mathbf{H}}^{(0)} } \\ {{\mathbf{E}}^{(0)} } \\ \end{array} } \right]} \right|_{z = - \infty } = {\mathbf{0}},$$(10)where \({\mathbf{E}}^{(0)}\) and \({\mathbf{H}}^{(0)}\) indicate the EM fields in the air.
Transformed governing equations
In this section, we adopt a classic method that has been widely used as a pretreatment before deriving semi-analytical solutions of wave-fields in 3D multi-layered media (e.g., Aki and Richards 1980; Chen 1999; Ren et al. 2007, 2009, 2010a, b, 2012). This pretreatment leads to transformed governing equations. The details are introduced below.
The involved wave-field vectors are expanded using a set of vector basis functions:
where \(Y_{k}^{m} (r,\theta ) = J_{m} (kr)e^{im\theta }\)(\(m = 0,\; \pm 1,\; \pm 2, \ldots\)) is the cylindrical harmonic function. The orthogonality and completeness of this set of vector basis functions, which have been proven in previous studies (Aki and Richards 1980; Chen 1999), can be found in Appendix A.
An arbitrary vector, for example, \({\mathbf{C}}(r,\theta ,z)\), can be expressed in terms of this set of function basis as:
where \(C_{T,m} (z,k)\), \(C_{S,m} (z,k)\), and \(C_{R,m} (z,k)\) are the expansion coefficients given by:
where the symbol * indicates the complex conjugate.
Transformed governing equations of elastic waves
For the double couple point source concerned in this study, the body force density F can be mathematically expressed as:
where \({\mathbf{r}}\) is the horizontal space variable, i.e., \({\mathbf{r}} = (r,\theta ) = (x,y)\); \({\mathbf{r}}_{s}\) denotes the horizontal space variable of source point; \(z_{s}\) indicates the source depth; \(\delta\) is the delta function; \({\mathbf{M}}(\omega )\) represents the spectrum of the source moment tensor. There is a trick in evaluating expansion coefficients of the source according to Eqs. (13)–(15): if an arbitrary cylindrical coordinate system is chosen, the order ‘m’ will theoretically go to infinity. However, if a ‘source-center’ cylindrical coordinate system, in which the point source is located in z-axis, is chosen, the order ‘m’ will be limited as \(\left| m \right| \le 2\). Therefore, we choose a source-center coordinate system for 3D problem (see Fig. 1). Then, the expansion coefficients of the double couple point source can be written as:
where:
\(M_{xx} (\omega )\), \(M_{xy} (\omega )\), \(M_{xz} (\omega )\), \(M_{yy} (\omega )\), \(M_{yz} (\omega )\), and \(M_{zz} (\omega )\) are the corresponding elements of the source moment tensor \({\mathbf{M}}(\omega )\). In this work, we take into account double couple point source representing a fault without tension (i.e., the displacement discontinuity across the fault is parallel to fault plane). For such kind of source, Eqs. (3.21) and (3.23) in Chapter 3 of Aki and Richards (1980) tell us that the source moment tensor is a symmetric tensor (Chen 1999).
The elastic wave-fields involved in Eqs. (1) and (2) can be rewritten in terms of expansion coefficients. Using the orthogonality of the vector basis functions (see Appendix A) and noticing Eqs. (17) and (18), we find that the expansion coefficients of \({\mathbf{u}}\) and \({{\varvec{\uptau}}}\) satisfy the following linear superposition:
where:
with \(n = 1,2\), \((\gamma_{s}^{(j)} )^{2} = k^{2} - (\omega s_{s}^{(j)} )^{2}\), \(s_{s}^{(j)} = \sqrt {{{\rho^{(j)} } \mathord{\left/ {\vphantom {{\rho^{(j)} } {G^{(j)} }}} \right. \kern-\nulldelimiterspace} {G^{(j)} }}}\); and
where:
with \(n = 0,1,2\), \(s_{p}^{(j)} = \sqrt {{{\rho^{(j)} } \mathord{\left/ {\vphantom {{\rho^{(j)} } {(\lambda^{(j)} + 2G^{(j)} )}}} \right. \kern-\nulldelimiterspace} {(\lambda^{(j)} + 2G^{(j)} )}}}\).
We can see, the two expansion coefficients associated with SH waves, \(u_{T,m}^{(j)} (z,k)\) and \(\tau_{T,m}^{(j)} (z,k)\), are independent of those associated with P and SV waves, \(u_{S,m}^{(j)} (z,k)\), \(u_{R,m}^{(j)} (z,k)\), \(\tau_{S,m}^{(j)} (z,k)\), and \(\tau_{R,m}^{(j)} (z,k)\). This fact leads to two uncoupled modes of elastic wave-fields; that is, SH mode governed by Eqs. (21)–(23) and PSV mode governed by Eqs. (24)–(28).
Expansion coefficients of the cross product \({\kern 1pt} {\mathbf{u}} \times {\mathbf{B}}^{{\text{a}}}\)
The induction electric current \(- i\omega \sigma {\mathbf{u}} \times {\mathbf{B}}^{{\text{a}}}\) acts as a source of EM fields. Determining the expansion coefficients of \({\kern 1pt} {\mathbf{u}} \times {\mathbf{B}}^{{\text{a}}}\) is the key of transforming Eq. (3) and solving EM fields. For 3-D case, the intersection angle between propagation direction of seismic wave and orientation of the ambient geomagnetic field varies for different azimuth angle. This makes the expansion of the vector \({\kern 1pt} {\mathbf{u}} \times {\mathbf{B}}^{{\text{a}}}\) and the derivation of EM field solutions in 3-D case more complicated and tedious than the 2-D case.
Now, let us define:
Note that seismic displacement can be expressed by expansion coefficients as:
and Eq. (11) can be rewritten as:
where \({\mathbf{e}}_{r}\) and \({\mathbf{e}}_{\theta }\) are the two horizontal unit vectors of cylindrical coordinate system.
Assuming the x-, y- and z-components of \({\mathbf{B}}^{{\text{a}}}\) are \(B_{x}^{{\text{a}}}\), \(B_{y}^{{\text{a}}}\), and \(B_{z}^{{\text{a}}}\), respectively, we can obtain the expression of \({\mathbf{B}}^{{\text{a}}}\) in cylindrical coordinate system as:
Substitution of Eqs. (29) and (30) into Eqs. (13)–(15) yields:
where, \(\xi = T,S,R\); and
For the above nine integration formulas, we need to find out their explicit expressions one by one.
For Eq. (34), we can replace \({\mathbf{T}}_{k}^{m} (r,\theta )\), \({\mathbf{T}}_{{k^{\prime}}}^{{m^{\prime}}} (r,\theta )\), and \({\mathbf{B}}^{{\text{a}}}\) with their expressions in cylindrical coordinate system. Utilizing Eqs. (31) and (32), we derive:
Then, we substitute Eq. (43) into Eq. (34) and use the relation \(\frac{1}{2\pi }\int\nolimits_{0}^{2\pi } {e^{{i(m - m^{\prime})\theta }} d\theta } = \delta_{{m,m^{\prime}}}\) to gain:
Utilizing the following property of Bessel function
we find:
Combination of Eqs. (31) and (32) also gives:
Substituting the above formula into Eq. (35) results in:
Notice another property of Bessel function
we gain:
From Eqs. (31) and (32), we can also obtain:
Further combining the equation \(\frac{1}{2\pi }\int\nolimits_{0}^{2\pi } {e^{{i(m - m^{\prime} \pm 1)\theta }} d\theta } = \delta_{{m,m^{\prime} \mp 1}}\) and the following recurrence relations of Bessel function:
we can rewrite Eq. (36) as:
Taking into account the following orthogonality of Bessel function:
we have:
Combining Eqs. (33), (46), (50), and (55) and replacing \(k^{\prime}\) with k, we finally obtain.
In a similar way, utilizing Eqs. (31)–(33), (37)–(42) and some properties of Bessel function, such as Eqs. (45), (49), (52), and (54), we gain:
and
Based on Eqs. (12) and (56)–(58), we find \({\mathbf{C}}(r,\theta ,z)\) can be divided into three parts, which are related with seismic displacement expansion coefficients of \(m^{\prime}\), \(m^{\prime} + 1\), and \(m^{\prime} - 1\) orders, respectively. For these three parts, we use \(m\) to replace \(m^{\prime}\), \(m^{\prime} + 1\) and \(m^{\prime} - 1\), respectively, to make the seismic displacement expansion coefficients have a uniform order; that is, \(u_{\xi ,m} (z,k)\) (\(\xi = T,S,R\)). Since the expansion coefficients of \(u_{T,m} (z,k)\) and \(\tau_{T,m} (z,k)\) (which correspond to SH waves) are not coupled with those of \(u_{S,m} (z,k)\), \(u_{R,m} (z,k)\), \(\tau_{S,m} (z,k)\), and \(\tau_{R,m} (z,k)\) (which correspond to P and SV waves), the SH and PSV modes will be solved separately. Correspondingly, we separate the induction electric current induced by SH waves from those induced by P and SV waves. Finally, \({\mathbf{C}}(r,\theta ,z)\) can be divided into six parts as:
Each part can be expressed in terms of expansion coefficients as:
where, \(p = 0, + 1, - 1\); \(\zeta = SH,PSV\); and
Transformed governing equations of EM fields
Each part of the induction electric current, i.e., \(- i\omega \sigma {\mathbf{C}}^{p,\zeta } (r,\theta ,z)\), correspondingly will induce partial EM fields that contribute to the total EM fields. From this viewpoint, the total EM fields can also be divided into six parts and written as:
for \(j = 0,1,2, \ldots ,N\).
Each part of EM fields can be expressed by expansion coefficients as:
where, \(j = 0,1,2, \ldots ,N\); \(p = 0, + 1, - 1\); \(\zeta = SH,PSV\).
The EM fields in solid media (i.e., \(j = 1,2, \ldots ,N\)) satisfy:
Rewriting the above two equations in terms of expansion coefficients and utilizing the orthogonality of the vector basis functions (see Appendix A), we obtain the general form of transformed governing equations of EM fields in solid (see Appendix B). Equations (170)–(172) involve the EM fields of TM mode (in which magnetic fields are transversely polarized), whereas Eqs. (173)-(175) involve the EM fields of TE mode (in which electric fields are transversely polarized).
Taking into account the specific expansion coefficients of \({\mathbf{C}}^{p,\zeta } (r,\theta ,z)\), i.e., Eqs. (60)–(64), we find that SH waves will not generate EM fields of TE mode, that is:
for \(p = 0, + 1, - 1\).
However, SH waves will generate EM fields of TM mode. The expansion coefficients of these TM-mode EM fields are actually determined by \(u_{T,m} (z,k)\). Further considering the linear superposition of \(u_{T,m} (z,k)\), i.e., Eq. (21), we obtain:
where \(j = 1,2, \ldots ,N\).
Considering SH waves with the case of \(p = 0\), we find \((\tilde{H}_{T,n}^{0,SH(j)} ,\tilde{E}_{S,n}^{0,SH(j)} ,\tilde{E}_{R,n}^{0,SH(j)} )\) with \(n = 1{,}2\) (that is, partial TM-mode EM fields) which satisfy the following equations:
where \({\mathbf{a}}^{TM(j)} = \left[ {\begin{array}{*{20}c} 0 & { - i\omega \tilde{\varepsilon }^{(j)} } \\ {{{i(\gamma_{em}^{(j)} )^{2} } \mathord{\left/ {\vphantom {{i(\gamma_{em}^{(j)} )^{2} } {(\omega \tilde{\varepsilon }^{(j)} )}}} \right. \kern-\nulldelimiterspace} {(\omega \tilde{\varepsilon }^{(j)} )}}} & 0 \\ \end{array} } \right]\) and \((\gamma_{em}^{(j)} )^{2} = k^{2} - \omega^{2} \mu^{(j)} \tilde{\varepsilon }^{(j)}\).
SH waves with the case of \(p = + 1, - 1\) determine another partial TM-mode EM fields, i.e., \((\tilde{H}_{T,n}^{1,SH(j)} ,\tilde{E}_{S,n}^{1,SH(j)} ,\tilde{E}_{R,n}^{1,SH(j)} )\) with \(n = 1, 2\):
We learn from Eqs. (170)-(172) that partial induction electric current \(- i\omega \sigma {\mathbf{C}}^{0,PSV}\) does not generate EM fields of TM mode, because of the fact \(C_{S,m}^{0,PSV} = C_{R,m}^{0,PSV} = 0\). Thus, we have:
However, another two parts of induction electric current, \(- i\omega \sigma {\mathbf{C}}^{ \pm 1,PSV}\), will induce TM-mode EM fields. The expansion coefficients of these EM fields are related to \(u_{S,m} (z,k)\) and \(u_{R,m} (z,k)\). Further considering the linear superposition of these two seismic-displacement expansion coefficients, i.e., Eq. (24), we obtain:
where \(j = 1,2, \ldots ,N\).
PSV-mode seismic waves with the case of \(p = + 1, - 1\) give rise to another partial TM-mode EM fields, i.e., \((\tilde{H}_{T,n}^{1,PSV(j)} ,\tilde{E}_{S,n}^{1,PSV(j)} ,\tilde{E}_{R,n}^{1,PSV(j)} )\) with \(n = 0,1,2\):
Equations (173)–(175) tell us that PSV-mode seismic waves will also induce TE-mode EM fields because of the three non-zero expansion coefficients, \(C_{T,m}^{0,PSV} (z,k)\), \(C_{T,m + 1}^{ + 1,PSV} (z,k)\), and \(C_{T,m - 1}^{ - 1,PSV} (z,k)\). Using a similar way as above, we find:
where \(j = 1,2, \ldots ,N\).
PSV-mode seismic waves with the case of \(p = 0\) determine partial TE-mode EM fields, i.e., \((\tilde{E}_{T,n}^{0,PSV(j)} ,\tilde{H}_{S,n}^{0,PSV(j)} ,\tilde{H}_{R,n}^{0,PSV(j)} )\) with \(n = 0,1,2\) as:
where \({\mathbf{a}}^{TE(j)} = \left[ {\begin{array}{*{20}c} 0 & {{{(\gamma_{em}^{(j)} )^{2} } \mathord{\left/ {\vphantom {{(\gamma_{em}^{(j)} )^{2} } {(i\omega \mu^{(j)} )}}} \right. \kern-\nulldelimiterspace} {(i\omega \mu^{(j)} )}}} \\ {i\omega \mu^{(j)} } & 0 \\ \end{array} } \right]\).
Another partial TE-mode EM fields \((\tilde{E}_{T,n}^{1,PSV(j)} ,\tilde{H}_{S,n}^{1,PSV(j)} ,\tilde{H}_{R,n}^{1,PSV(j)} )\) with \(n = 0,1,2\) are generated by PSV-mode seismic waves with the case of \(p = + 1, - 1\) as follows:
Since the air (above the free surface) is treated as non-conductive, i.e., \(\sigma^{(0)} = 0\), we do not consider any induction electric current in the air. The generation of EM fields in air actually results from the continuities of EM fields’ horizontal components at free surface. Using a similar way of deriving Eqs. (71)–(81), we can obtain the transformed governing equations of EM fields in air (see Appendix C).
Transformed governing equations written in matrix
SH waves are independent of P and SV waves for layered media considered in this study. Consequently, the transformed governing equations of displacement–stress–EM-wave-fields in solid media can be written as two sets of first-order ordinary differential equations associated with SH-mode and PSV-mode seismic waves, respectively. Although these two equation sets are different in dimension, they are identical in form:
where \(\zeta = SH,PSV\); \(j = 1,2, \ldots ,N\).
For SH waves and corresponding TM-mode EM fields in solid media, we have:
where \(j = 1,2, \ldots ,N\).
For P and SV waves and corresponding EM fields in solid media, we have:
where \(j = 1,2, \cdot \cdot \cdot ,N\). \({\mathbf{A}}^{PSV(j)} (1:4,1:4)\) represents a sub-matrix of \({\mathbf{A}}^{PSV(j)}\) including the elements in the rows from first to fourth and also in the columns from first to fourth. Other analogous matrices in the context, such as those in Eqs. (92)–(97), (123)–(125), (136), (137), (153), and (155), are done in the same manner.
From Appendix C, we can see the transformed governing equations of EM fields in air can also be written as two sets of first-order ordinary differential equations:
where \(\zeta = SH,PSV\); \(z \le z^{(1)}\); and
with \((\gamma_{em}^{(0)} )^{2} = k^{2} - \omega^{2} \mu_{0} \varepsilon_{0}\).
With the constraints of boundary conditions, all the expansion coefficients contained in vector \({\mathbf{y}}^{\zeta (j)} (z)\) (\(j = 0,1,2, \ldots ,N\)) can be determined by solving Eqs. (82) and (98). The expansion coefficients of EM fields’ vertical components, i.e., \(\tilde{E}_{R,n}^{q,\zeta (j)} (z,k)\) and \(\tilde{H}_{R,n}^{q,\zeta (j)} (z,k)\), are not contained in vector \({\mathbf{y}}^{\zeta (j)} (z)\). However, they can be calculated by the bottom rows of Eqs. (73), (74), (77), (80), (81), (182), (185), and (188), that is:
for \(n = 1,2\); and
for \(n = 0,1,2\).
Once \(\tilde{u}_{T,n}^{(j)} (z,k)\), \(\tilde{u}_{S,n}^{(j)} (z,k)\), \(\tilde{H}_{T,n}^{q,\zeta (j)} (z,k)\), and \(\tilde{E}_{T,n}^{q,\zeta (j)} (z,k)\) (\(q = 0,1\), \(\zeta = SH,PSV\)) are determined, the above two equations can be used to calculate the expansion coefficients of EM fields’ vertical components. Now, the key problem is to solve the first-order ordinary differential equations [Eqs. (82) and (98)].
General solutions
According to the general theory of ordinary differential equations, fundamental differential equation set (82) can be solved as:
for \(j = 1,2, \cdot \cdot \cdot ,s - 1\) or \(j = s + 1,s + 2, \cdot \cdot \cdot ,N\); and
Here, \(\zeta = SH,PSV\), \({\mathbf{b}}^{\zeta }\) is the wave-amplitude vector to be determined by boundary conditions, and \({\tilde{\mathbf{s}}}^{\zeta }\) is the source term determined by \({{\varvec{\Theta}}}^{\zeta (s)}\) and \({\mathbf{D}}^{\zeta } (z)\) (see Source term section). In obtaining the third row of Eq. (107), we have utilized the fact \(\vartriangle z \to 0\) which means that \(z^{(s - )} \to z_{s} - 0\) and \(z^{(s + )} \to z_{s} + 0\).
Matrices \({{\varvec{\Theta}}}^{\zeta }\) and \({{\varvec{\Lambda}}}^{\zeta } (z)\) are related with the eigen-decomposition of matrix \({\mathbf{A}}^{\zeta }\). The eigenvalues of \({\mathbf{A}}^{\zeta }\) actually have physical meanings: they are merely i times the vertical wavenumbers for down-going and up-going wave-fields (Aki and Richards 1980). In the following context, we use subscripts ‘d’ and ‘u’ to indicate the matrices (or vectors) associated with down-going and up-going wave-fields, respectively.
For the case \(\zeta = SH\), we define:
with \(j = 1,2, \cdot \cdot \cdot ,N\); and
Then, we have \({{\varvec{\Lambda}}}^{SH} (z)\) written as:
for \(j = 1,2, \cdot \cdot \cdot ,s - 1\) or \(j = s + 1,s + 2, \cdot \cdot \cdot ,N\); and
The matrix \({{\varvec{\Theta}}}^{SH(j)}\) \((j = 1,2, \cdot \cdot \cdot ,N)\) is given by:
where, \(\Delta_{s}^{(j)} = \frac{{\sigma^{(j)} }}{{(s_{s}^{(j)} )^{2} - \mu^{(j)} \tilde{\varepsilon }^{(j)} }}\), \(\gamma_{s}^{(j)} = \sqrt {k^{2} - (\omega s_{s}^{(j)} )^{2} }\), \(\gamma_{em}^{(j)} = \sqrt {k^{2} - \omega^{2} \mu^{(j)} \tilde{\varepsilon }^{(j)} }\). We define \({\text{Re}} \left\{ {\gamma_{s}^{(j)} } \right\} > 0\) and \({\text{Re}} \left\{ {\gamma_{em}^{(j)} } \right\} > 0\) so that \({{\varvec{\Lambda}}}_{d}^{SH(j)} (z)\) and \({{\varvec{\Lambda}}}_{u}^{SH(j)} (z)\) are related with down-going and up-going wave-fields, respectively. \(\pm \gamma_{s}^{(j)}\) and \(\pm \gamma_{em}^{(j)}\) are just the eigenvalues of \({\mathbf{A}}^{SH(j)}\) and \(\pm \gamma_{em}^{(j)}\) are double eigenvalues. The six column vectors of \({{\varvec{\Theta}}}^{SH(j)}\) are the eigenvectors of \({\mathbf{A}}^{SH(j)}\).
For the case \(\zeta = PSV\), we define:
with \(j = 1,2, \ldots ,N\); and
Then, we have \({{\varvec{\Lambda}}}^{PSV} (z)\) written as:
for \(j = 1,2, \cdot \cdot \cdot ,s - 1\) or \(j = s + 1,s + 2, \ldots ,N\); and
The matrix \({{\varvec{\Theta}}}^{PSV(j)}\) \((j = 1,2, \cdot \cdot \cdot ,N)\) is given by:
where, \(\Delta_{p}^{(j)} = \frac{{\sigma^{(j)} }}{{(s_{p}^{(j)} )^{2} - \mu^{(j)} \tilde{\varepsilon }^{(j)} }}\), \(\gamma_{p}^{(j)} = \sqrt {k^{2} - (\omega s_{p}^{(j)} )^{2} }\), \({\text{Re}} \left\{ {\gamma_{p}^{(j)} } \right\} > 0\).
In this study, the air medium is treated as a homogeneous half-space. Thus, there are only up-going waves in the air. Taking into account this fact, we find the general solution of Eq. (98) can be written as:
where \(\zeta = SH,PSV\); \({\mathbf{b}}_{u}^{\zeta (0)}\) is the unknown EM-wave–amplitude vector in the air; matrices \({{\varvec{\Theta}}}_{u}^{\zeta (0)}\) and \({{\varvec{\Lambda}}}_{u}^{\zeta (0)} (z)\) are related with the eigen-decomposition of matrix \({\mathbf{A}}^{\zeta (0)}\) and they are given by:
where, \(\gamma_{em}^{(0)} = \sqrt {k^{2} - \omega^{2} \mu_{0} \varepsilon_{0} }\), \({\text{Re}} \left\{ {\gamma_{em}^{(0)} } \right\} > 0\).
It should be mentioned that, in Eqs. (108), (109), (116), (117), and (127), the introduction of extra exponential factors like \(e^{{ - \upsilon z^{(j)} }}\) and \(e^{{\upsilon z^{(j + 1)} }}\) (in which \(\upsilon = \gamma_{s}^{(j)} ,\gamma_{p}^{(j)} {\text{ or }}\gamma_{em}^{(j)}\)) is an important pretreatment of the LAC GRT method. It guarantees all diagonal elements in matrix \({{\varvec{\Lambda}}}^{\zeta (j)} (z)\) are exponential decaying factors, which will provide a good stability in numerical calculation. The introduction of these extra exponential factors affects the vectors \({\mathbf{b}}^{\zeta (j)}\) and \({\mathbf{b}}^{\zeta (s)} + {\tilde{\mathbf{s}}}^{\zeta }\), which will further affect the LAC GRT coefficients defined in Eqs. (140) and (141).
Determining the semi-analytical solutions
To determine \({\mathbf{y}}^{\zeta (j)} (z)\) \((j = 0,1,2, \ldots ,N)\) through Eqs. (106), (107), and (126), we have to obtain the source term \({\tilde{\mathbf{s}}}^{\zeta }\) as well as the wave-amplitude vectors \({\mathbf{b}}^{\zeta (j)}\) (\(j = 1,2, \ldots ,N\) or \(j = s - ,s +\)) and \({\mathbf{b}}_{u}^{\zeta (0)}\).
Source term
After inserting the two artificial interfaces \(z = z^{(s - )} = z_{s} - \vartriangle z\) and \(z = z^{(s + )} = z_{s} + \vartriangle z\), the source term \({\tilde{\mathbf{s}}}^{\zeta }\) is given by (Chen 1999; Ren et al. 2010b):
where \(\zeta = SH,PSV\); \({{\varvec{\Psi}}}_{11}^{\zeta }\), \({{\varvec{\Psi}}}_{12}^{\zeta }\), \({{\varvec{\Psi}}}_{21}^{\zeta }\) and \({{\varvec{\Psi}}}_{22}^{\zeta }\) are the four sub-matrices of \({{\varvec{\Psi}}}^{\zeta }\), which is determined by:
\({\tilde{\mathbf{\Lambda }}}_{d}^{\zeta (s)} (\eta )\) and \({\tilde{\mathbf{\Lambda }}}_{d}^{\zeta (s)} (\eta )\) are diagonal matrices given by:
If the two artificial interfaces are excluded, the integration limits in Eq. (132), i.e., \(z^{(s - )}\) and \(z^{(s + )}\), will be replaced by \(z^{(s)}\) and \(z^{(s + 1)}\), respectively. Besides, the two terms \(\left[ {{\tilde{\mathbf{\Lambda }}}_{d}^{\zeta (s)} (\eta )} \right]^{ - 1}\) and \(\left[ {{\tilde{\mathbf{\Lambda }}}_{u}^{\zeta (s)} (\eta )} \right]^{ - 1}\) will be replaced by \(\left[ {{{\varvec{\Lambda}}}_{d}^{\zeta (s)} (\eta )} \right]^{ - 1}\) and \(\left[ {{{\varvec{\Lambda}}}_{u}^{\zeta (s)} (\eta )} \right]^{ - 1}\). That will make the source term contain exponential growth factors, such as \(e^{{\gamma_{s}^{(s)} (z_{s} - z^{(s)} )}}\) and \(e^{{\gamma_{s}^{(s)} (z^{(s + 1)} - z_{s} )}}\), leading to high-frequency instability problem (i.e., numerical overflow for high frequency) in the numerical calculation of the source term (Chen 1999; Ren et al. 2010b). The introduction of the two artificial interfaces \(z = z^{(s - )} \to z_{s} - 0\) and \(z = z^{(s + )} \to z_{s} + 0\) (as \(\vartriangle z \to 0\)) eliminates the exponential growth factors and therefore helps to solve the high-frequency instability problem without sacrificing any computational efficiency (Chen 1999; Ren et al. 2010b).
According to Eq. (132), \({\tilde{\mathbf{s}}}_{d}^{SH}\) and \({\tilde{\mathbf{s}}}_{u}^{SH}\) are 3 × 2 matrices while \({\tilde{\mathbf{s}}}_{d}^{PSV}\) and \({\tilde{\mathbf{s}}}_{u}^{PSV}\) are 5 × 3 matrices. Combination of Eqs. (19), (85), (90), and (132) leads to the following explicit expressions of the source term:
where
LAC GRT coefficients
Now, we apply the LAC GRT method (Luco and Apsel 1983; Chen 1993, 1999; Martin and Thomson 1997; Ge and Chen 2008; Ren et al. 2007, 2010a, b, 2012) to determine the wave-amplitude vectors \({\mathbf{b}}^{\zeta (j)}\) (\(j = 1,2, \cdot \cdot \cdot ,N\) or \(j = s - ,s +\)) and \({\mathbf{b}}_{u}^{\zeta (0)}\).
The vector \({\mathbf{b}}^{\zeta (j)}\) (\(j = 1,2, \ldots ,N\) or \(j = s - ,s +\)) can be divided into two sub-vectors,
where \({\mathbf{b}}_{d}^{\zeta (j)}\) and \({\mathbf{b}}_{u}^{\zeta (j)}\) represent the amplitudes of the down-going and up-going wave-fields, respectively.
For each interface above the source, we define a generalized up-going transmission coefficient and a generalized up–down reflection coefficient, \({\mathbf{T}}_{u}^{\zeta (j)}\) and \({\mathbf{R}}_{ud}^{\zeta (j)}\) (\(j = 1,2, \ldots ,s\) or \(j = s -\)). Meanwhile, for each interface below the source, we define a generalized down-going transmission coefficient and a generalized down–up reflection coefficient, \({\mathbf{T}}_{d}^{\zeta (j)}\) and \({\mathbf{R}}_{du}^{\zeta (j)}\) (\(j = s +\) or \(j = s + 1,s + 2, \ldots ,N + 1\)). The definitions are as follows:
The LAC GRT coefficients, \({\mathbf{T}}_{u}^{\zeta (j)}\), \({\mathbf{R}}_{ud}^{\zeta (j)}\), \({\mathbf{T}}_{d}^{\zeta (j)}\), and \({\mathbf{R}}_{du}^{\zeta (j)}\), describe the overall effects of multiple reflection and transmission due to the existence of interfaces (see Fig. 2). For the case of \(\zeta = SH\) and \(PSV\), they are 3 \(\times\) 3 and 5 \(\times\) 5 matrices, respectively, except that \({\mathbf{T}}_{u}^{SH(1)}\) and \({\mathbf{T}}_{u}^{PSV(1)}\) are 2 \(\times\) 3 and 3 \(\times\) 5 matrices, respectively.
The continuity boundary conditions, i.e., Eqs. (7) and (8), at subsurface interfaces help achieve the direct evaluation equations of the generalized reflection and transmission coefficients.
For the two artificial interfaces \(z = z^{(s - )}\) and \(z = z^{(s + )}\), the continuity boundary conditions yield:
where \({{\varvec{\Theta}}}_{11}^{\zeta (s)}\), \({{\varvec{\Theta}}}_{12}^{\zeta (s)}\), \({{\varvec{\Theta}}}_{21}^{\zeta (s)}\), and \({{\varvec{\Theta}}}_{22}^{\zeta (s)}\) (with \(\zeta = SH,PSV\)) are the four sub-matrices of \({{\varvec{\Theta}}}^{\zeta (s)}\), that is:
In deriving Eqs. (142) and (143), we have used the constraints \(z^{(s - )} \to z_{s} - 0\) and \(z^{(s + )} \to z_{s} + 0\), which result from the fact \(\vartriangle z \to 0\). Obviously, Eqs. (142) and (143) suggest that:
For \(j = 2,3, \ldots ,s\), we use the continuity boundary conditions to obtain:
Similarly, for \(j = s + 1,s + 2, \ldots ,N\), we gain:
Apparently, Eqs. (147) and (149) are recursive formulas for computing the LAC GRT coefficients. To evaluate these equations, we need to determine \({\mathbf{R}}_{ud}^{\zeta (1)}\) and \({\mathbf{R}}_{du}^{\zeta (N + 1)}\) first.
Since the Nth layer (bottom layer) is a half-space, the radiation boundary condition at \(z = z^{(N + 1)} = + \infty\), i.e., Eq. (9), gives:
On the free surface, the elastic wave-fields satisfy the traction-free condition, whereas the horizontal components of EM fields satisfy the continuity boundary condition. The combination of these two conditions leads to:
For the case of \(\zeta = SH\), \({\mathbf{N}}_{1}^{SH}\) and \({\mathbf{N}}_{2}^{SH}\), respectively, are 5 × 5 and 5 × 3 matrices given by:
and \({\mathbf{Q}}_{u}^{SH(1)}\) is a 3 × 3 diagonal matrix determined by:
where \(h_{1} = \min (z^{(2)} ,z_{s} ) - z^{(1)}\).
For the case of \(\zeta = PSV\), \({\mathbf{N}}_{1}^{PSV}\) and \({\mathbf{N}}_{2}^{PSV}\) respectively are 8 × 8 and 8 × 5 matrices given by
and \({\mathbf{Q}}_{u}^{PSV(1)}\) is a 5 × 5 diagonal matrix determined by:
Now, the LAC GRT coefficients for all interfaces (including the two artificial interfaces) can be computed by successively using Eqs. (152), (151), (147), (149), and (146).
The final solutions
After determining the source term and all the LAC GRT coefficients, we can calculate \({\mathbf{b}}_{d}^{\zeta (s)} + {\tilde{\mathbf{s}}}_{d}^{\zeta }\), \({\mathbf{b}}_{u}^{\zeta (s)} + {\tilde{\mathbf{s}}}_{u}^{\zeta }\), \({\mathbf{b}}_{d}^{\zeta (j)}\) and \({\mathbf{b}}_{u}^{\zeta (j)}\) (\(j = 0,1, \ldots ,s - 1\) or \(j = s - ,s +\) or \(j = s + 1,s + 2, \ldots ,N\)) through following equations:
Now, the vector \({\mathbf{y}}^{\zeta (j)} (z)\), which contains the expansion coefficients of elastic wave-fields and EM fields’ horizontal components, can be computed for a receiver at any depth by substituting the above six equations into Eqs. (106), (107), or (126). Then, the expansion coefficients of EM fields’ vertical components can be calculated through Eqs. (104) and (105). Thereafter, combining Eqs. (70)–(72), (75), (76), (78), (79), (179)–(181), (183), (184), (187), and (188) with Eqs. (66) and (67), we obtain the semi-analytical solutions of EM fields in the frequency–space domain. Similarly, the combination of Eqs. (21), (24), and (30) yields the semi-analytical solutions of seismic waves in the frequency–space domain. The wavenumber integration in Eqs. (30) and (67) can be numerically computed using the well-known discrete wavenumber method (Bouchon and Aki 1977; Bouchon 1981, 2003). The final transformation back to the time domain can be performed by the discrete inverse Fourier transform.
It should be mentioned, if the source and receiver are located at close or same depths, it will be extremely time-consuming to numerically calculate the semi-analytical solutions without applying any other technique, because the convergence of wavenumber integration will become very slow. The peak-trough averaging method (Zhang et al. 2001, 2003), which is mathematically simple and easy to implement in practice, has been proven an effective and efficient method to overcome this slow convergence problem. Application of the peak-trough averaging method in our derived semi-analytical solutions will make it possible to efficiently calculate both seismic and EM signals generated by an earthquake with a shallow focus.
Conclusions
Using a set of vector basis functions in cylindrical coordinate system (Aki and Richards 1980; Chen 1993) to expand the involved wave-fields and solving the expansion coefficients through the LAC GRT method (Luco and Apsel 1983; Chen 1993, 1999; Ge and Chen 2008; Ren et al. 2007, 2010a, b, 2012), we derive the semi-analytical solutions of seismo-electromagnetic signals arising from the motional induction in 3-D multi-layered media due to a double couple point source, as which an earthquake source can be treated under far-field condition (Aki and Richards 1980). The determination of the EM fields excited by the induction electric current in the 3-D case, which is the most complicated and tedious part of this work, is accomplished carefully and patiently.
The LAC GRT method adopted in the derivation has been proven numerically efficient and stable in previous studies (Martin and Thomson 1997; Chen 1999; Ge and Chen 2008). The analytical regularization approach (Chen 1999; Ren et al. 2010b), which introduces two artificial interfaces with distance \(\vartriangle z\) from the source and considers a limiting process of \(\vartriangle z \to 0\), is adopted in an effort to solve the high-frequency instability problem that exists in the numerical computation. Therefore, the derived semi-analytical solutions should have advantage of higher efficiency and stability in numerical computation. Besides, we propose using the peak-trough averaging method (Zhang et al. 2001, 2003) to overcome another computational problem, that is, the slow convergence problem which occurs when the source and receiver are located at close or same depths.
The derived semi-analytical solutions account for not only the seismo-electromagnetic signals in the solid but also those in the air. They indicate that SH waves only induce EM fields of TM mode, whereas P and SV waves induce EM fields of both TE and TM modes. On the basis of the semi-analytical solutions, expected characteristics of the seismo-electromagnetic signals arising from the motional induction in 3-D multi-layered media will be numerically investigated in a companion paper.
Availability of data and materials
No data and materials are used.
Abbreviations
- 3-D:
-
Three-dimensional
- 2-D:
-
Two-dimensional
- EM:
-
Electromagnetic
- TM:
-
Transverse magnetic
- TE:
-
Transverse electric
- LAC:
-
Luco–Apsel–Chen
- GRT:
-
Generalized reflection and transmission
- SH:
-
Shear horizontal
- SV:
-
Shear vertical
References
Aki K, Richards PG (1980) Quantitative seismology: theory and methods. W. H. Freeman and Co., London
Belov SV, Migunov NI, Sosolev GA (1974) Magnetic effect of strong earthquakes of Kamchatka. Geomag Aeron 14(3):380–382
Bouchon M (1981) A simple method to calculate Green-functions for elastic layered media. Bull Seismol Soci Am 71(4):957–971
Bouchon M (2003) A review of the Discrete wavenumber method. Pure Appl Geophys 160(3):445–465
Bouchon M, Aki K (1977) Discrete wave-number representation of seismic-source wave fields. Bull Seismol Soci Am 67(2):259–277
Chen X (1993) A systematic and efficient method for computing seismic normal modes in layered half-space. Geophys J Int 115:391–409
Chen X (1999) Seismogram synthesis in multi-layered half-space, Part I. Theor Formul Earthq Res China 13(2):149–174
Chen X (2007) Generation and propagation of seismic SH waves in multilayered media with irregular interfaces. Adv Geophys 48:191–264
Fraser-Smith AC, Bernardi A, McGill PR, Ladd ME, Helliwell RA, Villard OGJr, (1990) Low-frequency magnetic field measurements near the epicenter of the Ms 71 Loma Prieta Earthquake. Geophys Res Lett 17(9):1465–1468
Fujinawa Y, Noda Y (2015) Characteristics of seismoelectric wave fields associated with natural microcracks. Pure Appl Geophys 172:197–614
Fujinawa Y, Takahashi K, Noda Y, Iitaka H, Yazaki S (2011) Remote detection of electric field change induced at the seismic wave front from the start of fault rupturing. Int J Geophys 2011:752193
Gao Y, Chen X, Hu H, Wen J, Tang J, Fang G (2014) Induced electromagnetic field by seismic waves in Earth’s magnetic field. J Geophys Res Solid Earth 119:5615–5685
Gao Y, Wang D, Wen J, Hu H, Chen X, Yao C (2019) Electromagnetic responses to an earthquake source due to the motional induction effect in a 2-D layered model. Geophys J Int 219:563–593
Ge Z, Chen X (2008) An efficient approach for simulating wave propagation with the boundary element method in multilayered media with irregular interfaces. Bull Seismol Soc Am 98:3007–3016
Gershenzon NI, Gokhberg MB, Yunga SL (1993) On the electromagnetic field of an earthquake focus. Phys Earth Planet Inter 77:13–19
Gokhberg MB, Gufeld IL, Rozhnoy AA, Marenko VF, Yampolsky VS, Ponomarev EV (1989) Study of seismic influence on the ionosphere by super long-wave probing of the Earth-ionosphere waveguide. Phys Earth Planet Inter 57:64–67
Han P, Hattori K, Huang Q, Hirano T, Ishiguro Y, Yoshino C, Febriani F (2011) Evaluation of ULF electromagnetic phenomena associated with the 2000 Izu Islands earthquake swarm by wavelet transform analysis. Nat Hazards Earth Syst Sci 11:965–970
Han P, Hattori K, Hirokawa M, Zhuang J, Chen CH, Febriani F, Yamaguchi H, Yoshino C, Liu JY, Yoshida S (2014) Statistical analysis of ULF seismomagnetic phenomena at Kakioka, Japan, during 2001–2010. J Geophys Res Space Phys 119:4998–5011
Han P, Hattori K, Xu G, Ashida R, Chen C-H, Febriani F, Yamaguchi H (2015) Further investigations of geomagnetic diurnal variations associated with the 2011 off the Pacific coast of Tohoku earthquake (Mw 9.0). J Asian Earth Sci 114(2):321–326
Han P, Hattori K, Huang Q, Hirooka S, Yoshino C (2016) Spatiotemporal characteristics of the geomagnetic diurnal variation anomalies prior to the 2011 Tohoku earthquake (Mw 9.0) and the possible coupling of multiple pre-earthquake phenomena. J Asian Earth Sci 129:13–21
Han P, Hattori K, Zhuang J, Chen C-H, Liu J-Y, Yoshida S (2017) Evaluation of ULF seismo-magnetic phenomena in Kakioka, Japan by using Molchan’s error diagram. Geophys J Int 208(1):482–490
Hattori K, Han P, Yoshino C, Febriani F, Yamaguchi H, Chen C-H (2013) Investigation of ULF seismo-magnetic phenomena in Kanto, Japan during 2000–2010: case studies and statistical studies. Survey Geophys 34:293–316
Honkura Y, Işikara AM, Oshiman N, Ito A, Üçer B, Bariş Ş, Tunçer MK, Matsushima M, Pektaş R, Çelik C, Tank SB, Takahashi F, Nakanshi M, Yoshimura R, Ikeda Y, Komut T (2000) Preliminary results of multidisciplinary observations before, during and after the Kocaeli (Izmit) earthquake in the western part of the North Anatolian Fault Zone. Earth, Planets and Space 52:293–298
Honkura Y, Satoh H, Ujihara N (2004) Seismic dynamo effects associated with the M7.1 earthquake of 26 May 2003 off Miyagi prefecture and the M6.4 earthquake of 26 July 2003 in northern Miyagi prefecture. NE Japan Earth Planets and Space 56:109–114
Honkura Y, Ogawa Y, Matsushima M, Nagaoka S, Ujihara N, Yamawaki T (2009) A model for observed circular polarized electric fields coincident with the passage of large seismic waves. J Geophys Res Solid Earth 114:B10103. https://doi.org/10.1029/2008JB006117
Huang Q (2002) One possible generation mechanism of co-seismic electric signals. Proc Jpn Acad Series B 78(7):173–178
Huang Q (2011a) Retrospective investigation of geophysical data possibly associated with the Ms8.0 Wenchuan earthquake in Sichuan China. J Asian Earth Sci 41:421–427
Huang Q (2011b) Rethinking earthquake-related DC-ULF electromagnetic phenomena: towards a physics-based approach. Nat Hazards Earth Syst Sci 11(11):2941–2949
Huang Q, Ren H, Zhang D, Chen JY (2015) Medium effect on the characteristics of the coupled seismic and electromagnetic signals. Proc Jpn Acad Series B 91(1):17–24
Iyemori T, Kamei T, Tanaka Y, Takeda M, Hashimoto T, Araki T, Okamoto T, Watanabe K, Sumitomo N, Oshiman N (1996) Co-Seismic geomagnetic variations observed at the 1995 Hyogoken-Nanbu Earthquake. J Geomagn Geoelectr 48(8):1059–1070
Karakelian D, Beroza GC, Klemperer SL, Fraser-Smith AC (2002) Analysis of Ultralow-frequency electromagnetic field associated with the 1999 M 7.1 Hector Mine, California, Earthquake sequence. Bull Seismol Soc Am 92(4):1513–1524
Luco JE, Apsel RJ (1983) On the Green’s function for a layered halfspace: Part I. Bull Seismol Soc Am 73:909–927
Martin BE, Thomson CJ (1997) Modelling surfacewaves in anisotropic structures II: examples. Phys Earth Planet Inter 103:253–279
Matsushima M, Honkura Y, Oshiman N, Barış Ş, Tunçer MK, Tank SB, Çelik C, Takahashi F, Nakanishi M, Yoshimura R, Pektaş R, Komut T, Tolak E, Ito A, Iio Y, Işıkara AM (2002) Seismoelectromagnetic effect associated with the İzmit earthquake and its aftershocks. Bull Seismol Soc Am 92(1):350–360
Mizutani H, Ishido T, Yokokura T, Ohnishi S (1976) Electrokinetic phenomena associated with earthquakes. Geophys Res Lett 3:365–368
Nagao T, Orihara Y, Yamaguchi T, Takahashi I, Hattori K, Noda Y, Sayanagi K, Uyeda S (2000) Co-seismic geoelectric potential changes observed in Japan. Geophys Res Lett 27(10):1535–1538
Ogawa T, Utada H (2000) Coseismic piezoelectric effects due to a dislocation 1. An analytic far and early-time field solution in a homogeneous whole space. Phys Earth Planet Inter 121:273–288
Okubo K, Takeuchi N, Utsugi M, Yumoto K, Sasai Y (2011) Direct magnetic signals from earthquake rupturing: Iwate-Miyagi earthquake of M7.2. Jpn Earth Planet Sci Lett 305:65–72
Pride SR (1994) Governing equations for the coupled electromagnetics and acoustics of porous-media. Phys Rev B 50(21):15678–15696
Ren H (2009) Theoretical study of seismoelectric effect in fluid-saturated porous media. Ph. D. Thesis. Peking University
Ren H, Huang Q, Chen X (2007) Numerical simulation of seismoelectromagnetic waves in layered porous media. Proceeding of the 8th China International Geo-electromagnetic Workshop, Jingzhou, Hubei, China, 322–329
Ren H, Huang Q, Chen X (2010a) Analytical regularization of the high-frequency instability problem in numerical simulation of seismoelectric wave-fields in multi-layered porous media. Chin J Geophys 53(3):506–511
Ren H, Huang Q, Chen X (2010b) A new numerical technique for simulating the coupled seismic and electromagnetic waves in layered porous media. Earthquake Sci 23(2):167–176
Ren H, Chen X, Huang Q (2012) Numerical simulation of coseismic electromagnetic fields associated with seismic waves due to finite faulting in porous media. Geophys J Int 188(3):925–944
Ren H, Wen J, Huang Q, Chen X (2015) Electrokinetic effect combined with surface-charge assumption: a possible generation mechanism of coseismic EM signals. Geophys J Int 200(2):835–848
Ren H, Huang Q, Chen X (2016a) Numerical simulation of seismo-electromagnetic fields associated with a fault in a porous medium. Geophys J Int 206(1):205–220
Ren H, Huang Q, Chen X (2016b) Existence of evanescent electromagnetic waves resulting from seismoelectric conversion at a solid-porous interface. Geophys J Int 204(1):147–166
Ren H, Huang Q, Chen X (2020) Evanescent EM waves generated by seismoelectric conversion at an interface. In: Grobbe N, Revil A, Zhu Z, Slob E (eds) Seismoelectric exploration: theory, experiments, and applications. Wiley, New York
Sun Y-C, Uyeshima M, Ren H, Huang Q, Aizawa K, Tsukamoto K, Kanda W, Seki K, Kishita T, Ohminato T, Watanabe A, Ran J, Chen X (2019) Numerical simulations to explain the coseismic electromagnetic signals: a case study for a M5.4 aftershock of the 2016 Kumamoto earthquake. Earth Planets Space 71:143
Takeuchi N, Chubachi N, Narita K (1997) Observations of earthquake waves by the vertical earth potential difference method. Phys Earth Planet Interiors 101:157–161
Tang J, Zhan Y, Wang LF, Dong ZY, Zhao GZ, Xu JL (2010) Electromagnetic coseismic effect associated with aftershock of Wenchuan Ms 8.0 earthquake. Chin J Geophys 53(3):526–534
Ujihara N, Honkura Y, Ogawa Y (2004) Electric and magnetic field variations arising from the seismic dynamo effect for aftershocks of the M7.0 earthquake of 26 May 2003 off Miyagi Prefecture. NE Jpn Earth Planets Space 56:115–124
Xu G, Han P, Huang Q, Hattori K, Febriani F, Yamaguchi H (2013) Anomalous behaviors of geomagnetic diurnal variations prior to the 2011 off the Pacific coast of Tohoku earthquake (Mw9.0). J Asian Earth Sci 77:59–65
Yamazaki K (2012) Estimation of temporal variations in the magnetic field arising from the motional induction that accompanies seismic waves at a large distance from the epicentre. Geophys J Int 190:1393–1403
Yamazaki K (2016) Temporal variations in magnetic signals generated by the piezomagnetic effect for dislocation sources in a uniform medium. Geophys J Int 206:130–141
Zhang HM, Chen X, Chang S (2001) Peak-trough averaging method and its applications to computing synthetic seismograms with shallow focus. Chin J Geophys 44:805–813
Zhang HM, Chen X, Chang S (2003) An efficient method for computing synthetic seismograms for a layered half-space with sources and receivers at close or same depth. Pure Appl Geophys 160:467–486
Zhang D, Ren H, Huang Q (2013) Numerical simulation study of co-seismic electromagnetic signals in porous media. Chin J Geophys 56(8):2739–2747
Acknowledgements
All the authors appreciate the excellent review work of the three anonymous reviewers.
Funding
This study was supported by the National Natural Science Foundation of China (Grant Numbers: 41674074, 41974081, and 41874082).
Author information
Authors and Affiliations
Contributions
HR, KY, QH, and XC put forward the idea of this study. Y-CS, HR, KY, and LZ participated in deriving the semi-analytical solutions. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Ethics approval and consent to participate
Not applicable.
Consent for publication
Not applicable.
Competing interests
The authors declare that they have no competing interests.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A: Orthogonality and completeness of the vector basis functions
The orthogonality is as follows:
and the completeness is determined by:
where \(\delta ({\mathbf{r}} - {\mathbf{r^{\prime}}}) = \frac{1}{{\sqrt {r^{\prime}r} }}\delta (\theta - \theta^{\prime})\delta (r - r^{\prime})\); \({\mathbf{r}}\) and \({\mathbf{r^{\prime}}}\) are horizontal coordinate vectors;\({\mathbf{I}}\) is the identity matrix.
Appendix B: General form of transformed governing equations of EM fields in solid
where, \(p = 0, + 1, - 1\); \(\zeta = SH,PSV\); \(j = 1,2, \cdot \cdot \cdot ,N\); and \((\gamma_{em}^{(j)} )^{2} = k^{2} - \omega^{2} \mu^{(j)} \tilde{\varepsilon }^{(j)}\).
Appendix C: Detailed form of transformed governing equations of EM fields in air
The EM fields in air satisfy:
where \(p = 0, + 1, - 1\); and \(\zeta = SH,PSV\). The purpose of using Eq. (178) is to provide convenience for applying the continuity condition of EM fields’ horizontal components at free surface.
The expansion coefficients of EM fields (in air) associated with SH waves are governed by:
where \(q = 0,1\); \(n = 1,2\); \({\mathbf{a}}^{TM(0)} = \left[ {\begin{array}{*{20}c} 0 & { - i\omega \varepsilon_{0} } \\ {{{i(\gamma_{em}^{(0)} )^{2} } \mathord{\left/ {\vphantom {{i(\gamma_{em}^{(0)} )^{2} } {(\omega \varepsilon_{0} )}}} \right. \kern-\nulldelimiterspace} {(\omega \varepsilon_{0} )}}} & 0 \\ \end{array} } \right]\); and \(\gamma_{em}^{(0)} = \sqrt {k^{2} - \omega^{2} \mu_{0} \varepsilon_{0} }\) with \({\text{Re}} (\gamma_{em}^{(0)} ) > 0\).
The expansion coefficients of EM fields (in air) associated with P and SV waves are governed by:
where \(n = 0,1,2\); and
where \(q = 0,1\); \(n = 0,1,2\); and \({\mathbf{a}}^{TE(0)} = \left[ {\begin{array}{*{20}c} 0 & {{{(\gamma_{em}^{(0)} )^{2} } \mathord{\left/ {\vphantom {{(\gamma_{em}^{(0)} )^{2} } {(i\omega \mu_{0} )}}} \right. \kern-\nulldelimiterspace} {(i\omega \mu_{0} )}}} \\ {i\omega \mu_{0} } & 0 \\ \end{array} } \right]\).
Derivation of Eqs. (179) and (183) has taken into account Eqs. (70) and (75) as well as the continuity condition of EM fields’ horizontal components at free surface.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Sun, YC., Ren, H., Yamazaki, K. et al. Semi-analytical solutions of seismo-electromagnetic signals arising from the motional induction in 3-D multi-layered media: part I—theoretical formulations. Earth Planets Space 73, 20 (2021). https://doi.org/10.1186/s40623-020-01327-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s40623-020-01327-7