Application of graph neural networks to predict explosion-induced transient flow

Abstract

We illustrate an application of graph neural networks (GNNs) to predict the pressure, temperature and velocity fields induced by a sudden explosion. The aim of the work is to enable accurate simulation of explosion events in large and geometrically complex domains. Such simulations are currently out of the reach of existing CFD solvers, which represents an opportunity to apply machine learning. The training dataset is obtained from the results of URANS analyses in OpenFOAM. We simulate the transient flow following impulsive events in air in atmospheric conditions. The time history of the fields of pressure, temperature and velocity obtained from a set of such simulations is then recorded to serve as a training database. In the training simulations we model a cubic volume of air enclosed within rigid walls, which also encompass rigid obstacles of random shape, position and orientation. A subset of the cubic volume is initialized to have a higher pressure than the rest of the domain. The ensuing shock initiates the propagation of pressure waves and their reflection and diffraction at the obstacles and walls. A recently proposed GNN framework is extended and adapted to this problem. During the training, the model learns the evolution of thermodynamic quantities in time and space, as well as the effect of the boundary conditions. After training, the model can quickly compute such evolution for unseen geometries and arbitrary initial and boundary conditions, exhibiting good generalization capabilities for domains up to 125 times larger than those used in the training simulations.

Introduction

Many industrial operations are subject to the risk of vapor cloud explosions. These events potentially cause hazardous levels of pressure in their surroundings [1], involving the rapid combustion of a premixed cloud of flammable vapour and oxidizer. Once the premixed cloud ignites, it causes a deflagration flame front that propagates through the flammable gas mixture; congested environments can result in increased flow turbulence and, consequently, higher mixing, flame speed and radiated pressure waves [2]. Deflagration is a complex phenomenon posing considerable challenges when attempting its numerical and experimental modelling. Experimental research has been conducted to measure impulse distribution during explosive blasts [3,4,5], contributing valuable insights to this area of study, and computational fluid dynamics (CFD) codes can achieve accurate predictions of deflagration events. However, in the engineering practice it is often necessary to model very large and geometrically complex domains, as the fluid and combustion responses are highly sensitive to the geometrical details. In addition, the discretisation of the event in space and time must be fine, to capture the details of the fluid’s turbulent combustion. The combination of large and complex domains, fine meshes and small time increments poses a problem of computational resources when conducting these simulations. In this study we set out to mitigate this problem by applying machine learning, specifically graph neural networks (GNNs). We focus on the propagation, reflection and diffraction of shock-induced pressure waves in complex geometric environments, absent combustion, which we will examine in a companion paper.

Data-driven machine learning techniques have emerged as a natural solution to computational problems in engineering simulations, offering significant improvements in computation time. Physics-informed machine learning techniques have dominated the research on the response of fluid systems. The literature [6] presents techniques adopting observational biases (with training sets carefully built to reflect the physical principles that the model will have to obey) [7, 8], inductive biases (where the machine learning model’s architecture is designed to embed some of the system’s properties, i.e. symmetry or translation-invariance) [9,10,11,12,13,14], or learning biases, where the loss function is constructed to encourage the attainment of physically consistent solutions [15,16,17,18]. Of particular interest for this study are GNNs, which adopt a hybrid approach. GNNs operate directly on graphs, which bear a resemblance to meshed domains typically employed in numerical solvers such as CFD. As a result, there has been a growing interest in the application of GNN-based machine learning algorithms.

When employing deep learning to tackle physical problems, the data under consideration is frequently represented in Euclidean space. Machine learning architectures that operate effectively on data arranged in a grid-like format have been extensively investigated [19, 20]. These architectures possess a significant limitation, which is that they must operate on regular grids. Despite attempts to circumvent this constraint [21], it has emerged that data from physical simulations can be better handled using geometric deep learning [22], which aims at generalizing deep learning methods to non-Euclidean domains, and represented as directed or undirected graph [23]. From here, the development of GNNs, that were initially formulated in [24] and further developed in [25, 26]. Due to their ability to directly operate on graphs, GNNs have been intensely studied in the past decade [27,28,29] and they recently grew in popularity by being applied to a vast range of problems using supervised, semi-supervised, unsupervised, reinforcement learning [10]. In recent years, GNNs have been used in a variety of applications, such as double pendulum problems and relativity [13], cosmology [12], mass-spring systems [30], visual images [31, 32], physical systems dynamics prediction [33,34,35], traffic prediction [36, 37], point clouds [38], image classification [39] and also fluid dynamics [33, 40,41,42,43,44]. In this study we apply the MeshGraphNets [33] algorithm, after suitable modifications, to address the problem at hand. This code has been successful at capturing several 2D and 3D physical phenomena, including transient compressible flows in two dimensions, using velocity and density information as inputs. In the present study we code MeshGraphNets in 3D and we include velocity, density, pressure and temperature as input variables, to allow physically accurate predictions of the complex pressure, temperature and velocity fields induced by impulsive events in realistic, congested and geometrically complex domains occupied by a compressible fluid.

In the next section we summarise how the model works, in “Assembly of a training dataset and training of the surrogate” we describe the CFD simulations performed to create the training dataset, and in “Results and discussion” section we present and discuss the results.

Methodology

A graph is defined as $G=(V,E)$ where $V=\{{{\varvec{v}}}_{i}{\}}_{i=1:{N}^{v}}$ represents a set of nodes, with ${N}^{v}$ being the total number of nodes and ${{\varvec{v}}}_{i}$ a vector containing the node’s attributes, while $E=\{{\mathbf{e}}_{k},{r}_{k},{s}_{k}{\}}_{k=1:{N}^{e}}$ represents the set of edges connecting the nodes: ${s}_{k}$ and ${r}_{k}$ are the indexes of the sender’s and receiver’s nodes respectively, ${\mathbf{e}}_{k}$ is a vector of edge’s attributes and ${N}^{e}$ represents the total number of edges in the graph [45]. In the present study, a node will represent a node of the meshed domain of the simulation, with the node’s attributes being pressure, temperature and velocity at the node and a Boolean variable to distinguish the boundary nodes from those on the inner part of the fluid’s domain. An edge will represent a connection between these nodes, with edge attributes being the distance and relative displacement vector between the pair of connected nodes, as proposed in [33]. In Ref. [10], a graph network (GN) framework is introduced as a generalization of a variety of GNN architectures. A GN block receives as an input a graph $G=(V,E)$ and it returns an updated graph, based on a set of computations. The updated graph is calculated by taking into account the information received at each single node from the neighbouring ones via the connections between them (edges) [10, 34]. The GN block thus contains a set of “update” functions $\phi$ and “aggregation” functions $\rho$ [10], defined as follows:

$$ {\mathbf{e}}_{k}^{\prime } = \phi^{e} \left( {{\mathbf{e}}_{k} ,{\varvec{v}}_{{r_{k} }} ,{\varvec{v}}_{{s_{k} }} } \right) $$

(1)

$$ {\overline{\mathbf{e}}}_{i}^{\prime } = \rho^{e \to v} \left( {E_{i}^{\prime } } \right) $$

(2)

$$ {\varvec{v}}_{i}^{\prime } = \phi^{v} \left( {\overline{\varvec{e}}_{i}^{\prime } ,{\varvec{v}}_{i} } \right) $$

(3)

Where $E_{i}^{\prime } = \left\{ {\left( {{\mathbf{e}}_{k}^{\prime } ,r_{k} ,s_{k} } \right)} \right\}_{{r_{k} = i,{ }k = 1:N^{e} }}$ [10].

The update functions modify the attributes of nodes and edges; the aggregation functions condense the information needed to compute the updates, receiving as an input a set of numbers and reducing it to a single value. First, ${\phi }^{e}$ is applied to each edge in order to get per-edge updates, which are then aggregated by ${\rho }^{e\to v}$ into a single vector for all edges projecting into node $i$. Second, ${\phi }^{v}$ is applied to each node to obtain per-node updates, which are influenced by the single node attributes, as well as the aggregated information from the edges acting on the node. A schematic of the items involved in the update and aggregation functions is shown in Fig. 1.

Fig. 1

Representation of the update and aggregation functions for a graph architecture [10]

From a practical point of view, the update can be implemented using different functions, including neural networks, leading to the definition of graph neural networks. On the other hand, aggregation functions are usually implemented via element-wise summations [10]:

$$ \phi^{e} \left( {{\mathbf{e}}_{k} ,{\varvec{v}}_{{r_{k} }} ,{\varvec{v}}_{{s_{k} }} } \right) = {\text{NN}}_{{\text{e}}} \left( {\left[ {{\mathbf{e}}_{k} ,{\varvec{v}}_{{r_{k} }} ,{\varvec{v}}_{{s_{k} }} } \right]} \right) $$

(4)

$$ \phi^{v} \left( {{\overline{\mathbf{e}}}_{i}^{\prime } ,{\varvec{v}}_{i} } \right) = {\text{NN}}_{{\text{v}}} \left( {\left[ {{\overline{\mathbf{e}}}_{i}^{\prime } ,{\varvec{v}}_{i} } \right]} \right) $$

(5)

$$ \rho^{e \to v} \left( {E_{i}^{\prime } } \right) = \mathop \sum \limits_{{\left\{ {k:r_{k} = i} \right\}}} {\varvec{e}}_{k}^{\prime } $$

(6)

An architecture described by the GN formalism is the message-passing neural network (MPNN), introduced in [41]. It facilitates the calculation of updates that take into consideration message propagation from adjacent nodes, thereby enabling the adjustment of node attributes to depend on the attributes of nodes located at a considerable distance from them. This phenomenon is made possible by the transmission of information through the interconnected edges linking the nodes. A MPNN consists of two phases, namely a passing one and a readout one, operating on unidirected graphs $G$ with node features ${v}_{i}$ and edge features ${e}_{ij}$. Focusing on the message passing phase, given a message function ${K}_{m}$ and a node update function ${\phi }_{m}^{v}$, the ${q}_{i}^{m+1}$, quantities at each node after iteration $m+1$ will depend on messages ${k}_{v}^{m+1}$ in accordance to [46]:

$$ k_{v}^{m + 1} = \mathop \sum \limits_{j \in N\left( i \right)} K_{m} \left( {q_{i}^{m} ,q_{j}^{m} ,e_{ij} } \right) $$

(7)

$$ q_{i}^{m + 1} = \phi_{m}^{v} \left( {q_{i}^{m} ,k_{v}^{m + 1} } \right) $$

(8)

where $N(i)$ represents the neighbours of the node ${v}_{i}$. From Eqs. 7 and 8 it can be seen how, at each message passing time step (i.e. m-th iteration), the influence of nodes further away from the one being considered is accounted for in the update of ${q}_{i}$. Using the GN framework, we can see that ${K}_{m}$ can be represented by the edges update function ${\phi }^{e}$ taking ${\mathbf{e}}_{k}$, ${{\varvec{v}}}_{rk}$ and ${{\varvec{v}}}_{sk}$ as inputs, while ${\rho }^{e\to v}$ is given again by element-wise summation. The MPNN involves the repetition of the GN block for m times, which can be interpreted in the graph architecture as the collection of information from nodes further away from the selected one, as sketched in Fig. 2.

Fig. 2

Representation of the message passing algorithm for a graph. Each node ${v}_{i}$ is updated by gathering information from nodes in its neighbourhood, at a distance depending on the chosen value of m

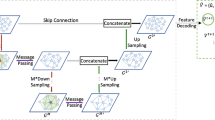
MeshGraphNets [30] has an Encode-Process-Decode structure as implemented in [47], followed by an integrator. The model is a generalization of the previously developed “Graph Network Simulator” (GNS) framework [48], a learnable simulator adopting a particle-based representation of physical systems. In the GNS framework, physical dynamics is predicted by modelling the interaction between neighbouring particles and how quantities are passed from one another. This can be seen as a message-passing on a graph, where the particles are the graph nodes and the edges effectively couple neighbouring nodes. MeshGraphNets uses a simulation mesh ${M}^{t}=(V, E)$, where $V$ are the mesh nodes and $E$ the mesh edges at a given time $t$. The mesh intrinsically has the same structure of a graph, naturally being eligible for the application of GN structures. The model is meant to predict dynamical quantities at the mesh nodes at time $t+\Delta t$ from knowledge of these quantities at time $t$ (as described by the mesh status ${M}^{t}$). This allows to iteratively predict the system’s status at the time steps subsequent to a given initial condition.

The model takes ${M}^{t}$ as input, and it is able to estimate ${M}^{t+\Delta t}$ through an Encode–Process–Decode architecture. The role of each section is sketched in Fig. 3 and described below.

• Encoder: ${M}^{t}$ is encoded into a multigraph $G=(V,E)$. This is obtained by defining the edges’ and nodes’ attributes starting from the simulation mesh. Positional features are given as relative values, so that the graph edges ${\text{e}}_{\text{ij}}\in {E}^{M}$, contain as attributes the relative displacement between neighbouring nodes ${\mathbf{u}}_{ij}={\mathbf{u}}_{i}-{\mathbf{u}}_{j}$ and its norm $|{\mathbf{u}}_{ij}|$. Then, the dynamical quantities at the nodes of the mesh (${{\varvec{q}}}_{i}^{t}$), where ${{\varvec{q}}}_{i}^{t}=({p}_{i}^{t}, {T}_{i}^{t}, {\mathbf{v}}_{i}^{t})$, with ${p}_{i}^{t}$ being the pressure at time t at the i-th node, ${T}_{i}^{t}$ the temperature, ${\mathbf{v}}_{i}^{t}$ the tri-dimensional velocity vector are defined and given as nodes attributes in ${{\varvec{v}}}_{i}$, together with${n}_{i}$, a flag (with value 0 or 1 in this study), distinguishing the boundary nodes from the internal ones, so that ${{\varvec{v}}}_{i}^{t}=({{\varvec{q}}}_{i}^{t}, {n}_{i})$. The final step is the encoding of all edges and nodes into latent vectors of customizable size, ${{\varvec{v}}}_{i}^{\text{E}}$ and ${{\varvec{e}}}_{ij}^{E}$. This is achieved with 2 multilayer perceptrons (MLPs), ${\epsilon }^{M}$ and ${\epsilon }^{V}$. In this step, the simulation mesh is transformed into the input to the machine learning model.

• Processor: a sequence of $m=15$ identical message passing steps (GN blocks, taking advantage of the message passing capabilities) are applied to the ${\mathbf{e}}_{ij}^{E}$ and ${{\varvec{v}}}_{i}^{\text{E}}$ obtained in the previous step:

  $$ {\mathbf{e}}_{ij}^{\prime E} \leftarrow f^{M} \left( {{\mathbf{e}}_{ij}^{E} ,{\varvec{v}}_{i}^{{\text{E}}} ,{\varvec{v}}_{j}^{{\text{E}}} } \right),\quad {\varvec{v}}_{i}^{{\prime {\text{E}}}} \leftarrow f^{V} \left( {{\varvec{v}}_{i}^{{\text{E}}} ,\mathop \sum \limits_{j} {\mathbf{e}}_{ij}^{\prime E} } \right) $$

  (9)

  where ${f}^{M}$ and ${f}^{V}$ are MLPs with a residual connection.

• Decoder: once the edges and the nodes have been processed, the temporal variation of the nodes’ attributes over a $\Delta t$ chosen during training, is estimated through an additional MLP ${\delta }^{V}$, applied to the latent node updated features ${{\varvec{v}}\mathbf{^{\prime}}}_{i}^{\text{E}}$. The model’s output are thus temporal variations of the nodes’ attributes $\Delta {q}_{i}^{(t+\Delta t)}$. By summing these to the original quantities at the nodes, it is possible to iteratively predict the system’s state ${M}^{t+\Delta t}$ at subsequent time steps.

Fig. 3

Schematics of the MeshGraphNets algorithm applied to CFD problems

Assembly of a training dataset and training of the surrogate

The data to train the model was obtained from a set of 413 CFD simulations conducted in OpenFOAM. In these simulations we considered a cubic volume (L = 0.1 m) of atmospheric air surrounded by rigid walls, and containing a rigid obstacle of random position, dimension, shape (prism, sphere, cone or cylinder) and orientation (examples are shown in Fig. 4). The decision to randomly assign attributes of shape, dimensions, and initial high-pressure areas within the domains was made to ensure adequate variability of inputs. Python scripts were used for the stochastic selection of these parameters, facilitating the automated generation of mesh files (gmsh format). The initial conditions for the fluid consisted of vanishing velocity ($\mathbf{v}=0$) and a uniform temperature and pressure (set to standard atmospheric air conditions) applied throughout the entire domain, with the exception of a subset of the fluid domain, which was initially assigned a higher pressure compared to the rest of the domain (randomly chosen between 3 and 15 bar). The shape of this particular subset was cuboidal with side lengths in the range 8–15 mm, and the location of its centroid was chosen randomly. We note that the choice of a cuboidal region of high pressure (over a more common spherical region) was made based on the simplicity of implementation, but also to further challenge the surrogate model with the prediction of the initial time evolution of this cuboidal region. This pressure difference induced a shock at $t=0$, triggering the propagation of pressure waves throughout the domain. As these waves interacted with the obstacles and walls, their reflection and diffraction occurred, leading to the formation of complex and transient flow conditions.

Fig. 4

Examples of meshed domains simulated to assemble the training dataset

The gas inside the domain was modelled as a perfect gas with heat capacity ratio $\gamma =1.4$, with the compressible, unsteady Navier–Stokes equations governing the flow behaviour. The conservation equations of mass, momentum and energy were solved in the unsteady Reynolds-averaged form (URANS) neglecting external forces:

$$ \frac{{\partial {\overline{\rho }}}}{\partial t} + \nabla \cdot \left( {{\overline{\rho }}\tilde{v}} \right) = 0 $$

(10)

$$ \frac{{\partial \left( {\overline{\rho }\tilde{\varvec{v}}} \right)}}{\partial t} + \nabla \cdot \left( {{\overline{\rho }}\tilde{v} \otimes \tilde{v}} \right) = - \nabla \overline{p} + \nabla \cdot \left( {{\tilde{\mathbf{\tau }}} - \overline{{{\uprho }v^{\prime\prime} \otimes v^{\prime\prime}}} } \right) $$

(11)

$$ \frac{{\partial \left( {\overline{\rho }\tilde{H}} \right)}}{\partial t} + \nabla \cdot \left( {{\overline{\rho }}\tilde{v}\tilde{H}} \right) = - \nabla \cdot \left( {{\upkappa }\nabla T - \overline{{{\uprho }v^{\prime\prime}H^{\prime\prime}}} } \right) + \nabla \cdot \left( {\tilde{v} \cdot {\overline{\mathbf{\tau }}} + \overline{{v^{\prime\prime} \cdot {{\varvec{\uptau}}}}} } \right) + \frac{{\partial \overline{p}}}{\partial t} $$

(12)

In Eqs. 10–12, $\rho$ represents the density, $t$ the time, $\mathbf{v}$ the velocity, $p$ the pressure, ${\varvec{\uptau}}$ the viscous stress tensor, $H$ the enthalpy and $\kappa$ is the coefficient of thermal diffusivity. The bar indicates ensemble averaged quantities, the tilde indicates density averaging, while the double prime refers to fluctuations around the density-averaged quantities. rhoCentralFoam, part of the C++ CFD toolbox OpenFOAM [49] was employed as solver. The k-ω-SST [50] model was used as turbulence closure. The turbulent kinetic energy k was initialized as $3.25*{10}^{-3}\frac{{\text{m}}^{2}}{{\text{s}}^{2}}$, while $\omega$ was calculated as $\omega =\frac{{k}^{0.5}}{{C}_{\mu }^{0.25}L}$, taking ${C}_{\mu }=0.09$ and L as 10% of the average cell size $\Delta c$. No-slip boundary conditions for the velocity field were applied on the surfaces of the obstacles and of the cubic enclosure. The integration schemes were of first order in time and second order in space. The time step was determined by imposing the Courant-Friedrichs Lewy (CFL) number to stay below 0.1. Kurganov and Tadmor’s scheme [51] was used for the interpolation of the convective terms, with Van Leer’s flux limiters [52].

For each of the simulation domains, meshing was obtained via the automatic meshing software Gmsh, with the average cell size $\Delta c$ randomly varying between different simulations between 3.0 and 4.2 mm. In 75% of the training simulations, refinement was imposed on the cells comprising the initial pressurised box and the obstacle wall, with $\Delta c$ varying between 1.5 and 2.5 mm, proportionally to the initial cell size. In the remaining cases, the meshes did not include any refinements. The use of different meshes was intended to test the GNN’s expected ability to handle arbitrary meshes. The outputs were recorded with a regular time spacing of $\Delta t=2*{10}^{-6}\text{ s}.$

The evolution of thermodynamical quantities during each pair of consecutive times in a simulation represented a unit training datapoint, with data at the initial time serving as an input and those at the final time as an output. The dataset comprised approximately 61,500 datapoints.

Following a preliminary study, the results presented below used 64 as the encoding dimension, which is half of what used in Pfaff et al. [33]. A summary of this preliminary study is reported in Appendix. The number of message-passing steps was set to 15, consistent with the original model [33]. Input standardization was applied to the input data. The model was trained on a single NVIDIA RTX 6000 GPU for 260 epochs by minimizing the mean square error (MSE) for the standardized values of pressure, temperature and velocity changes over $\Delta t$, defined as:

$$ \frac{1}{{N^{V} }}*\mathop \sum \limits_{i = 1}^{{N^{V} }} \left( {\left( {{\Delta }p_{i} - {\Delta }\hat{p}_{i} } \right)^{2} + \left( {{\Delta }T_{i} - {\Delta }\hat{T}_{i} } \right)^{2} + \left( {{\Delta }{\mathbf{v}}_{i} - {\Delta }{\hat{\mathbf{v}}}_{i} } \right)^{2} } \right). $$

(13)

Adams optimization with a decaying learning rate starting at 10^–3 and progressively reducing to 10^–9 was employed. The machine learning architecture was constructed using TensorFlow [53], TensorFlow Probability and dm-sonnet libraries, employing ragged tensors to manage the variability in input dimensions.

Results and discussion

Following training, the surrogate model was used to simulate explosion events and its predictions were compared to those of a new set of 38 simulations; these were set up as the CFD analyses described above and used for training, but they modelled unseen geometric domains, containing multiple obstacles. The fields of pressure, temperature and velocity were initialised at $t=0$; the surrogate model was then used to predict the next time step, iteratively advancing the solution. Cell sizes and initial pressures were randomly selected within the range of those present in the training dataset. The boundary condition $\mathbf{v}=0$ was enforced at the appropriate boundary nodes at all times; this choice was made for computational convenience, however the trained model was able to satisfy the boundary constraints on velocity effectively even in absence of the constraint ($\mathbf{v}=0$), albeit with an unavoidable small numerical error; by imposing vanishing velocity at the appropriate boundaries this error was avoided, and the model showed excellent predictions of the pressure, temperature and density fields at the boundaries, indicating that it had effectively learned the physics of the reflection and diffraction of a pressure wave at a wall. A qualitative comparison of the pressure fields predicted by CFD simulations and surrogate model is provided in Fig. 5.

Fig. 5

Predictions of the pressure field by CFD simulations and the surrogate model. The field at a time $5.6*10^{-5}$ s in a selected evaluation simulation is shown

Any error of the surrogate model tends to accumulate over time, as shown in Fig. 6a–c, which displays the average error in pressure, temperature and velocity components over the time duration $t=0.1$ ms of the 38 test simulations. This error in the predicted physical quantities remained low for the relatively long duration of the simulations. Maximum errors are shown in Fig. 6d–f; these were higher but still within acceptable limits. The maximum errors are calculated as the average of the maximum errors of all the 38 test simulations (the maximum was evaluated for each test case and these were averaged over the 38 test cases). We note that their evolution in time was not monotonic; the reasons for this were not investigated further here considering the high accuracy of the surrogate predictions.

Fig. 6

a Average error in pressure; b average error in temperature; c average errors in velocity; d maximum error in pressure; e maximum error in temperature; f maximum errors in velocity

Fig. 7

a First domain where the fluid domain is evaluated at points 1 and 2; b second domain where the fluid domain is evaluated at points 1 and 2

To further and more explicitly illustrate the level of accuracy of the surrogate model, for two selected points shown in Figs. 7, 8, 9, 10, 11 present time histories of the predicted thermodynamic quantities; the predictions are from two selected geometrical domains and at two selected points within these domains. In all cases, the surrogate model predicts histories of pressure, temperature and velocity extremely close to the CFD predictions.

Fig. 8

Comparison of the actual and predicted a) pressure, b) temperature, c) velocity components, d) velocity magnitude for point a-1 (Fig. 7)

Fig. 9

Comparison of the actual and predicted a pressure, b temperature, c velocity components, d velocity magnitude for point a-2 (Fig. 7)

Fig. 10

Comparison of the actual and predicted a pressure, b temperature, c velocity components, d velocity magnitude for point b-1 (Fig. 7)

Fig. 11

Comparison of the actual and predicted a pressure, b temperature, c velocity components, d velocity magnitude for point b-2 (Fig. 7)

Figure 12 illustrates the geometry of a selected test simulation, highlighting a particular rectangular plate representing one of the faces of a cuboidal rigid obstacle. The histories of average and maximum pressure on such plate are shown in Fig. 13, as predicted by CFD simulations or surrogate model. Again, the surrogate makes predictions very close to those of detailed CFD simulations.

Fig. 12

Geometry and initial conditions for a selected test simulation. The highlighted rectangle represents a plate over which maximum and average pressure are predicted

Fig. 13

Average (a) and maximum (b) pressure on the rectangular plate highlighted in Fig. 12

It is important to note that the trained model uses a simple loss function without differentiating weights between terms or including physically bounding terms. Remarkably, it achieves great accuracy despite its simplicity and minimal tuning. Incorporating additional terms in the loss function to account for physical laws (for example adding the residuals of governing equations) would ensure adherence to these laws. We shall explore the possible computational advantages (higher accuracy) and disadvantages (challenging training processes) of physics-informed approaches in future studies.

To assess the model’s generalisation capability, additional testing was conducted, predicting pressure wave propagation on larger and more complex domains. An additional set of simulations was conducted, modelling cubic domains of size L = 0.25 m and L = 0.5 m, containing three regions of initially higher pressure (therefore three sources of impulsive loading, at pressures of 6, 7.5 and 8.5 bar) and 8 obstacles, resulting in a highly congested environment and complex loading. These domains were discretised by structured meshes of different cell sizes Δc. An example of such domains and the corresponding initial conditions are shown in Fig. 14.

Fig. 14

Domain and initial conditions used for the evaluation of the model’s generalisation capabilities

Figure 15 summarises the findings, presenting the average and maximum errors in predictions of thermodynamical quantities in 3 different simulations, of geometry identical to that in Fig. 14 (apart from a scale factor) and three different combination of size L and cell size c, as indicated. We recall that the average cell size was 3.5 mm in the training simulations. The surrogate model demonstrates outstanding generalisation capability, with low errors in all cases, of similar magnitude as the errors displayed in Fig. 6 for smaller (L = 0.1 m) and geometrically much simpler domains. The accuracy of the surrogate model is higher when meshes similar to those used for training are used.

Fig. 15

Tests on larger and more complex domains. a Average error in pressure; b average error in temperature; c average error in velocity module; d maximum error in pressure; e maximum error in temperature; f maximum error in velocity

In Fig. 16 we provide examples of the computational cost of the CFD simulations and of the surrogate model’s (SM) predictions. We plot the computational time required to compute one time increment of length ${t}_{step}=2{*10}^{-6}$ s for simulations with different numbers of nodes (${N}^{V}$); the speed of the CFD simulations in OpenFOAM is compared to that of the surrogate model, executed either on a GPU (single NVIDIA T4) or on a CPU. The data are fitted by a power-law of type ${t}_{step}=\text{A}{{(N}^{V})}^{m}$. Least-square fits of such equation to the data gave $\text{A}=3.432*{10}^{-4},m=1.084; \text{A}=3.272*{10}^{-4},m=0.978;\text{A}=1.35*{10}^{-3},m=0.707;$ for the CFD simulations, SM on CPU, and SM on GPU, respectively. Assuming that such power-laws are valid at large number of nodes than those investigated here, the above data suggest computational speed-ups of approximately 50 for a simulation with 10⁶ nodes and of more than 100 for a simulation with 10⁷ nodes, intended as the time to perform a CFD simulation divided by the time to perform a corresponding surrogate prediction. The details of the type of hardware used in both CFD simulations and surrogate predictions, as well as the choice of parameters in the CFD simulations and surrogate models (e.g. the CFL number) can obviously affect the speed-ups recorded in this study. It is clear however that the surrogate model allows savings in computational time of a few orders of magnitude compared to CFD simulations, and the savings are higher in very large simulations. This can be game-changing in industrial applications, where deflagrations and detonations of entire industrial plants need to be simulated with high spatial and temporal resolution. Our future work will therefore aim at including additional physics in the surrogate model, namely combustion, deflagration and its transition to detonation.

Fig. 16

Computational time to complete a simulation time increment of ${t}_{step}=2{*10}^{-6}$ s, for CFD simulations or surrogate model’s predictions, performed on a CPU (SM_CPU) or on a GPU (SM_GPU). The figure includes power-law fits of ${t}_{step}=A{{(N}^{V})}^{m}$ through the data

Conclusions

We demonstrated the potential of GNNs, as implemented in MeshgraphNets and modified as described above, in predicting the transient flow response to impulsive events such as explosions. We applied a surrogate model to predict the transient fields of pressure, temperature and velocity following the sudden release of high pressure in finite regions of a fluid domain. We proposed a strategy to construct the training simulations to obtain from these suitable training data for a surrogate model.

The proposed surrogate exhibited high predictive accuracy. The model was trained on the results of URANS simulations of relatively small domains, however it was able to make accurate predictions also in the case of domains of volume up to 125x that of the training simulations, geometrically more complex, and with a coarser mesh than that used in the training simulations, which demonstrates excellent generalisation capabilities. The model also offers computational savings of at least one to two orders of magnitude compared to the CFD simulations used to train it, depending on the total number of cells. Such savings are expected to increase considerably as the number of cells increases.

Appendix

The dimensions used for encoding in the MeshGraphNets model, which determine the size of the latent vector where nodes’ and edges’ attributes are represented, significantly influence the model’s complexity. In the work conducted by Pfaff et al. [33] these dimensions were set to 128. Large encoding dimensions are commonly employed in GNNs to capture relevant information from a higher-dimensional space. By increasing the dimensionality of the problem, the model can assess linear and non-linear relationships among node features, representing them as vectors in the latent space. Nonetheless, augmenting the dimensions of the latent necessitates longer training times and make the model susceptible to overfitting. The encoding dimensions not only influence the training time but also impact the memory requirements. While longer training times may be acceptable, a higher demand for memory can pose challenges during GPU-based training. The larger memory requirements directly constrain the size of domains that can be utilized, limiting the number of nodes and cells within each simulation. This limitation arises from the fact that encoding causes the size of attributes considered for each node to grow by a multiplicative factor equal to the encoding dimension. For our training dataset, we observed that the time needed to make one update of the model was 1.67 times higher when employing 128 encoding dimensions instead of 64.

Figures 16, 17 and 18 show the average discrepancy and the average maximum discrepancy for pressure, temperature and velocity, comparing the performance of the surrogate model with encoding dimensions 64 and 128; the effect of the number of epochs is also explored. The results clearly showed that a model using encoding dimensions 64 may outperform one using dimension 128, at the expense of a longer training time (Fig. 19).

Fig. 17

Comparison of a Average discrepancy between the evaluated and expected calculated pressure over time for all the evaluation cases; b maximum discrepancy between the evaluated and expected calculated pressure at single points over time for all the evaluation cases; for the models comprising 64 and 128 encoding dimensions, trained for 163 and 260 epochs

Fig. 18

Comparison of a average discrepancy between the evaluated and expected calculated temperature over time for all the evaluation cases; b maximum discrepancy between the evaluated and expected calculated temperature at single points over time for all the evaluation cases; for the models comprising 64 and 128 encoding dimensions, trained for 163 and 260 epochs

Fig. 19

Comparison of a Average discrepancy between the evaluated and expected calculated velocities over time for all the evaluation cases; b maximum discrepancy between the evaluated and expected calculated velocities at single points over time for all the evaluation cases; for the models comprising 64 and 128 encoding dimensions, trained for 163 and 260 epochs