Abstract
An enriched homogenized model is developed based on a proposed homogenization strategy, to describe the wave propagation behaviour through periodic layered composites. The intrinsic parameters characterising the micro-inertia effect and non-local interactions are defined transparently in terms of the constituent materials’ properties and volume fractions. The framework starts with the introduction of an additional kinematic field to characterise the displacement of the stiff layer, before setting up macro kinematic fields to account for the average deformation of the constituent materials within a segmented unit cell. Relationships between these macro average strain fields are determined based on suitable micro-mechanical arguments. The Hill–Mandel condition is next applied to translate the energy statements from micro to macro. A system of coupled governing equations of motion is finally extracted naturally at the macro level via Hamilton’s Principle. Through a series of benchmark examples, it is shown that the proposed model exhibits excellent predictive capabilities over a broad range of loading frequencies.
Similar content being viewed by others
Introduction
Locally resonant metamaterials represent an emerging class of engineered morphologies which can exhibit unique wave attenuation and filtering characteristics. Periodic layered composites made up of at least three constituent materials belong to a subset of such metamaterials, as they can involve band gaps as well due to inner resonance arising from their specific microstructural arrangements [1,2,3]. When a wave propagates through a periodic heterogeneous media, a series of signal reflections and transmissions develop at the material interfaces. Relative to the minimum characteristic length of the constituent materials: (i) local resonance develops when the loading wavelength is much larger; (ii) Bragg scattering ensues when the loading wavelength is of the same order.
There exists a wide range of metamaterial designs in literature, e.g. a simple unit cell where a stiff inclusion coated by a compliant layer is embedded within a matrix [4,5,6,7,8], to complicated forms involving the bending vibration modes of cylindrical rods [9], thin flexible plates [10] and Timoshenko beams [11]. The focus of this contribution is on the one-dimensional viscoelastic plane wave propagation through the former, idealised as periodic layered composites representing the stiff inclusion, compliant layer and matrix material, for both sound and blast wave attenuation. The objective is to adequately describe the wave propagation process in a continuum formulation, without the explicit representation of the underlying constituent materials.
Classical continuum theories are non-dispersive, and are therefore ill-suited for such analyses. Full-scale numerical characterisation [8, 12,13,14] and/or laboratory experiments [15,16,17,18], while predictive, are often computationally/logistically expensive. Generalized continuum theories are thus developed to facilitate rapid analyses. In literature, the development of such theories typically follow either a bottom-up or a top-down approach.
A top-down strategy begins with a priori postulations of energy functions at the macro scale that incorporate additional higher-order contribution(s), with the associated length scale parameter(s) characterising the underlying micro-inertia effect and non-local interactions, otherwise not captured in a classical continuum. Such energy functions may not necessarily be attributed to the primary variable alone, as in the case of relaxed micromorphic theory [19, 20]. The relaxed model, which consists of an additional kinematic variable to track microstructural deformation, thus enriching the classical continuum, was employed to predict the frequency band-gaps as wave propagates through metamaterials [21]. Calibration of the parameters was later carried out based on numerical simulations with test data [22].
At the other end of the dichotomy, a bottom-up framework starts at the micro scale based on an identified unit cell, followed by a continualization or homogenization strategy towards a generalized continuum. Following the work on effective constitutive relations with respect to elastodynamics in heterogeneous media [23], the frequency-dependent effective mass was recast using a mass-in-mass lattice unit cell, into a multi-displacement model that tracks the movement of both apparent and hidden masses, hence averaging a negative mass near resonance [24]. A similar concept was extended to a two-dimensional setting [25]. The multi-displacement model was subsequently improved via non-local gradient effects, where the importance of ensuring numerical stability through carefully calibrated intrinsic parameters was emphasized [26]. Moreover, choices have to be made on the extent of the weighted interactions between the particles [27, 28].
Another popular bottom-up strategy is the asymptotic scheme, where both spatial and temporal scales are expanded into a series of fast and slow varying components, e.g. for bilaminate composites [29,30,31]. With regards to the modelling of inner resonance, the validity of the asymptotic homogenization scheme was demonstrated under the specific condition that the stiffness contrast between the matrix and compliant layer was of the order of the squared ratio between the loading wavelength and the size of the unit cell [3]. A similar strategy was employed to analyse viscoelastic wave propagation through a tri-material composite with low stiffness contrasts [2]. Since it was stated therewith that the accuracy of their asymptotic-based model reduces with increasing stiffness contrast, the approach is not yet directly applicable for locally resonant metamaterials. In order to achieve numerical stability [32], the model also adopted an approximating assumption during the derivation of boundary conditions.
In this contribution, an enriched model is developed, based on a proposed homogenization strategy that is fundamentally different from the approaches described above. A bottom-up strategy is adopted in our work, where an equivalence of energy is imposed across the scales. In contrast to an asymptotic homogenization scheme, our approach is directly applicable for locally resonant metamaterials. The approach presented here extends that for bilaminate composites [33], with the incorporation of an additional kinematic variable to provide a more refined resolution, for capturing the rapidly fluctuating responses within the unit cell. The practical applicability of the proposed model is examined by considering two locally resonant metamaterials from literature, applications of which pertain to sound wave transmission and blast wave propagation respectively. To broaden the scope of applicability, various degrees of viscoelasticity within compliant layer are also investigated. This is in line with recent reports on how viscoelasticity within the compliant layer can lead to overall enhanced wave attenuation properties [2, 34, 35]. Homogenized dispersion relations recovered using the proposed model based on infinitely long relaxation time, i.e. un-relaxed elastic configurations, are first benchmarked against analytical solutions. This is then followed by comparing homogenized responses from strongly viscoelastic configurations against reference solutions from Direct Numerical Simulations (DNS). It is shown that the proposed model exhibits excellent predictive capabilities over a broad range of loading frequencies.
This paper is organised as follows. An overview of the bottom-up strategy underlying the proposed enriched homogenized model is first provided. A macro kinematic variable is introduced to characterise the displacement of the stiff layer, together with suitable macro kinematic variables to account for the average deformation of different segments within a unit cell. The rapid fluctuating micro kinematic fields are then approximated up to the linear expansion of the corresponding macro quantities. The kinetic and potential energies of the unit cell are expressed in terms of the macro kinematic fields, before translating onto the macro scale via the Hill–Mandel condition. A system of homogenized governing equations of motions is next extracted through Hamilton’s Principle. Finally, the predictive capability of the proposed model is demonstrated with a series of benchmark examples.
Homogenization strategy
We first define a unit cell that is representative of the microstructural arrangement, with the objective of propagating the rapidly fluctuating responses within a unit cell onto the macro scale. To this end, we distinguish between two mechanisms underlying the transient behaviour:
Micro-inertia effect
When a macro point x is subjected to velocity v(x) in a standard homogenization framework, the transient response of the underlying unit cell is such that its average velocity corresponds to v(x). However, such an approach is unable to distinguish between the various possible deformation states, e.g. in Fig. 1i where the entire unit cell moves with the same velocity, or in Fig. 1ii where the stiff layer, compliant layers and matrix move at different velocities, though with an average value corresponding to v(x). The extent of non-uniformity in velocity within the unit cell translates onto the macro scale as a micro-inertia effect.
Non-local interactions
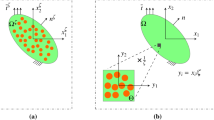
Consider the two length scale parameters, i.e. the loading wavelength \(\lambda \) and the size of a unit cell D, as depicted in Fig. 2i. When \(O(\lambda ) \gg O(D)\), the unit cell at each macro point x deforms locally to satisfy the imposed macro strain \(\varepsilon \), as shown in Fig. 2ii. For such cases with a clear separation of length scales between macro and micro, the standard homogenization approach can describe the micro-deformation adequately. However, when \(O(\lambda ) \rightarrow O(D)\), the interactions between neighbouring unit cells become more dominant. When subjected to an identical macroscopic strain as above-mentioned, the deformation within each unit cell is now furthermore influenced by the short range forces emanating from the neighbouring cells. The resulting response in Fig. 2iii can thus differ significantly from the reference case in Fig. 2ii. In a quasi-static setting, these non-local interactions manifest themselves at the macro level as size effect, which cannot be captured by a standard homogenization framework [36].
i Two length scale parameters \((\lambda , D)\) characterising the problem. ii When \(O(\lambda ) \gg O(D)\), a unit cell at each macro point x deforms locally to satisfy the imposed macro strain. iii When \(O(\lambda ) \rightarrow O(D)\), the deformation within each unit cell is furthermore influenced by the short range forces from neighbouring cells
In a generic loading, the macro behaviour results from the competition and interactions between the two mechanisms. To this end, we adopt a bottom-up strategy as summarized in Fig. 3. The general approach here broadly builds upon that for bilaminate composites [33], whereby the underlying micro-inertia effect and non-local interactions between constituent materials are captured via a linear variation of the average strain within each constituent material, followed by suitable micro-mechanical arguments towards homogenization. The micro-mechanisms are therefore allowed to propagate in a thermodynamically consistent manner and manifest themselves as intrinsic parameters naturally at the macro scale. A key departure (vis-à-vis that for bilaminate composites [33]) is the introduction of an additional kinematic variable to characterise the movement of the stiff layer. Specifically, the strategy in Fig. 3 encompasses the following:
- a.
The average deformation within a unit cell is characterised as per standard homogenization procedure. To distinguish between the different deformation modes for a given macroscopic loading, we introduce an additional kinematic variable to account for the displacement of the stiff layer. This is complemented with the characterisation of the average strains within the different segments of the unit cell. These macro kinematic fields thus provide critical information on the underlying deformation, which is not accounted for in a standard homogenization framework.
- b.
The kinetic and potential energies of each unit cell are written in terms of the macro kinematic variables and their gradients.
- c.
The Hill–Mandel condition, which states the equivalence of energy at the two scales, is adopted to translate the energy functions from micro to macro.
- d.
A system of homogenized governing equations of motion is next extracted naturally via Hamilton’s Principle, as per standard procedure.
Characterisation of unit cell and its underlying deformation
A typical periodic layered composite bar is illustrated in Fig. 4i. The corresponding elastic modulus and density for Material i are \(E_i\) and \(\rho _i\) respectively (\(i=1, 2, 3\)). Note that Material 1, 2 and 3 is attributed to the matrix, the compliant layer and the stiff layer respectively. A two-scale coordinate system is adopted, whereby x and y denote the macro and micro scales. To distinguish between quantities at the two scales, those that exist at the micro scale are denoted with a \({\widehat{}}\) symbol. We first define a unit cell of size D centred about a macro point x, with a symmetrical configuration about the origin of the micro coordinate y. The out-of-plane cross-sectional area is assumed as unity throughout the domain.
The unit cell is idealised as a series of springs over eight segments, as depicted in Fig. 4ii. To adequately capture the deformation of each constituent material within the unit cell, in addition to a (macro) kinematic variable \({\widetilde{U}}\) to account for the displacement of the stiff layer, we introduce micro kinematic fields \({{{\widehat{\varepsilon }}}_{(j)}}\) and \({{\widehat{U}}_{(j)}}\), to respectively characterise the strain and displacement underlying Segment j (\(j=\pm 1\), \(\pm 21\), \(\pm 23\), \(\pm 3\)). Note that the subscript 21 (or 23) refers to the segment containing Material 2 adjoining Material 1 (or 3), while − (or \(+\)) distinguishes between the two segments containing same material on the left (or right) of the unit cell. The volume fractions of Material 1, 2 and 3 are denoted by f, g and h respectively, such that \(f+g+h=1\). The mass of each constituent material is evenly distributed across each segment within the unit cell. While many kinematic variables are introduced at this stage, they will be later condensed out through suitable assumptions.
Average deformation of unit cell and its constituents
In the following, the kinematic fields are written with their arguments—(x, t) and (x, y, t) for macro and micro field respectively—for better clarity of presentation. Referring to Step (a) in Fig. 3, we characterise the deformation within different segments of the unit cell, in order to adequately capture the rapidly fluctuating response. As per standard homogenization approach, the macro strain that describes the average deformation of the unit cell is given by
where \({{\widehat{U}}(x,y,t)}\) denotes the displacement at a particular location within the unit cell at time t, while \(B^{(\pm )}\) refer to the boundaries of the unit cell.
The corresponding average strains between \(B^{(\pm )}\) and the midpoints of Material 2 within the unit cell \(I_{2m}^{(\pm )}\), as well as that between \(I_{2m}^{(\pm )}\) to the centre of the unit cell, can be written in terms of the micro displacements
Denoting the average strains within the eight segments of the unit cell as \({\varepsilon }_{(\pm 1)}\), \({\varepsilon }_{(\pm 21)}\), \({\varepsilon }_{(\pm 23)}\) and \({\varepsilon }_{(\pm 3)}\) respectively, the following kinematic relationship can be obtained, based on weighted sum of the average strains in the constituent materials
Combining (2) and (3) results in
At this juncture, there remains three micro displacement quantities on the right-hand side of (4). These quantities are approximated with the primary macro variables via (5a) and (5b), and with the newly introduced kinematic variable \({\widetilde{U}}\) that characterises the rigid body motion of the stiff layer via (5c), as
Substituting (5) into (4), we obtain
Note that the kinematic relationships in (6) hold true throughout the entire deformation process.
Decomposition of micro kinematic fields
The transient response of the unit cell is largely governed by the underlying deformation mode. To distinguish between the different transient modes as illustrated in Fig. 1, the micro strain within each segment of the unit cell is approximated by the linear expansion of the corresponding (macro) average strain in (7). This is a deliberate choice, as the gradient terms in (7) are required to capture the underlying non-local interactions illustrated in Fig. 2.
The micro strain rate within each segment of the unit cell is next approximated by the corresponding (macro) average strain rate via (8).
The linearisation for the micro strain rate (in a similar manner as the associated micro strain) is not done, because the present approach is already sufficient in accounting for the underlying micro-inertia effect and non-local interactions between the constituent materials. It will be demonstrated later that the current decomposition keeps the system of governing equations within a (manageable) fourth spatial order.
Energy functions of unit cell
A set of relations between the average strains (\({\varepsilon }_{(\pm 1)}\), \({\varepsilon }_{(\pm 21)}\), \({\varepsilon }_{(\pm 23)}\), \({\varepsilon }_{(\pm 3)}\)) and both primary and additional kinematic variables (U, \({\widetilde{U}}\)) have been determined in (6). In this section, we seek to establish another suitable relation between these macro strain fields, such that the kinetic and potential energies of a unit cell can be written solely in terms of macro kinematic fields, following Step (b) in Fig. 3.
Kinetic energy of unit cell
The transient response within a unit cell encompasses a series of reflections and transmissions of incident waves at the material interfaces, due to the jump in mechanical impedances. To capture this phenomenon adequately in the kinetic energy function, we refer to the energy fluxes of the constituent materials.
The mechanical impedance for Material i is defined as
For a given composite medium, the rate of energy transfer associated with a propagating wave is represented by its intensity within a specific segment of the unit cell
where \({{\widehat{\sigma }}_{(\pm j)}}\) denotes the stress within Segment j.
At the interface of the constituent materials, the ratio of reflected and transmitted intensities is given by
In general, it is difficult to determine a priori the actual stress states at the various interfaces within a unit cell. In order to establish a basic relation that captures the underlying transient behaviour without undue complexity, we approximate the stress rate at each side of the interface (\(I_{12}^{(\pm )}\), \(I_{32}^{(\pm )}\)) in Fig. 4ii, with the average stress rate within the corresponding segment,
Considering (10) to (12) yields
where \({\dot{\sigma }}=E{\dot{\varepsilon }}\) has been utilised for each segment.
The micro strain rates describing the dynamic process can thus be approximated with the macro fields from (6), (8) and (13) as
Utilising (14) and referring to Fig. 4ii, the velocity at different locations within the unit cell is thus
The total kinetic energy of the unit cell, \({\widehat{\Psi }}_{KE}\), is next obtained naturally as,
which can be written in terms of macro kinematic fields (\({\dot{U}}\), \(\dot{{\widetilde{U}}}\), \({\dot{\varepsilon }}\)) by utilising (14) and (15).
Potential energy of unit cell
The quasi-static response of a composite medium is governed by the non-local interactions between the constituent materials at the micro scale, which propagates onto the macro scale to influence the overall behaviour. Within a unit cell, the deformation is such that the equilibrium condition, taking into account the short-range forces induced by the neighbouring unit cells, has to be satisfied. To adequately capture the non-local interactions, we consider the stress continuity requirement at an interface, where
For simplicity, we approximate the inter-facial strains in (17) with the average strain of the corresponding segment,
Substituting (18) into (17), we obtain
The micro strain fields describing the quasi-static response can thus be approximated with the macro fields from (6), (7) and (19) as
where \({\widetilde{\varepsilon }}\) denotes the gradient of the additional kinematic variable \({\widetilde{U}}\).
The total potential energy of the unit cell, \({\widehat{\Psi }}_{PE}\), is thus
which can be written in terms of macro kinematic fields (U, \({{\widetilde{U}}}\), \({\varepsilon }\), \({{\widetilde{\varepsilon }}}\), \({\nabla \varepsilon }\)) by utilising (20).
Macroscopic energy densities
We next proceed to Step (c) in Fig. 3, where energy statements are translated from micro to macro via the Hill–Mandel condition. In the following, U and \({\widetilde{U}}\) are understood to be the macro displacements respectively at a given time t, and their argument (x, t) is dropped. Moreover, the expressions are written in terms of the primary variables U and \({\widetilde{U}}\) for better clarity of presentation. At a macro point, the kinetic and potential energy densities, \(\psi _{KE}\) and \(\psi _{PE}\) in (22), are obtained by smearing \({{\widehat{\Psi }}}_{KE}\) and \({{\widehat{\Psi }}}_{PE}\) respectively over the unit cell.
where the coefficients \(C_{(1)}\)–\(C_{(8)}\) are obtained from (16) and (21), with their definitions provided in A.
Note that \(C_{(1)}\), \(C_{(3)}\), \(C_{(4)}\) are non-negative for all constituent properties and volume fractions, since \(Z_3 \, > \, Z_2\). In addition, a numerical minimization done using ‘NMinimize’ in Mathematica, subjected to constraints \(E_1>0\), \(E_2>0\), \(E_3>0\) and \(\rho _1>1\), \(\rho _2>1\), \(\rho _3>1\) (greater than air density), \(0 \le f \le 1\), \(0 \le g \le 1\) and \(1<Z_1/Z_2<\)1,000,000, \(1<Z_2/Z_3<\)1,000,000, showed that \(C_{(2)} \ge 0\). Prima facie, the non-quadratic coupling term associated with \(C_{(4)}\) in (22a) may suggest a destabilizing effect in a dynamic analysis. To such concern, recall that the terms in (22a) have manifested themselves naturally, via a consistent propagation of microscopic kinetic energy via (16), onto the macro level. Accordingly, the formulation is well-posed. It will also be shown later through the benchmark examples, that the homogenized model is dynamically stable—results which are unlikely to be achieved with a non positive definite energy potential.
Enriched homogenized model
We now arrive at the final procedure, Step (d) in Fig. 3, where a system of homogenized governing equations of motion is extracted via Hamilton’s Principle. Consider a periodic layered composite bar, which is much longer than a unit cell \((x_1 \le x \le x_2)\), in absence of body forces. The action functional corresponding to the macro domain over a time interval \((t_1 \le t \le t_2)\) is given by
where T and Q represent the conventional traction and higher-order traction respectively, whereas \({\widetilde{T}}\) denotes the traction conjugate to the additional kinematic variable.
Hamilton’s Principle states that the variation of the action functional must vanish. Substituting (22) into (23), the variation of the action functional gives the system of homogenized governing equations of motion as
where the homogenized stresses and tractions are defined as
and
Referring to the system of governing equations of motion in (24), it is easily observed that a micro-inertia effect associated with the acceleration of the stiff layer is captured via \(\ddot{{\widetilde{U}}}\) while the non-uniformity in response within a unit cell given a deformation mode, is in turn captured via the difference between the two displacement fields (\({{U}}-{{\widetilde{U}}}\)). Finally, the non-local interactions between neighbouring unit cells manifest themselves as a higher-order term in (25a). The system of equations of motion in (24) thus govern the competition and interactions between the different mechanisms. Note that the intrinsic parameters \(C_{(1)}\)–\(C_{(8)}\) are defined transparently in terms of the constituent properties, without any need for calibrations.
Numerical results and discussions
The practical applicability of the proposed enriched homogenized model is demonstrated by considering two metamaterials from literature. The first belongs to a class of locally resonant units, where stiff lead inclusions coated with silicon rubber are embedded within an epoxy matrix for sound wave attenuation [4, 5], while the second is a metaconcrete variant that consist of lead inclusions similar to the first, albeit with different metal composition, coated with natural rubber arranged in mortar mix against blast wave propagation [6,7,8].
In this study, a generalized Maxwell viscoelastic model is adopted to represent the compliant layer [37, 38]. It accounts for contributions from multiple relaxation strengths and times via the Prony series as
where \(E_{2i}^r\) and \(\kappa _i\) represent the relaxation strength i with corresponding relaxation time i, while n denotes the total number of terms in the series.
For simplicity, a single relaxation strength and time are assumed for Material 2. The approach is similar to that reported for bi- and tri-material composites [2, 39]. The time-dependent elastic modulus for the compliant layer is therefore
where \(E_2^\infty \), \(E_2^0\) and \(\kappa \) represent the long-term modulus, initial modulus and relaxation time respectively.
The adopted parameters and information with respect to the two metamaterials are summarised in Table 1. In addition, the eight coefficients underlying the macro energy densities via (22), when evaluated based on material properties (\(E_1\), \(E_2^0\), \(E_3\), \(\rho _1\), \(\rho _2\), \(\rho _3\)) and volume fractions (f, g, h), are all positive, as shown in Table 2. It will be shown later that neither dispersive characteristics obtained from the proposed model nor the predicted homogenized displacement responses show any indication of ill-posedness. Referring to the discussions on gradient elasticity theories [32], the responses have not grown unbounded without any external work done. In essence, the stability of the formulation will be demonstrated.
For the problem statement described later, we consider two aspects of the model performance. First, the dispersive characteristics recovered using the proposed model based on infinitely long relaxation time, i.e. un-relaxed elastic cases, are benchmarked against the reference dispersion relations obtained by the transfer matrix method over the first Brillouin zone. The latter is a widely used technique in literature for such applications and elaborated in B. Second, we validate the proposed model’s predictive capability in capturing the wave propagation process by comparing the homogenized displacement responses against reference solutions from DNS under various degrees of viscoelasticity within compliant layer, i.e. Material 2. The semi-analytical solutions with the proposed model are obtained numerically via a Laplace Transform operation, as detailed in C.
Problem statement
The problem statement is illustrated in Fig. 5i. We consider a periodic layered composite bar of length 100D, with underlying unit cells each of size D given in Table 1. At the external surface \(x=0\), a sinusoidal load P, as depicted in Fig. 5ii, is applied. The tractions Q and \({\widetilde{T}}\) are assumed to vanish at the external surfaces. For an unit out-of-plane cross-sectional area, the Neumann boundary conditions are
where the angular frequency \(\omega =2\pi /t_d\).
i Schematics of a periodic layered composite bar with underlying unit cell of size D, subjected to a sinusoidal load P at \(x=0\) . ii Sinusoidal load P with amplitude \(E_{eff}\) over two periods, \(2t_d\). iii Normalised non-dispersive displacement response predicted by a standard elastic effective medium
With a standard effective elastic medium, load P produces a Gaussian-like displacement response over two periods, as shown in Fig. 5iii. Note that the amplitude of P is thus set at \(E_{eff}\) to facilitate the normalisation of displacement response with respect to \(\zeta =2c/ \omega \), where homogenized sound speed \(c=\sqrt{E_{eff}/\rho _{eff}}\).
The governing equation of motion for a standard elastic effective medium is
with the effective density and modulus defined as
At this juncture, it is worth noting that the normalised response calculated based on a standard elastic effective medium in accordance to (30) would always be non-dispersive as given in Fig. 5iii. It will be demonstrated later that such performance is not adequate to represent the actual dispersive characteristics within metamaterials, and hence the need for an enriched homogenized model.
Noting that the maximum impedance contrast between the respective constituent materials within the two configurations differ (by one order) in Table 1, it is therefore interesting to understand how they perform against a broad range of loading frequencies. In the following, for the purpose of benchmark examples, a total of two frequencies \((F=1/t_d)\), which represent typical range of excitation pertaining to sound wave transmission and blast wave propagation respectively, are selected per metamaterial as given in Table 3. For better clarity of presentation, the wavelength ratios (\({{\bar{\lambda }}}_1\), \({{\bar{\lambda }}}_2\), \({{\bar{\lambda }}}_3\)), i.e. the ratio between the loading wavelength in each constituent material and the width of each constituent layer, are also summarised. This allows us to examine the predictive capability of the proposed model in capturing the underlying dispersion from low to no separation of scales, as well as the resulting attenuation and filtering effect considering various degrees of viscoelasticity within compliant layer. Three stress relaxation times ([A], [B], [C]) with increasing intensity of strength degradation, are assumed per frequency in Table 3. Note that [A] pertains to infinitely extended periods to recover un-relaxed (elastic) cases.
Dispersive characteristics—un-relaxed (elastic) cases [A]
For the periodic layered medium in Fig. 5i, its dispersion relation obtained via the transfer matrix method is given below. This provides the reference solution for the benchmarking of dispersive characteristics of the proposed enriched homogenized model, based on infinitely long relaxation time, i.e. un-relaxed elastic cases via [A] in Table 3.
where parameter \(\xi _i=E_i k \), \(k={\omega }/{c_i}\) as per standard definition for wave number (\(i=1\), 2, 3). Equivalently, \(d_1=fD\), \(d_2=gD\) and \(d_3=hD\).
The proposed enriched homogenized model smears out the underlying discreteness, and captures the transient response through the system of governing equations of motion in (24), the solutions of which are given by
where \(\beta \) and \(\gamma \) each denotes a complex coefficient.
Substituting (32) into (24), we have
The dispersion relation of the proposed model is then obtained by setting the determinant of the \(2 \times 2\) matrix in (33) to null. For the two metamaterials considered, the dispersive characteristics obtained from the proposed model via (33) are compared against the reference solutions provided by (31) in Fig. 6. It can be observed that all dispersion relations based on the proposed model match the reference solutions very well across the acoustical branches with only very slight deviations towards higher normalised wave number kD, as opposed to the optical branches. This is likely due to the truncation during decomposition of micro kinematic fields, which has limited the spatial order within the coupled governing equations in (24). A better match to optical branches may likely be achieved by having higher temporal order in the governing equation of motion, i.e. second time-derivative of acceleration [2, 40]. In the literature, many of such formulations are motivated from a top-down strategy, in which the length scale parameters are either calibrated by matching the group velocity profile against the first band gap of the exact dispersion relation or approximated (non-physically) in order to preserve numerical stability. In this manuscript, a higher order temporal expansion is not adopted in order to limit the order of the homogenized model. Nevertheless, the general shape of both dispersion relations correlates well with those reported for periodic layered media [1] and acoustic metamaterials represented by diatomic crystal lattices [26]. Most importantly, it will be shown later that the mismatch in optical branches does not overly reduce the predictive capability of the homogenized model for the problems considered here, which are dominated by lower frequency wave components.
Homogenized displacement response
As a crucial assessment on the predictive capability of our model, the displacement profiles obtained by the proposed model are benchmarked against reference DNS solutions. For Metamaterial 1, the DNS consists of 42,000 linear truss elements (420 elements per unit cell) whereas that for Metamaterial 2 comprises a total of 60,000 elements (600 elements per unit cell). Time integration is applied using Newmark’s constant acceleration method, with a fixed time step of \(1 \times 10^{-6}\) s. Due consideration has been done with regards to the selection of both mesh size and associated time-step to ensure a sufficient spatial resolution across the compliant layers, where most dynamical reactions are expected to occur. Convergence studies have been carried out to ensure the overall adequacy of both spatial and temporal discretization in the DNS. The displacement in the periodic layered composite bar at macro point \(x=20D\) is extracted for benchmarking purpose.
Un-relaxed (elastic) cases [A]
The predicted homogenized displacement responses for Metamaterial 1 and 2, assuming infinitely long relaxation time, i.e. un-relaxed elastic cases via [A] in Table 3, are plotted against results from DNS for the specific examples of F at 1000 and 10,000 \(\mathrm {Hz}\), in Figs. 7i and 8i respectively. The predicted profiles correlate reasonably well with all reference DNS solutions, in terms of both time of arrival and amplitude of the leading wave front, as well as the trailing oscillations.
We next carry out Discrete Fourier Transform on the predicted homogenized responses in Figs. 7i and 8i. The objective of such analyses is to decompose the time-dependent solutions into the individual Fourier components over a range of frequencies, as shown in Figs. 7ii and 8ii respectively.
Noting that the response of the proposed enriched model matches DNS well, Discrete Fourier Transform is only performed on the former for a meaningful comparison to that of a standard effective medium. Recall that the normalised response calculated based on a standard elastic effective medium would always be non-dispersive and hence is not able to capture the actual propagation accurately, unlike the proposed enriched homogenized model.
The sampling frequency adopted for Metamaterial 1 is 4000 \(\mathrm {Hz}\) whereas that for Metamaterial 2, is 40,000 \(\mathrm {Hz}\). A total of 512 data points are used per analysis. It can be observed that each metamaterial has a specific cut-off frequency, beyond which, no more wave form can pass through. This is evidenced when the transformed predictions are set against that of the standard elastic effective medium. Such filtering limit tallies expectedly around the end of the 1st pass band (or start of the 1st stop band) of respective dispersion relations in Fig. 6, i.e. Metamaterial 1 (145 \(\mathrm {Hz}\)) and Metamaterial 2 (1610 \(\mathrm {Hz}\)). We also note that the amplitudes of the transformed predictions decreases as the loading frequency transits from within the 1st pass band to the 2nd stop band.
Viscoelastic cases [B, C]
Finally, the predicted homogenized displacement responses for Metamaterial 1 and 2, with respect to viscoelastic cases [B] and [C] in Table 3, are plotted against results from DNS, in Figs. 9 and 10 respectively. The predicted profiles again match all reference DNS solutions. The overall trend is consistent. For a given stress relaxation time \(\kappa \), the normalised peak amplitude dips with increasing frequency F, resulting from wave attenuation due to local resonance effect, typical of such engineered unit cells. On the other hand, at a given frequency F, the normalised peak amplitude dips with decreasing stress relaxation time \(\kappa \), i.e. faster strength degradation, due to dissipative effect of viscoelasticity. In this regard, it is clear that a standard effective elastic medium, as shown in Fig. 5(iii), is no longer applicable.
Metamaterial 1—Homogenized displacement profiles at \(x=20D\), with respect to relaxation time [B] \((\kappa =0.256s)\) for loading frequency F at i 50 \(\mathrm {Hz}\), ii 1000 \(\mathrm {Hz}\), and with respect to [C] \((\kappa =0.0255s)\) for F at iii 50 \(\mathrm {Hz}\), iv 1000 \(\mathrm {Hz}\)
Metamaterial 2—Homogenized displacement profiles at \(x=20D\), with respect to relaxation time [B] \((\kappa =0.026s)\) for loading frequency F at i 500 \(\mathrm {Hz}\), ii 10,000 \(\mathrm {Hz}\), and with respect to [C] \((\kappa =0.0026s)\) for F at iii 500 \(\mathrm {Hz}\), iv 10,000 \(\mathrm {Hz}\)
Conclusion
This paper presents a bottom-up homogenization strategy, leading to an enriched model that captures the dispersive effect during viscoelastic plane wave propagation through periodic layered composites. The proposed framework naturally incorporates the underlying micro-inertia effect and non-local interactions between constituent materials. The micro-mechanisms propagate in a thermodynamically consistent manner, and manifest themselves as intrinsic parameters at the macro scale, as opposed to the conventional top-down approach, where energy functions are postulated a priori, and requiring the calibration of many length scale parameters. The proposed framework also departs from the commonly adopted approach of having a frequency-dependent effective mass or an equivalent mass-in-mass lattice sub-model, to represent band gap phenomena within locally resonantly metamaterials.
In our framework, the constituent materials within a unit cell are idealised as a series of springs with uniformly distributed mass. An additional kinematic field is introduced to characterise the displacement of the stiff layer, complemented by the characterisation of the average strains within the different segments of the unit cell. These (macro) kinematic fields thus provide critical information of the underlying deformation, which are not accounted for in a standard homogenization approach. The ensuing kinetic and potential energies of a unit cell are next translated from micro to macro following the Hill–Mandel condition. Finally, a system of homogenized governing equations of motions is extracted via Hamilton’s Principle, where a fourth-order enriched model with micro-inertia effect is recovered. The intrinsic parameters are defined transparently in terms of the microstructural properties and volume fractions, without the need for any calibrations.
In situations with at least a weak separation of scales, predictions with the proposed model match the reference solutions very well for benchmark examples involving two locally resonant metamaterials from literature, applications of which pertain to sound wave transmission and blast wave propagation respectively. Having a viscoelastic compliant layer has certainly helped to dissipate more energy during wave transmission. It is consistently shown that, the shorter the time interval over which strength degradation takes place, the greater the amount of wave attenuation occurs.
Availability of data and materials
Not applicable.
References
Brun M, Guenneau S, Movchan AB, Bigoni D. Dynamics of structural interfaces: filtering and focussing effects for elastic waves. J Mech Phys Solids. 2010;58:1212–24.
Hu R, Oskay C. Nonlocal homogenization model for wave dispersion and attentuation in elastic and viscoelastic periodic layered media. J Appl Mech. 2017;84:031003–103100312.
Auriault J-L, Boutin C. Long wavelength inner-resonance cut-off frequencies in elastic composite materials. Int J Solids Struct. 2012;49:3269–81.
Liu ZY, Zhang XX, Mao YW, Zhu YY, Yang ZY, Chan CT, Sheng P. Locally resonant sonic materials. Science. 2000;289:1734–6.
Sheng P, Zhang XX, Liu ZY, Chan CT. Locally resonant sonic materials. Physica B Condens Matter. 2003;338:201–5.
Mitchell SJ, Pandolfi A, Ortiz M. Metaconcrete: designed aggregates to enhance dynamic performance. J Mech Phys Solids. 2014;65:69–81.
Mitchell SJ, Pandolfi A, Ortiz M. Investigation of elastic wave transmission in a metaconcrete slab. Mech Mater. 2015;91:295–303.
Mitchell SJ, Pandolfi A, Ortiz M. Effect of brittle fracture in a metaconcrete slab under shock loading. J Eng Mech. 2016;142:104016010.
Kim EH, Yang JK, Hwang HY, Shul CW. Impact and blast mitigation using locally resonant woodpile metamaterials. Int J Impact Eng. 2017;101:24–31.
Nouh M, Aldraihem O, Baz A. Wave propagation in metamaterial plates with periodic local resonances. J Sound Vib. 2015;341:53–73.
Sharma B, Sun CT. Local resonance and bragg bandgaps in sandwich beams containing periodically inserted resonators. J Sound Vib. 2016;364:133–46.
Krushynska AO, Miniaci M, Bosia F, Pugno NM. Coupling local resonance with Bragg band gaps in single-phase mechanical metamaterials. Extreme Mech Lett. 2017;12:30–6.
Tan KT, Huang HH, Sun CT. Blast-wave impact mitigation using negative effective mass density concept of elastic metamaterials. Int J Impact Eng. 2014;64:20–9.
Gupta S, Pramanik A, Ahmed M, Verma AK. Love wave propagation in prestressed piezoelectric layered structure. Int J Appl Mech. 2016;08:1650045–1165004516.
Kettenbeil C, Ravichandran G. Experimental investigation of the dynamic behavior of metaconcrete. Int J Impact Eng. 2018;111:199–207.
Rupin M, Roux P. A multi-wave elastic metamaterial based on degenerate local resonances. J Acoust Soc Am. 2017;142:75–81.
Briccola D, Ortiz M, Pandolfi A. Experimental validation of metaconcrete blast mitigation properties. J Appl Mech. 2016;84:031001–10310016.
Ang LYL, Koh YK, Lee HP. Acoustic metamaterials: a potential for cabin noise control in automobiles and armored vehicles. Int J Appl Mech. 2016;08:1650072–1165007235.
Neff P, Ghiba I-D, Madeo A, Placidi L, Rosi G. A unifying perspective: the relaxed linear micromorphic continuum. Continuum Mech Thermodyn. 2014;26:639–81.
Ghiba I-D, Neff P, Madeo A, Placidi L, Rosi G. The relaxed linear micromorphic continuum: existence, uniqueness and continuous dependence in dynamics. Math Mech Solids. 2015;20:1171–97.
Madeo A, Neff P, Ghiba I-D, Placidi L, Rosi G. Wave propagation in relaxed micromorphic continua: modeling metamaterials with frequency band-gaps. Continuum Mech Thermodyn. 2015;27:551–70.
Madeo A, Barbagallo G, d’Agostino MV, Placidi L, Neff P. First evidence of non-locality in real band-gap metamaterials: determining parameters in the relaxed micromorphic model. Proc R Soc A. 2016;472:20160169.
Milton GW, Willis JR. On modifications of Newton’s second law and linear continuum elastodynamics. Proc Math Phys Eng Sci. 2007;463(2079):855–80.
Huang HH, Sun CT, Huang GL. On the negative effective mass density in acoustic metamaterials. Int J Eng Sci. 2009;47:610–7.
Huang HH, Sun CT. Continuum modeling of a composite material with internal resonators. Mech Mater. 2012;46:1–10.
Zhou YH, Wei PJ, Li YQ, Tang QH. Continuum model of acoustic metamaterials with diatomic crystal lattice. Mech Adv Mater Struct. 2017;24:1059–73.
Metrikine AV, Askes H. One-dimensional dynamically consistent gradient elasticity models derived from a discrete microstructure: part 1: generic formulation. Eur J Mech A Solids. 2002;21:555–72.
Askes H, Metrikine AV. One-dimensional dynamically consistent gradient elasticity models derived from a discrete microstructure: part 2: static and dynamic response. Eur J Mech A Solids. 2002;21:573–88.
Bennett T, Gitman IM, Askes H. Elasticity theories with higher-order gradients of inertia and stiffness for the modelling of wave dispersion in laminates. Int J Fract. 2007;148:185–93.
Bagni C, Gitman IM, Askes H. A micro-inertia gradient visco-elastic motivation for proportional damping. J Sound Vib. 2015;347:115–25.
De Domenico D, Askes H. A new multi-scale dispersive gradient elasticity model with micro-inertia: formulation and \(C^0\)-finite element implementation. Int J Numer Methods Eng. 2016;108:485–512.
Askes H, Aifantis EC. Gradient elasticity in statics and dynamics: an overview of formulations, length scale identification procedures, finite element implementations and new results. Int J Solids Struct. 2011;48:1962–90.
Tan SH, Poh LH. Homogenized gradient elasticity model for plane wave propagation in bilaminate composites. J Eng Mech. 2018;144:04018075.
Lewińska MA, Kouznetsova VG, van Dommelen JAW, Krushynska AO, Geers MGD. The attenuation performance of locally resonant acoustic metamaterials based on generalised viscoelastic modelling. Int J Solids Struct. 2017;126–127:163–74.
Kuo C-W, Steve Suh C. On the dispersion and attenuation of guided waves in tubular section with multi-layered viscoelastic coating—part I: axial wave propagation. Int J Appl Mech. 2017;09:1750001–1175000118.
Biswas R, Poh LH. A micromorphic computational homogenization framework for heterogeneous materials. J Mech Phys Solids. 2017;102:187–208.
Park SW, Schapery RA. Methods of interconversion between linear viscoelastic material functions. Part I: a numerical method based on Prony series. Int J Solids Struct. 1999;36:1653–75.
Sorvari J, Hämäläinen J. Time integration in linear viscoelasticity—a comparative study. Mech Time Depend Mater. 2010;14:307–28.
Hui T, Oskay C. Laplace-domain, high-order homogenization for transient dynamic response of viscoelastic composites. Int J Numer Methods Eng. 2015;103:937–57.
Wautier A, Guzina BB. On the second-order homogenization of wave motion in periodic media and the sound of a chessboard. J Mech Phys Solids. 2015;78:382–414.
Banerjee B. An introduction to metamaterials and waves in composites. Boca Raton: CRC Press; 2011.
Li YH, Zhou XL, Bian ZG, Xing YF, Song JZ. Bandgap structures of SH-wave in a one-dimensional phononic crystal with viscoelastic interfaces. Int J Appl Mech. 2017;09:1750102–1175010215.
Valkó PP, Abate J. Comparison of sequence accelerators for the Gaver method of numerical laplace transform inversion. Comput Math Appl. 2004;48:629–36.
Acknowledgements
Not applicable.
Funding
Not applicable.
Author information
Authors and Affiliations
Contributions
All authors contributed in development of the proposed enriched homogenized model. The derivations, numerical studies and the draft of the manuscript were performed by SHT, under the supervision of LHP. Both authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A: Summary of coefficients underlying macroscopic energy densities
The kinetic and potential energy densities, \(\psi _{KE}\) and \(\psi _{PE}\) in (22), are obtained by smearing \({{\widehat{\Psi }}}_{KE}\) and \({{\widehat{\Psi }}}_{PE}\) from (16) and (21) respectively, over the unit cell. The underlying coefficients \(C_{(1)}\)–\(C_{(8)}\) can be obtained as
in which acoustic impedance mismatch \(z_{12}=Z_1-Z_2\) and \( z_{23}=Z_2-Z_3\), while the modulus of a standard elastic effective medium \(E_{eff}=\displaystyle {\frac{E_1E_2E_3}{fE_2E_3+gE_1E_3+hE_1E_2}}\) .
Appendix B: Dispersion relation using transfer matrix method
The standard equation of motion that describes elastic wave propagation through a homogeneous constituent layer, Material n, reads
where the displacement field within the individual layer is denoted by \(u_n\), while the elastic modulus and density are \(E_n\) and \(\rho _n\) respectively.
The solution to (35) when expressed in the complex exponential form is
where \(\alpha \) denotes a complex coefficient, k the wave number and \(\omega \) the angular frequency.
By substituting (36) into (35), the equation of motion that accounts for elastodynamics at fixed frequency (hence dropping the argument t) can be obtained as
where \(c_n=\sqrt{E_n / \rho _n}\) is the sound speed of Material n. Note that such manipulation is often employed in the study of waves through composites as it facilitates the correlation between solutions at fixed frequencies to the individual Fourier components of the time-dependent solution [41].
The solutions to (37) can be written as
We next relate the quantities between both ends of an individual layer, where \(m_{pq}^n\) represents the transfer sub-matrix applied over a finite distance of \(d_n\), after utilising (38) and Euler’s formula \(e^{\pm ikd_n}=\cos (kd_n) \pm i\sin (kd_n)\),
where
in which parameter \(\xi _n=E_n k \) and \(k={\omega }/{c_n}\) as per standard definition for wave number.
Derivations of the transfer sub-matrix are provided below.
At this juncture, it is pertinent to recognise that the two eigenvalues of the uni-modular \(m_{pq}^n\) in (39) correspond to \(e^{\pm ikd_n}\) and are indeed related to \(\cos (kd_n)\) via trigonometrical identity
We next derive a complete transfer matrix that relates displacement and stress quantities between both ends of the unit cell given in Fig. 4ii. As the unit cell consists of three materials distributed into five constituent layers, with finite thickness of \(d_i\) attributed to each Material i with the corresponding elastic modulus and density as \(E_i\) and \(\rho _i\) respectively (\(i=1\), 2, 3), we can therefore multiply five transfer sub-matrices from (39) sequentially with the necessary arguments to obtain the complete transfer matrix as
This is followed by solving for the eigenvalues \(\Lambda \) of \(M_{yz}\). The resulting determinant of the \(2 \times 2\) matrix in (42) is set to null as
Similar to (41), we impose that the unit cell behaves as if it is a homogenized entity [1, 42], in order to recover the exact Bloch-Floquet dispersion relation (31) for a periodic infinite medium made up of such unit cells by considering
where size of the unit cell \(D=d_1+d_2+d_3\), while \(\Lambda _1\) and \(\Lambda _2\) denote the first and second eigenvalue of \(M_{yz}\) via (43) respectively.
Appendix C: Solution of homogenized response
The system of homogenized governing equations of motion is solved semi-analytically with the Laplace Transform. In general, the procedure consists of three main steps. First, the partial differential equations of motion (PDE) in (24) are converted into two ordinary differential equations (ODE) using Laplace Transform. This is followed by solving the system of ODE in the complex angular frequency (s) domain. The final step reverts this solution to the time (t) domain via a numerical Inverse Laplace Transform procedure.
The primary variable U and the additional kinematic variable \({\widetilde{U}}\) are functions of both space and time. Performing the Laplace Transform, we obtain
Hereafter, \(U_s\) and \({\widetilde{U}}_s\) are understood to be the macro displacement and additional kinematic fields in the s domain respectively, and the argument (x, s) is dropped. In view of (45), (24) can be converted into ODE as
where the added superscript represents Laplace transform operator \({{\mathscr {L}}}\) on the various coefficients underlying the macro energy densities.
Recall that these coefficients involve \(E_2(t)\), the linear viscoelastic modulus in the compliant layer which is a function of time. It is therefore necessary to transform them accordingly with respect to the s domain [37].
With reference to (28), the operational modulus \(E_2^{{\mathscr {L}}}(s)\) for the present model is thus
The solutions to (46) are given by the harmonic waves
where A and B each denotes a complex coefficient.
Substituting (48) into (46) respectively, the system of ODE is given by
In order to solve the expression, the determinant of the \(2 \times 2\) matrix in (49) must be set to null. The resulting characteristic definition is a polynomial of order 6 in k, and that only three (out of six) roots have strictly positive imaginary parts. Denoting these three roots as \(k_1\), \(k_2\) and \(k_3\) with the corresponding complex coefficients as \(A_1\), \(A_2\) and \(A_3\) for the primary variable U, as well as \(B_1\), \(B_2\) and \(B_3\) for the additional kinematic variable \({\widetilde{U}}\), the solutions to (46) are obtained as
Given that \(k_1 \, \ll \, k_2\) and \(k_1 \, \ll \, k_3\) (50), can be further condensed to only capture the dominant harmonic wave component as
Note that the approximation (51) does not affect the accuracy of predictions at all, as evident from the benchmark examples in this study.
At this juncture, there remain two unknowns \((A_1\) and \(B_1)\) to be determined. To proceed, the Laplace Transform is performed on the boundary conditions in (29) to give
where
This is followed by substituting (51) into (52) to solve for \(A_1\) and \(B_1\) at \(x=0\), which completes the definition of (51). The final step is to revert \(U_s\) to the time domain using a numerical Inverse Laplace Transform procedure. Here, we adopt the sequence of Gaver functionals in tandem with Wynn’s Rho acceleration scheme [43].
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Tan, S.H., Poh, L.H. Enriched homogenized model for viscoelastic plane wave propagation in periodic layered composites. Adv. Model. and Simul. in Eng. Sci. 7, 4 (2020). https://doi.org/10.1186/s40323-020-0143-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s40323-020-0143-x