A minimally-intrusive fully 3D separated plate formulation in computational structural mechanics

Abstract

Most of mechanical systems and complex structures exhibit plate and shell components. Therefore, 2D simulation, based on plate and shell theory, appears as an appealing choice in structural analysis as it allows reducing the computational complexity. Nevertheless, this 2D framework fails for capturing rich physics compromising the usual hypotheses considered when deriving standard plate and shell theories. To circumvent, or at least alleviate this issue, authors proposed in their former works an in-plane–out-of-plane separated representation able to capture rich 3D behaviors while keeping the computational complexity the one of 2D simulations. In the present paper we propose an efficient integration of fully 3D descriptions into existing plate software.

Introduction

We consider the linear elastostatic problem defined in the plate domain $\Omega = \Omega _{xy} \times \Omega _z$, with $\Omega _{xy} = [0,H_x] \times [0,H_y]$ and $\Omega _z = [0,H_z]$ in which the thickness (out-of-plane) dimension is much lower than the other ones, i.e. $H_z \ll H_x, H_y$.

The linear elastic behavior relating the Cauchy’s stress $\varvec{\sigma }$ and the strain $\varvec{\varepsilon }$ using Voigt notation reads

$$\begin{aligned} \varvec{\sigma } = {\mathbf {C}} \, \varvec{\varepsilon }, \end{aligned}$$

(1)

where ${\mathbf {C}}$ is the elasticity matrix. The relation between strain $\varvec{\varepsilon }$ and displacement ${\mathbf {u}}$ (with components ${\mathbf {u}}=(u,v,w)$) writes

$$\begin{aligned} \varvec{\varepsilon } = \nabla _s {\mathbf {u}} = {\mathbf {G}} {\mathbf {u}}, \end{aligned}$$

(2)

where ${\mathbf {G}} = \nabla _s \bullet = \frac{1}{2} (\nabla \bullet + \nabla ^T \bullet )$ is the symmetric gradient operator.

Considering an homogeneous and isotropic material the behavior writes

$$\begin{aligned} {\mathbf {C}} = \frac{E}{(1+\nu )(1-2\nu )} \begin{bmatrix} 1-\nu&\quad \nu&\quad \nu&\quad 0&\quad 0&\quad 0 \\ \nu&\quad 1-\nu&\quad \nu&\quad 0&\quad 0&\quad 0 \\ \nu&\quad \nu&\quad 1-\nu&\quad 0&\quad 0&\quad 0 \\ 0&\quad 0&\quad 0&\quad \frac{(1-2\nu )}{2}&\quad 0&\quad 0 \\ 0&\quad 0&\quad 0&\quad 0&\quad \frac{(1-2\nu )}{2}&\quad 0 \\ 0&\quad 0&\quad 0&\quad 0&\quad 0&\quad \frac{(1-2\nu )}{2} \end{bmatrix} . \end{aligned}$$

(3)

With ${\mathbf {g}}({\mathbf {x}})$ the body forces, the displacement field ${\mathbf {u}} ({\mathbf {x}})$ for ${\mathbf {x}} \in \Omega$ is described by the linear momentum balance equation

$$\begin{aligned} \nabla \cdot \varvec{\sigma } + {\mathbf {g}} = {\mathbf {0}}. \end{aligned}$$

(4)

The domain boundary $\partial \Omega$ is partitioned into Dirichlet, $\Gamma _D$, and Neumann, $\Gamma _N$, boundaries, where displacement ${\mathbf {u}}_g$ and tractions ${\mathbf {T}}$ are enforced respectively. In what follows and without loss of generality we assume ${\mathbf {T}}={\mathbf {0}}$

The problem weak form associated to the strong form (4) lies in looking for the displacement field ${\mathbf {u}}$ verifying the Dirichlet boundary conditions such that the weak form

$$\begin{aligned} \int \limits _{\Omega } \varvec{\varepsilon }({\mathbf {u}}^*) \cdot \left( {\mathbf {C}} \cdot \varvec{\varepsilon }({\mathbf {u}}) \right) \, d{\mathbf {x}} = \int \limits _{\Omega } {\mathbf {u}}^* \cdot {\mathbf {g}} \, d{\mathbf {x}} , \end{aligned}$$

(5)

fulfills for any test function ${\mathbf {u}}^*$, with the trial and test fields defined in appropriate functional spaces.

Plate theory

The Reissner–Mindlin theory is based on the following fundamental hypotheses [1]: (i) on the middle plane $(z=0)$ the in-plane displacements vanish, i.e. $u(x,y,z=0)=v(x,y,z=0)=0$ that implies that points located in the middle-plane only moves vertically; (ii) the plate thickness remains unchanged; (iii) the plane stress assumption remains valid, i.e. $\sigma _{zz}=0$ and (v) a straight line normal to the undeformed middle plane remains straight but not necessarily orthogonal to the middle plane after deformation.

From these assumptions the displacement field can be written as:

$$\begin{aligned} {\left\{ \begin{array}{ll} u(x,y,z) = -\,z \theta ^x(x,y)\\ v(x,y,z) = -\,z \theta ^y(x,y)\\ w(x,y,z) = w(x,y) \end{array}\right. } \end{aligned}$$

(6)

where w is the vertical displacement (deflection) of the points on the middle plane and the rotations $\theta _x$ and $\theta _y$ coincide with the angles followed by the normal vectors contained in the planes xz and yz respectively in their motions.

We define the generalized displacement vector $\hat{{\mathbf {u}}}$

$$\begin{aligned} \hat{{\mathbf {u}}} = [\theta ^x, \theta ^y, w]^T \end{aligned}$$

(7)

defined at any point on the middle plane.

Injecting plate theory assumptions into the 3D elastostatic problem weak form, Eq. (5) reduces to the following 2D formulation

$$\begin{aligned} \int \limits _{\Omega _{xy}} \varvec{{\hat{\varepsilon }}}(\hat{{\mathbf {u}}}^{{\mathbf {*}}}) \cdot \left( \hat{{\mathbf {C}}} \varvec{{\hat{\varepsilon }}}(\hat{{\mathbf {u}}}) \right) \, d{\mathbf {x}} = \int \limits _{\Omega _{xy}} \hat{{\mathbf {u}}}^{\mathbf {*}} \cdot \hat{{\mathbf {g}}} \, d{\mathbf {x}}, \end{aligned}$$

(8)

whose standard finite element discretization leads to

$$\begin{aligned} {\mathbf {K}}_{xy} {\mathbf {U}} = {\mathbf {B}}_{xy} \end{aligned}$$

(9)

where for notational simplicity the hat symbol (${\hat{\bullet }}$) is omitted. In the previous expression (9), ${\mathbf {K}}_{xy}$ is the stiffness matrix and ${\mathbf {U}}$ and ${\mathbf {B}}_{xy}$ are the vector of the generalized displacements and forces, the former containing nodal rotations and deflections and the last the dual quantities: the nodal moments and vertical nodal forces. The 3D displacement field can be then recovered by using the relations (6).

In many cases, the complexity of the solution makes impossible the introduction of pertinent hypotheses for reducing the dimensionality of the model from 3D to 2D. In that case a fully 3D descriptions seem compulsory, and the in-plane–out-of-plane separated representations become particularly suitable.

PGD-based in-plane–out-of-plane decomposition

The in-plane–out-of-plane separated representation was applied in our former works to efficiently solve 3D elastic problems in plate geometries [2,3,4]. The elastic problem was defined in a plate domain $\Omega = \Omega _{xy} \times \Omega _z$ with $(x,y)\in \Omega _{xy}$, $\Omega _{xy} \subset {\mathbb {R}}^2$ and $z \in \Omega _z$, $\Omega _z \subset {\mathbb {R}}$. The separated representation of the displacement field ${\mathbf {u}} =(u,v,w)$ consists in a finite sum decomposition on N terms, each one of them consisting in the product of two unknown functions, one depending on the in-plane coordinates (x, y) and one on the out-of-plane coordinate z, i.e.:

$$\begin{aligned} {\mathbf {u}} (x,y,z)=\left( \begin{array}{c} u(x,y,z)\\ v(x,y,z)\\ w(x,y,z) \end{array}\right) \approx \sum _{i=1}^{N}{\left( \begin{array}{c} u^{i}_{xy}(x,y) \cdot u^{i}_z(z)\\ v^{i}_{xy}(x,y) \cdot v^{i}_z(z)\\ w^{i}_{xy}(x,y) \cdot w^{i}_z(z) \end{array}\right) }. \end{aligned}$$

(10)

Expression (10) can be written in a more compact form by using the Hadamard (component-to-component) product:

$$\begin{aligned} {\mathbf {u}}(x,y,z) \approx \sum _{i=1}^{N} {\mathbf {U}}^i_{xy} (x,y) \circ {\mathbf {U}}^i_z(z). \end{aligned}$$

(11)

Enriched formulations

As reported in the previous section plate kinematics can be written as a single-term separated decomposition

$$\begin{aligned} {\left\{ \begin{array}{ll} u(x,y,z) = \theta ^x(x,y) f^x(z)\\ v(x,y,z) = \theta ^y(x,y) f^y(z)\\ w(x,y,z) = w(x,y) f^z(z) \end{array}\right. }, \end{aligned}$$

(12)

with $f^x(z)=-\,z$, $f^y(z)=-\,z$ and $f^z(z)=1$.

For the sake of generality we are considering generic functions $f^x(z)$, $f^y(z)$ and $f^z(z)$ assumed known, but than can be different to the ones related to the standard Reissner–Mindlin plate theory, and its associated 3D kinematics given by Eq. (12). Consequently $\theta ^x$, $\theta ^y$ and w do not represent rotations and deflection anymore.

The displacements gradient becomes

$$\begin{aligned} \nabla {\mathbf {u}} = \left( \begin{array}{cll} \frac{\partial u}{\partial x} \\ \frac{\partial u}{\partial y} \\ \frac{\partial u}{\partial z} \\ \frac{\partial v}{\partial x} \\ \frac{\partial v}{\partial y} \\ \frac{\partial v}{\partial z} \\ \frac{\partial w}{\partial x} \\ \frac{\partial w}{\partial y} \\ \frac{\partial w}{\partial z} \\ \end{array} \right) = \left( \begin{array}{clll} \frac{\partial \theta ^x}{\partial x} \\ \frac{\partial \theta ^x}{\partial y} \\ \theta ^x \\ \frac{\partial \theta ^y}{\partial x} \\ \frac{\partial \theta ^y}{\partial y} \\ \theta ^y \\ \frac{\partial w}{\partial x} \\ \frac{\partial w}{\partial x} \\ w \\ \end{array} \right) \circ \left( \begin{array}{cll} f^x \\ f^x \\ \frac{d f^x(z)}{dz} \\ f^y \\ f^y \\ \frac{d f^y(z)}{dz}\\ f^z \\ f^z \\ \frac{df^z}{\partial z} \\ \end{array} \right) , \end{aligned}$$

(13)

that allows defining the strain separated form, that taking into account its symmetry reads

$$\begin{aligned} \varvec{\varepsilon }= & {} \left( \begin{array}{cll} \frac{\partial u}{\partial x} \\ \frac{\partial v}{\partial y} \\ \frac{\partial w}{\partial z} \\ \frac{\partial u}{\partial y} + \frac{\partial v}{\partial x} \\ \frac{\partial u}{\partial z} + \frac{\partial w}{\partial x} \\ \frac{\partial v}{\partial z} + \frac{\partial w}{\partial y} \end{array} \right) = \left( \begin{array}{clll} \frac{\partial \theta ^x}{\partial x} \\ \frac{\partial \theta ^y}{\partial y} \\ w \\ \frac{\partial \theta ^x}{\partial y} \\ \theta ^x \\ \theta ^y \\ \end{array} \right) \circ \left( \begin{array}{cll} f^x \\ f^y \\ \frac{df^z}{dz} \\ f^x \\ \frac{df^x}{dz} \\ \frac{df^y}{dz} \end{array} \right) + \left( \begin{array}{cll} 0 \\ 0 \\ 0 \\ \frac{\partial \theta ^y}{\partial x} \\ \frac{\partial w}{\partial x} \\ \frac{\partial w}{\partial y} \\ \end{array} \right) \circ \left( \begin{array}{cll} 0 \\ 0 \\ 0 \\ f^y \\ f^z \\ f^z \end{array} \right) \end{aligned}$$

(14)

$$\begin{aligned}= & {} \varvec{\Theta }^1(x,y) \circ {\mathbf {F}}^1(z) + \varvec{\Theta }^2(x,y) \circ {\mathbf {F}}^2(z). \end{aligned}$$

(15)

In the case of a general material the Hooke tensor can also be written as

$$\begin{aligned} {\mathbf {C}} (x,y,z) = \sum _{i=1}^{M} {\mathbf {C}}^i_{xy}(x,y) \circ {\mathbf {C}}^i_z(z). \end{aligned}$$

(16)

For an homogenous material we have simply

$$\begin{aligned} {\mathbf {C}} = {\mathbf {C}}^i_{xy} \circ {\mathbf {C}}^i_z. \end{aligned}$$

(17)

where ${\mathbf {C}}_z$ is given by Eq. (3) and ${\mathbf {C}}_{xy}$ is a tensor whose all the entries are 1,

$$\begin{aligned} {\mathbf {C}}_{xy} = \begin{bmatrix} 1&\quad 1&\quad 1&\quad 1&\quad 1&\quad 1 \\ 1&\quad 1&\quad 1&\quad 1&\quad 1&\quad 1 \\ 1&\quad 1&\quad 1&\quad 1&\quad 1&\quad 1 \\ 1&\quad 1&\quad 1&\quad 1&\quad 1&\quad 1 \\ 1&\quad 1&\quad 1&\quad 1&\quad 1&\quad 1 \\ 1&\quad 1&\quad 1&\quad 1&\quad 1&\quad 1 \end{bmatrix} . \end{aligned}$$

(18)

Taking this into consideration the method that we are going to explain can be used both for homogenous and not homogenous materials. For the sake of simplicity we are going to present it in the case where in expression (16) only one term appears in the sum, but it can be easily extended to involve more terms. The virtual work principle, expressed using a matrix notation, involves the internal work

$$\begin{aligned} \varvec{\varepsilon }^{*T} \varvec{\sigma }&= \varvec{\varepsilon }^{*T} {\mathbf {C}} \varvec{\varepsilon } \nonumber \\&= \{ \varvec{\Theta }^{1*}(x,y) \circ {\mathbf {F}}^1(z) + \varvec{\Theta }^{2*}(x,y) \circ {\mathbf {F}}^2(z) \}^T \{ {\mathbf {C}}_{xy}(x,y) \circ {\mathbf {C}}_z(z)\} \nonumber \\&\{ \varvec{\Theta }^1(x,y) \circ {\mathbf {F}}^1(z) + \varvec{\Theta }^2(x,y) \circ {\mathbf {F}}^2(z) \} \nonumber \\&= \varvec{\Theta }^{1*T}(x,y) \{{\mathbf {C}}_{xy}(x,y) \circ \hat{{\mathbf {C}}}_z^{11}(z)\} \varvec{\Theta }^1(x,y) +\varvec{\Theta }^{1*T}(x,y) \{{\mathbf {C}}_{xy}(x,y) \circ \hat{{\mathbf {C}}}_z^{12}(z)\} \nonumber \\&\varvec{\Theta }^2(x,y) + \varvec{\Theta }^{2*T}(x,y) \{{\mathbf {C}}_{xy}(x,y) \circ \hat{{\mathbf {C}}}_z^{21}(z)\} \varvec{\Theta }^1(x,y) + \varvec{\Theta }^{2*T}(x,y) \nonumber \\&\{{\mathbf {C}}_{xy}(x,y) \circ \hat{{\mathbf {C}}}_z^{22}(z)\} \varvec{\Theta }^2(x,y). \end{aligned}$$

(19)

In the previous expression matrices $\hat{{\mathbf {C}}}_z^{ij}(z)$ results

$$ \begin{aligned} \hat{{\mathbf {C}}}^{ij}_{z_{kl}}(z) = {\mathbf {C}}_{z_{kl}}(z) {\mathbf {F}}^i_k(z) {\mathbf {F}}^j_l(z), \ \quad i,j \in [1,2] \ \& \ k,l \in [1, \cdots , 6]. \end{aligned}$$

(20)

Now, the virtual work integral reads

$$\begin{aligned}&\int \limits _{\Omega _{xy} \times \Omega _z} \sum \limits _{i=1}^2 \sum \limits _{j=1}^2 \varvec{\Theta }^{i*T}(x,y) \{{\mathbf {C}}_{xy}(x,y) \circ \hat{{\mathbf {C}}}_z^{ij}(z) \} \varvec{\Theta }^j(x,y) \ dz \ dx \ dy\nonumber \\&\quad = \int \limits _{\Omega _{xy}} \sum \limits _{i=1}^2 \sum \limits _{j=1}^2 \varvec{\Theta }^{i*T}(x,y) {\mathbf {D}}^{ij}(x,y) \varvec{\Theta }^j(x,y) \ dx \ dy, \end{aligned}$$

(21)

where

$$\begin{aligned} {\mathbf {D}}^{ij}(x,y) = {\mathbf {C}}_{xy}(x,y) \circ \int _{\Omega _z} \hat{{\mathbf {C}}}_z^{ij}(z) \ dz . \end{aligned}$$

(22)

Now, if we assume an approximation based on a piecewise linear interpolation on a triangular finite element, related to an in-plane mesh of $\Omega _{xy}= \cup _{e=1}^{\texttt {E}} \Omega _{xy}^e$, with the shape functions defined by $N^e_i(x,y), \ i=1,2,3; \ e =1, \ldots , {\texttt {E}}$; it results

$$\begin{aligned} {\left\{ \begin{array}{ll} \theta ^{x,e}(x,y) = N^e_1(x,y) \theta ^{x,e}_1 + N_2^e(x,y) \theta ^{x,e}_2 + N_3^e(x,y) \theta ^{x,e}_3 \\ \theta ^{y,e}(x,y) = N^e_1(x,y) \theta ^{y,e}_1 + N_2^e(x,y) \theta ^{y,e}_2 + N_3^e(x,y) \theta ^{y,e}_3 \\ w^e(x,y) = N_1^e(x,y) w_1^e + N_2^e(x,y) w_2^e + N_3^e(x,y) w_3^e \\ \end{array}\right. } \end{aligned}$$

(23)

Using that approximation we can express vectors $\varvec{\Theta }^i(x,y)$ in each element $\Omega ^e$ from the generalized nodal displacements

$$\begin{aligned} {\mathbf {U}}^{eT}= (\theta ^{x,e}_1, \theta ^{y,e}_1,w^e_1,\theta ^{x,e}_2, \theta ^{y,e}_2,w^e_2, \theta ^{x,e}_3, \theta ^{y,e}_3,w^e_3), \end{aligned}$$

(24)

from

$$\begin{aligned} \varvec{\Theta }^i((x,y) \in \Omega _{xy}^e) = {\mathbf {B}}^{i,e}(x,y) {\mathbf {U}}^e, \end{aligned}$$

(25)

where ${\mathbf {B}}^{i,e}(x,y)$ contains the shape functions and theirs derivatives, according to the expressions involved in the components of $\varvec{\Theta }^i(x,y), \ i=1,2$.

Thus, integral (21) reads

$$\begin{aligned}&\sum \limits _{e=1}^{\texttt {E}} {\mathbf {U}}^{e*T} \left\{ \int _{\Omega _{xy}^e} \sum \limits _{i=1}^2 \sum \limits _{j=1}^2 {\mathbf {B}}^{i,eT}(x,y) {\mathbf {D}}^{ij}(x,y) {\mathbf {B}}^{j,e}(x,y) \ dx \ dy \right\} {\mathbf {U}}^e \nonumber \\&\quad = \sum \limits _{e=1}^{\texttt {E}} {\mathbf {U}}^{e*T} {\mathbf {K}}_{xy}^e {\mathbf {U}}^e = {\mathbf {U}}^{*T} {\mathbf {K}}_{xy} {\mathbf {U}}. \end{aligned}$$

(26)

Now, if we consider the virtual work of the body forces ${\mathbf {g}}({\mathbf {x}})$, it involves

$$\begin{aligned} {\mathbf {u}}^{*T} {\mathbf {g}}({\mathbf {x}}), \end{aligned}$$

(27)

where without loss of generality we assume

$$\begin{aligned} {\mathbf {u}}(x,y,z) = {\mathbf {V}} \circ {\mathbf {W}}, \end{aligned}$$

(28)

with ${\mathbf {V}}^T =(\theta ^x, \theta ^y , w)$ and ${\mathbf {W}}^T = (f^x(z),f^y(z),f^z(z))$, and the single-mode decomposition of the body forces given by

$$\begin{aligned} {\mathbf {g}}(x,y,z) = {\mathbf {G}} \circ {\mathbf {H}}, \end{aligned}$$

(29)

with ${\mathbf {G}}^T =(M^x(x,y), M^y(x,y), T(x,y))$ and ${\mathbf {H}}^T = (h^x(z),h^y(z),h^z(z))$. The fact of considering a single mode in the decomposition of the body force is not restrictive as discussed later.

The virtual work (27) can be expressed as

$$\begin{aligned} {\mathbf {u}}^{*T} {\mathbf {g}}({\mathbf {x}}) = {\mathbf {V}}^{*T}(x,y) \hat{{\mathbf {J}}}(z) {\mathbf {G}}(x,y), \end{aligned}$$

(30)

where matrix $\hat{{\mathbf {J}}}$ reads

$$\begin{aligned} \hat{{\mathbf {J}}}_{kl}(z) = {\mathbf {I}}_{kl} {\mathbf {W}}_k(z) {\mathbf {H}}_l(z), \end{aligned}$$

(31)

with ${\mathbf {I}}$ the identity matrix.

Now, the integral results

$$\begin{aligned} \int \limits _{\Omega _{xy} \times \Omega _z} {\mathbf {u}}^{*T} {\mathbf {g}}({\mathbf {x}}) \ dz \ dx \ dy = \int \limits _{\Omega _{xy}} {\mathbf {V}}^{*T}(x,y) {\mathbf {J}} {\mathbf {G}}(x,y) \ dx \ dy, \end{aligned}$$

(32)

with

$$\begin{aligned} {\mathbf {J}} = \int \limits _{\Omega _z} \hat{{\mathbf {J}}}(z) \ dz, \end{aligned}$$

(33)

Integrating in the mesh $\Omega _{xy}=\cup _{e=1}^{\texttt {E}} \Omega _{xy}^e$,

$$\begin{aligned} \int \limits _{\Omega _{xy}} {\mathbf {V}}^{*T}(x,y) {\mathbf {J}} {\mathbf {G}}(x,y) \ dx \ dy = \sum \limits _{e=1}^{\texttt {E}} \int \limits _{\Omega _{xy}^e} {\mathbf {V}}^{e *T}(x,y) {\mathbf {J}} {\mathbf {G}}^e(x,y) \ dx \ dy, \end{aligned}$$

(34)

where ${\mathbf {V}}^{e}(x,y)$ and ${\mathbf {G}}^e(x,y)$ are approximated respectively from

$$\begin{aligned} {\mathbf {V}}^{e}(x,y) = {\mathbf {N}} (x,y) {\mathbf {U}}^e, \end{aligned}$$

(35)

and

$$\begin{aligned} {\mathbf {G}}^{e}(x,y) = {\mathbf {N}} (x,y) {\mathbf {R}}^e, \end{aligned}$$

(36)

with ${\mathbf {R}}^e$ containing the nodal values of ${\mathbf {G}}(x,y)$ and ${\mathbf {N}} (x,y) = [{\mathbf {N}}_1(x,y) \ {\mathbf {N}}_2(x,y) \ {\mathbf {N}}_3(x,y)]$, and

$$\begin{aligned} {\mathbf {N}}_i = \left( \begin{array}{ccc} N_i^e(x,y) &{} \quad 0 &{} \quad 0 \\ 0 &{} \quad N_i^e(x,y) &{} \quad 0 \\ 0 &{} \quad 0 &{} \quad N_i^e(x,y) \\ \end{array} \right) . \end{aligned}$$

(37)

Thus, it results

$$\begin{aligned}&\sum \limits _{e=1}^{\texttt {E}} \int \limits _{\Omega _{xy}^e} {\mathbf {V}}^{e *T}(x,y) {\mathbf {J}} {\mathbf {G}}^e(x,y) \ dx \ dy = \sum \limits _{e=1}^{\texttt {E}} {\mathbf {U}}^{e *T} \left\{ \int \limits _{\Omega _{xy}^e} {\mathbf {N}}^T {\mathbf {J}} {\mathbf {N}} \ dx \ dy \right\} {\mathbf {R}}^e \nonumber \\&\quad = \sum \limits _{e=1}^{\texttt {E}} {\mathbf {U}}^{e *T} {\mathbf {A}}_{xy}^e {\mathbf {R}}^e = \sum \limits _{e=1}^{\texttt {E}} {\mathbf {U}}^{e *T} {\mathbf {B}}_{xy}^e = {\mathbf {U}}^{*T} {\mathbf {B}}_{xy}, \end{aligned}$$

(38)

from which, the principle of virtual works reads

$$\begin{aligned} {\mathbf {U}}^{*T} {\mathbf {K}}_{xy} {\mathbf {U}} = {\mathbf {U}}^{*T} {\mathbf {B}}_{xy}. \end{aligned}$$

(39)

Remark 1

In general the displacement decomposition within the PGD rationale involves more than a single mode, however, within the updating process, when calculating the n mode, the $n-1$ already computed move to the right hand member, acting as generalized body force.

Remark 2

Thus, the in-plane functions determining the kinematics can be obtained from a standard plate theory software by using the elementary rigidity and forces given respectively by ${\mathbf {K}}_{xy}^e$ and ${\mathbf {B}}_{xy}^e$ considered in expression (26) and (38).

Remark 3

If traction ${\mathbf {T}} \ne {\mathbf {0}}$ the same procedure can be applied to treat the corresponding terms.

Calculation of the out-of plane functions

The expression of solution obtained in the previous section is given by

$$\begin{aligned} {\mathbf {u}} (x,y,z)=\left( \begin{array}{c} u(x,y,z)\\ v(x,y,z)\\ w(x,y,z) \end{array}\right) = {\left( \begin{array}{c} \theta ^{x}(x,y) f^x(z)\\ \theta ^{y}(x,y) f^y(z)\\ w(x,y) f^z(z) \end{array}\right) } = {\mathbf {V}} (x,y) \circ {\mathbf {W}}(z), \end{aligned}$$

(40)

where

$$\begin{aligned} {\mathbf {V}} (x,y) = {\left( \begin{array}{c} \theta ^{x}(x,y)\\ \theta ^{y}(x,y)\\ w(x,y) \end{array}\right) } \end{aligned}$$

(41)

and

$$\begin{aligned} {\mathbf {W}}(z) = {\left( \begin{array}{c} f^x(z)\\ f^y (z)\\ f^z(z) \end{array}\right) }. \end{aligned}$$

(42)

Now, we proceed to updated the out-of-plane functions involved in ${\mathbf {W}}(z)$ from the just calculated in-plane functions ${\mathbf {V}}(x,y)$ by considering again the principle of virtual work

$$\begin{aligned} \int \limits _{\Omega _{xy} \times \Omega _{z}} \varvec{\varepsilon }(\mathbf {u}^*) \cdot \left( \mathbf {C} \cdot \varvec{\varepsilon }(\mathbf {u}\right) \, d\mathbf {x} = \int \limits _{\Omega _{xy} \times \Omega _{z}} \mathbf {u}^* \cdot {\mathbf {f}} \, d\mathbf {x} \end{aligned}$$

(43)

where now in Eq. (40) the in-plane functions are assumed known and we look for the ones involved in the out-of-plane contribution ${\mathbf {W}}(z)$. Thus, the previous integral form can be integrated on $\Omega _{xy}$, and then Eq. (43) reduced to a one dimensional problem in $\Omega _z$ involving as unknown functions $f^x(z)$, $f^y(z)$ and $f^z(z)$.

The same rationale that was previously addressed when performing the in-plane calculations is considered again but now with the test functions given by

$$\begin{aligned} \varvec{\varepsilon }^*= \varvec{\Theta }^1(x,y) \circ {\mathbf {F}}^{1 *}(z) + \varvec{\Theta }^2(x,y) \circ {\mathbf {F}}^{2 *}(z), \end{aligned}$$

(44)

and

$$\begin{aligned} \mathbf {u}^*(x,y,z) = {\mathbf {V}}(x,y) \circ {\mathbf {W}}^*(z). \end{aligned}$$

(45)

Now, from the updated out-of-plane functions in ${\mathbf {W}}(z)$, the in-plane functions in ${\mathbf {V}}(x,y)$ are again updated and the procedure repeats until reaching the convergence (fixed point). The procedure for computing the out-of-plane components in this minimally-intrusive way is detailed in Appendix A.

Numerical results

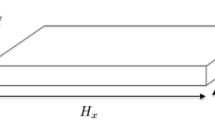
The problem taken into consideration is depicted in Fig. 1. The geometrical and mechanical properties of the plate domain $\Omega = [0,H_x] \times [0,H_y] \times [0,H_z]$ are defined in Table 1 On the right boundary face of the domain (the blue zone in Fig. 1) a vertical traction is enforced, ${\mathbf {T}} = (0,0,8\cdot 10^9) {\text {N}}/{\text {m}}^2$ and on the opposite face homogeneous Dirichlet boundary conditions are imposed. No volumetric body forces are considered. As in the considered domain the thickness (out-of-plane) dimension is not much lower than the other ones (in-plane dimensions), the linear variation of the displacement field along the thickness described by (2) is not more true as we can notice in Fig. 2 that compares the plate solution from the fully 3D solution assumed as reference. However using the just proposed minimally-intrusive fully 3D separated plate formulation we can notice how the solution is improved. Figure 3 shows the error of the solution respect to the 3D FEM solution, computed as

$$\begin{aligned} \xi \left( {\mathbf {u}}\right) = \dfrac{\left( \int _{\Omega } \left( {\mathbf {u}} - {\mathbf {u}}_{FEM} \right) ^2 d\,\mathbf {x}\right) ^{\frac{1}{2}}}{\left( \int _{\Omega } \left( {\mathbf {u}}_{FEM} \right) ^2 d\,\mathbf {x}\right) ^{\frac{1}{2}}}, \end{aligned}$$

(46)

as a function of the number of modes. The error of the plate theory solution results $\xi ({\mathbf {u}} _{plate}) = 0.0633$.

Fig. 1

The problem taken into consideration

Table 1 Model parameters

Fig. 2

Displacement field using: plate theory (a), minimally-intrusive fully 3D separated plate formulation (b), 3D FEM (c)

Fig. 3

Error of the enriched solution respect to the 3D solution for different number of modes

Fig. 4

Displacement field using: plate theory (a), minimally-intrusive fully 3D separated plate formulation (b), 3D FEM (c)

Fig. 5

Out-of-plane stress tensor components around the hole using the minimally-intrusive fully 3D separated plate formulation

Fig. 6

Out-of-plane stress tensor components in the $z = 65$ mm plane using the minimally-intrusive fully 3D separated plate formulation

We consider now the same problem as in the previous example but this time we suppose that there is an hole in the domain. As in the previous example, in Fig. 4 it is depicted the solution computed using the different techniques. Moreover in Figs. 5, 6 and 7 different perspectives of the out-of-plane stress tensor components are depicted. Let’s note how the proposed method is able to take into consideration the $\sigma _{zz}$ components, which is ignored in plate theory, and to obtain the parabolic evolution around the thickness for the $\sigma _{xz}$ and $\sigma _{yz}$ typical of a 3D solution (Fig. 7).

Fig. 7

Out-of-plane stress tensor components around the hole for $x = 146$ mm and $y = 97$ mm using the minimally-intrusive fully 3D separated plate formulation

In Figs. 8, 9 and 10 the same quantities are computed using a 3D finite element method, proving the good accuracy of the proposed method.

Fig. 8

Out-of-plane stress tensor components around the hole using 3D FEM

Fig. 9

Out-of-plane stress tensor components in the $z = 65$ mm plane using 3D FEM

Fig. 10

Out-of-plane stress tensor components around the hole for $x = 146$ mm and $y = 97$ mm using 3D FEM

Again, in Fig. 11 shows the error of the solution respect to the 3D FEM solution as a function of the number of modes. The error of the plate theory solution being $\xi ({\mathbf {u}} _{plate}) = 0.0638$.

Fig. 11

Error of the enriched solution respect to the 3D solution for different number of modes

Extension of the method to elasto-plastic dynamics

In this section we extend the method to dynamics problem in which plastic behavior can occur. With ${\mathbf {g}}({\mathbf {x}},t)$ the body forces, the displacement field evolution ${\mathbf {u}} (\mathbf {x},t)$ in the domain $\Omega$ and time interval $t \in I = (0,T]$ is described by the linear momentum balance equation

$$\begin{aligned} \rho \ddot{\mathbf {u}} (\mathbf {x},t) = \nabla \cdot \varvec{\sigma } + {\mathbf {g}}, \end{aligned}$$

(47)

where $\rho$ is the density (${\text{ kg }}/{\text {m}}^3$).

The boundary $\partial \Omega$ is decomposed according to $\partial \Omega = \Gamma _D \cup \Gamma _N$ where displacement and tractions ${\mathbf {T}} (t)$ are prescribed.

The behavior relating the Cauchy’s stress $\varvec{\sigma }$ and the elastic strain $\varvec{\varepsilon }^e$ reads [5]

$$\begin{aligned} \varvec{\sigma } = {\mathbf {C}} \varvec{\varepsilon }^e = {\mathbf {C}} (\varvec{\varepsilon } - \varvec{\varepsilon }^p), \end{aligned}$$

(48)

where $\mathbf {C}$ is the Hooke tensor, $\varvec{\varepsilon }$ is total strain and $\varvec{\varepsilon }^p$ is the plastic strain.

The problem weak form associated with the strong form (47) results in looking for the displacement field $\mathbf {u}$ verifying the initial and Dirichlet boundary conditions, and fulfilling

$$\begin{aligned} \rho \int \limits _{\Omega } \mathbf {u}^* \cdot \ddot{\mathbf {u}} \, d\mathbf {x} + \int \limits _{\Omega } \varvec{\varepsilon }(\mathbf {u}^*) \cdot \left( \mathbf {C} \, \left( \varvec{\varepsilon }(\mathbf {u}) - \varvec{\varepsilon }^p(\mathbf {u})\right) \right) \, d\mathbf {x} = \int \limits _{\Omega } \mathbf {u}^* \cdot {\mathbf {g}} \, d\mathbf {x} + \int \limits _{\Gamma _N} \mathbf {u}^* \cdot {\mathbf {T}}(t) \, d\mathbf {x}\nonumber \\ \end{aligned}$$

(49)

for any test function ${\mathbf {u}}^*$ in an appropriate functional space.

We consider at time $t_{j+1}$ the standard explicit time integration [6] (widely considered in commercial codes) given by

$$\begin{aligned}&\rho \int \limits _{\Omega } \mathbf {u^*} \cdot \dfrac{\mathbf {u}^{j+1} - 2\mathbf {u}^{j} + \mathbf {u}^{j-1}}{\Delta t^2} d\mathbf {x} + \int \limits _{\Omega } \varvec{\varepsilon }(\mathbf {u^*}) \cdot \left( \mathbf {C} \, \left( \varvec{\varepsilon }(\mathbf {u}^{j}) - \varvec{\varepsilon }^p(\mathbf {u}^{j}) \right) \right) d\mathbf {x} \nonumber \\&\quad =\int \limits _{\Omega } \mathbf {u}^* \cdot {\mathbf {g}} ^j \, d\mathbf {x} + \int \limits _{\Gamma _N}\mathbf {u^*} \cdot \mathbf {T}^{j} d\mathbf {x}, \end{aligned}$$

(50)

or, by putting all the explicit terms at the right hand side,

$$\begin{aligned}&\rho \int \limits _{\Omega } \mathbf {u^*} \cdot \mathbf {u}^{j+1} d\mathbf {x} = \rho \int \limits _{\Omega } \mathbf {u^*} \cdot \left( 2\mathbf {u}^{j} - \mathbf {u}^{j-1} \right) d\mathbf {x} \nonumber \\&\quad -\Delta t^2 \left( \int \limits _{\Omega } \varvec{\varepsilon }(\mathbf {u^*}) \cdot \left( \mathbf {C} \, \left( \varvec{\varepsilon }(\mathbf {u}^{j}) - \varvec{\varepsilon }^p(\mathbf {u}^{j}) \right) \right) d\mathbf {x} + \int \limits _{\Omega } \mathbf {u}^* \cdot {\mathbf {g}} ^j \, d\mathbf {x} + \int \limits _{\Gamma _N}\mathbf {u^*} \cdot \mathbf {T}^{j} d\mathbf {x} \right) .\qquad \end{aligned}$$

(51)

Recalling (28) we can write

$$\begin{aligned} {\mathbf {u}}^{j+1}(x,y,z) = {\mathbf {V}}^{j+1} \circ {\mathbf {W}}^{j+1}. \end{aligned}$$

(52)

Supposing the out-of-plane functions known, the left hand side term in (51) can be expressed as

$$\begin{aligned} {\mathbf {u}}^{*T} \mathbf {u}^{j+1}({\mathbf {x}}) = {\mathbf {V}}^{j+1,*T} (x,y) \hat{{\mathbf {J}}}^{j+1}(z) {\mathbf {V}}^{j+1}(x,y), \end{aligned}$$

(53)

where matrix $\hat{{\mathbf {J}}}^{j+1}$ reads

$$\begin{aligned} \hat{{\mathbf {J}}}_{kl}^{j+1}(z) = {\mathbf {I}}_{kl} {\mathbf {W}}_k^{j+1}(z) {\mathbf {W}}_l^{j+1}(z), \end{aligned}$$

(54)

with ${\mathbf {I}}$ the identity matrix.

Now, the integral results

$$\begin{aligned} \rho \int \limits _{\Omega } \mathbf {u^*} \cdot \mathbf {u}^{j+1} \ dz \ dx \ dy = \int \limits _{\Omega _{xy}} {\mathbf {V}}^{j+1,*T} (x,y) {\mathbf {J}}^{j+1} {\mathbf {V}}^{j+1}(x,y) \ dx \ dy, \end{aligned}$$

(55)

with

$$\begin{aligned} {\mathbf {J}}^{j+1} = \int \limits _{\Omega _z} \hat{{\mathbf {J}}}^{j+1}(z) \ dz, \end{aligned}$$

(56)

Integrating in the mesh $\Omega _{xy}=\cup _{e=1}^{\texttt {E}} \Omega _{xy}^e$,

$$\begin{aligned} \int \limits _{\Omega _{xy}} {\mathbf {V}}^{j+1,*T} {\mathbf {J}}^{j+1} {\mathbf {V}}^{j+1} \ dx \ dy = \sum \limits _{e=1}^{\texttt {E}} \int \limits _{\Omega _{xy}^e} {\mathbf {V}}^{j+1,e *T} {\mathbf {J}}^{j+1} {\mathbf {V}}^{j+1,e} \ dx \ dy, \end{aligned}$$

(57)

where ${\mathbf {V}}^{j+1,e} (x,y)$ is approximated from

$$\begin{aligned} {\mathbf {V}}^{j+1,e} (x,y) = {\mathbf {N}} (x,y) {\mathbf {U}}^{j+1,e}, \end{aligned}$$

(58)

with ${\mathbf {N}} (x,y) = [{\mathbf {N}}_1(x,y) \ {\mathbf {N}}_2(x,y) \ {\mathbf {N}}_3(x,y)]$, and

$$\begin{aligned} {\mathbf {N}}_i = \left( \begin{array}{ccc} N_i^e(x,y) &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad N_i^e(x,y) &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad N_i^e(x,y) \\ \end{array} \right) . \end{aligned}$$

(59)

Thus, it results

$$\begin{aligned}&\sum \limits _{e=1}^{\texttt {E}} \int \limits _{\Omega _{xy}^e} {\mathbf {V}}^{j+1,e *T} {\mathbf {J}}^{j+1} {\mathbf {V}}^{j+1,e} \ dx \ dy = \sum \limits _{e=1}^{\texttt {E}} {\mathbf {U}}^{j+1,e *T} \left\{ \int \limits _{\Omega _{xy}^e} {\mathbf {N}}^T {\mathbf {J}}^{j+1} {\mathbf {N}} \ dx \ dy \right\} {\mathbf {U}}^{j+1,e} \nonumber \\&\quad = \sum \limits _{e=1}^{\texttt {E}} {\mathbf {U}}^{j+1,e *T} {\mathbf M}_{xy}^{j+1,e} {\mathbf {U}}^{j+1,e} = {\mathbf {U}}^{j+1,*T} {\mathbf {M}}_{xy}^{j+1}{\mathbf {U}}^{j+1}. \end{aligned}$$

(60)

The different terms at the right hand side of (51) can be treated in a similar way, as already explained for the static case, so that at each time step j the virtual work principle reads

$$\begin{aligned} {\mathbf {U}}^{j+1,*T} {\mathbf {M}}_{xy}^{j+1} {\mathbf {U}}^{j+1} = {\mathbf {U}}^{j+1,*T} {\mathbf {B}}_{xy}^{j}. \end{aligned}$$

(61)

Remark 4

As for the static case, the in-plane functions determining the kinematics can be obtained from a standard plate theory software by using the elementary mass and forces given respectively by ${\mathbf {M}}_{xy}^{j+1,e}$ and ${\mathbf {B}}_{xy}^{j,e}$.

Remark 5

Again the out-of-plane functions can be obtained in a similar manner as already explained in the static case.

Fig. 12

The elasto-plastic dynamical problem taken into consideration

Table 2 Model parameters

Fig. 13

Horizontal loading for the elasto-plastic dynamical problem

Fig. 14

Displacement field using the three methods for $t = 0.1$ ms and $t = 0.5$ ms

For evaluating the performances of the method we consider the problem defined in Fig. 12. The geometrical and mechanical properties of the plate domain are defined in Table 2. On the right boundary face of the domain (the blue zone in Fig. 12) an horizontal traction is enforced, ${\mathbf {T}} = (2.7\cdot 10^8,0,0) N/m^2$ and on the opposite face homogeneous Dirichlet boundary conditions are imposed. No volumetric body forces are considered. For the sake of simplicity, we use the Von Mises criterion [7], assuming a Krupkowski isotropic hardening [8] given by the formula:

$$\begin{aligned} {\bar{\sigma }} = K \bigl ( {\bar{\varepsilon }} _0 + {\bar{\varepsilon }}_p \bigr )^p \end{aligned}$$

(62)

where ${\bar{\varepsilon }} _0 = 0.008$ is the initial equivalent plastic strain, ${\bar{\varepsilon }}_p$ is the equivalent plastic strain, $K = 0.4619$ GPa is a strength coefficient and $p = 0.1$ is the strain hardening exponent [9]. The problem is solved in the time interval [0, 50] ms with a time step $\Delta t = 10^{-4}$ ms which ensures the stability of the explicit method. In order to get the stationary solution the traction is applied gradually as depicted in Fig. 13 and a Rayleigh damping (proportional to the mass) is used. Figs. 14, 15 and 16 compares the solution obtained with the three methods at different times. For this problem the 2D solution is given by shell theory [1] as

$$\begin{aligned} {\left\{ \begin{array}{ll} u(x,y,z) = u_0(x,y) -z \theta _x(x,y)\\ v(x,y,z) = v_0(x,y) -z \theta _y(x,y)\\ w(x,y,z) = w_0(x,y) \end{array}\right. } \end{aligned}$$

(63)

where $u_0$, $v_0$ and $w_0$ are the displacements of the points on the middle plane along x, y and z respectively and the rotations $\theta _x$ and $\theta _y$ coincide with the angles followed by the normal vectors contained in the planes xz and yz respectively in their motions.

Fig. 15

Displacement field using the three methods for $t = 1$ ms and $t = 5$ ms

Fig. 16

Displacement field using the three methods for $t = 10$ ms and $t = 30$ ms

Again the solution computed using the proposed method is able to get a 3D behavior (as the one of the 3D FEM solution) with the striction along the thickness in the zone with a smaller section, which is typical of a 3D plastic solution.

Conclusions

Here we proposed a minimally intrusive formulation of mechanical problems (linear, elasto-plastic, static and dynamic) defined in separable domains, enabling 3D solutions expressed as a finite sum decomposition involving the product of functions defined in the plane and in the thickness. The main contribution of the present work is that the calculation of functions defined in the plane, the most expensive computationally, can be ensured by a standard plate solver, whereas the solution of those defined in the thickness, defining 1D problems extremely simple and cheap, is externalized and ensured by a function called by the plate solver.

The different numerical examples prove the procedure efficiency that allows computing 3D solutions while keeping the computational cost the one characteristic of standard 2D plate and shell calculations.

Appendix A: Calculation of the out-of plane functions in a minimally-intrusive manner

We write the virtual work principle

$$\begin{aligned} \varvec{\varepsilon }^{*T} \varvec{\sigma }&= \varvec{\varepsilon }^{*T} {\mathbf {C}} \varvec{\varepsilon } \nonumber \\&= \{ \varvec{\Theta }^{1}(x,y) \circ {\mathbf {F}}^{1*}(z) + \varvec{\Theta }^{2}(x,y) \circ {\mathbf {F}}^{2*}(z) \}^T \{ {\mathbf {C}}_{xy}(x,y) \circ {\mathbf {C}}_z(z)\} \nonumber \\&\{ \varvec{\Theta }^1(x,y) \circ {\mathbf {F}}^1(z) + \varvec{\Theta }^2(x,y) \circ {\mathbf {F}}^2(z) \} \nonumber \\&= \mathbf {F}^{1*T}(x,y) \{\hat{{\mathbf {C}}}^{11}_{xy}(x,y) \circ {\mathbf {C}}_z(z)\} \mathbf {F}^1(x,y) + \mathbf {F}^{1*T}(x,y) \ \{\hat{{\mathbf {C}}}^{12}_{xy}(x,y) \circ {\mathbf {C}}_z(z)\} \nonumber \\&\mathbf {F}^2(x,y) + \mathbf {F}^{2*T}(x,y) \{\hat{{\mathbf {C}}}^{21}_{xy}(x,y) \circ {\mathbf {C}}_z(z)\} \mathbf {F}^1(x,y) + \mathbf {F}^{2*T}(x,y) \nonumber \\&\{\hat{{\mathbf {C}}}^{22}_{xy}(x,y) \circ {\mathbf {C}}_z(z)\} \mathbf {F}^2(x,y). \end{aligned}$$

(64)

In the previous expression matrices $\hat{{\mathbf {C}}}_{xy}^{ij}(x,y)$ results

$$ \begin{aligned} \hat{{\mathbf {C}}}^{ij}_{xy_{kl}}(x,y) = \mathbf {C}_{xy_{kl}}(x,y) \varvec{\Theta }^i_k(x,y) \varvec{\Theta }^j_l(x,y), \quad \ \ i,j \in [1,2] \ \& \ \ \quad k,l \in [1, \cdots , 6]. \end{aligned}$$

(65)

Now, the virtual work integral reads

$$\begin{aligned}&\int \limits _{\Omega _{xy} \times \Omega _z} \sum \limits _{i=1}^2 \sum \limits _{j=1}^2 \mathbf {F}^{i*T}(z) \{\hat{{\mathbf {C}}}^{ij}_{xy}(x,y) \circ {\mathbf {C}}_z(z) \} \mathbf {F}^{j}(z) \ dz \ dx \ dy \nonumber \\&\quad = \int \limits _{\Omega _{z}} \sum \limits _{i=1}^2 \sum \limits _{j=1}^2 \mathbf {F}^{i*T}(z) {\mathbf {P}}^{ij}(z) \mathbf {F}^j(z) \ dz, \end{aligned}$$

(66)

where

$$\begin{aligned} {\mathbf {P}}^{ij}(z) = {\mathbf {C}}_{z}(z) \circ \int \limits _{\Omega _{xy}} \hat{{\mathbf {C}}}^{ij}_{xy}(x,y) \ dx \ dy. \end{aligned}$$

(67)

Now, if we assume for instance an approximation based on piecewise linear interpolations on the 1D finite element mesh of $\Omega _{z}= \cup _{q=1}^{\texttt {Q}} \Omega _z^q$, with the shape functions defined by $N^q_i(z), \ i=1,2; \ q =1, \ldots , {\texttt {Q}}$; it results

$$\begin{aligned} {\left\{ \begin{array}{ll} f^{x,q}(z) = N^q_1(z) f^{x,q}_1 + N_2^q(z) f^{x,q}_2 \\ f^{y,q}(z) = N^q_1(z) f^{y,q}_1 + N_2^q(z) f^{y,q}_2 \\ f^{z,q}(z) = N_1^q(z) f^{z,q}_1 + N_2^q(z) f^{z,q}_2 \\ \end{array}\right. } \end{aligned}$$

(68)

Using that approximation we can express vectors ${\mathbf {F}} ^i(z)$ in each element $\Omega _z^q$ from

$$\begin{aligned} {\mathbf {L}}^{qT}= (f^{x,q}_1, f^{y,q}_1,f^{z,q}_1,f^{x,q}_2, f^{y,q}_2,f^{z,q}_2), \end{aligned}$$

(69)

and

$$\begin{aligned} \mathbf {F}^i(z \in \Omega _z^q) = {\mathbf {T}}^{i,q}(z) {\mathbf {L}}^q, \end{aligned}$$

(70)

where ${\mathbf {T}}^{i,q}(z)$ contains the shape functions and theirs derivatives, according to the expressions involved in the components of $\mathbf {F}^i(z), \ i=1,2$.

Thus, integral (66) reads

$$\begin{aligned}&\sum \limits _{q=1}^{\texttt {Q}} {\mathbf {L}}^{q*T} \left\{ \int \limits _{\Omega _z^q} \sum \limits _{i=1}^2 \sum \limits _{j=1}^2 {\mathbf {T}}^{i,qT}(z) {\mathbf {P}}^{ij}(z) {\mathbf {T}}^{j,q}(z) \ dz \right\} {\mathbf {L}}^q \nonumber \\&\quad = \sum \limits _{q=1}^{\texttt {Q}} {\mathbf {L}}^{q*T} {\mathbf {K}}_z^q {\mathbf {L}}^q = {\mathbf {L}}^{*T} {\mathbf {K}}_z {\mathbf {L}}. \end{aligned}$$

(71)

The virtual work (27) of the body forces can be expressed as

$$\begin{aligned} {\mathbf {u}}^{*T} {\mathbf {g}}({\mathbf {x}}) = {\mathbf {W}}^{*T}(z) \hat{{\mathbf {O}}}(x,y) {\mathbf {H}}(z), \end{aligned}$$

(72)

where matrix $\hat{{\mathbf {O}}}$ reads

$$\begin{aligned} \hat{{\mathbf {O}}}_{kl}(x,y) = {\mathbf {I}}_{kl} {\mathbf {V}}_k(x,y) {\mathbf {G}}_l(x,y), \end{aligned}$$

(73)

with ${\mathbf {I}}$ the identity matrix.

Now, the integral results

$$\begin{aligned} \int \limits _{\Omega _{xy} \times \Omega _z} {\mathbf {u}}^{*T} {\mathbf {g}}({\mathbf {x}}) \ dz \ dx \ dy = \int \limits _{\Omega _{z}} {\mathbf {W}}^{*T}(z) {\mathbf {O}} {\mathbf {H}}(z) \ dz , \end{aligned}$$

(74)

with

$$\begin{aligned} {\mathbf {O}} = \int \limits _{\Omega _{xy}} \hat{{\mathbf {O}}}(x,y) \ dx \ dy, \end{aligned}$$

(75)

Integrating in the mesh $\Omega _{z}=\cup _{q=1}^{\texttt {Q}} \Omega _z^q$,

$$\begin{aligned} \int \limits _{\Omega _{z}} {\mathbf {W}}^{*T}(z) {\mathbf {O}} {\mathbf {H}}(z) \ dz = \sum \limits _{q=1}^{\texttt {Q}} \int \limits _{\Omega _z^q} {\mathbf {W}}^{q*T}(z) {\mathbf {O}} {\mathbf {H}}^q(z) \ dz , \end{aligned}$$

(76)

where ${\mathbf {W}}^{q}(z)$ and ${\mathbf {H}}^q(z)$ are approximated respectively from

$$\begin{aligned} {\mathbf {W}}^{q}(z) = {\mathbf {S}} (z) {\mathbf {L}}^q, \end{aligned}$$

(77)

and

$$\begin{aligned} {\mathbf {H}}^{q}(z) = {\mathbf {S}} (z) {\mathbf {M}}^q, \end{aligned}$$

(78)

with ${\mathbf {M}} ^q$ containing the nodal values of ${\mathbf {H}}(z)$ and ${\mathbf {S}}(z) = [{\mathbf {N}}_1(z) \ {\mathbf {N}}_2(z)]$, and

$$\begin{aligned} {\mathbf {N}}_i = \left( \begin{array}{ccc} N_i^q(z) &{} 0\\ 0 &{} N_i^q(z)\\ \end{array} \right) . \end{aligned}$$

(79)

Thus, it results

$$\begin{aligned}&\sum \limits _{q=1}^{\texttt {Q}} \int \limits _{\Omega ^q} {\mathbf {W}}^{q*T}(z) {\mathbf {O}} {\mathbf {H}}^q(z) \ dz = \sum \limits _{q=1}^{\texttt {Q}} {\mathbf {L}}^{q *T} \left\{ \int \limits _{\Omega _z^q} {\mathbf {S}}^T {\mathbf {O}} {\mathbf {S}} \ dz \right\} {\mathbf {M}}^q \nonumber \\&\quad = \sum \limits _{q=1}^{\texttt {Q}} {\mathbf {L}}^{q *T} {\mathbf {A}}_z^q {\mathbf {M}}^q = \sum \limits _{q=1}^{\texttt {Q}} {\mathbf {L}}^{q *T} {\mathbf {B}}_z^q = {\mathbf {L}}^{*T} {\mathbf {B}}_z, \end{aligned}$$

(80)

from which, the principle of virtual works reads

$$\begin{aligned} {\mathbf {L}}^{*T} {\mathbf {K}}_z {\mathbf {L}} = {\mathbf {L}}^{*T} {\mathbf {B}}_z. \end{aligned}$$

(81)

Thus, the out-of-plane functions determining the kinematics can be obtained from a standard 1D software by using the elementary rigidity and forces given respectively by ${\mathbf {K}}_{z}^q$ and ${\mathbf {B}}_{z}^q$ considered in expression (71) and (80).