Abstract
Composite structures are convenient structural solutions for many engineering fields, but their design is challenging and may lead to oversizing due to the significant amount of uncertainties concerning the current modeling capabilities. From a structural analysis standpoint, the finite element method is the most used approach and shell elements are of primary importance in the case of thin structures. Current research efforts aim at improving the accuracy of such elements with limited computational overheads to improve the predictive capabilities and widen the applicability to complex structures and nonlinear cases. The present paper presents shell elements with the minimum number of nodal degrees of freedom and maximum accuracy. Such elements compose the best theory diagram stemming from the combined use of the Carrera Unified Formulation and the Axiomatic/Asymptotic Method. Moreover, this paper provides guidelines on the choice of the proper higher-order terms via the introduction of relevance factor diagrams. The numerical cases consider various sets of design parameters such as the thickness, curvature, stacking sequence, and boundary conditions. The results show that the most relevant set of higher-order terms are third-order and that the thickness plays the primary role in their choice. Moreover, certain terms have very high influence, and their neglect may affect the accuracy of the model significantly.
Similar content being viewed by others
Introduction
The finite element method (FEM) is one of the most common tools for the design of structures and makes use of three-dimensional (3D), 2D and 1D elements to solve a broad variety of linear and nonlinear structural problems. 2D and 1D elements, although less accurate than 3D, can lead to reduced computational costs. 2D models are referred to as shell and plate finite elements (FE) and can model metallic and composite thin-walled structures. 2D models available in commercial codes rely on the classical theories of structures [1,2,3]. In a 2D model, the primary unknown variables depend on two coordinates, x, and y. On the other hand, assumed fields define the unknown distributions along the thickness direction, z. A structural theory has a given expansion of the unknowns along z. Such expansions characterize the accuracy of a theory and its computational costs. For instance, in FEM, the expansion terms, referred to as generalized unknown variables, define the nodal degrees of freedom (DOF) of the model [4].
Richer expansions lead to higher accuracies and computational costs [5] but wider application scenarios. For a given accuracy level, the choice of a structural theory is problem dependent. In the case of composite structures, the following characteristics may require structural models with richer expansions than classical ones [6]:
- 1.
Moderately thick or thick structures, i.e., \(\frac{a}{h}\) < 50, where a is the characteristic length of the structure and h is the thickness.
- 2.
Materials with high transverse deformability, e.g., common orthotropic materials, in which \(\frac{E_L}{E_T}\), \(\frac{E_L}{E_z} > 5\), and \(\frac{G}{E_L}<\frac{1}{10}\), where E and G are the Young and shear moduli and L is the fiber direction of the fiber and T, z are perpendicular to L.
- 3.
Transverse anisotropy due, for instance, to the presence of contiguous layers with different properties.
As well-known, such factors require the proper modeling of shear and normal transverse stresses, and variations of the displacement field at the interface between two layers with different mechanical properties, i.e., the Zig–Zag effect.
The development of structural theories, i.e., the selection of the expansion terms, can follow two main approaches, namely, the axiomatic and asymptotic ones. The axiomatic method introduces expansions related to hypotheses on the mechanical behavior to reduce the mathematical complexity of the 3D differential equations of elasticity as in the case of classical theories [1,2,3]. The asymptotic method introduces a mathematically rigorous expansion having known accuracy if compared to the 3D exact solution [7, 8]. Axiomatic models are easier than asymptotic ones to implement but may miss fundamental expansion terms. Asymptotic models are more rigorous but the simultaneous consideration of multiple problem parameters, e.g., thickness and orthotropic ratio, may be cumbersome.
Over the last decades, the research activity has focused on the development of shell and plate models incorporating the effects mentioned above [9, 10]. Most recent efforts describe well the open research topics and refinement techniques related to shells, such as, improvements of classical models [11] and higher-order models [12,13,14]; asymptotic approaches [15]; improvement of FE performances regarding membrane and shear locking [16,17,18,19,20,21], mesh accuracy [22], and distortion [23]; improved modeling of the interlaminar shear stresses [24]; Layer-Wise (LW) models [25, 26]; Zig–Zag models [27, 28]; mixed formulations [29,30,31]; variable kinematics finite elements with multifield effects [32]; extensions to non-linear problems [33, 34] and peridynamics [35]; innovative solution schemes such as the numerical manifold method [36].
Via the axiomatic/asymptotic method (AAM), this paper presents best theory diagrams (BTD) [37] providing the shell finite elements with the minimum computational cost and maximum accuracy for a given problem. In [37], the results stemmed from strong-form solutions restricting the analysis concerning boundary conditions and stacking sequences. This paper is the first contribution based on shell finite elements allowing the generation of BTD for various boundary conditions and stacking sequences. Moreover, this paper presents a novel metric referred to as Relevance Factor (RF) to evaluate the influence of terms and outline guidelines for the proper choice of the expansion terms. This paper is organized as follows: the governing equations and the methodology are in “Finite element formulation” and “Best theory diagram” sections, then, the “Results” and “Conclusions” sections follow.
Finite element formulation
The Carrera Unified Formulation (CUF) defines the displacement field of a 2D model as
where the Einstein notation acts on \(\tau \). \(\mathbf {u}\) is the displacement vector, (u\(_{x}\) u\(_{y}\) u\(_{z}\))\(^T\). F\(_{\tau }\) are the thickness expansion functions. \(\mathbf {u}_{\tau }\) is the vector of the generalized unknown displacements. M is the number of expansion terms. In the case of polynomial, Taylor-like expansions, a third-order model, hereinafter referred to as N = 3, has the following displacement field:
The third-order model has twelve nodal unknowns. The order and type of expansion is a free parameter. In other words, the theory of structure is an input of the analysis. This paper makes use of the Equivalent Single Layer (ESL) formulation and N = 4 as reference model to build the BTD.
The metric coefficients H\(^k_\alpha \), H\(^k_\beta \) and H\(^k_z\) of the k-th layer of the multilayered shell are
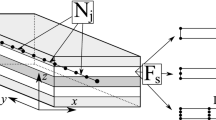
R\(^k_\alpha \) and R\(^k_\beta \) are the principal radii of the middle surface of the k-th layer, A\(^k\) and B\(^k\) the coefficients of the first fundamental form of \(\Omega _k\), see Fig. 1. This paper focused only on shells with constant radii of curvature with A\(^k = \) B\(^k = 1\). The geometrical relations are
where
The stress–strain relations are
where
The governing equations make use of the Principle of Virtual Displacements (PVD) and the finite element formulation exploits the MITC technique via nine-node shell elements. The displacement vector and its virtual variation are
\(\varvec{u}_{\tau _i}\) and \(\delta \varvec{u}_{s_j}\) are the nodal displacement vector and its virtual variation, respectively. Considering the constitutive and geometrical equations, and the PVD, the following governing equation holds
The \(3\times 3\) matrix \(\varvec{k}^{k}_{\tau s i j}\) is the fundamental mechanical nucleus whose expression is independent of the order of the expansion. \(\varvec{p}^k_{s j}\) is the load vector. More details regarding the finite element formulation are in [4].
Best theory diagram
One of the CUF extensions is the AAM as a tool to analyze the influence of expansion terms starting from a full axiomatic theory [38, 39], in this paper, the \(\hbox {N} = 4\). Via the AAM, asymptotic-like results related to the relevance of each variable are obtainable by varying problem parameters, e.g., thickness, orthotropic ratio, stacking sequence, boundary conditions. The AAM can follow various approaches, the one used in this paper has the following steps:
- 1.
Definition of parameters such as geometry, boundary conditions, materials, and layer layouts.
- 2.
Axiomatic choice of a starting theory and definition of the starting nodal unknowns. Usually, the starting theory provides 3D-like solutions.
- 3.
The CUF generates the governing equations for the theories considered. In particular, the CUF generates reduced models having combinations of the starting terms as generalized unknowns.
- 4.
For each reduced model, the accuracy evaluation makes use of one or more control parameters, in this paper, the maximum transverse displacement.
The number of active terms and the error identifies each theory on a Cartesian plane in which the abscissa reports the error and the ordinate reports the number of active terms. The best theory diagram (BTD) is the curve composed of all those models providing the minimum error with the least number of variables, see Fig. 2. Given the accuracy, models with fewer variables than those on the BTD do not exist. Given the number of variables, models with better accuracy than those on the BTD do not exist. The graphic notation makes use of black and white triangles to indicate active and inactive terms, respectively. In this paper, the control parameter for the error evaluation is the maximum u\(_z\), that is, error \(= 100\times \frac{|u_z - u_z^{N = 4}|}{|u_z^{N = 4}|}\).
Results
The numerical results focus on cases retrieved from [40]. The shell has a = b and \(\hbox {R}_{\alpha } = \hbox {R}_{\beta }\) = R. The load is bi-sinusoidal and applied on the top surface, \(\hbox {p}_z = \hat{p}_{z}\sin (\pi \alpha /\hbox {a})\sin (\pi \beta /\hbox {b})\). The material properties are \(\hbox {E}_1\)/\(\hbox {E}_2 = 25\), \(\hbox {G}_{12}\)/\(\hbox {E}_2 = \hbox {G}_{13}\)/\(\hbox {E}_2 = 0.5\), \(\hbox {G}_{13}\)/\(\hbox {E}_2 = 0.2\), \(\nu = 0.25\). The finite element model of a quarter of shell has a \(4\times 4\) mesh as this discretization provides sufficiently accurate results [40]. In all cases, the BTD vertical axis ranges from 5 to 15 since, more often than not, models with 4 or less DOF provide very high errors and are not of practical interest.
Simply-supported, 0/90/0
A simply-supported shell with symmetric lamination is the first numerical case. The analysis aims to study the influence of the thickness and curvature on the BTD. R/a and a/h vary to consider deep, shallow, thick and thin shells.
Table 1 presents the transverse displacement with comparisons against a 3D solution and an analytical model based on a fourth-order layer-wise model. As well-known, the accuracy of the present \(\hbox {N} = 4\) model decreases for thicker shells. However, given that the present work aims to investigate the role of higher-order terms and build BTD, the present \(\hbox {N} = 4\) model accuracy is satisfactory. Figure 3 presents the accuracy of all models stemming by the 2\(^{15}\) combinations of the \(\hbox {N} = 4\) model. In other words, each dot provides the accuracy of a structural theory based on a subset of the fifteen DOF full fourth-order expansion. The BTD is the lower boundary curve composed of those theories with the minimum number of terms for a given error. Figures 4 and 5 present the BTD for \(\hbox {R/a} = 5\) and 2, respectively. For comparison purposes, each plot shows the FSDT, \(\hbox {N} = 2\) and \(\hbox {N} = 3\) results. In the case of \(\hbox {a/h} = 5\), BTD with and without \(\hbox {N} = 2\) and FSDT are available to improve the readability of the results. Tables 2, 3 and 4 present each BTD model. For the sake of brevity, \(\hbox {R/a} = 2 \) is not reported since does not present any significant changes if compared to \(\hbox {R/a} = 5\). Each row shows the model providing the minimum error for a given number of DOF. For instance, for \(\hbox {R/a} = 5\), \(\hbox {a/h} = 100\), the 7 DOF BTD has the following displacement model:
The last row of each table shows the relevance factor (RF) of given order terms in the BTD. The RF is the ratio between the number of active instances and the total number of cases. For instance, \(\hbox {RF}_0 = 1\) indicates that the zeroth-order terms are always present in the BTD. \(\hbox {RF}_4 = 0.27\) because fourth-order terms are in the BTD nine times out of 33 cases. The RF provides a metric to measure the influence of a set of variables, higher the RF higher the relevance. Table 5 reports the error from all the 14 DOF models. Each row refers to a model indicated by the inactive term.
The results suggest that
In all cases, no more than six DOF are necessary to provide errors lower than 1%.
The analysis of all combinations shows that for thin shells there is a significant gap between models providing acceptable accuracies and those with errors larger than 70%. On the other hand, as the thickness increases, the distribution has fewer accuracy gaps. As shown in Table 5, the zeroth and first-order terms affect the gap width to a great extent. In thin shells, their role is predominant, whereas, in thick shells, higher-order terms gain relevance. A more regular accuracy distribution is an indication of more relevance of higher-order terms.
According to the distributions of accuracy from all combinations, the introduction of new terms in an expansion is ineffective if a very relevant term is not present. For instance, u\(_{x4}\) gains significance as the thickness increases.
For thin shells, the FSDT provides higher accuracy with less DOF than the BTD due to the correction of the Poisson locking. For moderately thick shells, a/h = 10, the FSDT matches the BTD but with moderate accuracy. The use of 6 DOF improves the accuracy to a great extent. As a/h decreases further, the FSDT is no longer on the BTD.
The \(\hbox {N} = 3 \) is always on the BTD, whereas the \(\hbox {N} = 2\) is a BTD only for thin shells.
The thickness ratio influences the BTD more than curvature.
The zeroth-order terms are active in each BTD independently of the thickness, i.e., \(\hbox {RF}_0 = 1\).
The relevance of first- and second-order terms decreases as the thickness increases.
The influence of third-order terms increases as the thickness increases.
The fourth-order terms are the least influential, although, at a/h \(= 5\), the RF increases considerably to the level of second-order terms.
Most of the zeroth-, first- and third-order terms present a regular pattern along a BTD table, i.e., as one of these terms becomes inactive, it does not appear in the BTD anymore. On the other hand, second- and fourth-order terms have a more irregular pattern indicating that their influence depends on the activation or deactivation of other terms.
Simply-supported, 0/90/0/90
The second numerical case deals with a different stacking sequence to investigate the effect of an asymmetric lamination on the BTD. All other parameters remain as those of the previous case. Moreover, this section considers two additional R/a values, 100 and 50, for a more comprehensive analysis on the effect of the curvature. Table 6 presents the transverse displacement values with comparisons with other models from literature, when available.
The all combination accuracy plot is in Fig. 6, whereas, Figs. 7 and 8 present the BTD for given R/a values and varying a/h, and Fig. 9 shows the BTD for a given a/h and varying R/a. The BTD models are in Tables 7, 8, 9, 10, and 11. The results suggest that
The present case has more uniform accuracy distributions than the previous one indicating higher relevances of the higher-order terms. For the thick case, there are no relevant gaps up to 60%, and the proper choice of terms can provide any accuracy level. For a/h \(= 10\), there is an accuracy gap between 20 and 35% meaning that there are not structural models that can provide such level of accuracy.
As in the previous case, the FSDT validity is confirmed for the thin case, whereas its accuracy is not sufficient from a/h \(= 10\) and below.
Unlike the previous case, from a/h = 10 and below, some ten DOF are necessary to have errors lower than 1%.
As the thickness increases, the RF distributions are similar to the previous case with a slightly higher influence of the higher-order terms and lower for zeroth- and first-order ones.
For a/h \(= 5\) the influence of higher-order terms is of particular relevance. For instance, the 5 DOF BTD differs significantly from the FSDT and requires third-order terms.
The variation of the curvature leads to less significant modifications of the BTD than the thickness.
Clamped-free, 0/90/0/90
The last numerical example proposes the 4-layer shell with two edges parallel to \(\beta \) clamped, and the other two free. The aim is to provide some insights into the effect of the geometrical boundary conditions on the BTD. All the other parameters are as in the previous case. Table 12 presents the transverse displacement from the \(\hbox {N} = 4\) model. The BTD for the present case are in Tables 13, 14, 15, and Fig. 10. The results show that the most relevant effect from the new set of boundary conditions is an increased relevance of higher-order terms at a/h \(= 10\).
Analysis of the relevance of generalized displacement variables
This section aims at investigating the role of each generalized unknowns in the BTD and how their relevance changes with varying parameters. To this purpose, the RF restricts to each variable as shown, for instance, in Fig. 11. In this case, RF = 1 means that a given variable is present in each BTD of the shell configuration considered. For instance, for the 0/90/0 case with R/a = 5, u\(_{x1}\), u\(_{y1}\) and u\(_{z1}\) are in all BTD independently of the thickness ratio. Each set of figures presents the RF for the three terms of a given order, see Figs. 11, 12, 13, 14, and 15. The discussion for each order follows.
Zeroth-order terms As expected, these terms have very high influence and are almost always present in BTD. Just u\(_{x1}\) presents RF lower than unity in three cases in which the 5 DOF BTD requires higher-order terms as discussed in previous sections.
First-order terms In-plane components have unitary RF in most cases. On the other hand, the out-of-plane component has lower relevance and is consistent with the appearance of the FSDT model as 5 DOF BTD for thin and moderately thick shells.
Second-order terms The influence of these terms varies consistently. u\(_{x3}\) has little relevance in the 0/90/0 case but higher in the asymmetric case, and such relevance tends to increase for higher thickness, and the curvature does not influence it. The u\(_{y3}\) relevance has smaller variations due to the thickness change. The thickness strongly influences the out-of-plane component and its influence decreases for thicker shells.
Third-order terms The in-plane components have significant influence which increases for thicker shells. The out-of-plane influence is relevant in the symmetric case and increases for thicker shells.
Fourth-order terms These terms are the less influential except for u\(_{x5}\) in the clamped-free case. The relevance of these terms should increase as soon as the BTD considers stress distributions.
Conclusions
This paper presented results on the accuracy of higher-order generalized displacement variables for composite shells. Investigations used the CUF and the AAM. The former provided the finite element matrices for any-order models, and the latter led to the analysis of the relevance of each generalized variable. The combined use of these tools generated the BTD and relevance factor diagrams. The BTD provides the minimum number of DOF for a given accuracy level. The RF diagrams measure the importance of a variable, or of a set of variables, as various parameters change, e.g., thickness, curvature, stacking sequence. All results considered the maximum transverse displacement as the control parameter. The analysis led to the following guidelines and recommendations:
For the cases considered in this paper, the thickness and stacking sequence are the most important factors for the choice of the primary variables. For thin shells, six DOF are sufficient to obtain errors lower than 1%. For thick shells, ten DOF are necessary.
In most cases, the accuracy level obtainable from combinations of a given set of variables is not continuous as the DOF decrease. In other words, there are no structural models that can satisfy certain accuracy of the solution.
Accuracy gaps indicate the presence of very effective terms that must be present in the expansion to ensure satisfactory accuracies. For instance, for thin shells, these terms coincide with the FSDT expansions. However, as the presence of non-classical effects due to asymmetries or high thickness increases, the relevance of higher-order terms increases and the accuracy gaps tend to disappear.
The FSDT and second-order model are BTD only for thin shells. The third-order model is close to the BTD in most cases.
As the thickness increases, the relevance of third-order variables increases significantly, and these terms can be the most relevant together with the zeroth-order ones.
The out-of-plane displacement variables tend to have less relevance than in-plane ones. Such a relevance should increase significantly as soon as the analysis considers stress distributions as control parameters.
The set of variables composing a BTD model depends on the boundary conditions; however, such a dependency is weaker than the thickness one.
Most immediate future developments should deal with the inclusion of all displacement and stress components as control parameters and the analysis of more complex configurations. In fact, for the boundary conditions adopted, the use of the transverse displacement is the minimum requirement for a BTD. The inclusion of other control parameters, e.g., transverse shear and axial stresses, may modify the BTD concerning accuracy and set of active terms with higher relevance of higher-order terms.
References
Kirchhoff G. Uber das gleichgewicht und die bewegung einer elastischen scheibe. J Reins Angewandte Mathematik. 1850;40:51–88.
Reissner E. The effect of transverse shear deformation on the bending of elastic plates. J Appl Mech. 1945;12:69–76.
Mindlin RD. Influence of rotatory inertia and shear in flexural motions of isotropic elastic plates. J Appl Mech. 1951;18:1031–6.
Carrera E, Cinefra M, Petrolo M, Zappino E. Finite element analysis of structures through unified formulation. Chichester: Wiley; 2014.
Washizu K. Variational methods in elasticity and plasticity. Oxford: Pergamon; 1968.
Carrera E. Developments, ideas and evaluations based upon the Reissner’s mixed variational theorem in the modeling of multilayered plates and shells. Appl Mech Rev. 2001;54:301–29.
Gol’denweizer AL. Theory of thin elastic shells. International series of monograph in aeronautics and astronautics. New York: Pergamon Press; 1961.
Cicala P. Systematic approximation approach to linear shell theory. Torino: Levrotto e Bella; 1965.
Kapania K, Raciti S. Recent advances in analysis of laminated beams and plates, part I: shear effects and buckling. AIAA J. 1989;27(7):923–35.
Carrera E. Historical review of zig–zag theories for multilayered plates and shells. Appl Mech Rev. 2003;56:287–308.
Endo M. An alternative first-order shear deformation concept and its application to beam, plate and cylindrical shell models. Compos Struct. 2016;146:50–61.
Katili I, Maknun IJ, Batoz JL, Ibrahimbegovic A. Shear deformable shell element DKMQ24 for composite structures. Compos Struct. 2018;160:586–93.
Thakur SN, Ray C, Chakraborty S. Response sensitivity analysis of laminated composite shells based on higher-order shear deformation theory. Arch Appl Mech. 2018;88(8):1429–59.
Reinoso J, Paggi M, Areias P, Blázquez A. Surface-based and solid shell formulations of the 7-parameter shell model for layered CFRP and functionally graded power-based composite structures. Mech Adv Mater Struct. (in press).
Chung SW, Hong SG. Pseudo-membrane shell theory of hybrid anisotropic materials. Compos Struct. 2017;160:586–93.
Ko Y, Lee Y, Lee PS, Bathe KJ. Performance of the MITC3+ and MITC4+ shell elements in widely-used benchmark problems. Comput Struct. 2017;193:187–206.
Jun H, Toon K, Lee PS, Bathe KJ. The MITC3+ shell element enriched in membrane displacements by interpolation covers. Comput Methods Appl Mech Eng. 2018;337:458–80.
Ko Y, Lee PS, Bathe KJ. The MITC4+ shell element and its performance. Comput Struct. 2016;169:57–68.
Ko Y, Lee PS, Bathe KJ. A new MITC4+ shell element. Comput Struct. 2017;182:404–18.
Ko Y, Lee PS, Bathe KJ. A new 4-node MITC element for analysis of two-dimensional solids and its formulation in a shell element. Comput Struct. 2017;192:34–49.
Rama G, Marinkovic D, Zehn M. High performance 3-node shell element for linear and geometrically nonlinear analysis of composite laminates. Compos B Eng. 2018;151:118–26.
Ho Nguyen Tan T, Kim HG. A new strategy for finite-element analysis of shell structures using trimmed quadrilateral shell meshes: a paving and cutting algorithm and a pentagonal shell element. Int J Numer Methods Eng. 2018;114(1):1–27.
Wisniewski K, Turska E. Improved nine-node shell element MITC9i with reduced distortion sensitivity. Comput Mech. 2018;62(3):499–523.
Gruttman F, Knust G, Wagner W. Theory and numerics of layered shells with variationally embedded interlaminar stresses. Comput Methods Appl Mech Eng. 2017;326:713–38.
Naumenko K, Eremeyev VA. A layer-wise theory of shallow shells with thin soft core for laminated glass and photovoltaic applications. Compos Struct. 2017;178:434–46.
Li DH, Zhang F. Full extended layerwise method for the simulation of laminated composite plates and shells. Comput Struct. 2017;187:101–13.
Coda HB, Paccola RR, Carrazedo R. Zig–Zag effect without degrees of freedom in linear and non linear analysis of laminated plates and shells. Compos Struct. 2017;161:32–50.
Ahmed A, Kapuria S. A four-node facet shell element for laminated shells based on the third order zigzag theory. Compos Struct. 2016;158(1):112–27.
Zucco G, Groh RMJ, Madeo A, Weaver PM. Mixed shell element for static and buckling analysis of variable angle tow composite plates. Compos Struct. 2016;152:324–38.
Cinefra M, Chinosi C, Della Croce L, Carrera E. Refined shell finite elements based on RMVT and MITC for the analysis of laminated structures. Compos Struct. 2014;113:492–7.
Chai Y, Li W, Liu G, Gong Z, Li T. A superconvergent alpha finite element method (SaFEM) for static and free vibration analysis of shell structures. Comput Struct. 2017;179:27–47.
Cinefra M, Petrolo M, Li G, Carrera E. Variable kinematic shell elements for composite laminates accounting for hygrothermal effects. J Therm Stress. 2017;40(12):1523–44.
Liang K. Koiter–Newton analysis of thick and thin laminated composite plates using a robust shell element. Compos Struct. 2017;161:530–9.
Punera D, Kant T. Elastostatics of laminated and functionally graded sandwich cylindrical shells with two refined higher order models. Compos Struct. 2017;182:505–23.
Chowdhury SR, Roy P, Roy D, Reddy JN. A peridynamic theory for linear elastic shells. Int J Solids Struct. 2016;84:110–32.
Guo H, Zheng H. The linear analysis of thin shell problems using the numerical manifold method. Thin-Walled Struct. 2018;124:366–83.
Carrera E, Cinefra M, Lamberti A, Petrolo M. Results on best theories for metallic and laminated shells including layer-wise models. Compos Struct. 2015;126:285–98.
Carrera E, Petrolo M. Guidelines and recommendation to construct theories for metallic and composite plates. AIAA J. 2010;48(12):2852–66.
Carrera E, Petrolo M. On the effectiveness of higher-order terms in refined beam theories. J Appl Mech. 2011;78:021013.
Cinefra M, Valvano S. A variable kinematic doubly-curved MITC9 shell element for the analysis of laminated composites. Mech Adv Mater Struct. 2016;23(11):1312–25.
Huang NN. Influence of shear correction factors in the higher-order shear deformation laminated shell theory. Int J Solids Struct. 1994;31:1263–77.
Authors' contributions
EC provided the CUF FEM framework. MP developed the AAM and obtained the BTD. Both authors read and approved the final manuscript.
Acknowledgements
Erasmo Carrera acknowledges the Russian Science Foundation under Grant No. 18-19-00092.
Competing interests
The authors declare that they have no competing interests.
Availability of data and materials
Data are available upon request.
Funding
This work was partially supported by the Russian Science Foundation under Grant No. 18-19-00092.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Petrolo, M., Carrera, E. Best theory diagrams for multilayered structures via shell finite elements. Adv. Model. and Simul. in Eng. Sci. 6, 4 (2019). https://doi.org/10.1186/s40323-019-0129-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s40323-019-0129-8