Background

Last few decades, soil erosion impacts natural resources and agricultural production globally (Bakker et al. 2005; Pimentel et al. 1995; Prasannakumar et al. 2012). In Mountain regions, soil erosion causes severe hazards, such as heavy rainfall, surface water flow on bare lands that contribute to land degradation (Ristić et al. 2012; Ashiagbor et al. 2013; Tamene and Vlek 2008). The primary soil erosion is onsite consequences impacts on soil fertility loss and degradation of soil resources quality, whereas pollution on water bodies and settling sediments are an offsite (Morgan et al. 1984; Blaikie and Brookfield 2015). It directly impacts on the environment, economy, and agriculture in mountain areas (Vanacker et al. 2003; Navas et al. 2004). Its rate increased through the change in precipitation and temperature pattern and eventually altering the runoff and land use, which causes flood, drought, and famine (Nearing et al. 2004; Thapa and Dhulikhel 2019; Zhao et al. 2013). On the other hand, the deposition of sediments on the river affects reservoir and dams, increases their costs of maintenance, and in the long run, makes them unusable (Samaras and Koutitas 2014). There have been several studies to understand this situation; their findings control soil erosion and ecological restoration (Samaras and Koutitas 2014; Shah et al. 1991). Although some attention regarding erosion modeling essential for inaccessible mountainous areas.

Mountain region is highly vulnerable to resource degradation caused by landslides, soil loss from steep slopes, and deforestation (TolIIrism 1995). In Nepal, approximately 45.5% of land erodes from the water in steeper areas (Chalise et al. 2019). One study shows that soil loss of agricultural land in the hills through surface erosion, other finds in 1992 and 1993 of Likhu Khola watershed soil loss and slightly degraded secondary forest (Shrestha 1997; Gardner and Jenkins 1995). Several models exist for prediction of soil erosion from empirical (USLE/RUSLE), and considerably varies in its data input. The RUSLE represents raindrop impacts on climate, soil, topography, and land use affect rill and inter rill soil erosion (Magdoff and Weil 2004). This method is widely used to estimate soil erosion loss and risk, which provides a guideline for the development of conservation plans and controlling erosion under different land-cover conditions, such as croplands, rangelands, and disturbed forest lands (Milward and Mersey 1999). The remote sensing and GIS techniques are feasible for soil erosion estimation and spatial distribution in larger areas (Milward and Mersey 1999; Bahadur 2012). The remote sensing, GIS, and RUSLE provide the potential to estimate soil erosion loss on a cell-by-cell basis (Milward and Mersey 1999). The RUSLE model with GIS used for estimation of the spatial distribution of soil erosion in Dolakha; however, the model is applicable only in the prediction of sheet and rill erosion, unable to estimate the rate of gully erosion (Wang et al. 2002). It provides a framework for decision-makers for planning activities to control erosion and contributes toward filling a gap of soil loss information of a particular district.

Materials and methods

Study area

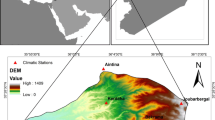
The study area is the Dolakha District, Nepal, situated in the northeast part of Kathmandu (Fig. 1; Dennison and Rana 2017). It’s fragile in the last few years for soil erosion, deforestation, and terrace farming on steep slopes and rapid population pressure on natural resources (Thapa and Upadhyaya 2020; Pei and Sharma 1998). Other significant contributors are land use and land cover change caused by a human that increases the erosion rate here (Fall et al. 2011).

Fig. 1
figure 1

Study area used for estimating soil erosion

Full size image

Data collection

The spatial datasets for this research are shown in Table 1.

Table 1 The datasets used for the RUSLE modelling
Full size table

Methods

The RUSLE model estimates soil damage for ground slopes in Geographic Information System (GIS) platform (Yitayew et al. 1999; Fig. 2). A combined equation of geophysical and land cover factors to evaluate the yearly soil loss from a unit of property. It assesses erosion risk in the research area, which has its qualities and application scopes (Ciesiolka et al. 1995; Boggs et al. 2001). Its global model to predict soil loss because of its convenience and compatibility with GIS (Milward and Mersey 1999; Tang et al. 2015; Jha and Paudel 2010; Šúri et al. 2002). GIS and remote sensing technology advancement enabled a more accurate estimation of the factors used for calculation (TolIIrism 1995; Park et al. 2005; Ganasri and Ramesh 2016; Atoma 2018). Each of the elements derived separately in raster data format and the erosion calculated using the map algebra functions. Figure 2 illustrates the framework for the RUSLE model calculation and expressed by an equation,

$${\text{A}} = \left[ {\text{R}} \right]*\left[ {\text{K}} \right]*\left[ {\text{LS}} \right]*\left[ {\text{C}} \right]*\left[ {\text{P}} \right],$$
(1)

where A = soil loss (mg ha−1 year−1), R = rainfall erosivity factor (mm ha−1 year−1), K = soil erodibility factor (mg ha−1 year−1), LS = slope-length and slope steepness factor (dimensionless), C = land management factor (dimensionless), and P = conservation practice factor (dimensionless).

Fig. 2
figure 2

The methodological framework for potential soil erosion using RUSLE model

Full size image

RUSLE parameters computation

  1. a.

    Rainfall erosivity factor (R)

This rainfall erosion factor (R) describes the intensity of precipitation at a particular location based on their amount on soil erosion (Koirala et al. 2019; Thapa and Upadhyaya 2019). Essential for soil erosion risk assessment under future land use and climate change (Stocking 1984). It quantifies an effect of raindrop amount and rate of runoff associate with rainfall and its unit expressed in mm ha−1 h−1 year−1. During this study, the rainfall map produced by the National Aeronautics and Space Administration (NASA) used to generate a rainfall erosion factor (Wischmeier and Smith 1978). This map shows mean annual precipitation over the district, equation integrated to make the R-factor given by Morgan et al. (1984).

$${\text{R}} = 3 8. 5+ 0. 3 5 {\text{P}},$$
(2)

where R = rainfall erosivity factor, P = mean annual rainfall in mm

  1. b.

    Soil erodibility factor (K)

The soil erodibility factor (K) measures the susceptible soil types and their particles to detachment and transport by rainfall and runoff. The K factor influenced by soil texture, organic matter, soil structure, and permeability of the soil profile (Erencin et al. 2000). The equation provided by reference used to estimate the soil loss (Kouli et al. 2009).

$${\text{K}} = {\text{Fcsand}}*{\text{Fsi-cl}}*{\text{Forgc}}*{\text{Fhisand}}*0. 1 3 1 7,$$
(3)

where

$${\text{Fcsand}} = \left[ {0. 2+ 0. 3 {\text{exp}}\left( { - 0.0 2 5 6 {\text{ SAN }}\left( { 1- \frac{SIL}{100}} \right)} \right)} \right],$$
(4)
$${\text{Fsi-cl}} = \left[ {\frac{SIL}{CLA + SIL}} \right]^{0. 3} ,$$
(5)
$${\text{Forgc}} = \left[ { 1.0 \, - \frac{{0.25 {\text{C}}}}{{C + \exp \left( {3.72 - 2.95 C} \right)}}} \right],$$
(6)
$${\text{Fhisand}} = \left[ { 1.0 \, - \frac{{0.70 {\text{SN}}1}}{{SN1 + \exp \left( { - 5.51 + 22.9 SN1} \right)}}} \right],$$
(7)

where SAN, SIL and CLA are % sand, silt and clay, respectively; C is the organic carbon content; and SN1 sand content subtracted from 1 and divided by 100. Fcsand = low soil erodibility factor for soil Fsi-cl = low soil erodibility factor with high clay to silt ratio. Forgc = factor that reduces soil erodibility for soil with high organic content. Fhisand = factor that reduces soil erodibility for soil with high sand content.

  1. c.

    Topographic factor (LS)

The topographic factor (LS) created from two sub-factors: a slope gradient factor (S) and a slope-length factor (L), both determined from the Digital Elevation Model (DEM). The slope-length and gradient parameter is crucial in the soil erosion modeling for calculating overland flow (surface runoff) (Morgan et al. 1992). The L and S represent the effect of slope length and steepness respectively on erosion, also when it increases soil loss per unit area rises. These calculated from the DEM and combined to result in the topographical factor grid using relation (Atoma 2018).

$${\text{L}} = \left( {\frac{\lambda }{22.13}} \right)^{\text{m}} ,$$
(8)

where L = slope length factor, λ = slope length (m), m = slope-length exponent

$${\text{m}} = \frac{F}{{1 + F^{\prime}}},$$
(9)
$${\text{F}} = \frac{\sin /0.0896}{{ 3 \left( {\sin } \right)_{0.8} + 0.56}},$$
(10)

where F = ratio between rill erosion and inter rill erosion, β = slope angle (°)

In ArcGIS, L was calculated as,

$$flow_{acc } + 625 {\text{L }} = \frac{{\left( {flow_{acc } + 625} \right)^{{\left( {m + 1} \right)}} {-}flow_{acc}^{{\left( {m + 1} \right)}} }}{{25^{{\left( {{\text{m}} + 2} \right)}} * 22.13^{\text{m}} }},$$
(11)

For slope gradient factor,

$${\text{S}} = {\text{Con}}\left( {\left( {{\text{Tan}}\left( {{\text{slope}}*0.0 1 7 4 5} \right) < 0.0 9} \right),\left( { 10. 8*{\text{Sin}}\left( {{\text{slope}}*0.0 1 7 4 5} \right) + 0.0 3} \right),\left( { 1 6. 8*{\text{Sin}}\left( {{\text{slope}}*0.0 1 7 4 5} \right) - 0. 5} \right)} \right),$$
(12)

Final,

$${\text{LS}} = {\text{L}}*{\text{S}},$$
(13)
  1. d.

    Cover management factor (C)

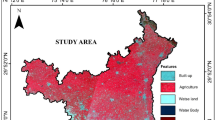
The cover-management factor (C) reflects the effect of cropping and other practices on erosion rates (Chalise et al. 2019). It’s the most spatiotemporal sensitive as it follows plant growth and rainfall dynamics (Nearing et al. 2004). This factor defined as a non-dimensional number between zero and one representing a rainfall erosion weighted ratio of soil loss for specified land and vegetated conditions to the corresponding loss from continuous bare fallow (Wischmeier and Smith 1978). In this study, LULC produced by the ICIMOD used for preparing a C-factor map (Sheikh et al. 2011). The raster map converted to polygon through raster to polygon tool and the attributes with the same land use type merged into a single class using ArcGIS 10.5 software, the study used eight types of land use (Table 2). Each land-use example, C values assigned through reference ranges from 0 to 1, where lower C means no loss, while higher indicates uncover and significant chances of soil loss (Erencin et al. 2000; Panagos et al. 2015).

Table 2 Cover management factor
Full size table
  1. e.

    Support practice factor (P)

The support practice factor indicates the rate of soil loss according to agricultural practice. There are three methods, such as contours, cropping, and terrace, and vital elements to control erosion (Park et al. 2005). This contouring method used with P values ranges from 0 to 1, where the value 0 represents proper anthropic erosion, and the value 1 indicates a non-anthropic erosion facility (Table 3, Kouli et al. 2009). It values for particular types of land cover used from published sources (Coughlan and Rose 1997; Yue-Qing et al. 2008).

Table 3 P factor values for slope (Kumar and Kushwaha 2013)
Full size table

Potential erosion map

The different data input processed in ArcGIS created five-factor maps: R, K, LS, C, and P (Fig. 3). These raster maps integrated within the ArcGIS environment using the RUSLE relation to generate composite maps of the estimated erosion loss on the study area (Ganasri and Ramesh 2016; Atoma 2018). Zonal statistics tool and calculating geometry used for computing an area-weighted mean of the potential erosion rates for its generated to explore the relationship between slope and LULC on erosion (Bastola et al. 2019). The slope map of Dolakha created from DEM in ArcGIS and then reclassified into eight classes (Gorr and Kurland 2010).

Fig. 3
figure 3

Five factor maps of soil erosion of study area, a Topographic factor map, b cover management factor map, c support practice factor, d soil erodibility factor map, e rainfall erosivity factor map

Full size image

Results

Factor maps

The results showed that the topographic factor (LS) value range between 0 and 12,073 (Fig. 3a); Rainfall erosivity factor (R) value ranges between 87.4938 and 1541.42 mm ha−1 year−1 (Fig. 3e); Soil erodibility factor (K) value ranged from 0.2 to 0.32 (Fig. 3d). The support practice factor (P) value for the entire area ranged from 0.55 to 1 (Fig. 3c). The cover management factor (C) value ranged between 0 and 0.45 (Fig. 3b).

Potential soil erosion rates of Nepal

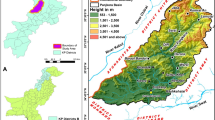
The potential soil erosion map of the Dolakha district produced multiplying the factor maps in ArcGIS (Fig. 4; Table 4). The soil erosion higher than 80% consists of a 5.01% area (Table 4). It shows that around 10% of high, very high, and severe risk zones need conservation to reduce the risk of soil erosion. The mean erosion rate high in barren lands, followed by agricultural lands, shrubs, grasslands, and forests, and the highest soil loss rates observed in steep slopes.

Fig. 4
figure 4

Potential map of soil erosion rate of Dolakha district

Full size image
Table 4 Potential soil erosion rate of Dolakha district
Full size table

The study area classified into six classes that remained constant in the different erosion classes shown bold in the diagonal cells. Greater than 80% of the study area remained in the high severe erosion risk class. The proportion area at low and moderate risk of erosion is 70% and 15%, respectively, while the space between the upper and very severe, around 15%, indicates a chance increasing.

Discussion

RUSLE is an empirical-based modeling approach that predicts the long-term average annual rate of soil erosion on slopes using five factors. It estimates soil loss with similar terrain and meteorological conditions (Prasannakumar et al. 2012). This research, a potential soil erosion rate map of Dolakha generated using different sources (Table 1) for the RUSLE model using ArcGIS software. Its the first time that such an approach to assess erosion risk across an entire mountainous region, and the methodology still has certain limitations. Again, it identifies priority areas for reducing soil erosion. Other research studies having similar geographic characteristics also used the same method (Prasannakumar et al. 2012; Panagos et al. 2015; Kumar and Kushwaha 2013). In an erosion model, proper consideration of R-factor, LS-factor, K-factor, P-factor, and C-factor should minimize the uncertainties. The LS-factor with a maximum slope in the study area used as original RUSLE formulations (McCool et al. 1989). According to the many research results, Nepal is vulnerable to soil erosion hazards due to five major factors, high annual precipitation, the soil characteristics, mainly texture and steep slopes, land covers, and soil conservation practices along the slopes (McCool et al. 1987, 1989). Its total soil erosion is comparatively higher than in other countries of the world (Koirala et al. 2019). This study also found that around 15% of the total area in district was between upper and very severe region, which is common in rates of erosion of countries like India, Ethiopia, United Kingdom, Europe, and Africa in their steeper slope area (Morgan et al. 1984; Stocking 1984; Wischmeier and Smith 1978). Here, the suggested range of erosion is almost equal to that of Australia, China, as estimated by Lu et al. (2003). The higher erosion rates in China and Australia indicate the vulnerability to an erosion of the semi-arid and semi-humid areas of the world (Suárez de Castro and Rodríguez Grandas 1962). The soil erosion rates in the mountainous regions, like Nepal, also rise with an increase in slope (Assouline and Ben-Hur 2006).

RUSLE is the most commonly applied soil loss estimation model (Mekelle 2015; Wang et al. 2013; Maetens et al. 2012; Erol et al. 2015). Moreover, RUSLE model strength lies in giving predicted soil loss using limited information, especially in developing countries where data are scarce (Tadesse 2016; Shahid 2013; Angima et al. 2003) although RUSLE widely used in mountainous terrain with steep slopes still questionable (Turnipseed et al. 2003; Cevik and Topal 2003). Some models, such as AGNPS or ANSWER, are unsuitable in Nepal due to large amounts of data and AGNPS, non-applicable to this Middle hill area (Kettner 1996; Ayalew 2020). On the other hand, modeling results are impressive but difficult to interpret and validate because of its complexity (Meyer and Flanagan 1992). Overall, such models include errors because they based on empirical rules. This model identifies areas at risk, where management actions needed (Rabia 2012; Roșca et al. 2012). It’s simple, flexible, and physical base for predicting the relative soil loss pattern; however, the high hills are heterogeneous on precipitation patterns and topography. It assesses soil erosion accuracy estimates from the models using ground observations. It’s impossible to validate the assessments and analyze error and bias by comparing model prediction with field-based measurements over a set of sites. There have been very few field-based studies in the area. However, the output compared with the estimated erosion levels of different studies from published articles and with other model-based results of mid and high hill areas in Nepal with similar characteristics to the Dolakha (Kebede 2001; Saxton and Rawls 2006).

The method contains limitations and potential for factors that drive erosion in the RUSLE model. Precipitation data from TRMM Data used for hill areas to calculate the rainfall erosion factor. Weather stations in the Himalayan region limited, and spatial precipitation data is low resolution. Furthermore, this approach is unable to capture the distribution of massive precipitation events, markedly impacting soil erosion. The cover management factor (C) and support practice factor (P) weighted at soil order level using published results (Uddin et al. 2018). Better estimates could determine the C-factor by remote sensing, have used vegetation indices such as the Normalized Difference Vegetation Index (NDVI) (Almagro et al. 2019a, b). Usually, NDVI directly correlated to the C-factor by linear or exponential regression (Yue-Qing et al. 2008; Van der Knijff et al. 1999). An alternative approach for an approximation of the P-factor based on empirical equations. For instance, Wener’s method assumes that the P-factor linked to topographical features, and slope gradient (Panagos et al. 2015; Terranova et al. 2009; Phinzi and Ngetar 2019). The RUSLE method reported overestimating erosion in high terrain (Ganasri and Ramesh 2016; Uddin et al. 2018). The Rich Mesic Forest (RMF) and Mesic Forest (MF) models better estimates over a slope with ground data (Fall et al. 2011; Bellemare et al. 2005). Comprehensive research appropriate for accurate estimation of erosion model and ground measurements.

Conclusions

The severity assessment of soil erosion GIS-based RUSLE equation considering rainfall, soil, DEM, land use, and land cover. The soil erosion rate categorized into six classes based on its severity, and 5.01% of the regions found under extreme risk (> 80 Mg ha−1 year−1) 70% of areas remained in a low-risk zone. This show area with high elevation along with prompt rainfall susceptible to soil erosion. The predicted severity can provide a basis for conservation and planning processes at the decision-makers. The regions with high to very severe soil erosion warrant special priority and control measures. While this model forms a basis on mapping and prediction using remote sensing and GIS-based analysis for vulnerability zones, such studies suggested for conservation and refining the model in the future.