Background

The seru production, conceived at Sony, is an innovation of assembly system used widely in the Japanese electronics industry and recognized a new production patten. Seru is a manufacturing organization (an assembly unit) that consists of simple equipment and one or several worker(s) that are dedicated to one or several product(s). In seru, worker(s) must be multi-skilled operators, i.e., workers can operate the most or all processes of production.

To compete in a turbulent market, in 1992, several mini-assembly units were created in one of Sony’s video-camera factories for an 8-mm CCD-TR55 video-camera, after dismantling a long assembly conveyor line. As did the original conveyor line, each mini-assembly unit produced the entire product. In 1994, Tatsuyoshi Kon, a former Sony staff, called this mini-assembly organization as seru, a Japanese word for cellular organism. Seru is similar to assembly cells, a widely adopted assembly system in western industries. Equipment, however, is less important for seru. As a human-centered assembly system, seru is an old-fashioned workshop where craftsperson, including jack-of-all-trades workers, assembles an entire product from-start-to-finish by her- or himself. This mini-assembly organization is regarded as an ideal combination of lean and agile production paradigms. By adopting seru production, Canon and Sony reduced 720,000 and 710,000 m2 of floor space, respectively (Stecke et al. 2012). Cost can also be reduced largely by using seru systems. After adopting seru systems, Canon’s costs were reduced significantly, by 55 billion yen in 2003, and by a total of 230 billion yen from 1998 to 2003. As a result, Canon emerged as a leading electronics maker. Its average productivity is higher than that of Toyota (Yin et al. 2008). Other benefits from seru systems include the reductions of throughput time, setup time, required labor hours, WIP inventories, and finished-product inventories. Some amazing cases related to the reductions in throughput time and required labor hours, the throughput time was reduced by 53 % at Sony Kohda and 35,976 required workers, equal to 25 % of Canon’s previous total workforce, have been saved.

There are three types of seru: divisional seru, rotating seru, and yatai. A divisional seru is a short line staffed with several partially cross-trained workers. Tasks within a divisional seru are divided into different sections. Each section is operated by one or more workers. Workers staffed within rotating seru or yatais are completely cross-trained. A rotating seru is often organized in a U-shaped layout with several workers. Each worker assembles an entire product from-start-to-finish without disruption. A yatai is the seru with a single worker who does all operational and managerial tasks. An NEC (Nippon Electric Company in Japan) completely cross-trained worker can assemble a word processor of 120 components in 18 min (Shinohara 1995; Stecke et al. 2012). In this research, the serus are rotating serus or yatai. A detailed introduction of seru system and its managerial mechanism can be found in Yin et al. (2008), Liu et al. (2010) and Stecke et al. (2012).

Due to the merit of seru production, many companies converted assembly line into seru system to increase the productivity. The line-seru (or line-cell) conversion was used widely in the Japanese electronics industry (Isa and Tsuru 1999; Miyake 2006; Sakazume 2005, 2012; Shinobu 2009; Yoshimoto 2003). Its essence is to convert traditional conveyor assembly line to a seru system in which one (or multiple) worker performs the most of all tasks the seru. The total productivity of manufacturers may be increased dramatically by line-seru conversion (Johnson 2005; Kaku et al. 2009; Stecke et al. 2012; Yin et al. 2008). Liu et al. (2014) proposed an implementation framework and process for converting the assembly line into a seru system.

The first issue of line-seru conversion is to establish the mathematical model. Such technical and decision making problems had been defined as line-seru conversion problems (Kaku et al. 2009). Kaku et al. (2009) considered three types of systems including a pure seru system (as shown in Fig. 1, where two serus are constructed, i.e., workers 2 and 5 in seru 1 and workers 1, 3 and 4 in seru 2), a pure assembly line and a hybrid system with serus and line. The pure seru system is very simple and a special case of all other seru assembly systems. The results obtained for pure seru system models not only provide insights into the pure seru system environment, they also provide a basis for heuristics that are applicable to more complicated assembly seru system environments. Therefore, many literatures focused on converting the assembly line to a pure seru system, such as Yu et al. (2012, 2013, 2014). Also, the research considers the assembly line is converted to a pure seru system.

Fig. 1
figure 1

An example of converting assembly line to a pure seru system (Yu et al. 2012)

Full size image

Another key of line-seru conversion is to evaluate the performance improvement created by the conversion. Kaku et al. (2009) used total throughput time (TTPT) and total labor hours (TLH) to evaluate the performance improvement created by line-seru conversion. Kaku et al. (2009) and Yu et al. (2012) investigated the operational influence factors to TTPT and TLH. They summarized several managerial insights that could be used to improve the performances of TTPT and TLH through line-seru conversion. Yu et al. (2013) evaluated the performance improvement from the perspective of manpower reduction. They established the line-seru conversion model towards reducing worker(s) and proposed an exact algorithm.

Also, the decision problem in line-seru conversion is widespread concerned. In fact, line-seru conversion includes two decision problems, i.e., seru formation and seru load (Yu et al. 2012, 2013, 2014). Most of previous researches focused on seru formation. Yu et al. (2012) investigated how to format serus to improve the performances of TTPT and TLH. Yu et al. (2013) clarified the complexity of seru formation towards reducing workers. Yu et al. (2014) revealed the mathematical characteristics of seru formation such as solution space, complexity and non-convex properties. Regarding seru load, most researches used given scheduling rule to assign product batches to serus, because seru load is NP-hard. Yu et al. (2012, 2013, 2014) used the FCFS (First Come First Severed) rule to dispatch product batches into serus. Therefore, the seru load should be investigated.

This paper, originally motivated by line-seru conversion applications of Sony and Canon, has two purposes. First, we demonstrate the influence of ten different scheduling rules usually used in seru load on the performance of line-seru conversion. Subsequently, we clarify exactly the complexities of seru load and line-seru conversion for the ten scheduling rules. Second, to obtain Pareto-optimal solutions for the large-scale instances of line-seru conversion, we propose two improved exact algorithms by decreasing time complexity and space complexity respectively.

The remainder of this study is organized as follows. The bi-objective model of converting the assembly line into a pure seru system with minimizing TTPT and TLH is given in the second section. The third section illustrates the influence of ten scheduling rules on the TTPT and TLH performances of seru system. The forth section clarifies exactly the complexities of seru load and line-seru conversion for ten scheduling rules. In the fifth section, two exact algorithms are developed based on reducing time complexity and space complexity. Several examples to illustrate the performance of the two proposed algorithms are given in the sixth section. In the last section conclusions and future research are given. All theorem proofs can be found in the “Appendix”.

Multi-objective model of converting the assembly line into a pure seru system

Assumption

The following assumptions are considered in this study.

  1. 1.

    The types and batches of products to be processed are known in advance. There are N product types that are divided into M product batches. Each batch contains a single product type.

  2. 2.

    The assembly tasks within a seru are manual so need only simple and cheap equipment and the cost of duplicating equipment is ignored (Stecke et al. 2012; Yu et al. 2012).

  3. 3.

    A product batch is assembled entirely within a seru.

  4. 4.

    All product types have the same assembly tasks. If a task is not used in a product, then we assume the task time for the product was zero.

  5. 5.

    In the assembly line, each task (or station) is in the charge of a single worker. That means that a worker only performs a single assembly task in the assembly line. Therefore, the total number of tasks in the line equals W.

  6. 6.

    The assembly tasks within each seru are the same as the ones within the line. A seru worker needs to perform all assembly tasks, assembles an entire product from-start-to-finish, and there is no disruption or delay between adjacent tasks.

Indices

i :

Index of workers (i = 1,2,…,w). w is the total number of workers in an assembly line.

j :

Index of serus (j = 1,2,…,J). J is the total number of serus in a seru system.

n :

Index of product types (n = 1, 2,…, N). N is the total number of product types.

m :

Index of product batches (m = 1, 2,…, M). M is the total number of product batches.

k :

Index of the sequence of product batches in a seru (k = 1, 2,…, M).

q :

Index of sub-sets of all the feasible seru systems (q = 1, 2,…, Q). Q is the total number of sub-sets.

Parameters

$$Vmn = \left\{ \begin{array}{ll} 1,&\quad{\text{if product type of product batch }}m{\text{ is }}n \hfill \\ 0,&\quad{\text{otherwise }} \hfill \\ \end{array} \right..$$
B m :

Size of product batch m.

T n :

Cycle time of product type n in the assembly line.

SL n :

setup time of product type n in the assembly line.

SCP n :

Setup time of product type n in a seru.

T mj :

Average task time of seru j assembling product batch m.

η i :

Upper bound on the number of tasks for worker i in a seru. If the number of tasks assigned to worker i is more than η i , worker i’s average task time within a seru will be longer than her or his task time within the original assembly line.

ε i :

Worker i’s coefficient of influencing level of doing multiple assembly tasks.

β ni :

Skill level of worker i for each task of product type n

.

Decision variables

$$Xij = \left\{ {\begin{array}{*{20}l} {1,} \hfill & {{\text{if}}\;{\text{worker}}\;i\;{\text{is}}\;{\text{assigned}}\;{\text{to}}\;{\text{seru}}\;j} \hfill \\ {0,} \hfill & {\text{otherwise }} \hfill \\ \end{array} } \right..$$
$$Zmjk = \left\{ {\begin{array}{*{20}l} {1,} \hfill & {{\text{if}}\;{\text{product}}\;{\text{batch}}\;m\;{\text{is}}\;{\text{assigned}}\;{\text{to}}\;{\text{seru}}\;j\;{\text{in}}\;{\text{sequence}}\;k} \hfill \\ {0,} \hfill & {\text{otherwise}} \hfill \\ \end{array} } \right..$$

Variables

C i :

Coefficient of variation of worker i’s increased task time after line-seru conversion, i.e., from a specialist to a completely cross-trained worker. if the number of worker i’s tasks within a seru is over her or his upper bound η i , i.e., w > η i , then the worker will cost more average task time than her or his task time within the original assembly line. c i is given in Eq. (1).

TC m :

Assembly task time of product batch m per station in a seru. In a seru, the task time of product type n is calculated by the average task time of workers in the seru. TC m is represented as Eq. (2).

FCB m :

Begin time of product batch m in a seru. There is no waiting time between two product batches so that FCB m is the aggregation of flow time and setup time of the product batches processed prior to product batch m in the same seru. FCB m is represented as Eq. (3).

SC m :

Setup time of product batch m in a seru. Setup time is considered when two different types of products are processed consecutively; otherwise the setup time is zero. For example, in Eq. (4), two adjacent assembled products in a seru are expressed as m and m′. If the product type of m is different with that of m′, i.e., V mn  = 1, \(V_{{m^{{\prime }} n}} = 0\), and then the setup time of batch m is SCP n V mn . However, if the product types of m and m′ are identical, i.e., \(V_{mn} = V_{{m^{{\prime }} n}} = 1\), and then the setup time of batch m is 0.

FC m :

Flow time of product batch m in a seru. FC m is represented as Eq. (5).

$$C_{i} = \left\{ {\begin{array}{*{20}l} {\begin{array}{*{20}l} {1 + \varepsilon_{i} (W - \eta_{i} ),} \hfill & {W > \eta_{i} } \hfill \\ {1,} \hfill & {W \le \eta_{i} } \hfill \\ \end{array} } \hfill & {\forall i} \hfill \\ \end{array} } \right.$$
(1)
$$TC_{m} = \frac{{\sum\nolimits_{n = 1}^{N} {\sum\nolimits_{i = 1}^{W} {\sum\nolimits_{j = 1}^{J} {\sum\nolimits_{k = 1}^{M} {V_{mn} T_{n} \beta_{ni} C_{i} X_{ij} Z_{mjk} } } } } }}{{\sum\nolimits_{i = 1}^{W} {\sum\nolimits_{j = 1}^{J} {\sum\nolimits_{k = 1}^{M} {X_{ij} Z_{mjk} } } } }}$$
(2)
$$FCB_{m} = \sum\limits_{s = 1}^{m - 1} {\sum\limits_{j = 1}^{J} {\sum\limits_{k = 1}^{m} {(FC_{s} + SC_{s} )Z_{mjk} Z_{sj(k - 1)} } } }$$
(3)
$$SC_{m} = \left\{ {\begin{array}{*{20}c} {\begin{array}{*{20}l} {SCP_{n} V_{mn} ,} \hfill & {V_{mn} = 1,\;V_{{m^{{\prime }} n}} = 0} \hfill \\ {0,} \hfill & {V_{mn} = V_{{m^{{\prime }} n}} = 1} \hfill \\ \end{array} } & {(m^{{\prime }} |Z_{mjk} = 1,\;Z_{{m^{{\prime }} j(k - 1)}} = 1,\quad \forall j,k)} \\ \end{array} } \right.$$
(4)
$$FC_{m} = \frac{{B_{m} TC_{m} W}}{{\sum\nolimits_{i = 1}^{W} {\sum\nolimits_{j = 1}^{J} {\sum\nolimits_{k = 1}^{M} {X_{ij} Z_{mjk} } } } }}$$
(5)

TTPT and TLH of the seru system

The total throughput time (TTPT) and the total labor hours (TLH) of the seru system are expressed as follows.

$${\text{TTPT}}\;{\text{of}}\;seru\;{\text{system}} = \mathop {\text{Max}}\limits_{m} (FCB_{m} + FC_{m} + SC_{m} )$$
(6)
$${\text{TLH}}\;{\text{of}}\;seru\;{\text{system}} = \sum\limits_{m = 1}^{M} {\sum\limits_{i = 1}^{W} {\left( {\sum\limits_{j = 1}^{J} {\sum\limits_{k = 1}^{M} {FC_{m} } } X_{ij} Z_{mjk} } \right)} }$$
(7)

TTPT of seru system is the completion time of the last completed product batch. TLH of seru system is the cumulative working time of all workers in the seru system. Given product batches, the seru systems should have shorter TTPT and TLH than the line.

Formulation of bi-objective line-seru conversion with minimizing TTPT and TLH

The mathematical model is formulated as Eqs. (8)–(13).

Objective functions:

$${\text{Min}}\;{\text{TTPT}}\;{\text{of}}\;seru\;{\text{system}}$$
(8)
$${\text{Min}}\;{\text{TLH}}\;{\text{of}}\;seru\;{\text{system}}$$
(9)

Subject to:

$$1 \le \sum\limits_{i = 1}^{W} {X_{ij} } \le W,\quad \forall j$$
(10)
$$\sum\limits_{j = 1}^{J} {X_{ij} } = 1,\quad \forall i$$
(11)
$$\sum\limits_{j = 1}^{J} {\sum\limits_{k = 1}^{M} {Z_{mjk} } } = 1,\quad \forall m$$
(12)
$$\sum\limits_{m = 1}^{M} {\sum\limits_{k = 1}^{M} {Z_{mjk} } } = 0,\quad \left(\forall j|\sum\limits_{i = 1}^{W} {X_{ij} } = 0\right)$$
(13)

where Eq. (8) minimizes the total throughput time (TTPT). Equation (9) minimizes the total labor hours (TLH). Equation (10) is the number constraint that the number of workers within a seru must be in the interval of [1, W]. Equation (11) is the worker assignment rule, i.e., each worker should be assigned to one and only one seru. Equation (12) is the product batch assignment rule, i.e., each batch should be assigned to one and only one seru. Equation (13) is the rule of assigning constraint, i.e., a product must be assigned to a seru in which at least one worker is assigned. In other words, for a seru without any worker, i.e., \(\forall j|\sum\nolimits_{i = 1}^{W} {X_{ij} } = 0\), any batch cannot be assigned into the seru, i.e., \(\sum\nolimits_{m = 1}^{M} {\sum\nolimits_{k = 1}^{M} {Z_{mjk} } } = 0\).

Influence of the scheduling rules on line-seru conversion

Line-seru conversion includes seru formation and seru load (Yu et al. 2012). Seru load determines which product batches are dispatched to the serus formed in seru formation. Seru formation determines how many serus to be constructed and how to assign the workers into serus. A detailed introduction of seru formation can be found in Yu et al. (2012, 2013, 2014).

Property 1

Given a seru formation, without a given scheduling rule seru load is NP-hard.

Explanation

Without a given scheduling rule, in seru load, each product batch can be assigned into any seru in the given seru formation. Therefore, seru load is an assignment and NP-hard problem.

Thus, for simplicity, earlier researches (Kaku et al. 2009; Yu et al. 2012, 2013, 2014) fixed the scheduling rules on seru load such as FCFS and SPT.

However, the different scheduling rules produce different performances or complexity of a system (Chuen and Robert 1993; Grabot and Geneste 1994; Holthaus and Rajendran 1997; Amirghasemi and Zamani 2014; Nurre and Sharkey 2014; Xu et al. 2015; Zeng et al. 2015). The comparative analysis of scheduling rules in some specific industrial environments can be found in Rajendran and Holthaus (1999), Kizil et al. (2006), Chiang and Fu (2007), Akturk (2011), and Li et al. (2015).

To investigate the influence of scheduling rules on the performance of line-seru conversion, we used a total of ten scheduling rules of seru load. The ten scheduling rules are selected from Seru production applications of Sony and Canon, because the ten rules are usually used in Seru production. The ten scheduling rules used in the paper are defined in detailed as follows.

To illustrate clearly that TTPT and TLH of line-seru conversion are influenced by the different scheduling rules, we used 5 product batches and 2 serus, where worker 1 in seru 1 and worker 2 in seru 2. The data of task time of 5 batches on 2 seru is shown in Table 1. The data of the earliest due date (EDD) of 5 batches is shown in Table 2.

Table 1 Task time of five batches on 2 serus
Full size table
Table 2 Earliest due date of 5 batches
Full size table

First come first served (FCFS)

This rule is often used as a bench-mark. FCFS of seru load is described as following: an arriving product batch is assigned to the empty seru with the smallest seru number. If all serus are occupied, the product batch is assigned to the seru with the earliest completion time. Result with FCFS on seru load shows in Fig. 2, where TTPT is 10 and TLH is 19.

Fig. 2
figure 2

Result of FCFS rule on seru load with the seru sequence of {1}–{2}

Full size image

Last come first served (LCFS)

LCFS of seru load is described as following: the last arriving product batch is assigned to the empty seru with the smallest seru number. If all serus are occupied, the product batch is assigned to the seru with the earliest completion time. Result with LCFS on seru load shows in Fig. 3, where TTPT is 7 and TLH is 14.

Fig. 3
figure 3

Result of LCFS rule on seru load with the seru sequence of {1}–{2}

Full size image

Shortest processing time (SPT)

This rule is perhaps the most commonly used rule for job shop scheduling. SPT of seru load is described as following: an arriving product batch is assigned to the seru with the shortest processing time for it. The shortest processing time (SPT) of batch m is \(\mathop {\hbox{min} }\nolimits_{j = 1}^{J} (Tmj)\), e.g., SPTs of batches 1 and 2 are 1 and 4 respectively. Result with SPT on seru load shows in Fig. 4, where TTPT is 10 and TLH is 13.

Fig. 4
figure 4

Result of SPT rule on seru load with the seru sequence of {1}–{2}

Full size image

Earliest completion time (ECT)

As shown in Fig. 4, SPT rule on seru load may cause the imbalance among serus. For example, the difference between the two serus in Fig. 4 is 7 = 10-3. Therefore, Yu et al. (2012) proposed that the balance among serus should be considered in seru load. ECT of seru load is described as following: an arriving product batch is assigned to the seru with the earliest completion time of finishing the batch. Result with ECT on seru load shows in Fig. 5, where TTPT is 7, TLH is 14, and the difference between the two serus is 0.

Fig. 5
figure 5

Result of ECT rule on seru load with the seru sequence of {1}–{2}

Full size image

Earliest due-date first (EDD)

This rule is often used in industries for its simplicity of implementation. EDD of seru load is described as following: the product batch with the earliest due-date is selected and assigned to the seru with the shortest processing time for the batch. Result with EDD on seru load shows in Fig. 6, where TTPT is 10 and TLH is 13.

Fig. 6
figure 6

Result of EDD rule on seru load with the seru sequence of {1}–{2}

Full size image

Modified earliest due-date first (MEDD)

MEDD of seru load is described as following: the product batch with the earliest due-date is selected and assigned to the seru with the earliest completion time of finishing the batch. Result with MEDD on seru load shows in Fig. 7, where TTPT is 8 and TLH is 16.

Fig. 7
figure 7

Result of MEDD rule on seru load with the seru sequence of {1}–{2}

Full size image

Minimal Shortest Processing Time first (MSPT)

MSPT of seru load is described as following: the product batch with the minimal shortest processing time is selected and assigned to the seru with the shortest processing time for it. MSPT is the minimal SPT of all batches, i.e., \(\mathop {\hbox{min} }\nolimits_{m = 1}^{M} \mathop {\hbox{min} }\nolimits_{j = 1}^{J} (Tmj)\). For example, MSPT of Table 1 is 1. Result with MSPT on seru load shows in Fig. 8, where TTPT is 10 and TLH is 13.

Fig. 8
figure 8

Result of MSPT rule on seru load with the seru sequence of {1}–{2}

Full size image

Modified minimal shortest processing time first (MMSPT)

MMSPT of seru load is described as following: the product batch with the minimal shortest processing time is selected and assigned to the seru with the earliest completion time of finishing the batch. Result with MMSPT on seru load shows in Fig. 9, where TTPT is 9 and TLH is 15.

Fig. 9
figure 9

Result of MMSPT rule on seru load with the seru sequence of {1}–{2}

Full size image

Longest shortest processing time first (LSPT)

LSPT of seru load is described as following: the product batch with the longest shortest processing time is selected and assigned to the seru with the shortest processing time for it. LSPT is the longest SPT of all batches, i.e., \(\mathop {\hbox{max} }\nolimits_{m = 1}^{M} \mathop {\hbox{min} }\nolimits_{j = 1}^{J} (Tmj)\). For example, LSPT of Table 1 is 4. Result with LSPT on seru load shows in Fig. 10, where TTPT is 10 and TLH is 13.

Fig. 10
figure 10

Result of LSPT rule on seru load with the seru sequence of {1}–{2}

Full size image

Modified longest shortest processing time first (MLSPT)

MLSPT of seru load is described as following: the product batch with the longest shortest processing time is selected and assigned to the seru with the earliest completion time of finishing the batch. Result with MLSPT on seru load shows in Fig. 11, where TTPT is 7 and TLH is 14.

Fig. 11
figure 11

Result of MLSPT rule on seru load with the seru sequence of {1}–{2}

Full size image

Based on Figs. 2, 3, 4, 5, 6, 7, 8, 9, 10 and 11, we can obtain Table 3. Table 3 shows that the different scheduling rules on seru load cause different TTPTs and TLHs of the converted seru system even though the seru formation is identical.

Table 3 Result of 10 scheduling rules used in seru load with the same seru formation
Full size table

From Table 3, we can see that scheduling rules have a significant effect on the performance of converted seru system with the same seru formation. For example, the best and worst TTPT in the ten scheduling rules are 7 and 10 respectively, and the best and worst TLH in the ten scheduling rules are 13 and 19. Therefore, the investigation on scheduling rules used in seru load is important for Seru production. Consequently, we clarify the complexities of solution spaces of seru load and line-seru conversion for the ten scheduling rules from the theoretical perspective. The clarification of complexity of solution space makes it possible to obtain the optimal solution or Pareto-optimal solutions of line-seru conversion.

Complexity of seru load and line-seru conversion for the different scheduling rules

The line-seru conversion is a two-stage decision process, i.e., seru formation and seru load (Yu et al. 2012, 2014). Therefore, the complexity of line-seru conversion should be clarified by combining the complexity of seru formation with the complexity of seru load.

Complexity of seru formation

Seru formation is the first step of line-seru conversion. Distinguished from the traditional manufacturing cell formation problems (Safaei and Tavakkoli-Moghaddam 2009; Wu et al. 2009), seru formation in line-seru conversion is to determine how many serus to be formed and how to assign workers into the serus (Yu et al. 2012). Seru formation is decided by decision variable X ij .

Property 2

Seru formation of line-seru conversion is an instance of the unordered set partition problem and NP-hard.

Explanation

Seru formation is to partition a conveyor line with W workers into pair-wise disjoint nonempty serus, and so seru formation is an instance of the unordered set partition problem. Set partitioning is a well-known NP-hard problem (Garey and Johnson 1979). The detailed proof can be found in Yu et al. (2013).

Since seru formation is an instance of the unordered set partition, the number of all the feasible solutions of seru formation can be expressed as:

$$F(W) = \sum\limits_{J = 1}^{W} {P (W ,J )}$$
(14)

where P(W, J) is the count of partitioning W workers in assembly line into J serus and can be expressed as the Stirling numbers of the second kind (Rennie and Dobson 1969; Williamson 1985; Knopfmacher and Mays 2006; Klazar 2003).

Complexities of seru load for the different scheduling rules

Seru load is the second step of line-seru conversion and is decided by decision variable Z mjk . It determines which product batches are dispatched to the serus formed in seru formation (Chen et al. 2013; Solimanpur and Elmi 2013).

According to Properties 1 and 2, line-seru conversion is a complex problem including two NP-hard problems (i.e., seru formation and seru load). For simplicity and without loss of generality, the scheduling rule in seru load is usually given. However, even given a scheduling rule in seru load, line-seru conversion is still an NP-hard problem because seru formation is NP-hard.

Different scheduling rules produce different performances or complexity of line-seru conversion. Up to now, the influences of scheduling rules to line-seru conversion are not investigated yet. Therefore, one objective of this study is to clarify the influence of different scheduling rules to complexity of line-seru conversion. Since the complexity of seru formation is independent of scheduling rule, we focus on clarifying the influence of different scheduling rules to complexity of seru load.

Gven a seru formation, the number of solutions (S) of seru load can be expressed by the number of serus (J).

Theorem 1

Given a seru formation with J serus, without given a scheduling rule, S =  J M.

Proof

See Proof of Theorem 1 in “Appendix”.

As described in Property 1 and Theorem 1, seru load is NP-hard and has J M feasible solutions. For simplicity, therefore, earlier researches used the typical scheduling rules such as FCFS and SPT.

In addition, the number of solutions (S) of seru load varies with the scheduling rules. For example, for the line with two workers labeled 1 and 2, there are two solutions of seru formation, i.e., {{1,2}} and {{1},{2}}. For the latter solution of {{1},{2}}, there are two seru sequences, i.e., {1}–{2} and {2}–{1}.

For the 5 product batches in Table 1, there are two results of seru load with FCFS. The result of {1}–{2} is shown in Fig. 2 and the result of {2}–{1} is shown in Fig. 12. This means the seru sequence does influence the result of seru load with FCFS.

Fig. 12
figure 12

Result with FCFS rule on seru load with the seru sequence of {2}–{1}

Full size image

However, for the 5 product batches in Table 1, there is only one result of seru load with SPT. For the seru sequence of {1}–{2}, the result of seru load with SPT is shown in Fig. 4. For the seru sequence of {2}–{1}, the result of seru load with SPT is shown in Fig. 13. By comparing Figs. 4 and 13, we can easily observe that the two results are identical. This is because regardless of the seru sequence, using SPT an arriving batch is always assigned to the seru with the shortest processing time for it. This means the seru sequence does not influence the result of seru load with SPT.

Fig. 13
figure 13

Result with SPT rule on seru load with the seru sequence of {2}–{1}

Full size image

Therefore, the ten scheduling rules are divided into two classes: (1) scheduling rules related to seru sequence (SRRSS); and (2) scheduling rules unrelated to seru sequence (SRUSS). A SRRSS rule is the one with which the seru load result is influenced by the seru sequence. However, a SRUSS rule means that the seru load result is independent of the seru sequence using the rule. In the ten scheduling rules, FCFS and LCFS belong to SRRSS, but the other eight scheduling rules belong to SRUSS. Thus, we clarify the complexity of seru load with the ten scheduling rules from the two classes.

Complexity (S) of seru load with SRRSS is clarified in Theorems 2–3. Complexity (S) of seru load with SRUSS is clarified in Theorem 4.

Theorem 2

Given a seru formation with J serus, if seru load uses a SRRSS and M ≥ J, S = J! = \(P_{J}^{J}\).

Proof

See Proof of Theorem 2 in “Appendix”.

Theorem 3

Given a seru formation with J serus, if seru load uses a SRRSS and M < J, S = \(C_{J}^{M} P_{M}^{M} = P_{J}^{M}\).

Proof

See Proof of Theorem 3 in “Appendix”.

Theorem 4

Given a seru formation with J serus, if seru load uses a SRUSS, S = 1.

Proof

See Proof of Theorem 4 in “Appendix”.

Subsequently, the complexity (T(W)) of line-seru conversion with the different scheduling rules can be clarified by combining the complexity of seru formation (F(W)) with the complexity of seru load (S).

Complexities of line-seru conversion with the different scheduling rules

The complexities (T(W)) of line-seru conversion with the different scheduling rules are summarized in Table 4.

Table 4 Complexities (T(W)) of line-seru conversion with the different scheduling rules
Full size table

The clarification of complexity of solution space makes it possible to obtain the optimal solution or Pareto-optimal solutions of line-seru conversion.

Two improved exact approaches for multi-objective line-seru conversion

Multi-objective decisions are often used in line-seru conversion (Kaku et al. 2009; Yu et al. 2013, 2014). However, multi-objective optimization is more difficult to solve than single-objective optimization (Ebrahimipour et al. 2015). Enumeration algorithm based on non-dominated sorting (Deb et al. 2002) for multi-objective line-seru conversion is described as follows.

figure a

Step (1) is to produce all the feasible solutions (N) with the given scheduling rule. Both time complexity and space complexity are O(N).

Step (2) is to calculate TTPT and TLH of each feasible solution. Time complexity is O(N), but space complexity is O(4N) for storing seru sequence, TTPT, TLH and the batches assigned in each seru.

Step (3) is to obtain exact Pareto-optimal solutions by non-dominated sorting of Deb et al. (2002). Time complexity of non-dominated sorting is O(2N 2), where 2 is the number of objectives. Space complexity is O(N).

Therefore, time complexity and space complexity of the enumeration algorithm are O(2N 2) and O(4N) respectively.

However, because of the higher time complexity (i.e., O(2N 2)), the enumeration cannot obtain the Pareto-optimal solutions for the instances with more than 6 workers using a SRRSS. We develop two improved exact algorithms for the large-scale instances by decreasing time complexity and space complexity respectively.

The improved exact algorithm by decreasing time complexity

When the solutions attending non-dominated sorting are reduced by R, the time complexity will be improved by \(\left( {1 - \frac{{(N - R)^{2} }}{{(N)^{2} }}*100\;\% } \right)\).

Therefore, we consider to cut off the solutions dominated by the certain Pareto-optimal solution(s) before running non-dominated sorting algorithm. The certain solutions are defined in Definitions 1 and 2.

Definition 1

mTTPT is the Pareto-optimal solution with the minimal TTPT.

Definition 2

mTLH is the Pareto-optimal solution with the minimal TLH.

By cutting off the solutions dominated by mTTPT or mTLH before non-dominated sorting, time complexity can be decreased greatly. The methods to find out the solutions dominated by mTTPT and mTLH are described in Theorems 5 and 6 respectively.

Theorem 5

If a solution’s TLH is more than mTTPT’s, then the solution must be dominated by mTTPT.

Proof

See Proof of Theorem 5 in “Appendix”.

Theorem 6

If a solution’s TTPT is more than mTLH’s, then the solution must be dominated by mTLH.

Proof

See Proof of Theorem 6 in “Appendix”.

The improved exact algorithm by decreasing time complexity is described as follows.

figure b

In step (1), both time complexity and space complexity are O(N).

In step (2), time complexity is O(N) and space complexity is O(4N).

Step (3) is to obtain mTTPT and mTLH by traversal all the feasible solutions. Both time complexity and space complexity are O(N).

Step (4) is to obtain the solutions non-dominated (assume the number is K) by mTTPT or mTLH by traversing all the feasible solutions. Both time complexity and space complexity are O(N).

Step (5) is to obtain the exact Pareto-optimal solutions by non-dominated sorting the K solutions obtained in step (4). The time complexity is O(2K 2) and space complexity is O(K).

The key of the improved exact algorithm by decreasing time complexity is leis in step (4), i.e., the operation of “S←S/{S i }”. That cuts off the solutions dominated by mTTPT or mTLH before non-dominated sorting, i.e., step (5).

Obviously, for the improved exact algorithm by decreasing time complexity, the time complexity is the maximum between O(2K 2) and O(N). Space complexity is O(4N) still. Therefore, we propose another improved exact algorithm by decreasing space complexity.

The improved exact algorithm by decreasing space complexity

If we partition all the feasible solutions (N) in several sub-sets to obtain the non-dominated solutions of each sub-set, then the space complexity will be decreased. Subsequently, the Pareto-optimal solutions can be obtained by sorting the non-dominated solutions in all sub-sets. The improved exact algorithm by decreasing space complexity is described as follows.

figure c

Step (1) is to initialize.

Step (2) is to partition all the produced feasible solutions into Q sub-sets. In each sub-set, there are approximately \(\frac{N}{Q}\) solutions.

Step (3) calculates the TTPT and TLH of each solution in each sub-set. The time complexity is \(O\left( {\frac{N}{Q}} \right)\) and space complexity is \(O\left( {4\frac{N}{Q}} \right)\).

Step (4) obtains non-dominated solutions (assume the number is S q ) of sub-set q using non-dominated sorting. The time complexity is \(O\left( {2\left( {\frac{N}{Q}} \right)^{2} } \right)\) and space complexity is \(O\left( {\frac{N}{Q}} \right)\).

Step (5) obtains the exact Pareto-optimal solutions by non-dominated sorting the \(\sum\nolimits_{q = 1}^{Q} {S_{q} }\) non-dominated solutions, where \(\sum\nolimits_{q = 1}^{Q} {S_{q} }\) non-dominated solutions refer to all sub-sets’ non-dominated solutions obtained in step (4). Time complexity is \(O\left( {2\left( {\sum\nolimits_{q = 1}^{Q} {S_{q} } } \right)}^{2} \right)\) and space complexity is \(O\left( {\sum\nolimits_{q = 1}^{Q} {S_{q} } } \right)\).

The key of the improved exact algorithm by decreasing space complexity lies in steps (2) and (4). Step (2) partitions the whole solution space into several sub-spaces. Step (4) produces the solutions to attend the final non-dominated sorting by aggregating the non-dominated solutions of all sub-spaces.

For the improved exact algorithm by decreasing space complexity, space complexity is the maximum between \(0\left( {4\frac{N}{Q}} \right)\) and \(O\left( {\sum\nolimits_{q = 1}^{Q} {S_{q} } } \right)\), and time complexity is the maximum between \(O\left( {2\left( {\frac{N}{Q}} \right)^{2} } \right)\) and \(O\left( 2{\left( {\sum\nolimits_{q = 1}^{Q} {S_{q} } } \right)^{2} } \right)\).

Computation experiments

Test instances

Tables 5, 6, 7, 8 and 9 show the parameters, data distribution and detail data of level of skill of workers, coefficient of influencing level of skill to multiple stations for workers and data of batches used in test, respectively. From the 5 Tables, it can be observed that the lot size of each batch is N(50,5) and the ability of workers is also different with stations and N(0.2,0.05). The detailed data of ε i and batches are given in Tables 7 and 8 respectively.

Table 5 Parameters in the experiments
Full size table
Table 6 Data distribution of worker’s level of skill (β ni )
Full size table
Table 7 Data of worker’s level of skill (β ni )
Full size table
Table 8 Coefficient of influencing level of skill to multiple stations for workers (ε i )
Full size table
Table 9 Data of batches
Full size table

Table 5 shows that the mean of skill level of each worker for product type n (β ni ) ranges from 1 to 1.2 and the standard deviations are fixed to 0.1. The detailed data of β ni are given in Table 6.

For the instance with W workers, we use the following data set from Tables 5, 6, 7, 8, 9: the entire Table 5, the first W rows of Tables 7 and 8, and the entire Table 9.

Hardware and software specifications

The two improved exact algorithms were coded in C# and executed on an Intel Core(TM) i7-4790 CPU @ 3.6 GHz under Windows 7 using 8 GB of RAM.

Computation results of the improved exact algorithm by decreasing time complexity

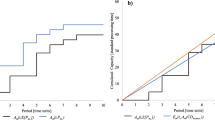
The enumeration based on non-dominated sorting cannot solve the instances with more than 6 workers using a SRRSS, such as FCFS. We use the improved exact algorithm by decreasing time complexity to solve the instances with 5, 6 and 7 workers. The computation results are shown in Figs. 14, 15, 16 respectively.

Fig. 14
figure 14

The solutions dominated by mTTPT and mTLH for the instance with 5 workers

Full size image
Fig. 15
figure 15

The solutions dominated by mTTPT and mTLH for the instance with 6 workers

Full size image
Fig. 16
figure 16

The solutions to attend non-dominated sorting for the instance with 7 workers

Full size image

Figure 14 shows 7 Pareto-optimal solutions, 541 feasible solutions, 493 solutions dominated by mTTPT or mTLH, and left 48 solutions to attend non-dominated sorting for the instance with 5 workers. Similarly, Fig. 15 shows 9 Pareto-optimal solutions, 4683 feasible solutions, 3831 solutions dominated by mTTPT or mTLH, and only left 852 solutions to attend non-dominated sorting for the instance with 6 workers. Figure 16 shows the Pareto-optimal solutions of the instance with 7 workers, where 10 Pareto-optimal solution and 2437 solutions to attend non-dominated sorting.

Table 10 shows the performance of the improved exact algorithm by decreasing time complexity for different instances.

Table 10 Performance of the improved exact algorithm by decreasing time complexity
Full size table

From Table 10, we can see that the improved exact algorithm by decreasing time complexity has a better performance than the enumeration based on non-dominated sorting because of cutting off approximately 89 % non Pareto-optimal solutions before running non-dominated sorting. Compared with the original non-dominated sorting algorithm, the step (5) saves approximately 98 % computational time. For example, for the instances with 5 and 6 workers, in step (5) the saved computational time are \(\left( {1 - \frac{0.002}{0.06}} \right)*100\;\% = 97\;\%\) and \(\left( {1 - \frac{0.03}{1.4}} \right)*100\;\% = 98\;\%\) respectively. That is because, by cutting off non-dominated solutions, the time complexities of non-dominated sorting are improved by \(\left( {\frac{48}{541}} \right)^{2} *100\;\%\) for the instance with 5 workers and by \(97\;\% = \left( {1 - \left( {\frac{852}{4,683}} \right)^{2} } \right)*100\;\%\) for the instance with 6 workers.

The enumeration based on non-dominated sorting cannot solve the instances with more than 6 workers. The improved exact algorithm by decreasing time complexity solves the instance with 7 workers in 2.87 s. The time complexities of non-dominated sorting are improved by \(99.7\;\% = \left( {1 - \left( {\frac{2,437}{47,293}} \right)^{2} } \right)*100\;\%\).

Moreover, we can easily observe the computation time of enumeration based on non-dominated sorting increases exponentially with the number of all solutions, however, the total time of the improved exact algorithm by decreasing time complexity increases linearly with the number of all solutions.

The improved exact algorithm by decreasing time complexity cannot solve the instance with more than 7 workers because 9749 left solutions cannot be solved by non-dominated sorting.

Computation results of the improved exact algorithm by decreasing space complexity

We use the improved exact algorithm by decreasing space complexity to solve the instances with 8 and 9 workers using FCFS rule. The numbers of sub-sets (Q) of instances with 8 and 9 workers are set as 8 and 9 respectively. The computation results are shown in Figs. 17 and 18 respectively.

Fig. 17
figure 17

The Pareto-optimal solutions of the instance with 8 workers

Full size image
Fig. 18
figure 18

The Pareto-optimal solutions of the instance with 9 workers

Full size image

Figure 17 shows that there are final 599 solutions to attend non-dominated sorting and 8 Pareto-optimal solutions for the instance with 8 workers. Similarly, Fig. 18 shows there are 19 Pareto-optimal solutions generated by non-dominated sorting final 1142 solutions in all 7,087,261 feasible solutions for the instance with 9 workers.

Table 11 shows the performance of the improved exact algorithm by decreasing space complexity for different instances.

Table 11 Performance of the improved exact algorithm by decreasing space complexity
Full size table

From Table 11, we can see that the improved exact algorithm by decreasing space complexity has a better performance than the improved exact algorithm by decreasing time complexity. That is because the improved exact algorithm by decreasing space complexity cuts off more non Pareto-optimal solutions before running final non-dominated sorting (i.e., Tables 10, 11). Moreover, the total time of the improved exact algorithm by decreasing space complexity increases linearly with the number of all solutions (N).

However when producing all the feasible solution (N) is not possible, the improved exact algorithm by decreasing space complexity cannot obtain the Pareto-optimal solutions. For example of the instance with 10 workers using FCFS rule, there are 102,247,563 feasible solutions of line-seru conversion, and the computer cannot produce all the feasible solutions.

Conclusions

Our contributions in this paper are summarized as following. First, we investigate the significant influence of the 10 selected scheduling rules on the TTPT and TLH performances of seru system. Subsequently, we clarify the complexities of seru load and line-seru conversion for ten different scheduling rules in detail. Second, we develop two improved exact algorithms based on reducing time complexity and space complexity respectively, to obtain Pareto-optimal solutions of multi-objective line-seru conversion. Compared with the enumeration based on non-dominated sorting, the two proposed algorithms greatly decrease time complexity and space complexity respectively and improve the computation performance by approximately 98 %.

The line-seru conversion is a real problem in Japan electronics industry, therefore there are still a lot of works should be performed. For example, the influence of scheduling rules on the performance improvements in line-seru conversion should be further researched. Furthermore, other important production performances of seru system should be evaluated, such as balancing (Esmaeilbeigi et al. 2015) and WIP. In addition, the situations under which workers can’t operate all tasks in a seru should be investigated, i.e., the fundamental principles of hybrid seru system with a short line and operation management of the seru system including divisional serus. Moreover, the further research should consider the number of assembly tasks varying with the product types. Also, the optimal methods to train the multi-skilled workers in seru production should be studied in future.