Abstract
The purpose of this paper is to introduce a new iterative algorithm for finding a common element of the set of solutions of a system of generalized mixed equilibrium problems, the set of common fixed points of a finite family of pseudo contraction mappings, and the set of solutions of the variational inequality for an inverse strongly monotone mapping in a real Hilbert space. We establish results on the strong convergence of the sequence by the proposed scheme to a common element of the above three solution sets. These results extend and improve some corresponding results in this area. Finally, we give a numerical example which supports our main theorem.
Similar content being viewed by others
1 Introduction
Let Θ be a bifunction from \(K\times K\) into the set of real numbers, R, where K is a nonempty closed convex subset of a real Hilbert space H. The equilibrium problem is to find a point \(x\in K\) such that
We denote the set of solutions of (1.1) by \(\operatorname{EP}(\Theta)\). The equilibrium problem includes the fixed point problem, the variational inequality problem, the optimization problem, the saddle point problem, the Nash equilibrium problem and so on, as its special cases [1, 2].
The generalized mixed equilibrium problem is to find a point \(x\in K\) such that
where φ is a function on K into R and A is a nonlinear mapping from K to H. The set of solutions of a generalized mixed equilibrium problem is denoted by \(\operatorname{GMEP}(\Theta,A,\varphi)\).
If we consider \(\Theta=0\) and \(\varphi=0\) in (1.2), then we have the classical variational inequality problem which is to find a point \(x\in K\) such that
The solution set of (1.3) is denoted by \(\operatorname{VI}(K, A)\).
To proceed we need to recall some definitions and concepts.
Definition 1.1
Let K be a nonempty closed convex subset of a real Hilbert space H.
-
(i)
A mapping \(S:K\rightarrow K\) is called nonexpansive if \(\| Sx-Sy\|\leq\|x-y\|\), for all \(x,y\in K\).
-
(ii)
A mapping \(T:K\rightarrow K\) is called k-strict pseudo contractive mapping, if for all \(x,y\in K\) there exists a constant \(0\leq k<1\) such that
$$ \Vert Tx-Ty\Vert ^{2}\leq \Vert x-y\Vert ^{2}+ k\bigl\Vert (I-T)x-(I-T)y\bigr\Vert ^{2},\quad \forall x,y\in K, $$(1.4)where I is the identity mapping on K.
-
(iii)
A mapping \(A:H\rightarrow H\) is called monotone if for each \(x,y\in H\),
$$\langle Ax-Ay,x-y\rangle\geq0. $$ -
(iv)
A mapping \(A:H\rightarrow H\) is called β-inverse strongly monotone if there exists \(\beta> 0\) such that
$$ \langle Ax-Ay,x-y\rangle\geq\beta\|Ax-Ay\|^{2},\quad \forall x,y\in H. $$ -
(v)
The mapping \(A:K\rightarrow H\) is L-Lipschitz continuous if there exists a positive real number L such that \(\|Ax-Ay\|\leq L\| x-y\|\) for all \(x,y\in H\). If \(0< L<1\), then the mapping A is a contraction with constant L.
Clearly a nonexpansive mapping is a 0-strict pseudo contractive mapping [3]. Note that in a Hilbert space, (1.4) is equivalent to the following inequality:
We denote \(F(T)=\{x\in K : Tx=x\}\), the set of fixed points of T. It can be shown that, for a k-strict pseudo contractive mapping \(T:K\rightarrow K\), the mapping \(I-T\) is demiclosed, i.e., if \(\{x_{n} \}\) is a sequence in K with \(x_{n}\rightharpoonup q\) and \(x_{n}-Tx_{n}\rightarrow0\), then \(q\in F(T)\) (refer to [4]). The symbols ⇀ and → denote weak and strong convergence, respectively.
A set valued mapping \(Q:H\rightarrow2^{H}\) is called monotone if for all \(x,y\in H\), \(f\in Q(x)\) and \(g\in Q(y)\) imply \(\langle x-y,f-g\rangle\geq0\). A monotone mapping \(Q:H\rightarrow2^{H}\) is maximal if the graph \(G(Q)\) of Q is not properly contained in the graph of any other monotone mapping. It is well known that a monotone mapping Q is maximal if and only if for \((x,f )\in H\times H\), \(\langle x-y,f-g\rangle \geq0\) for every \((y,g)\in G(Q)\) implies \(f\in Q(x)\) [5].
For any \(x\in H\) there exists a unique point in K denoted by \(P_{K}x\) such that \(\|x-P_{K}x\|\leq\|x-y\|\) for all \(y\in K\). It is well known that the operator \(P_{K}:H\rightarrow K\), which is called the metric projection, is a nonexpansive mapping and has the properties that, for each \(x\in H\), \(P_{K}x\in K\) and \(\langle x-P_{K}x,P_{K}x-y\rangle\geq0\), for all \(y\in K\). It is also known that \(\|P_{K}x-P_{K}y\|^{2}\leq\langle x-y, P_{K}x-P_{K}y\rangle\), for all \(x,y\in K\) [6]. In the context of the variational inequality problem, we obtain
Let I be an index set. For each \(i\in I\), let \(\Theta_{i}\) be a real valued bifunction on \(K\times K\), \(A_{i}\) a nonlinear mapping, and \(\varphi_{i}:K\rightarrow R\) a function. The system of generalized mixed equilibrium problems as an extension of problems (1.1), (1.2), and (1.3) is to find a point \(x\in K\) such that
Note that \(\bigcap_{i\in I}\operatorname{GMEP}(\Theta_{i},A_{i},\varphi_{i})\) is the solution set of (1.7).
Vast range of problems which arise in economics, finance, image reconstruction, transportation, network and so on, appear as a special case of problem (1.7); see for example [7–10]. This problem also covers various forms of feasibility problems. So, it seems reasonable to study the system of generalized mixed equilibrium problems. There are many authors who introduced some iterative processes for finding the solution set of these problems or common solution of someone with others, for instance see [2, 11–13] and the references therein. In 2010, Peng et al. [14] introduced the following iterative algorithm for finding a common element of fixed points of a family of infinite nonexpansive mappings and the set of solutions of a system of finite family of equilibrium problems:
Under suitable conditions, they presented and proved a strong convergence theorem for finding an element of \(\Omega=\bigcap_{i=1}^{\infty}F(T_{i})\cap \operatorname{VI}(K, A)\cap\bigcap_{k=1}^{m} \operatorname{EP}(\mathrm {F}_{k})\). In 2013, Cai and Bu [11] proposed an iterative method as follows:
They proved that under appropriate conditions, the sequences \(\{x_{n}\}\), \(\{z_{n}\}\), and \(\{u_{n}\}\) converge strongly to \(z=P_{\Omega}f(z)\), where \(\Omega=F(W)\cap\bigcap_{i=1}^{\infty}F(T_{i})\cap\bigcap_{k=1}^{m} \operatorname{GMEP}(\mathrm{F}_{k},\varphi_{k},B_{k}) \cap\bigcap_{j=1}^{N} \operatorname{VI}(K, A_{j})\) and f is a contractive mapping. The iterative method for solving a system of equilibrium problem has studied by many other authors; for example [7, 14, 15] and so on. Note that, for finding common fixed point of a finite family of mapping and solution set of other problems, authors usually have been using the so-called W-mapping [11, 16, 17]. For example Thianwan [16] proposed the following method for finding a common element of the set of solutions of an equilibrium problem, the set of common fixed points of a finite family of nonexpansive mappings, and the set of solutions of the variational inequality of an α-inverse strongly monotone mapping in a real Hilbert space:
He showed that under suitable conditions, the above algorithm strongly converges to \(\bigcap_{i=1}^{N} F(T_{i}) \cap \operatorname{EP}(\phi) \cap \operatorname{VI}(K, A)\), where for each \(i=1,\ldots,N\), \(T_{i}\) is a nonexpansive mapping and A is an α-inverse strongly monotone mapping.
In this paper, we present an iterative algorithm for finding a common solution of a system of finite generalized mixed equilibrium problems, a variational inequality problem for an inverse strongly monotone mapping and common fixed points of a finite family of strictly pseudo contractive mappings. We show that the algorithm strongly converges to a solution of the problem under certain conditions. Our results modify, improve and extend corresponding results of Takahashi and Takahashi [18], Zhang et al. [19], Shehu [20], Thianwan [16], and others. The rest of the paper is organized as follows. Section 2 briefly explains the necessary mathematical background. Section 3 presents the main results. A numerical example is provided in the final section.
2 Preliminaries
It is well known that in a (real) Hilbert space H
for all \(x, y \in H\) [12]. Furthermore, it is easy to see that
Lemma 2.1
([13])
Let \(\{a_{n}\}\), \(\{b_{n}\}\), and \(\{c_{n}\}\) be three nonnegative real sequences satisfying
with \(\{t_{n}\}\subset[0, 1]\), \(\sum_{n=1}^{\infty} t_{n} = \infty\), \(b_{n}=o(t_{n})\), and \(\sum_{n=1}^{\infty} c_{n} < \infty\). Then \(\lim_{n\rightarrow\infty}a_{n}=0 \).
Lemma 2.2
([21])
Let H be a (real) Hilbert space and \(\{x_{n}\}_{n=1}^{N}\) be a bounded sequence in H. Let \(\{a_{n}\} _{n=1}^{N}\) be a sequence of real numbers such that \(\sum_{n=1}^{N} a_{n}=1\). Then
Lemma 2.3
([22])
Let \(\{x_{n}\}\) and \(\{z_{n}\}\) be bounded sequences in a Banach space and \(\beta_{n}\) be a sequence of real numbers such that \(0<\liminf_{n\rightarrow\infty}\beta_{n}<\limsup_{n\rightarrow\infty}\beta_{n}<1\) for all \(n \geq0\). Suppose that \(x_{n+1} = (1-\beta_{n})z_{n} + \beta_{n}x_{n}\) for all \(n \geq0\) and \(\limsup_{n\rightarrow\infty}(\|z_{n+1}-z_{n}\|-\|x_{n+1}-x_{n}\|)\leq0\). Then \(\lim_{n\rightarrow\infty}\|z_{n}-x_{n}\|=0 \).
Let us assume that the bifunction Θ satisfies the following conditions:
-
(A1)
\(\Theta(x,x)=0\), \(\forall x\in K\);
-
(A2)
Θ is monotone on K, i.e., \(\Theta (x,y)+\Theta(y,x)\leq0\), \(\forall x,y\in K\);
-
(A3)
for all \(x,y,z\in K\), \(\lim_{t\rightarrow0^{+}}\Theta (tz+(1-t)x ,y)\leq\Theta(x,y)\);
-
(A4)
for all \(x\in K\), \(y\mapsto\Theta(x,y)\) is convex and lower semicontinuous.
Lemma 2.4
([1])
Let K be a nonempty closed convex subset of Hilbert space H and Θ be a real valued bifunction on \(K\times K\) satisfying (A1)-(A4). Let \(r>0\) and \(x\in H\), then there exists \(z\in K\) such that
Lemma 2.5
([2])
Suppose all conditions in Lemma 2.4 are satisfied. For any given \(r>0\), define a mapping \(T_{r}:H\rightarrow K\) as
for all \(x\in H\). Then the following conditions hold:
-
1.
\(T_{r}\) is single valued;
-
2.
\(T_{r}\) is firmly nonexpansive, i.e.,
$$\|T_{r} x-T_{r} y\|^{2}\leq\langle T_{r} x-T_{r} y,x-y\rangle, \quad \forall x,y\in H; $$ -
3.
\(F(T_{r})=\operatorname{EP}(\Theta)\);
-
4.
\(\operatorname{EP}(\Theta)\) is a closed and convex set.
Remark 2.6
For the generalized mixed equilibrium problem (1.2), if the nonlinear operator A is a monotone, Lipschitz continuous mapping, φ is a convex and lower semicontinuous function, and the real valued bifunction Θ admits the conditions (A1)-(A4), then it is easy to show that \(G(x,y)=\Theta(x,y)+\langle A x,y-x \rangle+ \varphi (y)-\varphi(x)\) also satisfies the conditions (A1)-(A4), and the generalized mixed equilibrium (1.2) is still the following equilibrium problem:
3 Main results
As is well known, the strict pseudo contraction mappings have more useful applications than nonexpansive mappings like in solving inverse problems [23]. In addition, various problems reduced to find the common element of the fixed point set of a family of nonlinear mappings such as image restoration (see for example [24]). For construction an algorithm which can used to obtain the fixed point set of a family of strictly pseudo contractive mappings we need to introduce the following proposition.
In the sequel, \(I=\{1,2,\ldots,m\}\) and \(J=\{1,2,\ldots,l\}\) are two index sets.
Proposition 3.1
Let \(T_{j}:K\rightarrow K\), \(j\in J\), be \(k_{j}\)-strict pseudo contractive mappings. Define \(S:K\rightarrow K\) by \(S=\gamma_{0}I+\gamma_{1}T_{1}+\cdots+\gamma_{l}T_{l}\), where the \(\{\gamma_{j}\}\), \(j\in J\), are in \((0,1)\) and, for each \(n\in N\), \(\sum_{j=0}^{l} \gamma_{j}=1\). If \(\gamma_{0}\in[k,1)\) such that \(k=\max\{ k_{1}, \ldots,k_{l}\}\), then S is a nonexpansive mapping and \(F(S)=\bigcap_{j\in J}F(T_{j})\).
Proof
By the definition of the mapping S, we have
On the other hand, from (1.4) and (2.2) we have
Furthermore, (1.5) implies that, for each \(j\in J\),
By substituting (3.2) and (3.3) in (3.1), we have
Then S is a nonexpansive mapping. Now, by the definition of S we obtain \(I-S=\sum_{j\in J} \gamma_{j} (I-T_{j} )\) and clearly \(F(S)=\bigcap_{j\in J}F(T_{j})\). □
Theorem 3.2
Let \(\Theta_{i}:K\times K\rightarrow R\), \(i\in I\), be bifunctions satisfying (A1)-(A4). Suppose that, for each \(i\in I\), the \(B_{i}\) are \(\theta_{i}\)-inverse strongly monotone mappings, the \(C_{i}\) are monotone and Lipschitz continuous mappings from K into H, and the \(\varphi_{i}\) are convex and lower semicontinuous functions from K into R. Let \(T_{j}:K\rightarrow K\), \(j\in J\), be \(k_{j}\)-strict pseudo contractive mappings and \(A:K\rightarrow H\) be a σ-inverse strongly monotone mapping. Let \(f:K\rightarrow K\) be an ε-contraction mapping and \(\{v_{n}\}\) be a convergent sequence in K with limit point v. Suppose that \(\Omega=\bigcap_{i\in I}\operatorname{GMEP}(\Theta_{i},B_{i},C_{i},\varphi_{i})\cap\bigcap_{j\in J}F(T_{j})\cap \operatorname{VI}(A,K) \) is nonempty. For any initial guess \(x_{1}\in K\), define the sequence \(\{x_{n} \}\) by
where for all \(n\in N\), \(\{\lambda_{n}\},\{r_{n,i}\}_{i\in I}\subseteq (0,\infty)\), and \(\{\alpha_{n}\}, \{\beta_{n}\}, \{\delta_{n,i}\}_{i\in I}, \{\gamma_{j}\}_{j\in J}\subseteq(0,1)\) are sequences satisfying the following control conditions:
-
1.
\(\lim_{n\rightarrow\infty}\alpha_{n}=0\), \(\sum_{n=1}^{\infty}\alpha _{n}=\infty\);
-
2.
\(0<\liminf_{n\rightarrow\infty}\beta_{n}\leq\limsup_{n\rightarrow \infty}\beta_{n}<1\);
-
3.
for some \(a,b\in(0,2\sigma)\), \(\lambda_{n}\in[a,b]\) and \(\lim_{n\rightarrow\infty}|\lambda_{n+1}-\lambda_{n}|=0\);
-
4.
for some \(d>0\), \(0< d\leq\delta_{n,i}\leq1\), \(\sum_{i\in I}\delta _{n,i}=1\) and \(\sum_{n=1}^{\infty}|\delta_{n+1,i}-\delta_{n,i}|<\infty\);
-
5.
for some \(c>0\), \(k\leq\gamma_{0}\leq c<1\) such that \(k=\max_{j\in J}\{k_{j}\}\) and \(\sum_{j\in J}\gamma_{j}=1\);
-
6.
for some \(\tau_{i},\rho_{i}\in(0,2\theta_{i})\), \(r_{n,i}\in[\tau_{i},\rho _{i}]\) and \(\sum_{n=1}^{\infty}|r_{n+1,i}-r_{n,i}|<\infty\), \(i\in I\).
Then the sequences \(\{x_{n} \}\) converges strongly to \(z\in\Omega\), where \(z=P_{\Omega}( v+f(z))\).
Proof
For \(x,y\in K\) and \(i\in I\), put \(G_{i}(x,y)=\Theta_{i} (x,y)+\langle C_{i} x,y-x \rangle+ \varphi_{i}(y)-\varphi_{i}(x)\). By Remark 2.6, \(G_{i}\) satisfies the conditions (A1)-(A4) and so the algorithm (3.5) can be rewritten as follows:
Claim 1
The sequences \(\{x_{n} \}\), \(\{y_{n} \}\), \(\{u_{n} \}\), \(\{t_{n} \}\), and \(\{k_{n} \}\) are bounded where, for each \(n\in N\), \(u_{n}=\sum_{i\in I}\delta_{n,i}u_{n,i}\), \(t_{n}=P_{K} (y_{n}-\lambda_{n} Ay_{n})\), and \(k_{n}=P_{K} (u_{n}-\lambda_{n} Au_{n} )\).
To prove the claim from (3.6) we have
Then, by using Lemma 2.5, for each \(i\in I\), we have \(u_{n,i}=T_{r_{n,i}}(x_{n}-r_{n,i} B_{i} x_{n})\), and, for any \(q\in\Omega\), \(q=T_{r_{n,i}}(q-r_{n,i} B_{i} q)\). Thus
So, we have
By the definition of \(t_{n}\) and \(k_{n}\) we have
and
Since \(\lim_{n\rightarrow\infty}v_{n}=v\), \(\{v_{n}\}\) is bounded,
where \(M_{1}=\sup_{n\geq1}\{\|v_{n}-q\|\}\). Putting \(S=\gamma_{0} I+\sum_{j\in J}\gamma_{j}T_{j}\), by Proposition 3.1, S is nonexpansive. On the other hand, for all \(n\in N\), we have
By induction, we deduce that
Therefore, \(\{x_{n}\}\) is bounded, and so are \(\{y_{n} \}\), \(\{u_{n} \}\), \(\{ u_{n,i}\}\), \(\{t_{n} \}\), and \(\{k_{n} \}\).
Claim 2
\(\|x_{n+1}-x_{n}\|\rightarrow0\) as \(n\rightarrow\infty\).
Let \(z_{n}=\frac{1}{1-\beta_{n}}x_{n+1}-\frac{\beta_{n}}{1-\beta_{n}}x_{n} \). Hence
Now, by the definition of \(t_{n}\) we have
Similarly,
By (3.17) and the definition of \(y_{n}\) we obtain
Furthermore, by the definition of \(u_{n}\),
From (3.7), since for each \(i\in I\), \(u_{n,i}, u_{{n+1},i}\in K\),
and
By adding the two inequalities (3.20), (3.21), and the monotonicity of \(G_{i}\) we have
So
Thus, for each \(i\in I\),
This yields
or
where \(\tau=\inf_{n\geq1}\{r_{{n},i}\}\) and \(M_{2}=\sup_{n\geq1}\{\| u_{n,i}-x_{n}\|\}\). Thus, from (3.15), (3.16), (3.18), (3.19), and (3.22) we obtain
So, by assumptions 1-6 of the theorem
and by Lemma 2.3, we have
But, since \(x_{n+1}-x_{n}=(1-\beta_{n})(z_{n}-x_{n})\), we have
Claim 3
\(\lim_{n\rightarrow\infty}\|x_{n}-S x_{n}\|=0\).
Note that
First we show that \(\lim_{n\rightarrow\infty}\|x_{n+1}-S t_{n}\|=0\). From (3.5)
Hence
This implies that
Now, we prove that \(\lim_{n\rightarrow\infty}\|t_{n}-x_{n}\|=0\). To do this, it suffices to show that \(\lim_{n\rightarrow\infty}\|x_{n}-u_{n}\|=0\) and \(\lim_{n\rightarrow\infty}\|u_{n}-t_{n}\|=0\). By the definition of \(t_{n}\) we have
So, by (3.26) and the convexity of \(\| \cdot \|^{2}\), we have
Hence
and then
Using the projection properties gives us
This implies that
From (3.28) and the convexity of \(\| \cdot \|^{2}\), one can see that, for \(q\in\Omega\),
Hence
and so by (3.27)
Next, we show that \(\lim_{n\rightarrow\infty}\|y_{n}-u_{n}\|=0\). The definition of \(k_{n}\) and a similar argument to (3.26) give us
Then
Hence
and therefore
Similar to (3.28) we can see that
From (3.32) and the convexity of \(\| \cdot \|^{2}\), we have
So
Then the above inequality and (3.31) imply that
But from (3.5),
So, from (3.33) we have
Then by (3.29) and (3.34) we have
Now, we show that \(\lim_{n\rightarrow\infty}\|x_{n}-u_{n}\|=0\). To do this, note that, for any \(i\in I\),
So, from (3.36) and the definition of \(u_{n}\), we obtain
Thus,
Since S is nonexpansive, we have
Hence
which yields
Since \(\|t_{n}-x_{n}\|\leq\|t_{n}-u_{n}\|+\|u_{n}-x_{n}\|\), from (3.35) and (3.38) we obtain
Inequality (3.24) and equations (3.25), (3.39), and \(\| x_{n}-x_{n+1}\|\rightarrow0\) imply that
Claim 4
\(\limsup_{n\rightarrow\infty}\langle v+ f(z)-z,y_{n}-z\rangle\leq0\), where \(z=P_{\Omega}( v+ f(z))\).
To prove the claim, let \(\{y_{n_{k}}\}\) be a subsequence of \(\{y_{n}\}\) such that
By boundedness of \(\{y_{n_{k}}\}\), there exists a subsequence of \(\{ y_{n_{k}}\}\) which is weakly convergent to \(z_{0}\in K\). Without loss of generality, we can assume that \(y_{n_{k}}\rightharpoonup z_{0}\). So, (3.41) reduces to
Therefore, by projection properties, to prove \(\langle v+ f(z)-z,z_{0}-z\rangle\geq0\), it suffices to show that \(z_{0}\in\Omega\).
(a) First we prove that \(z_{0}\in\bigcap_{j\in J}^{m}F(T_{j})\). From (3.40) and the demiclosedness property of S we obtain \(z_{0}\in F(S)\). So, by Proposition 3.1, \(z_{0}\in\bigcap_{j\in J}^{m}F(T_{j})\).
(b) Next we show that \(z_{0}\in \operatorname{VI}(A,K)\). Note that from boundedneess of \(\{x_{n}\}\), \(\{u_{n}\}\), and equation (3.33), there exist subsequences \(\{x_{n_{k}}\}\) and \(\{u_{n_{k}}\}\) of \(\{x_{n}\}\) and \(\{ u_{n}\}\), respectively, which converge weakly to \(z_{0}\). Suppose that \(N_{K}x\) is a normal cone to K at x and Q is a mapping defined by
It is well known that Q is a maximal monotone mapping and \(0\in Q(x)\) if and only if \(x\in \operatorname{VI}(A,K)\). For details see [2]. If \((x,u)\in G(Q)\), then \(u-Ax\in N_{K}x\). Since \(k_{n}=P_{K} (u_{n}-\lambda _{n} Au_{n} )\in K\), we have
In addition, from projection properties we have \(\langle x-k_{n},k_{n}-(u_{n}-\lambda_{n} Au_{n} )\rangle \geq0 \). Then \(\langle x-k_{n},\frac{k_{n}-u_{n}}{\lambda_{n}}+Au_{n} \rangle\geq0\). Hence, from (3.44) we have
Since A is a continuous mapping, from (3.34) and (3.45) we deduce that
Therefore, from maximal monotonicity of Q, we obtain \(0\in Q(z_{0})\) and hence \(z_{0}\in \operatorname{VI}(A,K)\).
(c) Now we prove that \(z_{0}\in\bigcap_{i\in I}\operatorname{GEP}(G_{i},B_{i})\). For all \(i\in I\), by (3.36),
and then
This implies that
Therefore, for any \(i\in I\),
So by (3.38),
Since \(\{u_{n,i}\}_{i\in I}\) is bounded, by (3.46), there exists a weakly convergent subsequence \(\{u_{n_{k},i}\}\) of \(\{u_{n,i}\}\) to \(z_{0}\). Now, we will show that, for any \(i\in I\), \(z_{0}\) is a member of \(\operatorname{GEP}(G_{i},B_{i})\). Since \(u_{n,i}=T_{r_{n,i}} (x_{n}-r_{n,i} B_{i} x_{n})\), for all \(y\in K\) we have
From (A2) we obtain
Hence, for all \(y\in K\),
Let \(y_{t}=ty+(1-t)z_{0}\), where \(t\in(0,1]\) and \(y\in K\). Then \(y_{t}\in K\) and by (3.47),
But \(B_{i}\) is a \(\theta_{i}\)-inverse strongly monotone mapping and \(\| u_{n_{k},i}-x_{n_{k}} \|\rightarrow0 \), so \(\|B_{i}u_{n_{k},i}-B_{i}x_{n_{k}} \| \rightarrow0\) and \(\langle y_{t}-u_{n_{k},i} ,B_{i}y_{t}-B_{i}u_{n_{k},i} \rangle \geq0\), for all \(i\in I\). As \(k\rightarrow\infty\), the relations \(\frac {u_{n_{k},i}-x_{n_{k}}}{r_{n_{k},i}} \rightarrow0\), \(u_{n_{k},i}\rightharpoonup0\), and condition (A4) imply that
From (A1), (A4), and (3.48) we have
Letting \(t\rightarrow0\), so for each \(y\in K\),
That is, \(z_{0}\in \operatorname{GEP}(G_{i},B_{i})\), for all \(i\in I\). Now by parts (a), (b) and (c), \(z_{0}\in\Omega\). Therefore, from (3.42) we obtain
Claim 5
The sequence \(\{x_{n}\}\) converges to z, where \(z=P_{\Omega}( v+ f(z))\).
From the convexity of \(\| \cdot \|^{2}\) and (2.1) we deduce that
where \(\gamma_{n}=2\alpha_{n}(1-\beta_{n})\langle v_{n}+ f(x_{n})-z,y_{n}-z\rangle \). On the other hand
Suppose that \(M_{0}=\sup_{n\in N}\{\|y_{n}-z\|\}\). So
Substitute (3.52) in (3.50), then
where \(M= (1+\varepsilon)M_{1}^{2}+ M_{0}^{2}\). Therefore from (3.49) and Lemma 2.1, we conclude that \(\lim_{n\rightarrow\infty}\|x_{n}-z\|=0 \). Also from (3.34) and (3.38) we can see that \(y_{n}\rightarrow z\) and \(u_{n}\rightarrow z\). This completes the proof. □
Let \(m=1\) in the index set I and take \(\delta_{n,1}=1\), so (3.5) becomes the following algorithm:
Put \(\varphi=0\), \(C=0\), and \(\{v_{n}\}=\{0\}\) in (3.53). If \(A=0\), then by the projection properties, \(k_{n}=P_{\Omega}u_{n}\). Since \(u_{n}\in C\), we have \(k_{n}=u_{n}\). So, we get the following corollary which is the so-called viscosity approximation method.
Corollary 3.3
Let \(\Theta:K\times K\rightarrow R\) be a bifunction satisfying (A1)-(A4) and B a θ-inverse strongly monotone. Let \(S:K\rightarrow K\) be a nonexpansive and \(f:K\rightarrow K\) be an ε-contraction mapping. Suppose that \(\Omega=\operatorname{GEP}(\Theta,B)\cap F(S)\) is nonempty. For any initial guess \(x_{1}\in K\), define the sequence \(\{x_{n} \}\) by
where \(\{r_{n}\}\) is a positive real sequence, \(\{\alpha_{n}\}\) and \(\{ \beta_{n}\}\) are sequences in \((0,1)\) satisfying the following conditions:
-
1.
\(\lim_{n\rightarrow\infty}\alpha_{n}=0\), \(\sum_{n=1}^{\infty}\alpha _{n}=\infty\);
-
2.
\(0<\liminf_{n\rightarrow\infty}\beta_{n}\leq\limsup_{n\rightarrow \infty}\beta_{n}<1\);
-
3.
for some \(\tau,\rho\in(0,2\theta)\), \(r_{n}\in[\tau,\rho]\) and \(\lim_{n\rightarrow\infty} (r_{n+1}-r_{n})=0\).
Then the sequence \(\{x_{n} \}\) converges strongly to \(z\in\Omega\), where \(z=P_{\Omega} fz\).
4 Numerical example
In this section, we present a numerical example which supports our algorithm.
Example 1
Suppose \(H=R\) and \(K= [-200,200]\). A system of generalized mixed equilibrium problem is to find a point \(x\in K\) such that, for each \(i \in I\),
For any \(i\in I\), define \(\varphi_{i}=0\), \(\Theta_{i}(x,y)=(y+ix)(y-x)\) and \(A_{i}x=ix\). It is easy to see that, for each \(i\in I\), \(\Theta _{i}(x,y)\) satisfies the conditions (A1)-(A4) and \(A_{i}\) is \(\frac {1}{i+1}\)-inverse strongly monotone mapping. We know that, for each \(i\in I\), \(T_{r_{i}}\) is single valued. Thus for any \(y\in k\) and \(r_{i}>0\), we have
Let \(Q_{i}(y)=r_{i}y^{2}+[(1+r_{i}(i-1))u_{i}-(1-ir_{i})x]y+[(1-ir_{i})u_{i}x-(1+i r_{i} )u_{i}^{2}]\). Since \(Q_{i}\) is a quadratic function relative to y, \(Q_{i}(y)\geq0\) for all \(y\in K \), if and only if the coefficient of \(y^{2} \) is positive and the discriminant \(\Delta_{i} \leq0 \). But
so we obtain
and then
From Lemma 2.5, we have \(F(T_{r_{i}} )=\operatorname{GEP}(\Theta, A_{i})={0}\). Define \(S:K \rightarrow K \) by \(S(x)=\sin(x) \). Then S is nonexpansive and \(F(\sin(x) )=\{0\}\). So, \(\Omega=\{0\}\). Assume that \(I=\{1,2\}\), \(A=0 \), \(\{v_{n}\}=\{0\}\), \(f(x)=\frac{x}{2} \), \(r_{n,i}=\frac {2n}{(n+1)(i+1)} \), \(\alpha_{n}=\frac{1}{n} \), \(\beta_{n}=\frac{1}{3}\) and \(\delta_{n,i}=\frac{1}{2}\), \(C_{i}=0\), \(i\in I\). Hence,
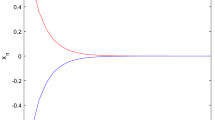
Then, by Theorem 3.2, the sequence \(\{x_{n} \}\) converges strongly to \(0\in\Omega\). Table 1 and Figure 1 indicate the behavior of \(x_{n}\) for algorithm (3.5) with \(x_{0}=10\) and \(x_{0}=-10\). We have used MATLAB with \(\varepsilon=10^{-4}\).
References
Blum, E, Oettli, W: From optimization and variational inequalities to equilibrium problems. Math. Stud. 63, 123-145 (1994)
Combettes, PL, Histoaga, SA: Equilibrium programming using proximal like algorithms. Math. Program. 78, 29-41 (1997)
Browder, FE, Petryshyn, WV: Construction of fixed points on nonlinear mappings in Hilbert spaces. J. Math. Anal. Appl. 20, 197-228 (1967)
Acedo, GL, Xu, HK: Iterative methods for strict pseudo-contraction in Hilbert spaces. Nonlinear Anal. 67, 2258-2271 (2007)
Rockafeller, RT: On maximality of sums of nonlinear operators. Trans. Am. Math. Soc. 149, 75-88 (1970)
Cegielski, A: Iterative Methods for Fixed Point Problems in Hilbert Spaces. Springer, London (2011)
Ansari, QH, Schaible, S, Yao, JC: The system of generalized vector equilibrium problems with applications. J. Glob. Optim. 22, 3-16 (2002)
Barbagallo, A: On the regularity of retarded equilibria in time-dependent traffic equilibrium problems. Nonlinear Anal. 71, 2406-2417 (2009)
Barbagallo, A, Daniele, P, Maugeri, A: Variational formulation for a general dynamic financial equilibrium problem: balance law and liability formula. Nonlinear Anal. 75, 1104-1123 (2012)
Huang, NJ, Fang, YP: Strong vector F-complementary problem and least element problem of feasible set. Nonlinear Anal. 61, 901-918 (2005)
Cai, G, Bu, S: A viscosity scheme for mixed equilibrium problems, variational inequality problems and fixed point problems. Math. Comput. Model. 57, 1212-1226 (2013)
Chang, SS, Joseph Lee, HW, Chan, CK: A new method for solving equilibrium problem fixed point problem and variational inequality problem with application to optimization. Nonlinear Anal. 70, 3307-3319 (2009)
Liu, LS: Ishikawa and Mann iterative process with errors for nonlinear strongly accretive mappings in Banach space. J. Math. Anal. Appl. 194, 114-125 (1995)
Peng, JW, Wu, SY, Yao, JC: A new iterative method for finding common solutions of a system of equilibrium problems, fixed-point problems, and variational inequalities. Abstr. Appl. Anal. (2010). doi:10.1155/2010/428293
He, Z, Du, WS: Strong convergence theorems for equilibrium problems and fixed point problems: a new iterative method, some comments and applications. Fixed Point Theory Appl. (2011). doi:10.1186/1687-1812-2011-33
Thianwan, S: Strong convergence theorems by hybrid methods for a finite family of nonexpansive mappings and inverse-strongly monotone mappings. Nonlinear Anal. Hybrid Syst. 3, 605-614 (2009)
Zhao, J, He, S: A new iterative method for equilibrium problems and fixed point problems of infinitely nonexpansive mappings and monotone mappings. Appl. Math. Comput. 215, 670-680 (2009)
Takahashi, S, Takahashi, W: Strong convergence theorem for a generalized equilibrium problem and a nonexpansive mapping in a Hilbert space. Nonlinear Anal. 69, 1025-1033 (2008)
Zhang, SS, Rao, RF, Huang, JL: Strong convergence theorem for a generalized equilibrium problem and a k-strict pseudocontraction in Hilbert spaces. Appl. Math. Mech. 30(6), 685-694 (2009)
Shehu, Y: Iterative method for fixed point problem, variational inequality and generalized mixed equilibrium problems with applications. J. Glob. Optim. 52, 57-77 (2012)
Hao, Y, Cho, SY, Qin, X: Some weak convergence theorems for a family of asymptotically nonexpansive nonself mappings. Fixed Point Theory Appl. 2010, Article ID 218573 (2010)
Suzuki, T: Strong convergence theorems for infinite families of nonexpansive mappings in general Banach spaces. J. Fixed Point Theory Appl. 1, 103-123 (2005)
Scherzer, O: Convergence criteria of iterative methods based on Landweber iteration for solving nonlinear problems. J. Math. Anal. Appl. 194, 911-933 (1991)
Kotzer, T, Cohen, N, Shamir, J: Image restoration by a novel method of parallel projection onto constraint sets. Optim. Lett. 20, 1772-1774 (1995)
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
All authors contributed equally, and they also read and finalized manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Payvand, M.A., Jahedi, S. System of generalized mixed equilibrium problems, variational inequality, and fixed point problems. Fixed Point Theory Appl 2016, 93 (2016). https://doi.org/10.1186/s13663-016-0583-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13663-016-0583-7