Stabilization of hybrid stochastic systems with time-varying delay by discrete-time state feedback control

Abstract

In this paper, we are concerned with the stabilization of hybrid stochastic systems with variable delay by discrete-time state feedback control. By using Lyapunov functionals, we obtain an upper bound $\tau ^{*}$ on the duration τ between two consecutive state observations. Meantime, we show that hybrid stochastic systems with variable delay can be stabilized by discrete-time state feedback control as long as $\tau <\tau ^{*}$. Finally, two examples are given to demonstrate the applicability of our work.

1 Introduction

In the real world, many systems are may experience abrupt changes in their structure and parameters caused by phenomena such as component failures or repairs and changing subsystem interconnections, and sudden environmental disturbances. Hybrid systems have been used to model these systems (see, e.g., [1, 2]). Since the underlying hybrid systems are in operation for a relatively long time, it is very important to study their asymptotic behavior. One of the important issues in the study of long run behavior is the analysis of stability. Some results on the asymptotic stability and exponential stability may be found in [3–6]. However, since some hybrid systems are not always stable, it is necessary to design a feedback control to make the controlled systems stable. It is well known that random noise can be utilized to stabilize an unstable system. The theory on stabilization by random noise has been studied by many authors (see, e.g., [7–10]).

On the other hand, one could design a deterministic feedback control in the drift coefficients so that the controlled stochastic systems become stable. For example, given an unstable hybrid stochastic system

$$ dx(t)=f\bigl(x(t),r(t),t\bigr)\,dt+g\bigl(x(t),r(t),t\bigr) \,dw(t), $$

(1.1)

Yuan [11] designed the linear feedback control $A(r(t))x(t)$ to stabilize the hybrid stochastic system (1.1), while Mao [12] and Hu [13] used the delay feedback control $u(x(t-\delta ),r(t),t)$ to make the hybrid stochastic system (1.1) become stable. Such a regular feedback control requires continuous observation of the state $x(t)$ or $x(t-\delta )$ for all times $t\ge 0$. Obviously, this continuous control strategy is not easy to implement in practice. In 2013, Mao [14] designed a feedback control $u(x([t/\tau ]\tau ),r(t),t)$ based on the discrete-time observations of the state $x(t)$ at times $0,\tau ,2\tau ,\dots$, and investigated the stabilization problem for hybrid stochastic systems. The latter is clearly more realistic and costs less in practice. Therefore, some recent results on stabilization with discrete time feedback control may be found in [15–18].

In the study of the above stabilization, the time delay τ is added in the feedback controller. However, the real phenomenon indicates that the uncontrolled system itself may be disturbed by the time delay. As we know, the time delay is inevitable in practice, which often leads to instability and poor performance of stochastic delay systems. Therefore, many scholars began to pay attention to the problem of stabilizing hybrid stochastic delay systems by using feedback control. In 2020, Li and Mao [19] considered a class of hybrid stochastic systems with constant delay

$$ dx(t)=f\bigl(x(t),x(t-\tau ),r(t),t\bigr)\,dt+g\bigl(x(t),x(t-\tau ),r(t),t\bigr)\,dw(t). $$

(1.2)

By applying the delay feedback control $u(x(t-\tau ),r(t),t)$, they showed that the controlled system

$$ \begin{aligned} dx(t)={}&\bigl[f\bigl(x(t),x(t-\tau ),r(t),t\bigr)+u\bigl(x(t-\tau ),r(t),t\bigr)\bigr]\,dt \\ &{} +g\bigl(x(t),x(t-\tau ),r(t),t\bigr)\,dw(t) \end{aligned} $$

(1.3)

is asymptotically stable and pth-moment exponentially stable. Since then, some scholars extended the stabilization results [19] to the discrete-time feedback control problem for Eq. (1.2) and achieved many results. For example, Mei et al. [20, 21] made use of the feedback controllers based on the discrete-time state observations to stabilize the unstable stochastic systems as in (1.2), and extended their stabilization results to the case of hybrid neutral stochastic delay systems. Lu et al. [22] discussed the stabilization of hybrid stochastic delay systems by feedback control based on the discrete-time observations of both state and mode, while Song et al. [23, 24] generalized the stabilization results of [22] to the case of highly nonlinear hybrid stochastic delay systems.

It is noted that the time delay in the above literature [19–24] is assumed to be a constant. However, many real stochastic delay models indicate that the time delay is a delay function. Therefore, a natural question is whether the discrete-time state feedback control can be used to stabilize such a stochastic system with variable delay. Recently, Dong and Mao [25] studied a class of hybrid stochastic systems with time-varying delay

$$ dx(t)=f\bigl(x(t),x\bigl(t-\tau (t)\bigr),r(t),t\bigr)\,dt+g \bigl(x(t),x\bigl(t-\tau (t)\bigr),r(t),t\bigr)\,dw(t). $$

(1.4)

They used the delay feedback control $u(x(t-\tau (t))$ to stabilize the hybrid stochastic delay systems as in (1.4). To the best of our knowledge, when the time-varying delay $\tau (t)$ is nondifferentiable, few authors have considered the problem of stabilization for hybrid stochastic delay systems by discrete-time state feedback control. Motivated by the above discussion, the main aim of this paper is to design a discrete-time feedback control $u(x([t/\tau ]\tau ),r(t),t)$ to stabilize the given unstable system, namely

$$ dx(t)=f\bigl(x(t),x\bigl(t-h(t)\bigr),r(t),t\bigr)\,dt+g \bigl(x(t),x\bigl(t-h(t)\bigr),r(t),t\bigr)\,dw(t). $$

(1.5)

Compared with the previous work, the main contributions of this paper include:

(1) When the delay function $h(t)$ is nondifferentiable, we are the first to study the feedback control for hybrid stochastic delay systems based on the discrete-time state observation, and an upper bound of the duration between two continuous state observations is obtained.

(2) By constructing the Lyapunov functional, we obtain sufficient conditions to ensure the stabilization of hybrid stochastic delay systems in the sense of $H_{\infty}$ stability, mean square asymptotic stability, and exponential stability.

The rest of the paper is organized as follows. In Sect. 2, we introduce some notations and hypotheses concerning systems (2.1). In Sect. 3, we investigate the stabilization of hybrid stochastic delay systems by feedback control based on discrete-time state observations. Then in Sect. 4 we give two examples to illustrate our theory.

2 Preliminaries and the global solution

Throughout this paper, unless other specified, we use the following notation. Let $|\cdot |$ denote the Euclidean norm in $\mathbb{R}^{n}$. If A is a vector or matrix, its transpose is denoted by $A^{\top}$. If A is a matrix, its trace norm is denoted by $|A|=\sqrt{\text{trace}(A^{\top}A)}$ while its operator norm is defined by $\|A\|=\sup \{|Ax|:|x|=1\}$. If A is a symmetric matrix, we denote by $\lambda _{\min}(A)$ and $\lambda _{\max}(A)$ its smallest and largest eigenvalues, respectively.

Let $(\Omega , {\mathcal {F}}, P)$ be a complete probability space with a filtration $\{{\mathcal {F}}_{t}\}_{t\ge t_{0}}$ satisfying the usual conditions. Let $w(t)$ be an m-dimensional Brownian motion defined on the probability space $(\Omega , {\mathcal {F}}, P)$. Let $\tau >0$ and $\mathbb{C}([{-\tau},0];\mathbb{R}^{n})$ denote the family of continuous functions ξ from $[{-\tau},0]$ to $\mathbb{R}^{n}$ with the norm $\|\xi \|=\sup_{{-\tau}\le u\le 0}|\xi (u)|$. Let $r(t)$, $t\ge 0$ be a right-continuous Markov chain on the probability space $(\Omega ,\mathcal {F},P)$ taking values in a finite state space $S=\{1,2,\dots ,N\}$ with generator $\Gamma =(\gamma _{ij})_{N\times N}$ given by

$$ {P}\bigl(r(t+\Delta )=j|r(t)=i\bigr)= \textstyle\begin{cases} \gamma _{ij}\Delta +o(\Delta ) , &\text{if } i\neq j, \\ 1+\gamma _{ii}\Delta +o(\Delta ), &\text{if } i=j, \end{cases} $$

where $\Delta >0$. Here $\gamma _{ij}\ge 0$ is the transition rate from i to j, $i\neq j$, while $\gamma _{ii}=-\sum_{j\neq i}\gamma _{ij}$. We assume that the Markov chain $r(\cdot )$ is independent of the Brownian motion $w(\cdot )$.

In this paper, we consider hybrid stochastic systems with time-varying delay of the form

$$ \begin{aligned} dx(t)={}&\bigl[f\bigl(x(t),x\bigl(t-h(t) \bigr),r(t),t\bigr)+u\bigl(x(\delta _{t}),r(t),t\bigr)\bigr]\,dt \\ & {} +g\bigl(x(t),x\bigl(t-h(t)\bigr),r(t),t\bigr)\,dw(t), \quad t\ge 0, \end{aligned} $$

(2.1)

with initial data $x(0)=x_{0}\in \mathbb{R}^{n}$, $r(0)=r_{0}\in S$, and

$$\begin{aligned}& f: \mathbb{R}^{n}\times \mathbb{R}^{n}\times S\times \mathbb{R}_{+} \to \mathbb{R}^{n}, \\& g:\mathbb{R}^{n} \times \mathbb{R}^{n}\times S \times \mathbb{R}_{+} \to \mathbb{R}^{n\times m}, \\& u:\mathbb{R}^{n} \times S \times \mathbb{R}_{+} \to \mathbb{R}^{n}. \end{aligned}$$

Here $h(t)$ is defined by Assumption 2.3, while $\delta _{t}=[t/\tau ]\tau$, in which $[t/\tau ]$ is the integer part of $t/\tau$, $\tau >0$.

In this paper, the following hypotheses are imposed on the coefficients f, g, and u.

Assumption 2.1

For each integer $d\ge 1$, there exists a positive constant $L_{d}$ such that

$$\begin{aligned} \bigl\vert f(x_{1},y_{1},i,t)-f(x_{2},y_{2},i,t) \bigr\vert \vee \bigl\vert g(x_{1},y_{1},i,t)-g(x_{2},y_{2},i,t) \bigr\vert \le L_{d}\bigl( \vert x_{1}-x_{2} \vert + \vert y_{1}-y_{2} \vert \bigr), \end{aligned}$$

for all $x_{1},y_{1},x_{2},y_{2}\in \mathbb{R}^{n}$ with $|x_{1}|\vee |y_{1}|\vee |x_{2}|\vee |y_{2}|\le d$ and any $(i,t)\in R_{+}\times S$. Moreover, we assume that there exists a constant $L_{0}>0$ such that

$$\begin{aligned} \bigl\vert f(x,y,i,t) \bigr\vert \vee \bigl\vert g(x,y,i,t) \bigr\vert \le L_{0}\bigl( \vert x \vert + \vert y \vert \bigr). \end{aligned}$$

for all $(x,y,i,t)\in \mathbb{R}^{n}\times \mathbb{R}^{n}\times S\times \mathbb{R}_{+}$.

Assumption 2.2

There exists a positive constant k such that

$$\begin{aligned} \bigl\vert u(x,i,t)-u(y,i,t) \bigr\vert \le k \vert x-y \vert \end{aligned}$$

for all $x,y\in \mathbb{R}^{n}$ and $(i,t)\in \mathbb{R}_{+}\times S$. Moreover, we assume that $u(0,i,t)=0$ for all $(i,t)\in \mathbb{R}_{+}\times S$.

Assumption 2.3

Assume that the time-varying delay $h(t)$ is a Borel measurable function from $\mathbb{R}_{+}$ to $[\underline{h},\bar{h}]$, with the following property:

$$\begin{aligned} h_{0}:=\limsup_{h\to 0} \biggl(\sup _{s\ge -\bar{h}} \frac{m(E_{s,h})}{h} \biggr)< \infty, \end{aligned}$$

(2.2)

where $\underline{h}$, h̄ are two positive constants with $\underline{h}<\bar{h}$, $E_{s,h}=\{t\in \mathbb{R}_{+}: t-h(t)\in [s,s+h)\}$ and $m(\cdot )$ denotes the Lebesgue measure on $\mathbb{R}_{+}$.

Remark 2.4

In the existing literature involving variable delay [19, 26, 27], the delay function $h(t):\mathbb{R}_{+}\to \mathbb{R}_{+}$ is either constant or differentiable, with its derivative being bounded by $\hat{h}\in (0,1)$. That is,

$$\begin{aligned} \frac{dh(t)}{dt} \le \hat{h} < 1, \quad \forall t\ge 0. \end{aligned}$$

(2.3)

If $h(t)=\tau$, then it follows that

$$\begin{aligned} \int _{T_{0}}^{T}\Psi (t-\tau )\,dt= \int _{T_{0}-\tau}^{T-\tau}\Psi (t)\,dt \le \int _{T_{0}-\tau}^{T}\Psi (t)\,dt. \end{aligned}$$

(2.4)

If $h(t)$ is differentiable with its derivative being bounded by $\hat{h}\in (0,1)$, then by applying a time change, it follows that

$$\begin{aligned} \int _{T_{0}}^{T}\Psi \bigl(t-h(t)\bigr)\,dt\le \frac{1}{1-\hat{h}} \int _{T_{0}-h(T_{0})}^{T} \Psi (t)\,dt. \end{aligned}$$

(2.5)

However, these two conditions might not be a natural feature of stochastic delay systems in the real world. For example, piecewise constant delays occur frequently in sampled-data controls but such functions are not differentiable.

Remark 2.5

In practice, there are many delay functions that satisfy Assumption 2.3. For example, consider the delay function $h(t)=0.1|\sin 2t|$ from $\mathbb{R}_{+}$ to $[0,0.1]$. Obviously, it obeys the Lipschitz condition

$$ \bigl\vert h(t)-h(s) \bigr\vert \le 0.2(t-s) $$

for any $0\le s< t<\infty$. In fact, it satisfies Assumption 2.3 with $h_{0}= 1.25$. In particular, if $h(t)$ is differentiable and its derivative is bounded by $\hat{h}\in (0,1)$, then $h(t)$ satisfies Assumption 2.3 with $h_{0}=1/(1-\hat{h})$.

Lemma 2.6

Let Assumptions 2.3hold. Let $T>T_{0}\ge 0$ and $\Psi :[-\bar{h},T-\underline{h}]\to \mathbb{R}_{+}$ be a continuous function. Then

$$\begin{aligned} \int _{T_{0}}^{T}\Psi \bigl(t-h(t)\bigr)\,dt\le h_{0} \int _{T_{0}-\bar{h}}^{T- \underline{h}}\Psi (t)\,dt. \end{aligned}$$

(2.6)

Proof

By Assumption 2.3, for any $\varepsilon >0$, there exists a positive constant h̃ such that

$$\begin{aligned} \sup_{s\ge -\bar{h}}\frac{m(E_{s,h})}{h}\le h_{0}+\varepsilon , \quad \forall h\in (0,\tilde{h}). \end{aligned}$$

Note that $-\bar{h}\le t-h(t) \le T-\underline{h}$ for $t\in [T_{0},T]$. Let n be any large integer such that $h:=(T-\underline{h}-T_{0}+\bar{h})/n<\tilde{h}$. Set $t_{q}=T_{0}-\bar{h}+qh$ for $q=0,1,\dots ,n-1$. Recalling the definition of the Riemann–Lebesgue integral, we have

$$\begin{aligned} \int _{T_{0}}^{T}\Psi \bigl(t-h(t)\bigr)\,dt=\lim _{n\to \infty}\sum_{q=0}^{n-1}m(E_{t_{q},h}) \Psi (t_{q}). \end{aligned}$$

Noting that $m(E_{t_{q},h})\le (h_{0}+\varepsilon )h$. Hence,

$$ \begin{aligned} \int _{T_{0}}^{T}\Psi \bigl(t-h(t)\bigr)\,dt&=\lim _{n\to \infty} \sum_{q=0}^{n-1}(h_{0}+ \varepsilon )h\Psi (t_{q}) \\ &=(h_{0}+\varepsilon ) \int _{T_{0}-\bar{h}}^{T-\underline{h}}\Psi (t)\,dt. \end{aligned} $$

Letting $\varepsilon \to 0$ yields the required assertion. □

Remark 2.7

In fact, Assumption 2.3 implies that $h_{0}\ge 1$. Letting $\psi (t)=1$ for all $t\ge -\bar{h}$, Lemma 2.6 shows that

$$ T-T_{0}\le (T-T_{0}+\bar{h}-\underline{h})h_{0} $$

for any $T> 0$, which implies

$$ h_{0}\ge \lim_{T\to \infty} \frac{T-T_{0}}{T-T_{0}+\bar{h}-\underline{h}}=1. $$

In particular, if $h(t)$ degenerates to the constant delay τ, then $h_{0}=1$.

Theorem 2.8

Let Assumptions 2.1–2.3hold, then Eq. (2.1) has a unique global solution $x(t)$ on $t\ge -\bar{h}$. Moreover, the solution has the property that

$$\begin{aligned} E \bigl\vert x(t) \bigr\vert ^{2}< \infty \end{aligned}$$

(2.7)

for any $t\ge 0$.

The proof of Theorem 2.8 is shown in the Appendix.

3 Main results

The main aim is to establish sufficient stability criteria for hybrid stochastic systems with time-varying delay. Let us denote by $C^{2,1}(\mathbb{R}^{n}\times S\times \mathbb{R}_{+};\mathbb{R}_{+})$ the family of all continuous nonnegative functions $U(x,i,t)$ defined on $\mathbb{R}^{n}\times S\times \mathbb{R}_{+}$ such that for each $i\in S$, they are continuously twice differentiable in x and once in t. For $U(x,i,t)\in C^{2,1}(\mathbb{R}^{n}\times S\times \mathbb{R}_{+}; \mathbb{R}_{+})$, we define the function $\mathcal{L}U: \mathbb{R}^{n}\times \mathbb{R}^{n} \times S\times \mathbb{R}_{+} \to \mathbb{R}$ by

$$ \begin{aligned} \mathcal{L}U(x,y,i,t)={}& U_{t}(x,i,t)+U_{x}(x,i,t)\bigl[f(x,y,i,t)+u(x,i,t)\bigr] \\ & {} +\frac{1}{2}\bigl[g^{\top}(x,y,i,t)U_{xx}(x,i,t)g(x,y,i,t) \bigr]+\sum_{j=1}^{N} \gamma _{ij}U(x,j,t), \end{aligned} $$

(3.1)

where

$$ \begin{aligned}&U_{t}(x,i,t)= {\frac{\partial U(x,i,t)}{\partial t}}, \\ & U_{x}(x,i,t) = \biggl( {\frac{\partial U(x,i,t)}{\partial x_{1}}}, \dots , { \frac{\partial U(x,i,t)}{\partial x_{n}}} \biggr), \\ &U_{xx}(x,i,t)= \biggl( {\frac{\partial ^{2} U(x,i,t)}{\partial x_{i} \partial x_{j}}} \biggr)_{n\times n}. \end{aligned} $$

Assumption 3.1

Assume that there exists a function $U\in C^{2,1}(\mathbb{R}^{n}\times S\times \mathbb{R}_{+};\mathbb{R}_{+})$ and three positive constants $\lambda _{i}$, $i=1,2,3$ such that

$$\begin{aligned} \mathcal{L}U(x,y,i,t)+\lambda _{1} \bigl\vert U_{x}(x,i,t) \bigr\vert ^{2}\le -\lambda _{2} \vert x \vert ^{2}+ \lambda _{3} \vert y \vert ^{2} \end{aligned}$$

(3.2)

for all $(x,y,i,t)\in \mathbb{R}^{n}\times \mathbb{R}^{n}\times S\times \mathbb{R}_{+}$.

We can now state our first result.

Theorem 3.2

Let Assumptions 2.1, 2.2, 2.3, and 3.1hold. If $\tau >0$ is sufficiently small for

$$\begin{aligned} \lambda _{2}>\lambda _{3}h_{0}+ \frac{k^{2}}{\lambda _{1}} \tau \bigl[(4 \tau +2)L_{0}^{2}(1+h_{0})+4k^{2} \tau \bigr] \quad \textit{and} \quad \tau \le \frac{1}{4k}, \end{aligned}$$

(3.3)

then the solution of equation (2.1) with the initial data has the property

$$\begin{aligned} \int _{0}^{\infty}E \bigl\vert x(t) \bigr\vert ^{2}\,dt< \infty . \end{aligned}$$

(3.4)

That is, Eq. (2.1) is $H_{\infty}$ stable in mean square.

Proof

For any $t\ge 2\bar{h}$, we define the segment processes $\hat{x}_{t}=\{x(t+s):-2\bar{h}\le s\le 0\}$ and $\hat{r}_{t}=\{x(t+s):-2\bar{h}\le s\le 0\}$. For $\hat{x}_{t}$ and $\hat{r}_{t}$ to be well defined for $0\le t\le 2\bar{h}$, we set $x(s)=x_{0}$ and $r(s)=r_{0}$ for $-2\bar{h}\le s \le 0$. The Lyapunov functional is defined by

$$\begin{aligned} V(\hat{x}_{t},\hat{r}_{t},t)=U \bigl(x(t),r(t),t\bigr)+ \frac{k^{2}}{\lambda _{1}} \int _{-\tau}^{0} \int _{t+s}^{t}\phi (v)\,dv\,ds \end{aligned}$$

(3.5)

for $t\ge 2\bar{h}$, where

$$ \begin{aligned} \phi (t)={}&\tau \bigl\vert f\bigl(x(t),x\bigl(t-h(t) \bigr),r(t),t\bigr)+u\bigl(x(\delta _{t}),r(t),t\bigr) \bigr\vert ^{2} \\ &{} + \bigl\vert g\bigl(x(t),x\bigl(t-h(t)\bigr),r(t),t\bigr) \bigr\vert ^{2}. \end{aligned} $$

By the Itô formula and the fundamental theorem of calculus, we obtain

$$\begin{aligned} EV(\hat{x}_{t},\hat{r}_{t},t)=EV( \hat{x}_{2\bar{h}},\hat{r}_{2\bar{h}},2 \bar{h})+ \int _{2\bar{h}}^{t}ELV(\hat{x}_{s}, \hat{r}_{s},s)\,ds \end{aligned}$$

(3.6)

for $t\ge 2\bar{h}$, where

$$ \begin{aligned} LV(\hat{x}_{t},\hat{r}_{t},t)={}& \mathcal{L}U\bigl(x(t),x\bigl(t-h(t)\bigr),r(t),t\bigr) \\ & {}-U_{x}\bigl(x(t),r(t),t\bigr)\bigl[u\bigl(x(t),r(t),t\bigr)-u \bigl(x(\delta _{t}),r(t),t\bigr)\bigr] \\ & {}+\frac{k^{2}}{\lambda _{1}}\tau \phi (t)- \frac{k^{2}}{\lambda _{1}} \int _{t-\tau}^{t}\phi (s)\,ds. \end{aligned} $$

By Assumptions 2.1, 2.2, and condition (3.3), we have

$$ \begin{aligned} &-U_{x}\bigl(x(t),r(t),t \bigr)\bigl[u\bigl(x(t),r(t),t\bigr)-u\bigl(x(\delta _{t}),r(t),t\bigr) \bigr] \\ &\quad \le \lambda _{1} \bigl\vert U_{x} \bigl(x(t),r(t),t\bigr) \bigr\vert ^{2}+\frac{k^{2}}{4\lambda _{1}} \bigl\vert x(t)-x( \delta _{t}) \bigr\vert ^{2} \end{aligned} $$

(3.7)

and

$$ \begin{aligned} \frac{k^{2}}{\lambda _{1}}\tau \phi (t)\le{}& \frac{k^{2}}{\lambda _{1}}\tau (4\tau +2)L^{2}\bigl( \bigl\vert x(t) \bigr\vert ^{2}+ \bigl\vert x\bigl(t-h(t)\bigr) \bigr\vert ^{2}\bigr)+2 \frac{k^{2}}{ \lambda _{1}}k^{2}\tau ^{2} \bigl\vert x(\delta _{t}) \bigr\vert ^{2} \\ \le{}& \biggl[\frac{k^{2}}{\lambda _{1}}\tau (4\tau +2)L_{0}^{2}+4 \frac{k^{4}}{\lambda _{1}}\tau ^{2} \biggr] \bigl\vert x(t) \bigr\vert ^{2}+ \frac{k^{2}}{\lambda _{1}} \tau (4\tau +2)L_{0}^{2} \bigl\vert x\bigl(t-h(t)\bigr) \bigr\vert ^{2} \\ & {} +\frac{k^{2}}{4\lambda _{1}} \bigl\vert x(t)-x(\delta _{t}) \bigr\vert ^{2}. \end{aligned} $$

(3.8)

Inserting (3.7) and (3.8) into (3.6), we get

$$ \begin{aligned} ELV(\hat{x}_{t}, \hat{r}_{t},t)={}&E\mathcal{L}U\bigl(x(t),x\bigl(t-h(t)\bigr),r(t),t \bigr)+ \lambda _{1}E \bigl\vert U_{x}\bigl(x(t),r(t),t \bigr) \bigr\vert ^{2} \\ &{} +\frac{k^{2}}{2\lambda _{1}}E \bigl\vert x(t)-x(\delta _{t}) \bigr\vert ^{2}+ \frac{k^{2}}{\lambda _{1}}\tau \bigl[(4\tau +2)L_{0}^{2}+4k^{2} \tau \bigr]E \bigl\vert x(t) \bigr\vert ^{2} \\ &{} +\frac{k^{2}}{\lambda _{1}} \tau (4\tau +2)L^{2}E \bigl\vert x \bigl(t-h(t)\bigr) \bigr\vert ^{2}- \frac{k^{2}}{\lambda _{1}} \int _{t-\tau}^{t}E\phi (s)\,ds. \end{aligned} $$

(3.9)

On the other hand, it follows from (2.1) that

$$\begin{aligned} E \bigl\vert x(t)-x(\delta _{t}) \bigr\vert ^{2}\le 2 \int _{\delta _{t}}^{t}E\phi (s)\,ds \le 2 \int _{t-\tau}^{t}E\phi (s)\,ds. \end{aligned}$$

By Assumption 3.1, it follows that

$$ \begin{aligned} EV(\hat{x}_{t}, \hat{r}_{t},t)={}&EV(\hat{x}_{2\bar{h}},\hat{r}_{2 \bar{h}},2 \bar{h})- \biggl\{ \lambda _{2}-\frac{k^{2}}{ \lambda _{1}}\tau \bigl[(4\tau +2)L_{0}^{2}+4k^{2}\tau \bigr] \biggr\} \int _{2 \bar{h}}^{t}E \bigl\vert x(s) \bigr\vert ^{2}\,ds \\ &{} +\biggl[\lambda _{3}+\frac{k^{2}}{\lambda _{1}} \tau (4\tau +2)L_{0}^{2}\biggr] \int _{2\bar{h}}^{t}E \bigl\vert x\bigl(s-h(s)\bigr) \bigr\vert ^{2}\,ds. \end{aligned} $$

By Lemma 2.6, we get

$$ \begin{aligned} \int _{2\bar{h}}^{t}E \bigl\vert x\bigl(s-h(s)\bigr) \bigr\vert ^{2}\,ds&\le h_{0} \int _{\bar{h}}^{t}E \bigl\vert x(s) \bigr\vert ^{2}\,ds \\ &\le h_{0} \int _{\bar{h}}^{2\bar{h}}E \bigl\vert x(s) \bigr\vert ^{2}\,ds+h_{0} \int _{2 \bar{h}}^{t}E \bigl\vert x(s) \bigr\vert ^{2}\,ds. \end{aligned} $$

Hence,

$$\begin{aligned}& EV(\hat{x}_{t},\hat{r}_{t},t) \\& \quad =Q_{1}- \biggl\{ \lambda _{2}-\lambda _{3}h_{0}- \frac{k^{2}}{\lambda _{1}} \tau \bigl[(4\tau +2)L_{0}^{2}(1+h_{0})+4k^{2} \tau \bigr] \biggr\} \int _{2\bar{h}}^{t}E \bigl\vert x(s) \bigr\vert ^{2}\,ds, \end{aligned}$$

(3.10)

where

$$ Q_{1}=EV(\hat{x}_{2\bar{h}},\hat{r}_{2\bar{h}},2\bar{h})+ \biggl[ \lambda _{3}+\frac{k^{2}}{\lambda _{1}} \tau (4\tau +2)L_{0}^{2} \biggr]h_{0} \int _{\bar{h}}^{2\bar{h}}E \bigl\vert x(s) \bigr\vert ^{2}\,ds $$

is a positive constant. It follows from (3.10) that

$$\begin{aligned} \int _{2\bar{h}}^{t}E \bigl\vert x(s) \bigr\vert ^{2}\,ds \le \frac{Q_{1}}{\lambda _{2}-\lambda _{3}h_{0}-\frac{k^{2}}{\lambda _{1}} \tau [(4\tau +2)L_{0}^{2}(1+h_{0})+4k^{2}\tau ]}. \end{aligned}$$

Letting $t\to \infty$, we obtain

$$\begin{aligned} \int _{2\bar{h}}^{\infty}E \bigl\vert x(s) \bigr\vert ^{2}\,ds \le \frac{Q_{1}}{\lambda _{2}-\lambda _{3}h_{0}-\frac{k^{2}}{\lambda _{1}} \tau [(4\tau +2)L_{0}^{2}(1+h_{0})+4k^{2}\tau ]}, \end{aligned}$$

as required. The proof is therefore complete. □

Theorem 3.3

Under the same assumptions of Theorem 3.2, the solution of equation (2.1) with the initial data has the property

$$\begin{aligned} \lim_{t\to \infty}E \bigl\vert x(t) \bigr\vert ^{2}=0. \end{aligned}$$

(3.11)

That is, Eq. (2.1) is asymptotically stable in mean square.

Proof

By the Itô formula, we have

$$ \begin{aligned} E \bigl\vert x(t) \bigr\vert ^{2} ={}& \bigl\vert x(2\bar{h}) \bigr\vert ^{2}+ E \int _{2\bar{h}}^{t} \bigl(2x^{\top}(s)\bigl[f \bigl(x(s),x\bigl(s-h(s)\bigr),r(s),s\bigr) \\ & {}+u\bigl(x(\delta _{s}),r(s),s\bigr)\bigr]+ \bigl\vert g \bigl(x(s),x\bigl(s-h(s)\bigr),r(s),s\bigr) \bigr\vert ^{2} \bigr) \,ds. \end{aligned} $$

By Assumptions 2.1, 2.2, and Lemma 2.6, we then get

$$ \begin{aligned} E \bigl\vert x(t) \bigr\vert ^{2} &\le \Vert \hat{x}_{2\bar{h}} \Vert ^{2}+ Q \int _{2 \bar{h}}^{t}\bigl(E \bigl\vert x(s) \bigr\vert ^{2}+E \bigl\vert x\bigl(s-h(s)\bigr) \bigr\vert ^{2}+E \bigl\vert x(s)-x(\delta _{s}) \bigr\vert ^{2}\bigr) \,ds \\ &\le \Vert \hat{x}_{2\bar{h}} \Vert ^{2} + Q \int _{2\bar{h}}^{t}\bigl(E \bigl\vert x(s) \bigr\vert ^{2}+E \bigl\vert x(s)-x( \delta _{s}) \bigr\vert ^{2}\bigr)\,ds + Q \int _{\bar{h}}^{t} E \bigl\vert x(s) \bigr\vert ^{2}\,ds, \end{aligned} $$

(3.12)

where Q denotes a positive constant. By using Assumptions 2.1 and 2.2 again, we derive

$$ \begin{aligned} E \bigl\vert x(s)-x(\delta _{s}) \bigr\vert ^{2})\,ds\le{}& 6(\tau +1)L_{0}^{2} \int _{\delta _{s}}^{s}\bigl(E \bigl\vert x(v) \bigr\vert ^{2}+E \bigl\vert x\bigl(v-h(v)\bigr) \bigr\vert ^{2} \bigr)\,dv \\ & {} +6\tau ^{2}k^{2}\bigl(E \bigl\vert x(s) \bigr\vert ^{2}+E \bigl\vert x(s)-x(\delta _{s}) \bigr\vert ^{2}\bigr). \end{aligned} $$

Noting that $6\tau ^{2}k^{2}<1$ by condition (3.3), we hence have

$$ \begin{aligned} E \bigl\vert x(s)-x(\delta _{s}) \bigr\vert ^{2})\,ds\le{}& \frac{6(\tau +1)L_{0}^{2}}{1-6\tau ^{2}k^{2}} \int _{\delta _{s}}^{s}\bigl(E \bigl\vert x(v) \bigr\vert ^{2}+E \bigl\vert x\bigl(v-h(v)\bigr) \bigr\vert ^{2} \bigr)\,dv \\ & {} +\frac{6(\tau +1)L_{0}^{2}}{1-6\tau ^{2}k^{2}}E \bigl\vert x(s) \bigr\vert ^{2}. \end{aligned} $$

(3.13)

Substituting this into (3.12) yields

$$ \begin{aligned} E \bigl\vert x(t) \bigr\vert ^{2}\le {}& \Vert \hat{x}_{2\bar{h}} \Vert ^{2}+ Q \int _{ \bar{h}}^{2\bar{h}}E \bigl\vert x(s) \bigr\vert ^{2}\,ds+2Q \int _{2\bar{h}}^{t}E \bigl\vert x(s) \bigr\vert ^{2}\,ds \\ & {} +Q \int _{2\bar{h}}^{t} \int _{\delta _{s}}^{s}\bigl(E \bigl\vert x(v) \bigr\vert ^{2}+E \bigl\vert x\bigl(v-h(v)\bigr) \bigr\vert ^{2} \bigr)\,dv\,ds. \end{aligned} $$

(3.14)

Using the substitution technique, we get

$$\begin{aligned}& \int _{2\bar{h}}^{t} \int _{\delta _{s}}^{s}\bigl(E \bigl\vert x(v) \bigr\vert ^{2}+E \bigl\vert x\bigl(v-h(v)\bigr) \bigr\vert ^{2} \bigr)\,dv\,ds \\& \quad \le \int _{2\bar{h}}^{t} \int _{s-\tau}^{s}\bigl(E \bigl\vert x(v) \bigr\vert ^{2}+E \bigl\vert x\bigl(v-h(v)\bigr) \bigr\vert ^{2} \bigr)\,dv\,ds \\& \quad \le \int _{v}^{v+\tau}\,ds \int _{2\bar{h}-\tau}^{t}\bigl(E \bigl\vert x(v) \bigr\vert ^{2}+E \bigl\vert x\bigl(v-h(v)\bigr) \bigr\vert ^{2} \bigr)\,dv \\& \quad =\tau \int _{2\bar{h}-\tau}^{t}\bigl(E \bigl\vert x(s) \bigr\vert ^{2}+E \bigl\vert x\bigl(s-h(s)\bigr) \bigr\vert ^{2} \bigr)\,ds. \end{aligned}$$

By Lemma 2.6, we have

$$ \begin{aligned} & \int _{2\bar{h}}^{t} \int _{\delta _{s}}^{s}\bigl(E \bigl\vert x(v) \bigr\vert ^{2}+E \bigl\vert x\bigl(v-h(v)\bigr) \bigr\vert ^{2} \bigr)\,dv\,ds \\ &\quad \le \tau \int _{2\bar{h}-\tau}^{t}E \bigl\vert x(s) \bigr\vert ^{2}\,ds+\tau h_{0} \int _{ \bar{h}-\tau}^{t}E \bigl\vert x(s) \bigr\vert ^{2}\,ds \\ &\quad \le \tau \biggl( \int _{2\bar{h}-\tau}^{2\bar{h}}E \bigl\vert x(s) \bigr\vert ^{2}\,ds+h_{0} \int _{\bar{h}-\tau}^{2\bar{h}}E \bigl\vert x(s) \bigr\vert ^{2}\,ds \biggr)+ \tau (1+h_{0}) \int _{2\bar{h}}^{t}E \bigl\vert x(s) \bigr\vert ^{2}\,ds. \end{aligned} $$

Inserting this into (3.14) and applying Theorem 3.2, we derive

$$ \begin{aligned} E \bigl\vert x(t) \bigr\vert ^{2}\le{}& \Vert \hat{x}_{2\bar{h}} \Vert ^{2}+ \bigl[Q+\tau (1+h_{0})\bigr] \int _{\bar{h}-\tau}^{2\bar{h}}E \bigl\vert x(s) \bigr\vert ^{2}\,ds \\ &{} +\bigl[2Q+\tau (1+h_{0})\bigr] \int _{2\bar{h}}^{t}E \bigl\vert x(s) \bigr\vert ^{2}\,ds \le \bar{Q} \end{aligned} $$

(3.15)

for any $t\ge 2\bar{h}$. By the Itô formula, it follows that

$$ \begin{aligned} E \bigl\vert x(t_{2}) \bigr\vert ^{2}-E \bigl\vert x(t_{2}) \bigr\vert ^{2} ={}&E \int _{t_{1}}^{t_{2}} \bigl(2x^{\top}(s)\bigl[f \bigl(x(s),x\bigl(s-h(s)\bigr),r(s),s\bigr) \\ & {} +u\bigl(x(\delta _{s}),r(s),s\bigr)\bigr]+ \bigl\vert g \bigl(x(s),x\bigl(s-h(s)\bigr),r(s),s\bigr) \bigr\vert ^{2} \bigr) \,ds \end{aligned} $$

for any $2\bar{h}\le t_{1}< t_{2}<\infty$. By using Assumptions 2.1, 2.2, and (3.15), we can show that

$$\begin{aligned} \bigl\vert E \bigl\vert x(t_{2}) \bigr\vert ^{2}-E \bigl\vert x(t_{2}) \bigr\vert ^{2} \bigr\vert \le \bar{Q}(t_{2}-t_{1}). \end{aligned}$$

This implies that $E|x(t)|^{2}$ is uniformly continuous in t on $[2\bar{h},\infty ]$. It then follows from (3.4) that $\lim_{t\to \infty}E|x(t)|^{2}=0$, as required. □

In the previous argument, we have discussed the asymptotic stabilization. However, this stability does not reveal the rate at which the solution tends to zero. So, we will discuss the exponential stabilization by the discrete-time state feedback control. For this purpose, we need to impose another condition.

Assumption 3.4

Assume that there exist two positive constants $C_{1}$ and $C_{2}$ such that

$$\begin{aligned} C_{1} \vert x \vert ^{2}\le U(x,i,t)\le C_{2} \vert x \vert ^{2} \end{aligned}$$

for all $x\in \mathbb{R}^{n}$, $i\in S$, and $t\in \mathbb{R}_{+}$.

Theorem 3.5

Let Assumptions 2.1, 2.2, 2.3, 3.1, and 3.4hold. Let $\tau >0$ be sufficiently small for (3.3) to hold, and set

$$\begin{aligned} \lambda =\lambda _{2}-\lambda _{3}h_{0}- \frac{k^{2}}{\lambda _{1}} \tau \bigl[(4\tau +2)L_{0}^{2}(1+h_{0})+4k^{2} \tau \bigr], \end{aligned}$$

(3.16)

then the solution of equation (2.1) satisfies

$$\begin{aligned} \limsup_{t\to \infty}\frac{\log (E \vert x(t) \vert ^{2})}{t}\le -\gamma \end{aligned}$$

(3.17)

and

$$\begin{aligned} \limsup_{t\to \infty}\frac{\log ( \vert x(t) \vert )}{t}\le - \frac{\gamma}{2} \quad \textit{a.s.} \end{aligned}$$

(3.18)

for all initial data $\hat{x}_{2\bar{h}}$ and $\hat{r}_{2\bar{h}}$, where $\gamma >0$ is the unique root to the following equation:

$$\begin{aligned} 2\gamma \tau (Q_{4}+Q_{6}\tau ) e^{2\tau \gamma}+2\gamma \tau (Q_{5}+Q_{6} \tau )h_{0}e^{2\tau \gamma +\bar{h}\gamma}+\gamma C_{2}=\lambda , \end{aligned}$$

(3.19)

here $Q_{4}=\frac{k^{2}}{\lambda _{1}}[(4\tau +2)\tau L_{0}^{2}+4\tau ^{2} k^{2}]+ \frac{24\tau ^{2}(\tau +1)k^{4}L_{0}^{2}}{\lambda _{1}(1-6\tau ^{2}k^{2})}$, $Q_{5}=(4\tau +2)L_{0}^{2}$, and $Q_{6}= \frac{24\tau ^{2}(\tau +1)k^{4}L_{0}^{2}}{\lambda _{1}(1-6\tau ^{2}k^{2})}$.

Proof

By the Itô formula, we have

$$\begin{aligned} E\bigl(e^{\gamma t}V(\hat{x}_{t},\hat{r}_{t},t) \bigr)=e^{2\bar{h}\gamma}EV( \hat{x}_{2\bar{h}}, \hat{r}_{2\bar{h}},2 \bar{h})+ \int _{2\bar{h}}^{t}e^{ \gamma s}\bigl[\gamma EV( \hat{x}_{s},\hat{r}_{s},s)+ELV(\hat{x}_{s}, \hat{r}_{s},s)\bigr]\,ds \end{aligned}$$

for $t\ge 2\bar{h}$. By Assumption 3.4 and using (3.10), we obtain

$$\begin{aligned} C_{1}e^{\gamma t}E \bigl\vert x(t) \bigr\vert ^{2}=Q_{3}+ \int _{2\bar{h}}^{t}e^{\gamma s}( \gamma EV( \hat{x}_{s},\hat{r}_{s},s)-\lambda E \bigl\vert x(s) \bigr\vert ^{2}\,ds, \end{aligned}$$

(3.20)

where

$$ Q_{3}=e^{2\bar{h}\gamma}EV(\hat{x}_{2\bar{h}}, \hat{r}_{2\bar{h}},2 \bar{h})+ \biggl[\lambda _{3}+ \frac{k^{2}}{\lambda _{1}} \tau (4\tau +2)L_{0}^{2} \biggr]h_{0} \int _{\bar{h}}^{2\bar{h}}e^{\gamma s}E \bigl\vert x(s) \bigr\vert ^{2}\,ds. $$

By the definition of Lyapunov functional (3.5) and Assumption 3.4, we then have

$$ \begin{aligned} EV(\hat{x}_{t},\hat{r}_{t},t)={}&C_{2}E \bigl\vert x(t) \bigr\vert ^{2}+E \biggl( \frac{k^{2}}{\lambda _{1}} \int _{-\tau}^{0} \int _{t+s}^{t}\phi (v)\,dv\,ds \biggr) \\ \le{}& C_{2}E \bigl\vert x(t) \bigr\vert ^{2}+ \frac{k^{2}}{\lambda _{1}}\tau \int _{t-\tau}^{t} \bigl(\bigl[(4\tau +2)L^{2}+4\tau k^{2}\bigr]E \bigl\vert x(s) \bigr\vert ^{2} \\ & {} + (4\tau +2)L_{0}^{2}E \bigl\vert x\bigl(s-h(s) \bigr) \bigr\vert ^{2}+4\tau k^{2}E \bigl\vert x(s)-x( \delta _{s}) \bigr\vert ^{2} \bigr)\,ds. \end{aligned} $$

By (3.13), we get

$$ \begin{aligned} EV(\hat{x}_{t}, \hat{r}_{t},t)\le{}& C_{2}E \bigl\vert x(t) \bigr\vert ^{2}+Q_{4} \int _{t-\tau}^{t}E \bigl\vert x(s) \bigr\vert ^{2}\,ds+Q_{5} \int _{t-\tau}^{t}E \bigl\vert x\bigl(s-h(s)\bigr) \bigr\vert ^{2}\,ds \\ &{} + Q_{6} \int _{t-\tau}^{t} \int _{\delta _{s}}^{s}\bigl(E \bigl\vert x(v) \bigr\vert ^{2}+E \bigl\vert x\bigl(v-h(v)\bigr) \bigr\vert ^{2} \bigr)\,dv\,ds, \end{aligned} $$

(3.21)

where $Q_{4}$, $Q_{5}$, and $Q_{6}$ have been defined in (3.19). But

$$ \begin{aligned} & \int _{t-\tau}^{t} \int _{\delta _{s}}^{s}\bigl(E \bigl\vert x(v) \bigr\vert ^{2}+E \bigl\vert x\bigl(v-h(v)\bigr) \bigr\vert ^{2} \bigr)\,dv\,ds \\ &\quad \le \int _{t-\tau}^{t} \int _{s-\tau}^{s}\bigl(E \bigl\vert x(v) \bigr\vert ^{2}+E \bigl\vert x\bigl(v-h(v)\bigr) \bigr\vert ^{2} \bigr)\,dv\,ds \\ &\quad \le \tau \int _{t-2\tau}^{t}\bigl(E \bigl\vert x(s) \bigr\vert ^{2}+E \bigl\vert x\bigl(s-h(s)\bigr) \bigr\vert ^{2}\bigr)\,ds. \end{aligned} $$

(3.22)

Inserting (3.21), (3.22) into (3.20), we can obtain that

$$ \begin{aligned} C_{1}e^{\gamma t}E \bigl\vert x(t) \bigr\vert ^{2}\le{}& Q_{3}+\gamma (Q_{4}+Q_{6} \tau ) \int _{2\bar{h}}^{t}e^{\gamma s} \biggl( \int _{s-2\tau}^{s}E \bigl\vert x(v) \bigr\vert ^{2}\,dv \biggr)\,ds \\ & {}+ \gamma (Q_{5}+Q_{6}\tau ) \int _{2\bar{h}}^{t}e^{\gamma s} \biggl( \int _{s-2\tau}^{s}E \bigl\vert x\bigl(v-h(v)\bigr) \bigr\vert ^{2}\,dv \biggr)\,ds \\ & {}-(\lambda -\gamma C_{2}) \int _{2\bar{h}}^{t}e^{\gamma s} E \bigl\vert x(s) \bigr\vert ^{2}\,ds. \end{aligned} $$

(3.23)

Using the substitution technique, we have

$$ \begin{aligned} \int _{2\bar{h}}^{t}e^{\gamma s} \biggl( \int _{s-2\tau}^{s}E \bigl\vert x(v) \bigr\vert ^{2}\,dv \biggr)\,ds &\le \int _{2\bar{h}-2\tau}^{t}E \bigl\vert x(v) \bigr\vert ^{2} \biggl( \int _{v}^{v+2 \tau}e^{\gamma s}\,ds \biggr)\,dv \\ &\le 2\tau e^{2\tau \gamma} \int _{2\bar{h}-2\tau}^{t}e^{\gamma s}E \bigl\vert x(s) \bigr\vert ^{2}\,ds \\ &\le 2\tau e^{2\tau \gamma} \biggl( \int _{2\bar{h}-2\tau}^{2\bar{h}}e^{ \gamma s}E \bigl\vert x(s) \bigr\vert ^{2}\,ds+ \int _{2\bar{h}}^{t}e^{\gamma s}E \bigl\vert x(s) \bigr\vert ^{2}\,ds \biggr) \end{aligned} $$

and

$$ \begin{aligned} & \int _{2\bar{h}}^{t}e^{\gamma s} \biggl( \int _{s-2\tau}^{s}E \bigl\vert x\bigl(v-h(v)\bigr) \bigr\vert ^{2}\,dv \biggr)\,ds \\ &\quad \le \int _{2\bar{h}-2\tau}^{t}E \bigl\vert x\bigl(v-h(v)\bigr) \bigr\vert ^{2} \biggl( \int _{v}^{v+2 \tau}e^{\gamma s}\,ds \biggr)\,dv \\ &\quad \le 2\tau e^{\gamma (2\tau +\bar{h})} \int _{2\bar{h}-2\tau}^{t}e^{ \gamma (s-h(s))}E \bigl\vert x \bigl(s-h(s)\bigr) \bigr\vert ^{2}\,ds \\ &\quad \le 2\tau h_{0}e^{\gamma (2\tau +\bar{h})} \int _{\bar{h}-2\tau}^{t}e^{ \gamma s}E \bigl\vert x(s) \bigr\vert ^{2}\,ds \\ &\quad \le 2\tau h_{0}e^{\gamma (2\tau +\bar{h})} \biggl( \int _{\bar{h}-2\tau}^{2 \bar{h}}e^{\gamma s}E \bigl\vert x(s) \bigr\vert ^{2}\,ds+ \int _{2\bar{h}}^{t}e^{\gamma s}E \bigl\vert x(s) \bigr\vert ^{2}\,ds \biggr). \end{aligned} $$

Substituting this into (3.23) yields

$$ \begin{aligned} &C_{1}e^{\gamma t}E \bigl\vert x(t) \bigr\vert ^{2} \\ &\quad \le Q_{7}+ \bigl(\gamma (Q_{4}+Q_{6} \tau )2\tau e^{2\tau \gamma} + \gamma (Q_{5}+Q_{6}\tau )2 \tau h_{0} e^{\gamma (2\tau +\bar{h})}+ \gamma C_{2}-\lambda \bigr) \\ &\qquad {}\times \int _{2\bar{h}}^{t}e^{\gamma s} E \bigl\vert x(s) \bigr\vert ^{2}\,ds, \end{aligned} $$

where

$$ \begin{aligned} Q_{7}={}&Q_{3}+\gamma (Q_{4}+Q_{6}\tau )2\tau e^{2\tau \gamma} \int _{2\bar{h}-2\tau}^{2\bar{h}}e^{\gamma s}E \bigl\vert x(s) \bigr\vert ^{2}\,ds \\ & {} + \gamma (Q_{5}+Q_{6}\tau )2\tau h_{0}e^{\gamma (2\tau + \bar{h})} \int _{\bar{h}-2\tau}^{2\bar{h}}e^{\gamma s}E \bigl\vert x(s) \bigr\vert ^{2}\,ds. \end{aligned} $$

Recalling (3.19), we obtain

$$ C_{1}e^{\gamma t}E \bigl\vert x(t) \bigr\vert ^{2}\le Q_{7}, \quad \forall t\ge 2\bar{h}, $$

(3.24)

which implies that (3.17) holds. Finally, by [1], we can obtain the other assertion (3.18) from (3.24). The proof is therefore complete. □

Corollary 3.6

Let Assumptions 2.1, 2.2, and 2.3hold. Assume that there exists a function $U\in C^{2,1}(\mathbb{R}^{n}\times S\times \mathbb{R}_{+};\mathbb{R}_{+})$ and some positive constants $C_{i},i=1,2$ and $\beta _{i}$, $i=1,2,3$ such that

$$ C_{1} \vert x \vert ^{2}\le U(x,i,t)\le C_{2} \vert x \vert ^{2} $$

(3.25)

and

$$ \mathcal{L}U(x,y,i,t)\le -\beta _{1} \vert x \vert ^{2}+\beta _{2} \vert y \vert ^{2}, \qquad \bigl\vert U_{x}(x,i,t) \bigr\vert ^{2} \le \beta _{3} \vert x \vert , $$

(3.26)

for all $x,y\in \mathbb{R}^{n}$, $i\in S$ and $t\in \mathbb{R}_{+}$. Let $\tau >0$ be sufficiently small for (3.3) to hold, and set

$$\begin{aligned} \lambda =\lambda _{2}-\lambda _{3}h_{0}- \frac{k^{2}}{\lambda _{1}} \tau \bigl[(4\tau +2)L_{0}^{2}(1+h_{0})+4k^{2} \tau \bigr]. \end{aligned}$$

Then the assertions of Theorem 3.5still hold, provided $\lambda _{1}<\beta _{1}/\beta _{3}^{2}$.

Proof

In fact, we only need to verify whether Assumption 3.1 is true. If $\lambda _{1}<\beta _{1}/\beta _{3}^{2}$, then it follows from (3.26) that

$$ \mathcal{L}U(x,y,i,t)+\lambda _{1} \bigl\vert U_{x}(x,i,t) \bigr\vert ^{2} \le -\bigl(\beta _{1}- \lambda _{1}\beta _{3}^{2}\bigr) \vert x \vert ^{2}+\beta _{2} \vert y \vert ^{2}, $$

Set $\lambda _{2}=\beta _{1}-\lambda _{1}\beta _{3}^{2}$ and $\lambda _{3}=\beta _{2}$, then Assumption 3.1 holds. □

4 Two examples

Let us now discuss two examples to illustrate our theory.

Example 4.1

Consider an unstable hybrid stochastic system with time-varying delay,

$$\begin{aligned} dx(t)=f\bigl(x(t),x\bigl(t-h(t)\bigr),r(t)\bigr)\,dt+g\bigl(x(t),x \bigl(t-h(t)\bigr),r(t)\bigr)\,dw(t), \end{aligned}$$

(4.1)

on $t\ge 0$, and assume that the coefficients f and g satisfy the linear growth condition, while the time delay $h(t)$ satisfies Assumption 2.3. Let us design a discrete-time state feedback control to stabilize system (4.1). Now, we use a linear controller $u(x,i,t)=F(i)x$, where $F(i)\in \mathbb{R}^{n\times n}$ for all $i\in S$. Therefore, the controlled hybrid stochastic systems with time-varying delay has the form

$$ \begin{aligned} dx(t)={}&\bigl[f\bigl(x(t),x\bigl(t-h(t) \bigr),r(t),t\bigr)+F\bigl(r(t)\bigr)x(\delta _{t})\bigr]\,dt \\ & {} +g\bigl(x(t),x\bigl(t-h(t)\bigr),r(t),t\bigr)\,dw(t). \end{aligned} $$

(4.2)

It is easy to obtain that Assumption 2.2 holds with $k=\max_{i\in S}\|F(i)\|$. Choose $U(x,i,t)=q_{i}|x|^{2}$, where $q_{i}>0$, then we have

$$ \begin{aligned} &\mathcal{L}U(x,y,i,t)\le x^{\top} \Biggl( \bigl[3q_{i}L_{0}+2q_{i}L_{0}^{2} \bigr]I+q_{i}\bigl[F(i)+F^{ \top}(i)\bigr]+\sum _{j=1}^{N}\gamma _{ij}q_{j}I \Biggr)x \\ &\hphantom{\mathcal{L}U(x,y,i,t)\le}{} +y^{\top}\bigl[\bigl(q_{i}L_{0}+2q_{i}L_{0}^{2} \bigr)I\bigr]y, \\ & \bigl\vert U_{x}(x,i,t) \bigr\vert ^{2}\le 2\max _{i\in S}q_{i} \vert x \vert . \end{aligned} $$

We assume that the following linear matrix inequalities:

$$\begin{aligned} \bigl[3q_{i}L_{0}+2q_{i}L_{0}^{2} \bigr]I+Y(i)+Y(i)^{\top}+\sum_{j=1}^{N} \gamma _{ij}q_{j}I< 0 \end{aligned}$$

(4.3)

have their solutions for $q_{i}>0$ and $Y_{i}\in \mathbb{R}^{n\times n}$ ($i\in S$). Set $F(i)=q_{i}^{-1}Y(i)$ and

$$\begin{aligned} &\beta _{1}=-\max_{i\in S}\lambda _{\max} \Biggl(\bigl[3q_{i}L_{0}+2q_{i}L_{0}^{2} \bigr]+Y(i)+Y(i)^{ \top}+\sum_{j=1}^{N} \gamma _{ij}q_{j} \Biggr), \\ &\beta _{2}=\max_{i\in S}\lambda _{\max}(q_{i}I),\qquad \beta _{3}=2 \max_{i\in S}\lambda _{\max} \bigl[\bigl(q_{i}L_{0}+2q_{i}L_{0}^{2} \bigr)I\bigr]. \end{aligned}$$

Then, we see that (3.26) is satisfied. The corresponding parameters in Corollary 3.6 become $C_{1}=\min_{i\in S}q_{i}$, $C_{2}=\max_{i\in S}q_{i}$. Choose $\lambda _{1}<\beta _{1}/\beta _{3}^{2}$, and set $\lambda _{2}=\beta _{1}-\lambda _{1}\beta _{3}^{2}$ and $\lambda _{3}=\beta _{2}$. Let $\tau >0$ be sufficiently small for (3.3) to hold, then, by Corollary 3.6, the controlled hybrid stochastic system with time-varying delay (4.2) is exponentially stable in mean square and almost surely as well.

Example 4.2

Let $r(t)$ be a right-continuous Markov chain on the state space $S=\{1,2\}$ with its generator

$$\mathrm{\Gamma }=\left[\begin{array}{cc}-1& 1\\ 1& -1\end{array}\right].$$

Consider the following one-dimensional hybrid stochastic system with time-varying delay:

$$\begin{aligned} dx(t)=f\bigl(x(t),x\bigl(t-h(t)\bigr),r(t),t\bigr)\,dt+g \bigl(x(t),x\bigl(t-h(t)\bigr),r(t),t\bigr)\,dw(t), \end{aligned}$$

(4.4)

on $t\ge 0$, where

$$\begin{aligned}& f(x,y,1)=-1.2x^{3}+0.2y, \qquad g(x,y,1)=0.3x+0.05y, \\& f(x,y,2)=-0.8x^{3}+0.5y, \qquad g(x,y,2)=0.4x+0.02y \end{aligned}$$

and

$$ \begin{aligned} h(t)={}&\sum_{k=0}^{\infty} \bigl\{ \bigl[0.25-0.2(t-3k)\bigr]I_{[3k,3k+1)}(t)+0.05I_{[3k+1,3k+2)}(t) \\ &{}+\bigl[0.05+0.2(t-3k-2)\bigr]I_{[3k+2,3k+3)}(t) \bigr\} . \end{aligned} $$

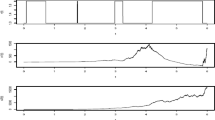
It is easy to obtain that Assumption 2.1 holds with $L_{0}=0.5$ and $h(t)$ satisfies Assumption 2.3 with $\underline{h}=0.05$, $\bar{h}=0.25$, and $h_{0}=1.25$. A computer simulation (Fig. 1) shows that Eq. (4.4) is not almost surely exponentially stable.

Figure 1

Computer simulation of the path of the hybrid stochastic system with time-varying delay (4.4) using the Euler–Maruyama method with step size 10⁻³ and initial values $x(0)=2$ and $r(0)=1$

Now consider the linear controller of the form $u(x,i,t)=F(i)x$ ($i=1,2$) and the controlled system given as follows:

$$ \begin{aligned} dx(t)={}&\bigl[f\bigl(x(t),x\bigl(t-h(t) \bigr),r(t),t\bigr)+F\bigl(r(t)\bigr)x(\delta _{t})\bigr]\,dt \\ & {} +g\bigl(x(t),x\bigl(t-h(t)\bigr),r(t),t\bigr)\,dw(t). \end{aligned} $$

(4.5)

Obviously, we derive that the linear matrix inequalities (4.5) have their solutions $q_{1}=1$, $q_{2}=2$, $Y(1)=-16$, and $Y(2)=-8$. Then, we have $F(1)=-16$ and $F(2)=-4$. Hence, we can obtain that $k=16$, $\beta _{1}=15$, $\beta _{2}=2$, and $\beta _{3}=4$. Choose $\lambda _{1}=0.5$ and set $\lambda _{2}=7$, $\lambda _{3}=2$. Let $\tau <2.42\times 10^{-3}$, then, by Corollary 3.6, the controlled hybrid stochastic system with time-varying delay (4.5) is exponentially stable in mean square and almost surely as well. A computer simulation (Fig. 2) clearly supports this result.

Figure 2

Computer simulation of the path of the controlled hybrid stochastic system with time-varying delay (4.5) with $\tau =10^{-3}$ using the Euler–Maruyama method with step size 10⁻³ and initial values $x(0)=2$ and $r(0)=1$

5 Conclusion

This paper is devoted to the stabilization of hybrid stochastic systems with time-varying delay by feedback controls based on discrete-time state observations. An upper bound $\tau ^{*}$ on the duration τ between two consecutive state observations is obtained by the method of Lyapunov functionals. In the meantime, some sufficient conditions in the sense of $H_{\infty}$ stability, mean-square asymptotic stability, and exponential stability have been established for the hybrid stochastic systems with time-varying delay as long as $\tau <\tau ^{*}$.

Appendix

Proof of Theorem 2.8

By Mao [1], we know that Assumptions 2.1 and 2.2 guarantee the existence of the unique maximal local solution $x(t)$ on $t\in [0,\sigma _{\infty})$, where $\sigma _{\infty}$ is the explosion time. Let $k_{0}$ be the bound for ξ. For each integer $k\ge k_{0}$, define the stopping time

$$ \tau _{k}=\inf \bigl\{ t\in [0,\sigma _{\infty}): \bigl\vert x(t) \bigr\vert \ge k\bigr\} . $$

Clearly, $\tau _{k}$ is increasing as $k\to \infty$. Set $\tau _{\infty}=\lim_{k\to \infty}\tau _{k}$, whence $\tau _{\infty}\le \sigma _{\infty}$ a.s. Note if we can show that $\tau _{\infty}=\infty$ a.s., then $\sigma _{\infty}=\infty$ a.s. So we just need to show that $\tau _{\infty}=\infty$ a.s. Now, we shall show that $\tau _{\infty } > \tau$ a.s. For any $k\ge k_{0}$ and $t\in [0,\tau ]$, by the Itô formula, it is easy to show that

$$ \begin{aligned} E \bigl\vert x(t\wedge \tau _{k}) \bigr\vert ^{2} ={}& \bigl\vert x(0) \bigr\vert ^{2}+ E \int _{0}^{ \tau _{k}\wedge t} \bigl(2x^{\top}(s)\bigl[f \bigl(x(s),x\bigl(s-h(s)\bigr),r(s),s\bigr) \\ & {}+u\bigl(x(\delta _{s}),r(s),s\bigr)\bigr]+ \bigl\vert g \bigl(x(s),x\bigl(s-h(s)\bigr),r(s),s\bigr) \bigr\vert ^{2} \bigr) \,ds. \end{aligned} $$

(6.1)

By Assumptions 2.1 and 2.2, we then get

$$\begin{aligned} E \bigl\vert x(t\wedge \tau _{k}) \bigr\vert ^{2} \le \bigl\vert \xi (0) \bigr\vert ^{2}+ E \int _{0}^{\tau _{k} \wedge t}\bigl(\alpha _{1} \bigl\vert x(s) \bigr\vert ^{2}+2k \bigl\vert x(\delta _{s}) \bigr\vert ^{2}+\alpha _{2} \bigl\vert x\bigl(s-h(s)\bigr) \bigr\vert ^{2}\bigr)\,ds, \end{aligned}$$

where $\alpha _{1}=3L+2L^{2}$, $\alpha _{2}=L+2L^{2}$, $H_{1}=\alpha _{2}\int _{0}^{\tau }E|x(s-h(s))|^{2}\,ds$. Noting that for $t\in [0,\tau ]$, $-\bar{h}\le t-h(t)\le \tau -\underline{h}\le 0$, we have

$$\begin{aligned} H_{1} =\alpha _{2} \int _{0}^{\tau }E \bigl\vert \xi \bigl(s-h(s)\bigr) \bigr\vert ^{2}\,ds=\alpha _{2} \tau \Vert \xi \Vert ^{2}< \infty . \end{aligned}$$

Then it follows that

$$\begin{aligned} \sup_{0\le t\le \tau}E \bigl\vert x(t\wedge \tau _{k}) \bigr\vert ^{2} \le \bigl\vert \xi (0) \bigr\vert ^{2}+H_{1}+ (\alpha _{1}+2k) \int _{0}^{t} \Bigl(\sup_{0\le s\le \tau}E \bigl\vert x(s\wedge \tau _{k}) \bigr\vert ^{2} \Bigr) \,ds. \end{aligned}$$

Hence, by the Gronwall inequality, we have

$$\begin{aligned} E \bigl\vert x(\tau _{k}\wedge t) \bigr\vert ^{2} \le \bigl( \bigl\vert \xi (0) \bigr\vert ^{2}+H_{1} \bigr)e^{(\alpha _{1}+2k) \tau}, \quad 0\le t\le \tau , \end{aligned}$$

(6.2)

for any $k\ge k_{0}$. In particular, $E|x(\tau _{k}\wedge \tau )|^{2} \le (|\xi (0)|^{2}+H_{1})e^{( \alpha _{1}+2k)\tau}$, $\forall k\ge k_{0}$. This implies $k^{2} P(\tau _{k}\le \tau ) \le (|\xi (0)|^{2}+H_{1})e^{(\alpha _{1}+2k) \tau}$. Letting $k\to \infty$, we hence obtain that $P(\tau _{\infty }\le \tau ) =0$, namely $P(\tau _{\infty } > \tau ) = 1$. Letting $k\to \infty$ in (6.2) yields

$$\begin{aligned} E \bigl\vert x(t) \bigr\vert ^{2} \le \bigl( \bigl\vert \xi (0) \bigr\vert ^{2}+H_{1}\bigr)e^{(\alpha _{1}+2k)\tau}, \quad 0\le t\le \tau . \end{aligned}$$

(6.3)

Let us now proceed to prove $\tau _{\infty } > 2\tau$ a.s., given that we have shown (6.3). For any $k\ge k_{0}$ and $t\in [0, 2\tau ]$, it follows from (6.1) that

$$\begin{aligned} E \bigl\vert x(t\wedge \tau _{k}) \bigr\vert ^{2} \le \bigl\vert \xi (0) \bigr\vert ^{2}+H_{2}+ E \int _{0}^{ \tau _{k}\wedge t}\bigl(\alpha _{1} \bigl\vert x(s) \bigr\vert ^{2}+2k \bigl\vert x(\delta _{s}) \bigr\vert ^{2}\bigr)\,ds, \end{aligned}$$

(6.4)

where $H_{2}=\alpha _{2}\int _{0}^{2\tau }E|x(s-h(s))|^{2}\,ds$. Note that for $t\in [0,2\tau ]$, $-\bar{h}\le t-h(t)\le \tau$. By Lemma 2.6 and (6.3), we have

$$ \begin{aligned} H_{2}&=H_{1}+\alpha _{2} \int _{\tau }^{2\tau }E \bigl\vert x\bigl(s-h(s)\bigr) \bigr\vert ^{2}\,ds \\ &\le H_{1}+\alpha _{2} h_{0} \int _{\tau -\bar{h}}^{2\tau - \underline{h}}E \bigl\vert x(s) \bigr\vert ^{2}\,ds \\ &\le H_{1}+\alpha _{2}h_{0}(\bar{h}-\tau ) \Vert \xi \Vert ^{2}+\alpha _{2}h_{0}\bigl( \bigl\vert \xi (0) \bigr\vert ^{2}+H_{1} \bigr)e^{(\alpha _{1}+2k)\tau}\tau \\ &< \infty . \end{aligned} $$

Consequently,

$$\begin{aligned} \sup_{0\le t\le 2\tau}E \bigl\vert x(t\wedge \tau _{k}) \bigr\vert ^{2} \le \bigl\vert \xi (0) \bigr\vert ^{2}+H_{2}+ (\alpha _{1}+2k) \int _{0}^{t} \Bigl(\sup_{0\le s\le 2\tau}E \bigl\vert x(s \wedge \tau _{k}) \bigr\vert ^{2} \Bigr) \,ds. \end{aligned}$$

Gronwall inequality then implies

$$\begin{aligned} E \bigl\vert x(t\wedge \tau _{k}) \bigr\vert ^{p}\le \bigl( \bigl\vert \xi (0) \bigr\vert ^{2}+H_{2} \bigr)e^{(\alpha _{1}+2k)2 \tau}, \quad 0\le t\le 2\tau . \end{aligned}$$

(6.5)

In particular, $E |x(\tau _{k}\wedge 2\tau |^{p} \le (|\xi (0)|^{2}+H_{2})e^{( \alpha _{1}+2k)2\tau}$, $\forall k\ge k_{0}$. This implies $k^{2} P(\tau _{k}\le 2\tau ) \le (|\xi (0)|^{2}+H_{2})e^{(\alpha _{1}+2k)2 \tau}$. Letting $k\to \infty$, we then obtain that $P(\tau _{\infty }\le 2\tau ) =0$, namely $P(\tau _{\infty } > 2\tau ) = 1$. Letting $k\to \infty$ in (6.5) yields

$$ E \bigl\vert x(t) \bigr\vert ^{2} \le \bigl( \bigl\vert \xi (0) \bigr\vert ^{2}+H_{2}\bigr)e^{(\alpha _{1}+2k)2\tau}, \quad 0\le t \le 2\tau . $$

Repeating this procedure, we can show that, for any integer $i\ge 1$, $\tau _{\infty } > i\tau$ a.s.,

$$ E \bigl\vert x(t) \bigr\vert ^{2} \le \bigl( \bigl\vert \xi (0) \bigr\vert ^{2}+H_{i}\bigr)e^{(\alpha _{1}+2k)i\tau}, \quad 0\le t \le i\tau , $$

where

$$ \begin{aligned} H_{i}&=\alpha _{2} \int _{0}^{i\tau }E \bigl\vert x\bigl(s-h(s)\bigr) \bigr\vert ^{2}\,ds \\ &=H_{i-1}+\alpha _{2} \int _{(i-1)\tau }^{i\tau }E \bigl\vert x\bigl(s-h(s)\bigr) \bigr\vert ^{2}\,ds \\ &\le H_{i-1}+\alpha _{2} h_{0} \int _{(i-1)\tau -\bar{h}}^{i\tau - \underline{h}}E \bigl\vert x(s) \bigr\vert ^{2}\,ds \\ &\le H_{i-1}+\alpha _{2}h_{0}\bar{h}\bigl( \bigl\vert \xi (0) \bigr\vert ^{2}+H_{i-1} \bigr)e^{( \alpha _{1}+2k)(i-1)\tau} \\ &< \infty . \end{aligned} $$

We must therefore have $\tau _{\infty } = \infty$ a.s., and the required assertion (2.7) holds as well. □