1 Introduction

Fractional derivatives and fractional differential equations have been shown to be a beneficial approach in physical phenomena modeling in different fields of engineering and science [1]. It is worth mentioning that many practical systems display memory and genetic characteristics, which can be better described by fractional calculus than by integer calculus, such as electromagnetic waves [2], hydroturbine-governing systems [3], viscoelastic systems [4], financial systems [5], and wind-turbine generators [6]. Also, many different definitions of fractional derivatives are introduced according to different kernels [7–9]. Theses definitions are used in Riesz-space fractional equations [10], time-fractional differential equations [11–13], complex network [14, 15], materials constitutive equations [16, 17], fractional diffusion modeling [18–20], fractional love models [21, 22], and control theories [23–25]. Furthermore, many types of synchronization such as complete, anti, projective, modified projective, and function synchronization have been introduced [26–30].

The generalized fractional derivative has many features over the integer derivatives and has potential in many applications. Since chaos in fractional-order models is more complex than in the integer cases, it has been proposed in image encryption [31, 32]. Recently, Anderson and Ulness used the generalized fractional derivative in quantum mechanics [33]. Ren and Zhai investigated a generalized fractional memristor-based impulsive neural network [34]. Chaotic fractional-order models with two parameters can recover secure communication and information transfer [31]. The GF derivative will be a novel direction in the fractional calculus due to its important usage in many fields [31]. In [35], the authors presented the chaotic GF Lorenz and Rössler systems. Odibat et al. introduced the GF differential equation with time delay and solved it using a modified predictor–corrector technique [36]. Ren and Zhai studied the stability analysis of GF neutral systems with time delays [37].

Numerous physical problems have been mobilized based on the Caputo fractional derivative as it is convenient for initial-value problems (IVPs) and has many criteria that resemble integer-order derivatives. Jarad et al. [38] introduced the generalized properties of the Caputo-type fractional derivative. They discussed the relation between the generalized fractional derivative operator and the generalized fractional integral operator. The Caputo version of the generalized derivative appears to be nearer to ordinary derivatives than other generalized derivatives. Thus, the objective of this work is to introduce the generalized fractional-order nonlinear dynamical systems governed by the generalized fractional derivative [38] as follows:

$$ {}^{C} \mathcal{D}^{\sigma ,\rho}x(t)=Ax(t)+f\bigl(x(t)\bigr), $$
(1.1)

where \({}^{C}\mathcal{D}^{\sigma ,\rho}\) denotes the left generalized Caputo-type fractional derivative, \(1<\sigma <2\), \(\rho \geq 0\), \(x\in R^{n}\) is a state variable, A is a \((n\times n)\) constant matrix, and \(f(x(t))\in R^{n}\) is a vector of continuous functions. The predictor–corrector (P–C) method is a numerical simulation purposed for Caputo fractional-order systems [39]. Odibat and Baleanu [40] introduced a modified P–C method for the numerical solution of generalized Caputo-type IVPs. We use the same procedure as in [40] to solve system (1.1).

Chaos synchronization and control theory in fractional calculus have become important topics in recent years. Several types of synchronization and different control techniques are used in many applications such as neural networks [41–43], biology [44, 45], and secure communications [46, 47]. The generalized fractional-order systems will be used in potential applications as an extension of classical fractional- and integer-order ones.

The previous papers on studying the stability of GFSs investigated with fractional-order lying in \((0,1)\), while this paper states the stability of GFSs with order lying in \((1, 2)\). The stability analysis of that system using the G–B Lemma, the M–L function, and the Laplace transform is illustrated. The M–L stability of GFS with order lying in \((1, 2)\) is investigated by the Lyapunov direct method. We show that chaotic solutions for GF models are more complicated than the classical fractional and integer cases [31]. We controlled the chaotic GFSs using linear feedback control [48]. By this technique of control, we synchronized two different chaotic GFSs. The paper is outlined as follows: In Sect. 2, we address some important preliminaries. In Sect. 3, using the G–B Lemma, the M–L function, and the Laplace transform, we prove the solution of the generalized fractional dynamical system on its approach to zero at infinity. By linear feedback control, a theorem to control chaotic GFS is investigated in Sect. 4. We give an example to test the validity of this theorem. In Sect. 5, the control functions that are used to achieve synchronization between two different chaotic GFSs are illustrated. An example of synchronization between different GFSs with orders lying in \((1, 2)\) is presented. Finally, the conclusion of our work is given in Sect. 6.

2 Preliminaries

We state the basic definitions of fractional derivatives and some lemmas in this section [7, 49–53]. The left-sided and right-sided fractional derivatives of order σ, are written as

$$ \bigl({}^{\mathrm{RL}}_{\ \ a}\mathcal{D}_{x}^{\sigma}g \bigr) (x)= \frac{1}{\Gamma (1-\sigma )} \frac{d}{dx} \int _{a}^{x} \frac{g(y)\,dy}{(x-y)^{\sigma}}, \quad x > a, $$
(2.1)

and

$$ \bigl({}^{\mathrm{RL}}_{\ \ x}\mathcal{D}_{b}^{\sigma}g \bigr) (x) = \frac{1}{\Gamma (1-\sigma )} \biggl(\frac{-d}{dx} \biggr) \int _{x}^{b} \frac{g(y)\,dy}{(y-x)^{\sigma}},\quad x < b. $$
(2.2)

The left and right RL fractional derivatives for \(\sigma \in (n-1, n)\), \(n\in \mathbb{N}\) take the forms:

$$ \bigl({}^{\mathrm{RL}}_{\ \ a}\mathcal{D}_{x}^{\sigma}g \bigr) (x)= \frac{1}{\Gamma (n-\sigma )} \biggl(\frac{d}{dx} \biggr)^{n} \int _{a}^{x} \frac{g(y)\,dy}{(x-y)^{-n+1+\sigma}},\quad x > a, $$
(2.3)

and

$$ \bigl({}^{\mathrm{RL}}_{\ \ x}\mathcal{D}_{b}^{\sigma}g \bigr) (x)= \frac{1}{\Gamma (n-\sigma )} \biggl(\frac{-d}{dx} \biggr)^{n} \int _{x}^{b} \frac{g(y)\,dy}{(y-x)^{-n+1+\sigma}},\quad x < b. $$
(2.4)

For \(\sigma \in (n-1, n)\), the corresponding left-sided and right-sided Caputo derivatives are defined as:

$$ \bigl({}^{C}_{a}\mathcal{D}_{x}^{\sigma}g \bigr) (x)= \frac{1}{ \Gamma (n-\sigma )} \int _{a}^{x} \frac{g^{(n)}(y)\,dy}{(x-y)^{-n+1+\sigma}},\quad x > a, $$
(2.5)

and

$$ \bigl({}^{C}_{x}\mathcal{D}_{b}^{\sigma}g \bigr) (x)= \frac{1}{\Gamma (n-\sigma )} \int _{x}^{b} \frac{(-1)^{n}g^{(n)}(y)\,dy}{(y-x)^{-n+1+\sigma}}, \quad x < b. $$
(2.6)

Definition 2.1

(Katugampola [54])

The generalized left-sided RL integral of f \({}^{\mathrm{RL}}_{\ \ a}\mathcal{I}_{x}^{\sigma ,\rho}f(x)\) order σ, when \(\sigma >0\), \(\rho \geq 0\), is

$$ \bigl({}^{\mathrm{RL}}_{\ \ a}\mathcal{I}_{x}^{\sigma ,\rho}f \bigr) (x)= \frac{\rho ^{1-\sigma}}{\Gamma (\sigma )} \int _{a}^{x} \frac{s^{\rho -1}f(s)\,ds}{(x^{\rho}-s^{\rho})^{1-\sigma}},\quad x > a. $$
(2.7)

For \(n-1 <\sigma <n\), \(n\in \mathbb{N}\), the generalized left-sided RL fractional derivatives of order σ is written as

$$ \begin{aligned} \bigl({}^{\mathrm{RL}}_{\ \ a}\mathcal{D}_{x}^{\sigma ,\rho}g \bigr) (x)&= \biggl(x^{1-\rho}\frac{d}{dx} \biggr)^{n} \bigl({}^{ \mathrm{RL}}_{\ \ a} \mathcal{I}_{x}^{n-\sigma ,\rho}g \bigr) (x) \\ &= \frac{\rho ^{\sigma -n+1}}{\Gamma (n-\sigma )} \biggl(x^{1-\rho} \frac{d}{dx} \biggr)^{n} \int _{a}^{x} \frac{y^{\rho -1}g(y)\,dy}{(x^{\rho}-y^{\rho})^{-n+1+\sigma}},\quad x > a. \end{aligned} $$
(2.8)

We recover the RL fractional derivative in (2.3) when \(\rho = 1\). Moreover, the generalized left-sided Caputo derivatives of order σ \((\sigma \in (n-1, n))\) are defined as

$$ \bigl({}^{C}_{a}\mathcal{D}_{x}^{\sigma ,\rho}g \bigr) (x)= \Biggl( {}^{\mathrm{RL}}_{\ \ a}\mathcal{D}_{x}^{\sigma ,\rho} \Biggl[g(t)-\sum_{i=0}^{n-1} \frac{g^{(i)}(a)}{i!}(t-a)^{i} \Biggr] \Biggr) (x) ,\quad x > a, $$
(2.9)

where \(n=\lceil \operatorname{Re}(\sigma )\rceil \).

Definition 2.2

(Jarad et al. [38])

The generalized left-sided Caputo derivative of order σ (\(n-1 <\sigma <n\)), \(n\in \mathbb{N}\) is written by

$$ \bigl({}^{C}_{a}\mathcal{D}_{x}^{\sigma ,\rho}g \bigr) (x)= \frac{\rho ^{\sigma -n+1}}{\Gamma (n-\sigma )} \int _{a}^{x}\bigl(x^{\rho}-y^{ \rho} \bigr)^{-n+1+\sigma} \biggl(y^{1-\rho}\frac{d}{dy} \biggr)^{n}g(y) \frac{dy}{y^{1-\rho}},\quad x > a, $$
(2.10)

further analysis includes

$$ {}^{\mathrm{RL}}_{\ \ a}\mathcal{I}_{x}^{\sigma ,\rho}{}^{C}_{ a} \mathcal{D}_{x}^{\sigma ,\rho}g(x)=g(x) -\sum _{i=0}^{n-1} \frac{ (y^{1-\rho}\frac{d}{dy} )^{i}g(y)|_{y=a}}{i!}\biggl( \frac{(t^{\rho}-a^{\rho}}{\rho}\biggr)^{i}. $$
(2.11)

We recover the Caputo fractional derivative (2.5) when \(\rho = 1\) in (2.10). The ρ-Laplace transform of the Caputo generalized fractional derivative is presented as [49]:

$$ \mathcal{L}_{\rho}\bigl\{ \bigl({}^{C} \mathcal{D}^{\sigma ,\rho} g \bigr) (t)\bigr\} =s^{ \sigma } \mathcal{L}_{\rho}\bigl\{ g(t)\bigr\} -\sum_{j=0}^{n-1}s^{n-j-1} \biggl(\biggl(t^{1-\rho}\frac{d}{dt}\biggr)^{j}g \biggr) (0), $$
(2.12)

where \({}^{C}\mathcal{D}^{\sigma ,\rho}={}^{C}_{0}\mathcal{D}_{x}^{\sigma , \rho}\) (i.e., the left generalized Caputo-type fractional derivative of order σ).

The ρ-Laplace transform of a function g is given as:

$$ \mathcal{L}_{\rho}\bigl\{ g(t)\bigr\} (s)= \int _{0}^{\infty}e^{-s \frac{t^{\rho}}{\rho}}g(t) \frac{dt}{t^{1-\rho}}. $$
(2.13)

Definition 2.3

([50])

The two-parameter Mittag–Leffler function is described as:

$$ E_{\sigma , \beta}(w)=\sum_{j=0}^{\infty} \frac{w^{j}}{\Gamma (\sigma j+\beta )}, \quad \sigma , \beta >0, w \in C. $$
(2.14)

Lemma 2.1

([51])

Let \(G(s)=\mathcal{L}\{g(t)\}\). If all poles of \(sG(s)\) are in the open left-half complex plane, then \(\lim_{t\rightarrow \infty}g(t)=\lim_{s\rightarrow 0}sG(s)\).

The Laplace transform of the function \(w^{\sigma l+\beta -1}E_{\sigma , \beta}^{(l)}(-aw^{\sigma})\) is:

$$ \mathcal{L}\bigl\{ w^{\sigma l+\beta -1}E_{\sigma , \beta}^{(l)} \bigl(-aw^{ \sigma}\bigr)\bigr\} =\frac{l!s^{\sigma -\beta}}{(s^{\sigma}\mp a)^{l+1}}\quad \bigl(R(s) \geq \vert a \vert ^{\frac{1}{\sigma}}\bigr), $$
(2.15)

where \(E_{\sigma , \beta}^{(l)}(w)\) is

$$ E_{\sigma , \beta}^{(l)}(w)= \frac{d^{l}}{dw^{l}}\sum_{k=0}^{\infty} \frac{w^{k}}{\Gamma (\sigma k+\beta )}=\sum_{k=0}^{\infty} \frac{(k+l)!w^{k}}{k!\Gamma (\sigma k+\sigma l+\beta )}. $$
(2.16)

From Definition 2.3, one obtains:

$$ \begin{aligned} \frac{dE_{\sigma , \beta}(w)}{dw}= \frac{E_{\sigma , \beta -1}(w)-(\beta -1)E_{\sigma , \beta}(w)}{\sigma w}. \end{aligned} $$
(2.17)

Using (2.17), we have:

$$ E_{\sigma , \beta}^{(m)}(w)=( \sigma w)^{-m}\sum_{k=0}^{m}d_{k}E_{ \sigma , \beta -k}(w), $$
(2.18)

where \(d_{k}\) (\(k=0, 1, \ldots, m\)) are real constants depend on β.

Lemma 2.2

([7])

The function \(g(z(t))\) satisfies the Lipschitz condition, if

$$ \bigl\| g(z)-g(w)\bigr\| \leq M\| z-w \| ,\quad M\in R^{+}. $$
(2.19)

Lemma 2.3

([55])

$$ E_{\sigma , \beta}(D)\leq \frac{C}{1+ \Vert D \Vert },\quad 0< \sigma < 2, D\in R^{n \times n}, C\in R^{+}, $$
(2.20)

where μ satisfies (i) \(\pi \sigma /2\leq \mu \leq \min\{\pi , \pi \sigma \}\) and (ii) \(\mu \leq |\arg (\operatorname{eig}(D))|\leq \pi \).

Lemma 2.4

(Gronwall–Bellman Lemma [53])

If

$$ h(x)\leq g(x)+ \int _{0}^{x}m(w)h(w)\,dw, $$
(2.21)

where \(m(x)\geq 0\), \(g(x)\), \(h(x)\) are continuous functions, \(0 \leq x \leq T\), then \(h(x)\) satisfies

$$ h(x)\leq g(x)+ \int _{0}^{x}m(w)g(w)\exp\biggl[ \int _{w}^{x}m(y)\,dy\biggr]\,dw. $$
(2.22)

3 Stability analysis

In this section, we introduce two methods to study the stability of system (1.1) for \(\sigma \in (1,2)\). The first one depends on the Gronwall–Bellman (G–B) Lemma, the Mittag–Leffler (M–L) function, and the Laplace transform, while the second method depends on the Lyapunov direct method and it is called M–L stability.

Theorem 3.1

The zero solution of a generalized Caputo fractional-order system (1.1) for \(\sigma \in (1,2)\) is stable if:

  1. 1.

    \(|\arg(\lambda _{i}(\frac{A}{\rho ^{\sigma}}))|>\pi \sigma /2\).

  2. 2.

    \(f(0)=0\), \(\lim_{\|x\|\rightarrow 0}\frac{\|f(x)\|}{\|x\|}=0\),

where \(x\in \mathbb{R}^{n\times 1}\), \(A\in \mathbb{R}^{n\times n}\), \(t\in \mathbb{R}^{+}\) and \(\lambda _{i}(\frac{A}{\rho ^{\sigma}})\) are the eigenvalues of matrix \(\frac{A}{\rho ^{\sigma}}\).

Proof

The initial conditions of system (1.1) are given as:

$$ \biggl(x^{1-\rho} \frac{d}{dt} \biggr)^{k}x(0)=x_{k},\quad k=0,1. $$
(3.1)

Using the ρ-Laplace transform and ρ-Laplace inverse transform, one obtains the solution of (1.1) with the initial conditions (3.1) as follows:

$$ \begin{aligned} x(t)={}& E_{\sigma , 1}\biggl[A\biggl(\frac{t^{\rho}}{\rho} \biggr)^{\sigma}\biggr] x_{1}+ \frac{t^{\rho}}{\rho}E_{\sigma , 2} \biggl[A\biggl(\frac{t^{\rho}}{\rho}\biggr)^{\sigma}\biggr] x_{2} \\ &{}+ \int _{0}^{t}\biggl(\frac{t^{\rho}-s^{\rho}}{\rho} \biggr)^{\sigma -1}E_{ \sigma , \sigma}\biggl[A\biggl(\frac{t^{\rho}-s^{\rho}}{\rho} \biggr)^{\sigma}\biggr]s^{\rho -1}f\bigl(x(s)\bigr) \,ds. \end{aligned} $$
(3.2)

By part 2 of Theorem 3.1, there exists \(C>0\) and \(\delta _{0}\) such that

$$ \bigl\Vert x(t) \bigr\Vert < \delta _{0} \quad \Rightarrow \quad \bigl\Vert f\bigl(x(t)\bigr) \bigr\Vert < \kappa \frac{(\sigma -1) \Vert A \Vert \Vert x(t) \Vert }{C}, \quad t\geq 0, 0< \kappa < 1. $$
(3.3)

Using Eq. (3.3) and Lemma 2.3, (3.2) gives

$$ \begin{aligned} \bigl\Vert x(t) \bigr\Vert &\leq \frac{c_{1} \Vert x_{1} \Vert }{1+ \Vert A \Vert (\frac{t^{\rho}}{\rho})^{\sigma}} + \frac{c_{2} \Vert x_{2} \Vert t^{\rho}}{1+ \Vert A \Vert (\frac{t^{\rho}}{\rho})^{\sigma}} \\ &\quad {}+\kappa \int _{0}^{t} \frac{(\frac{t^{\rho}-s^{\rho}}{\rho})^{\sigma -1}s^{\rho -1}(\sigma -1) \Vert A \Vert }{ (1+ \Vert A \Vert (\frac{t^{\rho}-s^{\rho}}{\rho})^{\sigma})} \bigl\Vert x(s) \bigr\Vert \,ds \\ &\leq \frac{c_{1} \Vert x_{1} \Vert }{(1+ \Vert A \Vert (\frac{t^{\rho}}{\rho})^{\sigma})^{\kappa}}+ \frac{c_{2} \Vert x_{2} \Vert t^{\rho}}{1+ \Vert A \Vert (\frac{t^{\rho}}{\rho})^{\sigma}} \\ &\quad {} +\kappa \int _{0}^{t} \frac{(\frac{t^{\rho}-s^{\rho}}{\rho})^{\sigma -1}s^{\rho -1}(\sigma -1) \Vert A \Vert }{ (1+ \Vert A \Vert (\frac{t^{\rho}-s^{\rho}}{\rho})^{\sigma})} \bigl\Vert x(s) \bigr\Vert \,ds. \end{aligned} $$
(3.4)

Using the Gronwall–Bellman Lemma 2.4 and Eq. (3.4), we obtain

$$\begin{aligned} \bigl\Vert x(t) \bigr\Vert &\leq \frac{c_{1} \Vert x_{1} \Vert }{(1+ \Vert A \Vert (\frac{t^{\rho}}{\rho})^{\sigma})^{\kappa}} + \frac{c_{2} \Vert x_{2} \Vert t^{\rho}}{1+ \Vert A \Vert (\frac{t^{\rho}}{\rho})^{\sigma}} \\ &\quad {} +\kappa \int _{0}^{t} \frac{(\frac{t^{\rho}-s^{\rho}}{\rho})^{\sigma -1}s^{\rho -1}(\sigma -1) \Vert A \Vert }{(1+ \Vert A \Vert (\frac{t^{\rho}-s^{\rho}}{\rho})^{\sigma})} \biggl( \frac{c_{1} \Vert x_{1} \Vert }{(1+ \Vert A \Vert (\frac{t^{\rho}}{\rho})^{\sigma})^{\kappa}}+ \frac{c_{2} \Vert x_{2} \Vert t^{\rho}}{1+ \Vert A \Vert (\frac{t^{\rho}}{\rho})^{\sigma}} \biggr) \\ &\quad {}\times \exp \biggl( \int _{ \tau}^{t}\kappa \frac{(\frac{t^{\rho}-s^{\rho}}{\rho})^{\sigma -1} s^{\rho -1}(\sigma -1) \Vert A \Vert }{(1+ \Vert A \Vert (\frac{t^{\rho}-s^{\rho}}{\rho})^{\sigma})}\,ds \biggr)\,d\tau \\ &= \frac{c_{1} \Vert x_{1} \Vert }{(1+ \Vert A \Vert (\frac{t^{\rho}}{\rho})^{\sigma})^{\kappa}}+ \frac{c_{2} \Vert x_{2} \Vert t^{\rho}}{1+ \Vert A \Vert (\frac{t^{\rho}}{\rho})^{\sigma}} \\ &\quad {}+\kappa \int _{0}^{t} \biggl( \frac{c_{1} \Vert x_{1} \Vert }{(1+ \Vert A \Vert (\frac{\tau ^{\rho}}{\rho})^{\sigma})^{\kappa}}+ \frac{c_{2} \Vert x_{2} \Vert \tau ^{\rho}}{1+ \Vert A \Vert (\frac{\tau ^{\rho}}{\rho})^{\sigma}} \biggr) \frac{(\frac{t^{\rho}-\tau ^{\rho}}{\rho})^{\sigma -1}\tau ^{\rho -1}(\sigma -1) \Vert A \Vert }{ (1+ \Vert A \Vert (\frac{t^{\rho}-\tau ^{\rho}}{\rho})^{\sigma})^{1-\kappa \frac{\sigma -1}{\sigma}}}\,d \tau \\ &\leq \frac{c_{1} \Vert x_{1} \Vert }{(1+ \Vert A \Vert (\frac{t^{\rho}}{\rho})^{\sigma})^{\kappa}}+ \frac{c_{2} \Vert x_{2} \Vert t^{\rho}}{1+ \Vert A \Vert (\frac{t^{\rho}}{\rho})^{\sigma}} \\ &\quad {}+\kappa \int _{0}^{t} \biggl( \frac{c_{1} \Vert x_{1} \Vert }{(1+ \Vert A \Vert (\frac{\tau ^{\rho}}{\rho})^{\sigma})^{\kappa}} + \frac{c_{2} \Vert x_{2} \Vert \tau ^{\rho}}{1+ \Vert A \Vert (\frac{\tau ^{\rho}}{\rho})^{\sigma}} \biggr) \biggl(\frac{t^{\rho}-\tau ^{\rho}}{\rho}\biggr)^{\kappa (\sigma -1)-1} \\ &\quad \times\tau ^{\rho -1}( \sigma -1) \Vert A \Vert ^{\kappa \frac{\sigma -1}{\sigma}} \,d \tau \\ &\leq \frac{c_{1} \Vert x_{1} \Vert }{(1+ \Vert A \Vert (\frac{t^{\rho}}{\rho})^{\sigma})^{\kappa}}+ \frac{c_{2} \Vert x_{2} \Vert }{t^{-\rho}+\rho ^{-\sigma} \Vert A \Vert t^{\rho \sigma -\rho}} \\ &\quad {}+\kappa c_{1}( \sigma -1)\|x_{1} \Vert A \Vert ^{\kappa \frac{\sigma -1}{\sigma}- \kappa} \int _{0}^{t}\tau ^{\rho -\rho \sigma -1} \bigl(t^{\rho}- \tau ^{\rho}\bigr)^{\kappa (\sigma -1)-1}\,d\tau \\ &\quad {} +\kappa c_{2}\|x_{2}\|(\sigma -1) \Vert A \Vert ^{\kappa \frac{\sigma -1}{\sigma}-1} \int _{0}^{t} \tau ^{2\rho -\rho \sigma -1} \bigl(t^{\rho}-\tau ^{\rho}\bigr)^{\kappa (\sigma -1)-1}\,d\tau \\ &= \frac{c_{1} \Vert x_{1} \Vert }{(1+ \Vert A \Vert (\frac{t^{\rho}}{\rho})^{\sigma})^{\kappa}}+ \frac{c_{2} \Vert x_{1} \Vert }{t^{-\rho} +\rho ^{-\sigma} \Vert A \Vert t^{\rho \sigma -\rho}} \\ &\quad {} +\kappa c_{1}( \sigma -1)\|x_{2} \Vert A \Vert ^{\kappa \frac{\sigma -1}{\sigma}- \kappa} \frac{\Gamma (1-\kappa \sigma )\Gamma (\kappa (\sigma -1)))}{ \rho \Gamma (1-\kappa )}t^{\rho (1-\kappa )-1} \\ &\quad {} +\kappa c_{2}(\sigma -1)\|x_{2} \Vert A \Vert ^{\kappa \frac{\sigma -1}{\sigma}-1} \frac{\Gamma (2-\sigma )\Gamma (\kappa (\sigma -1)))}{\rho \Gamma (2-\sigma +\kappa (\sigma -1))}t^{ \rho (2-\sigma +\kappa (\sigma -1)-1)}. \end{aligned}$$
(3.5)

Hence, the zero solution of (1.1) is locally asymptotically stable if \(\kappa <\frac{\sigma -1}{\sigma}\) and \(\rho <\frac{1}{1-\kappa}\). □

Remark 3.1

For the choice \(\rho =1\) in Theorem 3.1, we obtain the case of the classical fractional system with order lying in \(\sigma \in (1, 2)\) [1].

3.1 The Mittag–Leffler (M–L) stability for system (1.1)

The definition of M–L stability and its theorem stability for the case \(\sigma \in (0, 1)\) is introduced [34]. In this subsection, we present the definition of M–L stability for the case \(\sigma \in (1, 2)\). A theorem to prove that the solution of system (1.1) is M–L stable is investigated using the Lyapunov direct method.

Remark 3.2

From Theorem 3.1, for \(1<\sigma <2\), the solution of FDE

$$ \begin{aligned} &{}^{C} \mathcal{D}^{\sigma ,\rho}x(t)= \lambda x(t), \\ & \biggl(x^{1-\rho}\frac{d}{dt} \biggr)^{k}x(0)=x_{k},\quad k=0,1, \end{aligned} $$
(3.6)

is expressed as:

$$ x(t)\leq E_{\sigma , 1}\biggl[\lambda \biggl( \frac{t^{\rho}}{\rho}\biggr)^{\sigma}\biggr] x_{1}+ \frac{t^{\rho}}{\rho}E_{\sigma , 2}\biggl[\lambda \biggl(\frac{t^{\rho}}{\rho} \biggr)^{ \sigma}\biggr] x_{2}. $$
(3.7)

Lemma 3.1

Let \(x(t)\in C([0,\infty ],\mathbb{R})\) and \(\sigma \in (1,2)\), if

$$ \begin{aligned} &{}^{C} \mathcal{D}^{\sigma ,\rho}x(t)\leq \lambda x(t), \\ & \biggl(x^{1-\rho}\frac{d}{dt} \biggr)^{k}x(0)=x_{k},\quad k=0,1, \end{aligned} $$
(3.8)

then one has

$$ x(t)\leq E_{\sigma , 1}\biggl[\lambda \biggl( \frac{t^{\rho}}{\rho}\biggr)^{\sigma}\biggr] x_{1}+ \frac{t^{\rho}}{\rho}E_{\sigma , 2}\biggl[\lambda \biggl(\frac{t^{\rho}}{\rho} \biggr)^{ \sigma}\biggr] x_{2}. $$
(3.9)

Proof

In view of the inequality in (3.8), \(\exists \theta (t)\geq 0\) holds

$$ {}^{C} \mathcal{D}^{\sigma ,\rho}x(t)+ \theta (t)= \lambda x(t), $$
(3.10)

and from Theorem 3.1, we deduce that

$$ \begin{aligned} x(t)&=E_{\sigma , 1}\biggl[A\biggl(\frac{t^{\rho}}{\rho} \biggr)^{\sigma}\biggr] x_{1}+ \frac{t^{\rho}}{\rho}E_{\sigma , 2} \biggl[\lambda \biggl(\frac{t^{\rho}}{\rho}\biggr)^{ \sigma}\biggr] x_{2} \\ &\quad {}- \int _{0}^{t}\biggl(\frac{t^{\rho}-s^{\rho}}{\rho} \biggr)^{ \sigma -1}E_{\sigma , \sigma}\biggl[\lambda \biggl( \frac{t^{\rho}-s^{\rho}}{\rho}\biggr)^{ \sigma}\biggr]s^{\rho -1}\theta (s) \,ds. \end{aligned} $$
(3.11)

According to Remark 3.2, the equation \({}^{C}\mathcal{D}^{\sigma ,\rho}x(t)= \lambda x(t)\) has a solution \(z(t)\) as:

$$ z(t)=E_{\sigma , 1}\biggl[A\biggl(\frac{t^{\rho}}{\rho} \biggr)^{\sigma}\biggr] x_{1}+ \frac{t^{\rho}}{\rho}E_{\sigma , 2} \biggl[\lambda \biggl(\frac{t^{\rho}}{\rho}\biggr)^{ \sigma}\biggr] x_{2}, $$
(3.12)

furthermore, it has

$$ x(t)-z(t)=- \int _{0}^{t}\biggl(\frac{t^{\rho}-s^{\rho}}{\rho} \biggr)^{ \sigma -1}E_{\sigma , \sigma}\biggl[\lambda \biggl( \frac{t^{\rho}-s^{\rho}}{\rho}\biggr)^{ \sigma}\biggr]s^{\rho -1}\theta (s) \,ds, $$
(3.13)

since \(\theta (s)\geq 0\), \(E_{\sigma , \sigma}>0\) for \(1< \sigma <2\), then \(x(t)\leq z(t)\) for \(t\geq 0\). □

Definition 3.1

(M–L Stability)

The trivial solution of system

$$ \begin{aligned} &{}^{C} \mathcal{D}^{\sigma ,\rho}x(t)= f\bigl(t,x(t)\bigr), \\ & \biggl(x^{1-\rho}\frac{d}{dt} \biggr)^{k}x(0)=x_{k},\quad k=0,1, \end{aligned} $$
(3.14)

is M–L stable if it satisfies

$$ x(t)\leq \biggl\{ E_{\sigma , 1}\biggl[\lambda \biggl( \frac{t^{\rho}}{\rho}\biggr)^{ \sigma}\biggr] \varphi _{1}(x_{1})+ \frac{t^{\rho}}{\rho}E_{\sigma , 2}\biggl[ \lambda \biggl( \frac{t^{\rho}}{\rho}\biggr)^{\sigma}\biggr] \varphi _{2}(x_{2}) \biggr\} ^{ \frac{1}{\beta}}, $$
(3.15)

where \(\beta > 0\), \(\sigma \in (1, 2)\), \(\lambda \geq 0\), locally the Lipschitz function \(\varphi _{1}( x)\), \(\varphi _{2}(x)\) satisfies \(\varphi _{1}(0)=\varphi _{2}(0) = 0\), \(\varphi _{1}( x)\), \(\varphi _{2}(x)\geq 0\) with Lipschitz constants \(\varphi _{10}\), \(\varphi _{20}\).

Theorem 3.2

If a continuously differentiable function \(V(t, x(t)): [0, +\infty )\times S\rightarrow R^{+}\) is locally Lipschitz in x and

$$\begin{aligned}& \nu _{1} \bigl\Vert x(t) \bigr\Vert ^{l}\leq V\bigl(t, x(t)\bigr) \leq \nu _{2} \bigl\Vert x(t) \bigr\Vert ^{k}, \end{aligned}$$
(3.16)
$$\begin{aligned}& {}^{C}\mathcal{D}^{\sigma , \rho} V\bigl(t, x(t) \bigr) \leq -\nu _{3} \bigl\Vert x(t) \bigr\Vert ^{k}, \end{aligned}$$
(3.17)

where \(\sigma \in (1 , 2)\), \(x\in S\), \(l, k, \nu _{j}>0\) (\(j=1, 2, 3\)) are arbitrary constants, then the fixed point of system (1.1) is Mittag–Leffler (M–L) stable.

Proof

From the inequalities (3.16) and (3.17), we have

$$ {}^{C}\mathcal{D}^{\sigma , \rho} V\bigl(t, x(t) \bigr) \leq - \frac{\nu _{3}}{\nu _{2}}V\bigl(t, x(t)\bigr), $$
(3.18)

using Lemma 3.1, one has

$$ V\bigl(t, x(t)\bigr) \leq V\bigl(0, x(0)\bigr)E_{\sigma , 1} \biggl[-\frac{\nu _{3}}{\nu _{2}}\biggl( \frac{t^{\rho}}{\rho}\biggr)^{\sigma} \biggr]+\frac{t^{\rho}}{\rho} V\bigl(0, x^{(1)}(0)\bigr)E_{ \sigma , 2} \biggl[-\frac{\nu _{3}}{\nu _{2}}\biggl(\frac{t^{\rho}}{\rho}\biggr)^{\sigma} \biggr], $$
(3.19)

substituting (3.19) into (3.16), we obtain

$$ \bigl\Vert x(t) \bigr\Vert \leq \biggl( \frac{V(0, x(0))}{\nu _{1}}E_{\sigma , 1}\biggl[- \frac{\nu _{3}}{\nu _{2}}\biggl( \frac{t^{\rho}}{\rho}\biggr)^{\sigma}\biggr]+ \frac{V(0, x^{(1)}(0))}{\nu _{1}} \frac{t^{\rho}}{\rho} E_{\sigma , 2}\biggl[- \frac{\nu _{3}}{\nu _{2}}\biggl( \frac{t^{\rho}}{\rho}\biggr)^{\sigma}\biggr]\biggr)^{ \frac{1}{l}}. $$
(3.20)

Let \(\varphi _{1}=\frac{V(0, x(0))}{\nu _{1}}\) and \(\varphi _{2}=\frac{V(0, x^{(1)}(0))}{\nu _{1}}\), then (3.20) takes the form

$$ \bigl\Vert x(t) \bigr\Vert \leq \biggl(\varphi _{1} E_{\sigma , 1}\biggl[-\frac{\nu _{3}}{\nu _{2}}\biggl( \frac{t^{\rho}}{\rho}\biggr)^{\sigma}\biggr]+\varphi _{2} \frac{t^{\rho}}{\rho} E_{ \sigma , 2}\biggl[-\frac{\nu _{3}}{\nu _{2}}\biggl( \frac{t^{\rho}}{\rho}\biggr)^{\sigma}\biggr]\biggr)^{ \frac{1}{l}}. $$
(3.21)

Actually, \(V(t, x(t))\) is locally Lipschitz with respect to x, and \(V(0, x(0))=0\) and \(V(0, x^{(1)}(0))=0\) hold if and only if \(x(0)=0\) and \(x^{(1)}(0)=0\), respectively. Then, \(\varphi _{1}\) and \(\varphi _{2}\) also satisfy locally Lipschitz condition. From Definition 3.1, the fixed point of (1.1) is M–L stable. □

4 Control of chaotic generalized fractional systems (GFSs)

We introduce a technique to control the solutions of chaotic GFSs by linear feedback control. The GFS (1.1) can be written after adding the vector of control functions \(u(t)\) as:

$$ {}^{C} \mathcal{D}^{\sigma , \rho}x(t)=Ax(t)+f\bigl(x(t)\bigr)+u(t). $$
(4.1)

We can present the linear feedback control functions as \(u(t)=Kx(t)\), where K is \(n\times n\) constant matrix. Hence, the controlled system (4.1) becomes:

$$ {}^{C} \mathcal{D}^{\sigma , \rho}x(t)=(A+K)x(t)+f\bigl(x(t)\bigr). $$
(4.2)

We investigate the sufficient conditions to hold that system (4.2) is asymptotically stable in the following theorem.

Theorem 4.1

The system (4.2) is asymptotically stable for \(1<\sigma <2\) if:

  1. 1.

    We choose K s.t. the zero solution of \({}^{C}\mathcal{D}^{\sigma , \rho}x(t)=(A+K)x(t)\) is asymptotically stable.

  2. 2.

    \(\lim_{\|x\|\rightarrow 0}\frac{\|f(x)\|}{\|x\|}=0\).

Proof

The proof is similar to that of Theorem 3.1. □

We give an example of chaotic GFSs with order lying in \((1, 2)\) to test the validity of Theorem 4.1.

4.1 An example

In this subsection, we control the solution of chaotic GF Lü system with order lying in \((1, 2)\) using linear feedback control. The chaotic GF Lü system takes the form:

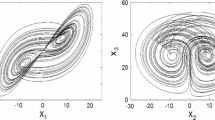
$$ \begin{aligned} &{}^{C} \mathcal{D}^{\sigma , \rho}x_{1}(t) =a(x_{2}-x_{1}), \\ &{}^{C}\mathcal{D}^{\sigma , \rho}x_{2}(t) =-x_{1}x_{3}+cx_{2}, \\ &{}^{C}\mathcal{D}^{\sigma , \rho}x_{3}(t) =x_{1}x_{2}-bx_{3}, \end{aligned} $$
(4.3)

where a, b, and c are constant parameters. For the choice \(a=36\), \(b=3\), \(c=20\), and \(\sigma =1.11\) and the initial values are \(x_{0}=(0.1, 0.3, 0.5)^{T}\) and \(\dot{x}_{0}=(0.2, 0.4, 0.6)^{T}\), system (4.3) has chaotic behavior, as shown in Fig. 1 for small time (\(t=10\)). System (4.3) has different chaotic behavior as shown in Figs. 1(a), (b), and (c) that correspond to the values \(\rho =1\), \(\rho =2.5\), and \(\rho =3\), respectively. Figure 1(a) shows the chaotic behavior of the classical fractional-order Lü system (\(\rho =1\)), while the chaotic behaviors of generalized fractional-order Lü systems for \(\rho =2.5\), and \(\rho =3\) are shown in Figs. 1(b) and (c). This means that the complicated solution behavior of system (4.3) depends on the value of parameter ρ.

Figure 1
figure 1

The chaotic behavior of the GF Lü system (4.3) in \((x_{1}, x_{2})\) space for: (a) \(\rho =1\) (classical fractional-order case), (b) \(\rho =2.5\), (c) \(\rho =3\)

Full size image

By adding control functions, system (4.3) can be written as

$$ \begin{aligned} &{}^{C} \mathcal{D}^{\sigma , \rho}x_{1}(t) =a(x_{2}-x_{1})+u_{1}, \\ &{}^{C}\mathcal{D}^{\sigma , \rho}x_{2}(t) =-x_{1}x_{3}+cx_{2}+u_{2}, \\ &{}^{C}\mathcal{D}^{\sigma , \rho}x_{3}(t) =x_{1}x_{2}-bx_{3}+u_{3}. \end{aligned} $$
(4.4)

We can write the control functions as

$$ \begin{pmatrix} u_{1} \\ u_{2} \\ u_{3} \end{pmatrix}= \begin{pmatrix} -10 x_{1} \\ -25 x_{2} \\ -20x_{3} \end{pmatrix}. $$
(4.5)

Using (4.5), the system (4.4) is obtained

$$ {}^{C} \mathcal{D}^{\sigma , \rho} \begin{pmatrix} x_{1} \\ x_{2} \\ x_{3} \end{pmatrix}= \begin{pmatrix} -46 & 36 & 0 \\ 0 & -5 & 0 \\ 0 & 0 & -23 \end{pmatrix} \begin{pmatrix} x_{1} \\ x_{2} \\ x_{3} \end{pmatrix}+ \begin{pmatrix} 0 \\ -x_{1}x_{3} \\ x_{1}x_{2} \end{pmatrix}, $$
(4.6)

where

$$ A+K= \begin{pmatrix} -46 & 36 & 0 \\ 0 & -5 & 0 \\ 0 & 0 & -23 \end{pmatrix}\quad \mbox{and}\quad f(x)= \begin{pmatrix} 0 \\ -x_{1}x_{3} \\ x_{1}x_{2} \end{pmatrix}. $$

System (4.6) holds Theorem 4.1 as:

  1. 1.

    Obviously, the zero solution of \({}^{C}\mathcal{D}^{\sigma , \rho}x(t)=(A+K)x(t)\) is asymptotically stable.

  2. 2.

    \(\lim_{\|x\|\rightarrow 0} \frac{\sqrt{x_{1}^{2}(x_{2}^{2}+x_{3}^{2})}}{\|x\|}\leq \lim_{ \|x\|\rightarrow 0}\|x\|=0\).

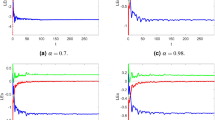
The zero solution of system (4.6) is asymptotically stable, as shown in Fig. 2 for the same choice of parameters and initial values as in Fig. 1(b).

Figure 2
figure 2

The behavior of the chaotic system after adding the control (4.4) in (a) \((t, x_{1})\) diagram, (b) \((t, x_{2})\) diagram, and (c) \((t, x_{3})\) diagram

Full size image

5 Synchronization between two different chaotic generalized fractional systems (GFSs)

In this section, we introduce the synchronization between two different chaotic GFSs using a linear feedback control method. We present an example to verify the validity of the proposed theorem of synchronization.

Definition 5.1

We can say that the drive system (1.1) is synchronized with the following response system

$$ {}^{C} \mathcal{D}^{\sigma , \rho}y=By+f\bigl(y(t)\bigr)+u, $$
(5.1)

if \(\|e(t)\|=\|y(t)-x(t)\|\rightarrow 0\) as \(t\rightarrow \infty \), where \(1<\sigma <2\), \(\rho \geq 0\), \(y\in R^{n}\) is a state variable, B is a \((n\times n)\) constant matrix and \(u\in R^{n}\) is a vector of control functions.

From systems (1.1) and (5.1), the error system can be written as:

$$ {}^{C} \mathcal{D}^{\sigma , \rho}e=Ae+(B-A)y+f(y)-f(x)+u. $$
(5.2)

We investigate a theorem to calculate the analytical formula of control functions that achieve synchronization between two different chaotic GFSs.

Theorem 5.1

The solution of the error system (5.2) can approach zero if the vector of control functions u takes the form

$$ u=(A-B)y-Ke, $$
(5.3)

where \(K=\operatorname{diag}(k_{1}, k_{2}, \ldots, k_{n})\) is again a matrix, \(\sigma \in (1, 2)\) and the initial values of the error system (5.2) are \(e^{(j)}(0)=e^{(j)}_{0}\), \(j=0, 1\).

Proof

Using the control functions (5.3), the system of the error (5.2) can be written as:

$$ {}^{C} \mathcal{D}^{\sigma , \rho}e=(A-K)e+f(y)-f(x), $$
(5.4)

by taking the ρ-Laplace transform for system (5.4), then

$$ s^{\sigma } \mathcal{L}_{\rho}\bigl\{ e(t)\bigr\} -\sum_{j=0}^{1}s^{2-j-1} \bigl(e^{(j)}\bigr) (0) =(A-K)\mathcal{L}_{\rho}\bigl\{ e(t) \bigr\} +\mathcal{L}_{\rho}\bigl\{ f(y)-f(x)\bigr\} , $$
(5.5)

then,

$$ \mathcal{L}_{\rho}\bigl\{ e(t)\bigr\} =\frac{1}{s^{\sigma }I-A+K} \mathcal{L}_{\rho}\bigl\{ f(y)-f(x) \bigr\} +\frac{1}{s^{\sigma }I-A+K}\sum_{j=0}^{1}s^{2-j-1} \bigl(e^{(j)}\bigr) (0), $$
(5.6)

using Lemma 2.1, we obtain

$$ \begin{aligned} \lim_{t\rightarrow \infty} e(t)&= \lim_{s \rightarrow 0}s\mathcal{L}_{\rho}\bigl\{ e(t)\bigr\} \\ &=\lim _{s \rightarrow 0}\Biggl[\frac{s}{s^{\sigma }I-A+K}\mathcal{L}_{\rho} \bigl\{ f(y)-f(x) \bigr\} +\frac{s}{s^{\sigma }I-A+K}\sum_{j=0}^{1}s^{2-j-1} \bigl(e^{(j)}\bigr) (0)\Biggr] \\ &=0, \end{aligned} $$
(5.7)

then the synchronization between the drive system (1.1) and the response system (5.1) can be achieved. □

5.1 Synchronization between two different chaotic generalized fractional (GF) Lü and Lorenz systems

We investigate the synchronization between two different chaotic generalized fractional Lü and Lorenz systems with order lying in \((1, 2)\) as an example for the synchronization scheme. The GF Lorenz system [35] has been written as:

$$ \begin{aligned} &{}^{C} \mathcal{D}^{\sigma , \rho}y_{1}(t) =a_{1}(y_{2}-y_{1}), \\ &{}^{C}\mathcal{D}^{\sigma , \rho}y_{2}(t) =c_{1}y_{1}-y_{1}y_{3}-y_{2}, \\ &{}^{C}\mathcal{D}^{\sigma , \rho}y_{3}(t) =y_{1}y_{2}-b_{1}y_{3}, \end{aligned} $$
(5.8)

where \(a_{1}\), \(b_{1}\), and \(c_{1}\) are constant parameters. For the choice \(a_{1}=10\), \(b_{1}=8/3\), \(c_{1}=28\), \(\sigma =1.11\), \(\rho =2.5\), and the initial values are \(y_{0}=(1, 0.5, 2)^{T}\) and \(\dot{y}_{0}=(0.5, 1, 1)^{T}\), the system (5.8) has chaotic behavior, as shown in Fig. 3.

Figure 3
figure 3

The chaotic behavior of the GF Lorenz system (5.8) in \((y_{3}, y_{1}, y_{2})\) space for \(\rho =2.5\) and \(\sigma =1.11\)

Full size image

We consider the drive system is the chaotic GF Lü system (4.3) and the chaotic GF Lorenz system (5.8) is the response system. The response system after adding the control functions can be written as:

$$ \begin{aligned} &{}^{C} \mathcal{D}^{\sigma , \rho}y_{1}(t) =a_{1}(y_{2}-y_{1})+u_{1}, \\ &{}^{C}\mathcal{D}^{\sigma , \rho}y_{2}(t) =c_{1}y_{1}-y_{1}y_{3}-y_{2}+u_{2}, \\ &{}^{C}\mathcal{D}^{\sigma , \rho}y_{3}(t) =y_{1}y_{2}-b_{1}y_{3}+u_{3}. \end{aligned} $$
(5.9)

By applying Theorem 5.1, the control functions are given as:

$$ \begin{pmatrix} u_{1} \\ u_{2} \\ u_{3} \end{pmatrix}= \begin{pmatrix} (a_{1}-a)(y_{1}-y_{2})-k_{1}e_{1} \\ -c_{1}y_{1}+(c+1)y_{2}-k_{2}e_{2} \\ (b_{1}-b)y_{3} \end{pmatrix}. $$
(5.10)

Using the drive system (4.3), the response system (5.9) and the control functions (5.10), the error system can be written as:

$$ \begin{aligned} &{}^{C} \mathcal{D}^{\sigma , \rho}e_{1}(t) =a(e_{2}-e_{1})-k_{1}e_{1}, \\ &{}^{C}\mathcal{D}^{\sigma , \rho}e_{2}(t) =x_{1}x_{3}-y_{1}y_{3}+(c-k_{2})e_{2}, \\ &{}^{C}\mathcal{D}^{\sigma , \rho}e_{3}(t) =y_{1}y_{2}-x_{1}x_{2}-(b+k_{3})e_{3}. \end{aligned} $$
(5.11)

In the numerical treatment, the values of the parameters and the initial conditions of the drive system (4.3) and for the response system (5.9) are the same values that are taken in Fig. 1(b) and Fig. 3, respectively. The synchronization is achieved and the results are shown in Figs. 4 and 5. Figure 4 shows the same chaotic attractor for drive system (4.3) and response system (5.9), while the synchronization errors approach zero, as given in Fig. 5.

Figure 4
figure 4

Chaotic attractors for (a) the drive system (4.3) in \((x_{1}, x_{3}, x_{2})\) space, (b) the response system (5.9) in \((y_{1}, y_{3}, y_{2})\) space

Full size image
Figure 5
figure 5

The synchronization errors of the drive system (4.3) and the response system (5.9) in (a) \((t, e_{1})\) diagram, (b) \((t, e_{2})\) diagram, and (c) \((t, e_{3})\) diagram

Full size image

6 Conclusion

We introduced the generalized fractional dynamical system with order in \((1, 2)\). In Theorem 3.1, the stability analysis of that system is investigated using the Mittag–Leffler function, the Gronwall–Bellman Lemma, and the Laplace transform. We proposed M–L stability of our system with order lying in \((1, 2)\) based on the Lyapunov direct method in Theorem 3.2. The chaotic GF Lü and Lorenz systems are presented. Using linear feedback control, we illustrated the control of chaotic GFS in general and an example is given to test the validity of Theorem 4.1. We investigated the synchronization between two different chaotic GFSs. The analytical formula of the control functions (5.3) that achieve synchronization are given in Theorem 5.1. Synchronization between the different GF Lü and Lorenz systems is achieved. Other examples of GFSs can be similarly studied.