Graphical structure of double controlled metric-like spaces with an application

Abstract

The aim of the manuscript is to present the concept of a graphical double controlled metric-like space (for short, GDCML-space). The structure of an open ball of the proposed space is also discussed, and the newly presented ideas are explained with a new technique by depicting appropriately directed graphs. Moreover, we present some examples in a graph structure to prove that our results are sharp compared to those in the previous papers. Further, the existence of a solution to the boundary value problem originating from the transverse oscillations of a homogeneous bar (TOHB) is obtained theoretically.

1 Introduction

To resolve many problems in mathematics, we require to use fixed point theory. This theory is also considered a remarkable tool in applied sciences and several other disciplines. The Banach fixed point theorem [1] is known as the essential theorem in the metric fixed point theory. This theorem has been generalized and extended in several directions using different topologies and/or variant contractions. Among these generalizations and extensions, we cite [2–10].

On the other hand, graph theory is a branch of mathematics that deals with networks of elements connected by lines. A graph is considered a structure amounting to a set of objects in which some pairs of objects are related in some sense. The beginning of the graph theory field originated in number games. It has a significant contribution to mathematical research, with applications in social sciences, operations research, chemistry, and computer science. For more details, we refer to [11–14].

In 2005, Echenique [15] initiated the combination of graph theory and fixed point theory by presenting a proof of the fixed point result of Tarski via graphs (using ordinal numbers). A year later, Espinola and Kirk [16] gave some fixed point theorems via graph theory. Precisely, they established some fixed point results for nonexpansive mappings defined on R-trees and used the obtained theorems to give some results in graph theory. Note that metric graphs correspond to spaces followed by considering a connected graph and metrizing the nontrivial edges of the graph as bounded intervals of $\mathbb{R}$. Going in the same direction, a fruitful contribution was made by Jachymski [17] in 2008 and Beg et al. [18] in 2010. Namely, variant generalizations of the Banach contraction principle to mappings on a metric space equipped with a graph have been provided. For further investigations of fixed point results using a graph, see [19–23].

Among the generalizations of a metric space, there is the concept of a double controlled metric-like space introduced by Mlaiki [24]. In this setting, double controlled control functions are considered on the right-hand-side of the modified triangular inequality. Also, self-distance may not be equal to zero. In this paper, we construct a suitable double controlled metric-like metric space equipped with a graph and some suitable graphical contraction mappings. We prove some related fixed point theorems. We also present some concrete examples and an application by ensuring the existence of a solution to a boundary value problem originating from TOHB.

2 Basic facts and primary definitions

This part is intended to review primary definitions of a controlled metric-type space, a double controlled metric-type space, and a double controlled metric-like space and some facts about the graph theory, which are very important for most of the statements of our paper.

Definition 2.1

([25])

Consider $\beta \neq \emptyset$ and a function $\rho :\beta ^{2}\rightarrow {}[ 1,\infty )$. Assume that a function $\xi :\beta ^{2}\rightarrow {}[ 0,\infty )$ satisfies the assumptions below for all $k,l,m\in \beta$:

$( \xi _{1})$:

$\xi (k,l)=0\Leftrightarrow k=l$;

$( \xi _{2})$:

$\xi (k,l)=\xi (l,k)$;

$( \xi _{3})$:

$\xi (k,l)\leq \rho (k,m)\xi (k,m)+\rho (m,l)\xi (m,l)$.

Then $(\beta ,\xi )$ is called a controlled metric-type space.

Abdeljawad et al. [26] extended the above definition to double controlled metric-type spaces as follows:

Definition 2.2

([26])

Consider $\beta \neq \emptyset$ and noncomparable functions $\rho ,\zeta :\beta ^{2}\rightarrow {}[ 1,\infty )$. Let the function $\sigma :\beta ^{2}\rightarrow {}[ 0,\infty )$ satisfy the assumptions below for all $k,l,m\in \beta$:

$(\sigma _{1})$:

$\sigma (k,l)=0\Leftrightarrow k=l$;

$( \sigma _{2})$:

$\sigma (k,l)=\sigma (l,k)$;

$( \sigma _{3})$:

$\sigma (k,l)\leq \rho (k,m)\sigma (k,m)+\zeta (m,l)\sigma (m,l)$.

Then $(\beta ,\sigma )$ is called a double controlled metric-type space (DCMT-space).

In 2020, Mlaiki [24] introduced the concept of a double controlled metric-like space (DCML-space) and showed that any DCMT-space is a DCML-space, but the opposite is not true. He also obtained the related Banach contraction principle under mild conditions and presented his definition as follows:

Definition 2.3

([24])

Consider a set $\beta \neq \emptyset$ and noncomparable functions $\rho ,\zeta :\beta ^{2}\rightarrow {}[ 1,\infty )$. Let the function $\theta :\beta ^{2}\rightarrow {}[ 0,\infty )$ satisfy the hypotheses below for all $k,l,m\in \beta$:

$( \theta _{1})$:

$\theta (k,l)=0\Leftrightarrow k=l$;

$( \theta _{2})$:

$\theta (k,l)=\theta (l,k)$;

$( \theta _{3})$:

$\theta (k,l)\leq \rho (k,m)\theta (k,m)+\zeta (m,l)\theta (m,l)$.

Then $(\beta ,\theta )$ is called a DCML-space.

Based on the results of Jachymski [17], let a set $J\neq \emptyset$ and Λ be the diagonal of the Cartesian product $J\times J$. Also, assume that $\Game =(\nu (\Game ),\vartheta (\Game ))$ is a directed graph without parallel edges, where $\nu (\Game )$ is the vertex set of ⅁ so that it coincides with the set J, and the set of edges will be denoted by $\vartheta (\Game )$ so that it contains all the loops of ⅁, i.e., $\Lambda \subseteq \vartheta (\Game )$.

The undirected graph is obtained from ⅁ by ignoring the direction of edges denoted by the letter ⅁̃. Actually, it will be more convenient for us to treat ⅁̃ as a directed graph for which the set of its edges is symmetric. Under this convention,

$$ \vartheta (\widetilde{\Game })=\vartheta (\Game )\cup \vartheta \bigl( \Game ^{-1}\bigr), $$

where $\Game ^{-1}$ is the graph obtained by reversing the direction of $\vartheta (\Game )$.

Assume that k and l are vertices of the directed graph ⅁, a path in ⅁ described as a sequence $\{k_{i}\}_{i=0}^{m}$ containing $( m+1 )$ vertices so that $k_{\circ }=k$, $k_{m}=l$ with $(k_{i-1},k_{i})\in \vartheta (\Game )$ for $i=1,2,\ldots,m$. Further, if there is a path between any two vertices, then a graph ⅁ is called connected, and ⅁ is weakly connected if ⅁̃ is connected. A graph $\Upsilon =(\nu (\Upsilon ),\vartheta (\Upsilon ))$ is called a subgraph of $\Game =(\nu (\Game ),\vartheta (\Game ))$ if $\nu (\Upsilon )\subseteq \nu (\Game )$ and $\vartheta (\Upsilon )\subseteq \vartheta (\Game )$.

The symbols below are due to Shukla et al. [27]:

A relation ℜ on J is defined by: $(k\Re l)_{\Game }$ if there is a directed path from k to l in ⅁, and we write $t\in (k\Re l)_{\Game }$ if t contained in some directed path from k to l in ⅁. Moreover, they denote $[k]_{\Game }^{n}=\{l\in J: \text{there is a direct path from }k\text{ to }l\text{ in } \Game \text{ with the length }n\}$.

Recall that a sequence $\{k_{i}\}\subset J$ is called ⅁-termwise connected (⅁-TWC) if $(k_{i}\Re k_{i+1})_{\Game }$, for all $i\in \mathbb{N}$. Henceforward, we shall consider all graphs are directed unless otherwise stated.

Chuensupantharat et al. [28] applied a directed graph in metric fixed point theory by introducing a graphical b-metric space to generalize a b-metric space. They were able to study the topological properties of this space and get examples and results about the fixed points that contribute significantly to the development of graph theory. For more examples and explanations, see [29].

3 Graphical double controlled metric-like spaces

Most of the results in metric fixed point theory depend on the fact that if the contractive condition holds for comparable elements p and q, and for q and r, it necessarily holds for p and r. Transitivity can be avoided while working in the structure of the graph.

Because of the importance of graphs in the metric fixed point, we commence the graphical version of double-controlled metric-like spaces as the following:

Definition 3.1

Assume that $J\neq \emptyset$ endowed with a graph ⅁ and noncomparable functions $\sigma ,\xi :J\times J\rightarrow {}[ 1,\infty )$. Let the function $d_{\Game _{\sigma \xi }}:J\times J\rightarrow {}[ 0,\infty )$ verify the following assertions $\forall k,l,m\in J$:

$(d_{\Game }1)$:

$d_{\Game _{\sigma \xi }}(k,l)=0\Rightarrow k=l$;

$(d_{\Game }2)$:

$d_{\Game _{\sigma \xi }}(k,l)=d_{\Game _{\sigma \xi } }(l,k)$;

$(d_{\Game }3)$:

$(k\Re l)_{\Game }$, $m\in (k\Re l)_{\Game }\Rightarrow d_{\Game _{\sigma \xi }}(k,l)\leq \sigma (k,m)d_{\Game _{\sigma \xi }}(k,m)+\xi (m,l)d_{\Game _{\sigma \xi }}(m,l)$.

Then $(J,d_{\Game _{\sigma \xi }})$ is called a graphical double-controlled metric-like space (GDCML-space).

Remark 3.2

• (i) If we take $\sigma =\xi$, then we have a new space called a graphical controlled metric-like space.

• (ii) It is clear that a GDCML-space is more general than a DCML-space.

• (iii) Every DCML-space is a GDCML-space.

To illustrate the above remark (iii), we give the following examples:

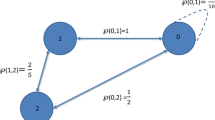
Example 3.3

Let $J=\{1,3,5,7,11\}$. Define $\sigma ,\xi :J\times J\rightarrow {}[ 1,\infty )$ by

$$ \sigma (k,l)=\textstyle\begin{cases} k, & \text{if }k,l\geq 1, \\ 1, & \text{otherwise,}\end{cases}\displaystyle \quad \text{and}\quad \xi (k,l)=\textstyle\begin{cases} \max \{k,l\}, & \text{if }k,l\geq 1, \\ 1, & \text{otherwise.}\end{cases} $$

Assume the set J is equipped with

$$ d_{\Game _{\sigma \xi }}(k,l)=\textstyle\begin{cases} 0, & \text{if }k=l, \\ \frac{1}{2}, & \text{if }k=0\text{ and }l=0, \\ \frac{1}{k}, & \text{if }k\geq 1\text{ and }0\leq l< 1, \\ \frac{1}{l}, & \text{if }l\geq 1\text{ and }0\leq k< 1, \\ 1, & \text{otherwise.}\end{cases} $$

The proof that the pair $(J,d_{\Game _{\sigma \xi }})$ is a DCML-space comes directly from paper [24].

Now, let the set of vertices be $J=\nu (\Game )$ and the set of edges be described as

$$ \vartheta (\Game )=\Lambda + \bigl\{ (1,3),(1,5),(3,5),(3,11),(5,7),(5,11),(7,1),(7,3),(11,1),(11,7) \bigr\} , $$

then $(J,d_{\Game _{\sigma \xi }})$ is a GDCML-space. The sketch of the graph ⅁ is illustrated in Fig. 1.

Figure 1

Graph describing DCML-space

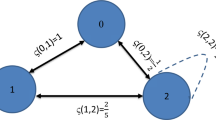
Example 3.4

A GDCML-space is not necessarily metric space. Assume that $J=\Phi \cup \Omega$, where $\Phi =\{\frac{1}{\varphi }:\varphi =1,2,3,4\}$ and $\Omega =\{2,3\}$. Define the GDCML $d_{\Game }:J\times J\rightarrow {}[ 0,\infty )$ as follows:

$$ d_{\Game }(k,l)=\textstyle\begin{cases} 0, & \text{if }k=l, \\ (k+l)^{2}, & \text{otherwise,}\end{cases} $$

equipped with the graph $\Game =(\nu (\Game ),\vartheta (\Game ))$ so that $J=\nu (\Game )$ with $\vartheta (\Game )$ as illustrated in Fig. 2. Explicitly, we can find that $(J,d_{\Game _{\sigma \xi }})$ is a DCML-space endowed with a graph ⅁ by setting $\sigma (k,l)=kl+26$ and $\xi (k,l)=13+kl$.

Figure 2

Graph associated with Example 3.4

It should be noted that $(J,d_{\Game _{\sigma \xi }})$ is not a graphical metric space and hence not a metric space because

$$ d_{\Game _{\sigma \xi }}(2,4)=36>d_{\Game _{\sigma \xi }}(2,1)+d_{ \Game _{\sigma \xi }}(1,4)=34. $$

Remark 3.5

A GDCML-space can be obtained from its ordered version.

Let $d_{\succcurlyeq _{\sigma \xi }}$ be an ordered double-controlled metric-like and $\Game _{d_{\sigma \xi }}=(\nu (\Game _{d_{\sigma \xi }}),\vartheta ( \Game _{d_{\sigma \xi }}))$ be a graph so that $\nu (\Game _{d_{\sigma \xi }})=J$ and $\vartheta (\Game _{d_{\sigma \xi }})= \{ (k,l)\in J\times J:k \succcurlyeq l \}$. It is clear that $(J,d_{\succcurlyeq _{\sigma \xi }})$ is a GDCML-space. Hence, we conclude that every ordered double-controlled metric-like space (ODCML-space) is a GDCML-space.

The following example confirms Remark 3.5.

Example 3.6

Consider $J=\{2,4,6,8,10\}$ equipped with the partial order ≽ described as

$$ \succcurlyeq :=\Lambda \cup \bigl\{ (k,l)\in J\times J:k,l\in J ,l \geq k \bigr\} . $$

Define $d_{\succcurlyeq _{\sigma \xi }}:J\times J\rightarrow {}[ 0, \infty )$ as follows:

$$ d_{\succcurlyeq _{\sigma \xi }}(k,l)=\textstyle\begin{cases} 0, & \text{if }k=l, \\ (k+l)^{2}, & k\neq l.\end{cases} $$

Surely, $(J,d_{\succcurlyeq _{\sigma \xi }})$ is an ODCML-space with the functions $\sigma ,\xi :J\times J\rightarrow {}[ 1,\infty )$ given as $\sigma (k,l)=\sqrt{k+l}$ and $\xi (k,l)=\sqrt{1+k+l}$.

Now, assume the graph $\Game _{d_{\sigma \xi }}$ is endowed with the partial order ≽ as illustrated in Fig. 3. Then $(J,d_{\succcurlyeq _{\sigma \xi }})$ is a GDCML-space with the same functions σ and ξ.

Figure 3

Graph associated with Example 3.6

It should be noted that a GDCML-space is not necessarily a DCML-space. In order to confirm this statement, we will explain the following example.

Example 3.7

Assume that $J=\{0,1,2,3\}$ is furnished with the GDCML $d_{\Game _{\sigma \xi }}:J\times J\rightarrow {}[ 0,\infty )$ described as

$$ d_{\Game _{\sigma \xi }}(k,l)=\textstyle\begin{cases} 0, & \text{if }k=l, \\ ( k+l ) ^{2}, & k\neq l,\end{cases} $$

including the graph $\Game =(\nu (\Game ),\vartheta (\Game ))$ so that $J=\nu (\Game )$ with $\vartheta (\Game )$ as spanned in Fig. 4. Clearly, $(J,d_{\Game _{\sigma \xi }})$ is a GDCML-space endowed with a graph ⅁ by taking $\sigma (k,l)=\sqrt{k+l}$ and $\xi (k,l)=\sqrt{1+k+l}$.

Figure 4

Graph Describing GDCML-space

Note that

$$\begin{aligned} d_{\Game _{\sigma \xi }}(2,3) =&25 \\ \geq &4\sqrt{2}+2(9) \\ =&\sigma (2,0)d_{\Game _{\sigma \xi }}(2,0)+\xi (0,3)d_{\Game _{ \sigma \xi }}(0,3). \end{aligned}$$

Hence, a GDCML-space is not necessarily a DCML-space.

To summarize the above results together with the remarkable work that has been completed in lead manuscripts [24, 27, 30, 31], we present the next flow diagram (Fig. 5) in order to gain a better understanding of the corresponding concepts.

Figure 5

Flow digram stand for the inclusions. The reverse is not true

Definition 3.8

Suppose that $(J,d_{\Game _{\sigma \xi }})$ is a GDCML-space. Then for $k\in J$ and $\sigma >0$, the $d_{\Game _{\sigma \xi }}$-open ball with radius σ and center m is

$$ O_{d_{\Game _{\sigma \xi }}}(k,\delta )= \bigl\{ m\in J:(k\Re m)_{ \Game},\delta >d_{\Game _{\sigma \xi }}(k,m) \bigr\} . $$

Because $\vartheta (\Game )\supseteq \Lambda$, then $m\in O_{d_{\Game _{\sigma \xi }}}(m,\delta )$, so this proves that for $k\in J$, $O_{d_{\Game _{\sigma \xi }}}(m,\delta )\neq \emptyset$ and $\delta >0$.

Encompassed by a GDCML, the set $\Phi = \{ O_{d_{\Game _{\sigma \xi }}}(k,\delta )\mid k\in J, \delta >0 \}$ forms a neighborhood system for the topology $\tau _{\Game }$ on J.

Furthermore, if for every $k\in Q$, there is $\delta >0$ so that $Q\supset O_{d_{\Game _{\sigma \xi }}}(k,\delta )$, then the subset Q of J is open. Certainly, a subset Q of J is closed if its complement is open.

Proposition 3.9

Let $(J,d_{\Game _{\sigma \xi }})$ be a GDCML-space with $\sigma (k,m)=\rho \in {}[ 1,\infty )$ and $\xi (k,m)=\ell \in {}[ 1,\infty )$ so that $\rho \neq \ell$ for $k,m\in J$. If $m\in O_{d_{\Game _{\sigma \xi }}}(k,\delta )$ for $\delta >0$, then there is $\varpi >0$ so that $O_{d_{\Game _{\sigma \xi }}}(k,\delta )\supseteq O_{d_{\Game _{ \sigma \xi }}}(m,\varpi )$.

Proof

Assume that $m\in O_{d_{\Game _{\sigma \xi }}}(k,\frac{\delta }{\rho })$. If $m=k$, then we select $\varpi =\frac{\delta }{\rho }$. Now, suppose that $m\neq k$, then we get $d_{\Game _{\sigma \xi }}(m,k)\neq 0$. Selecting $0<\varpi =\frac{1}{\rho } ( \delta -\ell d_{\Game _{\sigma \xi }}(m,k) )$ and consider $l\in O_{d_{\Game _{\sigma \xi }}}(m,\varpi )$, then based on the given assertions, we have $(k\Re m)_{\Game _{\sigma \xi }}$ and $(m\Re l)_{\Game _{\sigma \xi }}$ and hence $(k\Re l)_{\Game _{\sigma \xi }}$. According to the property of the GDCML-space, we get

$$\begin{aligned} d_{\Game _{\sigma \xi }}(l,k) \leq &\sigma (l,m)d_{\Game _{\sigma \xi }}(l,m)+\xi (m,k)d_{\Game _{\sigma \xi }}(m,k) \\ < &\rho \varpi +\ell d_{\Game _{\sigma \xi }}(m,k) \\ =&\rho \biggl( \frac{\delta }{\rho }-\frac{\ell }{\rho }d_{\Game _{ \sigma \xi }}(m,k) \biggr) +\ell d_{\Game _{\sigma \xi }}(m,k) \\ =&\delta . \end{aligned}$$

That is, $d_{\Game _{\sigma \xi }}(l,k)<\delta$, i.e., $l\in O_{d_{\Game _{\sigma \xi }}}(k,\delta )$. Hence, $O_{d_{\Game _{\sigma \xi }}}(k,\delta )\supseteq O_{d_{\Game _{ \sigma \xi }}}(m,\varpi )$. This completes the proof. □

Definition 3.10

Let $(J,d_{\Game _{\sigma \xi }})$ be a GDCML-space. The sequence $\{k_{i}\}\in J$ is called:

• (a) convergent to $k\in J$ if $\lim_{i\rightarrow \infty }d_{\Game _{\sigma \xi }}(k_{i},k)=d_{ \Game _{\sigma \xi }}(k,k)$;

• (b) ⅁-Cauchy sequence if $\lim_{i,j\rightarrow \infty }d_{\Game _{\sigma \xi }}(k_{i},k_{j})$ exists and is finite.

Definition 3.11

A GDCML-space $(J,d_{\Game _{\sigma \xi }})$ is called ⅁-complete if for every ⅁-Cauchy sequence $\{k_{i}\}$, there is $k\in J$ so that

$$ \lim_{i,j\rightarrow \infty }d_{\Game _{\sigma \xi }}(k_{i},k)=d_{ \Game _{\sigma \xi }}(k,k)= \lim_{i,j\rightarrow \infty }d_{\Game _{ \sigma \xi }}(k_{i},k_{j}). $$

4 Recent fixed point theorems

Assume that $\Game =(\nu (\Game ),\vartheta (\Game ))$ is a weighted graph containing all the loops. We say that a sequence $\{k_{i}\}\in J$ with the initial value $k_{0}\in J$ is an Ω-Picard sequence (Ω-PS) for an operator $\Omega :J\rightarrow J$ if $k_{i}=\Omega k_{i-1}=\Omega ^{i}k_{0}$, $\forall i\in \mathbb{N}$.

Furthermore, $\Game =(\nu (\Game ),\vartheta (\Game ))$ is said to justify the property (P) [27] if a ⅁-termwise connected Ω-PS $\{k_{i}\}$ converging in J guarantees that there are a limit $k\in J$ of $\{k_{i}\}$ and $k_{0}\in \mathbb{N}$ so that $(k_{i},k)\in \vartheta (\Game )$ or $(k,k_{i})\in \vartheta (\Game )$, for all $i>i_{0}$.

Now, we demonstrate our first main results by defining a graphical $\Game _{\sigma \xi }$-contraction as follows:

Definition 4.1

Let $(J,d_{\Game _{\sigma \xi }})$ be a GDCML-space endowed with a graph ⅁ containing all the loops. A mapping $\Omega :J\rightarrow J$ is called a graphical $\Game _{\sigma \xi }$-contraction on a GDCML-space $(J,d_{\Game _{\sigma \xi }})$ if the stipulations below hold:

$(\Game _{ \sigma \xi }S1)$:

J preserves edges of ⅁, i.e., $\forall k,l\in J$, If $(k,l)\in \vartheta (\Game )$, then $(\Omega k,\Omega l)\in \vartheta (\Game )$;

$(\Game _{ \sigma \xi }S2)$:

there are $\eta \in {}[ 0,1)$ and $\sigma (k,l),\xi (k,l)\in {}[ 1,\infty )$ for all $k,l\in J$ with $(k,l)\in \vartheta (\Game )$, we get

$$ d_{\Game _{\sigma \xi }}(\Omega k,\Omega l)\leq \eta d_{\Game _{ \sigma \xi }}(k,l). $$

(4.1)

Theorem 4.2

Let $(J,d_{\Game _{\sigma \xi }})$ be a ⅁-complete GDCML-space and $\Omega :J\rightarrow J$ be a graphical $\Game _{\sigma \xi }$-contraction. Assume that the hypotheses below hold:

• (1) the graph ⅁ verifies the property (p);

• (2) for some $n\in \mathbb{N}$, there is $k_{0}\in J$ so that $\Omega k_{0}\in {}[ k_{0}]_{\Game }^{n}$ and

  $$ \lim_{i,m\rightarrow \infty } \frac{\sigma (k_{i+1},k_{i+2})}{\sigma (k_{i},k_{i+1})}\xi (k_{i+1},k_{m})< \frac{1}{\eta }, $$

  (4.2)

  where $\{k_{i}\}$ is Ω-PS with initial value $k_{0}$;

• (3) for every $k\in J$, we have that $\lim_{i\rightarrow \infty }\sigma (k,k_{i})$ and $\lim_{i\rightarrow \infty }\xi (k_{i},k)$ exist and are finite.

Then there is $k^{\ast }\in J$ so that the Ω-PS $\{k_{i}\}$ is ⅁-TWC and converges to both $k^{\ast }$ and $\Omega k^{\ast }$.

Proof

Assume that $k_{0}\in J$ so that for some $n\in \mathbb{N}$, $\Omega k_{0}\in {}[ k_{0}]_{\Game }^{n}$. Because $\{k_{i}\}$ is a Ω-PS with initial value $k_{0}$, there is a path $\{l_{j}\}_{j=0}^{n}$ with $k_{0}=l_{0}$, $\Omega k_{0}=l_{n}$ and $( l_{j-1},l_{j} ) \in \vartheta (\Game )$ for $j=1,2,\ldots,n$. Based on $(\Game _{\sigma \xi }S1)$, for $j=1,2,\ldots,n$ we have $( \Omega l_{j-1},\Omega l_{j} ) \in \vartheta (\Game )$. This implies that $\{\Omega l_{j}\}_{j=0}^{n}$ is a path from $\Omega l_{0}=\Omega k_{0}=k_{1}$ to $\Omega l_{n}=\Omega ^{2}k_{0}=k_{2}$ having length n, and thus $k_{2}\in {}[ k_{1}]_{\Game }^{n}$. By repeating the same approach, we find that $\{\Omega ^{i}l_{j}\}_{j=0}^{n}$ is a path from $\Omega ^{i}l_{0}=\Omega ^{i}k_{0}=k_{i}$ to $\Omega ^{i}l_{n}=\Omega ^{i}\Omega k_{0}=k_{i+1}$ of length n, and thus $k_{i+1}\in {}[ k_{i}]_{\Game }^{n}$, for all $i\in \mathbb{N}$. This proves that $\{k_{i}\}$ is a ⅁-TWC sequence.

Now, $( \Omega ^{i}l_{j-1},\Omega ^{i}l_{j} ) \in \vartheta ( \Game )$ for $j=1,2,\ldots,n$ and $i\in \mathbb{N}$. By $(\Game _{\sigma \xi }S2)$, we get

$$ d_{\Game _{\sigma \xi }}\bigl(\Omega ^{i}l_{j-1},\Omega ^{i}l_{j}\bigr)\leq \eta d_{\Game _{\sigma \xi }}\bigl(\Omega ^{i-1}l_{j-1},\Omega ^{i-1}l_{j}\bigr). $$

By continuing with the same scenario, we have

$$\begin{aligned} d_{\Game _{\sigma \xi }}\bigl(\Omega ^{i}l_{j-1},\Omega ^{i}l_{j}\bigr) \leq & \eta d_{\Game _{\sigma \xi }}\bigl(\Omega ^{i-1}l_{j-1},\Omega ^{i-1}l_{j}\bigr) \\ \leq &\eta ^{2}d_{\Game _{\sigma \xi }}\bigl(\Omega ^{i-2}l_{j-1}, \Omega ^{i-2}l_{j}\bigr) \\ &{}\vdots \\ \leq &\eta ^{i}d_{\Game _{\sigma \xi }}(l_{j-1},l_{j}). \end{aligned}$$

(4.3)

Since $\{k_{i}\}$ is a ⅁-TWC sequence, by (4.3), we can write

$$\begin{array}{c}{d}_{{\mathrm{⅁}}_{\sigma \xi }}(k_i,k_{i+1})\hfill \\ =d_{{\mathrm{⅁}}_{\sigma \xi }}({\mathrm{\Omega }}^i{k}_0,{\mathrm{\Omega }}^{i+1}{k}_0)\hfill \\ =d_{{\mathrm{⅁}}_{\sigma \xi }}({\mathrm{\Omega }}^i{l}_0,{\mathrm{\Omega }}^i{l}_n)\hfill \\ \le \sigma ({\mathrm{\Omega }}^i{l}_0,{\mathrm{\Omega }}^i{l}_1)d_{{\mathrm{⅁}}_{\sigma \xi }}({\mathrm{\Omega }}^i{l}_0,{\mathrm{\Omega }}^i{l}_1)+\xi ({\mathrm{\Omega }}^i{l}_1,{\mathrm{\Omega }}^i{l}_n)d_{{\mathrm{⅁}}_{\sigma \xi }}({\mathrm{\Omega }}^i{l}_1,{\mathrm{\Omega }}^i{l}_n)\hfill \\ \le \sigma ({\mathrm{\Omega }}^i{l}_0,{\mathrm{\Omega }}^i{l}_1)d_{{\mathrm{⅁}}_{\sigma \xi }}({\mathrm{\Omega }}^i{l}_0,{\mathrm{\Omega }}^i{l}_1)+\xi ({\mathrm{\Omega }}^i{l}_1,{\mathrm{\Omega }}^i{l}_n)\sigma ({\mathrm{\Omega }}^i{l}_1,{\mathrm{\Omega }}^i{l}_2)d_{{\mathrm{⅁}}_{\sigma \xi }}({\mathrm{\Omega }}^i{l}_1,{\mathrm{\Omega }}^i{l}_2)\hfill \\ +\xi ({\mathrm{\Omega }}^i{l}_1,{\mathrm{\Omega }}^i{l}_n)\xi ({\mathrm{\Omega }}^i{l}_2,{\mathrm{\Omega }}^i{l}_n)d_{{\mathrm{⅁}}_{\sigma \xi }}({\mathrm{\Omega }}^i{l}_2,{\mathrm{\Omega }}^i{l}_n)\hfill \\ \le \sigma ({\mathrm{\Omega }}^i{l}_0,{\mathrm{\Omega }}^i{l}_1)d_{{\mathrm{⅁}}_{\sigma \xi }}({\mathrm{\Omega }}^i{l}_0,{\mathrm{\Omega }}^i{l}_1)+\xi ({\mathrm{\Omega }}^i{l}_1,{\mathrm{\Omega }}^i{l}_n)\sigma ({\mathrm{\Omega }}^i{l}_1,{\mathrm{\Omega }}^i{l}_2)d_{{\mathrm{⅁}}_{\sigma \xi }}({\mathrm{\Omega }}^i{l}_1,{\mathrm{\Omega }}^i{l}_2)\hfill \\ +\xi ({\mathrm{\Omega }}^i{l}_1,{\mathrm{\Omega }}^i{l}_n)\xi ({\mathrm{\Omega }}^i{l}_2,{\mathrm{\Omega }}^i{l}_n)\sigma ({\mathrm{\Omega }}^i{l}_2,{\mathrm{\Omega }}^i{l}_3)d_{{\mathrm{⅁}}_{\sigma \xi }}({\mathrm{\Omega }}^i{l}_2,{\mathrm{\Omega }}^i{l}_3)\hfill \\ +\xi ({\mathrm{\Omega }}^i{l}_1,{\mathrm{\Omega }}^i{l}_n)\xi ({\mathrm{\Omega }}^i{l}_2,{\mathrm{\Omega }}^i{l}_n)\xi ({\mathrm{\Omega }}^i{l}_3,{\mathrm{\Omega }}^i{l}_n)d_{{\mathrm{⅁}}_{\sigma \xi }}({\mathrm{\Omega }}^i{l}_3,{\mathrm{\Omega }}^i{l}_n)\hfill \\ \le \dots \hfill \\ \le \sigma ({\mathrm{\Omega }}^i{l}_0,{\mathrm{\Omega }}^i{l}_1)d_{{\mathrm{⅁}}_{\sigma \xi }}({\mathrm{\Omega }}^i{l}_0,{\mathrm{\Omega }}^i{l}_1)\hfill \\ +\sum _{r=1}^{n-2}\left(\prod _{j=1}^r\xi ({\mathrm{\Omega }}^i{l}_j,{\mathrm{\Omega }}^i{l}_n)\right)\sigma ({\mathrm{\Omega }}^i{l}_r,{\mathrm{\Omega }}^i{l}_{r+1})d_{{\mathrm{⅁}}_{\sigma \xi }}({\mathrm{\Omega }}^i{l}_r,{\mathrm{\Omega }}^i{l}_{r+1})\hfill \\ +\prod _{s=1}^{n-1}\xi ({\mathrm{\Omega }}^i{l}_s,{\mathrm{\Omega }}^i{l}_n)d_{{\mathrm{⅁}}_{\sigma \xi }}({\mathrm{\Omega }}^i{l}_{n-1},{\mathrm{\Omega }}^i{l}_n)\hfill \\ \le {\eta }^i\left\{\begin{array}{c}\sigma ({\mathrm{\Omega }}^i{l}_0,{\mathrm{\Omega }}^i{l}_1)d_{{\mathrm{⅁}}_{\sigma \xi }}(l_0,l_1)\\ +{\sum }_{r=1}^{n-2}({\prod }_{j=1}^r\xi ({\mathrm{\Omega }}^i{l}_j,{\mathrm{\Omega }}^i{l}_n))\sigma ({\mathrm{\Omega }}^i{l}_r,{\mathrm{\Omega }}^i{l}_{r+1})d_{{\mathrm{⅁}}_{\sigma \xi }}(l_r,l_{r+1})\\ +{\prod }_{r=1}^{n-1}\xi ({\mathrm{\Omega }}^i{l}_r,{\mathrm{\Omega }}^i{l}_n){\eta }^i{d}_{{\mathrm{⅁}}_{\sigma \xi }}(l_{n-1},l_n)\end{array}\right\}.\hfill \end{array}$$

Since r is finite, letting

$$Q_{{\mathrm{⅁}}_{\sigma \xi }}=\left\{\begin{array}{c}\sigma ({\mathrm{\Omega }}^i{l}_0,{\mathrm{\Omega }}^i{l}_1)d_{{\mathrm{⅁}}_{\sigma \xi }}(l_0,l_1)\\ +{\sum }_{r=1}^{n-2}({\prod }_{j=1}^r\xi ({\mathrm{\Omega }}^i{l}_j,{\mathrm{\Omega }}^i{l}_n))\sigma ({\mathrm{\Omega }}^i{l}_r,{\mathrm{\Omega }}^i{l}_{r+1}){\eta }^r{d}_{{\mathrm{⅁}}_{\sigma \xi }}(l_0,l_1)\\ +{\prod }_{r=1}^{n-1}\xi ({\mathrm{\Omega }}^i{l}_r,{\mathrm{\Omega }}^i{l}_n){\eta }^{n-1}{d}_{{\mathrm{⅁}}_{\sigma \xi }}(l_0,l_1)\end{array}\right\},$$

a finite quantity, we have

$$ d_{\Game _{\sigma \xi }}(k_{i},k_{i+1})\leq \eta ^{i}Q_{\Game _{ \sigma \xi }}. $$

(4.4)

Again, since $\{k_{i}\}$ is a ⅁-TWC sequence for $i,m\in \mathbb{N}$, $i< m$ and using (4.4), we obtain

$$\begin{aligned} d_{\Game _{\sigma \xi }}(k_{i},k_{m}) \leq &\sigma (k_{i},k_{i+1})d_{ \Game _{\sigma \xi }}(k_{i},k_{i+1})+ \xi (k_{i+1},k_{m})d_{\Game _{ \sigma \xi }}(k_{i+1},k_{m}) \\ \leq &\sigma (k_{i},k_{i+1})d_{\Game _{\sigma \xi }}(k_{i},k_{i+1})+ \xi (k_{i+1},k_{m})\sigma (k_{i+1},k_{i+2})d_{\Game _{\sigma \xi }}(k_{i+1},k_{i+2}) \\ &{}+\xi (k_{i+1},k_{m})\xi (k_{i+2},k_{m})d_{\Game _{\sigma \xi }}(k_{i+2},k_{m}) \\ \leq &\sigma (k_{i},k_{i+1})d_{\Game _{\sigma \xi }}(k_{i},k_{i+1})+ \xi (k_{i+1},k_{m})\sigma (k_{i+1},k_{i+2})d_{\Game _{\sigma \xi }}(k_{i+1},k_{i+2}) \\ &{}+\xi (k_{i+1},k_{m})\xi (k_{i+2},k_{m}) \sigma (k_{i+2},k_{i+3})d_{ \Game _{\sigma \xi }}(k_{i+2},k_{i+3}) \\ &{}+\xi (k_{i+1},k_{m})\xi (k_{i+2},k_{m}) \xi (k_{i+3},k_{m})d_{\Game _{ \sigma \xi }}(k_{i+3},k_{m}) \\ \leq &\cdots \\ \leq &\sigma (k_{i},k_{i+1})d_{\Game _{\sigma \xi }}(k_{i},k_{i+1})+ \sum_{q=i+1}^{m-2} \Biggl( \prod _{s=1}^{q}\xi (k_{s},k_{m}) \Biggr) \sigma (k_{q},k_{q+1})d_{\Game _{\sigma \xi }}(k_{q},k_{q+1}) \\ &{}+\prod_{p=i+1}^{m-1}\xi (k_{p},k_{m})d_{\Game _{\sigma \xi }}(k_{m-1},k_{m}) \\ \leq &\sigma (k_{i},k_{i+1})\eta ^{i}Q_{\Game _{\sigma \xi }}+ \sum_{q=i+1}^{m-2} \Biggl( \prod _{s=1}^{q}\xi (k_{s},k_{m}) \Biggr) \sigma (k_{q},k_{q+1})\eta ^{q}Q_{\Game _{\sigma \xi }} \\ &{}+\prod_{p=m+1}^{i-1}\xi (k_{p},k_{i})\eta ^{i-1}Q_{\Game _{ \sigma \xi }} \\ \leq &\sigma (k_{m},k_{m+1})\eta ^{m}Q_{\Game _{\sigma \xi }}+ \sum_{q=m+1}^{i-2} \Biggl( \prod _{s=1}^{q}\xi (k_{s},k_{i}) \Biggr) \sigma (k_{q},k_{q+1})\eta ^{q}Q_{\Game _{\sigma \xi }} \\ &{}+ \Biggl( \prod_{p=i+1}^{m-1}\xi (k_{p},k_{m}) \Biggr) \eta ^{m-1}\sigma (k_{m-1},k_{m})Q_{\Game _{\sigma \xi }} \\ =&\sigma (k_{i},k_{i+1})\eta ^{i}Q_{\Game _{\sigma \xi }}+ \sum_{q=i+1}^{m-1} \Biggl( \prod _{s=1}^{q}\xi (k_{s},k_{m}) \Biggr) \sigma (k_{q},k_{q+1})\eta ^{q}Q_{\Game _{\sigma \xi }} \\ \leq &\sigma (k_{i},k_{i+1})\eta ^{i}Q_{\Game _{\sigma \xi }}+ \sum_{q=i+1}^{m-1} \Biggl( \prod _{s=0}^{q}\xi (k_{s},k_{m}) \Biggr) \sigma (k_{q},k_{q+1})\eta ^{q}Q_{\Game _{\sigma \xi }}. \end{aligned}$$

Note that, we used the fact $\sigma (k,l),\xi (k,l)\geq 1$. Assume that

$$ \Psi _{h}=\sum_{q=0}^{h} \Biggl( \prod_{s=0}^{q}\xi (k_{s},k_{m}) \Biggr) \sigma (k_{q},k_{q+1}) \eta ^{q}. $$

Then, we get

$$ d_{\Game _{\sigma \xi }}(k_{i},k_{m})\leq Q_{\Game _{\sigma \xi }} \bigl( \eta ^{i}\sigma (k_{i},k_{i+1})+ ( \Psi _{m-1}-\Psi _{i} ) \bigr) . $$

(4.5)

From condition (4.2) and using the ratio test, we find that $\lim_{i\rightarrow \infty }\Psi _{i}$ exists, and hence and the real sequence $\{\Psi _{i}\}$ is a ⅁-Cauchy.

At the last, letting $m,i\rightarrow \infty$ in (4.5), we have

$$ \lim_{i,m\rightarrow \infty }d_{\Game _{\sigma \xi }}(k_{i},k_{m})=0. $$

This proves that the sequence $\{k_{i}\}$ is a ⅁-Cauchy in $(J,d_{\Game _{\sigma \xi }})$. The completeness of $(J,d_{\Game _{\sigma \xi }})$ implies that there is a sequence $\{k_{i}\}$ converges in J and from stipulation (1), there is $k^{\ast }\in J$, $i_{0}\in \mathbb{N}$ so that $(k_{i},k^{\ast })\in \vartheta (\Game )$ or $(k^{\ast },k_{i})\in \vartheta (\Game )$, $\forall i>i_{0}$ and

$$ \lim_{i\rightarrow \infty }d_{\Game _{\sigma \xi }}\bigl(k_{i},k^{\ast } \bigr)=d_{ \Game _{\sigma \xi }}\bigl(k,k^{\ast }\bigr)=\lim_{m,i\rightarrow \infty }d_{ \Game _{\sigma \xi }}(k_{i},k_{m})=0. $$

This assures that $\{k_{i}\}$ converges to $k^{\ast }$.

If $(k_{i},k^{\ast })\in \vartheta (\Game )$, then by stipulation $(\Game _{\sigma \xi }S2)$, we get

$$ d_{\Game _{\sigma \xi }}\bigl(k_{i+1},\Omega k^{\ast } \bigr)=d_{\Game _{\sigma \xi }}\bigl(\Omega k_{i},\Omega k^{\ast }\bigr) \leq Ld_{\Game _{\sigma \xi }}\bigl(k_{i},k^{ \ast }\bigr),\text{ for }i>i_{0}. $$

This implies that

$$ \lim_{i\rightarrow \infty }d_{\Game _{\sigma \xi }}\bigl(k_{i+1},\Omega k^{ \ast }\bigr)=0. $$

Also, if $(k^{\ast },k_{i})\in \vartheta (\Game )$, then with the same arguments as above, we find that

$$ \lim_{i\rightarrow \infty }d_{\Game _{\sigma \xi }}\bigl(\Omega k^{\ast },k_{i+1} \bigr)=0. $$

Therefore, $\{k_{i}\}$ converges to both $k^{\ast }$ and $\Omega k^{\ast }$, and this finishes the proof. □

In order to achieve the existence of the fixed point, we introduce the following results:

Definition 4.3

Let $(J,d_{\Game _{\sigma \xi }})$ be a GDCML-space and $\Omega :J\rightarrow J$ be self-mapping. A trio $(J,d_{\Game _{\sigma \xi }},\Omega )$ is said to satisfy the property (H) if: corresponding to two limits $k^{\ast }\in J$ and $l^{\ast }\in \Omega (J)$ of a ⅁-TWC Ω-PS $\{k_{i}\}$, we get $k^{\ast }=l^{\ast }$.

Theorem 4.4

Assume that all hypotheses of Theorem 4.2hold and suppose that a trio $(J,d_{\Game _{\sigma \xi }},\Omega )$ verifies the property (H). Then, Ω possesses a fixed point.

Proof

In Theorem 4.2, we were able to prove that the Ω-PS $\{k_{i}\}$ with initial value $k_{0}$ converges to both $k^{\ast }$ and $\Omega k^{\ast }$. As $k^{\ast }\in J$ and $\Omega k^{\ast }\in \Omega (J)$, therefore by our assumption, we have $k^{\ast }=\Omega k^{\ast }$. Hence, Ω has a fixed point. □

The below example supports Theorem 4.2.

Example 4.5

Let $J=\{0\}\cup \{\frac{1}{3^{i}}:i\in \mathbb{N} \}$ be endowed with a GDCML $d_{\Game _{\sigma \xi }}$ described as

$$ d_{\Game _{\sigma \xi }}(k,l)=\textstyle\begin{cases} 0, & \text{if }k=l, \\ ( k+l ) ^{2}, & k\neq l,\end{cases} $$

including the graph ⅁ so that $J=\nu (\Game )$ and $\vartheta (\Game )=\Lambda \cup \{(k,l)\in J^{2}:(k\Re l)_{\Game }, k-l\geq 0\}$. It is obvious that $(J,d_{\Game _{\sigma \xi }})$ is a GDCML-space with $\sigma (k,l)=2+k+l$ and $\xi (k,l)=3+k+l$. Define a self mapping $\Omega :J\rightarrow J$ by $\Omega (k)=\frac{k}{3}$, for all $k\in J$. It is obvious to see that there is $k_{0}=\frac{1}{3}$ so that $\Omega (\frac{1}{3})=\frac{1}{9}\in {}[ \frac{1}{3}]_{\Game }^{1}$, i.e., $(\frac{1}{3}\Re \frac{1}{9})_{\Game }$ and the contraction (4.1) is fulfilled with $\eta =\frac{1}{9}$. Hence, Ω is a graphical $\Game _{\sigma \xi }$-contraction on a GDCML-space $(J,d_{\Game _{\sigma \xi }})$ with $\sigma (k,l)=2+k+l$, $\xi (k,l)=1+k+l$ and $\eta =\frac{1}{9}$.

Since $\{k_{i}\}$ is a Ω-PS, for each $k\in J$, $\Omega ^{i}(k)=\frac{k}{3^{i}}$, such that, we get

$$\begin{aligned} \lim_{i,m\rightarrow \infty } \frac{\sigma (k_{i+1},k_{i+2})}{\sigma (k_{i},k_{i+1})}\xi (k_{i+1},k_{m}) =&\lim_{i,m\rightarrow \infty } \frac{\sigma (\Omega ^{i+1}k_{0},\Omega ^{i+2}k_{0})}{\sigma (\Omega ^{i}k_{0},\Omega ^{i+1}k_{0})} \xi \bigl(\Omega ^{i+1}k_{0},\Omega ^{m}k_{0}\bigr) \\ =&\lim_{i,m\rightarrow \infty } \frac{\sigma (\frac{k_{0}}{3^{i+1}},\frac{k_{0}}{3^{i+2}})}{\sigma (\frac{k_{0}}{3^{i}},\frac{k_{0}}{3^{i+1}})} \xi \biggl(\frac{k_{0}}{3^{i+1}},\frac{k_{0}}{3^{m}}\biggr) \\ =&\frac{\sigma (0,0)}{\sigma (0,0)}\xi (0,0)=3< 9=\frac{1}{\eta }. \end{aligned}$$

Moreover, since $k_{0}=\frac{1}{3}$ and $\Omega ^{i}(k)=\frac{k}{3^{i}}$, we see that $\lim_{i\rightarrow \infty }\sigma (k,k_{i})$ and $\lim_{i\rightarrow \infty }\xi (k_{i},k)$ exist and are finite. Therefore, all hypotheses of Theorem 4.2 are fulfilled, and 0 is the unique fixed point of Ω on J. Figure 6 presents the weighted graph for $\nu ^{\ast }(\Game )=\{0,\frac{1}{3},\frac{1}{3^{2}},\frac{1}{3^{3}}, \frac{1}{3^{4}},\frac{1}{3^{5}},\frac{1}{3^{6}}\}\subseteq \nu ^{\ast }(\Game )$, where the wight of edge $(k,l)$ is equal to the value of $d_{\Game _{\sigma \xi }}(k,l)$.

Figure 6

Weighted graph for Example 4.5

5 The existence of a solution for transverse oscillations

In this section, we apply the obtained theoretical results to discuss the existence of a solution to the boundary value problem originating from transverse oscillations of a homogeneous bar (TOHB).

The TOHB is a problem of paramount importance. Suppose that we have a homogeneous bar that is fixed at one end and free at the other one so that the axis of the homogeneous bar corresponds to the segment $(0,1)$ of the x-axis and the deviation parallel to the z-axis at the point c. The differential equation that describes the TOHB is written as:

$$ \textstyle\begin{cases} \frac{d^{4}k(c)}{dc^{4}}=\aleph ^{4}\hbar (c,k(c)),\quad c\in I=[0,1], \\ k(0)=k^{\prime }(0)=k^{\prime \prime }(1)=k^{\prime \prime \prime }(1)=0,\end{cases} $$

(5.1)

where $\hbar :[0,1]\times \mathbb{R} \rightarrow \mathbb{R}$ is a continuous function and $\aleph >0$ is a constant.

Problem (5.1) is written as an integral equation as follows:

$$ k(c)=\aleph ^{4} \int _{0}^{1}\beth (c,u)\hbar \bigl(u,k(u)\bigr) \,du, $$

(5.2)

where $\beth (c,u)$ is the Green function described by

$$ \beth (c,u)=\frac{1}{6}\textstyle\begin{cases} 3u^{2}c-u^{3}, &0\leq u\leq c\leq 1, \\ 3uc^{2}-c^{3}, &0\leq c\leq u\leq 1.\end{cases} $$

Assume that $J=C(I,\mathbb{R} )$ is the set of real continuous functions on I. Let

$$ \mho =\Bigl\{ k\in J:\inf_{c\in I}k(c)>0 \text{ \& } k(c)\leq 1,c \in I \Bigr\} . $$

Let ⅁ be a graph defined by $J=\nu (\Game )$ and

$$ \vartheta (\Game )=\Lambda \cup \bigl\{ \bigl(k,k^{\ast }\bigr)\in J^{2}:k,k^{\ast } \in \mho ,k(c)\leq k^{\ast }(c), \forall c\in I\bigr\} . $$

Suppose that $d_{\Game _{\sigma \xi }}:J\times J\rightarrow {}[ 0,\infty )$ is a GDCML described as

$$ d_{\Game _{\sigma \xi }}\bigl(k,k^{\ast }\bigr)=\sup_{c\in I} \bigl\vert k(c)+k^{ \ast }(c) \bigr\vert ^{2}, $$

for all $k,k^{\ast }\in J$ with $\sigma (k,k^{\ast })=s+k+k^{\ast }$ and $\sigma (k,k^{\ast })=t+k+k^{\ast }$, such that $s,t>2$ and $s\neq t$. Then $(J,d_{\Game _{\sigma \xi }})$ is a GDCML-space.

Now, we consider Problem (5.1) under the following hypotheses:

($H_{1}$):

There is a lower solution $\gamma \in J$ of Problem (5.2), i.e.,

$$ \gamma (c)\leq \aleph ^{4} \int _{0}^{1}\beth (c,u)\hbar \bigl(u,k(u)\bigr) \,du; $$

($H_{2}$):

Select ℵ suitably so that

$$ \inf_{c\in I}\beth (c,u)>0, \quad 0\leq \sup_{c\in I} \bigl( \daleth (\aleph ,c) \bigr) ^{2}< 1\quad \text{and}\quad \beth (c,u)\hbar (u,1) \leq \biggl( \frac{1}{\aleph } \biggr) ^{4}, $$

where $\daleth (\aleph ,c)=\frac{\aleph ^{4}}{6} ( \frac{c^{4}-4c^{3}+6c^{2}}{4} )$;

($H_{3}$):

The stipulation below holds, for each $c\in I$ and $k,l\in J$

$$ \bigl\vert \hbar \bigl(c,k(c)\bigr)+\hbar \bigl(c,l(c)\bigr) \bigr\vert \leq \bigl\vert k(c)+l(c) \bigr\vert . $$

Theorem 5.1

Under assumptions $(H_{1})$–$(H_{3})$, Problem (5.1) governs TOHB has a solution.

Proof

Let $\Omega :J\rightarrow J$ be an operator described by

$$ \Omega \bigl(k(c)\bigr)=\aleph ^{4} \int _{0}^{1}\beth (c,u)\hbar \bigl(u,k(u)\bigr) \,du,\quad \forall u\in I. $$

It is clear that the operator J is well-defined. Based on the given assumption, for $(k,l)\in \vartheta (\Game )$ with $k,l\in J$, we have

$$\begin{aligned} \bigl\vert \Omega \bigl(k(c)\bigr)+\Omega \bigl(l(c)\bigr) \bigr\vert =& \biggl\vert \aleph ^{4} \int _{0}^{1}\beth (c,u)\hbar \bigl(u,k(u)\bigr) \,du+\aleph ^{4} \int _{0}^{1}\beth (c,u)\hbar \bigl(u,l(u)\bigr) \,du \biggr\vert \\ \leq &\aleph ^{4} \int _{0}^{1}\beth (c,u) \bigl\vert \hbar \bigl(u,k(u)\bigr)+ \hbar \bigl(u,l(u)\bigr) \bigr\vert \,du \\ \leq &\aleph ^{4} \int _{0}^{1}\beth (c,u) \Bigl( \sup _{c \in I} \bigl\vert \hbar \bigl(c,k(c)\bigr)+\hbar \bigl(c,l(c) \bigr) \bigr\vert \Bigr)\,du \\ =&\aleph ^{4} \Bigl( \sup_{c\in I} \bigl\vert \hbar \bigl(c,k(c)\bigr)+\hbar \bigl(c,l(c)\bigr) \bigr\vert \Bigr) \int _{0}^{1}\beth (c,u)\,du \\ \leq &\frac{\aleph ^{4}}{6} \biggl( \frac{c^{4}-4c^{3}+6c^{2}}{4} \biggr) \Bigl( \sup _{c\in I} \bigl\vert k(c)+l(c) \bigr\vert \Bigr), \end{aligned}$$

which implies that

$$ \sup_{c\in I} \bigl\vert \Omega \bigl(k(c)\bigr)+\Omega \bigl(l(c)\bigr) \bigr\vert ^{2} \leq \sup_{c\in I} \bigl( \daleth (\aleph ,c) \bigr) ^{2}\sup_{c \in I} \bigl\vert k(c)+l(c) \bigr\vert ^{2}. $$

Using our assumptions, we take $\sup_{c\in I} ( \daleth (\aleph ,c) ) ^{2}=\eta \in {}[ 0,1)$, such that we get

$$ d_{\Game _{\sigma \xi }}(\Omega k,\Omega l)\leq \eta d_{\Game _{ \sigma \xi }}(k,l). $$

This verifies the stipulation $(\Game _{\sigma \xi }S2)$ of Theorem 4.2.

Now, for all $k,l\in \Omega$ so that $(k,l)\in \vartheta (\Game )$, we find that $k,l\in \mho$ and $k(c)\leq l(c)$, for all $c\in I$.

By the assertion $(H_{2})$, we obtain $\inf_{c\in I}\Omega (k)>0$,

$$ \Omega (k) (c)=\aleph ^{4} \int _{0}^{1}\beth (c,u)\hbar \bigl(u,k(u)\bigr) \,du \leq \aleph ^{4} \int _{0}^{1}\beth (c,u)\hbar (c,1)\,du\leq 1 $$

and

$$ \Omega (k) (c)=\aleph ^{4} \int _{0}^{1}\beth (c,u)\hbar \bigl(u,k(u)\bigr) \,du \leq \aleph ^{4} \int _{0}^{1}\beth (c,u)\hbar \bigl(u,l(u)\bigr) \,du= \Omega (l) (c). $$

In other words, $\Omega (k)(c)\in \mho$ and $(\Omega (k)(c),\Omega (l)(c))\in \vartheta (\Game )$.

Moreover, by condition $(H_{1})$, the existence of a lower solution of the integral equation (5.2) confirms that there is a solution, say $\varkappa \in \mho$, so that $\Omega (\varkappa )\in {}[ \varkappa ]_{\Game }^{1}$. This implies that the hypothesis (2) of Theorem 4.2 is fulfilled. Also, the remaining conditions of Theorem 4.2 can be verified easily. So, the mapping Ω has a fixed point, which is a solution of the ordinary differential equation (5.1). □

6 Some open problems

• Is it possible to expand the triangle inequality to become quadrilateral or rectangular to obtain new spaces under the same topological properties?

• Is it possible to extend the contraction condition given in our basic theorem, such as the equivalent results of Reich [32], Meir–Keelar [33], Kannan [34], Hardy–Rogers [35], Ciric [36], Edelstein [37], and De la Sen [38] in a GDCML-space?

• Can we apply the theoretical results to discuss the existence solution of the following integro-differential equation:

  $$ k(c)=\frac{1}{4} \int _{s}^{r}\beth (c,u) \bigl[ \hbar \bigl(u,k(u),k^{ \prime }(u)\bigr)+\wp \bigl(u,k(u)\bigr) \bigr]\,du, $$

  for $c\in {}[ s,r]$, where $\beth :[s,r]\times {}[ s,r]\rightarrow {}[ 1,\infty ]$, $\hbar :[s,r]\times {}[ 0,\infty )\times {}[ 0,\infty ) \rightarrow {}[ 0,\infty )$ and $\wp :[s,r]\times {}[ 0,\infty )\rightarrow {}[ 0,\infty )$ are continuous functions?

• What happens if the graphical $\Game _{\sigma \xi }$-contraction mapping $\Omega :J\rightarrow J$ is a cyclic mapping, and/or we add the notion of α-admissibility?