Abstract
Pneumonia is a highly transmitted disease in children. According to the World Health Organization (WHO), the most affected regions include South Asia and sub-Saharan Africa. 15% deaths of children are due to pneumonia. In 2017, 0.88 million children were killed under the age of five years. An analysis of pneumonia disease is performed with the help of a delayed mathematical modelling technique. The epidemiological system contemplates subpopulations of susceptible, carriers, infected and recovered individuals, along with nonlinear interactions between the members of those subpopulations. The positivity and the boundedness of the ongoing problem for nonnegative initial data are thoroughly proved. The system possesses pneumonia-free and pneumonia existing equilibrium points, whose stability is studied rigorously. Moreover, the numerical simulations confirm the validity of these theoretical results.
Similar content being viewed by others
1 Literature survey
In 2014, Mochan et al. presented the interhost immune response to bacterial pneumonia infection in murine strains in a simple ordinary differential equation model dynamically [1]. Drusano et al., in 2014, investigated the effects of granulocytes to eradicate bacterial pathogens, and there was no role of antimicrobial therapy [2]. In 2015, Ndelwa et al. expressed the dynamic properties for the transfer of pneumonia along with screening and medication mathematically and analysed to know the transmission and effects [3]. Kosasih et al., in 2015, analysed a mathematical model of cough sounds by wavelet-based crackle detection work for rapid diagnosis of bacterial pneumonia in children [4]. In 2016, César et al. estimated particulate matter in a model mathematically and medications for both pneumonia and asthma in children among the population [5]. Marchello et al., in 2016, gave atypical bacterial pathogens as the main causes for lower respiratory diseases like cough, bronchitis, CAP and analysed them [6]. In 2017, Cheng et al. provided an IAV-SP model mathematically and dynamically. A quantitative risk-assessment framework to improve respiratory health due to COPD gave the hope for improvements [7]. Kosasih et al., in 2017, gave a simple mathematical model showing the analysis of measurements for pneumonia diagnosis among children clinically [8]. Tilahun et al., in 2017, proposed a deterministic nonlinear model mathematically and analysed optical control strategies for the bacterial disease pneumonia; results are shown graphically [9]. In 2018, Raj et al. analysed the classification of asthma and pneumonia based upon mathematical features of cough sound in the poor regions of the population [10]. Kizito et al., in 2018, presented a mathematical model that shows the control of pneumonia spread by bacteria. Also, the dynamics of treatment and formulation of vaccines were given [11]. In 2018, Mbabazi et al. investigated a mathematical model nonlinearly that described the modelling of within-host coinfection influenza A virus and pneumonia [12]. Tilahun et al., in 2018, proposed a coinfection model for pneumonia-typhoid and mathematically analysed their characteristic relationship in case of cure and medical strategies [13]. In 2019, Tilahun et al. described a model of pneumonia-meningitis coinfection with the help of ordinary differential equations and some of the theorems. It explained different techniques for disease clearance [14]. Diah et al., in 2019, reviewed mathematical models of pneumonia dynamically followed by research in the past. An alternative method was proposed to estimate the risk of pneumonia [15]. In 2019, Kosasih et al. explained the main cause of pneumonia affecting children in early childhood in poor regions of the world [8]. In 2019, Tilahun et al. analysed a coinfection mathematical model for pneumonia and bacterial meningitis [16]. Mbabazi et al., in 2019, proposed a pneumococcal pneumonia model with time delays mathematically, Hopf-bifurcation was analysed [17]. In 2020, Otoo et al. analysed a model of pneumonia spread by bacteria. The analysis determined the effects of vaccination to control the disease [18]. In 2020, Zephaniah et al. presented the dynamics of mathematical models for pneumonia, showing the result graphically [19]. Ming et al., in 2020, described the spread of coronavirus pneumonia in Wuhan, China, and discussed the increasing cases of infected people [20]. In 2020, Jung et al. demonstrated the observations using different clinical tests and showed the cause of disease, a novel pathogen [21]. Adams et al., in 2020, showed the progress regarding pneumonia prevention and different strategies to treat and overcome bacterial pneumonia [22]. In 2013, Ong’ala et al. developed a mathematical model for bacteremic pneumonia among children under five years. Using stability of equilibrium points and bifurcation, they analysed the reducing ways or the transfer rates between the carriers and the infected class [23]. Minuci et al. presented the review of mathematical modelling of the inflammatory response in lungs infections and injuries. They emphasised that mathematical modelling is a great tool for understanding infectious diseases [24]. Huttinger et al., in 2017, developed a mechanistic mathematical model explaining the dynamic relationship between streptococcus pneumonia (Sp), immune cells and epithelial tissues for the better understanding of complex dynamically changing host–Sp interaction. They claimed that their model provides help to plan better disease management strategies from the diagnostic and treatment perspective [25]. In 2021, Wafula et al. presented an article describing optimal control treatment by developing a deterministic mathematical model pneumonia–HIV coinfection incorporating the use of anti-pneumonia and ART treatment interventions as controls [26]. Oluwatobi et al. studied the effect of treatment of pneumonia infection and investigated the basic and effective reproduction numbers existence and the stability of equilibrium points [27]. Epidemiology has a significant role in different disciplines like medicine, engineering, chemistry, physics, economics and many more. A diseases model is investigated with the help of well-known branches of mathematics like spatio-temporal, stochastic, fractional and fractal fractional [28–48].
Pneumonia is a terrible strain in developing regions such as Asia, Africa and Europe. Pneumonia vaccination has been introduced in developed countries, and even the United States is the largest donor for nefarious purposes. Delay modelling is a more general form of deterministic modelling. The delayed analysis is a more realistic, close nature and authentic tool to control infectious diseases. For example, in the recent strain of coronavirus, the only control strategy is delaying tactics like public holidays, restriction in travel, facemask, hand sanitiser, social distancing etc. This article claims that precautionary measures or delay tactics are the best revenge to control pneumonia-like diseases other than vaccination or medication etc. That is a reason why we move in delay modelling.
The paper strategy is as follows: Sect. 1 presents literature survey regarding pneumonia-like diseases. Section 2 deals with the formulation of the delayed model and its mathematical analysis. In Sects. 3 and 4 the stability of the model is described locally and globally, respectively. Section 5 presents the sensitivity of the parameters involved in the model. In Sect. 6 the numerical simulations with their results are given. Section 7 contains the concluding remarks of the work.
2 Formulation of the model
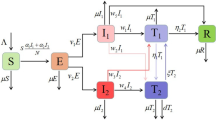
The formulation of the model is based on the theory of population dynamics. The population \(N ( t )\) is the sum of the following classes: susceptible \(S ( t )\), carriers \(C ( t )\), infected \(I ( t )\) and recovered \(R ( t )\). The modelling of pneumonia disease based on the law of mass action is performed (see Fig. 1). Furthermore, some assumptions are fixed during the delay modelling as follows:
-
Newly recruited individuals are assumed to be in the susceptible class.
-
The birth and death rates are approximately equal.
-
Vertical transmission is to be considered.
-
Susceptible types make attraction with the infected and carriers classes at any time \(( {t}-\tau )\).
-
Natural delay is assumed.
-
An artificial delay term like \({e}^{-\mu \tau }, \tau \geq 0\) (a decay term) is used for controlling the epidemic.
-
Once recovered, they may have chances to get the disease again.
-
The carriers may recover directly due to their internal immunity.
-
The carriers and infected classes have inverse interactions with each other.
-
Two types of death rates are considered: natural and due to the disease.
Table 1 presents the physical relevance of the constants as follows.
Based on the assumptions, the continuous model is defined with the help of the law of mass action. The nonlinear delay differential equations (DDEs) present the transmission flow of pneumonia type diseases as follows:
with nonnegative initial conditions \(S= S_{0}\geq0\), \(C=C_{0}\geq0\), \(I= I_{0}\geq0\), \(R= R_{0}\geq0\) and \({t}\geq 0, \tau \leq t\).
2.1 Model properties
To preserve the meaningful analysis of the model, all the variables \(S ( t ), C ( t ), I ( t ), R ( t )\) must be nonnegative. Consequently, the outcomes are achieved after studying the model for any time \(t \geq 0 \tau \leq t\) in a feasible region.
Theorem 2.1
The solutions \(({S}, {C}, {I}, {R}) \epsilon \mathbb{{R}}_{+}^{4}\) of system (1)–(4) are positive at \({t}\geq 0, \tau \leq {t}\) with given nonnegative initial conditions.
Proof
Obviously, system (1)–(4) is as follows:
Since all the parameters and derivatives of the model are nonnegative, system (1)–(4) admits a positive solution, as desired. □
Theorem 2.2
The solutions \(({S}, {C}, {I}, {R}) \epsilon \mathbb{{R}}_{+}^{4}\) of system (1)–(4) are bounded.
Proof
Consider the population function:
Using Gronwall’s inequality [49], we have
\(\lim_{{it}\longrightarrow \infty } \operatorname{Sup} {N}({t})\leq \frac{\Lambda }{\mu }\), as desired. □
2.2 Analysis of the model
This section shows a brief discussion of the equilibria of the pneumonia delayed model. We will discuss trivial pneumonia equilibrium (\(\mathcal{P}_{n} TE - {D}_{0}\)), pneumonia-free equilibrium (\(\mathcal{P}_{n} FE - {D}_{1} \)) and pneumonia existing equilibrium \(( \mathcal{P}_{n} EE - {D}_{2} )\) given by
2.3 Reproduction number
The idea of reproduction number by using the next-generation matrix method is presented in [50]. The next-generation matrix method is implanted into system (1)–(4) to calculate the reproduction number \(R_{0}\). After taking the carriers and infected classes from Eq. (1) to Eq. (4), along with the pneumonia-free equilibrium as follows:
where \(u_{1} = ( \mu +\beta +\pi )\) and \(u_{2} = ( \psi +\mu +\sigma )\), \(\theta _{1} = (1-\theta )\),
The spectral radius of \(A B^{-1} \vert _{{D}_{1}}\) is called reproduction number and is defined as
3 Local stability
In this section, we examine the local stability of the model at the equilibrium of the model using the following recognised results.
The Jacobian matrix of system (1)–(4) and its elements are given below:
\(J_{11} = - \kappa p( {I}+\omega {C} ) {e}^{-\mu \tau } -\mu, J_{12} = -\kappa p\omega {S} {e}^{-\mu \tau }, J_{13} = - \kappa p {S} {e}^{-\mu \tau }, J_{14} = \eta , J_{21} =\theta \kappa p( {I}+{C} ) {e}^{-\mu \tau }, J_{22} =\theta \kappa p\omega {S} {e}^{-\mu \tau } - u_{1}, J_{23} =\theta \kappa p {S} {e}^{-\mu \tau }, J_{24} =0, J_{31} =\kappa p( {I}+\omega {C} ) \theta _{1} {e}^{-\mu \tau }, J_{32} =\kappa p\omega {S} \theta _{1} {e}^{-\mu \tau } +\pi, J_{33} =\kappa p {S} \theta _{1} {e}^{-\mu \tau } - u_{2}, J_{34} =0, J_{41} =0, J_{42} = \beta, J_{43} = \psi, J_{44} =- ( \mu +\eta )\).
Theorem 3.1
The pneumonia trivial equilibrium (\(\mathcal{P}_{n}\)TE-\(D_{0}\)), \(D_{0} = ( S^{0}, C^{0}, I^{0}, R^{0} ) =(0,0,0,0)\) is locally asymptotically stable if \(\mathcal{R}_{0} =1\).
Proof
The Jacobian matrix (5) at \({D}_{0} = ( {S}^{0}, {C}^{0}, {I}^{0}, {R}^{0} ) =(0,0,0,0)\) is as follows:
The detailed proof is given in Appendix 1. So, by the Routh–Hurwitz criterion, the pneumonia trivial equilibrium point (\(\mathcal{P}_{n} {TE}- {D}_{0}\)) is locally asymptotically stable. □
Theorem 3.2
The pneumonia-free equilibrium, \(D_{1} = ( S^{1}, C^{1}, I^{1}, R^{1} ) = ( \frac{\Lambda }{\mu },0,0,0 )\) is locally asymptotically stable if \(\mathcal{R}_{0} <1\).
Proof
The Jacobian matrix (5) at \(D_{1} = ( S^{1}, C^{1}, I^{1}, R^{1} ) = ( \frac{\Lambda }{\mu },0,0,0 )\) is as follows:
The detailed proof is given in Appendix 2 since all the eigenvalues are negative. Therefore, by Routh–Hurwitz criterion for the 2nd-degree polynomial, both fixed values of \(x_{1}, x_{0} >0\) if \(\mathcal{R}_{0} <1\). Hence the pneumonia-free equilibrium (\(\mathcal{P}_{n} {FE}- {D}_{1}\)) of system (1)–(4) is locally asymptotically stable. In other circumstances, if \(\mathcal{R}_{0} >1\), then the Routh–Hurwitz condition does not hold. Thus, \(D_{1}\) is unstable. □
Theorem 3.3
Pneumonia existing equilibrium (\(\mathcal{P}_{n} {EE}- {D}_{2}\)), \(D_{2} = ( S^{*}, C^{*}, I^{*}, R^{*} )\) is locally asymptotically stable if \(\mathcal{R}_{0} >1\).
Proof
The Jacobian matrix (5) at \(D_{2} = ( S^{*}, C^{*}, I^{*}, R^{*} )\) is as follows:
The detailed proof is given in Appendix 3. By the Routh–Hurwitz criterion for the 4th-degree polynomial, the given constraint has been verified if \(\mathcal{R}_{0} >1\). Therefore pneumonia existing equilibrium (\(\mathcal{P}_{n} {EE}- {D}_{2}\)) of system (1)–(4) is locally asymptotically stable. □
4 Global stability
The following theorems are presented for the system’s stability (1)–(4) in the global sense.
Theorem 4.1
The pneumonia trivial equilibrium (\(\mathcal{P}_{n} TE - D_{0}\)), \(D_{0} = ( S^{0}, C^{0}, I^{0}, R^{0} ) =(0,0,0,0)\) is globally asymptotically stable if \(\mathcal{R}_{0} =1\).
Proof
The Lyapunov function \(\Omega: \mathcal{H}\rightarrow \mathbb{{R}}\) is defined as follows:
Hence \(D_{0}\) is globally asymptotically stable. □
Theorem 4.2
The pneumonia-free equilibrium (\(\mathcal{P}_{n}\)FE-\(D_{1}\)), \(D_{1} = ( S^{1}, C^{1}, I^{1}, R^{1} ) = ( \frac{\Lambda }{\mu },0,0,0)\) is globally asymptotically stable if \(\mathcal{R}_{0} <1\).
Proof
Define the Lyapunov function \(U:\mathcal{H}\rightarrow \mathbb{{R}}\) as follows:
The detailed proof is given in Appendix 4. \(\frac{dU}{dt} \leq 0\) if \(\mathcal{R}_{0} <1\) and \(\frac{dU}{dt} =0\) if \(S = S^{1}, C =0, I =0 \text{ and } R =0\). Since by the Lassalle invariance principle \(D_{1}\) is the only unique trajectory of system (1)–(4), \(D_{1}\) is globally asymptotically stable. □
Theorem 4.3
The pneumonia existence equilibrium (\(\mathcal{P}_{n}\)EE-\(D_{2}\)), \(D_{2} = ( S^{*}, C^{*}, I^{*}, R^{*} )\) is globally asymptotically stable if \(\mathcal{R}_{0} >1\).
Proof
Define the Volterra–Lyapunov function V \(:\mathcal{H}\rightarrow \mathbb{{R}}\) as follows:
The detailed proof is given in Appendix 5. \(\frac{dV}{dt} \leq 0\) if \(\mathcal{R}_{0} >1\) and \(\frac{dV}{dt} =0\) if \(S = S^{*},{C}= C^{*}, {I}= I^{*} \text{and} R = R^{*}\). Since by the Lassalle invariance principle \(D_{2}\) is the unique trajectory of system (1)–(4), \(D_{2}\) is globally asymptotically stable. □
5 Sensitivity analysis
We use the derivative-based local methods for the sensitivity analysis to take the partial derivatives of outputs concerning inputs as presented in [51]. The study highlights the importance of transmission rates that can change dynamics from pneumonia-free to pneumonia existing.
After that, the conclusion from the results mentioned above is that \(\kappa, p,\Lambda, \theta, \omega, \psi,\sigma,\pi,\beta \) are sensitive and μ is not sensitive, as desired.
6 Numerical simulations and results
Numerical simulations are presented by using the command build code of MATLAB software like DDE’s-23. The parameters have been taken from the scientific literature, as shown in [11] (see Table 1).
Example 1
(Results on pneumonia-free equilibrium (\(\mathcal{P}_{n}\)EE-\(D_{1}\)) without delay)
Figure 2(a) to (d) shows the solution at the pneumonia-free equilibrium (\(\mathcal{P}_{n}\)EE-\(D_{1} \)), when \(\tau =0\), \(D_{1} = ( S^{1}, C^{1}, I^{1}, R^{1} ) = ( 1,0,0,0 )\) with the nonnegative initial data and parameters presented in Table 1. Therefore, the value of the reproduction number is \(R_{0}< 1\). Moreover, Fig. 2(e) shows the combined behaviour of the system.
Example 2
(Simulation on pneumonia existing equilibrium (\(\mathcal{P}_{n}\)EE-\(D_{2}\)) without delay)
Fig. 3(a) to (d) displays the solution of system (1)–(4) at the pneumonia existing equilibrium (\(\mathcal{P}_{n}\)EE-\(D_{2} \)), when \(\tau =0\), \(D_{2} = ( S^{*}, C^{*}, I^{*}, R^{*} ) = ( 0.8863,0.01776,0.0238,0.04692 )\). Therefore, the value of the reproduction number is \(R_{0} >1\). Moreover, Fig. 3(e) shows the combined behaviour of the system.
Example 3
(Results on pneumonia existing equilibrium)
In this section, we have taken the effect of system (1)–(4) with active practices of artificial delay tactics. Anti-pneumonia ability could be increased as observed in Fig. 4(a) to (d). On the other hand, we can keep the infectivity of pneumonia patients decreasing and even moving to zero.
Example 4
(Behavior of reproduction number with the efficiency of delay tactics)
In Fig. 5, let \(\tau =1,2,3\). As apparent, the value decreases, which changes the dynamics of the system of pneumonia disease from prevailing scenario to disease-free equilibrium.
Example 5
(Behavior of infective class at different values of the delay parameter)
Fig. 6 exhibits that with the increase in the value of the delayed parameter, the infectivity reduces gradually and is controlled.
Example 6
(D-simulations of the system)
2D graphics are widely used in animation, providing a realistic but flat view of movement on the screen. We plotted the two-dimensional performance of the model with different subclasses for a better interpretation of the dynamics of pneumonia disease, as presented in Fig. 7(a)–(b) and 8(a)–(b) with and without delay effect, respectively, as desired.
7 Conclusion
In this article, we investigated the mathematical analysis of pneumonia delayed epidemic models with reliable delay strategies. The model is based on four types of subpopulations like the susceptible, the carriers, the infected and the recovered. Dynamical analysis of the model includes positivity, boundedness, equilibria and threshold parameter. The sensitivity of the parameters is one of the outcomes of the model. Linearisation of the model is developed by well-known results like the Jacobian and Routh–Hurwitz criterion. Lyapunov theory and the Lassale invariance principle are investigated for the global stability of the model. The following artificial control measures could support the eradication of the disease in the population: the cleanness of hands, extensive use of fruits and vegetables, calm sleeping, staying away from smoking, vaccination to the children under five years and being aware of your general health.
Availability of data and materials
All data files are available.
References
Mochan, E., Swigon, D., Ermentrout, G., Luken, S., Clermont, G.A.: Mathematical model of intrahost pneumococcal pneumonia infection dynamics in murine strains. J. Theor. Biol. 353, 44–54 (2014)
Drusano, G.L., Liu, W., Fikes, S., Cirz, R., Robbins, N., Kurhanewicz, S., Louie, A.: Interaction of drug-and granulocyte-mediated killing of pseudomonas aeruginosa in a murine pneumonia model. J. Infect. Dis. 210(8), 1319–1324 (2014)
Ndelwa, E.J., Kgosimore, M., Massawe, E.S., Namkinga, L.: Mathematical modelling and analysis of treatment and screening of pneumonia. Math. Theory Model. 5(10), 21–39 (2015)
Kosasih, K., Abeyratne, U.R., Swarnkar, V., Triasih, R.: Wavelet augmented cough analysis for rapid childhood pneumonia diagnosis. IEEE Trans. Biomed. Eng. 62(4), 1185–1194 (2015)
César, A.C.G., Nascimento, L.F.C., Mantovani, K.C.C., Vieira, L.C.P.: Fine particulate matter estimated by mathematical model and hospitalisations for pneumonia and asthma in children. Rev. Paul. Pediatr. (Engl. Ed.) 34(1), 18–23 (2016)
Marchello, C., Dale, A.P., Thai, T.N., Han, D.S., Ebell, M.H.: Prevalence of atypical pathogens in patients with cough and community-acquired pneumonia: a meta-analysis. Ann. Fam. Med. 14(6), 552–566 (2016)
Cheng, Y.H., You, S.H., Lin, Y.J., Chen, S.C., Chen, W.Y., Chou, W.C., Liao, C.M.: Mathematical modeling of post coinfection with influenza A virus and Streptococcus pneumoniae, with implications for pneumonia and COPD-risk assessment. Int. J. Chronic Obstr. Pulm. Dis. 12, 1973–1988 (2017)
Kosasih, K., Abeyratne, U.: Exhaustive mathematical analysis of simple clinical measurements for childhood pneumonia diagnosis. World J. Pediatr. 13(5), 446–456 (2017)
Tilahun, G.T., Makinde, O.D., Malonza, D.: Modelling and optimal control of pneumonia disease with cost-effective strategies. J. Biol. Dyn. 11(2), 400–426 (2017)
Raj, M., Reddy, M., Mufeed, M., Karthika, S.: HMM based cough sound analysis for classifying asthma and pneumonia in paediatric population. Int. J. Pure Appl. Math. 118(18), 609–616 (2018)
Kizito, M., Tumwiine, J.: A mathematical model of treatment and vaccination interventions of pneumococcal pneumonia infection dynamics. J. Appl. Math. 2018, Article ID 2539465 (2018)
Mbabazi, F.K., Mugisha, J.Y.T., Kimathi, M.: Modeling the within-host coinfection of influenza A virus and pneumococcus. Appl. Math. Comput. 339, 488–506 (2018)
Tilahun, G.T., Makinde, O.D., Malonza, D.: Co-dynamics of pneumonia and typhoid fever diseases with cost-effective optimal control analysis. Appl. Math. Comput. 316, 438–459 (2018)
Tilahun, G.T.: Optimal control analysis of pneumonia and meningitis coinfection. Comput. Math. Methods Med. 2019, 1–15 (2019)
Diah, I.M., Aziz, N.: Stochastic modelling for pneumonia incidence: a conceptual framework. In: In AIP Conference Proceedings, vol. 1, pp. 1–3. AIP, New York (2019)
Tilahun, G.T.: Modeling co-dynamics of pneumonia and meningitis diseases. Adv. Differ. Equ. 2019(1), 1 (2019)
Mbabazi, F.K., Mugisha, J.Y., Kimathi, M.: Hopf-bifurcation analysis of pneumococcal pneumonia with time delays. Abstr. Appl. Anal. 2019(1), 1 (2019)
Otoo, D., Opoku, P., Charles, S., Kingsley, A.P.: Deterministic epidemic model for (SVCSyCAsyIR) pneumonia dynamics, with vaccination and temporal immunity. Infect. Dis. Model. 5, 42–60 (2020)
Zephaniah, O.C., Nwaugonma, U.I.R., Chioma, I.S., Adrew, O.: A mathematical model and analysis of an SVEIR model for streptococcus pneumonia with saturated incidence force of infection. Math. Model. Appl. 5(1), 16 (2020)
Ming, W.K., Huang, J., Zhang, C.J.: Breaking down of healthcare system: mathematical modelling for controlling the novel coronavirus (2019-nCoV) outbreak in Wuhan, China. BioRxiv 1, 1–18 (2020)
Jung, S.M., Kinoshita, R., Thompson, R.N., Linton, N.M., Yang, Y., Akhmetzhanov, A.R., Nishiura, H.: Epidemiological identification of a novel pathogen in real-time: analysis of the atypical pneumonia outbreak in Wuhan, China, 2019—2020. J. Clin. Med. 9(3), 1–18 (2020)
Kwambana-Adams, B.A., Mulholland, E.K., Satzke, C.: State-of-the-art in the pneumococcal field: proceedings of the 11th international symposium on pneumococci and pneumococcal diseases (ISPPD-11). Pneumonia 12(1), 1–14 (2020)
Ong’ala, J., Oleche, P., Mugisha, J.Y.T.: Mathematical model for pneumonia dynamics with carriers. Int. J. Math. Anal. 7(50), 2457–2473 (2013)
Minucci, S.B., Heise, R.L., Reynolds, A.M.: Review of mathematical modeling of the inflammatory response in lung infections and injuries. Frontiers Appl. Math. Stat. 1, 1–25 (2020)
Huttinger, E.D., Boon, N.J., Clarke, T.B., Tanaka, R.J.: Mathematical modeling of Streptococcus pneumonia colonisation, invasive infection and treatment. Front. Physiol. 1, 1–14 (2017)
Wafula, N.M., Kwach, B.O., Marani, V.N.: Mathematical modeling and optimal control for controlling pneumonia- HIV coinfection. Int. J. Innov. Res. Dev. 10(1), 138–144 (2021)
Ouwatobi, K.I., Erinle-Ibrahim, L.M.: Mathematical modeling of pneumonia dynamics of children under the age of five. Res. Square 1, 1–16 (2021)
Ahmad, N., Elsonbaty, A., Raza, A., Rafiq, M., Adel, W.: Numerical simulation and stability analysis of a novel reaction-diffusion Covid-19 model. Nonlinear Dyn. 23, 01 (2021)
Noor, M.A., Raza, A., Arif, M.S., Rafiq, M., Nisar, K.S., Khan, I.: Non-standard computational analysis of the stochastic Covid-19 pandemic model: an application of computational biology. Alex. Eng. J. 00, 01 (2021)
Ahmed, N., Raza, A., Rafiq, M., Ahmadian, A., Batool, N., Salahshour, S.: Numerical and bifurcation analysis of SIQR model. Chaos Solitons Fractals 150, 01 (2021)
Diaz, J.E.M., Raza, A., Ahmed, N., Rafiq, M.: Analysis of a nonstandard computer method to simulate a nonlinear stochastic epidemiological model of coronavirus-like diseases. Comput. Methods Programs Biomed. 204, 1–10 (2021)
Akgul, A., Iqbal, M.S., Fatima, U., Ahmed, N., Iqbal, Z., Raza, A., Rafiq, M., Rehman, M.A.: Optimal existence of fractional order computer virus epidemic model and numerical simulations. Math. Methods Appl. Sci. 7437, 01 (2021)
Akgul, A., Ahmed, N., Raza, A., Iqbal, Z., Rafiq, M., Rehman, M.A., Baleanu, D.: A fractal fractional model for cervical cancer due to human papillomavirus infection. Fractals 29(05), 01 (2021)
Fatima, U., Baleanu, D., Ahmed, N., Azam, S., Raza, A., Rafiq, M., Aziz-Ur-Rehman, M.: Numerical study of computer virus reaction-diffusion epidemic model. Comput. Mater. Continua 66(03), 3183–3194 (2021)
Raza, A., Ahmadian, A., Rafiq, M., Salahshour, S., Laganà, I.R.: An analysis of a nonlinear susceptible-exposed-infected-quarantine-recovered pandemic model of a novel coronavirus with delay effect. Results Phys. 21, 01 (2021)
Shatanawi, W., Raza, A., Arif, M.S., Rafiq, M., Bibi, M., Mohsin, M.: Essential features preserving dynamics of stochastic Dengue model. Comput. Model. Eng. Sci. 126(01), 201–215 (2021)
Raza, A., Fatima, U., Rafiq, M., Ahmed, N., Khan, I., Nisar, K.S., Iqbal, Z.: Mathematical analysis and design of the nonstandard computational method for an epidemic model of computer virus with delay effect: application of mathematical biology in computer science. Results Phys. 21, 01 (2021)
Iqbal, Z., Aziz-ur Rehman, M., Baleanu, D., Ahmed, N., Raza, A., Rafiq, M.: Mathematical and numerical investigations of the fractional-order epidemic model with constant vaccination strategy. Rom. Rep. Phys. 73, 112 (2021)
Raza, A., Ahmadian, A., Rafiq, M., Salahshour, S., Naveed, M., Ferrara, M., Soori, A.H.: Modeling the effect of delay strategy on transmission dynamics of HIV/AIDS disease. Adv. Differ. Equ. 663, 01 (2020)
Rafiq, M., Diaz, J.E.M., Raza, A., Ahmed, N.: Design and stability analysis of a nonlinear SEIQR infectious model and its efficient non-local computational implementation. Appl. Math. Model. 89, 1835–1846 (2021)
Shatanawi, W., Raza, A., Arif, M.S., Abodayeh, K., Rafiq, M., Bibi, M.: Design of nonstandard computational method for stochastic susceptible-infected-treated-recovered dynamics of coronavirus model. Adv. Differ. Equ. 2960, 01 (2020)
Shatanawi, W., Raza, A., Arif, M.S., Rafiq, M., Abodayeh, K., Bibi, M.: An effective numerical method for the solution of a stochastic coronavirus (2019-nCovid) pandemic model. Comput. Mater. Continua 66(02), 1121–1137 (2021)
Naveed, M., Baleanu, D., Rafiq, M., Raza, A., Soori, A.H., Ahmed, N.: Dynamical behavior and sensitivity analysis of a delayed coronavirus epidemic model. Comput. Mater. Continua 65(01), 225–241 (2020)
Raza, A., Rafiq, M., Ahmed, N., Khan, I., Nisar, K.S., Iqbal, Z.: A structure preserving numerical method for solution of stochastic epidemic model of smoking dynamics. Comput. Mater. Continua 65(01), 263–278 (2020)
Naveed, M., Rafiq, M., Raza, A., Ahmed, N., Khan, I., Nisar, K.S., Soori, A.H.: Mathematical analysis of novel coronavirus (2019-nCov) delay pandemic model. Comput. Mater. Continua 64(03), 1401–1414 (2020)
Arif, M.S., Raza, A., Abodayeh, K., Rafiq, M., Nazeer, A.: A numerical efficient technique for the solution of susceptible infected recovered epidemic model. Comput. Model. Eng. Sci. 124(02), 477–491 (2020)
Rafiq, M., Ahmadian, A., Raza, A., Baleanu, D., Ehsan, M.S., Sathar, M.H.A.: Numerical control measures of stochastic malaria epidemic model. Comput. Mater. Continua 65(01), 33–51 (2020)
Shatanawi, W., Arif, M.S., Raza, A., Rafiq, M., Bibi, M., Abbasi, J.N.: Structure-preserving dynamics of stochastic epidemic model with the saturated incidence rate. Comput. Mater. Continua 64(02), 797–811 (2020)
Lin, S.Y.: New results for generalised Gronwall inequality and their application. Abstr. Appl. Anal. 2014, Article ID 168594 (2014)
Driekmann, O., Heesterbeek, J.A.P., Roberts, M.G.: The construction of next-generation matrices for compartmental epidemic models. J. R. Soc. Interface 07(47), 873–885 (2009)
White, E., Comiskey, C.: Heroin epidemics, treatment and ODE modeling. Math. Biosci. 208(1), 312–324 (2007)
Acknowledgements
The authors thank the editor and referees for their valuable time and feedback.
Funding
No funding is available for this research project.
Author information
Authors and Affiliations
Contributions
All the authors contributed equally. All authors read and approved the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Appendices
Appendix 1
Consider \(\vert J_{\mathcal{P}_{n}} \vert _{{D}_{0}} - \lambda I \vert =0\)
By solving the above determinant, we have the negative eigenvalues
Appendix 2
Consider \(\vert J_{\mathcal{P}_{n}} \vert _{{D}_{1}} - \lambda I \vert =0\)
The eigenvalues at \({D}_{1}\) are as follows:
And the polynomial \(\lambda ^{2} + x_{1} \lambda + x_{0} =0\), where \(x_{1} = ( u_{1} + u_{2} ) [ 1- \frac{\theta \kappa p\omega \Lambda {e}^{-\mu \tau } + \kappa p\Lambda \theta _{1} {e}^{-\mu \tau }}{\mu ( u_{1} + u_{2} )} ]\), \(x_{0} = u_{1} u_{2} [ 1- \frac{\kappa p\Lambda \theta _{1} {e}^{-\mu \tau }}{\mu u_{2}} - \frac{\kappa p\Lambda {e}^{-\mu \tau }}{\mu } ( \frac{\omega u_{2} + \pi }{u_{1} u_{2}} ) ]\).
Appendix 3
Consider \(\vert J_{\mathcal{P}_{n}} \vert _{{D}_{2}} - \lambda I \vert =0\)
where \(g_{1} = \kappa p( {I}^{*} +\omega {C}^{*} ) {e}^{-\mu \tau } \), \(g_{2} =\kappa p\omega {S}^{*} {e}^{-\mu \tau } \), \(g_{3} = \kappa p{S}^{*} {e}^{-\mu \tau } \), \(g_{4} = \theta \kappa p( {I}^{*} + {C}^{*} ) {e}^{-\mu \tau } \), \(g_{5} =\theta \kappa p\omega {S}^{*} {e}^{-\mu \tau } \), \(g_{6} = \theta \kappa p{S}^{*} {e}^{-\mu \tau } \), \(g_{7} = \kappa p( {I}^{*} +\omega {C}^{*} ) \theta _{1} {e}^{-\mu \tau } \), \(g_{8} =\kappa p\omega {S}^{*} \theta _{1} {e}^{-\mu \tau } \), \(g_{9} = \kappa p{S}^{*} \theta _{1} {e}^{-\mu \tau } \).
After solving \(\vert J_{\mathcal{P}_{n}} \vert _{{D}_{2}} - \lambda I \vert =0 \), we have
where \(y_{3} = [ ( \mu +\eta ) - g_{5} + u_{1} - g_{9} + u_{2} + g_{1} + \mu ]\),
Appendix 4
Appendix 5
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Naveed, M., Baleanu, D., Raza, A. et al. Modeling the transmission dynamics of delayed pneumonia-like diseases with a sensitivity of parameters. Adv Differ Equ 2021, 468 (2021). https://doi.org/10.1186/s13662-021-03618-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-021-03618-z