1 Introduction

The natural convection heat transfer from a vertical plate to a fluid has implementations in many industrial processes. The investigators have applied different sets of thermal conditions at the bounding plate. Ganesan et al. [1] have described the solutions for velocity and temperature applying continuous and well-defined conditions at the wall. Samiulhaq et al. [2] have presented the influence of radiation and porosity on the unsteady magnetohydrodynamic (MHD) flow. Chandran et al. [3] have worked on the unsteady free convection flow of an incompressible viscous fluid near a vertical plate with ramped wall temperature. Seth et al. [4, 5] have obtained the exact solutions of the MHD natural convection flow.

Over the set of functions [6],

$$ A=\bigl\{ r(t) \mid \exists N, \tau _{1},\tau _{2}>0, \bigl| r(t) \bigr| < N \exp \bigl(| t | /\tau _{j}\bigr), \text{if } t \in (-1)^{j} \times [0, \infty ) \bigr\} , $$
(1)

the Sumudu transform is defined as

$$ R(u)=S\bigl[r(t)\bigr]= \int _{0}^{\infty }r(ut)\exp (-t)\,dt,\quad u \in (-\tau _{1}, \tau _{2}). $$
(2)

The Sumudu transform method (STM) was started with Watugala [7] when he researched the engineering control problems. The implementations of the Sumudu transform method of the partial differential equations have been discussed in the literature [8]. Weerakoon [9] has investigated a complex inversion formula for the Sumudu transform. This transformation was initially discussed to be a theoretical dual of the Laplace transform. The Sumudu transform has very valuable features in the implementations of sciences and engineering. This transform has been utilized to investigate many problems without resorting to a new frequency domain having scale and unit-preserving features. Integro-differential equations have been investigated by Sumudu transform in [10]. Watugala [11] has investigated the transform for two variables with the emphasis on solutions to partial differential equations. Belgacem et al. [12, 13] have discussed the convolution-type integral equations with the focus on production problems. For more details, see [14–18].

We construct our paper as follows: We present the mathematical modeling of the problem in Sect. 2. We discuss the solution of the problem in Sect. 3. We give an alternative method in Sect. 4. We present the discussion in Sect. 5. We give the conclusion in the last section.

2 Mathematical modeling

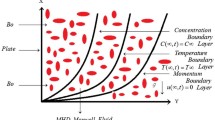
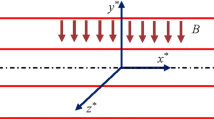
Let us assume that the unsteady MHD, natural convection, time dependent, incompressible viscous flow of second grade fluid near an infinite vertical plate is embedded in a porous medium with ramped wall temperature. In this case, we consider the Cartesian coordinate system. The plate is placed in the \((x , y)\) plane with x-axis oriented vertically and the y-axis in the normal direction. At the end of the wall, velocity and temperature are time dependent with certain limits of time identified as the characteristic time; velocity and temperature after that time attain constant values \(V_{0}\) and \(T_{\infty }\), respectively. The fundamental governing partial differential equations with small Reynolds number and usual Boussinesq’s approximation are given as [19–22]:

$$\begin{aligned}& \begin{aligned}[b] \frac{\partial {V(y,t)}}{\partial {t}}&=\upsilon \biggl(1+ \frac{\alpha _{1}}{\mu } \frac{\partial }{\partial {t}} \biggr) \frac{\partial ^{2}{V(y,t)}}{\partial {y}^{2}} +g\beta \bigl(T(y,t)-T_{ \infty } \bigr) \\ &\quad {}- \biggl[ \frac{{\sigma _{0}}M_{0}^{2}}{\rho }+ \frac{\upsilon \phi }{k_{0}} \biggl(1+ \frac{\alpha _{1}}{\mu } \frac{\partial }{\partial {t}} \biggr) \biggr] V(y,t), \end{aligned} \end{aligned}$$
(3)
$$\begin{aligned}& \frac{\partial {T(y,t)}}{\partial {t}}=\frac{k}{{\rho }{C_{p}}} \biggl(1+ \frac{16\sigma _{1}T_{\infty }^{3}}{3kK_{1}} \biggr) \frac{\partial ^{2}{T(y,t)}}{\partial {y}^{2}}, \end{aligned}$$
(4)

where \(V(y,t)\), \(T(y,t)\), ρ, υ, \(\alpha _{1}\), \(\beta _{T}\), g, k, and \(C_{p}\) denote the fluid velocity, temperature of the fluid, density, kinematic viscosity, second grade parameter, coefficient of volumetric thermal expansion, gravitational acceleration, thermal conductivity, and heat capacity at constant pressure, respectively.

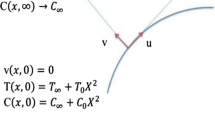
The appropriate initial and boundary conditions are presented as:

$$\begin{aligned}& V(y,0)=0, \qquad T(y,0)=T_{\infty },\qquad \frac{\partial {V(y,0)}}{\partial {t}} =0,\quad y \geq 0, \end{aligned}$$
(5)
$$\begin{aligned}& V(0,t)={f_{1}(t)},\qquad T(0,t)={f_{2}(t)}, \end{aligned}$$
(6)

where

$$\begin{aligned}& {f_{1}(t)}= \textstyle\begin{cases} V_{0}\frac{t}{t_{0}}, & 0< t\leq {t_{0}}, \\ V_{0}, & t>t_{0}, \end{cases}\displaystyle \quad \text{and}\quad {f_{2}(t)}= \textstyle\begin{cases} T_{\infty }+(T_{w}-T_{\infty })\frac{t}{t_{0}}, & 0< t\leq {t_{0}}, \\ T(0,t)=T_{w}, & t>t_{0}, \end{cases}\displaystyle \end{aligned}$$
(7)
$$\begin{aligned}& V(y,t)\to {0} ,\qquad T(y,t)\to {\infty },\quad \text{as } y \to { \infty }. \end{aligned}$$
(8)

Introducing the following dimensionless variables:

$$\begin{aligned}& \psi =\frac{V_{0}}{\upsilon }y,\qquad t^{\ast }= \frac{V_{0}^{2}}{\upsilon }t, \qquad V^{\ast }=\frac{V}{V_{0}}, \qquad \theta = \frac{T-T_{\infty }}{T_{w}-T_{\infty }}, \qquad G_{r}= \frac{g\beta t_{0}(T-T_{\infty })}{V_{0}^{3}}, \\& Nr =\frac{16\sigma _{1}T_{\infty }^{3}}{3kK_{1}}, \qquad M= \frac{{\sigma _{0}}M_{0}^{2}\upsilon }{{\rho }V_{0}^{2}},\qquad \mathit{Pr} = \frac{\upsilon {C_{p}}}{k},\qquad P{r_{0}}=\frac{\mathit{Pr} }{1+Nr}, \\& \alpha =\frac{{\alpha _{1}}{\rho }{V_{0}^{2}}}{\mu ^{2}},\qquad \frac{1}{K}=\frac{{\upsilon ^{2}}\phi }{k_{0}{V_{0}^{2}}}, \qquad a= M+ \frac{1}{K},\qquad b=\frac{\alpha }{K}, \end{aligned}$$

and removing the star notation, the required dimensionless momentum and energy equations are obtained as:

$$\begin{aligned}& \frac{\partial {V(\psi ,t)}}{\partial {t}} = \frac{\partial ^{2}{V(\psi ,t)}}{\partial {\psi }^{2}} +G_{r}\theta ( \psi ,t)-aV(\psi ,t)-b\frac{\partial {V(\psi ,t)}}{\partial {t}} + \alpha \frac{\partial ^{3}{V(\psi ,t)}}{{\partial {t}}\partial {\psi ^{2}}}, \end{aligned}$$
(9)
$$\begin{aligned}& \frac{\partial {\theta (\psi ,t)}}{\partial {t}} =\frac{1}{\mathit{Pr} _{0}} \frac{\partial ^{2}{\theta (\psi ,t)}}{\partial {\psi }^{2}}, \end{aligned}$$
(10)

and the corresponding initial and boundary conditions are presented as

$$\begin{aligned}& V(\psi ,0)=0, \qquad \theta (\psi ,0)=0,\qquad \frac{\partial {V(\psi ,t)}}{\partial {t}}{\bigg|}_{t=0}=0, \end{aligned}$$
(11)
$$\begin{aligned}& V(0,t)=f(t), \qquad \theta (0,t)=f(t), \quad \text{where } f(t)= \textstyle\begin{cases} t,& 0< t\leq 1, \\ 1,& t>1, \end{cases}\displaystyle \end{aligned}$$
(12)
$$\begin{aligned}& V(\psi ,t)\rightarrow 0, \qquad \theta (\psi ,t)\rightarrow 0\quad \text{as } \psi \rightarrow \infty . \end{aligned}$$
(13)

Also, a new version of Sumudu transform definition in modified form due to Watugala [7] is presented as

$$ R(u)=\mathbb{S}\bigl[r(t)\bigr]= \int _{0}^{\infty }\frac{r(t)e^{-\frac{t}{u}}}{u}\,dt. $$
(14)

Theorem 1

([14])

If \(R(u)\) is the Sumudu transform of \(r(t)\), then the Sumudu transform of the derivatives with integer order is as follows:

$$ \mathbb{S} \biggl[\frac{d^{n}r(t)}{dt^{n}} \biggr] = u^{-n} \Biggl[ R(u)- \sum_{\eta =0}^{n-1}u^{\eta } \frac{d^{n}r(t)}{dt^{n}} \bigg|_{t=0} \Biggr]. $$
(15)

Proof

The Sumudu transform of the first derivative of \(r(t)\), \(r'(t)=dr(t)/dt\), is given by

$$\begin{aligned} \mathbb{S} \biggl[\frac{dr(t)}{dt} \biggr] & = \int _{0}^{\infty }e^{-t} \frac{dr(ut)}{dt}\,dt= \lim_{\xi \to \infty } \int _{0}^{\xi }e^{-t} \frac{dr(ut)}{dt}\,dt \\ &= \lim_{\xi \to \infty } \biggl[ \frac{1}{u}e^{-\frac{t}{u}}r(t)\bigg|_{0}^{ \xi }+ \frac{1}{u^{2}} \int _{0}^{\xi }e^{-\frac{t}{u}}r(t)\,dt \biggr] \\ & = \lim_{\xi \to \infty } \biggl[ \frac{1}{u}e^{-\frac{t}{u}}r(t) \bigg\lvert _{0}^{\xi }+ \frac{1}{u} \biggl( \frac{1}{u} \int _{0}^{\xi }e^{- \frac{t}{u}}r(t)\,dt \biggr) \biggr] \\ & = \lim_{\xi \to \infty } \biggl[- \frac{1}{u}r(0)+ \frac{1}{u} \biggl( \frac{1}{u} \int _{0}^{\xi }e^{-\frac{t}{u}}r(t)\,dt \biggr) \biggr] \\ & = - \frac{1}{u}r(0) + \frac{1}{u}R(u). \end{aligned}$$
(16)

To get the Sumudu transformation for the second order derivative of the function \(r(t)\), proceeding in the same way, we obtain

$$ \mathbb{S} \biggl[\frac{d^{2}r(t)}{dt^{2}} \biggr] = \frac{1}{u^{2}} \biggl[ R(u)-r(0) -u \frac{dr(t)}{dt}\bigg|_{t=0} \biggr]. $$
(17)

To derive the general formula from this theorem for Sumudu transform of any integer order n, using mathematical induction, we get

$$ \mathbb{S} \biggl[\frac{d^{n}r(t)}{dt^{n}} \biggr] = u^{-n} \Biggl[ R(u)- \sum_{\eta =0}^{n-1}u^{\eta } \frac{d^{n}r(t)}{dt^{n}}\bigg|_{t=0} \Biggr] $$
(18)

which completes the proof. □

Next, defined for \(\operatorname{Re}(s)>0\), the Laplace transform for the function \(r(t)\) is given by

$$ F(s)=\mathcal{L}\bigl[r(t)\bigr]= \int _{0}^{\infty }e^{-st}r(t)\,dt. $$
(19)

In consideration of the definition in Eq. (14), the Laplace and Sumudu transforms exhibit a duality relation which is expressed in the following way:

$$ R\biggl(\frac{1}{s}\biggr)=sF(s),\qquad F\biggl( \frac{1}{u}\biggr)= u R(u), $$
(20)

which referred as Sumudu–Laplace duality and illustrates the fact that Laplace and Sumudu transformations interchange the images of Heaviside function \(H(t)\) and Dirac function \(\delta (t)\), since

$$ \mathcal{L}\bigl[\delta (t)\bigr]=\mathbb{S}\bigl[H(t)\bigr]=1,\qquad \mathcal{L}\bigl[H(t)\bigr]= \mathbb{S}\bigl[\delta (t)\bigr]= \frac{1}{u}. $$
(21)

Similarly, for the functions \(\cos (t)\) and \(\sin (t)\), we have

$$ \mathcal{L}\bigl[\sin (t)\bigr]=\mathbb{S}\bigl[\cos (t)\bigr]= \frac{1}{1+u^{2}}, \qquad \mathcal{L}\bigl[\cos (t)\bigr]=\mathbb{S}\bigl[\sin (t) \bigr]=\frac{u}{1+u^{2}}, $$
(22)

which is also consistent for the established result in Theorem 1 and integration formulas:

$$\begin{aligned}& \mathbb{S} \bigl[r'(t) \bigr]= \frac{\mathbb{S}[r(t)]-r(0)}{u}, \end{aligned}$$
(23)
$$\begin{aligned}& \mathbb{S} \biggl[ \int _{0}^{t} r(\tau ) \,d\tau \biggr]=u \mathbb{S}\bigl[r(t)\bigr]. \end{aligned}$$
(24)

The next theorem is very helpful for finding the solution of differential equations involving multiple integrals by using Sumudu transformation efficiently.

Theorem 2

([13])

Let \(r(t)\) be in A. The Sumudu transform \(R^{n}(u)\) of the nth antiderivative of \(r(t)\), obtained by n times successively integrating the function \(r(t)\),

$$ G^{n}(t)= \int \int _{0}^{t}\dots \int _{0}^{t}r(\tau ) (d \tau )^{n}, $$
(25)

can be obtained, for \(n \geq 1\), as

$$ R^{n}(u)=\mathbb{S}\bigl(G^{n}(t) \bigr)=u^{n}R(u). $$
(26)

Proof

For \(n=1\), Eq. (26) holds due to Eq. (24). To prove this theorem by induction, suppose that Eq. (26) holds for some n, and we prove it also holds for \(n+1\). Again using Eq. (24), we have

$$ R^{n+1}(u)=\mathbb{S}\bigl(G^{n+1}(t) \bigr)=\mathbb{S} \biggl[ \int _{0}^{t}G^{n}( \tau )\,d\tau \biggr]=u\mathbb{S}\bigl(G^{n}(t)\bigr)=u \bigl[ u^{n}R(u) \bigr] =u^{n+1}R(u). $$
(27)

This theorem generalizes the Sumudu convolution Theorem 4.1 as presented in Belgacem et al. [12], which states that the convolution of two functions g and h, defined as

$$ (g \star h) (t)= \int _{0}^{t}g(\tau )h(t-\tau )\,d\tau , $$
(28)

has its Sumudu transformation given by

$$ \mathbb{S} \bigl( (g \star h) (t) \bigr)=uG(u)H(u). $$
(29)

Similarly, the Sumudu transform of \((h_{1} \star h_{2} \star h_{3})\), with \(h_{1}\), \(h_{2}\), \(h_{3}\) in A, is given by

$$ \mathbb{S} \bigl( (h_{1} \star h_{2} \star h_{3}) (t) \bigr)=u^{2}H_{1}(u)H_{2}(u)H_{3}(u). $$
(30)

 □

3 Solution of the problem

In this section, the Sumudu transformation method is used to get the solution of the considered problem.

3.1 Exact solution of heat profile by Sumudu transformation

Theorem 3

Let \(\mathbb{S}\) be the Sumudu operator. Applying this operator on equation (10), along with initial and boundary conditions (11), (12) and (13), the exact solution of heat profile is

$$ {\theta }(\psi ,{t})={\theta }_{1}(\psi ,{t})-{\theta }_{2}(\psi ,{t}). $$

where

$$\begin{aligned} &{\theta }_{1}(\psi ,{t})=\mathbb{S}^{-1} \bigl(ue^{-\frac{a_{0}}{\sqrt{u}}}\bigr)= \int _{0}^{\tau }f(t)\,d(t) \quad \textit{with } f(t)= \operatorname{erfc}\biggl( \frac{a_{0}}{2\sqrt{t}}\biggr), a_{0}= \sqrt{P_{r_{0}}}\psi , \\ &{\theta }_{2}(\psi ,{t})={\theta }_{1}(\psi ,{\tau }-1)H({\tau }-1). \end{aligned}$$

Proof

Applying the Sumudu transformation technique to get the solution of Eq. (10) and taking into consideration Eq. (18) with given boundary conditions yields

$$ \frac{d^{2}{\bar{ \theta }(\psi ,u)}}{d{\psi }^{2}}- \frac{P_{r_{0}}}{u}{\bar{\theta }( \psi ,u)}=0, $$
(31)

with

$$ {\bar{\theta }(\psi ,u)}\rightarrow 0,\quad \text{as } \psi \rightarrow \infty \quad \text{and}\quad {\bar{\theta }(0,u)}=u\bigl(1-e^{-\frac{1}{u}}\bigr), $$

and its solution is given by

$$ \bar{\theta }(\psi ,u)=u\bigl(1-e^{-\frac{1}{u}}\bigr) e^{-\psi \sqrt{ \frac{P_{r_{0}}}{u}}}. $$
(32)

Further, it can be written as

$$ \bar{\theta }(\psi ,u)=\bigl(ue^{-\frac{a_{0}}{\sqrt{u}}} \bigr)-e^{-\frac{1}{u}} \bigl(ue^{-\frac{a_{0}}{\sqrt{u}}}\bigr),\quad \text{where } a_{0}= \sqrt{P_{r_{0}}} \psi . $$
(33)

Applying the Sumudu inverse transformation gives the solution

$$ {\theta }(\psi ,{t})={\theta }_{1}(\psi ,{t})-{ \theta }_{2}(\psi ,{t}), $$
(34)

where

$$\begin{aligned} &{\theta }_{1}(\psi ,{t})=\mathbb{S}^{-1} \bigl(ue^{-\frac{a_{0}}{\sqrt{u}}}\bigr)= \int _{0}^{\tau }f(t)\,d(t) \quad \text{and}\quad f(t)= \operatorname{erfc}\biggl( \frac{a_{0}}{2\sqrt{t}}\biggr), \end{aligned}$$
(35)
$$\begin{aligned} &{\theta }_{2}(\psi ,{t})={\theta }_{1}(\psi ,{\tau }-1)H({\tau }-1). \end{aligned}$$
(36)

 □

3.2 Exact solution of heat profile by Laplace transformation

Theorem 4

Let \(\mathscr{L}\) be the Laplace operator. Applying this operator on equation (10), along with initial and boundary conditions (11), (12), and (13), the exact solution of heat profile is

$$ {\theta }(\psi ,t)= {\theta }_{r}(\psi ,t)-{\theta }_{r}(\psi ,\tau _{0})H( \tau _{0}), $$

where

$$ {\theta }_{r}(\psi ,t)= \biggl(\frac{\mathit{Pr} _{0}}{2}{\psi }^{2}+t \biggr) \operatorname{erfc} \biggl(\sqrt{\frac{\mathit{Pr} _{0}}{4t}} { \psi } \biggr)- \biggl(\sqrt{ \frac{\mathit{Pr} _{0}t}{\pi }} {\psi } \biggr) e^{\frac{-\mathit{Pr} _{0}{\psi }^{2}}{4t}} $$

and \(H(\tau _{0})\) represents a standard Heaviside function with \(\tau _{0}=t -1\).

Proof

Applying Laplace transformation to get the solution of Eq. (10) and using appropriate boundary conditions yields

$$ \frac{\partial ^{2}{\bar{ \theta }(\psi ,m)}}{\partial {\psi }^{2}}-mPr_{0}{ \bar{\theta }(\psi ,m)}=0. $$
(37)

The solution of above differential equation (37) is obtained as

$$ \bar{\theta }(\psi ,m)= c_{1} e^{\psi \sqrt{mPr_{0}}} + c_{2} e^{- \psi \sqrt{mPr_{0}}}. $$
(38)

Applying the conditions to find unknowns \(c_{1}\) and \(c_{2}\) yields

$$ {\bar{\theta }(\psi ,m)}\rightarrow 0 \quad \text{as } \psi \rightarrow \infty \quad \text{and}\quad {\bar{\theta }(0,m)}= \biggl( \frac{1-e^{-m}}{m^{2}} \biggr). $$

We get

$$\begin{aligned}& \bar{\theta }(\psi ,m)= \biggl(\frac{1-e^{-m}}{m^{2}} \biggr) e^{- \psi \sqrt{mPr_{0}}}, \end{aligned}$$
(39)
$$\begin{aligned}& \bar{\theta }(\psi ,m) = \biggl( \frac{e^{-\psi \sqrt{mPr_{0}}}}{m^{2}} \biggr)-{e^{-m}} \biggl( \frac{e^{-\psi \sqrt{mPr_{0}}}}{m^{2}} \biggr)=\bar{\theta }_{r}(\psi ,m)-e^{-m} \bar{\theta }_{r}( \psi ,m). \end{aligned}$$
(40)

After applying inverse Laplace transformation on Eq. (40), we get

$$\begin{aligned}& {\theta }(\psi ,t)= {\theta }_{r}(\psi ,t)-{\theta }_{r}(\psi ,\tau _{0})H( \tau _{0}), \end{aligned}$$
(41)
$$\begin{aligned}& {\theta }_{r}(\psi ,t)= \biggl( \frac{\mathit{Pr} _{0}}{2}{\psi }^{2}+t \biggr) \operatorname{erfc} \biggl(\sqrt{ \frac{\mathit{Pr} _{0}}{4t}} {\psi } \biggr)- \biggl(\sqrt{ \frac{\mathit{Pr} _{0}t}{\pi }} {\psi } \biggr)e^{\frac{-\mathit{Pr} _{0}{\psi }^{2}}{4t}}, \end{aligned}$$
(42)

where \(H(\tau _{0})\) represents a standard Heaviside function with \(\tau _{0}=t -1\). □

3.3 Solution of velocity profile

Theorem 5

Let \(\mathbb{S}\) be the Sumudu operator. Applying this operator on equation (9), along with initial and boundary conditions (11), (12), and (13), the exact solution of velocity profile is given in equation (62).

Proof

The solution of Eq. (9) by using Sumudu transformation is obtained from

$$ \biggl(1+\frac{\alpha }{u} \biggr) \frac{d^{2}\bar{V}(\psi ,u)}{d{\psi }^{2}} - \biggl(\frac{1}{u}+a+ \frac{b}{u} \biggr)\bar{V}(\psi ,u)=- G_{r}{\bar{\theta } (\psi ,u )}. $$
(43)

Its general solution can be written as

$$ \bar{V} (\psi ,u ) =c_{1}e^{\psi \sqrt{ \frac{au + 1+b}{u + {\alpha }}}}+c_{2}e^{-\psi \sqrt{ \frac{au + 1+b}{u + {\alpha }}}}- \biggl( \frac{G_{r}u^{3}(1-e^{-\frac{1}{u}}) e^{-\psi \sqrt{\frac{P_{r0}}{u}}}}{(u+\alpha )P_{r_{0}}-u(au+1+b)} \biggr). $$
(44)

Since \({\bar{V}(\psi ,u)}\rightarrow 0\) as \(\psi \rightarrow \infty \) and \({\bar{V}(0,u)}=u(1-e^{-\frac{1}{u}})\), we get

$$\begin{aligned}& \begin{aligned}[b] \bar{V} (\psi ,u )={}& u\bigl(1-e^{-\frac{1}{u}}\bigr)e^{-\psi \sqrt{ \frac{au + 1+b}{u + {\alpha }}}} \\ &{}+ \frac{G_{r}u^{3}(1-e^{-\frac{1}{u}}) }{(u+\alpha )P_{r_{0}}-u(au+1+b)} \bigl[ e^{-\psi \sqrt{\frac{au + 1+b}{u + {\alpha }}}}-e^{-\psi \sqrt{ \frac{P_{r_{0}}}{u}}} \bigr], \end{aligned} \end{aligned}$$
(45)
$$\begin{aligned}& \bar{V} (\psi ,u )= \bar{v}_{1} (\psi ,u )+ \bar{v}_{2} (\psi ,u ). \end{aligned}$$
(46)

Applying Sumudu inverse transformation gives

$$ V(\psi ,t)= \mathbb{S}^{-1} \bigl( \bar{V} (\psi ,u ) \bigr)= \mathbb{S}^{-1} \bigl( \bar{v}_{1} (\psi ,u ) \bigr) + \mathbb{S}^{-1} \bigl(\bar{v}_{2} (\psi ,u ) \bigr), $$
(47)

where

$$\begin{aligned} &\bar{v}_{1} (\psi ,u )= u\bigl(1-e^{-\frac{1}{u}} \bigr)e^{-\psi \sqrt{\frac{au + c}{u + {\alpha }}}},\quad c=1+b, \end{aligned}$$
(48)
$$\begin{aligned} &\bar{v}_{2} (\psi ,u )= \frac{G_{r}u^{3}(1-e^{-\frac{1}{u}}) }{(u+\alpha )P_{r_{0}}-u(au+c)} \bigl[ e^{-\psi \sqrt{\frac{au + c}{u + {\alpha }}}}-e^{-\psi \sqrt{ \frac{P_{r_{0}}}{u}}} \bigr], \end{aligned}$$
(49)
$$\begin{aligned} & \bar{v}_{1} (\psi ,u )=\bar{v}_{11} (\psi ,u )- \bar{v}_{12} (\psi ,u ) , \end{aligned}$$
(50)
$$\begin{aligned} &\mathbb{S}^{-1} \bigl( \bar{v}_{1} (\psi ,u ) \bigr)={v}_{11} (\psi ,t )-{v}_{12} (\psi ,t ), \end{aligned}$$
(51)

where ∗ denotes the convolution. Then, we have

$$\begin{aligned}& {v}_{11} (\psi ,t ) =\mathbb{S}^{-1} \bigl(ue^{-\psi \sqrt{ \frac{au + c}{u + {\alpha }}}}\bigr)= \int _{0}^{t} f_{2}(\tau )\,d\tau , \end{aligned}$$
(52)
$$\begin{aligned}& {v}_{12} (\psi ,t ) =\mathbb{S}^{-1} \bigl[ e^{ \frac{-1}{u}}\bigl(ue^{-\psi \sqrt{\frac{au + c}{u + {\alpha }}}}\bigr) \bigr] \end{aligned}$$
(53)
$$\begin{aligned}& \hphantom{{v}_{12} (\psi ,t )} ={v}_{11} (\psi ,t-1 )H(t-1), \end{aligned}$$
(54)
$$\begin{aligned}& F_{2}(u) = e^{-\psi \sqrt{\frac{au + c}{u + {\alpha }}}}. \end{aligned}$$
(55)

It is complicated to find the Sumudu inverse of \(F_{2}(u)\) in exponential form, so we have to express it in its equivalent form as

$$ \begin{aligned} &F_{2}(u)=\sum_{n_{1}=0}^{\infty }\sum _{n_{2}=0}^{\infty }\sum _{n_{3}=0}^{ \infty } \frac{(-1)^{n_{3}}a^{\frac{n_{1}}{2}-n_{2}}(-\psi )^{n_{1}}d^{n_{2}}\Gamma ({\frac{n_{1}}{2}+1)}\Gamma {(n_{2} + n_{3})}}{n_{1}{!}n_{2}{!}n_{3}{!}(\alpha )^{n_{2} +n_{3}}\Gamma ({\frac{n_{1}}{2}+1-n_{2})}\Gamma {(n_{2})}}u^{n_{3}} , \quad \text{and} \\ &d=c-a \alpha . \end{aligned} $$
(56)

Applying Sumudu inverse transformation gives

$$\begin{aligned}& f_{2}(t) =\mathbb{S}^{-1}\bigl(F_{2}(u) \bigr)=\sum_{n_{1}=0}^{\infty }\sum _{n_{2}=0}^{ \infty }\sum_{n_{3}=0}^{\infty } \frac{(-1)^{n_{3}}a^{\frac{n_{1}}{2}-n_{2}}(-\psi )^{n_{1}}d^{n_{2}}\Gamma ({\frac{n_{1}}{2}+1)}\Gamma {(n_{2} + n_{3})}}{n_{1}{!}n_{2}{!}(n_{3}{!})^{2}(\alpha )^{n_{2} +n_{3}}\Gamma ({\frac{n_{1}}{2}+1-n_{2})}\Gamma {(n_{2})}}t^{n_{3}} , \end{aligned}$$
(57)
$$\begin{aligned}& \bar{v}_{2} ( \psi ,u ) =\frac{Gr}{a}u \biggl[ -1+ \frac{D}{1-a_{2} u}+\frac{E}{1+b_{2} u} \biggr]\bigl(1-e^{-\frac{1}{u}} \bigr) \bigl[ e^{-\psi \sqrt{\frac{au + c}{u + {\alpha }}}}-e^{-\psi \sqrt{ \frac{P_{r_{0}}}{u}}} \bigr] , \end{aligned}$$
(58)
$$\begin{aligned}& \bar{v}_{2} ( \psi ,u ) =\frac{Gr}{a}u \bigl[ -1+DF_{3}(u)+EF_{4}(u) \bigr]\bigl(1-e^{-\frac{1}{u}} \bigr) \bigl[F_{2}(u)-F_{1}(u) \bigr], \end{aligned}$$
(59)
$$\begin{aligned}& \bar{v}_{2} ( \psi ,u ) =\frac{Gr}{a} \bigl[-uF_{2}(u)+uF_{1}(u)+e^{- \frac{1}{u}} \bigl(uF_{2}(u)\bigr) -e^{-\frac{1}{u}}\bigl(uF_{1}(u) \bigr) \bigr] \\& \hphantom{\bar{v}_{2} ( \psi ,u ) ={}}{} +\frac{GrD}{a} \bigl[uF_{2}(u)F_{3}(u)-uF_{1}(u)F_{3}(u) \\& \hphantom{\bar{v}_{2} ( \psi ,u ) ={}}{}-e^{- \frac{1}{u}} \bigl(uF_{2}(u)F_{3}(u)\bigr)+e^{-\frac{1}{u}} \bigl(uF_{1}(u)F_{3}(u)\bigr) \bigr] \\& \hphantom{\bar{v}_{2} ( \psi ,u ) ={}}{} +\frac{GrE}{a} \bigl[uF_{2}(u)F_{4}(u)-uF_{1}(u)F_{4}(u) \\& \hphantom{\bar{v}_{2} ( \psi ,u ) ={}}{}-e^{- \frac{1}{u}} \bigl(uF_{2}(u)F_{4}(u)\bigr)+e^{-\frac{1}{u}} \bigl(uF_{1}(u)F_{4}(u)\bigr) \bigr], \end{aligned}$$
(60)

with

$$\begin{aligned}& j =\frac{P_{r_{0}}-c}{a}, \qquad r=\frac{\alpha P_{r_{0}}}{a},\qquad g= \frac{j}{2}, \qquad h= \sqrt{r+g^{2}},\qquad a_{2}=\frac{1}{h+g}, \\& b_{2} =\frac{1}{h-g}, \qquad D= \frac{a_{2} r+j}{(a_{2}+b_{2})(h^{2}-g^{2})},\qquad E= \frac{b_{2} r-j}{(a_{2}+b_{2})(h^{2}-g^{2})}, \\& F_{1}(u) =e^{-\psi \sqrt{\frac{P_{r_{0}}}{u}}}, \qquad F_{2}(u)=e^{- \psi \sqrt{\frac{au + c}{u + {\alpha }}}}, \\& F_{3}(u)= \frac{1}{1-a_{2}u},\qquad F_{4}(u)= \frac{1}{1+b_{2}u}. \end{aligned}$$
(61)

After applying the Sumudu inverse transformation, we obtain

$$\begin{aligned} v_{2}(\psi ,t) =&\frac{Gr}{a} \bigl[-\Phi _{1}(\psi ,t) +\Phi _{2}( \psi ,t)+\Phi _{1}(\psi ,t-1)H(t-1) -\Phi _{2}(\psi ,t-1)H(t-1) \bigr] \\ &{} +\frac{GrD}{a} \bigl[\Phi _{3}(\psi ,t) -\Phi _{4}(\psi ,t)- \Phi _{3}(\psi ,t-1)H(t-1) \\ &{}+\Phi _{4}(\psi ,t-1)H(t-1) \bigr] \\ &{} +\frac{GrE}{a} \bigl[\Phi _{5}(\psi ,t) -\Phi _{6}(\psi ,t)- \Phi _{5}(\psi ,t-1)H(t-1) \\ &{}+\Phi _{6}(\psi ,t-1)H(t-1) \bigr], \end{aligned}$$
(62)

where

$$\begin{aligned}& \Phi _{1}(\psi ,t) = \int _{0}^{t} f_{2}(\tau )\,d(\tau ), \end{aligned}$$
(63)
$$\begin{aligned}& \Phi _{2}(\psi ,t) = \int _{0}^{t} f_{1}(\tau )\,d(\tau ), \end{aligned}$$
(64)
$$\begin{aligned}& \Phi _{3}(\psi ,t) =(f_{2} \ast f_{3}) (t)= \int _{0}^{t} f_{2}(\tau )f_{3}(t- \tau )\,d(\tau ), \end{aligned}$$
(65)
$$\begin{aligned}& \Phi _{4}(\psi ,t) =(f_{1} \ast f_{3}) (t)= \int _{0}^{t} f_{1}(\tau )f_{3}(t- \tau )\,d(\tau ), \end{aligned}$$
(66)
$$\begin{aligned}& \Phi _{5}(\psi ,t) =(f_{2} \ast f_{4}) (t)= \int _{0}^{t} f_{2}(\tau )f_{4}(t- \tau )\,d(\tau ), \end{aligned}$$
(67)
$$\begin{aligned}& \Phi _{6}(\psi ,t) =(f_{1} \ast f_{4}) (t)= \int _{0}^{t} f_{1}(\tau )f_{4}(t- \tau )\,d(\tau ), \end{aligned}$$
(68)
$$\begin{aligned}& f_{1}(t) =\operatorname{erfc}\biggl( \frac{a_{1}}{2\sqrt{t}}\biggr), \quad \text{with } a_{1}= \sqrt{P_{r_{0}}}\psi , \end{aligned}$$
(69)
$$\begin{aligned}& f_{2}(t) =\sum_{n_{1}=0}^{\infty } \sum_{n_{2}=0}^{\infty }\sum _{n_{3}=0}^{ \infty } \frac{(-1)^{n_{3}}a^{\frac{n_{1}}{2}-n_{2}}(-\psi )^{n_{1}}d^{n_{2}} \Gamma ({\frac{n_{1}}{2}+1)}\Gamma {(n_{2} + n_{3})}}{n_{1}{!}n_{2}{!}(n_{3}{!})^{2}(\alpha )^{n_{2} +n_{3}}\Gamma ({\frac{n_{1}}{2}+1-n_{2})}\Gamma {(n_{2})}}t^{n_{3}} , \end{aligned}$$
(70)
$$\begin{aligned}& f_{3}(t) =e^{a_{2}t}, \end{aligned}$$
(71)
$$\begin{aligned}& f_{4}(t) =e^{-b_{2}t}. \end{aligned}$$
(72)

 □

4 Alternative method to calculate \(\bar{v}_{2} ( \psi ,u )\) by using discrete convolution (the Cauchy product)

$$\begin{aligned}& \bar{v}_{2} (\psi ,u ) = \frac{G_{r}u^{3}(1-e^{-\frac{1}{u}}) }{(u+\alpha )P_{r_{0}}-u(au+c)} \bigl[ e^{-\psi \sqrt{\frac{au + c}{u + {\alpha }}}}-e^{-\psi \sqrt{ \frac{P_{r_{0}}}{u}}} \bigr], \end{aligned}$$
(73)
$$\begin{aligned}& \begin{aligned}[b] \bar{v}_{2} ( \psi ,u ) ={}&\frac{Gr}{a} \biggl[-u-j+ \frac{1}{h^{2}-g^{2}} \biggl\lbrace \frac{D}{1-a_{2} u}+ \frac{E}{1+b_{2} u} \biggr\rbrace \biggr] \\ &\quad {}\times \bigl(1-e^{-\frac{1}{u}}\bigr) \bigl[ e^{- \psi \sqrt{\frac{au + c}{u + {\alpha }}}}-e^{-\psi \sqrt{ \frac{P_{r_{0}}}{u}}} \bigr] , \end{aligned} \end{aligned}$$
(74)
$$\begin{aligned}& \bar{v}_{2} ( \psi ,u ) =\frac{Gr}{a} \biggl[ -u-j+ \frac{1}{h^{2}-g^{2}} \bigl\lbrace DF_{4}(u)+EF_{5}(u) \bigr\rbrace \biggr]F_{1}(u) \bigl[F_{2}(u)-F_{3}(u) \bigr], \end{aligned}$$
(75)
$$\begin{aligned}& \begin{aligned}[b] \bar{v}_{2} ( \psi ,u ) ={}&\frac{Gr}{a} \bigl[-uF_{1}(u)F_{2}(u)+uF_{1}(u)F_{3}(u)-j \bigl(1-e^{- \frac{1}{u}}\bigr) \bigl(F_{2}(u)-F_{3}(u) \bigr) \bigr] \\ &{} +\frac{GrD}{a(h^{2}-g^{2})}\bigl(1-e^{-\frac{1}{u}}\bigr)F_{4}(u) \bigl[F_{2}(u)-F_{3}(u) \bigr] \\ &{}+\frac{GrE}{a(h^{2}-g^{2})} \bigl(1-e^{-\frac{1}{u}}\bigr)F_{5}(u) \bigl[F_{2}(u)-F_{3}(u) \bigr], \end{aligned} \end{aligned}$$
(76)
$$\begin{aligned}& \begin{aligned}[b] \bar{v}_{2} ( \psi ,u ) ={}&\frac{Gr}{a} \bigl[-S_{1}(u)+S_{2}(u)-j\bigl(F_{2}(u)-F_{3}(u) \bigr)-e^{- \frac{1}{u}}F_{2}(u)+e^{-\frac{1}{u}}F_{3}(u) \bigr] \\ &{} +\frac{GrD}{a(h^{2}-g^{2})} \bigl[F_{24}(u)-F_{34}(u)-e^{- \frac{1}{u}}F_{24}(u)+e^{-\frac{1}{u}}F_{34}(u) \bigr] \\ &{} +\frac{GrE}{a(h^{2}-g^{2})} \bigl[F_{25}(u)-F_{35}(u)-e^{- \frac{1}{u}}F_{25}(u)+e^{-\frac{1}{u}}F_{35}(u) \bigr], \end{aligned} \end{aligned}$$
(77)

with

$$\begin{aligned}& j =\frac{P_{r_{0}}-c}{a}, \qquad r=\frac{\alpha P_{r_{0}}}{a},\qquad z=j^{2}+r,\qquad e_{1}=j.r,\qquad g=\frac{j}{2},\qquad h=\sqrt{r+g^{2}}, \\& d =c-a \alpha , \qquad a_{2}=\frac{1}{h+g},\qquad b_{2}= \frac{1}{h-g}, \qquad D= \frac{a_{2} e_{1}+z}{(a_{2}+b_{2})},\qquad E= \frac{b_{2} e_{1}-z}{(a_{2}+b_{2})}, \\& c =1+b, \qquad F_{1}(u)=1-e^{-\frac{1}{u}},\qquad F_{2}(u)=e^{-\psi \sqrt{\frac{au + c}{u + {\alpha }}}},\qquad F_{3}(u)=e^{-\psi \sqrt{ \frac{P_{r_{0}}}{u}}}, \\& F_{4}(u) =\frac{1}{1-a_{2}u}, \qquad F_{5}(u)= \frac{1}{1+b_{2}u}. \end{aligned}$$
(78)

Employing the Sumudu inverse transformation, the solution is written as

$$\begin{aligned} v_{2}(\psi ,t) =&\frac{Gr}{a} \bigl[-S_{1}(\psi ,t) +S_{2}(\psi ,t)-j \bigl[f_{2}(\psi ,t)-f_{3}(\psi ,t)-f_{2}(\psi ,t-1)H(t-1) \\ &{}+f_{3}( \psi ,t-1)H(t-1) \bigr] \bigr] \\ &{} +\frac{GrD}{a(h^{2}-g^{2})} \bigl[f_{24}(\psi ,t)-f_{34}( \psi ,t)-f_{24}( \psi ,t-1)H(t-1) \\ &{}+f_{34}(\psi ,t-1)H(t-1) \bigr] \\ &{} +\frac{GrD}{a(h^{2}-g^{2})} \bigl[f_{25}(\psi ,t)-f_{35}( \psi ,t)-f_{25}( \psi ,t-1)H(t-1) \\ &{}+f_{35}(\psi ,t-1)H(t-1) \bigr], \end{aligned}$$
(79)

where

$$\begin{aligned}& S_{1}(\psi ,t) =(f_{1} \ast f_{2}) (t)= \int _{0}^{t} f_{1}(\tau )f_{2}(t- \tau )\,d(\tau ), \end{aligned}$$
(80)
$$\begin{aligned}& S_{2}(\psi ,t) =(f_{1} \ast f_{3}) (t)= \int _{0}^{t} f_{1}(\tau )f_{3}(t- \tau )\,d(\tau ), \end{aligned}$$
(81)
$$\begin{aligned}& \mathbb{S}^{-1}\bigl(e^{-\frac{1}{u}}F_{2}(u) \bigr) =f_{2}(t-1)H(t-1), \end{aligned}$$
(82)
$$\begin{aligned}& \mathbb{S}^{-1}\bigl(e^{-\frac{1}{u}}F_{3}(u) \bigr) =f_{3}(t-1)H(t-1), \end{aligned}$$
(83)

and

$$\begin{aligned}& f_{3}(t)=\operatorname{erfc}\biggl(\frac{a_{1}}{2\sqrt{t}}\biggr), \quad \text{with } a_{1}=\sqrt{P_{r_{0}}}\psi , \end{aligned}$$
(84)
$$\begin{aligned}& F_{24}(u)=F_{2}(u)F_{4}(u) \end{aligned}$$
(85)
$$\begin{aligned}& \begin{aligned} &\hphantom{F_{24}(u)}= \Biggl[ \sum_{n_{1}=0}^{\infty }\sum _{n_{2}=0}^{\infty }\sum_{n_{3}=0}^{ \infty } \frac{(-1)^{n_{3}}a^{\frac{n_{1}}{2}-n_{2}}(-\psi )^{n_{1}}d^{n_{2}}\Gamma ({\frac{n_{1}}{2}+1)}\Gamma {(n_{2} + n_{3})}}{n_{1}{!}n_{2}{!}n_{3}{!}(\alpha )^{n_{2} +n_{3}}\Gamma ({\frac{n_{1}}{2}+1-n_{2})}\Gamma {(n_{2})}}u^{n_{3}} \Biggr] \\ &\hphantom{F_{24}(u)={}}{}\times\Biggl[\sum _{l=0}^{\infty }\bigl(a_{2}(u) \bigr)^{l} \Biggr]. \end{aligned} \end{aligned}$$
(86)

Applying discrete convolution (the Cauchy product) with two truncated series, each of m terms, yields:

$$\begin{aligned}& =\sum_{n_{1}=0}^{\infty }\sum _{n_{2}=0}^{\infty }\sum_{n_{3}=0}^{m} \sum_{l=0}^{m} \frac{(-1)^{n_{3}}a^{\frac{n_{1}}{2}-n_{2}}(-\psi )^{n_{1}}d^{n_{2}}\Gamma ({\frac{n_{1}}{2}+1)}\Gamma {(n_{2} + n_{3})}}{n_{1}{!}n_{2}{!}n_{3}{!}(\alpha )^{n_{2} +n_{3}}\Gamma ({\frac{n_{1}}{2}+1-n_{2})}\Gamma {(n_{2})}}u^{n_{3}} \bigl(a_{2}(u)\bigr)^{m-l}, \end{aligned}$$
(87)
$$\begin{aligned}& f_{24}(\psi ,t) =\mathbb{S}^{-1}\bigl(F_{24}(u) \bigr) \end{aligned}$$
(88)
$$\begin{aligned}& \begin{aligned} &\hphantom{f_{24}(\psi ,t)} =\sum_{n_{1}=0}^{\infty }\sum _{n_{2}=0}^{\infty }\sum_{n_{3}=0}^{m} \sum_{l=0}^{m} \frac{(-1)^{n_{3}}a^{\frac{n_{1}}{2}-n_{2}}(-\psi )^{n_{1}}d^{n_{2}} \Gamma ({\frac{n_{1}}{2}+1)}\Gamma {(n_{2} + n_{3})}}{n_{1}{!}n_{2}{!}(n_{3}{!})^{2} (\alpha )^{n_{2} +n_{3}}\Gamma ({\frac{n_{1}}{2}+1-n_{2})}\Gamma {(n_{2})}} \\ &\hphantom{f_{24}(\psi ,t)=} {}\cdot\frac{t^{n_{3}+m-l}}{(n_{3}+m-l)!}(a_{2})^{m-l} , \end{aligned} \end{aligned}$$
(89)
$$\begin{aligned}& F_{34}(u) =F_{3}(u)F_{4}(u) \end{aligned}$$
(90)
$$\begin{aligned}& \hphantom{F_{34}(u)} = \Biggl[\sum_{\beta =0}^{\infty }\biggl( \frac{-a_{1}}{\sqrt{u}}\biggr)^{\beta } \frac{1}{\beta !} \Biggr] \Biggl[\sum_{\eta =0}^{\infty } \bigl(a_{2}(u)\bigr)^{ \eta } \Biggr]. \end{aligned}$$
(91)

By using Cauchy product or discrete convolution, we get the product of the above two series as a truncated double series

$$\begin{aligned}& =\sum_{\beta =0}^{\mu }\sum _{\eta =0}^{\mu } \frac{(-a_{1})^{\beta }(a_{2})^{\mu - \eta }}{\beta !}(u)^{ \frac{- \beta }{2}}(u)^{\mu - \eta }, \end{aligned}$$
(92)
$$\begin{aligned}& =\sum_{\beta =0}^{\mu }\sum _{\eta =0}^{\mu } \frac{(-a_{1})^{\beta }(a_{2})^{\mu - \eta }}{\beta !}(u)^{\mu - \eta - \frac{ \beta }{2}}, \end{aligned}$$
(93)
$$\begin{aligned}& f_{34}(\psi ,t) =\mathbb{S}^{-1}\bigl(F_{34}(u) \bigr), \end{aligned}$$
(94)
$$\begin{aligned}& \hphantom{f_{34}(\psi ,t)} =\sum_{\beta =0}^{\mu }\sum _{\eta =0}^{\mu } \frac{(-a_{1})^{\beta }(a_{2})^{\mu - \eta }}{\beta ! \Gamma (\mu - \eta - \frac{ \beta }{2}+1)}(t)^{ \mu - \eta - \frac{ \beta }{2}}, \end{aligned}$$
(95)
$$\begin{aligned}& \mathbb{S}^{-1}\bigl(e^{-\frac{1}{u}}F_{24}(u) \bigr) =f_{24}(t-1)H(t-1), \end{aligned}$$
(96)
$$\begin{aligned}& \mathbb{S}^{-1}\bigl(e^{-\frac{1}{u}}F_{34}(u) \bigr) =f_{34}(t-1)H(t-1), \end{aligned}$$
(97)
$$\begin{aligned}& f_{25}(\psi ,t) =\sum_{n_{1}=0}^{\infty } \sum_{n_{2}=0}^{\infty } \sum _{n_{3}=0}^{i}\sum_{w=0}^{i} \frac{(-1)^{n_{3}}a^{\frac{n_{1}}{2}-n_{2}}(-\psi )^{n_{1}}d^{n_{2}}\Gamma ({\frac{n_{1}}{2}+1)}\Gamma {(n_{2} + n_{3})}}{n_{1}{!}n_{2}{!}(n_{3}{!})^{2}(\alpha )^{n_{2} +n_{3}}\Gamma ({\frac{n_{1}}{2}+1-n_{2})}\Gamma {(n_{2})}} \end{aligned}$$
(98)
$$\begin{aligned}& \hphantom{f_{25}(\psi ,t) ={}}{} \times \frac{t^{n_{3}+i-w}}{(n_{3}+i-w)!}(-b_{2})^{i-w} , \end{aligned}$$
(99)
$$\begin{aligned}& f_{35}(\psi ,t) =\sum_{\beta _{1}=0}^{\mu _{1}} \sum_{\eta _{1}=0}^{ \mu _{1}} \frac{(-a_{1})^{\beta _{1}}(-b_{2})^{\mu _{1} - \eta _{1}}}{(\beta _{1}) ! \Gamma (\mu _{1} - \eta _{1}- \frac{ \beta _{1}}{2}+1)}(t)^{ \mu _{1} - \eta _{1}- \frac{ \beta _{1}}{2}}, \end{aligned}$$
(100)
$$\begin{aligned}& \mathbb{S}^{-1}\bigl(e^{-\frac{1}{u}}F_{25}(u) \bigr) =f_{25}(t-1)H(t-1), \end{aligned}$$
(101)
$$\begin{aligned}& \mathbb{S}^{-1}\bigl(e^{-\frac{1}{u}}F_{35}(u) \bigr) =f_{35}(t-1)H(t-1). \end{aligned}$$
(102)

5 Results and discussion

From Eqs. (34) and (41), we observe that the temperature profile has two different solution expressions calculated by Sumudu transformation in (34) and by Laplace transformation method in (41). These are graphically equivalent. Figure 1 presents the temperature illustration for various values of Pr. It has been declared that when the values of Pr increase, the temperature is falling in both cases.

Figure 1
figure 1

Temperature profile for different values of Pr via Laplace and Sumudu transformation

Full size image

6 Conclusion

We presented a new application of the Sumudu transform in this paper. The Sumudu transform is able to keep the unity of the function, the parity of the function, and has many other properties that are more valuable. Therefore, we investigated the Sumudu transform in this work. We compared the results with the results obtained by the Laplace transform. We proved the efficiency of the Sumudu transform for solutions of the unsteady convective flow of an MHD second grade fluid with ramped conditions.