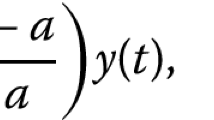1 Introduction

The integral equations of Urysohn–Stieltjes (U-S) type have been studied by some authors; see, for example, [3, 5, 11–15], and [16–22], and reference therein.

The quadratic Chandrasekhar integral equation

$$ x(t)=a(t) + x(t) \int _{0}^{1}\frac{t}{t+s}b_{1}(s)x(s) \,ds , \quad t\in I= [0,1] $$

has been studied in some papers; see, for example, [1, 4, 7–10], and [24] and references therein.

Our aim is to study the existence of solutions \(x\in C[0,1]\) of the U-S nonlinear functional integral inclusion

$$ x(t)-a(t)\in \int _{0}^{1}F \biggl(t,s,x(s), \int _{0}^{1}h \bigl(s,\theta ,x( \theta ) \bigr) \,d_{\theta }g_{2}(s,\theta ) \biggr)\,d_{s}g_{1}(t,s), \quad t\in I= [0,1]. $$
(1.1)

As applications, we will prove the existence of solutions \(x\in C[0,1]\) of the nonlinear Chandrasekhar functional integral inclusion

$$ x(t) - a(t) \in \int _{0}^{1}\frac{t}{t+s}F \biggl(b_{1}(s)x(s), \int _{0}^{1}\frac{s}{s+\theta } b_{2}(s) x( \theta ) \,d{\theta } \biggr)\,d{s}, \quad t\in I= [0,1], $$

and the Chandrasekhar quadratic integral equation

$$ x(t)=a(t)+ \int _{0}^{1}\frac{t}{t+s}b_{1}(s)x(s) \cdot \biggl( \int _{0}^{1} \frac{s}{s+\theta } b_{2}(s) x(\theta ) \,d{\theta } \biggr)\,d{s}, \quad t\in I= [0,1]. $$

The paper is organized as follows. In Sect. 2, we establish the existence and uniqueness results for single-valued nonlinear U-S equations. We also prove the continuous dependence of the unique solution on the \(g_{i} \) (\(i=1,2\)). As an application, we discuss some particular cases by presenting the existence of solutions of nonlinear Chandrasekhar quadratic functional integral equations. In Sect. 3, we add conditions to our problem in order to obtain a new existence result with an application. Our results are generalized in Sect. 4, where we discuss the existence of solutions for set-valued equation (1.1) with continuous dependence on the set \(S_{F}\) and demonstrate a particular case of inclusion by presenting the existence of solutions for set-valued Chandrasekhar nonlinear functional integral equations.

2 Single-valued problem

Here we consider the nonlinear single-valued functional integral equation of U-S type

$$ x(t) = a(t) + \int _{0}^{1}f \biggl(t,s,x(s), \int _{0}^{1}h \bigl(s,\theta ,x( \theta ) \bigr) \,d_{\theta }g_{2}(s,\theta ) \biggr)\,d_{s}g_{1}(t,s), \quad t\in [0,1]. $$
(2.1)

2.1 Existence of solutions I

Consider the U-S functional integral equation (2.1) under the following assumptions:

  1. (i)

    \(a: [0,1]\rightarrow [0,1] \) is a continuous function, with \(a = \sup_{t\in [0,1]} \vert a(t) \vert \).

  2. (ii)
    1. a)

      \(f:[0,1]\times [0,1]\times R \times R \rightarrow R \) is a continuous function, and there exist two continuous functions \(m_{1},k_{1}:[0,1]\times [0,1]\rightarrow R\) such that

      $$ \bigl\vert f(t,s,x,y) \bigr\vert \leq m_{1}(t,s)+k_{1}(t,s) \bigl( \vert x \vert + \vert y \vert \bigr). $$
    2. b)

      \(h:[0,1]\times [0,1]\times R \rightarrow R \) is a continuous function, and there exist two continuous functions \(m_{2},k_{2}:[0,1]\times [0,1]\rightarrow R\) such that

      $$ \bigl\vert h(t,s,x) \bigr\vert \leq m_{2}(t,s)+k_{2}(t,s) \vert x \vert . $$
    3. c)

      \(k=\sup \{ k_{i}(t,s):t, s\in [0,1]\}\), and \(m=\sup \{ m_{i}(t,s):t, s\in [0,1], i=1,2\}\).

  3. (iii)

    \(g_{i}:[0,1]\times R \rightarrow R\), \(i=1,2\), are continuous functions with

    $$ \mu =\max \bigl\{ \sup \bigl\vert g_{i}(t,1) \bigr\vert +\sup \bigl\vert g_{i}(t,0) \bigr\vert , \text{on } [0,1] \bigr\} . $$
  4. (iv)

    For all \(t_{1},t_{2}\in I\), \(t_{1}< t_{2}\), the functions \(s \rightarrow g_{i}(t_{2},s)-g_{i}(t_{1},s)\) are nondecreasing on \([0,1]\).

  5. (v)

    \(g_{i}(0,s)= 0\) for \(s \in [0,1]\).

  6. (vi)

    \(k\mu +k^{2}\mu ^{2}<1\).

Let E be a Banach space with the norm \(\Vert \cdot \Vert _{E}\), and let \(I = [0, 1]\). Denote by \(C = C (I, E)\) the space of all continuous functions on I taking values in the space E. This space becomes a Banach space with supnorm

$$ \Vert x \Vert _{C} = \sup_{t\in I} \bigl\Vert x(t) \bigr\Vert _{E}. $$

Remark 2.1

(see [11])

Note that the function \(s\rightarrow g(t,s)\) is nondecreasing on the interval \([0,1]\). Indeed, for \(s_{1}, s_{2}\in [0,1]\) with \(s_{1}< s_{2}\), from assumptions (iv) and (v) we obtain

$$ g(t,s_{2})-g(t,s_{1})= \bigl[g(t,s_{2})-g(0,s_{2}) \bigr]- \bigl[g(t,s_{1})-g(0,s_{1}) \bigr] \geq 0. $$

Lemma 2.2

([11])

Assume that a function g satisfies assumption (v). Then for arbitrary \(s_{1}, s_{2}\in I\) with \(s_{1}< s_{2}\), the function \(t\rightarrow g(t,s_{2})-g(t,s_{1})\) is nondecreasing on I.

Indeed, take \(t_{1},t_{2}\in [0,1]\) such that \(t_{1}< t_{2}\). Then by assumption (vi) we get

$$ \bigl[g(t_{2},s_{2})-g(t_{2},s_{1}) \bigr]- \bigl[g(t_{1},s_{2})-g(t_{1},s_{1}) \bigr]= \bigl[g(t_{2},s_{2})-g(t_{1},s_{2}) \bigr]- \bigl[g(t_{2},s_{1})-g(t_{1},s_{1}) \bigr] \geq 0. $$

For the existence of at least one solution of the U-S nonlinear functional integral equation (2.1), we have the following theorem.

Theorem 2.3

Let the assumptions (i)–(vi) be satisfied. Then the functional integral equation (2.1) has at least one solution \(x\in C[0,1]\).

Proof

Define the operator A by

$$ A x(t)= a(t)+ \int _{0}^{1}f \biggl(t,s,x(s), \int _{0}^{1}h \bigl(s,\theta ,x( \theta ) \bigr) \,d_{\theta }g_{2}(s,\theta ) \biggr)\,d_{s}g_{1}(t,s), \quad t\in I, $$
(2.2)

and define let the set

$$ Q_{r}= \bigl\{ x \in R: \vert x \vert \leq r \bigr\} \subseteq C[0,1], $$

where

$$ r=\frac{a+m\mu +km\mu ^{2}}{1-[k\mu +k^{2}\mu ^{2}]}. $$

It is clear that \(Q_{r}\) is a nonempty, bounded, closed, and convex set.

Let \(x\in Q_{r} \). Then

$$\begin{aligned} \bigl\vert A x(t) \bigr\vert =& \biggl\vert a(t)+ \int _{0}^{1}f \biggl(t,s,x(s), \int _{0}^{1}h \bigl(s, \theta ,x(\theta ) \bigr) \,d_{\theta }g_{2}(s,\theta ) \biggr)\,d_{s}g_{1}(t,s) \biggr\vert \\ \leq & \bigl\vert a(t) \bigr\vert + \int _{0}^{1} \biggl\vert f \biggl(t,s,x(s), \int _{0}^{1}h \bigl(s, \theta ,x(\theta ) \bigr) \,d_{\theta }g_{2}(s,\theta ) \biggr) \biggr\vert \,d_{s}g_{1}(t,s) \\ \leq &a+ \int _{0}^{1} \biggl(m_{1}(t,s)+k_{1}(t,s) \biggl( \bigl\vert x(t) \bigr\vert + \int _{0}^{1} \bigl\vert h \bigl(s, \theta ,x( \theta ) \bigr) \bigr\vert \,d_{\theta }g_{2}(s,\theta ) \biggr) \biggr)\,d_{s}g_{1}(t,s) \\ \leq &a+ \int _{0}^{1} \biggl(m_{1}(t,s)+k_{1}(t,s) \biggl( \bigl\vert x(t) \bigr\vert \\ &{}+ \int _{0}^{1} \bigl(m_{2}(s,\theta )+k_{2}(s,\theta ) \bigl\vert x(\theta ) \bigr\vert \,d_{ \theta }g_{2}(s,\theta ) \bigr) \biggr)\,d_{s}g_{1}(t,s) \biggr) \\ \leq &a+ \int _{0}^{1} (m_{1}(t,s)+k_{1}(t,s) \bigl( \bigl\vert x(t) \bigr\vert +(m+kr)\mu \bigr)\,d_{s}g_{1}(t,s) \\ \leq &a+ \bigl(m+k \bigl(r+(m+kr) \mu \bigr) \bigr)\mu \leq r. \end{aligned}$$

This proves that the operator \(A: Q_{r} \rightarrow Q_{r}\) and the class \(\{A x\}\) is uniformly bounded on \(Q_{r}\).

Then, for \(x\in Q_{r} \) and \(y(s)=\int _{0}^{1}h(s,\theta ,x(\theta )) \,d_{\theta }g_{2}(s,\theta )\), define the set

$$\begin{aligned} \theta (\delta ) ={}&\sup \bigl\{ \bigl\vert f(t_{2},s,x,y)-f(t_{1},s,x,y) \bigr\vert : t_{1},t_{2},s \in [0,1], t_{1}< t_{2}, \\ & \vert t_{2}-t_{1} \vert < \delta , \vert x \vert \leq r, \vert y \vert \leq r \bigr\} . \end{aligned}$$
(2.3)

Then from the uniform continuity of the function \(f: [0,1]\times [0,1]\times Q_{r}\times Q_{r} \rightarrow R \) and assumption (ii) we deduce that \(\theta (\delta ) \rightarrow 0 \) as \(\delta \rightarrow 0\), independently of \(x \in Q_{r}\).

Now let \(t_{2}, t_{1} \in [0,1]\), \(\vert t_{2}-t_{1} \vert <\delta\). Then we have

$$\begin{aligned}& \bigl\vert Ax(t_{2})- Ax(t_{1}) \bigr\vert \\ & \quad = \biggl\vert a(t_{2})+ \int _{0}^{1}f \biggl( t_{2},s,x(s), \int _{0}^{1}h \bigl(s, \theta ,x(\theta ) \bigr) \,d_{\theta }g_{2}(s,\theta ) \biggr)\,d_{s}g_{1}(t_{2},s) \\ & \quad\quad {} - a(t_{1})- \int _{0}^{1}f \biggl(t_{1},s,x(s), \int _{0}^{1}h \bigl(s, \theta ,x(\theta ) \bigr) \,d_{\theta }g_{2}(s,\theta ) \biggr)\,d_{s}g_{1}(t_{1},s) \biggr\vert \\ & \quad \leq \bigl\vert a(t_{2})- a(t_{1}) \bigr\vert + \biggl\vert \int _{0}^{1}f \biggl(t_{2},s,x(s), \int _{0}^{1}h \bigl(s,\theta ,x(\theta ) \bigr) \,d_{\theta }g_{2}(s,\theta ) \biggr)\,d_{s}g_{1}(t_{2},s) \\ & \quad\quad {} - \int _{0}^{1}f \biggl(t_{1},s,x(s), \int _{0}^{1}h \bigl(s,\theta ,x( \theta ) \bigr) \,d_{\theta }g_{2}(s,\theta ) \biggr)\,d_{s}g_{1}(t_{1},s) \biggr\vert \\ & \quad \leq \bigl\vert a(t_{2})- a(t_{1}) \bigr\vert \\ & \quad \quad {} + \biggl\vert \int _{0}^{1}f \bigl(t_{2},s,x(s),y(s) \bigr)\,d_{s}g_{1}(t_{2},s)- \int _{0}^{1}f \bigl(t_{1},s,x(s),y(s) \bigr)\,d_{s}g_{1}(t_{2},s) \\ & \quad \quad {} + \int _{0}^{1}f \bigl(t_{1},s,x(s),y(s) \bigr)\,d_{s}g_{1}(t_{2},s) - \int _{0}^{1}f \bigl(t_{1},s,x(s),y(s) \bigr)\,d_{s}g_{1}(t_{1},s) \biggr\vert \\ & \quad \leq \bigl\vert a(t_{2})- a(t_{1}) \bigr\vert + \int _{0}^{1} \bigl\vert (f \bigl(t_{2},s,x(s),y(s) \bigr)- f \bigl(t_{1},s,x(s),y(s) \bigr) \bigr\vert \,d_{s}g_{1}(t_{2},s) \\ & \quad \quad {} + \int _{0}^{1} \bigl\vert f \bigl(t_{1},s,x(s),y(s) \bigr) \bigr\vert \,d_{s} \bigl[g_{1}(t_{2},s)-g_{1}(t_{1},s) \bigr] \\ & \quad \leq \bigl\vert a(t_{2})- a(t_{1}) \bigr\vert + \int _{0}^{1}\theta (\delta )\,d_{s}g_{1}(t_{2},s) \\ & \quad\quad {} + \int _{0}^{1} \bigl(m_{1}(t, s)+k_{1}(t, s) \bigl( \vert x \vert + \vert y \vert \bigr) \bigr)\,d_{s} \bigl[g_{1}(t_{2},s)-g_{1}(t_{1},s) \bigr]. \end{aligned}$$

This inequality means that the class of functions \(\{A{x}\} \) is equicontinuous.

Therefore by the Arzelà–Ascoli theorem [25] A is compact.

Let \(\{x_{n}\}\subset Q_{r}\), \(x_{n}\rightarrow x\). Then

$$\begin{aligned}& Ax_{n}(t) \\& \quad =a(t) + \int _{0}^{1}f \biggl(t,s,x_{n}(s), \int _{0}^{1}h \bigl(s,\theta ,x_{n}( \theta ) \bigr) \,d_{\theta }g_{2}(s,\theta ) \biggr) \,d_{s}g_{1}(t,s), \\& \lim_{n\rightarrow \infty }Ax_{n}(t) \\& \quad =\lim_{n\rightarrow \infty } \biggl(a(t)+ \int _{0}^{1}f \biggl(t,s,x_{n}(s), \int _{0}^{1}h \bigl(s,\theta ,x_{n}( \theta ) \bigr)\,d_{\theta }g_{2}(s,\theta ) \biggr) \,d_{s}g_{1}(t,s) \biggr), \end{aligned}$$

and from assumption (ii) (see [23]) we get

$$\begin{aligned}& \lim_{n\rightarrow \infty } Ax_{n}(t) \\& \quad = a(t) + \int _{0}^{1}\lim_{n\rightarrow \infty } f \biggl(t,s,x_{n}(s), \int _{0}^{1}h \bigl(s,\theta ,x_{n}( \theta ) \bigr) \,d_{\theta }g_{2}(s,\theta ) \biggr) \,d_{s}g_{1}(t,s) \\& \quad = a(t) + \int _{0}^{1} f \biggl(t,s,\lim_{n\rightarrow \infty }x_{n}(s), \int _{0}^{1}h \Bigl(s,\theta ,\lim _{n\rightarrow \infty }x_{n}(\theta ) \Bigr)\,d_{ \theta }g_{2}(s, \theta ) \biggr)\,d_{s}g_{1}(t,s) \\& \quad = a(t)+ \int _{0}^{1}f \biggl(t,s,x(s), \int _{0}^{1} h \bigl(s,\theta ,x( \theta ) \bigr) \,d_{\theta }g_{2}(s,\theta ) \biggr)\,d_{s}g_{1}(t,s) \\& \quad = Ax(t). \end{aligned}$$

This proves that \(Ax_{n}(t)\rightarrow A x(t)\) and A is continuous.

Now (see [23]) A has at least one fixed point \(x \in Q_{r}\), and (2.1) has at least one solution \(x \in Q_{r}\subset C[0,1]\). □

2.2 Uniqueness of the solution

To prove the existence of a unique solution of U-S functional integral equation (2.1), let us replace condition (ii) by

\((\mathrm{ii})^{*}\):
  1. a)

    the function \(f:I\times I\times R \times R \rightarrow R \) is continuous and satisfies the Lipschitz condition

    $$ \bigl\vert f(t,s,x_{1},y_{1})-f(t,s,x_{2},y_{2}) \bigr\vert \leq k_{1} \bigl( \vert x_{1}-x_{2} \vert + \vert y_{1}-y_{2} \vert \bigr). $$
  2. b)

    \(h:I\times I\times R \rightarrow R \) is continuous and satisfies the Lipschitz condition

    $$ \bigl\vert h(t,s,x)-h(t,s,y) \bigr\vert \leq k_{2} \vert x-y \vert . $$

By condition \((\mathrm{ii})^{*}\) we have

$$ \bigl\vert f \bigl(t,s,x(s),y(s) \bigr) \bigr\vert - \bigl\vert f(t,s,0,0) \bigr\vert \leq \bigl\vert f \bigl(t,s,x(s),y(s) \bigr)-f(t,s,0,0) \bigr\vert \leq k_{1} \bigl( \vert x \vert + \vert y \vert \bigr). $$

Then

$$ \bigl\vert f \bigl(t,s,x(s),y(s) \bigr) \bigr\vert \leq k_{1} \bigl( \vert x \vert + \vert y \vert \bigr)+ \bigl\vert f_{1}(t,s,0,0) \bigr\vert , $$

and

$$ \bigl\vert f \bigl(t,s,x(s),y(s) \bigr) \bigr\vert \leq k_{1} \bigl( \vert x \vert + \vert y \vert \bigr)+m_{1}, $$

where \(m_{1}=\sup_{t\times s\in I\times I} \vert f(t,s,0,0) \vert \), and

$$ \bigl\vert h \bigl(t,s,x(s) \bigr) \bigr\vert - \bigl\vert h(t,s,0) \bigr\vert \leq \bigl\vert h \bigl(t,s,x(s) \bigr)-h(t,s,0) \bigr\vert \leq k_{2} \vert x \vert . $$

Then

$$ \bigl\vert h \bigl(t,s,x(s) \bigr) \bigr\vert \leq k_{2} \vert x \vert + \bigl\vert f_{2}(t,s,0) \bigr\vert , $$

and

$$ \bigl\vert h \bigl(t,s,x(s) \bigr) \bigr\vert \leq k_{2} \vert x \vert +m_{2}, $$

where \(m_{2}=\sup_{t\times s\in I\times I} \vert h(t,s,0) \vert \), \(m=\max \{m_{1},m_{2}\}\), and \(k=\max \{k_{1},k_{2}\}\).

Theorem 2.4

Let conditions (i), \((\mathit{ii})^{*}\), (iii), and (iv)–(v) be satisfied with \(\mu k+k^{2}\mu ^{2}\leq 1\). Then the functional integral equation (2.1) has unique solution \(x \in C[0,1] \).

Proof

Let \(x_{1}\), \(x_{2}\) be solutions of the integral equation (2.1). Then

$$\begin{aligned}& \bigl\vert x_{1}(t)-x_{2}(t) \bigr\vert \\& \quad = \biggl\vert a(t)+ \int _{0}^{1}f \biggl(t,s,x_{1}(s), \int _{0}^{1}h \bigl(s, \theta ,x_{1}( \theta ) \bigr) \,d_{\theta }g_{2}(s,\theta ) \biggr) \,d_{s}g_{1}(t,s) \\& \quad\quad {} - a(t)+ \int _{0}^{1}f \biggl(t,s,x_{2}(s), \int _{0}^{1}h \bigl(s,\theta ,x_{2}( \theta ) \bigr) \,d_{\theta }g_{2}(s,\theta ) \biggr) \,d_{s}g_{1}(t,s) \biggr\vert \\& \quad \leq \int _{0}^{1} \biggl\vert f \biggl(t,s,x_{1}(s), \int _{0}^{1}h \bigl(s,\theta ,x_{1}( \theta ) \bigr) \,d_{\theta }g_{2}(s,\theta ) \biggr) \\& \quad \quad {}-f \biggl(t,s,x_{2}(s), \int _{0}^{1}h \bigl(s,\theta ,x_{2}( \theta ) \bigr) \,d_{ \theta }g_{2}(s,\theta ) \biggr) \biggr\vert \,d_{s}g_{1}(t,s) \\& \quad \leq \int _{0}^{1}k_{1} \biggl( \bigl\vert x_{1}(s)-x_{2}(s) \bigr\vert + \int _{0}^{1} \bigl\vert \bigl(h \bigl(s, \theta ,x_{1}(\theta ) \bigr)-h \bigl(s,\theta ,x_{2}(\theta ) \bigr) \bigr) \bigr\vert \,d_{\theta }g_{2}(s, \theta ) \biggr) \,d_{s}g_{1}(t,s) \\& \quad \leq \int _{0}^{1}k_{1} \biggl( \bigl\vert x_{1}(s)-x_{2}(s) \bigr\vert + \int _{0}^{1}k_{2} \bigl( \bigl\vert x_{1}( \theta )-x_{2}(\theta ) \bigr\vert \bigr) \,d_{\theta }g_{2}(s,\theta ) \biggr)\,d_{s}g_{1}(t,s) \\& \quad \leq \int _{0}^{1}k_{1} \bigl( \bigl\vert x_{1}(s)-x_{2}(s) \bigr\vert +k_{2} \Vert x_{1}-x_{2} \Vert \mu \bigr)\,d_{s}g_{1}(t,s) \\& \quad \leq k \Vert x_{1}-x_{2} \Vert \mu +k^{2} \Vert x_{1}-x_{2} \Vert \mu ^{2}. \end{aligned}$$

Hence we have

$$ \Vert x_{1} -x_{2} \Vert \leq \bigl(\mu k+k^{2}\mu ^{2} \bigr) \Vert x_{1}-x_{2} \Vert $$

and

$$ \bigl(1- \bigl(\mu +k^{2}\mu ^{2} \bigr) \bigr) \Vert x_{1} -x_{2} \Vert \leq 0, $$

which implies

$$ x_{1}(t)=x_{2}(t). $$

 □

2.2.1 Continuous dependence of solution on functions \(g_{i}(t,s)\)

Here we show that the solution of U-S functional integral equation (2.1) continuously depends on the functions \(g_{i}\).

Definition 2.5

The solutions of functional integral equation (2.1) continuously depends on the functions \(g_{i}(t,s)\), \(i=1,2\), if for every \(\epsilon >0\), there exists \(\delta >0 \) such that

$$ \bigl\vert g_{i}(t,s)-g_{i}^{*}(t,s) \bigr\vert \leq \delta \quad \Rightarrow \quad \bigl\Vert x-x^{*} \bigr\Vert \leq \epsilon . $$

Theorem 2.6

Let the assumptions of Theorem 2.4be satisfied. Then the solution of (2.1) depends continuously on functions \(g_{i}(t,s)\), \(i=1,2\).

Proof

Let \(\delta >0\) be such that \(\vert g_{i}(t,s)-g_{i}^{*}(t,s) \vert \leq \delta \) for all \(t \geq 0 \). Then

$$\begin{aligned}& \bigl\vert x(t)-x^{*}(t) \bigr\vert \\& \quad = \biggl\vert a(t)+ \int _{0}^{1}f \biggl(t,s,x(s), \int _{0}^{1}h \bigl(s,\theta ,x( \theta ) \bigr) \,d_{\theta }g_{2}(s,\theta ) \biggr)\,d_{s}g_{1}(t,s) \\& \quad \quad {} - a(t)+ \int _{0}^{1}f \biggl(t,s,x^{*}(s), \int _{0}^{1}h \bigl(s,\theta ,x^{*}( \theta ) \bigr) \,d_{\theta }g^{*}_{2}(s,\theta ) \biggr) \,d_{s}g^{*}_{1}(t,s) \biggr\vert \\& \quad \leq \biggl\vert \int _{0}^{1}f \biggl(t,s,x(s), \int _{0}^{1}h \bigl(s,\theta ,x( \theta ) \bigr) \,d_{\theta }g_{2}(s,\theta ) \biggr)\,d_{s}g_{1}(t,s) \\& \quad \quad {} - \int _{0}^{1}f \biggl(t,s,x^{*}(s), \int _{0}^{1}h \bigl(s,\theta ,x^{*}( \theta ) \bigr) \,d_{\theta }g_{2}(s,\theta ) \biggr) \,d_{s}g_{1}(t,s) \\& \quad \quad {} + \int _{0}^{1}f \biggl(t,s,x^{*}(s), \int _{0}^{1}h \bigl(s,\theta ,x^{*}( \theta ) \bigr) \,d_{\theta }g_{2}(s,\theta ) \biggr) \,d_{s}g_{1}(t,s)) \\& \quad \quad {} - \int _{0}^{1}f \biggl(t,s,x^{*}(s), \int _{0}^{1}h \bigl(s,\theta ,x^{*}( \theta ) \bigr) \,d_{\theta }g^{*}_{2}(s,\theta ) \biggr) \,d_{s}g^{*}_{1}(t,s) \biggr\vert \\& \quad \leq \int _{0}^{1} \biggl\vert f \biggl(t,s,x(s), \int _{0}^{1} h \bigl(s, \theta ,x(\theta ) \bigr) \,d_{\theta }g_{2}(s,\theta ) \biggr) \\& \quad \quad {} - f \biggl(t,s,x^{*}(s), \int _{0}^{1} h \bigl(s,\theta ,x^{*}( \theta ) \bigr) \,d_{ \theta }g_{2}(s,\theta ) \biggr) \bigl\vert \,d_{s}g_{1}(t,s) \\& \quad\quad {} + \bigr\vert \int _{0}^{1}f \biggl(t,s,x^{*}(s), \int _{0}^{1} h \bigl(s,\theta ,x^{*}( \theta ) \bigr) \,d_{\theta }g_{2}(s,\theta ) \biggr) \\& \quad \quad {} - f \biggl(t,s,x^{*}(s), \int _{0}^{1} h \bigl(s,\theta ,x^{*}( \theta ) \bigr) \,d_{ \theta }g^{*}_{2}(s,\theta ) \biggr) \,d_{s}g^{*}_{1}(t,s) \biggr\vert \\& \quad \leq \int _{0}^{1}k_{1} \biggl( \bigl\vert x(s)-x^{*}(s) \bigr\vert \\& \quad \quad {} + \int _{0}^{1} \bigl\vert h \bigl(s,\theta ,x( \theta ) \bigr)-h \bigl(s,\theta ,x^{*}(\theta ) \bigr) \bigr\vert \,d_{ \theta }g_{2}(s,\theta ) \biggr)\,d_{s}g_{1}(t,s) \\& \quad\quad {} + \biggl\vert \int _{0}^{1}f \biggl(t,s,x^{*}(s), \int _{0}^{1}h \bigl(s,\theta ,x^{*}( \theta ) \bigr) \,d_{\theta }g_{2}(s,\theta ) \biggr) \,d_{s}g_{1}(t,s)) \\& \quad \quad {} - \int _{0}^{1}f \biggl(t,s,x^{*}(s), \int _{0}^{1}h \bigl(s,\theta ,x^{*}( \theta ) \bigr) \,d_{\theta }g^{*}_{2}(s,\theta ) \biggr) \,d_{s}g_{1}(t,s)) \\& \quad \quad {} + \int _{0}^{1}f \biggl(t,s,x^{*}(s), \int _{0}^{1}h \bigl(s,\theta ,x^{*}( \theta ) \bigr) \,d_{\theta }g^{*}_{2}(s,\theta ) \biggr) \,d_{s}g_{1}(t,s)) \\& \quad \quad {} - \int _{0}^{1}f \biggl(t,s,x^{*}(s), \int _{0}^{1}h \bigl(s,\theta ,x^{*}( \theta ) \bigr) \,d_{\theta }g^{*}_{2}(s,\theta ) \biggr) \,d_{s}g^{*}_{1}(t,s)) \biggr\vert \\& \quad \leq \int _{0}^{1}k \biggl( \bigl\vert x(s)-x^{*}(s) \bigr\vert + \int _{0}^{1}k \bigl\vert x(\theta )-x^{*}( \theta ) \bigr\vert \,d_{\theta }g_{2}(s, \theta ) \biggr)\,d_{s}g_{1}(t,s) \\& \quad \quad {} + \int _{0}^{1} \biggl\vert f \biggl(t,s,x^{*}(s), \int _{0}^{1}h \bigl(s,\theta ,x^{*}( \theta ) \bigr) \,d_{\theta }g_{2}(s,\theta ) \biggr) \\& \quad \quad {} - f \biggl(t,s,x^{*}(s), \int _{0}^{1}h \bigl(s,\theta ,x^{*}( \theta ) \bigr) \,d_{ \theta }g^{*}_{2}(s,\theta ) \biggr) \biggl\vert \,d_{s}g_{1}(t,s)) \\& \quad \quad {} + \int _{0}^{1} \biggr\vert f \biggl(t,s,x^{*}(s), \int _{0}^{1}h \bigl(s,\theta ,x^{*}( \theta ) \bigr) \,d_{\theta }g^{*}_{2}(s,\theta ) \biggr) \biggr\vert \bigl[d_{s}g_{1}(t,s)-d_{s}g^{*}_{1}(t,s) \bigr] \\& \quad \leq \int _{0}^{1}k \biggl( \bigl\vert x(s)-x^{*}(s) \bigr\vert + \int _{0}^{1}k \bigl\vert x(\theta )-x^{*}( \theta ) \bigr\vert \,d_{\theta }g_{2}(s, \theta ) \biggr)\,d_{s}g_{1}(t,s) \\& \quad \quad {} + \int _{0}^{1}k \biggl( \biggl\vert \int _{0}^{1}h \bigl(s,\theta ,x^{*}( \theta ) \bigr) \,d_{ \theta }g_{2}(s,\theta ) - \int _{0}^{1}h \bigl(s,\theta ,x^{*}( \theta ) \bigr) \,d_{ \theta }g^{*}_{2}(s,\theta ) \biggr\vert \biggr)\,d_{s}g_{1}(t,s)) \\& \quad \quad {} + \int _{0}^{1} \biggl\vert f \biggl(t,s,x^{*}(s), \int _{0}^{1}h \bigl(s,\theta ,x^{*}( \theta ) \bigr) \,d_{\theta }g^{*}_{2}(s,\theta ) \biggr) \biggr\vert \bigl[d_{s}g_{1}(t,s)-d_{s}g^{*}_{1}(t,s) \bigr] \\& \quad \leq \int _{0}^{1}k \biggl( \bigl\vert x(s)-x^{*}(s) \bigr\vert + \int _{0}^{1}k \bigl\vert x(\theta )-x^{*}( \theta ) \bigr\vert \,d_{\theta }g_{2}(s, \theta ) \biggr)\,d_{s}g_{1}(t,s) \\& \quad \quad {} + \int _{0}^{1}k \biggl( \int _{0}^{1} \bigl\vert h \bigl(s,\theta ,x^{*}(\theta ) \bigr) \bigr\vert \bigl[ d_{\theta }g_{2}(s, \theta )- d_{\theta }g^{*}_{2}(s,\theta ) \bigr] \biggr) \,d_{s}g_{1}(t,s)) \\& \quad \quad {} + \int _{0}^{1} \biggl[ m+ k \biggl( \bigl\vert x^{*}(s) \bigr\vert + \int _{0}^{1} \bigl\vert h \bigl(s,\theta ,x^{*}( \theta ) \bigr) \bigr\vert \,d_{\theta}g^{*}_{2}(s, \theta ) \biggr) \biggr] \bigl[d_{s}g_{1}(t,s)-d_{s}g^{*}_{1}(t,s) \bigr] \\& \quad \leq \int _{0}^{1}k \biggl( \bigl\vert x(s)-x^{*}(s) \bigr\vert + \int _{0}^{1}k \bigl\vert x(\theta )-x^{*}( \theta ) \bigr\vert \,d_{\theta}g_{2}(s, \theta ) \biggr)\,d_{s}g_{1}(t,s) \\& \quad \quad {} + \int _{0}^{1}k \biggl( \int _{0}^{1} \bigl[m+k \bigl\vert x^{*}( \theta ) \bigr\vert \bigr] \bigl[ d_{\theta }g_{2}(s, \theta )- d_{\theta }g^{*}_{2}(s,\theta ) \bigr] \biggr) \,d_{s}g_{1}(t,s) \\& \quad\quad {} + \int _{0}^{1} \biggl[m+ k \biggl( \bigl\vert x^{*}(s) \bigr\vert + \int _{0}^{1} \bigl[m+k \bigl\vert x^{*}( \theta ) \bigr\vert \bigr] \,d_{\theta}g^{*}_{2}(s, \theta ) \biggr) \biggr] \bigl[d_{s}g_{1}(t,s)-d_{s}g^{*}_{1}(t,s) \bigr] \\& \quad \leq k \mu \bigl\Vert x-x^{*} \bigr\Vert +k^{2}\mu ^{2} \bigl\Vert x-x^{*} \bigr\Vert +k[m+kr]\mu \bigl[ g_{2}(s,1)- g^{*}_{2}(s,1) \bigr] \\& \quad \quad {} + \bigl[m+k[r+m+kr] \bigr]\mu \bigl[ g_{1}(t,1)- g^{*}_{1}(t,1) \bigr]. \end{aligned}$$

Taking the supremum over \(t\in I\), we get

$$\begin{aligned} \bigl\Vert x-x^{*} \bigr\Vert \leq &k \mu \bigl\Vert x-x^{*} \bigr\Vert +k^{2}\mu ^{2} \bigl\Vert x-x^{*} \bigr\Vert +[km+kr] \mu \delta + \bigl[m+k[r+kr+m] \bigr]\mu \delta . \end{aligned}$$

Then

$$\begin{aligned} \bigl\Vert x-x^{*} \bigr\Vert \leq &\frac{(2km+2kr+k^{2}r+m)\mu \delta }{1-(k \mu +k^{2}\mu ^{2})}= \epsilon . \end{aligned}$$

Now we get that the solution of (2.1) continuously depends on the functions \(g_{i}\), \(i=1,2\). □

3 Existence of solutions II

Now we replace assumptions (ii) a), (vi) by

(\(\mathrm{ii} ^{*}\)):
\(\mathrm{a}^{*}\)):

\(f:[0,1]\times [0,1]\times R \times R \rightarrow R \) is a function, and there exist two continuous functions \(m_{1},k_{1}:[0,1]\times [0,1]\rightarrow R \) such that

$$ \bigl\vert f(t,s,x,y) \bigr\vert \leq m_{1}(t,s)+k_{1}(t,s) \vert x \vert \cdot \vert y \vert . $$
(\(\mathrm{vi} ^{*}\)):

There exists a positive root l of the algebraic equation

$$ \mu ^{2}k^{2} l^{2}+ \bigl(k\mu ^{2}m-1 \bigr) l+(a+m \mu )=0. $$

Theorem 3.1

Let the assumptions of Theorem 2.3be satisfied with (ii) a) and (vi) replaced by (\(ii^{*}\)) \(a^{*})\) and (\(vi^{*}\)), respectively. Then equation (2.1) has at least one solution \(x\in C[0,1]\).

Proof

Define the operator \(A^{*}\) by

$$ A^{*} x(t)= a(t)+ \int _{0}^{1}f \biggl(t,s,x(s), \int _{0}^{1}h \bigl(s, \theta ,x(\theta ) \bigr) \,d_{\theta}g_{2}(s,\theta ) \biggr)\,d_{s}g_{1}(t,s), \quad t\in [0,1], $$

and define the set

$$ Q_{l}= \bigl\{ x \in R: \vert x \vert \leq l \bigr\} \subseteq C \bigl([0,1] \bigr), $$

where l is a positive root of the algebraic equation

$$ \mu ^{2}k^{2} l^{2}+ \bigl(k\mu ^{2}m-1 \bigr) l+(a+m \mu )=0. $$

It is clear that \(Q_{l}\) is a nonempty, bounded, closed, and convex set.

Now let \(x\in Q_{l} \). Then

$$\begin{aligned}& \bigl\vert A^{*} x(t) \bigr\vert \\& \quad = \biggl\vert a(t)+ \int _{0}^{1}f \biggl(t,s,x(s), \int _{0}^{1}h \bigl(s,\theta ,x( \theta ) \bigr) \,d_{\theta}g_{2}(s,\theta ) \biggr)\,d_{s}g_{1}(t,s) \biggr\vert \\& \quad \leq a+ \int _{0}^{1} \biggl\vert f \biggl(t,s,x(s), \int _{0}^{1}h \bigl(s,\theta ,x( \theta ) \bigr) \,d_{\theta}g_{2}(s,\theta ) \biggr) \biggr\vert \,d_{s}g_{1}(t,s) \\& \quad \leq a+ \int _{0}^{1} \biggl(m_{1}(t,s)+k_{1}(t,s) \biggl( \bigl\vert x(t) \bigr\vert \cdot \biggl\vert \int _{0}^{1}h \bigl(s,\theta ,x(\theta ) \bigr) \,d_{\theta}g_{2}(s,\theta ) \biggr) \biggr) \biggr\vert \,d_{s}g_{1}(t,s) \\& \quad \leq a+ \int _{0}^{1} (m_{1}(t,s)+k_{1}(t,s) ( \bigl\vert x(t) \bigr\vert \cdot \int _{0}^{1} \bigl(m_{2}(s, \theta )+k_{2}(s,\theta ) \bigl\vert x(\theta ) \bigr\vert \,d_{\theta}g_{2}(s,\theta ) \bigr)\,d_{s}g_{1}(t,s) \\& \quad \leq a+ \int _{0}^{1}(m_{1}(t,s)+k_{1}(t,s) \bigl( \bigl\vert x(t) \bigr\vert \cdot (m+kl) \mu \bigr) \,d_{s}g_{1}(t,s) \\& \quad \leq a+ \bigl(m+k \bigl(l\cdot (m+k l) \mu \bigr) \bigr)\mu \leq l. \end{aligned}$$

This proves that \(A^{*}: Q_{l} \rightarrow Q_{l} \) and the class \(\{A^{*} x\}\) is uniformly bounded on \(Q_{l}\).

Now for \(x\in Q_{r} \) and \(y(s)=\int _{0}^{1}h(s,\theta ,x(\theta )) \,d_{\theta}g_{2}(s,\theta )\), define the set

$$\begin{aligned} \theta (\delta )={}&\sup \bigl\{ \bigl\vert f(t_{2},s,x,y)-f(t_{1},s,x, y) \bigr\vert : t_{1},t_{2}, s \in [0,1], t_{1}< t_{2}, \\ & \vert t_{2}-t_{1} \vert < \delta , \vert x \vert \leq l, \vert y \vert \leq l \bigr\} . \end{aligned}$$

Then from the uniform continuity of the function \(f: [0,1]\times [0,1]\times Q_{l}\times Q_{l} \rightarrow R \) and assumption (\(\mathrm{ii} ^{*}\)) we deduce that \(\theta (\delta ) \rightarrow 0 \) as \(\delta \rightarrow 0\), independently of \(x \in Q_{l}\).

Now let \(t_{2}, t_{1} \in [0,1] \) be such that \(\vert t_{2}-t_{1} \vert <\delta \). Then we have

$$\begin{aligned}& \bigl\vert A^{*}x(t_{2})- A^{*}x(t_{1}) \bigr\vert \\& \quad = \biggl\vert a(t_{2})+ \int _{0}^{1}f \biggl( t_{2},s,x(s), \int _{0}^{1}h \bigl(s, \theta ,x(\theta ) \bigr) \,d_{\theta}g_{2}(s,\theta ) \biggr)\,d_{s}g_{1}(t_{2},s) \\& \quad \quad {} - a(t_{1})- \int _{0}^{1}f \biggl(t_{1},s,x(s), \int _{0}^{1}h \bigl(s, \theta ,x(\theta ) \bigr) \,d_{\theta}g_{2}(s,\theta ) \biggr)\,d_{s}g_{1}(t_{1},s) \biggr\vert \\& \quad \leq \bigl\vert a(t_{2})- a(t_{1}) \bigr\vert + \biggl\vert \int _{0}^{1}f \biggl(t_{2},s,x(s), \int _{0}^{1}h \bigl(s,\theta ,x(\theta ) \bigr) \,d_{\theta}g_{2}(s,\theta ) \biggr)\,d_{s}g_{1}(t_{2},s) \\& \quad \quad {} - \int _{0}^{1}f \biggl(t_{1},s,x(s), \int _{0}^{1}h \bigl(s,\theta ,x( \theta ) \bigr) \,d_{\theta}g_{2}(s,\theta ) \biggr)\,d_{s}g_{1}(t_{1},s) \biggr\vert \\& \quad \leq \bigl\vert a(t_{2})- a(t_{1}) \bigr\vert \\& \quad \quad {} + \biggl\vert \int _{0}^{1}f \bigl(t_{2},s,x(s),y(s) \bigr)\,d_{s}g_{1}(t_{2},s)- \int _{0}^{1}f \bigl(t_{1},s,x(s),y(s) \bigr)\,d_{s}g_{1}(t_{2},s) \\& \quad \quad {} + \int _{0}^{1}f \bigl(t_{1},s,x(s),y(s) \bigr)\,d_{s}g_{1}(t_{2},s)- \int _{0}^{1}f \bigl(t_{1},s,x(s),y(s) \bigr)\,d_{s}g_{1}(t_{1},s) \biggr\vert \\& \quad \leq \bigl\vert a(t_{2})- a(t_{1}) \bigr\vert + \int _{0}^{1} \bigl\vert \bigl(f \bigl(t_{2},s,x(s),y(s) \bigr)- f \bigl(t_{1},s,x(s),y(s) \bigr) \bigr) \bigr\vert \,d_{s}g_{1}(t_{2},s) \\& \quad \quad {} + \int _{0}^{1} \bigl\vert f \bigl(t_{1},s,x(s),y(s) \bigr) \bigr\vert \,d_{s} \bigl[g_{1}(t_{2},s)-g_{1}(t_{1},s) \bigr] \\& \quad \leq \bigl\vert a(t_{2})- a(t_{1}) \bigr\vert \\& \quad \quad {} + \int _{0}^{1}\theta (\delta )\,d_{s}g_{1}(t_{2},s) + \int _{0}^{1} \bigl(m_{1}(t, s)+k_{1}(t, s) \bigl( \vert x \vert \cdot \vert y \vert \bigr) \bigr)\,d_{s} \bigl[g_{1}(t_{2},s)-g_{1}(t_{1},s) \bigr]. \end{aligned}$$

This inequality means that the class of functions \(\{A^{*}{x}\} \) is equicontinuous. Therefore \(A^{*} \) is compact by the Arzelà–Ascoli theorem [25].

Let \(\{x_{n}\}\subset Q_{l}\), \(x_{n}\rightarrow x\). Then

$$\begin{aligned}& A^{*}x_{n}(t) =a(t)+ \int _{0}^{1}f \biggl(t,s,x_{n}(s), \int _{0}^{1}h \bigl(s, \theta ,x_{n}( \theta ) \bigr) \,d_{\theta}g_{2}(s,\theta ) \biggr) \,d_{s}g_{1}(t,s), \\& \begin{aligned} \lim_{n\rightarrow \infty } A^{*}x_{n}(t)&= \lim _{n\rightarrow \infty } \biggl(a(t) \\ &\quad {} + \int _{0}^{1}f \biggl(t,s,x_{n}(s), \int _{0}^{1}h \bigl(s,\theta ,x_{n}( \theta ) \bigr) \,d_{\theta}g_{2}(s,\theta ) \biggr) \,d_{s}g_{1}(t,s) \biggr), \end{aligned} \end{aligned}$$

and by assumption (\(\mathrm{ii} ^{*}\)) (see [23]) we get

$$\begin{aligned}& \lim_{n\rightarrow \infty } A^{*}x_{n}(t) \\& \quad = a(t)+ \int _{0}^{1}\lim_{n\rightarrow \infty } f \biggl(t,s,x_{n}(s), \int _{0}^{1}h \bigl(s,\theta ,x_{n}( \theta ) \bigr)\,d_{\theta}g_{2}(s,\theta ) \biggr) \,d_{s}g_{1}(t,s) \\& \quad = a(t)+ \int _{0}^{1} f \biggl(t,s,\lim_{n\rightarrow \infty }x_{n}(s), \int _{0}^{1}h \Bigl(s,\theta ,\lim _{n\rightarrow \infty }x_{n}(\theta ) \Bigr)\,d_{ \theta }g_{2}(s, \theta ) \biggr)\,d_{s}g_{1}(t,s) \\& \quad = a(t)+ \int _{0}^{1}f \biggl(t,s,x(s), \int _{0}^{1} h \bigl(s,\theta ,x( \theta ) \bigr) \,d_{\theta}g_{2}(s,\theta ) \biggr)\,d_{s}g_{1}(t,s) = A^{*} x(t). \end{aligned}$$

This proves that \(A^{*}x_{n}(t)\rightarrow A^{*} x(t)\) and \(A^{*}\) is continuous. So (see [23]) \(A^{*}\) has at least one fixed point \(x \in Q_{r}\), and (2.1) has at least one solution \(x \in Q_{l}\subset C([0,1])\). □

3.1 Application

Let in equation (2.1), \(h(t,s,x(s))=b_{2}(t)x(s)\),

$$\begin{aligned} g_{1}(t,s) =& \textstyle\begin{cases} t \ln \frac{t+s}{t} & \text{for }t\in (0,1], s\in I, \\ 0 & \text{for }t=0, s\in I, \end{cases}\displaystyle \end{aligned}$$

and

$$\begin{aligned} g_{2}(s,\theta ) =& \textstyle\begin{cases} s \ln \frac{s+\theta }{s} & \text{for }s\in (0,1], \theta \in I, \\ 0 & \text{for }s=0, \theta \in I. \end{cases}\displaystyle \end{aligned}$$

Then \(g_{1}\), \(g_{2}\) satisfy our assumptions (iii)–(v), and we obtain the nonlinear Chandrasekhar functional integral equation

$$ x(t)=a(t)+ \int _{0}^{1}\frac{t}{t+s}f \biggl(t,s,x(s), \int _{0}^{1} \frac{s}{s+\theta }b_{2}(s)x( \theta )\,d\theta \biggr)\,ds. $$
(3.1)

Let, in equation (3.1), \(f(t,s,x(s),y(s))=b_{1}(s)x(s)\cdot y(s)\), where

$$ y(s)= \int _{0}^{1}\frac{s}{s+\theta }b_{2}(s)x( \theta )\,d\theta . $$

Then we obtain the Chandrasekhar quadratic functional integral equation of the form

$$ x(t)=a(t)+ \int _{0}^{1}\frac{t}{t+s}b_{1}(s)x(s) \cdot \biggl( \int _{0}^{1} \frac{s}{s+\theta }b_{2}(s)x( \theta )\,d\theta \biggr)\,ds. $$
(3.2)

Now, under the assumptions of Theorem 3.1, the Chandrasekhar quadratic functional integral equation (3.2) has at least one solution \(x\in C[0,1]\).

3.2 Example

Consider the following Chandrasekhar quadratic functional integral equation:

$$ x(t)=\frac{e^{-t}}{9+e^{t}}+ \int _{0}^{1}\frac{t}{t+s}\cdot \frac{2\cos (s) x(s)}{7e^{2s} (1+\cos ^{2} (s))}\cdot \biggl( \int _{0}^{1} \frac{s}{s+\theta }\cdot \frac{\sin (s)}{4(1+\sin ^{2}(s))} x(\theta )\,d \theta \biggr)\,ds. $$
(3.3)

First, note that equation (3.3) is a particular case of equation (3.2) if we put

$$\begin{aligned} &a(t)=\frac{e^{-t}}{9+e^{t}}, \\ &h \bigl(t,s,x(s) \bigr)=\frac{\sin (t)}{4(1+\sin ^{2}(t))} x(s), \\ &f \bigl(t,s,x(s),y(s) \bigr)=\frac{2\cos (s) x(s)}{7e^{2s} (1+\cos ^{2} (s))} \cdot y(s), \\ &y(s)= \int _{0}^{1}\frac{s}{s+\theta } \frac{\sin (s)}{4(1+\sin ^{2}(s))}x( \theta )\,d\theta , \end{aligned}$$

\(b_{1}(s)=\frac{2\cos (s) }{7e^{2s} (1+\cos ^{2} (s))}\), \(b_{2}(s)=\frac{\sin (s)}{4(1+\sin ^{2}(s))}\), with \(k_{1}=\frac{2}{7}\) and \(k_{2}=\frac{1}{4}\).

Thus conditions (i), (\(\mathrm{ii} ^{*}\)) and (iii) are satisfied with \(a=\frac{1}{10}\), \(k=\frac{1}{4}\), and \(m=0\). By all facts established above, we deduce that condition (\(\mathrm{vi} ^{*}\)) of the form

$$ \mu ^{2}k^{2} l^{2}+ \bigl(k\mu ^{2} m-1 \bigr) l+(a+m \mu )=0 $$

has a positive solution l. For example, if \(l \thickapprox 0.1\) or \(l \thickapprox 33\), then assumption (\(\mathrm{vi} ^{*}\)) will be satisfied if we choose one of this values.

As all the conditions of Theorem 3.1 are satisfied, equation (3.3) has at least one solution \(x\in C[0,1]\).

4 Set-valued problem

Consider the U-S nonlinear functional integral inclusion (1.1),

$$ x(t)\in a(t)+ \int _{0}^{1}F \biggl(t,s,x(s), \int _{0}^{1}h \bigl(s,\theta ,x( \theta ) \bigr) \,d_{\theta}g_{2}(s,\theta ) \biggr)\,d_{s}g_{1}(t,s), \quad t\in I, $$

under the following assumptions:

(i):

\(a: [0,1]\rightarrow [0,1] \) is a continuous function.

\((\mathrm{ii})^{***}\):
  1. (a)

    \(F : [0,1] \times [0,1] \times R \times R \rightarrow P(R) \), is a Lipschitzian set-valued map with a nonempty compact convex subset of \(2^{R}\), with a Lipschitz constant \(k_{1} > 0\):

    $$ \bigl\Vert F(t, s,x_{1},y_{1}) - F(t,s,x_{2},y_{2}) \bigr\Vert \leq k_{1} \bigl( \vert x_{1}-x_{2} \vert + \vert y_{1}-y_{2} \vert \bigr). $$

    Remark. From this assumption and Theorem 1 from [2, Sect. 9, Chap. 1] on the existence of Lipschitzian selection we deduce that the set of Lipschitz selections of F is not empty and there exists \(f\in F\) such that

    $$ \bigl\vert f(t,s,x_{1},y_{1})-f(t,s,x_{2},y_{2}) \bigr\vert \leq k_{1} \bigl( \vert x_{1}-x_{2} \vert + \vert y_{1}-y_{2} \vert \bigr). $$
  2. (b)

    \(h:[0,1]\times [0,1]\times R \rightarrow R \) is a continuous function such that

    $$ \bigl\vert h(t,s,x) \bigr\vert \leq m_{2}(t,s)+k_{2}(t,s) \vert x \vert . $$
  3. (c)

    \(k=\sup_{(t, s)\in [0,1]\times [0,1]} k_{i}(t,s)\) and \(m=\sup_{(t, s)\in [0,1]\times [0,1]} m_{i}(t,s)\).

(iii):

\(g_{i}:[0,1]\times R \rightarrow R\), \(i=1,2\), are continuous with

$$ \mu =\max \bigl\{ \sup \bigl\vert g_{i} \bigl(t,\varphi (t) \bigr) \bigr\vert +\sup \bigl\vert g_{i}(t,0) \bigr\vert \text{ on } [0,1] \bigr\} . $$
(iv):

For all \(t_{1},t_{2}\in [0,1]\), \(t_{1}< t_{2}\), the functions \(s\rightarrow g_{i}(t_{2},s)-g_{i}(t_{1},s)\) are nondecreasing on \([0,1]\).

(v):

\(g_{i}(0,s)= 0\) for any \(s \in [0,1]\).

(vi):

\(k\mu +k^{2}\mu ^{2}<1\).

4.1 Existence of solution

Theorem 4.1

Let assumptions \((i)\)–\((ii)^{***}\), and \((iv)\)–\((vi)\) be satisfied. Then (1.1) has at least one solution \(x\in C[0,1]\).

Proof

By assumption \((\mathrm{ii})^{***}\)-(a) it is clear that the set of Lipschitz selection of F is nonempty. So, the solution of the single-valued (2.1) where \(f \in S_{F}\) is a solution to (1.1).

Note that the Lipschitz selection \(f: [0,1]\times [0,1]\times R \times R \rightarrow R\) satisfies

$$ \bigl\vert f(t,s,x_{1},y_{1})-f(t,s,x_{2},y_{2}) \bigr\vert \leq k_{1} \bigl( \vert x_{1}-x_{2} \vert + \vert y_{1}-y_{2} \vert \bigr). $$

From this condition with \(m_{1}=\sup_{(t,s) \in I \times I} \vert f(t,s,0,0) \vert \) we have

$$ \bigl\vert f \bigl(t,s,x(s),y(s) \bigr) \bigr\vert - \bigl\vert f(t,s,0,0) \bigr\vert \leq \bigl\vert f \bigl(t,s,x(s),y(s) \bigr)-f(t,s,0,0) \bigr\vert \leq k_{1} \bigl( \vert x \vert + \vert y \vert \bigr). $$

Then

$$ \bigl\vert f \bigl(t,s,x(s),y(s) \bigr) \bigr\vert \leq k_{1} \bigl( \vert x \vert + \vert y \vert \bigr)+ \bigl\vert f(t,s,0,0) \bigr\vert , $$

and

$$ \bigl\vert f \bigl(t,s,x(s),y(s) \bigr) \bigr\vert \leq k_{1} \bigl( \vert x \vert + \vert y \vert \bigr)+m_{1}, $$

that is, assumption (ii) of Theorem 2.3 is satisfied. So, all conditions of Theorem 2.3 hold.

Note that if \(x \in C(I,R)\) is a solution of (2.1), then x is a solution to (1.1). □

4.1.1 Continuous dependence on the set of selection \(S_{F}\)

Here we study the continuous dependence on the set \(S_{F}\) of all selections of the set-valued function F.

Definition 4.2

The solution of (1.1) continuously depends on the set \(S_{F}\) if for all \(\epsilon >0\), there exists \(\delta >0 \) such that if

$$\begin{aligned} \bigl\vert f(t,s,x,y)-f^{*}(t,s,x,y) \bigr\vert < &\delta , \quad f, f^{*} \in S_{F} , t\in [0,1], \end{aligned}$$

then \(\Vert x - x^{*} \Vert < \epsilon \).

Now we have the following theorem.

Theorem 4.3

Let the assumptions of Theorem 4.1be satisfied with

$$ \bigl\vert h(t,s,x)-h(t,s,y) \bigr\vert \leq k_{2} \vert x-y \vert . $$

Then the solution of (1.1) continuously depends on the set \(S_{F}\) of all Lipschitzian selections of F.

Proof

For two solutions \(x(t)\) and \(x^{*}(t)\) of (1.1) corresponding to two selections \(f, f^{*} \in S_{F}\), we have

$$\begin{aligned}& \bigl\vert x(t)-x^{*}(t) \bigr\vert \\& \quad = \biggl\vert a(t)+ \int _{0}^{1}f \biggl(t,s,x(s), \int _{0}^{1}f \bigl(s, \theta ,x(\theta ) \bigr) \,d_{\theta}g_{2}(s,\theta ) \biggr)\,d_{s}g_{1}(t,s) \\& \quad \quad {} - a(t)+ \int _{0}^{1}f^{*} \biggl(t,s,x^{*}(s), \int _{0}^{1}h \bigl(s, \theta ,x^{*}( \theta ) \bigr) \,d_{\theta}g_{2}(s,\theta ) \biggr) ) \,d_{s}g_{1}(t,s) \biggr\vert \\& \quad \leq \int _{0}^{1} \biggl\vert f \biggl(t,s,x(s), \int _{0}^{1} h \bigl(s, \theta ,x(\theta ) \bigr) \,d_{\theta}g_{2}(s,\theta ) \biggr) \\& \quad \quad {} - f^{*} \biggl(t,s,x^{*}(s), \int _{0}^{1}h \bigl(s,\theta ,x^{*}( \theta ) \bigr)\,d_{ \theta }g_{2}(s,\theta ) \biggr) ) \biggr\vert \,d_{s} g_{1}(t,s) \\& \quad \leq \int _{0}^{1} \biggl\vert f \biggl(t,s,x(s), \int _{0}^{1} h \bigl(s, \theta ,x(\theta ) \bigr) \,d_{\theta}g_{2}(s,\theta ) \biggr) \\& \quad \quad {} - f \biggl(t,s,x^{*}(s), \int _{0}^{1} h \bigl(s,\theta ,x^{*}( \theta ) \bigr)\,d_{ \theta }g_{2}(s,\theta ) \biggr) \biggl\vert \,d_{s}g_{1}(t,s) \\& \quad \quad {} + \int _{0}^{1} \biggr\vert f \biggl(t,s,x^{*}(s), \int _{0}^{1} h \bigl(s, \theta ,x^{*}( \theta ) \bigr)\,d_{\theta}g_{2}(s,\theta ) \biggr) \\& \quad \quad {} - f^{*} \biggl(t,s,x^{*}(s), \int _{0}^{1} h \bigl(s,\theta ,x^{*}( \theta ) \bigr)\,d_{ \theta }g_{2}(s,\theta ) \biggr) \biggr\vert \,d_{s}g_{1}(t,s) \\& \quad \leq \int _{0}^{1} \biggl\vert f \biggl(t,s,x(s), \int _{0}^{1} h \bigl(s,\theta ,x( \theta ) \bigr) \,d_{\theta}g_{2}(s,\theta ) \biggr) \\& \quad \quad {} - f \biggl(t,s,x^{*}(s), \int _{0}^{1}h \bigl(s,\theta ,x^{*}( \theta ) \bigr)\,d_{\theta}g_{2}(s, \theta ) \biggr) \biggr\vert \,d_{s}g_{1}(t,s) + \delta \int _{0}^{1} \,d_{s}g_{1}(t,s) \\& \quad \leq \int _{0}^{1} \biggl\vert f \biggl(t,s,x(s), \int _{0}^{1} h \bigl(s,\theta ,x( \theta ) \bigr) \,d_{\theta}g_{2}(s,\theta ) \biggr) \\& \quad \quad {} - f \biggl(t,s,x^{*}(s), \int _{0}^{1}h \bigl(s,\theta ,x(\theta ) \bigr) \,d_{\theta}g_{2}(s, \theta ) \biggr) \biggr\vert \,d_{s}g_{1}(t,s) \\& \quad \quad {} + \int _{0}^{1} \biggl\vert f \biggl(t,s,x^{*}(s), \int _{0}^{1}h \bigl(s,\theta ,x( \theta ) \bigr) \,d_{\theta}g_{2}(s,\theta ) \biggr) \\& \quad \quad {} - f \biggl(t,s,x^{*}(s), \int _{0}^{1}h \bigl(s,\theta ,x^{*}( \theta ) \bigr)\,d_{\theta}g_{2}(s, \theta ) \biggr) \biggr\vert \,d_{s}g_{1}(t,s) + \delta \int _{0}^{1} \,d_{s}g_{1}(t,s) \\& \quad \leq \int _{0}^{1}k_{1} \biggl( \bigl\vert x(s)-x^{*}(s) \bigr\vert + \int _{0}^{1} \bigl\vert h \bigl(s, \theta ,x( \theta ) \bigr) -h \bigl(s,\theta ,x^{*}(\theta ) \bigr) \bigr\vert \,d_{\theta}g_{2}(s, \theta ) \biggr) \,d_{s}g_{1}(t,s) \\& \quad \quad {} + \delta \int _{0}^{1} \,d_{s}g_{1}(t,s) \\& \quad \leq \int _{0}^{1} k_{1} \biggl( \bigl\vert x(s)-x^{*}(s) \bigr\vert + \int _{0}^{1} k_{2} \bigl\vert x( \theta )-x^{*}(\theta ) \bigr\vert \,d_{\theta}g_{2}(s, \theta ) \biggr) \,d_{s}g_{1}(t,s) \\& \quad \quad {} + \delta \int _{0}^{1} \,d_{s}g_{1}(t,s). \end{aligned}$$

Now, taking the supremum over \(t\in I\), we get

$$\begin{aligned} \bigl\Vert x-x^{*} \bigr\Vert \leq & k\mu \bigl\Vert x-x^{*} \bigr\Vert + k^{2}\mu ^{2} \bigl\Vert x-x^{*} \bigr\Vert + \delta \mu . \end{aligned}$$

Hence

$$\begin{aligned} \bigl\Vert x-x^{*} \bigr\Vert \leq \frac{\delta \mu }{1-(k\mu + k^{2}\mu ^{2})}=\epsilon . \end{aligned}$$

Thus from last inequality we get

$$\begin{aligned} \bigl\Vert x-x^{*} \bigr\Vert \leq & \epsilon . \end{aligned}$$

This proves the continuous dependence of the solution on the set \(S_{F}\). □

4.2 Set-valued Chandrasekhar nonlinear quadratic functional integral inclusion

Now, as an application of the nonlinear set-valued functional integral equations of U-S type (1.1), we have the following. Let the functions \(g_{i} \) be defined by

$$\begin{aligned} g_{1}(t,s) =& \textstyle\begin{cases} t \ln \frac{t+s}{t} & \text{for }t\in (0,1], s\in I, \\ 0 & \text{for }t=0, s\in I, \end{cases}\displaystyle \end{aligned}$$

and

$$\begin{aligned} g_{2}(s,\theta ) =& \textstyle\begin{cases} s \ln \frac{s+\theta }{s} & \text{for }s\in (0,1], \theta \in I, \\ 0 & \text{for }s=0, \theta \in I. \end{cases}\displaystyle \end{aligned}$$

Let, in (1.1), \(h(t,s,x(s))=b_{2}(s) x(s)\) and \(F (t,s,x(s),y(s) )=F (b_{1}(s) x(s),y(s) )\), where

$$ y(s)= \int _{0}^{s}\frac{s}{s+\theta }b_{2}(s)x( \theta )\,d\theta . $$

Further, since the functions \(g_{i}\) satisfy assumptions (iii)–(v) (see [6]), we obtain the nonlinear Chandrasekhar functional integral inclusion

$$ x(t)\in a(t)+ \int _{0}^{1} \frac{t}{t+s}F \biggl(b_{1}(s)x(s), \int _{0}^{1} \frac{s}{s+\theta } b_{2}(s)x( \theta )\,d\theta \biggr)\,ds, \quad t\in [0,1]. $$
(4.1)

Now we can state the following existence result for (4.1).

Theorem 4.4

Under the assumptions of Theorem 4.1, inclusion (4.1) has at least one continuous solution \(x \in C[0,1]\).

4.3 Example

Consider the following nonlinear Chandrasekhar functional integral inclusion:

$$ x(t)\in te^{-4t}+ \int _{0}^{1} \frac{t}{t+s} \frac{\sqrt{\pi } e^{-2t}x(s)}{\pi +e^{t}} \int _{0}^{1} \frac{s}{s+\theta } \frac{\sqrt{s}}{e^{s+1} }x( \theta )\,d\theta \,ds ,\quad t\in [0,1]. $$
(4.2)

Note that this inclusion is a particular case of inclusion (4.1) if we choose \(F:[0,1]\times \mathbb{R}\to 2^{\mathbb{R}^{+}}\) in (4.2) as follows:

$$ F \bigl(b_{1}(s)x(s),y(s) \bigr)= \biggl[0,\frac{s}{s^{2}+1}x(s) \int _{0}^{1} \frac{s}{s+\theta } \frac{\sqrt{s}}{e^{s+1} } x(\theta ) \,d\theta \,ds \biggr]. $$

Further, note that now the terms involved in (4.1) have the form

$$ a(t)= te^{-4t}, \quad\quad y(s)= \int _{0}^{s}\frac{s}{s+\theta } \frac{1}{{s^{2}+1}}x( \theta )\,d\theta , \quad\quad h \bigl(t,s,x(s) \bigr)= \frac{\sqrt{s}}{e^{s+1}} x( \theta ), $$

with \(b_{1}(s)=\frac{1}{{s^{2}+1}}\) and \(b_{2}(s)=\frac{\sqrt{s}}{e^{s+1}}\).

Let \(f:[0,1]\times {R}\to {R}\) be a continuous map. Note that if \(f \in S_{F}\), then we have

$$ \bigl\vert f \bigl(b_{1}(s)x_{1}(s),y_{1}(s) \bigr)-f \bigl(b_{1}(s)x_{2}(s),y_{2}(s) \bigr) \bigr\vert \leq \frac{\sqrt{\pi }}{e^{2} (\pi +1 )} \vert x_{1}-x_{2} \vert $$

and

$$ \bigl\vert h \bigl(t,s,x_{1}(t) \bigr)-h \bigl(t,s,x_{2}(t) \bigr) \bigr\vert \leq \frac{1}{e^{2}} \vert x_{1}-x_{2} \vert . $$

Thus conditions (i) and \((\mathrm{ii})^{*}\) are satisfied with \(a=e\), \(k_{1}=\frac{\sqrt{\pi }}{e^{2} (\pi +1 )}\), and \(k_{2}=\frac{1}{e^{2}}\).

Moreover, we have

$$ k \mu +k^{2} \mu ^{2}\thickapprox 0.102607< 1. $$

This shows that assumption (vii) is satisfied. So, as all the conditions of Theorem 4.4 are satisfied, inclusion (4.2) has at least one solution \(x \in C[0,1]\).