Asymptotic behavior of Clifford-valued dynamic systems with D-operator on time scales

Abstract

In this paper, a general class of Clifford-valued neutral high-order neural network (HNN) with D-operator on time scales is investigated. In this model, time-varying delays and continuously distributed delays are taken into account. As an extension of the real-valued neural network, the Clifford-valued neural network, which includes a familiar complex-valued neural network and a quaternion-valued neural network as special cases, has been an active research field recently. By utilizing this novel method, which incorporates the differential inequality techniques and the fixed point theorem and time-scale theory of computation, we derive a few sufficient conditions to ensure the existence, uniqueness, and exponential stability of the pseudo almost periodic (PAP) solution of the considered model. The results in this paper are new, even if time scale $\mathbb{T}=\mathbb{R}$ or $\mathbb{T}=\mathbb{Z}$, and complementary to the previously existing works. Furthermore, an example and its numerical simulations are included to demonstrate the validity and advantage of the obtained results.

1 Introduction

The well-known Hopfield neural network (HNN) has been widely studied since it was introduced by John Hopfield in [1]. It has been successfully applied in many different fields, for example, signal processing, combinatorial optimization, and pattern recognition, see [2–5] and the references therein. One of the most critical problems in the study of HNNs with time delays is global exponential stability of the pseudo almost periodic (PAP) solutions. If so, the notion of pseudo-almost periodicity, which is the principal object of this work, was first presented by Zhang [6]. Dads et al. in [7] noted that it will be very valuable to investigate the dynamics of PAP systems with delays. The PAP solutions, which are more complicated and general than anti-periodic, periodic, and than almost periodic solutions, in the context of neural network were investigated in [8–10].

Moreover, some controversial opinions arise due to the ability of continuous neural networks and discrete neural networks to play similar roles in different implementations and applications. But it is not easy to investigate the dynamic properties of continuous-time systems and discrete-time systems, respectively. It is important to note that, in several references, the networks are characterized either by difference equations or by differential equations, i.e., dynamical systems are defined as $\mathbb{Z}$ or $\mathbb{R}$. In his doctoral thesis in 1990, Stefan Hilger [11] first proposed the famous dynamic equation on time scale theory, which has been largely investigated and developed in recent years [12–18]. For example, in [14], the authors investigated the weighted PAP functions on time scales with applications to delayed cellular neural networks. In [12], the authors studied global exponential stability of unique equilibrium for complex-valued neural networks on time scales. The existence and uniqueness of equilibrium for delayed interval neural networks with impulses on time scales was studied in [13].

On the other hand, because high-order Hopfield neural networks (HHNNs) have stronger approximation property, higher fault tolerance, greater storage capacity, and faster convergence rate than lower-order HNNs, the study of HHNNs has recently gained much attention, and there have been many results on the problem of the existence and global exponential stability of equilibrium, anti-periodic solutions, periodic solutions, almost periodic solutions, and PAP solutions of HHNNs in the literature [19–23]. For instance, in [19] the authors discussed a class of impulsive HHNNs system involving leakage time-varying delays. Sufficient conditions for the existence and some kinds of stability of a unique equilibrium point were established by using contraction mapping principle theorem and Lyapunov–Krasovskii functional. In [20], a class of HHNNs with impulse systems was considered. By virtue of Krasnoselski’s fixed point theorem and Lyapunov functions with inequality techniques, they investigated the anti-periodic solutions of this system. Existence and stability of periodic HHNNs with impulses and delays were studied by Zhang and Gui [23]. By using a fixed point theorem, differential inequality techniques, and Lyapunov functional method, Yu and Cai in [22] analyzed the existence and exponential stability of almost-periodic solutions for HHNNs. In [21], the authors investigated the PAP solutions for delayed HHNNs by using differential inequality techniques and Lyapunov functional method.

In addition, Clifford’s algebra was first introduced by William K. Clifford. It has been applied with success to different areas, in particular robot vision, control problems, neural computing, signal processing, and other areas due to its powerful and practical framework for the solution of geometric problems [24, 25]. As generalizations of real, complex, and quaternion-valued neural networks, Clifford-valued neural networks are a family of neural networks whose states and connection weights are Clifford algebraic elements. Since Clifford-valued neural networks have the ability to employ multi-state activation functions to process multi-level information, they have become actively researched in recent years. Recently, the dynamic behaviors of Clifford-valued neural networks were investigated in [9, 26–32].

As well it is known, in biochemical tests of the dynamics of neural networks, the neuronal information may be transferred through chemical reactivity, resulting in a neutral type process. In the recent past, greater effort has been given to the exponential convergence, existence, and analysis of the stability of equilibrium point and PAP solutions for neutral type neural networks (NTNNs) [33–37]. Namely, all NTNNs models taken into account in the above references can be characterized as non-operator-based neutral functional differential equations. In addition, NTNNs with D operator have better meaning than non-operator-based ones in various applications of neural network dynamics [38–44].

Inspired by the above discussions, the aim of this paper is to discuss exponential stability of PAP solution neutral type Clifford HHNNs with D-operator, time-varying delays, and infinite distributed delay on time scales. By using fixed point theorem, the existence and uniqueness of PAP solution of the system are proved. Furthermore, by the differential inequality theory and time-scale theory, sufficient conditions for the global exponential stability of PAP solution are obtained. Finally, an example and their simulations are given to show the effectiveness of the proposed theory. To do this, our contributions lie in four aspects: (a) The study of the existence, the uniqueness, and the global exponential stability of pseudo almost periodic solutions for neutral Clifford-valued HHNNs with D-operator, time-varying delays, and infinite distributed delay on time scales is first advanced. (b) The inclusion of different types of delay: infinite distributed delay and time-varying delay. We generalize the results of the papers [45–47]. (c) In our system, we not only consider the effects of mixed delays on Clifford-valued neural networks, but also the influences of neutral terms on the networks. (d) The neutral Clifford-valued HHNNs with mixed delay on time scales in this paper are more general than those of numerous previous works [9, 20, 45–47].

In this work, we consider the neutral Clifford HHNNs with time-varying delays and D operator as follows:

$$\begin{aligned} & \biggl[x_{i}(t)-p_{i}(t) \int _{0}^{\infty }r_{i}(s) x_{i}(t-s) \nabla s \biggr]^{\nabla } \\ &\quad = - c_{i}(t) x_{i}(t)+\sum _{j=1}^{n} d_{ij}(t) g_{j} \bigl(x_{j}(t) \bigr) +\sum_{j=1}^{n} a_{ij}(t) g_{j} \bigl(x_{j} \bigl(t-\tau _{ij}(t) \bigr) \bigr) \\ &\quad\quad{} +\sum_{j=1}^{n} \sum _{l=1}^{n} \alpha _{ijl}(t) g_{j} \bigl(x_{j} \bigl(t- \eta _{ijl}(t) \bigr) \bigr) g_{l} \bigl(x_{l} \bigl(t-\nu _{ijl}(t) \bigr) \bigr) \\ &\quad\quad{} +\sum_{j=1}^{n} \sum _{l=1}^{n} \beta _{ijl}(t) \int _{0}^{\infty } H_{ijl}(u) g_{j} \bigl(x_{j}(t-u) \bigr)\nabla u \int _{0}^{\infty } K_{ijl}(u) g_{l} \bigl(x_{l}(t-u) \bigr)\nabla u \\ &\quad\quad{} +\sum_{j=1}^{n} b_{ij}(t) \int _{0}^{\infty } N_{ij}(u) g_{j} \bigl(x_{j}(t-u) \bigr) \nabla u+I_{i}(t), \quad t\in \mathbb{T}, \end{aligned}$$

(1)

in which

• n: The number of neurons in layers.

• $\mathbb{T}$ is an almost periodic time scale, which is defined in Sect. 2. The synaptic efficiency.

• $x_{i}\in \mathcal{A}$: The state vector of the ith neuron.

• $c_{i}(\cdot )\in \mathbb{R}^{+}$: The continuous functions.

• $d_{ij}(\cdot )\in \mathcal{A}$: The connection weights at time t.

• $a_{ij}(\cdot ), \alpha _{ijl}(\cdot )\in \mathcal{A}$: The discretely delayed connection weights.

• $b_{ij}(\cdot ), \beta _{ijl}(\cdot ), p_{i}(\cdot )\in \mathcal{A}$ The distributively delayed connection weights.

• $\tau _{ij}(\cdot ), \eta _{ijl}(\cdot ), \nu _{ijl}(\cdot )\in \mathbb{R}^{+}$: Transmission delay.

• $N_{ij}(\cdot ), K_{ijl}(\cdot ), H_{ijl}(\cdot ), r_{i}(\cdot ) \in \mathbb{R}^{+}$: The kernel.

• $I_{i}(\cdot )\in \mathcal{A}$: The external inputs.

• $g_{j}(\cdot )\in \mathcal{A}$: The activation functions.

We should point out that

$$ \textstyle\begin{cases} x^{\Delta }(t)=\frac{dx(t)}{dt}\quad \text{if } \mathbb{T}=\mathbb{R}, \\ x^{\Delta }(t)=\Delta x(t)= x(t+1)- x(t)\quad \text{if } \mathbb{T}= \mathbb{Z}. \end{cases} $$

The initial conditions associated with model (1) are of the following form:

$$\begin{aligned} x_{i}(s)=\varphi _{i}(s), \quad s\in (- \infty ,0]_{\mathbb{T}}, 1\leq i \leq n, \end{aligned}$$

(2)

where $\varphi _{i}(\cdot )$ denotes a real-valued bounded right-dense continuous function defined on $(-\infty ,0]_{\mathbb{T}}$.

For any interval J of $\mathbb{R}$, we indicate by $J_{\mathbb{T}}= J \cap \mathbb{T}$.

Remark 1.1

If $\mathbb{T}=\mathbb{R}$, then model (1) can be reduced to

$$\begin{aligned} & \biggl[x_{i}(t)-p_{i}(t) \int _{0}^{\infty }r_{i}(s) x_{i}(t-s)\,d s \biggr]' \\ &\quad = c_{i}(t) x_{i}(t)+ \sum _{j=1}^{n} d_{ij}(t) g_{j} \bigl(x_{j}(t) \bigr) +\sum_{j=1}^{n} a_{ij}(t) g_{j} \bigl(x_{j} \bigl(t-\tau _{ij}(t) \bigr) \bigr) \\ &\quad\quad{}+\sum_{j=1}^{n} \sum _{l=1}^{n} \alpha _{ijl}(t) g_{j} \bigl(x_{j} \bigl(t- \eta _{ijl}(t) \bigr) \bigr) g_{l} \bigl(x_{l} \bigl(t-\nu _{ijl}(t) \bigr) \bigr) \\ &\quad\quad{} +\sum_{j=1}^{n} \sum _{l=1}^{n} \beta _{ijl}(t) \int _{0}^{\infty } H_{ijl}(u) g_{j} \bigl(x_{j}(t-u) \bigr)\,d u \int _{0}^{\infty } K_{ijl}(u) g_{l} \bigl(x_{l}(t-u) \bigr)\,du \\ &\quad\quad{} +\sum_{j=1}^{n} b_{ij}(t) \int _{0}^{\infty } N_{ij}(u) g_{j} \bigl(x_{j}(t-u) \bigr) \,d u+I_{i}(t), \quad t\in \mathbb{R}, \end{aligned}$$

(3)

if $\mathbb{T}=\mathbb{Z}$, then model (1) can be reduced to

$$\begin{aligned} & \biggl[x_{i}(k+1)-p_{i}(k+1) \int _{0}^{\infty }r_{i}(s) x_{i}(k+1-s)\,d s \biggr]- \biggl[x_{i}(k)-p_{i}(k) \int _{0}^{\infty }r_{i}(s) x_{i}(k-s)\,d s \biggr] \\ &\quad = - c_{i}(k) x_{i}(k)+ \sum _{j=1}^{n} d_{ij}(k) g_{j} \bigl(x_{j}(k) \bigr) + \sum_{j=1}^{n} a_{ij}(k) g_{j} \bigl(x_{j} \bigl(k-\tau _{ij}(k) \bigr) \bigr) \\ &\quad\quad{} + \sum_{j=1}^{n} \sum _{l=1}^{n} \alpha _{ijl}(k) g_{j} \bigl(x_{j} \bigl(k-\eta _{ijl}(t) \bigr) \bigr) g_{l} \bigl(x_{l} \bigl(k-\nu _{ijl}(t) \bigr) \bigr) \\ &\quad\quad{} + \sum_{j=1}^{n} \sum _{l=1}^{n} \beta _{ijl}(k) \int _{0}^{\infty } H_{ijl}(u) g_{j} \bigl(x_{j}(k-u) \bigr)\,d u \int _{0}^{\infty } K_{ijl}(u) g_{l} \bigl(x_{l}(k-u) \bigr)\,du \\ &\quad\quad{} + \sum_{j=1}^{n} b_{ij}(k) \int _{0}^{\infty } N_{ij}(u) g_{j} \bigl(x_{j}(k-u) \bigr) \,d u+I_{i}(k), \quad k\in \mathbb{Z}. \end{aligned}$$

(4)

To our knowledge, no published papers exist on the existence and global exponential stability of PAP solutions for neural networks (3) and (4).

This paper is organized as follows. In Sect. 2, we present several definitions and make some preparations for later sections. In Sects. 3 and 4, on the basis of the results presented in the previous sections, ∇-differential inequalities on time scales, and Banach’s fixed-point theorem, we present sufficient conditions that assure the existence and global exponential stability of PAP solutions to (1). In Sect. 5, we give an illustrative example to show the feasibility and effectiveness of the obtained results in Sects. 3 and 4. Finally, some conclusions are highlighted in Sect. 6.

2 Preliminary

2.1 The time scales calculus

Definition 2.1

([38])

Let $\mathbb{T}$ be a nonempty closed subset (time scale) of $\mathbb{R}$. For $t\in \mathbb{T}$, we define the forward jump operator $\sigma : \mathbb{T}\rightarrow \mathbb{T}$ by $\sigma (t)=\inf \{ s\in \mathbb{T}:s>t \}$, while the backward jump operator $\rho : \mathbb{T}\rightarrow \mathbb{T}$ is defined by $\rho (t)=\sup \{ s\in \mathbb{T}:s< t \}$. The graininess function $\nu : \mathbb{T}\rightarrow \mathbb{R}^{+}$ is defined by $\nu (t)=\sigma (t)-t$.

Definition 2.2

([38])

A point $t\in \mathbb{T}$ is said to be

$$\begin{aligned}& \textstyle\begin{cases} \text{left-dense if } t>\inf \mathbb{T} \text{ and } \rho (t)=t, \\ \text{left-scattered if } \rho (t)< t, \\ \text{right-dense if } t< \sup \mathbb{T} \text{ and } \sigma (t)=t, \\ \text{right-scattered if }\sigma (t)>t. \end{cases}\displaystyle \end{aligned}$$

If $\mathbb{T}$ has a right-scattered minimum m, then $\mathbb{T}_{k}=\mathbb{T}\setminus \{m\}$; otherwise $\mathbb{T}_{k}=\mathbb{T}$.

If $\mathbb{T}$ has a left-scattered maximum m, then $\mathbb{T}^{k}=\mathbb{T}\setminus \{m\}$; otherwise $\mathbb{T}^{k}=\mathbb{T}$.

Definition 2.3

([38])

Let $f:\mathbb{T}\rightarrow \mathbb{R}$ be a function.

f is rd-continuous provided it is continuous at each right-dense point in $\mathbb{T}$ and has a left-sided limit at each left-dense point in $\mathbb{T}$.

The set of rd-continuous functions $f:\mathbb{T}\rightarrow \mathbb{R}$ will be designated by $\mathrm{C}_{\mathrm{rd}}(\mathbb{T},\mathbb{R})$.

Definition 2.4

([38])

Let

∘:

$\rho :\mathbb{T}\rightarrow \mathbb{R}$ be called ν-regressive provided $1+\nu (t)\rho (t)\neq 0$ for all $t\in \mathbb{T}^{k}$.

∘:

$\rho :\mathbb{T}\rightarrow \mathbb{R}$ be called positively regressive provided $1+\nu (t)\rho (t)>0$ for all $t \in \mathbb{T}^{k}$.

∘:

The set of all regressive and rd-continuous functions $\rho : \mathbb{T}\rightarrow \mathbb{R}$ be denoted by $\mathcal{R}=\mathcal{R}(\mathbb{T},\mathbb{R})$,

∘:

The set of all positively regressive and rd-continuous functions $\rho : \mathbb{T}\rightarrow \mathbb{R}$ be denoted by $\mathcal{R}^{+}=\mathcal{R}^{+}(\mathbb{T},\mathbb{R})$.

Definition 2.5

([38])

If $p\in \mathcal{R}$, then we define the exponential function by

$$\begin{aligned} e_{p}(t,s)=\exp \biggl( \int _{s}^{t}\hat{\xi }_{\nu (\tau )} \bigl(p( \tau ) \bigr)\Delta \tau \biggr), \quad \forall t, s\in \mathbb{T}, \end{aligned}$$

where cylinder transformation is as in

$$ \hat{\xi }_{h}(s):= \textstyle\begin{cases} -\frac{1}{h}\log (1+sh) &\text{if } h\neq 0, \\ -s &\text{if } h=0. \end{cases} $$

Definition 2.6

([38])

Let $p_{1}, p_{2}:\mathbb{T}\rightarrow \mathbb{R}$ be two regressive functions, define

• a) $(p_{1}\oplus p_{2})(t)=p_{1}(t)+p_{2}(t)-\nu p_{1}(t)p_{2}(t)$,

• b) $\ominus p_{1}(t)=-\frac{p_{1}(t)}{1-\nu p_{1}(t)}$,

• c) $p_{1}\ominus p_{2}=p_{1}\oplus (\ominus p_{2})$.

Lemma 2.7

([38])

For $t\geq s$, suppose that $c(t)\geq 0$, then $e_{c}(t,s)\geq 1$.

Lemma 2.8

([38])

For all $t, s \in \mathbb{T}$, suppose that $c\in \mathcal{R}^{+}$, then $e_{c}(t,s)>0$.

Lemma 2.9

([38])

For a function $f:\mathbb{T}\rightarrow \mathbb{R}$ and $t\in \mathbb{T}^{k}$, we define the delta derivative of f at t, denoted by $f^{\Delta }(t)$, to be the number (provided it exists) with the property that given any $\epsilon > 0$ there is a neighborhood U of t such that

$$ \bigl\vert f \bigl(\sigma (t) \bigr)-f(s)-f^{\Delta }(t) \bigl(\sigma (t)-s \bigr) \bigr\vert < \epsilon \bigl\vert \sigma (t)-s \bigr\vert $$

for all $s \in \mathbb{T}$.

Lemma 2.10

([38])

Let f, g be a Δ-differentiable function on $\mathbb{T}$, then

$(a)$:

$(fg)^{\Delta }(t)=f^{\Delta }(t)g(t)+f(\sigma (t))g^{\Delta }(t)=f(t)g^{\Delta }(t)+f^{\Delta }(t)g(\sigma (t))$,

$(b)$:

$(\rho _{1}f+\rho _{2}g)^{\Delta }=\rho _{1}f^{\Delta }+\rho _{2}g^{\Delta }$ for any constant $\rho _{1}$, $\rho _{2}$.

Definition 2.11

([38])

If f is rd-continuous, then there exists a function F such that $F^{\Delta }(t) = f(t)$, and we define $\int _{a}^{b}f(t)\Delta t=F(b)-F(a)$.

Lemma 2.12

([38])

Assume that $c:\mathbb{T}\rightarrow \mathbb{R}$ is a regressive function, then

• 1) $e_{0}(t,s)\equiv 1$ and $e_{c}(t,t)\equiv 1$,

• 2) $e_{c}(t,s)=\frac{1}{e_{p}(s,t)}=e_{\ominus _{p}}(s,t)$,

• 3) $e_{c}(t,s)e_{c}(s,r)=e_{c}(t,r)$,

• 4) $(e_{c}(t,s))^{\Delta }=c(t)e_{c}(t,s)$,

• 5) $e_{c}(\sigma (t),s)= (1+\nu (t)c(t) )e_{c}(t,s)$,

• 6) $\int _{p}^{q} c(t) e_{c}(a, \sigma (t)) \Delta t=e_{c}(a, p)-e_{c}(a, q)$, $\forall a, p, q\in \mathbb{T}$.

Throughout this article, we restrict our analysis on almost periodic time scales.

Definition 2.13

([14])

A time scale $\mathbb{T}$ is said to be an almost periodic time scale if

$$ \Pi = \{ \tau \in \mathbb{R}, t\pm \tau \in \mathbb{T}, \forall t\in \mathbb{R} \} \neq \{0\}. $$

2.2 Clifford algebra

In this sub-section, we review some definitions, notations, and some basic results of Clifford’s algebra. For further details, the reader is referred to [48, 49]. Clifford’s real algebra on $\mathbb{R}^{p}$ is defined as

$$ \mathcal{A}= \biggl\{ \sum_{A\subseteq \{1, \ldots ,p\}} a_{A}e_{A},a_{A}\in \mathbb{R} \biggr\} , $$

where

✓:

$e_{A}=e_{h_{1}}e_{h_{2}}\cdots e_{h_{v}}$, $A= \{ h_{1},\ldots ,h_{v} \}$, $1\leq h_{1}< h_{2}<\cdots <h_{v} \leq p$.

✓:

$e_{\varnothing }=e_{0}=1$ and $e_{\{h\}}=e_{h}$, $h=1,\ldots ,p$, are called Clifford generators which satisfy the relations

• $e_{j}^{2}=-1$, $j=1,\ldots ,p$,

• $e_{j}e_{i}+e_{i}e_{j}=0$, $j\neq i$, $j, i=1,\ldots ,p$.

✓:

$e_{h_{1}}e_{h_{2}}\cdots e_{h_{v}}=e_{h_{1}h_{2}\cdots h_{v}}$ (the product of Clifford generators).

Let $\Theta = \{ \varnothing ,1,\ldots ,A,\ldots ,12\cdots p \}$, then it is clear to see that

$$ \mathcal{A}= \biggl\{ \sum_{A} a_{A}e_{A},a_{A} \in \mathbb{R} \biggr\} , $$

where $\sum_{A}$ is short for $\sum_{A\in \Theta }$ and $\mathcal{A}$ is isomorphic to $\mathbb{R}^{2p}$. The involution of z is defined as $\overline{z}=\sum_{A} z_{A}\overline{e}_{A}$ for any $z=\sum_{A\in \Theta } z_{A}\in \mathcal{A}$, where $\overline{e}_{A}=(-1)^{\frac{\mu [A](\mu [A]+1)}{2}}e_{A}$, and

$$ \mu [A]= \textstyle\begin{cases} 0 &\text{if } A=\varnothing , \\ v &\text{if } A=h_{1}h_{2}\cdots h_{v}. \end{cases} $$

It is directly deduced from the definition that $e_{A}\overline{e}_{A}=\overline{e}_{A} e_{A}=1$. In addition, for any Clifford number $z =\sum_{A} z^{A} e_{A}$, its involution can be indicated by $\overline{z}=\sum_{A} z^{A} \overline{e}_{A}$. For a Clifford-valued function $y=\sum_{A} y^{A} e_{A}:\mathbb{R}\rightarrow \mathcal{A}$, its derivative is donated by $\dot{y}(t)=\sum_{A} \dot{y}^{A} e_{A}$, where $y^{A}:\mathbb{R}\rightarrow \mathbb{R}$, $A\in \Theta$. Due to $e_{B}\overline{e}_{A}=(-1)^{\frac{\mu [A](\mu [A]+1)}{2}}e_{B}e_{A}$, we can simplify and express $e_{B}\overline{e}_{A}=e_{C}$ or $e_{B}\overline{e}_{A}=-e_{C}$, with $e_{C}$ being a basis for Clifford’s algebra $\mathcal{A}$, meaning that we can get a unique corresponding basis $e_{C}$ for given $e_{B}\overline{e}_{A}$. Define

$$ \chi [B.\overline{A}]= \textstyle\begin{cases} 0 &\text{if } e_{B}\overline{e}_{A}=e_{C}, \\ 1 &\text{if } e_{B}\overline{e}_{A}=-e_{C}, \end{cases} $$

then $e_{B}\overline{e}_{A}=(-1)^{\chi [B.\overline{A}]}e_{C}$. Furthermore, we can find unique $F^{C}$ satisfying $F^{B.\overline{A}}=(-1)^{\chi [B.\overline{A}]}F^{C}$ for $e_{B}\overline{e}_{A}=(-1)^{\chi [B.\overline{A}]}e_{C}$, for any $F\in \mathcal{A}$. Therefore,

$$\begin{aligned} F^{B.\overline{A}}e_{B}\overline{e}_{A}=F^{B.\overline{A}}(-1)^{\chi [B. \overline{A}]}e_{C}=(-1)^{\chi [B.\overline{A}]}F^{C}(-1)^{\chi [B. \overline{A}]}e_{C}=F^{c}e_{C}, \end{aligned}$$

and $F=\sum_{C} F^{C} e_{C}\in \mathcal{A}$. We set the norm of $\mathcal{A}$ as $\Vert x \Vert _{\mathcal{A}}=\max_{A}\{ \vert x^{A} \vert \}$.

2.3 Notations

The following notations and concepts are introduced throughout this work:

• $\mathbb{R}^{n}$: Indicates the set of all n real matrices.

• $\mathcal{A}^{n}$: Means an n-dimensional real Clifford vector space. For $x= (x_{1},\ldots ,x_{n} )^{T}\in \mathcal{A}^{n}$, we define $\Vert x \Vert _{\mathcal{A}^{n}}=\max_{1\leq i\leq n}\{ \Vert x_{i} \Vert _{\mathcal{A}}\}$.

• $C(\mathbb{R},\mathcal{A})$: Means the set of continuous functions from $\mathbb{T}$ to $\mathcal{A}$.

• $C^{1}(\mathbb{T},\mathcal{A})$: Means the set of continuous functions with continuous derivatives from $\mathbb{T}$ to $\mathcal{A}$.

• $BC(\mathbb{T},\mathcal{A}^{n})$: Indicates the set of all bounded continuous functions from $\mathbb{T}$ to $\mathcal{A}^{n}$. It should be noted that $(BC(\mathbb{T},\mathcal{A}^{n}), \Vert \cdot \Vert _{0} )$ is a Banach space with the norm $\Vert x \Vert _{0}=\max_{1\leq i\leq n} \{ \sup_{t\in \mathbb{T}} \Vert x_{i}(t) \Vert _{\mathcal{A}} \}$, where $x= (x_{1},\ldots ,x_{n} )^{T}\in BC(\mathbb{T}, \mathcal{A}^{n})$.

2.4 Pseudo almost periodic function on time scales

We recall in this sub-section some basic definitions, notations, and results of almost periodicity and pseudo almost periodicity on time scales.

Definition 2.14

([44])

Let $\mathbb{T}$ be an almost periodic time scale. A function $f_{0}: \mathbb{T} \rightarrow X^{n}$ is said to be almost periodic on $\mathbb{T}$ if, for any $\epsilon > 0$, the set

$$ E(\epsilon , f_{0} ) = \bigl\{ \omega \in \Pi : \bigl\Vert f_{0} (t + \omega ) - f_{0} (t) \bigr\Vert < \epsilon , \forall t \in \mathbb{T} \bigr\} $$

is relatively dense, meaning that, for any $\epsilon > 0$, there is a constant $l(\epsilon ) > 0$ such that each interval of length $l(\epsilon )$ contains at least one $\omega \in E(\epsilon , f )$ such that

$$ \bigl\Vert f_{0} (t +\omega ) - f_{0} (t) \bigr\Vert < \epsilon , \quad \forall t \in \mathbb{T}. $$

The set $E(\epsilon , f_{0} )$ is said to be the ϵ-translation set of $f_{0} (t)$, ω is said to be the ϵ-translation number of $f_{0} (t)$, and $l(\epsilon )$ is said to be the inclusion of $E(\epsilon , f_{0} )$.

We introduce a few notations in the following:

$$ \begin{aligned} \operatorname{PAP}_{0} \bigl(\mathbb{T},\mathbb{R}^{n} \bigr)={}& \biggl\{ f_{1}\in BC \bigl( \mathbb{T},X^{n} \bigr) : f_{1} \text{ is } \Delta \text{-measurable},\\ &{} \lim _{\mu \rightarrow +\infty } \frac{1}{2 \mu } \int _{-\mu }^{\mu } \bigl\Vert f_{1}(s) \bigr\Vert \Delta s =0, \mu \in \Pi \biggr\} . \end{aligned} $$

Definition 2.15

([44])

A function $f(\cdot ) \in BC(\mathbb{T},X^{n})$ is called pseudo almost periodic if $f(\cdot ) = f_{0} (\cdot )+ f_{1}(\cdot )$, where $f_{0}(\cdot ) \in \operatorname{AP}(\mathbb{T},X^{n})$ and $f_{1}(\cdot )\in \operatorname{PAP}_{0}(\mathbb{T},X^{n})$.

We refer to all of these functions as $\operatorname{PAP}(\mathbb{T},X^{n})$.

Remark 2.16

Note that an almost periodic pseudo function decomposition on the time scales given in Definition 2.15 is unique.

Lemma 2.17

([44])

Let $B(t)$ be an $n\times n$ rd-continuous matrix function on $\mathbb{T}$, the linear system

$$\begin{aligned} z^{\Delta }(t) = B(t)z(t),\quad t\in \mathbb{T} \end{aligned}$$

(5)

is said to admit an exponential dichotomy on $\mathbb{T}$ if there exist positive constants K, ξ, projection q, and a fundamental solution matrix $Z(t)$ of system (1) satisfying the following inequality:

$$\begin{aligned} \begin{gathered} \bigl\vert Z(t)q Z^{-1}(s) \bigr\vert \leq K e_{\ominus (t,s)}; \quad s, t\in \mathbb{T}, t \geq s, \\ \bigl\vert Z(t) (I - q)Z^{-1}(s) \bigr\vert \leq Ke_{\ominus (s,t)}; \quad s,t \in \mathbb{T}, t \leq s, \end{gathered} \end{aligned}$$

where $\vert \cdot \vert$ is a matrix norm on $\mathbb{T}$.

Lemma 2.18

([44])

Assume that $B(\cdot )$ is almost periodic and suppose that $h(\cdot )\in \operatorname{PAP}(\mathbb{T},X^{n})$, system (5) admits an exponential dichotomy, therefore the system

$$\begin{aligned} z^{\Delta }(t) = B(t)z(t) + h(t), \quad t \in \mathbb{T}, \end{aligned}$$

(6)

has a unique and bounded solution $z(\cdot )\in \operatorname{PAP}(\mathbb{T},X^{n})$, and $z(\cdot )$ is described as the following:

$$\begin{aligned} z(t)= \int _{-\infty }^{t}Z(t)q Z^{-1} \bigl(\sigma (s) \bigr)h(s) \Delta s- \int ^{+\infty }_{t}Z(t) (I - q) Z^{-1} \bigl( \sigma (s) \bigr)h(s) \Delta s, \end{aligned}$$

where $Z(\cdot )$ is the fundamental solution matrix of system (5).

Lemma 2.19

([44])

Let $b_{i}(\cdot )>0$ and $-b_{i}(\cdot )\in \mathcal{R}^{+}$. If $\min_{1\leq i\leq n} \{ \inf_{t\in \mathbb{T}}b_{i}(t) \} >0$, therefore the linear system

$$ z^{\Delta }(t)=\operatorname{diag} \bigl(-b_{1}(t),\ldots ,-b_{n}(t) \bigr)z(t) $$

admits an exponential dichotomy on $\mathbb{T}$.

Definition 2.20

([9])

The PAP solution $x^{*}(t)= (x^{*}_{1}(t),\ldots ,x^{*}_{n}(t) )^{T}$ of neural networks (1) with the initial value $\varphi ^{*}(s)= (\varphi _{1}^{*}(t),\ldots ,\varphi _{n}^{*}(t) )^{T}$ is called globally exponentially stable. There exist a constant $\lambda >0$ and $M>1$ such that every solution $x(t)= (x_{1}(t),\ldots ,x_{n}(t) )$ of neural networks (1) with the initial value $\varphi (t)= (\varphi _{1}(t),\ldots ,\varphi _{n}(t) )^{T}$ satisfies $\Vert x(t)-x^{*}(t) \Vert _{\mathcal{A}^{n}}\leq Me^{-\lambda t} \Vert \varphi - \varphi ^{*} \Vert _{\xi }$ for all $t\in (0,+\infty )$, where

$$\begin{aligned} \bigl\Vert \varphi -\varphi ^{*} \bigr\Vert _{\xi } =& \sup_{t\leq 0} \biggl\{ \max_{1\leq i\leq n}\xi ^{-1}_{i} \biggl\Vert \biggl[\varphi _{i}(t)-p_{i}(t) \int _{0}^{\infty } r_{i}(s)\varphi _{i}(t-s)\Delta s \biggr] \\ & {} - \biggl[\varphi ^{*}_{i}(t)-p_{i}(t) \int _{0}^{\infty } r_{i}(s) \varphi ^{*}_{i}(t-s)\Delta s \biggr] \biggr\Vert _{\mathcal{A}} \biggr\} . \end{aligned}$$

3 Existence of pseudo almost periodic solution

Now, for $i,j,l = 1,2,\dots ,n$, we assume throughout this paper that $c_{i}(\cdot )$ is almost periodic on $\mathbb{T}$ and $d_{ij}(\cdot )$, $a_{ij}(\cdot )$, $b_{ij}(\cdot )$, $\alpha _{ijl}(\cdot )$, $\beta _{ijl}(\cdot )$, $p_{i}(\cdot )$, $I_{i}(\cdot )$ are PAP functions on $\mathbb{T}$, and let the positive constant $d_{ij}^{+}$, $a^{+}_{ij}$, $b^{+}_{ij}$, $\alpha ^{+}_{ijl}$, $\beta ^{+}_{ijl}$, $c_{i}^{+}$, $c_{i}^{-}$, and $I_{i}^{+}$ such that

$$\begin{aligned}& a^{+}_{ij} = \sup_{t \in \mathbb{T}} \bigl\Vert a_{ij}(t) \bigr\Vert _{\mathcal{A}}, \quad\quad b^{+}_{ij} = \sup_{t \in \mathbb{R}} \bigl\Vert b_{ij}(t) \bigr\Vert _{\mathcal{A}}, \quad\quad \alpha ^{+}_{ijl} = \sup _{t \in \mathbb{T}} \bigl\Vert \alpha _{ijl}(t) \bigr\Vert _{\mathcal{A}}, \\& \beta ^{+}_{ijl} = \sup _{t \in \mathbb{T}} \bigl\Vert \beta _{ijl}(t) \bigr\Vert _{ \mathcal{A}}, \quad\quad p^{+}_{i} = \sup_{t \in \mathbb{T}} \bigl\Vert p_{i}(t) \bigr\Vert _{\mathcal{A}}, \quad\quad d^{+}_{ij} = \sup_{t \in \mathbb{T}} \bigl\Vert d_{ij}(t) \bigr\Vert _{\mathcal{A}}, \\& I^{+}_{i} = \sup _{t \in \mathbb{T}} \bigl\Vert I_{i}(t) \bigr\Vert _{\mathcal{A}}, \quad\quad c^{+}_{i} = \sup _{t \in \mathbb{T}} \bigl\Vert c_{i}(t) \bigr\Vert _{\mathcal{A}}, \quad\quad c^{-}_{i} = \inf_{t \in \mathbb{T}} \bigl\Vert c_{i}(t) \bigr\Vert _{\mathcal{A}}. \end{aligned}$$

To study the existence and the uniqueness of PAP solutions on time scales of neural networks (1), we first require some lemmas and the following assumptions:

$\mathbf{(A.S_{1})}$:

The function $g_{j}(\cdot )\in C(\mathcal{A},\mathcal{A})$, and there exist nonnegative constants $L^{g}_{j}$ and $M^{g}_{j}$ such that

$$ g_{j}(0)= 0, \quad\quad \bigl\Vert g_{j}(u_{1})-g_{j}(u_{2}) \bigr\Vert _{\mathcal{A}}\leq L_{j}^{g} \Vert u_{1}-u_{2} \Vert _{\mathcal{A}}, \quad\quad \bigl\Vert g_{j}(u_{1}) \bigr\Vert _{\mathcal{A}} \leq M^{g}_{j}, \quad u_{1}, u_{2} \in \mathbb{T}. $$

$\mathbf{(A.S_{2})}$:

The delay kernels, $r_{i}$, $e_{i}$, $N_{ij}$, $H_{ijl}$, $K_{ijl} :[0,\infty )_{\mathbb{T}} \longrightarrow [0, \infty )$ are continuous, and there exist nonnegative constants $r_{i}^{+}$, $N^{+}_{ij}$, $H^{+}_{ijl}$, $K^{+}_{ijl}$ such that

$$ \begin{gathered} r^{+}_{i}= \int _{0}^{\infty } r_{i}(s)\Delta s, \quad \quad N^{+}_{ij}= \int _{0}^{ \infty } N_{ij}(s)\Delta s, \quad \quad H^{+}_{ijl}= \int _{0}^{\infty } H_{ijl}(s) \Delta s, \\ K^{+}_{ijl}= \int _{0}^{\infty } K_{ijl}(s)\Delta s, \quad i, j, l \in \{1,2,\dots ,n\}. \end{gathered} $$

$\mathbf{(A.S_{3})}$:

Let $c_{i}(\cdot )\in \operatorname{AP}(\mathbb{T},\mathbb{R}^{+})$ with $-c_{i}(\cdot )\in \mathcal{R}^{+}$, $\min_{1\leq i\leq n} \{ \inf_{t\in \mathbb{T}}c_{i}(t) \} >0$.

Let $\tau _{ij}(\cdot ), \eta _{ijl}(\cdot ), \nu _{ijl}(\cdot )\in \operatorname{AP}(\mathbb{T},\mathbb{R}^{+})\cap C^{1}(\mathbb{T},\Pi )$, and

$$ \inf_{t\in \mathbb{T}} \bigl(1-\tau _{ij}^{\Delta }(t) \bigr)>0, \quad\quad \inf_{t\in \mathbb{T}} \bigl(1-\eta _{ijl}^{\Delta }(t) \bigr)>0, \quad\quad \inf_{t\in \mathbb{T}} \bigl(1-\nu _{ijl}^{\Delta }(t) \bigr)>0. $$

$\mathbf{(A.S_{4})}$:

Let us assume that there are nonnegative constants L, p, and q such that

$$\begin{aligned}& L =\max_{1 \leq i \leq 2n} \biggl\{ \frac{I_{i}^{+}}{\xi _{i}c_{i}^{-}} \biggr\} , \\& \begin{aligned} p &=\max_{1 \leq i \leq n} \Biggl\{ p_{i}^{+}r_{i}^{+}+ \frac{1}{c_{i}^{-}} \Biggl[ c_{i}^{+}p_{i}^{+}r_{i}^{+} +\xi _{i}^{-1} \Biggl(\sum_{j=1}^{n} d_{ij}^{+} \xi _{j} L_{j}^{g} +\sum_{j=1}^{n} a^{+}_{ij} \xi _{j} L^{g}_{j} \\ &\quad {} +\sum_{j=1}^{n} b^{+}_{ij} N^{+}_{ij}\xi _{j} L^{g}_{j}+ \sum_{j=1}^{n} \sum_{l=1}^{n} \alpha ^{+}_{ijl} \xi _{j} L^{g}_{j} M^{g}_{l}+ \sum_{j=1}^{n} \sum _{l=1}^{n} \beta ^{+}_{ijl} H^{+}_{ijl} K^{+}_{ijl} \xi _{j}L^{g}_{j}M_{j}^{g} \Biggr) \Biggr] \Biggr\} < 1, \end{aligned} \\& \begin{aligned} q &= \max_{1 \leq i \leq n} \Biggl\{ p_{i}^{+}r_{i}^{+} + \frac{1}{c_{i}^{-}} \Biggl[p_{i}^{+} c_{i}^{+}r_{i}^{+}+ \xi _{i}^{-1} \sum_{j=1}^{n}d_{ij}^{+} \xi _{j} L_{j}^{g}+\xi _{i}^{-1} \sum_{j=1}^{n} a^{+}_{ij} \xi _{j} L^{g}_{j} \\ &\quad {} +\xi _{i}^{-1}\sum_{j=1}^{n} b^{+}_{ij} N^{+}_{ij} \xi _{j}L^{g}_{j}+ \xi _{i}^{-1} \sum_{j=1}^{n} \sum _{l=1}^{n} \alpha ^{+}_{ijl} \bigl( \xi _{j} L^{g}_{j} M^{g}_{l}+ M^{g}_{j}\xi _{l} L^{g}_{l} \bigr) \\ &\quad {} + \xi _{i}^{-1}\sum_{j=1}^{n} \sum_{l=1}^{n} \beta _{ijl}^{+} H^{+}_{ijl} K^{+}_{ijl} \bigl(\xi _{j} L^{g}_{j} M^{g}_{l} + M^{g}_{j} \xi _{l} L^{g}_{l} \bigr) \Biggr] \Biggr\} < 1. \end{aligned} \end{aligned}$$

Lemma 3.1

Consider $h(\cdot ), f(\cdot )\in \operatorname{PAP}(\mathbb{T},\mathcal{A}^{n})$, therefore $h(\cdot )\times f(\cdot ) \in \operatorname{PAP}(\mathbb{T},\mathcal{A}^{n})$.

Proof

By Definition 2.15, we have

$$ h=h_{1}+h_{2}, \quad\quad f=f_{1}+f_{2}, $$

where $h_{1}, f_{1} \in \operatorname{AP}(\mathbb{T},\mathcal{A}^{n})$ and $h_{2}, f_{2}\in \operatorname{PAP}_{0}(\mathbb{T},\mathcal{A}^{n})$. Then $h\times f=h_{1} f_{1}+h_{1} f_{2}+ h_{2} f_{1}+h_{2} f_{2}$.

Obviously, $h_{1} f_{1} \in \operatorname{AP}(\mathbb{T},\mathcal{A}^{n})$. Also,

$$\begin{aligned} &\lim_{\mu \rightarrow \infty } \frac{1}{2\mu } \int _{-\mu }^{\mu } \Vert h_{1} f_{2}+h_{2} f_{1}+h_{2} \psi _{2} \Vert _{\mathcal{A}^{n}} \Delta t \\ &\quad \leq \lim_{\mu \rightarrow \infty } \frac{1}{2\mu } \int _{-\mu } \bigl( \Vert f_{1} \Vert _{0} \Vert f_{2} \Vert _{\mathcal{A}^{n}}+ \Vert h_{2} \Vert _{\mathcal{A}^{n}} \Vert f_{1} \Vert + \Vert h_{2} \Vert _{0} \Vert f_{2} \Vert _{\mathcal{A}^{n}} \bigr)\Delta t =0, \end{aligned}$$

which implies that $(h_{1} f_{2}+h_{2}f_{1}+h_{2}f_{2} ) \in \operatorname{PAP}_{0}(\mathbb{T},\mathcal{A}^{n})$. Then $h\times f \in \operatorname{PAP}(\mathbb{T},\mathcal{A}^{n})$. □

By Definition 2.15, analogous to the proofs of the results in [44], the following lemmas can be proven.

Lemma 3.2

Let $h^{1}(\cdot ), h^{2}(\cdot )\in \operatorname{PAP}(\mathbb{T},\mathcal{A}^{n})$, therefore $h^{1}(\cdot ) + h^{2}(\cdot )\in \operatorname{PAP}(\mathbb{T},\mathcal{A}^{n})$.

Lemma 3.3

Let $\chi \in \mathbb{R}$, $h(\cdot )\in \operatorname{PAP}(\mathbb{T},\mathcal{A}^{n})$, then $\chi h(\cdot ) \in \operatorname{PAP}(\mathbb{T},\mathcal{A}^{n})$.

Lemma 3.4

Let $h(\cdot )\in C(\mathcal{A},\mathcal{A}^{n})$, $k(\cdot )\in \operatorname{PAP}(\mathbb{T},\mathcal{A}^{n})$, therefore $h(k(\cdot )) \in \operatorname{PAP}(\mathbb{T},\mathcal{A}^{n})$.

Lemma 3.5

Let $h(\cdot ) \in \operatorname{PAP}(\mathbb{T},\mathcal{A}^{n})$, therefore $h(\cdot-\lambda ) \in \operatorname{PAP}(\mathbb{T},\mathcal{A}^{n})$.

Lemma 3.6

Let $h(\cdot )\in \operatorname{PAP}(\mathbb{T},\mathcal{A})$, $\varsigma (\cdot )\in \operatorname{AP}(\mathbb{T},\mathrm{R})\cap C^{1}( \mathbb{T},\Pi )$, where $\vert \varsigma (t) \vert \leq \varsigma ^{+}$ and $\dot{\varsigma }(t)\leq \dot{\varsigma }^{+}<1$, then $h(\cdot-\varsigma (\cdot )) \in \operatorname{PAP}(\mathbb{T},\mathcal{A}^{n})$.

Proof

Since $h(\cdot ) \in \operatorname{PAP}(\mathbb{T},\mathcal{A}^{n})$, then

$$ h(\cdot )=h^{1}(\cdot ) +h^{2}(\cdot ), $$

where $h^{1}(\cdot ) \in \operatorname{AP}(\mathbb{T},\mathcal{A}^{n})$ and $h^{2}(\cdot )\in \operatorname{PAP}_{0}(\mathbb{T},\mathcal{A}^{n})$. Consequently, we have

$$ h \bigl(t-\varsigma (t) \bigr)=h^{1} \bigl(t-\varsigma (t) \bigr)+h^{2} \bigl(t-\varsigma (t) \bigr). $$

From $h^{1}(\cdot -\varsigma (\cdot )) \in \operatorname{AP} (\mathbb{R}, \mathcal{A}^{n} )$ it follows that $h^{1}(\cdot )$ is uniformly continuous. Therefore, for each $\epsilon >0$, there exists a positive constant $s\in (0, \frac{\epsilon }{2} )$ such that, for any $t_{1}, t_{2} \in \mathbb{T}$ with $\vert t_{1}-t_{2} \vert < s$,

$$\begin{aligned} \bigl\Vert h^{1}(t_{1})-h^{1}(t_{2}) \bigr\Vert _{\mathcal{A}^{n}}< \frac{\epsilon }{2} \end{aligned}$$

(7)

since $\varsigma (\cdot )$ and $h^{1}(\cdot )$ are almost periodic, for this $s>0$, there exists $l(s)>0$ such that in every interval with length $l(s)$, there is θ satisfying

$$\begin{aligned} \bigl\vert \varsigma (t_{1}+\theta )-\varsigma (t_{1}) \bigr\vert < s, \quad\quad \bigl\Vert h^{1}(t_{1}+ \theta )-h^{1}(t_{1}) \bigr\Vert _{\mathcal{A}^{n}}< s \end{aligned}$$

(8)

for all $t_{1} \in \mathbb{T}$. It follows from (7) and (8) that

$$\begin{aligned} & \bigl\Vert h^{1} \bigl(t_{1}+\theta -\varsigma (t_{1}+\theta ) \bigr)-h^{1} \bigl(t_{1}- \varsigma (t_{1}) \bigr) \bigr\Vert _{\mathcal{A}^{n}} \\ &\quad \leq \bigl\Vert h^{1} \bigl(t_{1}+\theta - \varsigma (t_{1}+\theta ) \bigr)-h^{1} \bigl(t_{1}+ \theta - \varsigma (t_{1}) \bigr) \bigr\Vert _{\mathcal{A}^{n}} \\ &\quad\quad {} + \bigl\Vert h^{1} \bigl(t_{1}+\theta - \varsigma (t_{1}) \bigr)-h^{1} \bigl(t_{1}- \varsigma (t_{1}) \bigr) \bigr\Vert _{\mathcal{A}^{n}} < \frac{\epsilon }{2}+ \frac{\epsilon }{2}, \end{aligned}$$

which implies that $h^{1}(\cdot -\varsigma (\cdot ))\in \operatorname{PAP}_{0}(\mathbb{T}, \mathcal{A}^{n})$.

Moreover, let $u=t_{1}-\varsigma (t_{1})$ and noticing that $h^{2}(\cdot ) \in \operatorname{PAP}_{0}(\mathbb{T},\mathcal{A}^{n}) \subset B C (\mathbb{T}, \mathcal{A}^{n} )$, we find

$$\begin{aligned} &\lim_{\mu \rightarrow +\infty }\frac{1}{2 \mu } \int _{-\mu }^{\mu } \bigl\Vert h^{2} \bigl(t_{1}-\varsigma (t_{1}) \bigr) \bigr\Vert _{\mathcal{A}^{n}} \Delta t_{1} \\ &\quad \leq \lim_{\mu \rightarrow +\infty } \frac{1}{2 \mu } \int _{-\mu - \varsigma (-\mu )}^{\mu -\varsigma (\mu )} \frac{1}{1-\varsigma ^{\Delta }(u)} \bigl\Vert h^{2}(u) \bigr\Vert _{ \mathcal{A}^{n}} \Delta u \\ &\quad \leq \lim_{\mu \rightarrow +\infty } \frac{1}{1-\dot{\varsigma }^{+}} \frac{1}{2 \mu } \int _{-(\mu + \varsigma ^{+})}^{(\mu +\varsigma ^{+})} \bigl\Vert h^{2}(u) \bigr\Vert _{ \mathcal{A}^{n}} \Delta u \\ &\quad = \lim_{\mu \rightarrow +\infty } \frac{1}{1-\dot{\varsigma }^{+}} \frac{\mu -\varsigma ^{+}}{\mu } \frac{1}{2(\mu -\varsigma ^{+})} \int _{-(\mu +\varsigma ^{+})}^{(\mu +\varsigma ^{+})} \bigl\Vert h^{2}(u) \bigr\Vert _{\mathcal{A}^{n}} \Delta u=0, \end{aligned}$$

which implies that $h^{2}(\cdot -\varsigma (\cdot )) \in \operatorname{PAP}_{0}(\mathbb{T}, \mathcal{A}^{n})$. Hence, $h(\cdot -\varsigma (\cdot )) \in \operatorname{PAP}(\mathbb{T},\mathcal{A}^{n})$. □

Lemma 3.7

Let us assume that hypotheses $\mathbf{{(A.S_{1})}}$, $\mathbf{{(A.S_{2})}}$ hold. For all $1\leq j \leq n$, $x_{j}(\cdot ) \in \operatorname{PAP}(\mathbb{T},\mathcal{A}^{n})$. Therefore, the function

$$ \Omega _{i}: t \longmapsto \int _{-\infty }^{t} N_{ij}(t-s) g_{j} \bigl(x_{j}(s) \bigr) \Delta s\in \operatorname{PAP}(\mathbb{T}, \mathcal{A}), \quad 1 \leq i \leq n. $$

Proof

Since

$$\begin{aligned} \bigl\Vert \Omega _{i}(t) \bigr\Vert _{\mathcal{A}} =& \biggl\Vert \int _{-\infty }^{t} N_{ij}(t-s) g_{j}(x_{j}(s) \Delta s \biggr\Vert _{\mathcal{A}}\leq \int _{-\infty }^{t} N_{ij}(t-s) \Vert g \Vert \Delta s = N_{ij}^{+} \Vert g \Vert , \end{aligned}$$

which proves that the function $\Omega _{i}(\cdot )$ is absolutely convergent, $\Omega _{ij}(\cdot )\in BC(\mathbb{T},\mathcal{A})$. Then we will demonstrate the continuity of the function $\Omega _{i}(\cdot )$. For all rd-dense points $w\in \mathbb{T}$, we can select a sequence $(w_{n})_{n}\in \mathbb{T}$ with $w_{n}> w$ and $w_{n} \rightarrow w$, as $n \rightarrow \infty$. For any $\epsilon >0$, by the continuity of $x_{ij}$, there is a constant $N \in \mathbb{N}$ such that, for any integer $n>N$, $s \in \mathbb{T}$ with $w_{n}-s \in \mathbb{T}$ and $w-s \in \mathbb{T}$, we have

$$ \bigl\Vert x_{ij} (w_{n}-s )-x_{ij}(t-s) \bigr\Vert _{ \mathcal{A}} \leq \frac{\epsilon }{N_{ij}^{+} L^{g}_{j}}. $$

It follows that

$$\begin{aligned} & \bigl\Vert \Omega _{i}(t+w_{n})- \Omega _{i}(t) \bigr\Vert _{\mathcal{A}} \\ &\quad = \biggl\Vert \int _{-\infty }^{t+w_{n}} N_{ij}(t+w_{n}-s)g_{j} \bigl(x_{j}(s) \bigr) \Delta s- \int _{-\infty }^{t} N_{ij}(t-s) g_{j} \bigl(x_{j}(s) \bigr) \Delta s \biggr\Vert _{\mathcal{A}} \\ &\quad \leq \int _{-\infty }^{t} N_{ij}(t-s) L_{j}^{g} \bigl\Vert x_{j}(s+w_{n}) - x_{j}(s) \bigr\Vert _{\mathcal{A}} \Delta s \\ &\quad \leq L_{j}^{g} \int _{-\infty }^{t} N_{ij}(t-s) \Delta s \frac{\epsilon }{L_{j}^{g} N_{ij}^{+}}< \epsilon . \end{aligned}$$

In the same way, we can establish the ld-continuity of function $\Omega _{i}(\cdot )$, thus $\Omega _{i}(\cdot )$ is continuous on $\mathbb{T}$. Next, it remains to be demonstrated that the function $\Omega _{i}(\cdot )$ belongs to $\operatorname{PAP}(\mathbb{R},\mathcal{A}^{n})$. First, consider that with Lemma 3.4 and condition $\mathbf{{(A.S_{1})}}$, $g_{j}(x_{j}(\cdot ))$ can be written as $g_{j}(x_{j}(\cdot ))= u_{j}(\cdot )+v_{j}(\cdot )$, where $u_{j}(\cdot ) \in \operatorname{AP}(\mathbb{T},\mathcal{A}^{)}$ and $v_{j} (\cdot )\in \operatorname{PAP}_{0}(\mathbb{T},\mathcal{A})$. Consequently,

$$\begin{aligned} \Omega _{i}(t) =& \int _{-\infty }^{t} N_{ij}(t-s) \bigl[u_{j}(s)+v_{j}(s) \bigr] \Delta s \\ =& \int _{-\infty }^{t} N_{ij}(t-s) u_{j}(s) \Delta s + \int _{- \infty }^{t} N_{ij}(t-s) v_{j}(s) \Delta s=\Omega _{i}^{1}(t)+\Omega _{i}^{2}(t). \end{aligned}$$

Let us demonstrate the almost periodicity of the function $t \mapsto \Omega _{i}^{1}(t)$. For $\epsilon >0$, we consider, in view of the almost periodicity of $u_{j}(\cdot )$, that it is also possible to get a real number $L_{\epsilon }$. For each interval with length $L_{\epsilon }$, there exists a number δ with the property that $\sup_{\xi \in \mathbb{T}} \Vert u_{j}(\xi +\delta )-u_{j}(\xi ) \Vert _{\mathcal{A}}<\frac{\epsilon }{N_{ij}^{+}}$. Afterwards, we can write

$$\begin{aligned} \bigl\Vert \Omega _{i}^{1}(t+\delta )-\Omega _{i}^{1}(t) \bigr\Vert _{ \mathcal{A}} =& \biggl\Vert \int _{-\infty }^{t+\delta }N_{ij}(t+\delta -s)u_{j}(s) \Delta s- \int _{-\infty }^{t}N_{ij}(t-s)u_{j}(s) \Delta s \biggr\Vert _{ \mathcal{A}} \\ =& \biggl\Vert \int _{-\infty }^{t}N_{ij}(t-s)u_{j}(s+ \delta )\Delta s- \int _{-\infty }^{t}N_{ij}(t-s)u_{j}(s) \Delta s \biggr\Vert _{\mathcal{A}} \\ \leq & \int _{-\infty }^{t}N_{ij}(t-s) \bigl\Vert u_{j}(s+\delta )-u_{j}(s) \bigr\Vert _{ \mathcal{A}} \Delta s \\ \leq & \frac{\epsilon }{N_{ij}^{+}} \int _{0}^{+\infty }N_{ij}(s) \Delta s=\epsilon . \end{aligned}$$

This implies that $\Omega _{i}^{1}(\cdot )\in \operatorname{AP}(\mathbb{T},\mathcal{A})$. Now, let us demonstrate that, for all $1\leq i\leq n$, the function $\Omega _{i}^{2}(\cdot )\in \operatorname{PAP}_{0}(\mathbb{T},\mathcal{A})$. The following estimate can be obtained immediately:

$$\begin{aligned} \lim_{\mu \rightarrow +\infty } \frac{1}{2\mu } \int _{-\mu }^{\mu } \int ^{+\infty }_{0} N_{ij}(s) \bigl\Vert v_{j}(t-s) \bigr\Vert _{\mathcal{A}} \Delta s \Delta t =&\lim _{\mu \rightarrow +\infty } \int ^{+\infty }_{0} N_{ij}(s) \Omega _{\mu }(s)\Delta s, \end{aligned}$$

where

$$\begin{aligned} \Omega _{\mu }(s) =& \frac{1}{2\mu } \int _{-\mu }^{\mu } \bigl\Vert v_{j}(t-s) \bigr\Vert _{ \mathcal{A}} \Delta t \leq \frac{1}{2\mu } \int _{-\mu - \vert s \vert }^{\mu + \vert s \vert } \bigl\Vert v_{j}(u) \bigr\Vert _{\mathcal{A}} \Delta u \\ =&\frac{(\mu + \vert s \vert )}{\mu } \frac{1}{2(\mu + \vert s \vert )} \int _{-\mu - \vert s \vert }^{ \mu + \vert s \vert } \bigl\Vert v_{j}(u) \bigr\Vert _{\mathcal{A}} \Delta u, \end{aligned}$$

one can easily see that $\Omega _{\mu }\rightarrow 0$ as $\mu \rightarrow \infty$. Next, because $\Omega _{\mu }(\cdot )$ is bounded, based on the Lebesgue dominated convergence theorem, it results that

$$ \lim_{\mu \rightarrow \infty } \biggl\{ \int ^{+\infty }_{0} N_{ij}(s) \Omega _{\mu }(s) \Delta s \biggr\} =0, $$

and hence $\int _{-\infty }^{t} N_{ij}(t-s) g_{j}(x_{j}(s))\Delta s \in \operatorname{PAP}(\mathbb{T},\mathcal{A})$. □

Lemma 3.8

Let $b_{i}: \mathbb{T} \rightarrow (0,+\infty )$ with $-b_{i}(\cdot ) \in \mathcal{R}^{+}$ be almost periodic. Then, for any $\epsilon >0$, there exists $l(\varepsilon )>0$ such that any interval of length $l(\varepsilon )$ contains at least one $\tau \in \Pi$ such that, for $i=1,2, \ldots , n$,

$$\begin{aligned} & \bigl\vert e_{-a_{i}} \bigl(t+\tau , \sigma (s+\tau ) \bigr)-e_{-a_{i}} \bigl(t, \sigma (s) \bigr) \bigr\vert < \frac{\epsilon }{b_{i}^{-}}e_{-b_{i}} \bigl(t,\sigma (s) \bigr), \quad t \geq \sigma (s), t, s \in \mathbb{T}. \end{aligned}$$

Proof

Since $b_{i}(\cdot )$ is almost periodic, then for any $\epsilon >0$, there is $l(\epsilon )>0$ such that any interval of length $l(\epsilon )$ contains at least one $\tau \in \Pi$ such that

$$ \bigl\vert b_{i}(t+\tau )-b_{i}(t) \bigr\vert < \epsilon , \quad \forall t \in \mathrm{T}. $$

Such as $(e_{-b_{i}}(t, s) )^{\Delta }=-b_{i}(t) e_{-b_{i}}(t, s)$, we have the following:

$$\begin{aligned} \bigl(e_{-b_{i}} \bigl(t+\tau , \sigma (s)+\tau \bigr) \bigr)^{\Delta } =& -b_{i}(t)e_{-b_{i}} \bigl(t+ \tau , \sigma (s)+\tau \bigr) \\ &{}+ \bigl(b_{i}(t)-b_{i}(t+\tau ) \bigr) e_{-b_{i}} \bigl(t+\tau , \sigma (s)+ \tau \bigr). \end{aligned}$$

Then we have

$$\begin{aligned} &e_{-b_{i}} \bigl(t+\tau , \sigma (s)+\tau \bigr)-e_{-b_{i}} \bigl(t, \sigma (s) \bigr) \\ &\quad = \int _{t}^{\sigma (s)}e_{-b_{i}} \bigl(t, \sigma (u) \bigr) \bigl(b_{i}(u+ \tau )-b_{i}(u) \bigr)e_{-a_{i}} \bigl(u+\tau , \sigma (s)+\tau \bigr) \Delta u. \end{aligned}$$

Hence, we have that

$$\begin{aligned} & \bigl\vert e_{-b_{i}} \bigl(t+\tau , \sigma (s+\tau ) \bigr)-e_{-b_{i}} \bigl(t, \sigma (s) \bigr) \bigr\vert \\ &\quad = \bigl\vert e_{-b_{i}} \bigl(t+\tau , \sigma (s)+\tau \bigr)-e_{-b_{i}} \bigl(t, \sigma (s) \bigr) \bigr\vert \\ &\quad = \biggl\vert \int _{t}^{\sigma (s)}e_{-b_{i}} \bigl(t, \sigma (u) \bigr) \bigl(b_{i}(u+ \tau )-b_{i}(u) \bigr)e_{-a_{i}} \bigl(u+\tau , \sigma (s)+\tau \bigr) \Delta u \biggr\vert \\ &\quad \leq \biggl\vert \int _{t}^{\sigma (s)}e_{-b_{i}} \bigl(t, \sigma (u) \bigr) \bigl(b_{i}(u+ \tau )-b_{i}(u) \bigr) \Delta u \biggr\vert \\ &\quad \leq \epsilon \int _{t}^{\sigma (s)}e_{-b_{i}} \bigl(t, \sigma (u) \bigr) \Delta u \\ &\quad =-\frac{1}{b_{i}} \bigl(e_{-b_{i}}(t, t)-e_{-b_{i}} \bigl(t, \sigma (s) \bigr) \bigr)\epsilon =\frac{\epsilon }{b_{i}^{-}}e_{-b_{i}} \bigl(t, \sigma (s) \bigr), \quad i=1,2, \ldots , n. \end{aligned}$$

 □

Theorem 3.9

Let conditions $\mathbf{{(A.S_{1})}}$–$\mathbf{{(A.S_{4})}}$ hold. Therefore, there exists a unique PAP solution of neural networks (1) in the region

$$ B = \biggl\{ \varphi / \varphi \in \operatorname{PAP} \bigl(\mathbb{T}, \mathcal{A}^{n},u \bigr), \Vert \varphi - \varphi _{0} \Vert _{0} \leq \frac{p L }{1-p} \biggr\} , $$

where

$$\begin{aligned}& \varphi _{0}(t)= \biggl( \int _{-\infty }^{t} e_{-c_{1}}\bigl(t, \sigma (s) \bigr)\frac{I_{1}(s)}{\xi _{1}} \Delta s, \cdots , \int _{-\infty }^{t} e_{-c_{n}}\bigl(t,\sigma (s) \bigr) \frac{I_{n}(s)}{\xi _{n}}\Delta s \biggr)^{T} . \end{aligned}$$

Proof

Let $u_{i}(t)=\xi _{i}^{-1}x_{i}(t)$ and $U_{i}(t)=u_{i}(t)-p_{i}(t)\int _{0}^{\infty }r_{i}(s) u_{i}(t-s) \Delta s$. We obtain from system (1) that

$$\begin{aligned} U_{i}^{\Delta }(t) =& - c_{i}(t)U_{i}(t)-c_{i}(t)p_{i}(t) \int _{0}^{\infty }r_{i}(s) u_{i}(t-s)\Delta s+\frac{1}{\xi _{i}}\sum _{j=1}^{n} d_{ij}(t) g_{j} \bigl( \xi _{j}u_{j}(t) \bigr) \\ &{}+\frac{1}{\xi _{i}}\sum_{j=1}^{n} a_{ij}(t) g_{j} \bigl(\xi _{j}u_{j} \bigl(t- \tau _{ij}(t) \bigr) \bigr)+\frac{1}{\xi _{i}}\sum _{j=1}^{n} b_{ij}(t) \int _{0}^{\infty } N_{ij}(u) g_{j} \bigl(\xi _{j}u_{j}(t-u) \bigr) \Delta u \\ &{}+\frac{1}{\xi _{i}}\sum_{j=1}^{n} \sum _{l=1}^{n} \beta _{ijl}(t) \int _{0}^{\infty } H_{ijl}(u) g_{j} \bigl( \xi _{j}u_{j}(t-u) \bigr)\Delta u \int _{0}^{\infty } K_{ijl}(u) g_{l} \bigl(\xi _{l}u_{l}(t-u) \bigr)\Delta u \\ &{}+\frac{1}{\xi _{i}}\sum_{j=1}^{n} \sum _{l=1}^{n} \alpha _{ijl}(t) g_{j} \bigl(\xi _{j}u_{j} \bigl(t-\eta _{ijl}(t) \bigr) \bigr)g_{l} \bigl(\xi _{l}u_{l} \bigl(t- \nu _{ijl}(t) \bigr) \bigr)+\frac{1}{\xi _{i}}I_{i}(t). \end{aligned}$$

(9)

For any given $\varphi = (\varphi _{1},\ldots ,\varphi _{n} )^{T}\in B$, we consider the following system:

$$\begin{aligned} U_{i}^{\Delta }(s) =& -c_{i}(s)U_{i}(s)+F_{i} \bigl(s,\varphi (s) \bigr), \end{aligned}$$

(10)

where

$$\begin{aligned} F_{i} \bigl(s,\varphi (s) \bigr) =& -c_{i}(s)p_{i}(s) \int _{0}^{\infty }r_{i}(u) \varphi _{i}(s-u)\Delta u +\frac{1}{\xi _{i}} \Biggl[ \sum _{j=1}^{n} d_{ij}(s) g_{j} \bigl( \xi _{j} \varphi _{j}(s) \bigr) \\ &{}+ \sum_{j=1}^{n} a_{ij}(s) g_{j} \bigl(\xi _{j} \varphi _{j} \bigl(s-\tau _{ij}(s) \bigr) \bigr) + \sum_{j=1}^{n} b_{ij}(s) \int _{0}^{\infty } N_{ij}(u) g_{j} \bigl(\xi _{j}\varphi _{j}(s-u) \bigr) \Delta u \\ &{}+ \sum_{j=1}^{n}\sum _{l=1}^{n} \beta _{ijl}(s) \int _{0}^{\infty } H_{ijl}(u) g_{j} \bigl(\xi _{j}\varphi _{j}(s-u) \bigr) \Delta u \int _{0}^{\infty } K_{ijl}(u) g_{l} \bigl(\xi _{j} \varphi _{l}(s-u) \bigr)\Delta s \\ &{}+ \sum_{j=1}^{n} \sum _{l=1}^{n} \alpha _{ijl}(s) g_{j} \bigl(\xi _{l}\varphi _{j} \bigl(s-\eta _{ijl}(s) \bigr) \bigr) g_{l} \bigl( \xi _{l}\varphi _{l} \bigl(s-\nu _{ijl}(s) \bigr) \bigr) \Biggr]. \end{aligned}$$

By Lemma 2.19 and $(\mathbf{{A.S_{3}})}$, we see that the linear system

$$\begin{aligned} U_{i}^{\Delta }(s) =& -c_{i}(s)U_{i}(s) \end{aligned}$$

(11)

admits an exponential dichotomy on $\mathbb{T}$. Therefore, via Lemma 2.18, don’t we get that (10) has a unique solution bounded

$$\begin{aligned} (\Gamma _{\phi }) (t)=x_{i\varphi }(t) =& \begin{pmatrix} \int _{-\infty }^{t} e_{-c_{1}}(t,\sigma (s))F_{1}(s, \phi (s))\Delta s \\ \vdots \\ \int _{-\infty }^{t} e_{-c_{n}}(t,\sigma (s))F_{n}(s, \phi (s))\Delta s \end{pmatrix}. \end{aligned}$$

The theorem will be proved by the following steps:

• Step 1: We will demonstrate $\Gamma _{\phi }(\cdot ) \in \operatorname{PAP}(\mathbb{T},\mathcal{A}^{n})$. According to $\mathbf{{(A.S_{1})}}$ and $\mathbf{{(A.S_{4})}}$, it is easy to see that $x_{i\varphi }(\cdot ) \in BC(\mathbb{T},\mathcal{A})$. From Lemmas 3.1–3.6 and Lemma 3.7, we obtain that there are $F_{1i}(\cdot )\in \operatorname{AP}(\mathbb{T},\mathcal{A})$ and $F_{2i}(\cdot )\in \operatorname{PAP}_{0}(\mathbb{T},\mathcal{A})$ such that

  $$ F_{i}(\cdot )=F_{1i}(\cdot )+F_{2i}(\cdot )\in \operatorname{PAP}( \mathbb{T},\mathcal{A}). $$

  Hence

  $$\begin{aligned} x_{i\varphi }(t) =& \int _{-\infty }^{t} e_{-c_{i}} \bigl(t,\sigma (s) \bigr)F_{i} \bigl(s, \phi (s) \bigr)\Delta s \\ =& \int _{-\infty }^{t} e_{-c_{i}} \bigl(t,\sigma (s) \bigr)F_{1i} \bigl(s,\phi (s) \bigr) \Delta s + \int _{-\infty }^{t} e_{-c_{i}} \bigl(t,\sigma (s) \bigr)F_{2i} \bigl(s,\phi (s) \bigr) \Delta s \\ =&\Theta _{1i}(t)+\Theta _{2i}(t). \end{aligned}$$

  We will prove that $\Theta _{1i}(\cdot )\in \operatorname{AP}(\mathbb{T}, \mathcal{A})$. For every $\epsilon >0$, since $F_{1i}(\cdot )\in \operatorname{AP}(\mathbb{T}, \mathcal{A}^{n})$, it is possible to find a real number $l=l(\epsilon )>0$. For each interval with length $l(\epsilon )$, there exists a number ς in this interval such that $\Vert F_{1i}(t+\varsigma )-F_{1i}(t) \Vert _{\mathcal{A}}< \epsilon$, then

  $$\begin{aligned}& \bigl\Vert \Theta _{1i}(t+\varsigma )-\Theta _{1i}(t) \bigr\Vert _{ \mathcal{A}} \\& \quad = \biggl\Vert \int _{-\infty }^{t+\varsigma } e_{-c_{i}} \bigl(t+\varsigma , \sigma (s) \bigr) F_{1i}(s) \Delta s - \int _{-\infty }^{t} e_{-c_{i}} \bigl(t, \sigma (s) \bigr) F_{1i}(s) \Delta s \biggr\Vert _{\mathcal{A}} \\& \quad = \biggl\Vert \int _{-\infty }^{t}e_{-c_{i}} \bigl(t+\varsigma , \sigma (s+ \varsigma ) \bigr)F_{1i}(s+\varsigma ) \Delta s - \int _{-\infty }^{t} e_{-c_{i}} \bigl(t, \sigma (s) \bigr) F_{1i}(s)\Delta s \biggr\Vert _{\mathcal{A}} \\& \quad = \biggl\Vert \int _{-\infty }^{t} e_{-c_{i}} \bigl(t+\varsigma , \sigma (s+ \varsigma ) \bigr) F_{1i}(s+\varsigma ) \Delta s - \int _{-\infty }^{t} e_{-c_{i}} \bigl(t, \sigma (s) \bigr) F_{1i}(s+\varsigma ) \Delta s \biggr\Vert _{\mathcal{A}} \\& \quad \quad {} + \biggl\Vert \int _{-\infty }^{t} e_{-c_{i}} \bigl(t,\sigma (s) \bigr) F_{1i}(s+ \varsigma ) \Delta s - \int _{-\infty }^{t} e_{-c_{i}} \bigl(t,\sigma (s) \bigr) F_{1i}(s) \Delta s \biggr\Vert _{\mathcal{A}} \\& \quad \leq \biggl\Vert \int _{-\infty }^{t} \bigl(e_{-c_{i}} \bigl(t+ \varsigma , \sigma (s+\varsigma ) \bigr)+e_{-c_{i}} \bigl(t,\sigma (s) \bigr) \bigr) F_{1i}(s+ \varsigma )\Delta s \biggr\Vert _{\mathcal{A}} \\& \quad\quad {} + \biggl\Vert \int _{-\infty }^{t} e_{-c_{i}} \bigl(t,\sigma (s) \bigr) \bigl(F_{1i}(s+ \varsigma )-F_{1i}(s) \bigr) \Delta s \biggr\Vert _{\mathcal{A}} \\& \quad \leq \int _{-\infty }^{t} \bigl\vert e_{-c_{i}} \bigl(t+ \varsigma ,\sigma (s+ \varsigma ) \bigr)+e_{-c_{i}} \bigl(t,\sigma (s) \bigr) \bigr\vert \bigl\Vert F_{1i}(s+ \varsigma ) \bigr\Vert _{\mathcal{A}}\Delta s \\& \quad \quad {} + \int _{-\infty }^{t} \bigl\vert e_{-c_{i}} \bigl(t, \sigma (s) \bigr) \bigr\vert \bigl\Vert F_{1i}(s+\varsigma )-F_{1i}(s) \bigr\Vert _{\mathcal{A}} \Delta s. \end{aligned}$$

  By Lemma 3.8, and since $F_{1i}(\cdot )\in \operatorname{AP}(\mathbb{T},\mathcal{A})$ is a uniformly continuous and bounded function, we get that

  $$\begin{aligned}& \bigl\Vert \Theta _{1i}(t+\varsigma )-\Theta _{1i}(t) \bigr\Vert _{ \mathcal{A}}\leq \frac{\epsilon }{(c_{i}^{-})^{2}} \bigl[ \Vert F_{1} \Vert +c_{i}^{-} \bigr], \end{aligned}$$

  which implies that $\Theta _{1i}(\cdot )\in \operatorname{AP}(\mathbb{T}, \mathcal{A})$.

  Next, we are going to show that $\Theta _{2i}(\cdot )\in \operatorname{PAP}_{0}(\mathbb{T}, \mathcal{A})$. On the other hand,

  $$\begin{aligned}& \frac{1}{2\mu } \int _{-\mu }^{\mu } \biggl\Vert \int _{-\infty }^{t} e_{-c_{i}} \bigl(t, \sigma (s) \bigr) F_{2i}(s) \Delta s \biggr\Vert _{\mathcal{A}} \Delta s \\& \quad \leq \frac{1}{2\mu } \int _{-\mu }^{\mu } \Delta t \int _{-\infty }^{t} e_{-c_{i}} \bigl(t, \sigma (s) \bigr) \bigl\Vert F_{2i}(s) \bigr\Vert _{\mathcal{A}} \Delta s \\& \quad =\frac{1}{2\mu } \int _{-\mu }^{\mu } \Delta t \biggl( \int _{-\infty }^{- \mu } e_{-c_{i}} \bigl(t, \sigma (s) \bigr) \bigl\Vert F_{2i}(s) \bigr\Vert _{\mathcal{A}} \Delta s \\& \quad \quad {}+ \int ^{t}_{-\mu } e_{-c_{i}} \bigl(t, \sigma (s) \bigr) \bigl\Vert F_{2i}(s) \bigr\Vert _{\mathcal{A}} \Delta s \biggr) \\& \quad =\frac{1}{2\mu } \biggl[ \int _{-\infty }^{-\mu } \bigl\Vert F_{2i}(s) \bigr\Vert _{\mathcal{A}} \Delta s \int _{-\mu }^{\mu } e_{-c_{i}} \bigl(t, \sigma (s) \bigr) \Delta t \\& \quad \quad {} + \int _{-\mu }^{\mu } \bigl\Vert F_{2i}(s) \bigr\Vert _{\mathcal{A}} \Delta s \int _{s}^{\mu } e_{-c_{i}} \bigl(t, \sigma (s) \bigr) \Delta t \biggr] = \Pi _{1}+\Pi _{2}, \end{aligned}$$

  where

  $$\begin{aligned} \Pi _{1} =&\frac{1}{2\mu } \int _{-\infty }^{-\mu } \bigl\Vert F_{2i}(s) \bigr\Vert _{\mathcal{A}} \Delta s \int _{-\mu }^{\mu } e_{-c_{i}} \bigl(t, \sigma (s) \bigr) \Delta t \\ \leq &\frac{1}{2\mu c_{i}^{-}} \int _{-\infty }^{-\mu } \bigl\Vert F_{2i}(s) \bigr\Vert _{\mathcal{A}} \bigl[e_{-c_{i}^{-}} \bigl(-\mu , \sigma (s) \bigr)-e_{-c_{i}^{-}} \bigl( \mu , \sigma (s) \bigr) \bigr] \Delta s \\ \leq & \frac{ \Vert F_{2i} \Vert }{2\mu c_{i}^{-}} \int _{-\infty }^{- \mu } \bigl[e_{-c_{i}^{-}} \bigl(-\mu , \sigma (s) \bigr)-e_{-c_{i}^{-}} \bigl(\mu , \sigma (s) \bigr) \bigr] \Delta s \\ =&\frac{ \Vert F_{2i} \Vert }{2\mu (c_{i}^{-} )^{2} } \bigl[1-e_{-c_{i}^{-}}(-\mu ,-\infty )-e_{-c_{i}^{-}}(\mu ,-\mu )+e_{-c_{i}^{-}}( \mu ,-\infty ) \bigr] \\ \rightarrow & 0 \quad (\text{as } \mu \rightarrow \infty ) \end{aligned}$$

  and

  $$\begin{aligned} \Pi _{2} =&\frac{1}{2\mu } \int _{-\mu }^{\mu } \bigl\Vert F_{2i}(s) \bigr\Vert _{\mathcal{A}} \Delta s \int _{s}^{\mu } e_{-c_{i}} \bigl(t, \sigma (s) \bigr) \Delta t \\ \leq & \frac{1}{2\mu } \int _{-\mu }^{\mu } \bigl\Vert F_{2i}(s) \bigr\Vert _{ \mathcal{A}}\frac{1}{c_{i}^{-}} \bigl[e_{-c_{i}^{-}} \bigl(s, \sigma (s) \bigr)-e_{-c_{i}^{-}} \bigl( \mu , \sigma (s) \bigr) \bigr] \Delta s \\ \leq & \frac{1}{2\mu } \int _{-\mu }^{\mu } \bigl\Vert F_{2i}(s) \bigr\Vert _{ \mathcal{A}} \frac{1}{c_{i}^{-}} e_{-c_{i}^{-}} \bigl(s, \sigma (s) \bigr) \Delta s \\ =&\frac{1}{2\mu } \int _{-\mu }^{\mu } \bigl\Vert F_{2i}(s) \bigr\Vert _{ \mathcal{A}}\frac{1}{c_{i}^{-} (1-\nu (s) c_{i}^{-} )} \Delta s \\ \leq & \frac{1}{c_{i}^{-} (1-\bar{\nu } c_{i}^{-} )} \frac{1}{2\mu } \int _{-\mu }^{\mu } \bigl\Vert F_{2i}(s) \bigr\Vert _{ \mathcal{A}}\Delta s \\ \leq & \frac{1}{c_{i}^{-} (1-\bar{\nu }c_{i}^{-} )} \frac{1}{2\mu } \int _{-\mu }^{\mu } \bigl\Vert F_{2i}(s) \bigr\Vert _{ \mathcal{A}} \Delta s \rightarrow 0 \quad (\text{as } \mu \rightarrow \infty ), \end{aligned}$$

  where $\bar{\nu }=\sup_{t \in \mathbb{T}} \nu (t)$. Hence, $\int _{-\infty }^{t} e_{-c_{i}}(t, \sigma (s)) F_{2i}(s) \Delta s \in \operatorname{PAP}_{0}(\mathbb{T}, \mathcal{A})$, and then $x_{i\varphi }(\cdot )\in \operatorname{PAP}(\mathbb{T}, \mathcal{A})$. We now define a mapping $T :\operatorname{PAP}(\mathbb{T},\mathcal{A}^{n}) \rightarrow \operatorname{PAP}( \mathbb{T},\mathcal{A}^{n})$ by defining

  $$ (T_{\varphi }) (t)=x_{i\varphi }(t)+p_{i}(t) \int _{0}^{\infty }r_{i}(s) \varphi _{i}(t-s)\Delta s. $$

• Step 2: We will prove $T_{\phi }(\cdot )\in B$ for all $\varphi =(\varphi _{1},\ldots ,\varphi _{n})^{T}\in B$. In accordance with the definition of the norm of Banach space $\operatorname{PAP}(\mathbb{T},\mathcal{A}^{n})$, we have

  $$\begin{aligned} \Vert \varphi _{0} \Vert _{0} =&\max _{1 \leq i \leq n} \biggl\{ \sup_{t \in \mathbb{T}} \int _{-\infty }^{t} e_{-c_{i}} \bigl(t, \sigma (s) \bigr)\frac{ I_{i}(s)}{\xi _{i}} \Delta s \biggr\} \leq \max_{1 \leq i \leq n} \biggl\{ \frac{I_{i}^{+}}{\xi _{i}c_{i}^{-}} \biggr\} = L. \end{aligned}$$

  (12)

  Then, for $\varphi \in B$, we get

  $$\begin{aligned} \Vert \varphi \Vert _{0} \leq & \Vert \varphi - \varphi _{0} \Vert _{0} + \Vert \varphi _{0} \Vert _{0} \leq \frac{pL}{1-p} + L = \frac{L}{1-p}. \end{aligned}$$

  (13)

  Now, we prove that the mapping T is a self-mapping from B to B. In fact, for all $\phi \in B$ with (13), we obtain

  $$\begin{aligned}& \bigl\Vert (T_{\varphi }- \varphi _{0}) \bigr\Vert _{0} \\& \quad \leq \max_{1\leq i\leq n}\sup_{t\in \mathbb{T}} \Biggl\{ \int _{-\infty }^{t} e_{- c_{i}^{-}} \bigl(t,\sigma (s) \bigr) \Biggl[c_{i}^{+}p_{i}^{+} \int _{0}^{\infty }r_{i}(s) \bigl\Vert \varphi _{i}(t-s) \bigr\Vert _{\mathcal{A}}\Delta s \\& \quad \quad {} +\frac{1}{\xi _{i}} \sum_{j=1}^{n} d_{ij}^{+}\xi _{j}L^{g}_{j} \bigl\Vert \varphi _{j}(s) \bigr\Vert _{\mathcal{A}} + \frac{1}{\xi _{i}}\sum_{j=1}^{n} a^{+}_{ij} \xi _{j} L^{g}_{j} \bigl\Vert \varphi _{j} \bigl(s-\tau _{ij}(s) \bigr) \bigr\Vert _{\mathcal{A}} \\& \quad\quad {} +\frac{1}{\xi _{i}} \sum_{j=1}^{n} b^{+}_{ij} \int _{0}^{\infty }N_{ij}(u)\xi _{j}L^{g}_{j} \bigl\Vert \varphi _{j}(s-u) \bigr\Vert _{ \mathcal{A}}\Delta u \\& \quad\quad {} +\frac{1}{\xi _{i}}\sum_{j=1}^{n} \sum_{l=1}^{n} \beta ^{+}_{ijl} \xi _{j} L^{g}_{j} M^{g}_{l} K_{ijl}^{+} \int _{0}^{\infty }H_{ijl}(u) \bigl\Vert \varphi _{j}(s-u) \bigr\Vert _{\mathcal{A}} \Delta u \\& \quad \quad {} +\frac{1}{\xi _{i}}\sum_{j=1}^{n} \sum_{l=1}^{n} \alpha ^{+}_{ijl} \xi _{j}L^{g}_{j} M^{g}_{l} \bigl\Vert \varphi _{j} \bigl(s- \eta _{ijl}(s) \bigr) \bigr\Vert _{\mathcal{A}} \Biggr]\Delta s \\& \quad \quad {}+p_{i}^{+} \int _{0}^{\infty }r_{i}(s) \bigl\Vert \varphi _{i}(t-s) \bigr\Vert _{\mathcal{A}} \Delta s \Biggr\} \\& \quad \leq \max_{1\leq i\leq n} \Biggl\{ \int _{-\infty }^{t} e_{- c_{i}^{-}} \bigl(t, \sigma (s) \bigr) \Biggl[ c_{i}^{+}p_{i}^{+}r_{i}^{+} \Vert \varphi \Vert _{0} +\frac{1}{\xi _{i}} \sum _{j=1}^{n} d_{ij}^{+}\xi _{j}L^{g}_{j} \Vert \varphi \Vert _{0} \\& \quad\quad {} + \frac{1}{\xi _{i}}\sum_{j=1}^{n} a^{+}_{ij} \xi _{j} L^{g}_{j} \Vert \varphi \Vert _{0} +\frac{1}{\xi _{i}} \sum _{j=1}^{n} b^{+}_{ij}N_{ij}^{+} \xi _{j}L^{g}_{j} \Vert \varphi \Vert _{0} \\& \quad \quad {}+ \frac{1}{\xi _{i}} \sum_{j=1}^{n} \sum_{l=1}^{n} \alpha ^{+}_{ijl} \xi _{j}L^{g}_{j} M^{g}_{l} \Vert \varphi \Vert _{0} \\& \quad \quad {} +\frac{1}{\xi _{i}}\sum_{j=1}^{n} \sum_{l=1}^{n} \beta ^{+}_{ijl} H_{ijl}^{+}K_{ijl}^{+} \xi _{j} L^{g}_{j} M^{g}_{l} \Vert \varphi \Vert _{0} \Biggr] \Delta s+p_{i}^{+} r_{i}^{+} \Vert \varphi \Vert _{0} \Biggr\} \\& \quad =\max_{1\leq i\leq n} \Biggl\{ \frac{1}{c_{i}^{-}} \Biggl[ c_{i}^{+}p_{i}^{+} r_{i}^{+}+ \xi _{i}^{-1}\sum_{j=1}^{n} d_{ij}^{+} \xi _{j} L_{j}^{g}+ \xi _{i}^{-1}\sum_{j=1}^{n} a^{+}_{ij} \xi _{j} L^{g}_{j}+ \xi _{i}^{-1} \sum_{j=1}^{n} b^{+}_{ij} N^{+}_{ij}\xi _{j} L^{g}_{j} \\& \quad \quad {} +\xi _{i}^{-1} \sum _{j=1}^{n} \sum_{l=1}^{n} \alpha ^{+}_{ijl} \xi _{j} L^{g}_{j} M^{g}_{l} +\xi _{i}^{-1}\sum _{j=1}^{n} \sum_{l=1}^{n} \beta ^{+}_{ijl} H^{+}_{ijl} K^{+}_{ijl} \xi _{j}L^{g}_{j} M^{g}_{l} \Biggr] +p_{i}^{+}r_{i}^{+} \Biggr\} \Vert \varphi \Vert _{0} \\& \quad =p \Vert \varphi \Vert _{0}\leq \frac{p L }{1-p}, \end{aligned}$$

  it implies that $T_{\varphi }(\cdot ) \in B$.

• Step 3: We will show that T is a contraction mapping. For any given $\varphi , \overline{\varphi }\in B$, we have

  $$\begin{aligned}& \Vert T_{\varphi }-T_{\overline{\varphi }} \Vert _{0} \\& \quad =\max_{1\leq i\leq n}\sup_{t\in \mathbb{T}} \Biggl\{ \Biggl\Vert \int _{-\infty }^{t} e_{-c_{i}} \bigl(t,\sigma (s) \bigr) \\& \quad \quad {}\times \Biggl[-c_{i}(s)p_{i}(s) \int _{0}^{\infty }r_{i}(u) \bigl(\varphi _{i}(s-u) - \overline{\varphi }_{i}(s-u) \bigr)\Delta u \\& \quad \quad {} +\xi _{i}^{-1} \sum _{j=1}^{n} d_{ij}(s) \bigl(g_{j} \bigl(\xi _{j} \varphi _{j}(s) \bigr)- g_{j} \bigl(\xi _{j}\overline{\varphi }_{j}(s) \bigr) \bigr) \\& \quad \quad {} +\xi _{i}^{-1}\sum _{j=1}^{n} a_{ij}(s) \bigl(g_{j} \bigl(\xi _{j} \varphi _{j} \bigl(s-\tau _{ij}(s) \bigr) \bigr)- g_{j} \bigl(\xi _{j}\overline{\varphi }_{j} \bigl(s- \tau _{ij}(s) \bigr) \bigr) \bigr) \\& \quad \quad {} +\xi _{i}^{-1}\sum _{j=1}^{n} b_{ij}(s) \int _{0}^{\infty } N_{ij}(u) \bigl(g_{j} \bigl(\xi _{j}\varphi _{j}(s-u) \bigr)- g_{j} \bigl(\xi _{j} \overline{\varphi }_{j}(s-u) \bigr) \bigr) \Delta u \\& \quad \quad {} +\xi _{i}^{-1}\sum _{j=1}^{n} \sum_{l=1}^{n} \alpha _{ijl}(s) ( g_{j} \bigl(\xi _{j}\varphi _{j} \bigl(s-\eta _{ijl}(s) \bigr) \bigr) g_{l} \bigl( \xi _{l} \varphi _{l} \bigl(s-\nu _{ijl}(s) \bigr) \bigr) \\& \quad \quad {} - g_{j} \bigl(\xi _{j}\overline{\varphi }_{j} \bigl(s-\eta _{ijl}(s) \bigr) \bigr) g_{l} \bigl(\xi _{l}\varphi _{l} \bigl(s-\nu _{ijl}(s) \bigr) \bigr) \\& \quad \quad {} +g_{j} \bigl(\xi _{j}\overline{\varphi }_{j} \bigl(s-\eta _{ij}(s) \bigr) \bigr) g_{l} \bigl(\xi _{l} \varphi _{l} \bigl(s-\nu _{ijl}(s) \bigr) \bigr) \\& \quad \quad {} - g_{j} \bigl(\xi _{j}\overline{\varphi }_{j} \bigl(s-\eta _{ijl}(s) \bigr) \bigr) g_{l} \bigl( \xi _{l}\overline{\varphi }_{l} \bigl(s-\nu _{ijl}(s) \bigr) \bigr) ) \\& \quad \quad {} +\xi _{i}^{-1}\sum _{j=1}^{n} \sum_{l=1}^{n} \beta _{ijl}(s) ( \int _{0}^{\infty } H_{ijl}(u) g_{j} \bigl(\xi _{j}\varphi _{j}(s-u) \bigr) \\& \quad \quad {} \times \Delta u \int _{0}^{\infty } K_{ijl}(u) g_{l} \bigl(\xi _{l}\varphi _{l}(s-u) \bigr) \Delta u \\& \quad \quad {} - \int _{0}^{\infty } H_{ijl}(u) g_{j} \bigl(\xi _{j}\overline{\varphi }_{j}(s-u) \bigr) \Delta u \int _{0}^{\infty } K_{ijl}(u) g_{l} \bigl(\xi _{l}\varphi _{l}(s-u) \bigr) \Delta u \\& \quad \quad {} + \int _{0}^{\infty } H_{ijl}(u) g_{j} \bigl(\xi _{j}\overline{ \varphi }_{j}(s-u) \bigr) \Delta u \int _{0}^{\infty } K_{ijl}(u) g_{l} \bigl(\xi _{l} \varphi _{l}(s-u) \bigr) \Delta u \\& \quad \quad {} - \int _{0}^{\infty } H_{ijl}(u) g_{j} \bigl(\xi _{j} \overline{\varphi }_{j}(s-u) \bigr) \Delta u \int _{0}^{\infty } K_{ijl}(u) g_{l} \bigl( \xi _{l}\overline{\varphi }_{l}(s-u) \bigr) \Delta u ) \Biggr]\Delta s \\& \quad \quad {} + p_{i}(t) \int _{0}^{\infty }r_{i}(s) \bigl(\varphi _{i}(t-s) -\overline{\varphi }_{i}(t-s) \bigr)\Delta s \Biggr\Vert _{\mathcal{A}} \Biggr\} \\& \quad \leq \max_{1\leq i\leq n}\sup_{t\in \mathbb{T}} \Biggl\{ \int _{-\infty }^{t} e_{-c_{i}} \bigl(t,\sigma (s) \bigr) \Biggl[c_{i}^{+}p_{i}^{+} \int _{0}^{\infty }r_{i}(u) \bigl\Vert \varphi _{i}(s-u) - \overline{\varphi }_{i}(s-u) \bigr\Vert _{\mathcal{A}}\Delta u \\& \quad \quad {} +\xi _{i}^{-1} \sum _{j=1}^{n} d_{ij}^{+} L_{j}^{g}\xi _{j} \bigl\Vert \varphi _{j}(s)- \overline{\varphi }_{j}(s) \bigr\Vert _{\mathcal{A}} \\& \quad \quad {} +\xi _{i}^{-1}\sum _{j=1}^{n} a_{ij}^{+} L_{j}^{g}\xi _{j} \bigl\Vert \varphi _{j} \bigl(s-\tau _{ij}(s) \bigr)- \overline{\varphi }_{j} \bigl(s-\tau _{ij}(s) \bigr) \bigr\Vert _{\mathcal{A}} \\& \quad \quad {} +\xi _{i}^{-1}\sum _{j=1}^{n} b_{ij}^{+}L_{j}^{g} \xi _{j} \int _{0}^{ \infty } N_{ij}(u) \bigl\Vert \varphi _{j}(s-u)-\overline{\varphi }_{j}(s-u) \bigr\Vert _{\mathcal{A}} \Delta u \\& \quad \quad {} +\xi _{i}^{-1}\sum _{j=1}^{n}\sum_{l=1}^{n} \alpha _{ijl}^{+} \bigl(L_{j}^{g}\xi _{j} M_{l}^{g} \bigl\Vert \varphi _{j} \bigl(s-\eta _{ijl}(s) \bigr)- \overline{\varphi }_{j} \bigl(s-\eta _{ijl}(s) \bigr) \bigr\Vert _{\mathcal{A}} \\& \quad \quad {} +M_{j}^{g} L_{l}^{g} \xi _{l} \bigl\Vert \varphi _{l} \bigl(s-\nu _{ijl}(s) \bigr) - \overline{\varphi }_{l} \bigl(s-\nu _{ijl}(s) \bigr) \bigr\Vert _{\mathcal{A}} \bigr) \\& \quad \quad {} +\xi _{i}^{-1}\sum _{j=1}^{n} \sum_{l=1}^{n} \beta _{ijl}^{+} \biggl( \xi _{j} L_{j}^{g} K_{ijl}^{+} M_{l}^{g} \int _{0}^{\infty } H_{ijl}(u) \bigl\Vert \varphi _{j}(s-u)-\overline{\varphi }_{j}(s-u) \bigr\Vert _{\mathcal{A}} \Delta u \\& \quad \quad {} +H_{ijl} M_{j}^{g} L_{l}^{g}\xi _{l} \int _{0}^{ \infty } K_{ijl}(u) \bigl\Vert \varphi _{l}(s-u)-\overline{\varphi }_{l}(s-u) \bigr\Vert _{\mathcal{A}} \Delta u \biggr) \Biggr]\Delta s \\& \quad \quad {} + p_{i}^{+} \int _{0}^{\infty }r_{i}(s) \bigl\Vert \varphi _{i}(t-s) -\overline{\varphi }_{i}(t-s) \bigr\Vert _{\mathcal{A}} \Delta s \Vert _{\mathcal{A}} \Biggr\} \\& \quad \leq \max_{1\leq i\leq n}\sup_{t\in \mathbb{T}} \Biggl\{ \int _{-\infty }^{t} e_{-c_{i}^{-}} \bigl(t,\sigma (s) \bigr) \Biggl[c_{i}^{+}p_{i}^{+} r_{i}^{+} \Vert \varphi - \overline{\varphi } \Vert _{0} +\sum_{i=1}^{n} d_{ij}^{+} \xi _{j} L_{j}^{g} \Vert \varphi - \overline{\varphi } \Vert _{0} \\& \quad \quad {} +\xi _{i}^{-1}\sum _{j=1}^{n} a^{+}_{ij} \xi _{j} L^{g}_{j} \Vert \varphi - \overline{ \varphi } \Vert _{0} +\xi _{i}^{-1} \sum _{j=1}^{n} b^{+}_{ij} N^{+}_{ij} \xi _{j}L^{g}_{j} \Vert \varphi - \overline{\varphi } \Vert _{0} \\& \quad \quad {} +\xi _{i}^{-1}\sum _{j=1}^{n} \sum_{l=1}^{n} \alpha ^{+}_{ijl} \bigl(\xi _{j} L^{g}_{j} M^{g}_{l}+ M^{g}_{j} \xi _{l} L^{g}_{l} \bigr) \Vert \varphi - \overline{\varphi } \Vert _{0} \\& \quad \quad {} +\xi _{i}^{-1} \sum _{j=1}^{n} \sum_{l=1}^{n} \beta ^{+}_{ijl} H^{+}_{ijl} K^{+}_{ijl} \bigl(\xi _{j}L^{g}_{j} M^{g}_{l}+ M^{g}_{j} \xi _{l} L^{g}_{l} \bigr) \Vert \varphi - \overline{\varphi } \Vert _{0} \Biggr] \Delta s \\& \quad \quad {}+p_{i}^{+}r_{i}^{+} \Vert \varphi - \overline{\varphi } \Vert _{0} \Biggr\} \\& \quad =\max_{1\leq i\leq n} \Biggl\{ p_{i}^{+}r_{i}^{+} + \frac{1}{c_{i}^{-}} \Biggl[p_{i}^{+} c_{i}^{+}r_{i}^{+}+ \xi _{i}^{-1} \sum_{j=1}^{n}d_{ij}^{+} \xi _{j} L_{j}^{g}+\xi _{i}^{-1} \sum_{j=1}^{n} a^{+}_{ij} \xi _{j} L^{g}_{j} \\& \quad \quad {} +\xi _{i}^{-1}\sum _{j=1}^{n} b^{+}_{ij} N^{+}_{ij} \xi _{j}L^{g}_{j}+ \xi _{i}^{-1}\sum_{j=1}^{n} \sum_{l=1}^{n} \alpha ^{+}_{ijl} \bigl( \xi _{j} L^{g}_{j} M^{g}_{l}+ M^{g}_{j}\xi _{l} L^{g}_{l} \bigr) \\& \quad \quad {} + \xi _{i}^{-1}\sum _{j=1}^{n} \sum_{l=1}^{n} \beta _{ijl}^{+} H^{+}_{ijl} K^{+}_{ijl} \bigl(\xi _{j} L^{g}_{j} M^{g}_{l} + M^{g}_{j} \xi _{l} L^{g}_{l} \bigr) \Biggr] \Biggr\} \Vert \varphi - \overline{\varphi } \Vert _{0} \\& \quad =q \Vert \varphi - \overline{\varphi } \Vert _{0}< \Vert \varphi - \overline{\varphi } \Vert _{0}. \end{aligned}$$

  It is clear that the mapping T is a contraction. Therefore the mapping T possesses a unique fixed point $x^{*} \in B$, $T(x^{*}) = x^{*}$. So $x^{*}$ is a PAP solution of neural networks (1) in the region B.

 □

4 Exponential stability of pseudo almost periodic solution

We establish in this section several results for the global exponential stability of the unique PAP solutions of neural networks (1).

Theorem 4.1

Let $\mathbf{{(A.S_{1})}}$–${\mathbf{(A.S_{4})}}$ hold. Therefore, the unique pseudo almost periodic on time scales solution of neural networks (1) is globally exponentially stable.

Proof

It results from Theorem 3.9 that the neural networks (1) have a unique PAP on time scales $x^{*}(t)= (x_{1}^{*}(t),\ldots ,x_{n}^{*}(t) )^{T}$ with the initial value $\varphi ^{*}(t)$. Let $x(t)= (x_{1}(t),\ldots ,x_{n}(t) )^{T}$ be an arbitrary solution of (1) associated with the initial value $\varphi (t)= (\varphi _{1}(t),\ldots ,\varphi _{n}(t) )^{T}$. Set

$$\begin{aligned} \textstyle\begin{cases} y^{*}_{i}(t)=\xi ^{-1}_{i}x^{*}_{i}(t), \quad\quad Y^{*}_{i}(t)=y^{*}_{i}(t)-p_{i}(t) \int _{0}^{\infty } r_{i}(s) y^{*}_{i}(t-s)\Delta s, \\ y_{i}(t)=\xi ^{-1}_{i}x_{i}(t), \quad\quad Y_{i}(t)=y_{i}(t)-p_{i}(t) \int _{0}^{\infty } r_{i}(s) y_{i}(t-s)\Delta s, \end{cases}\displaystyle \end{aligned}$$

(14)

and

$$\begin{aligned} u_{i}(t)=y_{i}(t)-y^{*}_{i}(t), \quad\quad U_{i}(t)=Y_{i}(t)-Y^{*}_{i}(t), \quad\quad \phi _{i}(t)=\varphi _{i}(t)-\varphi _{i}^{*}(t). \end{aligned}$$

Then system (1) can be rewritten as follows:

$$\begin{aligned} U^{\Delta }_{i}(t) =& \bigl[Y_{i}(t)-Y^{*}_{i}(t) \bigr]^{\Delta } \\ =& -c_{i}(t)U_{i}(t)-p_{i}(t)c_{i}(t) \int _{0}^{\infty }r_{i}(s) u_{i}(t-s)\Delta s \\ &{}+\xi ^{-1}_{i} \sum_{j=1}^{n} d_{ij}(t) \bigl[g_{j} \bigl(\xi _{j}y_{j}(t) \bigr)-g_{j} \bigl(\xi _{j}y^{*}_{j}(t) \bigr) \bigr] \\ &{}+\xi ^{-1}_{i} \sum_{j=1}^{n}a_{ij}(t) \bigl[g_{j} \bigl( \xi _{j}y_{j} \bigl(t-\tau _{ij}(t) \bigr) \bigr)-g_{j} \bigl(\xi _{j}y^{*}_{j} \bigl(t-\tau _{ij}(t) \bigr) \bigr) \bigr] \\ &{}+\xi ^{-1}_{i} \sum_{j=1}^{n}b_{ij}(t) \int _{0}^{ \infty }N_{ij}(u) \bigl[g_{j} \bigl(\xi _{j}y_{j}(t-u) \bigr)-g_{j} \bigl(\xi _{j}y^{*}_{j}(t-u) \bigr) \bigr]\Delta u \\ &{}+\xi ^{-1}_{i} \sum_{j=1}^{n} \sum_{l=1}^{n} \alpha _{ijl}(t) \bigl[ g_{j} \bigl(\xi _{j}y_{j} \bigl(t-\eta _{ijl}(t) \bigr) \bigr) g_{l} \bigl( \xi _{l}y_{l} \bigl(t-\nu _{ijl}(t) \bigr) \bigr) \\ &{}- g_{j} \bigl(\xi _{j}y^{*}_{j} \bigl(t-\eta _{ijl}(t) \bigr) \bigr) g_{l} \bigl(\xi _{l}y^{*}_{l} \bigl(t- \nu _{ijl}(t) \bigr) \bigr) \bigr] \\ &{}+\xi ^{-1}_{i} \sum_{j=1}^{n} \sum_{l=1}^{n} \beta _{ijl}(t) \biggl[ \int _{0}^{\infty } H_{ijl}(u)g_{j} \bigl( \xi _{j}y_{j}(t-u) \bigr)\Delta u \int _{0}^{\infty } K_{ijl}(u) g_{l} \bigl(\xi _{l}y_{l}(t-u) \bigr)\Delta u \\ &{}- \int _{0}^{\infty } H_{ijl}(u)g_{j} \bigl(\xi _{j}y^{*}_{j}(t-u) \bigr) \Delta u \int _{0}^{\infty } K_{ijl}(u) g_{l} \bigl(\xi _{l}y^{*}_{l}(t-u) \bigr) \Delta u \biggr]. \end{aligned}$$

(15)

From $\mathbf{{(A.S_{4})}}$, there exists a constant $\lambda \in (0, \min_{1 \leq i \leq n} \{ c_{i}^{-}, d_{i}^{-} \} )$ such that

$$ 1-p_{j}^{+} \int _{0}^{\infty } r_{j}(\theta ) \exp ( \lambda \theta ) \Delta \theta >0, \quad\quad \frac{\Sigma _{ij}^{1}}{c_{i}^{-}-\lambda }< 1, $$

where

$$\begin{aligned} \Sigma _{ij}^{1} =&\frac{\exp (\lambda \sup_{s \in \mathbb{T}}\nu (s) )}{1-p_{j}^{+} \int _{0}^{\infty } r_{j}(\theta ) \exp (\lambda \theta ) \Delta \theta } \Biggl[c_{i_{0}}^{+}p_{i_{0}}^{+} \int _{0}^{\infty }r_{i_{0}}( \theta ) \exp ( \lambda \theta )\Delta \theta +\xi ^{-1}_{i_{0}} \sum _{j=1}^{n}d_{ij}^{+}L^{g}_{j} \\ &{}+ \xi ^{-1}_{i_{0}} \sum_{j=1}^{n}a_{ij}^{+}L^{g}_{j} \xi _{j} \exp \bigl(\lambda \tau _{ij}^{+} \bigr) +\xi ^{-1}_{i_{0}} \sum_{j=1}^{n}b_{ij}^{+} \int _{0}^{\infty }N_{ij}(u)L^{g}_{j} \exp (\lambda u)\Delta u \\ &{}+ \xi ^{-1}_{i_{0}} \sum_{j=1}^{n} \sum_{l=1}^{n}\alpha _{ijl}^{+} \bigl(M^{g}_{l}L^{g}_{j}\xi _{j} \exp \bigl(\lambda \eta _{ijl}^{+} \bigr) +M^{g}_{j}L^{g}_{l}\xi _{l} \exp \bigl(\lambda \nu _{ijl}^{+} \bigr) \bigr) \\ &{}+ \xi ^{-1}_{i_{0}} \sum_{j=1}^{n} \sum_{l=1}^{n}\beta _{ijl}^{+} \biggl(M^{g}_{l} K_{ijl}^{+}L^{g}_{j} \xi _{j} \int _{0}^{\infty }H_{ijl}(u)\exp (\lambda u) \\ &{}+ M^{g}_{j} H_{ijl}^{+}L^{g}_{l} \xi _{l} \int _{0}^{\infty }K_{ijl}(u)\exp (\lambda u) \Delta u \biggr) \Biggr]. \end{aligned}$$

For any $t_{0}>0$, let $K>1$ be a constant which satisfies

$$\begin{aligned} \bigl\Vert U(t_{0}) \bigr\Vert _{\mathcal{A}^{n}} < & \bigl( \Vert \phi \Vert _{\xi }+\epsilon \bigr) \end{aligned}$$

(16)

and

$$\begin{aligned} \bigl\Vert U(t) \bigr\Vert _{\mathcal{A}^{n}}< \bigl( \Vert \phi \Vert _{\xi }+\epsilon \bigr)e_{ \ominus _{\lambda }}(t,t_{0})< K \bigl( \Vert \phi \Vert _{\xi }+\epsilon \bigr)e_{ \ominus \lambda }(t,t_{0}), \quad \forall t\in (-\infty ,0]_{\mathbb{T}}. \end{aligned}$$

(17)

In the next part, we demonstrate

$$\begin{aligned} \bigl\Vert U(t) \bigr\Vert _{\mathcal{A}^{n}} < &K \bigl( \Vert \phi \Vert _{\xi }+\epsilon \bigr)e_{ \ominus \lambda }(t,t_{0}), \quad t>0. \end{aligned}$$

(18)

If not, there must exist $i_{0}\in \{1,2,\ldots ,n\}$ and $t_{1} > 0$ such that

$$\begin{aligned} \textstyle\begin{cases} \Vert U_{i}(t_{1}) \Vert _{\mathcal{A}}= \Vert U(t_{1}) \Vert _{\mathcal{A}^{n}}=K ( \Vert \Phi \Vert _{1}+\epsilon )e_{\ominus \lambda }(t_{1},t_{0}), \\ \Vert U(t) \Vert _{\mathcal{A}^{n}}< K ( \Vert \Phi \Vert _{1}+\epsilon )e_{ \ominus \lambda }(t,t_{0}), \quad \forall t\in (-\infty ,t_{1}]_{\mathbb{T}}. \end{cases}\displaystyle \end{aligned}$$

(19)

Besides,

$$\begin{aligned} &e_{\lambda }(t_{2},t_{0}) \bigl\Vert u_{j}(t_{2}) \bigr\Vert _{\mathcal{A}} \\ &\quad \leq e_{\lambda }(t_{2},t_{0}) \biggl\Vert u_{j}(t_{2})-p_{j}(t_{2}) \int _{0}^{ \infty } r_{j}(\theta )u_{j}(t_{2}-u)\Delta \theta \biggr\Vert _{ \mathcal{A}} \\ &\quad\quad{} +e_{\lambda }(t_{2},t_{0}) \biggl\Vert p_{j}(t_{2}) \int _{0}^{\infty } r_{j}( \theta )u_{j}(t_{2}-\theta )\Delta \theta \biggr\Vert _{\mathcal{A}} \\ &\quad \leq e_{\lambda }(t_{2},t_{0}) \bigl\Vert U_{j}(t_{2}) \bigr\Vert _{\mathcal{A}}+p_{j}^{+} \int _{0}^{\infty } r_{j}(\theta ) e_{\lambda }(\theta ,t_{0}) e_{ \lambda }(t_{2}- \theta ,t_{0}) \bigl\Vert u_{j}(t_{2}-\theta ) \bigr\Vert _{\mathcal{A}} \Delta \theta \\ &\quad \leq K \bigl( \Vert \phi \Vert _{\xi }+\epsilon \bigr)+p_{j}^{+} \int _{0}^{ \infty } r_{j}(\theta ) \exp ( \lambda \theta ) \Delta \theta \sup_{s\in (-\infty ,t]}e_{\lambda }(s,t_{0}) \bigl\Vert u_{j}(s) \bigr\Vert _{\mathcal{A}} \end{aligned}$$

(20)

for all $t_{2}\leq t$; $t < t_{1}$, $j=1,2,\ldots ,n$, which implies that

$$\begin{aligned} e_{\lambda }(t,t_{0}) \bigl\Vert u_{j}(t) \bigr\Vert _{\mathcal{A}} \leq & \sup_{s\in (-\infty ,t]}e_{\lambda }(s,t_{0}) \bigl\Vert u_{j}(s) \bigr\Vert _{\mathcal{A}} \\ \leq &\frac{K ( \Vert \phi \Vert _{\xi }+\epsilon )}{1-p_{j}^{+} \int _{0}^{\infty } r_{j}(\theta ) \exp (\lambda \theta ) \Delta \theta }. \end{aligned}$$

(21)

Furthermore,

$$\begin{aligned} &U^{\Delta }_{i}(s)+ c_{i}(s)U_{i}(s) \\ &\quad =- c_{i}(s)p_{i}(s) \int _{0}^{\infty }r_{i}(\theta ) u_{i}(s- \theta ) \Delta \theta +\xi ^{-1}_{i} \sum_{j=1}^{n} d_{ij}(s) \bigl[g_{j} \bigl(\xi _{j}y_{j}(s) \bigr)-g_{j} \bigl(\xi _{j}y^{*}_{j}(s) \bigr) \bigr] \\ &\quad\quad{} +\xi ^{-1}_{i} \sum _{j=1}^{n}a_{ij}(s) \bigl[g_{j} \bigl( \xi _{j}y_{j} \bigl(s-\tau _{ij}(s) \bigr) \bigr)-g_{j} \bigl(\xi _{j}y^{*}_{j} \bigl(s-\tau _{ij}(s) \bigr) \bigr) \bigr] \\ &\quad\quad{} +\xi ^{-1}_{i} \sum _{j=1}^{n}b_{ij}(s) \int _{0}^{ \infty }N_{ij}(u) \bigl[g_{j} \bigl(\xi _{j}y_{j}(s-u) \bigr)-g_{j} \bigl(\xi _{j}y^{*}_{j}(s-u) \bigr) \bigr]\Delta u \\ &\quad\quad{} +\xi ^{-1}_{i} \sum _{j=1}^{n}\sum_{l=1}^{n} \alpha _{ijl}(s) \bigl[ g_{j} \bigl(\xi _{j}y_{j} \bigl(s-\eta _{ijl}(s) \bigr) \bigr)g_{l} \bigl( \xi _{l}y_{l} \bigl(s-\nu _{ijl}(s) \bigr) \bigr) \\ &\quad\quad{} - g_{j} \bigl(\xi _{j}y^{*}_{j} \bigl(s-\eta _{ijl}(s) \bigr) \bigr) g_{l} \bigl(\xi _{l}y^{*}_{l} \bigl(s- \nu _{ijl}(s) \bigr) \bigr) \bigr] \\ &\quad\quad{} +\xi ^{-1}_{i} \sum _{j=1}^{n} \sum_{l=1}^{n} \beta _{ijl}(s) \biggl[ \int _{0}^{\infty } H_{ijl}(u)g_{j} \bigl( \xi _{j}y_{j}(s-u) \bigr)\Delta u \int _{0}^{\infty } K_{ijl}(u) g_{l} \bigl(\xi _{l}y_{l}(s-u) \bigr)\Delta u \\ &\quad\quad{} - \int _{0}^{\infty } H_{ijl}(u)g_{j} \bigl(\xi _{j}y^{*}_{j}(s-u) \bigr) \Delta u \int _{0}^{\infty } K_{ijl}(u) g_{l} \bigl(\xi _{l}y^{*}_{l}(s-u) \bigr) \Delta u \biggr], \end{aligned}$$

(22)

where $s\in [0,t]_{\mathbb{T}}$, $t\in [0,t_{1}]_{\mathbb{T}}$, $i\in \{1,2,\ldots ,n\}$. Multiplying both sides of (22) by $e_{-c_{i}}(t_{0},\sigma (s))$ and integrating it on $[t_{0},t]_{ \mathbb{T} }$, we have

$$\begin{aligned} U_{i}(t) =&U_{i}(t_{0})e_{-c_{i}}(t,t_{0})+ \int _{t_{0}}^{t}e_{-c_{i}} \bigl(t, \sigma (s) \bigr) \Biggl\{ -c_{i}(s)p_{i}(s) \int _{0}^{\infty }r_{i}( \theta ) u_{i}(s-\theta ) \Delta \theta \\ &{}+\xi ^{-1}_{i} \sum_{j=1}^{n} d_{ij}(s) \bigl[g_{j} \bigl(\xi _{j}y_{j}(s) \bigr)-g_{j} \bigl(\xi _{j}y^{*}_{j}(s) \bigr) \bigr] \\ &{}+\xi ^{-1}_{i} \sum_{j=1}^{n}a_{ij}(s) \bigl[g_{j} \bigl( \xi _{j}y_{j} \bigl(s-\tau _{ij}(s) \bigr) \bigr)-g_{j} \bigl(\xi _{j}y^{*}_{j} \bigl(s-\tau _{ij}(s) \bigr) \bigr) \bigr] \\ &{}+\xi ^{-1}_{i} \sum_{j=1}^{n}b_{ij}(s) \int _{0}^{ \infty }N_{ij}(u) \bigl[g_{j} \bigl(\xi _{j}y_{j}(s-u) \bigr)-g_{j} \bigl(\xi _{j}y^{*}_{j}(s-u) \bigr) \bigr]\Delta u \\ &{}+\xi ^{-1}_{i} \sum_{j=1}^{n} \sum_{l=1}^{n} \alpha _{ijl}(s) \bigl[ g_{j} \bigl(\xi _{j}y_{j} \bigl(s-\eta _{ijl}(s) \bigr) \bigr)g_{l} \bigl( \xi _{l}y_{l} \bigl(s-\nu _{ijl}(s) \bigr) \bigr) \\ &{}- g_{j} \bigl(\xi _{j}y^{*}_{j} \bigl(s-\eta _{ijl}(s) \bigr) \bigr) g_{l} \bigl(\xi _{l}y^{*}_{l} \bigl(s- \nu _{ijl}(s) \bigr) \bigr) \bigr] \\ &{}+\xi ^{-1}_{i} \sum_{j=1}^{n} \sum_{l=1}^{n} \beta _{ijl}(s) \biggl[ \int _{0}^{\infty } H_{ijl}(u)g_{j} \bigl( \xi _{j}y_{j}(s-u) \bigr)\Delta u \int _{0}^{\infty } K_{ijl}(u) g_{l} \bigl(\xi _{l}y_{l}(s-u) \bigr)\Delta u \\ &{}- \int _{0}^{\infty } H_{ijl}(u)g_{j} \bigl( \xi _{j}y^{*}_{j}(s-u) \bigr)\Delta u \int _{0}^{\infty } K_{ijl}(u) g_{l} \bigl(\xi _{l}y^{*}_{l}(s-u) \bigr)\Delta u \biggr] \Biggr\} \Delta s \end{aligned}$$

(23)

for all $t\in [0,t_{1}]_{\mathbb{T}}$. Thus, from (16), (17), (19), and (21), we have

$$\begin{aligned} & \bigl\Vert U_{i_{0}}(t_{1}) \bigr\Vert _{\mathcal{A}} \\ &\quad \leq \bigl\Vert U_{i_{0}}(t_{0}) \bigr\Vert _{\mathcal{A}}e_{-c_{i}}(t_{1},t_{0})+ \int _{t_{0}}^{t}e_{-c_{i}} \bigl(t_{1}, \sigma (s) \bigr) \Biggl[ c_{i_{0}}^{+}p_{i_{0}}^{+} \int _{0}^{\infty }r_{i_{0}}(\theta ) \bigl\Vert u_{i_{0}}(s- \theta ) \bigr\Vert _{\mathcal{A}} \Delta \theta \\ &\quad\quad{} + \sum_{j=1}^{n} d_{ij}^{+}L^{g}_{j}\xi _{j} \bigl\Vert u_{j}(s) \bigr\Vert _{\mathcal{A}} + \sum _{j=1}^{n}a_{ij}^{+}L^{g}_{j} \xi _{j} \bigl\Vert u_{j} \bigl(s-\tau _{ij}(s) \bigr) \bigr\Vert _{\mathcal{A}} \\ &\quad\quad{} + \sum_{j=1}^{n}b_{ij}^{+} \int _{0}^{\infty }N_{ij}(u)L^{g}_{j} \bigl\Vert u_{j}(s-u) \bigr\Vert _{\mathcal{A}}\Delta u \\ &\quad\quad {} + \sum_{j=1}^{n}\sum _{l=1}^{n} \alpha _{ijl}^{+} \bigl(M^{g}_{l}L^{g}_{j}\xi _{j} \bigl\Vert u_{j} \bigl(s-\eta _{ijl}(s) \bigr) \bigr\Vert _{\mathcal{A}} +M^{g}_{j}L^{g}_{l} \xi _{l} \bigl\Vert u_{l} \bigl(s-\nu _{ijl}(s) \bigr) \bigr\Vert _{\mathcal{A}} \bigr) \\ &\quad\quad{} + \sum_{j=1}^{n}\sum _{l=1}^{n}\beta _{ijl}^{+} \biggl(K_{ijl}^{+}M^{g}_{l} L^{g}_{j}\xi _{j} \int _{0}^{ \infty }H_{ijl}(u) \bigl\Vert u_{j}(s-u) \bigr\Vert _{\mathcal{A}}\Delta u \\ &\quad\quad{} + L^{g}_{l}M^{g}_{j} \xi _{l}H_{ijl}^{+} \int _{0}^{\infty }K_{ijl}(u) \bigl\Vert u_{l}(s-u) \bigr\Vert _{\mathcal{A}}\Delta u \biggr) \Biggr]\Delta s \\ &\quad \leq \bigl( \Vert \phi \Vert _{\xi }+\epsilon \bigr)e_{-c_{i}}(t_{1},t_{0}) + \frac{K ( \Vert \phi \Vert _{\xi }+\epsilon )e_{\ominus \lambda }(t_{1},t_{0})}{1-p_{j}^{+} \int _{0}^{\infty } r_{j}(\theta ) \exp (\lambda \theta ) \Delta \theta } \int _{t_{0}}^{t}e_{-c_{i}\oplus \lambda } \bigl(t_{1}, \sigma (s) \bigr) \\ &\quad\quad{} \times \Biggl[ c_{i_{0}}^{+}p_{i_{0}}^{+} \int _{0}^{\infty }r_{i_{0}}(\theta ) e_{\lambda } \bigl(\sigma (s),s-\theta \bigr)\Delta \theta +\xi ^{-1}_{i_{0}} \sum_{j=1}^{n} d_{ij}^{+}L^{g}_{j} e_{\lambda } \bigl(\sigma (s),s \bigr) \\ &\quad\quad{} +\xi ^{-1}_{i_{0}} \sum _{j=1}^{n}a_{ij}^{+}L^{g}_{j} \xi _{j} e_{\lambda } \bigl(\sigma (s),s-\tau _{ij}(s) \bigr) +\xi ^{-1}_{i_{0}} \sum_{j=1}^{n}b_{ij}^{+} \int _{0}^{\infty }N_{ij}(u)L^{g}_{j} e_{\lambda } \bigl(\sigma (s),s-u \bigr)\Delta u \\ &\quad\quad{} +\xi ^{-1}_{i_{0}} \sum _{j=1}^{n}\sum_{l=1}^{n} \alpha _{ijl}^{+} \bigl(M^{g}_{l}L^{g}_{j} \xi _{j} e_{\lambda } \bigl(\sigma (s),s-\eta _{ijl}(s) \bigr) +M^{g}_{j}L^{g}_{l} \xi _{l}e_{\lambda } \bigl(\sigma (s),s-\nu _{ijl}(s) \bigr) \bigr) \\ &\quad\quad{} +\xi ^{-1}_{i_{0}} \sum _{j=1}^{n}\sum_{l=1}^{n} \beta _{ijl}^{+} \biggl(M^{g}_{l} K_{ijl}^{+}L^{g}_{j} \xi _{j} \int _{0}^{\infty }H_{ijl}(u)e_{\lambda } \bigl( \sigma (s),s-u \bigr)\Delta u \\ &\quad\quad{} +M^{g}_{j} H_{ijl}^{+}L^{g}_{l} \xi _{l} \int _{0}^{\infty }K_{ijl}(u)e_{\lambda } \bigl(\sigma (s),s-u \bigr) \Delta u \biggr) \Biggr]\Delta s \\ &\quad \leq K \bigl( \Vert \phi \Vert _{\xi }+\epsilon \bigr)e_{\ominus \lambda }(t_{1},t_{0}) \Biggl\{ \frac{1}{K}e_{-c_{i_{0}}\oplus \lambda }(t_{1},t_{0}) + \frac{\exp (\lambda \sup_{s \in \mathbb{T}}\nu (s) )}{1-p_{j}^{+} \int _{0}^{\infty } r_{j}(\theta ) \exp (\lambda \theta ) \Delta \theta } \\ &\quad\quad{} \times \Biggl[c_{i_{0}}^{+}p_{i_{0}}^{+} \int _{0}^{\infty }r_{i_{0}}(\theta ) \exp ( \lambda \theta )\Delta \theta +\xi ^{-1}_{i_{0}} \sum _{j=1}^{n}d_{ij}^{+}L^{g}_{j} +\xi ^{-1}_{i_{0}} \sum_{j=1}^{n}a_{ij}^{+}L^{g}_{j} \xi _{j} \exp \bigl(\lambda \tau _{ij}^{+} \bigr) \\ &\quad\quad{} +\xi ^{-1}_{i_{0}} \sum _{j=1}^{n}b_{ij}^{+} \int _{0}^{\infty }N_{ij}(u)L^{g}_{j} \exp (\lambda u)\Delta u +\xi ^{-1}_{i_{0}} \sum _{j=1}^{n}\sum_{l=1}^{n} \alpha _{ijl}^{+} \bigl(M^{g}_{l}L^{g}_{j} \xi _{j}\exp \bigl(\lambda \eta _{ijl}^{+} \bigr) \\ &\quad\quad{} +M^{g}_{j}L^{g}_{l}\xi _{l}\exp \bigl(\lambda \nu _{ijl}^{+} \bigr) \bigr) +\xi ^{-1}_{i_{0}} \sum_{j=1}^{n} \sum_{l=1}^{n}\beta _{ijl}^{+} \biggl(M^{g}_{l} K_{ijl}^{+}L^{g}_{j} \xi _{j} \int _{0}^{\infty }H_{ijl}(u)\exp (\lambda u) \\ &\quad\quad{} + M^{g}_{j} H_{ijl}^{+}L^{g}_{l} \xi _{l} \int _{0}^{\infty }K_{ijl}(u)\exp (\lambda u) \Delta u \biggr) \Biggr] \int _{t_{0}}^{t}e_{-c_{i}\oplus \lambda } \bigl(t_{1}, \sigma (s) \bigr)\Delta s \Biggr\} \\ &\quad < K \bigl( \Vert \phi \Vert _{\xi }+\epsilon \bigr)e_{\ominus \lambda }(t_{1},t_{0}) \biggl[ \frac{e_{-(c_{i_{0}}- \lambda )}(t_{1},t_{0})}{K} + \frac{1-e_{-(c_{i_{0}}- \lambda )}(t_{1},t_{0})}{c_{i_{0}}^{-}-\lambda } \Xi _{ij}^{1} \biggr] \\ &\quad = K \bigl( \Vert \phi \Vert _{\epsilon }+\epsilon \bigr)e_{\ominus \lambda }(t_{1},t_{0}) \biggl[ \biggl( \frac{1}{K}-\frac{\Xi _{ij}^{1}}{c_{i_{0}}^{-}-\lambda } \biggr)e_{-(c_{i_{0}}- \lambda )}(t_{1},t_{0})+ \frac{\Xi _{ij}^{1}}{c_{i_{0}}^{-}-\lambda } \biggr] \\ &\quad < K \bigl( \Vert \Phi \Vert _{1}+\epsilon \bigr)e_{\ominus \lambda }(t_{1},t_{0}), \end{aligned}$$

(24)

which contradicts (19). Therefore, (18) holds. Letting $\epsilon \rightarrow 0^{+}$ leads to

$$\begin{aligned} \bigl\Vert Y(t) \bigr\Vert \leq &K \Vert \Phi \Vert _{1}e_{\ominus \lambda }(t_{1},t_{0}), \quad \forall t>0. \end{aligned}$$

(25)

Then, using the same arguments as in the proof of (20) and (21), in view of (25), we can prove

$$\begin{aligned} e_{\lambda }(t_{1},t_{0}) \bigl\Vert y_{j}(t) \bigr\Vert _{\mathcal{A}} \leq & \sup_{s\in (-\infty ,t]_{\mathbb{T}}}e_{ \lambda }(s,t_{0}) \bigl\Vert y_{j}(s) \bigr\Vert _{\mathcal{A}} \leq \frac{K \Vert \phi \Vert _{\xi }}{1-p_{j}^{+} \int _{0}^{\infty } r_{j}(\theta ) \exp (\lambda \theta ) \Delta \theta } \end{aligned}$$

and

$$\begin{aligned} \bigl\Vert y_{j}(t) \bigr\Vert _{\mathcal{A}} \leq & \frac{K \Vert \phi \Vert _{\xi }}{1-p_{j}^{+} \int _{0}^{\infty } r_{j}(\theta ) \exp (\lambda \theta ) \Delta \theta }e_{ \ominus \lambda }(t_{1},t_{0}), \quad \forall t>0, j=1,2,\ldots ,n. \end{aligned}$$

 □

Remark 4.2

The existence and global exponential stability of pseudo almost periodic solutions for Clifford’s high-order neural networks with D-operator on time scale are studied using the direct method. In other words, we do not decompose system (1) into a real-valued system, but we study Clifford-valued systems directly.

Remark 4.3

Even when system (1) is degenerated into quaternion-valued system or complex-valued system, that is, when A has only two or one Clifford generators, the conclusion of Theorem (1) remains new.

Remark 4.4

The sufficient condition for the global exponential stability of Clifford-valued HNNs has been obtained by the method of variation parameter and inequality technique. When the system deduces to real-valued or complex-valued HNNs, the corresponding stability criterion could be gotten.

5 Example

We present an example in this section to show the feasibility of our main findings in this work.

In model (1), let $n = p = 2$, and for $i=j = 1,2$, take

$$\begin{aligned}& c_{i}(t)=4+\sin ^{2}(t), \quad\quad p_{i}(t)=0.3+0.5 \sin (t), \quad\quad \tau _{ij}(t)=3- \sin \frac{\sqrt{5}}{7} t, \\& \nu _{ijl}(t)=\eta _{ijl}(t)=2+\cos \frac{\sqrt{3}}{2} t, \\& g_{i}(x)=\frac{1}{48} e_{0} \sin \bigl(x_{j}^{0}+x_{j}^{12} \bigr)+ \frac{1}{40} e_{1} \sin \bigl(x_{j}^{2}-x_{j}^{1} \bigr) + \frac{1}{30} e_{2} \sin \bigl(x_{j}^{1}+x_{j}^{12} \bigr)+ \frac{1}{36} e_{12} \sin \bigl(x_{j}^{0}+x_{j}^{2} \bigr), \\& \begin{aligned} I_{1}(t)= {}&0.2 e_{0} \biggl(\sin 3 t-\frac{2}{1+t^{2}} \biggr)+0.3 e_{1} \cos \sqrt{3} t +0.15 e_{2} \cos 2 t \\ &{}+0.1 e_{12} \biggl(\cos 4 t+ \frac{3}{1+t^{2}} \biggr), \end{aligned} \\& \begin{aligned} I_{2}(t)= {}&0.1 e_{0} \cos 3 t+0.5 e_{1} \biggl( \sin \sqrt{3} t+ \frac{3}{1+t^{2}} \biggr) +0.4 e_{2} \biggl(\cos \sqrt{2} t- \frac{\sqrt{7}}{1+t^{2}} \biggr) \\ &{}+0.3 e_{12} \sin \sqrt{2} t, \end{aligned} \\& {d_{11}(t)=0.3 e_{0} \sin \sqrt{2} t+0.06 e_{1} \cos \sqrt{2} t+0.1 e_{2} \cos 3 t+0.1e_{12} \sin \sqrt{3} t}, \\& {d_{12}(t)=0.05 e_{0} \sin 2 t+0.2 e_{1} \cos 4 t+0.2e_{2} \sin \sqrt{5} t+0.05 e_{12} \sin \sqrt{7} t}, \\& {d_{21}(t)=0.04 e_{0} \cos 3 t+ e_{1} \biggl(0.05+ \frac{0.05}{1+t^{2}} \biggr)+0.07 e_{2} \cos \sqrt{2} t+0.2 e_{12} \cos 4 t}, \\& {d_{22}(t)=0.05 e_{0} \cos ^{2}t+0.1 e_{1} \frac{1}{1+t^{2}}+0.05 e_{2} \cos 2 t+0.2 e_{12} \cos t}, \\& {a_{11}(t)=0.3 e_{0} \sin ^{2} t+0.04 e_{1} \sin \sqrt{7} t+0.1 e_{2} \sin ^{2} t+ e_{12} (0.1+0.1\cos \sqrt{3} t )}, \\& {a_{12}(t)=0.1e_{0} \cos 2 t+ e_{1} (0.1+0.1 \cos 4 t )+ e_{2} \biggl(0.1\cos (\sqrt{5} t)+\frac{0.1}{1+t^{2}} \biggr)+e_{12} \frac{0.05}{1+t^{2}}}, \\& {a_{21}(t)=0.06 e_{0} \sin ^{2}t+e_{1} 0.1\sin 9 t+0.03 e_{2} \frac{1}{1+t^{2}}+0.2 e_{12} \sin 4 t}, \\& {a_{22}(t)=0.05 e_{0} \sin 3 t+0.1 e_{1} \cos \sqrt{3} t+0.1e_{2} \cos 2 t+0.1 e_{12} \sin 5 t}, \\& b_{11}(t) = \bigl(0.1+0.1\sin ^{2}(t) \bigr) e_{0}+0.1 e_{1} \sin \sqrt{2} t+0.05e_{2} \sin \sqrt{2} t+ e_{12} (0.1+0.2 \sin \sqrt{5} t ), \\& b_{22}(t) =0.1 e_{0} \cos 3 t+0.3 e_{1} \sin 9 t+0.4 e_{2} \cos 2 t+0.5 e_{12} \sin \sqrt{2} t, \\& b_{12}(t) =0.1 e_{0}\frac{1}{1+t^{2}} +0.2e_{1} \sin \sqrt{5} t+e_{2} \biggl(0.04\sin ^{2} t+0.06 \frac{1}{1+t^{2}} \biggr)+0.2 e_{12} \sin 3 t, \\& b_{21}(t) =0.1 e_{0} \cos 3 t+0.2 e_{1} \sin \sqrt{5} t+0.1 e_{2} \sin ^{2}t+0.05 e_{12} \cos 2 t, \\& \alpha _{111}(t)=\alpha _{121}=\alpha _{122}= \alpha _{211}(t)= \alpha _{221}=\alpha _{222}=0, \\& \alpha _{112}=0.3 e_{0} \cos 2 t+e_{1} \biggl(0.2\sin (3t)+ \frac{0.2}{1+t^{2}} \biggr)+0.05 e_{2} \cos ^{2} t+0.1 e_{12} \sin \sqrt{5} t, \\& \alpha _{212}=0.1 e_{0} \cos 3 t+0.3 e_{1} \sin 9 t+0.4 e_{2} \cos 2 t+0.5 e_{12} \sin \sqrt{2} t, \\& \beta _{111}(t)=\beta _{121}=\beta _{122}=\beta _{211}(t)=\beta _{221}= \beta _{222}=0, \\& \beta _{112}=0.4 e_{0} \sin \sqrt{2} t+0.1 e_{1} \sin \sqrt{2} t+0.3 e_{2} \sin \sqrt{5} t+0.2 e_{12} \cos 4 t, \\& \beta _{212}=0.1 e_{0} \frac{1}{1+t^{2}}+0.3 e_{1} \cos \sqrt{5} t+0.1 e_{2} \sin 2 t+0.1e_{12} \cos 2 t, \\& r_{i}(t)=N_{ij}(t)=K_{ijl}(t)=H_{ijl}(t)=e^{-t}. \end{aligned}$$

By a simple calculation, we have

$$\begin{aligned}& L_{j}^{g}=\frac{1}{15}, \quad\quad M_{j}^{g}=\frac{1}{30}, \quad\quad d_{11}^{+}=0.3, \quad\quad d_{12}^{+}=0.2, \quad\quad d_{21}^{+}=0.2, \quad\quad d_{22}^{+}=0.2, \\& a_{11}^{+}=0.3, \quad\quad a_{12}^{+}=0.2, \quad\quad a_{21}^{+}=0.2, \quad\quad a_{22}^{+}=0.1, \quad\quad b_{11}^{+}=0.3, \quad\quad b_{12}^{+}=0.2, \\& b_{21}^{+}=0.2, \quad\quad b_{22}^{+}=0.5, \quad\quad \alpha _{112}^{+}=0.4, \quad\quad \alpha _{212}^{+}=0.5, \quad\quad \beta _{112}^{+}=0.4, \quad\quad \beta _{212}^{+}=0.3, \end{aligned}$$

and

$$\begin{aligned}& \begin{aligned} p &=\max_{1 \leq i \leq n} \Biggl\{ p_{i}^{+}r_{i}^{+}+ \frac{1}{c_{i}^{-}} \Biggl[ c_{i}^{+}p_{i}^{+}r_{i}^{+} +\xi _{i}^{-1} \Biggl(\sum_{j=1}^{n} d_{ij}^{+} \xi _{j} L_{j}^{g} +\sum_{j=1}^{n} a^{+}_{ij} \xi _{j} L^{g}_{j} \\ &\quad {} +\sum_{j=1}^{n} b^{+}_{ij} N^{+}_{ij}\xi _{j} L^{g}_{j}+ \sum_{j=1}^{n} \sum_{l=1}^{n} \alpha ^{+}_{ijl} \xi _{j} L^{g}_{j} M^{g}_{l}+ \sum_{j=1}^{n} \sum _{l=1}^{n} \beta ^{+}_{ijl} H^{+}_{ijl} K^{+}_{ijl} \xi _{j}L^{g}_{j}M_{j}^{g} \Biggr) \Biggr] \Biggr\} \\ &=\max \{ 0.4470; 0.4457 \} , \end{aligned} \\& \begin{aligned} q &= \max_{1 \leq i \leq n} \Biggl\{ p_{i}^{+}r_{i}^{+} + \frac{1}{c_{i}^{-}} \Biggl[p_{i}^{+} c_{i}^{+}r_{i}^{+}+ \xi _{i}^{-1} \sum_{j=1}^{n}d_{ij}^{+} \xi _{j} L_{j}^{g}+\xi _{i}^{-1} \sum_{j=1}^{n} a^{+}_{ij} \xi _{j} L^{g}_{j} \\ &\quad {} +\xi _{i}^{-1}\sum_{j=1}^{n} b^{+}_{ij} N^{+}_{ij} \xi _{j}L^{g}_{j}+ \xi _{i}^{-1} \sum_{j=1}^{n} \sum _{l=1}^{n} \alpha ^{+}_{ijl} \bigl( \xi _{j} L^{g}_{j} M^{g}_{l}+ M^{g}_{j}\xi _{l} L^{g}_{l} \bigr) \\ &\quad {} + \xi _{i}^{-1}\sum_{j=1}^{n} \sum_{l=1}^{n} \beta _{ijl}^{+} H^{+}_{ijl} K^{+}_{ijl} \bigl(\xi _{j} L^{g}_{j} M^{g}_{l} + M^{g}_{j} \xi _{l} L^{g}_{l} \bigr) \Biggr] \Biggr\} \\ &=\max \{ 0.4474; 0.4460 \} < 1. \end{aligned} \end{aligned}$$

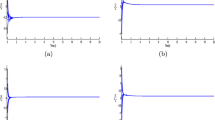
It is easy to verify that all conditions in Theorems 3.9 and 4.1 hold. By Theorems 3.9 and 4.1, system (1) has a unique PAP solution, which is globally exponentially stable, see Fig. 1 and Fig. 2.

Figure 1

(a) Curves of $x_{i}^{0}(t)$ of the continuous case $\mathbb{T}=\mathbb{R}$; (b) Curves of $x_{i}^{1}(t)$ of the continuous case $\mathbb{T}=\mathbb{R}$; (c) Curves of $x_{i}^{2}(t)$ of the continuous case $\mathbb{T}=\mathbb{R}$; (d) Curves of $x_{i}^{12}(t)$ of the continuous case $\mathbb{T}=\mathbb{R}$

Figure 2

(a) Curves of $x_{i}^{0}(t)$ of the discrete case $\mathbb{T}=\mathbb{Z}$; (b) Curves of $x_{i}^{1}(t)$ of the discrete case $\mathbb{T}=\mathbb{Z}$; (c) Curves of $x_{i}^{2}(t)$ of the discrete case $\mathbb{T}=\mathbb{Z}$; (d) Curves of $x_{i}^{12}(t)$ of the discrete case $\mathbb{T}=\mathbb{Z}$

6 Conclusion and open problems

The existence and global exponential stability of almost periodic pseudo solutions for high-order Clifford’s neural networks on a time scale with the D-operator have been obtained in this paper using the direct method. The results and the methods in this work are completely new. This work presents methods that can be used to investigate the problem of PAP solutions of other types of Clifford-valued neural networks like Clifford-valued cellular neural networks, Clifford-valued BAM networks, and Clifford-valued shunt inhibiting cellular neural networks. The study of the dynamics of fuzzy Clifford neural networks is our future research.