Abstract
In this paper, we introduce the non-convex interval-valued functions for fuzzy-interval-valued functions, which are called  -convex fuzzy-interval-valued functions, by means of fuzzy order relation. This fuzzy order relation is defined level-wise through Kulisch–Miranker order relation given on the interval space. By using the
-convex fuzzy-interval-valued functions, by means of fuzzy order relation. This fuzzy order relation is defined level-wise through Kulisch–Miranker order relation given on the interval space. By using the  -convexity concept, we present fuzzy-interval Hermite–Hadamard inequalities for fuzzy-interval-valued functions. Several exceptional cases are debated, which can be viewed as useful applications. Interesting examples that verify the applicability of the theory developed in this study are presented. The results of this paper can be considered as extensions of previously established results.
-convexity concept, we present fuzzy-interval Hermite–Hadamard inequalities for fuzzy-interval-valued functions. Several exceptional cases are debated, which can be viewed as useful applications. Interesting examples that verify the applicability of the theory developed in this study are presented. The results of this paper can be considered as extensions of previously established results.
Similar content being viewed by others
1 Introduction
The following integral inequality is known in the literature as the Hermite–Hadamard inequality [16, 17]:
where \(\mathcal{F}: K \rightarrow \mathbb{R}\) is a convex function on the interval \(K= [ {u}, \vartheta ]\) with \({u<} \vartheta \). So the concept of convexity in an integral problem is an interesting area for research. Therefore, much attention has been given to studying and characterizing different directions of classical convexity. Recently, many extensions and generalizations Hermite–Hadamard inequality for generalized convex functions have been established. For more useful details, see [1, 3–5, 7, 10, 19–23, 28] and the references therein.
On the other hand, the theory of interval analysis fell in to oblivion for a long time because of lack of applications in other sciences. The concept of interval analysis was proposed and investigated by Moore [26] and Kulish and Miranker [25]. For the first time it was used in numerical analysis to determine the error bounds of numerical solutions of a finite state machine. For fundamental details and applications, we refer the readers to the papers [14, 27, 32, 33] and the references therein. Inspired by the above literature, in 2018, Zhao et al. introduced  -convex interval-valued functions and proved the Hermite–Hadamard-type inequality for
-convex interval-valued functions and proved the Hermite–Hadamard-type inequality for  -convex interval-valued functions [34]. As a step forward, An et al. [2] presented the class of
-convex interval-valued functions [34]. As a step forward, An et al. [2] presented the class of  -convex interval-valued functions and established the following interval-valued Hermite–Hadamard-type inequality for such functions:
-convex interval-valued functions and established the following interval-valued Hermite–Hadamard-type inequality for such functions:
Theorem 1
Let \(\mathcal{F}: [ {u}, \vartheta ] \subset \mathbb{R} \rightarrow \mathcal{K}_{C}^{+}\) be a  -convex interval-valued function given by \(\mathcal{F} ( x ) = [ \mathcal{F}_{*} ( x ), \mathcal{F}^{*} ( x ) ]\) for all \(x \in [ {u}, \vartheta ]\), with
-convex interval-valued function given by \(\mathcal{F} ( x ) = [ \mathcal{F}_{*} ( x ), \mathcal{F}^{*} ( x ) ]\) for all \(x \in [ {u}, \vartheta ]\), with  and
and  , where \(\mathcal{F}_{*} ( x )\) and \(\mathcal{F}^{*} ( x )\) both are
, where \(\mathcal{F}_{*} ( x )\) and \(\mathcal{F}^{*} ( x )\) both are  -concave functions. If \(\mathcal{F}\) is Riemann integrable (in short, IR-integrable), then
-concave functions. If \(\mathcal{F}\) is Riemann integrable (in short, IR-integrable), then

We refer to the readers for further analysis of the literature on the applications and properties of generalized convex functions and Hermite–Hadamard integral inequalities to [6, 8, 9, 13, 15, 17, 24, 30, 31] and the references therein.
There are some integrals to deal with fuzzy-interval-valued functions, where the integrands are fuzzy-interval-valued functions. For instance, Oseuna-Gomez et al. [29] and Costa et al. [11] constructed Jensen’s integral inequality for fuzzy-interval-valued functions. By using the same approach, Costa and Roman-Flores also presented Minkowski and Beckenbach’s inequalities, where the integrands are fuzzy-interval-valued functions. Motivated by [11, 12, 29] and [34], we generalize integral inequality (2) by constructing fuzzy-interval integral inequality for convex fuzzy-interval-valued functions, where the integrands are convex fuzzy-interval-valued functions.
This study is organized as follows: Sect. 2 presents preliminaries and results in the interval space, in the space of fuzzy-intervals, and for fuzzy integrals. Section 3 introduces the new classes of  -convex fuzzy-interval-valued functions and investigates their properties. Section 4 obtains fuzzy-interval Hermite–Hadamard inequalities via
-convex fuzzy-interval-valued functions and investigates their properties. Section 4 obtains fuzzy-interval Hermite–Hadamard inequalities via  -convex fuzzy-interval-valued functions. In addition, some interesting examples are also given to verify our results. Section 4 gives conclusions and directions for future works.
-convex fuzzy-interval-valued functions. In addition, some interesting examples are also given to verify our results. Section 4 gives conclusions and directions for future works.
2 Preliminaries
Let \(\mathcal{K}_{C}\) be the collection of all closed and bounded intervals of \(\mathbb{R}\), that is, \(\mathcal{K}_{C} = \{ [ \omega _{*}, \omega ^{*} ]: \omega _{*}, \omega ^{*} \in\mathbb{R} \mbox{ and } \omega _{*} \leq \omega ^{*} \} \). If \(\omega _{*} \geq 0\), then \([ \omega _{*}, \omega ^{*} ]\) is called a positive interval. The set of all positive intervals is denoted by \(\mathcal{K}_{C}^{+}\) and defined as \(\mathcal{K}_{C}^{+} = \{ [ \omega _{*}, \omega ^{*} ]: [ \omega _{*}, \omega ^{*} ] \in \mathcal{K}_{C} \mbox{ and } \omega _{*} \geq 0 \} \).
We now discuss some properties of intervals under the arithmetic operations of addition, multiplication, and scalar multiplication. If \([ \mu _{*}, \mu ^{*} ], [ \omega _{*}, \omega ^{*} ] \in \mathcal{K}_{C}\), and \(\rho \in \mathbb{R}\), then these arithmetic operations are defined by
For \([ \mu _{*}, \mu ^{*} ], [ \omega _{*}, \omega ^{*} ] \in \mathcal{K}_{C}\), the inclusion “⊆” is defined by
Remark 1
The relation “\(\leq _{I}\)” is defined on \(\mathcal{K}_{C}\) by
for all \([ \mu _{*}, \mu ^{*} ], [ \omega _{*}, \omega ^{*} ] \in \mathcal{K}_{C}\), it is an order relation, see [25]. For given \([ \mu _{*}, \mu ^{*} ], [ \omega _{*}, \omega ^{*} ] \in \mathcal{K}_{C}\), we say that \([ \mu _{*}, \mu ^{*} ] \leq _{I} [ \omega _{*}, \omega ^{*} ]\) if and only if \(\mu _{*} \leq \omega _{*}\), \(\mu ^{*} \leq \omega ^{*}\) or \(\mu _{*} \leq \omega _{*}\), \(\mu ^{*} <\omega ^{*}\).
The concept of Riemann integral for interval-valued functions first introduced by Moore [26] and is defined as follows:
Theorem 2
([26])
If \(\mathcal{F}:[c,d]\subset \mathbb{R} \rightarrow \mathcal{K}_{C}\) is an interval-valued function on such that \([ \mathcal{F}_{*}, \mathcal{F}^{*} ]\), then \(\mathcal{F}\) is Riemann integrable on \([c, d]\) if and only if \(\mathcal{F}_{*}\) and \(\mathcal{F}^{*}\) both are Riemann integrable on \([ c,d ]\) and such that
The collections of all Riemann integrable real-valued functions and Riemann integrable interval-valued functions are denoted by \(\mathcal{R}_{[c, d]}\) and \(\mathcal{IR}_{[c, d]}\), respectively.
Let \(\mathbb{R}\) be the set of real numbers. A fuzzy subset set \(\mathcal{A}\) of \(\mathbb{R}\) is distinguished by a function \(\varphi :\mathbb{R} \rightarrow [0,1]\) called the membership function. In this study this depiction is approved. Moreover, the collection of all fuzzy subsets of \(\mathbb{R}\) is denoted by \(\mathbb{F} ( \mathbb{R} ) \).
A real fuzzy-interval φ is a fuzzy set in \(\mathbb{R}\) with the following properties:
-
(1)
φ is normal, i.e., there exists \(x \in \mathbb{R}\) such that \(\varphi ( x ) =1\);
-
(2)
φ is upper semicontinuous, i.e., for every \(x \in \mathbb{R}\) and \(\varepsilon >0\) there exists \(\delta >0\) such that \(\varphi ( x ) -\varphi ( y ) <\varepsilon \) for all \(y \in \mathbb{R}\) with \(\vert x-y \vert < \delta \).
-
(3)
φ is fuzzy convex, i.e., \(\varphi ( ( 1-\tau ) x+\tau y ) \geq \min ( \varphi ( x ), \varphi ( y ) )\), \(\forall x,y \in \mathbb{R}\) and \(\tau \in [0, 1]\);
-
(4)
φ is compactly supported, i.e., \(\operatorname{cl} \{ x \in \mathbb{R}\mid \varphi ( x ) > 0 \} \) is compact.
The collection of all real fuzzy-intervals is denoted by \(\mathbb{F}_{C} ( \mathbb{R} )\).
Since \(\mathbb{F}_{C} ( \mathbb{R} )\) denotes the set of all real fuzzy-intervals, \(\varphi \in \mathbb{F}_{C} ( \mathbb{R} )\) is a real fuzzy-interval if and only if each γ-level \([ \varphi ]^{\gamma } \) is a nonempty compact convex set of \(\mathbb{R}\). This is represented by
From these definitions, we have
where
Thus a real fuzzy-interval φ can be identified by parametrized triples
This leads to the following characterization of a real fuzzy-interval in terms of the two end point functions, \(\varphi _{*} ( \gamma )\) and \(\varphi ^{*} ( \gamma ) \).
Theorem 3
Suppose that \(\varphi _{*} ( \gamma ):[0,1] \rightarrow \mathbb{R}\) and \(\varphi ^{*} ( \gamma ):[0,1] \rightarrow \mathbb{R}\) satisfy the following conditions:
-
(1)
\(\varphi _{*} ( \gamma )\) is a nondecreasing function;
-
(2)
\(\varphi ^{*} ( \gamma )\) is a nonincreasing function;
-
(3)
\(\varphi _{*} ( 1 ) \leq \varphi ^{*} ( 1 )\);
-
(4)
\(\varphi _{*} ( \gamma )\) and \(\varphi ^{*} ( \gamma )\) are bounded and left continuous on (0, 1], and right continuous at \(\gamma =0\).
Moreover, if \(\varphi :\mathbb{R} \rightarrow [0,1]\) is a real fuzzy-interval given by \([ \varphi _{*} ( \gamma ), \varphi ^{*} ( \gamma ) ]\), then functions \(\varphi _{*} ( \gamma )\) and \(\varphi ^{*} ( \gamma )\) satisfy conditions (1)–(4).
Proposition 1
([12])
Let \(\varphi ,\phi \in \mathbb{F}_{C} ( \mathbb{R} )\). Then the relation “≼” given on \(\mathbb{F}_{C} ( \mathbb{R} )\) by
it is a partial order relation.
Now we discuss some properties of real fuzzy-intervals under addition, scalar multiplication, multiplication, and division. If \(\varphi ,\phi \in \mathbb{F}_{C} ( \mathbb{R} )\) and \(\rho \in \mathbb{R}\), then these arithmetic operations are defined by
If \(\psi \in \mathbb{F}_{C} ( \mathbb{R} )\) is such that \(\varphi =\phi \mathbin{\tilde{+}} \psi \), then we have the existence of Hukuhara difference of φ and ϕ, and we say that ψ is the H-difference of φ and ϕ, which is denoted by \(\varphi \tilde{-} \phi \) . If the H-difference exists, then
Remark 2
Obviously, \(\mathbb{F}_{C} ( \mathbb{R} )\) is closed under addition and nonnegative scalar multiplication. And the above-defined properties on \(\mathbb{F}_{C} ( \mathbb{R} )\) are equivalent to those derived from the usual extension principle. Furthermore, for each scalar number \(\rho \in \mathbb{R}\),
Theorem 4
The space \(\mathbb{F}_{C} ( \mathbb{R} )\) equipped with a supremum metric, i.e., for \(\psi , \phi \in \mathbb{F}_{C} ( \mathbb{R} )\)
it is a complete metric space, where H denote the well-known Hausdorff metric on the space of intervals.
Definition 1
([12])
A fuzzy-interval-valued map \(\mathcal{F}:K\subset \mathbb{R} \rightarrow \mathbb{F}_{C} ( \mathbb{R} )\) is called a fuzzy-interval-valued function. For each \(\gamma \in [ 0, 1 ]\), the γ-levels define the family of interval-valued functions \(\mathcal{F}_{\gamma }:K\subset \mathbb{R} \rightarrow \mathcal{K}_{C}\) given by \(\mathcal{F}_{\gamma } ( x ) = [ \mathcal{F}_{*} ( x,\gamma ), \mathcal{F}^{*} ( x, \gamma ) ]\) for all \(x \in K \). Here, for each \(\gamma \in [ 0, 1 ]\), the end point real functions \(\mathcal{F}_{*} (\cdot,\gamma ), \mathcal{F}^{*} (\cdot, \gamma ):K\rightarrow \mathbb{R}\) are called lower and upper functions of \(\mathcal{F}\).
Remark 3
Let \(\mathcal{F}:K\subset \mathbb{R} \rightarrow \mathbb{F}_{C} ( \mathbb{R} )\) be a fuzzy-interval-valued function. Then \(\mathcal{F} ( x )\) is said to be continuous at \(x\in K\) if, for each \(\gamma \in [ 0, 1 ]\), both end point functions \(\mathcal{F}_{*} ( x,\gamma )\) and \(\mathcal{F}^{*} ( x, \gamma )\) are continuous at \(x\in K\).
From the above literature review, the following results can be concluded; see [12, 18, 24, 26].
Definition 2
The map \(\mathcal{F}:[c, d]\subset \mathbb{R} \rightarrow \mathbb{F}_{C} ( \mathbb{R} )\) is called a fuzzy-interval-valued function. The fuzzy integral of \(\mathcal{F}\) over \([ c, d ]\), denoted by \(( FR ) \int _{c}^{d} \mathcal{F} ( x ) \,dx\), it is defined level-wise by
for all \(\gamma \in [ 0, 1 ]\), where \(\mathcal{R}_{[c, d]}\) is the collection of end point functions of interval-valued functions; \(\mathcal{F}\) is \(( FR )\)-integrable over \([c, d]\) if \(( FR ) \int _{c}^{d} \mathcal{F} ( x ) \,dx \in \mathbb{F}_{C} ( \mathbb{R} ) \). Note that if both end point functions are Lebesgue-integrable, then \(\mathcal{F}\) is a fuzzy Annum integrable function; see [18, 24, 26].
Theorem 5
Let \(\mathcal{F}:[c, d]\subset \mathbb{R} \rightarrow \mathbb{F}_{C} ( \mathbb{R} )\) be a fuzzy-interval-valued function, whose γ-levels define the family of interval-valued functions \(\mathcal{F}_{\gamma }:[c, d]\subset \mathbb{R} \rightarrow \mathcal{K}_{C}\) given by \(\mathcal{F}_{\gamma } ( x ) = [ \mathcal{F}_{*} ( x,\gamma ), \mathcal{F}^{*} ( x, \gamma ) ]\) for all \(x \in [c, d]\) and for all \(\gamma \in [ 0, 1 ] \). Then \(\mathcal{F}\) is \(( FR )\)-integrable over \([c, d]\) if and only if \(\mathcal{F}_{*} ( x,\gamma )\) and \(\mathcal{F}^{*} ( x, \gamma )\) both are R-integrable over \([c, d]\). Moreover, if \(\mathcal{F}\) is \(( FR )\)-integrable over \([ c, d ]\), then
for all \(\gamma \in [ 0, 1 ] \).
The families of all \(( FR )\)-integrable fuzzy-interval-valued functions and R-integrable functions over \([c, d]\) are denoted by \(\mathcal{IR}_{ ( [ c, d ], \gamma )}\) and \(\mathcal{R}_{ ( [ c, d ], \gamma )}\), respectively, for all \(\gamma \in [ 0, 1 ] \).
3
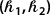 -Convex fuzzy-interval-valued functions
-Convex fuzzy-interval-valued functions
In this section, we put forward the definitions of  -convex fuzzy-interval-valued functions and investigate their basic properties.
-convex fuzzy-interval-valued functions and investigate their basic properties.
Definition 3
Let K be a convex set and  such that
such that  . Then a fuzzy-interval-valued function \(\mathcal{F}: K \rightarrow \mathbb{F}_{C} ( \mathbb{R} )\) is said to be:
. Then a fuzzy-interval-valued function \(\mathcal{F}: K \rightarrow \mathbb{F}_{C} ( \mathbb{R} )\) is said to be:
-
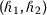 -convex on K if
-convex on K if 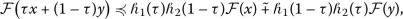 (11)
(11)for all \(x, y\in K\), \(\tau \in [ 0, 1 ]\) where \(\mathcal{F}(x) \succcurlyeq \tilde{0}\);
-
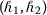 -concave on K if inequality (11) is reversed;
-concave on K if inequality (11) is reversed; -
affine
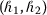 -convex on K if
-convex on K if 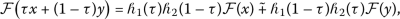 (12)
(12)for all \(x, y\in K\), \(\tau \in [ 0, 1 ] \) where \(\mathcal{F}(x) \succcurlyeq \tilde{0}\).
Remark 4
The  -convex fuzzy-interval-valued functions have some very nice properties similar to those of convex fuzzy-interval-valued functions:
-convex fuzzy-interval-valued functions have some very nice properties similar to those of convex fuzzy-interval-valued functions:
-
(1)
If \(\mathcal{F}\) is an
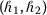 -convex fuzzy-interval-valued function, then \(\Upsilon \mathcal{F}\) is also
-convex fuzzy-interval-valued function, then \(\Upsilon \mathcal{F}\) is also 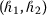 -convex for \(\Upsilon \geq 0\).
-convex for \(\Upsilon \geq 0\). -
(2)
If \(\mathcal{F}\) and \(\mathcal{T}\) both are
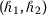 -convex fuzzy-interval-valued functions, then \(\max ( \mathcal{F}( x), \mathcal{T}( x) )\) is also an
-convex fuzzy-interval-valued functions, then \(\max ( \mathcal{F}( x), \mathcal{T}( x) )\) is also an 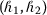 -convex fuzzy-interval-valued function.
-convex fuzzy-interval-valued function.
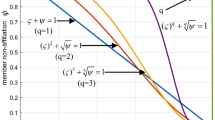
Now we discuss some special cases of  -convex fuzzy-interval-valued functions:
-convex fuzzy-interval-valued functions:
-
(i)
If
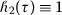 , then an
, then an 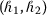 -convex fuzzy-interval-valued function becomes
-convex fuzzy-interval-valued function becomes 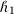 -convex fuzzy-interval-valued function, that is,
-convex fuzzy-interval-valued function, that is, 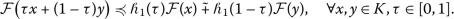
-
(ii)
If
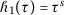 ,
, 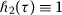 , then an
, then an 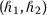 -convex fuzzy-interval-valued function becomes an s-convex fuzzy-interval-valued function, that is, $$ \mathcal{F} \bigl( \tau x+ ( 1-\tau ) y \bigr) \preccurlyeq \tau ^{s} \mathcal{F} ( x ) \mathbin{\tilde{+}} ( 1-\tau )^{s} \mathcal{F} ( y ), \quad \forall x, y\in K, \tau \in [ 0, 1 ]. $$
-convex fuzzy-interval-valued function becomes an s-convex fuzzy-interval-valued function, that is, $$ \mathcal{F} \bigl( \tau x+ ( 1-\tau ) y \bigr) \preccurlyeq \tau ^{s} \mathcal{F} ( x ) \mathbin{\tilde{+}} ( 1-\tau )^{s} \mathcal{F} ( y ), \quad \forall x, y\in K, \tau \in [ 0, 1 ]. $$ -
(iii)
If
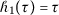 ,
,  , then an
, then an  -convex fuzzy-interval-valued function becomes a convex fuzzy-interval-valued function, that is, $$ \mathcal{F} \bigl( \tau x+ ( 1-\tau ) y \bigr) \preccurlyeq \tau \mathcal{F} ( x ) \mathbin{\tilde{+}} ( 1-\tau ) \mathcal{F} ( y ), \quad \forall x, y\in K, \tau \in [ 0, 1 ]. $$
-convex fuzzy-interval-valued function becomes a convex fuzzy-interval-valued function, that is, $$ \mathcal{F} \bigl( \tau x+ ( 1-\tau ) y \bigr) \preccurlyeq \tau \mathcal{F} ( x ) \mathbin{\tilde{+}} ( 1-\tau ) \mathcal{F} ( y ), \quad \forall x, y\in K, \tau \in [ 0, 1 ]. $$ -
(iv)
If
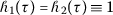 , then an
, then an 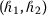 -convex fuzzy-interval-valued function becomes a P-convex fuzzy-interval-valued function, that is, $$ \mathcal{F} \bigl( \tau x+ ( 1-\tau ) y \bigr) \preccurlyeq \mathcal{F} ( x ) \mathbin{\tilde{+}} \mathcal{F} ( y ), \quad \forall x, y\in K, \tau \in [ 0, 1 ]. $$
-convex fuzzy-interval-valued function becomes a P-convex fuzzy-interval-valued function, that is, $$ \mathcal{F} \bigl( \tau x+ ( 1-\tau ) y \bigr) \preccurlyeq \mathcal{F} ( x ) \mathbin{\tilde{+}} \mathcal{F} ( y ), \quad \forall x, y\in K, \tau \in [ 0, 1 ]. $$
Theorem 6
Let K be a convex set,  such that
such that  , and let \(\mathcal{F}: K \rightarrow \mathbb{F}_{C} ( \mathbb{R} )\) be a fuzzy-interval-valued function whose γ-levels define the family of interval valued functions \(\mathcal{F}_{\gamma }:[c, d]\subset \mathbb{R} \rightarrow \mathcal{K}_{C}^{+}\) given by
, and let \(\mathcal{F}: K \rightarrow \mathbb{F}_{C} ( \mathbb{R} )\) be a fuzzy-interval-valued function whose γ-levels define the family of interval valued functions \(\mathcal{F}_{\gamma }:[c, d]\subset \mathbb{R} \rightarrow \mathcal{K}_{C}^{+}\) given by

Proof
Assume that for each \(\gamma \in [ 0, 1 ], \mathcal{F}_{*} ( x, \gamma )\) and \(\mathcal{F}^{*} ( x, \gamma )\) are  -convex on K. Then from (11), we have
-convex on K. Then from (11), we have

and

Then by (13), (3), and (5), we obtain

that is,

Hence, \(\mathcal{F}\) is an  -convex fuzzy-interval-valued function on K.
-convex fuzzy-interval-valued function on K.
Conversely, let \(\mathcal{F}\) be an  -convex fuzzy-interval-valued function on K. Then for all \(x,y\in K\) and \(\tau \in [ 0, 1 ]\), we have
-convex fuzzy-interval-valued function on K. Then for all \(x,y\in K\) and \(\tau \in [ 0, 1 ]\), we have  . Therefore, from (13), we have
. Therefore, from (13), we have
Again, from (13), (3), and (5), we obtain

for all \(x,y\in K\) and \(\tau \in [ 0, 1 ] \). Then by the  -convexity of \(\mathcal{F}\), we have for all \(x,y\in K\) and \(\tau \in [ 0, 1 ]\) that
-convexity of \(\mathcal{F}\), we have for all \(x,y\in K\) and \(\tau \in [ 0, 1 ]\) that

and

for each \(\gamma \in [ 0, 1 ] \). Hence, the result follows. □
Example 1
We consider  ,
,  , for \(\tau \in [ 0, 1 ]\) and the fuzzy-interval-valued functions \(\mathcal{F}:[0, 1] \rightarrow \mathbb{F}_{C} ( \mathbb{R} )\) defined by
, for \(\tau \in [ 0, 1 ]\) and the fuzzy-interval-valued functions \(\mathcal{F}:[0, 1] \rightarrow \mathbb{F}_{C} ( \mathbb{R} )\) defined by
Then, for each \(\gamma \in [ 0, 1 ]\), we have \(\mathcal{F}_{\gamma } ( x ) = [ 2\gamma x^{2}, (4-2\gamma ) x^{2} ]\). Since the end point functions \(\mathcal{F}_{*} ( x,\gamma )\), \(\mathcal{F}^{*} ( x, \gamma )\) are  -convex functions for each \(\gamma \in [0, 1]\), \(\mathcal{F} ( x )\) is an
-convex functions for each \(\gamma \in [0, 1]\), \(\mathcal{F} ( x )\) is an  -convex fuzzy-interval-valued function.
-convex fuzzy-interval-valued function.
Hermite–Hadamard-type inequalities for fuzzy-interval-valued functions
Theorem 7
Let \(\mathcal{F}: [ {u}, \vartheta ] \rightarrow \mathbb{F}_{C} ( \mathbb{R} )\) be an  -convex fuzzy-interval-valued function with
-convex fuzzy-interval-valued function with  and
and  , whose γ-levels define the family of interval valued functions \(\mathcal{F}_{\gamma }: [ {u}, \vartheta ] \subset \mathbb{R} \rightarrow \mathcal{K}_{C}^{+}\) given by \(\mathcal{F}_{\gamma } ( x ) = [ \mathcal{F}_{*} ( x,\gamma ), \mathcal{F}^{*} ( x, \gamma ) ]\) for all \(x \in [ {u}, \vartheta ]\) and for all \(\gamma \in [ 0, 1 ]\). If \(\mathcal{F}\in \mathcal{IR}_{ ( [ {u}, \vartheta ], \gamma )}\), then
, whose γ-levels define the family of interval valued functions \(\mathcal{F}_{\gamma }: [ {u}, \vartheta ] \subset \mathbb{R} \rightarrow \mathcal{K}_{C}^{+}\) given by \(\mathcal{F}_{\gamma } ( x ) = [ \mathcal{F}_{*} ( x,\gamma ), \mathcal{F}^{*} ( x, \gamma ) ]\) for all \(x \in [ {u}, \vartheta ]\) and for all \(\gamma \in [ 0, 1 ]\). If \(\mathcal{F}\in \mathcal{IR}_{ ( [ {u}, \vartheta ], \gamma )}\), then

Proof
Let \(\mathcal{F}: [ {u}, \vartheta ] \rightarrow \mathbb{F}_{C} ( \mathbb{R} )\) be an  -convex fuzzy-interval-valued function. Then, by hypothesis, we have
-convex fuzzy-interval-valued function. Then, by hypothesis, we have

Therefore, for every \(\gamma \in [0, 1]\), we have

Then

It follows that

That is,

Thus,

In a similar way as above, we have

Combining (16) and (17), we have

Hence, the required result follows. □
Remark 5
If  , then Theorem 7 reduces to the result for
, then Theorem 7 reduces to the result for  -convex fuzzy-interval-valued functions:
-convex fuzzy-interval-valued functions:

If  and
and  , then Theorem 7 reduces to the result for s-convex fuzzy-interval-valued functions:
, then Theorem 7 reduces to the result for s-convex fuzzy-interval-valued functions:
If  and
and  , then Theorem 7 reduces to the result for convex fuzzy-interval-valued functions:
, then Theorem 7 reduces to the result for convex fuzzy-interval-valued functions:
If  , then Theorem 7 reduces to the result for P-convex fuzzy-interval-valued functions:
, then Theorem 7 reduces to the result for P-convex fuzzy-interval-valued functions:
If \(\mathcal{F}_{*} ( {u}, \gamma ) = \mathcal{F}^{*} ( \vartheta , \gamma )\) then Theorem 7 reduces to the result for  -convex functions:
-convex functions:

Example 2
We consider  ,
,  , for \(\tau \in [ 0, 1 ]\), and the fuzzy function \(\mathcal{F}: [ {u}, \vartheta ] =[0, 2] \rightarrow \mathbb{F}_{C} ( \mathbb{R} )\) defined by
, for \(\tau \in [ 0, 1 ]\), and the fuzzy function \(\mathcal{F}: [ {u}, \vartheta ] =[0, 2] \rightarrow \mathbb{F}_{C} ( \mathbb{R} )\) defined by
Then, for each \(\gamma \in [ 0, 1 ]\), we have \(\mathcal{F}_{\gamma } ( x ) = [ 2\gamma x^{2}, (4-2\gamma ) x^{2} ]\). Since the end point functions \(\mathcal{F}_{*} ( x,\gamma ) =2\gamma x^{2}\), \(\mathcal{F}^{*} ( x, \gamma ) = (4-2\gamma ) x^{2}\) are  -convex functions for each \(\gamma \in [0, 1]\), \(\mathcal{F} ( x )\) is an
-convex functions for each \(\gamma \in [0, 1]\), \(\mathcal{F} ( x )\) is an  -convex fuzzy-interval-valued function. We verify the following by computing appropriate quantities:
-convex fuzzy-interval-valued function. We verify the following by computing appropriate quantities:

for all \(\gamma \in [ 0, 1 ] \). This means
Similarly, it can be easily show that

for all \(\gamma \in [ 0, 1 ]\), such that

from which it follows that
that is,
Hence,

Theorem 8
Let \(\mathcal{F}: [ {u}, \vartheta ] \rightarrow \mathbb{F}_{C} ( \mathbb{R} )\) be an  -convex fuzzy-interval-valued function with
-convex fuzzy-interval-valued function with  and
and  , whose γ-levels define the family of interval valued functions \(\mathcal{F}_{\gamma }: [ {u}, \vartheta ] \subset \mathbb{R} \rightarrow \mathcal{K}_{C}^{+}\) given by \(\mathcal{F}_{\gamma } ( x ) = [ \mathcal{F}_{*} ( x,\gamma ), \mathcal{F}^{*} ( x, \gamma ) ]\) for all \(x \in [ {u}, \vartheta ]\) and for all \(\gamma \in [ 0, 1 ]\). If \(\mathcal{F}\in \mathcal{IR}_{ ( [ {u}, \vartheta ], \gamma )}\), then
, whose γ-levels define the family of interval valued functions \(\mathcal{F}_{\gamma }: [ {u}, \vartheta ] \subset \mathbb{R} \rightarrow \mathcal{K}_{C}^{+}\) given by \(\mathcal{F}_{\gamma } ( x ) = [ \mathcal{F}_{*} ( x,\gamma ), \mathcal{F}^{*} ( x, \gamma ) ]\) for all \(x \in [ {u}, \vartheta ]\) and for all \(\gamma \in [ 0, 1 ]\). If \(\mathcal{F}\in \mathcal{IR}_{ ( [ {u}, \vartheta ], \gamma )}\), then

where

and  ,
,  .
.
Proof
Taking \([ {u}, \frac{{u}+ \vartheta }{2} ]\), we have

Therefore, for every \(\gamma \in [0, 1]\), we have

As a consequence, we obtain

That is,

It follows that

In a similar way as above, we have

Combining (18) and (19), we have

By using Theorem 7, we have

Therefore, for every \(\gamma \in [0, 1]\), we have

that is,

hence the result follows. □
Example 3
If we consider  ,
,  , for \(\tau \in [ 0, 1 ]\), and the fuzzy-interval-valued function \(\mathcal{F}: [ {u}, \vartheta ] =[0, 2] \rightarrow \mathbb{F}_{C} ( \mathbb{R} )\) defined by \(\mathcal{F}_{\gamma } ( x ) = [ 2\gamma x^{2}, (4-2\gamma ) x^{2} ]\), as in Example 2, then \(\mathcal{F}( x)\) is and
, for \(\tau \in [ 0, 1 ]\), and the fuzzy-interval-valued function \(\mathcal{F}: [ {u}, \vartheta ] =[0, 2] \rightarrow \mathbb{F}_{C} ( \mathbb{R} )\) defined by \(\mathcal{F}_{\gamma } ( x ) = [ 2\gamma x^{2}, (4-2\gamma ) x^{2} ]\), as in Example 2, then \(\mathcal{F}( x)\) is and  -convex fuzzy-interval-valued function satisfying inequality (15). We have \(\mathcal{F}_{*} ( x, \gamma ) = \gamma x\) and \(\mathcal{F}^{*} ( x, \gamma ) = ( 4-2\gamma ) x\). We now compute the following:
-convex fuzzy-interval-valued function satisfying inequality (15). We have \(\mathcal{F}_{*} ( x, \gamma ) = \gamma x\) and \(\mathcal{F}^{*} ( x, \gamma ) = ( 4-2\gamma ) x\). We now compute the following:

Then we obtain
Hence, Theorem 8 is verified.
Theorem 9
Let \(\mathcal{F},\mathcal{J}: [ {u}, \vartheta ] \rightarrow \mathbb{F}_{C} ( \mathbb{R} )\) be two  -convex fuzzy-interval-valued functions with
-convex fuzzy-interval-valued functions with  and
and  , whose γ-levels define the family of interval valued functions \(\mathcal{F}_{\gamma }, \mathcal{J}_{\gamma }: [ {u}, \vartheta ] \subset \mathbb{R} \rightarrow \mathcal{K}_{C}^{+}\) given by \(\mathcal{F}_{\gamma } ( x ) = [ \mathcal{F}_{*} ( x,\gamma ), \mathcal{F}^{*} ( x, \gamma ) ]\) and \(\mathcal{J}_{\gamma } ( x ) = [ \mathcal{J}_{*} ( x,\gamma ), \mathcal{J}^{*} ( x, \gamma ) ]\) for all \(x \in [ {u}, \vartheta ]\) and for all \(\gamma \in [ 0, 1 ]\). If \(\mathcal{F}\), \(\mathcal{J}\) and \(\mathcal{FJ} \in \mathcal{IR}_{ ( [ {u}, \vartheta ], \gamma )}\), then
, whose γ-levels define the family of interval valued functions \(\mathcal{F}_{\gamma }, \mathcal{J}_{\gamma }: [ {u}, \vartheta ] \subset \mathbb{R} \rightarrow \mathcal{K}_{C}^{+}\) given by \(\mathcal{F}_{\gamma } ( x ) = [ \mathcal{F}_{*} ( x,\gamma ), \mathcal{F}^{*} ( x, \gamma ) ]\) and \(\mathcal{J}_{\gamma } ( x ) = [ \mathcal{J}_{*} ( x,\gamma ), \mathcal{J}^{*} ( x, \gamma ) ]\) for all \(x \in [ {u}, \vartheta ]\) and for all \(\gamma \in [ 0, 1 ]\). If \(\mathcal{F}\), \(\mathcal{J}\) and \(\mathcal{FJ} \in \mathcal{IR}_{ ( [ {u}, \vartheta ], \gamma )}\), then

where \(\mathcal{M} ( {u}, \vartheta ) =\mathcal{F} ( {u} ) \mathcal{J} ( {u} ) \mathbin{\tilde{+}} \mathcal{F} ( \vartheta ) \mathcal{J} ( \vartheta )\), \(\mathcal{N} ( {u}, \vartheta ) =\mathcal{F} ( {u} ) \mathcal{J} ( \vartheta ) \mathbin{\tilde{+}} \mathcal{F} ( \vartheta ) \mathcal{J} ( {u} )\), and \(\mathcal{M}_{\gamma } ( {u}, \vartheta ) = [ \mathcal{M}_{*} ( ( {u}, \vartheta ), \gamma ), \mathcal{M}^{*} ( ( {u}, \vartheta ), \gamma ) ]\) and \(\mathcal{N}_{\gamma } ( {u}, \vartheta ) = [ \mathcal{N}_{*} ( ( {u}, \vartheta ), \gamma ), \mathcal{N}^{*} ( ( {u}, \vartheta ), \gamma ) ] \).
Example 4
We consider  ,
,  , for \(\tau \in [ 0, 1 ]\), and the fuzzy-interval-valued functions \(\mathcal{F}, \mathcal{J}: [ {u}, \vartheta ] =[0, 1] \rightarrow \mathbb{F}_{C} ( \mathbb{R} )\) defined by
, for \(\tau \in [ 0, 1 ]\), and the fuzzy-interval-valued functions \(\mathcal{F}, \mathcal{J}: [ {u}, \vartheta ] =[0, 1] \rightarrow \mathbb{F}_{C} ( \mathbb{R} )\) defined by
Then, for each \(\gamma \in [ 0, 1 ]\), we have \(\mathcal{F}_{\gamma } ( x ) = [ 2\gamma x^{2}, (4-2\gamma ) x^{2} ]\) and \(\mathcal{J}_{\gamma } ( x ) = [ \gamma x, (2-\gamma ) x ] \). Since the end point functions \(\mathcal{F}_{*} ( x,\gamma ) =2\gamma x^{2}\), \(\mathcal{F}^{*} ( x, \gamma ) = (4-2\gamma ) x^{2}\) and \(\mathcal{J}_{*} ( x,\gamma ) =\gamma x\), \(\mathcal{J}^{*} ( x, \gamma ) =(2-\gamma ) x\) are  -convex functions for each \(\gamma \in [0, 1]\), \(\mathcal{F}\), \(\mathcal{J}\) are also
-convex functions for each \(\gamma \in [0, 1]\), \(\mathcal{F}\), \(\mathcal{J}\) are also  -convex fuzzy-interval-valued functions. We now compute the following:
-convex fuzzy-interval-valued functions. We now compute the following:

for each \(\gamma \in [ 0, 1 ]\), which means
hence Theorem 9 is demonstrated.
Theorem 10
Let \(\mathcal{F},\mathcal{J}: [ {u}, \vartheta ] \rightarrow \mathbb{F}_{C} ( \mathbb{R} )\) be two  -convex fuzzy-interval-valued functions with
-convex fuzzy-interval-valued functions with  and
and  , whose γ-levels define the family of interval valued functions \(\mathcal{F}_{\gamma }, \mathcal{J}_{\gamma }: [ {u}, \vartheta ] \subset \mathbb{R} \rightarrow \mathcal{K}_{C}^{+}\) given by \(\mathcal{F}_{\gamma } ( x ) = [ \mathcal{F}_{*} ( x,\gamma ), \mathcal{F}^{*} ( x, \gamma ) ]\) and \(\mathcal{J}_{\gamma } ( x ) = [ \mathcal{J}_{*} ( x,\gamma ), \mathcal{J}^{*} ( x, \gamma ) ]\) for all \(x \in [ {u}, \vartheta ]\) and for all \(\gamma \in [ 0, 1 ]\). If \(\mathcal{F}\), \(\mathcal{J}\) and \(\mathcal{FJ} \in \mathcal{IR}_{ ( [ {u}, \vartheta ], \gamma )}\), then
, whose γ-levels define the family of interval valued functions \(\mathcal{F}_{\gamma }, \mathcal{J}_{\gamma }: [ {u}, \vartheta ] \subset \mathbb{R} \rightarrow \mathcal{K}_{C}^{+}\) given by \(\mathcal{F}_{\gamma } ( x ) = [ \mathcal{F}_{*} ( x,\gamma ), \mathcal{F}^{*} ( x, \gamma ) ]\) and \(\mathcal{J}_{\gamma } ( x ) = [ \mathcal{J}_{*} ( x,\gamma ), \mathcal{J}^{*} ( x, \gamma ) ]\) for all \(x \in [ {u}, \vartheta ]\) and for all \(\gamma \in [ 0, 1 ]\). If \(\mathcal{F}\), \(\mathcal{J}\) and \(\mathcal{FJ} \in \mathcal{IR}_{ ( [ {u}, \vartheta ], \gamma )}\), then

where \(\mathcal{M} ( {u}, \vartheta ) =\mathcal{F} ( {u} ) \mathcal{J} ( {u} ) \mathbin{\tilde{+}} \mathcal{F} ( \vartheta ) \mathcal{J} ( \vartheta )\), \(\mathcal{N} ( {u}, \vartheta ) =\mathcal{F} ( {u} ) \mathcal{J} ( \vartheta ) \mathbin{\tilde{+}} \mathcal{F} ( \vartheta ) \mathcal{J} ( {u} )\), and \(\mathcal{M}_{\gamma } ( {u}, \vartheta ) = [ \mathcal{M}_{*} ( ( {u}, \vartheta ), \gamma ), \mathcal{M}^{*} ( ( {u}, \vartheta ), \gamma ) ]\) and \(\mathcal{N}_{\gamma } ( {u}, \vartheta ) = [ \mathcal{N}_{*} ( ( {u}, \vartheta ), \gamma ), \mathcal{N}^{*} ( ( {u}, \vartheta ), \gamma ) ] \).
Proof
By hypothesis, for each \(\gamma \in [ 0, 1 ]\), we have

that is,

FR-integrating over \([ 0, 1 ]\), we have

hence the required result follows. □
Example 5
If we consider  ,
,  , for \(\tau \in [ 0, 1 ]\), and the fuzzy-interval-valued functions \(\mathcal{F}, \mathcal{J}: [ {u}, \vartheta ] =[0, 1] \rightarrow \mathbb{F}_{C} ( \mathbb{R} )\) defined, for each \(\gamma \in [ 0, 1 ]\), by \(\mathcal{F}_{\gamma } ( x ) = [ 2\gamma x^{2}, (4-2\gamma ) x^{2} ]\) and \(\mathcal{J}_{\gamma } ( x ) = [ \gamma x, (2-\gamma ) x ]\), as in Example 4, then \(\mathcal{F}\), \(\mathcal{J}\) both are
, for \(\tau \in [ 0, 1 ]\), and the fuzzy-interval-valued functions \(\mathcal{F}, \mathcal{J}: [ {u}, \vartheta ] =[0, 1] \rightarrow \mathbb{F}_{C} ( \mathbb{R} )\) defined, for each \(\gamma \in [ 0, 1 ]\), by \(\mathcal{F}_{\gamma } ( x ) = [ 2\gamma x^{2}, (4-2\gamma ) x^{2} ]\) and \(\mathcal{J}_{\gamma } ( x ) = [ \gamma x, (2-\gamma ) x ]\), as in Example 4, then \(\mathcal{F}\), \(\mathcal{J}\) both are  -convex fuzzy-interval-valued functions. We have \(\mathcal{F}_{*} ( x,\gamma ) =2\gamma x^{2}\), \(\mathcal{F}^{*} ( x, \gamma ) = ( 4-2\gamma ) x^{2}\), and \(\mathcal{J}_{*} ( x,\gamma ) =\gamma x\), \(\mathcal{J}^{*} ( x, \gamma ) =(2-\gamma ) x\). We now compute the following:
-convex fuzzy-interval-valued functions. We have \(\mathcal{F}_{*} ( x,\gamma ) =2\gamma x^{2}\), \(\mathcal{F}^{*} ( x, \gamma ) = ( 4-2\gamma ) x^{2}\), and \(\mathcal{J}_{*} ( x,\gamma ) =\gamma x\), \(\mathcal{J}^{*} ( x, \gamma ) =(2-\gamma ) x\). We now compute the following:

for each \(\gamma \in [ 0, 1 ]\), which means
hence the result follows.
4 Conclusion
In this work, we introduce the concept of  -convex fuzzy-interval-valued functions. With the new concept, we construct new versions of Hermite–Hadamard inequalities, called fuzzy-interval Hermite–Hadamard-type inequalities for
-convex fuzzy-interval-valued functions. With the new concept, we construct new versions of Hermite–Hadamard inequalities, called fuzzy-interval Hermite–Hadamard-type inequalities for  -convex fuzzy-interval-valued functions by means of a fuzzy order relation. Some special cases are also discussed, which can be viewed as applications. Useful examples that verify the applicability of the theory developed in this study are presented. We intend to use various types of convex fuzzy-interval-valued functions to construct fuzzy-interval inequalities for fuzzy-interval-valued functions. The concepts and techniques of this paper may be a starting point for further research in this area.
-convex fuzzy-interval-valued functions by means of a fuzzy order relation. Some special cases are also discussed, which can be viewed as applications. Useful examples that verify the applicability of the theory developed in this study are presented. We intend to use various types of convex fuzzy-interval-valued functions to construct fuzzy-interval inequalities for fuzzy-interval-valued functions. The concepts and techniques of this paper may be a starting point for further research in this area.
Availability of data and materials
Not applicable.
References
Alomari, M., Darus, M., Dragomir, S.S., Cerone, P.: Ostrowski type inequalities for functions whose derivatives are s-convex in the second sense. Appl. Math. Lett. 23, 1071–1076 (2010)
An, Y., Ye, G., Zhao, D., Liu, W.: Hermite–Hadamard type inequalities for interval \((h_{1}, h_{2})\)-convex functions. Mathematics 7, 436 (2019)
Anderson, G.D., Vamanamurthy, M.K., Vuorinen, M.: Generalized convexity and inequalities. J. Math. Anal. Appl. 335, 1294–1308 (2007)
Avci, M., Kavurmaci, H., Ozdemir, M.E.: New inequalities of Hermite–Hadamard type via s-convex functions in the second sense with applications. Appl. Math. Comput. 217, 5171–5176 (2011)
Awan, M.U., Noor, M.A., Noor, K.I.: Hermite–Hadamard inequalities for exponentially convex functions. Appl. Math. Inf. Sci. 12, 405–409 (2018)
Bede, B.: Mathematics of Fuzzy Sets and Fuzzy Logic. Studies in Fuzziness and Soft Computing, vol. 295. Springer, Berlin (2013)
Cerone, P., Dragomir, S.S.: Ostrowski type inequalities for functions whose derivatives satisfy certain convexity assumptions. Demonstr. Math. 37, 299–308 (2004)
Chalco-Cano, Y., Flores-Franulič, A., Román-Flores, H.: Ostrowski type inequalities for interval-valued functions using generalized Hukuhara derivative. Comput. Appl. Math. 31, 457–472 (2012)
Chalco-Cano, Y., Lodwick, W.A., Condori-Equice, W.: Ostrowski type inequalities and applications in numerical integration for interval-valued functions. Soft Comput. 19, 3293–3300 (2015)
Chen, F., Wu, S.: Integral inequalities of Hermite–Hadamard type for products of two h-convex functions. Abstr. Appl. Anal. 6, 1–6 (2014)
Costa, T.M.: Jensen’s inequality type integral for fuzzy-interval-valued functions. Fuzzy Sets Syst. 327, 31–47 (2017)
Costa, T.M., Roman-Flores, H.: Some integral inequalities for fuzzy-interval-valued functions. Inf. Sci. 420, 110–125 (2017)
Costa, T.M., Román-Flores, H., Chalco-Cano, Y.: Opial-type inequalities for interval-valued functions. Fuzzy Sets Syst. 358, 48–63 (2019)
de Weerdt, E., Chu, Q.P., Mulder, J.A.: Neural network output optimization using interval analysis. IEEE Trans. Neural Netw. 20, 638–653 (2009)
Diamond, P., Kloeden, P.E.: Metric Spaces of Fuzzy Sets: Theory and Applications. World Scientific, Singapore (1994)
Fang, Z.B., Shi, R.: On the \((p, h)\)-convex function and some integral inequalities. J. Inequal. Appl. 2014, 45 (2014)
Goetschel, R. Jr., Voxman, W.: Elementary fuzzy calculus. Fuzzy Sets Syst. 18, 31–43 (1986)
Hadamard, J.: Étude sur les propriétés des fonctions entières et en particulier d’une fonction considérée par Riemann. J. Math. Pures Appl. 5, 171–215 (1893)
Hermite, C.: Sur deux limites d’une intégrale définie. Mathesis 3, 1–82 (1883)
Hudzik, H., Maligranda, L.: Some remarks on s-convex functions. Aequ. Math. 48, 100–111 (1994)
Iscan, I.: A new generalization of some integral inequalities for \((\alpha , m)\)-convex functions. Math. Sci. 7, 1–8 (2013)
Iscan, I.: Hermite–Hadamard type inequalities for harmonically convex functions. Hacet. J. Math. Stat. 43, 935–942 (2014)
Iscan, I.: Hermite–Hadamard type inequalities for p-convex functions. Int. J. Anal. Appl. 11, 137–145 (2016)
Kaleva, O.: Fuzzy differential equations. Fuzzy Sets Syst. 24, 301–317 (1987)
Kulish, U., Miranker, W.: Computer Arithmetic in Theory and Practice. Academic Press, New York (2014)
Moore, R.E.: Interval Analysis. Prentice Hall, Englewood Cliffs (1966)
Moore, R.E., Kearfott, R.B., Cloud, M.J.: Introduction to Interval Analysis. SIAM, Philadelphia (2009)
Nanda, S., Kar, K.: Convex fuzzy mappings. Fuzzy Sets Syst. 48, 129–132 (1992)
Osuna-Gómez, R., Jiménez-Gamero, M.D., Chalco-Cano, Y., Rojas-Medar, M.A.: Hadamard and Jensen inequalities for s-convex fuzzy processes. In: Soft Methodology and Random Information Systems. Advances in Soft Computing, vol. 26, pp. 1–15. Springer, Berlin (2004)
Puri, M.L., Ralescu, D.A.: Fuzzy random variables. Read. Fuzzy Sets Intell. Syst. 114, 409–422 (1986)
Román-Flores, H., Chalco-Cano, Y., Lodwick, W.A.: Some integral inequalities for interval-valued functions. Comput. Appl. Math. 37, 1306–1318 (2018)
Rothwell, E.J., Cloud, M.J.: Automatic error analysis using intervals. IEEE Trans. Ed. 55, 9–15 (2012)
Snyder, J.M.: Interval analysis for computer graphics. SIGGRAPH Comput. Graph. 26, 121–130 (1992)
Zhao, D.F., An, T.Q., Ye, G.J., Liu, W.: New Jensen and Hermite–Hadamard type inequalities for h-convex interval-valued functions. J. Inequal. Appl. 2018, 302 (2018)
Acknowledgements
The authors would like to thank the Rector, COMSATS University Islamabad, Islamabad, Pakistan, for providing excellent research and academic environment.
Funding
The research is supported by the National Natural Science Foundation of China (Grant No. 61673169).
Author information
Authors and Affiliations
Contributions
All authors contributed equally to the writing of this paper. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Khan, M.B., Noor, M.A., Noor, K.I. et al. New Hermite–Hadamard-type inequalities for  -convex fuzzy-interval-valued functions.
Adv Differ Equ 2021, 149 (2021). https://doi.org/10.1186/s13662-021-03245-8
-convex fuzzy-interval-valued functions.
Adv Differ Equ 2021, 149 (2021). https://doi.org/10.1186/s13662-021-03245-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-021-03245-8


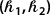 -Convex fuzzy-interval-valued functions
-Convex fuzzy-interval-valued functions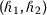 -convex on K if
-convex on K if 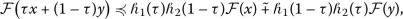
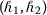 -concave on K if inequality (
-concave on K if inequality (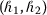 -convex on K if
-convex on K if 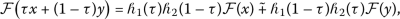
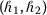 -convex fuzzy-interval-valued function, then
-convex fuzzy-interval-valued function, then 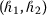 -convex for
-convex for 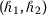 -convex fuzzy-interval-valued functions, then
-convex fuzzy-interval-valued functions, then 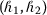 -convex fuzzy-interval-valued function.
-convex fuzzy-interval-valued function.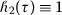 , then an
, then an 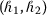 -convex fuzzy-interval-valued function becomes
-convex fuzzy-interval-valued function becomes 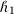 -convex fuzzy-interval-valued function, that is,
-convex fuzzy-interval-valued function, that is, 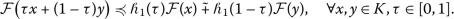
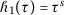 ,
, 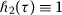 , then an
, then an 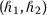 -convex fuzzy-interval-valued function becomes an s-convex fuzzy-interval-valued function, that is,
-convex fuzzy-interval-valued function becomes an s-convex fuzzy-interval-valued function, that is, 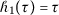 ,
,  , then an
, then an  -convex fuzzy-interval-valued function becomes a convex fuzzy-interval-valued function, that is,
-convex fuzzy-interval-valued function becomes a convex fuzzy-interval-valued function, that is, 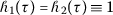 , then an
, then an 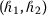 -convex fuzzy-interval-valued function becomes a P-convex fuzzy-interval-valued function, that is,
-convex fuzzy-interval-valued function becomes a P-convex fuzzy-interval-valued function, that is,  -convex fuzzy-interval-valued functions
-convex fuzzy-interval-valued functions