1 Introduction

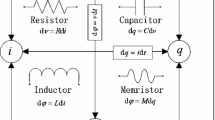
It is well known that Chua in [1] postulated the existence of the fourth circuit element in 1971, and he named this element memristor as a contraction of memory and resistor, Chua also pointed out that the memristor can memorize its past dynamic history, such a memory characteristic makes it as a potential candidate for simulating biological synapses, and it has been shown that a simple memristive system can exhibit a plethora of complex dynamical behaviors. Until 2008, William and his research group at Hewlett-Packard Laboratory proclaimed that the fourth circuit element is realized by building a prototype of a solid-state memristor [2], since then, many efforts have been made devoted to the analysis and synthesis of memristive systems, see [3–5] and the references therein.

Especially, the so-called memristive neural networks (MNNs) are constructed by introducing resistors into artificial or biological neural networks, which greatly expand the application scope of neural networks, for example, MNNs can provide an important approach to better understand the neural processes in the human brain [3]. In addition, in the process of design and implementation of NNs, communication delays are ubiquitous in the real world owing to the finite velocity of signal switching and delivery, and it often becomes a source of some undesirable side-effects such as oscillation and divergence in a real-world network [6]. Recently, the research on the dynamics of many types of delayed MNNs has been today’s hot topics and there are many excellent works have been reported, such as [7–13] and the references therein.

Synchronization, as an important nonlinear dynamical nature, has extensive applications in practical engineering fields. Under the drive–response (or master–slave) framework proposed by Pecora and Carroll in [14], many theoretical results have been established on the synchronization of two MNNs, for example, the synchronization dynamics of kinds of delayed MNNs have been well studied, such as the global exponential synchronization [15], reliable asymptotic anti-synchronization [16], non-fragile \(H_{\infty }\) synchronization [17], projective synchronization [18], and so on. Looking through the above-mentioned literature, the trajectories of the response system can reach the trajectories of deriving system over the infinite horizon. In the application point of view, the synchronization is usually required to be realized in finite time, which is more important in some engineering processes, for instance, secure communication and artificial intelligence [19, 20]. For finite-time synchronization, it is noteworthy that the settling time depends heavily on the initial states of the system, which limits practical applications because the information of initial conditions may be hard to adjust or even impossible to estimate. To satisfy the need of fact, the fixed-time stability was originally introduced by Polyakov in [21], if it is globally finite-time stable and the settling time function is uniformly bounded for any initial values, which means that the settling or halting time is not dependent on the initial states. Nowadays, fixed-time control has been extensively applied in many areas such as power systems [22], rigid spacecraft [23], etc. According to the significant biological and engineering backgrounds of finite-time or fixed-time synchronization control, such an issue of delayed MNNs has attracted considerable attention, see [10, 24–30] and the references therein. It is noteworthy that for the majority of the aforementioned studies, a common method is based on the generalized finite-time convergence theorem under the Filippov differential inclusion theory, and the corresponding criteria are established via constructing Lyapunov (or Lyapunov–Krasovskii) functionals.

Motivated by recent works in [31, 32] and combining with the framework for studying MNNs proposed in [33], in this paper, we further study the finite-time synchronization of a basic delayed MNN model. The main contribution of this paper lies in the following aspects.

  1. (1)

    Different from the theoretical results on dynamics of the aforementioned delayed MNNs, in this paper, the differential inclusion theory and the nonsmooth analysis techniques are abandoned, our results complement the earlier publications.

  2. (2)

    Existing finite-time synchronization results on delayed MNNs are mainly based on some generalized finite-time convergence theorem (see, e.g., [10, 24, 26, 27]), in this paper, we study the finite-time synchronization without using them, the employed approach enriches the analysis method of MNNs.

  3. (3)

    The theoretical results established in this paper are closely related to the location of the initial error states, which presents a new viewpoint of finite-time synchronization process.

The rest of this paper is arranged as follows. In Sect. 2, the model description and some preliminary works are presented. Section 3 discusses the finite-time synchronization of the drive–response MNNs with a state feedback controller. In Sect. 4, a numerical example is given to substantiate the theoretical analysis. Finally, conclusions are drawn in Sect. 5.

2 Preliminaries

In this paper, we consider the following delayed MNN model described by Guo et al. in [33],

$$ \frac{{\mathrm{d}}x_{i}(t)}{{\mathrm{d}}t}=-d_{i}x_{i}(t)+\sum _{j=1}^{n}a_{ij}(x_{i})f_{j} \bigl(x_{j}(t)\bigr)+ \sum_{j=1}^{n}b_{ij}(x_{i})g_{j} \bigl(x_{j}(t-\theta )\bigr)+I_{i}, $$
(2.1)

where \(x_{i}(t)\) denotes the neuron current activity level, \(d_{i}>0\) is the neuronal self-inhibition, \(f_{j}(\cdot )\), \(g_{j}(\cdot )\) are two activation functions, \(I_{i}\) stands for the input or bias, θ represents the transmission delay, and \(a_{ij}(\cdot )\) and \(b_{ij}(\cdot )\) are dependent on the variation directions of \(f_{j}(x_{j}(t))- x_{i}(t)\) and \(g_{j}(x_{j}(t-\theta ))-x_{i}(t)\) along time t, respectively. More concretely, in light of the current–voltage characteristics of memristor [33], the state-dependent parameters \(a_{ij}(\cdot )\) and \(b_{ij}(\cdot )\) can be specifically expressed as

$$\begin{aligned}& \begin{aligned} &a_{ij}(x_{i})= \textstyle\begin{cases} a_{ij}^{*}, & D^{-}f_{ij}(t)< 0, \\ \text{unchanged}, & D^{-}f_{ij}(t)=0, \\ a_{ij}^{**}, & D^{-}f_{ij}(t)> 0, \end{cases}\displaystyle \\ &b_{ij}(x_{i})= \textstyle\begin{cases} b_{ij}^{*}, & D^{-}g_{ij}(t-\theta )< 0, \\ \text{unchanged}, & D^{-}g_{ij}(t-\theta )= 0, \\ b_{ij}^{**}, & D^{-}g_{ij}(t-\theta )> 0, \end{cases}\displaystyle \end{aligned} \end{aligned}$$
(2.2)

in which \(a_{ij}^{*}\), \(a_{ij}^{**}\) and \(b_{ij}^{*}\), \(b_{ij}^{**}\) are different constants, \(D^{-}(\cdot )\) means the left upper Dini-derivation, and \(f_{ij}(t)=f_{j}(x_{j}(t))-x_{i}(t)\), \(g_{ij}(t-\theta )=f_{j}(x_{j}(t- \theta ))-x_{i}(t)\). The initial condition is equipped with \(x_{i}(t)=\varphi _{i}(t)\in C([-\theta , 0], \mathbb{R})\).

In the following, we routinely regard system (2.1) as the drive system and the corresponding response system is presented as follows:

$$ \frac{{\mathrm{d}}y_{i}(t)}{{\mathrm{d}}t}=-d_{i}y_{i}(t)+\sum _{j=1}^{n}a_{ij}(y_{i})f_{j} \bigl(y_{j}(t)\bigr)+ \sum_{j=1}^{n}b_{ij}(y_{i})g_{j} \bigl(y_{j}(t-\theta )\bigr)+I_{i}+\mathbb{C}_{i}(t), $$
(2.3)

in which \(y_{i}(t)\) stands for the state variable of the ith neuron of response system and \(\mathbb{C}_{i}(t)\) corresponds to the control input. The initial condition associated with system (2.3) is given by \(y_{i}(t)=\tilde{\varphi }_{i}(t)\in C([-\theta , 0], \mathbb{R})\).

Let us define the synchronization error function as , and subtract (2.3) from (2.1), we obtain the following error system:

(2.4)

With regard to neural networks (2.1) and (2.3), the initial condition of system (2.4) is correspondingly given as follows,

Definition 2.1

([20, 32])

If for a suitable designed controller and any initial state , \(s\in [-{ \theta }, 0]\), there is a time \(\mathbb{T}(\tilde{\boldsymbol{\varphi }},{\boldsymbol{\varphi }})\) such that

$$ \lim_{t\to \mathbb{T}(\tilde{\varphi },\varphi )} \bigl\vert { y_{i}(t)-x_{i}(t)} \bigr\vert =0 $$

and

$$ \bigl\vert {y_{i}(t)-x_{i}(t)} \bigr\vert \equiv 0,\quad \mbox{for } t\geq \mathbb{T}({\tilde{\boldsymbol{\varphi }}},{\boldsymbol{\varphi }}), i=1,2,\ldots,n. $$

Then the drive system-response systems (2.1) and (2.3) are said to achieve finite-time synchronization. The function \(\mathbb{T}\) is called the settling-time function.

Definition 2.2

([20, 32])

If drive–response systems (2.1) and (2.3) are finite-time synchronization and the settling time function \(\mathbb{T}(\tilde{\boldsymbol{\varphi }},{\boldsymbol{\varphi }})\) is uniformly bounded, that is, there is a constant \(\mathbb{T}_{\max }>0\) such that \(\mathbb{T}(\tilde{\boldsymbol{\varphi }},{\boldsymbol{\varphi }})\leq \mathbb{T}_{ \max }\). Then the drive system (2.1) and response system (2.3) are said to achieve fixed-time synchronization.

It is easy to see from the preknowledge that the finite-time synchronization problem in this paper is converted to finite-time stability problem of (2.4). In order to achieve this objective, further assumptions on the activations are made in the following.

Assumption 2.1

The activation functions \(f_{i}(\cdot )\) and \(g_{i}(\cdot )\) satisfy globally Lipschitz conditions and are bounded, that is, there exist positive constants \(L_{i}^{f}\), \(L_{i}^{g}\) and \(M_{i}^{f}\), \(M_{i}^{g}\) such that

$$ \bigl\vert f_{i}(u)-f_{i}(v) \bigr\vert \leq L_{i}^{f} \vert u-v \vert ,\qquad \bigl\vert g_{i}(u)-g_{i}(v) \bigr\vert \leq L_{i}^{g} \vert u-v \vert , $$

and

$$ \bigl\vert f_{i}(u) \bigr\vert \leq M_{i}^{f},\qquad \bigl\vert g_{i}(u) \bigr\vert \leq M_{i}^{g}, $$

hold for all \(u, v\in \mathbb{R}\), \(i=1,2,\ldots,n\).

3 Main results

For notational convenience, in what follows we denote \(\hat{a}_{ij}=\max \{|a_{ij}^{*}|,|a_{ij}^{**}| \}\), \(\hat{b}_{ij}= \max \{|b_{ij}^{*}|, |b_{ij}^{**}| \}\), \(d_{ij}^{a}=|\max \{a_{ij}^{*}, a_{ij}^{**} \}-\min \{a_{ij}^{*}, a_{ij}^{**}\}|\), \(d_{ij}^{b}=|\max \{b_{ij}^{*}, b_{ij}^{**} \}-\min \{b_{ij}^{*}, b_{ij}^{**}\}|\), \(\tilde{k}_{\min }= \min_{1 \leq i\leq n}\{k_{i}\}\).

We are now in a position to state our main results as follows.

Theorem 3.1

Let Assumption 2.1hold, if the error system (2.4) is controlled with the control law

where the control parameters \(\alpha _{i}\), \(\beta _{i}\), \(k_{i}\)are positive constants satisfying

$$ \alpha _{i}>-d_{i}+\sum _{j=1}^{n}\hat{a}_{ij}L_{j}^{f}+2^{ \frac{\mu }{1-\mu }} \sum_{j=1}^{n}\hat{b}_{ij}L_{j}^{g} $$
(3.1)

and

$$ \beta _{i}\geq 2^{\frac{\mu }{1-\mu }} \bigl((1-\mu ) \tilde{k}_{\min } \theta \bigr)^{\frac{1}{1-\mu }}\sum _{j=1}^{n}\hat{b}_{ij}L_{j}^{g}+ \sum_{j=1}^{n}d_{ij}^{a}M_{j}^{f}+ \sum_{j=1}^{n}d_{ij}^{b}M_{j}^{g},\quad i=1,2,\ldots,n, $$
(3.2)

then the response system (2.3) can in finite–time synchronize with the drive system (2.1).

In order to prove the main results, we first establish the following two lemmas.

Lemma 3.2

Let Assumption 2.1hold and conditions (3.1) and (3.2) be satisfied. Then, for each of system (2.4) with , it would finite–timely cross the hyperplane with .

Proof

Observe from (3.1), (3.2) and \(0<\mu <1\) that

$$ \alpha _{i}>- d_{i}+\sum _{j=1}^{n}\hat{a}_{ij}L_{j}^{f}+ \sum_{j=1}^{n} \hat{b}_{ij}L_{j}^{g} $$
(3.3)

and

$$ \beta _{i}>\sum_{j=1}^{n}d_{ij}^{a}M_{j}^{f} +\sum_{j=1}^{n}d_{ij}^{b}M_{j}^{g}. $$
(3.4)

Firstly, we obtain from the continuity argument and (3.1) that there exists a sufficiently small ε satisfying

$$ \varepsilon -\alpha _{i}-d_{i}+\sum _{j=1}^{n}\hat{a}_{ij}L_{j}^{f}+e^{ \varepsilon \theta } \sum_{j=1}^{n}\hat{b}_{ij}L_{j}^{g}< 0,\quad i=1,2,\ldots,n. $$
(3.5)

Set

One can easily see that , \(i=1,2,\ldots,n\), and we shall discuss it into the following two cases:

Case I: , \(i=1,2,\ldots,n\). We know from the continuity argument that there exists a constant \(\sigma >0\) such that , \(i=1,2,\ldots,n\), and , for \(s\in (t, t+\sigma )\).

Case II: If there exists an index \(i_{0}\) and a time \(t_{0}\geq 0\) such that , then we have

(3.6)

Note from

that

Then we deduce from (3.4), (3.5) and (3.6) that

Therefore, there must exist a constant \(\sigma >0\) such that , and , for \(s\in (t_{0}, t_{0}+\sigma )\).

We conclude from the above two cases that is non-increasing and , \(t\geq 0\), which means that

Therefore, as time t increases, \(\sup_{t-\theta \leq s\leq t} (\max_{i=1,2,\ldots,n}|e_{i}(s)| )\) would be less than 1. Denote the first time satisfying \(\sup_{t-\theta \leq s\leq t} (\max_{i=1,2,\ldots,n}|e_{i}(s)| )=1\) as \(\mathbb{T}_{1}\), then we have

That is to say, every error function would cross the hyperplane

$$ \sup_{t-\theta \leq s\leq t} \Bigl(\max_{i=1,2,\ldots,n}\bigl|e_{i}(s)\bigr| \Bigr)=1, $$

and the time it takes is no more than \(\mathbb{T}_{1}\). The proof of Lemma 3.2 is complete. □

Lemma 3.3

Let Assumption 2.1and conditions (3.1)–(3.2) be satisfied, if

$$ \alpha _{i}>-d_{i}+\sum_{j=1}^{n} \hat{a}_{ij}L_{j}^{f}+2^{ \frac{\mu }{1-\mu }}\sum _{j=1}^{n}\hat{b}_{ij}L_{j}^{g} $$

and

$$ \beta _{i}>2^{\frac{\mu }{1-\mu }} \bigl((1-\mu )\tilde{k}_{\min } \theta \bigr)^{\frac{1}{1-\mu }}\sum_{j=1}^{n} \hat{b}_{ij}L_{j}^{g}+\sum _{j=1}^{n}d_{ij}^{a}M_{j}^{f}+ \sum_{j=1}^{n}d_{ij}^{b}M_{j}^{g}, $$

hold for all \(i=1,2,\ldots,n\), then for each of system (2.4) with

would fixed–timely flow to 0.

Proof

Define

(3.7)

It is easy to see that

and if there exist an index \(i_{1}\) and a time \(t_{1}\geq 0\) such that , then one has

(3.8)

Notice that

(3.9)

Elementary calculation from (3.9) produces

(3.10)

which, together with (3.8), leads to

(3.11)

which means that there exists some \(\varsigma >0\) such that holds for all \(s\in (t_{1}, t_{1}+\varsigma )\).

Therefore, we obtain from the above discussions that

which reduces to

and hence one can easily deduce that, as time t increases, would flow to 0. Denote \(\mathbb{T}_{2}\) as the time such that , we then have

which implies that the time–taken for each from 1 to 0 is no more than \(\frac{1}{\tilde{k}_{\min }(1-\mu )}\), \(i=1,2,\ldots,n\). The proof of Lemma 3.3 is complete. □

Based on Lemmas 3.2 and 3.3, we are ready to prove Theorem 3.1.

Proof of Theorem 3.1

For every solution of error system (2.4), we treat it into two cases according to the location of initial error function:

Case I: .

In this case, we obtain from Lemma 3.3 that each error state component \(e_{i}(t)\), \(i=1,2,\ldots,n\), would flow to 0, and the time–taken is no more than \(\frac{1}{\tilde{k}_{\min }(1-\mu )}\). In other words, the drive–response system (2.1) and (2.3) under control law (3.1) achieve fixed-time synchronization.

Case II: .

In this case, we conclude from Lemma 3.2 that would flow to 1 with a finite time, which is no more than , and then in a similar manner to that carried out in Lemma 3.3, we see that each would continue to flow 0 in fixed time, which is no more than \(\frac{1}{\tilde{k}_{\min }(1-\mu )}\). In short, as time t increases, each \(e_{i}(t)\) would finally achieve 0 in finite time \(\mathbb{T}_{\mathrm{total}}\) with . □

Remark 3.1

The proof of the previous results provides a new perspective for better understanding the finite-time synchronization of MNNs. That is to say, if the absolute value of initial error function is less than or equal to 1, then each error function will achieve 0 in a fixed time; if the absolute value of initial error function is greater than 1, then each error function will firstly from the initial function to 1 in a finite time, and then further reach 0 in a fixed time. When the control parameter \(\mu >1\), whether there is such a mechanism process to realize fixed-time synchronization is another issue worth studying and discussing.

Remark 3.2

With the differential inclusion theory and nonsmooth finite (or fixed)-time convergence theorem, the researchers studied the finite (or fixed)-time synchronization of MNNs (see, e.g., [10, 24, 26, 27] and the references therein). Different from the method employed in those works, in this paper, we directly study the finite-time synchronization of the delayed MNNs (2.1) without using the theory of differential equations with discontinuous right-hand sides. Therefore, the theoretical results established in this paper enrich the already existing finite-time synchronization methods.

Remark 3.3

Different from some existing finite-time controllers with time delays in such as [24, 30, 34], the designed control law in Theorem 3.1 depends only on the current states at time t, it does not involve any information on the past states, which is much easier to be verified and realized in practice. Therefore, the designed finite-time control scheme is some less conservative. On the other hand, to realize the finite-time synchronization of discontinuous NNs, some useful Lyapunov functions or Lyapunov–Krasovskii functions are constructed based on the nonsmooth finite-time convergence theorem together differential inequality techniques; see, e.g., [20, 28, 30, 34]. In this paper, we investigate the finite-time synchronization problem of the considered delayed system by some mathematical analysis techniques via constructing different Lyapunov functions.

4 Numerical simulations

In this section, we will present a numerical example to illustrate the obtained theoretical results. For convenience, we denote \(f_{ij}(t)=a_{j}(x_{j}(t))-x_{i}(t)\) and \(g_{ij}(t-\theta )=b_{j}(x_{j}(t-\theta ))-x_{i}(t)\).

Example 4.1

Consider a two-neuron memristive neural network model as follows:

$$ \textstyle\begin{cases} \dot{x}_{1}(t)=-6.75x_{1}(t)+a_{11}(t)f_{1}(x_{1}(t))+a_{12}f_{2}(x_{2}(t)) \\ \hphantom{\dot{x}_{1}(t)={}}{}+b_{11}(t)g_{1}(x_{1}(t-0.45))+b_{12}g_{2}(x_{2}(t-0.45))+I_{1}, \\ \dot{x}_{2}(t)=-5x_{2}(t)+a_{21}f_{1}(x_{1}(t))+a_{22}(t)f_{2}(x_{2}(t)) \\ \hphantom{\dot{x}_{2}(t)={}}{}+b_{21}g_{1}(x_{1}(t-0.45))+b_{22}(t)g_{2}(x_{2}(t-0.45))+I_{2}, \end{cases} $$
(4.1)

where

$$\begin{aligned}& f_{i}(s)=g_{i}(s)=\frac{ \vert s+1 \vert - \vert s-1 \vert }{2},\quad i=1,2, \\& a_{12}=-4.8,\qquad a_{21}=6.1,\qquad b_{12}=0.8,\qquad b_{21}=-1.2,\qquad I_{1}=I_{2}=1.2, \end{aligned}$$

and

$$\begin{aligned}& a_{11}(t)= \textstyle\begin{cases} 0.856,& D^{-}f_{11}(t)< 0, \\ 1.628,& D^{-}f_{11}(t)>0, \\ a_{11}(t^{-}),& D^{-}f_{11}(t)=0, \end{cases}\displaystyle \qquad a_{22}(t)= \textstyle\begin{cases} -1.276,& D^{-}f_{22}(t)< 0, \\ 3.462,& D^{-}f_{22}(t)>0, \\ a_{22}(t^{-}),& D^{-}f_{22}(t)=0, \end{cases}\displaystyle \\& b_{11}(t)= \textstyle\begin{cases} -3.726,& D^{-}g_{11}(t-0.45)< 0, \\ 2.346,& D^{-}g_{11}(t-0.45)>0, \\ b_{11}(t^{-}),& D^{-}g_{11}(t-0.45)=0, \end{cases}\displaystyle \qquad b_{22}(t)= \textstyle\begin{cases} -2.224,& D^{-}g_{22}(t-0.45)< 0, \\ -2.216,& D^{-}g_{22}(t-0.45)>0, \\ b_{11}(t^{-}),& D^{-}g_{22}(t-0.45)=0. \end{cases}\displaystyle \end{aligned}$$

We can verify that the activation functions satisfy Assumption 2.1 with \(L_{i}^{f}=L_{i}^{g}=1\), \(M_{i}^{f}=M_{i}^{g}=1\). Moreover, the response system is described by

$$ \textstyle\begin{cases} \dot{y}_{1}(t)=-6.75y_{1}(t)+a_{11}(t)f_{1}(y_{1}(t))+a_{12}(f_{2}(y_{2}(t)) \\ \hphantom{\dot{y}_{1}(t)={}}{}+b_{11}(t)g_{1}(y_{1}(t-0.45))+b_{12}g_{2}(y_{2}(t-0.45))+I_{1}+ \mathbb{C}_{1}(t), \\ \dot{y}_{2}(t)=-5y_{2}(t)+a_{21}f_{1}(y_{1}(t))+a_{22}(t)f_{2}(y_{2}(t)) \\ \hphantom{\dot{y}_{2}(t)={}}{}+b_{21}g_{1}(y_{1}(t-0.45))+b_{22}(t)g_{2}(y_{2}(t-0.45))+I_{2}+ \mathbb{C}_{2}(t), \end{cases} $$
(4.2)

where the activation functions and system parameters are the same as that in system (4.1), and the controllers are designed as follows:

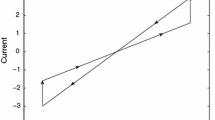
It follows from simple computations that conditions (3.1) and (3.2) are satisfied. Therefore, we conclude from Theorem 3.1 that the finite-time synchronization between system (4.1) and system (4.2) is achieved. Figures 1–2 show the simulation results with the initial conditions \(x_{1}(s)=8.5\), \(x_{2}(s)=-2.5\), \(y_{1}(s)=4.5\), \(y_{2}(s)=3.4\), \(s\in [-4.5, 0]\). Specifically, Fig. 1 shows the trajectories of the state evolution of system (4.1) and system (4.2), we can observe that the state of networks (4.2) in finite time synchronizes with system (4.1). Figure 2 shows the finite-time synchronization between system (4.1) and system (4.2), it is readily seen that the state evolution error approaches zero quickly as time goes.

Figure 1
figure 1

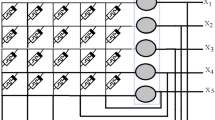
Time behaviors of state variables in \(x_{i}(t)\), \(y_{i}(t)\) of MNNs (4.1), \(i=1,2\)

Full size image
Figure 2
figure 2

The synchronization errors between the drive–response systems in Example 4.1

Full size image

5 Conclusion

This paper performed a finite-time synchronization analysis of delayed MNNs based on the previous works [31–33]. Different from the existing works, we turn to the synchronization analysis by discussing the MNNs directly. Some new criteria ensuring finite-time synchronization of delayed MNNs were established by designing the suitable controller and constructing some novel Lyapunov functions. It is worth mentioning that the presented methodology herein without employing the differential inclusion theory and nonsmooth finite time convergence theorem, which are usually used to handle the finite-time synchronization problem. Finally, a numerical example is presented to substantiate the results. The future work will focus on the investigation of the finite-time synchronization of MNNs with mixed time-varying delays or leakage delays or impulse disturbance.