1 Introduction

Since the advent of tobacco in 6000 BC, smoking has contributed heavily not only to problems leading to serious illness or even death, but it has also done harm to the whole society [1–3]. According to the third edition of cancer atlas jointly released by International Agency for Research on Cancer (IARC), American Cancer Society (ACS), and Union for International Cancer Control (UICC) on October 16, 2019, smoking causes more preventable cancer deaths than any other risk factor, and in 2017 alone, 2.3 million people worldwide died from smoking, which accounts for 24% of all cancer deaths. On the other hand, based on the WHO global report on trends in prevalence of tobacco use 2000–2025 [4], every year more than 8 million people die from tobacco use, accounting for about half of its users. More than 7 million of them died from direct smoking, while about 1.2 million were non-smokers who died from being exposed to second-hand smoke.

Owing to these facts, and the astronomical public health burden associated with smoking, smoking has been a prevalent problem all over the world that requires intervention for eradication urgently. For this goal, some mathematical models have become important tools to characterize smoking behavior since the smart work of Castello et al. [5]. In the transmission of smoking epidemics, incidence rate plays a vital role. Thus, in recent years, scholars at home and abroad have formulated different forms of smoking models with linear incidence rate [6–9], saturated incidence rate [10, 11], square root type incidence rate [12–14], and harmonic mean type incidence rate [15]. Several others presented fractional smoking models [16–20] and age-structured smoking models [2, 21]. It is worth noting that all the smoking models above neglect the fact that the use of tobacco also occurs in the form of snuffing. Due to this fact, Alzahrani and Zeb proposed the following tobacco smoking model containing snuffing class [22]:

$$ \textstyle\begin{cases} \frac{dX(t)}{dt} = A-\beta _{1} X(t)H_{1}(t)-\mu X(t)+\alpha Y(t), \\ \frac{dH_{1}(t)}{dt} = \beta _{1} X(t)H_{1}(t)-\beta _{2} H_{1}(t)H_{2}(t)-( \rho +\mu )H_{1}(t), \\ \frac{dH_{2}(t)}{dt} = \beta _{2} H_{1}(t)H_{2}(t)-(d+\varpi +\mu )H_{2}(t), \\ \frac{dY(t)}{dt} = \varpi H_{2}(t)-(\alpha +\gamma +\mu )Y(t), \\ \frac{dZ(t)}{dt} = \gamma Y(t)-\mu Z(t), \end{cases} $$
(1)

for the description of variables and parameters used in model, see Table (1) in [22]. Here, \(X(t)\), \(H_{1}(t)\), \(H_{2}(t)\), \(Y(t)\), and \(Z(t)\) stand for the numbers of susceptible smokers, snuffing class, irregular smokers, regular smokers, and quit smokers at time t, respectively. A is the recruitment rate of the susceptible population; \(\beta _{1}\) is the rate at which the susceptible population becomes the snuffing class; \(\beta _{2}\) is the rate at which the snuffing class becomes the irregular smokers; μ is the natural death rate of all the populations; ρ is the death rate of the snuffing class because of tobacco use; d is the death rate of the irregular smokers because of the tobacco related diseases; α is the relapse rate of the regular smokers, and γ is the quitting rate of the regular smokers.

Obviously, system (1) assumes that the regular smokers quit smoking instantaneously, which is not consistent with the reality, because it usually takes a certain period of time for a regular smoker to quit smoking once he has been addicted to tobacco. In addition, delay differential equations exhibit much more complicated dynamics than ordinary differential equations. Specially, time delay can cause occurrence of Hopf bifurcation and periodic solutions for dynamical systems. And delay differential equations have been used for analysis in many areas such as population dynamics [23–26], epidemiology [27–29], and computer networks [30–33]. Thus, to achieve better compatibility with the reality and motivated by the work above, we investigate the following smoking model with time delay:

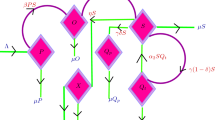
$$ \textstyle\begin{cases} \frac{dX(t)}{dt} = A-\beta _{1} X(t)H_{1}(t)-\mu X(t)+\alpha Y(t), \\ \frac{dH_{1}(t)}{dt} = \beta _{1} X(t)H_{1}(t)-\beta _{2} H_{1}(t)H_{2}(t)-( \rho +\mu )H_{1}(t), \\ \frac{dH_{2}(t)}{dt} = \beta _{2} H_{1}(t)H_{2}(t)-(d+\varpi +\mu )H_{2}(t), \\ \frac{dY(t)}{dt} = \varpi H_{2}(t)-(\alpha +\mu )Y(t)-\gamma Y(t- \tau ), \\ \frac{dZ(t)}{dt} = \gamma Y(t-\tau )-\mu Z(t), \end{cases} $$
(2)

where τ is the time delay due to the period that the regular smokers use to quit smoking. The flow diagram of system (2) is as shown in Fig. 1.

Figure 1
figure 1

The flow diagram of system (2)

Full size image

The initial conditions for the above system are as follows:

$$ \textstyle\begin{cases} X(\theta ) = \phi _{1}(\theta ), \quad \phi _{1}(\theta )\geq 0, \phi _{1}(0)> 0, \\ H_{1}(\theta ) = \phi _{2}(\theta ), \quad \phi _{2}(\theta )\geq 0, \phi _{2}(0)> 0, \\ H_{2}(\theta ) = \phi _{3}(\theta ), \quad \phi _{3}(\theta )\geq 0, \phi _{3}(0)> 0, \\ Y(\theta ) = \phi _{4}(\theta ), \quad \phi _{4}(\theta )\geq 0, \phi _{4}(0)>0, \\ Z(\theta ) = \phi _{5}(\theta ), \quad \phi _{5}(\theta )\geq 0, \phi _{5}(0)> 0, \theta \in C[-\tau ,0], \end{cases} $$
(3)

where \((\phi _{1}(\theta ),\phi _{2}(\theta ),\phi _{3}(\theta ),\phi _{4}( \theta ),\phi _{5}(\theta ) )\in ( C[-\tau ,0],\mathbb {R}^{5}_{+0} )\) is the Banach space of continuous functions mapping the interval \([-\tau ,0]\) into \(\mathbb {R}^{5}_{+0}\). It is easy to show that (2) has positive solutions with initial conditions (3).

The subsequent parts of this paper are organized as follows. In Sect. 2, the local stability and existence of Hopf bifurcation are analyzed. Section 3 is about the direction and stability of Hopf bifurcation. Section 4 is devoted to global exponential stability results for smoking present equilibrium. Numerical simulation is carried out in Sect. 5, and finally the conclusions are given in Sect. 6.

2 Local stability and existence of Hopf bifurcation

By solving the following algebraic equation

$$ \textstyle\begin{cases} A-\beta _{1} X^{*}H_{1}^{*}-\mu X^{*}+\alpha Y^{*}=0, \\ \beta _{1} X^{*}H_{1}^{*}-\beta _{2} H_{1}^{*}H_{2}^{*}-(\rho +\mu )H_{1}^{*}=0, \\ \beta _{2} H_{1}^{*}H_{2}^{*}-(d+\varpi +\mu )H_{2}^{*}=0, \\ \varpi H_{2}^{*}-(\alpha +\gamma +\mu )Y^{*}=0, \\ \gamma Y^{*}-\mu Z^{*}=0, \end{cases} $$
(4)

we know that if

$$ R_{0}= \frac{A\beta _{1}\beta _{2}}{(\rho +\mu )[\beta _{1}(d+\varpi +\mu )+\beta _{2}\mu ]}>1, $$

then system (2) has the unique smoking present equilibrium \(E^{*}(X^{*}, H_{1}^{*}, H_{2}^{*}, Y^{*}, Z^{*})\), where

$$\begin{aligned} X^{*} =&\frac{\rho +\mu +\beta _{2} H_{2}^{*}}{\beta _{1}},\qquad H_{1}^{*}= \frac{d+\varpi +\mu }{\beta _{2}}, \\ H_{2}^{*} =&\frac{(\alpha +\mu +\gamma )[A\beta _{1}\beta _{2}-(\rho +\mu ) (\beta _{1}(d+\varpi +\mu )+\beta _{2}\mu )]}{\beta _{1}\beta _{2}\varpi (\mu +\gamma )+\beta _{2}(\alpha +\mu +\gamma )[\beta _{1}(d+\mu )+\beta _{2}\mu ]}, \\ Y^{*} =&\frac{\varpi H_{2}^{*}}{\alpha +\mu +\gamma },\qquad Z^{*}= \frac{\gamma Y^{*}}{\mu }. \end{aligned}$$

The linear equations of system (2) at \(E^{*}(X^{*}, H_{1}^{*}, H_{2}^{*}, Y^{*}, Z^{*})\) take the form

$$ \textstyle\begin{cases} \frac{dX(t)}{dt} = -(\beta _{1}H_{1}^{*}+\mu ) X(t)-\beta _{1}X^{*} H_{1}(t)+ \alpha Y(t), \\ \frac{dH_{1}(t)}{dt} = \beta _{1}H_{1}^{*} X(t)-\beta _{2} H_{1}^{*}H_{2}(t), \\ \frac{dH_{2}(t)}{dt} = \beta _{2} H_{2}^{*}H_{1}(t), \\ \frac{dY(t)}{dt} = \varpi H_{2}(t)-(\alpha +\mu )Y(t)-\gamma Y(t- \tau ), \\ \frac{dZ(t)}{dt} = \gamma Y(t-\tau )-\mu Z(t). \end{cases} $$
(5)

Then the associated characteristic equation of system (5) reads

$$ \mathrm{det} \begin{pmatrix} \lambda +\beta _{1}H_{1}^{*}+\mu & \beta _{1}X^{*} & {0} & -\alpha & {0} \\ -\beta _{1}H_{1}* & \lambda & \beta _{2}H_{1}^{*} & {0} & {0} \\ {0} & -\beta _{2}H_{2}^{*} & \lambda & {0} & {0} \\ {0} & {0} & -\varpi &\lambda +\alpha +\mu +\gamma e^{-\lambda \tau } & {0} \\ {0} & {0} & {0} & -\gamma e^{-\lambda \tau } & \lambda +\mu \end{pmatrix} =0. $$
(6)

It follows from Eq. (6) that

$$ \lambda ^{5}+\mu _{4}\lambda ^{4}+\mu _{3}\lambda ^{3}+\mu _{2} \lambda ^{2}+\mu _{1}\lambda +\mu _{0}+\bigl(\gamma _{4}\lambda ^{4}+ \gamma _{3}\lambda ^{3}+\gamma _{2}\lambda ^{2}+\gamma _{1}\lambda + \gamma _{0} \bigr)e^{-\lambda \tau }=0, $$
(7)

where

$$\begin{aligned}& \mu _{0} = b_{1}b_{2}b_{4}\mu , \qquad \mu _{1}=b_{4}(b_{1}\mu +b_{2}\mu +b_{1}b_{2})+b_{2}b_{3} \mu , \\& \mu _{2} = b_{4}(b_{1}+b_{2}+ \mu )+b_{3}(b_{2}+\mu )+b_{1}b_{2} \mu , \\& \mu _{3} = b_{3}+b_{4}+\mu (b_{1}+b_{2})+b_{1}b_{2}, \qquad \mu _{4}=b_{1}+b_{2}+ \mu , \\& \gamma _{0} = b_{1}b_{4}\mu \gamma ,\qquad \gamma _{1}=b_{4}(b_{1}+\mu ) \gamma +b_{3}\mu \gamma , \\& \gamma _{2} = b_{4}\gamma +b_{3}\gamma +b_{1}\mu \gamma ,\qquad \gamma _{3}=(b_{1}+ \mu )\gamma ,\qquad \gamma _{4}=\gamma , \end{aligned}$$

with

$$ b_{1}=\beta _{1}H_{1}^{*}+\mu ,\qquad b_{2}=\alpha +\mu ,\qquad b_{3}=\beta _{1}^{2}X^{*}H_{1}^{*},\qquad b_{4}=\beta _{2}^{*}H_{1}^{*}H_{2}^{*}. $$

For \(\tau =0\), Eq. (7) becomes

$$ \lambda ^{5}+(\mu _{4}+\gamma _{4})\lambda ^{4}+(\mu _{3}+\gamma _{3}) \lambda ^{3}+(\mu _{2}+\gamma _{2})\lambda ^{2}+(\mu _{1}+\gamma _{1}) \lambda +\mu _{0}+\gamma _{0}=0. $$
(8)

From the expressions of \(\mu _{4}\) and \(\gamma _{4}\), we can obtain

$$ \mu _{4}+\gamma _{4}=b_{1}+b_{2}+ \mu +\gamma =\beta _{1}H_{1}^{*}+2 \mu + \alpha +\gamma >0. $$

Thus, in view of Routh–Hurwitz criteria, if condition \((H_{1})\) Eq. (9)–(12) holds,

$$\begin{aligned}& \mathrm{det}_{1}=\mu _{0}+\gamma _{0}>0, \end{aligned}$$
(9)
$$\begin{aligned}& \mathrm{det}_{2}= \begin{vmatrix} \mu _{4}+\gamma _{4} &{1} \\ \mu _{2}+\gamma _{2} &\mu _{3}+\gamma _{3} \end{vmatrix}>0, \end{aligned}$$
(10)
$$\begin{aligned}& \mathrm{det}_{3}= \begin{vmatrix} \mu _{4}+\gamma _{4} &{1} &{0} \\ \mu _{2}+\gamma _{2} &\mu _{3}+\gamma _{3} &\mu _{4}+\gamma _{4} \\ {0} &\mu _{1}+\gamma _{1} &\mu _{2}+\gamma _{2} \end{vmatrix}>0, \end{aligned}$$
(11)
$$\begin{aligned}& \mathrm{det}_{4}= \begin{vmatrix} \mu _{4}+\gamma _{4} &{1} &{0} &{0} \\ \mu _{2}+\gamma _{2} &\mu _{3}+\gamma _{3} &\mu _{4}+\gamma _{4} &{1} \\ \mu _{0}+\gamma _{0} &\mu _{1}+\gamma _{1} &\mu _{2}+\gamma _{2} &\mu _{3}+\gamma _{3} \\ {0} &{0} &\mu _{0}+\gamma _{0} &\mu _{1}+\gamma _{1} \end{vmatrix}>0, \end{aligned}$$
(12)

then all roots of Eq. (8) have a negative real part.

For \(\tau >0\), let \(\lambda =i\omega _{0}\), \(\tau =\tau _{0}\) in Eq. (7) and still denote \(\omega _{0}\) and \(\tau _{0}\) by ω and τ, respectively. Then we obtain

$$ \textstyle\begin{cases} (\gamma _{1}\omega -\gamma _{3}\omega ^{3})\sin \tau \omega +(\gamma _{4} \omega ^{4}-\gamma _{2}\omega ^{2}+\gamma _{0})\cos \tau \omega =\mu _{2} \omega ^{2}-\mu _{4}\omega ^{4}-\mu _{0}, \\ (\gamma _{1}\omega -\gamma _{3}\omega ^{3})\cos \tau \omega -(\gamma _{4} \omega ^{4}-\gamma _{2}\omega ^{2}+\gamma _{0})\sin \tau \omega =\mu _{3} \omega ^{3}-\omega ^{5}-\mu _{1}\omega , \end{cases} $$
(13)

which leads to

$$ \omega ^{10}+\gamma _{04}\omega ^{8}+\gamma _{03}\omega ^{6}+\gamma _{02} \omega ^{4}+\gamma _{01}\omega ^{2}+\gamma _{00}=0, $$
(14)

with

$$\begin{aligned}& \gamma _{00} = \mu _{0}^{2}-\gamma _{0}^{2}, \\& \gamma _{01} = \mu _{1}^{2}-2\mu _{0}\mu _{2}-\gamma _{1}^{2}+2 \gamma _{0}\gamma _{2}, \\& \gamma _{02} = \mu ^{2}-2\mu _{1}\mu _{3}+2\mu _{0}\mu _{4}+2\gamma _{1} \gamma _{3}-\gamma _{2}^{2}-2 \gamma _{0}\gamma _{4}, \\& \gamma _{03} = \mu _{3}^{2}+2\mu _{1}-2\mu _{2}\mu _{4}-\gamma _{3}^{2}+2 \gamma _{2}\gamma _{4}, \\& \gamma _{04} = \mu _{4}^{2}-2\mu _{3}-\gamma _{4}^{2}. \end{aligned}$$

Let \(\omega ^{2}=\chi \), then Eq. (14) is equivalent to

$$ \chi ^{5}+\gamma _{04}\chi ^{4}+\gamma _{03}\chi ^{3}+\gamma _{02} \chi ^{2}+\gamma _{01}\chi +\gamma _{00}=0. $$
(15)

In what follows, we present some lemmas to establish the distribution of Eq. (15) based on the discussion about the distribution of the roots of Eq. (15) in [34].

Lemma 1

If\(\gamma _{00}<0\), then Eq. (15) has at least one positive root.

Let

$$ L(\chi )=\chi ^{5}+\gamma _{04}\chi ^{4}+\gamma _{03}\chi ^{3}+ \gamma _{02}\chi ^{2}+\gamma _{01}\chi +\gamma _{00}. $$
(16)

Then

$$ L^{\prime }(\chi )=5\chi ^{4}+4\gamma _{04}\chi ^{3}+3\gamma _{03}\chi ^{2}+2 \gamma _{02}\chi +\gamma _{01}. $$
(17)

Denote

$$ 5\chi ^{4}+4\gamma _{04}\chi ^{3}+3\gamma _{03}\chi ^{2}+2\gamma _{02} \chi +\gamma _{01}=0. $$
(18)

Let \(\chi =y-\frac{\gamma _{04}}{5}\). Then Eq. (18) becomes

$$ y^{4}+\varPhi _{2}y^{2}+\varPhi _{1}y+\varPhi _{0}=0, $$
(19)

where

$$\begin{aligned}& \varPhi _{0} = -\frac{3}{625}\gamma _{04}^{4}+ \frac{3}{125}\gamma _{04}^{2} \gamma _{03}-\frac{2}{25}\gamma _{04}\gamma _{02}+\frac{1}{5}\gamma _{01}, \\& \varPhi _{1} = \frac{8}{125}\gamma _{04}^{3}+ \frac{6}{25}\gamma _{04} \gamma _{03}+ \frac{2}{3}\gamma _{02}, \\& \varPhi _{2} = -\frac{6}{25}\gamma _{04}^{2}+ \frac{3}{5}\gamma _{03}. \end{aligned}$$

If \(\varPhi _{1}=0\), then we obtain four roots of Eq. (19) as follows:

$$\begin{aligned}& y_{1} = \sqrt{\frac{-\varPhi _{2}+\sqrt{\varTheta _{0}}}{2}},\qquad y_{2}=-\sqrt{ \frac{-\varPhi _{2}+\sqrt{\varTheta _{0}}}{2}}, \\& y_{3} = \sqrt{\frac{-\varPhi _{2}-\sqrt{\varTheta _{0}}}{2}},\qquad y_{2}=-\sqrt{ \frac{-\varPhi _{2}-\sqrt{\varTheta _{0}}}{2}}, \end{aligned}$$

where \(\varTheta _{0}=\varPhi _{2}^{2}-4\varPhi -0\). Thus, \(\chi _{j}=y_{j}-\frac{\gamma _{04}}{5}\) (\(j=1, 2, 3, 4\)) are the roots of Eq. (18). Then we have the following lemma.

Lemma 2

Assume that\(\gamma _{00}\geq 0\)and\(\varPhi _{1}=0\).

  1. (i)

    If\(\varTheta _{0}<0\), then Eq. (15) has no positive roots;

  2. (ii)

    If\(\varTheta _{0}\geq 0\), \(\varPhi _{2}\geq 0\), and\(\varPhi _{0}>0\), then Eq. (15) has no positive roots;

  3. (iii)

    If (i) and (ii) are not satisfied, then Eq. (15) has positive roots if and only if there exists at least one\(\chi _{*}\in \{\chi _{1}, \chi _{2}, \chi _{3}, \chi _{4}\}\)such that\(\chi _{*}>0\)and\(L(\chi _{*})\leq 0\).

In what follows, we suppose that \(\varPhi _{1}\neq 0\) and consider the resolvent of Eq. (19)

$$ \varPhi _{1}^{2}-4(S-\varPhi _{2}) \biggl(\frac{S^{2}}{4}-\varPhi _{0} \biggr)=0, $$
(20)

which equals to

$$ S^{3}-\varPhi _{2}S^{2}-4\varPhi _{0}S_{1}+4\varPhi _{2}\varPhi _{0}- \varPhi _{1}^{2}=0. $$
(21)

Define

$$\begin{aligned}& \varGamma _{1} = \frac{1}{3}\varPhi _{2}^{2}-4 \varPhi _{0},\qquad \varUpsilon _{1}=- \frac{2}{27}\varPhi _{2}^{3}+\frac{8}{3}\varPhi _{2}\varPhi _{0}-\varPhi _{1}^{2}, \\& \varTheta _{1} = \frac{1}{27}\varGamma _{1}^{3}+ \frac{1}{4}\varUpsilon _{1}^{2},\qquad \varPsi _{1}=\frac{1}{2}+\frac{\sqrt{3}}{2}i. \end{aligned}$$

By the Cardan formula, Eq. (19) has roots:

$$\begin{aligned}& S_{1} = \sqrt[3]{-\frac{\varGamma _{1}}{2}+\sqrt{\varTheta _{1}}}+ \sqrt[3]{-\frac{\varGamma _{1}}{2}-\sqrt{\varTheta _{1}}}+ \frac{\varPhi _{2}}{3}, \\& S_{2} = \varPsi _{1}\sqrt[3]{-\frac{\varGamma _{1}}{2}+\sqrt{ \varTheta _{1}}}+ \varPsi _{1}^{2}\sqrt[3]{- \frac{\varGamma _{1}}{2}-\sqrt{\varTheta _{1}}}+ \frac{\varPhi _{2}}{3}, \\& S_{3} = \varPsi _{1}^{2} \sqrt[3]{- \frac{\varGamma _{1}}{2}+\sqrt{\varTheta _{1}}}+\varPsi _{1} \sqrt[3]{-\frac{\varGamma _{1}}{2}-\sqrt{\varTheta _{1}}}+ \frac{\varPhi _{2}}{3}. \end{aligned}$$

Let \(S_{*}=S_{1}\neq \varPhi _{2}\). Then Eq. (19) becomes

$$ y^{4}+S_{*}y^{2}+ \frac{S_{*}^{2}}{4}- \biggl[(S_{*}-\varPhi _{2})y^{2}- \varPhi _{1}y+\frac{S_{*}^{2}}{4}-\varPhi _{0} \biggr]=0. $$
(22)

If \(S_{*}>\varPhi _{2}\), then Eq. (22) is

$$ \biggl(y^{2}+\frac{S_{*}}{2} \biggr)^{2}- \biggl(\sqrt{S_{*}-\varPhi _{2}y}- \frac{\varPhi _{1}}{2\sqrt{S_{*}-\varPhi _{2}}} \biggr)^{2}=0. $$
(23)

After factorization, then

$$ y^{2}+\sqrt{S_{*}-\varPhi _{2}y}-\frac{\varPhi _{1}}{S_{*}-\varPhi _{2}}+ \frac{S_{*}}{2}=0 $$
(24)

and

$$ y^{2}-\sqrt{S_{*}-\varPhi _{2}y}+\frac{\varPhi _{1}}{S_{*}-\varPhi _{2}}+ \frac{S_{*}}{2}=0. $$
(25)

Denote

$$ \varTheta _{2}=-S_{*}-\varPhi _{2}+ \frac{2\varPhi _{1}}{\sqrt{S_{*}-\varPhi _{2}}}, \qquad \varTheta _{3}=-S_{*}-\varPhi _{2}- \frac{2\varPhi _{1}}{\sqrt{S_{*}-\varPhi _{2}}}. $$

Thus, we obtain the roots of Eq. (19):

$$\begin{aligned}& y_{1} = \frac{-\sqrt{S_{*}-\varPhi _{2}}+\sqrt{\varTheta _{2}}}{2},\qquad y_{2}= \frac{-\sqrt{S_{*}-\varPhi _{2}}-\sqrt{\varTheta _{2}}}{2}, \\& y_{3} = \frac{\sqrt{S_{*}-\varPhi _{2}}+\sqrt{\varTheta _{3}}}{2},\qquad y_{4}= \frac{\sqrt{S_{*}-\varPhi _{2}}-\sqrt{\varTheta _{3}}}{2}. \end{aligned}$$

Then \(\chi _{i}=y_{i}-\frac{\gamma _{04}}{5}\) (\(i=1, 2, 3, 4\)) are the roots of Eq. (18). Therefore, we have the following lemma.

Lemma 3

Suppose that\(\gamma _{00}\geq 0\)and\(S_{*}>\varPhi _{2}\).

  1. (i)

    If\(\varTheta _{2}<0\)and\(\varTheta _{3}<0\), then Eq. (15) has no positive roots;

  2. (ii)

    If (i) is not satisfied, then Eq. (15) has positive roots if and only if there exists at least one\(\chi _{*}\in \{\chi _{1}, \chi _{2}, \chi _{3}, \chi _{4}\}\)such that\(\chi _{*}>0\)and\(L(\chi _{*})\leq 0\).

At last, if \(S_{*}<\varPhi _{2}\), then Eq. (22) is

$$ \biggl(y^{2}+\frac{S_{*}}{2} \biggr)^{2}- \biggl(\sqrt{\varPhi _{2}-S_{*}y}- \frac{\varPhi _{1}}{2\sqrt{\varPhi _{2}-S_{*}}} \biggr)^{2}=0. $$
(26)

Let \(\bar{\chi }=\frac{\varPhi _{1}}{\varPhi _{2}-S_{*}}-\frac{\gamma _{04}}{5}\). Thus, we have the following lemma.

Lemma 4

Suppose that\(\gamma _{00}\geq 0\), \(\varPhi _{1}\neq 0\), and\(S_{*}<\varPhi _{2}\). Then Eq. (15) has positive roots if and only if\(\frac{\varPhi _{1}^{2}}{4(\varPhi _{2}-S_{*})^{2}}+\frac{S_{*}}{2}=0\)and\(\bar{\chi }>0\), \(L(\bar{\chi })\leq 0\).

Next, we suppose that the coefficients in Eq. (15) satisfy one of the conditions in \((H_{2})\).

\((H_{2})\):

(a) \(\gamma _{00}<0\); (b) \(\gamma _{00}\geq 0\), \(\varPhi _{1}=0\), and \(\varPhi _{2}<0\) or \(\varPhi _{0}>0\), and there exists at least one \(\chi _{*}\in \{\chi _{1}, \chi _{2}, \chi _{3}, \chi _{4}\}\) such that \(\chi _{*}>0\) and \(L(\chi _{*})\leq 0\); (c) \(\gamma _{00}\geq 0\), \(\varPhi _{1}\neq 0\), \(S_{*}>\varPhi _{2}\), \(\varTheta _{2}\geq 0\), or \(\varTheta _{3}\geq 0\), and there exists at least one \(\chi _{*}\in \{\chi _{1}, \chi _{2}, \chi _{3}, \chi _{4}\}\) such that \(\chi _{*}>0\) and \(L(\chi _{*})\leq 0\); (d) \(\gamma _{00}\geq 0\), \(\varPhi _{1}\neq 0\), \(S_{*}<\varPhi _{2}\), \(\frac{\varPhi _{1}^{2}}{4(\varPhi _{2}-S_{*})^{2}}+\frac{S_{*}}{2}=0\), and \(\bar{\chi }>0\), \(L(\bar{\chi })\leq 0\).

Without loss of generality, we assume that Eq. (15) has five positive roots \(\omega _{s}\), (\(s=1, 2, \ldots , 5\)). It follows from Eq. (13) that

$$ \tau _{s}^{(j)}=\frac{1}{\omega _{s}} \times \arccos \biggl\{ \frac{S_{1}(\omega _{s})}{S_{2}(\omega _{s})}+2j\pi \biggr\} , $$
(27)

where \(s=1, 2, \ldots , 5\) and \(j =0, 1, 2, \ldots \) , and

$$\begin{aligned}& \begin{aligned} S_{1}(\omega _{s})&=(\gamma _{3}-\mu _{4}\gamma _{4})\omega _{s}^{8}+( \mu _{2}\gamma _{4}-\gamma _{1}-\mu _{3}\gamma _{3}+\mu _{4}\gamma _{2}) \omega _{s}^{6} \\ &\quad {}+(\mu _{3}\gamma _{1}+\mu _{1}\gamma _{3}-\mu _{0}\gamma _{4}-\mu _{2} \gamma _{2}-\mu _{4}\gamma _{0})\omega _{s}^{4} \\ &\quad {}+(\mu _{0}\gamma _{2}+\mu _{2}\gamma -0- \mu _{1}\gamma _{1})\omega _{s}^{2}- \mu _{0}\gamma _{0}, \end{aligned} \\& \begin{aligned} S_{2}(\omega _{s})&=\gamma _{4}\omega _{s}^{8}+\bigl(\gamma _{3}^{2}-2 \gamma _{2}\gamma _{4}\bigr)\omega _{s}^{6}+ \bigl(\gamma _{2}^{2}+2\gamma -0 \gamma _{4}-2 \gamma _{1}\gamma _{3}\bigr)\omega _{s}^{4} \\ &\quad {}+\bigl(\gamma _{1}^{2}-2\gamma _{0} \gamma _{2}\bigr)\omega _{s}^{2}+\gamma _{0}^{2}. \end{aligned} \end{aligned}$$

Define

$$ \tau _{0}=\min\bigl\{ \tau _{s}^{(0)}\bigr\} , \quad s=1, 2, \ldots , 5, $$
(28)

and when \(\tau =\tau _{0}\), Eq. (7) has a pair of purely imaginary roots \(\pm i\omega _{0}\). Then one has

$$\begin{aligned} \biggl[\frac{d\lambda }{d\tau } \biggr]^{-1} =&- \frac{5\lambda ^{4}+4\mu _{4}\lambda ^{3}+3\mu _{3}\lambda ^{2}+2\mu _{2}\lambda +\mu _{1}}{\lambda (\lambda ^{5}+\mu _{4}\lambda ^{4}+\mu _{3}\lambda ^{3}+\mu _{2}\lambda ^{2}+\mu _{1}\lambda +\mu _{0})} \\ &{}+ \frac{4\gamma _{4}\lambda ^{3}+3\gamma _{3}\lambda ^{2} +2\gamma _{2}\lambda +\gamma _{1}}{\lambda (\gamma _{4}\lambda ^{4} +\gamma _{3}\lambda ^{3}+\gamma _{2}\lambda ^{2}+\gamma _{1}\lambda +\gamma _{0})}- \frac{\tau }{\lambda }. \end{aligned}$$
(29)

Thus,

$$ \operatorname{Re} \biggl[\frac{d\lambda }{d\tau } \biggr]^{-1}_{\tau =\tau _{0}}= \frac{f^{\prime }(\chi _{0})}{S_{2}(\omega _{0})}, $$
(30)

where \(f(\chi )=\chi ^{5}+\gamma _{04}\chi ^{4}+\gamma _{03}\chi ^{3}+ \gamma _{02}\chi ^{2}+\gamma _{01}\chi +\gamma _{00}\) and \(\chi _{0}=\omega _{0}^{2}\).

Now we make the assumption as follows: \((H_{3})\)\(f^{\prime }(\chi _{0})\neq 0\). Under condition \((H_{3})\), then \(\operatorname{Re}[d\lambda /d\tau ]^{-1}_{\tau =\tau _{0}}\neq 0\). In conclusion, we have the following results.

Theorem 1

For system (2), if\(R_{0}>1\)and conditions\((H_{1})\)–\((H_{3})\)hold, then the smoking present equilibrium point\(E^{*}(X^{*}, H_{1}^{*}, H_{2}^{*}, Y^{*}, Z^{*})\)is locally asymptotically stable when\(\tau \in [0, \tau _{0})\); system (2) undergoes a Hopf bifurcation at\(E^{*}(X^{*}, H_{1}^{*}, H_{2}^{*}, Y^{*}, Z^{*})\)when\(\tau =\tau _{0}\)and a family of periodic solutions bifurcate from\(E^{*}(X^{*}, H_{1}^{*}, H_{2}^{*}, Y^{*}, Z^{*})\).

3 Direction and stability of Hopf bifurcation

Let \(t=s\tau \), \(v_{1}(t)=X(t)-X^{*}\), \(v_{2}(t)=H_{1}(t)-H_{1}^{*}\), \(v_{3}(t)=H_{2}(t)-H_{2}^{*}\), \(v_{4}(t)=Y(t)-Y^{*}\), \(v_{5}(t)=Z(t)-Z^{*}\), and \(\tau =\tau _{0}+\varrho \), \(\varrho \in R\). Then system (2) becomes

$$ \dot{v}(t)=L_{\varrho }v_{t}+F(\varrho , v_{t}), $$
(31)

where \(v_{t}=(v_{1}(t), v_{2}(t), v_{3}(t), v_{4}(t), v_{5}(t))^{T}=(X, H_{1}, H_{2}, Y, Z)^{T} \in R^{5}\), \(v_{t}(\theta )=v(t+\theta )\in C=C([-1, 0], R^{5})\), and \(L_{\varrho }\): \(C\rightarrow R^{5}\), \(F(\varrho , u_{t})\rightarrow R^{5}\) are defined respectively as follows:

$$ L_{\varrho }\phi =(\tau _{0}+\varrho ) \bigl(P\phi (0)+Q\phi (-1)\bigr) $$
(32)

and

$$ F(\varrho , \phi )= \begin{pmatrix} -\beta _{1}\phi _{1}(0)\phi _{2}(0) \\ \beta _{1}\phi _{1}(0)\phi _{2}(0)-\beta _{2}\phi _{2}(0)\phi _{3}(0) \\ \beta _{2}\phi _{2}(0)\phi _{3}(0) \\ {0} \\ {0} \end{pmatrix}, $$
(33)

with

$$\begin{aligned}& P= \begin{pmatrix} -(\beta _{1}H_{1}^{*}+\mu ) &-\beta _{1}X^{*} &{0} &\alpha &{0} \\ \beta _{1}H_{1}^{*} &{0} &-\beta _{2}H_{1}^{*} &{0} &{0} \\ {0} &\beta _{2}H_{2}^{*} &{0} &{0} &{0} \\ {0} &{0} &\varpi &-(\alpha +\mu ) &{0} \\ {0} &{0} &{0} &{0} &-\mu \end{pmatrix}, \\& Q= \begin{pmatrix} {0} &{0} &{0} &{0} &{0} \\ {0} &{0} &{0} &{0} &{0} \\ {0} &{0} &{0} &{0} &{0} \\ {0} &{0} &{0} &-\gamma &{0} \\ {0} &{0} &{0} &\gamma &{0} \end{pmatrix}. \end{aligned}$$

By the Riesz representation theorem, there exists a matrix \(\eta (\theta , \varrho )\) such that

$$ L_{\varrho }\phi = \int _{-1}^{0}d\eta (\theta , \varrho )\phi ( \theta ). $$
(34)

In fact, choosing

$$ \eta (\theta , \varrho )=(\tau _{0}+\varrho )P \delta (\theta )+Q \delta (\theta +1)), $$
(35)

where \(\delta (\theta )\) is Dirac function, then Eq. (34) is fulfilled.

For \(\phi \in C([-1,0], R^{5})\), define

$$ A(\varrho )\phi = \textstyle\begin{cases} \frac{d\phi (\theta )}{d\theta },& {-}1\leq \theta < 0, \\ \int _{-1}^{0}d\eta (\theta ,\varrho )\phi (\theta ),& \theta =0, \end{cases} $$

and

$$ R(\varrho )\phi = \textstyle\begin{cases} 0,& {-}1\leq \theta < 0, \\ F(\varrho ,\phi ),& \theta =0. \end{cases} $$

Then system (31) is equivalent to

$$ \dot{v}(t)=A(\varrho )v_{t}+R(\varrho )v_{t}. $$
(36)

For \(\varphi \in C^{1}([0, 1], (R^{5})^{*})\), define

$$ A^{*}(\varphi )= \textstyle\begin{cases} -\frac{d\varphi (s)}{ds},& 0< s\leq 1, \\ \int _{-1}^{0}d{\eta }^{T}(s,0)\varphi (-s),& s=0. \end{cases} $$

For \(\phi \in C([-1,0], R^{5})\) and \(\varphi \in C^{1}([0, 1], (R^{5})^{*})\), define

$$ \bigl\langle \varphi (s),\phi (\theta )\bigr\rangle =\bar{ \varphi }(0)\phi (0)- \int _{\theta =-1}^{0} \int _{\xi =0}^{\theta }\bar{\varphi }(\xi - \theta )\, d\eta (\theta )\phi (\xi )\, d\xi , $$
(37)

where \(\eta (\theta )=\eta (\theta , 0)\).

Define the vector \(\rho (\theta )=(1, \rho _{2}, \rho _{3}, \rho _{4}, \rho _{5})^{T}e^{i \omega _{0}\tau _{0}\theta }\), \(\theta \in [-1, 0]\), is the eigenvector of \(A(0)\) corresponding to \(+i\omega _{0}\tau _{0}\), and \(\rho ^{*}(s)=D(1, \rho _{2}^{*}, \rho _{3}^{*}, \rho _{4}^{*}, \rho _{5}^{*})e^{i \omega _{0}\tau _{0}s}\), \(s\in [0, 1]\), is the eigenvector of \(A^{*}\) corresponding to \(-i\omega _{0}\tau _{0}\). By computations, one has

$$\begin{aligned}& \rho _{2} = - \frac{i\omega _{0}+\beta _{1}H_{1}^{*}+\mu }{\beta _{1}X^{*}},\qquad \rho _{3}=- \frac{i\omega _{0}\rho _{2}-\beta _{1}H_{1}^{*}}{\beta _{2}H_{1}^{*}}, \\& \rho _{4} = \frac{\varpi \rho _{3}}{i\omega _{0}+\alpha +\mu +\gamma e^{-i\omega _{0}\tau _{0}}},\qquad \rho _{5}= \frac{\gamma e^{-i\omega _{0}\tau _{0}}}{i\omega _{0}+\mu }, \\& \rho _{2}^{*} = - \frac{i\omega _{0}-\beta _{1}H_{1}^{*}-\mu }{\beta _{1}H_{1}^{*}},\qquad \rho _{3}^{*}= \frac{\beta _{1}X^{*}}{i\omega _{0}+\beta _{2}H_{2}^{*}}, \\& \rho _{4}^{*} = \frac{\beta _{2}H_{1}^{*}\rho _{2}^{*}-i\omega _{0}\rho _{3}^{*}}{\varpi },\qquad \rho _{5}^{*}=- \frac{\gamma e^{i\omega _{0}\tau _{0}}\rho _{4}^{*}}{i\omega _{0}-\alpha -\mu -\gamma e^{i\omega _{0}\tau _{0}}}. \end{aligned}$$

Furthermore, we have

$$ \bar{D}=\bigl[1+\rho _{2}\bar{\rho }_{2}^{*}+\rho _{3}\bar{\rho }_{3}^{*}+ \rho _{4}\bar{\rho }_{4}^{*}+\rho _{5}\bar{\rho }_{5}^{*}+\tau _{0}e^{-i \omega _{0}\tau _{0}}\gamma \rho _{4}\bigl(\bar{\rho }_{5}^{*}-\bar{\rho }_{4}^{*}\bigr)\bigr]^{-1}, $$
(38)

which leads to \(\langle \rho ^{*}, \rho \rangle =1\) and \(\langle \rho ^{*}, \bar{\rho }\rangle =0\).

Next, based on the algorithms in [35] and the similar computation process as that in [36–38], we obtain

$$\begin{aligned}& g_{20} = 2\tau _{0}\bar{D}\bigl[\bigl(\bar{\rho }_{2}^{*}-1\bigr)\beta _{1}\rho _{2}+\bigl( \bar{\rho }_{3}^{*}-\bar{\rho }_{2}^{*}\bigr)\beta _{2}\rho _{2}\rho _{3}\bigr], \\& g_{11} = \tau _{0}\bar{D}\bigl[\bigl(\bar{\rho }_{2}^{*}-1\bigr)\beta _{1}(\rho _{2}+ \bar{\rho }_{2})+\bigl(\bar{\rho }_{3}^{*}-\bar{\rho }_{2}^{*} \bigr) (\rho _{2} \bar{\rho }_{3}+\bar{\rho }_{2}\rho _{3})\bigr], \\& g_{02} = 2\tau _{0}\bar{D}\bigl[\bigl(\bar{\rho }_{2}^{*}-1\bigr)\beta _{1}\bar{\rho }_{2}+\bigl( \bar{\rho }_{3}^{*}-\bar{\rho }_{2}^{*}\bigr)\beta _{2}\bar{\rho }_{2} \bar{\rho }_{3}\bigr], \\& \begin{aligned} g_{21} &= 2\tau _{0}\bar{D} \biggl\{ \bigl(\bar{\rho }_{2}^{*}-1\bigr)\beta _{1} \biggl[W_{11}^{(1)}(0)\rho _{2}+ \frac{1}{2}W_{11}^{(1)}(0)\bar{\rho }_{2}+W_{11}^{(2)}(0)+ \frac{1}{2}W_{20}^{(2)}(0) \biggr] \\ &\quad {} +\bigl(\bar{\rho }_{3}^{*}-\bar{\rho }_{2}^{*}\bigr)\beta _{2} \biggl[W_{11}^{(2)}(0) \rho _{3}+ \frac{1}{2}W_{11}^{(2)}(0)\bar{\rho }_{3}+W_{11}^{(3)}(0) \rho _{2}+ \frac{1}{2}W_{20}^{(3)}(0)\bar{\rho }_{2} \biggr] \biggr\} , \end{aligned} \end{aligned}$$

where

$$\begin{aligned}& W_{20}(\theta ) = \frac{ig_{20}\rho (0)}{\tau _{0}\omega _{0}}e^{i \tau _{0}\omega _{0}\theta }+ \frac{i\bar{g}_{02}\bar{\rho }(0)}{3\tau _{0}\omega _{0}}e^{-i\tau _{0} \omega _{0}\theta }+E_{1}e^{2i\tau _{0}\omega _{0}\theta }, \\& W_{11}(\theta ) = -\frac{ig_{11}\rho (0)}{\tau _{0}\omega _{0}}e^{i \tau _{0}\omega _{0}\theta }+ \frac{i\bar{g}_{11}\bar{\rho }(0)}{\tau _{0}\omega _{0}}e^{-i\tau _{0} \omega _{0}\theta }+E_{2} \end{aligned}$$

with

$$\begin{aligned}& \begin{aligned} E_{1}&=2 \begin{pmatrix} 2i\omega _{0}+\beta _{1}H_{1}^{*}+\mu &\beta _{1}X^{*} &0 &-\alpha &{0} \\ -\beta _{1}H_{1}^{*} &2i\omega _{0} &\beta _{2}H_{1}^{*} &{0} &{0} \\ {0} &-\beta _{2}H_{2}^{*} & 2i\omega _{0} &{0} &{0} \\ {0} &{0} &-\varpi &2i\omega _{0}+\alpha +\mu +\gamma e^{-2i\omega _{0}\tau _{0}} &{0} \\ {0} &{0} &{0} &-\gamma e^{-2i\omega _{0}\tau _{0}} &2i\omega _{0}+\mu \end{pmatrix}^{-1} \\ &\quad {}\times \begin{pmatrix} -\beta _{1}\rho _{2} \\ \beta _{1}\rho _{2}-\beta _{2}\rho _{2}\rho _{3} \\ \beta _{2}\rho _{2}\rho _{3} \\ {0} \\ {0} \end{pmatrix}, \end{aligned} \\& \begin{aligned} E_{2}&=- \begin{pmatrix} -(\beta _{1}H_{1}^{*}+\mu ) &-\beta _{1}X^{*} &{0} &\alpha &{0} \\ \beta _{1}H_{1}^{*} &{0}& -\beta _{2}H_{1}^{*} &{0} &{0} \\ {0} &\beta _{2}H_{2}^{*} &{0} &{0} &{0} \\ {0} &{0} &\varpi &-(\alpha +\mu +\gamma ) &{0} \\ {0} &{0} &{0} &\gamma &-\mu \end{pmatrix}^{-1} \\ &\quad {}\times \begin{pmatrix} -\beta _{1}(\rho _{2}+\bar{\rho }_{2}) \\ \beta _{1}(\rho _{2}+\bar{\rho }_{2})-\beta _{2}(\rho _{2}\bar{\rho }_{3}+ \bar{\rho }_{2}\rho _{3}) \\ \beta _{2}(\rho _{2}\bar{\rho }_{3}+\bar{\rho }_{2}\rho _{3}) \\ {0} \\ {0} \end{pmatrix}. \end{aligned} \end{aligned}$$

Thus, one has

$$\begin{aligned}& C_{1}(0)= \frac{i}{2\tau _{0}\omega _{0}} \biggl(g_{11}g_{20}-2 \vert g_{11} \vert ^{2}- \frac{ \vert g_{02} \vert ^{2}}{3} \biggr)+ \frac{g_{21}}{2} \\& \mu _{2} =- \frac{\operatorname{Re}\{C_{1}(0)\}}{\operatorname{Re}\{\lambda '(\tau _{0})\}}, \\& \beta _{2}=2\operatorname{Re}\bigl\{ C_{1}(0)\bigr\} , \\& T_{2}=- \frac{\operatorname{Im}\{C_{1}(0)\}+\mu _{2}\operatorname{Im} \{\lambda '(\tau _{0})\}}{\tau _{0}\omega _{0}}. \end{aligned}$$
(39)

In conclusion, we have the following results.

Theorem 2

For system (2), if\(\mu _{2}>0\) (\(\mu _{2}<0\)), then the Hopf bifurcation is supercritical (subcritical); if\(\beta _{2}<0\) (\(\beta _{2}>0\)), then the bifurcating periodic solutions are stable (unstable); if\(T_{2}>0\) (\(T_{2}<0\)), then the period of the bifurcating periodic solutions increases (decreases).

4 Global stability criteria

Theorem 3

Suppose that there exist positive definite symmetric matrices\(J_{i}>0\), \(i=1,2,3,4,5\), \(P_{i}>0\), \(i=1,\ldots,8\)\(L^{*}>0\), and scalars\(\mu _{i}>0\), \(i=1,2,\ldots,8\), such that

whererepresents symmetric term in a symmetric matrix andIis the identity matrix with appropriate dimension. Then the endemic equilibrium\(E^{*} ( X^{*},H^{*}_{1},H^{*}_{2},Y^{*},Z^{*} )\)of model (5) is globally exponentially stable.

Proof

Consider the following Lyapunov functional:

$$\begin{aligned} V(t) =& X^{T}(t)J_{1} X(t) + H_{1}^{T}(t)J_{2} H_{1}(t)+H_{2}^{T}(t)J_{3} H_{2}(t) +Y^{T}(t)J_{4} Y(t)+Z^{T}(t)J_{5} Z(t) \\ &{}+\gamma (\mu _{7}+\mu _{8}) \int ^{t}_{t-\tau }Y^{T}(\omega )Y( \omega )\,d\omega +\frac{1}{\tau } \int ^{0}_{-\tau } \int ^{t}_{t+ \omega }Y^{T}(\kappa )L^{*}Y(\kappa ) \,d\kappa \,d\omega . \end{aligned}$$
(40)

Then the time derivative of \(V(t)\) along the trajectories of system (5) yields

$$\begin{aligned} \dot{V}(t) =& 2 \bigl[X^{T}(t)J_{1} \bigl(-\bigl(\beta _{1}H_{1}^{*}+\mu \bigr) X(t)- \beta _{1}X^{*} H_{1}(t)+\alpha Y(t) \bigr) \\ &{}+H_{1}^{T}(t)J_{2} \bigl( \beta _{1}H_{1}^{*} X(t)-\beta _{2} H_{1}^{*}H_{2}(t) \bigr) +H_{2}^{T}(t)J_{3} \bigl(\beta _{2} H_{2}^{*}H_{1}(t) \bigr) \\ &{}+Y^{T}(t)J_{4} \bigl( \varpi H_{2}(t)-( \alpha +\mu )Y(t)- \gamma Y(t-\tau ) \bigr) +Z^{T}(t)J_{4} \bigl(\gamma Y(t-\tau )-\mu Z(t) \bigr) \bigr] \\ &{}+\gamma (\mu _{7}+\mu _{8})Y^{T}(t) Y(t)-\gamma (\mu _{7}+ \mu _{8})Y^{T}(t- \tau ) Y(t-\tau )+Y^{T}(t)L^{*} Y(t) \\ &{}-\frac{1}{\tau } \int ^{t}_{t-\tau }Y^{T}(\omega )L^{*}Y(\omega ) \,d\omega \\ \leq & -2 \bigl(\beta _{1}H_{1}^{*}+\mu \bigr)X^{T}(t)J_{1}X(t)-2(\alpha +\mu )Y^{T}(t)J_{4} Y(t)-2\mu Z^{T}(t)J_{5} Z(t) \\ &{}+\beta _{1}X^{*} \bigl[\mu ^{-1}_{1}X^{T}(t)J_{1}J^{T}_{1} X(t)+ \mu _{1} H_{1}^{T}(t) H_{1}(t) \bigr] \\ &{}+\alpha \bigl[\mu ^{-1}_{2}X^{T}(t)J_{1}J^{T}_{1} X(t)+\mu _{2} Y^{T}(t) Y(t) \bigr] \\ &{}+\beta _{1}H_{1}^{*} \bigl[\mu ^{-1}_{3} H_{1}^{T}(t)J_{2}J^{T}_{2} H_{1}(t)+\mu _{3} X^{T}(t) X(t) \bigr] \\ &{}+ \beta _{2}H_{1}^{*} \bigl[\mu ^{-1}_{4} H_{1}^{T}(t)J_{2}J^{T}_{2} H_{1}(t)+\mu _{4} H_{2}^{T}(t) H_{2}(t) \bigr] \\ &{}+\beta _{2}H_{2}^{*} \bigl[ \mu ^{-1}_{5} H_{2}^{T}(t)J_{3}J^{T}_{3} H_{2}(t) +\mu _{5} H_{1}^{T}(t) H_{1}(t) \bigr] \\ &{}+\varpi \bigl[\mu ^{-1}_{6} Y^{T}(t)J_{4}J^{T}_{4} Y(t)+\mu _{6} H_{2}^{T}(t) H_{2}(t) \bigr] \\ &{}+\gamma \bigl[\mu ^{-1}_{7} Y^{T}(t)J_{4}J^{T}_{4} Y(t)+\mu _{7} Y^{T}(t-\tau ) Y(t-\tau ) \bigr] \\ &{}+ \gamma \bigl[\mu ^{-1}_{8} Z^{T}(t)J_{5}J^{T}_{5} Z(t)+\mu _{8} Y^{T}(t-\tau ) Y(t-\tau ) \bigr] \\ &{}+\gamma ( \mu _{7}+ \mu _{8})Y^{T}(t) Y(t)-\gamma (\mu _{7}+\mu _{8})Y^{T}(t-\tau ) Y(t- \tau ) \\ &{}+Y^{T}(t)L^{*} Y(t) -\frac{1}{\tau } \int ^{t}_{t-\tau }Y^{T}( \omega )L^{*}Y(\omega )\,d\omega \\ =&X^{T}(t)\varPsi _{1} X(t) + H_{1}^{T}(t) \varPsi _{2} H_{1}(t)+H_{2}^{T}(t) \varPsi _{3} H_{2}(t) +Y^{T}(t)\varPsi _{4} Y(t)+Z^{T}(t)\varPsi _{5} Z(t) \\ &{}-\frac{1}{\tau } \int ^{t}_{t-\tau }Y^{T}(\omega )L^{*}Y(\omega ) \,d\omega . \end{aligned}$$
(41)

It follows from \(\varPsi _{i}<0\), \(i=1,\ldots,5\), that there exists a sufficiently small constant \(0<\delta \leq \tau ^{-1}\) such that

$$\begin{aligned} \varPi =& \max \bigl\{ \lambda _{M} (\varPsi _{1} ), \lambda _{M} (\varPsi _{2} ), \lambda _{M} (\varPsi _{3} ), \lambda _{M} (\varPsi _{4} )+\gamma ( \mu _{7}+\mu _{8} )\delta \tau e^{ \delta \tau }, \lambda _{M} (\varPsi _{5} ) \bigr\} \\ &{}+\delta \max \bigl\{ \lambda _{M} (J_{1} ), \lambda _{M} (J_{2} ), \lambda _{M} (J_{3} ), \lambda _{M} (J_{4} ), \lambda _{M} (J_{5} ) \bigr\} \leq 0. \end{aligned}$$
(42)

Let us take

$$ G(t)=e^{\delta t}V(t). $$
(43)

From (40)–(42), we have

$$\begin{aligned} \dot{G}(t) =&\delta e^{\delta t}V(t)+e^{\delta t}\dot{V}(t) \\ =& \delta e^{\delta t} \biggl[ X^{T}(t)J_{1} X(t) + H_{1}^{T}(t)J_{2} H_{1}(t)+H_{2}^{T}(t)J_{3} H_{2}(t) +Y^{T}(t)J_{4} Y(t)+Z^{T}(t)J_{5} Z(t) \\ &{}+\gamma (\mu _{7}+\mu _{8}) \int ^{t}_{t-\tau }Y^{T}(\omega )Y( \omega )\,d\omega + \int ^{t}_{t-\tau }Y^{T}(\omega )L^{*}Y( \omega )\,d\omega \biggr] \\ &{}+e^{\delta t} \biggl[ X^{T}(t)\varPsi _{1} X(t) + H_{1}^{T}(t)\varPsi _{2} H_{1}(t)+H_{2}^{T}(t) \varPsi _{3} H_{2}(t) +Y^{T}(t)\varPsi _{4} Y(t) \\ &{}+Z^{T}(t) \varPsi _{5} Z(t)-\frac{1}{\tau } \int ^{t}_{t-\tau }Y^{T}(\omega )L^{*}Y(\omega ) \,d\omega \biggr] \\ \leq & \delta e^{\delta t} \biggl[ X^{T}(t)J_{1} X(t) + H_{1}^{T}(t)J_{2} H_{1}(t)+H_{2}^{T}(t)J_{3} H_{2}(t) +Y^{T}(t)J_{4} Y(t)+Z^{T}(t)J_{5} Z(t) \\ &{}+\gamma (\mu _{7}+\mu _{8}) \int ^{t}_{t-\tau }Y^{T}(\omega )Y( \omega )\,d\omega \biggr] +e^{\delta t} \bigl[ X^{T}(t)\varPsi _{1} X(t) + H_{1}^{T}(t) \varPsi _{2} H_{1}(t) \\ &{}+H_{2}^{T}(t) \varPsi _{3} H_{2}(t)+Y^{T}(t)\varPsi _{4} Y(t)+Z^{T}(t)\varPsi _{5} Z(t) \bigr]. \end{aligned}$$
(44)

Then, by using (42) and integrating both sides of (44) from 0 to t, we obtain

$$\begin{aligned} \dot{G}(t) \leq & \biggl[ X^{T}(0)J_{1} X(0) + H_{1}^{T}(0)J_{2} H_{1}(0)+H_{2}^{T}(0)J_{3} H_{2}(0) +Y^{T}(0)J_{4} Y(0)+Z^{T}(0)J_{5} Z(0) \\ &{}+\gamma (\mu _{7}+\mu _{8}) \int ^{0}_{-\tau }Y^{T}(\omega )Y( \omega )\,d\omega +\frac{1}{\tau } \int ^{0}_{-\tau } \int ^{0}_{ \omega }Y^{T}(\kappa )L^{*}Y(\kappa )\,d\kappa \,d\omega \biggr] \\ &{}+ \int ^{t}_{0} \biggl[\delta e^{\delta \omega } \bigl[ X^{T}( \omega )J_{1} X(\omega ) + H_{1}^{T}(\omega )J_{2} H_{1}( \omega )+H_{2}^{T}( \omega )J_{3} H_{2}(\omega ) +Y^{T}(\omega )J_{4} Y(\omega ) \\ &{}+Z^{T}(\omega )J_{5} Z(\omega ) \bigr]+e^{\delta \omega } \bigl[ X^{T}( \omega )\varPsi _{1} X(\omega ) + H_{1}^{T}(\omega )\varPsi _{2} H_{1}( \omega )+H_{2}^{T}(\omega )\varPsi _{3} H_{2}(\omega ) \\ &{}+Y^{T}(\omega )\varPsi _{4} Y(\omega )+Z^{T}(\omega )\varPsi _{5} Z( \omega ) \bigr] \,d\omega \\ &{}+\gamma (\mu _{7}+\mu _{8}) \delta \int ^{t}_{0}e^{\delta \omega } \int ^{\omega }_{\omega -\tau }Y^{T}( \kappa )Y( \kappa )\,d\kappa \,d\omega \biggr] \\ \leq & \biggl[ X^{T}(0)J_{1} X(0) + H_{1}^{T}(0)J_{2} H_{1}(0)+H_{2}^{T}(0)J_{3} H_{2}(0) +Y^{T}(0)J_{4} Y(0)+Z^{T}(0)J_{5} Z(0) \\ &{}+\gamma \tau (\mu _{7}+\mu _{8}) \Vert \phi _{4} \Vert ^{2}+ \frac{\tau }{2}\lambda _{M}\bigl(L^{*}\bigr) \Vert \phi _{4} \Vert ^{2} +\gamma \tau ( \mu _{7}+\mu _{8})\delta e^{\delta \tau } \Vert \phi _{4} \Vert ^{2} \biggr] \\ &{}+ \int ^{t}_{0}\delta e^{\delta \omega } \varPi \bigl( \bigl\Vert X(\omega ) \bigr\Vert ^{2} + \bigl\Vert H_{1}(\omega ) \bigr\Vert ^{2} + \bigl\Vert H_{2}(\omega ) \bigr\Vert ^{2} + \bigl\Vert Y(\omega ) \bigr\Vert ^{2} + \bigl\Vert Z(\omega ) \bigr\Vert ^{2} \bigr)\,d\omega \\ \leq & \Delta \bigl( \Vert \phi _{1} \Vert ^{2} + \Vert \phi _{2} \Vert ^{2} + \Vert \phi _{3} \Vert ^{2} + \Vert \phi _{4} \Vert ^{2} + \Vert \phi _{5} \Vert ^{2} \bigr), \end{aligned}$$
(45)

where

$$ \Delta = \max \biggl\{ \lambda _{M} (J_{1} ), \lambda _{M} (J_{2} ), \lambda _{M} (J_{3} ), \lambda _{M} (J_{4} )+ \tau \gamma (\mu _{7}+\mu _{8})\bigl[1+\delta e^{\delta \tau } \bigr] + \frac{\tau }{2}\lambda _{M}\bigl(L^{*} \bigr), \lambda _{M} (J_{5} ) \biggr\} . $$

Also, it is easy to obtain that

$$\begin{aligned} G(t) \geq & e^{\delta t} \bigl[ \min \bigl\{ \lambda _{m} (J_{1} ), \lambda _{m} (J_{2} ), \lambda _{m} (J_{3} ), \lambda _{m} (J_{4} ), \lambda _{m} (J_{5} ) \bigr\} \bigr] \\ &{}\times \bigl( \bigl\Vert X(t) \bigr\Vert ^{2} + \bigl\Vert H_{1}(t) \bigr\Vert ^{2} + \bigl\Vert H_{2}(t) \bigr\Vert ^{2} + \bigl\Vert Y(t) \bigr\Vert ^{2} + \bigl\Vert Z(t) \bigr\Vert ^{2} \bigr). \end{aligned}$$
(46)

From (45) and (46), it follows that

$$\begin{aligned}& \bigl\| X(t)\bigr\| ^{2} +\bigl\| H_{1}(t)\bigr\| ^{2} +\bigl\| H_{2}(t)\bigr\| ^{2} +\bigl\| Y(t)\bigr\| ^{2} +\bigl\| Z(t)\bigr\| ^{2} \\& \quad \leq \frac{e^{-\delta t} G(t)}{\min \{\lambda _{m} (J_{1} ), \lambda _{m} (J_{2} ), \lambda _{m} (J_{3} ), \lambda _{m} (J_{4} ), \lambda _{m} (J_{5} ) \}} \\& \quad \leq \varLambda \bigl( \Vert \phi _{1} \Vert ^{2} + \Vert \phi _{2} \Vert ^{2} + \Vert \phi _{3} \Vert ^{2} + \Vert \phi _{4} \Vert ^{2} + \Vert \phi _{5} \Vert ^{2} \bigr)e^{-\delta t}, \end{aligned}$$
(47)

where

$$ \varLambda = \frac{\max \{\lambda _{M} (J_{1} ), \lambda _{M} (J_{2} ), \lambda _{M} (J_{3} ), \lambda _{M} (J_{4} )+\tau \gamma (\mu _{7}+\mu _{8})[1+\delta e^{\delta \tau }] +\frac{\tau }{2}\lambda _{M}(L^{*}), \lambda _{M} (J_{5} ) \}}{\min \{\lambda _{m} (J_{1} ), \lambda _{m} (J_{2} ), \lambda _{m} (J_{3} ), \lambda _{m} (J_{4} ), \lambda _{m} (J_{5} ) \}}. $$

This implies that the endemic equilibrium \(E^{*} ( X^{*},H^{*}_{1},H^{*}_{2},Y^{*},Z^{*} )\) of model (5) is globally exponentially stable. This ends the proof. □

5 Numerical simulation

Choosing \(A=0.1\), \(\beta _{1}=0.003\), \(\beta _{2}=0.002\), \(\mu =0.002\), \(\alpha =0.003\), \(\rho =0.003\), \(d=0.003\), \(\varpi =0.004\), \(\gamma =0.05\).

$$ \textstyle\begin{cases} \frac{dX(t)}{dt} = 0.1-0.003 X(t)H_{1}(t)-0.002 X(t)+0.003 Y(t), \\ \frac{dH_{1}(t)}{dt} = 0.003 X(t)H_{1}(t)-0.002 H_{1}(t)H_{2}(t)-0.005 H_{1}(t), \\ \frac{dH_{2}(t)}{dt} = 0.002 H_{1}(t)H_{2}(t)-0.009H_{2}(t), \\ \frac{dY(t)}{dt} = 0.004 H_{2}(t)-0.005Y(t)-0.05 Y(t-\tau ), \\ \frac{dZ(t)}{dt} = 0.05 Y(t-\tau )-0.002 Z(t). \end{cases} $$
(48)

Calculation reveals that the unique smoking present equilibrium of system (48) is \(E^{*}(6.5548, 4.5, 7.3322, 0.5333, 13.3325)\). Then we obtain \(\omega _{0}=0.7202\) and the critical value of time delay \(\tau _{0}=32.0957\).

According to Theorem 1, system (48) is locally asymptotically stable at the smoking present equilibrium \(E^{*}(6.5548, 4.5, 7.3322, 0.5333, 13.3325)\) when \(\tau \in [0, \tau _{0}=32.0957)\), as shown in Fig. 2. That is, smoking continuously propagates with a fixed number in populations. When we choose \(\tau =33.5625>\tau _{0}=32.0957\), system (48) loses its stability and oscillation occurs, and periodic solutions emerge from the smoking present equilibrium \(E^{*}(6.5548, 4.5, 7.3322, 0.5333, 13.3325)\), as observed in Fig. 3. This implies that smoking explosively spreads in populations. In addition, since \(\mu _{2}=24.7558>0\), \(\beta _{2}=-0.4258<0\), and \(T_{2}=-6.2623<0\), we can conclude that the Hopf bifurcation is supercritical; the bifurcating periodic solutions are stable and decreasing.

Figure 2
figure 2

Time plots of X, \(H_{1}\), \(H_{2}\)Y, and Z with \(\tau = 31.0082<\tau _{0}=32.0957\)

Full size image
Figure 3
figure 3

Time plots of X, \(H_{1}\), \(H_{2}\)Y, and Z with \(\tau = 33.5625>\tau _{0}=32.0957\)

Full size image

6 Conclusions

Over 7000 chemical compounds and toxins are included in cigarettes affecting nearly every organ in the body. Therefore, smoking is a sorely destructive problem. What is more serious is that smoking addiction not only increases the disease burden but also adds an economic burden on the society. According to the 2019 global tobacco epidemic report released by the World Health Organization, about 5 billion people have been covered by at least one tobacco control measure recommended by the organization, reaching the highest level of achievement, but 59 countries still have no tobacco control measure reaching the highest level of implementation. Thus, it is very important to try to simulate and reveal the nature of smoking addiction. This paper is concerned with a delayed tobacco smoking model containing users in the form of snuffing by incorporating the time delay due to the period that the regular smokers use to quit smoking into the model formulated in the literature [22]. Its dynamics is studied in terms of stability and Hopf bifurcation.

It has been shown that when the value of delay is below the critical value \(\tau _{0}\), the populations in system (2) are in ideal stable state. In this case, it is easy to predict and control smoking addiction. However, once the value of delay is above \(\tau _{0}\), populations in system (2) may coexist in an oscillatory mode under some conditions. Therefore, we should control and postpone the occurrence of Hopf bifurcation in system (2). From this point of view, we can conclude that people who would like to quit smoking should quit it as soon as possible. Specially, specific formulas determining the stability and direction of the Hopf bifurcation are derived with the aid of the normal form theory and the manifold center theorem. Global exponential stability of smoking present equilibrium is presented by using LMI techniques. Computer simulations are implemented to explain the obtained analytical results.

It is worth noting that we only consider the effect of time delay on system (2). Very recently, fractional-order modeling in various fields such as epidemics [39–42], system control [43–45], and neural network [46–49], has shown more advantage and consistency compared with integer-order mathematical modeling. Thus, it is more interesting to investigate the fractional-order smoking model with time delay. We leave this as our near future research work.