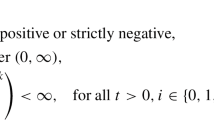1 Introduction

In this paper, we study the central limit theorem for a fractional stochastic heat equation in spatial dimension \(\mathbb {R}^{d}\) driven by a spatially correlated noise:

$$ \textstyle\begin{cases} \frac{\partial u^{\varepsilon }}{\partial t}(t,x)= \mathcal{D}_{ \underline{\delta }}^{\underline{\alpha }}u^{\varepsilon }(t,x)+b(u^{\varepsilon }(t,x))+ \sqrt{\varepsilon }\sigma (u^{\varepsilon }(t,x)) \dot{F}(t,x), \\ u^{\varepsilon }(0,x)=0, \end{cases} $$
(1)

where \(\varepsilon >0\), \((t,x)\in [0,T]\times \mathbb {R}^{d}\), \(d\ge 1\), \(\underline{\alpha }=(\alpha _{1},\ldots,\alpha _{d})\), \(\underline{\delta }=(\delta _{1},\ldots,\delta _{d})\), and we will assume that \(\alpha _{i}\in \mathopen{]}0,2\mathclose{]}\setminus \{1\}\) and \(\vert \delta _{i} \vert \le \min \{\alpha _{i},2-\delta _{i}\}\), \(i=1,\ldots, d\), Ḟ is the “formal” derivative of the Gaussian perturbation and \(\mathcal{D}_{\underline{\delta }}^{\underline{\alpha }}\) denotes a non-local fractional differential operator on \(\mathbb {R}^{d}\) defined by \(\mathcal{D}_{\underline{\delta }}^{\underline{\alpha }}:=\sum_{i=1}^{d} D_{ \delta _{i}}^{\alpha _{i}} \). Here, \(D_{\delta _{i}}^{\alpha _{i}}\) denotes the fractional differential derivative with respect to the ith coordinate defined via its Fourier transform \(\mathcal{F}\) by

$$ \mathcal{F}\bigl(\mathcal{D}_{\underline{\delta }}^{\underline{\alpha }}\phi \bigr) (\xi )=- \vert \xi \vert ^{\alpha _{i}}\exp \biggl(-\imath \delta _{i} \frac{\pi }{2}\operatorname{sgn}{ \xi } \biggr)\mathcal{F}(\phi ) (\xi ), $$

with \(\imath ^{2}+1=0\). The noise \(F(t,x)\) is a martingale measure in the sense of Walsh [12] and Dalang [4]. From now on, we shall refer to Eq. (1) as \(\mathit{Eq}_{\underline{\delta },\varepsilon }^{\underline{\alpha }}(d, b, \sigma )\). See Sect. 2 for details.

As the parameter ε tends to zero, the solutions \(u^{\varepsilon }\) of (1) will tend to the solution of the deterministic equation defined by

$$ \textstyle\begin{cases} \frac{\partial u^{0}}{\partial t}(t,x)= \mathcal{D}_{\underline{\delta }}^{ \underline{\alpha }}u^{0}(t,x)+b(u^{0}(t,x)), \\ u^{0}(0,x)=0. \end{cases} $$
(2)

It is always interesting to investigate deviations of \(u^{\varepsilon } \) from \(u^{0}\), as ε decreases to 0, that is, the asymptotic behavior of the trajectory

$$ X^{\varepsilon }(t,x):= \frac{1}{\sqrt{\varepsilon }\lambda (\varepsilon )} \bigl(u^{ \varepsilon } -u^{0} \bigr) (t,x),\quad (t,x)\in [0,T]\times \mathbb {R}^{d}, $$

where \(\lambda (\varepsilon )\) is some deviation scale which strongly influences the asymptotic behavior of \(X^{\varepsilon }\) (see Freidlin and Wentzell [8]):

  • The case \(\lambda (\varepsilon )=1/ \sqrt{\varepsilon }\) provides some large deviation estimates. El Mellali and Mellouk [7] proved that the law of the solution \(u^{\varepsilon }\) satisfies a large deviation principle.

  • When the deviation scale satisfies

    $$ \lambda (\varepsilon )\to +\infty ,\qquad \sqrt{\varepsilon }\lambda ( \varepsilon )\to 0\quad \text{as }\varepsilon \to 0, $$

    it is the moderate deviations. Li et al. [11] proved that \(\frac{1}{\sqrt{\varepsilon }\lambda (\varepsilon )} (u^{ \varepsilon } -u^{0} )\) satisfies a moderate deviation principle by the weak convergence method.

  • When the deviation scale satisfies \(\lambda (\varepsilon )=1\), we are in the domain of the central limit theorem. In this paper, we prove that the process \((u^{\varepsilon }-u^{0})/\sqrt{\varepsilon }\) converges to a random field.

The central limit theorem is a traditional topic in the theory of probability and statistics. Recently, the study of the central limit theorem for stochastic (partial) differential equation has been carried out, see e.g. [2, 9, 11, 13] etc.

The rest of this paper is organized as follows. In Sect. 2, the precise framework is stated. In Sect. 3, we state the central limit theorem and prove it by establishing some moment convergence results of SPDE.

Throughout the paper, \(C_{p}\) is a positive constant depending on the parameter p, and \(C, C_{1},\ldots \) are constants depending on no specific parameter (except T and the Lipschitz constants), whose value may be different from line to line by convention.

2 Framework

In this section, let us give the framework taken from Boulanba et al. [1], El Mellali and Mellouk [7].

2.1 The operator \(\mathcal{D}_{\underline{\delta }}^{\underline{\alpha }}\)

According to [6, 10], \(D_{\delta }^{\alpha }\) can be represented for \(1<\alpha <2\) by

$$ D_{\delta }^{\alpha }= \int _{-\infty }^{+\infty } \frac{\phi (x+y)-\phi (x)-y\phi '(x)}{ \vert y \vert ^{1+\alpha }}\bigl(\kappa _{-}^{ \delta }\mathbf{1}_{(-\infty ,0)}(y)+\kappa _{+}^{\delta }\mathbf{1}_{(0,+ \infty )}(y)\bigr)\,dy, $$

and for \(0<\alpha <1\) by

$$ D_{\delta }^{\alpha }= \int _{-\infty }^{+\infty } \frac{\phi (x+y)-\phi (x)}{ \vert y \vert ^{1+\alpha }}\bigl(\kappa _{-}^{\delta } \mathbf{1}_{(-\infty ,0)}(y)+\kappa _{+}^{\delta }\mathbf{1}_{(0,+ \infty )}(y)\bigr)\,dy, $$

where \(\kappa _{-}^{\delta }\) and \(\kappa _{+}^{\delta }\) are two non-negative constants satisfying \(\kappa _{-}^{\delta }+\kappa _{+}^{\delta }>0\) and ϕ is a smooth function for which the integral exists, and \(\phi '\) stands for its derivative.

Let \(G_{\alpha ,\delta }(t,x)\) denote the fundamental solution of the equation \(\mathit{Eq}_{\delta ,1}^{\alpha }(1,0,0)\), that is, the unique solution of the Cauchy problem

$$ \textstyle\begin{cases} \frac{\partial u}{\partial t}(t,x)= D_{\delta }^{\alpha }u(t,x), \\ u(0,x)=\delta _{0}(x), \quad t>0, x\in \mathbb {R}, \end{cases} $$

where \(\delta _{0}\) is the Dirac distribution. Using Fourier’s calculus, one gets

$$ G_{\alpha ,\delta }(t,x)=\frac{1}{2\pi } \int _{-\infty }^{\infty }\exp \biggl(-\imath zx-t \vert z \vert ^{\alpha }\exp \biggl(-\imath \delta \frac{\pi }{2}\operatorname{sgn}(z) \biggr) \biggr)\,dz. $$
(3)

Here, \(\alpha \in \mathopen{]}0,2\mathclose{]}\) and \(\vert \delta \vert \le \min \{\alpha ,2-\alpha \}\).

For higher dimension \(d\ge 1\) and any multi index \(\underline{\alpha }=(\alpha _{1},\ldots, \alpha _{d})\) and \(\underline{\delta }=(\delta _{1},\ldots,\delta _{d})\), let \({\mathbf{G}}_{\underline{\alpha },\underline{\delta }}(t,x)\) be the Green function of the deterministic equation \(\mathit{Eq}_{\underline{\delta }}^{\underline{\alpha }}(d,0,0)\). Clearly,

$$\begin{aligned} {\mathbf{G}}_{\underline{\alpha },\underline{\delta }}(t,x)={}&\prod _{i=1}^{d}G_{ \alpha _{i},\delta _{i}}(t,x_{i}) \\ ={}&\frac{1}{(2\pi )^{d}} \int _{\mathbb {R}^{d}}\exp \Biggl(-\imath \langle \xi ,x \rangle -t\sum _{i=1}^{d} \vert \xi _{i} \vert ^{\alpha _{i}}\exp \biggl(-\imath \delta _{i}\frac{\pi }{2} \operatorname{sgn}(\xi _{i}) \biggr) \Biggr)\,d\xi , \end{aligned}$$
(4)

where \(\langle \cdot ,\cdot \rangle \) stands for the inner product in \(\mathbb {R}^{d}\).

2.2 The driving noise F

Let \(\mathcal{S}(\mathbb {R}^{d+1})\) be the space of Schwartz test functions. On a complete probability space \((\varOmega , \mathcal{G},\mathbb {P})\), the noise \(F=\{F(\phi ),\phi \in \mathcal{S}(\mathbb {R}^{d+1})\}\) is assumed to be an \(L^{2}(\varOmega ,\mathcal{G},\mathbb {P})\)-valued Gaussian process with mean zero and covariance functional given by

$$ J(\varphi ,\psi ):=\mathbb {E}\bigl[F(\phi )F(\psi ) \bigr]= \int _{\mathbb {R}_{+}}\,ds \int _{\mathbb {R}^{d}} \bigl(\phi (s,\star )\ast \tilde{\psi }(s,\star ) \bigr) (x)\varGamma (dx)\,ds,\quad \phi ,\psi \in \mathcal{S}\bigl(\mathbb {R}^{d+1}\bigr), $$

where \(\tilde{\psi }(s,x):=\psi (s,-x)\) and Γ is a non-negative and non-negative definite tempered measure, therefore symmetric. The symbol ∗ denotes the convolution product and ⋆ stands for the spatial variable.

Let μ be the spectral measure of Γ, which is a tempered measure, that is, \(\mu =\mathcal{F}^{-1}(\varGamma )\), and this gives

$$ J(\phi ,\psi )= \int _{\mathbb {R}_{+}}\,ds \int _{\mathbb {R}^{d}}\mu (d\xi )\mathcal{F}\phi (s, \star ) (\xi )\overline{ \mathcal{F}\psi (s,\star )}(\xi ), $$
(5)

where z̄ is the complex conjugate of z.

As in Dalang [4], the Gaussian process F can be extended to a worthy martingale measure, in the sense of Walsh [12],

$$ M:=\bigl\{ M_{t}(A), t\in \mathbb {R}_{+}, A\in \mathcal{B}_{b}\bigl(\mathbb {R}^{d}\bigr)\bigr\} , $$

where \(\mathcal{B}_{b}(\mathbb {R}^{d})\) denotes the collection of all bounded Borel measurable sets in \(\mathbb {R}^{d}\). Let \(\mathcal{G}_{t}\) be the completion of the σ-field generated by the random variables \(\{F(s,A);0\le s\le t, A\in \mathcal{B}_{b}(\mathbb {R}^{d})\}\).

Boulanba et al. [1] gave a rigorous meaning to the solution of equation \(\mathit{Eq}_{\underline{\delta },\varepsilon }^{\underline{\alpha }}(d,b, \sigma )\) by means of a joint measurable and \(\mathcal{G}_{t}\)-adapted process \(\{u^{\varepsilon }(t,x);(t,x)\in \mathbb {R}_{+}\times \mathbb {R}^{d}\}\) satisfying, for each \(t\ge 0\) and for almost all \(x\in \mathbb {R}^{d}\), the following evolution equation:

$$\begin{aligned} u^{\varepsilon }(t,x)={}& \sqrt{\varepsilon } \int _{0}^{t} \int _{\mathbb {R}^{d}} \mathbf{G}_{\underline{\alpha }, \underline{\delta }}(t-s,x-y)\sigma \bigl(u^{\varepsilon }(s,y)\bigr)F(\,ds\,dy) \\ &{} + \int _{0}^{t}\,ds \int _{\mathbb {R}^{d}}\mathbf{G}_{\underline{\alpha }, \underline{\delta }}(t-s,x-y)b\bigl(u^{\varepsilon }(s,y) \bigr)\,dy. \end{aligned}$$
(6)

In order to prove our result, we are going to give another equivalent approach to the solution of \(\mathit{Eq}_{\underline{\delta },\varepsilon }^{\underline{\alpha }}(d,b, \sigma )\), see [5]. To start with, let us denote by \(\mathcal{H}\) the Hilbert space obtained by the completion of \(\mathcal{S}(\mathbb {R}^{d})\) with the inner product

$$\begin{aligned} \langle \phi ,\psi \rangle _{\mathcal{H}}:={}& \int _{\mathbb {R}^{d}}\varGamma (dx) ( \phi \ast \tilde{\psi }) (x) \\ ={}& \int _{\mathbb {R}^{d}}\mu (d\xi )\mathcal{F}\phi (\xi )\overline{\mathcal{F}\psi }(\xi ), \quad \phi ,\psi \in \mathcal{S}\bigl(\mathbb {R}^{d}\bigr). \end{aligned}$$

The norm induced by \(\langle \cdot ,\cdot \rangle _{\mathcal{H}}\) is denoted by \(\Vert \cdot \Vert _{\mathcal{H}}\).

By Walsh’s theory of the martingale measures [12], for \(t\ge 0\) and \(h\in \mathcal{H}\), the stochastic integral

$$ B_{t}(h)= \int _{0}^{t} \int _{\mathbb {R}^{d}}h(y)F(ds,dy) $$

is well defined and the process \(\{B_{t}(h); t\ge 0, h\in \mathcal{H}\}\) is a cylindrical Wiener process on \(\mathcal{H}\). Let \(\{e_{k}\}_{k\ge 1}\) be a complete orthonormal system of the Hilbert space \(\mathcal{H}\), then

$$ \biggl\{ B_{t}^{k}:= \int _{0}^{t} \int _{\mathbb {R}^{d}}e_{k}(y)F(ds,dy);k \ge 1 \biggr\} $$

defines a sequence of independent standard Wiener processes, and we have the following representation:

$$ B_{t}:=\sum_{k\ge 1}B_{t}^{k}e_{k}. $$
(7)

Let \(\{\mathcal{F}_{t}\}_{t\in [0,T]}\) be the σ-field generated by the random variables \(\{B_{s}^{k};s\in [0,t], k\ge 1\}\). We define the predictable σ-field in \(\varOmega \times [0,T]\) generated by the sets \(\{\mathopen{]}s,t\mathclose{]}\times A;A\in \mathcal{F}_{s}, 0\le s\le t\le T\}\). In the following, we can define the stochastic integral with respect to cylindrical Wiener process \(\{B_{t}(h)\}_{t\ge 0}\) (see e.g. [3] or [5]) of any predictable square-integrable process with values in \(\mathcal{H}\) as follows:

$$ \int _{0}^{t} \int _{\mathbb {R}^{d}}g\cdot dB:=\sum_{k\ge 1} \int _{0}^{t} \bigl\langle g(s),e_{k} \bigr\rangle _{\mathcal{H}} \,dB_{s}^{k}. $$

In the sequel, we shall consider the mild solution to equation \(\mathit{Eq}_{\underline{\delta },\varepsilon }^{\underline{\alpha }}(d,b, \sigma )\) given by

$$\begin{aligned} u^{\varepsilon }(t,x)={}&\sqrt{\varepsilon }\sum_{k\ge 1} \int _{0}^{t} \bigl\langle \mathbf{G}_{\underline{\alpha }, \underline{\delta }}(t-s,x-\cdot ) \sigma \bigl(u^{\varepsilon }(s,\star )\bigr), e_{k}\bigr\rangle _{\mathcal{H}} \,dB_{s}^{k} \\ & {} + \int _{0}^{t} \bigl[\mathbf{G}_{\underline{\alpha },\underline{\delta }}(t-s) \ast b\bigl(u^{\varepsilon }(s,\star )\bigr) \bigr](x)\,ds \end{aligned}$$
(8)

for any \(t\in [0,T]\), \(x\in \mathbb {R}^{d}\).

2.3 Existence, uniqueness, and Hölder regularity to equation

For a multi-index \(\underline{\alpha }=(\alpha _{1},\ldots,\alpha _{d})\) such that \(\alpha _{i}\in \mathopen{]}0,2\mathclose{]}\setminus \{1\}\), \(i=1,\ldots, d\), and any \(\xi \in \mathbb {R}^{d}\), let \(S_{\underline{\alpha }}(\xi )=\sum_{i=1}^{d} \vert \xi _{i} \vert ^{\alpha _{i}} \). Assume the following assumptions on the functions σ, b and the measure μ:

(C)::

The functionsσandbare Lipschitz, that is, there exists some constantLsuch that, for all\(x,y\in \mathbb {R}\),

$$ \bigl\Vert \sigma (x)-\sigma (y) \bigr\Vert \le L \vert x-y \vert , \qquad \bigl\vert b(x)-b(y) \bigr\vert \le L \vert x-y \vert . $$
(9)
\((H_{\eta }^{\underline{\alpha }})\)::

Let\(\underline{\alpha }\)be as defined above and\(\eta \in\mathopen{]}0,1\mathclose{]}\), it holds that

$$ \int _{\mathbb {R}^{d}} \frac{\mu (d\xi )}{(1+ S_{\underline{\alpha }}(\xi ))^{\eta }}< + \infty . $$

From Boulanba et al. [1], we know the following result.

Proposition 2.1

([1, Theorem 3.1])

Under assumptions (C) and\((H_{\eta }^{\underline{\alpha }})\), Eq. (8) admits a unique continuous solution\(u^{\varepsilon }\), which satisfies

$$ \sup_{t\in [0,T],x\in \mathbb {R}^{d}}\mathbb {E}\bigl[ \bigl\vert u^{\varepsilon }(t,x) \bigr\vert ^{p} \bigr]< +\infty . $$
(10)

2.4 Convergence of solutions

The next result is concerned with the convergence of \(u^{\varepsilon }\) as \(\varepsilon \to 0\).

Proposition 2.2

Assume (C) and\((H_{\eta }^{\underline{\alpha }})\). Then, for any\(T>0\), there exists some constant\(C(p, K, T)\)depending onp, K, Tsuch that

$$ \sup_{0\le t\le T, x\in \mathbb {R}^{d}}\mathbb {E}\bigl[ \bigl\vert u^{\varepsilon }(t,x)-u^{0}(t,x) \bigr\vert ^{p} \bigr]\le \varepsilon ^{\frac{p}{2}} c(p, L, T). $$
(11)

Proof

For any \((t,x)\in [0,T]\times \mathbb {R}^{d}\), we have

$$\begin{aligned} u^{\varepsilon }(t,x)-u^{0}(t,x)={}&\sqrt{\varepsilon }\sum _{k\ge 1} \int _{0}^{t} \bigl\langle \mathbf{G}_{\underline{\alpha }, \underline{\delta }}(t-s,x-\cdot ) \sigma \bigl(u^{\varepsilon }(s,\star )\bigr), e_{k}\bigr\rangle _{\mathcal{H}} \,dB_{s}^{k} \\ & {} + \int _{0}^{t} \bigl[\mathbf{G}_{\underline{\alpha },\underline{\delta }}(t-s) \ast \bigl( b\bigl(u^{\varepsilon }(s,\star )\bigr)-b\bigl(u^{0}(s,\star ) \bigr) \bigr) \bigr](x)\,ds \\ =:{}& A_{1}^{\varepsilon }+A_{2}^{\varepsilon }. \end{aligned}$$
(12)

Let

$$ \mathcal{J}(t):= \int _{\mathbb {R}^{d}}\mu (d\xi ) \bigl\vert \mathcal{F}\mathbf{G}_{\underline{\alpha }, \underline{\delta }}(t) (\xi ) \bigr\vert ^{2}. $$
(13)

For the first term \(A_{1}^{\varepsilon }\), by Burkholder’s inequality, the Lipschitz property of σ, and (10), we have that, for any \((t,x)\in [0,T]\times \mathbb {R}^{d}\), \(p\ge 2\),

$$\begin{aligned} \mathbb {E}\bigl[ \bigl\vert A_{1}^{\varepsilon }(t,x) \bigr\vert ^{p} \bigr]\le{}&\varepsilon ^{ \frac{p}{2}}c(p)\mathbb {E}\biggl[ \biggl\vert \int _{0}^{t} \bigl\Vert \mathbf{G}_{ \underline{\alpha },\underline{\delta }}(t-s,x-\star )\sigma \bigl(u^{ \varepsilon }(s,\star )\bigr) \bigr\Vert _{\mathcal{H}}^{2}\,ds \biggr\vert ^{\frac{p}{2}} \biggr] \\ \le{}&\varepsilon ^{\frac{p}{2}} c(p,T)\mathbb {E}\biggl[ \int _{0}^{t} \bigl\Vert \mathbf{G}_{\underline{\alpha },\underline{\delta }}(t-s,x-\star )\sigma \bigl(u^{ \varepsilon }(s,\star )\bigr) \bigr\Vert _{\mathcal{H}}^{p}\,ds \biggr] \\ \le{}&\varepsilon c(p,L, T) \int _{0}^{t}\mathcal{J}(t-s) \Bigl(1+\sup _{(r,y) \in [0,s]\times \mathbb {R}^{d}}\mathbb {E}\bigl[ \bigl\vert u^{\varepsilon }(r,y) \bigr\vert ^{p} \bigr] \Bigr)\,ds \\ \le{}& \varepsilon c(p, L, T). \end{aligned}$$
(14)

For the second term \(A_{2}^{\varepsilon }\), by the Lipschitz property of b and Fubini’s theorem, we have

$$\begin{aligned} \mathbb {E}\bigl[ \bigl\vert A_{2}^{\varepsilon }(t,x) \bigr\vert ^{p} \bigr]\le{}& c(p,T) \mathbb {E}\biggl[ \int _{0}^{t} \int _{\mathbb {R}^{d}}\mathbf{G}_{\underline{\alpha }, \underline{\delta }}(t-s, x-y) \bigl\vert u^{\varepsilon }(s,y)-u^{0}(s,y) \bigr\vert ^{p}\,dy\,ds \biggr] \\ \le{}& c(p,L,T) \int _{0}^{t} \int _{\mathbb {R}^{d}}\mathbf{G}_{\underline{\alpha }, \underline{\delta }}(t-s, x-y)\mathbb {E}\Bigl[\sup _{0\le l\le s,z\in \mathbb {R}^{d}} \bigl\vert u^{\varepsilon }(l,z)-u^{0}(l,z) \bigr\vert ^{p} \Bigr]\,dy\,ds \\ \le{}& c(p,L,T) \int _{0}^{t}\mathbb {E}\Bigl[\sup_{0\le l\le s,z\in \mathbb {R}^{d}} \bigl\vert u^{\varepsilon }(l,z)-u^{0}(l,z) \bigr\vert ^{p} \Bigr]\,ds. \end{aligned}$$
(15)

Set \(\zeta ^{\varepsilon }(t):=\sup_{0\le s\le t, x\in \mathbb {R}^{d}}\mathbb {E}[ \vert u^{\varepsilon }(s,x)-u^{0}(s,x) \vert ^{p} ]\). By (12), (14), and (15), we have that, for any \(t\in [0,T]\),

$$ \zeta ^{\varepsilon }(t)\le \varepsilon ^{\frac{p}{2}} c_{1}(p, L, T)+ c_{2}(p, L, T) \int _{0}^{t}\zeta ^{\varepsilon }(s)\,ds. $$

Hence, by Gronwall’s lemma, there exists a constant \(c(p,L,T)\) independent of ε such that

$$ \zeta ^{\varepsilon }(T)\le \varepsilon ^{\frac{p}{2}}c(p,L,T). $$

The proof is complete. □

3 Central limit theorem

To study the central limit theorem for \(u^{\varepsilon }\), we furthermore suppose that

(D)::

The functionbis differentiable, and its derivative\(b'\)is Lipschitz. More precisely, there exists a positive constant\(L'\)such that

$$ \bigl\vert b'(y)-b'(z) \bigr\vert \le L' \vert y-z \vert \quad \text{for all } y,z\in \mathbb {R}. $$
(16)

Combined with the Lipschitz continuity of b, we conclude that

$$ \bigl\vert b'(z) \bigr\vert \le L,\quad \forall z\in \mathbb {R}. $$
(17)

Consider the stochastic partial differential equation

$$\begin{aligned} \frac{\partial X}{\partial t}(t,x)=\mathcal{D}_{\underline{\delta }}^{ \underline{\alpha }}X(t,x)+b' \bigl(u^{0}(t,x)\bigr)X(t,x)+ \sigma \bigl(u^{0}(t,x)\bigr) \dot{F}(t,x), \end{aligned}$$
(18)

with \(X(0,x)\equiv 0\). Using the same strategy in the proof of the existence and uniqueness for the solution to Eq. (1), one can obtain the following result. Here we omit its proof.

Proposition 3.1

Assuming conditions (C), \((H_{\eta }^{\underline{\alpha }})\), and (D), there exists a unique continuous solutionXto Eq. (18) in the following form: for any\(t\in [0,T]\), \(x\in \mathbb {R}^{d}\),

$$\begin{aligned} X(t,x)={}&\sum_{k\ge 1} \int _{0}^{t}\bigl\langle \mathbf{G}_{\underline{\alpha }, \underline{\delta }}(t-s,x-\cdot )\sigma \bigl(u^{0}(s,\star )\bigr), e_{k} \bigr\rangle _{\mathcal{H}} \,dB_{s}^{k} \\ & {} + \int _{0}^{t} \bigl[\mathbf{G}_{\underline{\alpha },\underline{\delta }}(t-s) \ast \bigl[b'\bigl(u^{0}(s,\star )\bigr)X(s,\star )\bigr] \bigr](x)\,ds. \end{aligned}$$
(19)

Our main result is the following central limit theorem.

Theorem 3.2

Assuming conditions (C), \((H_{\eta }^{\underline{\alpha }})\), and (D), for any\((t,x)\in [0,T]\times \mathbb {R}^{d}\), the process\((u^{\varepsilon }(t,x)-u^{0}(t,x))/\sqrt{\varepsilon }\)converges in\(L^{2}\)to a random field\(X(t,x)\).

Proof

Let

$$ X^{\varepsilon }=\bigl(u^{\varepsilon }(t,x)-u^{0}(t,x)\bigr)/\sqrt{ \varepsilon }. $$

Then, for any \((t,x)\in [0,T]\times \mathbb {R}^{d}\),

$$\begin{aligned} &X^{\varepsilon }(t,x)-X(t,x) \\ &\quad = \sum_{k\ge 1} \int _{0}^{t} \bigl\langle \mathbf{G}_{\underline{\alpha }, \underline{\delta }}(t-s,x-\star ) \bigl[\sigma \bigl(u^{\varepsilon }(s, \star ) \bigr)-\sigma \bigl(u^{0}(s,\star ) \bigr) \bigr], e_{k} \bigr\rangle _{\mathcal{H}}\,dB_{s}^{k} \\ &\quad\quad{} + \int _{0}^{t} \biggl\{ \mathbf{G}_{\underline{\alpha }, \underline{\delta }}(t-s) \ast \biggl[ \frac{b (u^{\varepsilon }(s,\star ) ) -b(u^{0}(s,\star ) )}{\sqrt{\varepsilon }} -b'\bigl(u^{0}(s,\star ) \bigr)X(s,\star ) \biggr](x) \biggr\} \,ds \\ &\quad = \sum_{k\ge 1} \int _{0}^{t} \bigl\langle \mathbf{G}_{\underline{\alpha }, \underline{\delta }}(t-s,x-\star ) \bigl[\sigma \bigl(u^{\varepsilon }(s, \star ) \bigr)-\sigma \bigl(u^{0}(s,\star ) \bigr) \bigr], e_{k} \bigr\rangle _{\mathcal{H}}\,dB_{s}^{k} \\ &\quad\quad{} + \int _{0}^{t} \biggl\{ \mathbf{G}_{\underline{\alpha }, \underline{\delta }}(t-s) \ast \biggl[ \frac{b (u^{\varepsilon }(s,\star ) ) -b(u^{0}(s,\star ) )}{\sqrt{\varepsilon }} -b'\bigl(u^{0}(s,\star ) \bigr)X^{\varepsilon }(s,\star ) \biggr](x) \biggr\} \,ds \\ &\quad\quad{} + \int _{0}^{t} \bigl\{ \mathbf{G}_{\underline{\alpha }, \underline{\delta }}(t-s) \ast \bigl[b'\bigl(u^{0}(s,\star )\bigr) \bigl(X^{\varepsilon }(s,\star )-X(s,\star )\bigr) \bigr](x) \bigr\} \,ds \\ &\quad =:A_{1}^{\varepsilon }(t,x)+A_{2}^{\varepsilon }(t,x)+A_{3}^{ \varepsilon }(t,x). \end{aligned}$$
(20)

For the first term \(A_{1}^{\varepsilon }\), by the Lipschitz continuity of σ and Proposition 2.2, we have

$$\begin{aligned} \mathbb {E}\bigl[ \bigl\vert A_{1}^{\varepsilon }(t,x) \bigr\vert ^{2} \bigr]={}&\mathbb {E}\biggl[ \int _{0}^{t} \bigl\Vert \mathbf{G}_{\underline{\alpha },\underline{\delta }}(t-s,x-\star )\bigl[ \sigma \bigl(u^{\varepsilon }(s,\star )\bigr) -\sigma \bigl(u^{0}(s,\star )\bigr) \bigr] \bigr\Vert _{\mathcal{H}}^{2}\,ds \biggr] \\ \le{}& L^{2}\mathbb {E}\biggl[ \int _{0}^{t} \bigl\Vert \mathbf{G}_{\underline{\alpha }, \underline{\delta }}(t-s,x-\star ) \bigl\vert u^{\varepsilon }(s,\star ) -u^{0}(s, \star ) \bigr\vert \bigr\Vert _{\mathcal{H}}^{2} \,ds \biggr] \\ \le{}&L^{2} \int _{0}^{t}\,ds \Bigl(\sup_{(r,y)\in [0,s]\times \mathbb {R}^{d}} \mathbb {E}\bigl\vert u^{\varepsilon }(r,y) - u^{0}(r,y) \bigr\vert ^{2} \Bigr)\times \mathcal{J}(t-s) \\ \le{}& \varepsilon c(L,T). \end{aligned}$$
(21)

By Taylor’s formula, there exists a random field \(\eta ^{\varepsilon }\) taking values in \((0,1)\) such that

$$\begin{aligned} b\bigl(u^{\varepsilon }\bigr)-b\bigl(u^{0}\bigr)=b\bigl(u^{0}+ \sqrt{\varepsilon }X^{ \varepsilon }\bigr)-b\bigl(u^{0}\bigr) =\sqrt{ \varepsilon }b' \bigl( u^{0}+\sqrt{ \varepsilon } \eta ^{\varepsilon } X^{\varepsilon } \bigr)X^{ \varepsilon }. \end{aligned}$$

Since \(b'\) is Lipschitz continuous, we have

$$\begin{aligned} \biggl\vert \frac{1}{\sqrt{\varepsilon }} \bigl[b\bigl(u^{0}+\sqrt{\varepsilon } X^{ \varepsilon }\bigr)-b\bigl(u^{0}\bigr) \bigr]-b' \bigl(u^{0}\bigr)X^{\varepsilon } \biggr\vert \le{}& \sqrt{\varepsilon }L' \bigl\vert X^{\varepsilon } \bigr\vert ^{2}. \end{aligned}$$

Thus, by Proposition 2.2, we have

$$\begin{aligned} \mathbb {E}\bigl[ \bigl\vert A_{2}^{\varepsilon }(t,x) \bigr\vert ^{2} \bigr] \le{}& \varepsilon L^{\prime 2} \mathbb {E}\biggl[ \biggl( \int _{0}^{t}\mathbf{G}_{\underline{\alpha }, \underline{\delta }}(t-s)\ast \bigl\vert X^{\varepsilon }(s,\star ) \bigr\vert ^{2} (x) \,ds \biggr)^{2} \biggr] \\ \le{}& \varepsilon c\bigl(L',T\bigr) \int _{0}^{t} \int _{\mathbb {R}^{d}}\mathbf{G}_{ \underline{\alpha }, \underline{\delta }}(t-s,x-y) \mathbb {E}\bigl[ \bigl\vert X^{ \varepsilon }(s,y) \bigr\vert ^{4} \bigr] \,ds\,dy \\ \le{}& \varepsilon c\bigl(L',T\bigr) \int _{0}^{t} \int _{\mathbb {R}^{d}}\mathbf{G}_{ \underline{\alpha }, \underline{\delta }}(t-s,x-y) \sup _{(r,z)\in [0,s] \times \mathbb {R}^{d}} \mathbb {E}\bigl[ \bigl\vert X^{\varepsilon }(r,z) \bigr\vert ^{4} \bigr] \,ds\,dy \\ \le{}& \varepsilon c\bigl(L, L',T\bigr). \end{aligned}$$
(22)

For the third term, by the boundedness of \(b'\), we have

$$\begin{aligned} \mathbb {E}\bigl[ \bigl\vert A_{3}^{\varepsilon }(t,x) \bigr\vert ^{2} \bigr] \le{}& c(L,T) \mathbb {E}\biggl[ \int _{0}^{t} \int _{\mathbb {R}^{d}}\mathbf{G}_{\underline{\alpha }, \underline{\delta }}(t-s,x-y) \bigl\vert X^{\varepsilon }(s,y)-X(s,y) \bigr\vert ^{2} (x) \,ds\,dy \biggr] \\ \le{}& c(L,T) \int _{0}^{t} \int _{\mathbb {R}^{d}}\mathbf{G}_{\underline{\alpha }, \underline{\delta }}(t-s,x-y)\sup _{(r,z)\in [0,s]\times \mathbb {R}^{d}} \mathbb {E}\bigl[ \bigl\vert X^{\varepsilon }(r,z)-X(r,z) \bigr\vert ^{2} \bigr] \,ds\,dy \\ \le{}& c(L,T) \int _{0}^{t}\sup_{(r,z)\in [0,s]\times \mathbb {R}^{d}} \mathbb {E}\bigl[ \bigl\vert X^{\varepsilon }(r,z)-X(r,z) \bigr\vert ^{2} \bigr] \,ds. \end{aligned}$$
(23)

By (20)–(23), we have that, for any \(t\in [0,T]\),

$$ \begin{gathered} \sup_{(r,x)\in [0,t]\times \mathbb {R}^{d}} \mathbb {E}\bigl[ \bigl\vert X^{ \varepsilon }(r,x)-X(r,x) \bigr\vert ^{2} \bigr] \\ \quad \le \varepsilon c\bigl(L,L',T \bigr)+ \int _{0}^{t}\sup_{(r,z)\in [0,s]\times \mathbb {R}^{d}} \mathbb {E}\bigl[ \bigl\vert X^{ \varepsilon }(r,z)-X(r,z) \bigr\vert ^{2} \bigr] \,ds.\end{gathered} $$

Hence, by Gronwall’s lemma, there exists a constant \(c(L, L', T)\) independent of ε such that

$$ \sup_{(t,x)\in [0,T]\times \mathbb {R}^{d}} \mathbb {E}\bigl[ \bigl\vert X^{ \varepsilon }(t,x)-X(t,x) \bigr\vert ^{2} \bigr]\le \varepsilon c\bigl(L, L', T \bigr). $$

The proof is complete. □