Abstract
In this paper, asymptotical stability of the exact solutions of nonlinear impulsive ordinary differential equations is studied under Lipschitz conditions. Under these conditions, asymptotical stability of Runge–Kutta methods is studied by the theory of Padé approximation. And two simple examples are given to illustrate the conclusions.
Similar content being viewed by others
1 Introduction
The impulsive differential equations (IDEs) are widely applied in numerous fields of science and technology: theoretical physics, mechanics, population dynamics, pharmacokinetics, industrial robotics, chemical technology, biotechnology, economics, etc. Recently, the theory of IDEs has been an object of active research. Especially, stability of the exact solutions of IDEs has been widely studied (see [1, 2, 9, 16, 18] and the references therein). However, many IDEs cannot be solved analytically or their solving is more complicated. Hence taking numerical methods is a good choice.
In recent years, the stability of numerical methods for IDEs has attracted more and more attention (see [11, 12, 15, 17, 22, 29] etc.). Stability of Runge–Kutta methods with the constant stepsize for scalar linear IDEs has been studied by [17]. Runge–Kutta methods with variable stepsizes for multidimensional linear IDEs has been investigated in [12]. Collocation methods for linear nonautonomous IDEs has been considered in [29]. An improved linear multistep method for linear IDEs has been investigated in [13]. Stability of the exact and numerical solutions of nonlinear IDEs has been studied by the Lyapunov method in [11]. Stability of Runge–Kutta methods for a special kind of nonlinear IDEs has been investigated by the properties of the differential equations without impulsive perturbations in [15]. Stability and asymptotic stability of implicit Euler method for stiff IDEs in Banach space has been studied by [22]. There is a lot of significant work on the numerical solution of impulsive differential equations, for example [6, 7, 10, 14, 23–27]. However, in this work the authors did not investigate the stability of the numerical methods for non-stiff nonlinear IDEs under Lipschitz conditions. Consider the equation of the form
where \(x(t^{+})\) is the right limit of \(x(t)\), \(t_{0}=\tau_{0}<\tau_{1}<\tau _{2}<\cdots\), \(\lim_{k\rightarrow\infty}\tau_{k}=\infty\), the function \(f:[t_{0},+\infty)\times\mathbb{C}^{d}\rightarrow\mathbb{C}^{d}\) is continuous in t and Lipschitz continuous with respect to the second variable in the following sense: there is a positive real constant α such that
for arbitrary \(t\in[t_{0},\infty)\), \(x_{1},x_{2}\in\mathbb{C}^{d}\), where \(\| \cdot\|\) is any convenient norm on \(\mathbb{C}^{d}\). And also assume that each function \(I_{k}\), \(k=1,2,\ldots \) is Lipschitz continuous i.e. there is a positive constant \(\beta_{k}\) such that
Definition 1.1
(See [1])
A function \(x:[t_{0},\infty)\rightarrow\mathbb{C}^{d}\) is said to be a solution of (1), if
- (i)
\(\lim_{t\rightarrow t_{0}^{+}}x(t)=x_{0}\),
- (ii)
for \(t\in(t_{0},+\infty)\), \(t\neq\tau_{k}\), \(k=1,2,\dots\), \(x(t)\) is differentiable and \(x'(t)=f(t,x(t))\),
- (iii)
\(x(t)\) is left continuous in \((t_{0},+\infty)\) and \(x(\tau _{k}^{+})=I_{k}(x(\tau_{k}))\), \(k=1,2,\dots\).
2 Asymptotical stability of the exact solution
In this section, we study the asymptotical stability of the exact solution of (1). In order to investigate the asymptotical stability of \(x(t)\), consider Eq. (1) with another initial data:
where \(\mathbb{Z}^{+}=\{1,2,\ldots\}\).
Definition 2.1
The exact solution \(x(t)\) of (1) is said to be
- 1
stable if, for an arbitrary \(\epsilon>0\), there exists a positive number \(\delta=\delta(\epsilon)\) such that, for any other solution \(y(t)\) of (4), \(\|x_{0}-y_{0}\|<\delta\) implies
$$ \bigl\Vert x(t)-y(t) \bigr\Vert < \epsilon,\quad \forall t>t_{0}; $$ - 2
asymptotically stable, if it is stable and \(\lim_{t\rightarrow\infty}\|x(t)-y(t)\|=0\).
Theorem 2.2
Assume that there exists a positive constantγsuch that \(\tau _{k}-\tau_{k-1}\leq\gamma\), \(k\in\mathbb{Z}^{+}\). The exact solution of (1) is asymptotically stable if there is a positive constantCsuch that
for arbitrary \(k\in\mathbb{Z}^{+}\).
Proof
For arbitrary \(t\in(\tau_{k}, \tau_{k+1}]\), \(k=0,1,2,\dots \), we obtain
By the Gronwall theorem, for arbitrary \(t\in(\tau_{k}, \tau_{k+1}]\), \(k=0,1,2,\dots\), we have
which implies, by Definition 2.1(iii),
which also implies
Therefore, by the method of introduction and the conditions (3) and (5), for arbitrary \(t\in(\tau_{k}, \tau _{k+1}]\), \(k=0,1,2,\dots\), we obtain
which implies \(\|x(\tau_{k+1})-y(\tau_{k+1})\| \leq C^{k}\|x_{0}-y_{0}\| \mathrm{e}^{\alpha\gamma}\) and \(\|x(\tau^{+}_{k+1})-y(\tau^{+}_{k+1})\| \leq\|x_{0}-y_{0}\| C^{k+1}\). Hence for an arbitrary \(\epsilon>0\), there exists \(\delta=\mathrm {e}^{-\alpha\gamma}\epsilon\) such that \(\|x_{0}-y_{0}\|<\delta\) implies
for arbitrary \(t\in(\tau_{k}, \tau_{k+1}]\), \(k=0,1,2,\dots\), i.e.
So the exact solution of (1) is stable. Obviously, for arbitrary \(t\in(\tau_{k}, \tau_{k+1}]\), \(k=0,1,2,\dots\),
Similarly, we also obtain
and
Consequently, the exact solution of (1) is asymptotically stable. □
From the proof of Theorem 2.2, we can obtain the following result.
Remark 2.3
If the condition (5) of Theorem 2.2 is changed into the weaker condition
then the exact solution of (1) is stable.
3 Runge–Kutta methods
In this section, Runge–Kutta methods for (1) can be constructed as follows:
where \(h_{k}=\frac{\tau_{k+1}-\tau_{k}}{m}\), \(t_{k,l}=\tau_{k}+l h_{k}\), \(t_{k,l}^{i}=t_{k,l}+c_{i}h_{k}\), \(x_{k,l}\) is an approximation to the exact solution \(x(t_{k,l})\) and \(X_{k,l}^{i}\) is an approximation to the exact solution \(x(t_{k,l}^{i})\), \(k\in\mathbb{N}=\{0,1,2,\ldots\}\), \(l=0,1,\ldots,m-1\), \(i=1,2,\ldots,s\), s is referred to as the number of stages. The weights \(b_{i}\), the abscissae \(c_{i}=\sum_{j=1}^{s} a_{ij}\) and the matrix \(A=[a_{ij}]_{i,j=1}^{s}\) will be denoted by \((A, b, c)\). Similarly, the Runge–Kutta methods for (4) can be constructed as follows:
Definition 3.1
The Runge–Kutta method (7) for impulsive differential equation (1) is said to be
- 1
stable, if \(\exists M>0\), \(m\geq M\), \(h_{k}=\frac{\tau_{k+1}-\tau _{k}}{m}\), \(k\in\mathbb{N}\),
- (i)
\(I-zA\) is invertible for all \(z=\alpha h_{k}\),
- (ii)
for an arbitrary \(\epsilon>0\), there exists such a positive number \(\delta=\delta(\epsilon)\) that, for any other numerical solutions of (8), \(\|x_{0}-y_{0}\|<\delta\) implies
$$ \bigl\Vert \vert X_{k}-Y_{k} \vert \bigr\Vert < \epsilon, \quad\forall k\in\mathbb{N}, $$where \(X_{k}=(x_{k,0},x_{k,1},\ldots,x_{k,m})^{T}\), \(Y_{k}=(y_{k,0},y_{k,1},\ldots,y_{k,m})^{T}\) and
$$\bigl\Vert \vert X_{k}-Y_{k} \vert \bigr\Vert = \max_{0\leq l \leq m}\bigl\{ \Vert x_{k,l}-y_{k,l} \Vert \bigr\} ; $$
- (i)
- 2
asymptotically stable, if it is stable and if \(\exists M_{1}>0\), for any \(m\geq M_{1}\), \(h_{k}=\frac{\tau_{k+1}-\tau_{k}}{m}\), \(k\in\mathbb {N}\), the following holds:
$$ \lim_{k\rightarrow\infty} \bigl\Vert \vert X_{k}-Y_{k} \vert \bigr\Vert =0. $$
Lemma 3.2
The \((\mathbf{j},\mathbf{k})\)-Padé approximation to \(\mathrm{e}^{z}\)is given by
where
with error
It is the unique rational approximation to \(\mathrm{e}^{z}\)of order \(\mathbf{j}+\mathbf{k}\), such that the degrees of numerator and denominator arejandk, respectively.
Lemma 3.3
Assume that \(\mathbf{R}(z)\)is the \((\mathbf{j},\mathbf{k})\)-Padé approximation to \(\mathrm{e}^{z}\). Then \(\mathbf{R}(z)<\mathrm{e}^{z}\)for all \(z>0\)if and only ifkis even, when \(z>0\).
Theorem 3.4
Assume that \(\mathbf{R}(z)\)is the stability function of Runge–Kutta method (7) i.e.
Under the conditions of Theorem 2.2, Runge–Kutta method (7) with nonnegative coefficients (\(a_{ij}\geq0\)and \(b_{i}\geq 0\), \(1\leq i\leq s\), \(1\leq j\leq s\)) for (1) is asymptotically stable for \(h_{k}=\frac{\tau_{k+1}-\tau_{k}}{m}\), \(k\in \mathbb{N}\), \(m\in\mathbb{Z}^{+}\)and \(m\geq M\), ifkis even, where \(M=\inf\{m: I-zA\)is invertible and \((I-zA)^{-1}e\geq0, z=\alpha h_{k}, k\in\mathbb{N}, m\in\mathbb{Z}^{+}\}\). (The last inequality should be interpreted entrywise.)
Proof
Because \(a_{ij}\geq0\) and \(b_{i}\geq0\), \(1\leq i\leq s\), \(1\leq j\leq s\), we obtain
And when \(m\geq M\), \((I-zA)^{-1}e\geq0\), \(z=\alpha h_{k}\), \(k\in\mathbb {Z}^{+}\), so
where \([\|X_{k,l}^{i}-Y_{k,l}^{i}\|]=(\|X_{k,l}^{1}-Y_{k,l}^{1}\|,\| X_{k,l}^{2}-Y_{k,l}^{2}\|,\ldots, \|X_{k,l}^{s}-Y_{k,l}^{s}\|)^{T}\). By Lemma 3.2 and Lemma 3.3, we can obtain
Hence for arbitrary \(k=0,1,2,\ldots\) and \(l=0,1,\ldots,m\), we have
Therefore, by the method of the introduction and the condition (5), we obtain
which implies that Runge–Kutta method for (1) is asymptotically stable for \(h_{k}=\frac{\tau_{k+1}-\tau_{k}}{m}\), \(k\in \mathbb{N}\), \(m\in\mathbb{Z}^{+}\) and \(m\geq M\). □
Remark 3.5
-
(1)
For z sufficiently close to zero, the matrix \(I-zA\) is invertible and \((I-zA)^{-1}e\geq0\). Therefore, taking stepsizes \(h_{k}=\frac{\tau_{k+1}-\tau_{k}}{m}\), \(k\in\mathbb{N}\), \(m\in\mathbb {Z}^{+}\) and \(m\geq M\) and \(M=\inf\{m: I-zA\text{ is invertible}, (I-zA)^{-1}e\geq0, z=\alpha h_{k}, k\in\mathbb{N}, m\in\mathbb{Z}^{+}\}\) in Theorem 3.4 is reasonable.
-
(2)
Under the conditions of Remark 2.3, Runge–Kutta method (7) with nonnegative coefficients (\(a_{ij}\geq0\) and \(b_{i}\geq0\), \(1\leq i\leq s\), \(1\leq j\leq s\)) for (1) is stable for \(h_{k}=\frac{\tau_{k+1}-\tau_{k}}{m}\), \(k\in\mathbb{N}\), \(m\in \mathbb{Z}^{+}\) and \(m\geq M\), if k is even, where \(M=\inf\{ m: I-zA\) is invertible and \((I-zA)^{-1}e\geq0, z=\alpha h_{k}, k\in\mathbb {N}, m\in\mathbb{Z}^{+}\}\).
By Theorem 3.4 as \(\mathbf{k}=0\), we can obtain the following corollary.
Corollary 3.6
Under the conditions of Theorem 2.2, the followingp-stagepth order explicit Runge–Kutta methods with nonnegative coefficients (\(a_{ij}\geq0\)and \(b_{i}\geq0\), \(1\leq j< i\), \(1\leq i\leq p\)) for (1) are asymptotically stable for \(h_{k}=\frac{\tau_{k+1}-\tau _{k}}{m}\), \(k\in\mathbb{N}\), \(m\in\mathbb{Z}^{+}\), when \(p\leq4\).
- (1)
Explicit Euler method;
- (2)
2-stage second order explicit Runge–Kutta methods
- (3)
3-stage third order explicit Runge–Kutta methods
- (4)
The classical 4-stage fourth order explicit Runge–Kutta method
$$ \textstyle\begin{array}{c|cccc} 0 & 0 &0 &0 &0\\ \frac{1}{2} & \frac{1}{2} &0 &0 &0\\ \frac{1}{2} &0 &\frac{1}{2} &0 &0\\ \vphantom{\displaystyle\sum_{a}}1 &0 &0 &1 &0\\ \hline &\frac{1}{6}&\frac{1}{3}&\frac{1}{3}&\frac{1}{6} \end{array} $$
Unfortunately, we cannot obtain the p-stage explicit Runge–Kutta methods of order p for \(p\geq5\), because of the Butcher barriers (see [4, Theorem 370B, pp. 259] or [8, Theorem 5.1 pp. 173]).
In the following of this section, we will consider the θ-method for (1):
where \(h_{k}=\frac{\tau_{k+1}-\tau_{k}}{m}\), \(m\geq1\), m is an integer, \(k=0,1,2,\dots\).
Lemma 3.7
(See [19])
For \(m>\sup\{\alpha\tau _{k}-\tau_{k-1}\}\)and \(z_{k}=h_{k} \alpha\), \(h=\frac{\tau_{k}-\tau_{k-1}}{m}\), \(m, k\in\mathbb{Z}^{+}\), then
if and only if \(0\leq\theta\leq\varphi(1)\), where \(\varphi(x)=\frac{1}{x}-\frac{1}{\mathrm{e}^{x}-1}\).
Theorem 3.8
Under the conditions of Theorem 2.2, if \(0\leq \theta\leq\varphi(1)\), there is a positiveMsuch thatθmethod for (1) is asymptotically stable for \(h_{k}=\frac{\tau _{k+1}-\tau_{k}}{m}\), \(k\in\mathbb{N}\), \(m\in\mathbb{Z}^{+}\)and \(m\geq M\).
Proof
Obviously, we can obtain
which implies
Therefore, by Lemma 3.7 and the method of introduction, we obtain
So θ-method for (1) is asymptotically stable for \(h_{k}=\frac{\tau_{k+1}-\tau_{k}}{m}\), \(k\in\mathbb{N}\), \(m\in\mathbb {Z}^{+}\) and \(m> \sup\{\alpha(\tau_{k+1}-\tau_{k})\}\), if \(0\leq\theta \leq\varphi(1)\). □
4 Numerical experiments
In this section, two simple numerical examples in real space are given.
Example 4.1
Consider the following scalar impulsive differential equation:
Obviously, for arbitrary \(x,y\in\mathbb{R}\), we obtain
which implies the Lipschitz coefficient \(\alpha=1\). Hence, for \(k\geq2\),
Therefore, by Theorem 2.2, the exact solution of (11) is asymptotically stable.
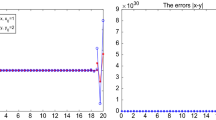
By Corollary 3.6, the explicit Euler method (see Fig. 1) and classical 4-stage fourth order explicit Runge–Kutta method (see Fig. 2) for (11) are asymptotically stable for \(h_{0}=\frac{3}{2m}\) and \(h_{k}=\frac{1+2^{-(k+1)}-2^{-k}}{m}\), \(k\in\mathbb {Z}^{+}\), \(m\in\mathbb{Z}^{+}\) and \(m\geq2\).
Explicit Euler method for (11)
The classical 4-stage fourth order Runge–Kutta method for (11)
Example 4.2
Consider the following scalar nonlinear impulsive differential equation:
Obviously, for arbitrary \(x,y\in\mathbb{R}\), we have
which implies the Lipschitz constant \(\alpha=\frac{1}{2}\). So
Therefore, by Theorem 2.2, the exact solution of (12) is asymptotically stable.
By Corollary 3.6, the explicit Euler method (see Fig. 3) and classical 4-stage fourth order explicit Runge–Kutta methods (see Fig. 4) for (12) are asymptotically stable for \(h_{k}=\frac{1}{m}\), \(k\in\mathbb{N}\), m is an arbitrary positive integer.
Explicit Euler method for (12) as \(h=\frac{1}{10}\)
The classical 4-stage fourth order Runge–Kutta method for (12) as \(h=\frac{1}{10}\)
From Tables 1 and 2, we can see that the Runge–Kutta methods conserve their orders of convergence.
References
Bainov, D.D., Simeonov, P.S.: Systems with Impulsive Effect: Stability, Theory and Applications. Ellis Horwood, Chichester (1989)
Bainov, D.D., Simeonov, P.S.: Impulsive Differential Equations: Asymptotic Properties of the Solutions. World Scientific, Singapore (1995)
Butcher, J.C.: The Numerical Analysis of Ordinary Differential Equations: Runge–Kutta and General Linear Methods. Wiley, New York (1987)
Butcher, J.C.: Numerical Methods for Ordinary Differential Equations. Wiley, Chichester (2003)
Dekker, K., Verwer, J.G.: Stability of Runge–Kutta Methods for Stiff Nonlinear Differential Equations. North-Holland, Amsterdam (1984)
Ding, X.H., Wu, K.N., Liu, M.Z.: Convergence and stability of the semi-implicit Euler method for linear stochastic delay integro-differential equations. Int. J. Comput. Math. 83, 753–763 (2006)
Ding, X.H., Wu, K.N., Liu, M.Z.: The Euler scheme and its convergence for impulsive delay differential equations. Appl. Math. Comput. 216, 1566–1570 (2010)
Hairer, E., Nørsett, S.P., Wanner, G.: Solving Ordinary Differential Equations II, Stiff and Differential Algebraic Problems. Springer, New York (1993)
Lakshmikantham, V., Bainov, D.D., Simeonov, P.S.: Theory of Impulsive Differential Equations. World Scientific, Singapore (1989)
Liang, H., Liu, M.Z.: Extinction and permanence of the numerical solution of a two-prey one-predator system with impulsive effect. Int. J. Comput. Math. 88, 1305–1325 (2014)
Liang, H., Song, M.H., Liu, M.Z.: Stability of the analytic and numerical solutions for impulsive differential equations. Appl. Numer. Math. 61, 1103–1113 (2011)
Liu, M.Z., Liang, H., Yang, Z.W.: Stability of Runge–Kutta methods in the numerical solution of linear impulsive differential equations. Appl. Math. Comput. 192, 346–357 (2007)
Liu, X., Song, M.H., Liu, M.Z.: Linear multistep methods for impulsive differential equations. Discrete Dyn. Nat. Soc. 2012, Article ID 652928 (2012). https://doi.org/10.1155/2012/652928
Liu, X., Zeng, Y.M.: Linear multistep methods for impulsive delay differential equations. Appl. Numer. Math. 321, 553–563 (2018)
Liu, X., Zhang, G.L., Liu, M.Z.: Analytic and numerical exponential asymptotic stability of nonlinear impulsive differential equations. Appl. Numer. Math. 81, 40–49 (2014)
Mil’man, V.D., Myshkis, A.D.: On the stability of motion in the presence of impulses. Sib. Math. J. 1, 233–237 (1960)
Ran, X.J., Liu, M.Z., Zhu, Q.Y.: Numerical methods for impulsive differential equation. Math. Comput. Model. 48, 46–55 (2008)
Samoilenko, A.M., Perestyuk, N.A., Chapovsky, Y.: Impulsive Differential Equations. World Scientific, Singapore (1995)
Song, M.H., Yang, Z.W., Liu, M.Z.: Stability of θ-methods for advanced differential equations with piecewise continuous arguments. Comput. Math. Appl. 49, 1295–1301 (2005)
Wang, Q., Qiu, S.: Oscillation of numerical solution in the Runge–Kutta methods for equation \(x'(t) = ax(t) + a_{0} x([t])\). Acta Math. Appl. Sin. Engl. Ser. 30, 943–950 (2014)
Wanner, G., Hairer, E., Nørsett, S.P.: Order stars and stability theorems. BIT Numer. Math. 18, 475–489 (1978)
Wen, L.P., Yu, Y.S.: The analytic and numerical stability of stiff impulsive differential equations in Banach space. Appl. Math. Lett. 24, 1751–1757 (2011)
Wu, K.N., Liu, X.Z., Yang, B.Q., Lim, C.C.: Mean square finite-time synchronization of impulsive stochastic delay reaction–diffusion systems. Commun. Nonlinear Sci. Numer. Simul. 79, Article ID 104899 (2019)
Wu, K.N., Na, M.Y., Wang, L.M., Ding, X.H., Wu, B.Y.: Finite-time stability of impulsive reaction–diffusion systems with and without time delay. Appl. Math. Comput. 363, Article ID 124591 (2019)
Wu, K.Z., Ding, X.H.: Impulsive stabilization of delay difference equations and its application in Nicholson’s blowflies models. Adv. Differ. Equ. 2012, Article ID 88 (2012). https://doi.org/10.1186/1687-1847-2012-88
Wu, K.Z., Ding, X.H.: Stability and stabilization of impulsive stochastic delay differential equations. In: Mathematical Problems in Engineering 2012 (2012). https://doi.org/10.1155/2012/176375
Wu, K.Z., Ding, X.H., Wang, L.M.: Stability and stabilization of impulsive stochastic delay difference equations. Discrete Dyn. Nat. Soc. 2010, Article ID 592036 (2010). https://doi.org/10.1155/2010/592036
Yang, Z.W., Liu, M.Z., Song, M.H.: Stability of Runge–Kutta methods in the numerical solution of equation \(u'(t) = au(t) + a_{0} u([t])+a_{1} u([t-1])\). Appl. Math. Comput. 162, 37–50 (2005)
Zhang, Z.H., Liang, H.: Collocation methods for impulsive differential equations. Appl. Math. Comput. 228, 336–348 (2014)
Acknowledgements
The author would like to thank the handling editors and the anonymous reviewers.
Availability of data and materials
The datasets used or analysed during the current study are available from the corresponding author on reasonable request.
Funding
This work is supported by the NSF of P.R. China (No. 11701074).
Author information
Authors and Affiliations
Contributions
The author read and approved the current manuscript.
Corresponding author
Ethics declarations
Competing interests
The author declares that there is no conflict of interests regarding the publication of this paper.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Zhang, GL. Asymptotical stability of Runge–Kutta methods for nonlinear impulsive differential equations. Adv Differ Equ 2020, 42 (2020). https://doi.org/10.1186/s13662-019-2473-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-019-2473-x