1 Introduction

Fluids that have both viscous and elastic behaviors are referred to as viscoelastic fluids, for example, polymers, castor oil, engine oil, etc. Viscoelastic fluid has very significant applications in the field of medicine, automobiles, polymers solutions, electrochemistry, and mechanics [1]. Due to contrasting simulations compared to Newtonian fluids, Navier–Stokes equations are no longer reliable to describe the rheology of viscoelastic fluids. Due to vast implementation in many areas, it got great attention of the scholars so that various models have been formulated. One of the well-known models among them is Jeffrey fluid model, which deals with the time derivative instead of the convective derivative. Second grade fluid model and viscous fluid model can be deduced from it by letting their parameters tend to zero. Keeping in mind the above mentioned facts, Jeffrey model was considered by many scholars like Hayat et al. [2] who studied Jeffrey fluid in the presence of thermal radiation. They developed velocity and temperature field via HPM and also showed variations in the fluid behavior due to embedded parameters. In another study, Hayat et al. [3] discussed the phenomenon of heat transfer of Jeffrey fluid over a moving surface, in which Jeffrey fluid model was considered as a rheological model. The authors studied Jeffrey fluid in the presence of thermal radiation effect and solved the governing equations by using HAM. Turkyilmazoglu et al. [4] investigated the heat transfer phenomena of Jeffrey fluid flow near the stagnation point. Furthermore, Elahi et al. [5] examined the simultaneous effects of magneto-hydrodynamic and partial slip on peristaltic flow of Jeffrey fluid in rectangular duct. The closed-form solution for the velocity field was obtained by a separation of variables procedure. In the above studies, low thermal conductivity was reported by the researchers for the considered fluids. To circumvent this issue, the idea of suspension of nanosized particles was adopted by the researchers and scholars. The first successful attempt was done by Eastman [6] in 1995. Eastman showed 40% enhancement in the thermal conductivity of ethylene glycol, when copper nanoparticles were dispersed at 0.3% volume fraction in ethylene glycol. Inspired from the work of Eastman and Choi, many researchers did their work on the above mentioned idea; see, e.g., Dinvarad et al. [7], Mohyud din et al. [8], Parekh and Lee [9], and Loganath [10]. They have noticed that nanoparticles are responsible for the enhancement of thermal conductivity and viscous forces. They also observed that nanofluids are more stable and do not have the sedimentation problem.

Magneto-hydrodynamic flow in a rotating frame has huge beneficial applications in various phenomena like cosmic and geographic flow, Earth rotation, formation of galaxies, circulation of oceans, electro-magnetic pumping, turbines and power generation, etc. Motivated by the above tremendous applications in mentioned fields, many researchers worked on the rotating phenomenon. The influence of silver nanoparticles on Jeffrey fluid flow was discussed by Atirah et al. [11]. They highlighted that velocity shows acceleration/deceleration at both primary and secondary positions when the rotation parameter varies. They also observed great variation in heat transfer rate when nanoparticles were uniformly dispersed in the fluid. Singh et al. [12] discussed the convective flow in the presence of transverse magnetic field past over an accelerated porous plate in a rotating channel. They highlighted the impact of several parameters like suction/injection, Prandtl number, and rotation parameter on flow behavior and also have shown the results graphically. Seth et al. [13] discussed the Couette flow under the effect of inclined magnetic field in a rotatory channel. They observed that the angle of inclination of applied magnetic field is responsible for deceleration of primary and secondary velocity throughout the channel. Ali et al. [14] studied the magneto-hydrodynamic flow of a Brinkman-type nanofluid in a rotating disk with Hall effect. They observed a 6.35% increase in the rate of heat transfer when MoS2 nanoparticles were dispersed uniformly in the considered fluid. Furthermore, Ali et al. [15] studied the different shapes of MoS2, namely (platelets, cylinders, bricks, and blades) taking engine and kerosene oil as base fluids in a rotating frame.

The effect of heat and mass transfer phenomena occur due to the differences in temperature and concentration. In modern technology, heat and mass transfer phenomena play a key role, especially in engineering, and due to this reason most researchers are attracted to further investigate this topic. Moreover, heat and mass transfer have a wide range of industrial and practical life applications, like freeze-drying food. Blums [16] as well as Incropera and De Witt [17] discussed in details heat and mass transfer with several thermal and concentration applications. The phenomenon of heat and mass transfer is very important because of many physical uses in science and modern technology, as discussed in the book of Nield and Bejan [18]. In heat and mass transfer phenomena, the transfer of thermal energy from one system to another is happening not only due to temperature gradient but also due to concentration gradient. The transfer of thermal energy due to concentration gradient is referred to as diffusion-thermo (Dufour effect). Already in 1952 Chapman and Cowling [19] developed the effect of diffusion-thermo on the transport of heat and mass from kinetic molecular theory of gases. Based on the above effects, different investigations have been carried out, e.g., Reddy et al. [20] discussed numerically the effect of diffusion-thermo and thermal diffusion in the presence of Hall current in a rotating frame for the fluid flowing in a porous medium. They highlighted that Dufour effect is responsible for the rise in the velocity and temperature field. Kafoussias et al. [21] analyzed the Dufour and Soret effects on a mixed convective flow along with temperature-dependent viscosity. The impact of Dufour and Soret numbers on a time-independent mixed convective flow of heat and mass transfer flowing over a semiinfinite plate under the influence of magnetic field was discussed by Alam et al. [22]. Zafer and William [23] studied the effect of diffusion-thermo and thermal diffusion on a natural convection flow over a vertical surface. They assumed helium–air mixture as a fluid and solved the governing equations analytically.

The concept of a fractional derivative was presented about 300 years ago, and it is known as the natural generalization of the ordinary calculus because it includes the derivatives and integrals of noninteger order. The idea of fractional calculus is based on a question [24] which was asked by L’Hospital in 1695 and addressed to Leibnitz about his notation that he used for the nth derivative of a function in his research publication, namely, what would happen if we take \(n=1/2\)? Leibniz responded that it would be an apparent paradox, but since then fruitful results were drawn. In the beginning, they did not get that much attention from mathematicians due to an abstract approach. But for the last three decades fractional calculus has shown remarkable development, and it changes from a pure mathematical formulation to different applied fields like bioengineering, physics, rheology, viscoelasticity, biophysics, and electrochemistry [25]. Especially, it has been proved that fractional calculus is a useful tool to deal with viscoelastic behavior [26]. The concept of fractional order calculus is used by various researchers in their work, and we refer to [27,28,29,30,31] for details. We note that there are some differences in the use of the involved operators. To successfully deal with the problem of a singular kernel, a new operator with exponential function for the fractional derivative was presented by Caputo and Fabrizio [32] in 2015. Using the concept of CF fractional derivative, Sheikh et al. [33] studied a generalized second grade fluid in a porous medium. Furthermore, Ali et al. [34] used time-fractional derivative for the influence of magnetic field on the blood flow of Casson fluid. Ali et al. [34] analyzed the two-phase blood flow of magnetic particles using CF fractional operators. Saqib et al. [35] studied a free convection flow of generalized Jeffrey fluid using CF fractional model. Although the existing fractional derivatives have been efficiently used in real world problems, there are still many things to be improved. For example, in the case of CF derivative [32], the operator is nonsingular, unlike in [24], but still it has a problem of nonlocality. Therefore, to fix this non-locality problem, Atangana and Baleanu [29, 36] in 2016 used the generalized Mittag-Leffler function and proposed a new operator for a fractional derivative having nonlocal and nonsingular kernel. Now the Atangana–Baleanu definition will be more significant when discussing real world problems and will also have a great advantage while using Laplace transform method to solve physical problems with initial conditions. By using the idea of AB fractional derivative, Sheikh et al. [37] developed exact an expression for the velocity distribution of Casson fluid. Variation in the velocity profile was also displayed graphically for various parameters. Some other interesting work based on time fractional derivative can be found in [38,39,40,41,42,43,44].

Inspired by the above literature review, the objective of the present investigation is to analyze the electrically conducted mixed convection flow of generalized Jeffrey nanofluid in a rotating frame past over an infinite oscillating plate saturated in a porous medium along with thermal radiation and diffusion-thermo. Tiwari and Das nanofluid model [45], along with Boussinesq approximation [46], is used for the development of the governing equations of the considered phenomenon. After that the governing equations are reduced to Atangana–Baleanu fractional model. Exact expressions for the velocity, heat, and mass distributions are obtained by using the Laplace transform method. To check the influence of pertinent parameters on the velocity profile, heat and mass distributions, exact expressions are plotted graphically. Variations in Sherwood and Nusselt numbers are also expressed in tabular form. It is worth noting that the rate of heat transfer is enhanced by 15.04% when the values of volume fraction of silver nanoparticles vary from 0.00 to 0.04.

2 Preliminaries

Definition 1

([47])

If \(f ( t )\) is a piecewise continuous function for \(t \ge 0\) and of exponential order m, then the Laplace transform \(F ( p )\) of \(f ( t )\) exists for all \(p > m\) and is given by

$$ L \bigl[ f ( t );p \bigr] = \int _{0}^{\infty } f ( t )e^{ - pt}\,dt. $$
(1)

Definition 2

([29])

Let \(f\in H^{1} ( a,b ). b > a\) and \(\alpha \in [0, 1]\), then the Atangana–Baleanu fractional derivative is given as;

$$ {}^{AB}\wp _{t}^{\alpha } f(t) = \frac{N(\alpha )}{1 - \alpha } \int _{0} ^{\tau } \mathrm{E}_{\boldsymbol{\alpha }} \biggl( \frac{ - \alpha ( \tau - t )}{1 - \alpha } \biggr) f' ( t )\,dt. $$
(2)

The Atangana–Baleanu fractional derivative operator is known to be helpful and is frequently used to discuss the real world phenomena. The AB time fractional derivative has huge beneficial applications when the Laplace transform technique is used to solve fractional differential equations.

The Laplace transform of Atangana–Baleanu time fractional operator is given as [29]:

$$ \text{\pounds}\bigl\{ {}^{AB}\wp _{t}^{\alpha } f(t) \bigr\} = \frac{N ( \alpha )}{1 - \alpha } \frac{p^{\alpha } \text{\pounds} ( f ( t ) )p - p^{\alpha - 1}f ( 0 )}{p ^{\alpha } + \frac{\alpha }{1 - \alpha }}. $$
(3)

2.1 Mathematical formulation of the problem

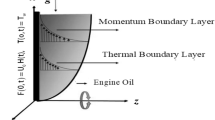
Assume Cartesian coordinate system for the study of the unsteady, incompressible Jeffrey nanofluid embedded in a porous medium. Fluid occupies space \(z \ge 0\). The whole system is assumed in a rigid body rotation. Jeffrey nanofluid is flowing along the x-axis which is taken vertically upward and rotating about the z-axis with fixed angular velocity Ω as shown in Fig. 1.

Figure 1
figure 1

Geometry of the flow

Full size image

A uniform magnetic field of strength \(B_{0}\) is applied transversely to the fluid motion which is parallel to the z-axis. Initially, both the fluid and plate are at stationary position. At time \(t = 0^{ +} \), the plate starts its motion due to cosine oscillations, while the temperature and concentration of the fluid are raised to Tw and Cw, respectively. Keeping in mind the above assumptions and under Boussinesq’s approximation, the governing equations are given as [46]:

$$\begin{aligned}& \rho _{nf} \biggl( \frac{\partial F ( z,t )}{\partial t} + 2 \varOmega iF ( z,t ) \biggr) \\& \quad = \frac{\mu _{nf}}{1 + \lambda _{1}} \biggl( 1 + \lambda _{2}\frac{\partial }{\partial t} \biggr)\frac{ \partial ^{2}F ( z,t )}{\partial z^{2}} - \frac{\mu _{nf} \phi _{1}}{k^{*} ( 1 + \lambda _{1} )} \biggl( 1 + \lambda _{2}\frac{\partial }{\partial t} \biggr)F ( z,t ) \\& \qquad {}- \sigma B_{0}^{2}F ( z,t ) + ( \rho \beta _{T} ) _{nf}g ( T - T_{\infty } ) + ( \rho \beta _{C} ) _{nf}g ( C - C_{\infty } ), \end{aligned}$$
(4)
$$\begin{aligned}& \frac{\partial T ( z,t )}{\partial t} = \frac{K_{nf}}{ ( \rho c_{p} )_{nf}}\frac{\partial ^{2}T ( z,t )}{ \partial z^{2}} - \frac{\partial q_{r}}{\partial z} + \frac{D_{m}K _{T}}{c_{s} ( c_{p} )_{nf}}\frac{\partial ^{2}C ( z,t )}{\partial z^{2}}, \end{aligned}$$
(5)
$$\begin{aligned}& \frac{\partial C ( z,t )}{\partial t} = D_{nf}\frac{ \partial ^{2}C ( z,t )}{\partial z^{2}}, \end{aligned}$$
(6)

where all the parameters and quantities are defined in the nomenclature section.

Physical initial and boundary conditions for the velocity, temperature and concentration profiles are as follows:

$$ \begin{aligned} &F ( z,0 ) = 0,&\quad & T ( z,0 ) = T_{\infty },&\quad & C ( z,0 ) = C_{\infty }, \\ &F ( 0,t ) = U_{0}H ( t )\cos wt,&\quad & T ( 0,t ) = T_{w},&\quad & C ( 0,t ) = C_{w}, \\ &F ( \infty ,t ) = 0, &\quad &T ( \infty ,t ) = T_{ \infty },&\quad & C ( \infty ,t ) = C_{\infty }. \end{aligned} $$
(7)

Nanofluid expressions involved in the governing equations are given as [48]:

$$ \begin{aligned} & ( \rho \beta _{T} )_{nf} = ( 1 - \varphi ) ( \rho \beta _{T} )_{f} + \varphi ( \rho \beta _{T} ) _{s}, \qquad ( \rho c_{p} )_{nf} = ( 1 - \varphi ) ( \rho c_{p} )_{f} + \varphi ( \rho c_{p} ) _{s}, \\ &\mu _{nf} = \mu _{f} ( 1 - \varphi )^{ - 2.5}, \qquad \rho _{nf} = ( 1 - \varphi )\rho _{f} + \varphi \rho _{s},\qquad D_{nf} = ( 1 - \varphi )D_{f}, \\ &k_{nf} = k_{f} \biggl( \frac{k_{s} + 2k_{f} - 2\varphi ( k_{f} - k_{s} )}{k_{s} + 2k_{f} + 2\varphi ( k_{f} - k_{s} )} \biggr). \end{aligned} $$
(8)

The mentioned nanofluid expressions are applicable for spherical shaped nanosized particles. The thrmophysical properties of nanoparticles and base fluids are given in Table 1. The term for radiative heat flux by using Rosseland approximation [49] is given as:

$$ q_{r} = \frac{ - 4\sigma ^{*}\partial T^{4}}{3k_{1}^{*}\partial z}. $$
(9)

In order to linearize \(T^{4}\), we use Taylor expansion about \(T_{\infty } \) up to two terms, and then \(T^{4}\) takes the form:

$$ T^{4} = 4TT_{\infty }^{3} - 3T_{\infty }^{4}. $$
(10)

Incorporating Eq. (9) into Eq. (8) and differentiating with respect to z, we get

$$ \frac{\partial q_{r}}{\partial z} = \frac{16\sigma ^{*}T_{\infty }^{3}}{3k _{1}^{*}}\frac{\partial ^{2}T}{\partial z^{2}}. $$
(11)
Table 1 The thermo-physical properties of the base fluid and nanosized particles
Full size table

For dimensional analysis, the dimensionless variables are:

$$ F^{*} = \frac{F}{U_{0}},\qquad z^{*} = \frac{zU_{0}}{\nu },\qquad t^{*} = \frac{tU_{0}^{2}}{\nu },\qquad \theta = \frac{T - T_{\infty }}{T_{w} - T _{\infty }},\qquad \phi = \frac{C - C_{\infty }}{C_{w} - C_{\infty }} . $$
(12)

Using expressions defined in Eq. (10) and dimensionless variables defined in (11), the governing equations take the following form:

$$\begin{aligned}& \begin{aligned}[b] \frac{\partial F ( z,t )}{\partial t} + 2irF ={}& \frac{a _{1}}{1 + \lambda _{1}} \biggl( 1 + \lambda \frac{\partial }{\partial t} \biggr)\frac{\partial ^{2}F ( z,t )}{ \partial z^{2}} - \frac{a_{1}}{k ( 1 + \lambda _{1} )} \biggl( 1 + \lambda \frac{\partial }{\partial t} \biggr)F ( z,t ) \\ &{} - \biggl( \frac{Ha}{a_{3}} \biggr)F ( z,t ) + d_{1}\theta ( z,t ) + d_{2}\phi ( z,t ), \end{aligned} \end{aligned}$$
(13)
$$\begin{aligned}& \frac{\partial \theta ( z,t )}{\partial t} = a_{4}\frac{ \partial ^{2}\theta ( z,t )}{\partial z^{2}} + d_{3} \frac{ \partial ^{2}\phi ( z,t )}{\partial z^{2}}, \end{aligned}$$
(14)
$$\begin{aligned}& \frac{\partial \phi ( z,t )}{\partial t} = a_{5}\frac{ \partial ^{2}\phi ( z,t )}{\partial z^{2}}. \end{aligned}$$
(15)

And dimensionless initial and boundary conditions are:

$$ \begin{aligned} &F ( z,0 ) = 0,&\quad & T ( z,0 ) = 0,&\quad & C ( z,0 ) = 0, \\ &F ( 0,t ) = \cos wt,&\quad & T ( 0,t ) = 1,&\quad & C ( 0,t ) = 1, \\ &F ( \infty ,t ) = 0,&\quad & T ( \infty ,t ) = 0,&\quad & C ( \infty ,t ) = 0. \end{aligned} $$
(16)

In the dimensionalization process the constants and parameters are:

$$\begin{aligned}& r = \frac{\varOmega \nu }{U_{0}^{2}},\qquad \lambda = \frac{\lambda _{2}U_{0} ^{2}}{\nu }, \qquad \frac{1}{K} = \frac{\phi _{1}\nu }{K_{1}^{*}U_{0}^{2}},\qquad Ha = \frac{\sigma ^{*}\beta _{0}^{2}\nu }{\rho U_{0}^{2}}, \\& Gr = \frac{g \beta _{T}\nu (T_{w} - T_{\infty } )}{U_{0}^{3}}, \qquad Gm = \frac{g\beta _{C}\nu (C_{w} - C_{\infty } )}{U_{0}^{3}},\qquad d_{1} = a _{2}Gr,\qquad d_{2} = a_{6}Gm, \\& \Pr = \frac{\nu _{f}}{\alpha _{f}},\qquad R_{d} = \frac{16\sigma ^{*}T^{3}}{k_{f}k_{1}^{*}},\qquad Sc = \frac{\nu }{D _{f}},\qquad m_{1} = (1 - \varphi ) + \varphi \frac{(\rho c_{p})_{s}}{( \rho c_{p})_{f}}, \\& m_{2} = \frac{k_{s} + 2k_{f} - 2\varphi (k_{f} - k _{s})}{k_{s} + 2k_{f} + \varphi (k_{f} - k_{s})}, \qquad a_{1} = \biggl( ( 1 - \varphi )^{2.5} \biggl\{ ( 1 - \varphi ) + \varphi \frac{\rho _{s}}{\rho _{f}} \biggr\} \biggr) ^{ - 1}, \\& a_{2} = \frac{1}{\rho _{nf}} \biggl( ( 1 - \varphi ) \rho _{f} + \frac{ ( \beta _{T} )_{s}}{ ( \beta _{T} ) _{f}} \biggr), \qquad a_{3} = ( 1 - \varphi ) + \varphi \frac{\rho _{s}}{\rho _{f}},\qquad a_{4} = \frac{m_{2} + R_{d}}{m_{1}\Pr }, \\& a_{5} = \frac{S_{c}}{1 - \varphi },\qquad a_{6} = \frac{1}{\rho _{nf}} \biggl( ( 1 - \varphi ) \rho _{f} + \frac{ ( \beta _{C} )_{s}}{ ( \beta _{C} ) _{f}} \biggr), \\& Df = \frac{D_{m}K_{T}}{c_{s}c_{p}\nu } \biggl( \frac{C_{w} - C_{ \infty }}{T_{w} - T_{\infty }} \biggr),\qquad d_{3} = \frac{Df}{m_{1}}. \end{aligned}$$

2.2 Atangana–Baleanu fractional model

To transform the classical model defined in Eqs. (12), (13) and (14) into AB fractional model, we used \({}^{AB}\wp _{t}^{\alpha } \) instead of \(\frac{\partial }{\partial t}(\cdot)\) and got

$$\begin{aligned}& {}^{AB}\wp _{t}^{\alpha } F ( z,t ) + 2irF ( z,t ) \\& \quad = \frac{a_{1}}{1 + \lambda _{1}} \bigl( 1 + \lambda ^{AB}\wp _{t}^{ \alpha } \bigr)\frac{\partial ^{2}F ( z,t )}{\partial z ^{2}} + \frac{a_{1}}{1 + \lambda _{1}} \bigl( 1 + \lambda ^{AB}\wp _{t} ^{\alpha } \bigr)F ( z,t ) \\& \qquad {}- \biggl( \frac{Ha}{a_{3}} \biggr)F ( z,t ) + d_{1} \theta ( z,t ) + d_{2}\phi ( z,t ), \end{aligned}$$
(17)
$$\begin{aligned}& {}^{AB}\wp _{t}^{\alpha } \theta ( z,t ) = a_{4}\frac{ \partial ^{2}\theta ( z,t )}{\partial z^{2}} + d_{3}\frac{ \partial ^{2}\phi ( z,t )}{\partial z^{2}}, \end{aligned}$$
(18)
$$\begin{aligned}& {}^{AB}\wp _{t}^{\alpha } \phi ( z,t ) = a_{4}\frac{\partial ^{2}\theta ( z,t )}{\partial z^{2}}, \end{aligned}$$
(19)

where the operator of AB fractional derivative [29] is

$$ ^{AB}\wp _{t}^{\alpha } f(t) = \frac{N(\alpha )}{1 - \alpha } \int _{0} ^{\tau } \mathrm{E}_{\boldsymbol{\alpha }} \biggl( \frac{ - \alpha ( \tau - t )}{1 - \alpha } \biggr) f' ( t )\,dt, $$
(20)

where \(N ( 0 ) = N ( 1 ) = 1\), \(0 < \alpha < 1\) and \(E_{\alpha } \) is Mittag-Leffler function.

2.3 Exact solutions

Applying Laplace transform on Eqs. (16), (17) and (18), and using initial conditions defined in Eq. (15), we get

$$\begin{aligned}& \frac{d^{2}\overline{\phi } ( z,p )}{dz^{2}} - \biggl( \frac{ \delta _{3}p^{\alpha }}{p^{\alpha } + \delta _{1}} \biggr)\overline{ \phi } ( z,p ) = 0, \end{aligned}$$
(21)
$$\begin{aligned}& \frac{d^{2}\overline{\theta } ( z,p )}{dz^{2}} - \biggl( \frac{\delta _{2}p^{\alpha }}{p^{\alpha } + \delta _{1}} \biggr)\overline{ \theta } ( z,p ) = \frac{d_{3}}{p} \biggl( \frac{\delta _{3}p^{\alpha }}{p^{\alpha } + \delta _{1}} \biggr)\exp \biggl( - z\sqrt{ \frac{ \delta _{3}p^{\alpha }}{p^{\alpha } + \delta _{1}}} \biggr), \end{aligned}$$
(22)
$$\begin{aligned}& \frac{d^{2}\overline{F} ( z,p )}{dz^{2}} - \biggl( \frac{ \delta _{6}p^{\alpha } + \delta _{7}}{\delta _{4}p^{\alpha } + \delta _{5}} \biggr)\overline{F} ( z,p ) = \frac{ - d_{1} ( p^{\alpha } + \delta _{1} )}{\delta _{4}p^{\alpha } + \delta _{5}}\overline{ \theta } ( z,p ) - \frac{ - d_{2} ( p^{\alpha } + \delta _{1} )}{\delta _{4}p^{\alpha } + \delta _{5}}\overline{ \phi } ( z,p ), \end{aligned}$$
(23)

and the transformed boundary conditions are

$$ \begin{aligned} &\overline{F} ( 0,p ) = \frac{p}{p^{2} + \omega ^{2}}, &\quad &\overline{ \theta } ( 0,p ) = \frac{1}{p},&\quad & \overline{\phi } ( 0,p ) = \frac{1}{p}, \\ &\overline{F} ( \infty ,p ) = 0,&\quad & \overline{\theta } ( \infty ,p ) = 0, & \quad &\overline{\phi } ( \infty ,p ) = 0, \end{aligned} $$
(24)

where

$$\begin{aligned}& \delta _{0} = \frac{1}{1 - \alpha }, \qquad \delta _{1} = \alpha \delta _{0},\qquad \delta _{2} = \frac{\delta _{0}}{a_{4}}, \qquad \delta _{3} = a_{5}\delta _{0}, \qquad b_{1} = 1 + \frac{a_{1}\lambda }{k ( 1 + \lambda _{1} )}, \\& b_{2} = \frac{a_{1}}{1 + \lambda _{1}},\qquad b_{3} = \frac{a_{1}\lambda\delta _{0}}{1 + \lambda _{1}}, \qquad b_{4} = \frac{Ha}{a_{3}} + \frac{a_{1}}{k ( 1 + \lambda _{1} )} + 2ir, \qquad \delta _{4} = b_{2} + b_{3}, \\& \delta _{5} = b_{2}\delta _{1},\qquad \delta _{6} = b_{1}\delta _{0} + b_{4},\qquad \delta _{7} = \delta _{1}b_{4}, \end{aligned}$$

where, employing transformed boundary conditions defined in Eq. (23), the solution of Eqs. (20), (21) and (22) will be

$$\begin{aligned}& \overline{\phi } ( z,p ) = \frac{1}{p^{1 - \alpha }} \overline{ \phi _{3}^{*}} ( z,p,0,\delta _{3},0,\delta _{1} ), \end{aligned}$$
(25)
$$\begin{aligned}& \overline{\theta } ( z,p ) = \frac{1}{p^{1 - \alpha }} \bigl[ \delta _{2}^{*}\overline{\phi _{3}^{*}} ( z,p,0,\delta _{2},0, \delta _{1} ) + \delta _{1}^{*}\overline{\phi _{3}^{*}} ( z,p,0, \delta _{3},0,\delta _{1} ) \bigr], \end{aligned}$$
(26)
$$\begin{aligned}& \overline{F} ( z,p ) \\& \quad = \frac{p}{p^{2} + \omega ^{2}}\overline{ \phi _{1}^{*}} ( z,p, \delta _{6},\delta _{7},\delta _{21},\sqrt{ \delta _{4}} ) \\& \qquad {}+ \frac{1}{p^{1 - \alpha }} \begin{bmatrix} \Re _{1}\overline{\phi _{2}^{*}} ( z,p,0,\delta _{6},\delta _{7}, \delta _{21},\sqrt{\delta _{4}} ) + \Re _{2}\overline{\phi _{2} ^{*}} ( z,p,\delta _{12},\delta _{6},\delta _{7},\delta _{21},\sqrt{ \delta _{4}} ) \\ {}+ \Re _{3}\overline{\phi _{2}^{*}} ( z,p,\delta _{13},\delta _{6}, \delta _{7},\delta _{21},\sqrt{\delta _{4}} ) + \Re _{4}\overline{ \phi _{2}^{*}} ( z,p,0,\delta _{6},\delta _{7},\delta _{21},\sqrt{ \delta _{4}} ) \\ {}+ \Re _{5}\overline{\phi _{2}^{*}} ( z,p,\varGamma _{1},\delta _{6}, \delta _{7},\delta _{21},\sqrt{\delta _{4}} ) + \Re _{6}\overline{ \phi _{2}^{*}} ( z,p,\delta _{12},\varGamma _{2},\delta _{7},\delta _{21},\sqrt{ \delta _{4}} ) \end{bmatrix} \\& \qquad {}- \frac{1}{p^{1 - \alpha }} \begin{bmatrix} \Re _{1}\overline{\phi _{3}^{*}} ( z,p,0,\delta _{2},0,\delta _{1} ) + \Re _{2}\overline{\phi _{3}^{*}} ( z,p,\delta _{12},\delta _{2},0,\delta _{1} ) \\ {}+ \Re _{3}\overline{\phi _{3}^{*}} ( z,p,\delta _{13},\delta _{2},0, \delta _{1} ) \end{bmatrix} \\& \qquad {}- \frac{1}{p^{1 - \alpha }} \begin{bmatrix} \Re _{4}\overline{\phi _{3}^{*}} ( z,p,0,\delta _{3},0,\delta _{1} ) + \Re _{5}\overline{\phi _{3}^{*}} ( z,p,\varGamma _{1},\delta _{3},0,\delta _{1} ) \\ {}+ \Re _{6}\overline{\phi _{3}^{*}} ( z,p, \varGamma _{2},\delta _{3},0,\delta _{1} ) + \Re _{7}\overline{\phi _{3}^{*}} ( z,p,0,\delta _{3},0,\delta _{1} ) \\ {}+ \Re _{8}\overline{\phi _{3}^{*}} ( z,p,\varGamma _{1},\delta _{3},0,\delta _{1} ) + \Re _{9}\overline{\phi _{3}^{*}} ( z,p, \varGamma _{2},\delta _{3},0,\delta _{1} ) \end{bmatrix}, \end{aligned}$$
(27)

where

$$\begin{aligned}& \overline{\phi }_{1}^{*} ( z,p,m_{1},m_{2},m_{3},m_{4} ) = \exp \biggl( - \frac{z}{m_{4}}\sqrt{\frac{m_{1}p^{\alpha } + m_{2}}{p ^{\alpha } + m_{3}}} \biggr), \end{aligned}$$
(28)
$$\begin{aligned}& \overline{\phi }_{2}^{*} ( z,p,m_{1},m_{2},m_{3},m_{4},m_{5} ) = \frac{1}{p^{\alpha } + m_{1}}\exp \biggl( - \frac{z}{m_{5}}\sqrt{\frac{m_{2}p^{\alpha } + m_{3}}{p^{\alpha } + m _{4}}} \biggr), \end{aligned}$$
(29)
$$\begin{aligned}& \overline{\phi }_{3}^{*} ( z,p,m_{1},m_{2},m_{3},m_{4} ) = \frac{1}{p^{\alpha } + m_{1}}\exp \biggl( - z\sqrt{\frac{m_{2}p^{ \alpha } + m_{3}}{p^{\alpha } + m_{4}}} \biggr), \end{aligned}$$
(30)

and

$$\begin{aligned}& \delta _{8} = \frac{\delta _{2}\delta _{5} - \delta _{1}\delta _{6} - \delta _{7}}{\delta _{2}\delta _{4} - \delta _{6}},\qquad \delta _{9} = \frac{ \delta _{1}\delta _{7}}{\delta _{2}\delta _{4} - \delta _{6}}, \qquad \delta _{10} = \frac{\delta _{8}}{2}, \qquad \delta _{11} = \sqrt{ ( \delta _{10} ) ^{2} + \delta _{9}}, \\& \delta _{12} = \delta _{10} + \delta _{11}, \qquad \delta _{13} = \delta _{10} - \delta _{11},\qquad \delta _{14} = \frac{\delta _{1}^{2}}{\delta _{12}\delta _{13}},\qquad \delta _{15} = \frac{ ( \delta _{1} - \delta _{13} )^{2}}{\delta _{12} - \delta _{13}}, \\& \delta _{16} = \frac{ ( \delta _{1} - \delta _{13} )^{2}}{\delta _{13} ( \delta _{13} - \delta _{12} )},\qquad \delta _{17} = \frac{ \delta _{3}\delta _{5} - \delta _{1}\delta _{6} - \delta _{7}}{\delta _{3} \delta _{4} - \delta _{6}}, \qquad \delta _{18} = \frac{\delta _{1}\delta _{7}}{\delta _{3}\delta _{4} - \delta _{6}},\qquad \delta _{19} = \frac{\delta _{17}}{2}, \\& \delta _{20} = \sqrt{ ( \delta _{19} )^{2} + \delta _{18}}, \qquad \varGamma _{1} = \delta _{19} + \delta _{20}, \qquad \varGamma _{2} = \delta _{19} - \delta _{20},\qquad \varGamma _{3} = \frac{\delta _{1}^{2}}{\varGamma _{1}\varGamma _{2}}, \\& \varGamma _{4} = \frac{ ( \delta _{1} - \varGamma _{1} )^{2}}{ \varGamma _{1} ( \varGamma _{1} - \varGamma _{2} )},\qquad \varGamma _{5} = \frac{ ( \delta _{1} - \varGamma _{2} )^{2}}{\varGamma _{2} ( \varGamma _{1} - \varGamma _{2} )}, \qquad \delta ^{*} = \delta _{3} - \delta _{2},\qquad \delta _{1}^{*} = \frac{d_{3}\delta _{3}}{a_{4}\delta ^{*}}, \\& \delta _{2} ^{*} = 1 - \delta _{1}^{*}, \qquad d_{2}^{*} = d_{1}\delta _{1}^{*}, \qquad \Re _{1} = d_{1}\delta _{14}, \qquad \Re _{2} = d_{1}\delta _{15}, \qquad \Re _{3} = d _{1}\delta _{16}, \\& \Re _{4} = d_{1}\varGamma _{3},\qquad \Re _{5} = d_{1}\varGamma _{4},\qquad \Re _{6} = d_{1}\varGamma _{5},\qquad \Re _{7} = d_{2}\varGamma _{3}, \\& \Re _{8} = d_{2}\varGamma _{4}, \qquad \Re _{9} = d_{2}\varGamma _{5}. \end{aligned}$$

By taking the inverse Laplace transform, Eqs. (24), (25) and (26) will take the form:

$$\begin{aligned}& \phi ( z,t ) = h ( t )*\phi _{3}^{*} ( z,t,0, \delta _{3},0,\delta _{1} ), \end{aligned}$$
(31)
$$\begin{aligned}& \theta ( z,t ) = h ( t )* \bigl[ \delta _{2} ^{*}\phi _{3}^{*} ( z,t,0,\delta _{2},0,\delta _{1} ) + \delta _{1}^{*}\phi _{3}^{*} ( z,t,0,\delta _{3},0,\delta _{1} ) \bigr], \end{aligned}$$
(32)
$$\begin{aligned}& F ( z,t ) \\& \quad = \cos wt*\phi _{1}^{*} ( z,t,\delta _{6}, \delta _{7},\delta _{21},\sqrt{\delta _{4}} ) \\& \qquad {}+ h ( t )*\begin{bmatrix} \Re _{1}\phi _{2}^{*} ( z,t,0,\delta _{6},\delta _{7},\delta _{21},\sqrt{ \delta _{4}} ) + \Re _{2}\phi _{2}^{*} ( z,t,\delta _{12}, \delta _{6},\delta _{7},\delta _{21},\sqrt{\delta _{4}} ) \\ {}+ \Re _{3}\phi _{2}^{*} ( z,t,\delta _{13},\delta _{6},\delta _{7}, \delta _{21},\sqrt{\delta _{4}} ) + \Re _{4}\phi _{2}^{*} ( z,t,0,\delta _{6},\delta _{7},\delta _{21},\sqrt{\delta _{4}} ) \\ {}+ \Re _{5}\phi _{2}^{*} ( z,t,\varGamma _{1},\delta _{6},\delta _{7}, \delta _{21},\sqrt{\delta _{4}} ) + \Re _{6}\phi _{2}^{*} ( z,t,\delta _{12},\varGamma _{2},\delta _{7},\delta _{21},\sqrt{\delta _{4}} ) \end{bmatrix} \\& \qquad {}- h ( t )*\begin{bmatrix}\Re _{1}\phi _{3}^{*} ( z,t,0,\delta _{2},0,\delta _{1} ) + \Re _{2}\phi _{3}^{*} ( z,t,\delta _{12},\delta _{2},0,\delta _{1} )\\ {} + \Re _{3}\phi _{3}^{*} ( z,t, \delta _{13},\delta _{2},0,\delta _{1} ) \end{bmatrix} \\& \qquad {}- h ( t )*\begin{bmatrix} \Re _{4}\phi _{3}^{*} ( z,t,0,\delta _{3},0,\delta _{1} ) + \Re _{5}\phi _{3}^{*} ( z,t,\varGamma _{1},\delta _{3},0,\delta _{1} )\\ {} + \Re _{6}\phi _{3}^{*} ( z,t,\varGamma _{2},\delta _{3},0, \delta _{1} ) + \Re _{7}\phi _{3}^{*} ( z,t,0,\delta _{3},0,\delta _{1} ) \\ {}+ \Re _{8}\phi _{3}^{*} ( z,t,\varGamma _{1},\delta _{3},0,\delta _{1} ) + \Re _{9}\phi _{3}^{*} ( z,t,\varGamma _{2},\delta _{3},0, \delta _{1} ) \end{bmatrix}. \end{aligned}$$
(33)

Here * shows convolution-product and

$$h ( t ) = L^{ - 1} \biggl[ \frac{1}{p^{1 - \alpha }} \biggr] = \frac{1}{t^{\alpha } \varGamma ( 1 - \alpha )}. $$

Here

$$\begin{aligned}& \phi _{1}^{*} ( z,t,m_{1},m_{2},m_{3},m_{4} ) \\& \quad = \frac{1}{ \pi } \int _{0}^{\infty } \int _{0}^{\infty } \varPsi _{1} ( z,u,c_{1},c _{2},c_{3},c_{4} )\exp \bigl( \mathrm{tr}_{1} - r_{2}r_{1}^{\alpha } \cos \alpha \pi \bigr)\sin \bigl( r_{2}r_{1}^{\alpha } \sin \alpha \pi \bigr)\,dr_{1}\,dr_{2}, \\& \phi _{2}^{*} ( z,t,m_{1},m_{2},m_{3},m _{4},m_{5} ) \\& \quad = \frac{1}{\pi } \int _{0}^{\infty } \int _{0}^{ \infty } \varPsi _{2} ( z,u,c_{1},c_{2},c_{3},c_{4},c_{5} ) \exp \bigl( \mathrm{tr}_{1} - r_{2}r_{1}^{\alpha } \cos \alpha \pi \bigr) \\& \qquad {}\times \sin \bigl( r_{2}r_{1}^{\alpha } \sin \alpha \pi \bigr)\,dr_{1}\,dr_{2}, \\& \phi _{3}^{*} ( z,t,m_{1},m_{2},m_{3},m_{4} ) \\& \quad = \frac{1}{ \pi } \int _{0}^{\infty } \int _{0}^{\infty } \varPsi _{3} ( z,u,c_{1},c _{2},c_{3},c_{4} )\exp \bigl( \mathrm{tr}_{1} - r_{2}r_{1}^{\alpha } \cos \alpha \pi \bigr)\sin \bigl( r_{2}r_{1}^{\alpha } \sin \alpha \pi \bigr)\,dr_{1}\,dr_{2}, \end{aligned}$$

in which

$$\begin{aligned}& \varPsi _{1} ( z,t,c_{1},c_{2},c_{3},c_{4} ) \\& \quad = e^{\frac{ - z}{c _{4}}\sqrt{c_{1}}} - \frac{z\sqrt{c_{2} - c_{1}c_{3}}}{2c_{4}\sqrt{ \pi t}} \int _{0}^{\infty } \frac{1}{r_{2}}\exp \biggl( \frac{ - z^{2}}{4c _{4}^{2}r_{2}} - c_{1}r_{2} \biggr)\cdot I_{1} \bigl( 2\sqrt{ ( c _{2} - c_{1}c_{3} )r_{2}t} \bigr)\,dr_{2}, \\& \varPsi _{2} ( z,t,c _{1},c_{2},c_{3},c_{4},c_{5} ) \\& \quad = e^{ - c_{1}t - \frac{ - z}{c _{5}}\sqrt{c_{1}}} - \frac{z\sqrt{c_{3} - c_{2}c_{4}}}{2c_{5}\sqrt{ \pi }} \\& \qquad\times {} \int _{0}^{\infty } \int _{0}^{t} \frac{e^{ - c_{1}t}}{ \sqrt{t}} \exp \biggl( c_{1}t - c_{4}t - \frac{ - z^{2}}{4c_{5}r_{2}} - c_{2}r_{2} \biggr)\cdot I_{1} \bigl( 2\sqrt{ ( c_{3} - c_{2}c _{4} )r_{2}t} \bigr)\,dt \,dr_{2}, \\& \varPsi _{3} ( z,t,c_{1},c_{2},c _{3},c_{4} ) \\& \quad = e^{ - c_{1}t - z\sqrt{c_{2}}} - \frac{z\sqrt{c _{3} - c_{2}c_{4}}}{2c_{5}\sqrt{\pi }} \\& \qquad\times {} \int _{0}^{\infty } \int _{0} ^{t} \frac{e^{ - c_{1}t}}{\sqrt{t}} \exp \biggl( c_{1}t - c_{4}t - \frac{ - z^{2}}{4r_{2}} - c_{2}r_{2} \biggr)\cdot I_{1} \bigl( 2\sqrt{ ( c_{3} - c_{2}c_{4} )r_{2}t} \bigr)\,dt \,dr_{2}. \end{aligned}$$

2.4 Nusselt number

Nusselt number in dimensionless form is represented as

$$ Nu = - \frac{k_{nf}}{k_{f}} \frac{\partial \theta }{\partial z} \bigg|_{z = 0}. $$
(34)

2.5 Sherwood number

The dimensionless form of Sherwood number is

$$ S_{h} = - D_{nf} \biggl( \frac{\partial \phi }{\partial z} \biggr) _{z = 0}. $$
(35)

3 Results and discussion

This section deals with the interpretation of the obtained results. After transforming the classical model to Atangana–Baleanu time fractional model, exact expressions were obtained via the Laplace transform technique. In order to highlight the effects the relative parameters, namely, Dufour effect Df, Schmidt number Sc, thermal Grashof number Gr, mass Grashof number Gm, rotation parameter r, Hartman number Ha, permeability parameter K, material parameters of Jeffrey fluid λ and \(\lambda _{1}\) on the velocity, temperature, and concentration profile, plots were drawn using MATHCAD.

Variation in the velocity profile due to volume fraction φ can be observed from Fig. 2. By increasing the volume fraction φ, the engine oil retards. This is due to the fact that, when value of φ increases, the fluid becomes more viscous and the friction force between the fluid particles increases, as a result the fluid decelerates. The range for the volume fraction of nanoparticles is chosen between 0.01 and 0.04; if this selected limit is crossed then sedimentation and clogging will be caused.

Figure 2
figure 2

Impact of φ on the velocity distribution of Jeffrey nanofluid

Full size image

Figure 3 depicts the influence of magnetic parameter Ha on the velocity profile. It can be observed that, as the values of Ha increase, the fluid slows down. The physics behind this phenomenon is that, when magnetic field is applied to the fluid flow, it creates Lorentz forces which act as an opposing agent to the fluid motion and produce resistive forces to the fluid particles, as a result the fluid retards.

Figure 3
figure 3

Impact of Ha on the velocity distribution of Jeffrey nanofluid

Full size image

Figure 4 shows that increasing the values of Gr from 5 to 20 makes the velocity of the fluid increase. This is true because, for higher values of Gr, the buoyancy forces increase, as a result the thickness of the momentum boundary layer decreases, which leads to velocity increase.

Figure 4
figure 4

Impact of Gr on the velocity distribution of Jeffrey nanofluid

Full size image

The effect of material parameter λ on the velocity profile can be seen from Fig. 5. It is interesting to note that, as the values of λ increase, a fall in the velocity is noticed. This is due to an increase in the viscosity and elasticity of the fluid.

Figure 5
figure 5

Impact of λ on the velocity distribution of Jeffrey nanofluid

Full size image

In Fig. 6, an enhancement in the velocity profile can be observed for higher values of Jeffrey fluid parameter \(\lambda _{1}\). It is true because \(\lambda _{1}\) is the ratio between relaxation and retardation time parameters. So that, as we increase the value of \(\lambda _{1}\), immediate response is received to shear stress and so the fluid accelerates.

Figure 6
figure 6

Impact of \(\lambda _{1}\) on the velocity distribution of Jeffrey nanofluid

Full size image

Under the influence of K, the velocity profile is displayed in Fig. 7. As the value of K increases, the motion of the fluid increases. Physically, it is true because, for higher values of K, the resistance from porous medium reduces, and as a result the fluid accelerates.

Figure 7
figure 7

Impact of K on the velocity distribution of Jeffrey nanofluid

Full size image

The velocity profile under the influence of mass Grashof number Gm can be noticed form Fig. 8, which shows a rise in the velocity profile when the value of mass Grashof number is increased. This happened due to the concentration gradient which raised the buoyancy forces in the fluid, and consequently the velocity increased.

Figure 8
figure 8

Impact of Gm on the velocity distribution of Jeffrey nanofluid

Full size image

Figure 9 shows the behavior of the fluid under the influence of Schmidt number Sc. It can be seen that the velocity of the fluid decreases for higher values of Sc. This is true because for higher values of Sc the viscosity of the fluid increases, the mass diffusion rate decreases, and as a result the velocity diminishes.

Figure 9
figure 9

Impact of Sc on the velocity distribution of Jeffrey nanofluid

Full size image

Figure 10 illustrates the effect of the rotation parameter r on the fluid motion. The velocity of the fluid decreases as the values of r increases. This is due to the fact that the rotation parameter is directly proportional to the kinematic viscosity, so when increasing the value of r, the fluid motion decreases.

Figure 10
figure 10

Impact of r on the velocity distribution of Jeffrey nanofluid

Full size image

The effect of Dufour number Df can be seen from Fig. 11. Enhancement in the velocity profile is noticed for higher values of Df. Physically, it is true because, when Df increases, the rate of mass diffusion increases, kinematic viscosity of fluid decreases, and consequently, velocity increases.

Figure 11
figure 11

Impact of Df on the velocity distribution of Jeffrey nanofluid

Full size image

Figure 12 displays a rise in the temperature profile of the fluid for higher values of Df. This is due to the effect of the increase of thermal conductivity and decrease of specific heat capacity of the fluid, while enhancement in the heat transfer rate due to volume fraction φ can be noticed from Fig. 13. As the volume fraction of the nanoparticle increases, viscous forces in the fluid increase, which leads to a rise in the boiling and freezing points of EO, and consequently, the Nusselt number enhances which means, that the lubrication properties of EO become more effective and efficient. Variation reported in Fig. 12 for Nusselt number is identical to the variation in Table 2. The influence of Schmidt number on concentration profile is shown in Fig. 14. A fall in the concentration profile is reported when increasing Sc. As Sc has an inverse relation with mass diffusivity, an increase in Sc will decrease the rate of mass diffusion, and as a result the concentration of fluid will decrease. Moreover, the rate of mass distribution under the effect of volume fraction φ of nanoparticles is presented numerically in Table 3. One can observe that when increasing the volume fraction φ, viscous forces increase, which leads to a slowdown of the fluid flow, and consequently, the rate of mass distribution decreases.

Figure 12
figure 12

Impact of Df on the temperature profile

Full size image
Figure 13
figure 13

Variation in Nusselt number for the volume fraction

Full size image
Figure 14
figure 14

Influence of Sc on the concentration profile

Full size image
Table 2 Variation in Nusselt number
Full size table
Table 3 Variations in Sherwood number
Full size table

4 Concluding remarks

In the presence of Dufour effect, thermal radiation, heat and mass transfer, the rotating Jeffrey nanofluid embedded in a porous medium is examined. Nanofluid is formed by dispersing silver (AgNps) nanosize particles in engine oil. Exact expressions are obtained through the Laplace transform technique for the velocity, temperature and concentration profiles. The influence of various parameters is plotted graphically. Variation in Nusselt and Sherwood numbers is calculated numerically. The main points from the study are listed below.

  • Increasing the fractional parameter α decreases the velocity.

  • Velocity profile increases with the increasing values of Df, Gr and Gm.

  • For higher values of λ, r, Sc and φ, the viscosity of the engine oil increases, which cause a rise in the boiling point of the engine oil. This will intensely increase the heat carrying capacity and lubrication properties of the oil.

  • For MHD and permeability parameters, the viscosity of the engine oil decreases, as a result the motion of the fluid retards.

  • Temperature profile is enhanced when increasing the value of Df, which is due an increase in the thermal conductivity and decrease in the specific heat capacity of the engine oil.

  • The rate of heat transfer increases by 15.04% when the volume friction is 0.04.

  • By increasing of volume friction of nanoparticles, the rate of mass distribution increases by 22.07%.