1 Introduction

The Degasperis–Procesi equation with the form

$$ \phi _{x}-\phi _{txx}+4\phi \phi _{x}=3\phi _{x}\phi _{xx}+\phi \phi _{xxx}, $$
(1)

was discovered in [1], which is one of three integrable equations within a certain family of third-order nonlinear dispersive PDEs. It is a representative model for shallow water dynamics, so many scholars have investigated this equation by different methods (see [2,3,4,5,6,7]). The Degasperis–Procesi equation possesses smooth solutions that develop singularities in finite time by capturing the essential features of breaking waves [8], the solutions remain bounded, but their slopes become unbounded.

Recently, Lai et al. [9] studied the generalized Degasperis–Procesi equation

$$ \phi _{x}-\phi _{txx}+k\phi _{x}+m\phi \phi _{x}=3\phi _{x}\phi _{xx}+ \phi \phi _{xxx}. $$
(2)

The objective of this work is to investigate the modified Degasperis–Procesi equation in the form [10]

$$\begin{aligned}& \begin{aligned}[b] \phi _{t}-\phi _{txx}+\beta f^{\prime }(\phi )\phi _{x}&=f^{\prime \prime \prime }(\phi )\phi _{x}^{3}+3f^{\prime \prime }(\phi )\phi _{x}\phi _{xx}+f^{\prime }(\phi )\phi _{xxx} \\ &\quad{} +\alpha m \bigl[(m-1)\phi ^{m-2}\phi _{x}^{2}+ \phi ^{m-1}\phi _{xx} \bigr]-\alpha \phi ^{m}, \end{aligned} \end{aligned}$$
(3)

where \(\alpha ,\beta \in R\), \(m\geq 2\), \(f(\phi )\) is a polynomial function of order n (\(n\geq 2\)). Setting \(\alpha =0\), \(\beta =4\), \(f( \phi )=\frac{\phi ^{2}}{2}\), Eq. (3) reduces to the Degasperis–Procesi equation (1).

In the present paper, \(\alpha =0\), \(f(\phi )=\phi ^{n}\), \(n\in Z^{+}\) is considered, and then Eq. (3) becomes

$$ \phi _{t}-\phi _{txx}+\beta n\phi ^{n-1}\phi _{x}=n(n-1) (n-2)\phi ^{n-3} \phi _{x}^{3}+3n(n-1) \phi ^{n-2}\phi _{x}\phi _{xx}+n\phi ^{n-1} \phi _{xxx}, $$
(4)

by substituting the traveling wave transformation \(\phi (x,t)=\phi (x-ct)= \phi (\xi )\), where c is the wave speed. Integrating once and neglecting the integral constant, the partial differential equation (4) changes to the following ordinary differential equation:

$$ -c\phi +c\phi ^{\prime \prime }+\beta \phi ^{n}=n(n-1)\phi ^{n-2} \phi ^{\prime 2}+n\phi ^{n-1}\phi ^{\prime \prime }. $$
(5)

Equation (5) is equivalent to the two-dimensional system as follows:

$$ \frac{d\phi }{d\xi }=y, \quad\quad \frac{dy}{d\xi }=\frac{c\phi -\beta \phi ^{n}+n(n-1)\phi ^{n-2}y^{2}}{c-n \phi ^{n-1}}, $$
(6)

with the first integral being

$$ H(\phi ,y)=\frac{1}{2} \bigl(c-n\phi ^{n-1} \bigr)^{2}y^{2}- \phi \biggl(\frac{c ^{2}}{2}\phi -\frac{cn+c\beta }{n+1}\phi ^{n}+ \frac{\beta }{2}\phi ^{2n-1} \biggr)=h. $$
(7)

Obviously, Eq. (5) is a three-parameter planar dynamical system depending on the parameter triplet \((c,\beta ,n)\). Since the phase orbits defined by the vector fields of Eq. (5) determine all traveling wave solutions of Eq. (4), we will investigate the bifurcations of phase portraits of Eq. (5) in the phase plane \((\phi ,y)\) when the parameters \((c,\beta ,n)\) change. For the given physical model, we aim to find the bounded solutions of Eq. (5) which are meaningful in physics.

Suppose that \(\phi (\xi )\) is a continuous solution of (6) for \(\xi \in (-\infty ,+\infty )\) and \(\lim_{\xi \rightarrow -\infty } \phi (\xi )=\alpha \) as well as \(\lim_{\xi \rightarrow +\infty } \phi (\xi )=\beta \). If \(\alpha =\beta \), \(\phi (x,t)\) is called a solitary wave solution. If \(\alpha \neq \beta \), \(\phi (x,t)\) is called a kink (anti-kink) wave solution. A solitary wave solution corresponds to a homoclinic orbit, a kink (anti-kink) wave solution corresponds to a heteroclinic orbit, a periodic orbit corresponds to a periodic traveling wave solution.

This paper is organized as follows. In Sect. 2, we discuss the bifurcations of phase portraits of system (6) under different parameter conditions. In Sect. 3, we prove the existence of solitary wave, periodic, and loop solutions of (6). A brief conclusion is given in Sect. 4.

2 Bifurcations of phase portraits of (6) and (8)

In this section, the phase portraits of Eq. (6) will be considered. First, let \(d\tau =(c-n\phi ^{n-1})\,d\xi \), then Eq. (6) becomes

$$ \frac{d\phi }{d\tau }= \bigl(c-n\phi ^{n-1} \bigr)y, \quad\quad \frac{dy}{d\tau }=c\phi -\beta \phi ^{n}+n(n-1)\phi ^{n-2}y^{2}. $$
(8)

Obviously, Eq. (8) has the same topological phase portraits as Eq. (6) except for the straight line \(c-n\phi ^{n-1}=0\), and Eqs. (8) and (6) are integrable, which have the same first integral as (7). For a fixed h, (7) determines a set of invariant curves of (8), which contains different branches of curves. As h is varied, (7) defines different families of orbits of (8) with different dynamical behaviors.

Denoting \(F(\phi )=c\phi -\beta \phi ^{n}\), to investigate the critical points of the system, we need to find all zeros of the equation \(F(\phi )=0\). In the \((\phi ,y)\)-phase plane, the abscissas of equilibrium points of Eq. (6) on the ϕ-axis are the zeros of \(F(\phi )\). Notice that \(F^{\prime }(\phi )=c-\beta n\phi ^{n-1}\), for an odd n and \(c\beta >0\), \(F^{\prime }(\phi )\) has two zeros \(\phi _{\pm }=\pm (\frac{c}{\beta n})^{\frac{1}{n-1}}\); for an even n, \(F^{\prime }(\phi )\) has one zero \(\phi _{+}=(\frac{c}{\beta n})^{ \frac{1}{n-1}}\). Then the distribution of the zeros of \(F(\phi )\) on the ϕ-axis is presented. For an odd n, there exist three equilibrium points of Eq. (8) at \(O(0,0)\) and \(E(\phi _{a,b},0)\) when \(c\beta >0\), where \(\phi _{a}=(\frac{c}{\beta n})^{\frac{1}{n-1}}\), \(\phi _{b}=-(\frac{c}{ \beta n})^{\frac{1}{n-1}}\). For an even n, there exist two equilibrium points of \(O(0,0)\) and \(E(\phi _{c},0)\), where \(\phi _{c}=(\frac{c}{ \beta n})^{\frac{1}{n-1}}\).

Let \(E(\phi _{i},0)\) be an equilibrium point of (8) and \(M(\phi _{i},0)\) be the coefficient matrix of the linearized system of Eq. (8) at an equilibrium point \(E(\phi _{i},0)\). We obtain

$$J(\phi _{i},0)=\det M(\phi _{i},0)=- \bigl(c-n\phi _{i}^{n-1} \bigr) \bigl(c-\beta n \phi _{i}^{n-1} \bigr). $$

By the theory of planar dynamical systems, the equilibrium point \(E(\phi _{i},0)\) of the Hamiltonian system is a center if \(J(\phi _{i},0)> 0\); \(E(\phi _{i},0)\) is a saddle if \(J(\phi _{i},0)< 0\); while if \(J(\phi _{i},0)=0\) and Poincaré index of this equilibrium point is zero, then \(E(\phi _{i},0)\) is a cusp.

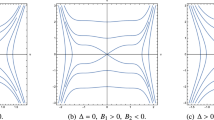
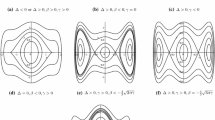
From the analysis above, we obtain the different phase portraits of Eq. (6) shown in Fig. 1.

Figure 1
figure 1

Phase portraits of (8) under different parameter conditions, for \(m\in Z^{+}\) and \(m\geq 1\)

Full size image

3 Some exact traveling wave solutions of (6) and (8)

In this section, we will use the phase portrait analytical technique [11,12,13,14,15,16,17,18,19,20,21] to get smooth solitary, loop and periodic wave solutions under some conditions.

1. If \(n=2\), we notice that the curves defined by \(H(\phi ,y)=h=0\) correspond to the orbits consisting of two stable manifolds, two unstable manifolds of the saddle point \(O(0,0)\) and two open curves passing through the points \((\phi _{c}, 0)\), respectively (see the red orbits in Fig. 1-6). From Eq. (7), it is obvious that the arch curve on the left-hand side of the straight line \(\phi =\frac{c}{2}\) has the algebraic equation

$$ y^{2}=\frac{\phi ^{2}(c^{2}-\frac{2c(2+\beta )}{3}\phi +\beta \phi ^{2})}{(c-2 \phi )^{2}}=\frac{(-\beta )\phi ^{2}(\phi _{1}-\phi )(\phi -\phi _{2})}{(c-2 \phi )^{2}}, $$
(9)

where \(\phi _{1,2}=\frac{c(2+\beta )}{3}\pm \frac{c}{3}\sqrt{\beta ^{2}-5\beta +4}\). By Eq. (9) and the above standard phase portrait analysis, integrating along the stable and unstable manifolds, approaching the straight line \(\phi =\frac{c}{2}\) to the saddle point \(O(0,0)\) and two open curves passing through the points \((\phi _{2},0)\), we obtain the following representations:

$$ \xi = \int _{\phi }^{\frac{1}{2}\phi _{1}} \eta _{1}(\phi )\,d\phi =- \frac{1}{\sqrt{- \beta }} \biggl[\varPhi _{1}(\phi )+\varPhi _{2}( \phi )-\varPhi _{1} \biggl(\frac{1}{2}\phi _{1} \biggr)- \varPhi _{2} \biggl(\frac{1}{2}\phi _{1} \biggr) \biggr] $$
(10)

and

$$ \xi = \int _{\phi }^{\phi _{2}} \eta _{1}(\phi )\,d\phi =- \frac{1}{\sqrt{- \beta }} \bigl[\varPhi _{1}(\phi )+\varPhi _{2}( \phi )-\varPhi _{1}(\phi _{2})-\varPhi _{2}( \phi _{2}) \bigr], $$
(11)

where \(\eta _{1}(\phi )=\frac{c-2\phi }{\sqrt{-\beta }\phi \sqrt{( \phi _{1}-\phi )(\phi -\phi _{2})}}\), \(\varPhi _{1}(\phi )=\frac{c}{\sqrt{- \phi _{1}\phi _{2}}}\cosh ^{-1} (\frac{\phi _{1}+\phi _{2}-\frac{2\phi _{1}\phi _{2}}{\phi }}{\phi _{1}-\phi _{2}} )\), and \(\varPhi _{2}( \phi )= 2 \arcsin (\frac{2\phi -\phi _{1}-\phi _{2}}{\phi _{1}-\phi _{2}})\). Employing (10) and (11), we obtain a loop solution.

Remark

The loop solution is a solitary wave solution with a singularity, which possesses infinite derivatives at certain points, and consist of two or more independent branches. The loop solution illustrated in (10) and (11) may be regarded as a composite solution made up of three single-valued solutions. The notion of composite solutions for the Camassa–Holm equation is discussed in detail in [15,16,17,18,19].

2. If \(n=2\), we notice that the curves defined by \(H(\phi ,y)=h\in (h _{1},0)\) corresponding to a family of periodic orbits (see the blue orbits in Fig. 1-6). Under this condition, the algebraic equation is obtained as follows:

$$ y^{2}=\frac{2h+\phi ^{2}(c^{2}-\frac{2c(2+\beta )}{3}\phi +\beta \phi ^{2})}{(c-2\phi )^{2}}=\frac{(-\beta )(\phi -\phi _{3})(\phi -\phi _{4})( \phi -\phi _{5})(\phi _{6}-\phi )}{(c-2\phi )^{2}}, $$
(12)

where \(\phi _{3}<\phi _{4}<0<\phi _{5}<\phi _{6}\), and \(\phi _{3}=-\phi _{5}\), \(\phi _{4}=-\phi _{6}\). Thus, we have parametric representations for the family of periodic solutions as follows:

$$ \vert \xi \vert =\frac{c-2\phi _{3}}{\sqrt{-\beta \phi _{6}\phi _{5}}}F(\varphi ,k)-\frac{2(\phi _{6}-\phi _{3})}{\sqrt{\phi _{6}\phi _{5}}}\varPi \biggl(\varphi ,\frac{\phi _{5}-\phi _{6}}{\phi _{5}-\phi _{3}},k \biggr), $$
(13)

where \(\varphi =\arcsin \sqrt{\frac{(\phi _{5}-\phi _{3})(\phi _{6}- \phi )}{(\phi _{6}-\phi _{5})(\phi -\phi _{3})}}\), \(k^{2}=\frac{(\phi _{6}-\phi _{5})(\phi _{4}-\phi _{3})}{(\phi _{6}-\phi _{4})(\phi _{5}-\phi _{3})}\); \(F(\varphi ,k)\) and \(\varPi (\varphi ,\frac{\phi _{5}-\phi _{6}}{ \phi _{5}-\phi _{3}},k)\) are the Legendre’s incomplete elliptic integrals of the first and third kind, respectively (see [22]).

3. If \(n=3\), we notice that the curves defined by \(H(\phi ,y)=h=0\) correspond to two homoclinic orbits passing through the saddle point \(O(0,0)\) (see the red orbits in Fig. 1-5). Under this condition, the algebraic equation is obtained as follows:

$$ y^{2}=\frac{\phi ^{2}(c^{2}-\frac{c(3+\beta )}{2}\phi ^{2}+\beta \phi ^{4})}{(c-3\phi ^{2})^{2}} =\frac{\beta \phi ^{2}(\phi -z_{1})(\phi -z _{2})(\phi -z_{3})(\phi -z_{4})}{(c-3\phi ^{2})^{2}}, $$
(14)

where \(z_{i}\) (\(i=1-4\)) are complex numbers, \(z_{2}\) is conjugate to \(z_{1}\), and \(z_{4}\) is conjugate to \(z_{3}\). Thus, by using the first equation of (6) and Eq. (14), we obtain the parametric representation of two homoclinic orbits:

$$ \vert \xi \vert =\frac{1}{\sqrt{\beta }} \bigl[\omega _{1}F(\varphi _{1},k_{1})+ \omega _{2}\varPi \bigl(\varphi _{1},1+\alpha ^{2},k_{1} \bigr)+\omega _{3}\varPi \bigl(\varphi _{1},1+g_{1}^{2},k_{1} \bigr)+\omega _{4}f_{2} \bigr], $$
(15)

where \(\omega _{1}=\frac{gc\alpha (1+g_{1}\alpha )}{(a_{1}+b_{1}g_{1})(1+ \alpha ^{2})}- \frac{3g(b_{1}-a_{1}g_{1})(1+\alpha g_{1})}{(1+g_{1}^{2})}\), \(\omega _{2}=\frac{gc\alpha ^{2}(\alpha -g_{1})}{(a_{1}+b_{1}g_{1})(1+ \alpha ^{2})}\), \(\omega _{3}=\frac{3gg_{1}^{2}(b_{1}-g_{1}a_{1})(g_{1}- \alpha )}{g_{1}(1+g_{1}^{2})}\), and \(\omega _{4}=\frac{\alpha gc( \alpha -g_{1})}{a_{1}+b_{1}g_{1}}-\frac{3g_{1}(b_{1}-g_{1}a_{1})(g _{1}-\alpha )}{g_{1}}\). It gives rise to two smooth solitary solutions. The details of the computation can be seen in Appendix.

4. If \(n=3\), the curves defined by \(H(\phi ,y)=h=0\) correspond to different orbits of Eq. (8) consisting of two stable manifolds, two unstable manifolds of the saddle point \((0,0)\), and two open curves passing through the points \((\phi _{a}, 0)\) (see the red orbits in Fig. 1-7). On the right-hand side of the vertical axis, from Eq. (7), the arch curve on the right-hand side of the straight line \(\phi =( \frac{c}{3})^{\frac{1}{2}}\) is

$$\begin{aligned}& \begin{aligned}[b] y^{2}&=\frac{\phi ^{2}(c^{2}-\frac{c(3+\beta )}{2}\phi ^{2}+\beta \phi ^{4})}{(c-3\phi ^{2})^{2}} =\frac{\beta \phi ^{2}(\phi -\phi _{7})( \phi -\phi _{8})(\phi -z_{5})(\phi -z_{6})}{(c-3\phi ^{2})^{2}} \\ &=\frac{\beta \phi ^{2}(\phi -\phi _{7})(\phi -\phi _{8})[(\phi -b_{1})^{2}+a _{1}^{2}]}{(c-3\phi ^{2})^{2}},\end{aligned} \end{aligned}$$
(16)

where \(\phi _{7}\), \(\phi _{8}\) are real numbers, \(z_{5}\), \(z_{6}\) are complex numbers, and \(\phi _{7}>\phi _{8}\), \(z_{6}\) is conjugate to \(z_{5}\). By Eq. (16) and the above standard phase portrait analysis, integrating along the stable and unstable manifolds, approaching the straight line \(\phi =(\frac{c}{3})^{\frac{1}{2}}\) to the saddle point \(O(0,0)\) and the open-end curve passing through the points \((\phi _{c},0)\), integrating on the intervals \([0,\phi )\) and \((\phi ,\frac{\phi _{c}}{2}]\), we obtain the following representations:

$$\begin{aligned}& \begin{aligned}[b] \xi &=\frac{1}{\sqrt{\beta }} \biggl[\omega _{5}F( \varphi _{2},k_{2})+\omega _{6}\varPi \biggl( \varphi _{2},\frac{\alpha _{1}^{2}}{\alpha _{1}^{2}-1},k_{2} \biggr) + \omega _{7}\varPi \biggl(\varphi _{2},\frac{\alpha _{2}^{2}}{\alpha _{2}^{2}-1},k _{2} \biggr) \\ &\quad{} +\omega _{8}\arctan \biggl(\sqrt{ \frac{k_{2}^{2}+(1-k_{2}^{2})\alpha _{1} ^{2}}{1-\alpha _{1}^{2}}}s\,du \biggr) +\omega _{9}\arctan \biggl(\sqrt {\frac{k_{2} ^{2}+(1-k_{2}^{2})\alpha _{2}^{2}}{1-\alpha _{2}^{2}}}s\,du \biggr) \biggr], \end{aligned} \end{aligned}$$
(17)

where \(\eta _{2}(\phi )=\frac{c-3\phi ^{2}}{\sqrt{\beta }\phi \sqrt{( \phi -\phi _{7})(\phi -\phi _{8})(\phi -z_{5})(\phi -z_{6})}}\), \(\varphi _{2}=\arccos (\frac{(A-B)\phi +\phi _{7}B-\phi _{8}A}{(A+B) \phi -\phi _{7}B-\phi _{8}A})\), \(A^{2}=(\phi _{7}-b_{1})^{2}+a_{1}^{2}\), \(B^{2}=(\phi _{8}-b_{1})^{2}+a_{1}^{2}\), \(k_{2}^{2}=\frac{(A+B)^{2}-( \phi _{7}-\phi _{8})}{4AB}\), \(\omega _{5}=\frac{cg_{2}\alpha _{2}(B-A)}{ \phi _{7}B+\phi _{8}A}- \frac{3g_{2}\alpha _{1}(\phi _{7}B-\phi _{8}A)}{A+B}\), \(\omega _{6}=\frac{cg _{2}(B-A)(\alpha _{1}-\alpha _{2})}{(\phi _{7}B+\phi _{8}A)(1-\alpha _{1} ^{2})}\), \(\omega _{7}=-\frac{3g_{2}(\phi _{7}B-\phi _{8}A)(\alpha _{2}- \alpha _{1})}{(A+B)(1-\alpha _{2}^{2})}\), \(\omega _{8}=-\frac{\alpha _{1}cg _{2}(B-A)(\alpha _{1}-\alpha _{2})}{(\phi _{7}B+\phi _{8}A)(1-\alpha _{1} ^{2})}\sqrt{\frac{1-\alpha _{1}^{2}}{k_{2}^{2}+(1-k_{2}^{2})\alpha _{1}^{2}}}\), and \(\omega _{9}=\frac{3\alpha _{2}g_{2}(\phi _{7}B-\phi _{8}A)(\alpha _{2}-\alpha _{1})}{(A+B)(1-\alpha _{2}^{2})} \sqrt{\frac{1- \alpha _{2}^{2}}{k_{2}^{2}+(1-k_{2}^{2})\alpha _{2}^{2}}}\). It gives rise to a loop solitary solution like in (10) and (11). Paralleling with the orbits on the right-hand side of the vertical axis, another loop solution can be found which consists of orbits on the left-hand side of the y-axis in Fig. 1-7.

4 Conclusion

In summary, we have obtained the bifurcations of the parameters and proved the existence of some exact traveling wave solutions for the modified Degasperis–Procesi equation, with the aid of dynamical systems theory. We have shown that modified Degasperis–Procesi equation has smooth solitary wave solutions, periodic wave solutions and loop solitary solutions under some parameter conditions.