Dynamics of difference equation $x_{n+1}=f( x_{n-l},x_{n-k})$

Abstract

In this paper, we present the asymptotic behavior of the solutions for a general class of difference equations. We introduce general theorems in order to study the stability and periodicity of the solutions. Moreover, we use a new technique to study the existence of periodic solutions of this general equation. By using our general results, we can study many special cases that have not been studied previously and some problems that were raised previously. Some numerical examples are provided to illustrate the new results.

1 Introduction

Amid the most recent two decades, there has been an extraordinary research of the utilization of difference equations in the solution of numerous issues that emerge in economy, statistics, and engineering science. Likewise, difference equations have been utilized as approximations to ordinary and partial differential equations (ODEs and PDEs) because of the improvement of rapid advanced processing hardware. It tends to be said that difference equations identify with differential equations as discrete mathematics identifies with continuous mathematics. Any individual who has made an investigation of differential equations will realize that even elementary examples can be difficult to solve. By contrast, elementary difference equations are moderately simple to study. For many reasons, computer scientists take an interest difference equations. For instance, difference equations often emerge while determining the cost of an algorithm in big-O notation. In 1943, the difference equations were commonly used for solving partial differential equations. Problems involving time-dependent fluid flows, neutron diffusion and transport, radiation flow, thermonuclear reactions, and problems involving the solution of several simultaneous partial differential equations are being solved by the use of difference equations. Other than the utilization of difference equations as approximations to ODEs and PDEs, they afford a powerful method for the analysis of electrical, mechanical, thermal, and other systems in which there is a recurrence of identical sections. By using the difference equations, the investigation of the conduct of electric-wave filters, multistage amplifiers, magnetic amplifiers, insulator strings, continuous beams of equal span, crankshafts of multicylinder engines, acoustical filters, etc., is enormously facilitated. The standard techniques for solving such systems are generally very lengthy when the number of elements involved is large. The use of difference equations greatly reduces the complexity and labor in problems of this type.

As a result of the many applications of difference equations in various fields, many mathematicians are interested in the asymptotic behavior of different types of difference equations; see [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36]. Also, many powerful methods for studying qualitative behavior of difference equations have been established and developed; see [5, 20] and [30].

In particular, we review some difference equations that are special cases of the general studied equation. In [11], Devault et al. studied the recursive sequence

$$ x_{n+1}=\frac{A}{x_{n}}+\frac{1}{x_{n-2}}, $$

where A is a real number. Khuong in [23] investigated the behavior of the positive solutions of the difference equation

$$ x_{n+1}=a+ \biggl( \frac{x_{n-l}}{x_{n-k}} \biggr) ^{\alpha }, $$

(1.1)

where l, k and α are positive integers , $a>-1$ and $0\leq k< l$. In [33], Stevic investigated the behavior of the positive solutions of the difference equation (1.1) when a and α are positive real numbers, $l=1$ and $k=0$. The case $\alpha =1$ has been considered in [10]. In [19], Elsayed studied the periodicity and the boundedness of the positive solutions of the difference equation

$$ x_{n+1}=a+\frac{bx_{n-l}+cx_{n-k}}{dx_{n-l}+ex_{n-k}}, $$

(1.2)

where a, b, c, d and e are positive real number. For further study of Eq. (1.2) with $a=0$, see [12, 17, 22] and [26]. Elsayed in [20] and Moaaz in [29] studied the qualitative behavior of solutions of the equation

$$ x_{n+1}=a+b\frac{x_{n-1}}{x_{n}}+c\frac{x_{n}}{x_{n-1}}, $$

where a, b and c are real number.

Our aim in this paper is to investigate the qualitative behavior of the solutions of the difference equation

$$ x_{n+1}=f ( x_{n-l},x_{n-k} ) ,\quad n=0,1,\ldots, $$

(E)

where l and k are positive integers, the function $f ( u,v )$ is a continuous real function and is homogeneous with degree α and the initial conditions $x_{-\mu }, x_{-\mu +1}, \ldots, x_{0}$ are real numbers for $\mu =\max \{ l,k \}$. In this paper, we study the local/global stability and periodicity character of solutions of the difference equation in a general form using a homogeneous function. We use a new and powerful method to study the prime period two solution of this equation. Moreover, we apply general results on some special cases. We can use our results to answer some of the problems raised earlier, as

Problem 1

(Kulenovic and Ladas [25])

Suppose that a, b, c and d are real numbers. Investigate the forbidden set of the difference equation

$$ x_{n+1}=\frac{ax_{n}+bx_{n-1}}{cx_{n}+dx_{n-1}}x_{n} $$

(1.3)

and investigate the asymptotic behavior and the periodic nature of its solution.

2 Existence of periodic solutions

The following theorems state a new necessary and sufficient condition that Eq. (E) has periodic solution of prime period two.

Theorem 2.1

Assume that l and k are odd or l and k are even. If $\alpha \neq 1$, then Eq. (E) has no prime positive period two solution.

Proof

On the contrary, we assume that Eq. (E) has a prime period two distinct solution

$$ \ldots,\rho ,\sigma ,\rho ,\sigma ,\ldots. $$

If l and k are odd, then we have $x_{n-l}=x_{n-k}=\rho$. From Eq. (E), we get

$$\begin{aligned}& \rho = f ( \rho ,\rho ) , \\& \sigma = f ( \sigma ,\sigma ) . \end{aligned}$$

Thus, we obtain

$$ \rho =\sigma =f^{1/ ( 1-\alpha ) } ( 1,1 ) . $$

This is a contradiction.

Next, we let l and k be even. Then we get $x_{n-l}=x_{n-k}=\sigma$, and hence

$$\begin{aligned} \rho =&f ( \sigma ,\sigma ) , \\ \sigma =&f ( \rho ,\rho ) . \end{aligned}$$

Therefore

$$\begin{aligned} \rho =&\sigma^{\alpha }f ( 1,1 ) \\ =& \bigl( \rho^{\alpha }f ( 1,1 ) \bigr) ^{\alpha }f ( 1,1 ) \\ =&\rho^{\alpha^{2}}f^{\alpha +1} ( 1,1 ) \end{aligned}$$

and so

$$ \rho =f^{1/ ( 1-\alpha ) } ( 1,1 ) . $$

Hence,

$$\begin{aligned} \sigma =&\rho^{\alpha }f ( 1,1 ) \\ =&f^{\alpha / ( 1-\alpha ) } ( 1,1 ) f ( 1,1 ) \\ =&f^{1/ ( 1-\alpha ) } ( 1,1 ) =\rho , \end{aligned}$$

which is a contradiction. Thus, the proof is completed. □

Theorem 2.2

Assume that l is odd and k is even. Equation (E) has a prime period two solution $\ldots, \rho , \sigma , \rho , \sigma , \ldots$ if and only if

$$ \begin{aligned} &f ( \tau ,1 ) =\tau f ( 1,\tau ) \quad \textit{if }\alpha\neq 1; \\ &f ( \tau ,1 ) =\tau\quad \textit{and} \quad f ( 1,\tau ) =1 \quad \textit{if } \alpha=1,\end{aligned} $$

(2.1)

where $\tau =\rho /\sigma$.

Proof

We suppose without loss of generality that $l>k$. Now, we assume that Eq. (E) has a prime period two solution

$$ \ldots,\rho ,\sigma ,\rho ,\sigma ,\ldots. $$

Since l is odd and k is even, we have $x_{n-l}=\rho$ and $x_{n-k}=\sigma$. From Eq. (E), we get

$$\begin{aligned}& \rho = f ( \rho ,\sigma ) =\sigma^{\alpha }f \biggl( \frac{ \rho }{\sigma },1 \biggr) , \\& \sigma = f ( \sigma ,\rho ) =\sigma^{\alpha }f \biggl( 1,\frac{ \rho }{\sigma } \biggr) . \end{aligned}$$

Then

$$ \tau =\frac{f ( \tau ,1 ) }{f ( 1,\tau ) }. $$

On the other hand, we let (2.1) hold. If $\alpha \neq 1$, then we choose

$$\begin{aligned}& x_{-l+2\mu } = \frac{f ( \tau ,1 ) }{f^{\alpha / ( \alpha -1 ) } ( 1,\tau ) }, \\& x_{-l+2\mu +1} = \frac{1}{f^{1/ ( \alpha -1 ) } ( 1, \tau ) }, \end{aligned}$$

for $\mu =0,1,\ldots, ( l-1 ) /2$, where $\tau \in \mathbb{R} \backslash \{ 1 \}$. Hence, we obtain

$$\begin{aligned}& x_{1} =f ( x_{-l},x_{-k} )=f \biggl( \frac{f ( \tau ,1 ) }{f^{\alpha / ( \alpha -1 ) } ( 1,\tau ) },\frac{1}{f^{1/ ( \alpha -1 ) } ( 1,\tau ) } \biggr) . \end{aligned}$$

From (2.1), we have

$$ x_{1}=f \biggl( \frac{\tau }{f^{1/ ( \alpha -1 ) } ( 1, \tau ) },\frac{1}{f^{1/ ( \alpha -1 ) } ( 1,\tau ) } \biggr) . $$

Since f is homogeneous with degree α, we get

$$ x_{1}=\frac{1}{f^{\alpha / ( \alpha -1 ) } ( 1,\tau ) }f ( \tau ,1 ) . $$

Also, we have

$$\begin{aligned} x_{2} =&f ( x_{-l+1},x_{-k+1} ) \\ =&f \biggl( \frac{1}{f^{1/ ( \alpha -1 ) } ( 1,\tau ) },\frac{f ( \tau ,1 ) }{f^{\alpha / ( \alpha -1 ) } ( 1,\tau ) } \biggr) \\ =&f \biggl( \frac{1}{f^{1/ ( \alpha -1 ) } ( 1,\tau ) },\frac{\tau }{f^{1/ ( \alpha -1 ) } ( 1,\tau ) } \biggr) \\ =&\frac{1}{f^{\alpha / ( \alpha -1 ) } ( 1,\tau ) }f ( 1,\tau ) \\ =&\frac{1}{f^{1/ ( \alpha -1 ) } ( 1,\tau ) }. \end{aligned}$$

Hence, it is concluded by induction that

$$ x_{2n-1}=\frac{f ( \tau ,1 ) }{f^{\alpha / ( \alpha -1 ) } ( 1,\tau ) } \quad \mbox{and} \quad x_{2n}= \frac{1}{f ^{1/ ( \alpha -1 ) } ( 1,\tau ) } \quad \text{for all }n>0. $$

Therefore, Eq. (E) has a prime period two solution. If $\alpha =1$, then we choose

$$ x_{-l+2\mu }=c\tau \quad \mbox{and} \quad x_{-l+2\mu +1}=c, \quad \mu =0,1,\ldots, ( l-1 ) /2, $$

where $\tau \in \mathbb{R} \backslash \{ 1 \}$ and c arbitrary real number. Thus, we get

$$\begin{aligned} x_{1} =&f ( x_{-l},x_{-k} ) \\ =&f ( c\tau ,c ) \\ =&cf ( \tau ,1 ) =c\tau \end{aligned}$$

and

$$\begin{aligned} x_{2} =&f ( x_{-l+1},x_{-k+1} ) \\ =&f ( c,c\tau ) \\ =&cf ( 1,\tau ) =c. \end{aligned}$$

Then it is concluded by induction that $x_{2n-1}=c\tau$ and $x _{2n}=c$ for all $n>0$. Therefore, Eq. (E) has a prime period two solution and the proof is completed. □

Theorem 2.3

Assume that l is even and k is odd. Equation (E) has a prime period two solution $\ldots, \rho , \sigma , \rho , \sigma , \ldots$ , if and only if

$$ \begin{aligned} &f ( 1,\tau ) =\tau f ( \tau ,1 ) \quad \textit{if }\alpha\neq 1; \\ &f ( 1,\tau ) =\tau \quad \textit{and}\quad f ( \tau ,1 ) =1 \quad \textit{if } \alpha=1, \end{aligned} $$

(2.2)

where $\tau =\rho /\sigma$.

Proof

The proof is similar to that of proof of Theorem 2.2 and hence is omitted. □

Example 2.1

Let the difference equation

$$ x_{n+1}=ax_{n}^{\alpha }+bx_{n-1}^{\alpha }, $$

(2.3)

where α is an integer, a and b are positive real numbers and $\vert \alpha \vert \neq 1$. From Theorem 2.3, Eq. (2.3) has a prime period two solution

$$ \rho =\frac{a+b\tau^{\alpha }}{ ( a\tau^{\alpha }+b ) ^{ \alpha / ( \alpha -1 ) }} \quad \mbox{and} \quad \sigma =\frac{1}{ ( a\tau^{\alpha }+b ) ^{1/\alpha -1}},\quad \tau \in \mathbf{\mathbb{R} }^{+}\backslash \{ 1 \} , $$

if and only if

$$ a+b\tau^{\alpha }=\tau \bigl( a\tau^{\alpha }+b \bigr) $$

and so

$$ \frac{b}{a}=\frac{1-\tau^{\alpha +1}}{\tau ( 1-\tau^{\alpha -1} ) }. $$

(2.4)

We have

$$ H ( \tau ) :=\frac{1-\tau^{\alpha +1}}{\tau ( 1- \tau^{\alpha -1} ) }> \min_{\tau \in \mathbf{\mathbb{R} }^{+}}H ( \tau ) = \frac{\alpha +1}{\alpha -1},\quad \alpha >1 $$

and

$$ H ( \tau ) < \max_{\tau \in \mathbf{\mathbb{R} }^{+}}H ( \tau ) =\frac{\alpha +1}{\alpha -1},\quad \alpha < -1, $$

which with (2.4) gives $b ( \alpha -1 ) >a ( \alpha +1 )$. For example, for $\alpha =-2$, $a=7$, $b=2$, $x_{1}=3.107$ and $x_{0}=1.553$, the prime period two solution of (2.3) is shown in Fig. 1.

Figure 1

Prime period two solution of Eq. (2.3)

3 Stability of Equation (E)

In this section, we study the local stability and global attractivity of the equilibrium point of Eq. (E).

Lemma 3.1

If $\alpha \neq 1$, then Eq. (E) has a positive equilibrium point

$$ \overline{x}=f^{1/ ( 1-\alpha ) } ( 1,1 ) . $$

(3.1)

Also, if $\alpha =1$ and $f ( 1,1 ) \neq 1$, then Eq. (E) has only zero equilibrium point.

Proof

The equilibrium point of Eq. (E) is given by $\overline{x}=f ( \overline{x},\overline{x} )$. Since f is homogeneous with degree α, we obtain

$$ \overline{x}=\overline{x}^{\alpha }f ( 1,1 ) . $$

If $\alpha \neq 1$, then $\overline{x}=0$ or $\overline{x}=f^{1/ ( 1-\alpha ) } ( 1,1 )$. Otherwise, if $\alpha =1$ and $f ( 1,1 ) \neq 1$, then we have $\overline{x}=0$. Thus, the proof is completed. □

Theorem 3.1

The zero equilibrium point of Eq. (E) is locally asymptotically stable if $\alpha >1$, or

$$ \alpha =1\quad \textit{and}\quad \bigl\vert f_{u} ( 1,1 ) \bigr\vert + \bigl\vert f_{v} ( 1,1 ) \bigr\vert < 1. $$

(3.2)

Proof

Since f homogeneous with degree α, we have $f_{u}$ and $f_{v}$ are homogeneous with degree $\alpha -1$. Now, if $\alpha >1$, then we get $f_{u} ( \overline{x},\overline{x} ) = \overline{x}^{\alpha -1}f_{u} ( 1,1 ) =0$ and $f_{v} ( \overline{x},\overline{x} ) =0$, for $\overline{x}=0$. Hence, $\overline{x}=0$ is locally asymptotically stable. Next, if $\alpha =1$, then $f_{u} ( \overline{x},\overline{x} ) =f _{u} ( 1,1 )$ and $f_{v} ( \overline{x},\overline{x} ) =f_{v} ( 1,1 )$. By using Theorem 1.3.7 in [24], we see that Eq. (E) is locally stable if

$$ \bigl\vert f_{u} ( 1,1 ) \bigr\vert + \bigl\vert f_{v} ( 1,1 ) \bigr\vert < 1, $$

which completes the proof. □

Theorem 3.2

The positive equilibrium point of Eq. (E) is locally asymptotically stable if

$$ \bigl\vert f_{u} ( 1,1 ) \bigr\vert + \bigl\vert f_{v} ( 1,1 ) \bigr\vert < f ( 1,1 ) $$

(3.3)

or

$$\begin{aligned} &0< \alpha < 1, \quad \textit{for } f_{u}>0,f_{v}>0; \\ &-1< \alpha < 0, \quad \textit{for }f_{u}< 0,f_{v}< 0; \\ &2f_{u} ( 1,1 ) < ( 1+\alpha ) f ( 1,1 ), \quad \textit{for }f_{u}>0,f_{v}< 0; \\ &2f_{v} ( 1,1 ) < ( 1+\alpha ) f ( 1,1 ),\quad \textit{for }f_{u}< 0,f_{v}>0. \end{aligned}$$

Proof

The linearized equation of (E) about x̅ is the linear difference equation

$$ y_{n+1}= \frac{\partial f}{\partial u}\biggm| _{ (\overline{x},\overline{x} ) }y_{n-l}+ \frac{\partial f}{\partial v}\biggm| _{ ( \overline{x},\overline{x} ) }y_{n-k}. $$

(3.4)

From Theorem 1.3.7 in [24], Eq. (3.4) is locally stable if

$$ \bigl\vert f_{u} ( \overline{x},\overline{x} ) \bigr\vert + \bigl\vert f_{v} ( \overline{x},\overline{x} ) \bigr\vert < 1. $$

Using Corollary 2 in [7], we see that $f_{u}$ and $f_{v}$ are homogeneous with degree $\alpha -1$. This implies

$$ \bigl\vert f_{u} ( 1,1 ) \bigr\vert + \bigl\vert f_{v} ( 1,1 ) \bigr\vert < f ( 1,1 ) . $$

If we admit that $f_{u}>0$ and $f_{v}>0$, then we obtain

$$ f_{u} ( \overline{x},\overline{x} ) +f_{v} ( \overline{x}, \overline{x} ) < 1. $$

(3.5)

From Euler’s homogeneous function theorem, we deduce that

$$ uf_{u}+vf_{v}=\alpha f, $$

(3.6)

which with (3.5) gives $0<\alpha <1$. Similarly, if $f_{u}<0$ and $f_{v}<0$, then we get $-1<\alpha <0$.

In the case where $f_{u}>0$ and $f_{v}<0$, we have

$$ f_{u} ( \overline{x},\overline{x} ) -f_{v} ( \overline{x}, \overline{x} ) < 1. $$

(3.7)

Combining (3.6) with (3.7), we get

$$ 2f_{u} ( 1,1 ) < ( 1+\alpha ) f ( 1,1 ) . $$

Finally, if $f_{u}<0$ and $f_{v}>0$, then we find

$$ 2f_{v} ( 1,1 ) < ( 1+\alpha ) f ( 1,1 ) . $$

Hence, the proof is completed. □

Example 3.1

Let the difference equation

$$ x_{n+1}=ax_{n}^{\alpha }+bx_{n-1}^{\alpha }, $$

(3.8)

where α, a and b are real numbers $,~a>0$, $b>0$ and $\alpha \neq 1$. Since $f ( u,v ) =au^{\alpha }+bv^{\alpha }$, we get

$$ \alpha f_{u}>0 \quad \mbox{and} \quad \alpha f_{v}>0. $$

By using Theorem 3.2, the positive equilibrium point $\overline{x}= ( a+b ) ^{1/ ( 1-\alpha ) }$ of Eq. (3.8) is locally asymptotically stable if $\vert \alpha \vert <1$. For example, for $\alpha =0.6$, $a=0.2$, $b=0.7$, $x_{1}=2.0$ and $x_{0}=0.2$, the stable solution of (3.8) is shown in Fig. 2.

Figure 2

Stable solution of difference Eq. (3.8)

Remark 3.1

If $\alpha =0$, then $uf_{u}+vf_{v}=0$ and $f_{u}f_{v}<0$. Thus, Eq. (3.8) is locally asymptotically stable if

$$ \bigl\vert f_{u} ( 1,1 ) \bigr\vert < \frac{1}{2}f ( 1,1 ) . $$

(3.9)

Theorem 3.3

Assume that f has non-positive partial derivatives. Then Eq. (E) has a unique positive equilibrium x̅ and every solution of Eq. (E) converges to x̅.

Proof

Let $( m,M )$ is a solution of the system

$$\begin{aligned}& m = f ( M,M ) , \\& M = f ( m,m ) . \end{aligned}$$

This implies

$$\begin{aligned}& m = M^{\alpha }f ( 1,1 ) , \\& M = m^{\alpha }f ( 1,1 ) , \end{aligned}$$

and so

$$ \bigl( m^{\alpha +1}-M^{\alpha +1} \bigr) f ( 1,1 ) =0. $$

Hence, we get $m=M$. By Theorem 1.4.7 in [26], we see that every solution of Eq. (E) converges to x̅. Hence, the proof is completed. □

Remark 3.2

Assume that $f_{u}>0$ and $f_{v}<0$. By Theorem 1.4.5 in [26], if we were able to obtain a condition that ensures that

$$ \frac{f ( z,1 ) -zf ( 1,z ) }{1-z^{\alpha +1}} \neq 0, $$

(3.10)

for all $z\in ( 0,\infty )$, then the equilibrium point x̅ would be a global attractor of Eq. (E).

Remark 3.3

Assume that $f\in C ( [ 0,\infty ) \times [ 0, \infty ) , [ 0,\infty ) )$, $f_{u}f_{v}>0$, $\vert \alpha \vert <1,~l=0$ and $k=1$. Then, by Euler’s homogeneous function theorem, we see that

$$\begin{aligned} u\vert f_{u}\vert +v\vert f_{v}\vert =&\vert uf _{u}+vf_{v}\vert \\ =&\vert \alpha \vert f \\ < &f, \end{aligned}$$

for all $u,v\in ( 0,\infty )$. Thus, by using Theorem 1.4.4 in [26], Eq. (E) has exactly one of the following three cases for all solutions (stability trichotomy):

• (a) $\lim_{n\rightarrow \infty }x_{n} =\infty$ for $x_{-1}x_{0} \neq 0$.

• (b) $\lim_{n\rightarrow \infty }x_{n} =0$ and Eq. (E) has only a zero equilibrium point.

• (c) $\lim_{n\rightarrow \infty }x_{n} =\overline{x}$ for $x_{-1}x _{0}\neq 0$ and x̅ is the only positive equilibrium point.

4 Discussion and numerical examples

Corollary 4.1

Assume that l and k are odd or l and k are even. If $f_{u}<0$ and $f_{v}>0$, then Eq. (E) has a unique equilibrium x̅ and every solution of Eq. (E) converges to x̅.

Proof

From Theorem 2.1, if l and k are odd or l and k are even, then Eq. (E) has no prime period two solution. Thus, by Theorem 1.4.6 in [26], we see that every solution of Eq. (E) converges to x̅. □

Remark 4.1

Notice that equations that have been studied in [2, 3, 10,11,12,13,14,15,16,17,18,19,20,21,22,23, 26] and [31,32,33,34] are special cases of Eq. (E). For example, Elsayed in [19] investigated the stability character and the periodicity of solutions of Eq. (1.2). From Remark 3.1, the positive equilibrium point of Eq. (1.2) is locally asymptotically stable if

$$ \biggl\vert \frac{be-cd}{ ( d+e ) ^{2}} \biggr\vert < \frac{1}{2} \biggl( a+ \frac{b+c}{d+e} \biggr) \quad \text{(Theorem 3.1 in [19])}. $$

Next, if $be>cd$, then we have $f_{u}>0$ and $f_{v}<0$. Note that the condition $c\geq b$ ensures that

$$ \bigl( cd+ad^{2}z+cdz^{2}+ade+aze^{2}+ ( c-b ) ze+bdz+cdz+adz ^{2}e \bigr) \neq 0. $$

This implies

$$ \frac{1}{1-z} \biggl( a+\frac{bz+c}{dz+e}-z \biggl( a+\frac{b+cz}{d+ez} \biggr) \biggr) =\frac{f ( z,1 ) -zf ( 1,z ) }{1-z^{\alpha +1}}\neq 0. $$

Hence, by Remark 3.2, the equilibrium point is a global attractor of (E) if $be>cd$ and $c\geq b$ (Theorem 5.2 in [19]). Finally, by using Theorem 2.2 and 2.3, we can obtain the results of Theorem 6.1 in [19].

In the following, two special cases are given to validate the asymptotic behavior of the proposed new class of difference equations.

Example 4.1

Consider the difference equation (1.3). We have

$$ f ( u,v ) =\frac{au+bv}{cu+dv}u $$

homogeneous with degree $one$. Then the partial derivatives of f are

$$ f_{u} ( u,v ) =\frac{bdv^{2}+au ( cu+2dv ) }{ ( cu+dv ) ^{2}} \quad \mbox{and} \quad f_{v} ( u,v ) =\frac{ ( bc-ad ) u^{2}}{ ( cu+dv ) ^{2}}. $$

From Lemma 3.1, Eq. (1.3) has only zero equilibrium point if $a+b\neq c+d$. By Theorem 3.1, the zero equilibrium point of Eq. (1.3) is locally asymptotically stable if one of the following cases holds:

• (i) $bc>ad$ and $a+b< c+d$,

• (ii) $bc< ad$ and $a ( c+3d ) +b ( d-c ) < ( c+d) ^{2}$.

For the periodicity of solutions of Eq. (1.3), we assume that a, b, c and d are real numbers, $\vert c\vert +\vert d\vert \neq 0$ and $\vert a\vert +\vert d\vert \neq 0$. Using Theorem 2.3, we see that Eq. (1.3) has a prime period two solution if and only if

$$ \frac{a+b\tau }{c+d\tau }=\tau \quad \mbox{and}\quad \frac{a\tau +b}{c\tau +d}\tau =1. $$

Then

$$ a+ ( b-c ) \tau -d\tau^{2}=0 $$

and

$$ d- ( b-c ) \tau -a\tau^{2}=0. $$

Thus, we get $a+d=0$ and

$$ \frac{2 ( c-b ) }{a-d}=\frac{1+\tau^{2}}{\tau }. $$

We define the function $H ( \tau ) := ( 1+\tau^{2} ) /\tau$. Then we find

$$ H ( \tau ) > \min_{\tau \in \mathbf{\mathbb{R} }^{+}\backslash \{ 1 \} }H ( \tau ) =2\quad \text{and}\quad H ( \tau ) < \underset{\tau \in \mathbf{\mathbb{R} }^{-}\backslash \{ -1 \} }{\max }H ( \tau ) =-2. $$

Therefore, Eq. (1.3) has a prime period two solution if $a+d=0$ and one of the following conditions holds:

• (a) $\frac{c-b}{a-d} >1$ for $x_{-1}x_{0}>0$,

• (b) $\frac{c-b}{a-d} <-1$ for $x_{-1}x_{0}<0$.

For a numerical example, we take $a=b=1$, $c=3.5$, $d=-1$, $x_{-1}=2$ and $x_{0}=1$; see Fig. 3.

Figure 3

Prime period two solution of Eq. (1.3)

Example 4.2

Consider the difference equation

$$ x_{n+1}=ax_{n-l}^{\alpha }e^{- ( bx_{n-l}/x_{n-k} ) }, $$

(4.1)

where α, a and b are real numbers, $a>0$ and $b>0$. We have

$$ f ( u,v ) =au^{\alpha }e^{-bu/v}, $$

homogeneous with degree α. Then the partial derivatives of f are

$$\begin{aligned}& f_{u} ( u,v ) = a \biggl[ \alpha -b\frac{u}{v} \biggr] u^{ \alpha -1}e^{bu/v}, \\& f_{v} ( u,v ) = ab\frac{u^{\alpha +1}}{v^{2}}e^{bu/v}. \end{aligned}$$

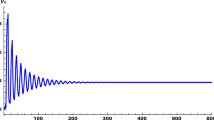
If $\alpha <0$, then $f_{u}<0$ and $f_{v}>0$. By Theorem 3.2, we see that the positive equilibrium point $\overline{x}= ( ae^{-b} ) ^{1/ ( 1-\alpha ) }$ of Eq. (4.1) is locally asymptotically stable if $b<\alpha <1$ or $2b<1+\alpha$. For a numerical example, we take $l=0$, $k=1$, $\alpha =0.5$, $a=2$ and $b=0.1$; see Fig. 4.

Figure 4

Stable solution of difference Eq. (4.1)

For the periodicity of solutions of Eq. (4.1), we assume that l is odd and k is even. By using Theorem 2.2, we see that Eq. (4.1) has a prime period two solution

$$ \rho =\tau \bigl( ae^{-b/\tau } \bigr) ^{1/ ( 1-\alpha ) }\quad \text{and }\quad \sigma = \bigl( ae^{-b/\tau } \bigr) ^{1/ ( 1- \alpha ) },\quad \tau \in \mathbf{ \mathbb{R} }^{+}\backslash \{ 1 \} , $$

if and only if

$$ \frac{b}{ ( \alpha -1 ) }=\frac{\tau \ln \tau }{ ( \tau^{2}-1 ) }. $$

(4.2)

We have

$$ G ( \tau ) :=\frac{\tau \ln \tau }{ ( \tau^{2}-1 ) }< \underset{\tau \in \mathbb{R} ^{+}}{ \max }G ( \tau ) = \frac{1}{2}\quad \text{for }\tau \in \mathbf{\mathbb{R}}^{+}\backslash \{ 1 \} , $$

which with (4.2) gives $2b< ( \alpha -1 )$. For a numerical example, we take $l=1$, $k=0$, $\alpha =-2$, $a=1$, $b=2\ln 2$, $x_{-1}=2\sqrt[3]{2}$ and $x_{0}=\sqrt[3]{2}$; see Fig. 5.

Figure 5

Prime period two solution of Eq. (4.1)