1 Introduction

For an atomic nucleus in nonlinear media, its internal wave evolution is of considerable interest for many applications in science and modern industry technology (see, e.g., [1, 2]). Mathematical theory of propagation of a nonlinear wave for a nucleon field interacting with a neutral meson field is often based on the study of the so-called Klein–Gordon–Schrödinger (KGS) system which has the form

$$\begin{aligned} &iu_{t}+\frac{1}{2}u_{xx}=-nu, \end{aligned}$$
(1.1)
$$\begin{aligned} &n_{tt}-n_{x x}+M^{2}n=|u|^{2}, \end{aligned}$$
(1.2)

where \(u(x,t)\) denotes the conserved complex nucleon field, and \(n(x,t)\) represents the real scalar meson field. This system describes the dynamics of a nucleon field interacting with a neutral meson field through the Yukawa coupling [1]. Up to now, there is a series of work on global existence and asymptotic behavior for this system (1.1)–(1.2) in different topology spaces [3–9]. However, in recent years, modern physics has shown increased interest from different experimental and theoretical groups in the study of the exact solutions. The construction of exact and analytical traveling wave solutions of a nonlinear system is one of the most important and essential tasks in quantum mechanics and chaos theory [10], as these solutions describe very well the various physical phenomena, such as vibrations, solitons, and propagation with a finite speed. To this end, many reliable methods have been developed [11–17], and many interesting research results were reported.

For KGS system, Li–Yang–Wang [14] and Wang–Zhou [12] investigated the periodic wave solutions by using F-expansion method, and Wang–Xia [18] applied Exp-function method to get some generalized solitary wave solutions. Based on a series hypothesis, Darwish [13] has recently obtained multiple exact explicit solutions of the KGS system (1.1)–(1.2). However, to the best of our knowledge, there are few report on the existence of some particular physical waves, such as bright and dark solitons [19]. The main reason is that these methods always omit the original properties of this system.

Our original purpose in this paper is to find a particular type solitary wave solution. For this, we assume that the solution \((u,n)\) for the system (1.1)–(1.2) has the form \(u=f(\tau )^{p_{1}}\exp\{i\phi\}\) and \(n=g(\tau)^{p_{2}}\), respectively, where both \(f(\tau)\) and \(g(\tau)\) are the basis wave functions, \(p_{1}\) and \(p_{2}\) will be determined later by balancing the coefficients. In this paper we explicitly obtain the bright 1-solitons and the bell-shaped regular solitons with the appropriate choice of f and g. Moreover, taking into account the superposition of wave components, we also get the interacting wave \((u,n)\) having the form \(u=[f_{1}(\tau)^{p_{1}}+f_{2}(\tau )^{p_{1}}]\exp\{i\phi\}\) and \(n=g_{1}(\tau)^{p_{2}}+g_{2}(\tau)^{p_{2}}\), respectively. It is regretful that the usual dark soliton cannot be derived, because it strongly depends on the coefficients for Yukawa interaction terms. But fortunately, it may induce a large class of periodic wave solutions that would not be provided by the exposed standard methods.

2 Mathematical analysis

In order to solve (1.1)–(1.2) using the traveling wave hypothesis, it is assumed that

$$ u(x,t)=f(\tau)^{p_{1}}\exp\{i\phi\}, \qquad n(x,t)=g( \tau)^{p_{2}}, $$
(2.1)

where \(f(\tau)\) and \(g(\tau)\) represent the solitary wave profiles, \(\tau=B\eta=B(x-vt)\) and \(\phi=-\kappa x+\omega t+\theta\). Here v is the velocity of soliton and B is the inverse width of the soliton. Also κ is the frequency of the soliton, while ω is the wave number of the soliton and θ is the phase constant. The exponents \(p_{1}\) and \(p_{2}\) are unknown real constants at this point and their values will appear in the process of deriving the solution of this model. Substituting the derivatives of u, n into equation (1.1) and decomposing into real and imaginary parts, respectively, we have

$$ -Bp_{1}(v+\kappa)f(\tau)^{p_{1}-1}f'( \tau)=0 $$
(2.2)

and

$$\begin{aligned} &\biggl(-\omega-\frac{\kappa^{2}}{2}\biggr)f(\tau)^{p_{1}}+ \frac {1}{2}B^{2}p_{1}(p_{1}-1)f( \tau)^{p_{1}-2}f'(\tau)^{2} \\ &\quad {}+\frac{1}{2}B^{2}p_{1}f( \tau)^{p_{1}-1}f''(\tau)+f(\tau)^{p_{1}}g(\tau )^{p_{2}}=0, \end{aligned}$$
(2.3)

while equation (1.2) reduces to

$$\begin{aligned} &p_{2}(p_{2}-1)B^{2}\bigl(v^{2}-1 \bigr)g(\tau)^{p_{2}-2}g'(\tau)^{2} \\ &\quad {}+p_{2}B^{2}\bigl(v^{2}-1\bigr)g( \tau)^{p_{2}-2}g''(\tau)+M^{2}g(\tau )^{p_{2}}-f(\tau)^{2p_{1}}=0. \end{aligned}$$
(2.4)

In (2.2), as a necessary condition, \(v=-\kappa\) is restricted to avoid the trivial solution. In the next section, we mainly treat the rest equations (2.3) and (2.4) in different cases.

3 Solitary wave

In this section we consider the regular solitary wave for the KGS system (1.1)–(1.2) and present some particular solutions which play important roles in the physical traveling wave theory.

The first investigation is concerned with the bright soliton which has the following form:

$$ u(x,t)=\frac{A_{1}}{\cosh^{p_{1}}\tau}\exp\{i\phi\},\qquad n(x,t)= \frac {A_{2}}{\cosh^{p_{2}}\tau}, $$
(3.1)

where \(A_{1}\) and \(A_{2}\) are real and represent the amplitudes of the u- and n-soliton, respectively. Substituting (3.1) into (2.3) and (2.4), respectively, we have

$$ \frac{-\omega A_{1}+\frac{1}{2}A_{1}(p_{1}^{2}B^{2}-\kappa^{2})}{\cosh ^{p_{1}} \tau}-\frac{1}{2}\frac{p_{1}(p_{1}+1)A_{1}B^{2}}{\cosh ^{p_{1}+2} \tau}+ \frac{A_{1}A_{2}}{\cosh^{p_{1}+p_{2}}\tau}=0 $$
(3.2)

and

$$ \frac{A_{2}p_{2}^{2}B^{2}(v^{2}-1)+M^{2}A_{2}}{\cosh^{p_{2}}\tau}-\frac {A_{2}B^{2}p_{2}(p_{2}+1)(v^{2}-1)}{\cosh^{p_{2}+2}\tau}- \frac{A_{1}^{2}}{\cosh^{2p_{1}}\tau}=0. $$
(3.3)

From (3.2), equating the exponents \(p_{1}+2\) and \(p_{1}+p_{2}\) gives \(p_{2}=2\) to get a nontrivial solution. In what follows, we proceed by investigating the cases \(p_{1}=1\) and \(p_{1}=2\).

Case 1

By virtue of (3.3), the first possibility is for the exponents to satisfy \(2p_{1}=p_{2}\), that is, \(p_{1}=1\). Setting the coefficient of the linearly independent \(\frac {1}{\cosh^{p_{1}+j}\tau}\) (\(j=0,2\)) to zero in (3.2), we have

$$\begin{aligned}& -\omega A_{1}+\frac{1}{2}A_{1}\bigl(B^{2}- \kappa^{2}\bigr) =0, \\& -A_{1}B^{2}+A_{1}A_{2} =0. \end{aligned}$$

Solving the above equations, we obtain

$$ B^{2}=2\omega+\kappa^{2}=A_{2} , $$
(3.4)

which implies \(A_{2}> 0\) and \(\omega=\frac{A_{2}-\kappa^{2}}{2}\). In addition, from (3.3), setting the coefficients of the linearly independent function \(\frac{1}{\cosh^{p_{1}+j}\tau}\) (\(j=0,2\)) to 0, we obtain

$$\begin{aligned}& 4A_{2}B^{2}\bigl(v^{2}-1\bigr)+A_{2}M^{2}-A_{1}^{{2}}= 0, \\& -6A_{2}B^{2}\bigl(v^{2}-1\bigr)= 0. \end{aligned}$$

Note that \(A_{2}B\neq0\), thus from the above algebraic equations we get

$$ v^{2}=1 , \qquad A_{2}M^{2}=A_{1}^{2}. $$
(3.5)

Therefore, inserting equations (3.4) and (3.5) into (3.1) leads to

$$\begin{aligned}& u_{1}(x,t) =\frac{\pm BM}{\cosh(B\eta)}\exp\{i\phi\}, \end{aligned}$$
(3.6)
$$\begin{aligned}& n_{1}(x,t) =\frac{B^{2}}{\cosh^{2}(B\eta)}, \end{aligned}$$
(3.7)

where

$$ \phi=vx+\omega t+\theta,\qquad \omega=\frac{B^{2}-1}{2},\qquad v^{2}=1, $$
(3.8)

and B is an arbitrary real nonzero constant. The above expression, as in the case of the particular physical wave, clearly shows the existence of the bright soliton for KGS system (1.1) and (1.2). The propagation profile of the bright soliton is depicted in Fig. 1.

Figure 1
figure 1

Bright soliton with \(B=\sqrt{3}\), \(M=1\) and \(v=1\): (a) the real part of u; (b) the modulus of n

Full size image

Remark 3.1

From the solution (3.6)–(3.7), one has \(M^{2}n=|u|^{2}\), which suggests \(n_{tt}-n_{xx}=0\). Setting \(u=p+iq\), this system becomes

$$\begin{aligned}& p_{t}+\frac{1}{2}q_{xx}+nq= 0, \\& -q_{t}+\frac{1}{2}p_{xx}+np= 0, \\& n_{tt}-n_{xx}=0. \end{aligned}$$

In fact, the KGS system reduces to a system of conservation laws \(\partial_{t} T+\partial_{x} S=0\) with \(T=\frac{1}{2}(p^{2}+q^{2}+2n_{t})\) and \(S=-\frac{1}{2}p_{x}q+\frac{1}{2}pq_{x}-n_{x}\).

Case 2

In (3.3), one can have \(2p_{1}=p_{2}+2\), that is, \(p_{1}=2\). In a similar way to Case 1, one has the following equations:

$$\begin{aligned}& -\omega A_{1}+\frac{1}{2}A_{1}\bigl(4B^{2}- \kappa^{2}\bigr) =0, \\& -3A_{1}B^{2}+A_{1}A_{2} =0, \\& 4A_{2}B^{2}\bigl(v^{2}-1\bigr)+A_{2}M^{2} =0, \\& -6A_{2}B^{2}\bigl(v^{2}-1\bigr)-A_{1}^{2} =0, \end{aligned}$$

which yields

$$ B^{2}=\frac{2\omega+\kappa^{2}}{4}=\frac{A_{2}}{3}=\frac {-M^{2}}{4(v^{2}-1)}=- \frac{A_{1}^{2}}{6A_{2}(v^{2}-1)} $$
(3.9)

with \(A_{2}> 0\) and \(v^{2}<1\). Moreover, we obtain \(3M^{2}A_{2}=2A_{1}^{2}\). In this case, the soliton solution of (1.1)–(1.2) can be written as

$$\begin{aligned}& u_{2}(x,t) =\pm\frac{3BM}{\sqrt{2}\cosh^{2}(B \eta)}\exp\{i\phi\} , \end{aligned}$$
(3.10)
$$\begin{aligned}& n_{2}(x,t) =\frac{3B^{2}}{\cosh^{2}(B \eta)}, \end{aligned}$$
(3.11)

where

$$ \phi=v x+\omega t+\theta, \qquad \omega=2B^{2}+ \frac{M^{2}}{8B^{2}}-\frac {1}{2},\qquad v^{2}=1-\frac{M^{2}}{4B^{2}}. $$
(3.12)

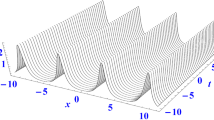
Figure 2 presents the propagation process of the soliton solution. This solution is the so-called bell-profile solitary wave, which is also reported in the existing literature [17, 18].

Figure 2
figure 2

Bell-profile soliton with \(B=M=1\): (a) the real part of u; (b) the modulus of n

Full size image

Remark 3.2

This solution has a strong space location requirement. Indeed, any tiny upper and lower translation is ineffective, that is, if one sets \(u(x,t)=(A_{1}\operatorname{sech}^{p_{1}}\tau +C_{1})\exp\{i\phi\}\) and \(n(x,t)=A_{2}\operatorname{sech}^{p_{2}}\tau+C_{2}\) with real constants \(C_{1}\) and \(C_{2}\), then one can deduce that \(C_{1}=C_{2}=0\) with \(p_{1}=1\) or 2 and \(p_{2}=2\).

As \(\operatorname{sech}^{2}(\alpha-i\pi/2)=-\operatorname{csch}^{2}(\alpha)\), shifting x by \(i\pi /2\) in \(u_{2}\), \(n_{2}\), we obtain

$$\begin{aligned}& u_{3}(x,t)=\pm\frac{3BM}{\sqrt{2}}\operatorname{csch}^{2}(B\eta)\exp\{i\phi \}, \end{aligned}$$
(3.13)
$$\begin{aligned}& n_{3}(x,t)=-3B^{2}\operatorname{csch}^{2}(B\eta), \end{aligned}$$
(3.14)

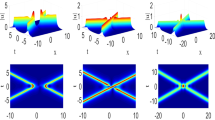
with ϕ, ω and v as in (3.12). Similar to the bell-shaped soliton, any tiny change of the amplitude for this solution is not allowed, although the shock wave brings about the singularity along some characteristic direction (e.g., \(x-vt=0\)). The evolution of the real part for u and \(|n|\) is displayed in Fig. 3.

Figure 3
figure 3

Singular soliton with \(B=M=1\): (a) the real part of u; (b) the singularity of n

Full size image

Using the formula \(\operatorname{csch}^{2}(\alpha)-\operatorname{sech}^{2}(\alpha)=4\operatorname{csch}^{2}(2\alpha)\), we can get

$$\begin{aligned}& u_{4}(x,t) =\pm\frac{3BM}{4\sqrt{2}}\bigl(\operatorname{csch}^{2}(B\eta/2)- \operatorname{sech}^{2}(B\eta /2)\bigr)\exp\{i\phi\}, \end{aligned}$$
(3.15)
$$\begin{aligned}& n_{4}(x,t) =-\frac{3B^{2}}{4}\bigl(\operatorname{csch}^{2}(B\eta/2)- \operatorname{sech}^{2}(B\eta/2)\bigr), \end{aligned}$$
(3.16)

with ϕ, ω and v as in (3.12) as well.

Remark 3.3

We will also attempt to find a dark soliton of the form \(u=A_{1}\tanh(\tau)\exp\{i\phi\}\) and \(n=A_{2}\tanh ^{2}(\tau)\). It is regretful that the homogeneous balancing technique cannot produce a nontrivial solution because it strongly depends on the sign of the coefficients for Yukawa interaction terms. However, we can deduce a solution with \(\tanh(\tilde{B}(x-vt))+\tilde{C}\) where B̃ is a pure imaginary number. Noting that \(\tanh(ix)=i\tan x\), we will then have the solution in Sect. 4.

4 Periodic wave

The search for the dark solitons shows the existence of a solution with the form \(\tanh(i\tilde{B}(x-vt))+\tilde{C}\) (see Remark 3.3), which inspires us to exert fresh efforts.

It is well known that \(\tanh(ix)=i\tan x\) and that \(\tanh(i\tilde {B}(x-vt))\) type solution implies the existence of a tangent wave of KGS system (1.1)–(1.2). As a generalization, here we consider the following translation wave:

$$ u(x,t)=\bigl(A_{1}\tan^{p_{1}} \tau+C_{1}\bigr)\exp\{i\phi\},\qquad n(x,t)=A_{2} \tan ^{p_{2}}\tau+C_{2}, $$
(4.1)

where \(A_{1} \), \(A_{2}\), \(C_{1} \), \(C_{2} \), \(p_{1} \), \(p_{2}\) are real and \(C_{1}\), \(C_{2}\) are free nonzero parameters. Substituting the derivatives of u, n into (1.1) and (1.2) yields

$$\begin{aligned} &\biggl(-\omega A_{1}-\frac{1}{2}\kappa^{2}A_{1} \biggr)\tan^{p_{1}}\tau-\omega C_{1}-\frac{1}{2} \kappa^{2}C_{1}+\frac{1}{2}A_{1}p_{1}(p_{1}-1)B^{2} \tan ^{p_{1}-2}\tau \\ &\quad {}+A_{1}p_{1}^{2}B^{2} \tan^{p_{1}}\tau+\frac {1}{2}A_{1}p_{1}(p_{1}+1)B^{2} \tan^{p_{1}+2}\tau+A_{1}A_{2}\tan ^{p_{1}+p_{2}}\tau \\ &\quad {}+A_{1}C_{2}\tan^{p_{1}}\tau+A_{2}C_{1} \tan^{p_{2}}\tau+C_{1}C_{2}=0 \end{aligned}$$
(4.2)

and

$$\begin{aligned} &A_{2}p_{2}(p_{2}-1)B^{2} \bigl(v^{2}-1\bigr)\tan^{p_{2}-2}\tau +2A_{2}p_{2}^{2}B^{2} \bigl(v^{2}-1\bigr)\tan^{p_{2}}\tau \\ &\quad {}+A_{2}p_{2}(p_{2}+1)B^{2} \bigl(v^{2}-1\bigr)\tan^{p_{2}+2}\tau+M^{2} \bigl(A_{2}\tan ^{p_{2}}\tau+C_{2}\bigr) \\ &\quad {}- \bigl(A_{1}^{2}\tan^{2p_{1}} \tau+2A_{1}C_{1}\tan^{p_{1}}\tau +C_{1}^{2} \bigr)=0. \end{aligned}$$
(4.3)

An effective matching and the independent 0-coefficients for \(\tan ^{p_{1}+j}\tau\) (\(j=-2,0,2\)) show \(p_{1}=p_{2}=2\) and the equations

$$\begin{aligned}& -\omega A_{1}-\frac{1}{2}\kappa ^{2}A_{1}+4A_{1}B^{2}+A_{1}C_{2}+A_{2}C_{1} =0, \end{aligned}$$
(4.4)
$$\begin{aligned}& -\omega C_{1}-\frac{1}{2}\kappa^{2}C_{1}+A_{1}B^{2}+C_{1}C_{2} =0 , \end{aligned}$$
(4.5)
$$\begin{aligned}& 3A_{1}B^{2}+A_{1}A_{2} =0, \end{aligned}$$
(4.6)

which produce \(B^{2}=-\frac{A_{2}}{3}\). And from (4.4)/\(A_{1}\)–(4.5)/\(C_{1}\), we can obtain \(-\frac{4}{3}+\frac{C_{1}}{A_{1}}=-\frac{A_{1}}{3C_{1}}\) which yields \(\frac{C_{1}}{A_{1}}=1\) or \(\frac{C_{1}}{A_{1}}=\frac{1}{3}\). Moreover, in (4.3), setting the coefficients of the function \(\frac {1}{\tan^{p_{2}+j}\tau}\) (\(j=-2,0,2\)) to 0, we have

$$\begin{aligned}& 2A_{2}B^{2}\bigl(v^{2}-1\bigr)+M^{2}C_{2}-C_{1}^{2} =0, \end{aligned}$$
(4.7)
$$\begin{aligned}& 8A_{2}B^{2}\bigl(v^{2}-1\bigr)+M^{2}A_{2}-2A_{1}C_{1} =0, \end{aligned}$$
(4.8)
$$\begin{aligned}& 6A_{2}B^{2}\bigl(v^{2}-1\bigr)-A_{1}^{2} =0. \end{aligned}$$
(4.9)

From (4.9), we have \(A_{1}^{2}=-2A_{2}^{2}(v^{2}-1)\) for \(v^{2}-1<0\). Equations (4.7)–(4.8) reduce to

$$\begin{aligned}& A_{1}^{2}+3M^{2}C_{2}-3C_{1}^{2} =0, \end{aligned}$$
(4.10)
$$\begin{aligned}& 4A_{1}^{2}+3M^{2}A_{2}-6A_{1}C_{1} =0. \end{aligned}$$
(4.11)

If \(\frac{C_{1}}{A_{1}}=1\), form (4.11), we get \(A_{2}=\frac {2A_{1}^{2}}{3M^{2}}>0\), which contradicts \(B^{2}=-\frac{A_{2}}{3}\). Otherwise, if \(\frac{C_{1}}{A_{1}}=\frac{1}{3}\), we have \(C_{2}=\frac{1}{3}A_{2}=-\frac{2A_{1}^{2}}{9M^{2}}\). Hence, the solution of KGS system (1.1)–(1.2) is given by

$$\begin{aligned}& u_{5}(x,t) =\pm\frac{3KM}{\sqrt{2}} \biggl(\tan^{2}(K\eta)+ \frac{1}{3} \biggr)\exp\{i\phi\} , \end{aligned}$$
(4.12)
$$\begin{aligned}& n_{5}(x,t) =-3K^{2} \biggl(\tan^{2}(K\eta)+ \frac{1}{3} \biggr), \end{aligned}$$
(4.13)

where

$$ \phi=v x+\omega t+\theta,\qquad \omega=2K^{2}+ \frac{M^{2}}{8K^{2}}-\frac {1}{2},\qquad v^{2}=1-\frac{M^{2}}{4K^{2}}, $$
(4.14)

and K is an arbitrary real nonzero constant. For the propagation of the solution, one can refer to Fig. 4.

Figure 4
figure 4

Tangent type wave with \(M=K=1\): (a) the real part of u; (b) the periodical singularity of n

Full size image

As \(\tan^{2}(\alpha-\pi/2)=\cot^{2}(\alpha)\), shifting x by \(i\pi/2\) in \(u_{5}\), \(n_{6}\), we have

$$\begin{aligned}& u_{6}(x,t) =\pm\frac{3KM}{\sqrt{2}} \biggl(\cot^{2}(K\eta)+ \frac{1}{3} \biggr)\exp\{i\phi\} , \end{aligned}$$
(4.15)
$$\begin{aligned}& n_{6}(x,t) =-3K^{2} \biggl(\cot^{2}(K\eta)+ \frac{1}{3} \biggr), \end{aligned}$$
(4.16)

with ϕ, ω and v as in (4.14). This solution admits a similar periodical change process as for the tangent type wave.

Using the formula \(\cot^{2}(\alpha)+\tan^{2}(\alpha)=4\cot^{2}(2\alpha )+2\), we also have

$$\begin{aligned}& u_{7}(x,t) =\pm\frac{3KM}{4\sqrt{2}} \biggl(\cot^{2}(K\eta/2)+ \tan^{2}(K\eta /2)-\frac{2}{3} \biggr)\exp\{i\phi\}, \end{aligned}$$
(4.17)
$$\begin{aligned}& n_{7}(x,t) =-\frac{3K^{2}}{4} \biggl(\cot^{2}(K\eta/2)+ \tan^{2}(K\eta /2)-\frac{2}{3} \biggr), \end{aligned}$$
(4.18)

with ϕ, ω and v as in (4.14) as well.

5 Conclusion

In this paper, the ansatz method is applied to the \((1+1)\)-dimensional KGS system for some particular solitary waves, and a series of explicit exact solutions are constructed. Most of them cannot be derived by the existing standard procedures, particularly, the bright solitons and singular wave that play essential role in plasma and fluid physics. More importantly, their amplitudes are not only strongly dependent on the wave speed, but also related to the mass of the meson. As for the existence of dark solitons of another form, we will make further discussion in the forthcoming work.