1 Introduction

The nonlinear systems have been widely studied in the real world [1–7]. During the past 30 years, neural networks have become one of the most important nonlinear systems and have been intensively applied to solve various optimization problems [8]. On the other hand, time-delay may often occur in many practical systems such as neural networks [9–12]. At the same time, it can lead to many complex dynamic behaviors such as divergence, oscillation and instability of the neural networks [13]. It is very important that the stability analysis for delayed neural networks between theoretical and practical systems.

In the past decades, synchronization and anti-synchronization of neural networks have caused wide attention because of its potential application in various fields of science and humanity worldwide, such as image encryption [14], physical systems [15], secure communication [16] and laser technology [17]. Meanwhile, many control methods and techniques have been proposed to synchronize the behavior of neural networks. These control methods are divided into adaptive control [18], nonlinear control [19], active control [20], etc. Most of these methods are based on continuous control and discontinuous control strategies are rarely studied. The intermittent control [21] is a kind of discontinuous control methods and control of the system in a discontinuous time period. It is a more effective and economical approach than continuous control. So far, it is widely applied to solve the synchronization problem of neural networks [22–24].

We say that two systems achieve anti-synchronization when they have the same amplitude but opposite signs. Then the sum of two signals will converge to zero when the anti-synchronization phenomenon occurs. Therefore, the authors have studied the anti-synchronization phenomenon on neural networks and some relevant theoretical results have been established [25–27]. In the current research of synchronization theory, most authors studying the anti-synchronization of neural networks have based themselves on the convergence time being large enough. This indicates that the control can drive the slave system to anti-synchronize the master system after the infinite horizon. The control of infinite time is not difficult to realize in the actual system, but it takes a higher cost. We hope to control the cost as much as possible and to reach stability of the system as quickly as possible. In order to realize the stability and synchronization of the system quickly, one can use finite-time techniques to get a faster convergent speed. Finite-time synchronization of complex networks has been investigated in [28, 29]. Unfortunately, there are few papers considering the finite-time anti-synchronization of neural networks via feedback control with intermittent adjustment.

Motivated by the above discussion, this paper will investigate the finite-time anti-synchronization of time-varying delayed neural networks. Furthermore, by applying an inequality technique and the Lyapunov stability theorem, the finite-time anti-synchronization can be realized between the drive and response systems by designing an intermittent adjustment feedback controller. Lastly, two numerical examples are given to prove the correctness of the proposed method.

The remainder of this paper is organized as follows. In Section 2, the model formulation and some preliminaries are given. The main results will be obtained in Section 3. Two examples are given to show the effectiveness of our results in Section 4. Finally, conclusions are drawn in Section 5.

Notations: Throughout this paper, \(\mathbb{R}^{n}\) denotes n dimensional real numbers set, \(\mathbb{N}\) denotes natural numbers set. \(A_{m \times n}\) and \(I_{N}\) refer to \(m \times n\) matrix and \(N \times N\) identity matrix, respectively. The superscript T denotes vector transposition. \(\Vert \cdot \Vert \) is the Euclidean norm in \(\mathbb{R}^{n}\). If A is a matrix, \(\Vert A \Vert \) denotes its operator norm. If not explicitly stated, matrices are assumed to have compatible dimensions.

2 Model description and preliminaries

In this section, a neural network model and definition will be introduced. Furthermore, some useful lemmas will also be given, which will be used later.

The model of the neural network with time-varying delay can be described by

$$ \dot{x}_{i}(t) = - c_{i}x_{i}(t) + \sum_{j = 1}^{n} a_{ij} f_{j} \bigl(x_{j}(t) \bigr) + \sum _{j = 1}^{n} b_{ij}f_{j} \bigl(x_{j} \bigl(t - \tau (t) \bigr) \bigr) , \quad i = 1,2,\ldots,n, $$
(1)

where \({x_{i}}(t)\) denotes the state variable associated with the ith neuron. In compact matrix form, (1) can be rewritten as

$$ \dot{x}(t) = - Cx(t) + Af \bigl(x(t) \bigr) + Bf \bigl(x \bigl(t - \tau(t) \bigr) \bigr), $$
(2)

where \(x(t) = {({x_{1}}(t),{x_{2}}(t),\ldots,{x_{n}}(t))^{T}} \in{\mathbb {R}^{n}}\) is the state vector of the neural networks at time t. \({c_{i}} > 0\) (\(i = 1,2,\ldots,n\)) are constants, \(C = \operatorname {diag}({c_{1}},{c_{2}},\ldots ,{c_{n}})\) is diagonal matrix. \(A = {({a_{ij}})_{n \times n}}\), \(B = {({b_{ij}})_{n \times n}}\) represent the connect weight matrix and the delayed connection weight matrix with proper dimension. \({a_{ij}}\), \({b_{ij}}\) denote the strengths of connectivity between the cell i and j at time t and at time \(t - \tau(t)\), respectively; \(f(x(t)) = ({f_{1}}({x_{1}}(t)),\ldots,{f_{n}}({x_{n}}(t)))^{T}\) is the activation function of the neurons and satisfy the global Lipschitz conditions with Lipschitz constants \(L > 0\). \(\tau(t)\) is the time-varying delay of neural network, \(0 \leq{\tau_{1}} \leq\tau(t) \leq{\tau_{2}}\), \(\dot{\tau}(t) \le h < 1\), \({\tau _{1}}\), \({\tau_{2}}\) and h are constants. In addition, the initial conditions of system (2) are given by \(x(s) = \phi(s) = {({\phi_{1}}(s),{\phi_{2}}(s),\ldots,{\phi_{n}}(s))^{T}}\).

In this paper, we consider system (2) as the drive system, and the corresponding response system is given by

$$ \dot{y}_{i}(t) = - c_{i}y_{i}(t) + \sum_{j = 1}^{n} a_{ij} f_{j} \bigl(y_{j}(t) \bigr) + \sum _{j = 1}^{n} b_{ij}f_{j} \bigl(y_{j} \bigl(t - \tau (t) \bigr) \bigr) + u_{i}(t), \quad i = 1,2,\ldots,n, $$
(3)

or equivalently

$$ \dot{y}(t) = - Cy(t) + Af \bigl(y(t) \bigr) + Bf \bigl(y \bigl(t - \tau(t) \bigr) \bigr) + u(t), $$
(4)

where the initial conditions \(y(s) = \omega(s) = {({\omega _{1}}(s),{\omega_{2}}(s),\ldots,{\omega_{n}}(s))^{T}} \in\mathbb{R}^{n}\), \(y(t) = ({y_{1}}(t),{y_{2}}(t), \ldots,{y_{n}}(t))^{T}\) is the response state vector of the neural networks at time t. \(u(t) = ({u_{1}}(t),{u_{2}}(t), \ldots,{u_{n}}(t))^{T}\) is an intermittent adjustment feedback controller that will be designed to achieve the anti-synchronization between drive-response systems.

Define the anti-synchronization errors \({e_{i}}(t) = {y_{i}}(t) + {x_{i}}(t)\), \(i = 1,2,\ldots,n\). \({x_{i}}(t)\) and \({y_{i}}(t)\) are the state variables of drive system (1) and response system (3), respectively. Therefore, the error system can be derived as follows:

$$ \dot{e}_{i}(t) = -c_{i}e_{i}(t) + \sum_{j = 1}^{n} a_{ij} F_{j} \bigl(e_{j}(t) \bigr) + \sum _{j = 1}^{n} b_{ij} F_{j} \bigl(e_{j} \bigl(t - \tau (t) \bigr) \bigr) + u_{i}(t), \quad i = 1,2,\ldots,n, $$
(5)

or equivalently

$$ \dot{e}(t) = - Ce(t) + AF \bigl(e(t) \bigr) + BF \bigl(e \bigl(t - \tau(t) \bigr) \bigr) + u(t), $$
(6)

with initial conditions \({\psi_{i}}(t) = {\omega_{i}}(t) + {\phi_{i}}(t)\), \(i = 1,2,\ldots,n\). Here \(e(t) = {({e_{1}}(t),{e_{2}}(t),\ldots,{e_{n}}(t))^{T}} \in{\mathbb{R}^{n}}\), \({F_{j}}({e_{j}}(t)) = {f_{j}}({y_{j}}(t)) + {f_{j}}({x_{j}}(t))\), \({F_{j}}({e_{j}}(t - \tau(t))) = {f_{j}}({y_{j}}(t - \tau (t))) + {f_{j}}({x_{j}}(t - \tau(t)))\).

Through this paper, in order to obtain the anti-synchronization results, we give the following assumption, definition and some useful lemmas.

Assumption 1

[30]

There exists a constant \(L > 0\), for any \(x(t),y(t) \in{\mathbb{R}^{n}}\), such that

$$\bigl\Vert f \bigl(x(t) \bigr) + f \bigl(y(t) \bigr) \bigr\Vert \le L \bigl\Vert x(t) + y(t) \bigr\Vert , $$

therefore, we can obtain \(\Vert {F(e(t))} \Vert \le L \Vert {e(t)} \Vert \).

Definition 1

[23]

System (1) and (3) are said to be finite-time anti-synchronization if for suitable intermittent adjustment feedback controller \({u_{i}}(t)\), there exists a constant \(\bar{T} > 0\) such that

$$\lim_{t \to\bar{T} } \bigl\Vert {{e_{i}}(t)} \bigr\Vert = 0, \quad i = 1,2,\ldots,n, $$

and \(\Vert {{e_{i}}(t)} \Vert = 0\) for \(t > \bar{T} \), where T̄ is a function about the initial state vector value, The function T̄ is named the settling-time function and its value is called the settling time.

Lemma 1

[31]

If \({a_{1}},{a_{2}},\ldots,{a_{n}}\) are positive number and \(0 < p < q\), then

$$\Biggl(\sum_{i = 1}^{n} a_{i}^{q} \Biggr)^{\frac{1}{q}} \le \Biggl(\sum_{i = 1}^{n} a_{i}^{p} \Biggr)^{\frac{1}{p}}. $$

Lemma 2

[32]

Suppose that a function \(V(t)\) is continuous and non-negative when \(t \in[ {0, + \infty} )\), and it satisfies the following conditions:

$$\textstyle\begin{cases} \dot{V}(t) \le- \alpha{V^{\eta}}(t), \quad HT \le t < HT + \theta T,\\ \dot{V}(t) \le0, \quad HT + \theta T \le t < (H + 1)T, \end{cases} $$

where \(\alpha> 0\), \(T > 0\), \(0 < \eta< 1\), \(0 < \theta< 1\), \(H \in\mathbb {N}\), then the following inequality holds:

$$V^{1 - \eta}(t) \le V^{1 - \eta}(0) - \alpha\theta(1 - \eta)t, \quad 0 \le t \le \bar{T} , $$

and the constant T̄ is the settling time.

Lemma 3

[33]

Given any real matrices A, B, Q of appropriate dimensions and a scalar \(m > 0\), such that \(0 < Q = {Q^{T}}\). Then the following inequality holds:

$$A^{T}B + B^{T}A \le mA^{T}QA + m^{-1}B^{T}Q^{-1}B. $$

3 Main results

In this section, the finite-time anti-synchronization of neural networks will be studied between system (1) and system (3). In order to obtain the results, an intermittent adjustment feedback controller can be designed as follows:

$$ \textstyle\begin{cases} u_{i}(t)=-\frac{\beta}{2}e_{i}(t) +v_{i}(t),\\ v_{i}(t)=- \frac{k}{2}\operatorname {sgn}(e_{i}(t)) \vert e_{i}(t) \vert ^{\alpha}\\ \hphantom{v_{i}(t)=}{}-\frac{k}{2}(\int_{t - \tau(t)}^{t} e^{2}_{i}(s)\,ds) ^{\frac{1 + \alpha }{2}}(\frac{e_{i}(t)}{ \Vert e_{i}(t) \Vert ^{2}}), \quad HT \le t < HT + \delta, i = 1,2,\ldots,n,\\ {u_{i}}(t) = -\frac{\beta}{2}e_{i}(t), \quad HT + \delta\le t < (H + 1)T,i = 1,2,\ldots,n, \end{cases} $$
(7)

where \(0 < \alpha< 1\), \(\beta> 0\) is a positive constant called control gain, \(k > 0\) is a tunable real constant, \(\operatorname {sgn}( \cdot)\) is the sign function. \(H \in\mathbb{N}\), \(T > 0\) is the control period, \(\delta> 0\) is called the control duration.

In the same way, (7) can be expressed by the following form:

$$ \textstyle\begin{cases} u(t) = - \frac{\beta}{2}e(t) + v(t),\\ v(t)=- \frac{k}{2}\operatorname {sgn}(e(t)){{ \vert {e(t)} \vert }^{\alpha}}\\ \hphantom{v(t)=}{}- \frac{k}{2}{{(\int_{t - \tau(t)}^{t} {e^{T}}(s)e(s)\,ds)}^{\frac{{1 + \alpha}}{2}}}(\frac{{e(t)}}{{{{ \Vert {e(t)} \Vert }^{2}}}}),\quad HT \le t < HT + \delta,\\ u(t) = - \frac{\beta}{2}e(t), \quad HT + \delta\le t < (H + 1)T, \end{cases} $$
(8)

where

$$\begin{aligned}& \bigl\vert e(t) \bigr\vert ^{\alpha}= \bigl( \bigl\vert e_{1}(t) \bigr\vert ^{\alpha}, \bigl\vert e_{2}(t) \bigr\vert ^{\alpha},\ldots, \bigl\vert e_{n}(t) \bigr\vert ^{\alpha} \bigr)^{T}, \\& \operatorname {sgn}\bigl(e(t) \bigr)=\operatorname {diag}\bigl(\operatorname {sgn}\bigl(e_{1}(t) \bigr),\operatorname {sgn}\bigl(e_{2}(t) \bigr),\ldots, \operatorname {sgn}\bigl(e_{n}(t) \bigr) \bigr)^{T}. \end{aligned}$$

Let \(\theta= \frac{\delta}{T}\) be the ratio of the control width δ to the control period T, which is called the control rate. Then, substituting (8) into (6), the error system between (2) and (4) can be expressed as

$$ \textstyle\begin{cases} \dot{e}(t) = - Ce(t) + AF(e(t)) + BF(e(t - \tau(t))) - \frac{\beta}{2}e(t)- \frac{k}{2}\operatorname {sgn}(e(t)){ \vert {e(t)} \vert ^{\alpha}} \\ \hphantom{\dot{e}(t) =}{}- \frac{k}{2}{(\int_{t - \tau(t)}^{t} {{e^{T}}(s)e(s)\,ds} ) ^{\frac{{1 + \alpha}}{2}}}(\frac{{e(t)}}{{{{ \Vert {e(t)} \Vert }^{2}}}}),\quad HT \le t < HT + \theta T, H \in\mathbb{N},\\ \dot{e}(t) = - Ce(t) + AF(e(t)) + BF(e(t - \tau(t))) \\ \hphantom{\dot{e}(t) =}{}- \frac{\beta}{2}e(t), \quad HT + \theta T \le t < (H + 1)T. \end{cases} $$
(9)

Remark 1

When \(HT \le t < HT + \theta T\), \(H \in\mathbb{N}\). If \(0 < \alpha< 1\), the controller \(u(t)\) is a continuous function with respect t. If \(\alpha= 0\), \(u(t)\) turns to be discontinuous one, which is similar to the controller that have been considered in [34]. If \(\alpha= 1\), the controller will become typical feedback control issues, which only can realize an asymptotical anti-synchronization in an infinite time.

Theorem 1

Suppose Assumption  1 holds, and there exists a positive constant \({m_{1}}\) such that the following condition:

$$ - 2 \Vert C \Vert + {m_{1}} \bigl\Vert {A{A^{T}}} \bigr\Vert + {m_{1}}^{ - 1}L + \frac{L}{{1 - h}} \bigl\Vert {B{B^{T}}} \bigr\Vert + 1 -\beta\le0, $$
(10)

then system (2) and system (4) can realize finite-time anti-synchronization under the intermittent adjustment feedback controller (8) in a finite time:

$$\bar{T} = \frac{{{V^{(1 - \alpha)/2}}(0)}}{{k\theta(1 - \alpha)/2}} , $$

where \(V(0) = {e^{T}}(0)e(0) = \sum_{i = 1}^{n} ({e_{i}}(0))^{2} \), \(e(0) = y(0) + x(0)\).

Proof

Constructing the following Lyapunov function:

$$ V(t) = {e^{T}}(t)e(t) + \int_{t - \tau(t)}^{t} {{e^{T}}(s)e(s)} \,ds, $$
(11)

at the same time, \({e^{T}}(t)e(t)\) also can be described as \(\sum_{i = 1}^{n} ({e_{i}}(t))^{2}\). Then the derivative of \(V(t)\) with respect to time t along the solutions of equation (9) can be calculated as follows.

When \(HT \le t < HT + \theta T\), \(H \in\mathbb{N}\),

$$\begin{aligned} \dot{V}(t)& = \dot{e}^{T}(t)e(t) + e^{T}(t)\dot{e} (t) + e^{T}(t)e(t) - e^{T} \bigl(t - \tau(t) \bigr)e \bigl(t - \tau(t) \bigr) \bigl(1 - \dot{\tau}(t) \bigr) \\ &= -e^{T}(t) \bigl(C + C^{T} \bigr)e(t) + e^{T}(t)A \bigl(f \bigl(y(t) \bigr) + f \bigl(x(t) \bigr) \bigr) \\ &\quad {}+ \bigl[A \bigl(f \bigl(y(t) \bigr) + f \bigl(x(t) \bigr) \bigr) \bigr]^{T}e(t) \\ &\quad {}+ e^{T}(t)B \bigl(f \bigl(y \bigl(t - \tau(t) \bigr) \bigr) + f \bigl(x \bigl(t - \tau(t) \bigr) \bigr) \bigr) \\ &\quad {}+ \bigl[B \bigl(f \bigl(y \bigl(t - \tau(t) \bigr) \bigr) + f \bigl(x \bigl(t - \tau(t) \bigr) \bigr) \bigr) \bigr]^{T}e(t) \\ &\quad {}- e^{T}(t)\beta e(t) - ke^{T}(t)\operatorname {sgn}\bigl(e(t) \bigr) \bigl\vert e(t) \bigr\vert ^{\alpha}\\ &\quad {}- k \biggl( \int_{t - \tau(t)}^{t} e^{T}(s)e(s)\,ds \biggr)^{\frac{1 + \alpha}{2}} e^{T}(t) \biggl(\frac{e(t)}{ \Vert e(t) \Vert ^{2}} \biggr) \\ &\quad {}+ e^{T}(t)e(t) - e^{T} \bigl(t - \tau(t) \bigr)e \bigl(t - \tau(t) \bigr) \bigl(1 - \dot{\tau }(t) \bigr) \\ &= - 2e^{T}(t)Ce(t) + e^{T}(t)A \bigl(f \bigl(y(t) \bigr) + f \bigl(x(t) \bigr) \bigr) \\ &\quad {}+ \bigl[A \bigl(f \bigl(y(t) \bigr) + f \bigl(x(t) \bigr) \bigr) \bigr]^{T}e(t) \\ &\quad {}+ e^{T}(t)B \bigl(f \bigl(y \bigl(t - \tau(t) \bigr) \bigr) + f \bigl(x \bigl(t - \tau(t) \bigr) \bigr) \bigr) \\ &\quad {}+ \bigl[B \bigl(f \bigl(y \bigl(t - \tau(t) \bigr) \bigr) + f \bigl(x \bigl(t - \tau(t) \bigr) \bigr) \bigr) \bigr]^{T}e(t) \\ &\quad {}- e^{T}(t)\beta e(t) - ke^{T}(t)\operatorname {sgn}\bigl(e(t) \bigr) \bigl\vert e(t) \bigr\vert ^{\alpha}- k \biggl( \int_{t - \tau(t)}^{t} e^{T}(s)e(s)\,ds \biggr)^{\frac{1 + \alpha }{2}} \\ &\quad {}+ e^{T}(t)e(t) - e^{T} \bigl(t - \tau(t) \bigr)e \bigl(t - \tau(t) \bigr) \bigl(1 - \dot{\tau}(t) \bigr). \end{aligned}$$

Using Lemma 3 and Assumption 1, the following inequality can be established:

$$ \begin{aligned}[b] & e^{T}(t)A \bigl(f \bigl(y(t) \bigr) + f \bigl(x(t) \bigr) \bigr) + \bigl[A \bigl(f \bigl(y(t) \bigr) + f \bigl(x(t) \bigr) \bigr) \bigr]^{T}e(t) \\ & \quad \le m_{1}e^{T}(t)AA^{T}e(t) + m_{1}^{-1} \bigl[f \bigl(y(t) \bigr) + f(x(t) \bigr]^{T} \bigl[f \bigl(y(t) \bigr) + f \bigl(x(t) \bigr) \bigr] \\ & \quad \le m_{1}e^{T}(t)AA^{T}e(t) + m_{1}^{-1}Le^{T}(t)e(t). \end{aligned} $$
(12)

Similarly,

$$ \begin{aligned}[b] & e^{T}(t)B \bigl(f \bigl(y \bigl(t - \tau(t) \bigr) \bigr) + f \bigl(x \bigl(t - \tau(t) \bigr) \bigr) \bigr) \\ &\quad\quad{} + \bigl[B \bigl(f \bigl(y \bigl(t - \tau(t) \bigr) \bigr) + f \bigl(x \bigl(t - \tau(t) \bigr) \bigr) \bigr) \bigr]^{T}e(t) \\ &\quad \le\frac{L}{1 - h}e^{T}(t)BB^{T}e(t) + (1 - h)e^{T} \bigl(t - \tau(t) \bigr)e \bigl(t - \tau(t) \bigr). \end{aligned} $$
(13)

Substituting (13) and (14) into \(\dot{V}(t)\)

$$\begin{aligned} \dot{V}(t) \le&{} - 2e^{T}(t)Ce(t) + m_{1}e^{T}(t)AA^{T}e(t) + m_{1}^{-1}Le^{T}(t)e(t) \\ &{} + \frac{L}{1 - h}e^{T}(t)BB^{T}e(t) + (1 - h)e^{T} \bigl(t - \tau(t) \bigr)e \bigl(t - \tau(t) \bigr) - e^{T}(t)\beta e(t) \\ &{} - k\sum_{i = 1}^{n} e_{i}(t) \operatorname {sgn}\bigl(e_{i}(t) \bigr) \bigl\vert e_{i}(t) \bigr\vert ^{\alpha}- k \biggl( \int_{t - \tau(t)}^{t} e^{T}(s)e(s)\,ds \biggr)^{\frac{1 + \alpha}{2}} \\ &{} + e^{T}(t)e(t) - (1 - h)e^{T} \bigl(t - \tau(t) \bigr)e \bigl(t - \tau(t) \bigr) \\ \le&{} - 2 \Vert C \Vert \bigl\Vert e(t) \bigr\Vert ^{2} + m_{1} \bigl\Vert AA^{T} \bigr\Vert \bigl\Vert e(t) \bigr\Vert ^{2} + m_{1}^{-1}L \bigl\Vert e(t) \bigr\Vert ^{2} \\ &{} + \frac{L}{1 - h} \bigl\Vert BB^{T} \bigr\Vert \bigl\Vert e(t) \bigr\Vert ^{2} + (1 - \beta) \bigl\Vert e(t) \bigr\Vert ^{2} \\ & {}- k\sum_{i = 1}^{n} \bigl\vert e_{i}(t) \bigr\vert ^{\alpha+ 1} - k \biggl( \int_{t - \tau(t)}^{t} e^{T}(s)e(s)\,ds \biggr)^{\frac{1 + \alpha}{2}}. \end{aligned}$$

From Lemma 1, we get

$$\Biggl(\sum_{i = 1}^{n} { \bigl\vert {{e_{i}}(t)} \bigr\vert }^{2} \Biggr)^{1/2} \le \Biggl(\sum_{i = 1}^{n} { \bigl\vert {{e_{i}}(t)} \bigr\vert }^{\alpha+ 1} \Biggr)^{1/\alpha+ 1}. $$

Hence,

$$ \Biggl(\sum_{i = 1}^{n} \bigl\vert {{e_{i}}(t)} \bigr\vert ^{2} \Biggr)^{\alpha+ 1/2} \le\sum_{i = 1}^{n} \bigl\vert {{e_{i}}(t)} \bigr\vert ^{\alpha+ 1}. $$
(14)

Therefore, according to the condition (10)

$$\begin{aligned} \dot{V}(t) &\le \biggl( - 2 \Vert C \Vert + m_{1} \bigl\Vert AA^{T} \bigr\Vert + m_{1}^{-1}L + \frac{L}{1 - h} \bigl\Vert BB^{T} \bigr\Vert + 1 - \beta \biggr) \bigl\Vert e(t) \bigr\Vert ^{2} \\ &\quad{} - k \Biggl(\sum_{i = 1}^{n} \bigl\vert e_{i}(t) \bigr\vert ^{2} \Biggr)^{\frac{ \alpha+ 1}{2}} - k \biggl( \int_{t - \tau(t)}^{t} e^{T}(s)e(s)\,ds \biggr)^{\frac{\alpha+ 1}{2}} \\ & \le- k \Biggl(\sum_{i = 1}^{n} \bigl\vert e_{i}(t) \bigr\vert ^{2} \Biggr)^{\frac{\alpha+ 1}{2}} - k \biggl( \int_{t - \tau(t)}^{t} e^{T}(s)e(s)\,ds \biggr)^{\frac{\alpha+ 1}{2}}. \end{aligned}$$

According to (14), the results can be obtained

$$\dot{V}(t) \le- kV^{\frac{\alpha+ 1}{2}}(t). $$

When \(HT + \theta T \le t < (H + 1)T\), \(H \in\mathbb{N}\), according to the condition (10),

$$\begin{aligned} \dot{V}(t) &= \dot{e}^{T}(t)e(t) + e^{T}(t)\dot{e} (t) + e^{T}(t)e(t) - e^{T} \bigl(t - \tau(t) \bigr)e \bigl(t - \tau(t) \bigr) \bigl(1 - \dot{\tau}(t) \bigr) \\ &= - 2e^{T}(t)Ce(t) + e^{T}(t)A \bigl(f \bigl(y(t) \bigr) + f \bigl(x(t) \bigr) \bigr) + \bigl[A \bigl(f \bigl(y(t) \bigr) + f \bigl(x(t) \bigr) \bigr) \bigr]^{T}e(t) \\ &\quad {} + e^{T}(t)B \bigl(f \bigl(y \bigl(t - \tau(t) \bigr) \bigr) + f \bigl(x \bigl(t - \tau(t) \bigr) \bigr) \bigr) \\ &\quad {}+ \bigl[B \bigl(f \bigl(y \bigl(t - \tau(t) \bigr) \bigr) + f \bigl(x \bigl(t - \tau(t) \bigr) \bigr) \bigr) \bigr]^{T}e(t) \\ &\quad {}- e^{T}(t)\beta e(t) + e^{T}(t)e(t) - e^{T} \bigl(t - \tau(t) \bigr)e \bigl(t - \tau (t) \bigr) \bigl(1 - \dot{\tau}(t) \bigr) \\ &\le - 2e^{T}(t)Ce(t) + m_{1}e^{T}(t)AA^{T}e(t) + m_{1}^{-1}Le^{T}(t)e(t) \\ & \quad {}+ \frac{L}{1 - h}e^{T}(t)BB^{T}e(t) + (1 - h)e^{T} \bigl(t - \tau(t) \bigr)e \bigl(t - \tau(t) \bigr) \\ & \quad {}- e^{T}(t)\beta e(t)+ e^{T}(t)e(t) - (1 - h)e^{T} \bigl(t - \tau(t) \bigr)e \bigl(t - \tau(t) \bigr) \\ &\le - 2 \Vert C \Vert \bigl\Vert e(t) \bigr\Vert ^{2} + m_{1} \bigl\Vert AA^{T} \bigr\Vert \bigl\Vert e(t) \bigr\Vert ^{2} + m_{1}^{-1}L \bigl\Vert e(t) \bigr\Vert ^{2} \\ &\quad {} + \frac{L}{1 - h} \bigl\Vert BB^{T} \bigr\Vert \bigl\Vert e(t) \bigr\Vert ^{2} - \beta \bigl\Vert e(t) \bigr\Vert ^{2} + \bigl\Vert e(t) \bigr\Vert ^{2} \\ &= \biggl( - 2 \Vert C \Vert + m_{1} \bigl\Vert AA^{T} \bigr\Vert + m_{1}^{-1}L + \frac{L}{1 - h} \bigl\Vert BB^{T} \bigr\Vert + 1-\beta \biggr) \bigl\Vert e(t) \bigr\Vert ^{2} \\ &\le 0. \end{aligned}$$

Then we have

$$\textstyle\begin{cases} \dot{V}(t) \le- k{V^{\frac{{\alpha+ 1}}{2}}}(t),\quad HT \le t < HT + \theta T,\\ \dot{V}(t) \le0,\quad HT + \theta T \le t < (H + 1)T. \end{cases} $$

According to Lemma 2, the following inequality can be obtained:

$$V^{1 - \eta}(t) \le V^{1 - \eta}(0) - \alpha\theta(1 - \eta)t . $$

Letting \(\eta= \frac{{\alpha+ 1}}{2}\), \(\alpha=k\), it is easy to get

$$\bar{T} = \frac{{{V^{(1 - \alpha)/2}}(0)}}{{k\theta(1 - \alpha)/2}}. $$

Hence, the error vector \(e(t)\) will converge to zero within T̄. Consequently, under controller (8), systems (2) and (4) realize finite-time anti-synchronization. This completes the proof of the theorem. □

Remark 2

The settling time of anti-synchronization can be estimated in a finite time. The sufficient conditions given in Theorem 1 can avoid the problem that the neural network only realizes anti-synchronization when time tends to infinity efficiently, and this has significant meanings in real engineering applications of network synchronization.

Remark 3

The larger of the control rate θ, the faster convergence speed. When \(\theta= 0\), the intermittent adjustment feedback controller (8) can be described as \(u(t) = - \frac{\beta}{2}e(t)\), and the systems (2) and (4) can achieve asymptotical anti-synchronization. When \(\theta= 1\), the controller (8) is degenerated to a continuous control input. If we change the controller (8) to the following form:

$$ \begin{aligned}[b] u(t) =&{} - \frac{\beta}{2}e(t) - \frac{k}{2} \operatorname {sgn}\bigl(e(t) \bigr)\bigl\vert e(t) \bigr\vert ^{\alpha}\\ & {}- \frac{k}{2} \biggl( \int_{t - \tau(t)}^{t} e^{T}(s)e(s)\,ds \biggr)^{\frac{1 + \alpha}{2}} \biggl(\frac{e(t)}{ \Vert e(t) \Vert ^{2}} \biggr),\quad t \ge0, \end{aligned} $$
(15)

then the following corollary can be derived.

Corollary 1

Suppose Assumption  1 holds, the systems (2) and (4) can realize finite-time anti-synchronization via continuous controller (15), if there exists a positive constant \({m_{1}}\) such that the following conditions hold:

$$- 2 \Vert C \Vert + m_{1} \bigl\Vert AA^{T} \bigr\Vert + m_{1}^{-1}L + \frac{L}{1 - h} \bigl\Vert BB^{T} \bigr\Vert + 1 - \beta\le0. $$

Then system (2) and system (4) can realize finite-time anti-synchronization under the controller (15) in a finite time:

$$\bar{T} = \frac{{{V^{(1 - \alpha)/2}}(0)}}{{k\theta(1 - \alpha)/2}} , \quad \textit{where }V(0) = e^{T}(0)e(0) = \sum_{i = 1}^{n} e_{i}^{T}(0)e_{i}(0) . $$

4 Numerical simulations

In this section, two numerical examples are given to show the effectiveness of Theorem 1.

Example 1

Considering the following model as the master system:

$$ \dot{x}(t) = - Cx(t) + Af \bigl(x(t) \bigr) + Bf \bigl(x \bigl(t - \tau(t) \bigr) \bigr), $$
(16)

where \(x(t) = {({x_{1}}(t),{x_{2}}(t))^{T}}\), \(f(x(t)) = {(f({x_{1}}(t)),f({x_{2}}(t)))^{T}}\), \(f(x) = \tanh(x)\),

$$A = \left ( \textstyle\begin{array}{@{}c@{\quad}c@{}} 2&{ - 0.1}\\ { - 5}&{4.5} \end{array}\displaystyle \right ),\quad\quad B = \left ( \textstyle\begin{array}{@{}c@{\quad}c@{}} { - 1.5}&{ - 0.1}\\ { - 0.2}&{ - 3.2} \end{array}\displaystyle \right ),\quad\quad C = \left ( \textstyle\begin{array}{@{}c@{\quad}c@{}} 1&0\\ 0&1 \end{array}\displaystyle \right ). $$

Next, the corresponding slave system is considered as follows:

$$ \dot{y}(t) = - Cy(t) + Af \bigl(y(t) \bigr) + Bf \bigl(y \bigl(t - \tau(t) \bigr) \bigr) + u(t). $$
(17)

When \(\tau(t) = 1\), \(u(t)\) is the form of (8), system (16) has a chaotic attractor, as shown in Figure 1. According to system (16) and (17), the state trajectories can be drawn without the controller (8) in Figure 2 and Figure 3. In Figure 4, it is referring to the anti-synchronization errors without the controller (8).

Figure 1
figure 1

The chaotic attractor of system ( 16 ) and ( 17 ).

Full size image
Figure 2
figure 2

The state trajectories of \(\pmb{x_{1}}\) , \(\pmb{y_{1}}\) without the controller ( 8 ).

Full size image
Figure 3
figure 3

The state trajectories of \(\pmb{x_{2}}\) , \(\pmb{y_{2}}\) without the controller ( 8 ).

Full size image
Figure 4
figure 4

The anti-synchronization errors \(\pmb{e_{1}}\) , \(\pmb{e_{2}}\) without the control ( 8 ).

Full size image

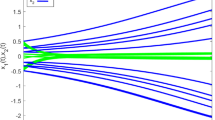
In this simulation, the values of the parameters for the intermittent adjustment feedback controller (8) are taken as \(\beta= 25.1\), \(k = 12\), \(\alpha= 0.95\), \(T = 2\) and \(\theta= 0.6\). when \(L = 1\), \(h = 0.1\), \({m_{1}} = 0.2\). The initial values are taken as \(x(0) = (0.2,0.5)\), \(y(0) = (0.3,0.6)\). By using Matlab toolbox, \(- 2 \Vert C \Vert + m_{1} \Vert AA^{T} \Vert + m_{1}^{-1}L + \frac{L}{1 - h} \Vert BB^{T} \Vert + 1 - \beta= - 0.0755 < 0 \), the settling time \(\bar{T}= 5.5246\), it can be verified that the condition (10) in Theorem 1 are satisfied. And the state trajectories can be drawn with the controller (8) in Figure 5 and Figure 6. The anti-synchronization errors with the controller (8) are drawn in Figure 7.

Figure 5
figure 5

The state trajectories of \(\pmb{x_{1}}\) , \(\pmb{y_{1}}\) under the controller ( 8 ).

Full size image
Figure 6
figure 6

The state trajectories of \(\pmb{x_{2}}\) , \(\pmb{y_{2}}\) under the controller ( 8 ).

Full size image
Figure 7
figure 7

The anti-synchronization errors \(\pmb{e_{1}}\) , \(\pmb{e_{2}}\) under the control ( 8 ).

Full size image

Example 2

Considering the following model as the master system:

$$ \dot{x}(t) = - Cx(t) + Af \bigl(x(t) \bigr) + Bf \bigl(x \bigl(t - \tau(t) \bigr) \bigr), $$
(18)

where \(x(t) = {({x_{1}}(t),{x_{2}}(t),{x_{3}}(t))^{T}}\), \(f(x(t)) = {(f({x_{1}}(t)),f({x_{2}}(t)),f(x_{3}(t)))^{T}}\), \(f(x) = \tanh(x)\),

$$A = \left ( \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{}} {1.15}&{ - 3.0}&{ - 3.0}\\ { - 3.0}&{1.0}&{ - 4.0}\\ { - 3.0}&{4.0}&{0.9} \end{array}\displaystyle \right ), \quad\quad B = \left ( \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{}} { 0.1}&{ - 0.2}&{ - 0.2}\\ { - 0.2}&{ 0.1}&{ - 0.4}\\ { - 0.2}&{0.4}&{0.1} \end{array}\displaystyle \right ), \quad\quad C = \left ( \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{}} 1&0&0\\ 0&1&0\\ 0&0&1 \end{array}\displaystyle \right ). $$

Next, the corresponding slave system is considered as follows:

$$ \dot{y}(t) = - Cy(t) + Af \bigl(y(t) \bigr) + Bf \bigl(y \bigl(t - \tau(t) \bigr) \bigr) + u(t). $$
(19)

When \(\tau(t) = 1\), system (18) has a chaotic attractor, as shown in Figure 8. At the same time, the state trajectories of system (18) and (19) can be drawn without the intermittent adjustment feedback controller (8) in Figure 9. In Figure 10, it is referring to the anti-synchronization errors without the controller (8).

Figure 8
figure 8

The chaotic attractor of system ( 18 ) and ( 19 ).

Full size image
Figure 9
figure 9

The state trajectories of \(\pmb{x_{i}}\) , \(\pmb{y_{i}}\) , \(\pmb{i=1,2,3}\) without the controller ( 8 ).

Full size image
Figure 10
figure 10

The anti-synchronization errors \(\pmb{e_{1}}\) , \(\pmb{e_{2}}\) , \(\pmb{e_{3}}\) without the control ( 8 ).

Full size image

In this simulation, the values of the parameters for controller (8) are taken as \(\beta= 13\), \(k = 12\), \(\alpha= 0.94\), \(T = 3\) and \(\theta= 0.6\). when \(L = 1\), \(h = 0.1\), \({m_{1}} = 0.2\). The initial values are taken as \(x(0) = (0.2,0.5,0.7)\), \(y(0) = (0.3,0.6,0.8)\). By using Matlab toolbox, \(- 2 \Vert C \Vert + m_{1} \Vert AA^{T} \Vert + m_{1}^{-1}L + \frac{L}{1 - h} \Vert BB^{T} \Vert + 1 - \beta= -0.2795 < 0 \), the settling time \(\bar{T}= 4.7276\), it can be verified that the condition (10) in Theorem 1 are satisfied. And the state trajectories can be drawn with the controller (8) in Figure 11. The anti-synchronization errors with the controller (8) are drawn in Figure 12.

Figure 11
figure 11

The state trajectories of \(\pmb{x_{i}}\) , \(\pmb{y_{i}}\) , \(\pmb{i=1,2,3}\) under the controller ( 8 ).

Full size image
Figure 12
figure 12

The anti-synchronization errors \(\pmb{e_{1}}\) , \(\pmb{e_{2}}\) , \(\pmb{e_{3}}\) under the control ( 8 ).

Full size image

Remark 4

In the intermittent adjustment feedback controller (7) and (8), the parameter k plays an important part in improving the convergence speed. The larger the parameter k, the shorter the settling time T̄. Examples 1 and 2 shows the simulation results when \(k = 12 \). Table 1 gives the settling times when the values of k are different in Examples 1 and 2.

Table 1 The settling time \(\pmb{\bar{T}}\)
Full size table

Remark 5

In this paper, our theorem conditions and the settling time can simply the calculation through Matlab to get the desired results. As regards references [19] and [30], our research is based on them, which can make the system stable in a shorter time. Therefore, it has higher research value in the actual system.

5 Conclusion

In this paper, we investigate the finite-time anti-synchronization by using Lyapunov functional method. A simple intermittent adjustment feedback controller is designed to control the states of two systems to achieve anti-synchronization within a finite time. Some sufficient conditions are put forward for the anti-synchronization of drive-response systems, it plays an important role in practical application. The main contribution of this paper is that system (1) and (3) can realize anti-synchronization in a finite time.

Furthermore, two numerical simulation examples are provided to verify the rightness of the proposed anti-synchronization criteria. It is important to note that the intermittent adjustment feedback control can reduce the control time and cost rather than the continuous control. Therefore, our method has very extensive application in transportation, communications and other areas. Finally, it is still a big challenge to investigate the finite-time anti-synchronization of neural networks with discontinuous dynamic behaviors; these problems will be considered in the next papers.