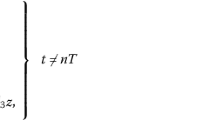1 Introduction

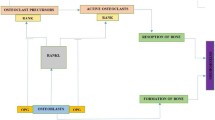
Bone is a highly organized tissue. Apart from attending to its own structural integrity, the skeleton must also respond to systemic needs for adequate amounts of calcium in the extracellular fluid. In order to maintain normal functions of bone and calcium homeostasis, bone remodeling process is needed to be taken into account. In bone remodeling process, osteoclasts act as bone resorbing cells, while osteoblasts act as bone forming cells. The process begins with the appearance of active osteoclasts on a previously inactive surface of bone, after which a lacuna will be excavated. Subsequently, osteoblasts then refill the resorption cavity and become inactive osteoblasts [1–3]. Serious health conditions such as osteoporosis may occur when the bone remodeling process is imbalanced (e.g. there is excessively deep resorption space produced by osteoclasts, or the replenishment of the resorption space by the activation of osteoblasts is incomplete). For a better understanding of bone remodeling process, the basic knowledge about osteoblasts, osteoclasts and the involving hormones such as parathyroid hormone (PTH) and calcitonin (CT) is necessary.

Osteoblasts derived from mesenchymal cells are responsible for bone formation. The stromal stem cells proliferate preosteoblast precursors, and then preosteoblasts precursors proliferate preosteoblasts. After that, preosteoblasts differentiate into osteoblasts, and then osteoblasts become osteocytes or resting osteoblasts [4]. Note that the differentiation and activation of osteoclasts require direct physical contact with osteoblasts that produce at least two indispensable cytokines [1]. On the other hand, osteoclasts derived from the hemopoietic cells are responsible for bone resorption. The hemopoietic stem cells proliferate preosteoclast precursor cells, and then preosteoclasts precursors differentiate into preosteoclasts. After that, preosteoclasts differentiate into osteoclasts [4].

PTH and CT are principal hormones involved in bone formation and resorption. PTH is secreted from the parathyroid glands in response to the low calcium level in blood. It increases calcium concentration in blood by various direct and indirect actions on bone, kidney and intestine [1]. On bone, PTH enhances bone resorption by stimulating the activation of osteoclasts indirectly through osteoblasts since osteoclasts do not possess PTH receptors while osteoblast precursors possess them. Moreover, PTH has both stimulating and inhibiting effects on the differentiation and activation of osteoblasts [1]. PTH stimulates the differentiation of mesenchymal stem cells to preosteoblasts, but it inhibits the differentiation of osteoblasts in mature cells through the process of down-regulation of PTH receptors on osteoblasts [5–7]. In contrast to PTH, CT produced by the parafollicular cells of the thyroid gland inhibits bone resorption by acting on osteoclasts resulting in the decrease of calcium level in blood [1, 2].

As discussed above, an excessively deep resorption space produced by osteoclasts or an incomplete replenishment of the resorption space by the activation of osteoblasts can result in bone remodeling imbalance. If remodeling imbalance exists after the completion of a remodeling cycle, the degree of bone loss will be exacerbated and that leads to osteoporosis [8]. Osteoporosis is a bone metabolic disease which is characterized by low bone mass, the structural deterioration of bone and an increased risk of fracture. It occurs most frequently in postmenopausal women [3]. An increase in the activation frequency of new bone remodeling units and an increase in remodeling imbalance, especially resulting from the increase of osteoclastic formation, are observed when estrogen is deficient [8–12]. In osteoporosis patients, estrogen replacement therapy has been widely used to prevent menopausal bone loss and reduce the risk of fracture [8–12]. Kanatani et al. [10] and Riggs et al. [12] reported that the presence of estrogen results in the decrease of bone resorption by inhibiting the activity of osteoclasts. The works of Prestwood et al. [9] and Albright et al. [11] indicated the decrease in the values of biochemical markers of bone turnover due to the short-term estrogen treatment. However, there are some serious risks and side effects from the estrogen replacement therapy such as breast cancer and heart disease [8, 13]. High doses of estrogen results in weight loss in rats, and an increase in tumor formation was observed in aging rats with long-term treatment of estrogen [14]. Hence, the appropriate dose and duration of estrogen treatment are necessary and need to be investigated in details.

Mathematical models of bone remodeling process were proposed and analyzed theoretically and numerically [15–20]. However, the model that incorporates the effects of PTH, CT and the impulsive treatments of estrogen has not been proposed and analyzed yet. In the next section, we will develop a system of impulsive differential equations to study the effects of PTH, CT and the impulsive estrogen replacement therapy on bone remodeling process.

2 Model development

In bone remodeling process, estrogen is responsible for many osteoclast suppressing activities both directly and indirectly. Estrogen limits the size of preosteoclast and osteoclast populations, and it also limits the production of osteoclasts by restraining the production and secretion of cytokine that stimulate a stimulator of osteoclast development [21–30]. Moreover, in the presence of estrogen, osteoblastic stromal cells synthesize more anti-osteoclast OPG than osteoclast-stimulating receptor activator RANKL. Since OPG is a soluble decoy RANK-like receptor that binds to and covers up RANKL molecules sticking out of the surfaces of osteoblastic stromal cells, then the more OPG means the less RANKL available on the osteoblastic stromal cells’ surfaces for binding to their real RANK receptors, and that reduces the RANK signals needed to drive differentiation of the osteoclast progenitors into mature osteoclasts. Hence, the increase in the level of estrogen results in the decrease in the number of osteoclasts [21–30]. On the other hand, it has been reported that estrogen also has stimulating effects on osteoblasts as well by attenuating PTH-induced inhibition of osteoblast proliferation [31, 32]. Estrogen also directly modulates differentiation of bipotential stromal cells into the osteoblast and adipocyte lineages, causing a lineage shift toward the osteoblast, which leads to direct stimulation of bone formation [33]. We then propose an impulsive model to investigate the effects of PTH, CT and impulsive estrogen treatments on bone remodeling process as follows:

figure a

with

figure b

where \(x(t)\) denotes the concentration of PTH above the basal level in blood at time t, \(y(t)\) denotes the concentration of CT above the basal level in blood at time t, \(z(t)\) denotes the number of active osteoclasts at time t, \(w(t)\) denotes the number of active osteoblasts at time t and all parameters in the model are positive constant. \(\Delta z(t)=z({{t}^{+}})-z(t),\Delta w(t)=w({{t}^{+}})-w(t)\), T represents the period of impulsive treatment of estrogen, \(n\in{{Z}_{+}}\), \({{Z}_{+}}=\{1,2,3,\ldots\}\), ρ represents the inhibiting effect of estrogen supplement on osteoclasts, \(0<\rho<1\), and μ represents the stimulating effect of estrogen supplement on osteoblasts, \(\mu>0\).

Here, the rate of change of PTH concentration in blood is represented by (1a). The first term on the right-hand side accounts for the secretion rate of PTH from the parathyroid glands which is inhibited by the increase in the calcium levels indicated by the increase in the number of active osteoclasts [1].

The rate of change of CT concentration in blood is represented by (1b). The elevation of calcium levels indicated by the increase in the number of active osteoclasts stimulates the secretion of CT from the thyroid gland, whereas the increase in the level of PTH suppresses the secretion of CT as reported in [34]. Hence, the secretion rate of CT is then assumed to be represented by the first term on the right-hand side of (1b).

The rate of change of the number of active osteoclasts is represented by (1c). The first term on the right-hand side accounts for the stimulating effect of PTH and the inhibiting effect of CT on the reproduction of active osteoclasts which requires the cell to cell interaction of osteoclasts and osteoblasts as indicated in [20].

The rate of change of the number of active osteoblasts is represented by (1d). The first and the second terms on the right-hand side account for the stimulating effect and the inhibiting effect of PTH on the reproduction and differentiation of active osteoblasts as mentioned in [20], respectively.

The last terms of (1a)-(1d) account for the removal rates of PTH, CT, active osteoclasts and active osteoblasts, respectively.

The inhibition effect of estrogen treatment on the number of active osteoclasts is represented by (1e), while the stimulating effect of estrogen treatment on the number of active osteoblasts is represented by (1f).

As it has been observed clinically in [1, 35, 36], the dynamics of PTH and CT are very fast compared to the changes in the number of active osteoclasts and active osteoblasts. We then assume in what follows that PTH and CT equilibrate quickly to the level at which \(\frac{dx}{dt}=0\) and \(\frac{dy}{dt}=0\), respectively. That is,

$$ x=\frac{a_{1}}{{b_{1}}({k_{1}}+z)}\equiv{{f}_{1}}(z) $$
(2)

and

$$ y=\frac{a_{2}}{b_{2}} \biggl(\frac{z}{{k_{2}}+{f_{1}}(z)} \biggr)= \frac {{a_{2}}{b_{1}}z ({k_{1}}+z )}{{b_{2}} [{a_{1}}+{b_{1}}{k_{2}} ({k_{1}}+z ) ]}\equiv{f_{2}}(z). $$
(3)

Hence, system (1a)-(1f) can be reduced to the system of (4a)-(4d) as follows:

figure c

with

figure d

3 Preliminaries

Let

$$V:{R_{+}}\times R_{+}^{2}\to{R_{+}}, $$

where \({R_{+}}=[0,\infty),{ R}_{+}^{2}=\{S\in{R^{2}}:S=(z,w), z\ge0,w\ge 0\}\). The map defined by the right-hand side of (4a)-(4b) is denoted by \(F=({F_{1}},{F_{2}})\).

Definition 1

The function V defined in (4a) is said to belong to class \({V_{0}}\) if

  1. (a)

    V is continuous in \((nT,(n+1)T]\times R_{+}^{2}\to{R_{+}}\) and for each \(S\in R_{+}^{2},n\in{Z_{+}}\), \(\lim_{(t,Y)\to(nT^{+},S)} V(t,Y)=V(nT^{+},S)\) exists, and

  2. (b)

    V is locally Lipschitzian in S.

Definition 2

Suppose \(V\in{V_{0}}\). For \((t,S)\in(nT,(n+1)T]\times R_{+}^{2}\), the upper right derivative of \(V(t,S)\) with respect to (4a)-(4d) is defined by

$${D^{+}}V(t,S)=\limsup_{h \to0^{+}}\frac{1}{h}\bigl[V \bigl(t+h,S+hF(t,S)\bigr)-V(t,S)\bigr], $$

where \(F=({F_{1}},{F_{2}})\).

In what follows, we assume that the solution of (4a)-(4d), \(S(t)=(z(t),w(t))\), is a piecewise continuous function. That is, \(S(t):{R_{+}}\to{R}_{+}^{2}\), \(S(t)\) is continuous on \((nT,(n+1)T],n\in{Z_{+}}\) and \(\lim_{t\to nT^{+}}S(t)=S(nT^{+})\) exists. Then the global existence and uniqueness of solution to (4a)-(4d) is guaranteed by the smoothness properties of F (see [37] for more details).

Since \(\frac{dz}{dt}=0\) whenever \(z(t)=0, t\ne nT,\frac {dw}{dt}>0\) whenever \(w(t)=0, t\ne nT\) and \(z(n{{T}^{+}})=(1-\rho )z(nT), 0<\rho<1\), \(w(n{{T}^{+}})=w(n{{T}})+\mu, \mu>0\), we have the following lemma.

Lemma 1

Suppose \(S(t)=(z(t),w(t))\) is a solution of (4a)-(4d) with \(S({{0}^{+}})\ge0\). Then \(S(t)\ge0\) for all \(t\ge0\).

Lemma 2

There exists a constant \(M>0\) such that, for sufficiently large t, \(z(t)\le M\) and \(w(t)\le M\) provided that

$$ {b_{4}}>\frac{{a_{1}}{a_{3}}}{{b_{1}}{k_{3}}{k_{4}}}, $$
(5)

where \((z(t),w(t))\) is a solution of (4a)-(4d).

Proof

We let \(v(t)=z(t)+w(t)\), \({M_{1}}=\sup z{f_{1}}(z)=\frac{a_{1}}{b_{1}}\) and \({M_{2}}=\sup{f_{1}}(z)=\frac{a_{1}}{{b_{1}}{k_{1}}}\).

For \(t\ne nT\), we choose a positive constant c for which

$$c=\min \biggl\{ {b_{3}},{b_{4}}-\frac{{a_{3}}{M_{1}}}{{k_{3}}{k_{4}}} \biggr\} . $$

Then

$$\begin{aligned} D^{+}v+cv={}&\frac{dz}{dt}+\frac{dw}{dt}+cz+cw \\ ={}&\frac{{a_{3}}{f_{1}}(z)zw}{ ({k_{3}}+f_{1}^{2}(z) ) ({k_{4}}+{f_{2}}(z) )}-{b_{3}}z+\frac {{a_{4}}{f_{1}}(z)}{{k_{5}}+{f_{1}}(z)}- \frac {{a_{5}}{f_{1}}(z)w}{{k_{6}}+{f_{1}}(z)}-{b_{4}}w \\ &{}+cz+cw \\ \le{}&(c-{b_{3}})z+ \biggl(\frac{{a_{3}}{M_{1}}}{{k_{3}}{k_{4}}}-{b_{4}}+c \biggr)w+\frac{{a_{4}}{M_{2}}}{k_{5}} \\ \le{}& \frac{{a_{4}}{M_{2}}}{k_{5}} \equiv{M_{0}}. \end{aligned}$$

Hence \(D^{+}v\le-cv+{M_{0}}\).

For \(t=nT\),

$$\begin{aligned} v\bigl(n{{T}^{+}}\bigr)&=z\bigl(n{T^{+}}\bigr)+w\bigl(n{T^{+}}\bigr) \\ &=(1-\rho)z(nT)+w(nT)+\mu \\ &=z(nT)+w(nT)+\mu-\rho z(nT) \\ &\le v(nT)+\mu. \end{aligned}$$

Therefore, Lemma 2.2 of Liu et al. [38] implies that, for \(t\in(nT,(n+1)T]\),

$$\begin{aligned} v(t)&\le v(0){e^{-ct}}+ \int_{0}^{t}{{M_{0}} {e^{-c(t-s)}}\,ds}+ \sum_{0< {t_{n}}< t}{\mu} {e^{-c(t-{t_{n}})}} \\ &\le v(0){e^{-ct}}+{M_{0}} \biggl(\frac{1}{c}- \frac{e^{-ct}}{c} \biggr)+\mu \biggl(\frac{{e^{-c(t-T)}}-{e^{-c(t-{t_{n+1}})}}}{1-{e^{cT}}} \biggr) \\ &< \frac{M_{0}}{c}+\mu \biggl(\frac{e^{cT}}{{e^{cT}}-1} \biggr)\equiv M \quad\text{as } t \to\infty. \end{aligned}$$

Thus, \(v(t)\) is uniformly ultimately bounded, and hence there exists a constant \(M>0\) such that \(z(t)\le M\) and \(w(t)\le M\) for sufficiently large t. □

4 Stability when there is no active osteoclast

Now, let us consider the reduced impulsive system (4a)-(4d) when there is no active osteoclast \((z=0)\):

$$\begin{aligned} &\frac{dw}{dt}= A-Bw, \quad t\ne nT, \end{aligned}$$
(6)
$$\begin{aligned} &w\bigl(nT^{+}\bigr)= w(nT)+\mu,\quad t= nT, \end{aligned}$$
(7)
$$\begin{aligned} &w\bigl(0^{+}\bigr)= w_{0}, \end{aligned}$$
(8)

where \(A\equiv\frac{{a_{1}}{a_{4}}}{{b_{1}}{k_{1}}{k_{5}}+{a_{1}}}\) and \(B\equiv\frac {{a_{1}}{a_{5}}}{{b_{1}}{k_{1}}{k_{6}}+{a_{1}}}+{b_{4}}\). Note that \(A>0\) and \(B>0\). We can see that

$$ \tilde{w}(t)=\frac{\mu{e^{-B(t-nT)}}}{1-{e^{-BT}}}+\frac{A}{B}, \quad t \in\bigl(nT,(n+1)T\bigr] $$
(9)

is a periodic solution of (6)-(8) with \(\tilde{w}(0^{+})=\frac{\mu}{1-{e^{-BT}}}+\frac{A}{B}>0\).

Hence, the positive solution of (6)-(8) is

$$w(t)= \biggl({w_{0}}-\frac{A}{B}-\frac{\mu}{1-{e^{-BT}}} \biggr){e^{-Bt}}+\tilde{w}(t),\quad t\in\bigl(nT,(n+1)T\bigr]. $$

This leads to the following result.

Lemma 3

System (6)-(8) has a positive periodic solution \(\tilde{w}(t)\), and for every solution \(w(t)\) of (6)-(8), we have \(w(t)\to\tilde{w}(t)\) as \(t\to\infty \).

Therefore, system (4a)-(4d) has a periodic solution at the vanishing level of active osteoclasts

$$\bigl(0,\tilde{w}(t) \bigr)= \biggl(0,\frac{\mu {e^{-B(t-nT)}}}{1-{e^{-BT}}}+\frac{A}{B} \biggr) $$

for \(t\in(nT,(n+1)T]\) and \(\tilde{w}(nT^{+})=\tilde{w}(0^{+})=\frac{\mu }{1-{e^{-BT}}}+\frac{A}{B}, n\in{Z_{+}}\).

Theorem 1

The solution \((0,\tilde{w}(t))\) of (4a)-(4d) is locally asymptotically stable provided that

$$\begin{aligned} &0< T< T_{\mathrm{max}}, \end{aligned}$$
(10)
$$\begin{aligned} &b_{3}< \frac{AD}{B} , \end{aligned}$$
(11)
$$\begin{aligned} &\frac{D\mu}{B}< \ln \biggl(\frac{1}{1-\rho} \biggr), \end{aligned}$$
(12)

where \({T_{\mathrm{max}}}\equiv\frac{1}{ (\frac{AD}{B}-{b_{3}} )} [\ln (\frac{1}{1-\rho} )-\frac{D\mu}{B} ]\) and \(D\equiv \frac{{a_{1}}{a_{3}}{b_{1}}{k_{1}}}{{k_{4}} ({{a_{1}}^{2}}+{{b_{1}}^{2}}{{k_{1}}^{2}}{k_{3}} )}\).

Proof

Consider a small perturbation from the point \((0,\tilde{w}(t))\)

$$\begin{aligned} &z(t)={u_{1}}(t), \\ &w(t)=\tilde{w}(t)+{u_{2}}(t). \end{aligned}$$

Then we may write

$$ \left ( \begin{matrix} {u_{1}}(t) \\ {u_{2}}(t) \end{matrix} \right )=\Phi(t) \left ( \begin{matrix} {u_{1}}(0) \\ {u_{2}}(0) \end{matrix} \right ), \quad 0< t< T, $$

where \({\Phi}(t)\) satisfies

$$\frac{d{\Phi}(t)}{dt}=\left ( \begin{matrix} D\tilde{w}(t)-{b_{3}} & 0 \\ * &-B \end{matrix} \right ){\Phi}(t) $$

and \({\Phi}(0)=I\), the identity matrix. Hence, the fundamental solution matrix is

$${\Phi}(t)=\left ( \begin{matrix} \exp\int_{0}^{t}({D\tilde{w}(s)-{b_{3}}})\,ds & 0& \\ * & \exp\int_{0}^{t}{(-B)}\,ds \end{matrix} \right ). $$

Since the term (∗) is not required in further analysis, it is not necessary to find the exact expression for (∗).

Linearization of (4c)-(4d) yields

$$\left ( \begin{matrix} {u_{1}}(nT^{+}) \\ {u_{2}}(nT^{+}) \end{matrix} \right )=\left ( \begin{matrix} 1-\rho& 0 \\ 0 & 1 \end{matrix} \right )\left ( \begin{matrix} {u_{1}}(nT) \\ {u_{2}}(nT) \end{matrix} \right ). $$

According to Floquet theory, the solution \((0,\tilde{w}(t))\) of (4a)-(4d) is locally stable if \(\vert \lambda_{i} \vert <1\), \(i=1,2\), where \(\lambda_{i}\) is an eigenvalue of

$$M=\left ( \begin{matrix} 1-\rho& 0 \\ 0 & 1 \end{matrix} \right ){ \Phi}(T). $$

Note that the eigenvalues of M are

$$\begin{aligned} &\lambda_{1}=(1-\rho)\exp\int_{0}^{T}\bigl({D\tilde {w}(s)-{b_{3}}}\bigr)\,ds=(1-\rho)\exp \biggl(\frac{D\mu}{B}+\frac {ADT}{B}-{b_{3}}T \biggr),\\ &\lambda_{2}=\exp\int_{0}^{T}(-B)\,ds=\exp(-BT). \end{aligned}$$

Since \(0<\rho<1\), \(B>0\) and (10)-(12) hold, then

$$\biggl(\frac{AD}{B}-{b_{3}} \biggr)T< \ln \biggl( \frac{1}{1-\rho} \biggr)-\frac {D\mu}{B}. $$

Hence,

$$\vert \lambda_{1} \vert =(1-\rho)\exp \biggl(\frac{D\mu}{B}+\frac {ADT}{B}-{b_{3}}T \biggr)< 1 $$

and

$$\vert \lambda_{2} \vert =\exp(-BT)< 1. $$

Therefore, Floquet theory implies that the solution \((0,\tilde{w}(t))\) of (4a)-(4d) is locally stable and the proof is complete. □

5 Permanence of the system

Definition 3

The reduced impulsive system (4a)-(4d) is said to be permanent if there are constants \(m, M>0\) (independent of the initial values) and a finite time \({t_{0}}\) such that for all solutions with initial values \(z(0^{+})>0\), and \(w(0^{+})>0\),

$$\begin{aligned} m \le{}&z(t) \le M, \end{aligned}$$
(13)
$$\begin{aligned} m \le{}&w(t) \le M, \end{aligned}$$
(14)

for all \(t>{t_{0}}\). Note that \({t_{0}}\) may depend on the initial values.

Theorem 2

Suppose that

$$\begin{aligned} b_{3}&< \frac{DE}{B}, \end{aligned}$$
(15)
$$\begin{aligned} T&>T^{*}. \end{aligned}$$
(16)

System (4a)-(4d) is permanent if (5) holds where \(E \equiv{a_{4}}{b_{2}}{k_{4}}({a_{1}}+{b_{1}}{k_{1}}{k_{2}})\) and \(T^{*} \equiv \frac{B}{E}\ln (\frac{1}{1-\rho} )\).

Proof

Suppose that \(S(t)=(z(t),w(t))\) is a solution of system (4a)-(4d) with \(z(0^{+})>0\) and \(w(0^{+})>0\). Since (5) holds, Lemma 2 implies that there is a constant \(M>0\) such that, for sufficiently large t, \(z(t)\le M\) and \(w(t)\le M\).

Since \(\frac{{a_{4}}{f_{1}(z)}}{{k_{5}}+{f_{1}(z)}}>0\) and \((\frac {{a_{5}}{f_{1}(z)}}{{k_{6}}+{f_{1}(z)}}+{b_{4}} )\) is a decreasing function when \(z>0\), (4b) implies that

$$\begin{aligned} &\frac{dw}{dt} \ge -Bw,\quad t\ne nT, \\ &w\bigl(nT^{+}\bigr)= w(nT)+\mu,\quad t= nT \end{aligned}$$

and then we have

$$w(t)>\tilde{w}(t)-\frac{A}{B}-\varepsilon $$

for some \(\varepsilon>0\) and for sufficiently large t.

Hence,

$$w(t)>\frac{\mu{e^{-BT}}}{1-{e^{-BT}}}-\varepsilon\equiv{m_{1}} $$

for sufficiently large t.

Therefore, we only need to show that there exists a constant \({m_{2}}>0\) such that \(z(t)>{m_{2}}\). In order to do so, for some \({m_{3}}>0\), we first let

$$\begin{aligned} &\hat{M}_{1}=a_{1}^{2}+b_{1}^{2}{k_{3}} {{({k_{1}}+{m_{3}})}^{2}}, \\ &\hat{M}_{2}={b_{2}} {k_{4}} \bigl({a_{1}}+{b_{1}} {k_{2}} ({k_{1}}+{m_{3}} ) \bigr)+{a_{2}} {b_{1}} {m_{3}} ({k_{1}}+{m_{3}} ), \\ &\hat{M}_{3}=\frac{{a_{1}}{a_{3}}{b_{1}}{b_{2}}{k_{1}} ({a_{1}}+{b_{1}}{k_{1}}{k_{2}} )}{{\hat{M}_{1}}{\hat{M}_{2}}}, \\ &\hat{M}_{4}=\frac{{a_{1}}{a_{4}}}{B({a_{1}}+{b_{1}}{k_{5}}({k_{1}}+{m_{3}}))}. \end{aligned}$$

Next, we do the two steps as follows.

Step 1. We will prove by contradiction that there exists \(t_{1}\) such that \(z(t_{1})\ge{m_{3}}\).

Suppose that \(z(t)<{m_{3}}\) for all positive t. We observe from (4b) and (4d) that

$$\begin{aligned} &\frac{dw}{dt}=\frac{{a_{4}}{f_{1}}(z)}{{k_{5}}+{f_{1}}(z)}-\frac {{a_{5}}{f_{1}}(z)w}{{k_{6}}+{f_{1}}(z)}-{b_{4}}w,\quad t\ne nT \\ &\phantom{\frac{dw}{dt}}\ge\frac{{a_{1}}{a_{4}}}{{a_{1}}+{b_{1}}{k_{5}}({k_{1}}+z)}-Bw \\ &\phantom{\frac{dw}{dt}}\ge \frac{{a_{1}}{a_{4}}}{{a_{1}}+{b_{1}}{k_{5}}({k_{1}}+{m_{3}})}-Bw, \\ &w\bigl(t^{+}\bigr)=w(t)+\mu,\quad t= nT. \end{aligned}$$

Consider the comparison system

$$\begin{aligned} &\frac{dP}{dt}=\frac{{a_{1}}{a_{4}}}{{a_{1}}+{b_{1}}{k_{5}}({k_{1}}+{m_{3}})}-BP, \quad t\ne nT, \end{aligned}$$
(17)
$$\begin{aligned} &P\bigl(t^{+}\bigr) = P(t)+\mu,\quad t= nT, \end{aligned}$$
(18)
$$\begin{aligned} &P\bigl(0^{+}\bigr) = w\bigl(0^{+}\bigr). \end{aligned}$$
(19)

Hence,

$$ \tilde{P}(t)\equiv\frac{\mu{e^{-B(t-nT)}}}{1-{e^{-BT}}}+\frac {{a_{1}}{a_{4}}}{B({a_{1}}+{b_{1}}{k_{5}}({k_{1}}+{m_{3}}))},\quad t \in\bigl(nT,(n+1)T\bigr] $$
(20)

is a periodic solution of (17)-(19) with \(\tilde {P}(0^{+})\equiv\frac{\mu}{1-{e^{-BT}}}+\frac{A}{B}>0\). The positive solution of (17)-(19) is

$$ P(t)= \biggl(P\bigl(0^{+}\bigr)-\frac {{a_{1}}{a_{4}}}{B({a_{1}}+{b_{1}}{k_{5}}({k_{1}}+{m_{3}}))}- \frac{\mu }{1-{e^{-BT}}} \biggr){e^{-Bt}}+\tilde{P}(t) $$
(21)

for \(t\in(nT,(n+1)T]\) and \(P(t)\to\tilde{P}(t)=\frac{\mu {e^{-B(t-nT)}}}{1-{e^{-BT}}}+\frac {{a_{1}}{a_{4}}}{B({a_{1}}+{b_{1}}{k_{5}}({k_{1}}+{m_{3}}))} \text{ as } t\to\infty\).

The comparison theorem [37] then implies that \(w(t)\geq P(t)\).

Next, let us consider (4a)

$$\begin{aligned} \frac{dz}{dt}&=\frac{{a_{3}}{f_{1}}(z)zw}{ ({k_{3}}+f_{1}^{2}(z) ) ({k_{4}}+{f_{2}}(z) )}-{b_{3}}z \\ &=\frac{{a_{1}}{a_{3}}{b_{1}}{b_{2}} ({k_{1}}+z ) ( {a_{1}}+{b_{1}}{k_{2}} ({k_{1}}+z ) )zw}{ (a_{1}^{2}+b_{1}^{2}{k_{3}}{{ ({k_{1}}+z )}^{2}} ) ({b_{2}}{k_{4}} ({a_{1}}+{b_{1}}{k_{2}} ({k_{1}}+z ) )+{a_{2}}{b_{1}}z ({k_{1}}+z ) )}-{b_{3}}z \\ &\ge \biggl(\frac{{a_{1}}{a_{3}}{b_{1}}{b_{2}}{k_{1}} ({a_{1}}+{b_{1}}{k_{1}}{k_{2}} )w}{{\hat{M}_{1}}{\hat{M}_{2}}}-{b_{3}} \biggr)z. \end{aligned}$$

Since \(w(t)\geq P(t)\), there is \({T_{1}}>0\) such that

$$ \tilde{P}(t)-{\varepsilon_{1}}< P(t)\le w(t),\quad t\ne nT, t \ge{T_{1}} $$

for a sufficiently small \({\varepsilon_{1}}>0\).

Therefore,

$$\begin{aligned} \frac{dz}{dt} &\ge \bigl({\hat{M}_{3}} \bigl(\tilde{P}(t)-{ \varepsilon _{1}} \bigr)-{b_{3}} \bigr)z,\quad t\ne nT, t \ge{T_{1}}, \\ z\bigl(t^{+}\bigr) &= (1-\rho)z(t),\quad t= nT, t\ge{T_{1}}. \end{aligned}$$

Letting \(N\in{Z_{+}}\) and \(NT\ge{T_{1}}\), and integrating over \((nT,(n+1)T], n\ge N\), then we obtain

$$\begin{aligned} z\bigl((n+1)T\bigr)&\ge z(nT) (1-\rho)\exp \biggl( \int_{nT}^{(n+1)T}{ \bigl({\hat {M}_{3}} \bigl(\tilde{P}(t)-{\varepsilon_{1}} \bigr)-{b_{3}} \bigr)\,dt} \biggr) \\ &=z(nT) (1-\rho)\exp \biggl(({\hat{M}_{3}} {\hat{M}_{4}}-{ \varepsilon_{1}} {\hat {M}_{3}}-{b_{3}})T+ \frac{{\hat{M}_{3}}\mu}{B} \biggr) \\ &= z(nT){\eta}, \end{aligned}$$

where \(\eta\equiv(1-\rho)\exp (({\hat{M}_{3}}{\hat{M}_{4}}-{\varepsilon _{1}}{\hat{M}_{3}}-{b_{3}})T+\frac{{\hat{M}_{3}}\mu}{B} )\).

Consider

$$\ln\eta=\ln(1-\rho)+({\hat{M}_{3}} {\hat{M}_{4}}-{ \varepsilon_{1}} {\hat {M}_{3}}-{b_{3}})T+ \frac{{\hat{M}_{3}}\mu}{B}. $$

For sufficiently small \({\varepsilon_{1}}>0\),

$$\begin{aligned} \ln\eta&\approx \ln(1-\rho)+({\hat{M}_{3}} {\hat{M}_{4}}-{b_{3}})T+ \frac {{\hat{M}_{3}}\mu}{B} \\ &>\ln(1-\rho)+({\hat{M}_{3}} {\hat{M}_{4}}-{b_{3}})T. \end{aligned}$$

Since (15) and (16) hold, we can choose a small \({m_{3}}>0\) such that \(\ln\eta>0\), and hence

$$ \eta\equiv(1-\rho)\exp \biggl(({\hat{M}_{3}} { \hat{M}_{4}}-{\varepsilon _{1}} {\hat{M}_{3}}-{b_{3}})T+ \frac{{\hat{M}_{3}}\mu}{B} \biggr)>1. $$
(22)

Then \(z((n+k)T)\ge z(nT)\eta^{k}\to\infty\) as \(k\to\infty\). It contradicts the boundedness of \(z(t)\). Hence, there is \({t_{1}}>0\) such that \(z(t_{1})\ge{m_{3}}\).

Step 2. If \(z(t)\ge{m_{3}}\) for all \(t>{t_{1}}\), then the proof is complete. Otherwise, \(z(t)<{m_{3}}\) for some \(t>{t_{1}}\). Letting \(t^{*}=\inf_{t>t_{1}}\{z(t)< m_{3}\}\). There are two possible subcases.

Case 1: \({t^{*}}={n_{1}}T\) for some \({n_{1}}\in{Z_{+}}\). This means \(z(t)\ge {m_{3}}\) for \(t\in(t_{1},t^{*}]\) and, by the continuity of \(z(t)\), we have \(z(t^{*})={m_{3}}\).

Since there are \(M>0\) and \(m_{1}>0\) such that \(z(t)< M\), and \(m_{1}< w(t)< M\) for sufficiently large t, we choose \(M'>0\) and \(m'_{1}>0\) such that

$$z(t)< M' \quad\text{and} \quad m'_{1}< w(t)< M' $$

and

$$ m'_{1}< \frac{b_{3}}{\hat{M}_{3}} $$
(23)

such that

$$ \biggl\vert w\bigl(t^{*+}\bigr)-\frac {{a_{1}}{a_{4}}}{B({a_{1}}+{b_{1}}{k_{5}}({k_{1}}+{m_{3}}))}- \frac{\mu }{1-{e^{-BT}}} \biggr\vert -\mu< M'. $$
(24)

Then choose \(n_{2},n_{3}\in{Z_{+}}\) such that

$$ {n_{2}}T>\frac{1}{B}\ln \biggl(\frac{M'+\mu}{\varepsilon_{1}} \biggr) $$
(25)

and

$$ (1-\rho)^{n_{2}}\exp\bigl(( {n_{2}}+1){\eta_{1}}T \bigr)\eta^{n_{3}}>1, $$
(26)

where

$$ \eta_{1}\equiv{\hat{M}_{3}} {m'_{1}}-{b_{3}}< 0. $$

Let \({T}'={n_{2}}T+{n_{3}}T\). We claim that there is \(t_{2}\in(t^{*},t^{*}+T']\) such that \(z(t_{2})>{m_{3}}\). Otherwise, considering (21) with \(P(t^{*+})=w(t^{*+})\), we have

$$\begin{aligned} P(t)= \biggl(P\bigl(t^{*+}\bigr)-\frac {{a_{1}}{a_{4}}}{B({a_{1}}+{b_{1}}{k_{5}}({k_{1}}+{m_{3}}))}-\frac{\mu }{1-{e^{-BT}}} \biggr){e^{-B(t-{t^{*}})}}+\tilde{P}(t) \end{aligned}$$

for \(t\in(nT,(n+1)T]\) and \(n_{1}\le n\le n_{1}+n_{2}+n_{3}\).

For \({n_{2}}T\le t-{t^{*}}\le T'\), we have

$$\begin{aligned} \bigl\vert P(t)-\tilde{P}(t) \bigr\vert &=\biggl\vert P \bigl(t^{*+}\bigr)-\frac {{a_{1}}{a_{4}}}{B({a_{1}}+{b_{1}}{k_{5}}({k_{1}}+{m_{3}}))}-\frac{\mu }{1-{e^{-BT}}} \biggr\vert {e^{-B(t-{t^{*}})}} \\ &= \biggl\vert w\bigl(t^{*+}\bigr)-\frac {{a_{1}}{a_{4}}}{B({a_{1}}+{b_{1}}{k_{5}}({k_{1}}+{m_{3}}))}- \frac{\mu }{1-{e^{-BT}}} \biggr\vert {e^{-B(t-{t^{*}})}} \\ &< \bigl(M'+\mu\bigr){e^{-B(t-{t^{*}})}} \\ &< \bigl(M'+\mu\bigr){e^{-B{n_{2}}T}} \\ &< {\varepsilon_{1}.} \end{aligned}$$

Then

$$ \tilde{P}(t)-{\varepsilon_{1}}< P(t)< w(t). $$

As in Step 1, we have

$$\begin{aligned} z\bigl({{t}^{*}}+{T}'\bigr)&=z({n_{1}}T+{n_{2}}T+{n_{3}}T) \\ &\ge z\bigl(t^{*}+{n_{2}}T\bigr)\eta^{n_{3}}. \end{aligned}$$

From (4a), we have

$$\begin{aligned} &\frac{dz}{dt}=\frac{{a_{3}}{f_{1}}(z)zw}{ ({k_{3}}+f_{1}^{2}(z) ) ({k_{4}}+{f_{2}}(z) )}-{b_{3}}z, \quad t\ne nT \\ &\phantom{\frac{dz}{dt}}\ge({\hat{M}_{3}}w-{b_{3}})z \\ &\phantom{\frac{dz}{dt}}\ge\bigl({\hat{M}_{3}} {m'_{1}}-{b_{3}} \bigr)z \\ &\phantom{\frac{dz}{dt}}={\eta_{1}}z, \\ &z\bigl({{t}^{+}}\bigr)=(1-\rho)z(t),\quad t= nT. \end{aligned}$$
(27)

Integrating the above over \([t^{*},t^{*}+{n_{2}}T]\), we obtain

$$\begin{aligned} z\bigl(t^{*}+{n_{2}}T\bigr)&\ge z\bigl(t^{*} \bigr){{(1-\rho)}^{n_{2}}}\exp \biggl( \int _{{n_{1}}T}^{{n_{1}}T+{n_{2}}T}{{\eta_{1}}\,dt} \biggr) \\ &\ge{m_{3}} {{(1-\rho)}^{n_{2}}}\exp({n_{2}} { \eta_{1}}T) \\ &\ge{m_{3}} {{(1-\rho)}^{n_{2}}}\exp\bigl(({n_{2}}+1){ \eta_{1}}T\bigr), \end{aligned}$$

and hence

$$\begin{aligned} z\bigl(t^{*}+T'\bigr)&\ge z\bigl(t^{*}+{n_{2}}T \bigr)\eta^{n_{3}} \\ &\ge{m_{3}} {{(1-\rho)}^{n_{2}}}\exp\bigl(({n_{2}}+1){ \eta_{1}}T\bigr)\eta^{n_{3}} \\ &>m_{3}, \end{aligned}$$

which contradicts the definition of \(m_{3}\). Hence, there is \(t_{2}\in (t^{*},t^{*}+T']\) such that \(z(t_{2})>{m_{3}}\).

Now, let \(\tilde{t}=\inf_{t>t^{*}}\{z(t)>m_{3}\}\). Then \(z(t)< {m_{3}}\) for \(t\in(t^{*},\tilde{t})\), and by the continuity of \(z(t)\), we have \(z(\tilde{t})={m_{3}}\). We choose \(l\in{Z_{+}}\) such that \(l\le{n_{2}}+{n_{3}}\) and \(t^{*}+lT\ge\tilde{t}\), and suppose \(t\in (t^{*}+(l-1)T,t^{*}+lT]\). From (27), we have

$$\begin{aligned} z(t)&\ge z\bigl(t^{*+}\bigr) (1-\rho)^{l-1}\exp\bigl((l-1){ \eta_{1}}T\bigr)\exp\bigl({\eta _{1}}\bigl(t- \bigl(t^{*}+(l-1)T\bigr)\bigr)\bigr) \\ &=z\bigl(t^{*}\bigr) (1-\rho)^{l}\exp\bigl((l-1){\eta_{1}}T \bigr)\exp\bigl({\eta _{1}}\bigl(t-\bigl(t^{*}+(l-1)T\bigr) \bigr)\bigr) \\ &={m_{3}}(1-\rho)^{l}\exp\bigl({\eta_{1}} \bigl(t-t^{*}\bigr)\bigr) \\ &\ge{m_{3}}(1-\rho)^{{n_{2}}+{n_{3}}}\exp({\eta_{1}}lT) \\ &\ge{m_{3}}(1-\rho)^{{n_{2}}+{n_{3}}}\exp\bigl(({n_{2}}+{n_{3}}){ \eta_{1}}T\bigr). \end{aligned}$$

Since \({\eta_{1}}<0\) and \(l\le{n_{2}}+{n_{3}}\), letting

$$ \bar{m}_{2}={m_{3}}(1-\rho)^{{n_{2}}+{n_{3}}}\exp \bigl(({n_{2}}+{n_{3}}){\eta_{1}}T\bigr), $$

we have \(z(t)\ge\bar{m}_{2}\) for \(t\in(t^{*},\tilde{t})\). We can continue in the same way by using t̃ instead of \(t^{*}\). Then we shall have \(z(t)\ge\bar{m}_{2}\) for all t large enough.

Case 2: \(t^{*}\ne nT\) for all \(n\in{Z_{+}}\). This means \(z(t)\ge{m_{3}}\) for \(t\in[t_{1},t^{*})\) and \(z(t^{*})={m_{3}}\). Suppose \(t^{*} \in ({n'_{1}}T,({n'_{1}}+1)T)\) for some \({n'_{1}}\in{Z_{+}}\). There are two possible subcases.

Case 2.1: \(z(t)\le{m_{3}}\) for all \(t\in(t^{*},({n'_{1}}+1)T]\). We claim that there is \({t'_{2}}\in[({n'_{1}}+1)T,({n'_{1}}+1)T+T']\) such that \(z(t'_{2})>{m_{3}}\). Otherwise, considering (21) with \(P(({n'_{1}}+1){T^{+}})=w(({n'_{1}}+1){T^{+}})\). For \(t\in(nT,(n+1)T]\), \({n'_{1}}+1\le n\le{n'_{1}}+1+{n_{2}}+{n_{3}}\), we obtain

$$\begin{aligned} P(t)={}& \biggl(P\bigl(\bigl({n'_{1}}+1\bigr){T^{+}}\bigr)- \frac {{a_{1}}{a_{4}}}{B({a_{1}}+{b_{1}}{k_{5}}({k_{1}}+{m_{3}}))}-\frac{\mu }{1-{e^{-BT}}} \biggr){e^{-B(t-({n'_{1}}+1)T)}} +\tilde{P}(t). \end{aligned}$$

Similarly to Case 1, for \({n_{2}}T\le t-{t^{*}}\), we obtain

$$ \bigl\vert P(t)-\tilde{P}(t) \bigr\vert < \varepsilon_{1}. $$

Then

$$ \tilde{P}(t)-\varepsilon_{1}< P(t)\le w(t). $$

Since \({n_{2}}T\le({n'_{1}}+1+{n_{2}})T-{t^{*}}\), we have

$$\begin{aligned} z\bigl(\bigl({n'_{1}}+1+{n_{2}}\bigr)T\bigr)& \ge z\bigl(t^{*}\bigr) (1-\rho)^{n_{2}}\exp\bigl({\eta _{1}}\bigl( \bigl({n'_{1}}+1+{n_{2}}\bigr)T-{t^{*}}\bigr) \bigr) \\ &\ge {m_{3}}(1-\rho)^{n_{2}}\exp\bigl({\eta_{1}} \bigl(\bigl({n'_{1}}+1+{n_{2}} \bigr)T-{n'_{1}}T\bigr)\bigr) \\ &\ge{m_{3}}(1-\rho)^{n_{2}}\exp\bigl(({n_{2}}+1){ \eta_{1}}T\bigr). \end{aligned}$$

Then

$$\begin{aligned} z\bigl(\bigl({n'_{1}}+1+{n_{2}}+{n_{3}} \bigr)T\bigr)&\ge z\bigl(\bigl({n'_{1}}+1+{n_{2}} \bigr)T\bigr)\eta^{n_{3}} \\ &\ge {m_{3}}(1-\rho)^{n_{2}}\exp\bigl(({n_{2}}+1){ \eta_{1}}T\bigr)\eta^{n_{3}} \\ &>m_{3}, \end{aligned}$$

which contradicts the definition of \(m_{3}\). Hence, there is \(t'_{2} \in [({n'_{1}}+1)T,({n'_{1}}+1)T+T']\) such that \(z(t'_{2})>{m_{3}}\).

Now, let \(\bar{t}=\inf_{t>t^{*}}\{z(t)>m_{3}\}\). Then \(z(t)\le {m_{3}}\) for \(t\in[t^{*},\bar{t})\), and \(z(\bar{t})={m_{3}}\). We choose \(l'\in{Z_{+}}\) such that \(l'\le{n_{2}}+{n_{3}}+1\) and suppose \(t\in ({n'_{1}}T+(l'-1)T,{n'_{1}}T+l'T]\). From (27), we have

$$\begin{aligned} z(t)&\ge z\bigl({\bigl({n'_{1}}T+\bigl(l'-1 \bigr)T\bigr)^{+}}\bigr)\exp\bigl({\eta_{1}}\bigl(t-\bigl({n'_{1}}T+ \bigl(l'-1\bigr)T\bigr)\bigr)\bigr) \\ &= z\bigl({n'_{1}}T+\bigl(l'-1\bigr)T\bigr) (1-\rho)\exp\bigl({\eta_{1}}\bigl(t-\bigl({n'_{1}}T+ \bigl(l'-1\bigr)T\bigr)\bigr)\bigr) \\ &\ge z\bigl(t^{*}\bigr){{(1-\rho)}^{l-1}}\exp\bigl({\eta_{1}} \bigl(t-{t^{*}}\bigr)\bigr) \\ &\ge {m_{3}}(1-\rho)^{l'-1}\exp\bigl({\eta_{1}} \bigl(t-{t^{*}}\bigr)\bigr). \end{aligned}$$

Since \({\eta_{1}}<0\) and \(t-{t^{*}}\le l'T\), hence

$$ z(t)\ge{m_{3}}(1-\rho)^{{n_{2}}+{n_{3}}}\exp\bigl(({n_{2}}+{n_{3}}+1){ \eta_{1}}T\bigr). $$

Letting

$$ m_{2}={m_{3}}(1-\rho)^{{n_{2}}+{n_{3}}}\exp \bigl(({n_{2}}+{n_{3}}+1){\eta_{1}}T\bigr), $$

we have \(z(t)\ge{m_{2}}\) for \(t\in(t^{*},\bar{t})\). We can continue in the same way by using t̄ instead of \(t^{*}\). Then we shall have \(z(t)\ge{m_{2}}\) for all t large enough.

Case 2.2: There is \(t''\in(t^{*},({n'_{1}}+1)T]\) such that \(z(t'')>{m_{3}}\). Let \(\underline{t}=\inf_{t>t^{*}}\{z(t)>m_{3}\}\). Hence, \(z(t)<{m_{3}}\) for \(t\in[t^{*},\underline{t})\), and \(z(\underline {t})={m_{3}}\). For \(t\in[t^{*},\underline{t})\), (27) holds, we have

$$\begin{aligned} z(t)&\ge z\bigl(t^{*}\bigr)\exp \biggl( \int_{t^{*}}^{t}{\eta_{1}}\,dt \biggr) \\ &={m_{3}}\exp\bigl({\eta_{1}}\bigl(t-{t^{*}}\bigr)\bigr) \\ &\ge {m_{3}}\exp({\eta_{1}}T) \\ &>{m_{2}} \end{aligned}$$

since \(t<{n'_{1}}T+T<{t^{*}}+T\).

For \(t>\underline{t}\), we can continue in the same way since \(z(\underline{t})\ge{m_{3}}\). Since \({m_{2}}<{\bar{m}_{2}}<{m_{3}}\), we have \(z(t)\ge{m_{2}}\) for \(t\ge{t_{1}}\). The proof is complete. □

6 Existence and stability of positive periodic solution

We now investigate the possibility of bifurcation of positive periodic solution to system (4a)-(4d) near \((0,\tilde{w}(t))\). In order to do so, it is more convenient to exchange the state variables and consider the following system instead:

$$\begin{aligned} &\frac{dz}{dt}=\frac{{a_{4}}{f_{1}}(w)}{{k_{5}}+{f_{1}}(w)}-\frac {{a_{5}}{f_{1}}(w)z}{{k_{6}}+{f_{1}}(w)}-{b_{4}}z,\quad t\neq nT, \end{aligned}$$
(28)
$$\begin{aligned} &\frac{dw}{dt}=\frac {{a_{3}}{f_{1}}(w)zw}{({k_{3}}+f_{1}^{2}(w))({k_{4}}+{f_{2}}(w))}-{b_{3}}w,\quad t\neq nT \end{aligned}$$
(29)

with

$$\begin{aligned} &\Delta z(t)=\mu,\quad t=nT, \end{aligned}$$
(30)
$$\begin{aligned} &\Delta w(t)=-\rho w(t),\quad t=nT. \end{aligned}$$
(31)

Let

$$\begin{aligned} &F_{1}(z,w)\equiv\frac{{a_{4}}{f_{1}}(w)}{{k_{5}}+{f_{1}}(w)}-\frac {{a_{5}}{f_{1}}(w)z}{{k_{6}}+{f_{1}}(w)}-{b_{4}}z, \\ &F_{2}(z,w)\equiv\frac {{a_{3}}{f_{1}}(w)zw}{({k_{3}}+f_{1}^{2}(w))({k_{4}}+{f_{2}}(w))}-{b_{3}}w. \end{aligned}$$

According to Lakmeche and Arino [39],

$$\begin{aligned} &\Theta_{1}(z,w)=z+\mu,\qquad {\Theta_{2}}(z,w)=(1-\rho)w,\qquad \varsigma(t)=\bigl(\tilde {w}(t),0\bigr)^{T},\\ & S_{0}=\bigl( \tilde{w}(\tau_{0}),0\bigr)^{T},\quad \tau_{0}=T_{\mathrm{max}} \end{aligned}$$

and

$$\begin{aligned} &\frac{\partial{\Phi_{1}}(\tau_{0},S_{0})}{\partial\tau}=\frac{\partial\tilde {w}(\tau_{0},S_{0})}{\partial t}=\frac{-B\mu\exp(-B\tau_{0})}{1-\exp(-B\tau _{0})}< 0, \\ &\frac{\partial{\Phi_{1}}(\tau_{0},S_{0})}{\partial z}=\exp \biggl( \int _{0}^{\tau_{0}}{\frac{{\partial F_{1}}(\varsigma(r))}{\partial z}\,dr} \biggr)=\exp(-B \tau_{0}), \\ & \frac{\partial{\Phi_{1}}(\tau_{0},S_{0})}{\partial w}= \int_{0}^{\tau _{0}}{\exp \biggl( \int_{\upsilon}^{\tau_{0}}{\frac{\partial{F_{1}}\varsigma (r)}{\partial z}\,dr} \biggr) \frac{\partial F_{1}( \varsigma(\upsilon ))}{\partial w}}\exp \biggl( \int_{0}^{\upsilon}{\frac{\partial F_{2}(\varsigma(r))}{\partial w}\,dr} \biggr)\,d\upsilon \\ &\phantom{\frac{\partial{\Phi_{1}}(\tau_{0},S_{0})}{\partial w}}= \int_{0}^{\tau_{0}}{\exp\bigl(-B(\tau_{0}- \upsilon)\bigr){f'_{1}}(0) \biggl( \frac {{a_{4}}{k_{5}}}{{({k_{5}}+{f_{1}}(0))}^{2}}- \frac{{a_{5}}{k_{6}}\tilde{w}(\upsilon )}{{({k_{6}}+{f_{1}}(0))}^{2}} \biggr)} \\ &\phantom{\frac{\partial{\Phi_{1}}(\tau_{0},S_{0})}{\partial w}=}{}\times\exp \biggl( \int_{0}^{\upsilon}{\bigl(D\tilde{w}(r)-{b_{3}} \bigr)\,dr} \biggr)\,d\upsilon, \\ &\frac{\partial{\Phi_{2}}(\tau_{0},S_{0})}{\partial w}=\exp \biggl( \int _{0}^{\tau_{0}}{\frac{\partial F_{2}(\varsigma(r))}{\partial w}\,dr} \biggr)=\exp \biggl( \int_{0}^{\tau_{0}}{\bigl(D\tilde{w}(r)-{b_{3}} \bigr)\,dr} \biggr), \\ &\frac{{\partial^{2}}\Phi_{2}(\tau_{0},S_{0})}{\partial z\,\partial w}= \int _{0}^{\tau_{0}}{\exp \biggl( \int_{\upsilon}^{\tau_{0}}{\frac{\partial F_{2}(\varsigma(r))}{\partial w}\,dr} \biggr) \frac{{\partial^{2}}F_{2}(\varsigma (\upsilon))}{\partial z\,\partial w}\exp \biggl( \int_{0}^{\upsilon}{\frac {\partial F_{2}(\varsigma(r))}{\partial w}\,dr} \biggr)\,d \upsilon} \\ &\phantom{\frac{{\partial^{2}}\Phi_{2}(\tau_{0},S_{0})}{\partial z\,\partial w}}=\frac{D\tau_{0}}{1-\rho}>0, \\ &\frac{{\partial^{2}}\Phi_{2}(\tau_{0},S_{0})}{\partial w^{2}}= \int_{0}^{\tau _{0}}{\exp \biggl( \int_{\upsilon}^{\tau_{0}}{\frac{\partial F_{2}( \varsigma (r))}{\partial w}\,dr} \biggr) \frac{{\partial^{2}}F_{2}(\varsigma( \upsilon ))}{\partial w^{2}}\exp \biggl( \int_{0}^{\upsilon}{\frac{\partial F_{2}(\varsigma(r))}{\partial w}\,dr} \biggr)\,d \upsilon} \\ &\phantom{\frac{{\partial^{2}}\Phi_{2}(\tau_{0},S_{0})}{\partial z\,\partial w}=}{}+ \int_{0}^{\tau_{0}}{ \biggl[\exp \biggl( \int_{\upsilon}^{\tau_{0}}{\frac {\partial F_{2}(\varsigma(r))}{\partial w}\,dr} \biggr) \frac{{\partial ^{2}}F_{2}(\varsigma(\upsilon))}{\partial z\,\partial w} \biggr]} \\ &\phantom{\frac{{\partial^{2}}\Phi_{2}(\tau_{0},S_{0})}{\partial z\, \partial w}=}{}\times \biggl[ \int_{0}^{\upsilon}\exp \biggl( \int_{\theta}^{\upsilon }{\frac{\partial F_{1}(\varsigma(r))}{\partial z}\,dr} \biggr) \frac{\partial F_{1}(\varsigma(\theta))}{\partial w}\\ &\phantom{\frac{{\partial^{2}}\Phi_{2}(\tau_{0},S_{0})}{\partial z\, \partial w}=}{}\times \exp \biggl( \int_{0}^{\theta}{\frac {\partial F_{2}(\varsigma(r))}{\partial w}\,dr} \biggr)\,d\theta \biggr]\,d\upsilon \\ &\phantom{\frac{{\partial^{2}}\Phi_{2}(\tau_{0},S_{0})}{\partial z\,\partial w}}= \int_{0}^{\tau_{0}}{\frac{2{a_{3}}\tilde{w}(\upsilon)}{1-\rho} \biggl( \frac {{k_{4}}{f'_{1}}(0)({k_{3}}-2f_{1}^{2}(0))-{f_{1}}(0){f'_{2}}(0)({k_{3}}+f_{1}^{2}(0))}{k_{4}^{2}{({k_{3}}+f_{1}^{2}(0))}^{2}} \biggr)\,d\upsilon} \\ &\phantom{\frac{{\partial^{2}}\Phi_{2}(\tau_{0},S_{0})}{\partial z\,\partial w}=}{}+D{f'_{1}}(0) \int_{0}^{\tau_{0}}{ \biggl[\exp \biggl( \int_{\upsilon}^{\tau _{0}}{\bigl(D\tilde{w}(r)-{b_{3}} \bigr)\,dr} \biggr) \biggr]} \\ &\phantom{\frac{{\partial^{2}}\Phi_{2}(\tau_{0},S_{0})}{\partial z\,\partial w}=}{}\times \biggl[ \int_{0}^{\upsilon}{ \biggl(\frac{{a_{4}}{k_{5}}}{{({k_{5}} +{f_{1}}(0))}^{2}} - \frac{{a_{5}}{k_{6}}\tilde{w}(\theta)}{{({k_{6}} +{f_{1}}(0))}^{2}} \biggr)} \\ &\phantom{\frac{{\partial^{2}}\Phi_{2}(\tau_{0},S_{0})}{\partial z\,\partial w}=}{}\times\exp \biggl( \int_{0}^{\theta}{\bigl(D\tilde{w}(r) -{b_{3}}\bigr)\,dr -B(\upsilon -\theta)} \biggr)\,d\theta \biggr]\, d\upsilon, \\ &\frac{\partial^{2}{\Phi_{2}}(\tau_{0},S_{0})}{\partial w\,\partial\tau}=\frac {\partial F_{2}(\varsigma(\tau_{0}))}{\partial w}\exp \biggl( \int_{0}^{\tau _{0}}{\frac{\partial F_{2}(\varsigma(r))}{\partial w}\,dr} \biggr) \\ &\phantom{\frac{\partial^{2}{\Phi_{2}}(\tau_{0},S_{0})}{\partial w\,\partial\tau}}=\bigl(D\tilde{w}(\tau_{0})-{b_{3}}\bigr)\exp \biggl( \int_{0}^{\tau_{0}}{\bigl(D\tilde {w}(r)-{b_{3}} \bigr)\,dr} \biggr) \\ &\phantom{\frac{\partial^{2}{\Phi_{2}}(\tau_{0},S_{0})}{\partial w\,\partial\tau}}=\frac{1}{1-\rho} \biggl[\frac{D\mu\exp(-B\tau_{0})}{1-\exp(-B\tau _{0})}+\frac{AD}{B}-b_{3} \biggr]. \end{aligned}$$

Now, we can compute

$$\begin{aligned} d'_{0}=1-{ \biggl(\frac{\partial\Theta_{2}}{\partial w}\frac{\partial\Phi _{2}}{\partial w} \biggr)}_{(\tau_{0},S_{0})}=1-(1-\rho)\exp \biggl( \int _{0}^{\tau_{0}}{\bigl(D\tilde{w}(r)-{b_{3}} \bigr)\,dr} \biggr), \end{aligned}$$

where \(\tau_{0}\) is the root of \(d'_{0}=0\). Note that \(d'_{0}>0\) if \(T< T_{\mathrm{max}}\) and \(d'_{0}<0\) if \(T>T_{\mathrm{max}}\). We can also compute

$$\begin{aligned} &a'_{0}=1-{ \biggl(\frac{\partial\Theta_{1}}{\partial z}\frac{\partial\Phi _{1}}{\partial z} \biggr)}_{(\tau_{0},S_{0})}=1-\exp(-B{\tau_{0}})>0, \\ &b'_{0}=-{ \biggl(\frac{\partial\Theta_{1}}{\partial z}\frac{\partial\Phi _{1}}{\partial w}+ \frac{\partial\Theta_{1}}{\partial w}\frac{\partial\Phi _{2}}{\partial w} \biggr)}_{(\tau_{0},S_{0})} \\ &\phantom{b'_{0}}=-\frac{\partial\Phi_{1}(\tau_{0},S_{0})}{\partial w} \\ &\phantom{b'_{0}}=- \int_{0}^{\tau_{0}}{\exp\bigl(-B({\tau_{0}}- \upsilon)\bigr){f'_{1}}(0) \biggl(\frac {{a_{4}}{k_{5}}}{{({k_{5}}+{f_{1}}(0))}^{2}}- \frac{{a_{5}}{k_{6}}\tilde{w}(\upsilon )}{{({k_{6}}+{f_{1}}(0))}^{2}} \biggr)} \\ &\phantom{b'_{0}=}{}\times \exp \biggl( \int_{0}^{\upsilon}{\bigl(D\tilde{w}(r)-{b_{3}} \bigr)\,dr} \biggr)\,d\upsilon, \\ &B^{*}=- \biggl[ \biggl(\frac{D\mu\exp(-B{\tau_{0}})}{1-\exp(-B{\tau_{0}})} \biggr) \biggl(1-\frac{B{\tau_{0}}}{1-\exp(-B{\tau_{0}})} \biggr)+\frac{AD}{B}-{b_{3}} \biggr], \\ &C^{*}=2(1-\rho)\frac{b'_{0}}{a'_{0}}\frac{{\partial^{2}}{\Phi_{2}}}{\partial z\partial w}-(1-\rho)\frac{{\partial^{2}}{\Phi_{2}}}{\partial w^{2}}. \end{aligned}$$

Note that \(C^{*} > 0\) and \(B^{*}<0\) if

$$\begin{aligned} &{k_{4}} {f'_{1}}(0) \bigl({k_{3}}-2f_{1}^{2}(0) \bigr)< {f_{1}}(0){f'_{2}}(0) \bigl({k_{3}}+f_{1}^{2}(0)\bigr), \end{aligned}$$
(32)
$$\begin{aligned} &\frac{{a_{4}}{k_{5}}}{{({k_{5}}+{f_{1}}(0))}^{2}}>\frac{{a_{5}}{k_{6}}}{{({k_{6}}+{f_{1}}(0))}^{2}} \biggl[\frac{\mu}{1-\exp(-B{\tau_{0}})}+ \frac{A}{B} \biggr] \end{aligned}$$
(33)

and

$$ \frac{AD}{B}-{b_{3}}-D\mu>0. $$
(34)

Hence, the following result is obtained according to Lakmeche and Arino [39].

Theorem 3

System (28)-(31) has a positive periodic solution which is supercritical provided

$$ T>T_{\mathrm{max}} $$
(35)

and (5), (11)-(12), (32)-(34) hold.

7 Numerical simulations

In this section, numerical simulations are carried out in order to support our theoretical predictions.

Firstly, all parameters are chosen to satisfy all conditions in Theorem 1. In Figure 1, we can see that the solution of system (4a)-(4d) converges asymptotically to the oscillatory solution \((0,\tilde{w}(t))\) as time passes conforming with our theoretical prediction. Figure 2 shows that the solution of system (4a)-(4d) is bounded within a positive range as time passes when all parameters are chosen to satisfy all conditions in Theorem 2. Here, the simulation result also agrees with our theoretical prediction. Finally, the solution trajectory of system (4a)-(4d) shown in Figure 3 exhibits the sustained oscillations as time passes when all parameters are chosen to satisfy all conditions in Theorem 3. A limit cycle occurs as theoretically predicted.

Figure 1
figure 1

Numerical simulation of equations (4a)-(4d). The solution trajectory approaches oscillatory solution \((0,\tilde {w}(t))\) as time passes. Here, all parameters are chosen to satisfy the conditions in Theorem 1, i.e., \({a_{1}}=0.65\), \({a_{2}}=0.3\), \({a_{3}}=0.3\), \({a_{4}}=0.9\), \({a_{5}}=0.1\), \({b_{1}}=0.5\), \({b_{2}}=0.2\), \({b_{3}}=0.425\), \({b_{4}}=0.5\), \({k_{1}}=0.1\), \({k_{2}}=0.5\), \({k_{3}}=0.1\), \({k_{4}}=0.5\), \({k_{5}}=0.01\), \({k_{6}}=0.75\), \(\mu=0.1\), \(\rho=0.1\), \(T=1\), \(z(0)=0.0001\), and \(w(0)=0.0001\). (a) The solution trajectory projected on \((z,w)\)-plane. (b) The corresponding time course of the number of active osteoclasts \((z)\) tending towards zero. (c) The corresponding time course of the number of active osteoblasts \((w)\) exhibiting positive oscillation.

Full size image
Figure 2
figure 2

Numerical simulation of equations (4a)-(4d). The solution trajectory is bounded within a positive range as time passes. Here, all parameters are chosen to satisfy the conditions in Theorem 2, \({a_{1}}=0.2\), \({a_{2}}=0.3\), \({a_{3}}=0.21\), \({a_{4}}=0.9\), \({a_{5}}=0.4\), \({b_{1}}=0.7\), \({b_{2}}=0.5\), \({b_{3}}=0.1\), \({b_{4}}=0.3\), \({k_{1}}=0.5\), \({k_{2}}=1.9\), \({k_{3}}=0.9\), \({k_{4}}=0.9\), \({k_{5}}=0.01\), \({k_{6}}=0.75\), \(\mu=0.5\), \(\rho=0.5\), \(T=10\), \(z(0)=0.7\), and \(w(0)=3\). (a) The solution trajectory projected on \((z,w)\)-plane. (b) The corresponding time course of the number of active osteoclasts \((z)\) and (c) The corresponding time course of the number of active osteoblasts \((w)\).

Full size image
Figure 3
figure 3

Numerical simulation of equations (4a)-(4d). The solution trajectory approaches a limit cycle as time passes. Here, all parameters are chosen to satisfy the conditions in Theorem 3, \({a_{1}}=0.75\), \({a_{2}}=0.3\), \({a_{3}}=0.35\), \({a_{4}}=0.9\), \({a_{5}}=0.4\), \({b_{1}}=0.7\), \({b_{2}}=0.5\), \({b_{3}}=0.1\), \({b_{4}}=0.6\), \({k_{1}}=0.5\), \({k_{2}}=2.9\), \({k_{3}}=0.9\), \({k_{4}}=0.95\), \({k_{5}}=0.21\), \({k_{6}}=0.7\), \(\mu=0.2\), \(\rho=0.5\), \(T=20\), \(z(0)=0.13\), and \(w(0)=5\). (a) The solution trajectory projected on \((z,w)\)-plane. (b) The corresponding time course of the number of active osteoclasts \((z)\). (c) The corresponding time course of the number of active osteoblasts \((w)\).

Full size image

8 Conclusion

We have developed an impulsive system of bone remodeling process in order to investigate the effect of estrogen supplements. The model is then analyzed theoretically so that the conditions on the system parameters, for which the desirable behaviors of the solution of the system can be expected, are derived. We can see that the frequency of estrogen treatments \(\frac{1}{T}\), the dosages of estrogen supplements indicated by μ and ρ play important roles in controlling the number of active osteoclasts and active osteoblasts, the different frequencies and dosages of estrogen supplements might lead to the undesirable behavior of the system. For example, the solution of the system might be unbounded, which means that the number of active osteoclasts, bone resorbing cells, might increase to very high levels or the number of active osteoblasts, bone forming cells, decreases to very low levels resulting in the net bone resorption instead of bone formation, which is the expected outcome of the estrogen supplements.

Moreover, a condition needed to guarantee the existence of positive oscillation in the number of active osteoblasts and active osteoclasts resembling clinical observation stated in Theorem 3 is \(T>T_{\mathrm{max}}\), where \(T_{\mathrm{max}}\) depends on μ and ρ. Hence, if the dosage of estrogen supplement reflected by μ and ρ is fixed, an appropriate frequency of estrogen supplement \(\frac{1}{T}\) can be chosen so that \(T>T_{\mathrm{max}}\) as required by Theorem 3 to guarantee the desirable levels of active osteoblasts and active osteoclasts. Therefore, the dosage and the frequency of estrogen supplement are the keys to the effectiveness of estrogen supplement in osteoporosis patients.