1 Introduction

We consider a one-space dimensional quasi-linear hyperbolic equation of the type

$$ u_{tt} = A(x, t, u)u_{xx} + f(x, t, u, u_{x}, u_{t}),\quad 0 < x < 1, t > 0, $$
(1.1)

with the following initial conditions:

$$ u(x, 0) = p(x),\qquad u_{t}(x, 0) = q(x), \quad 0 \le x \le1, $$
(1.2)

and boundary conditions

$$ u(0, t) = r_{0}(t),\qquad u(1, t) = r_{1}(t),\quad t \ge0. $$
(1.3)

We assume that the functions \(A(x, t, u)\) and \(u(x, t)\) are sufficiently smooth, the required higher order partial derivatives of \(A(x, t, u)\) and \(u(x, t)\) exist in the solution domain \(\Omega\equiv \{ (x, t)|0 < x < 1, t > 0 \}\), and the conditions (1.2) and (1.3) are given with sufficient smoothness to maintain the order of accuracy in the numerical method under consideration. Further, we assume that the initial and boundary value problem (1.1)-(1.3) has a unique smooth solution \(u(x, t)\) in the solution domain Ω. The details of existence and uniqueness of the above initial boundary value problem have already been discussed in [1].

A wave is a time evolution phenomenon that we generally model mathematically using partial differential equations (pdes) which have a dependent variable \(u(x, t)\), which represents the wave value, an independent variable, time t and one or more independent spatial variables. The actual form that the wave takes is strongly dependent upon the system’s initial conditions, boundary conditions and disturbances in the system.

Wave equation is an important second-order linear partial differential equation for the description of waves as they occur in real life such as ripples on a lake, wind waves on water, tidal surges in estuaries, transverse waves travelling on a long string, transverse vibrations of strings and membranes, traffic density waves, seismic waves, acoustic waves and electromagnetic wave currents in coaxial cables.

Problems involving the propagation of nonlinear waves have become of increasing interest in various branches of science and engineering. In general, waves of finite amplitude governed by a nonlinear evolution equation are called nonlinear waves. As is well known, the principle of superposition of solutions is not valid in nonlinear equations. Therefore the methods familiar to physicists and engineers, like the use of Fourier or Laplace transforms, are no longer applicable with the result that the study of nonlinear waves has not yet become well established. However, in recent years, a number of interesting phenomena involving nonlinear waves have been found, and with the development of digital computers remarkable progress has been made in the research into nonlinear waves.

There has been a consistent effort in developing efficient and high accuracy finite difference methods to solve quasi-linear hyperbolic equations. In 1968 to 1969, Bickley and Fyfe [2, 3] developed a cubic spline method for two-point boundary value problems. Papamichael and Whiteman [4] also developed a cubic spline technique for the solution of one-dimensional heat conduction equation. Raggett and Wilson [5] used a cubic spline technique to give a fully implicit finite difference approximation to the one-dimensional wave equation. Fleck Jr. [6] proposed a cubic spline method for solving a wave equation of nonlinear optics. Jain and Aziz [7, 8] studied spline function approximations and a cubic spline solution of two-point boundary value problems with significant first derivative terms. Jain et al. [9] discussed difference schemes based on splines in compression for the solution of conservation laws. Kadalbajoo and Patidar [10, 11] analyzed numerical methods of singularly perturbed two-point boundary value problems by spline in compression and tension approximations. Khan and Aziz [12] derived a parametric cubic spline approach to the solution of system of two-point boundary value problems. Kadalbajoo and Aggarwal [13] discussed a cubic spline method for solving singular two-point boundary value problems. Mohanty et al. [14–17] gave spline in compression methods for singularly perturbed two-point singular boundary value problems and gave convergent spline in tension methods for singularly perturbed two-point singular boundary value problems. Rashidinea et al. [18, 19] discussed spline methods for the solution of hyperbolic and parabolic equations. Islam et al. [20, 21] studied non-polynomial spline approximations for the solution of boundary value problems. Ding and Zhang [22] studied parametric spline methods for the solution of hyperbolic equations. Mohanty and Jain [23] studied the use of a cubic spline method for the solution of 1D quasilinear parabolic equations. Recently, Mohanty et al. [24, 25] derived numerical methods based on non-polynomial spline approximations for the solution of 1D quasilinear hyperbolic equations. In these methods, they have used full-step grid points, hence these methods are not directly applicable to problems in polar coordinates. Mohanty et al. [26–35] have also used different techniques for the solution of one-dimensional nonlinear wave equations. Most recently, Mohanty and Khurana [36] have proposed a high accuracy numerical method based on off-step discretization for the solution of 2D quasilinear hyperbolic equations. To the authors’ knowledge, no numerical method based on half-step spline in compression approximation has been developed for the one-dimensional quasi-linear hyperbolic equation from the consistency condition so far. In this paper, we propose a method derived from the consistency condition, which is applicable to hyperbolic equations irrespective of coordinate systems.

Our paper is arranged as follows. In Section 2, we discuss the properties of spline in compression approximations. In Section 3, we discuss a detailed derivation of a new half-step three-level implicit method based on spline in compression approximations. In Section 4, we extend our technique to solve the system of nonlinear second-order quasi-linear hyperbolic equations. In Section 5, we discuss the stability analysis when the method is applied to a telegraphic equation, and we show it to be unconditionally stable. We also establish the stability condition to solve fourth-order linear hyperbolic partial differential equation. In Section 6, we solve some benchmark problems and compare our results with other existing methods. In Section 7, we give concluding remarks.

2 Spline in compression approximations

We discretize the solution domain \([0, 1] \times[0,J]\) into \((N + 1) \times J\) by a set of grid points \((x_{l}, t_{j})\), where \(0 = x_{0} < x_{1} < \cdots< x_{N + 1} = 1\), and \(0 = t_{0} < t_{1} < \cdots< t_{J} = J\), N being a positive integer with uniform mesh spacing \(h = x_{l} - x_{l - 1}\), \(k = t_{j} - t_{j - 1}\); \(l = 1(1)N + 1\), \(j = 1(1)J\). Let \(u_{l}^{j}\) and \(U_{l}^{j}\) be the approximate and exact solutions of \(u(x, t)\) at the grid point \((x_{l}, t_{j})\), respectively.

Now, for each subinterval \([x_{l - 1}, x_{l}]\), \(l = 1(1)N + 1\), we define the non-polynomial spline in compression function \(S_{j}(x)\) of the function \(u(x, t)\) at the mesh point \((x_{l}, t_{j})\) as follows:

$$\begin{aligned} S_{j}(x) =& a_{l}^{j} + b_{l}^{j}(x - x_{l}) + c_{l}^{j}\sin\omega(x - x_{l}) \\ &{}+ d_{l}^{j}\cos\omega(x - x_{l}),\quad l = 1(1)N + 1, x \in[x_{l - 1}, x_{l}], \end{aligned}$$
(2.1)

where \(a_{l}^{j}\), \(b_{l}^{j}\), \(c_{l}^{j}\) and \(d_{l}^{j}\) are unknown coefficients and ω is an arbitrary parameter to be determined. Here \(S_{j} \in C^{2}[0, 1]\) and it interpolates \(u(x, t)\) at the mesh point \((x_{l}, t_{j})\) at jth time level.

The derivatives of function \(S_{j}\) at x are given by

$$\begin{aligned}& S'_{j}(x) = b_{l}^{j} + \omega c_{l}^{j}\cos\omega(x - x_{l}) - \omega d_{l}^{j}\sin\omega(x - x_{l}), \end{aligned}$$
(2.2)
$$\begin{aligned}& S''_{j}(x) = - \omega^{2} \bigl[c_{l}^{j}\sin\omega(x - x_{l}) + d_{l}^{j}\cos \omega(x - x_{l})\bigr]. \end{aligned}$$
(2.3)

We denote

$$ M_{l}^{j} = S''_{j}(x_{l}) = U_{xx_{l}}^{j},\qquad M_{l \pm1/2}^{j} = S''_{j}(x_{l \pm1/2}) = U_{xx_{l} \pm\frac{1}{2}}^{j}. $$
(2.4)

Using the notations of (2.4) and putting \(x = x_{l}\) and \(x_{l - 1/2}\) in (2.3), we get the following values of \(a_{l}^{j}\), \(b_{l}^{j}\), \(c_{l}^{j}\) and \(d_{l}^{j}\):

$$ \begin{aligned} &a_{l}^{j} = U_{l}^{j} + \frac{M_{l}^{j}}{\omega^{2}},\qquad b_{l}^{j} = \frac{U_{l}^{j} - U_{l - 1}^{j}}{h} + \frac{M_{l}^{j}}{\omega\theta} - \frac{M_{l - 1/2}^{j}}{\omega\theta} \cos\theta, \\ &c_{l}^{j} = \frac{M_{l - 1/2}^{j} - M_{l}^{j}\cos\theta}{\omega^{2}\sin \theta},\qquad d_{l}^{j} = \frac{ - M_{l}^{j}}{\omega^{2}}, \end{aligned} $$
(2.5)

where \(\theta= \frac{\omega h}{2}\).

Substituting the values of (2.5) in (2.2), we get

$$\begin{aligned} S'_{j}(x) =& \frac{U_{l}^{j} - U_{l - 1}^{j}}{h} + \frac {M_{l}^{j}}{\omega \theta} - \frac{M_{l - 1/2}^{j}}{\omega\theta} \cos\theta+ \frac {(M_{l - 1/2}^{j} - M_{l}^{j}\cos\theta)}{\omega\sin\theta} \cos\omega(x - x_{l}) \\ &{}+ \frac{M_{l}^{j}}{\omega} \sin\omega(x - x_{l}),\quad x \in[x_{l - 1}, x_{l}]. \end{aligned}$$
(2.6)

Similarly,

$$\begin{aligned} S'_{j}(x) =& \frac{U_{l + 1}^{j} - U_{l}^{j}}{h} - \frac {M_{l}^{j}}{\omega \theta} + \frac{M_{l + 1/2}^{j}}{\omega\theta} \cos\theta+ \frac{(M_{l}^{j}\cos\theta- M_{l + 1/2}^{j})}{\omega\sin\theta} \cos \omega(x - x_{l}) \\ &{}+ \frac{M_{l}^{j}}{\omega} \sin\omega(x - x_{l}),\quad x \in[x_{l}, x_{l + 1}]. \end{aligned}$$
(2.7)

From the condition of continuity \(S'_{j}(x_{l} - ) = S'_{j}(x_{l} + )\), we obtain the following consistency condition:

$$ U_{l + 1}^{j} - 2U_{l}^{j} + U_{l - 1}^{j} = h^{2}\bigl[\alpha M_{l + 1/2}^{j} + 2\beta M_{l}^{j} + \alpha M_{l - 1/2}^{j} \bigr] + O\bigl(h^{6}\bigr),\quad l = 1(1)N, $$
(2.8)

where

$$\begin{aligned}& \alpha= \frac{1}{2\theta^{2}}\biggl(\frac{\theta}{\sin\theta} - \cos \theta\biggr) = \frac{1}{3} - \frac{\theta^{2}}{90} + O\bigl(\theta^{4} \bigr), \end{aligned}$$
(2.9a)
$$\begin{aligned}& \beta= \frac{1}{2\theta^{2}}(1 - \theta\cot\theta) = \frac{1}{6} + \frac{\theta^{2}}{90} + O\bigl(\theta^{4}\bigr). \end{aligned}$$
(2.9b)

Equating the coefficient of \(M_{l}^{j}\), from (2.8), we obtain the condition

$$ 2(\alpha+ \beta) = 1. $$
(2.10)

Substituting the values of (2.9a)-(2.9b) in (2.10) and neglecting \(O(\theta^{4})\) terms, we get

$$ \tan\frac{\theta}{2} = \frac{\theta}{2}. $$
(2.11)

The above equation has infinitely many roots, the smallest positive non-zero root is given by

$$ \theta= 8.986818916. $$
(2.12)

When \(\omega\to0\), i.e., when \(\theta\to0\), then \((\alpha,\beta) \to ( \frac{1}{3},\frac{1}{6} )\), and relation (2.8) reduces to a cubic spline relation.

Now, we give two important properties of non-polynomial spline in compression

$$\begin{aligned}& m_{l - 1/2}^{j} = S'_{j}(x_{l - 1/2}) \\& \hphantom{m_{l - 1/2}^{j}}= \frac{U_{l}^{j} - U_{l - 1}^{j}}{h} + \frac{(M_{l}^{j} - M_{l - 1/2}^{j}\cos\theta)}{\omega\theta} +\frac{(M_{l - 1/2}^{j} - M_{l}^{j}\cos\theta)\cos\theta}{\omega \sin \theta} - \frac{M_{l}^{j}\sin\theta}{\omega}, \end{aligned}$$
(2.13)
$$\begin{aligned}& m_{l + 1/2}^{j} = S'_{j}(x_{l + 1/2}) \\& \hphantom{m_{l + 1/2}^{j}}= \frac{U_{l + 1}^{j} - U_{l}^{j}}{h} - \frac{(M_{l}^{j} - M_{l + 1/2}^{j}\cos\theta)}{\omega\theta} + \frac{(M_{l}^{j}\cos\theta- M_{l + 1/2}^{j})\cos\theta}{\omega\sin \theta} + \frac{M_{l}^{j}\sin\theta}{\omega}. \end{aligned}$$
(2.14)

On simplifying (2.13) and (2.14), we get

$$\begin{aligned}& S_{j}^{\prime} (x_{l - 1/2}) = \frac{U_{l}^{j} - U_{l - 1}^{j}}{h} + \frac{h(2\beta M_{l - 1/2}^{j} - \alpha M_{l}^{j})}{4}, \end{aligned}$$
(2.15)
$$\begin{aligned}& S_{j}^{\prime} (x_{l + 1/2}) = \frac{U_{l + 1}^{j} - U_{l}^{j}}{h} + \frac{h(\alpha M_{l}^{j} - 2\beta M_{l + 1/2}^{j})}{4}. \end{aligned}$$
(2.16)

Relations (2.15) and (2.16) are two important properties of non-polynomial spline in compression function \(S_{j}(x)\).

3 Method based on non-polynomial spline in compression approximations

For the sake of simplicity, we first consider the one-space dimensional nonlinear hyperbolic partial differential equation

$$ u_{tt} = A(x, t)u_{xx} + f(x, t, u, u_{x}, u_{t}),\quad 0 < x < 1, t > 0, $$
(3.1)

with the initial and boundary conditions prescribed by (1.2) and (1.3), respectively. At the grid point \((x_{l}, t_{j})\), we define \(A_{l}^{j} = A(x_{l}, t_{j})\), \(U_{t_{l}}^{j} = u_{t}(x_{l},t_{j})\), \(U_{tt_{l}}^{j} = u_{tt}(x_{l},t_{j})\), \(U_{x_{l}}^{j} = u_{x}(x_{l},t_{j})\), \(U_{xx_{l}}^{j} = u_{xx}(x_{l},t_{j}) = M_{l}^{j}\), and we may rewrite differential equation (3.1) at the grid point \((x_{l}, t_{j})\) as

$$ U_{tt_{l}}^{j} - A_{l}^{j}U_{xx_{l}}^{j} = f\bigl(x_{l}, t_{j}, U_{l}^{j}, U_{x_{l}}^{j}, U_{t_{l}}^{j}\bigr) \equiv F_{l}^{j}\quad (\mbox{say}). $$
(3.2)

Similarly, at the grid point \((x_{l \pm1/2},t_{j})\), we can write differential equation (3.1) as

$$ U_{tt_{l \pm1/2}}^{j} - A_{l \pm1/2}^{j}U_{xx_{l \pm1/2}}^{j} = f\bigl(x_{l \pm1/2}, t_{j}, U_{l \pm1/2}^{j}, U_{x_{l \pm1/2}}^{j}, U_{t_{l \pm 1/2}}^{j}\bigr) \equiv F_{l \pm1/2}^{j}. $$
(3.3)

Now we simplify the consistency condition (2.8) with the aid of differential equation (3.1) to get its modified form.

By the help of (2.4), (3.2), (3.3), we may rewrite (2.8) as

$$\begin{aligned} U_{l + 1}^{j} - 2U_{l}^{j} + U_{l - 1}^{j} =& h^{2} \biggl[ \frac{\alpha}{ A_{l + 1/2}^{j}} \bigl(U_{tt_{l + 1/2}}^{j} - F_{l + 1/2}^{j}\bigr) + \frac{2\beta}{ A_{l}^{j}}\bigl(U_{tt_{l}}^{j} - F_{l}^{j} \bigr) \\ &{}+ \frac{\alpha}{A_{l - 1/2}^{j}}\bigl(U_{tt_{l - 1/2}}^{j} - F_{l - 1/2}^{j}\bigr) \biggr] + O\bigl(h^{6}\bigr). \end{aligned}$$
(3.4)

We use the following expansions:

$$\begin{aligned}& \frac{1}{A_{l \pm\frac{1}{2}}^{j}} = \frac{1}{A_{l}^{j}} \biggl[ 1 \mp \frac{h}{2} \biggl( \frac{A_{x_{l}}^{j}}{A_{l}^{j}} \biggr) - \frac{h^{2}}{8A_{l}^{j}} \biggl( A_{xx_{l}}^{j} - 2\frac{{A_{x_{l}}^{j}}^{2}}{A_{l}^{j}} \biggr) \mp O\bigl(h^{3}\bigr) \biggr], \end{aligned}$$
(3.5)
$$\begin{aligned}& {U_{tt_{l \pm1/2}}^{j}} = {U_{tt_{l}}^{j}} \pm \frac{h}{2}{U_{ttx_{l}}^{j}} + \frac{h^{2}}{8}{U_{ttxx_{l}}^{j}} \pm O\bigl(h^{3}\bigr). \end{aligned}$$
(3.6)

With the aid of (2.9a), (2.9b), (3.5), (3.6), from (3.4), we obtain

$$\begin{aligned} A_{l}^{j}\bigl(U_{l + 1}^{j} - 2U_{l}^{j} + U_{l - 1}^{j}\bigr) =& h^{2} \biggl[ 2(\alpha+ \beta)U_{tt_{l}}^{j} - \frac{\alpha h^{2}}{4A_{l}^{j}}\biggl(A_{xx_{l}}^{j} - 2\frac{{A_{x_{l}}^{j}}^{2}}{A_{l}^{j}} \biggr)U_{tt_{l}}^{j} \\ &{}- \frac{\alpha h^{2}}{2}\frac{A_{x_{l}}^{j}}{A_{l}^{j}}U_{ttx_{l}}^{j} + \frac{\alpha h^{2}}{4}U_{ttxx_{l}}^{j} \biggr] \\ &{}- h^{2}\biggl[ \biggl( \frac{1}{3} - \frac{\theta^{2}}{90} \biggr) \biggl( 1 - \frac{h}{2}\frac{A_{x_{l}}^{j}}{A_{l}^{j}} - \frac{h^{2}}{8A_{l}^{j}} \biggl(A_{xx_{l}}^{j} - 2\frac{{A_{x_{l}}^{j}}^{2}}{A_{l}^{j}}\biggr) \biggr)F_{l + \frac{1}{2}}^{j} \\ &{}+ \biggl( \frac{1}{3} - \frac{\theta^{2}}{90} \biggr) \biggl( 1 + \frac{h}{2}\frac{A_{x_{l}}^{j}}{A_{l}^{j}} - \frac{h^{2}}{8A_{l}^{j}}\biggl(A_{xx_{l}}^{j} - 2\frac{{A_{x_{l}}^{j}}^{2}}{A_{l}^{j}}\biggr) \biggr)F_{l - \frac{1}{2}}^{j} \\ &{}+ \biggl( \frac{1}{3} + \frac{2\theta^{2}}{90} \biggr)F_{l}^{j} \biggr] + O\bigl(h^{6}\bigr). \end{aligned}$$
(3.7)

Now, using (2.9a) and (2.9b) in (3.7), we get

$$\begin{aligned} A_{l}^{j}\bigl(U_{l + 1}^{j} - 2U_{l}^{j} + U_{l - 1}^{j}\bigr) =& \frac{h^{2}}{12} \biggl[ 12U_{tt_{l}}^{j} - \frac{h^{2}}{A_{l}^{j}} \biggl( A_{xx_{l}}^{j}- 2\frac{{A_{x_{l}}^{j}}^{2}}{A_{l}^{j}} \biggr)U_{tt_{l}}^{j} \\ &{} - 2h^{2}\frac{A_{x_{l}}^{j}}{A_{l}^{j}}U_{ttx_{l}}^{j} + h^{2}{U_{tt}}_{xx_{l}}^{j} \biggr] \\ &{}- \frac{h^{2}}{3} \biggl[ \biggl( 1 - \frac{h}{2} \frac{A_{x_{l}}^{j}}{A_{l}^{j}} \biggr)F_{l + \frac{1}{2}}^{j} + \biggl( 1 + \frac{h}{2}\frac{A_{x_{l}}^{j}}{A_{l}^{j}} \biggr)F_{l - \frac{1}{2}}^{j} + F_{l}^{j} \biggr] \\ &{}+ \frac{h^{4}}{24A_{l}^{j}} \biggl[ \biggl( A_{xx_{l}}^{j} - 2\frac{{A_{x_{l}}^{j}}^{2}}{A_{l}^{j}} \biggr) \bigl( F_{l + \frac{1}{2}}^{j} + F_{l - \frac{1}{2}}^{j} \bigr) \biggr] \\ &{}+ \frac{h^{2}\theta^{2}}{90} \biggl[ \biggl( 1 - \frac{h}{2} \frac{A_{x_{l}}^{j}}{A_{l}^{j}} \biggr)F_{l + \frac{1}{2}}^{j} + \biggl( 1 + \frac{h}{2}\frac{A_{x_{l}}^{j}}{A_{l}^{j}} \biggr)F_{l - \frac{1}{2}}^{j} - 2F_{l}^{j} \biggr] \\ &{}+ O\bigl(h^{6}\bigr). \end{aligned}$$
(3.8)

Now we use the following approximations:

$$\begin{aligned}& 2hU_{ttx_{l}}^{j} = U_{tt_{l + 1}}^{j} - U_{tt_{l - 1}}^{j} + O\bigl(h^{3}\bigr), \end{aligned}$$
(3.9a)
$$\begin{aligned}& h^{2}U_{ttxx_{l}}^{j} = U_{tt_{l + 1}}^{j} - 2U_{tt_{l}}^{j} + U_{tt_{l - 1}}^{j} + O \bigl(h^{4}\bigr), \end{aligned}$$
(3.9b)
$$\begin{aligned}& F_{l + 1/2}^{j} + F_{l - 1/2}^{j} = 2F_{l}^{j} + O\bigl(h^{2}\bigr) = 2 \bigl(U_{tt_{l}}^{j} - A_{l}^{j}U_{xx_{l}}^{j} \bigr) + O\bigl(h^{2}\bigr), \end{aligned}$$
(3.9c)
$$\begin{aligned}& F_{l + 1/2}^{j} - F_{l - 1/2}^{j} = hF_{{x}_{l}}^{j} + O\bigl(h^{3}\bigr), \end{aligned}$$
(3.9d)
$$\begin{aligned}& h^{2}U_{xx_{l}}^{j} = U_{l + 1}^{j} - 2U_{l}^{j} + U_{l - 1}^{j} + O \bigl(h^{4}\bigr). \end{aligned}$$
(3.9e)

Using the approximations (3.9a)-(3.9d) in (3.8) and neglecting high order terms, we get

$$\begin{aligned} A_{l}^{j}\bigl(U_{l + 1}^{j} - 2U_{l}^{j} + U_{l - 1}^{j}\bigr) =& \frac{h^{2}}{12} \biggl[ 10U_{tt_{l}}^{j} - \frac{h^{2}}{A_{l}^{j}} \biggl( A_{xx_{l}}^{j} - 2\frac{{A_{x_{l}}^{j}}^{2}}{A_{l}^{j}} \biggr)U_{tt_{l}}^{j} \\ &{}- h\frac{A_{x_{l}}^{j}}{A_{l}^{j}} \bigl( U_{tt_{l + 1}}^{j} - U_{tt_{l - 1}}^{j} \bigr) + \bigl( U_{tt_{l + 1}}^{j} + U_{tt_{l - 1}}^{j} \bigr) \biggr] \\ &{}- \frac{h^{2}}{3} \biggl[ \biggl( 1 - \frac{h}{2} \frac{A_{x_{l}}^{j}}{A_{l}^{j}} \biggr)F_{l + \frac{1}{2}}^{j} + \biggl( 1 + \frac{h}{2}\frac{A_{x_{l}}^{j}}{A_{l}^{j}} \biggr)F_{l - \frac{1}{2}}^{j} + F_{l}^{j} \biggr] \\ &{}+ \frac{h^{4}}{12A_{l}^{j}} \biggl[ \biggl( A_{xx_{l}}^{j} - 2 \frac{{A_{x_{l}}^{j}}^{2}}{A_{l}^{j}} \biggr) \bigl( U_{tt_{l}}^{j} - A_{l}^{j}U_{xx_{l}}^{j} \bigr) \biggr] + O \bigl(h^{6}\bigr). \end{aligned}$$
(3.10)

Using approximation (3.9e) and re-arranging the terms in (3.10), we obtain a modified version of the consistency condition

$$\begin{aligned}& \biggl[ A_{l}^{j} + \frac{h^{2}}{12} \biggl( A_{xx_{l}}^{j} - 2\frac{A_{x_{l}}^{j}}{A_{l}^{j}}A_{x_{l}}^{j} \biggr) \biggr]\bigl(U_{l + 1}^{j} - 2U_{l}^{j} + U_{l - 1}^{j}\bigr) \\& \quad = \frac{h^{2}}{12} \biggl[ \biggl( 1 - h\frac{A_{x_{l}}^{j}}{A_{l}^{j}} \biggr)U_{tt_{l + 1}}^{j} + \biggl( 1 + h\frac{A_{x_{l}}^{j}}{A_{l}^{j}} \biggr)U_{tt_{l - 1}}^{j} + 10U_{tt_{l}}^{j} \biggr] \\& \qquad {}- \frac{h^{2}}{3} \biggl[ \biggl( 1 - \frac{h}{2} \frac{A_{x_{l}}^{j}}{A_{l}^{j}} \biggr)F_{l + \frac{1}{2}}^{j} + \biggl( 1 + \frac{h}{2}\frac{A_{x_{l}}^{j}}{A_{l}^{j}} \biggr)F_{l - \frac{1}{2}}^{j} + F_{l}^{j} \biggr] + O\bigl(h^{6}\bigr). \end{aligned}$$
(3.11)

Since \(F_{l}^{j}\) contains the term \(u_{tt}\) and first derivative terms, then from (3.11) the spline in compression method for hyperbolic equation (3.1) can be written as

$$\begin{aligned}& \biggl[ A_{l}^{j} + \frac{h^{2}}{12} \biggl( A_{xx_{l}}^{j} - 2\frac{A_{x_{l}}^{j}}{A_{l}^{j}}A_{x_{l}}^{j} \biggr) \biggr]\bigl(U_{l + 1}^{j} - 2U_{l}^{j} + U_{l - 1}^{j}\bigr) \\& \quad = \frac{h^{2}}{12} \biggl[ \biggl(1 - h\frac{A_{x_{l}}^{j}}{A_{l}^{j}}\biggr) \overline{U}_{tt_{l + 1}}^{j} + \biggl(1 + h\frac{A_{x_{l}}^{j}}{A_{l}^{j}}\biggr) \overline{U}_{tt_{l - 1}}^{j} + 10\overline{U}_{tt_{l}}^{j} \biggr] \\& \qquad {}- \frac{h^{2}}{3} \biggl[ \biggl( 1 - \frac{h}{2} \frac{A_{x_{l}}^{j}}{A_{l}^{j}} \biggr)\hat{F}_{l + \frac{1}{2}}^{j} + \biggl( 1 + \frac{h}{2}\frac{A_{x_{l}}^{j}}{A_{l}^{j}} \biggr)\hat{F}_{l - \frac{1}{2}}^{j} + \hat{F}_{l}^{j} \biggr] + \hat{T}_{l}^{j}, \end{aligned}$$
(3.12)

where \(\hat{T}_{l}^{j}= O(k^{2}h^{2} + k^{2}h^{4} + h^{6})\) and we use the following approximations:

$$\begin{aligned}& \overline{U}_{l \pm1/2}^{j} = \frac{U_{l \pm1}^{j} + U_{l}^{j}}{2}, \end{aligned}$$
(3.13a)
$$\begin{aligned}& \overline{U}_{t_{l}}^{j} = \frac{U_{l}^{j + 1} - U_{l}^{j - 1}}{2k}, \end{aligned}$$
(3.13b)
$$\begin{aligned}& \overline{U}_{t_{l \pm1}}^{j} = \frac{U_{l \pm1}^{j + 1} - U_{l \pm1}^{j - 1}}{2k}, \end{aligned}$$
(3.13c)
$$\begin{aligned}& \overline{U}_{t_{l \pm1/2}}^{j} = \frac{\overline{U}_{t_{l \pm1}}^{j} + \overline{U}_{t_{l}}^{j}}{2}, \end{aligned}$$
(3.13d)
$$\begin{aligned}& \overline{U}_{tt_{l}}^{j} = \frac{U_{l}^{j + 1} - 2U_{l}^{j} + U_{l}^{j - 1}}{k^{2}}, \end{aligned}$$
(3.13e)
$$\begin{aligned}& \overline{U}_{tt_{l \pm1}}^{j} = \frac{U_{l \pm1}^{j + 1} - 2U_{l \pm 1}^{j} + U_{l \pm1}^{j - 1}}{k^{2}}, \end{aligned}$$
(3.13f)
$$\begin{aligned}& \overline{U}_{tt_{l \pm1/2}}^{j} = \frac{\overline{U}_{tt_{l \pm 1}}^{j} + \overline{U}_{tt_{l}}^{j}}{2}, \end{aligned}$$
(3.13g)
$$\begin{aligned}& \overline{U}_{x_{l}}^{j} = \frac{U_{l + 1}^{j} - U_{l - 1}^{j}}{2h}, \end{aligned}$$
(3.13h)
$$\begin{aligned}& \overline{U}_{x_{l \pm1/2}}^{j} = \frac{\overline{U}_{x_{l \pm1}}^{j} + \overline{U}_{x_{l}}^{j}}{2}, \end{aligned}$$
(3.13i)
$$\begin{aligned}& \overline{U}_{xx_{l}}^{j} = \frac{U_{l + 1}^{j} - 2U_{l}^{j} + U_{l - 1}^{j}}{h^{2}}. \end{aligned}$$
(3.13j)

Simplifying (3.13a)-(3.13j), we obtain

$$\begin{aligned}& \overline{U}_{l \pm1/2}^{j} = U_{l \pm1/2}^{j} + \frac{h^{2}}{8}U_{xx_{l}}^{j} \pm O\bigl(h^{3} \bigr), \end{aligned}$$
(3.14a)
$$\begin{aligned}& \overline{U}_{t_{l}}^{j} = U_{t_{l}}^{j} + O \bigl(k^{2}\bigr), \end{aligned}$$
(3.14b)
$$\begin{aligned}& \overline{U}_{t_{l \pm1}}^{j} = U_{t_{l \pm1}}^{j} + O \bigl(k^{2}\bigr), \end{aligned}$$
(3.14c)
$$\begin{aligned}& \overline{U}_{t_{l \pm1/2}}^{j} = U_{t_{l \pm1/2}}^{j} + \frac{h^{2}}{8}U_{xxt_{l}}^{j} + O\bigl(k^{2} \pm h^{3}\bigr), \end{aligned}$$
(3.14d)
$$\begin{aligned}& \overline{U}_{tt_{l}}^{j} = U_{tt_{l}}^{j} + O \bigl(k^{2}\bigr), \end{aligned}$$
(3.14e)
$$\begin{aligned}& \overline{U}_{tt_{l \pm1}}^{j} = U_{tt_{l \pm1}}^{j} + O \bigl(k^{2} + k^{2}h^{2} + h^{4} \bigr), \end{aligned}$$
(3.14f)
$$\begin{aligned}& \overline{U}_{tt_{l \pm1/2}}^{j} = U_{tt_{l \pm1/2}}^{j} + \frac{h^{2}}{8}U_{xxtt_{l}}^{j} + O\bigl(k^{2} \pm h^{3}\bigr) \end{aligned}$$
(3.14g)
$$\begin{aligned}& \overline{U}_{x_{l}}^{j} = U_{x_{l}}^{j} + \frac {h^{2}}{6}U_{xxx_{l}}^{j} + O\bigl(h^{4} \bigr), \end{aligned}$$
(3.14h)
$$\begin{aligned}& \overline{U}_{x_{l \pm1/2}}^{j} = U_{x_{l \pm1/2}}^{j} + \frac{h^{2}}{24}U_{xxx_{l}}^{j} \pm O\bigl(h^{3} \bigr), \end{aligned}$$
(3.14i)
$$\begin{aligned}& \overline{U}_{xx_{l}}^{j} = U_{xx_{l}}^{j} + \frac{h^{2}}{12}U_{xxxx_{l}}^{j} + O\bigl(h^{4}\bigr). \end{aligned}$$
(3.14j)

We define the following approximations:

$$\begin{aligned}& \overline{F}_{l}^{j} = f\bigl(x_{l},t_{j},U_{l}^{j}, \overline{U}_{x_{l}}^{j},\overline {U}_{t_{l}}^{j} \bigr), \end{aligned}$$
(3.15a)
$$\begin{aligned}& \overline{F}_{l \pm1/2}^{j} = f\bigl(x_{l \pm1/2},t_{j}, \overline{U}_{l \pm 1/2}^{j},\overline{U}_{x_{l \pm1/2}}^{j}, \overline{U}_{t_{l \pm 1/2}}^{j}\bigr). \end{aligned}$$
(3.15b)

Then, using the approximations (3.14b), (3.14h) in (3.15a) and (3.14a), (3.14d), (3.14i) in (3.15b), respectively, we get

$$\begin{aligned}& \overline{F}_{l}^{j} = F_{l}^{j} + O \bigl(h^{2} + k^{2}\bigr), \end{aligned}$$
(3.16a)
$$\begin{aligned}& \overline{F}_{l \pm1/2}^{j} = F_{l \pm1/2}^{j} + O \bigl(h^{2} + k^{2}\bigr). \end{aligned}$$
(3.16b)

Let

$$\begin{aligned}& \overline{M}_{l}^{j} = \frac{1}{A_{l}^{j}}\bigl( \overline{U}_{tt_{l}}^{j} - \overline{F}_{l}^{j} \bigr), \end{aligned}$$
(3.17a)
$$\begin{aligned}& \overline{M}_{l \pm1/2}^{j} = \frac{1}{A_{l \pm 1/2}^{j}}\bigl( \overline{U}_{tt_{l \pm1/2}}^{j} - \overline{F}_{l \pm 1/2}^{j} \bigr). \end{aligned}$$
(3.17b)

Then, using the approximations (3.14e), (3.16a) in (3.17a), and (3.14g), (3.16b) in (3.17b), respectively, we get

$$\begin{aligned}& \overline{M}_{l}^{j} = M_{l}^{j} + O \bigl(h^{2} + k^{2}\bigr), \end{aligned}$$
(3.18a)
$$\begin{aligned}& \overline{M}_{l \pm1/2}^{j} = M_{l \pm1/2}^{j} + O \bigl(h^{2} + k^{2}\bigr). \end{aligned}$$
(3.18b)

Next we define

$$\begin{aligned}& \hat{U}_{x_{l + 1/2}}^{j} = \frac{U_{l + 1}^{j} - U_{l}^{j}}{h} + \frac{h(\alpha\overline{M}_{l}^{j} - 2\beta\overline{M}_{l + 1/2}^{j})}{4}, \end{aligned}$$
(3.19a)
$$\begin{aligned}& \hat{U}_{x_{l - 1/2}}^{j} = \frac{U_{l}^{j} - U_{l - 1}^{j}}{h} + \frac{h(2\beta\overline{M}_{l - 1/2}^{j} - \alpha \overline{M}_{l}^{j})}{4}. \end{aligned}$$
(3.19b)

Then, using the approximations (3.18a), (3.18b) in (3.19a) and (3.19b), we get

$$\begin{aligned}& \hat{U}_{x_{l + 1/2}}^{j} = U_{x_{l + 1/2}}^{j} + O \bigl(k^{2} + h^{3}\bigr), \end{aligned}$$
(3.20a)
$$\begin{aligned}& \hat{U}_{x_{l - 1/2}}^{j} = U_{x_{l - 1/2}}^{j} + O \bigl(k^{2} + h^{3}\bigr). \end{aligned}$$
(3.20b)

We further define

$$ \hat{F}_{l \pm\frac{1}{2}}^{j} = f\bigl(x_{l \pm \frac{1}{2}},t_{j}, \overline{U}_{l \pm\frac{1}{2}}^{j},\hat{U}_{x_{l \pm \frac{1}{2}}}^{j}, \overline{U}_{t_{l \pm\frac{1}{2}}}^{j}\bigr). $$
(3.21)

Then, using the approximations (3.14a), (3.14d), (3.20a), (3.20b) in (3.21) and simplifying, we get

$$ \hat{F}_{l \pm1/2}^{j} = F_{l \pm1/2}^{j} + \frac{h^{2}}{8}\bigl(U_{xx_{l}}^{j}f_{u_{l}}^{j} + U_{xxt_{l}}^{j}f_{u_{t_{l}}}^{j}\bigr) + O \bigl(k^{2} \pm h^{3}\bigr). $$
(3.22)

Now we define

$$\begin{aligned}& \hat{U}_{l}^{j} = U_{l}^{j} + ah^{2}\bar{U}_{xx_{l}}^{j}, \end{aligned}$$
(3.23a)
$$\begin{aligned}& \hat{U}_{t_{l}}^{j} = \overline{U}_{t_{l}}^{j} + c\bigl(\bar{U}_{t_{l + 1}}^{j} - 2\overline{U}_{t_{l}}^{j} + \overline{U}_{t_{l - 1}}^{j}\bigr), \end{aligned}$$
(3.23b)

where ‘a’ and ‘c’ are parameters to be determined. Then, using the approximations (3.14j) in (3.23a) and (3.14b), (3.14c) in (3.23b), respectively, we get

$$\begin{aligned}& \hat{U}_{l}^{j} = U_{l}^{j} + ah^{2}U_{xx_{l}}^{j} + O\bigl(h^{4}\bigr), \end{aligned}$$
(3.24a)
$$\begin{aligned}& \hat{U}_{t_{l}}^{j} = U_{t_{l}}^{j} + ch^{2}U_{xxt_{l}}^{j} + O\bigl(k^{2} + h^{4}\bigr). \end{aligned}$$
(3.24b)

Further, let

$$ \hat{U}_{x_{l}}^{j} = \overline{U}_{x_{j}}^{j} + \alpha bh\bigl(\overline{M}_{l + 1/2}^{j} - \overline{M}_{l - 1/2}^{j}\bigr), $$
(3.25)

where \(\alpha= \frac{1}{3} + O(\theta^{2})\), and ‘b’ is a parameter to be determined.

Then, using the approximations (3.14h), (3.18b) in (3.25), we get

$$ \hat{U}_{x_{l}}^{j} = U_{x_{l}}^{j} + \frac{h^{2}}{6}(1 + 6\alpha b)U_{xxx_{l}}^{j} + O \bigl(k^{2} + h^{4}\bigr). $$
(3.26)

Thus,

$$ \hat{U}_{x_{l}}^{j} = U_{x_{l}}^{j} + O \bigl(k^{2} + h^{4}\bigr) $$
(3.27)

if \(b = \frac{ - 1}{2}\).

Let

$$ \hat{F}_{l}^{j} = F\bigl(x_{l},t_{j}, \hat{U}_{l}^{j},\hat{U}_{x_{l}}^{j}, \hat{U}_{t_{l}}^{j}\bigr). $$
(3.28)

Then, using the approximations (3.24a), (3.24b), (3.27) in (3.28), we get

$$ \hat{F}_{l}^{j} = F_{l}^{j} + h^{2}\bigl(aU_{xx_{l}}^{j}f_{ul}^{j} + cU_{xxt_{l}}^{j}f_{u_{t_{l}}}^{j}\bigr) + O \bigl(h^{4} + k^{2}\bigr). $$
(3.29)

Using the approximations (3.14e), (3.14f), (3.22), (3.29) in (3.12), we obtain

$$\begin{aligned}& \biggl[ A_{l}^{j} + \frac{h^{2}}{12} \biggl( A_{xx_{l}}^{j} - 2\frac{A_{x_{l}}^{j}}{A_{l}^{j}}A_{x_{l}}^{j} \biggr) \biggr]\bigl(U_{l + 1}^{j} - 2U_{l}^{j} + U_{l - 1}^{j}\bigr) \\& \quad = \frac{h^{2}}{12}\biggl[ \biggl(1 - h\frac{A_{x_{l}}^{j}}{A_{l}^{j}} \biggr)U_{tt_{l + 1}}^{j} + 10U_{tt_{l}}^{j} + \biggl(1 + h\frac{A_{x_{l}}^{j}}{A_{l}^{j}}\biggr)U_{tt_{l - 1}}^{j} \biggr] \\& \qquad {}- \frac{h^{2}}{3}\biggl[ \biggl(1 - \frac{h}{2}\frac{A_{x_{l}}^{j}}{A_{l}^{j}}\biggr) \biggl\{ F_{l + 1/2}^{j} + \frac{h^{2}}{8}\bigl(U_{xx_{l}}^{j}f_{u_{l}}^{j} + U_{xxt_{l}}^{j}f_{u_{t_{l}}}^{j}\bigr)\biggr\} \\& \qquad {}+ \bigl\{ F_{l}^{j} + h^{2} \bigl(aU_{xx_{l}}^{j}f_{u_{l}}^{j} + cU_{xxt_{l}}^{j}f_{u_{t_{l}}}^{j}\bigr)\bigr\} \\& \qquad {} + \biggl(1 + \frac{h}{2}\frac{A_{x_{l}}^{j}}{A_{l}^{j}}\biggr)\biggl\{ F_{l - 1/2}^{j} + \frac{h^{2}}{8}\bigl(U_{xx_{l}}^{j}f_{u_{l}}^{j} + U_{xxt_{l}}^{j}f_{u_{t_{l}}}^{j}\bigr)\biggr\} \biggr] + \hat{T}_{l}^{j}. \end{aligned}$$
(3.30)

Comparing (3.11) and (3.30), we obtain the local truncation error

$$ \hat{T}_{l}^{j} = \frac{h^{4}}{12}\bigl[(1 + 4a)U_{xx_{l}}^{j}f_{u_{l}}^{j} + (1 + 4c)U_{xxt_{l}}^{j}f_{u_{t_{l}}}^{j}\bigr] + O \bigl(k^{2}h^{2} + k^{2}h^{4} + h^{6}\bigr). $$
(3.31)

Now the local truncation error of the proposed method to be \(O(k^{2}h^{2} + k^{2}h^{4} + h^{6})\), the coefficients of \(h^{4}\) in (3.31) must vanish, that is,

$$ 1 + 4a = 0, \qquad 1 + 4c = 0. $$
(3.32)

On solving (3.32), we get \(a = c = -1/4\).

Now, we consider the numerical method of \(O(k^{2} + k^{2}h^{2} + h^{4})\) for the solution of quasi-linear hyperbolic equation (1.1). Here, we use the techniques discussed in [37–45]. Scheme (3.12) has to be modified suitably when the coefficient \(A = A(x, t, u)\). In order to understand the concept in devising the method for the quasi-linear case, we consider the following differential equation:

$$ u'' = A(x),\quad 0 < x < 1. $$
(3.33)

A fourth-order method for differential equation (3.33) is given by

$$ U_{l + 1} - 2U_{l} + U_{l - 1} = \frac{h^{2}}{12} \bigl[12A_{l} + h^{2}A_{xx_{l}}\bigr] + O \bigl(h^{6}\bigr), $$
(3.34)

where

$$U_{l} = U(x_{l}),\qquad A_{l} = A(x_{l}),\qquad A_{xx_{l}} = A_{xx}(x_{l}). $$

Whenever differential equation (3.33) is of the form \(u'' = A(x,u)\), the evaluation of \(A_{xx}\) is difficult and formula (3.34) needs to modified suitably. Substituting \(h^{2}A_{xx_{l}} = A_{l + 1} - 2A_{l} + A_{l - 1} + O(h^{4})\) in (3.34), we obtain the modified version of (3.34) due to Numerov as follows:

$$ U_{l + 1} - 2U_{l} + U_{l - 1} = \frac{h^{2}}{12}[A_{l + 1} + A_{l - 1} + 10A_{l}] + O\bigl(h^{6} \bigr), $$
(3.35)

where \(A_{l} = A(x_{l},U_{l})\). Note that (3.35) is consistent with the differential equation \(u'' = A(x,u)\).

Now, we use the above concept to derive the numerical method for quasi-linear equation (1.1). Since the coefficient A is not only the function of x and t, but also of the dependent variable u, difference scheme (3.12) cannot be applied directly as the first and second derivatives of u are unknown at the internal grid points. Thus, further discretizations of \(u_{x}\) and \(u_{{xx}}\) are required in method (3.12) without affecting its order. For this purpose, we need the following estimates:

$$\begin{aligned}& A_{x_{l}}^{j} = \frac{\overline{A}_{l + 1/2}^{j} - \overline{A}_{l - 1/2}^{j}}{h} + O\bigl(h^{2} \bigr), \end{aligned}$$
(3.36a)
$$\begin{aligned}& A_{xx_{l}}^{j} = \frac{4(\overline{A}_{l + 1/2}^{j} - 2A_{l}^{j} + \overline{A}_{l - 1/2}^{j})}{h^{2}} + O\bigl(h^{2} \bigr), \end{aligned}$$
(3.36b)

where \(A_{l}^{j} = A(x_{l}, t_{j}, U_{l}^{j})\), \(\overline{ A}_{l \pm1/2}^{j} = A(x_{l \pm1/2}, t_{j}, \overline{U}_{l \pm1/2}^{j})\).

Substituting the above approximations (3.36a) and (3.36b) into (3.12), the order of method (3.12) is retained, and hence we obtain the required numerical method of \(O(k^{2} + k^{2}h^{2} + h^{4})\) based on spline in compression approximations (see [37–45]) for differential equation (1.1).

Note that the initial and Dirichlet boundary conditions are given by (1.2) and (1.3), respectively. Incorporating the initial and boundary conditions, we can write the spline in compression method in a tridiagonal form. If differential equation (1.1) is linear, we use the Gauss elimination (tridiagonal solver) method; in the nonlinear or quasilinear case, we can use the Newton-Raphson iterative method (see [46–48]).

4 Method extended to a system of quasi-linear hyperbolic equations

Next, we consider the system of one-space dimensional hyperbolic equations of the form:

$$\begin{aligned} \frac{\partial^{2}u^{(i)}}{\partial t^{2}} =& A^{(i)}(x,t)\frac{\partial^{2}u^{(i)}}{\partial x^{2}} \\ &{}+ f^{(i)} \bigl(x,t,u^{(1)},u^{(2)},\ldots ,u^{(M)},u_{x}^{(1)},u_{x}^{(2)}, \ldots ,u_{x}^{(M)},u_{t}^{(1)},u_{t}^{(2)}, \ldots,u_{t}^{(M)}\bigr), \\ & 0 < x < 1, t > 0, i = 1(1)M, \end{aligned}$$
(4.1)

subject to the initial and boundary conditions

$$\begin{aligned}& u^{(i)}(x,0) = u_{0}^{(i)}(x),\qquad u_{t}^{(i)}(x,0) = u_{1}^{(i)}(x),\quad 0 \le x \le1, \end{aligned}$$
(4.2)
$$\begin{aligned}& u^{(i)}(0,t) = g_{0}^{(i)}(t),\qquad u^{(i)}(1,t) = g_{1}^{(i)}(t),\quad t \ge0, i = 1(1)M, \end{aligned}$$
(4.3)

which is defined in a semi-infinite region \(\Omega= \{ (x,t)|0 < x < 1, t > 0\}\).

For \(i = 1(1)M\), we need the following approximations:

$$\begin{aligned}& \overline{U}_{l \pm\frac{1}{2}}^{(i)j} = \frac{U_{l \pm1}^{(i)j} + U_{l}^{(i)j}}{2}, \end{aligned}$$
(4.4)
$$\begin{aligned}& \overline{U}_{t_{l}}^{(i)j} = \frac{U_{l}^{(i)j + 1} - U_{l}^{(i)j - 1}}{2k}, \end{aligned}$$
(4.5)
$$\begin{aligned}& \overline{U}_{t_{l \pm1}}^{(i)j} = \frac{U_{l \pm1}^{(i)j + 1} - U_{l \pm 1}^{(i)j - 1}}{2k}, \end{aligned}$$
(4.6)
$$\begin{aligned}& \overline{U}_{t_{l \pm\frac{1}{2}}}^{(i)j} = \frac{\overline{U}_{t_{l \pm 1}}^{(i)j} + \overline{U}_{t_{l}}^{(i)j}}{2}, \end{aligned}$$
(4.7)
$$\begin{aligned}& \overline{U}_{tt_{l}}^{(i)j} = \frac{U_{l}^{(i)j + 1} - 2U_{l}^{(i)j} + U_{l}^{(i)j - 1}}{k^{2}}, \end{aligned}$$
(4.8)
$$\begin{aligned}& \overline{U}_{tt_{l \pm1}}^{(i)j} = \frac{U_{l \pm1}^{(i)j + 1} - 2U_{l \pm 1}^{(i)j} + U_{l \pm1}^{(i)j - 1}}{k^{2}}, \end{aligned}$$
(4.9)
$$\begin{aligned}& \overline{U}_{tt_{l \pm\frac{1}{2}}}^{(i)j} = \frac{\overline{U}_{tt_{l \pm 1}}^{(i)j} + \overline{U}_{tt_{l}}^{(i)j}}{2}, \end{aligned}$$
(4.10)
$$\begin{aligned}& \overline{U}_{x_{l}}^{(i)j} = \frac{U_{l + 1}^{(i)j} - U_{l - 1}^{(i)j}}{2h}, \end{aligned}$$
(4.11)
$$\begin{aligned}& \overline{U}_{x_{l \pm\frac{1}{2}}}^{(i)j} = \frac{ \pm(U_{l \pm 1}^{(i)j} - U_{l}^{(i)j})}{h}, \end{aligned}$$
(4.12)
$$\begin{aligned}& \overline{U}_{xx_{l}}^{(i)j} = \frac{U_{l + 1}^{(i)j} - 2U_{l}^{(i)j} + U_{l - 1}^{(i)j}}{h^{2}}. \end{aligned}$$
(4.13)

We define

$$\begin{aligned}& \overline{F}_{l}^{(i)j} = f^{(i)} \bigl(x_{l},t_{j},\overline{U}_{l}^{(1)j}, \overline {U}_{l}^{(2)j},\ldots,\overline{U}_{l}^{(M)j}, \overline{U}_{x_{l}}^{(1)j},\overline{U}_{x_{l}}^{(2)j}, \ldots, \\& \hphantom{\overline{F}_{l}^{(i)j} ={}}{}\overline {U}_{x_{l}}^{(M)j},\overline{U}_{t_{l}}^{(1)j}, \overline{U}_{t_{l}}^{(2)j},\ldots ,\overline{U}_{t_{l}}^{(M)j} \bigr), \end{aligned}$$
(4.14)
$$\begin{aligned}& \overline{F}_{l \pm\frac{1}{2}}^{(i)j} = f^{(i)} \bigl(x_{l \pm \frac{1}{2}},t_{j},\overline{U}_{l \pm\frac{1}{2}}^{(1)j}, \overline{U}_{l \pm\frac{1}{2}}^{(2)j},\ldots,\overline{U}_{l \pm \frac{1}{2}}^{(M)j}, \overline{U}_{x_{l} \pm \frac{1}{2}}^{(1)j},\overline{U}_{x_{l} \pm \frac{1}{2}}^{(2)j}, \ldots, \\& \hphantom{\overline{F}_{l \pm\frac{1}{2}}^{(i)j} ={}}{}\overline{U}_{x_{l \pm \frac{1}{2}}}^{(M)j},\overline{U}_{t_{l \pm \frac{1}{2}}}^{(1)j}, \overline{U}_{t_{l \pm \frac{1}{2}}}^{(2)j},\ldots,\overline{U}_{t_{l \pm \frac{1}{2}}}^{(M)j} \bigr), \end{aligned}$$
(4.15)
$$\begin{aligned}& \overline{M}_{l}^{(i)j} = \frac{1}{A_{l}^{(i)j}}\bigl[ \overline{U}_{tt_{l}}^{(i)j} - \overline{F}_{l}^{(i)j} \bigr], \end{aligned}$$
(4.16)
$$\begin{aligned}& \overline{M}_{l \pm\frac{1}{2}}^{(i)j} = \frac{1}{A_{l \pm \frac{1}{2}}^{(i)j}} \bigl( \overline{U}_{tt_{l \pm\frac{1}{2}}}^{(i)} - \overline{F}_{l \pm1/2}^{(i)j} \bigr), \end{aligned}$$
(4.17)
$$\begin{aligned}& \hat{U}_{l}^{(i)j} = U_{l}^{(i)j} - \frac{1}{4}h^{2}\overline{U}_{xx_{l}}^{(i)j}, \end{aligned}$$
(4.18)
$$\begin{aligned}& \hat{U}_{x_{l}}^{(i)j} = \overline{U}_{x_{l}}^{(i)j} - \frac{\alpha h}{2}\bigl(\overline{M}_{l + \frac{1}{2}}^{(i)j} - \overline{M}_{l - \frac{1}{2}}^{(i)j}\bigr), \end{aligned}$$
(4.19)
$$\begin{aligned}& \hat{U}_{t_{l}}^{(i)j} = \overline{U}_{t_{l}}^{(i)j} - \frac{1}{4}\bigl(\overline{U}_{t_{l + 1}}^{(i)j} - 2 \overline{U}_{t_{l}}^{(i)j} + \overline{U}_{t_{l - 1}}^{(i)j} \bigr), \end{aligned}$$
(4.20)
$$\begin{aligned}& \hat{U}_{x_{l + \frac{1}{2}}}^{(i)j} = \frac{U_{l + 1}^{(i)j} - U_{l}^{(i)j}}{h} + \frac{h}{4} \bigl( \alpha\overline{M}_{l}^{(i)j} - 2\beta \overline{M}_{l + \frac{1}{2}}^{(i)j} \bigr), \end{aligned}$$
(4.21)
$$\begin{aligned}& \hat{U}_{x_{l - \frac{1}{2}}}^{(i)j} = \frac{U_{l}^{(i)j} - U_{l - 1}^{(i)j}}{h} + \frac{h}{4} \bigl( 2\beta\overline{M}_{l - \frac{1}{2}}^{(i)j} - \alpha \overline{M}_{l}^{(i)j} \bigr), \end{aligned}$$
(4.22)

where the values of α and β are defined in Section 2.

Further, we define

$$\begin{aligned}& \hat{F}_{l \pm\frac{1}{2}}^{(i)j} = f^{(i)}\bigl(x_{l \pm \frac{1}{2}},t_{j}, \overline{U}_{l \pm\frac{1}{2}}^{(1)j},\overline{U}_{l \pm\frac{1}{2}}^{(2)j}, \ldots,\overline{U}_{l \pm \frac{1}{2}}^{(M)j},\hat{U}_{x_{l} \pm\frac{1}{2}}^{(1)j}, \hat{U}_{x_{l} \pm \frac{1}{2}}^{(2)j},\ldots, \\& \hphantom{\hat{F}_{l \pm\frac{1}{2}}^{(i)j} ={}}{}\hat{U}_{x_{l} \pm \frac{1}{2}}^{(M)j}, \overline{U}_{t_{l \pm \frac{1}{2}}}^{(1)j},\overline{U}_{t_{l \pm \frac{1}{2}}}^{(2)j}, \ldots,\overline{U}_{t_{l \pm \frac{1}{2}}}^{(M)j}\bigr), \end{aligned}$$
(4.23)
$$\begin{aligned}& \hat{F}_{l}^{(i)j} = f^{(i)}\bigl(x_{l},t_{j}, \hat{U}_{l}^{(1)j},\hat{U}_{l}^{(2)j}, \ldots,\hat {U}_{l}^{(M)j},\hat{U}_{x_{l}}^{(1)j}, \hat{U}_{x_{l}}^{(2)j},\ldots, \\& \hphantom{\hat{F}_{l}^{(i)j} ={}}{}\hat {U}_{x_{l}}^{(M)j}, \hat{U}_{t_{l}}^{(1)j},\hat{U}_{t_{l}}^{(2)j}, \ldots,\hat {U}_{t_{l}}^{(M)j}\bigr). \end{aligned}$$
(4.24)

Then the new method based on spline in compression approximations for the system of equations (4.1) may be written as

$$\begin{aligned}& \biggl[ A_{l}^{(i)j} + \frac{h^{2}}{12} \biggl( A_{xx_{l}}^{(i)j} - 2\frac{A_{x_{l}}^{(i)j}}{A_{l}^{(i)j}}A_{x_{l}}^{(i)j} \biggr) \biggr]\bigl(U_{l + 1}^{(i)j} - 2U_{l}^{(i)j} + U_{l - 1}^{(i)j}\bigr) \\& \quad = \frac{h^{2}}{12} \biggl[ \biggl( 1 - \frac{hA_{x_{l}}^{(i)j}}{A_{l}^{(i)j}} \biggr) \overline{U}_{tt_{l + 1}}^{(i)j} + \biggl( 1 + \frac{hA_{x_{l}}^{(i)j}}{A_{l}^{(i)j}} \biggr)\overline{U}_{tt_{l - 1}}^{(i)j} + 10\overline{U}_{tt_{l}}^{(i)j} \biggr] \\& \qquad {}- \frac{h^{2}}{3} \biggl[ \biggl( 1 - \frac{hA_{x_{l}}^{(i)j}}{2A_{l}^{(i)j}} \biggr) \hat{F}_{l + \frac{1}{2}}^{(i)j} + \biggl( 1 + \frac{hA_{x_{l}}^{(i)j}}{2A_{l}^{(i)j}} \biggr) \hat{F}_{l - \frac{1}{2}}^{(i)j} + \hat{F}_{l}^{(i)j} \biggr]+ \hat{T}_{l}^{(i)j}, \end{aligned}$$
(4.25)

where \(\hat{T}_{l}^{(i)j} = O(k^{2}h^{2} + k^{2}h^{4} + h^{6})\). Using the technique discussed in the previous section, we can obtain the spline in compression method of \(O(k^{2} +k^{2} h^{2} +h^{4} )\) for the solution of the system of quasi-linear hyperbolic equations.

5 Application to a telegraphic equation and stability analysis

In this section we first discuss the background of ‘telegraphic equation’, application of the proposed method to the telegraphic equation with forcing function say f and stability analysis.

It would be difficult to imagine a world without communication systems. A plethora of guided fixed line telephones as well as a multitude of unguided systems to serve cellular phones are evident in our surrounding world. In order to optimize guided communication systems, it is necessary to determine or project power and signal losses in the system since all systems have such losses. To determine these losses and eventually ensure a maximum output, it is necessary to formulate some kind of equation with which to calculate these losses. We give mathematical derivation for the telegraphic equation in terms of voltage and current for a section of a transmission line. The telegraphic equations are a pair of linear differential equations which describe the voltage and current on an electrical transmission line with distance and time. The equations come from Oliver Heaviside who developed the transmission line model in the 1880s. The theory applies to high-frequency transmission lines (such as telegraph wires and radio frequency conductors), but it is also important for designing high-voltage energy transmission lines. In order to be able to model the telegraphic equations, it is necessary to understand the basic principles of electricity. Ohm’s law describes the relationship between voltage, current and resistance in an electrical circuit. Ohm’s law states that if one volt is applied to one ohm resistance, the current that flows will be one ampere.

It states that:

$$V = I\cdot R, $$

where:

  • \(V= \mbox{voltage measured in volts}\),

  • \(I= \mbox{current measured in ampere}\),

  • \(R = \mbox{resistance measured in ohm}\).

Kirchhoff’s first law states that the current flowing into a junction, in a circuit or node, must be equal to the current flowing out of the junction or node. The current flow is described by

$$I_{\mathrm{total}} = I_{1} + I_{2} + I_{3}. $$

Kirchhoff’s second law states that, for any closed loop path around a circuit, the sum of voltage gains and voltage drops equals zero. This implicates that no energy can be lost or gained by the circuit, with result that the total voltage change must be zero. The voltage in a closed circuit is described by

$$V_{\mathrm{in}} = V_{1} + V_{2} + V_{3}. $$

The challenge is to model an infinite small piece of telegraph wire as an electric circuit since it has a load and a source as indicated by Ohm’s and Kirchhoff’s laws. The characteristics of a small piece of telegraph wire and that of a long transmission line are the same, thus it is sufficient to model an infinite small piece of telegraph wire to represent a transmission line over distance.

Assume that the cable is imperfectly insulated so that there are both capacitance and current leakage to ground as shown in Figure 1. No two conductors can be perfectly insulated due to the current that flows through them as well as the potential difference in the conductors.

Figure 1
figure 1

Telegraph wire with leakage.

Full size image

Let

  • \(x= \mbox{distance from sending end of the cable}\),

  • \(e(x, t)= \mbox{potential at any point on the cable at any time}\),

  • \(i(x, t)= \mbox{current at any point on the cable at any time}\),

  • \(R= \mbox{resistance of the cable}\),

  • \(L= \mbox{inductance of the cable}\),

  • \(G= \mbox{conductance to ground}\),

  • \(C = \mbox{capacitance to ground}\).

Voltage drop across the resistor, according to Ohm’s law, is given by

$$ V = I\cdot R. $$
(5.1)

According to Ohm’s law, voltage drop across the capacitor, where a capacitor gives an integrator circuit, is given by

$$ V = \frac{1}{C} \int i\, dt, $$
(5.2)

and voltage drop across the inductor, where an inductor gives a differentiator circuit, is given by

$$ V = L\frac{di}{dt}. $$
(5.3)

The potential at Q is equal to the potential at P, minus the drop in potential along the element PQ. Therefore, if (5.1)-(5.3) are combined, it leads to the following equation:

$$e(x + dx, t) = e(x, t) - (R\, dx)i - L(dx)\frac{\partial i}{\partial t}. $$

Thus

$$ e(x + dx, t) - e(x, t) = - (R\, dx)i - L(dx)\frac{\partial i}{\partial t}. $$
(5.4)

Dividing the above equation by dx and letting \(dx \to0\), we get

$$ \frac{\partial e}{\partial x} = - Ri - L\frac{\partial i}{\partial t}. $$
(5.5)

Likewise, the current at Q is equal to the current at P minus the current loss through leakage to ground. Using the equation for current through the capacitor,

$$ i = C\frac{de}{dt}, $$
(5.6)

the equation for current now becomes

$$i(x + dx, t) = i(x, t) - (G\, dx)i - (C\, dx)\frac{\partial e}{\partial t}. $$

Thus

$$ i(x + dx, t) - i(x, t) = - (G\, dx)i - (C\, dx)\frac{\partial e}{\partial t}. $$
(5.7)

Dividing the above equation by dx and letting \(dx \to0\), we get

$$ \frac{\partial i}{\partial x} = - Gi - C\frac{\partial e}{\partial t}. $$
(5.8)

If (5.5) is now differentiated with respect to x and (5.8) with respect to t, the respective results are

$$ \frac{\partial^{2}e}{\partial x^{2}} = - R\frac{\partial i}{\partial x} - L\frac{\partial i^{2}}{\partial x\, \partial t} $$
(5.9)

and

$$ \frac{\partial^{2}i}{\partial t\, \partial x} = - G\frac{\partial e}{\partial t} - C\frac{\partial^{2}e}{\partial t^{2}}. $$
(5.10)

Using (5.10) in (5.9), we get

$$ \frac{\partial^{2}e}{\partial x^{2}} = - R\frac{\partial i}{\partial x} - L\biggl( - G\frac{\partial e}{\partial t} - C \frac{\partial^{2}e}{\partial t^{2}}\biggr). $$
(5.11)

Using (5.8) in (5.11), we get

$$ \frac{\partial^{2}e}{\partial x^{2}} = LC\frac{\partial^{2}e}{\partial t^{2}} + (RC + LG)\frac{\partial e}{\partial t} + (GR)e. $$
(5.12)

Similarly, we can obtain

$$ \frac{\partial^{2}i}{\partial x^{2}} = LC\frac{\partial^{2}i}{\partial t^{2}} + (RC + LG)\frac{\partial i}{\partial t} + (GR)i. $$
(5.13)

Two equations (5.12) and (5.13) are known as the telegraphic equations.

Now we apply the proposed method to the following telegraphic equation with the forcing functionfto study the stability of the proposed method

$$ \varphi_{tt} + (\alpha_{0} + \beta_{0}) \varphi_{t} + \alpha_{0}\beta_{0}\varphi= \varphi_{xx} + f(x, t),\quad 0 < x < 1, t > 0, $$
(5.14)

where \(\alpha_{0} > 0\), \(\beta_{0} \ge0\) are real parameters. For \(\beta_{0} = 0\), equation (5.14) represents a damped wave equation. The initial and boundary conditions of type (1.2) and (1.3) are prescribed.

We denote \(a_{0} = \frac{(\alpha_{0} + \beta_{0})^{2}k^{2}}{4}\), \(b_{0} = \alpha_{0}\beta_{0}k^{2}\), \(\lambda= \frac{k}{h}\) and \(f_{l}^{j} = f(x_{l}, t_{j})\).

Applying method (3.12) to differential equation (5.14) and neglecting local truncation error, we obtain a numerical approximation of \(O(k^{2} + h^{4})\) as

$$\begin{aligned}& \delta_{t}^{2}\varphi_{l}^{j} + \sqrt{a_{0}} (2\mu_{t}\delta_{t}) \varphi_{l}^{j} + \frac{\sqrt{a_{0}}}{ 12}\bigl(2 \delta_{x}^{2}\mu_{t}\delta_{t}\bigr) \varphi_{l}^{j} + \biggl(\frac {b_{0}}{12} - \lambda^{2}\biggr)\delta_{x}^{2} \varphi_{l}^{j} + b_{0}\varphi_{l}^{j} + \frac{\delta_{x}^{2}\delta_{t}^{2}}{12}\varphi_{l}^{j} \\& \quad = \frac{k^{2}}{3}\bigl[f_{l + 1/2}^{j} + f_{l}^{j} + f_{l - 1/2}^{j} \bigr], \end{aligned}$$
(5.15)

where

$$\begin{aligned}& \delta_{t}^{2}\varphi_{l}^{j} = \varphi_{l}^{j + 1} - 2\varphi_{l}^{j} + \varphi_{l}^{j - 1}, \qquad \delta_{x}^{2} \varphi_{l}^{j} = \varphi_{l + 1}^{j} - 2 \varphi_{l}^{j} + \varphi_{l - 1}^{j}, \\& 2\mu_{x}\delta_{x}\varphi _{l}^{j} = \varphi_{l + 1}^{j} - \varphi_{l - 1}^{j}, \qquad 2\mu_{t}\delta_{t}\varphi_{l}^{j} = \varphi_{l}^{j + 1} - \varphi _{l}^{j - 1}. \end{aligned}$$

The above scheme is conditionally stable (see [26, 27]).

In order to obtain an unconditionally stable scheme, we may rewrite the above scheme as

$$\begin{aligned}& \bigl(1 + \eta b_{0}^{2}\bigr)\delta_{t}^{2} \varphi_{l}^{j} + \sqrt{a_{0}} (2 \mu_{t}\delta_{t})\varphi_{l}^{j} + \frac{\sqrt{a_{0}}}{ 12}\bigl(2\delta_{x}^{2}\mu_{t} \delta_{t}\bigr)\varphi_{l}^{j} + \biggl( \frac {b_{0}}{12} - \lambda^{2}\biggr)\delta_{x}^{2} \varphi_{l}^{j} + b_{0}\varphi_{l}^{j} \\& \quad {}+ \frac{\delta_{x}^{2}\delta_{t}^{2}}{12}\varphi_{l}^{j} - \gamma \lambda^{2}\delta_{x}^{2}\delta_{t}^{2} \varphi_{l}^{j} = \frac{k^{2}}{3}\bigl[f_{l + 1/2}^{j} + f_{l}^{j} + f_{l - 1/2}^{j} \bigr], \end{aligned}$$
(5.16)

where ‘η’ and ‘γ’ are free parameters to be determined.

The additional terms are of high order and do not affect the accuracy of the scheme.

The exact solution \(\Theta_{l}^{j}\) satisfies

$$\begin{aligned}& \bigl(1 + \eta b_{0}^{2}\bigr)\delta_{t}^{2} \Theta_{l}^{j} + \sqrt{a_{0}} (2\mu_{t} \delta_{t})\Theta_{l}^{j} + \frac{\sqrt{a_{0}}}{ 12} \bigl(2\delta_{x}^{2}\mu_{t}\delta_{t} \bigr)\Theta_{l}^{j} + \biggl(\frac {b_{0}}{12} - \lambda^{2}\biggr)\delta_{x}^{2} \Theta_{l}^{j} + b_{0}\Theta_{l}^{j} \\& \quad {}+ \frac{\delta_{x}^{2}\delta_{t}^{2}}{12}\Theta_{l}^{j} - \gamma \lambda^{2}\delta_{x}^{2}\delta_{t}^{2} \Theta_{l}^{j} = \frac{k^{2}}{3}\bigl[f_{l + 1/2}^{j} + f_{l}^{j} + f_{l - 1/2}^{j}\bigr] + T_{l}^{j}, \end{aligned}$$
(5.17)

where \(T_{l}^{j} = O(k^{2}h^{2} + h^{6})\).

Let \(\varepsilon_{l}^{j} = \Theta_{l}^{j} - \varphi_{l}^{j}\) be the discretization error at the grid point \((x_{l}, t_{j})\). Then subtracting (5.16) from (5.17), we get the error equation

$$\begin{aligned}& \bigl(1 + \eta b_{0}^{2}\bigr)\delta_{t}^{2} \varepsilon_{l}^{j} + \sqrt{a_{0}} (2 \mu_{t}\delta_{t})\varepsilon_{l}^{j} + \frac{\sqrt{a_{0}}}{ 12}\bigl(2\delta_{x}^{2}\mu_{t} \delta_{t}\bigr)\varepsilon_{l}^{j} + \biggl( \frac{b_{0}}{12} - \lambda^{2}\biggr)\delta_{x}^{2} \varepsilon_{l}^{j} + b_{0}\varepsilon_{l}^{j} \\& \quad {}+ \frac{\delta_{x}^{2}\delta_{t}^{2}}{12}\varepsilon_{l}^{j} - \gamma \lambda^{2}\delta_{x}^{2}\delta_{t}^{2} \varepsilon_{l}^{j} = T_{l}^{j}. \end{aligned}$$
(5.18)

For stability, we put \(\varepsilon_{l}^{j} = \xi^{j}e^{i\psi l}\) in the homogeneous part of the error equation; we get the characteristic equation

$$ A\xi^{2} + B\xi+ C = 0, $$
(5.19)

where

$$\begin{aligned}& A = 1 + \eta b_{0}^{2} + \sqrt{a_{0}} - \frac{\sqrt{a_{0}}}{ 3}\sin^{2}\biggl(\frac{\psi}{2}\biggr) - \frac{1}{3}\sin^{2}\biggl(\frac{\psi}{2}\biggr) + 4\gamma \lambda^{2}\sin^{2}\biggl(\frac{\psi}{2} \biggr), \end{aligned}$$
(5.20a)
$$\begin{aligned}& B = - 2 - 2\eta b_{0}^{2} + 4\biggl(\lambda^{2} - \frac{b_{0}}{12}\biggr)\sin^{2}\biggl(\frac{\psi}{2}\biggr) + b_{0} + \frac{2}{3}\sin^{2}\biggl( \frac{\psi}{2}\biggr) \\& \hphantom{B ={}}{}- 8\gamma \lambda^{2}\sin^{2} \biggl(\frac{\psi}{2}\biggr), \end{aligned}$$
(5.20b)
$$\begin{aligned}& C = 1 + \eta b_{0}^{2} - \sqrt{a_{0}} + \frac{\sqrt{a_{0}}}{ 3}\sin^{2}\biggl(\frac{\psi}{2}\biggr) - \frac{1}{3}\sin^{2}\biggl(\frac{\psi}{2}\biggr) + 4\gamma \lambda^{2}\sin^{2}\biggl(\frac{\psi}{2}\biggr). \end{aligned}$$
(5.20c)

Using the transformation \(\xi= \frac{1 + z}{1 - z}\), the characteristic equation (5.19) reduces to

$$ (A - B + C)z^{2} + 2(A - C)z + (A + B + C) = 0. $$
(5.21)

According to the Routh-Hurwitz criterion, the necessary and sufficient conditions for \(|\xi| < 1\) are \(A + B + C > 0\), \(A - C > 0\), \(A - B + C > 0\).

Thus for stability we have the conditions

$$\begin{aligned}& A + B + C = b_{0}\cos^{2}\biggl(\frac{\psi}{2}\biggr) + 4\lambda^{2}\sin^{2}\biggl(\frac{\psi}{2}\biggr) + \frac{2b_{0}}{3}\sin^{2}\biggl(\frac{\psi}{2}\biggr) > 0, \\& A - C = 2\sqrt{a_{0}} \biggl[\cos^{2}\biggl( \frac{\psi}{2}\biggr) + \frac{2}{3}\sin^{2}\biggl( \frac{\psi}{2}\biggr)\biggr] > 0, \\& A - B + C = 4 + 4\eta b_{0}^{2} - b_{0} + \frac{b_{0}}{3}\sin^{2}\biggl(\frac{\psi}{2}\biggr) + 4 \biggl[(4\gamma- 1)\lambda^{2} - \frac{1}{3}\biggr] \sin^{2}\biggl(\frac{\psi}{2}\biggr) > 0. \end{aligned}$$

The first two conditions are satisfied for all choices of variable angle ψ. Multiplying the third condition by 16η, we get

$$\begin{aligned}& (64\eta- 1) + (8\eta b_{0} - 1)^{2} + \frac{16\eta b_{0}}{3} \sin^{2}\biggl(\frac{\psi}{2}\biggr) \\& \quad {}+ 64\eta\biggl[(4\gamma- 1) \lambda^{2} - \frac{1}{3}\biggr]\sin^{2}\biggl( \frac{\psi}{2}\biggr) > 0. \end{aligned}$$
(5.22)

Thus the scheme is stable if \(\eta\ge\frac{1}{64}\), \(\gamma\ge\frac{1 + 3\lambda^{2}}{12\lambda^{2}}\), \(\alpha_{0} > 0\), \(\beta_{0} \ge0\) for all ψ except \(\psi=0\) and 2π (when \(b_{0} = 0\)). We treat this case separately.

For \(\psi=0\) or 2π (when \(b_{0} = 0\)), we have the characteristic equation

$$ (1 + \sqrt{a_{0}} )\xi^{2} - 2\xi+ (1 - \sqrt{a_{0}} ) = 0, $$
(5.23)

whose roots are \(\xi_{1,2} = 1\), \(\frac{1 - \sqrt{a_{0}}}{1 + \sqrt{a_{0}}}\). In this case also \(|\xi| \le1\).

Hence, for \(\alpha_{0} > 0\), \(\beta_{0} \ge0\), \(\eta\ge\frac{1}{64}\), \(\gamma \ge \frac{1 + 3\lambda^{2}}{12\lambda^{2}}\), scheme (5.16) is stable for all choices of \(h > 0\) and \(k > 0\).

Now we consider the fourth-order hyperbolic equation

$$ \biggl( \frac{\partial^{2}}{\partial t^{2}} - \frac{\partial ^{2}}{\partial x^{2}} \biggr)^{2}u = f(x,t),\quad0 < x < 1, t > 0. $$
(5.24)

The initial values of u, \(u_{t}\), \(u_{tt}\), \(u_{{ttt}}\) at \(t=0\) are known and the boundary values of u, \(u_{{xx}}\) are known at \(x=0\) and \(x=1\).

Equation (5.24) in a coupled form can be written as

$$\begin{aligned}& \biggl( \frac{\partial^{2}}{\partial t^{2}} - \frac{\partial ^{2}}{\partial x^{2}} \biggr)u = v,\quad0 < x < 1, t > 0, \end{aligned}$$
(5.25a)
$$\begin{aligned}& \biggl( \frac{\partial^{2}}{\partial t^{2}} - \frac{\partial ^{2}}{\partial x^{2}} \biggr)v = f(x,t),\quad0 < x < 1, t > 0. \end{aligned}$$
(5.25b)

Since the grid lines are parallel to coordinate axis, the successive tangential derivatives of u and its normal derivatives are known on the boundary, that is, the values of \(u_{t}, u_{tt},\ldots\) are known at \(x=0\) and \(x=1\), and the values of \(u_{xx}, u_{{xxt}},\ldots\) are known at \(t=0\). Hence the initial values of u, \(u_{t}\), v, \(v_{t}\) are known at \(t=0\), and the values of u, v are known at \(x=0\) and \(x=1\). Thus, applying scheme (4.25) to the system of equations (5.25a) and (5.25b), we get the following two equations:

$$\begin{aligned}& U_{l + 1}^{j} - 2U_{l}^{j} + U_{l - 1}^{j} = \frac{h^{2}}{12}\bigl[\overline{U}_{tt_{l + 1}}^{j} + 10\overline{U}_{tt_{l}}^{j} + \overline{U}_{tt_{l - 1}}^{j} \bigr] \\& \hphantom{U_{l + 1}^{j} - 2U_{l}^{j} + U_{l - 1}^{j} ={}}{}- \frac{h^{2}}{3}\bigl[\overline{V}_{l + 1/2}^{j} + \hat{V}_{l}^{j} + \overline{V}_{l - 1/2}^{j} \bigr] + \hat{T}_{1l}^{j}, \end{aligned}$$
(5.26a)
$$\begin{aligned}& V_{l + 1}^{j} - 2V_{l}^{j} + V_{l - 1}^{j} = \frac{h^{2}}{12}\bigl[\overline{V}_{tt_{l + 1}}^{j} + 10\overline{V}_{tt_{l}}^{j} + \overline{V}_{tt_{l - 1}}^{j} \bigr] \\& \hphantom{V_{l + 1}^{j} - 2V_{l}^{j} + V_{l - 1}^{j} ={}}{}- \frac{h^{2}}{3}\bigl[f_{l + 1/2}^{j} + f_{l}^{j} + f_{l - 1/2}^{j}\bigr] + \hat{T}_{2l}^{j}, \end{aligned}$$
(5.26b)

where \(U_{l}^{j}\) and \(V_{l}^{j}\) are the exact solutions of (5.25a) and (5.25b), respectively, and \(\hat{T}_{1l}^{j}\) and \(\hat{T}_{2l}^{j}\) are of \(O(k^{2}h^{2} + k^{2}h^{4} + h^{6})\).

Multiplying throughout by \(p^{2} = (k^{2}/h^{2})\), we may write the above system of equations in an operator form

$$\begin{aligned}& \bigl(12 + \delta_{x}^{2}\bigr)\delta_{t}^{2}U_{l}^{j} = 12p^{2}\delta_{x}^{2}U_{l}^{j} + k^{2}\bigl(12 + \delta_{x}^{2} \bigr)V_{l}^{j} + p^{2}\hat{T}_{1l}^{j}, \end{aligned}$$
(5.27a)
$$\begin{aligned}& \bigl(12 + \delta_{x}^{2}\bigr)\delta_{t}^{2}V_{l}^{j} = 12p^{2}\delta_{x}^{2}V_{l}^{j} + k^{2}\bigl(f_{l + 1/2}^{j} + f_{l}^{j} + f_{l - 1/2}^{j}\bigr) + p^{2}\hat{T}_{2l}^{j}. \end{aligned}$$
(5.27b)

Let \(u_{l}^{j}\) and \(v_{l}^{j}\) be the approximate solutions of (5.25a) and (5.25b), respectively, which satisfy

$$\begin{aligned}& \bigl(12 + \delta_{x}^{2}\bigr)\delta_{t}^{2}u_{l}^{j} = 12p^{2}\delta_{x}^{2}u_{l}^{j} + k^{2}\bigl(12 + \delta_{x}^{2} \bigr)v_{l}^{j}, \end{aligned}$$
(5.28a)
$$\begin{aligned}& \bigl(12 + \delta_{x}^{2}\bigr)\delta_{t}^{2}v_{l}^{j} = 12p^{2}\delta_{x}^{2}v_{l}^{j} + k^{2}\bigl(f_{l + 1/2}^{j} + f_{l}^{j} + f_{l - 1/2}^{j}\bigr). \end{aligned}$$
(5.28b)

Let \((\varepsilon_{u})_{l}^{j} = U_{l}^{j} - u_{l}^{j}\) and \((\varepsilon_{v})_{l}^{j} = V_{l}^{j} - v_{l}^{j}\) be the errors at the grid point \((x_{l},t_{j})\).

Subtracting (5.28a) from (5.27a) and (5.28b) from (5.27b), we get the following two error equations:

$$\begin{aligned}& \bigl(12 + \delta_{x}^{2}\bigr)\delta_{t}^{2}( \varepsilon_{u})_{l}^{j} = 12p^{2} \delta_{x}^{2}(\varepsilon_{u})_{l}^{j} + k^{2}\bigl(12 + \delta_{x}^{2}\bigr) ( \varepsilon_{v})_{l}^{j} + p^{2} \hat{T}_{1l}^{j}, \end{aligned}$$
(5.29a)
$$\begin{aligned}& \bigl(12 + \delta_{x}^{2}\bigr)\delta_{t}^{2}( \varepsilon_{v})_{l}^{j} = 12p^{2} \delta_{x}^{2}(\varepsilon_{v})_{l}^{j} + p^{2}\hat{T}_{2l}^{j}. \end{aligned}$$
(5.29b)

Substituting \((\varepsilon_{v})_{l}^{j} = e^{i\psi_{0}j}e^{i\theta_{0}l}\) into the homogeneous part of error equation (5.29b), we get

$$ \sin^{2}\biggl(\frac{\psi_{0}}{2}\biggr) = \frac{3p^{2}\sin^{2}(\frac{\theta_{0}}{2})}{3 - \sin^{2}(\frac{\theta_{0}}{2})}. $$
(5.30)

Since \(0 \le\sin^{2}(\frac{\psi_{0}}{2}) \le1\), from (5.30), we have

$$ 3p^{2}\sin^{2}\biggl(\frac{\theta_{0}}{2}\biggr) \le3 - \sin^{2}\biggl(\frac{\theta_{0}}{2}\biggr). $$
(5.31)

The above inequality holds if

$$ \max\biggl[3p^{2}\sin^{2}\biggl(\frac{\theta_{0}}{2}\biggr) \biggr] \le\min\biggl[3 - \sin^{2}\biggl(\frac{\theta_{0}}{2}\biggr) \biggr], $$
(5.32)

that is, if

$$ 0 < p \le\sqrt{\frac{2}{3}} \approx0.816. $$
(5.33)

Hence scheme (5.28b) is stable for \(0 < p \le0.816\).

Numerically, first we compute (5.28b) using the value \(0 < p \le0.816\) and then (5.28a). Assume that the value of \((\varepsilon_{v})_{l}^{j}\) is known in (5.29a). Then substituting \((\varepsilon_{u})_{l}^{j} = e^{i\phi_{0}j}e^{i\beta_{0}l}\) into the homogeneous part of (5.29a), we get

$$ \sin^{2}\biggl(\frac{\phi_{0}}{2}\biggr) = \frac{3p^{2}\sin^{2}(\frac{\beta_{0}}{2})}{3 - \sin^{2}(\frac{\beta_{0}}{2})}. $$
(5.34)

Proceeding as above, it is easy to verify that scheme (5.28a) is also stable for \(0 < p \le0.816\).

6 Numerical results

In this section, we have computed some benchmark problems using the proposed scheme and compared our results obtained by the existing methods for the solution of 1D quasi-linear wave equation. The exact solutions are provided in each case. The right-hand side homogeneous functions, initial and boundary conditions may be obtained by using the exact solution as a test procedure. The linear difference equations have been solved using tridiagonal solver, whereas nonlinear difference equations have been solved using the Newton-Raphson method. While using the Newton-Raphson method, the iterations were stopped when absolute error tolerance ≤10−12 had been achieved. All computations were carried out using MATLAB codes.

The proposed scheme is a three-level scheme. The value ofuat\(t =0\) is known from the initial condition. To begin the computation, we need the numerical value of u of required accuracy at \(t = k\), so we discuss an explicit method of \(O(k^{2})\) for calculating the value of u at first time level in order to solve the differential equation (1.1) using the proposed scheme (3.12) which is applicable to problems both in Cartesian and polar coordinates.

Since the values of u and \(u_{t}\) are known explicitly at \(t = 0\), so the values of successive tangential derivatives \(u, u_{x}, u_{xx}, \ldots, u_{tx}, u_{txx}, \ldots\) etc. are known at \(t = 0\). An approximation for u at \(t=k\) may be written as

$$ u_{l}^{1} = u_{l}^{0} + k(u_{t})_{l}^{0} + \frac{k^{2}}{2}(u_{tt})_{l}^{0} + O\bigl(k^{3}\bigr). $$
(6.1)

From equation (1.1), we have

$$ (u_{tt})_{l}^{0} = \bigl[A(x, t, u)u_{xx} + f(x, t, u, u_{x}, u_{t}) \bigr]_{l}^{0}. $$
(6.2)

Then, using the initial values and their successive tangential derivative values from (6.2), we obtain the value of \(u_{tt}\) at \(t = 0\), and then subsequently from (6.1), we can compute the value of u at first time level, i.e., at \(t = k\).

The relation between the exact solution\(u_{exact}\)and the approximate solution \(u(h)\) is given by the following equation:

$$ u_{\mathrm{exact}} = u(h) + Mh^{p} + \cdots\mbox{higher order terms}, \quad 0 < x, y < 1, $$
(6.3)

where h is the measure of the mesh discretization, M is a constant and p is the order (rate) of convergence. If the meshes are to be refined sufficiently, the higher order terms can be neglected. Then the maximum absolute errors \(E_{h}\) can be approximated as

$$ E_{h} = \operatorname{Max} \bigl\vert u_{\mathrm{exact}} - u(h) \bigr\vert \cong Mh^{p}. $$
(6.4)

Taking the logarithm of both sides of (6.4), we obtain

$$ \log(E_{h}) = \log(M) + p\log(h). $$
(6.5)

For two different refined mesh spacing \(h_{1}\) and \(h_{2}\), we have the following two relations:

$$\begin{aligned}& \log(E_{h_{1}}) = \log(M) + p\log(h_{1}), \end{aligned}$$
(6.6a)
$$\begin{aligned}& \log(E_{h_{2}}) = \log(M) + p\log(h_{2}), \end{aligned}$$
(6.6b)

where \(E_{h_{1}}\) and \(E_{h_{2}}\) are maximum absolute errors for two uniform mesh sizes \(h_{1}\) and \(h_{2}\), respectively. For computation of order of convergence, we have considered \(h_{1} = 1/32\) and \(h_{2} = 1/64\) for all five problems, for a fixed value of \(\sigma= k/(h^{2})\), and results are reported in Table 1. Assume \(|E(h)|\) to be the maximum absolute error for u at a certain time level for a fixed value of \(\sigma= k/(h^{2})\), then the error behaves like \(|E(h)| \cong|Mh^{p}|\), implying that \(\log|E(h)| \cong\log(M) + p\log|h|\). Thus, on log-log scale the error behaves linearly with a slope that is equal to p, the order of convergence.

Table 1 Order of convergence
Full size table

Problem 6.1

Telegraphic equation

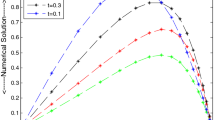
$$ u_{tt} + (\alpha_{0} + \beta_{0})u_{t} + \alpha_{0}\beta_{0}u = u_{xx} + f(x, t),\quad 0 < x < 1, t > 0. $$
(6.7)

The exact solution is given by \(u = e^{ - 2t}\sinh x\). The maximum absolute errors (MAE) are tabulated in Table 2 at \(t = 2\) for different values of \(\alpha_{0}\), \(\beta_{0}\), η, γ for a fixed value of \(\sigma= 3.2\). Figures 2(a) and 2(b) represent the exact vs numerical solution at \(t =2\), \(\sigma= 3.2\), \(\alpha_{0} = 12\), \(\beta_{0} = 8\), \(\eta= 1\), \(\gamma= 1\), \(h=1/16\), and log-log error plot at \(t =2\), \(\alpha_{0} = \pi\), \(\beta_{0} = \pi\), \(\eta=0.75\), \(\gamma= 1.5\), \(\sigma= 3.2\), respectively.

Figure 2
figure 2

Plots of Problem 6.1 .

Full size image
Table 2 Problem 6.1 : The maximum absolute errors
Full size table

Problem 6.2

Van-der-Pol type nonlinear wave equation

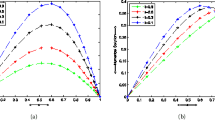
$$ u_{tt} = u_{xx} + \varepsilon\bigl(u^{2} - 1 \bigr)u_{t} + f(x, t),\quad 0 < x < 1, t > 0. $$
(6.8)

The exact solution is given by \(u = e^{ - t}\sin(\pi x)\). The MAE at \(t=1 \mbox{ and }2\) are tabulated in Table 3 for a fixed value of \(\sigma= 0.8\) and \(\varepsilon= 0.01,0.001\). Figures 3(a) and 3(b) represent the exact vs numerical solution at \(t = 2\), \(\varepsilon= 0.001\), \(h =1/16\) and log-log error plot at \(t=1\), \(\varepsilon= 0.01\), respectively.

Figure 3
figure 3

Plots of Problem 6.2 .

Full size image
Table 3 Problem 6.2 : The maximum absolute errors
Full size table

Problem 6.3

Nonlinear wave equation

$$ u_{tt} = u_{xx} + \gamma u(u_{x} + u_{t}) + f(x, t),\quad 0 < x < 1, t > 0. $$
(6.9)

The exact solution is given by \(u = e^{ - 2t}\cosh x\). The MAE are tabulated in Table 4 at \(t = 1\) for \(\gamma= 0.5\mbox{ and }2\) for a fixed value of \(\sigma= 3.2\). Figures 4(a) and 4(b) represent the exact vs numerical solution at \(t =1\), \(\gamma= 2\), \(h =1/64\) and log-log error plot at \(t =1\), \(\gamma= 0.5\), respectively.

Figure 4
figure 4

Plots of Problem 6.3 .

Full size image
Table 4 Problem 6.3 : The maximum absolute errors
Full size table

Problem 6.4

Quasi-linear equation

$$ u_{tt} = \bigl(1 + u^{2}\bigr)u_{xx} + \gamma uu_{x} + f(x, t),\quad 0 < x < 1, t > 0. $$
(6.10)

The exact solution is given by \(u = e^{ - 2t}\sin(\pi x)\). The MAE are tabulated in Table 5 at \(t = 1\) for \(\gamma= 2\mbox{ and }20\) for a fixed value of \(\sigma= 3.2\). Figures 5(a) and 5(b) represent the exact vs numerical solution at \(t =1\), \(\gamma= 2\), \(h =1/32\) and log-log error plot at \(t =1\), \(\gamma= 20\), respectively.

Figure 5
figure 5

Plots of Problem 6.4 .

Full size image
Table 5 Problem 6.4 : The maximum absolute errors
Full size table

Problem 6.5

Fourth-order nonlinear hyperbolic equation

$$ \biggl( \frac{\partial^{2}}{\partial t^{2}} - \frac{\partial ^{2}}{\partial x^{2}} \biggr)^{2}u = \alpha uu_{x} + f(x,t),\quad0 < x < 1, t > 0. $$
(6.11)

The initial values (at \(t=0\)) of u, \(u_{t}\), \(u_{tt}\), \(u_{{ttt}}\) are known and the values of u, \(u_{{xx}}\) are known at \(x=0\) and \(x=1\).

In order to solve (6.11), we put

$$ \biggl( \frac{\partial^{2}}{\partial t^{2}} - \frac{\partial ^{2}}{\partial x^{2}} \biggr)u = v. $$
(6.12)

Hence (6.11) reduces to a system of coupled nonlinear equations of the form

$$\begin{aligned}& \biggl( \frac{\partial^{2}}{\partial t^{2}} - \frac{\partial ^{2}}{\partial x^{2}} \biggr)u = v,\quad0 < x < 1, t > 0, \end{aligned}$$
(6.13)
$$\begin{aligned}& \biggl( \frac{\partial^{2}}{\partial t^{2}} - \frac{\partial ^{2}}{\partial x^{2}} \biggr)v = \alpha uu_{x} + f(x,t),\quad0 < x < 1, t > 0. \end{aligned}$$
(6.14)

Since the grid lines are parallel to coordinate axis, successive tangential derivatives of u and its normal derivatives are known on the boundary. Hence the initial values of u, \(u_{t}\), v, \(v_{t}\) are known at \(t=0\), and the values of u, v are known at \(x=0\) and \(x=1\). Thus applying scheme (5.14), we can solve the system of equations (6.13) and (6.14).

The exact solution is \(u=e^{-t} \sin(\pi x)\). The maximum absolute errors for u are tabulated in Table 6 at \(t=1\) for \(\alpha= 0.5\mbox{ and }0.05\) for a fixed value of \(\sigma= 1.6\). Figures 6(a) and 6(b) represent the exact vs numerical solution at \(t=1\), \(\alpha= 0.5\), \(h = 1/32\) and log-log error plot at \(t = 1\), \(\alpha= 0.05\), respectively.

Figure 6
figure 6

Plots of Problem 6.5 .

Full size image
Table 6 Problem 6.5 : The maximum absolute errors
Full size table

7 Concluding remarks

In this paper, using two half-step points and a central point, we have derived a new stable half-step spline in compression method of \(O(k^{2} + h^{4})\) accuracy for the solution of quasi-linear hyperbolic equation (1.1). Our method has been derived directly from the consistency condition which is fourth-order accurate, and we have used properties of spline in compression function in derivation of the method. For a fixed parameter \(\sigma= k/h^{2}\), the proposed method behaves like a fourth-order method. The accuracy and efficiency of the proposed method are exhibited from the numerical computations. The proposed method for scalar equation has been extended in a vector form to solve the system of quasi-linear hyperbolic pdes. For the telegraphic equation, the method is shown to be unconditionally stable, and the stability condition for solving a fourth-order linear hyperbolic pde has also been established. The method is directly applicable to quasilinear hyperbolic pdes irrespective of the coordinate system, which brings an edge over other existing methods.