1 Introduction

Recently, increasing interests and considerable researches have been given to fractional differential equations (FDEs) thanks to its applications in wide areas of applied science and engineering. The formulations based on FDEs are more adequate than the previously used classical integer-order models. It is usually recommended to employ the fractional models for describing diverse physical phenomena such as fluid mechanics, plasma physics, electrochemistry, mathematical biology, probability and statistics, finance, electrical networks, rheology, optics, and signal processing to maintain not only the behavior of the original systems but also all of its historical states. It is a well-known fact that there is no generally applicable method to seek the exact solution of most FDEs. The procedures such as linearization or discretization are inevitable. For this reason, it is particularly important to propose and develop a new computationally efficient method for obtaining the numerical solution of FDEs. In order to accommodate the reader who is not acquainted with the concept of fractional calculus, it is perhaps important to recall that fractional calculus is a discipline concerning the possibility of taking non-integer or fractional powers to the derivatives and integrals. As is well known, there are many different types of fractional derivatives. A most frequently and widely used one was proposed by Caputo [1], which will be explained here briefly. The initial conditions for the differential equations with fractional order by Caputo’s definition take on the same form as for the ones with integer order, whose physically meaningful interpretation is very clear. Moreover, an exceptionally good benefit of the fractional derivative interpreted in Caputo’s viewpoint is that, from the physical perspective, some characteristic properties of classical derivative that the derivative of any constant function is zero should be preserved. Of course not all aspects of current or past interest in fractional calculus can be covered in this section, but the aim is at least to provide up to date information in as much detail as possible as well as to generate curiosity and encourage further investigation of the potential applications of this branch of mathematics. To give the reader insight and understanding as regards fractional calculus in more depth, we refer to the books of Oldham and Spanier [2], Miller and Ross [3], Podlubny [4], Kilbas et al. [5] and the references cited therein.

The Navier-Stokes equations (NSE) are a set of coupled nonlinear second-order partial differential equations that are conventionally regarded as the appropriate mathematical formulation to describe the numerical simulation being relevant to the unsteady, compressible, and viscous fluid flows. Generally, incompressible flows can be modeled using the NSE in two different formulations which may be based on either primitive (velocity and pressure) or derived (such as velocity and vorticity) variables. The velocity-vorticity approach, generally known as the stream function-vorticity approach, requires the transformation of NSE into equations of velocity and vorticity components and does not include the pressure term. Notwithstanding the advantage that the number of equations to be solved in velocity-vorticity form is two and three for two- and three-dimensional problems, respectively, which is fewer than those in the primitive variables approach, they have lost some of their attractiveness and have received very little attention. Imposition of boundary conditions of the transformed equations is a major drawback that has to be tackled, especially for three-dimensional problems. It may require substantial effort related to the boundary treatment to circumvent this problem, whereas the use of method based on primitive variables is quite common and definitely more straightforward. As a consequence, the incompressible NSE are most frequently solved by the formulation of primitive variables which will be considered here. In 2004 El-Shahed and Salem [6] have proposed the generalized NSE by simply replacing the first-order time derivative term by a derivative of fractional order but still retaining the first- and second-order space derivatives. Afterward, the published research articles with regard to solving a viscous fluid problem in a tube in cylindrical coordinates have emerged continuously. The approximated solutions for the problem as above have been given among others by Momani and Odibat [7] using the Adomian decomposition method (ADM), Ragab et al. [8] using the homotopy analysis method (HAM), Kumar et al. [9] by the ADM and Laplace transform method (LTM), Kumar et al. [10] with the new homotopy perturbation transform method (HPTM), and Wang and Liu [11] using the modified reduced differential transform method (DTM) and new iterative Elzaki transform method. Besides those mentioned above, the new development in solving nonlinear FDEs has been proposed by Kumar and his colleagues. The HAM together with the Laplace transform was applied to solve the nonlinear shock wave equation of fractional order arising in the flow of gases [12]. The implementation of the homotopy analysis Sumudu transform method (HASTM), an inventive coupling of Sumudu transform and well-known homotopy analysis technique, to derive the analytical and numerical solutions of a nonlinear fractional differential-difference problem was shown in [13]. They also pointed out that the most important advantage of the HASTM over the ADM and HPTM is without making use of Adomian’s and He’s polynomials. Other pioneering work can be found in [14, 15].

Meanwhile, numerical methods turn out to be an alternative way of attaining an approximate solution of FDEs. Solving FDEs by the classical mesh-dependent numerical methods such as the finite difference methods (FDM), the finite volume methods (FVM), and the finite element methods (FEM) requires the mesh generation, which appears to be computationally costly. The use of meshes restricted by their applications leads to many difficulties in some specific problems. Attempts to get rid of the aforementioned problem have been devoted to developing the so-called meshless (or meshfree) methods. They have some advantages when compared to the grid based methods by virtue of the flexibility and simplicity of placing nodes at arbitrary locations. The academic work regarding the remarkable progress on meshless methods has thus far received considerable interest and has been published continually both theoretically and numerically (see [16–25]). One of the extensively popularized meshless methods in solving initial and boundary value problems is the meshless local Petrov-Galerkin (MLPG) method originating with Atluri and Zhu [26]. This is one of the truly meshless methods just because the requirement of background cells for integration is not needed.

In meshless procedure, construction of shape function is one of the main challenges that must be taken into account. Originally, the MLPG approach is numerically implemented using the moving least squares (MLS) approximation to the spatially discretized domain. Even though the MLS approximation seems to be one of the most commonly used methods, it is not always advantageous. The only notable imperfection for MLS shape functions is that they do not have the Kronecker delta property, so the techniques like the Lagrange multiplier or penalty method are required to enforce essential (Dirichlet) boundary conditions. On the other hand, the so-called method of kriging is one of the most immensely used techniques in geostatistics for spatial interpolation. This subsequently became another way to enhance the accuracy and efficiency for the meshfree methods. The moving kriging (MK) interpolation was first proposed by Gu [27] and successfully demonstrated the effectiveness in solving steady-state heat conduction problems. In addition to the consistency property, the MK shape functions have the delta property which allows essential boundary conditions to easily be imposed in a similar way to the FEM. The kriging interpolation is shown to be essentially the same as the radial point interpolation method (RPIM) on condition that the same basis functions are used [28].

As mentioned in the second paragraph, virtually all the accomplishments to acquire the solution of fractional NSE in the literature can only be limited to the one dimension. Only the simplest cases are solved analytically so that an exact solution can be obtained. The theoretical study for solving such a problem in higher space dimensions is connected with great difficulties. Evidently, seeking the analytical solution of the time-fractional NSE in multiple dimensions has not been easy by reason of the nonlinearity which makes them very complicated or almost not possible to achieve, not to mention containing unknown function (velocity components and pressure) of several independent variables (space and time) more than one and its partial derivatives with respect to those variables. Up to now, only little attention has been paid to the development of the MLPG method so as to solve the fractional model of fluid flow in Cartesian coordinates. Additionally, as far as the authors are concerned, stability of meshfree methods for a fractional model is rather hard to investigate and needs many efforts, especially for a governing equation considered with nonlinear term. To fill this gap, the main contribution of this paper is to investigate and analyze the stability of a fractional model for unsteady-state flow problem developed based on the meshless methods.

The organization of the remainder of this article is as follows. In Section 2, mathematical preliminaries may be helpful for whoever is about to begin with FDE, so we give a short description and basic concepts of fractional calculus. Also we provide a discrete approximation for the fractional derivative based on a quadrature rule. In Section 3, we first introduce the governing nonlinear time-fractional NSE in two dimensions and then explain how to solve the nonlinear system. We show the stability of the meshfree method, and the sensitivity of several important parameters is also studied and discussed. In Section 4, two numerical tests are examined and discussed to show the validation of stability for the present method. Finally, we end the current work with concluding remarks in Section 5.

2 Mathematical preliminaries

This section can be useful for the reader who is unfamiliar with the fractional derivative. We briefly give some important concepts and definitions of fractional calculus.

Definition 1

A real function \(f ( x )\) with \(x>0\) is said to be in the space \(C_{\mu},\mu\in \mathbf{R}\) if there exists a real number \(p>\mu\) such that \(f ( x ) = x^{p} f_{1} ( x )\), where \(f_{1} ( x ) \in C(0,\infty)\) and for \(m\in \mathbf{N}\) it is said to be in \(C_{\mu}^{m}\) if \(f^{(m)} \in C_{\mu}\).

Definition 2

The left-sided Riemann-Liouville fractional integral operator of order \(\alpha\geq0\) for a function \(f\in C_{\mu},\mu\geq-1\) is defined as

$$ J_{a}^{\alpha} f ( x ) = \textstyle\begin{cases} \frac{1}{\Gamma ( \alpha )} \int_{a}^{x} ( x - \tau )^{\alpha -1} f ( \tau ) \,d\tau,& \alpha >0, x>a,\\ f ( x ),& \alpha =0, \end{cases} $$
(2.1)

where \(\Gamma ({\cdot})\) stands for the gamma function. The lower bound of integration a is commonly set to be zero.

Definition 3

If n be the smallest integer that exceeds α, the Caputo time-fractional derivative operator of order \(\alpha>0\) for any causal function of time, \(i.e\). vanishing for \(t<0\) is defined as

$$ D_{t}^{\alpha} f ( x,t ) = \frac{\partial^{\alpha} f ( x, t )}{\partial t^{\alpha}} = \textstyle\begin{cases} J_{t}^{n-\alpha} ( \frac{\partial^{n} f ( x,t )}{\partial t^{n}} ),& n-1< \alpha< n,\\ \frac{\partial^{n} f ( x,t )}{\partial t^{n}}, &\alpha=n, \end{cases} $$
(2.2)

or equivalently

$$ D_{t}^{\alpha} f ( x,t ) = \textstyle\begin{cases} \frac{1}{\Gamma ( n-\alpha )} \int_{0}^{t} ( t-\tau )^{n-\alpha-1} \frac{\partial^{n} f(x,\tau)}{\partial \tau^{n}} \,d\tau, & n-1< \alpha< n\\ \frac{\partial^{n} f ( x,t )}{\partial t^{n}},& \alpha=n, \end{cases} $$
(2.3)

and the space fractional derivative operator of order \(\beta>0\) is defined as

$$ D_{x}^{\beta} f ( x,t ) = \textstyle\begin{cases} \frac{1}{\Gamma ( n-\beta )} \int_{0}^{x} ( x-\theta )^{n-\beta-1} \frac{\partial^{n} f(\theta,t)}{\partial \theta^{n}} \,d\theta,& n-1< \beta< n,\\ \frac{\partial^{n} f ( x,t )}{\partial x^{n}},& \beta=n. \end{cases} $$
(2.4)

In addition we also provide the derivation of discrete approximation for the Caputo fractional derivative based on a quadrature formula. Given the time interval [\(0, T\) ] discretized uniformly into k subintervals. The values at nodal points in time domain are defined by \(t_{n} =n\Delta t\), \(n=0,1,2,\dots,k\) where \(\Delta t = T/k\). For simplicity we denote the approximate solutions of function f at the points \(x_{i}\) and \(t_{n}\) by \(f_{i}^{n}\). The approximate formula at time level n can be obtained as follows:

$$\begin{aligned} D_{t}^{\alpha} f ( x_{i}, t_{n} ) ={}& \frac{1}{\Gamma ( 1-\alpha )} \int_{0}^{t_{n}} \frac{\partial f ( x_{i},\phi )}{\partial\phi} ( t_{n} - \phi )^{-\alpha} \,d\phi \\ ={}& \frac{1}{\Gamma ( 1-\alpha )} \sum_{k=1}^{n} \int_{ ( k-1 ) \Delta t}^{k \Delta t} \biggl( \frac{f_{i}^{k} - f_{i}^{k-1}}{ \Delta t} +O( \Delta t ) \biggr) ( n\Delta t-\phi )^{-\alpha} \,d\phi \\ ={}& \frac{1}{\Gamma ( 2-\alpha )} \sum_{k=1}^{n} \biggl\{ \biggl( \frac{f_{i}^{k} - f_{i}^{k-1}}{\Delta t} +O( \Delta t ) \biggr) \bigl( ( n-k+1 )^{1-\alpha} - ( n-k )^{1-\alpha} \bigr) \biggr\} \Delta t^{1-\alpha} \\ ={}& \frac{\Delta t^{-\alpha}}{\Gamma ( 2-\alpha )} \sum_{k=1}^{n} \bigl( f_{i}^{k} - f_{i}^{k-1} \bigr) \bigl( ( n-k+1 )^{1-\alpha} - ( n-k )^{1-\alpha} \bigr)\\ &{} + \frac{1}{ \Gamma ( 2-\alpha )} \sum_{k=1}^{n} \bigl( ( n-k+1 )^{1-\alpha} - ( n-k )^{1-\alpha} \bigr) O \bigl( \Delta t^{2-\alpha} \bigr)\\ ={}& \sigma_{\alpha,k} \sum _{k=1}^{n} \omega_{\alpha,k} \bigl( f_{i}^{n-k+1} - f_{i}^{n-k} \bigr) + O ( \Delta t ), \end{aligned}$$

where \(\omega_{\alpha,k} = k^{1-\alpha} - ( k-1 )^{1-\alpha}\) and \(\sigma_{\alpha, \Delta t} = \frac{\Delta t^{-\alpha}}{\Gamma (2-\alpha)}\). The notation O is the higher-order residuals truncated of Taylor series. Therefore the discretized formula for the Caputo fractional derivative which is of first-order accuracy in time can be obtained:

$$ D_{t}^{\alpha} f ( x_{i}, t_{n} ) \approx \sigma_{\alpha,k} \sum_{k=1}^{n} \omega_{\alpha,k} \bigl( f_{i}^{n-k+1} - f_{i}^{n-k} \bigr). $$
(2.5)

3 Numerical procedure

Most incompressible fluid models for unsteady-state flow problem can be described mathematically by the two-dimensional time-fractional NSE in primitive form with the source terms included as

$$\begin{aligned} &\frac{\partial^{\alpha} u}{\partial t^{\alpha}} +u \frac{\partial u}{ \partial x} +v \frac{\partial u}{\partial y} =- \frac{\partial p}{ \partial x} + \frac{1}{{Re}} \biggl( \frac{\partial^{2} u}{\partial x^{2}} + \frac{\partial^{2} u}{\partial y^{2}} \biggr) + s_{x}, \end{aligned}$$
(3.1)
$$\begin{aligned} &\frac{\partial^{\alpha} v}{\partial t^{\alpha}} +u \frac{\partial v}{ \partial x} +v \frac{\partial v}{\partial y} =- \frac{\partial p}{ \partial y} + \frac{1}{{Re}} \biggl( \frac{\partial^{2} v}{\partial x^{2}} + \frac{\partial^{2} v}{\partial y^{2}} \biggr) + s_{y}, \end{aligned}$$
(3.2)
$$\begin{aligned} &\frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} =0, \end{aligned}$$
(3.3)

where u and v are the velocities in the x and y directions, p is the pressure, respectively, Re represents the Reynolds number, \(s_{x}\) and \(s_{y}\) are the source functions along the x and y directions, respectively, α is the fractional parameter, \(0<\alpha<1\), and the Caputo time-fractional derivative presented in this work is defined by

$$ \frac{\partial^{\alpha} u ( \mathbf{x}, t )}{\partial t^{\alpha}} = \frac{1}{\Gamma ( 1- \alpha )} \int_{0}^{t} \frac{\partial u ( \mathbf{x}, \xi )}{\partial\xi} ( t - \xi )^{- \alpha} \,d\xi. $$
(3.4)

We omit the derivation details for the standard local weak formulation, spatial discretization, and temporal discretization here to save space and refer to Thamareerat et al. [25].

3.1 Solving the nonlinear system

The discretized system of nonlinear algebraic equations which corresponds to equations (3.1), (3.2), and (3.3) can be written as

$$ \sigma_{\alpha, \Delta t} \mathbf{A} \sum_{k=1}^{n} \omega_{\alpha,k} \bigl( \mathbf{U}^{n-k+1} - \mathbf{U}^{n-k} \bigr) + \mathbf{B}^{n} \mathbf{U}^{n} = \mathbf{S}^{n}, $$
(3.5)

where \(\mathbf{A}= \left[{\scriptsize\begin{matrix}{} \mathbf{I} & \mathbf{0} & \mathbf{0}\cr \mathbf{0} & \mathbf{I} & \mathbf{0}\cr \mathbf{0} & \mathbf{0} & \mathbf{0}\end{matrix}} \right]\), \(\mathbf{B}= \left[{\scriptsize\begin{matrix}{} \mathbf{B}_{{11}} & \mathbf{0} & \mathbf{B}_{{13}}\cr \mathbf{0} & \mathbf{B}_{{22}} & \mathbf{B}_{{23}}\cr \mathbf{B}_{{31}} & \mathbf{B}_{{32}} & \mathbf{0}\end{matrix}} \right]\), \(\mathbf{S}= \left[{\scriptsize\begin{matrix}{} \mathbf{S}_{{x}}\cr \mathbf{S}_{{y}}\cr \mathbf{0}\end{matrix}} \right]\), \(\mathbf{U}= \left[{\scriptsize\begin{matrix}{} \hat{\mathbf{U}}\cr \hat{\mathbf{V}}\cr \hat{\mathbf{P}}\end{matrix}} \right]\),

$$\begin{aligned} &\mathbf{B}_{{11}} = \bigl[ \varphi_{ij} ( u, v ) \bigr]; \qquad \varphi_{ij} ( u, v ) = u ( \mathbf{x}_{i} ) \phi_{j, x} ( \mathbf{x}_{i} ) + v ( \mathbf{x}_{i} ) \phi_{j, y} ( \mathbf{x}_{i} ) - \frac{1}{{Re}} \bigl( \phi_{j, xx} ( \mathbf{x}_{i} ) + \phi_{j, yy} ( \mathbf{x}_{i} ) \bigr), \\ &\mathbf{B}_{{13}} = \bigl[ \phi_{j,x} ( \mathbf{x}_{i} ) \bigr], \qquad\mathbf{B}_{{22}} = \mathbf{B}_{{11}},\qquad \mathbf{B}_{{23}} = \bigl[ \phi_{j, y} ( \mathbf{x}_{i} ) \bigr],\qquad \mathbf{B}_{{31}} = \mathbf{B}_{{13}},\qquad \mathbf{B}_{{32}} = \mathbf{B}_{{23}}, \\ &\mathbf{S}_{{x}} = [ s_{x1}\ s_{x2}\ s_{x3}\ \dots\ s_{xN} ]^{T}, \qquad \mathbf{S}_{{y}} = [ s_{y1}\ s_{y2}\ s_{y3}\ \dots\ s_{yN} ]^{T}, \\ &\hat{\mathbf{U}} = [ \hat{u}_{1}\ \hat{u}_{2}\ \hat{u}_{3}\ \dots\ \hat{u}_{N} ]^{T},\qquad \hat{ \mathbf{V}} = [ \hat{v}_{1}\ \hat{v}_{2}\ \hat{v}_{3}\ \dots\ \hat{v}_{N} ]^{T}, \qquad\hat{ \mathbf{P}} = [ \hat{p}_{1}\ \hat{p}_{2}\ \hat{p}_{3}\ \dots\ \hat{p}_{N} ]^{T}, \\ & \text{$\mathbf{I}$ is the $N\times N$ identity matrix and $\mathbf{0}$ is the $N\times N$ zeros matrix,} \end{aligned}$$

which can be rearranged to give

$$ \sigma_{\alpha,\Delta t} \mathbf{A} \bigl( \mathbf{U}^{n} - \mathbf{U}^{n -1} \bigr) + \mathbf{B}^{n} \mathbf{U}^{n} = - \sigma_{\alpha,\Delta t} \mathbf{A} \sum_{k =2}^{n} \omega_{\alpha,k} \bigl( \mathbf{U}^{n - k +1} - \mathbf{U}^{n - k} \bigr) + \mathbf{S}^{n}. $$
(3.6)

At the first time level, when \(n=1\),

$$ \bigl( \sigma_{\alpha, \Delta t} \mathbf{A} + \mathbf{B}^{1} \bigr) \mathbf{U}^{1} = \sigma_{\alpha, \Delta t} \mathbf{A U}^{0} + \mathbf{S}^{1}, $$
(3.7)

and when \(n\geq2\),

$$ \bigl( \sigma_{\alpha, \Delta t} \mathbf{A} + \mathbf{B}^{n} \bigr) \mathbf{U}^{n} = \sigma_{\alpha, \Delta t} \mathbf{A} \Biggl( \mathbf{U}^{n-1} - \sum_{k=2}^{n} \omega_{\alpha,k} \bigl( \mathbf{U}^{n-k+1} - \mathbf{U}^{n-k} \bigr) \Biggr) + \mathbf{S}^{n}. $$
(3.8)

Equation (3.8) can be expressed more conveniently as

$$ \mathbf{U}^{n} = \mathbf{G}^{n} \Biggl( \mathbf{U}^{n-1} - \sum_{k=2}^{n} \omega_{\alpha,k} \bigl( \mathbf{U}^{n-k+1} - \mathbf{U}^{n-k} \bigr) + ( \sigma_{\alpha, \Delta t} \mathbf{A} )^{-1} \mathbf{S}^{n} \Biggr), $$
(3.9)

where \(\mathbf{G}^{n} = \sigma_{\alpha, \Delta t} ( \sigma_{\alpha, \Delta t} \mathbf{A} + \mathbf{B}^{n} )^{-1} \mathbf{A}\). It should be noted that so long as the matrix \(\sigma_{\alpha, \Delta t} \mathbf{A} + \mathbf{B}^{n}\) is non-singular, \(i.e\). invertible, we have a unique solution for the unknown vector \(\mathbf{U}^{n}\) in each time step. The non-singularity of this matrix often entails the value of correlation parameter which is unable to prove in general. In many of the practical problems, nonetheless, the singularities are rare. To obtain solution values at time level n, we need the previous solutions at all time levels \(0,1,2,\dots,n -1\) expressed inside the parentheses on the right-hand side of equation (3.9). Owing to the coefficient matrix \(\mathbf{G}^{n}\) containing an unknown function of u and v, now we have 3N nonlinear equation and also 3N unknown values. To deal with the nonlinear part in a simple way, we might just as well use the quantities at the previous time step to approximate those at the new time step. This choice is possible if there should be not much difference of solution between n and \(n+1\). In other words, two consecutive time levels should be sufficiently small. Instead of doing like that, a better way to get more accuracy is by a conventional iterative method such as fixed point. We can rewrite equation (3.9) in the form of recursive formula as

$$\begin{aligned} &\mathbf{U}^{n, l} = \mathbf{G} \bigl( \mathbf{U}^{n, l -1} \bigr) \Biggl( \mathbf{U}^{n -1} - \sum_{k =2}^{n} \omega_{\alpha,k} \bigl( \mathbf{U}^{n - k +1} - \mathbf{U}^{n - k} \bigr) + ( \sigma_{\alpha,\Delta t} \mathbf{A} )^{-1} \mathbf{S}^{n} \Biggr), \\ &\quad l =1,2,3,\dots, \end{aligned}$$
(3.10)

where a superscript \(n,l\) denotes the time level n and lth fixed point iteration. In the first step, \(l=1\), we pick \(\mathbf{U}^{0}\) as initial guess, i.e. \(\mathbf{U}^{0,0} = \mathbf{U}^{0}\). When the solution is updated, the resulting solution from the previous stage will be used as the initial guess for the next iteration. This process is repeated again and again until the following terminating condition is met:

$$ \bigl\Vert \mathbf{U}^{n,l} - \mathbf{U}^{n,l -1} \bigr\Vert _{\infty} \leq \varepsilon, $$
(3.11)

where \(\Vert {\cdot} \Vert _{\infty}\) is the infinity norm, and ε is a small prescribed value depending on the accuracy requirement. To put it another way, the process is repeated until the computed values at all grid points have a little change with every subsequent iteration. This means that an initial guess is close enough to the new time level solution. Once the criterion of convergence as prescribed above is fulfilled, we can move on to the next time level. In the meshfree method, it is important to note that the accuracy and stability of the method is conditional upon the correlation parameter ω, the nodal spacing h (h is the average nodal distance between any two points), and also the Reynolds number Re. In the next section, we will investigate these in a thorough manner.

3.2 Stability analysis

In this section a mathematical analysis technique based on the eigenvalue of the matrix is applied to verify condition on the stability for the meshless method. It is possible to consider only its homogeneous part in that inhomogeneous terms do not alter the stability properties. Let \(\mathbf{e}^{n} = \mathbf{U}^{n} - \tilde{\mathbf{U}}^{n}\) be the perturbation or error vector at the nth time level where \(\mathbf{U}^{n}\) and \(\tilde{\mathbf{U}}^{n}\) denote the exact and approximate solution at the nth time level, respectively. So from equation (3.9) we have

$$ \mathbf{e}^{n} = \mathbf{G}^{n} \Biggl( \mathbf{e}^{n -1} - \sum_{k =2}^{n} \omega_{\alpha,k} \bigl( \mathbf{e}^{n - k +1} - \mathbf{e}^{n - k} \bigr) \Biggr). $$
(3.12)

The perturbation vector will be propagated forward in time according to the equation \(\mathbf{e}^{n} = \mathbf{G}^{n} \mathbf{e}^{0}\). The Euclidean matrix and vector norms are compatible or consistent. This allows us to write

$$ \bigl\Vert \mathbf{e}^{n} \bigr\Vert \leq \bigl\Vert \mathbf{G}^{n} \bigr\Vert \bigl\Vert \mathbf{e}^{0} \bigr\Vert . $$
(3.13)

For fixed nodal distance the difference equation (3.9) will be stable if \(\mathbf{e}^{n}\) remains bounded as n increases indefinitely. That is when there exists a positive number M, independent of n and distance for each pair of nodes, such that \(\Vert \mathbf{G}^{n} \Vert \leq M\). This obviously limits the amplification of any initial perturbation, and therefore of any arbitrary round off errors, since \(\Vert \mathbf{e}^{n} \Vert \leq M \Vert \mathbf{e}^{0} \Vert \). To prove that the statement given in equation (3.13) is established for all natural numbers, we will consider the inequality (3.12) in the case of \(n=1\) and \(n\geq2\) separately. When \(n=1\), it is rather easy to see that \(\Vert \mathbf{e}^{1} \Vert \leq \Vert \mathbf{e}^{0} \Vert \) if \(\Vert \mathbf{G}^{1} \Vert \leq1\). In the case of \(n\geq2\), this can be done by means of mathematical induction. Let \(P(n)\) be the statement \(\Vert \mathbf{e}^{n} \Vert \leq \Vert \mathbf{G}^{n} \Vert \Vert \mathbf{e}^{0} \Vert ,n\geq2\). We first rearrange equation (3.12) as follows:

$$\begin{aligned} \mathbf{e}^{n} &= \mathbf{G}^{n} \Biggl( \mathbf{e}^{n -1} - \sum_{k =2}^{n} \omega_{\alpha,k} \bigl( \mathbf{e}^{n - k +1} - \mathbf{e}^{n - k} \bigr) \Biggr) \\ &= \mathbf{G}^{n} \Biggl( \mathbf{e}^{n -1} - \sum _{k =2}^{n -1} \omega_{\alpha,k} \bigl( \mathbf{e}^{n - k +1} - \mathbf{e}^{n - k} \bigr) - \omega_{\alpha,n} \bigl( \mathbf{e}^{1} - \mathbf{e}^{0} \bigr) \Biggr) \\ &= \mathbf{G}^{n} \Biggl( \mathbf{e}^{n -1} - \sum _{k =1}^{n -2} \omega_{\alpha,k+1} \mathbf{e}^{n - k} + \sum_{k =2}^{n -1} \omega_{\alpha,k} \mathbf{e}^{n - k} - \omega_{\alpha,n} \bigl( \mathbf{e}^{1} - \mathbf{e}^{0} \bigr) \Biggr) \\ &= \mathbf{G}^{n} \Biggl( \mathbf{e}^{n -1} - \sum _{k =1}^{n -1} \omega_{\alpha,k+1} \mathbf{e}^{n - k} + \sum_{k =2}^{n -1} \omega_{\alpha,k} \mathbf{e}^{n - k} + \omega_{\alpha,n} \mathbf{e}^{0} \Biggr) \\ &= \mathbf{G}^{n} \Biggl( \mathbf{e}^{n -1} + \sum _{k =2}^{n -1} ( \omega_{\alpha,k} - \omega_{\alpha,k+1} ) \mathbf{e}^{n - k} - \omega_{\alpha,2} \mathbf{e}^{n -1} + \omega_{\alpha,n} \mathbf{e}^{0} \Biggr) \\ &= \mathbf{G}^{n} \Biggl( ( 1- \omega_{\alpha,2} ) \mathbf{e}^{n -1} + \sum_{k =2}^{n -1} ( \omega_{\alpha,k} - \omega_{\alpha,k+1} ) \mathbf{e}^{n - k} + \omega_{\alpha,n} \mathbf{e}^{0} \Biggr). \end{aligned}$$
(3.14)

Taking the norm of both sides of equation (3.14), making use of the compatibility condition for matrix and vector norms, and then applying the triangle inequality, we can write

$$ \bigl\Vert \mathbf{e}^{n} \bigr\Vert \leq \bigl\Vert \mathbf{G}^{n} \bigr\Vert \Biggl( ( 1- \omega_{\alpha,2} ) \bigl\Vert \mathbf{e}^{n-1} \bigr\Vert + \sum _{k=2}^{n-1} ( \omega_{\alpha,k} - \omega_{\alpha,k+1} ) \bigl\Vert \mathbf{e}^{n-k} \bigr\Vert + \omega_{\alpha,n} \bigl\Vert \mathbf{e}^{0} \bigr\Vert \Biggr). $$
(3.15)

There are basically two steps to infer \(P(n)\) holds for each positive integer \(n\geq2\). The first step, known as the base case, intends to show the given statement for a certain number, \(n=2\). We have

$$\begin{aligned} \bigl\Vert \mathbf{e}^{2} \bigr\Vert &\leq \bigl\Vert \mathbf{G}^{2} \bigr\Vert \bigl( ( 1- \omega_{\alpha,2} ) \bigl\Vert \mathbf{e}^{1} \bigr\Vert + \omega_{\alpha,2} \bigl\Vert \mathbf{e}^{0} \bigr\Vert \bigr) \\ &\leq \bigl\Vert \mathbf{G}^{2} \bigr\Vert \bigl( ( 1- \omega_{\alpha,2} ) \bigl\Vert \mathbf{G}^{1} \bigr\Vert \bigl\Vert \mathbf{e}^{0} \bigr\Vert + \omega_{\alpha,2} \bigl\Vert \mathbf{e}^{0} \bigr\Vert \bigr) \\ &< \bigl\Vert \mathbf{G}^{2} \bigr\Vert \bigl( ( 1- \omega_{\alpha,2} ) \bigl\Vert \mathbf{e}^{0} \bigr\Vert + \omega_{\alpha,2} \bigl\Vert \mathbf{e}^{0} \bigr\Vert \bigr) \\ &= \bigl\Vert \mathbf{G}^{2} \bigr\Vert \bigl\Vert \mathbf{e}^{0} \bigr\Vert , \end{aligned}$$
(3.16)

which is obviously fulfilled. The second step called the inductive case is to prove that equation (3.13) for any positive integer implies the formula for its successor. Suppose that \(\Vert \mathbf{e}^{m} \Vert \leq \Vert \mathbf{G}^{m} \Vert \Vert \mathbf{e}^{0} \Vert ,\forall m\geq2\). We have to show that \(\Vert \mathbf{e}^{m+1} \Vert \leq \Vert \mathbf{G}^{m+1} \Vert \Vert \mathbf{e}^{0} \Vert \). From inequality (3.15) we can write

$$\begin{aligned} \bigl\Vert \mathbf{e}^{m +1} \bigr\Vert \leq{}& \bigl\Vert \mathbf{G}^{m+1} \bigr\Vert \Biggl( ( 1- \omega_{\alpha,2} ) \bigl\Vert \mathbf{e}^{m} \bigr\Vert + \sum_{k =2}^{m} ( \omega_{\alpha,k} - \omega_{\alpha,k+1} ) \bigl\Vert \mathbf{e}^{m +1- k} \bigr\Vert + \omega_{\alpha,m+1} \bigl\Vert \mathbf{e}^{0} \bigr\Vert \Biggr) \\ < {}& \bigl\Vert \mathbf{G}^{m+1} \bigr\Vert \Biggl( ( 1- \omega_{\alpha,2} ) \bigl\Vert \mathbf{G}^{m} \bigr\Vert \bigl\Vert \mathbf{e}^{0} \bigr\Vert \\ &{}+ \sum _{k=2}^{m} ( \omega_{\alpha,k} - \omega_{\alpha,k+1} ) \bigl\Vert \mathbf{G}^{m + 1-k} \bigr\Vert \bigl\Vert \mathbf{e}^{0} \bigr\Vert + \omega_{\alpha,m+1} \bigl\Vert \mathbf{e}^{0} \bigr\Vert \Biggr) \\ < {}& \bigl\Vert \mathbf{G}^{m+1} \bigr\Vert \bigl\Vert \mathbf{e}^{0} \bigr\Vert \Biggl( 1- \omega_{\alpha,2} + \sum _{k=2}^{m} (\omega_{\alpha,k} - \omega_{\alpha,k+1} ) + \omega_{\alpha,m+1} \Biggr) \\ ={}& \bigl\Vert \mathbf{G}^{m+1} \bigr\Vert \bigl\Vert \mathbf{e}^{0} \bigr\Vert , \end{aligned}$$
(3.17)

which completes the proof. Our proof shows that the error made at each time level of calculation will be no more than the error made at the initial step as long as \(\Vert \mathbf{G}^{n} \Vert \leq1\), which means \(\rho ( \mathbf{G} ) \leq1\) where \(\rho( \mathbf{G} )\) is the largest modulus of the eigenvalues of G, called the spectral radius of G. In other words, all eigenvalues of the matrix \(\mathbf{G} = \sigma_{\alpha, \Delta t} ( \sigma_{\alpha, \Delta t} \mathbf{A} + \mathbf{B} )^{-1} \mathbf{A}\) satisfy the following condition:

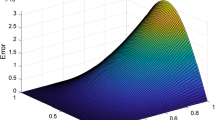
$$ \biggl\vert \frac{\sigma_{\alpha, \Delta t} \lambda_{A}}{\sigma_{\alpha, \Delta t} \lambda_{A} + \lambda_{B}} \biggr\vert \leq1, $$
(3.18)

where \(\lambda_{A}\) and \(\lambda_{B}\) are the eigenvalues of the matrices A and B, respectively. Seeing that A is a block diagonal matrix with \(3\times3\) blocks whose elements are the identity and zero matrices, the eigenvalues of matrix A can be either 0 or 1 only. In case \(\lambda_{A} =0\) we can see that the inequality (3.18) is automatically satisfied for all \(\lambda_{B} \neq0\). This implies \(\lambda_{B}\) can be any arbitrary except zero. Provided that \(\lambda_{A} =1\), the above inequality is always satisfied when \(\lambda_{B}\) must not exceed \(-2 \sigma_{\alpha, \Delta t}\) or must be non-negative only. Consequently, we can say that the scheme is unconditionally stable so long as \(\lambda_{B} \leq-2 \sigma_{\alpha, \Delta t}\) or \(\lambda_{B} \geq0\). As mentioned above, the eigenvalues of matrix B is highly dependent upon the correlation parameter (ω), the distance between any two nodal points (h), and the Reynolds number (Re), which significantly affect the solution. Since it is impossible to explicitly define a relationship among these parameters, we investigate this dependence numerically. Also we show how maximum eigenvalue \(\operatorname{Re}(\lambda)\) of matrix B varies along a range of horizontal and vertical components of velocity and pressure solution. So all we need to do is whether the largest eigenvalue of B will be non-negative.

In the first three Figures, 1(a) (horizontal velocity), (b) (vertical velocity), and (c) (pressure) show the real part of maximum eigenvalue of B when the solutions are varied. We see that there is no difference between Figure 1(a) and (b), and they really look alike. This indicates that no matter what the values of horizontal and vertical velocities are, the eigenvalues of the matrix B still have positive real parts. The scheme is always stable for all values of u and v, whereas the numerical stability shown in Figure 1(c) is not surprising. It seems to be nothing more than just a line parallel to the x-axis and without any change of \(\operatorname{Re} (\lambda)_{\mathrm{max}}\) simply because B is independent of pressure solution. Figure 1(d) shows that for Reynolds numbers up to 1,000 a stable computation is still possible. For a fixed Reynolds number and a distance between each node, Figure 1(e) displays \(\operatorname{Re} (\lambda)_{\mathrm{max}}\) of matrix B while the correlation parameter is varied. The effect of nodal spacing for eigenvalue of B is observed in Figure 1(f) when the Reynolds number and correlation parameter are constant. All in all a detailed study of this section shows that in all cases depicted in Figure 1, the scheme satisfies the stability condition for a wide range of these parameters, which can be chosen freely, and it remains stable versus to any values of time step as well.

Figure 1
figure 1

The effect of the (a) horizontal velocity, (b) vertical velocity, (c) pressure, (d) Reynolds number, (e) correlation parameter, and (f) nodal spacing for eigenvalue of matrix B.

Full size image

4 Illustrative examples

In this section numerical experiments are performed and discussed in detail to confirm the applicability, reliability, and robustness of the proposed meshless method and also to make sure of the theoretical result analyzed. Two common types of estimators like maximum error and root mean square error (RMSE) are used to make comparison between the numerical result and analytical solution:

$$\begin{aligned} &E_{\infty} = \max \bigl\{ \vert U_{i} - u_{i} \vert , 1\leq i\leq N \bigr\} , \end{aligned}$$
(4.1)
$$\begin{aligned} &\operatorname{RMSE}= \sqrt{\frac{1}{N} \sum _{i=1}^{N} ( U_{i} - u_{i} )^{2}}, \end{aligned}$$
(4.2)

where \(U_{i}\) and \(u_{i}\) are the exact and approximate solutions at locations \(\mathbf{x}_{i}\), respectively. For some natural numbers \(M_{1}\) and \(M_{2}\), let \(\Delta x =( b-a )/ M_{1}\) and \(\Delta y =( d-c ) / M_{2}\) be the step size of space variables along x and y directions, respectively. The space domain is subdivided into equal size subintervals to give the set of nodes \(x_{i} =a+i \Delta x, i=0,1,2,\dots M_{1}\) and \(y_{j} =c+j \Delta y, j=0,1,2,\dots, M_{2}\). In all of the presented numerical experiments, the nodal distribution is placed on a unit square domain \(\Omega = \{ (x,y)| 0\leq x,y\leq1 \}\).

Example 1

Consider the time-fractional NSE in the presence of a body force with the following the exact solution:

$$\begin{aligned} &u ( x,y,t ) =2 x^{2} y ( 1-x )^{2} ( 1-y ) ( 1-2y ) e^{-t}, \end{aligned}$$
(4.3)
$$\begin{aligned} &v ( x,y,t ) =-2x y^{2} ( 1-x ) ( 1-2x ) ( 1-y )^{2} e^{-t}, \end{aligned}$$
(4.4)
$$\begin{aligned} &p ( x,y,t ) = \bigl(x^{2} - y^{2} \bigr)e^{-t}, \end{aligned}$$
(4.5)

which automatically satisfies the initial and boundary conditions. Table 1 gives the maximum and RMSEs of the velocity and pressure for Example 1 with various choices of Δt on regular points. When Δt is taken smaller, the error in the numerical time integration will be reduced. We must keep it reasonably small, provided that we want to closely approximate the exact value of the problem. The exact solutions together with its approximate solutions and corresponding errors at time \(T=1\) with \(\alpha=0.99, \Delta x= \Delta y =0.1,\Delta t=0.1\) are represented graphically in Figure 2. Furthermore, we can observe the behavior of fractional models as the fractional derivative parameter is changed gradually. The approximate solutions are computed for various values of α, some of which are depicted in Figures 3 and 4. It can be seen from Figure 4(c) that the curves of the pressure solution for each value of α varied are nearly identical to each other and too close to be distinguishable. In order to assess the meshless method, the computational results using uneven nodal distribution are also reported in Table 2. For the purpose of comparison, the step size of time variable Δt is chosen to be the same as regularly arranged nodes. When taking account of an overview of RMS error, we can observe that there is very little difference between the results of horizontal and vertical velocities, whereas the pressure results in the case of uneven nodal points are apparently better than those obtained using regular nodal points. The presented numerical results through the figures and tables illustrate and corroborate the high accuracy and validity of the proposed method.

Figure 2
figure 2

The graphs of approximate and exact solutions and corresponding absolute errors at \(\pmb{t=1}\) with \(\pmb{\alpha=0.99}\) , \(\pmb{\Delta x= \Delta y =0.1}\) , \(\pmb{\Delta t=0.1}\) , \(\pmb{{Re}=100}\) for Example 1 : (a), (b) the horizontal and (c), (d) vertical components of velocity and (e), (f) pressure.

Full size image
Figure 3
figure 3

The solution curves for Example 1 at \(\pmb{y=0.4}\) with \(\pmb{\Delta x= \Delta y =0.1}\) , \(\pmb{{Re}=100}\) when \(\pmb{\alpha=0.25}\) (a), (b), (c), \(\pmb{\alpha=0.5}\) (d), (e), (f), and \(\pmb{\alpha=0.75}\) (g), (h), (i).

Full size image
Figure 4
figure 4

The solution curves with different values of α for Example 1 : (a) the horizontal and (b) vertical components of velocity at \(\pmb{x=y=0.4}\) and (c) pressure at \(\pmb{x=0.6}\) and \(\pmb{y=0.4}\) with \(\pmb{\Delta x= \Delta y =0.1}\) , \(\pmb{{Re}=100}\) .

Full size image
Table 1 The maximum and RMSEs of the velocity and pressure for Example 1 with different choices of Δ t on regular points
Full size table
Table 2 The maximum and RMSEs of the velocity and pressure for Example 1 with different choices of Δ t on uneven points
Full size table

Example 2

Consider the most extensively used test problem known as decaying Taylor-Green vortices, for which an analytical closed form solution is available as follows:

$$\begin{aligned} &u ( x,y,t ) = \sin (x) \cos (y) e^{\frac{-2t}{{Re}}}, \end{aligned}$$
(4.6)
$$\begin{aligned} &v ( x,y,t ) =- \cos ( x) \sin (y) e^{\frac{-2t}{{Re}}}, \end{aligned}$$
(4.7)
$$\begin{aligned} &p ( x,y,t ) = \frac{1}{4} \bigl( \cos (2x) + \cos (2y) \bigr) e^{\frac{-4t}{{Re}}}, \end{aligned}$$
(4.8)

which automatically satisfies the initial and boundary conditions. In Table 3 we show the RMSEs of the approximated solution for velocity and pressure with regular nodes\(, \alpha=0.99, N=121, \Delta t=0.1\), and \({Re}=100\) at different times up to \(t=2\). Also the errors found with different values of correlation parameter ω are reported in Table 4. As we see when the correlation parameter \(\omega\in[0.2,1.5]\) becomes larger, the pressure error is reduced gradually. Figure 5 shows the graphs of resulting absolute errors at time \(t=1\) with \(\alpha=0.99, N=121,\Delta t=0.1,{Re}=10\) for both regular and irregular distributions. The same conclusion as Example 1 that not much difference for the velocity solutions is found can be stated. To observe the behavior of fractional models, we compute the numerical solutions for different values of α, some of which are shown in Figures 6 and 7. Taking everything into consideration, it is evident that the computed numerical solutions from the results presented graphically reveal the performance, high accuracy, and validity of the proposed method.

Figure 5
figure 5

The graphs of absolute errors obtained for Example 2 on regular (left-hand side) and irregular (right-hand side) distributions of nodes at time \(\pmb{t=1}\) with \(\pmb{\alpha=0.99}\) , \(\pmb{N=121}\) , \(\pmb{\Delta t=0.1}\) , \(\pmb{{Re}=10}\) : (a), (b) the horizontal and (c), (d) vertical components of velocity and (e), (f) pressure.

Full size image
Figure 6
figure 6

The solution curves for Example 2 at \(\pmb{y=0.4}\) with \(\pmb{\Delta x= \Delta y =0.1}\) , \(\pmb{{Re}=100}\) when \(\pmb{\alpha=0.3}\) (a), (b), (c), \(\pmb{\alpha=0.5}\) (d), (e), (f), and \(\pmb{\alpha=0.7}\) (g), (h), (i).

Full size image
Figure 7
figure 7

The solution curves with different values of α for Example 2 : (a) the horizontal and (b) vertical components of velocity and (c) pressure at \(\pmb{x=0.4}\) and \(\pmb{y=0.4}\) with \(\pmb{\Delta x= \Delta y=0.1}\) , \(\pmb{{Re}=100}\) .

Full size image
Table 3 The RMSEs of the velocity and pressure with regular nodes and fixed \(\pmb{\alpha=0.99}\) , \(\pmb{N=121}\) , \(\pmb{\Delta t=0.1}\) , \(\pmb{{Re}=100}\) at some time levels t for Example 2
Full size table
Table 4 The RMSEs of the velocity and pressure with different values of correlation parameter ω for Example 2
Full size table

5 Concluding remarks

In the numerical experiment, an important point that is worth mentioning here is that due to the fact that the exact solution of the system of equations (3.1)-(3.3) is unavailable, the obtained results have to be compared with analytical solution of classical NSE, which are congruous with what we expected when \(\alpha\rightarrow1\). The most important feature of fractional models is the convergence of the approximation to the classical model. The solution for the integer-order system must be recovered. The reliability of the solutions with α not approaching 1 is guaranteed by the theoretical study shown in Section 3.2. We prove the unconditional stability using a technique based on eigenvalue of the matrix, and the effect of many important parameters on the solution is also investigated thoroughly. The present study is motivated by lack of detailed experimental study and stability analysis in the literature related to a fractional model of full NSE in Cartesian system of coordinate. As we can see, the applications of FDE are manifold and important, but for the multidimensional unsteady-state flow problem it is in its beginning stage and needs further work. In the end, the authors definitely believe that the insights and source of information drawn in this paper with emphasis on the theoretical analysis and numerical study will be of use to the readers interested in fluid flow problem and to the science and engineering community.