Finite-time control for uncertain systems with nonlinear perturbations

Abstract

This study investigates the problem of finite-time control for uncertain systems with nonlinear perturbations. The aim is to design the state-feedback and output-feedback controller which ensure finite-time boundedness and with a desired $H_{\infty}$ performance index υ. Specifically, first, we divide the time-varying delay into non-uniformly subintervals and decompose the corresponding integral intervals to estimate the bounds of integral terms exactly. Second, the conditions obtained in this paper are formulated in terms of linear matrix inequalities (LMIs), which can be efficiently solved via standard numerical software. Finally, numerical examples are presented to demonstrate the effectiveness and advantages of the theoretical results.

1 Introduction

Much work has been done on the robust control of linear systems over the past 20 years [1, 2]. Most of the results in this field relate to the stability and performance criteria defined over an infinite time interval. In many practical applications, however, the main concern is the behavior of the system over a fixed finite time interval. In this sense it appears reasonable to define as stable a system whose state, given some initial conditions, remains within prescribed bounds in the fixed time interval, and as unstable a system which does not. Many are the practical problems in which this kind of stability (FTS) or short-time stability [3, 4] plays an important role: for instance the problem of not exceeding some given bounds for the state trajectories, when some saturation elements are present in the control loop; or the problem of controlling the trajectory of a space vehicle from an initial point to a final point in a prescribed time interval. Time delay frequently occurs in various practical engineering systems, such as static neural networks systems [5, 6], singular systems [7–10], Markovian jump systems [11–15], genetic regulatory network systems [16] and networked control systems (NCS) [17–21].

It is well known that the nonlinearities, as time delays also cause instability and poor performance of practical systems. Therefore, the stability problem of time-delay systems with nonlinear perturbations has received increased attention [22–25]. The free-weighting matrices approach was adopted in [22–24]. Recently, a less conservative delay-dependent stability criterion was provided in [23] by partitioning the delay interval into two segments of equal length, and evaluating the time derivative of a candidate LKF in each segment of the delay interval into two segments of equal length, having this at our disposal, more information on the variation interval of the delay can be employed. Nevertheless, there still exists room for further improvement.

In many practical systems, time delay is unavoidable; see [26–34]. In such cases, a method of FTS has been applied to investigate the system with time varying; see [17, 28]. Motivated by the above discussions, this paper investigates the problem of finite-time control for uncertain systems with nonlinear perturbations. The contributions of this paper can be summarized as follows:

• We divide the variation of the delay into N parts with equal length, and construct a new LKF for these delay intervals, which can be regarded as an extension of the method of [17], consequently, use more information of the delay range, and hence yield less conservative delay-range bounds.

• The system is assumed to be exactly known to designers in [28], i.e., there are no uncertainties in the system, while in this paper, the existence of norm-bounded uncertainties is considered, which will increase the difficulty of FTS analysis.

• Only the state-feedback control is considered in [28], in this paper, we design both the state-feedback and the output-feedback controllers, the output-feedback controller design is much more difficult than the state-feedback one.

• It is well known that a disturbance effect is often the source of instability and poor performance of a system, thus, the disturbance attenuation performance studied via the $H_{\infty}$ control approach is worth to be considered. Compared with [18, 29], we added external disturbance $w(t)$ and unknown nonlinear perturbations $f(x(t),t)$, $g(x(t-\tau(t)),t)$, and this motivates the research.

In this paper, we deal with the problem of finite-time $H_{\infty}$ controller design for uncertain systems with nonlinear perturbations. Both state-feedback controller and output-feedback controller have been considered. By means of LMI techniques, some sufficient LMI-based conditions for the existence of the state-feedback controller and output-feedback controller are given.

The rest of the current paper is organized as follows. Section 2 introduces the problem formulation and some definitions on FTB and finite-time $H_{\infty}$ control. Some FTB criteria obtained for the systems are presented in Section 3. In Section 3, the problem of finite-time $H_{\infty}$ control via state-feedback and output-feedback is discussed. Section 4 gives some numerical examples to demonstrate the effectiveness of our main results. Finally, Section 5 draws the conclusion.

Notation

The superscripts T and $(-1)$ stand for matrix transposition and matrix inverse, respectively; $\mathbb{R}^{n}$ denotes the n-dimensional Euclidean space; the notation $X>Y$ ($X\ge Y$), where X, Y are symmetric matrices, means that $X-Y$ is positive definite (positive semidefinite). ∗ denotes the term that is induced by symmetry. $\operatorname{col}\{x_{1}, x_{2}, \ldots, x_{n}\}$ means $[x_{1}^{T},x_{2}^{T}, \ldots,x_{n}^{T}]^{T}$ and $\operatorname{Sym} \{X\}=X+X^{T}$. The shorthand notation $\operatorname{diag}\{ M_{1}, M_{2}, \ldots, M_{n}\}$ denotes a block diagonal matrix with diagonal blocks being the matrices $M_{1},M_{2}, \ldots, M_{n}$. $\lambda_{\min}(\cdot)$ and $\lambda_{\max}(\cdot)$ denote the smallest and largest eigenvalue of ⋅. $L_{2}^{n}[0 \ N]$ is the space of n-dimensional square integrable function vectors over $[0 \ N]$. Matrices, if their dimensions are not explicitly stated, are assumed to have appropriate dimensions for algebraic operations.

2 Problem formulation and preliminaries

In this paper, we consider the neural networks with time-varying delay systems as follows:

$$ \textstyle\begin{cases} \dot{x}(t)= [A+\Delta A (t ) ]x (t )+ [A_{d}+\Delta A_{d} (t ) ]x (t-\tau (t ) )+ Ff (x (t ),t )\\ \hphantom{\dot{x}(t)=}{}+Gg (x (t-\tau (t ) ),t )+Bu (t ) +Ew (t ),\\ y (t )=Cx (t )+C_{d}x (t-\tau (t ) ),\\ x (t )=\varphi (t ),\quad t\in [-2\tau_{M},0 ], \end{cases} $$

(1)

where $x(t)\in \mathbb{R}^{n}$ is the state vector of the neural network associated with n neurons; $\tau(t)$ is time-varying delay satisfying $0< \tau_{m} \leq\tau(t)\leq\tau_{M}$, $\tilde{\tau}_{d}\leq\dot{\tau}(t)\leq\bar{\tau}_{d}$; $\varphi(\cdot)\in L_{2}[-2\tau_{M}\ 0]$ is an initial function; $u(t)\in\mathbb{R}^{l}$ is the control input and $y(t)\in\mathbb {R}^{m}$ is the measured output. $w(t)\in L_{2}^{q}[0\ {+}\infty]$ is the external disturbances; A, $A_{d}$, C, $C_{d}$, F, G, B, E are known real constant matrices with appropriate dimensions. $\Delta A(t)$, $\Delta A_{d}(t)$ are real-valued unknown matrices representing time-varying parameter uncertainties, and they are assumed to be of the form

$$ \bigl[ \textstyle\begin{array}{@{}c@{\quad}c} \Delta A (t )&\Delta A_{d} (t ) \end{array}\displaystyle \bigr] =L\Sigma (t ) \bigl[ \textstyle\begin{array}{@{}c@{\quad}c} E_{a}&E_{d} \end{array}\displaystyle \bigr], $$

(2)

where L and $E_{i}$ ($i=a,d$) are known real constant matrices and $\Sigma(t)$ is unknown time-varying matrix functions satisfying $\Sigma^{T}(t)\Sigma(t)\leq I$, ∀t. $f(x(t),t)\in \mathbb{R}^{n}$ and $g(x(t-\tau(t)),t)\in \mathbb{R}^{n}$ are unknown nonlinear perturbations with $x(t)$ and $x(t-\tau(t))$, respectively. They satisfy $f(0,t)\equiv 0$, $g(0,t)\equiv0$, and

$$ \textstyle\begin{cases} f^{T} (x (t ),t )f (x (t ),t )\leq \alpha^{2}x^{T} (t )x (t ),\\ g^{T} (x (t-\tau (t ) ),t )g (x (t-\tau (t ) ),t )\leq\beta^{2} x^{T} (t-\tau (t ) )x (t-\tau (t ) ), \end{cases} $$

(3)

where $\alpha\geq0$, $\beta\geq0$ are known scalars. For simplicity we denote $f=f(x(t),t)$, $g=g(x(t-\tau(t),t))$.

Assumption 2.1

For any given positive number η, the external disturbances input $w(t)$ is time varying and satisfies

$$ \int_{0}^{T}w^{T} (t )w (t )\,dt\leq\eta, \quad \eta\geq0. $$

(4)

In this paper, the objective is to find a state-feedback controller and output-feedback controller for the system (1) that will render the corresponding closed-loop dynamic system FTB with a desired $H_{\infty}$ index υ. The definitions of FTS, FTB and finite-time $H_{\infty}$ control are introduced as follows.

Definition 2.1

[21] (FTS)

The time-delay system (1) with $w(t)=0$ is said to be FTS with respect to $(c_{1},c_{2},T,R)$, where $c_{1}>0$, and $R>0$, if there exists a constant $c_{2}$ ($>c_{1}$), such that

$$ x^{T} (t )Rx (t )\leq c_{1},\quad\forall t\in (-\tau _{M},0 ] \quad\Rightarrow\quad x^{T} (t )Rx (t )\leq c_{2},\quad\forall t\in (0,T ], $$

Definition 2.2

[19] (FTB)

Given positive constants $c_{1}$, η, T and a symmetric matrix $R>0$, the time-delay system (1) with $w(t)$ satisfying (5) guaranteed by the state-feedback/output-feedback controller is said to be robustly FTB with respect to $(c_{1},c_{2},T, R,\eta)$, if there exists a constant $c_{2}$ ($>c_{1}$), such that

$$ x^{T} (t )Rx (t )\leq c_{1},\quad\forall t\in (-\tau _{M},0 ] \quad\Rightarrow\quad x^{T} (t )Rx (t )\leq c_{2},\quad\forall t\in (0,T ], $$

Definition 2.3

[19]

If there exists a state-feedback/an output-feedback controller, such that the closed-loop system is FTB with respect to $(c_{1},c_{2},T,R,\eta)$ and under the assumed zero initial condition, the system output satisfies the following cost function inequality for $T>0$ and for all admissible $w(t)$ which satisfy (5):

$$ \int_{0}^{T}y^{T} (t )y (t )\,dt\leq \upsilon^{2} \int _{0}^{T}w^{T} (t )w (t )\,dt. $$

(5)

Then the state-feedback/out-putback controller is called the robust finite-time $H_{\infty}$ controller of the system (1).

Remark 1

FTS and asymptotic stability

It is worth noting that asymptotic stability and FTS are independent concepts: a system which is FTS may not be asymptotically stable, while an asymptotically stable system may not be FTS.

Remark 2

It is easy to see that, given Definition 2.2 of FTB, FTS can be recovered as a particular case by letting $\eta=0$.

Remark 3

From system (1), combining (2), (3), (4), it follows that

$$ \begin{aligned}[b] \bigl\| \dot{\varphi} (t )\bigr\| &\leq \bigl[ \|A\|+\|A_{d}\|+\|L\| \bigl(\|E_{a}\|+\|E_{d}\| \bigr)+ \alpha\|F\|+\beta\|G\| \bigr] \|\varphi\|+\|E\|\eta \\ &=\sqrt{\rho}, \quad\forall t\in [-\tau_{M},0 ]. \end{aligned} $$

(6)

We note that

$$ \rho= \bigl\{ \bigl[ \|A\|+\|A_{d}\|+\|L\| \bigl(\|E_{a}\|+ \|E_{d}\| \bigr)+ \alpha\|F\|+\beta\|G\| \bigr] \|\varphi\|+\|E\|\eta \bigr\} ^{2}. $$

Remark 4

FTB and reachable sets

Since the concept of FTB is, in some way, related to the concept of researchable sets, it is important to clarify the differences between the two ideas. Reachable sets are defined as the set of states that a dynamical system attains given some bounded inputs and starting from some given initial conditions (see [35]). On the other hand, according to Definition 2.2, FTB explores if, given a bound on the state variables and a set of admissible initial states, the state remains confined within the prescribed bound when both non-zero initial conditions and external constant disturbances are considered. An important difference between the two approaches is that in the reachable set analysis the assumption of the system asymptotic stability is exploited [36], while the FTB analysis condition provided in this paper allows one to establish FTB for $t\in[0,T]$ of the system even if it is not asymptotically stable (see also Remark 1).

Lemma 2.1

[5]

For any positive matrix Z and for differentiable signal x in $[\alpha,\beta]\rightarrow\mathbb{R}^{n}$, the following inequality holds:

$$ \int_{\alpha}^{\beta} \dot{x}^{T} (u )Z \dot{x} (u )\geq\frac{1}{\beta-\alpha}\hat{\Omega}^{T} \bar{Z}\hat{\Omega}, $$

where $\bar{Z}=\operatorname{diag} \{Z,3Z\}$ and

$$ \hat{\Omega}= \begin{bmatrix} x (\beta )-x (\alpha )\\ x (\beta )+x (\alpha )-\frac{2}{\beta-\alpha}\int _{\alpha}^{\beta}x (u )\,du \end{bmatrix}. $$

Lemma 2.2

[19]

Let H, E, and $F(t)$ be real matrices of appropriate dimension with $F(t)$ satisfying

$$ F^{T} (t )F (t )\leq I. $$

Then for any scalar $\varepsilon> 0$

$$ HF (t )E+ \bigl(HF (t )E \bigr)^{T}\leq\varepsilon ^{-1}HH^{T}+ \varepsilon E^{T}E. $$

3 Main results

In this section, we shall establish our main results based on LMI framework. Let $N> 0$ be an integer and $\tau_{j}$ ($j=1,2,\ldots,N+1$) be some scalars satisfying

$$ \tau_{m}=\tau_{1}< \tau_{2}< \cdots< \tau_{N}< \tau_{N+1}=\tau_{M}. $$

We can divide the delay interval $[\tau_{m},\tau_{M}]$ into N equidistant subintervals, where $\tau_{m}=\tau_{1}$, $\tau_{N+1}=\tau_{M}$, we denote by $\tau_{\star}$ the length of the subinterval $[\tau_{i},\tau_{i+1}]$, that is, $\tau_{\star}=\tau_{i+1}-\tau_{i}=\frac{(\tau_{M}-\tau_{m})}{N}$. Firstly, we derive sufficient conditions which guarantee the FTB of system in equation (1) under ignoring the control input $u(t)$, secondly, we will consider an unstable system, respectively, design the state-feedback and output-feedback controller to make the system FTB.

3.1 A new model transformation

To extract the time-varying term in $\tau(t)$, we express $x(t-\tau (t))$ as

$$ x \bigl(t-\tau (t ) \bigr)=\delta x (t-\tau_{i} )+ (1- \delta )x (t-\tau_{i+1} ) +\delta\tau_{\star}\chi_{d} (t ), $$

(7)

where $\delta\in(0,1]$, $\delta x(t-\tau_{i})+(1-\delta)x(t-\tau _{i+1})$ denotes the approximation of $x(t-\tau(t))$, $\delta\tau_{\star}\chi_{d}(t)$ is the approximation error. Ignoring the control input $u(t)$, by using equation (7), the system in (1) can be regarded as

$$ \dot{x} (t )=\bar{A}x (t )+\delta\bar{A_{d}}x (t- \tau_{i} ) + (1-\delta )\bar{A_{d}}x (t-\tau_{i+1} )+\delta\tau _{\star} \bar{A_{d}} \chi_{d} (t )+Ff+Gg+Ew (t ), $$

(8)

where

$$ \bar{A}=A+\Delta A (t ),\qquad \bar{A_{d}}=A_{d}+\Delta A_{d} (t ). $$

Remark 5

In [17], $x(t-\tau(t))$ is expressed by $x(t-\tau(t))=\frac{1}{2}x(t-\tau_{1})+\frac{1}{2}(t-\tau_{2})+\frac {\tau_{\star}}{2}\chi_{d}(t)$. In this paper, we use δ ($\delta\in(0,1]$) instead of $\frac {1}{2}$. In this way, we can get less conservative criteria for delay systems via adjusting the parameter δ.

By defining $y_{d}(t)=\dot{x}(t)$, we can rewrite $\chi_{d}(t)$ as

$$ \begin{aligned}[b] \chi_{d} (t )&= \frac{1}{\delta\tau_{\star}} \bigl[x \bigl(t-\tau (t ) \bigr)-\delta x (t- \tau_{i} )- (1-\delta )x (t-\tau_{i+1} ) \bigr] \\ &=\frac{1}{\delta\tau_{\star}} \bigl\{ (1-\delta ) \bigl[x \bigl(t-\tau (t ) \bigr)- x (t- \tau_{i+1} ) \bigr]-\delta \bigl[x (t-\tau_{i} )-x \bigl(t- \tau (t ) \bigr) \bigr] \bigr\} \\ &=\frac{1-\delta}{\delta\tau_{\star}} \int_{t-\tau_{i+1}}^{t-\tau (t )}\dot{x} (s )\,ds- \frac{1}{\tau_{\star}} \int_{t-\tau (t )}^{t-\tau_{i}}\dot {x} (s )\,ds \\ &=\frac{1}{\tau_{\star}} \int_{t-\tau_{i+1}}^{t-\tau_{i}}\sigma (\theta )y_{d} ( \theta )\,d\theta, \end{aligned} $$

(9)

where

$$ \sigma (\theta )= \textstyle\begin{cases} \frac{1-\delta}{\delta}, & t-\tau_{i+1}\leq\theta< t-\tau (t ),\\ -1, & t-\tau (t )\leq\theta\leq t-\tau_{i}. \end{cases} $$

Hence, equation (1) can be written as

$$ \begin{bmatrix} y_{d} (t )\\ y (t ) \end{bmatrix} = \begin{bmatrix} \Gamma_{1}\\ \Gamma_{2} \end{bmatrix} \begin{bmatrix} \zeta (t )\\ \chi_{d} (t ) \end{bmatrix}, $$

(10)

where

$$\begin{aligned}& \zeta (t )= \operatorname{col} \biggl\{ x (t ),x (t-\tau_{i} ),x (t-\tau _{i+1} ),f, g, \int_{t-\tau_{i}}^{t}x (s )\,ds, \int_{t-\tau_{i+1}}^{t-\tau_{i}}x (s )\,ds,w (t ) \biggr\} , \\& \Gamma_{1}^{T}=\operatorname{col} \bigl\{ \bar{A}^{T},\delta \bar{A}_{d}^{T}, (1-\delta )\bar{A}_{d}^{T}, F^{T},G^{T},0,0,E^{T},\delta\tau_{\star} \bar{A}_{d}^{T} \bigr\} , \\& \Gamma_{2}^{T}=\operatorname{col} \bigl\{ C^{T},\delta C_{d}^{T}, (1-\delta )C_{d}^{T},0,0,0,0,0, \delta\tau_{\star}C_{d}^{T} \bigr\} . \end{aligned}$$

For convenience of representation, the following notation is introduced:

$$\begin{aligned}& e_{i}=\operatorname{col} \{\underbrace{0_{n},\ldots ,0_{n}}_{i-1},I_{n}, \underbrace{0_{n},\ldots,0_{n}}_{9-i} \}, \\& \xi^{T} (t )=\bigl[ \textstyle\begin{array}{@{}c@{\quad}c} \zeta^{T} (t )&\chi_{d}^{T} (t ) \end{array}\displaystyle \bigr]. \end{aligned}$$

In order to derive less conservative criteria, we firstly analyze the method of choosing LKF for the above-mentioned systems (10) and asymptotically stable conditions are presented in this section.

3.2 FTB analysis

In this subsection, we aim to analyze the FTB of the system consisting of (10) and derive the sufficient conditions of FTB.

Theorem 3.1

For some given scalars α, β, $c_{1}$, η, $0< \tau _{m}\leq\tau_{M}$, $\tilde{\tau}_{d}$, ψ, $\bar{\tau}_{d}$, $\delta \in(0,1]$, $T>0$, $\gamma\geq1$, ρ, the system in (10) is FTB with respect to $(c_{1},c_{2},T,\psi,\eta)$, if there exist symmetric positive matrices

$$P= \begin{bmatrix} P_{11}&P_{12}&P_{13}\\ \ast&P_{22}&P_{23}\\ \ast&\ast&P_{33} \end{bmatrix} \in\mathbb{R}^{3n\times3n}, $$

$Q_{1},Q_{2}, X_{1},X_{2},X_{3},X_{4},X_{5}\in\mathbb{R}^{n\times n}$, positive scalars $c_{2}$, $\omega_{j}$ ($j=1,2,\ldots,12$), ε, and any positive scalars $\varepsilon_{1}$, $\varepsilon_{2}$, such that, for $i=1,2,3,\ldots,N$, the following LMIs hold:

$$\begin{aligned}& \begin{bmatrix} \psi- P_{11}&0\\ \ast&P_{11}-2\psi \end{bmatrix}< 0, \end{aligned}$$

(11)

$$\begin{aligned}& \begin{bmatrix} -c_{2}e^{-\gamma T}&\sqrt{2c_{1}+\eta (1-e^{-\gamma T} )} &\theta_{1}&\theta_{2}&\cdots&\theta_{12}\\ \ast&-I&0&0&\cdots&0\\ \ast&\ast&-\omega_{1}&0&\cdots&0\\ \ast&\ast&\ast&-\omega_{2}&\cdots&0\\ \vdots&\vdots&\vdots&\vdots&\ddots&\vdots\\ \ast&\ast&\ast&\ast&\cdots&-\omega_{12} \end{bmatrix}< 0, \end{aligned}$$

(12)

where

$$\begin{aligned}& \theta_{1}=\sqrt{\frac{\tau_{i}^{3}}{2}\rho} \omega_{1},\qquad \theta_{2}=\sqrt{ \frac{\tau_{i+1}^{3}}{2}\rho}\omega_{2},\qquad \theta_{3}=\sqrt {\frac{\tau_{\star}^{2} (\tau_{i}+\tau_{i+1} )}{2}\rho}\omega_{3}, \\& \theta_{4}=\sqrt{\tau_{\star} \biggl[- \frac{\tau_{i}^{2}}{2}+ \frac{\tau_{i+1}^{2}}{2} \biggr]\rho}\omega_{4}, \qquad \theta_{5}=\sqrt{\tau_{\star} \biggl[ \frac{\tau_{i+1}^{2}}{2}- \frac{\tau_{i}^{2}}{2} \biggr]\rho}\omega_{5},\qquad \theta_{6}=\tau_{i}\sqrt{\frac{c_{1}}{\lambda_{\min} (\psi )}} \omega_{6}, \\& \theta_{7}=\tau_{i+1}\sqrt{ \frac{c_{1}}{\lambda_{\min} (\psi )}}\omega_{7},\qquad \theta_{8}=\sqrt{ \frac{2\tau_{i}c_{1}}{\lambda_{\min} (\psi )}}\omega_{8}, \qquad \theta_{9}=\sqrt{\frac{2\tau_{i+1}c_{1}}{\lambda_{\min} (\psi )}}\omega_{9}, \\& \theta_{10}=\sqrt{\frac{2\tau_{i}\tau_{i+1}c_{1}}{\lambda_{\min} (\psi )}}\omega_{10},\qquad \theta_{11}=\sqrt{\frac{\tau_{i}c_{1}}{\lambda_{\min} (\psi )}}\omega_{11},\qquad \theta_{12}=\sqrt{\frac{\tau_{i+1}c_{1}}{\lambda_{\min} (\psi )}}\omega_{12}, \\& \begin{bmatrix} \Pi&\Phi_{1}&\Phi_{2}&\Phi_{3}&\Phi_{4}&\Phi_{5}&\Phi_{6}&\Phi_{7}\\ \ast&-X_{1}&0&0&0&0&\varepsilon\tau_{i}X_{1}L&0\\ \ast&\ast&-X_{2}&0&0&0&\varepsilon\tau_{i+1}X_{2}L&0\\ \ast&\ast&\ast&-X_{3}&0&0&\varepsilon\tau_{\star}X_{3}L&0\\ \ast&\ast&\ast&\ast&-X_{4}&0&\varepsilon\tau_{\star}X_{4}L&0\\ \ast&\ast&\ast&\ast&\ast&-X_{5}&\varepsilon\tau_{\star}X_{5}L&0\\ \ast&\ast&\ast&\ast&\ast&\ast&-\varepsilon I&0\\ \ast&\ast&\ast&\ast&\ast&\ast&\ast&-\varepsilon I \end{bmatrix}< 0, \end{aligned}$$

(13)

where $\Pi=(\Pi_{ij})_{9\times9}$ with

$$\begin{aligned}& \Pi_{11}=P_{11}A+A^{T}P_{11} +P_{12}+P_{12}^{T}+P_{13}+P_{13}^{T}+ Q_{1}+Q_{2}+\varepsilon_{1}\alpha^{2}I-4 \Sigma_{1}-4\Sigma_{2}-\gamma P_{11}, \\& \Pi_{12}=\delta P_{11}A_{d}-P_{12}-2 \Sigma_{1},\qquad \Pi_{13}= (1-\delta )P_{11}A_{d}-P_{13}-2 \Sigma_{2},\qquad\Pi_{14}= P_{11}F,\\& \Pi_{15}=P_{11}G, \qquad \Pi_{16}=P_{22}+P_{23}+P_{23}^{T}+P_{33}+A^{T}P_{12}+A^{T}P_{13} +\frac{6}{\tau_{i}}\Sigma_{1}+\frac{6}{\tau_{i+1}}\Sigma_{2}, \\& \Pi_{17}=A^{T}P_{13}+P_{23}+ \frac{6}{\tau_{i+1}}\Sigma_{2}+P_{33},\qquad \Pi_{18}=P_{11}E, \qquad \Pi_{19}=\delta\tau_{\star}P_{11}A_{d}, \\& \Pi_{22}=-Q_{1}+\varepsilon_{2} \beta^{2} \delta^{2}I-4\Sigma_{1}, \qquad \Pi_{23}=\varepsilon_{2}\beta^{2}\delta (1-\delta )I,\\& \Pi_{26}=-P_{22}-P_{23} +\delta A_{d}^{T} (P_{12}+P_{13} )+ \frac{6}{\tau_{i}}\Sigma _{1}, \qquad \Pi_{27}=-P_{23}+\delta A_{d}^{T}P_{13}, \\& \Pi_{29}=\varepsilon_{2}\beta^{2} \delta^{2}\tau_{\star}I,\qquad \Pi_{33}=-Q_{2}-4 \Sigma_{2}+\beta^{2}\varepsilon_{2} (1-\delta )^{2}I, \\& \Pi_{36}=\frac{6}{\tau_{i+1}}\Sigma_{2}+ (1-\delta ) A_{d}^{T} (P_{12}+P_{13} )-P_{23}^{T}-P_{33},\\& \Pi_{37}= \frac{6}{\tau_{i+1}}\Sigma_{2}+ (1-\delta )A_{d}^{T}P_{13}-P_{33}, \qquad \Pi_{39}=\varepsilon_{2}\beta^{2} (1-\delta ) \delta\tau_{\star }I, \\& \Pi_{44}=-\varepsilon_{1}I,\qquad \Pi_{46}=F^{T} (P_{12}+P_{13} ),\qquad \Pi_{47}=F^{T}P_{13},\qquad \Pi_{55}=-\varepsilon_{2}I,\\& \Pi_{56}=G^{T} (P_{12}+P_{13} ),\qquad \Pi_{57}=G^{T}P_{13}, \qquad \Pi_{66}=-\frac{12}{\tau_{i}^{2}}\Sigma_{1}-\frac{12}{\tau _{i+1}^{2}} \Sigma_{2},\\& \Pi_{67}=-\frac{12}{\tau_{i+1}^{2}} \Sigma_{2},\qquad \Pi_{68}= \bigl(P_{12}^{T}+P_{13}^{T} \bigr)E,\qquad \Pi_{69}=\delta\tau_{\star} \bigl(P_{12}^{T}+P_{13}^{T} \bigr)A_{d},\\& \Pi_{77}=-\frac{12}{\tau_{i+1}^{2}} \Sigma_{2}, \qquad \Pi_{78}=P_{13}^{T}E,\qquad \Pi_{79}= \delta\tau_{\star}P_{13}^{T}A_{d},\\& \Pi_{88}=-\gamma I,\qquad \Pi_{99}=-\tau_{\star}M+ \varepsilon_{2}\beta^{2}\delta^{2} \tau_{\star}^{2}I. \end{aligned}$$

The other entries of Π are zeros. We have

$$\begin{aligned}& X_{1}-\frac{\tau_{\star}\bar{\tau}_{d}}{\tau_{i}}X_{4}\geq0, \end{aligned}$$

(14)

$$\begin{aligned}& 0< X_{i}< \omega_{i}I,\quad i=1,2,3,4,5, \end{aligned}$$

(15)

$$\begin{aligned}& 0< P_{22}< \omega_{6}I,\quad 0< P_{33}< \omega_{7}I,\quad |P_{23}|< \omega_{10}I,\quad 0< Q_{1}< \omega_{11}I,\quad 0< Q_{2}< \omega_{12}I, \\& |P_{12}|< \omega_{8}I,\qquad |P_{13}|< \omega_{9}I, \\& \begin{aligned}[b] \varpi={}& \bigl( \tau_{i}^{2} \omega_{6} +\tau_{i+1}^{2}\omega_{7} +2 \tau_{i}\omega_{8} +2\tau_{i+1} \omega_{9} +2\tau_{i}\tau_{i+1} \omega_{10} +\tau_{i}\omega_{11} + \tau_{i+1}\omega_{12} \bigr)\frac{c_{1}}{\lambda_{\min} (\psi )} \\ &{}+ \biggl\{ \frac{\tau_{i}^{3}}{2}\omega_{1} + \frac{\tau_{i+1}^{3}}{2}\omega_{2} +\frac{\tau_{\star}^{2}}{2} (\tau_{i}+ \tau_{i+1} )\omega_{3} +\tau_{\star} \omega_{4} \biggl[-\frac{\tau_{i}^{2}}{2}+\frac{\tau_{i+1}^{2}}{2} \biggr] \\ &{}+\tau_{\star}\omega_{5} \biggl[-\frac{\tau_{i}^{2}}{2}+ \frac{\tau_{i+1}^{2}}{2} \biggr] \biggr\} \rho, \end{aligned} \\& {{\bar{\Phi}_{1}= \bigl[ \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{}} \tau_{i}X_{1}\bar{A}&\tau_{i}\delta X_{1}\bar{A}_{d}& \tau_{i} (1-\delta )X_{1}\bar{A}_{d}&\tau_{i} X_{1}F&\tau_{i}X_{1}G&0&0& \tau_{i} X_{1}E&\tau_{\star} \tau_{i}\delta X_{1}\bar{A}_{d} \end{array}\displaystyle \bigr]^{T}}}, \\& {{\bar{\Phi}_{2}= \bigl[ \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{}} \tau_{i+1}X_{2}\bar{A}&\tau_{i+1}\delta X_{2}\bar{A}_{d}& \tau_{i+1} (1-\delta )X_{2}\bar{A}_{d}&\tau_{i+1} X_{2}F&\tau_{i+1}X_{2}G&0&0& \tau_{i+1} X_{2}E&\tau_{\star} \tau _{i+1}\delta X_{2}\bar{A}_{d} \end{array}\displaystyle \bigr]^{T}}}, \\& {{\bar{\Phi}_{3}= \bigl[ \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{}} \tau_{\star}X_{3}\bar{A}&\tau_{\star}\delta X_{3}\bar{A}_{d}& \tau_{\star} (1-\delta )X_{3}\bar{A}_{d}&\tau_{\star} X_{3}F&\tau_{\star}X_{3}G&0&0& \tau_{\star}X_{3}E&\tau_{\star }^{2}\delta X_{3}\bar{A}_{d} \end{array}\displaystyle \bigr]^{T}}}, \\& {{\bar{\Phi}_{4}= \bigl[ \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{}} \tau_{\star}X_{4}\bar{A}&\tau_{\star}\delta X_{4}\bar{A}_{d}& \tau_{\star} (1-\delta )X_{4}\bar{A}_{d}&\tau_{\star} X_{4}F&\tau_{\star}X_{4}G&0&0& \tau_{\star}X_{4}E&\tau_{\star }^{2}\delta X_{4}\bar{A}_{d} \end{array}\displaystyle \bigr]^{T}}}, \\& {{\bar{\Phi}_{5}= \bigl[ \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{}} \tau_{\star}X_{5}\bar{A}&\tau_{\star}\delta X_{5}\bar{A}_{d}& \tau_{\star} (1-\delta )X_{5}\bar{A}_{d}&\tau_{\star} X_{5}F&\tau_{\star}X_{5}G&0&0&\tau_{\star}X_{5}E& \tau_{\star }^{2}\delta X_{5}\bar{A}_{d} \end{array}\displaystyle \bigr]^{T}}}, \\& {{\Phi_{1}= \bigl[ \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{}} \tau_{i}X_{1}A&\tau_{i}\delta X_{1}A_{d}& \tau_{i} (1-\delta )X_{1}A_{d}&\tau_{i} X_{1}F&\tau_{i}X_{1}G&0&0& \tau_{i}X_{1}E&\tau_{\star} \tau_{i}\delta X_{1}A_{d} \end{array}\displaystyle \bigr]^{T}}}, \\& {{\Phi_{2}= \bigl[ \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{}} \tau_{i+1}X_{2}A&\tau_{i+1}\delta X_{2}A_{d}& \tau_{i+1} (1-\delta )X_{2}A_{d}&\tau_{i+1} X_{2}F&\tau_{i+1}X_{2}G&0&0& \tau_{i+1}X_{2}E&\tau_{\star} \tau _{i+1}\delta X_{2}A_{d} \end{array}\displaystyle \bigr]^{T}}}, \\& {{\Phi_{3}= \bigl[ \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{}} \tau_{\star}X_{3}A&\tau_{\star}\delta X_{3}A_{d}& \tau_{\star} (1-\delta )X_{3}A_{d}&\tau_{\star} X_{3}F&\tau_{\star}X_{3}G&0&0& \tau_{\star}X_{3}E&\tau_{\star }^{2}\delta X_{3}A_{d} \end{array}\displaystyle \bigr]^{T}}}, \\& {{\Phi_{4}= \bigl[ \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{}} \tau_{\star}X_{4}A&\tau_{\star}\delta X_{4}A_{d}& \tau_{\star} (1-\delta )X_{4}A_{d}&\tau_{\star} X_{4}F&\tau_{\star}X_{4}G&0&0&\tau_{\star}X_{4}E& \tau_{\star }^{2}\delta X_{4}A_{d} \end{array}\displaystyle \bigr]^{T}}}, \\& {{\Phi_{5}= \bigl[ \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{}} \tau_{\star}X_{5}A&\tau_{\star}\delta X_{5}A_{d}& \tau_{\star} (1-\delta )X_{5}A_{d}&\tau_{\star} X_{5}F&\tau_{\star}X_{5}G&0&0&\tau_{\star}X_{5}E& \tau_{\star }^{2}\delta X_{5}A_{d} \end{array}\displaystyle \bigr]^{T}}}, \\& {{\Phi_{6}= \bigl[ \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{}} \varepsilon L^{T}P_{11}&0&0&0&0&\varepsilon L^{T} (P_{12}+P_{13} ) &\varepsilon L^{T}P_{13} &0&0 \end{array}\displaystyle \bigr]^{T}}}, \\& {{\Phi_{7}= \bigl[ \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{}} E_{a}&\delta E_{d}& (1-\delta ) E_{d}&0&0&0&0&0&\delta\tau_{\star}E_{d} \end{array}\displaystyle \bigr]^{T}}}, \\& \Omega_{1}=\operatorname{Sym} \bigl\{ [e_{1},e_{6},e_{6}+e_{7} ] P \bigl[\Gamma_{1}^{T},e_{1}-e_{2},e_{1}-e_{3} \bigr]^{T} \bigr\} , \\& \Omega_{2}=e_{1} (Q_{1}+Q_{2} )e_{1}^{T}-e_{2}Q_{1}e_{2}^{T}-e_{3}Q_{2}e_{3}^{T}, \\& \Pi_{1}=\Gamma_{1}^{T} S \Gamma_{1},\qquad \Pi_{2}=- \bigl[ \textstyle\begin{array}{@{}c@{\quad}c@{}} e_{1}-e_{2}&e_{1}+e_{2}-2\frac{1}{\tau_{i}}e_{6} \end{array}\displaystyle \bigr] \bar{ \Sigma}_{1} \bigl[ \textstyle\begin{array}{@{}c@{\quad}c@{}} e_{1}-e_{2}&e_{1}+e_{2}-2\frac{1}{\tau_{i}}e_{6} \end{array}\displaystyle \bigr]^{T}, \\& \Pi_{3}=- \bigl[ \textstyle\begin{array}{@{}c@{\quad}c@{}} e_{1}-e_{3}&e_{1}+e_{3}-2\frac{1}{\tau_{i+1}} (e_{6}+e_{7} ) \end{array}\displaystyle \bigr] \bar{ \Sigma}_{2} \bigl[ \textstyle\begin{array}{@{}c@{\quad}c@{}} e_{1}-e_{3}&e_{1}+e_{3}-2\frac{1}{\tau_{i+1}} (e_{6}+e_{7} ) \end{array}\displaystyle \bigr]^{T}, \\& \Pi_{4}=-\tau_{\star}e_{9}Me_{9}^{T},\qquad \Pi_{5}=\varepsilon_{1} \bigl(-e_{4}e_{4}^{T}+ \alpha ^{2}e_{1}e_{1}^{T} \bigr),\qquad \Pi_{6}=\varepsilon_{2} \bigl(-e_{5}e_{5}^{T}+ \beta^{2}\Gamma_{3}\Gamma _{3}^{T} \bigr), \\& \Gamma_{3}=\delta e_{2}+ (1-\delta )e_{3}+\delta\tau_{\star }e_{9}, \qquad \Sigma_{1}= X_{1}-\frac{\tau_{\star}\bar{\tau}_{d}}{\tau_{i}}X_{4}, \qquad \bar{\Sigma}_{1}=\operatorname{diag} \{\Sigma_{1},3 \Sigma_{1} \}, \\& \Sigma_{2}= X_{2}+ \frac{\tau_{\star}\tilde{\tau}_{d}}{\tau_{i}}X_{5}, \qquad \bar{\Sigma}_{2}= \operatorname{diag} \{\Sigma_{2},3\Sigma_{2} \}, \\& S=\tau_{i}^{2}X_{1}+\tau_{i+1}^{2}X_{2}+ \tau_{\star}^{2}X_{3} +\tau_{\star}^{2}X_{4}+ \tau_{\star}^{2}X_{5}, \qquad P_{11}= \psi^{\frac{1}{2}}\tilde{P}_{11}\psi^{\frac{1}{2}}, \\& \lambda_{1}=\lambda_{\min}(\tilde{P}_{11}),\qquad \lambda_{2}=\lambda_{\max }(\tilde{P}_{11}), \end{aligned}$$

(16)

Proof

When $\tau(t)\in[\tau_{i},\tau_{i+1}]$, construct a LKF candidate:

$$\begin{aligned} V_{i} ( x_{t} )=\sum_{j=1}^{6}V_{ij} ( x_{t} ), \end{aligned}$$

(17)

where

$$\begin{aligned}& V_{i1} ( x_{t} ) =\eta^{T} (t )P\eta (t ), \\& V_{i2} ( x_{t} ) = \int_{t-\tau_{i}}^{t}x^{T} (s )Q_{1}x (s )\,ds + \int_{t-\tau_{i+1}}^{t}x^{T} (s )Q_{2}x (s )\,ds, \\& V_{i3} ( x_{t} ) =\tau_{i} \int_{-\tau_{i}}^{0} \int _{t+\theta}^{t}\dot{x}^{T} (s )X_{1} \dot{x} (s )\,ds\,d\theta+\tau_{i+1} \int_{-\tau_{i+1}}^{0} \int _{t+\theta}^{t}\dot{x}^{T} (s )X_{2} \dot{x} (s )\,ds\,d\theta, \\& V_{i4} ( x_{t} ) =\tau_{\star} \int_{-\tau_{i+1}}^{-\tau _{i}} \int_{t+\theta}^{t} \dot{x}^{T} (s )X_{3} \dot{x} (s )\,ds\,d\theta, \\& V_{i5} ( x_{t} ) =\tau_{\star} \int_{-\tau (t ) }^{-\tau_{i}} \int_{t+\theta}^{t} \dot{x}^{T} (s )X_{4} \dot{x} (s )\,ds\,d\theta, \\& V_{i6} ( x_{t} ) =\tau_{\star} \int_{-\tau_{i+1} }^{-\tau (t )} \int_{t+\theta}^{t} \dot{x}^{T} (s )X_{5} \dot{x} (s )\,ds\,d\theta, \end{aligned}$$

with

$$ \eta (t )=\operatorname{col} \biggl\{ x (t ), \int_{t-\tau_{i}}^{t}x (s )\,ds, \int_{t-\tau_{i+1}}^{t}x (s )\,ds \biggr\} . $$

Calculating the time derivative of $V(x_{t})$ along the solution of (10), we can get

$$ \dot{V}_{i} ( x_{t} )= \sum_{j=1}^{6} \dot{V}_{ij} ( x_{t} ), $$

(18)

where

$$\begin{aligned}& \dot{V_{i1}} (x_{t} )=2 \eta^{T} (t )P\dot{\eta }^{T} (t ) =2 \bigl[ \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{}} x^{T} (t )&\int_{t-\tau_{i}}^{t}x^{T} (s )\,ds&\int _{t-\tau_{i+1}}^{t}x^{T} (s )\,ds \end{array}\displaystyle \bigr] \times \begin{bmatrix} P_{11}&P_{12}&P_{13}\\ \ast&P_{22}&P_{23}\\ \ast&\ast&P_{33} \end{bmatrix} \\& \hphantom{\dot{V_{i1}} (x_{t} )=}{}\times \begin{bmatrix} \dot{x} (t )\\ x (t )-x (t-\tau_{i} )\\ x (t )-x (t-\tau_{i+1} ) \end{bmatrix} \\& \hphantom{\dot{V_{i1}} (x_{t} )}=\xi^{T} (t )\Omega_{1}\xi (t ), \end{aligned}$$

(19)

$$\begin{aligned}& \begin{aligned}[b] \dot{V}_{i2} (x_{t} )&=x^{T} (t ) (Q_{1}+Q_{2} )x (t )- x^{T} (t- \tau_{i} )Q_{1}x (t-\tau_{i} ) -x^{T} (t-\tau_{i+1} )Q_{2}x (t-\tau_{i+1} ) \\ &=\xi^{T} (t )\Omega_{2}\xi (t ), \end{aligned} \end{aligned}$$

(20)

$$\begin{aligned}& \begin{aligned}[b] \dot{V}_{i3} (x_{t} )={}& \dot{x}^{T} (t ) \bigl[\tau _{i}^{2}X_{1} +\tau_{i+1}^{2}X_{2} \bigr]\dot{x} (t ) - \tau_{i} \int_{t-\tau_{i}}^{t}\dot{x}^{T} (s )X_{1}\dot{x} (s )\,ds \\ &{}- \tau_{i+1} \int_{t-\tau_{i+1}}^{t}\dot{x}^{T} (s )X_{2}\dot {x} (s )\,ds, \end{aligned} \end{aligned}$$

(21)

$$\begin{aligned}& \dot{V}_{i4} (x_{t} )=\tau_{\star}^{2} \dot{x}^{T} (t ) X_{3}\dot{x} (t )- \tau_{\star} \int_{t-\tau_{i+1}}^{t-\tau_{i}}\dot{x}^{T} (s ) X_{3}\dot{x} (s )\,ds, \end{aligned}$$

(22)

$$\begin{aligned}& \begin{aligned}[b] \dot{V}_{i5} (x_{t} )={}& \tau_{\star} \bigl(\tau (t )-\tau_{i} \bigr) \dot{x}^{T} (t )X_{4} \dot{x} (t )-\tau_{\star} \bigl(1-\dot{\tau} (t ) \bigr) \int_{t-\tau (t )}^{t-\tau_{i}}\dot{x}^{T} (s ) X_{4}\dot{x} (s )\,ds \\ &{}+\tau_{\star}\dot{\tau} (t ) \int_{t-\tau_{i}}^{t}\dot {x}^{T} (s ) X_{4}\dot{x} (s )\,ds, \end{aligned} \end{aligned}$$

(23)

$$\begin{aligned}& \begin{aligned}[b] \dot{V}_{i6} (x_{t} )={}& \tau_{\star} \bigl(\tau_{i+1}-\tau (t ) \bigr) \dot{x}^{T} (t )X_{5}\dot{x} (t ) -\tau_{\star} \bigl(1-\dot{\tau} (t ) \bigr) \int_{t-\tau _{i+1}}^{t-\tau (t )} \dot{x}^{T} (s )X_{5}\dot{x} (s )\,ds \\ &{}-\tau_{\star}\dot{\tau} (t ) \int_{t-\tau_{i+1}}^{t} \dot{x}^{T} (s )X_{5}\dot{x} (s )\,ds, \end{aligned} \end{aligned}$$

(24)

Using Lemma 2.1, one obtains

$$\begin{aligned} &-\tau_{i} \int_{t-\tau_{i}}^{t}\dot{x}^{T} (s ) X_{1}\dot{x} (s )\,ds+\tau_{\star}\dot{\tau} (t ) \int _{t-\tau_{i}}^{t}\dot{x}^{T} (s ) X_{4}\dot{x} (s )\,ds \\ &\quad=-\tau_{i} \int_{t-\tau_{i}}^{t}\dot{x}^{T} (s ) \biggl[ X_{1}-\frac{\tau_{\star}\dot{\tau} (t )}{\tau_{i}}X_{4} \biggr]\dot{x} (s )\,ds \\ &\quad\leq-\tau_{i} \int_{t-\tau_{i}}^{t}\dot{x}^{T} (s ) \biggl[ X_{1}-\frac{\tau_{\star}\bar{\tau}_{d}}{\tau_{i}}X_{4} \biggr]\dot {x} (s )\,ds \\ &\quad\leq- \begin{bmatrix} x (t )-x (t-\tau_{i} )\\ x (t )+x (t-\tau_{i} )-2\frac{1}{\tau_{i}}\int_{t-\tau _{i}}^{t} x (s )\,ds \end{bmatrix} ^{T} \bar{\Sigma}_{1} \begin{bmatrix} x (t )-x (t-\tau_{i} )\\ x (t )+x (t-\tau_{i} )-2\frac{1}{\tau_{i}}\int_{t-\tau _{i}}^{t} x (s )\,ds \end{bmatrix} \\ &\quad=\xi^{T} (t )\Pi_{2}\xi (t ), \end{aligned}$$

(25)

where

$$\begin{aligned}& X_{1}-\frac{\tau_{\star}\bar{\tau}_{d}}{\tau_{i}}X_{4}\geq0, \end{aligned}$$

(26)

$$\begin{aligned}& \begin{aligned}[b] &{-}\tau_{i+1} \int_{t-\tau_{i+1}}^{t}\dot{x}^{T} (s )X_{2}\dot {x} (s )\,ds -\tau_{\star}\dot{\tau} (t ) \int_{t-\tau_{i+1}}^{t} \dot{x}^{T} (s )X_{5}\dot{x} (s )\,ds \\ &\quad=-\tau_{i+1} \int_{t-\tau_{i+1}}^{t}\dot{x}^{T} (s ) \biggl[X_{2}+\frac{\tau_{\star}\dot{\tau} (t )}{\tau _{i+1}}X_{5} \biggr] \dot{x} (s )\,ds \\ &\quad\leq-\tau_{i+1} \int_{t-\tau_{i+1}}^{t}\dot{x}^{T} (s ) \biggl[X_{2}+\frac{\tau_{\star}\tilde{\tau}_{d}}{\tau_{i+1}}X_{5} \biggr] \dot{x} (s )\,ds \\ &\quad\leq- \begin{bmatrix} x (t )-x (t-\tau_{i+1} )\\ x (t )+x (t-\tau_{i+1} )-2\frac{1}{\tau_{i+1}}\int _{t-\tau_{i+1}}^{t} x (s )\,ds \end{bmatrix} ^{T}\\ &\qquad{}\times \bar{\Sigma}_{2} \begin{bmatrix} x (t )-x (t-\tau_{i+1} )\\ x (t )+x (t-\tau_{i+1} )-2\frac{1}{\tau_{i+1}}\int _{t-\tau_{i+1}}^{t} x (s )\,ds \end{bmatrix} \\ &\quad=\xi^{T} (t )\Pi_{3}\xi (t ), \end{aligned} \end{aligned}$$

(27)

there exists $\delta\in(0,1]$, subject to $\tau_{\star}X_{3}+\tau _{\star}(1-\bar{\tau}_{d})X_{4} =(\frac{\delta}{1-\delta})^{2}[\tau_{\star}X_{3}+\tau_{\star}(1-\bar {\tau}_{d})X_{5}]$, we define it as M, using Jensen’s inequality [23]

$$ \begin{aligned}[b] &{-}\tau_{\star} \int_{t-\tau_{i+1}}^{t-\tau_{i}}\dot{x}^{T} (s ) X_{3}\dot{x} (s )\,ds-\tau_{\star} \bigl(1-\dot{\tau} (t ) \bigr) \int_{t-\tau (t )}^{t-\tau_{i}} \dot{x}^{T} (s )X_{4}\dot{x} (s )\,ds \\ &\qquad{}-\tau_{\star} \bigl(1-\dot{\tau} (t ) \bigr) \int_{t-\tau_{i+1}}^{t-\tau (t )} \dot{x}^{T} (s )X_{5}\dot{x} (s )\,ds \\ &\quad\leq- \int_{t-\tau (t )}^{t-\tau_{i}} \dot{x}^{T} (s )M\dot{x} (s )\,ds- \int_{t-\tau _{i+1}}^{t-\tau (t )} \dot{x}^{T} (s ) \biggl( \frac{1-\delta}{\delta} \biggr)^{2}M\dot{x} (s )\,ds \\ &\quad=- \int_{t-\tau_{i+1}}^{t-\tau_{i}}\dot{x}^{T} (s ) \sigma^{2} (s )M \dot{x}^{T} (s )\,ds \\ &\quad\leq-\tau_{\star}\chi_{d}^{T} (t )M \chi_{d} (t ). \end{aligned} $$

(28)

Combining equations (21)-(28), we obtain

$$ \dot{V_{i3}} (x_{t} )+\dot{V_{i4}} (x_{t} ) +\dot{V_{i5}} (x_{t} )+ \dot{V_{i6}} (x_{t} )\leq \xi^{T} (t ) ( \Pi_{1}+\Pi_{2}+\Pi_{3}+\Pi_{4} ) \xi (t ). $$

(29)

On the other hand, for any scalars $\varepsilon_{1}\geq0$, $\varepsilon _{2}\geq0$, it follows from (3) that

$$\begin{aligned}& \varepsilon_{1} \bigl[f^{T}f-\alpha^{2}x^{T} (t )x (t ) \bigr]\leq0, \end{aligned}$$

(30)

$$\begin{aligned}& \varepsilon_{2} \bigl[g^{T}g-\beta^{2}x^{T} \bigl(t-\tau (t ) \bigr)x \bigl(t-\tau (t ) \bigr) \bigr]\leq0. \end{aligned}$$

(31)

With the expression of system in (10) and combining equations (19)-(31), $\dot{V}_{i}(x_{t})$ can be finally written as

$$ \dot{V}_{i} ( x_{t} )\leq\xi^{T} (t ) \Biggl[\Omega_{1}+\Omega_{2}+ \sum _{i=1}^{6}\Pi_{i} \Biggr] \xi (t )= \xi^{T} (t ) \hat{\Pi} \xi (t ), $$

(32)

where $\hat{\Pi}=(\hat{\Pi}_{ij})_{9\times9}$.

$$\begin{aligned}& \hat{\Pi}_{11}=P_{11}\bar{A}+\bar{A}^{T}P_{11} +P_{12}+P_{12}^{T}+P_{13}+P_{13}^{T}+Q_{1}+Q_{2}+ \varepsilon_{1}\alpha^{2}I +\bar{A}^{T}S\bar{A}-4 \Sigma_{1}-4\Sigma_{2}, \\& \hat{\Pi}_{12}=\delta P_{11}\bar{A}_{d}-P_{12} +\delta\bar{A}^{T}S \bar{A}_{d} -2\Sigma_{1}, \\& \hat{\Pi}_{13}= (1-\delta )P_{11}\bar{A}_{d}-P_{13} + (1-\delta )\bar{A}^{T}S\bar{A}_{d} -2\Sigma_{2}, \qquad \hat{\Pi}_{14}= P_{11}F+\bar{A}^{T}SF,\\& \hat{\Pi}_{15}=P_{11}G+\bar{A}^{T}SG, \\& \hat{ \Pi}_{16}=P_{22} +P_{23}+P_{23}^{T}+P_{33}+ \bar{A}^{T}P_{12} +\bar{A}^{T}P_{13}+ \frac{6}{\tau_{i}}\Sigma_{1}+\frac{6}{\tau _{i+1}}\Sigma_{2}, \\& \hat{\Pi}_{17}=\bar{A}^{T}P_{13}+P_{23}+P_{33}+ \frac{6}{\tau _{i+1}}\Sigma_{2},\qquad \hat{\Pi}_{18}= \bar{A}^{T}SE+P_{11}E,\\& \hat{\Pi}_{19}=\delta \tau_{\star}P_{11}\bar{A}_{d} +\delta \tau_{\star}\bar{A}^{T}S\bar{A}_{d}, \qquad \hat{\Pi}_{22}=-Q_{1}+\delta^{2} \bar{A}_{d}^{T}S\bar{A}_{d}+\varepsilon _{2}\beta^{2} \delta^{2}I-4\Sigma_{1}, \\& \hat{\Pi}_{23}= \delta (1-\delta ) \bar{A}_{d}^{T}S \bar{A}_{d}+ \varepsilon_{2}\beta^{2}\delta (1- \delta )I, \qquad \hat{\Pi}_{24}= \delta\bar{A}_{d}^{T} SF,\qquad \hat{\Pi}_{25}=\delta\bar{A}_{d}^{T}SG,\\& \hat{\Pi}_{26}=-P_{22}-P_{23}+\delta \bar{A}_{d}^{T} (P_{12}+P_{13} )+ \frac{6}{\tau_{i}}\Sigma_{1}, \qquad \hat{\Pi}_{27}=-P_{23}+\delta\bar{A}_{d}^{T}P_{13}, \\& \hat{\Pi}_{28}=\delta\bar{A}_{d}^{T}SE, \qquad \hat{\Pi}_{29}=\delta^{2}\tau_{\star}\bar{ A}_{d}^{T}S \bar {A}_{d}+\varepsilon_{2} \beta^{2} \delta^{2}\tau_{\star}I, \\& \hat{\Pi}_{33}=-Q_{2}-4\Sigma_{2}+ \beta^{2}\varepsilon_{2} (1-\delta )^{2}I + (1- \delta )^{2}\bar{A}_{d}^{T}S\bar{A}_{d}, \qquad \hat{\Pi}_{34}= (1-\delta )\bar{A}_{d}^{T}SF, \\& \hat{\Pi}_{35}= (1-\delta )\bar{A}_{d}^{T}SG, \qquad \hat{\Pi}_{36}=\frac{6}{\tau_{i+1}}\Sigma_{2} + (1-\delta ) \bar{A}_{d}^{T} (P_{12}+P_{13} )-P_{23}^{T}-P_{33},\\& \hat{ \Pi}_{37}=\frac{6}{\tau_{i+1}}\Sigma_{2} + (1-\delta ) \bar{A}_{d}^{T}P_{13}-P_{33}, \qquad \hat{\Pi}_{38}= (1-\delta )\bar{A}_{d}^{T}SE, \\& \hat{\Pi}_{39}=\varepsilon_{2}\beta^{2} (1- \delta )\delta\tau _{\star}I + (1-\delta )\delta\tau_{\star} \bar{A}_{d}^{T}S\bar{A}_{d},\qquad \hat{ \Pi}_{44}=-\varepsilon_{1}I+F^{T}SF,\\& \hat{ \Pi}_{45}=F^{T}SG, \qquad \hat{\Pi}_{46}=F^{T} (P_{12}+P_{13} ), \qquad \hat{\Pi}_{47}=F^{T}P_{13},\\& \hat{\Pi}_{48}=F^{T}SE,\qquad \hat{\Pi}_{49}=\delta \tau_{\star}F^{T}S\bar{A}_{d},\qquad \hat{ \Pi}_{55}=-\varepsilon_{2}I+G^{T}SG, \\& \hat{\Pi}_{56}=G^{T} (P_{12}+P_{13} ), \qquad \hat{\Pi}_{57}=G^{T}P_{13},\qquad\hat{ \Pi}_{58}=G^{T}SE,\qquad \hat{\Pi}_{59}=\delta \tau_{\star}G^{T}S\bar{A}_{d},\\& \hat{ \Pi}_{66}=-\frac{12}{\tau_{i}^{2}}\Sigma_{1}-\frac{12}{\tau _{i+1}^{2}} \Sigma_{2}, \qquad \hat{\Pi}_{67}=-\frac{12}{\tau_{i+1}^{2}}\Sigma_{2},\qquad \hat{ \Pi}_{68}= \bigl(P_{12}^{T}+P_{13}^{T} \bigr)E,\\& \hat{\Pi}_{69}=\delta\tau_{\star} \bigl(P_{12}^{T}+P_{13}^{T} \bigr) \bar{A}_{d},\qquad \hat{\Pi}_{77}=-\frac{12}{\tau_{i+1}^{2}} \Sigma_{2},\qquad \hat{\Pi}_{78}=P_{13}^{T}E, \\& \hat{\Pi}_{79}=\delta\tau_{\star}P_{13}^{T} \bar{A}_{d},\qquad \hat{\Pi}_{88}=E^{T}SE,\qquad \hat{\Pi}_{89}=\delta\tau_{\star}E^{T}S \bar{A}_{d},\\& \hat{\Pi}_{99}=-\tau_{\star}M+ \varepsilon_{2}\beta^{2}\delta^{2} \tau _{\star}^{2}I +\delta^{2}\tau_{\star}^{2} \bar{A}_{d}^{T}S\bar{A}_{d}. \end{aligned}$$

Next, choosing a supplementary function as $\mathfrak{J}_{1}(t)=\dot {V}_{i}(x_{t})- \gamma x^{T}(t)P_{11}x(t)-\gamma w^{T}(t)w(t)$, it follows that

$$ \mathfrak{J}_{1} (t )\leq\xi^{T} (t )\tilde{\Pi}\xi (t ), $$

(33)

where $\tilde{\Pi}=(\tilde{\Pi}_{ij})_{9\times9}$,

$$\begin{aligned}& \begin{aligned}[b] \tilde{\Pi}_{11}={}&P_{11}\bar{A}+\bar{A}^{T}P_{11} +P_{12}+P_{12}^{T}++P_{13}+P_{13}^{T}+Q_{1}+Q_{2}+ \varepsilon_{1}\alpha^{2}I \\ &{}+\bar{A}^{T}S\bar{A}-4 \Sigma_{1}-4\Sigma_{2}-\gamma P_{11}, \end{aligned}\\& \tilde{\Pi}_{88}=E^{T}SE-\gamma I, \end{aligned}$$

and the other entries of Π̃ are the same as Π̂. The matrix Π̃ can be rewritten as

$$ \tilde{\Pi}=\check{\Pi}-\sum\limits _{j=1}^{5} \bar{\Phi}_{j} (-X_{j} )^{-1}\bar{ \Phi}_{j}^{T}< 0, $$

(34)

where

$$\begin{aligned}& \check{\Pi}_{11}=P_{11}\bar{A}+\bar{A}^{T}P_{11} +P_{12}+P_{12}^{T}+P_{13}+P_{13}^{T}+ Q_{1}+Q_{2}+\varepsilon_{1}\alpha^{2}I-4 \Sigma_{1}-4\Sigma_{2}-\gamma P_{11}, \\& \check{\Pi}_{12}=\delta P_{11}\bar{A}_{d}-P_{12}-2 \Sigma_{1},\qquad \check{\Pi}_{13}= (1-\delta )P_{11}\bar{A}_{d}-P_{13}-2\Sigma _{2}, \qquad\check{\Pi}_{14}= P_{11}F,\\& \check{ \Pi}_{15}=P_{11}G, \qquad \check{\Pi}_{16}=\hat{\Pi}_{16},\qquad \check{ \Pi}_{17}=\hat{\Pi}_{17},\qquad \check{\Pi}_{18}=P_{11}E, \qquad \check{\Pi}_{19}=\delta\tau_{\star}P_{11} \bar{A}_{d},\\& \check{\Pi}_{22}=-Q_{1}+ \varepsilon_{2}\beta^{2} \delta^{2}I-4 \Sigma_{1},\qquad \check{\Pi}_{23}=\varepsilon^{2} \beta^{2}\delta (1-\delta )I, \qquad \check{\Pi}_{26}=\hat{\Pi}_{26},\\& \check{ \Pi}_{27}=\hat{\Pi}_{27},\qquad \check{\Pi}_{29}= \varepsilon_{2}\beta^{2}\delta^{2} \tau_{\star}I,\qquad \check{\Pi}_{33}=-Q_{2}-4 \Sigma_{2}+\beta^{2}\varepsilon_{2} (1-\delta )^{2}I,\\& \check{\Pi}_{36}=\hat{\Pi}_{36}, \qquad \check{\Pi}_{37}=\hat{\Pi}_{37}, \qquad \check{\Pi}_{39}=\varepsilon_{2}\beta^{2} (1- \delta )\delta \tau_{\star}I,\qquad \check{\Pi}_{44}=- \varepsilon_{1}I,\\& \check{\Pi}_{46}=\hat{ \Pi}_{46},\qquad \check{\Pi}_{47}=\hat{\Pi}_{47}, \qquad\check{\Pi}_{55}=-\varepsilon_{2}I,\qquad \check{ \Pi}_{56}=\hat{\Pi}_{56},\qquad \check{\Pi}_{57}= \hat{\Pi}_{57}, \\& \check{\Pi}_{66}=\hat{\Pi}_{66},\qquad \check{ \Pi}_{67}=\hat{\Pi}_{67},\qquad \check{\Pi}_{68}= \hat{\Pi}_{68},\qquad \check{\Pi}_{69}=\hat{ \Pi}_{69},\qquad \check{\Pi}_{77}=\hat{\Pi}_{77}, \\& \check{\Pi}_{78}=\hat{\Pi}_{78},\qquad \check{ \Pi}_{79}=\hat{\Pi}_{79},\qquad \check{\Pi}_{88}=- \gamma I, \qquad \check{\Pi}_{99}=-\tau_{\star}M+\varepsilon_{2} \beta^{2}\delta^{2} \tau _{\star}^{2}I. \end{aligned}$$

By using the Schur complement [29], it is obvious that the inequality in equation (34) is equivalent to

$$ \begin{bmatrix} \check{\Pi}&\bar{\Phi}_{1}&\bar{\Phi}_{2}&\bar{\Phi}_{3}&\bar{\Phi }_{4}&\bar{\Phi}_{5}\\ \ast&-X_{1}&0&0&0&0\\ \ast&\ast&-X_{2}&0&0&0\\ \ast&\ast&\ast&-X_{3}&0&0\\ \ast&\ast&\ast&\ast&-X_{4}&0\\ \ast&\ast&\ast&\ast&\ast&-X_{5} \end{bmatrix} < 0. $$

(35)

Using equation (2), the inequality in equation (35) can be rewritten as

$$\begin{aligned} & \begin{bmatrix} \Pi&\Phi_{1}&\Phi_{2}&\Phi_{3}&\Phi_{4}&\Phi_{5}\\ \ast&-X_{1}&0&0&0&0\\ \ast&\ast&-X_{2}&0&0&0\\ \ast&\ast&\ast&-X_{3}&0&0\\ \ast&\ast&\ast&\ast&-X_{4}&0\\ \ast&\ast&\ast&\ast&\ast&-X_{5} \end{bmatrix} \\ &\quad{}+\operatorname{Sym} \left \{\varepsilon^{-1} \begin{bmatrix} \Phi_{6}\\ \varepsilon\tau_{i}X_{1}L\\ \varepsilon\tau_{i+1}X_{2}L\\ \varepsilon\tau_{\star}X_{3}L\\ \varepsilon\tau_{\star}X_{4}L\\ \varepsilon\tau_{\star}X_{5}L \end{bmatrix} \Sigma (t ) \bigl[ \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{}} \Phi_{7}^{T}&0&0&0&0&0 \end{array}\displaystyle \bigr] \right \}< 0. \end{aligned}$$

(36)

Applying Lemma 2.2, the inequality in equation (36) is equivalent to equation (13). Hence, if the condition in equation (13) holds, we have $\mathfrak{J}_{1}(t)\leq\xi ^{T}(t)\tilde{\Pi}\xi(t)<0$. Then we can obtain

$$ \dot{V}_{i} ( x_{t} ) < \gamma x^{T} (t )P_{11}x (t )+ \gamma w^{T} (t )w (t ) < \gamma V_{i} ( x_{t} )+\gamma w^{T} (t )w (t ). $$

(37)

Multiplying the above inequality by $e^{-\gamma t}$, it yields

$$ \frac{d}{dt} \bigl(e^{-\gamma t}V (x_{t} ) \bigr)< \gamma e^{-\gamma t}w^{T} (t )w (t ). $$

(38)

By integrating the aforementioned inequality between 0 and t, we obtain

$$ \begin{aligned}[b] V (x_{t} )&< e^{\gamma t}V (x_{0} )+ \gamma e^{\gamma t} \int_{0}^{t}e^{-\gamma s }w^{T} (s )w (s )\,ds \\ &\leq e^{\gamma T}V (x_{0} )+e^{\gamma T}\eta \bigl(1-e^{-\gamma T} \bigr),\quad t\in (0,T ]. \end{aligned} $$

(39)

On the other hand, note that $P_{11}=\psi^{\frac{1}{2}}\tilde {P}_{11}\psi^{\frac{1}{2}}$, the following relation is true:

$$\begin{aligned}& \lambda_{\min} (\tilde{P}_{11} ) x^{T} (0 )\psi x (0 ) \leq x^{T} (0 )P_{11}x (0 ) \leq\lambda_{\max} ( \tilde{P}_{11} ) x^{T} (0 )\psi x (0 ) \leq \lambda_{\max} (\tilde{P}_{11} ) c_{1}, \end{aligned}$$

(40)

$$\begin{aligned}& \lambda_{\min} (\psi ) x^{T} (0 )x (0 ) \leq x^{T} (0 )\psi x (0 )\leq c_{1},\qquad \lambda_{\min} ( \tilde{P}_{11} ) x^{T} (t )\psi x (t ) \leq V_{i} (x ), \end{aligned}$$

(41)

The initial value of LKF can be written as

$$ \begin{aligned}[b] V_{i} (x_{0} )={}&\sum _{j=1}^{6}V_{ij} (x_{0} ) \\ ={}&\eta^{T} (0 )P\eta (0 )+ \int_{-\tau_{i}}^{0}x^{T} (s )Q_{1}x (s )\,ds + \int_{-\tau_{i+1}}^{0}x^{T} (s )Q_{2}x (s )\,ds \\ &{}+\tau_{i} \int_{-\tau_{i}}^{0} \int_{\theta}^{0}\dot{x}^{T} (s )X_{1} \dot{x} (s )\,ds\,d\theta+\tau_{i+1} \int_{-\tau_{i+1}}^{0} \int _{\theta}^{0}\dot{x}^{T} (s )X_{2} \dot{x} (s )\,ds\,d\theta \\ &{}+\tau_{\star} \int_{-\tau_{i+1}}^{-\tau_{i}} \int_{\theta}^{0} \dot{x}^{T} (s )X_{3} \dot{x} (s )\,ds\,d\theta +\tau_{\star} \int_{-\tau (0 ) }^{-\tau_{i}} \int_{\theta}^{0} \dot{x}^{T} (s )X_{4} \dot{x} (s )\,ds\,d\theta \\ &{}+\tau_{\star} \int_{-\tau_{i+1} }^{-\tau (0 )} \int_{\theta}^{0} \dot{x}^{T} (s )X_{5} \dot{x} (s )\,ds\,d\theta \\ \leq{}& x^{T} (0 )P_{11}x (0 )+\tilde{\varpi}\leq x^{T} (0 )P_{11}x (0 )+\varpi, \end{aligned} $$

(42)

where

$$\begin{aligned}[b] \tilde{\varpi}={}& \bigl[ \tau_{i}^{2} \lambda_{\max} (P_{22} ) +\tau_{i+1}^{2} \lambda_{\max} (P_{33} ) +2\tau_{i} \lambda_{\max} (P_{12} ) +2\tau_{i+1} \lambda_{\max} (P_{13} ) \\ &{}+2\tau_{i} \tau_{i+1}\lambda_{\max} (P_{23} )+\tau_{i} \lambda_{\max} (Q_{1} ) +\tau_{i+1} \lambda_{\max} (Q_{2} ) \bigr] \frac{c_{1}}{\lambda_{\min} (\psi )} \\ &{}+ \biggl\{ \frac{\tau_{i}^{3}}{2}\lambda_{\max} (X_{1} ) +\frac{\tau_{i+1}^{3}}{2}\lambda_{\max} (X_{2} ) +\frac{\tau_{\star}^{2}}{2} (\tau_{i}+\tau_{i+1} ) \lambda_{\max } (X_{3} ) \\ &{}+\tau_{\star}\lambda_{\max} (X_{4} ) \biggl[- \frac{\tau_{i}^{2}}{2}+\frac{\tau^{2} (0 )}{2} \biggr] +\tau_{\star} \lambda_{\max} (X_{5} ) \biggl[-\frac{\tau^{2} (0 )}{2}+ \frac{\tau_{i+1}^{2}}{2} \biggr] \biggr\} \rho \\ \leq{}&\varpi. \end{aligned} $$

In addition, combining equations (37)-(42), we have

$$ \lambda_{\min} (\tilde{P}_{11} )x^{T} (t )\psi x (t ) \leq e^{\gamma T} \bigl(x^{T} (0 )P_{11}x (0 )+\varpi \bigr) +e^{\gamma T} \eta \bigl(1-e^{-\gamma T} \bigr), \quad t\in (0,T ], $$

(43)

it follows from (43) that

$$ x^{T} (t ) \psi x (t )\leq \frac{c_{1}\lambda_{\max} (\tilde{P}_{11} )+\varpi+\eta (1-e^{-\gamma T} )}{ \lambda_{\min} (\tilde{P}_{11} )e^{-\gamma T}}. $$

(44)

Now, we proceed to show the derivation of conditions of (11) and (12). In order to transform (44) into a LMI-based condition, we assume that inequality (11) is true, that is,

$$ \left . \textstyle\begin{array}{r@{}} \psi< P_{11}\\ P_{11}< 2\psi \end{array}\displaystyle \right \}\quad\Rightarrow\quad I< \psi^{-1/2}P_{11} \psi^{-1/2}< 2I. $$

The above relations imply that $\lambda_{1}>1$, $\lambda_{2}<2$. By considering these relations, one can obtain the following:

$$ \textstyle\begin{cases} c_{1}\lambda_{2}+\omega+\eta (1-e^{-\gamma T} )< 2c_{1}+ \omega+\eta (1-e^{-\gamma T} ),\\ c_{2}\lambda_{1}e^{-\gamma T}>c_{2}e^{-\gamma T}. \end{cases} $$

Defining $\lambda_{1}=\lambda_{\min}(\tilde{P}_{11})$, $\lambda _{2}=\lambda_{\max}(\tilde{P}_{11})$, we arrive at $x^{T}(t)\psi x(t)< c_{2}$ from LMIs (11) and (12). That is, the system in (10) is FTB when ignoring the control input $u(t)$. This completes the proof. □

Remark 6

Different from the delay-partitioning approach used in [28], when the delay-partitioning number becomes larger, there are involved more decision variables, so that the conditions become more complicated and the computational cost increases. However, in our method, there are no additional matrix variables apart from those associated in the corresponding LKF, that is, P, $Q_{i}$ ($i=1,2$), $X_{j}$ ($j=1,2,3,4,5$). One can see that when the delay-partitioning number becomes larger, the derived criteria can lead to an improvement. Furthermore, the cost of computation and the complexity of the obtained criteria do not increase.

Remark 7

If there is no perturbation, that is, $f=0$, $g=0$, $w(t)=0$, the FTB problem of system (1) is reduced to analyzing the FTS of the system

$$ \textstyle\begin{cases} \dot{x} (t )= [A+\Delta A (t ) ]x (t )+ [A_{d}+\Delta A_{d} (t ) ]x (t-\tau (t ) )+ Bu (t ),\\ y (t )=Cx (t )+C_{d}x (t-\tau (t ) ),\\ x (t )=\varphi (t ),\quad t\in [-\tau_{M},0 ]. \end{cases} $$

This problem has been widely studied in the recent literature (see [18]) and the FTS criterion for the deterministic system is addressed below.

Remark 8

In the proof of Theorem 3.1, a new integral inequality, called a Wirtinger-based inequality, is employed to bound the derivative of LKF, which was proposed in [6] and was shown to be tighter than the one employed in [26]. Therefore, the condition obtained in this paper may be less conservative than [26].

Remark 9

The inequalities in equations (11)-(16) are LMIs, which can be calculated by the LMI toolbox in MATLAB. The results depend on the selected parameters $(c_{1},c_{2},T,\psi,\eta )$, the lower and upper bounds of the time-varying delay, and scalars ε and γ. Further, in order to obtain a minimum state upper bound $c_{2}$, we choose a value of the parameter ε, then the minimum searching function (such as the “mincx” in MATLAB) can be used to search an optimal γ which can guarantee the upper bound $c_{2}$ minimum.

3.3 State-feedback controller design

In this subsection, we consider the following state-feedback controller for the system (1):

$$ u(t)=Kx (t ), $$

(45)

where the state-feedback controller gain K is to be determined in the course of the design. Then we can get the following closed-loop system:

$$ \textstyle\begin{cases} \dot{x} (t )= [A+\Delta A (t )+BK ]x (t )+ [A_{d}+\Delta A_{d} (t ) ]x (t-\tau (t ) )+ Ff+Gg+Ew (t ),\\ y (t )=Cx (t )+C_{d}x (t-\tau (t ) ),\\ x (t )=\varphi (t ),\quad t\in [-\tau_{M},0 ]. \end{cases} $$

(46)

Theorem 3.2 gives sufficient conditions, which guarantee the resulting closed-loop system (46) is FTB with respect to the given $(c_{1},c_{2},T,\psi,\eta)$.

Theorem 3.2

For some given scalars α, β, $c_{1}$, η, $0< \tau _{m}\leq\tau_{M}$, $\tilde{\tau}_{d}$, ψ, $\bar{\tau}_{d}$, $\delta \in(0,1]$, $T>0$, $\gamma\geq1$, ρ, the system in (46) by the state-feedback controller (45) is FTB with respect to $(c_{1},c_{2},T,\psi,\eta)$ and satisfies the cost function equation (5) for all admissible $w(t)$, if there exist symmetric positive matrices $P= \Bigl[{\scriptsize\begin{matrix}{} P_{11}&P_{12}&P_{13}\cr \ast&P_{22}&P_{23}\cr \ast&\ast&P_{33} \end{matrix}}\Bigr]\in\mathbb{R}^{3n\times3n}$ ($P_{12}=\kappa _{1}P_{11}$, $P_{13}=\kappa_{2}P_{11}$, $\kappa_{1}>0$, $\kappa_{2}>0$), $Q_{1},Q_{2},X_{1},X_{2},X_{3},X_{4},X_{5} \in\mathbb{R}^{n\times n}$, positive scalars $c_{2}$, $\omega_{j}$ ($j=1,2,\ldots,7$), $\omega_{10}$, $\omega_{11}$, $\omega_{12}$, ε, σ, and any positive scalars $\varepsilon_{1}$, $\varepsilon_{2}$, and real matrix W, $W_{1}$, $W_{2}$, $W_{3}$, $W_{4}$, $W_{5}$ such that, for $i=1,2,3,\ldots,N$, the following LMIs and conditions (11), (14)-(15) hold:

$$ \begin{bmatrix} -c_{2}e^{-\gamma T}&\sqrt{2c_{1}+\eta (1-e^{-\gamma T} )}& \bar{\theta}_{1}&\theta_{2}&\cdots&\theta_{7}&\theta_{10}&\theta _{11}&\theta_{12}\\ \ast&-I&0&0&\cdots&0&0&0&0\\ \ast&\ast&-\omega_{1}&0&\cdots&0&0&0&0\\ \ast&\ast&\ast&-\omega_{2}&\cdots&0&0&0&0\\ \vdots&\vdots&\vdots&\vdots&\ddots&\vdots&\vdots&\vdots&\vdots\\ \ast&\ast&\ast&\ast&\cdots&-\omega_{7}&0&0&0\\ \ast&\ast&\ast&\ast&\cdots&\ast&-\omega_{10}&0&0\\ \ast&\ast&\ast&\ast&\cdots&\ast&\ast&-\omega_{11}&0\\ \ast&\ast&\ast&\ast&\cdots&\ast&\ast&\ast&-\omega_{12} \end{bmatrix}< 0, $$

(47)

where

$$\begin{aligned}& \bar{\theta}_{1}=\sqrt{\frac{\tau_{i}^{3}}{2}\rho+ \frac{2 ( \tau_{i}k_{1}+\tau_{i+1}k_{2} )c_{1} }{\lambda_{\min} (\psi )}}\omega_{1}, \\& \begin{bmatrix} \vec{\Pi}&\vec{\Phi}_{1}&\vec{\Phi}_{2}&\vec{\Phi}_{3}&\vec{\Phi }_{4}&\vec{\Phi}_{5} &\vec{\Phi}_{6}&\Phi_{7}\\ \ast&-X_{1}&0&0&0&0&\varepsilon\tau_{i}X_{1}L&0\\ \ast&\ast&-X_{2}&0&0&0&\varepsilon\tau_{i+1}X_{2}L&0\\ \ast&\ast&\ast&-X_{3}&0&0&\varepsilon\tau_{\star}X_{3}L&0\\ \ast&\ast&\ast&\ast&-X_{4}&0&\varepsilon\tau_{\star}X_{4}L&0\\ \ast&\ast&\ast&\ast&\ast&-X_{5}&\varepsilon\tau_{\star}X_{5}L&0\\ \ast&\ast&\ast&\ast&\ast&\ast&-\varepsilon I&0\\ \ast&\ast&\ast&\ast&\ast&\ast&\ast&-\varepsilon I \end{bmatrix} < 0, \end{aligned}$$

(48)

where $\vec{\Pi}=(\vec{\Pi}_{ij})_{9\times9}$ with

$$\begin{aligned}& \begin{aligned}[b] \vec{\Pi}_{11}={}&P_{11}A+A^{T}P_{11}+W+W^{T} +2 (\kappa_{1}+\kappa_{2} )P_{11}+ Q_{1}+Q_{2}\\ &{}+\varepsilon_{1}\alpha^{2}I-4 \Sigma_{1}-4\Sigma_{2}-\gamma P_{11}+ \frac{1}{\sigma}C^{T}C, \end{aligned} \\& \vec{\Pi}_{12}=\delta P_{11}A_{d}- \kappa_{1}P_{11}-2\Sigma_{1}+\frac {1}{\sigma} \delta C^{T}C_{d},\\& \vec{\Pi}_{13}= (1-\delta )P_{11}A_{d}-\kappa _{2}P_{11}-2 \Sigma_{2}+\frac{1}{\sigma} (1-\delta ) C^{T}C_{d}, \qquad \vec{\Pi}_{14}=P_{11}F,\qquad \vec{\Pi}_{15}=P_{11}G, \\& \vec{\Pi}_{16}=P_{22}+P_{23}+P_{23}^{T}+P_{33}+ (\kappa_{1}+\kappa _{2} ) \bigl(A^{T}P_{11}+W^{T} \bigr)+\frac{6}{\tau_{i}}\Sigma_{1}+\frac {6}{\tau_{i+1}} \Sigma_{2}, \\& \vec{\Pi}_{17}=\kappa_{2} \bigl(A^{T}P_{11}+W^{T} \bigr)+P_{23}+\frac {6}{\tau_{i+1}}\Sigma_{2} +P_{33}, \qquad\vec{\Pi}_{18}=P_{11}E,\\& \vec{\Pi}_{19}= \delta\tau_{\star}P_{11}A_{d}+\frac{1}{\sigma}\delta \tau_{\star}C^{T}C_{d}, \qquad \vec{\Pi}_{22}=-Q_{1}+\varepsilon_{2} \beta^{2} \delta^{2}I-4\Sigma_{1}+ \frac{1}{\sigma}\delta^{2}C_{d}^{T}C_{d},\\& \vec{\Pi}_{23}=\varepsilon_{2}\beta^{2}\delta (1- \delta )I+ \frac{1}{\sigma}\delta (1-\delta )C_{d}^{T}C_{d}, \\& \vec{\Pi}_{26}=-P_{22}-P_{23}+\delta ( \kappa_{1}+\kappa_{2} )A_{d}^{T}P_{11} +\frac{6}{\tau_{i}}\Sigma_{1},\qquad \vec{\Pi}_{27}=-P_{23}+ \delta\kappa_{2}A_{d}^{T}P_{11}, \\& \vec{\Pi}_{29}=\varepsilon_{2}\beta^{2} \delta^{2}\tau_{\star}I+\frac{1}{\sigma}\delta^{2} \tau_{\star}C_{d}^{T}C_{d},\\& \vec{ \Pi}_{33}=-Q_{2}-4\Sigma_{2}+\beta^{2} \varepsilon_{2} (1-\delta )^{2}I+ \frac{1}{\sigma} (1-\delta )^{2}C_{d}^{T}C_{d}, \\& \vec{\Pi}_{36}=\frac{6}{\tau_{i+1}}\Sigma_{2}+ (1-\delta ) ( \kappa_{1}+\kappa_{2} )A_{d}^{T}P_{11}-P_{23}^{T}-P_{33},\\& \vec{\Pi}_{37}=\frac{6}{\tau_{i+1}}\Sigma_{2}+ (1-\delta ) \kappa_{2}A_{d}^{T}P_{11}-P_{33}, \\& \vec{\Pi}_{39}=\varepsilon_{2}\beta^{2} (1-\delta )\delta\tau _{\star}I+ \frac{1}{\sigma} (1-\delta )\delta \tau_{\star}C_{d}^{T}C_{d}, \qquad\vec{ \Pi}_{44}=-\varepsilon_{1}I,\qquad \vec{\Pi}_{46}= (\kappa_{1}+\kappa_{2} )F^{T}P_{11}, \\& \vec{\Pi}_{47}=\kappa_{2}F^{T}P_{11}, \qquad \vec{\Pi}_{55}=-\varepsilon_{2}I,\qquad \vec{ \Pi}_{56}= (\kappa_{1}+\kappa_{2} )G^{T}P_{11},\qquad \vec{\Pi}_{57}= \kappa_{2}G^{T}P_{11},\\& \vec{ \Pi}_{66}=-\frac{12}{\tau_{i}^{2}}\Sigma_{1}-\frac{12}{\tau _{i+1}^{2}} \Sigma_{2},\qquad \vec{\Pi}_{67}=-\frac{12}{\tau_{i+1}^{2}} \Sigma_{2}, \qquad \vec{\Pi}_{68}= (\kappa_{1}+\kappa_{2} )P_{11}E,\\& \vec{\Pi}_{69}=\delta\tau_{\star} ( \kappa_{1}+\kappa_{2} )P_{11}A_{d}, \qquad \vec{\Pi}_{77}=-\frac{12}{\tau_{i+1}^{2}}\Sigma_{2},\qquad \vec{\Pi}_{78}=\kappa_{2}P_{11}E,\\& \vec{ \Pi}_{79}=\delta\tau_{\star}\kappa_{2}P_{11}A_{d}, \qquad \vec{\Pi}_{88}=-\gamma I,\qquad \vec{\Pi}_{99}=- \tau_{\star}M+\varepsilon_{2}\beta^{2} \delta^{2} \tau _{\star}^{2}I+ \frac{1}{\sigma} \delta^{2}\tau_{\star}^{2}C_{d}^{T}C_{d}. \end{aligned}$$

The other entries of Π⃗ are the same as Π in Theorem  3.1. We have

$$\begin{aligned}& {{\vec{\Phi}_{1}=\bigl[ \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{}} \tau_{i} (X_{1}A+W_{1} )&\tau_{i}\delta X_{1}A_{d}& \tau_{i} (1-\delta )X_{1}A_{d}&\tau_{i} X_{1}F&\tau_{i}X_{1}G&0&0& \tau_{i}X_{1}E&\tau_{\star} \tau_{i}\delta X_{1}A_{d} \end{array}\displaystyle \bigr]^{T}}},\\& {{\vec{\Phi}_{2}=\bigl[ \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{}} \tau_{i+1} (X_{2}A+W_{2} )&\tau_{i+1}\delta X_{2}A_{d}& \tau_{i+1} (1-\delta )X_{2}A_{d}&\tau_{i+1} X_{2}F&\tau_{i+1}X_{2}G&0&0 \end{array}\displaystyle }}\\& {{\hphantom{\vec{\Phi}_{2}=\bigl[} \textstyle\begin{array}{@{}c@{\quad}c@{}} \tau_{i+1}X_{2}E&\tau_{\star} \tau _{i+1}\delta X_{2}A_{d} \end{array}\displaystyle \bigr]^{T}}}, \\& {{\vec{\Phi}_{3}=\bigl[ \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{}} \tau_{\star} (X_{3}A+W_{3} )&\tau_{\star}\delta X_{3}A_{d}& \tau_{\star} (1-\delta )X_{3}A_{d}&\tau_{\star} X_{3}F&\tau_{\star}X_{3}G&0&0& \tau_{\star}X_{3}E&\tau_{\star }^{2}\delta X_{3}A_{d} \end{array}\displaystyle \bigr]^{T}}}, \\& {{\vec{\Phi}_{4}=\bigl[ \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{}} \tau_{\star} (X_{4}A+W_{4} )&\tau_{\star}\delta X_{4}A_{d}& \tau_{\star} (1-\delta )X_{4}A_{d}&\tau_{\star} X_{4}F&\tau_{\star}X_{4}G&0&0&\tau_{\star}X_{4}E& \tau_{\star }^{2}\delta X_{4}A_{d} \end{array}\displaystyle \bigr]^{T}}}, \\& {{\vec{\Phi}_{5}=\bigl[ \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{}} \tau_{\star} (X_{5}A+W_{5} )&\tau_{\star}\delta X_{5}A_{d}& \tau_{\star} (1-\delta )X_{5}A_{d}&\tau_{\star} X_{5}F&\tau_{\star}X_{5}G&0&0&\tau_{\star}X_{5}E& \tau_{\star }^{2}\delta X_{5}A_{d} \end{array}\displaystyle \bigr]^{T}}}, \\& {{\vec{\Phi}_{6}=\bigl[ \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{}} \varepsilon L^{T}P_{11}&0&0&0&0&\varepsilon (\kappa_{1}+\kappa _{2} )L^{T}P_{11} &\varepsilon\kappa_{2}L^{T}P_{11} &0&0 \end{array}\displaystyle \bigr]^{T}}}, \\& \begin{aligned}[b] \varpi^{\ast}={}& \bigl( \tau_{i}^{2} \omega_{6} +\tau_{i+1}^{2}\omega_{7} +2 \tau_{i}\kappa_{1}\omega_{1} +2 \tau_{i+1}\kappa_{2}\omega_{1} +2\tau_{i} \tau_{i+1}\omega_{10} +\tau_{i}\omega_{11} +\tau_{i+1}\omega_{12} \bigr)\frac{c_{1}}{\lambda_{\min} (\psi )} \\ &{}+ \biggl\{ \frac{\tau_{i}^{3}}{2}\omega_{1} + \frac{\tau_{i+1}^{3}}{2}\omega_{2} +\frac{\tau_{\star}^{2}}{2} (\tau_{i}+ \tau_{i+1} )\omega_{3} +\tau_{\star} \omega_{4} \biggl[-\frac{\tau_{i}^{2}}{2}+\frac{\tau_{i+1}^{2}}{2} \biggr] \\ &{}+\tau_{\star}\omega_{5} \biggl[-\frac{\tau_{i}^{2}}{2}+ \frac{\tau_{i+1}^{2}}{2} \biggr] \biggr\} \rho. \end{aligned} \end{aligned}$$

In this case, a suitable state-feedback controller gain can be obtained by $K=(B^{T}B)^{-1} B^{T}P_{11}^{-1}W$.

Proof

Select the same KLF as Theorem 3.1 and define the following function:

$$ \mathfrak{J}_{2} (t )=\dot{V}_{i}(x_{t})- \gamma x^{T} (t )P_{11}x (t )-\gamma w^{T} (t )w (t )+ \frac{1}{\sigma}y^{T} (t )y (t ). $$

Recalling the condition equation (49), we have the following relation along the trajectories of system:

$$ \mathfrak{J}_{2} (t )< 0. $$

Then we obtain the following equation through some similar algebraic manipulations of the proof in Theorem 3.1:

$$ \int_{0}^{T}y^{T} (t )y (t )\,dt< \sigma \gamma e^{\gamma T} \int_{0}^{T}w^{T} (t )w (t )\,dt. $$

Therefore, condition (5) can be guaranteed by letting $v=\sqrt{\sigma \gamma e^{\gamma T}}$. By means of the change of variable $W=P_{11}BK$, $W_{1}=X_{1}BK$, $W_{2}=X_{2}BK$, $W_{3}=X_{3}BK$, $W_{4}=X_{4}BK$, $W_{5}=X_{5}BK$, the proof procedure is similar to that of Theorem 3.1, and it is omitted here. □

3.4 Output-feedback controller design

In this subsection, we consider the following output-feedback controller for the system (1):

$$ u(t)=Ky (t ), $$

(49)

where the state-feedback controller gain K is to be determined in the course of the design. Then we can get the following closed-loop system:

$$ \left \{ \textstyle\begin{array}{@{}l} \dot{x} (t ) = [A+\Delta A (t )+BKC ]x (t )+ [A_{d}+\Delta A_{d} (t )+BKC_{d} ]x (t-\tau (t ) )\\ \hphantom{\dot{x} (t ) =}{}+Ff+Gg+Ew (t ),\\ y (t )=Cx (t )+C_{d}x (t-\tau (t ) ),\\ x (t )=\varphi (t ),\quad t\in [-\tau_{M},0 ]. \end{array}\displaystyle \right . $$

(50)

Theorem 3.3 presents some sufficient conditions which guarantee the resulting closed-loop system (51) is FTB with respect to the given $(c_{1},c_{2},T,\psi,\eta)$.

Theorem 3.3

For some given scalars α, β, $c_{1}$, η, $0< \tau _{m}\leq\tau_{M}$, $\tilde{\tau}_{d}$, ψ, $\bar{\tau}_{d}$, $\delta \in(0,1]$, $T>0$, $\gamma\geq1$, ρ, the system in (50) by the output-feedback controller (49) is FTB with respect to $(c_{1},c_{2},T,\psi,\eta)$ and satisfies the cost function equation (5) for all admissible $w(t)$, if there exist symmetric positive matrices

$$P= \begin{bmatrix} P_{11}&P_{12}&P_{13}\\ \ast&P_{22}&P_{23}\\ \ast&\ast&P_{33} \end{bmatrix} \in\mathbb{R}^{3n\times3n} $$

($P_{12}=\kappa _{1}P_{11}$, $P_{13}=\kappa_{2}P_{11}$, $\kappa_{1}>0$, $\kappa_{2}>0$), $Q_{1},Q_{2}, X_{1},X_{2},X_{3},X_{4},X_{5}\in\mathbb{R}^{n\times n}$, positive scalars $c_{2}$, m, $\omega_{j}$ ($j=1,2,\ldots,7$), $\omega_{10}$, $\omega_{11}$, $\omega_{12}$, ε, σ, and any positive scalars $\varepsilon_{1}$, $\varepsilon_{2}$, and real matrices $W^{o}$, $W_{1}^{o}$, $W_{2}^{o}$, $W_{3}^{o}$, $W_{4}^{o}$, $W_{5}^{o}$ such that, for $i=1,2,3,\ldots,N$, the following LMI and conditions (14)-(15), (47)-(48) hold:

$$ \begin{bmatrix} \vec{\Pi}^{o}&\vec{\Phi}^{o}_{1}&\vec{\Phi}^{o}_{2}&\vec{\Phi }^{o}_{3}&\vec{\Phi}^{o}_{4}&\vec{\Phi}^{o}_{5} &\vec{\Phi}_{6}&\Phi_{7}\\ \ast&-X_{1}&0&0&0&0&\varepsilon\tau_{i}X_{1}L&0\\ \ast&\ast&-X_{2}&0&0&0&\varepsilon\tau_{i+1}X_{2}L&0\\ \ast&\ast&\ast&-X_{3}&0&0&\varepsilon\tau_{\star}X_{3}L&0\\ \ast&\ast&\ast&\ast&-X_{4}&0&\varepsilon\tau_{\star}X_{4}L&0\\ \ast&\ast&\ast&\ast&\ast&-X_{5}&\varepsilon\tau_{\star}X_{5}L&0\\ \ast&\ast&\ast&\ast&\ast&\ast&-\varepsilon I&0\\ \ast&\ast&\ast&\ast&\ast&\ast&\ast&-\varepsilon I \end{bmatrix}< 0, $$

(51)

where $\vec{\Pi}^{o}=(\vec{\Pi}^{o}_{ij})_{9\times9}$ with

$$\begin{aligned}& \begin{aligned}[b] \vec{\Pi}^{o}_{11}={}&P_{11}A+A^{T}P_{11}+W^{o}C+C^{T} \bigl(W^{0} \bigr)^{T} +2 (\kappa_{1}+ \kappa_{2} )P_{11}+ Q_{1}+Q_{2}\\ &{}+ \varepsilon_{1}\alpha^{2}I-4\Sigma_{1}-4 \Sigma_{2}-\gamma P_{11}+\frac{1}{\sigma}C^{T}C, \end{aligned}\\& \vec{\Pi}^{o}_{12}=\delta \bigl(P_{11}A_{d}+W^{o}C_{d} \bigr)-\kappa _{1}P_{11}-2\Sigma_{1}+ \frac{1}{\sigma}\delta C^{T}C_{d},\\& \vec{ \Pi}_{13}= (1-\delta ) \bigl(P_{11}A_{d}+W^{o}C_{d} \bigr) -\kappa_{2}P_{11}-2\Sigma_{2}+ \frac{1}{\sigma} (1-\delta ) C^{T}C_{d}, \\& \vec{\Pi}^{o}_{16}=P_{22}+P_{23}+P_{23}^{T}+P_{33}+ (\kappa _{1}+\kappa_{2} ) \bigl[A^{T}P_{11}+C^{T} \bigl(W^{o} \bigr)^{T} \bigr]+ \frac{6}{\tau_{i}} \Sigma_{1}+\frac{6}{\tau_{i+1}}\Sigma_{2}, \\& \vec{\Pi}^{o}_{17}=\kappa_{2} \bigl[A^{T}P_{11}+C^{T} \bigl(W^{o} \bigr)^{T} \bigr] +P_{23}+\frac{6}{\tau_{i+1}} \Sigma_{2} +P_{33},\\& \vec{\Pi}^{o}_{19}= \delta\tau_{\star} \bigl(P_{11}A_{d}+W^{o}C_{d} \bigr)+\frac{1}{\sigma}\delta\tau_{\star}C^{T}C_{d}, \\& \vec{\Pi}^{o}_{26}=-P_{22}-P_{23}+ \delta (\kappa_{1}+\kappa _{2} ) \bigl[A_{d}^{T}P_{11}+C_{d}^{T} \bigl(W^{o} \bigr)^{T} \bigr] +\frac{6}{\tau_{i}} \Sigma_{1},\\& \vec{\Pi}^{o}_{27}=-P_{23}+ \delta\kappa_{2} \bigl[A_{d}^{T}P_{11}+C_{d}^{T} \bigl(W^{o} \bigr)^{T} \bigr], \\& \vec{\Pi}^{o}_{36}=\frac{6}{\tau_{i+1}}\Sigma_{2}+ (1-\delta ) (\kappa_{1}+\kappa_{2} ) \bigl[A_{d}^{T}P_{11}+C_{d}^{T} \bigl(W^{o} \bigr)^{T} \bigr] -P_{23}^{T}-P_{33}, \\& \vec{\Pi}^{o}_{37}=\frac{6}{\tau_{i+1}}\Sigma_{2}+ (1-\delta ) \kappa_{2} \bigl[A_{d}^{T}P_{11}+C_{d}^{T} \bigl(W^{o} \bigr)^{T} \bigr]-P_{33}, \\& \vec{\Pi}^{o}_{69}=\delta\tau_{\star} ( \kappa_{1}+\kappa _{2} ) \bigl(P_{11}A_{d}+W^{o}C_{d} \bigr),\qquad \vec{\Pi}^{o}_{79}=\delta\tau_{\star} \kappa_{2} \bigl(P_{11}A_{d}+W^{o}C_{d} \bigr), \\& \vec{\Phi}^{o}_{1}= \bigl[\textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{}} \tau_{i}M_{1}&\tau_{i}\delta M_{1d}& \tau_{i} (1-\delta )M_{1d}&\tau_{i} X_{1}F&\tau_{i}X_{1}G&0&0 & \tau_{i}X_{1}E&\tau_{\star} \tau_{i}\delta M_{1d} \end{array}\displaystyle \bigr] ^{T}, \\& \vec{\Phi}^{o}_{2}= \bigl[\textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{}} \tau_{i+1}M_{2}&\tau_{i+1}\delta M_{2d}& \tau_{i+1} (1-\delta )M_{2d}&\tau_{i+1} X_{2}F&\tau_{i+1}X_{2}G&0&0 \end{array}\displaystyle \\& \hphantom{\vec{\Phi}^{o}_{2}= \bigl[}\textstyle\begin{array}{@{}c@{\quad}c@{}} \tau_{i+1}X_{2}E&\tau_{\star} \tau _{i+1}\delta M_{2d} \end{array}\displaystyle \bigr] ^{T}, \\& \vec{\Phi}^{o}_{3}=\bigl[ \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{}} \tau_{\star}M_{3}&\tau_{\star}\delta M_{3d}& \tau_{\star} (1-\delta )M_{3d}&\tau_{\star} X_{3}F&\tau_{\star}X_{3}G&0&0& \tau_{\star}X_{3}E&\tau_{\star }^{2}\delta M_{3d} \end{array}\displaystyle \bigr]^{T}, \\& \vec{\Phi}^{o}_{4}=\bigl[ \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{}} \tau_{\star}M_{4}&\tau_{\star}\delta M_{4d}& \tau_{\star} (1-\delta )M_{4d}&\tau_{\star} X_{4}F&\tau_{\star}X_{4}G&0&0&\tau_{\star}X_{4}E& \tau_{\star }^{2}\delta M_{4d} \end{array}\displaystyle \bigr]^{T}, \\& \vec{\Phi}^{o}_{5}=\bigl[ \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{}} \tau_{\star}M_{5}&\tau_{\star}\delta M_{5d}& \tau_{\star} (1-\delta )M_{5d}&\tau_{\star} X_{5}F&\tau_{\star}X_{5}G&0&0&\tau_{\star}X_{5}E& \tau_{\star }^{2}\delta M_{5d} \end{array}\displaystyle \bigr]^{T}, \\& X_{i}A+W_{i}^{o}C=M_{i},\qquad X_{i}A_{d}+W_{i}^{o}C_{d}=M_{id} \quad (i=1,2,3,4,5 ). \end{aligned}$$

The other entries of $\vec{\Pi}^{o}$ are the same as Π⃗ in Theorem  3.2. In this case, a suitable state-feedback controller gain can be obtained by $K=(B^{T}B)^{-1}B^{T}P_{11}^{-1}W^{o}$.

Proof

The closed-loop system in equation (50) can be written as

$$ \dot{x} (t )= \bigl[A+\Delta A (t )+BKC \bigr] x (t )+ \bigl[A_{d}+\Delta A_{d} (t )+BKC_{d} \bigr]x \bigl(t-\tau (t ) \bigr) +Ff+Gg+Ew (t ). $$

(52)

Defining $W^{o}=P_{11}BK$, $W^{o}_{1}=X_{1}BK$, $W^{o}_{2}=X_{2}BK$, $W^{o}_{3}=X_{3}BK$, $W^{o}_{4}=X_{4}BK$, $W^{o}_{5}=X_{5}BK$. The proof procedure is similar to that of Theorem 3.2, and it is not difficult to get the conclusion. This completes the proof. □

4 Numerical examples and simulation

Example 1

Consider the system (46) with the parameters [18]

$$\begin{aligned} &A= \begin{bmatrix} 0.15&0.4\\ 0.1&0.3 \end{bmatrix},\qquad A_{d}= \begin{bmatrix} -0.1&0\\ 0.15&0 \end{bmatrix}, \qquad B= \begin{bmatrix} 0.1\\ 0.2 \end{bmatrix}, \qquad C=[ \textstyle\begin{array}{@{}c@{\quad}c@{}} 0.05&0 \end{array}\displaystyle ],\\ &C_{d}=[ \textstyle\begin{array}{@{}c@{\quad}c@{}} 0.1&0 \end{array}\displaystyle ], \qquad L= \begin{bmatrix} 0.01\\ 0 \end{bmatrix},\qquad E_{a}=[ \textstyle\begin{array}{@{}c@{\quad}c@{}} 1&0 \end{array}\displaystyle ],\\ & E_{d}= [ \textstyle\begin{array}{@{}c@{\quad}c@{}} 0.5&0 \end{array}\displaystyle ],\qquad F=G=E= \begin{bmatrix} 0&0\\ 0&0 \end{bmatrix}. \end{aligned}$$

• State-feedback case: We choose $\alpha=0$, $\beta=0$, $\eta=0.5$, $\rho=1.0572$, $T=1.5$, $c_{1}=2.002$, $\varepsilon=1{,}000$, $\psi=I$, $k_{1}=0.01$, $k_{2}=0.01$, $\tilde{\tau}_{d}=0.01$, $\bar{\tau}_{d}=0.02$, $\tau _{m}=0.1$, $\tau_{M}=21.1$, $N=10$. By using Theorem 3.2, the control gain matrix K and the minimum upper bound of state variable are calculated by LMIs in equations (11), (14), (15), (47), (48) for $\gamma=1.005$. When i=1, $\tau(t)\in[0.1,2.2]$

$$\begin{aligned}& \min \{c_{2} \}= 8.3992e+04, \\& P_{11}= \begin{bmatrix} 1.5701 & 0.0000\\ 0.0000 & 1.5701 \end{bmatrix}, \qquad W= 1.0e+03 * \begin{bmatrix} -2.6634 & 0.0002\\ -0.0008 & -2.6048 \end{bmatrix}, \\& K= 1.0e+03 *[ \textstyle\begin{array}{@{}c@{\quad}c@{}} -3.3949 &-6.6357 \end{array}\displaystyle ]. \end{aligned}$$

• Output-feedback case: We choose $\alpha=0$, $\beta=0$, $\eta=0.5$, $\rho=1.0572$, $T=1.5$, $c_{1}=2.002$, $\varepsilon=1{,}000$, $\psi=I$, $k_{1}=0.01$, $k_{2}=0.02$, $\tilde{\tau}_{d}=0.01$, $\bar{\tau}_{d}=0.02$, $\tau _{m}=0.1$, $\tau_{M}=4.1$, $N=10$. By using Theorem 3.3, the control gain matrix K and the minimum upper bound of state variable are calculated by LMIs in equations (14), (15), (47), (48), (51), for $\gamma=1.135$. When $i=1$, $\tau(t)\in[0.1,0.5]$,

$$\begin{aligned}& \min \{c_{2} \} =1.4127e+04, \\& P_{11} = \begin{bmatrix} 1.4252 &-0.2448\\ -0.2448 & 1.7067 \end{bmatrix}, \qquad W^{o}= \begin{bmatrix} -234.3653\\ -6.4364 \end{bmatrix},\qquad K= [ \textstyle\begin{array}{@{}c@{}} -450.7111 \end{array}\displaystyle ]. \end{aligned}$$

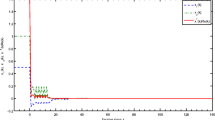
The curves of state values with state-feedback controller and output-feedback controller are shown in Figures 1-6.

Figure 1

State response $\pmb{x(t)}$ of the system with state-feedback controller and time-varying delay $\pmb{0.1\leq\tau(t)\leq2.2}$ .

Figure 2

Time-delay state response $\pmb{x(t-\tau(t))}$ of the system with state-feedback controller and time-varying delay $\pmb{0.1\leq\tau(t)\leq2.2}$ .

Figure 3

State response $\pmb{x(t)}$ of the system with output-feedback controller and time-varying delay $\pmb{0.1\leq\tau(t)\leq0.5}$ .

From Figures 1-4, it can be seen that state values satisfy the following condition with the state-feedback controller: $K=1.0e+03 * [ -3.3949 \ {-}6.6357 ]$, which makes the unstable system in (46) FTB with respect to $(2.001,83{,}992,1.5,I,0.5)$. We have

$$ x^{T} (t )\psi x (t )< c_{2}=83{,}992, \quad\forall t \in(0,1.5]. $$

Further, with the output-feedback controller $K= [ -450.7111 ]$, state responses satisfy the following condition, which proves that the system is FTB with respect to $(2.001,14{,}127,1.5, I,0.5)$:

$$ x^{T} (t )\psi x (t )< c_{2}=14{,}127, \quad\forall t \in(0,1.5]. $$

Figure 4

Time-delay state response $\pmb{x(t-\tau(t))}$ of the system with state-feedback controller and time-varying delay $\pmb{0.1\leq\tau(t)\leq0.5}$ .

When $\tau_{m}=0.1$, $k_{1}=0.01$, $k_{2}=0.02$, $\alpha=\beta=0$, the minimum allowable upper bounds for $c_{2}$ are given in Table 1 for different values of i. From Table 1, it is also seen that the FTB criteria can still be applicable when the range of $c_{2}$ is greater by adjusting the parameter i. From Figures 5-8, we can see that with output-feedback controller, the state values are larger and the rate of convergence is faster than those with state-feedback controller.

Figure 5

The system with state-feedback controller when $\pmb{i=2}$ .

Figure 6

The system with state-feedback controller when $\pmb{i=3}$ .

Figure 7

The system with output-feedback controller when $\pmb{i=2}$ .

Figure 8

The system with output-feedback controller when $\pmb{i=3}$ .

Table 1 The minimum allowable $\pmb{c_{2}}$ upper bound for $\pmb{\tau_{m}}$ with different values i

Example 2

We consider the above time-delay systems (1) with the following parameters given in [23, 25, 30, 31]:

$$\begin{aligned} &A= \begin{bmatrix} -1.2&0.1\\ -0.1&-1 \end{bmatrix},\qquad A_{d}= \begin{bmatrix} -0.6&0.7\\ -1&-0.8 \end{bmatrix}, \qquad B= \begin{bmatrix} 0\\ 0 \end{bmatrix}, \qquad C=[ \textstyle\begin{array}{@{}c@{\quad}c@{}} 0&0 \end{array}\displaystyle ], \\ & C_{d}=[ \textstyle\begin{array}{@{}c@{\quad}c@{}} 0&0 \end{array}\displaystyle ],\qquad L= \begin{bmatrix} 0\\ 0 \end{bmatrix},\qquad E_{a}=[ \textstyle\begin{array}{@{}c@{\quad}c@{}} 0&0 \end{array}\displaystyle ],\qquad E_{d}= [ \textstyle\begin{array}{@{}c@{\quad}c@{}} 0&0 \end{array}\displaystyle ],\\ &F=G= \begin{bmatrix} 1&0\\ 0&1 \end{bmatrix}, \qquad E= \begin{bmatrix} 0&0\\ 0&0 \end{bmatrix}. \end{aligned}$$

For given values of $\alpha=0.1$, $\beta=0.1$, $c_{1}=2.002$, $\rho = 13.9104$, $\eta=0.5$, $\tilde{\tau}_{d}=6.5$, $\bar{\tau}_{d}=7.5$, $\varepsilon=100$, $\delta =0.9$, $T=1.5$, $\tau_{m}=7$, $\tau_{M}=7.5$, $\psi=I$, $N=1$, we provide a part of the feasible solution here (due to the limitation of the length of this paper):

$$\begin{aligned}& c_{2} \{\min \}=8.8196e+06, \\& Q_{1 }= \begin{bmatrix} 3.8893 & 0.4102\\ 0.4102 & 2.3616 \end{bmatrix}, \qquad Q_{2}= \begin{bmatrix} 0.0675&-0.0057\\ -0.0057&0.0574 \end{bmatrix}, \\& \varepsilon_{1} =29.8198,\qquad \varepsilon_{2}=18.6851. \end{aligned}$$

Let $f(x)=0.01x(t)\sin (x(t))$, $g(x(t-\tau(t)))=0.1x(t-\tau(t))\cos (x(t-\tau(t)))$, in this example, Figures 9 and 10 show the trajectory of variables $x(t)$ with $\tau_{M}=8.3618$ and $\tau(t)=8+0.25 \sin t$ under the initial condition $[0.3,0.6]$, respectively.

Figure 9

Trajectories of $\pmb{x(t)}$ with $\pmb{\tau=8.3618}$ .

Figure 10

Trajectories of $\pmb{x(t)}$ with $\pmb{\tau(t)=8+0.25 \sin(t)}$ .

When $\alpha=\beta=0.1$, $\tau_{m}=7$, $\tau_{M}=7.5$, $\tilde{\tau }_{d}=6.5$, $\bar{\tau}_{d}=7.5$, the minimum allowable $c_{2}$ are given in Table 2 for different values of δ. From Table 2, it is also to see the FTB criteria can still be applicable when the range of $c_{2}$ is greater by adjusting the parameter δ.

Table 2 The minimum allowable $\pmb{c_{2}}$ upper bound for $\pmb{\tau_{m}}$ with different values δ

Example 3

We consider the above time-delay systems (1) with the following parameters given in [22]:

$$\begin{aligned} &A= \begin{bmatrix} -2&0.1\\ 0&-1 \end{bmatrix},\qquad A_{d}= \begin{bmatrix} -1&0\\ -1&-1 \end{bmatrix}, \qquad B= \begin{bmatrix} 0\\ 0 \end{bmatrix},\qquad C=[ \textstyle\begin{array}{@{}c@{\quad}c@{}} 0&0 \end{array}\displaystyle ], \\ & C_{d}=[ \textstyle\begin{array}{@{}c@{\quad}c@{}} 0&0 \end{array}\displaystyle ],\qquad L= \begin{bmatrix} 0\\ 0 \end{bmatrix}, \qquad E_{a}=[ \textstyle\begin{array}{@{}c@{\quad}c@{}} 0&0 \end{array}\displaystyle ], \qquad E_{d}= [ \textstyle\begin{array}{@{}c@{\quad}c@{}} 0&0 \end{array}\displaystyle ],\\ & F=G= \begin{bmatrix} 1&0\\ 0&1 \end{bmatrix}, \qquad E= \begin{bmatrix} 0&0\\ 0&0 \end{bmatrix}. \end{aligned}$$

Let $f(x(t))=0.05x(t)*\sin(x(t))$, $g(x(t-\tau(t)))=0.1x(t-\tau(t))*\cos (x(t-\tau(t)))$, $\tau_{M}=8.5419$. Figure 11 shows the trajectory of variable $x(t)$ under the initial condition $[0.4,0.8]^{T}$.

Figure 11

Trajectories of $\pmb{x(t)}$ with $\pmb{\tau=8.5419}$ .

For given values of α, β and $\bar{\tau }_{d}$, we apply Theorem 3.1 to calculate the maximal allowable value $\tau_{M}$ that guarantees the asymptotical stability of the system listed in Table 3. From the table, it is easy to see that our proposed stability criterion gives much less conservative results than those in [24], since the proposed analysis uses delay-partitioning approach as well as tighter bounding on the time derivative of the LKF.

Table 3 Maximum bounds $\pmb{\tau_{M}}$ for $\pmb{\tau_{m}=0.5,1}$

5 Conclusions

In this paper, we investigated the finite-time $H_{\infty}$ control problem for a class of continuous-time nonlinear system with time-varying norm-bounded parameter uncertainties and admissible external disturbances. Some sufficient conditions for the existence of the robust state-feedback controller and output-feedback controller have been provided in terms of LMIs. Finally, numerical examples are provided to demonstrate the effectiveness of the proposed method.