1 Introduction

Iterative learning control (ILC) is an effective control scheme in handling a system that repetitively perform the same task with a view to sequentially improving the accuracy on a finite interval. The research of ILC is of great significance for dynamic systems with complex modeling, strong nonlinear coupling effects, and uncertainty [1–5]. The aim of ILC is to look for a proper learning control algorithm of the controlled systems so that the output state can track the given desired trajectory over a finite interval time and in the meantime the constructed learning control sequences can uniformly converge to the desired control. Since Arimito proposed the concept of iterative learning control in 1984, the research of ILC has become a topic of focus in the field of control and fruitful research progress has been made in theory and application [6–12].

Singular systems have been a subject of interest over the last two decades due to their many practical applications. For instance, we have engineering systems, social systems, economic systems, biological systems, network analysis, time-series analysis, etc. [13, 14]. Such systems describe a wider class of systems, including physical models and non-dynamic constraints. Currently, ILC of singular system has also attracted the attentions of many scholars. The existing ILC methods of singular discrete systems use either a P-type algorithm or a D-type algorithm to track the desired output trajectory. Compared with these existing ILC methods, we use a PD-type algorithm related to the current error and the following error to improve the accuracy. Considering the equivalence of two norms, we use the λ norm in the paper to prove the convergence of the PD-type algorithm. Reference [15] studied the state tracking problem of the singular system with time-delay and proved that the iterative learning algorithm is convergent under certain conditions. In [16], the convergence of the P-type iterative learning control algorithm for a fast subsystem of a linear singular system is proved under a certain sufficient condition. Reference [17] proposes the convergence results for a continue linear time-invariant singular system by the close-loop PD-type iterative learning control algorithm. In [18], a new iterative learning control algorithm to study the state tracking for a class of singular systems is proposed and the convergence of the algorithm is completely analyzed.

As a result, the PD-type iterative learning control algorithm is applied to study the state tracking for a class of discrete singular systems. And then the convergence conditions are proposed and analyzed from the theoretical perspective. Finally, the numerical simulation results, showing that the given ILC algorithm for the state tracking of singular system is effective, are presented.

2 Description of singular discrete system

A repeatable discrete singular system is descried as follows:

$$ Ex_{k}(i+1) = Ax_{k}(i)+Bu_{k}(i), $$
(1)

where \(E,A\in R^{n\times n}\), \(B\in R^{n\times m}\) are constant matrices. E is singular matrix and \(\operatorname{rank}(E)= q< n\). i denotes the time index and \(i\in[0,1,\ldots,T]\), k is the repetitive time and \(k=1,2,\ldots \) .

According to the theorem in [13, 14], the system (1) could be expressed as

$$ \left \{ \textstyle\begin{array}{l} x_{k}^{(1)}(i+1) = A_{11}x_{k}^{(1)}(i)+A_{12}x_{k}^{(2)}(i)+B_{1}u_{k}(i), \\ 0 = A_{21}x_{k}^{(1)}(i)+A_{22}x_{k}^{(2)}(i)+B_{2}u_{k}(i), \end{array}\displaystyle \right . $$
(2)

where \(x_{k}^{(1)}(i)\in R^{q}\), \(x_{k}^{(2)}(i)\in R^{(n-q)}\), \(x_{k}(i)=[x_{k}^{(1)}(i)\ x_{k}^{(2)}(i)]^{T}\).

Based on decomposed form of the singular discrete system in (2), we propose the following PD-type iterative learning control algorithm:

$$ u_{k+1}(i)=u_{k}(i)+\varGamma _{1}e_{1k}(i+1)+ \varGamma _{2}e_{2k}(i), $$
(3)

where \(e_{1k}(i)=x_{d}^{(1)}(i)-x_{k}^{(1)}(i)\), \(e_{2k}(i)=x_{d}^{(2)}(i)-x_{k}^{(2)}(i)\). \(\varGamma _{1}\in R^{m\times q}\), \(\varGamma _{2}\in R^{m\times(n-q)}\) are the iterative learning gain matrices.

Since the target of this paper is to discuss the state tracking problem of the discrete system, in the following context, we can consider the singular discrete system (2). Assume that the singular discrete system (2) satisfies the following conditions:

  1. (1)

    The singular discrete system is regular, controllable, and observable, \(A_{22}\) is invertible.

  2. (2)

    The system (2) satisfies the initial conditions: \(x_{k}(0)=x_{d}(0)\), \(k=0,1,\ldots\) .

  3. (3)

    For a given desired target \(x_{d}(i)\), there always exists a corresponding control input \(u_{d}(i)\) over the finite interval \([0, T]\), such that

    $$ \left \{ \textstyle\begin{array}{l} x_{d}^{(1)}(i+1) = A_{11}x_{d}^{(1)}(i)+A_{12}x_{d}^{(2)}(i)+B_{1}u_{d}(i), \\ 0 = A_{21}x_{d}^{(1)}(i)+A_{22}x_{d}^{(2)}(i)+B_{2}u_{d}(i). \end{array}\displaystyle \right . $$
    (4)

3 Convergence analysis of PD-type iterative learning control algorithm

Throughout this paper, we will use the following notation.

The λ norm of the discrete-time vector \(h:\{0,1,\ldots,T\} \rightarrow R^{n}\) is defined as

$$ \Vert h\Vert _{\lambda}=\sup_{0\leqslant i\leqslant T}\bigl\{ \lambda^{i}\bigl\Vert h(i)\bigr\Vert \bigr\} \quad (0< \lambda< 1) , $$

where \(\|\cdot\|\) is a kind of vector norm in \(R^{n}\). For \(\lambda ^{T}\leqslant\lambda^{i}\leqslant\lambda^{0}\) (\(0\leqslant i\leqslant T\)), it is straightforward to get

$$\Vert h\Vert _{\lambda}\leqslant\sup_{0\leqslant i\leqslant T}\bigl\Vert h(i)\bigr\Vert \leqslant\lambda^{-T}\Vert h\Vert _{\lambda},\quad h:\{0,1,\ldots,T\}\rightarrow R^{n}. $$

Theorem 1

Assuming that the discrete singular system (2) satisfies the given conditions (1)-(3), if the condition \(\|G\|<1\) holds, where

$$G=I-\varGamma _{1}\hat{B}_{1}+\varGamma _{2} \hat{B}_{2},\quad \hat{B}_{2}=A_{22}^{-1}B_{2}, \hat{B}_{1}=B_{1}-A_{12}\hat{B}_{2}, $$

then the PD-type iterative learning control algorithm (3) is uniformly convergent on \([0,T]\). Furthermore, the state \(x_{k}(i)\) of the system (2) uniformly converges to the desired trajectory \(x_{d}(i)\) on \([0,T]\), when the iteration \(k\rightarrow\infty\), that is,

$$\lim_{k\rightarrow\infty}{x_{k}(i)}=x_{d}(i),\quad i \in[0,1,\ldots,T]. $$

Proof

Since \(0=A_{21}x_{k}^{(1)}(i)+A_{22}x_{k}^{(2)}(i)+B_{2}u_{k}(i)\) and \(A_{22}\) is an invertible matrix,

$$ x_{k}^{(2)}(i)=-A_{22}^{-1}A_{21}x_{k}^{(1)}(i)-A_{22}^{-1}B_{2}u_{k}(i). $$
(5)

Denoting \(\hat{A}_{21}=A_{22}^{-1}A_{21}\), \(\hat{B}_{2}=A_{22}^{-1}B_{2}\), then (5) can be written as

$$ x_{k}^{(2)}(i)=-\hat{A}_{21}x_{k}^{(1)}(i)- \hat{B}_{2} u_{k}(i). $$
(6)

Substituting (6) into the system (2), we get

$$ x_{k}^{(1)}(i+1)=(A_{11}-A_{12} \hat{A}_{21})x_{k}^{(1)}(i)+(B_{1}-A_{12} \hat {B}_{2})u_{k}(i); $$
(7)

letting \(\hat{A}_{11}=A_{11}-A_{12}\hat{A}_{21}\), \(\hat {B}_{1}=B_{1}-A_{12}\hat{B}_{2}\), then (7) becomes

$$ x_{k}^{(1)}(i+1)=\hat{A}_{11}x_{k}^{(1)}(i)+ \hat{B}_{1}u_{k}(i). $$
(8)

Denote \(\varDelta u_{k}(i)=u_{d}(i)-u_{k}(i)\). From (3), we obtain

$$ \varDelta u_{k+1}(i)=\varDelta u_{k}(i)-\bigl( \varGamma _{1}e_{1k}(i+1)+\varGamma _{2}e_{2k}(i) \bigr). $$
(9)

From (6) and (8), one derives that

$$ e_{1k}(i+1)=x_{d}^{(1)}(i+1)-x_{k}^{(1)}(i+1)= \hat{A}_{11}e_{1k}(i)+\hat {B}_{1}\varDelta u_{k}(i) $$
(10)

and

$$ e_{2k}(i)=x_{d}^{(2)}(i)-x_{k}^{(2)}(i)=- \hat{A}_{21}e_{1k}(i)-\hat {B}_{2}\varDelta u_{k}(i). $$
(11)

Substituting (10), (11) into (9), we have

$$ \varDelta u_{k+1}(i)=\varDelta u_{k}(i)-( \varGamma _{1}\hat{A}_{11}-\varGamma _{2}\hat {A}_{21})e_{1k}(i)-(\varGamma _{1}\hat{B}_{1}- \varGamma _{2}\hat{B}_{2})\varDelta u_{k}(i); $$
(12)

labeling \(G=I-\varGamma _{1}\hat{B}_{1}+\varGamma _{2}\hat{B}_{2}\), \(H=\varGamma _{2}\hat {A}_{21}-\varGamma _{1}\hat{A}_{11}\), then

$$ \varDelta u_{k+1}(i)=He_{1k}(i)+G\varDelta u_{k}(i). $$
(13)

Considering the initial condition \(x_{k}(0)=x_{d}(0)\), \(k=0,1,\ldots\) , and (10), we have

$$\begin{aligned} e_{1k}(i) =&\hat{A}_{11}^{i}e_{1k}(i)+ \sum_{j=0}^{i-1} \hat {A}_{11}^{i-j-1} \hat{B}_{1}\varDelta u_{k}(j) \\ =&\sum_{j=0}^{i-1} \hat {A}_{11}^{i-j-1}\hat{B}_{1}\varDelta u_{k}(j). \end{aligned}$$
(14)

Thus, (13) can be rewritten as

$$ \varDelta u_{k+1}(i)=H\sum_{j=0}^{i-1} \hat{A}_{11}^{i-j-1}\hat{B}_{1}\varDelta u_{k}(j)+G\varDelta u_{k}(i). $$
(15)

Taking norms on both sides of (15) and multiplying by \(\lambda^{i}\), we obtain

$$ \lambda^{i}\bigl\Vert \varDelta u_{k+1}(i)\bigr\Vert \leqslant\lambda^{i}\Vert H\Vert \sum _{j=0}^{i-1} \bigl\Vert \hat{A}_{11}^{i-j-1} \hat{B}_{1}\bigr\Vert \bigl\Vert \varDelta u_{k}(j)\bigr\Vert +\lambda^{i}\Vert G\Vert \bigl\Vert \varDelta u_{k}(i)\bigr\Vert . $$
(16)

Denote \(h=\|H\|\), \(b=\sup_{\substack{1\leqslant i\leqslant T\\ 0\leqslant j\leqslant{i-1}}}\|\hat{A}_{11}^{i-j-1}\hat{B}_{1}\|\). According to the definition of the λ norm, it yields

$$\begin{aligned} \lambda^{i}\bigl\Vert \varDelta u_{k+1}(i)\bigr\Vert \leqslant&\lambda^{i}h\sum_{j=0}^{i-1}b \bigl\Vert \varDelta u_{k}(j)\bigr\Vert +\lambda^{i}\Vert G\Vert \bigl\Vert \varDelta u_{k}(i)\bigr\Vert \\ \leqslant&\Vert G\Vert \Vert \varDelta u_{k}\Vert _{\lambda}+hb\sum_{j=0}^{i-1} \lambda ^{i-j}\Vert \varDelta u_{k}\Vert _{\lambda} \\ \leqslant&\biggl( \Vert G\Vert +hb\frac{\lambda}{1-\lambda}\biggr)\Vert \varDelta u_{k}\Vert _{\lambda}. \end{aligned}$$
(17)

Because the right side of (17) is irrespective of time, we obtain

$$\begin{aligned} \|\varDelta u_{k+1}\|_{\lambda}\leqslant\biggl( \|G \|+hb\frac{\lambda}{1-\lambda }\biggr)\|\varDelta u_{k}\|_{\lambda}. \end{aligned}$$
(18)

For \(\|G\|<1\), there exists a λ small enough such that

$$ \|G\|+hb\frac{\lambda}{1-\lambda}< 1. $$
(19)

Then it follows from (18) and (19) that as long as λ is small enough, one derives that

$$ \lim_{k\rightarrow\infty}\|\varDelta u_{k} \|_{\lambda}=0. $$
(20)

According to the properties of λ-norm we have \(\sup_{1\leqslant i\leqslant T}\|\varDelta u_{k}(i)\| \leqslant\lambda^{-T}\|\varDelta u_{k}\|_{\lambda}\), which yields

$$ \lim_{k\rightarrow\infty}\sup_{1\leqslant i\leqslant T}\bigl\Vert \varDelta u_{k}(i)\bigr\Vert =0. $$
(21)

That means algorithm (3) is uniformly convergent.

For λ to meet (19), taking norms on both sides of (5) and multiplying by λ, we get

$$\begin{aligned} \lambda^{i}\bigl\Vert e_{1k}(i)\bigr\Vert \leqslant&\sum_{j=0}^{i-1} \bigl\Vert \hat {A}_{11}^{i-j-1}\hat{B}_{1}\bigr\Vert \lambda^{i-j}\lambda^{j}\bigl\Vert \varDelta u_{k}(j)\bigr\Vert \\ \leqslant& b\frac{\lambda}{1-\lambda} \Vert \varDelta u_{k}\Vert _{\lambda}. \end{aligned}$$
(22)

Similar to the derivation of (18), we have

$$ \|e_{1k}\|_{\lambda}\leqslant b\frac{\lambda}{1-\lambda}\| \varDelta u_{k}\| _{\lambda}. $$
(23)

Combining (20) and (21), we obtain

$$ \lim_{k\rightarrow\infty}\sup_{1\leqslant i\leqslant T}\bigl\Vert e_{1k}(i)\bigr\Vert =0. $$
(24)

Similarly,we have

$$ \lim_{k\rightarrow\infty}\sup_{1\leqslant i\leqslant T}\bigl\Vert e_{2k}(i)\bigr\Vert =0. $$
(25)

We have

$$ x_{d}(i)-x_{k}(i)= \begin{pmatrix} x_{d}^{(1)}(i) \\ x_{d}^{(2)}(i) \end{pmatrix}- \begin{pmatrix} x_{k}^{(1)}(i)\\ x_{k}^{(2)}(i) \end{pmatrix} = \begin{pmatrix} e_{1k}(i)\\ e_{2k}(i) \end{pmatrix}. $$

Therefore \(\lim_{k\rightarrow\infty}{x_{k}(i)}=x_{d}(i)\) is true on the interval \([0,T]\). □

4 Simulation of the new algorithm

In the paper, we discussed a two-dimensional singular discrete-time system. A system model is mentioned as follows:

$$ \begin{bmatrix} 1 & 0 \\ 0 & 0 \end{bmatrix} \begin{pmatrix} x_{k}^{1}(i+1) \\ x_{k}^{2}(i+1) \end{pmatrix} = \begin{bmatrix}1 & 2 \\ 1 & 1 \end{bmatrix} \begin{pmatrix} x_{k}^{1}(i) \\ x_{k}^{2}(i) \end{pmatrix} + \begin{bmatrix}1 & 0 \\ 0 & 1 \end{bmatrix} \begin{pmatrix} u_{k}^{1}(i) \\ u_{k}^{2}(i) \end{pmatrix} . $$

As shown above, we can see that

$$ E= \begin{bmatrix}1 & 0 \\ 0 & 0 \end{bmatrix} ,\qquad A= \begin{bmatrix}1 & 2 \\ 1 & 1 \end{bmatrix} ,\qquad B= \begin{bmatrix}1 & 0 \\ 0 & 1 \end{bmatrix} . $$

From the restricted equivalence transformation of singular systems, we have the following form:

$$ \left \{ \textstyle\begin{array}{l} x_{k}^{1}(i+1)=x_{k}^{1}(i)+2x_{k}^{2}(i)+u_{k}^{1}(i), \\ 0=x_{k}^{1}(i)+x_{k}^{2}(i)+u_{k}^{2}(i). \end{array}\displaystyle \right . $$
(26)

According to the PD-type algorithm (3), let the gain matrix be

$$\begin{aligned}& \varGamma _{1}= \bigl[\textstyle\begin{array}{@{}c@{\quad}c@{}} 0.4 & -0.06 \end{array}\displaystyle \bigr] ^{T}, \\& \varGamma _{2}= \bigl[\textstyle\begin{array}{@{}c@{\quad}c@{}}-0.9 & -0.5 \end{array}\displaystyle \bigr] ^{T}, \end{aligned}$$

and E, A, B satisfy the conditions in Theorem 1. We denote

$$ x_{d}(i)=\left \{ \textstyle\begin{array}{l} x_{d}^{(1)}(i) =5\sin(0.6i), \\ x_{d}^{(2)}(i) =10-10e^{-i}, \end{array}\displaystyle \right . $$

with the initial conditions of \(x_{k}(0)= [0 \ 0] ^{T}\), \(u_{0}(t)= [0 \ 0]^{T}\), and it satisfies the condition \(\max \|G\|=0.7<1\), where

$$G=I-\varGamma _{1}\hat{B}_{1}+\varGamma _{2} \hat{B}_{2}= \begin{bmatrix}0.6 & -0.1 \\ 0.06 & 0.38 \end{bmatrix} $$

and we take

$$\max \Vert G\Vert =\max\bigl\{ \Vert G\Vert _{1},\Vert G \Vert _{2},\Vert G\Vert _{\infty}\bigr\} ; $$

then the simulation results are shown in Figures 1-4.

Figure 1
figure 1

The system state tracking of \(\pmb{x_{d}^{(1)}(i)}\) .

Full size image

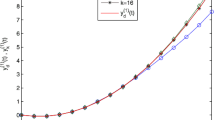
Figure 1 shows the tracking process of the desired trajectory \(x_{d}^{(1)}(i)\) of the discrete singular system by using iterative learning control algorithm (3) at 18th and 25th iterations. According to the definition of complete tracking and the simulation data we can derive that the algorithm can track the desired trajectory completely at the 30th iteration.

Figure 2 shows the tracking process of the desired trajectory \(x_{d}^{(2)}(i)\) of the discrete singular system by using iterative learning control algorithm (3) at the 18th and 25th iterations. According to the definition of complete tracking and the simulation data we can derive that the algorithm can track the desired trajectory completely at the 30th iterations.

Figure 2
figure 2

The system state tracking of \(\pmb{x_{d}^{(2)}(i)}\) .

Full size image

Figures 3 and 4 show the variation curves of the maximum tracking error. With the increase number of iterations, the state tracking error can converge to zero.

Figure 3
figure 3

The variation curves of the maximum tracking error of \(\pmb{x_{d}^{(1)}(i)}\) .

Full size image
Figure 4
figure 4

The variation curves of the maximum tracking error of \(\pmb{x_{d}^{(2)}(i)}\) .

Full size image

The simulation examples illustrate the effectiveness of PD-type iterative learning control algorithm for discrete singular systems. It shows that the research on discrete iterative learning control problem of a class of singular systems has obtained good results in this paper.

5 Conclusions

In this paper, an iterative learning control problem for a class of discrete singular systems is studied by using the dynamic decomposition standard of singular systems. The PD-type iterative learning control algorithm and the sufficient condition are designed, and we have proved in theory the algorithm can guarantee that the output can track the desired trajectory completely on a finite time interval. The simulation example shows the effectiveness of PD-type iterative learning control algorithm for the discrete singular system.