1 Introduction

The Zakharov-Kuznetsov (ZK) equation is a generalization of the Korteweg-de Vries (KdV) equation. It was obtained by Zakharov and Kuznetsov [1] to describe the behavior of weakly nonlinear ion-acoustic waves in a plasma comprising cold ions and hot isothermal electrons in the presence of a uniform magnetic field. If a magnetic field is directed along the x-axis, the ZK equation in renormalized variables [2] takes the form

$$ u_{t}+auu_{x}+\nabla^{2}u_{x}=0, $$
(1.1)

where \(\nabla^{2}=\partial^{2}_{x}+\partial^{2}_{y}+\partial^{2}_{z}\) is the isotropic Laplacian. The ZK equation is given by

$$ u_{t}+auu_{x}+(u_{xx}+u_{yy})_{x}=0 $$
(1.2)

and

$$ u_{t}+auu_{x}+(u_{xx}+u_{yy}+u_{zz})_{x}=0, $$
(1.3)

in two- and three-dimensional spaces, respectively. Several properties of this equation, including the existence and stability of solitary wave solutions, have been extensively studied in the literature (see [3, 4] and references therein).

Many numerical schemes have been proposed for some well-known one-dimensional equations, however, little numerical analysis has been published for the multi-dimensional cases. Few numerical methods have been proposed for solving the ZK equation. Xu and Shu [5] discussed a local discontinuous Galerkin (LDG) method for the ZK equation, which is different from the DG method in our paper. Ren et al. [6] proposed an implicit fully discrete LDG method for the fractional Zakharov-Kuznetsov equation and proved the stability and convergence. In [7], Cheng and Shu presented a new DG method for solving some kinds of time dependent partial differential equations in one dimension. The method could be used to solve the problems without introducing any auxiliary variables or rewriting the original equation into a larger system.

For the sake of simplicity, we will only consider the problem in two dimension on a rectangular domain, \(\Omega=[a,b]\times[c,d]\). However, the method in our paper could easily be generalized to higher dimensions.

In this paper, we will present and analyze a DG method for the ZK equation:

$$ u_{t}+f(u)_{x}+u_{xxx}+u_{xyy}=0, $$
(1.4)

with an initial condition

$$ u(x,y,0)=u_{0}(x,y), $$
(1.5)

and periodic boundary conditions. Here \(f(u)\) is a nonlinear function.

The rest of this paper is as follows. In Section 2, some notations and auxiliary results are introduced, which will be used later in this paper. In Section 3, the DG method for ZK equation is presented, and a stability error estimate is discussed in Section 4. Some numerical experiments are given to illustrate the accuracy and capability of the method in Section 5. Finally some concluding remarks and comments for future work are given in Section 6.

2 Notations

2.1 Basic notations

For the sake of simplicity, a rectangular mesh is assumed to cover the computational domain \([a,b]\times[c,d]\),

$$ I_{i,j} =\bigl\{ (x,y):x_{i-\frac{1}{2}}\leq x\leq x_{i+\frac{1}{2}},y_{j-\frac{1}{2}} \leq y\leq y_{j+\frac{1}{2}}\bigr\} , $$

for \(i=1,\ldots, N_{x}\), \(j=1,\ldots, N_{y}\), where

$$ a=x_{\frac{1}{2}}< x_{\frac{3}{2}}< \cdots< x_{N_{x}+\frac{1}{2}}=b $$

and

$$ c=y_{\frac{1}{2}}< y_{\frac{3}{2}}< \cdots< y_{N_{y}+\frac{1}{2}}=d $$

are discretizations in x over \([a,b]\) and y over \([c,d]\), respectively. The center of the element in the x-direction is \(x_{i} =(x_{i-1/2}+x_{i+1/2})/2\); the center of the element in the y-direction is \(y_{j} =(y_{j-1/2}+y_{j+1/2})/2\). We define \(I_{i}\) and \(J_{j}\) by \(I_{i}=[x_{i-\frac{1}{2}},x_{i+\frac{1}{2}}] \), \(J_{j}=[y_{j-\frac{1}{2}}, y_{j+\frac{1}{2}}] \) for \(i=1,\ldots, N_{x}\), \(j=1,\ldots, N_{y}\). We have \(I_{i,j}=I_{i}\times J_{j}\).

We denote by \(u_{i+\frac{1}{2},y}^{+}\) and \(u_{i+\frac{1}{2},y}^{-}\) the values of u at \(x_{i+1/2}\), and by \(u_{x,j+1/2}^{+}\) and \(u_{x,j+1/2}^{-}\) the values of u at \(y_{j+1/2}\), from the top cell \(I_{i}\times J_{j+1}\) and from the bottom cell \(I_{i}\times J_{j}\), respectively.

Denote the cell lengths

$$ \Delta x_{i}=x_{i+\frac{1}{2}}-x_{i-\frac{1}{2}},\quad 1\leq i\leq N_{x}, \qquad \Delta y_{j}=y_{j+\frac{1}{2}}-y_{j-\frac{1}{2}}, \quad 1\leq j\leq N_{y}, $$

and \(h=\max(\max_{1\leq i\leq N_{x}}\Delta x_{i},\max_{1\leq j\leq N_{y}}\Delta y_{j})\).

Assume the mesh is regular, namely there is a constant \(c>0\) independent of h such that

$$ \Delta x_{i}\geq ch, \quad 1\leq i\leq N_{x}, \qquad \Delta y_{j}\geq ch, \quad 1\leq j\leq N_{y}. $$

Define the space \(V_{h}^{k}\) as the space of tensor product piecewise polynomials of degree at most k in each variable on every element

$$ V_{h}^{k}=\bigl\{ v:v\in Q^{k}(I_{i} \times J_{j}),\forall(x,y)\in I_{i}\times J_{j}, i=1,\ldots,N_{x},j=1,\ldots,N_{y}\bigr\} . $$
(2.1)

In this paper we use C to denote a positive constant, which may have a different value in a different occurrence. For any integer \(s\geq0\), let \(H^{s}(\Omega)\) represent the well-known Sobolev space equipped with the norm \(\|\cdot\|_{s}\). Let the scalar inner product on \(L^{2}\) be denoted by \((\cdot,\cdot)\), and the associated norm by \(\|\cdot\|\). Furthermore, let \(\|\cdot\|_{\infty}\) represent the norm on \(L^{\infty}\) [8].

2.2 Projection

In order to give an error estimates for two-dimensional problems in Cartesian meshes, we will give the projection in one dimension, which has been used in [7, 9, 10]. When \(k\geq3\), we could choose a projection \(\mathcal{P}\) such that, for any u, \(\mathcal{P}u\) satisfies

$$ \int_{I_{i}}uv\, dx= \int_{I_{i}}\mathcal{P}uv\, dx, $$

for any \(v\in V_{h}^{k-3}\) and

$$ \mathcal{P}u^{+}=u^{+},\qquad (\mathcal{P}u)_{x}^{+}=u_{x}^{+}, \qquad (\mathcal {P}u)_{xx}^{-}=u_{xx}^{-}, $$

at all \(x_{i+\frac{1}{2}}\).

Denote by \(\eta=u-\mathcal{P}u\) the projection error. It is easy to show [11]

$$ \|\eta\|+h\|\eta\|_{\infty}+h^{\frac{1}{2}}\|\eta\|_{\tau_{h}} \leq Ch^{k+1}, $$

where C is a positive constant that depends on k and \(\|u\|_{k+1}\) of the function u, \(\tau_{h}\) denotes the set of boundary points of all elements \(I_{i}\).

Next we give the projection in two dimensions. On a rectangle \([a,b]\times[c,d]\), define

$$ \mathbb{P}\omega=\mathcal{P}_{x}\otimes \mathcal{P}_{y}\omega, $$
(2.2)

where the subscripts indicate the application of the one dimensional operators \(\mathcal{P}\). Some properties for the projection \(\mathbb {P}\) are listed thus:

$$ \int_{I_{i}} \int_{J_{j}}\bigl(\mathbb{P}\omega(x,y)-\omega(x,y)\bigr)v(x,y)\, dy\, dx=0, $$
(2.3)

for any \(v(x,y)\in(P^{k-3}(I_{i})\otimes P^{k}(J_{j}))\cup (P^{k}(I_{i})\otimes P^{k-3}(J_{j}))\). Also

$$ \begin{aligned} & \int_{J_{j}}\bigl(\mathbb{P}\omega\bigl(x_{i-\frac{1}{2}}^{+},y \bigr)-\omega (x_{i-\frac{1}{2}},y)\bigr)v\bigl(x_{i-\frac{1}{2}}^{+},y\bigr)\,dy=0, \quad \forall v\in Q^{k}(I_{i}\otimes J_{j}), \\ & \int_{J_{j}}\bigl(\bigl(\mathbb{P}\omega\bigl(x_{i-\frac{1}{2}}^{+},y \bigr)\bigr)_{x}-\bigl(\omega (x_{i-\frac{1}{2}},y)\bigr)_{x} \bigr)v\bigl(x_{i-\frac{1}{2}}^{+},y\bigr)\,dy=0, \quad \forall v\in Q^{k}(I_{i}\otimes J_{j}), \\ & \int_{J_{j}}\bigl(\bigl(\mathbb{P}\omega\bigl(x_{i+\frac{1}{2}}^{-},y \bigr)\bigr)_{xx}-\bigl(\omega (x_{i+\frac{1}{2}},y)\bigr)_{xx} \bigr)v\bigl(x_{i+\frac{1}{2}}^{-},y\bigr)\,dy=0, \quad \forall v\in Q^{k}(I_{i}\otimes J_{j}), \end{aligned} $$
(2.4)

and

$$ \begin{aligned} & \int_{I_{i}}\bigl(\mathbb{P}\omega\bigl(x,y_{j-\frac{1}{2}}^{+} \bigr)-\omega (x,y_{j-\frac{1}{2}})\bigr)v\bigl(x,y_{j-\frac{1}{2}}^{+}\bigr)\,dx=0, \quad \forall v\in Q^{k}(I_{i}\otimes J_{j}), \\ & \int_{J_{j}}\bigl(\bigl(\mathbb{P}\omega\bigl(x_{i-\frac{1}{2}}^{+},y \bigr)\bigr)_{y}-\bigl(\omega (x_{i-\frac{1}{2}},y)\bigr)_{y} \bigr)v\bigl(x_{i-\frac{1}{2}}^{+},y\bigr)\,dy=0, \quad \forall v\in Q^{k}(I_{i}\otimes J_{j}), \\ & \int_{I_{i}}\bigl(\bigl(\mathbb{P}\omega\bigl(x,y_{j+\frac{1}{2}}^{-} \bigr)\bigr)_{xy}-\bigl(\omega (x,y_{j+\frac{1}{2}})\bigr)_{xy} \bigr)v\bigl(x,y_{j+\frac{1}{2}}^{+}\bigr)\,dx=0, \quad \forall v\in Q^{k}(I_{i}\otimes J_{j}). \end{aligned} $$
(2.5)

Similar to the one-dimensional case, there are some important approximation results for the projection (2.2),

$$ \|\eta\|+h\|\eta\|_{\infty}+h^{\frac{1}{2}}\|\eta \|_{\tau _{h}}\leq Ch^{k+1}, $$
(2.6)

where \(\eta=\mathbb{P}\omega-\omega\). \(\tau_{h}\) denotes the set of boundary points of all elements \(I_{i}\times J_{j}\), and we define

$$\begin{aligned} \|\eta\|_{\tau_{h}} =&\biggl(\sum_{1\leq i\leq N_{x}} \int_{c}^{d}\bigl(\bigl(\eta^{+}_{i+\frac{1}{2},y} \bigr)^{2}+\bigl(\eta^{-}_{i+\frac {1}{2},y}\bigr)^{2}\bigr)\,dy \\ &{}+\sum_{1\leq j\leq N_{y}} \int_{a}^{b}\bigl(\bigl(\eta^{+}_{x,j+\frac{1}{2}} \bigr)^{2}+\bigl(\eta^{-}_{x,j+\frac {1}{2}}\bigr)^{2}\bigr)\,dx \biggr)^{\frac{1}{2}}. \end{aligned}$$

3 DG scheme

In this section we define the discontinuous Galerkin method for equation (1.4): find \(u_{h}\in V_{h}^{k}\), such that for all test functions \(v_{h}\in V_{h}^{k}\),

$$\begin{aligned}& \int_{J_{j}} \int_{I_{i}}(u_{h})_{t}v_{h}\,dx \,dy- \int_{J_{j}} \int _{I_{i}}f(u_{h}) (v_{h})_{x} \,dx\,dy- \int_{J_{j}} \int_{I_{i}}u_{h}(v_{h})_{xxx}\,dx \,dy \\& \quad {}- \int_{J_{j}} \int_{I_{i}}u_{h}(v_{h})_{xyy}\,dx \,dy+ \int _{J_{j}}\bigl(\hat{f}\bigl(u_{h}^{-},u_{h}^{+} \bigr) (v_{h})^{-}\bigr)_{i+\frac{1}{2},y}\,dy \\& \quad {}- \int_{J_{j}}\bigl(\hat{f}\bigl(u_{h}^{-},u_{h}^{+} \bigr) (v_{h})^{+}\bigr)_{i-\frac {1}{2},y}\,dy+ \int_{J_{j}}\bigl((\hat{u}_{h})_{xx}v_{h}^{-} \bigr)_{i+\frac {1}{2},y}\,dy \\& \quad {}- \int_{J_{j}}\bigl((\hat{u}_{h})_{xx}v_{h}^{+} \bigr)_{i-\frac {1}{2},y}\,dy- \int_{J_{j}}\bigl((\hat{u}_{h})_{x}(v_{h})_{x}^{-} \bigr)_{i+\frac {1}{2},y}\,dy \\& \quad {}+ \int_{J_{j}}\bigl((\hat{u}_{h})_{x}(v_{h})_{x}^{+} \bigr)_{i-\frac {1}{2},y}\,dy+ \int_{J_{j}}\bigl(\hat{u}_{h}(v_{h})_{xx}^{-} \bigr)_{i+\frac {1}{2},y}\,dy \\& \quad {}- \int_{J_{j}}\bigl(\hat{u}_{h}(v_{h})_{xx}^{+} \bigr)_{i-\frac {1}{2},y}\,dy+ \int_{I_{i}}\bigl((\overline{u}_{h})_{xy}v_{h}^{-} \bigr)_{x,j+\frac {1}{2}}\,dx \\& \quad {}- \int_{I_{i}}\bigl((\overline{u}_{h})_{xy}v_{h}^{+} \bigr)_{x,j-\frac {1}{2}}\,dx- \int_{J_{j}}\bigl((\overline{u}_{h})_{y}(v_{h})_{y}^{-} \bigr)_{i+\frac {1}{2},y}\,dy \\& \quad {}+ \int_{J_{j}}\bigl((\overline{u}_{h})_{y}(v_{h})_{y}^{+} \bigr)_{i-\frac {1}{2},y}\,dy+ \int_{I_{i}}\bigl(\overline{u}_{h}(v_{h})_{xy}^{-} \bigr)_{x,j+\frac {1}{2}}\,dx \\& \quad {}- \int_{I_{i}}\bigl(\overline{u}_{h}(v_{h})_{xy}^{+} \bigr)_{x,j-\frac{1}{2}}\,dx=0. \end{aligned}$$
(3.1)

The flux \(\hat{f}(w^{-},w^{+})\) is a monotone flux. Some examples of monotone fluxes can be found in [12]. In this paper we could use the Lax-Friedriches flux,

$$\begin{aligned}& \hat{f}^{LF}\bigl(w^{-},w^{+}\bigr) = \frac{1}{2}\bigl(f\bigl(w^{-} \bigr)+f\bigl(w^{+}\bigr)-\alpha \bigl(w^{+}-w^{-}\bigr)\bigr), \\& \quad \alpha=\max_{\inf u_{0}\leq w\leq\sup u_{0}}\bigl\vert f'(w)\bigr\vert . \end{aligned}$$

The other ‘hat’ terms in (3.1) are the boundary terms that emerge from integration by parts. In order to ensure the stability, we could take the simple choices such that

$$ \begin{aligned} &\hat{u}_{h}=u_{h}^{+}, \qquad ( \hat{u}_{h})_{x}=(u_{h})_{x}^{+}, \qquad (\hat {u}_{h})_{xx}=(u_{h})_{xx}^{-}, \\ &\overline{u}_{h}=u_{h}^{+},\qquad (\overline{u}_{h})_{y}=(u_{h})_{y}^{+}, \qquad (\overline {u}_{h})_{xy}=(u_{h})_{xy}^{-}, \end{aligned} $$
(3.2)

or

$$ \begin{aligned} &\hat{u}_{h}=u_{h}^{-}, \qquad ( \hat{u}_{h})_{x}=(\hat {u}_{h})_{x}^{+}, \qquad (\hat{u}_{h})_{xx}=(\hat{u}_{h})_{xx}^{+}, \\ &\overline{u}_{h}=u_{h}^{-}, \qquad (\overline{u}_{h})_{y}=(u_{h})_{y}^{+}, \qquad (\overline {u}_{h})_{xy}=(u_{h})_{xy}^{+}. \end{aligned} $$
(3.3)

It is crucial that we take \((\hat{u}_{h})_{x}=(u_{h})_{x}^{+}\), \((\overline{u}_{h})_{y}=(u_{h})_{y}^{+}\) and the pair of fluxes \(\hat{u}_{h}\), \((\hat{u}_{h})_{xx}\) from the opposite directions; likewise for the pair \(\overline{u}_{h}\) and \((\overline{u}_{h})_{xy}\).

Equation (3.1) defines the DG method in integral form. To describe the algebraic problem to which the equation leads, let \(\{\varphi^{s}_{i}\theta^{m}_{j}\}\) be a tensor product local basis function system for \(Q^{k}(I_{i}\times J_{j})\), where \(\{\varphi^{s}_{i}\}_{s=1}^{k}\) and \(\{\theta^{m}_{j}\}_{m=1}^{k}\) are bases for the subspaces \(P^{k}(I_{i})\) and \(P^{k}(J_{j})\), respectively. Let

$$ u_{h}(x,y,t)=\sum_{s=1}^{k} \sum_{m=1}^{k}\alpha ^{sm}_{ij}(t) \varphi^{s}_{i}(x)\theta^{m}_{j}(y), \quad (x,y)\in I_{i,j}. $$
(3.4)

If in (3.1) we choose \(v_{h}=\varphi^{q}_{i}\theta^{r}_{j}\), \(1\leq q\leq k\), \(1\leq r\leq k\), then we can obtain

$$ \sum_{s=1}^{k}\sum _{m=1}^{k} \int_{I_{i}}\varphi ^{s}_{i} \varphi^{q}_{i}\,dx \int_{J_{j}}\theta^{m}_{j} \theta^{r}_{j}\,dy\frac{d\alpha ^{sm}_{ij}(t)}{dt}=F^{qr}_{ij}(v_{h}), $$
(3.5)

where \(F^{qr}_{ij}(v_{h})\) consists of terms from the left hand side of equation (3.1) except the first term.

We use the third order explicit TVD Runge-Kutta method in time direction [13]. The definition of the algorithm is now complete.

4 Stability analysis

Theorem 4.1

The solution \(u_{h}\) of the DG scheme (3.1) satisfies the following stability result:

$$ \bigl\Vert u_{h}(t)\bigr\Vert \leq\bigl\Vert u_{h}(0)\bigr\Vert . $$
(4.1)

Proof

We introduce a short-hand notation:

$$\begin{aligned} B_{ij}(u_{h},v_{h}) =& \int_{J_{j}} \int_{I_{i}}(u_{h})_{t}v_{h}\,dx \,dy- \int _{J_{j}} \int_{I_{i}}f(u_{h}) (v_{h})_{x} \,dx\,dy \\ &{} - \int_{J_{j}} \int_{I_{i}}u_{h}(v_{h})_{xxx}\,dx \,dy- \int_{J_{j}} \int _{I_{i}}u_{h}(v_{h})_{xyy}\,dx \,dy \\ &{} + \int_{J_{j}}\bigl(\hat{f}\bigl(u_{h}^{-},u_{h}^{+} \bigr) (v_{h})^{-}\bigr)_{i+\frac {1}{2},y}\,dy- \int_{J_{j}}\bigl(\hat{f}\bigl(u_{h}^{-},u_{h}^{+} \bigr) (v_{h})^{+}\bigr)_{i-\frac {1}{2},y}\,dy \\ &{} + \int_{J_{j}}\bigl((u_{h})_{xx}^{-}v_{h}^{-} \bigr)_{i+\frac{1}{2},y}\,dy- \int _{J_{j}}\bigl((u_{h})_{xx}^{-}v_{h}^{+} \bigr)_{i-\frac{1}{2},y}\,dy \\ &{} - \int_{J_{j}}\bigl((u_{h})_{x}^{+}(v_{h})_{x}^{-} \bigr)_{i+\frac{1}{2},y}\,dy+ \int _{J_{j}}\bigl((u_{h})_{x}^{+}(v_{h})_{x}^{+} \bigr)_{i-\frac{1}{2},y}\,dy \\ &{} + \int_{J_{j}}\bigl(u_{h}^{+}(v_{h})_{xx}^{-} \bigr)_{i+\frac{1}{2},y}\,dy- \int _{J_{j}}\bigl(u_{h}^{+}(v_{h})_{xx}^{+} \bigr)_{i-\frac{1}{2},y}\,dy \\ &{} + \int_{I_{i}}\bigl((u_{h})_{xy}^{-}v_{h}^{-} \bigr)_{x,j+\frac{1}{2}}\,dx- \int _{I_{i}}\bigl((u_{h})_{xy}^{-}v_{h}^{+} \bigr)_{x,j-\frac{1}{2}}\,dx \\ &{} - \int_{J_{j}}\bigl((u_{h})_{y}^{+}(v_{h})_{y}^{-} \bigr)_{i+\frac{1}{2},y}\,dy+ \int _{J_{j}}\bigl((u_{h})_{y}^{+}(v_{h})_{y}^{+} \bigr)_{i-\frac{1}{2},y}\,dy \\ &{} + \int_{I_{i}}\bigl(u_{h}^{+}(v_{h})_{xy}^{-} \bigr)_{x,j+\frac{1}{2}}\,dx- \int _{I_{i}}\bigl(u_{h}^{+}(v_{h})_{xy}^{+} \bigr)_{x,j-\frac{1}{2}}\,dx \\ =& \int_{J_{j}} \int _{I_{i}}(u_{h})_{t}v_{h}\,dx \,dy+E^{1}_{ij}(u_{h},v_{h})+E^{2}_{ij}(u_{h},v_{h})+E^{3}_{ij}(u_{h},v_{h}), \end{aligned}$$
(4.2)

where

$$\begin{aligned}& E^{1}_{ij}(u_{h},v_{h})= - \int_{J_{j}} \int_{I_{i}}f(u_{h}) (v_{h})_{x} \,dx\,dy+ \int _{J_{j}}\bigl(\hat{f}\bigl(u_{h}^{-},u_{h}^{+} \bigr) (v_{h})^{-}\bigr)_{i+\frac{1}{2},y}\,dy \\& \hphantom{E^{1}_{ij}(u_{h},v_{h})={}}{}- \int_{J_{j}}\bigl(\hat{f}\bigl(u_{h}^{-},u_{h}^{+} \bigr) (v_{h})^{+}\bigr)_{i-\frac{1}{2},y}\,dy, \end{aligned}$$
(4.3)
$$\begin{aligned}& E^{2}_{ij}(u_{h},v_{h})= - \int_{J_{j}} \int_{I_{i}}u_{h}(v_{h})_{xxx}\,dx \,dy \\& \hphantom{E^{2}_{ij}(u_{h},v_{h})={}}{}+ \int_{J_{j}}\bigl((u_{h})_{xx}^{-}v_{h}^{-} \bigr)_{i+\frac{1}{2},y}\,dy- \int _{J_{j}}\bigl((u_{h})_{xx}^{-}v_{h}^{+} \bigr)_{i-\frac{1}{2},y}\,dy \\& \hphantom{E^{2}_{ij}(u_{h},v_{h})={}}{} - \int_{J_{j}}\bigl((u_{h})_{x}^{+}(v_{h})_{x}^{-} \bigr)_{i+\frac{1}{2},y}\,dy+ \int _{J_{j}}\bigl((u_{h})_{x}^{+}(v_{h})_{x}^{+} \bigr)_{i-\frac{1}{2},y}\,dy \\& \hphantom{E^{2}_{ij}(u_{h},v_{h})={}}{} + \int_{J_{j}}\bigl(u_{h}^{+}(v_{h})_{xx}^{-} \bigr)_{i+\frac{1}{2},y}\,dy- \int _{J_{j}}\bigl(u_{h}^{+}(v_{h})_{xx}^{+} \bigr)_{i-\frac{1}{2},y}\,dy, \end{aligned}$$
(4.4)
$$\begin{aligned}& E^{3}_{ij}(u_{h},v_{h})= - \int_{J_{j}} \int_{I_{i}}u_{h}(v_{h})_{xyy}\,dx \,dy \\& \hphantom{E^{3}_{ij}(u_{h},v_{h})={}}{}+ \int_{I_{i}}\bigl((u_{h})_{xy}^{-}v_{h}^{-} \bigr)_{x,j+\frac{1}{2}}\,dx- \int _{I_{i}}\bigl((u_{h})_{xy}^{-}v_{h}^{+} \bigr)_{x,j-\frac{1}{2}}\,dx \\& \hphantom{E^{3}_{ij}(u_{h},v_{h})={}}{} - \int_{J_{j}}\bigl((u_{h})_{y}^{+}(v_{h})_{y}^{-} \bigr)_{i+\frac{1}{2},y}\,dy+ \int _{J_{j}}\bigl((u_{h})_{y}^{+}(v_{h})_{y}^{+} \bigr)_{i-\frac{1}{2},y}\,dy \\& \hphantom{E^{3}_{ij}(u_{h},v_{h})={}}{} + \int_{I_{i}}\bigl(u_{h}^{+}(v_{h})_{xy}^{-} \bigr)_{x,j+\frac{1}{2}}\,dx- \int _{I_{i}}\bigl(u_{h}^{+}(v_{h})_{xy}^{+} \bigr)_{x,j-\frac{1}{2}}\,dx. \end{aligned}$$
(4.5)

We will prove Theorem 4.1 by analyzing the above three terms \(E^{1}_{ij}\), \(E^{2}_{ij}\), \(E^{3}_{ij}\). Take \(v_{h}=u_{h}\) in the scheme (3.1), and denote \(F(u)=\int f(u)\, du\), then we have

$$\begin{aligned} E^{1}_{ij}(u_{h},u_{h}) =&- \int_{J_{j}}\bigl(F\bigl((u_{h})_{i+\frac {1}{2},y}^{-} \bigr)-F\bigl((u_{h})_{i-\frac{1}{2},y}^{+}\bigr)\bigr)\,dy \\ &{}+ \int_{J_{j}}\bigl(\bigl(\hat{f}\bigl(u_{h}^{-},u_{h}^{+} \bigr) (u_{h})^{-}\bigr)_{i+\frac {1}{2},y}-\bigl(\hat{f} \bigl(u_{h}^{-},u_{h}^{+}\bigr) (u_{h})^{+} \bigr)_{i-\frac {1}{2},y}\bigr)\,dy \\ =& \int_{J_{j}}(\widetilde{F}_{i+\frac{1}{2},y}-\widetilde {F}_{i-\frac{1}{2},y}+\Theta_{i-\frac{1}{2},y})\,dy, \end{aligned}$$
(4.6)

where

$$\begin{aligned}& \widetilde{F}_{i+\frac{1}{2},y} = -F\bigl((u_{h})_{i+\frac {1}{2},y}^{-} \bigr)+\bigl(\hat{f}\bigl(u_{h}^{-},u_{h}^{+}\bigr) (u_{h})^{-}\bigr)_{i+\frac {1}{2},y}, \\& \Theta_{i-\frac{1}{2},y} = -F\bigl((u_{h})_{i-\frac{1}{2},y}^{-}\bigr)+\bigl( \hat {f}\bigl(u_{h}^{-},u_{h}^{+}\bigr) (u_{h})^{-} \bigr)_{i-\frac{1}{2},y} \\& \hphantom{\Theta_{i-\frac{1}{2},y} ={}}{}+F\bigl((u_{h})_{i-\frac{1}{2},y}^{+}\bigr)-\bigl(\hat {f} \bigl(u_{h}^{-},u_{h}^{+}\bigr) (u_{h})^{+} \bigr)_{i-\frac{1}{2},y}. \end{aligned}$$
(4.7)

It is easy to obtain

$$\begin{aligned} \Theta =&-F\bigl((u_{h})_{i-\frac{1}{2},y}^{-}\bigr)+\bigl( \hat {f}\bigl(u_{h}^{-},u_{h}^{+}\bigr) (u_{h})^{-} \bigr)_{i-\frac{1}{2},y} \\ &{}+F\bigl((u_{h})_{i-\frac{1}{2},y}^{+}\bigr)-\bigl(\hat {f} \bigl(u_{h}^{-},u_{h}^{+}\bigr) (u_{h})^{+} \bigr)_{i-\frac{1}{2},y} \\ =&\bigl(F^{\prime}(\xi)-\hat{f}\bigr) \bigl(u_{h}^{+}-u_{h}^{-} \bigr) \\ \geq& 0, \end{aligned}$$
(4.8)

here we drop the subscript \(i-\frac{1}{2}\), y for simplicity because all quantities are evaluated in \(\Theta_{i-\frac{1}{2},y}\). The mean value theorem is applied and ξ is a value between \(u^{-}\) and \(u^{+}\), and we have used the fact \(F^{\prime}(\xi)= f(\xi)\) and the monotonicity of the flux function f̂ to obtain inequality (4.8).

For the term \(E^{2}_{ij}\), we obtain

$$\begin{aligned} E^{2}_{ij}(u_{h},u_{h}) =& \int_{J_{j}} \int _{I_{i}}(u_{h})_{x}(u_{h})_{xx} \,dx\,dy \\ &{}+ \int_{J_{j}}\bigl(u_{h}^{+}(u_{h})_{xx}^{-} \bigr)_{i+\frac{1}{2},y}\,dy- \int _{J_{j}}\bigl((u_{h})_{xx}^{-}u_{h}^{+} \bigr)_{i-\frac{1}{2},y}\,dy \\ &{}- \int_{J_{j}}\bigl((u_{h})_{x}^{+}(u_{h})_{x}^{-} \bigr)_{i+\frac{1}{2},y}\,dy+ \int _{J_{j}}\bigl((u_{h})_{x}^{+}(u_{h})_{x}^{+} \bigr)_{i-\frac{1}{2},y}\,dy \\ =& \int_{J_{j}}\frac{1}{2}\bigl((u_{h})^{-}_{x} \bigr)^{2}_{i+\frac{1}{2},y}\,dy- \int _{J_{j}}\frac{1}{2}\bigl((u_{h})^{+}_{x} \bigr)^{2}_{i-\frac{1}{2},y}\,dy \\ &{}+ \int_{J_{j}}\bigl(u_{h}^{+}(u_{h})_{xx}^{-} \bigr)_{i+\frac{1}{2},y}\,dy- \int _{J_{j}}\bigl((u_{h})_{xx}^{-}u_{h}^{+} \bigr)_{i-\frac{1}{2},y}\,dy \\ &{}- \int_{J_{j}}\bigl((u_{h})_{x}^{+}(u_{h})_{x}^{-} \bigr)_{i+\frac{1}{2},y}\,dy+ \int _{J_{j}}\bigl((u_{h})_{x}^{+}(u_{h})_{x}^{+} \bigr)_{i-\frac{1}{2},y}\,dy \\ =& \int_{J_{j}}\mathcal{H}_{i+\frac{1}{2},y}\,dy- \int_{J_{j}}\mathcal {H}_{i-\frac{1}{2},y}\,dy+ \int_{J_{j}}\Lambda_{i-\frac{1}{2},y}\,dy, \end{aligned}$$
(4.9)

where

$$\begin{aligned}& \mathcal{H}_{i+\frac{1}{2},y} = \biggl(\frac {1}{2} \bigl((u_{h})^{-}_{x}\bigr)^{2}+u_{h}^{+}(u_{h})_{xx}^{-}-(u_{h})_{x}^{+}(u_{h})_{x}^{-} \biggr)_{i+\frac {1}{2},y}, \\& \Lambda_{i-\frac{1}{2},y} = \biggl(\frac{1}{2}\bigl((u_{h})^{-}_{x} \bigr)^{2}-\frac {1}{2}\bigl((u_{h})^{+}_{x} \bigr)^{2}-(u_{h})_{x}^{+}(u_{h})_{x}^{-}+(u_{h})_{x}^{+}(u_{h})_{x}^{+} \biggr)_{i-\frac {1}{2},y} \\& \hphantom{\Lambda_{i-\frac{1}{2},y}} = \frac{1}{2}\bigl[(u_{h})_{x} \bigr]^{2}_{i-\frac{1}{2},y}. \end{aligned}$$
(4.10)

Summing over i, j in (4.9), we have

$$ \sum_{i,j}E^{2}_{ij}(u_{h},u_{h})= \int_{c}^{d}\sum_{i} \frac{1}{2}\bigl[(u_{h})_{x}\bigr]^{2}_{i-\frac{1}{2},y} \,dy\geq 0. $$
(4.11)

Now we consider the term \(E^{3}_{ij}\). By a similar argument to that used for \(E^{2}_{ij}\), we can obtain

$$ \sum_{i,j}E^{3}_{ij}(u_{h},v_{h})= \int_{c}^{d}\sum_{i} \frac{1}{2}\bigl[(u_{h})_{y}\bigr]^{2}_{i-\frac{1}{2},y} \,dy\geq 0. $$
(4.12)

Summing over i, j in (4.2), we have

$$ \frac{1}{2}\frac{d}{dt} \int_{c}^{d} \int_{a}^{b}u_{h}^{2}\,dx\,dy+ \int_{c}^{d}\sum_{i} \biggl(\frac{1}{2}\bigl(\bigl[(u_{h})_{x} \bigr]^{2}+\bigl[(u_{h})_{y}\bigr]^{2} \bigr)+\Theta \biggr)_{i-\frac{1}{2},y}\,dy=0, $$
(4.13)

there is no boundary term left because of the periodic boundary condition. Now, combining (4.8), (4.11), and (4.12), we complete the proof. □

Next we state an error estimate for our scheme (3.1) for the linear case \(f(u)=u\). We obtain the following theorem.

Theorem 4.2

Let u be the exact solution of the problem (1.4), and \(u_{h}\) be the numerical solution of scheme (3.1). If we use \(V_{h}^{k}\) space with \(k\geq3\), then we have the error estimate

$$\bigl\Vert u_{h}(t)-u(t)\bigr\Vert \leq Ch^{k+1}, $$

where the constant C depends on k, t, \(\|u\|\).

Proof

Using the notation in (4.2), the DG scheme (3.1) could be written as

$$ B_{i,j}(u_{h},v_{h})=0, $$
(4.14)

for all \(v_{h}\in V_{h}^{k}\). Note that the scheme (3.1) is satisfied when the numerical solutions \(u_{h}\) are replaced by the exact solutions u; we have

$$ B_{i,j}(u;v_{h})=0, $$
(4.15)

for all \(v_{h}\in V_{h}^{k}\). Then the error equation is obtained,

$$ B_{i,j}(u-u_{h};v_{h})=0, $$
(4.16)

for all \(v_{h}\in V_{h}^{k}\). We denote

$$ e_{h}=\mathbb{P}u-u_{h}, \qquad \varepsilon_{h}=u-\mathbb{P}u, $$
(4.17)

and we take the test function \(v_{h}=e_{h}\), then

$$ B_{i,j}(e_{h};e_{h})=-B_{i,j}( \varepsilon_{h};e_{h}). $$
(4.18)

For the left side of (4.18), from the stability result (4.13) we have

$$ \sum_{i,j}B_{i,j}(e_{h};e_{h}) \geq \frac{1}{2}\frac{d}{dt} \int _{c}^{d} \int_{a}^{b}e_{h}^{2}\,dx\,dy. $$
(4.19)

To the right side of (4.18), we write out all the terms

$$\begin{aligned} B_{ij}(\varepsilon_{h};e_{h}) =& \int_{J_{j}} \int_{I_{i}}(\varepsilon _{h})_{t}e_{h} \,dx\,dy- \int_{J_{j}} \int_{I_{i}}\varepsilon_{h}(e_{h})_{x} \,dx\,dy \\ &{}- \int _{J_{j}} \int_{I_{i}}\varepsilon_{h}(e_{h})_{xxx} \,dx\,dy \\ &{} - \int_{J_{j}} \int_{I_{i}}\varepsilon_{h}(e_{h})_{xyy} \,dx\,dy- \int _{J_{j}}\bigl(\varepsilon_{h}^{+}(e_{h})^{-} \bigr)_{i+\frac{1}{2},y}\,dy \\ &{} + \int_{J_{j}}\bigl(\varepsilon_{h}^{+}(e_{h})^{+} \bigr)_{i-\frac {1}{2},y}\,dy+ \int_{J_{j}}\bigl((\varepsilon_{h})_{xx}^{-}e_{h}^{-} \bigr)_{i+\frac {1}{2},y}\,dy \\ &{} - \int_{J_{j}}\bigl((\varepsilon_{h})_{xx}^{-}e_{h}^{+} \bigr)_{i-\frac {1}{2},y}\,dy- \int_{J_{j}}\bigl((\varepsilon_{h})_{x}^{+}(e_{h})_{x}^{-} \bigr)_{i+\frac {1}{2},y}\,dy \\ &{} + \int_{J_{j}}\bigl((\varepsilon_{h})_{x}^{+}(e_{h})_{x}^{+} \bigr)_{i-\frac {1}{2},y}\,dy+ \int_{J_{j}}\bigl(\varepsilon_{h}^{+}(e_{h})_{xx}^{-} \bigr)_{i+\frac {1}{2},y}\,dy \\ &{} - \int_{J_{j}}\bigl(\varepsilon_{h}^{+}(e_{h})_{xx}^{+} \bigr)_{i-\frac {1}{2},y}\,dy+ \int_{I_{i}}\bigl((\varepsilon_{h})_{xy}^{-}e_{h}^{-} \bigr)_{x,j+\frac {1}{2}}\,dx \\ &{} - \int_{I_{i}}\bigl((\varepsilon_{h})_{xy}^{-}e_{h}^{+} \bigr)_{x,j-\frac {1}{2}}\,dx- \int_{J_{j}}\bigl((\varepsilon_{h})_{y}^{+}(e_{h})_{y}^{-} \bigr)_{i+\frac {1}{2},y}\,dy \\ &{} + \int_{J_{j}}\bigl((\varepsilon_{h})_{y}^{+}(e_{h})_{y}^{+} \bigr)_{i-\frac {1}{2},y}\,dy+ \int_{I_{i}}\bigl(\varepsilon_{h}^{+}(e_{h})_{xy}^{-} \bigr)_{x,j+\frac {1}{2}}\,dx \\ &{} - \int_{I_{i}}\bigl(\varepsilon_{h}^{+}(e_{h})_{xy}^{+} \bigr)_{x,j-\frac{1}{2}}\,dx. \end{aligned}$$
(4.20)

Note that by the properties of the projection \(\mathbb{P}^{-}\), we know that the right terms except the first one in (4.20) are zeros, so (4.20) becomes

$$\begin{aligned} -B_{ij}(\varepsilon_{h};e_{h}) =&- \int_{I_{i}} \int_{J_{j}}(\varepsilon _{h})_{t}e_{h} \,dx\,dy \\ \leq& \frac{1}{2}\biggl( \int_{I_{i}} \int_{J_{j}}\bigl((\varepsilon_{h})_{t} \bigr)^{2}\,dx\,dy+ \int _{I_{i}} \int_{J_{j}}(e_{h})^{2}\,dx\,dy\biggr). \end{aligned}$$
(4.21)

Now we plug (4.19) and (4.21) into the equality (4.18), sum over i, j, and use the approximate result (2.6), and we have

$$ \frac{d}{dt} \int_{c}^{d} \int_{a}^{b}(e_{h})^{2}\,dx\,dy \leq \int_{c}^{d} \int_{a}^{b}(e_{h})^{2}\,dx \,dy+Ch^{2k+2}. $$
(4.22)

From Gronwall’s inequality and the fact that the initial error is

$$ \bigl\Vert u(\cdot,0)-u_{h}(\cdot,0)\bigr\Vert \leq Ch^{k+1}, $$
(4.23)

the approximate result (2.6) finally gives the error estimate.

Then Theorem 4.2 follows for \(k\geq3\). □

5 Numerical results

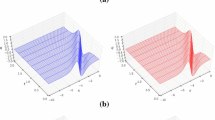
In this example we show the numerical results for the equation

$$ u_{t}+uu_{x}+\varepsilon(u_{xxx}+u_{xyy})=0; $$
(5.1)

the steady progressive wave solution is of the form

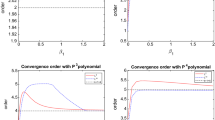
$$ u(x,y,t)=3c\operatorname{sech}^{2}\biggl(0.5\sqrt{\frac{c}{\varepsilon }} \bigl((x-ct)\cos\theta+y\sin\theta\bigr)\biggr), $$
(5.2)

where θ is an inclined angle with respect to the x-axis. We choose the constants \(c=0.01\), \(\varepsilon=0.01\). We use the third order Runge-Kutta method [13] and the time-space restriction is taken as \(\Delta t= \mathrm{CFL}\, h^{3}\). The optimal CFL number can be obtained by a standard von Neumann analysis. Here we simply choose a CFL number by numerical experiments to make the scheme stable. All the computations were performed in double precision. We can see in Tables 1 and 2 that the method with \(Q^{k}\) elements gives a \((k+1)\)th order of accuracy for the uniform meshes when \(k\geq2\), for \(Q^{0}\) and \(Q^{1}\), the scheme is not consistent.

Table 1 Accuracy test for equation ( 5.1 )
Full size table
Table 2 Accuracy test for equation ( 5.1 )
Full size table

6 Concluding remarks

In the paper a discontinuous Galerkin (DG) method for the two-dimensional nonlinear Zakharov-Kuznetsov (ZK) equation is presented and analyzed. Compared to the LDG method, stability and an error estimate is proved. Numerical examples are given to illustrate the accuracy and capability of the methods. In the future, we will develop this class of DG method for more general PDEs in multi-dimensions, and on nonrectangular regions.