Dynamic analysis of a nonautonomous impulsive single-species system in a random environment

Abstract

This paper is concerned with a nonautonomous single-species model, in which the population dynamics is affected by impulsive perturbations and environmental noise. Sufficient conditions for the extinction, stochastic permanence, and global attractivity of system are obtained, respectively. The above results reveal that the white noise plays a very important role in the dynamic behaviors. However, it is found that the bounded impulse does not affect the above properties. Some numerical simulation results are presented to support the analytical findings.

1 Introduction

The analysis of mathematical models of dynamic process has been of importance in improving our understanding of biological systems in a fluctuating environment. On the one hand, species living in such a fluctuating medium might experience abrupt changes of relatively short duration due to certain external effects. The duration of these changes is often negligible in comparison with that of the entire evolution process and hence the abrupt changes can be well approximated as impulses (see [1, 2]). On the other hand, population systems are often subject to environmental noise (see [3–7]). In recent research results, Mao et al. [8] revealed that different structures of environmental noise can have different influences on the population systems, while Mao et al. [9, 10] indicated that environmental noise may suppress a potential population explosion. Since impulsive effect and environmental noise are two essential ingredients of ecological processes, one is led to consider ISDE (impulsive stochastic differential equations) which would make for a suitable model. In recent years, many ISDE models have been extensively investigated in applied sciences and many good results have been obtained (see [11–18]). In this paper, we formulate a novel nonautonomous impulsive single-species system in a random environment. Motivated by the works of [18–20], we explore and analyze the asymptotic behaviors of the target system, and a good understanding of extinction, stochastic permanence, and global attractivity of the system is obtained. The rest of this paper is organized as follows. In the next section, a novel nonautonomous impulsive single-species model in a random environment is proposed, and some preliminaries are given. Sufficient conditions for the extinction, stochastic permanence, and global attractivity are established in Sections 3 and 4, respectively. In Section 5, some specific numerical examples and corresponding simulations are provided to verify our theoretical results.

2 Model and preliminaries

In [21], Ludwig et al. introduced the budworm population dynamics to be modeled by the equation

$$ y'(t)=y(t) \bigl(r-ay(t) \bigr)-h(y). $$

(2.1)

Here $y(t)$ stands for the density of species y, the positive constants r and a are the intrinsic growth rate and self-inhibition rate, respectively. The $h(y)$-term is predation. To be specific Murray [22] chose the form for $h(y)$ suggested by Ludwig et al. [21], that is, ${cy^{2}(t)}/{(b+y^{2}(t))}$, and discussed the stability of the following system:

$$ y'(t)=y(t) \bigl(r-ay(t) \bigr)-\frac{cy^{2}(t)}{b+y^{2}(t)}, $$

(2.2)

where ${cy^{2}(t)}/{(b+y^{2}(t))}$ is an S-shaped function and the pair of positive constants c and d are measures of saturation. Furthermore, in recent investigations Liu et al. [19, 20] considered the following nonautonomous version with impulsive perturbations:

$$ \left \{ \textstyle\begin{array}{@{}l} \dot{y}(t)=y(t) (r(t)-a(t)y(t) )-\frac {c(t)y^{2}(t)}{b(t)+y^{2}(t)},\quad t\neq\tau_{k},\\ y(\tau_{k}^{+})=(1+\lambda_{k})y(\tau_{k}),\quad t=\tau_{k}, k\in\mathbb{N}, \end{array}\displaystyle \right . $$

(2.3)

where $\mathbb{N}$ is the set of positive integers. The impulsive points satisfy $0<\tau_{1}<\tau_{2}<\cdots$, $\lim_{k\rightarrow+\infty}\tau_{k}=+\infty$, and the impulsive effects satisfy $\lambda_{k}>-1$, in particular, $\lambda_{k}>0$ represent stocking, while $\lambda_{k}<0$ denote harvesting.

In this contribution, we consider that environmental noise mainly affects the intrinsic growth rate $r(t)$. If we still use $r(t)$ to denote the average growth rate at time t, then we usually estimate it by an average value plus an error term, and we obtain

$$ r(t)\rightarrow r(t)+\sigma(t)\dot{B}(t), $$

(2.4)

where $\dot{B}(t)$ is a white noise and $\sigma^{2}(t)$ represents the intensity of the noise. Thus, a revised version can be described by ISDE

$$ \left \{ \textstyle\begin{array}{@{}l} dy(t)=y(t) (r(t)-a(t)y(t)- \frac {c(t)y(t)}{b(t)+y^{2}(t)} )\,dt+\sigma(t)y(t)\,dB(t),\quad t\neq\tau_{k},\\ y(\tau_{k}^{+})=(1+\lambda_{k})y(\tau_{k}),\quad t=\tau_{k}, k\in\mathbb{N}, \end{array}\displaystyle \right . $$

(2.5)

where the initial value $y(0)>0$. $B(t)$ is a standard Brownian motion defined on a complete probability space $(\Omega, \mathcal{F}, \{\mathcal{F}_{t}\}_{t\geq0},\mathbf{P})$ with a filtration $\{\mathcal{F}_{t}\}_{t\geq0}$ satisfying the usual conditions (i.e., it is right continuous and increasing while $\mathcal{F}_{0}$ contains all P-null sets), and the coefficients $r(t)$, $a(t)$, $c(t)$, $b(t)$ and $\sigma(t)$ are all positive continuous bounded functions on $R_{+}=[0,+\infty)$.

For convenience, we define

$$f^{l}= \inf f(t),\qquad f^{u}= \sup f(t),\quad t\in R_{+}, $$

where $f(t)$ is a continuous bounded function. Throughout this paper, it is assumed that

• (S) there exist two positive constants m and M such that $m\leq\prod_{0<\tau_{k}<t}(1+h_{k})\leq M$, and a product equals unity if the number of factors is zero.

Definition 2.1

(see [18])

Consider the following ISDE:

$$ \left \{ \textstyle\begin{array}{@{}l} dX(t)=F(t,X(t))\,dt+G(t,X(t))\,dW(t),\quad t\neq\tau_{k},\\ X(\tau_{k}^{+})-X(\tau_{k})=B_{k}X(\tau_{k}), \quad t=\tau_{k}, k\in\mathbb{N}, \end{array}\displaystyle \right . $$

(2.6)

with initial condition $X(0)$. A stochastic process $X(t)=(X_{1}(t),\ldots,X_{n}(t))$, $t\in[0,+\infty)$, is said to be a solution of (2.6) if

• (1) $X(t)$ is $\mathcal{F}_{t}$-adapted and is continuous on $(0,\tau_{1})$ and each interval $(\tau_{k},\tau_{k+1})$, $k\in\mathbb{N}$; $F(t,X(t))\in L^{1}([0,+\infty);R^{n})$, $G(t,X(t))\in L^{2}([0,+\infty);R^{n})$, where $L^{k}([0,+\infty);R^{n})$ is all $R^{n}$ valued measurable $\mathcal{F}_{t}$-adapted processes $\psi(t)$ satisfying $\int_{0}^{T}|\psi(t)|^{k}\,dt<\infty$ a.s. for every $T>0$;

• (2) for each $\tau_{k}$, $k\in\mathbb{N}$, $X(\tau_{k}^{+})=\lim_{t\rightarrow\tau_{k}^{+}}X(t)$ and $X(\tau_{k}^{-})=\lim_{t\rightarrow\tau_{k}^{-}}X(t)$ exist and $X(\tau_{k})=X(\tau_{k}^{-})$ with probability 1;

• (3) $X(t)$ obeys the equivalent integral equation of (2.6) for almost every $t\in[0,+\infty)\backslash\{\tau_{k}\}$ and satisfies the impulsive conditions at each $t=\tau_{k}$, $k\in\mathbb{N}$ with probability 1.

Definition 2.2

For a positive solution $y(t)$ of system (2.5), then

• (1) system (2.5) is said to be extinctive if $\lim_{t\rightarrow+\infty}y(t)=0$;

• (2) system (2.5) is said to be stochastically permanent if every $\varepsilon\in(0,1)$, there exist constants $\beta>0$ and $\delta>0$ such that for any initial value $y(0)\in R_{+}$, $y(t)$,

  $$\liminf_{t\rightarrow+\infty}\mathbf{P}\bigl\{ y(t)\geq\beta\bigr\} \geq1- \varepsilon, \qquad \liminf_{t\rightarrow+\infty}\mathbf{P}\bigl\{ y(t)\leq\delta \bigr\} \geq1-\varepsilon. $$

Definition 2.3

Let $y_{1}(t)$, $y_{2}(t)$ be, respectively, any two solutions of system (2.5) with positive initial values $y_{1}(0)$ and $y_{2}(0)$. If $\lim_{t\rightarrow+\infty}|y_{1}(t)- y_{2}(t)|=0$ a.s., then system (2.5) is globally attractive.

Lemma 2.1

(see [23])

Assume that an n-dimensional stochastic process $X(t)$ on $t\geq0$ satisfies the condition

$$E\bigl|X(t)-X(s)\bigr|^{\alpha}\leq c|t-s|^{1+\beta},\quad 0\leq s, t< +\infty, $$

for positive constants α, β, c. Then there exists a continuous version $\tilde{X}(t)$ of $X(t)$ which has the property that for every $\vartheta\in(0,\beta/\alpha)$, there is a positive random variable $\varphi(\omega)$ such that

$$\mathbf{P} \biggl\{ \omega:\sup_{0< |t-s|< \varphi(\omega), 0\leq s,t< +\infty}\frac{|\tilde{X}(t,\omega)-X(t,\omega)|}{|t-s|^{\vartheta }}\leq \frac{2}{1-2^{-\vartheta}} \biggr\} =1. $$

In other words, almost every sample path of $\tilde{X}(t)$ is locally but uniformly Hölder continuous with exponent ϑ.

Lemma 2.2

([24])

Suppose that $a_{1}, a_{2}, \ldots, a_{n}$ are real numbers; the inequality

$$|a_{1}+a_{2}+\cdots+a_{n}|^{p}\leq C_{p}\bigl(|a_{1}|^{p}+|a_{2}|^{p}+ \cdots+|a_{n}|^{p}\bigr) $$

holds, where $p>0$ and

$$C_{p}=\left \{ \textstyle\begin{array}{@{}l@{\quad}l} 1, & 0< p\leq1,\\ n^{p-1},& p>1. \end{array}\displaystyle \displaystyle \right . $$

Lemma 2.3

([25])

Let f be a non-negative function on $t\geq0$ such that f is integrable on $t\geq0$ and is uniformly continuous on $t\geq0$. Then $\lim_{t\rightarrow+\infty}f(t)=0$.

Lemma 2.4

For any given initial value $y(0)>0$, there is a unique solution $y(t)$ to system (2.5) for all $t\geq0$ and $y(t)$ will remain in $R_{+}^{1}=\{y|y\in R:y>0\}$ with probability 1.

Proof

Let us consider the following SDE without impulsive perturbations:

$$\begin{aligned} dx(t)={}& x(t) \biggl(r(t)-a(t) \prod_{0< \tau_{k}< t}(1+ \lambda_{k})x(t)- \frac{c(t) \prod_{0< \tau_{k}< t}(1+\lambda_{k})x(t)}{b(t) + [ \prod_{0< \tau_{k}< t}(1+\lambda_{k})x(t) ]^{2}} \biggr)\,dt \\ &{}+\sigma(t)x(t)\,dB(t) \end{aligned}$$

(2.7)

with initial value $x(0)=y(0)$.

It follows from the theory of SDE [6] that (2.7) has a unique local solution $x(t)$ on $[0,t_{e})$, where $t_{e}$ is the explosion time. To show this solution is global, we only need to prove that $t_{e}=+\infty$ a.s. Let $n_{0}$ be sufficiently large such that $x(0)$ remains in the interval $[ \frac{1}{n_{0}}, n_{0}]$. For each integer $n\geq n_{0}$, define the stopping time

$$ t_{n}=\inf \biggl\{ t\in[0,t_{e}): x(t)\notin\biggl( \frac{1}{n}, n\biggr) \biggr\} . $$

(2.8)

Clearly, $t_{n}$ is increasing as $n\rightarrow+\infty$. Set $t_{+\infty}=\lim_{n\rightarrow+\infty}t_{n}$, whence $t_{+\infty}\leq t_{e}$ a.s. To complete the proof, we only need to show that $t_{+\infty}=+\infty$ a.s. If this statement is false, then there exist a pair of constants $T>0$ and $\varepsilon\in(0, 1)$ such that $\mathbf{P} \{t_{+\infty}\leq T \}>\varepsilon$. As a result, there is an integer $n_{1}\geq n_{0}$ such that

$$\mathbf{P} \{t_{n}\leq T \}\geq\varepsilon, \quad\mbox{for all } n \geq n_{1}. $$

Define a $C^{2}$-function $\bar{V}: R_{+}\rightarrow R_{+}$ by

$$ \bar{V}(x)=x-1-\ln x. $$

(2.9)

The nonnegativity of $\bar{V}(x)$ is obvious. One derives, by Itô’s formula, that

$$\begin{aligned} d\bar{V}={}& \biggl(1-\frac{1}{x}\biggr)\,dx+0.5 \frac{1}{x^{2}}(dx)^{2} \\ ={}& \biggl\{ \bigl(x(t)-1 \bigr) \biggl[r(t)-a(t)\prod _{0< \tau_{k}< t}(1+\lambda_{k})x(t)- \frac{c(t)\prod_{0< \tau_{k}< t}(1+\lambda_{k})x(t)}{b(t)+ [\prod_{0< \tau_{k}< t}(1+\lambda_{k})x(t)]^{2}} \biggr] \\ &{}+0.5\sigma^{2}(t) \biggr\} \,dt+ \bigl(x(t)-1 \bigr)\sigma(t)\,dB(t) \\ ={}& \biggl[r(t) \bigl(x(t)-1 \bigr)+\bigl(1-x(t)\bigr)a(t)\prod _{0< \tau_{k}< t}(1+\lambda_{k})x(t) \\ &{}+ \frac{(1-x(t))c(t)\prod_{0< \tau_{k}< t}(1+\lambda_{k})x(t)}{b(t)+ [\prod_{0< \tau_{k}< t}(1+\lambda_{k})x(t)]^{2}} +0.5\sigma^{2}(t) \biggr]\,dt+ \bigl(x(t)-1 \bigr)\sigma(t)\,dB(t) \\ \leq{}& \biggl[r(t)x(t)+a(t)\prod_{0< \tau_{k}< t}(1+ \lambda_{k})x(t) +\frac{c(t)\prod_{0< \tau_{k}< t}(1+\lambda_{k})x(t)}{b(t)}+0.5\sigma ^{2}(t) \biggr]\,dt \\ &{}+ \bigl(x(t)-1 \bigr)\sigma(t)\,dB(t) \\ \leq{}& \biggl[\biggl(r^{u}+a^{u}M+\frac{c^{u}M}{b^{l}} \biggr)x(t)+0.5\bigl(\sigma^{u}\bigr)^{2} \biggr]\,dt+ \bigl(x(t)-1 \bigr)\sigma(t)\,dB(t). \end{aligned}$$

(2.10)

Let

$$L_{1}=r^{u}+a^{u}M+\frac{c^{u}M}{b^{l}},\qquad L_{2}=0.5\bigl(\sigma^{u}\bigr)^{2}. $$

Notice that $x\leq2(x-1-\ln x)+2$, for $x>0$, we know that

$$\begin{aligned} d\bar{V}&\leq \bigl[L_{1}x(t)+L_{2} \bigr]\,dt+ \bigl(x(t)-1 \bigr)\sigma(t)\,dB(t) \\ &\leq \bigl\{ 2L_{1}\bigl(\bar{V}(x)+1\bigr)+L_{2} \bigr\} \,dt+ \bigl(x(t)-1 \bigr)\sigma (t)\,dB(t) \\ &= \bigl\{ 2L_{1}\bar{V}(x)+2L_{1}+L_{2} \bigr\} \,dt+ \bigl(x(t)-1 \bigr)\sigma(t)\,dB(t). \end{aligned}$$

(2.11)

So

$$ \int_{0}^{t_{k}\wedge T}\,d\bar{V}(x)\leq\int _{0}^{t_{k}\wedge T} \bigl\{ 2L_{1}\bar{V}(x) +2L_{1}+L_{2} \bigr\} \,dt+\int_{0}^{t_{k}\wedge T} \bigl(x(t)-1 \bigr)\sigma(t)\,dB(t). $$

(2.12)

Taking expectations leads to

$$\begin{aligned} E\bar{V} \bigl(x(t_{k}\wedge T) \bigr)&\leq \bar{V} \bigl(x(0)\bigr)+(2L_{1}+L_{2})E(t_{k}\wedge T) +2L_{1} \int_{0}^{t_{k}\wedge T}E\bar{V}\bigl(x(t) \bigr)\,dt \\ &\leq\bar{V}\bigl(x(0)\bigr)+(2L_{1}+L_{2})T +2L_{1} \int_{0}^{T}E\bar{V} \bigl(y(t_{k}\wedge T)\bigr)\,dt. \end{aligned}$$

(2.13)

It then follows from the Gronwall inequality that

$$ E\bar{V} \bigl(x(t_{k}\wedge T) \bigr)\leq \bigl(\bar{V}\bigl(x(0) \bigr)+(2L_{1}+L_{2})T \bigr)e^{2L_{1}T}. $$

(2.14)

Let $\Omega_{n}=\{t_{n}\leq T\}$, $n\geq n_{1}$, then $\mathbf{P}(\Omega_{n})\geq\varepsilon$. Notice that for arbitrary $\omega\in \Omega_{n}$, $x(t_{n},\omega)$ equals either n or $\frac{1}{n}$, and thus $\bar{V}(y(t_{n},\omega))$ is no less than $n-1-\ln n$ or $\frac{1}{n}-1+\ln n$. Then

$$\begin{aligned} \bigl(\bar{V}\bigl(x(0)\bigr)+(2L_{1}+L_{2})T \bigr)e^{2L_{1}T}&\geq E\bigl[1_{\Omega_{n}}(\omega)\bar{V} \bigl(x(t_{n},\omega)\bigr)\bigr] \\ &\geq\varepsilon \biggl[(n-1-\ln n)\wedge\biggl(\frac{1}{n}-1+\ln n\biggr) \biggr], \end{aligned}$$

(2.15)

where $1_{\Omega_{n}}$ is the indicator function of $\Omega_{n}$. Letting $n\rightarrow\infty$ results in the contradiction

$$+\infty> \bigl(\bar{V}\bigl(x(0)\bigr)+(2L_{1}+L_{2})T \bigr)e^{2L_{1}T}=+\infty. $$

Thus we obtain $t_{+\infty}=+\infty$ a.s.

In the following, we need to show that $y(t)$ is the solution of (2.5). Denote

$$ y(t)=\prod_{0< \tau_{k}< t}(1+\lambda_{k})x(t). $$

(2.16)

One can see that $y(t)$ is continuous on each interval $(\tau_{k},\tau_{k+1})\subset R_{+}$ and for any $t\neq\tau_{k}$,

$$\begin{aligned} dy(t)={}&d \biggl( \prod_{0< \tau_{k}< t}(1+ \lambda_{k})x(t) \biggr)=\prod_{0< \tau_{k}< t}(1+ \lambda_{k})\,dx(t) \\ ={}& \prod_{0< \tau_{k}< t}(1+\lambda_{k}) x(t) \biggl(r(t)-a(t) \prod_{0< \tau_{k}< t}(1+\lambda_{k})x(t) \\ &{}- \frac{c(t) \prod_{0< \tau_{k}< t}(1+\lambda _{k})x(t)}{b(t)+[ \prod_{0< \tau_{k}< t}(1+\lambda _{k})x(t)]^{2}} \biggr)\,dt + \prod_{0< \tau_{k}< t}(1+ \lambda_{k})\sigma(t)x(t)\,dB(t) \\ ={}&y(t) \biggl(r(t)-a(t)y(t)- \frac{c(t)y(t)}{b(t)+y^{2}(t)} \biggr)\,dt+\sigma(t)y(t)\,dB(t). \end{aligned}$$

(2.17)

Moreover, for every $k\in N$ and $\tau_{k}\in[0,+\infty)$,

$$\begin{aligned} y\bigl(\tau_{k}^{+}\bigr)&= \lim _{t\rightarrow\tau_{k}^{+}}\prod_{0< \tau_{j}< t}(1+ \lambda_{j})x(t)=\prod_{0< \tau_{j}\leq \tau_{k}}(1+ \lambda_{j})x\bigl(\tau_{k}^{+}\bigr) \\ &=(1+\lambda_{k}) \prod_{0< \tau_{j}< \tau_{k}}(1+ \lambda_{j})x(\tau_{k}) =(1+\lambda_{k})y( \tau_{k}). \end{aligned}$$

(2.18)

Meanwhile,

$$\begin{aligned} y\bigl(\tau_{k}^{-}\bigr)&= \lim _{t\rightarrow\tau_{k}^{-}}\prod_{0< \tau_{j}< t}(1+ \lambda_{j})x(t)=\prod_{0< \tau_{j}< \tau_{k}}(1+ \lambda_{j})x\bigl(\tau_{k}^{-}\bigr) \\ &= \prod_{0< \tau_{j}< \tau_{k}}(1+\lambda_{j})x( \tau_{k})=y(\tau_{k}). \end{aligned}$$

(2.19)

The proof of Lemma 2.4 is complete. □

3 Extinction and stochastic permanence

We first consider the extinction of system (2.5). Denote

$$ \varphi(t)=r(t)-0.5\sigma^{2}(t). $$

(3.1)

Theorem 3.1

System (2.5) is extinct provided that

$$\limsup_{t\rightarrow+\infty}t^{-1} \biggl(\sum _{0< \tau_{k}< t}\ln(1+\lambda _{k})+\int_{0}^{t} \varphi(s)\,ds \biggr)< 0. $$

Proof

Applying Itô’s formula to (2.7), one derives that

$$\begin{aligned} d\ln x(t)={}& \frac{dx(t)}{x(t)}-\frac {(dx(t))^{2}}{2x^{2}(t)} \\ ={}& \biggl(r(t)-a(t)\prod_{0< \tau_{k}< t}(1+ \lambda_{k})x(t)- \frac{c(t) \prod_{0< \tau_{k}< t}(1+\lambda_{k})x(t)}{b(t)+ [ \prod_{0< \tau_{k}< t}(1+\lambda_{k})x(t) ]^{2}}-0.5\sigma^{2}(t) \biggr)\,dt \\ &{}+\sigma(t)\,dB(t) \\ ={}& \biggl(\varphi(t)-a(t)y(t)- \frac{c(t)y(t)}{b(t)+y^{2}(t)} \biggr)\,dt+\sigma(t)\,dB(t). \end{aligned}$$

(3.2)

Integrating both sides from 0 to t gives

$$ \ln x(t)-\ln x(0)=\int_{0}^{t}\varphi(s)\,ds-\int _{0}^{t}a(s)y(s)\,ds-\int_{0}^{t} \frac {c(s)y(s)}{b(s)+y^{2}(s)}\,ds+\mathcal{N}(t), $$

(3.3)

where $\mathcal{N}(t)= \int_{0}^{t}\sigma(s)\,dB(s)$, and $\mathcal{N}(t)$ is a local martingale with quadratic variation

$$ \bigl\langle \mathcal{N}(t), \mathcal{N}(t)\bigr\rangle =\int_{0}^{t} \sigma^{2}(s)\,ds\leq\bigl(\sigma ^{u}\bigr)^{2}t. $$

(3.4)

We obtain from the strong law of large numbers for local martingales

$$ \lim_{t\rightarrow+\infty}\frac{\mathcal{N}(t)}{t}=0 \quad\mbox{a.s.} $$

(3.5)

On the other hand, it follows from (3.3) that

$$\begin{aligned} \sum_{0< \tau_{k}< t}\ln(1+\lambda_{k})+ \ln x(t)-\ln x(0)={}&\sum_{0< \tau_{k}< t}\ln(1+ \lambda_{k})+\int_{0}^{t}\varphi(s)\,ds- \int_{0}^{t}a(s)y(s)\,ds \\ &{}-\int_{0}^{t}\frac{c(s)y(s)}{b(s)+y^{2}(s)}\,ds+ \mathcal{N}(t), \end{aligned}$$

(3.6)

that is,

$$\begin{aligned} \ln y(t)-\ln y(0)={}& \sum_{0< \tau_{k}< t}\ln(1+ \lambda _{k})+\int_{0}^{t}\varphi(s)\,ds- \int_{0}^{t}a(s)y(s)\,ds \\ &{} -\int_{0}^{t}\frac {c(s)y(s)}{b(s)+y^{2}(s)}\,ds+ \mathcal{N}(t). \end{aligned}$$

(3.7)

Hence

$$ \ln y(t)-\ln y(0)\leq \sum_{0< \tau_{k}< t}\ln(1+ \lambda_{k})+\int_{0}^{t}\varphi(s)\,ds+ \mathcal{N}(t). $$

(3.8)

Then the desired assertion follows from (3.5) immediately. □

Next, we turn to studying the stochastic permanence of system (2.5).

Theorem 3.2

If $\varphi^{l}>0$, then system (2.5) is stochastically permanent, where $\varphi(t)$ is defined in (3.1).

Proof

We first prove, for given $0<\varepsilon<1$, that there exists a positive constant β such that $\liminf_{t\rightarrow+\infty}\mathbf{P}\{y(t)\geq\beta\}\geq1-\varepsilon$. Define

$$ V_{1}(x)=\frac{1}{x}, \quad\mbox{for } x>0. $$

(3.9)

Then applying Itô’s formula to (2.7), one can see that

$$\begin{aligned} dV_{1}(x)={}& {-}\frac{1}{x^{2}}\,dx+ \frac{1}{x^{3}}(dx)^{2} \\ ={}&{-}V_{1}(x) \biggl(r(t)-a(t) \prod_{0< \tau_{k}< t}(1+ \lambda_{k})x(t) -\frac{c(t) \prod_{0< \tau_{k}< t}(1+\lambda _{k})x(t)}{b(t)+ [ \prod_{0< \tau_{k}< t}(1+\lambda _{k})x(t) ]^{2}} \biggr)\,dt \\ &{} +V_{1}(x)\sigma^{2}(t)\,dt-V_{1}(x) \sigma(t)\,dB(t). \end{aligned}$$

(3.10)

Since $\varphi^{l}>0$, we can choose a suitable positive constant θ such that

$$ \varphi^{l}>0.5\theta\bigl(\sigma^{u}\bigr)^{2}. $$

(3.11)

Define

$$ V_{2}(x)=\bigl(1+V_{1}(x)\bigr)^{\theta}, $$

(3.12)

then it follows from Itô’s formula, the assumption (S), and (3.11) that

$$\begin{aligned} dV_{2}(x)={}&\theta\bigl(1+V_{1}(x) \bigr)^{\theta-1}dV_{1}(x)+0.5\theta(\theta -1) \bigl(1+V_{1}(x)\bigr)^{\theta-2}\bigl(dV_{1}(x) \bigr)^{2} \\ ={}&\theta\bigl(1+V_{1}(x)\bigr)^{\theta-2} \biggl\{ - \bigl(1+V_{1}(x)\bigr)V_{1}(x) \biggl(r(t)-a(t) \prod _{0< \tau_{k}< t}(1+\lambda_{k})x(t) \\ &{}- \frac{c(t)\prod_{0< \tau_{k}< t}(1+\lambda _{k})x(t)}{b(t)+ [\prod_{0< \tau_{k}< t}(1+\lambda_{k})x(t) ]^{2}} \biggr) +\bigl(1+V_{1}(x) \bigr)V_{1}(x)\sigma^{2}(t) \\ &{}+ 0.5(\theta-1)V_{1}^{2}(x)\sigma^{2}(t) \biggr\} \,dt -\theta\bigl(1+V_{1}(x)\bigr)^{\theta-1}V_{1}(x) \sigma(t)\,dB(t) \\ ={}&\theta\bigl(1+V_{1}(x)\bigr)^{\theta-2} \biggl\{ -V_{1}^{2}(x) \bigl(r(t)-0.5\theta\sigma^{2}(t)-0.5 \sigma^{2}(t) \bigr) \\ &{}+V_{1}(x) \biggl(-r(t)+\sigma^{2}(t)+a(t) \prod _{0< \tau _{k}< t}(1+\lambda_{k}) + \frac{c(t)\prod_{0< \tau_{k}< t}(1+\lambda_{k})}{b(t) + [\prod_{0< \tau_{k}< t}(1+\lambda_{k})x(t) ]^{2}} \biggr) \\ &{}+ \frac{c(t)\prod_{0< \tau_{k}< t}(1+\lambda _{k})}{b(t)+ [\prod_{0< \tau_{k}< t}(1+\lambda_{k})x(t) ]^{2}}+ a(t) \prod_{0< \tau_{k}< t}(1+ \lambda_{k}) \biggr\} \,dt \\ &{}-\theta\bigl(1+V_{1}(x)\bigr)^{\theta-1}V_{1}(x) \sigma(t)\,dB(t) \\ \leq{}&\theta\bigl(1+V_{1}(x)\bigr)^{\theta-2} \biggl\{ -V_{1}^{2}(x) \bigl(\varphi^{l}-0.5\theta\bigl( \sigma^{u}\bigr)^{2} \bigr) +V_{1}(x) \biggl(\bigl( \sigma^{u}\bigr)^{2} +a^{u}M+ \frac{c^{u}M}{b^{l}} \biggr) \\ &{} +a^{u}M+ \frac{c^{u}M}{b^{l}} \biggr\} \,dt -\theta \bigl(1+V_{1}(x)\bigr)^{\theta-1}V_{1}(x)\sigma(t)\,dB(t). \end{aligned}$$

(3.13)

Choose a sufficient small constant $\rho>0$ such that

$$ 0< \frac{\rho}{\theta}< \varphi^{l}-0.5\theta\bigl(\sigma^{u} \bigr)^{2}. $$

(3.14)

Define

$$ V_{3}(x)=e^{\rho t}V_{2}(x). $$

(3.15)

Applying Itô’s formula leads to

$$\begin{aligned} dV_{3}(x)={}&\rho e^{\rho t}V_{2}(x)\,dt+e^{\rho t}dV_{2}(x) \\ \leq{}&\theta e^{\rho t}\bigl(1+V_{1}(x)\bigr)^{\theta-2} \biggl\{ \frac{\rho}{\theta }\bigl(1+V_{1}(x)\bigr)^{2}-V_{1}(x)^{2} \bigl(\varphi^{l} -0.5\theta\bigl(\sigma^{u} \bigr)^{2} \bigr)+V_{1}(x) \biggl(\bigl(\sigma^{u} \bigr)^{2} \\ &{}+a^{u}M+ \frac{c^{u}M}{b^{l}} \biggr)+a^{u}M+ \frac{c^{u}M}{b^{l}} \biggr\} \,dt-\theta e^{\rho t}\bigl(1+V_{1}(x) \bigr)^{\theta-1}V_{1}(x)\sigma(t)\,dB(t) \\ ={}&\theta e^{\rho t}\bigl(1+V_{1}(x)\bigr)^{\theta-2} \biggl\{ -V_{1}(x)^{2} \biggl(\varphi^{l} -0.5\theta \bigl(\sigma^{u}\bigr)^{2}- \frac{\rho}{\theta} \biggr)+V_{1}(x) \biggl(\bigl(\sigma^{u}\bigr)^{2} +a^{u}M \\ &{}+ \frac{c^{u}M}{b^{l}}+\frac{2\rho}{\theta} \biggr) +a^{u}M+ \frac{c^{u}M}{b^{l}}+\frac{\rho}{\theta} \biggr\} \,dt -\theta e^{\rho t} \bigl(1+V_{1}(x)\bigr)^{\theta-1}V_{1}(x)\sigma(t)\,dB(t) \\ ={}&e^{\rho t}\Gamma(x)\,dt-\theta e^{\rho t}\bigl(1+V_{1}(x) \bigr)^{\theta-1}V_{1}(x)\sigma(t)\,dB(t), \end{aligned}$$

(3.16)

where

$$\begin{aligned} \Gamma(x)={}&\theta\bigl(1+V_{1}(x)\bigr)^{\theta-2} \biggl\{ -V_{1}(x)^{2} \biggl(\varphi^{l} -0.5\theta\bigl( \sigma^{u}\bigr)^{2}- \frac{\rho}{\theta} \biggr)+V_{1}(x) \biggl(\bigl(\sigma^{u}\bigr)^{2} +a^{u}M \\ &{}+\frac{c^{u}M}{b^{l}}+\frac{2\rho}{\theta} \biggr) +a^{u}M+ \frac{c^{u}M}{b^{l}}+\frac{\rho}{\theta} \biggr\} . \end{aligned}$$

It is not difficult to prove that $\Gamma(x)$ is upper bounded, namely, $\Gamma_{1}=\sup_{x>0}\Gamma(x)<+\infty$. This, together with (3.16), indicates that

$$ dV_{3}(x)\leq\Gamma_{1}e^{\rho t}\,dt-\theta e^{\rho t}\bigl(1+V_{1}(x)\bigr)^{\theta-1}V_{1}(x) \sigma(t)\,dB(t). $$

(3.17)

Integrating and taking expectations result in

$$ E\bigl[V_{3} \bigl(x(t) \bigr)\bigr]=E\bigl[e^{\rho t} \bigl(1+V_{1}\bigl(x(t)\bigr) \bigr)^{\theta}\bigr]\leq \bigl(1+V_{1}\bigl(x(0)\bigr) \bigr)^{\theta }+ \frac{\Gamma_{1}e^{\rho t}}{\rho}. $$

(3.18)

As a consequence

$$ \limsup_{t\rightarrow\infty}E\bigl[V_{1}^{\theta}\bigl(x(t) \bigr)\bigr]\leq \limsup_{t\rightarrow\infty}E\bigl[(1+V_{1} \bigl(x(t)\bigr)^{\theta}\bigr]\leq\frac{\Gamma _{1}}{\rho}, $$

(3.19)

which, together with (2.16), yields

$$ \limsup_{t\rightarrow\infty}E\bigl[1/y^{\theta}(t)\bigr]= \limsup _{t\rightarrow\infty} \biggl(\prod_{0< \tau_{k}< t}(1+ \lambda_{k}) \biggr)^{-\theta}E\bigl[1/x^{\theta}(t)\bigr] \leq m^{-\theta}\frac{\Gamma_{1}}{\rho}=\Gamma_{2}. $$

(3.20)

Thus for any $\varepsilon>0$, let $\beta=\varepsilon^{\frac{1}{\theta}}/\Gamma_{2}^{\frac{1}{\theta}}$, by Chebyshev’s inequality, we have

$$ \mathbf{P} \bigl\{ y(t)< \beta \bigr\} =\mathbf{P} \bigl\{ y^{-\theta}(t)> \beta^{-\theta} \bigr\} \leq\frac{E[y^{-\theta}(t)]}{\beta^{-\theta}}=\beta^{\theta}E \bigl[y^{-\theta }(t)\bigr], $$

(3.21)

which implies that

$$\limsup_{t\rightarrow+\infty}\mathbf{P} \bigl\{ y(t)< \beta \bigr\} \leq \beta^{\theta}\Gamma_{2}=\varepsilon, $$

namely

$$ \liminf_{t\rightarrow+\infty}\mathbf{P} \bigl\{ y(t)\geq\beta \bigr\} \geq1- \varepsilon. $$

(3.22)

Next, we will prove that for arbitrary fixed $0<\varepsilon<1$, there exists a constant $\delta>0$ such that $\liminf_{t\rightarrow+\infty}\mathbf{P} \{y(t)\leq\delta \} \geq1-\varepsilon$. Choose $q>1$ arbitrarily, we define

$$ V_{4}(x)=x^{q}(t). $$

(3.23)

Applying Itô’s formula to (2.7) and recalling the assumption (S) yield

$$\begin{aligned} dV_{4}(x)={}&qx^{q-1}\,dx+0.5q(q-1)x^{q-2}(dx)^{2} \\ ={}&qx^{q} \biggl(r(t)-a(t) \prod_{0< \tau _{k}< t}(1+ \lambda_{k})x(t)+0.5(q-1)\sigma^{2}(t) \\ &{}- \frac{c(t) \prod_{0< \tau_{k}< t}(1+\lambda _{k})x(t)}{b(t)+ [\prod_{0< \tau_{k}< t}(1+\lambda_{k})x(t) ]^{2}} \biggr)\,dt +qx^{q}\sigma(t)\,dB(t) \\ \leq&{} qx^{q} \bigl(r(t)-a(t)mx(t)+0.5(q-1)\sigma^{2}(t) \bigr)\,dt+qx^{q}\sigma(t)\,dB(t). \end{aligned}$$

(3.24)

Integrating and taking expectations give

$$ E\bigl(x^{q}(t)\bigr)-E\bigl(x^{q}(0)\bigr)\leq q\int _{0}^{t}E \bigl\{ x^{q}(s) \bigl(r(s)-a(s)mx(s)+0.5(q-1)\sigma ^{2}(s) \bigr) \bigr\} \,ds. $$

(3.25)

So

$$ \frac{dE(x^{q}(t))}{dt}\leq qE\bigl(x^{q}(t)\bigr)\bigl[r(t)+0.5(q-1) \sigma^{2}(t)\bigr]-ma(t)qE\bigl(x^{q+1}(t) \bigr). $$

(3.26)

It follows from Hölder’s inequality that

$$E\bigl(x^{q+1}\bigr)\geq\bigl(E\bigl(x^{q}\bigr) \bigr)^{\frac{q+1}{q}}. $$

As a consequence

$$ \frac{dE(x^{q}(t))}{dt}\leq qE\bigl(x^{q}(t)\bigr)\bigl[r(t)+0.5(q-1) \sigma^{2}(t)\bigr]-qma(t) \bigl(E\bigl(x^{q}\bigr) \bigr)^{\frac {q+1}{q}}. $$

(3.27)

Denote

$$z(t)=E\bigl(x^{q}(t)\bigr), $$

then (3.27) can be rewritten as

$$\begin{aligned} \frac{dz}{dt}&\leq qz(t)\bigl[r(t)+0.5(q-1) \sigma^{2}(t)-ma(t)z^{\frac{1}{q}}(t)\bigr] \\ &\leq qz(t)\bigl[r^{u}+0.5q\bigl(\sigma^{u} \bigr)^{2}-ma^{l}z^{\frac{1}{q}}(t)\bigr]. \end{aligned}$$

(3.28)

By the standard comparison theorem, we have

$$ \limsup_{t\rightarrow+\infty}E\bigl(x^{q}(t)\bigr)\leq \biggl( \frac{r^{u}+0.5q(\sigma ^{u})^{2}}{ma^{l}} \biggr)^{q}=\triangle (q). $$

(3.29)

So

$$\begin{aligned} \limsup_{t\rightarrow+\infty}E\bigl(y^{q}(t)\bigr) =& \limsup_{t\rightarrow+\infty } \biggl(\prod_{0< \tau_{k}< t}(1+ \lambda_{k}) \biggr)^{q}E\bigl(x^{q}(t)\bigr) \\ \leq& \biggl(M\frac{r^{u}+0.5q(\sigma^{u})^{2}}{ma^{l}} \biggr)^{q}=\Re(q). \end{aligned}$$

(3.30)

On the other hand, let $\delta=\Re^{\frac{1}{q}}(q)/\varepsilon^{\frac{1}{q}}$, then we have

$$ \mathbf{P}\{y>\delta\}=\mathbf{P}\bigl\{ y^{q}>\delta^{q} \bigr\} \leq\frac{E(y^{q}(t))}{\delta^{q}}. $$

(3.31)

Thus it follows from (3.30) and (3.31) that

$$\limsup_{t\rightarrow+\infty} \mathbf{P}\{y>\delta\} \leq\frac{\Re(q)}{\delta^{q}}= \varepsilon, $$

which implies that

$$ \liminf_{t\rightarrow+\infty}\mathbf{P}\{y\leq\delta\} \geq1- \varepsilon, $$

(3.32)

which, together with (3.22), completes the proof of Theorem 3.2. □

4 Global attractivity

In this section, we first give Lemma 4.1 which is useful for the proof of global attractivity.

Lemma 4.1

For a solution $x(t)$ of (2.7) with initial value $x(0)>0$, almost every sample path of $x(t)$ is uniformly continuous for $t\geq0$.

Proof

Denote

$$ \mathcal{L}(q)=\max\bigl\{ \triangle(q), x^{q}(0)\bigr\} . $$

(4.1)

It follows from (3.28)-(3.29), for all $t\geq0$, that

$$ E\bigl(x^{q}(t)\bigr)\leq\mathcal{L}(q). $$

(4.2)

Notice that (2.7) is equivalent to the following integral equation:

$$\begin{aligned} x(t)={}&x(0)+ \int_{0}^{t}x(s) \biggl[r(s)- a(s)\prod_{0< \tau_{k}< t}(1+\lambda_{k})x(s) - \frac{c(s)\prod_{0< \tau_{k}< t}(1+\lambda_{k})x(s)}{b(s)+ [\prod_{0< \tau_{k}< t}(1+\lambda_{k})x(s) ]^{2}} \biggr]\,ds \\ &{} + \int_{0}^{t}\sigma(s)x(s)\,dB(s). \end{aligned}$$

(4.3)

At the same time, by Lemma 2.2 one sees that

$$\begin{aligned} &E \biggl|x(t) \biggl[r(t)-a(t) \prod_{0< \tau_{k}< t}(1+ \lambda_{k})x(t) -\frac{c(t)\prod_{0< \tau_{k}< t}(1+\lambda_{k})x(t)}{b(t) + [\prod_{0< \tau_{k}< t}(1+\lambda_{k})x(t) ]^{2}} \biggr] \biggr|^{q} \\ &\quad =E \biggl( \bigl|x(t) \bigr|^{q} \biggl|r(t)-a(t) \prod _{0< \tau _{k}< t}(1+\lambda_{k})x(t) -\frac{c(t)\prod_{0< \tau_{k}< t}(1+\lambda_{k})x(t)}{b(t) + [\prod_{0< \tau_{k}< t}(1+\lambda_{k})x(t) ]^{2}} \biggr|^{q} \biggr) \\ &\quad \leq0.5E\bigl|x(t)\bigr|^{2q}+0.5E \biggl|r(t)- a(t)\prod _{0< \tau_{k}< t}(1+\lambda_{k})x(t) -\frac{c(t)}{b(t)+ [\prod_{0< \tau_{k}< t}(1+\lambda_{k})x(t) ]^{2}} \biggr|^{2q} \\ &\quad\leq0.5 \biggl\{ \mathcal {L}(2q)+3^{2q-1} \biggl(\bigl|r^{u}\bigr|^{2q}+\biggl| \frac {c^{u}}{b^{l}}\biggr|^{2q}+\bigl|a^{u}M\bigr|^{2q}\mathcal {L}(2q) \biggr) \biggr\} =K(q). \end{aligned}$$

(4.4)

By the moment inequality for stochastic integrals, we obtain, for $0\leq t_{1}\leq t_{2}$ and $q>2$,

$$\begin{aligned} E \biggl| \int_{t_{1}}^{t_{2}}\sigma(s)x(s)\,dB(s) \biggr|^{q} &\leq\bigl(\sigma^{u}\bigr)^{q} \biggl[ \frac{q(q-1)}{2} \biggr]^{\frac {q}{2}}(t_{2}-t_{1})^{\frac{q-2}{2}} \int_{t_{1}}^{t_{2}}E\bigl|x(s)\bigr|^{q}\,ds \\ &\leq\bigl(\sigma^{u}\bigr)^{q} \biggl[ \frac{q(q-1)}{2} \biggr]^{\frac {q}{2}}(t_{2}-t_{1})^{\frac{q}{2}}\mathcal {L}(q). \end{aligned}$$

(4.5)

Then for

$$0< t_{1}< t_{2}< +\infty,\qquad t_{2}-t_{1} \leq1, \qquad \frac{1}{p}+\frac{1}{q}=1, $$

we can derive that

$$\begin{aligned} &E \bigl|x(t_{2})-x(t_{1}) \bigr|^{q} \\ &\quad=E \biggl| \int_{t_{1}}^{t_{2}}x(s) \biggl[r(s)- a(s) \prod_{0< \tau_{k}< t}(1+\lambda_{k})x(s) \\ &\qquad{} - \frac{c(s)\prod_{0< \tau _{k}< t}(1+h_{k})x(s)}{b(s)+[\prod_{0< \tau_{k}< t}(1+h_{k})x(s)]^{2}} \biggr]\,ds + \int_{t_{1}}^{t_{2}} \sigma(s)x(s)\,dB(s) \biggr|^{q} \\ &\quad\leq2^{q-1}E \biggl| \int_{t_{1}}^{t_{2}}x(s) \biggl[r(s)- a(s)\prod_{0< \tau_{k}< t}(1+\lambda_{k})x(s) \\ &\qquad{}-\frac{c(s)\prod_{0< \tau _{k}< t}(1+\lambda_{k})x(s)}{b(s) +[\prod_{0< \tau_{k}< t}(1+\lambda_{k})x(s)]^{2}} \biggr]\,ds \biggr|^{q}+2^{q-1}E \biggl|\int _{t_{1}}^{t_{2}}\sigma(s)x(s)\,dB(s) \biggr|^{q} \\ &\quad\leq2^{q-1}(t_{2}-t_{1})^{\frac{q}{p}} \int _{t_{1}}^{t_{2}}E \biggl|x(s) \biggl[r(s)- a(s)\prod _{0< \tau_{k}< t}(1+h_{k})x(s) \\ &\qquad{}- \frac{c(s)\prod_{0< \tau _{k}< t}(1+h_{k})x(s)}{b(s)+[\prod_{0< \tau_{k}< t}(1+h_{k})x(s)]^{2}} \biggr] \biggr|^{q}\,ds+2^{q-1}\bigl( \sigma^{u}\bigr)^{q} \biggl[\frac{q(q-1)}{2} \biggr]^{\frac {q}{2}}(t_{2}-t_{1})^{\frac{q}{2}}\mathcal {L}(q) \\ &\quad \leq2^{q-1}(t_{2}-t_{1})^{\frac {q}{p}+1}K(q)+2^{q-1} \bigl(\sigma^{u}\bigr)^{q} \biggl[\frac{q(q-1)}{2} \biggr]^{\frac {q}{2}}(t_{2}-t_{1})^{\frac{q}{2}}\mathcal {L}(q) \\ &\quad \leq2^{q-1}(t_{2}-t_{1})^{\frac{q}{2}} \biggl[(t_{2}-t_{1})^{\frac{q}{2}}+ \biggl[\frac{q(q-1)}{2} \biggr]^{\frac{q}{2}} \biggr]\mathcal {D}(q) \\ &\quad \leq2^{q-1}(t_{2}-t_{1})^{\frac{q}{2}} \biggl[1+ \biggl[\frac {q(q-1)}{2} \biggr]^{\frac{q}{2}} \biggr]\mathcal {D}(q), \end{aligned}$$

(4.6)

where $\mathcal{D}(q)=\max\{K(q), (\sigma^{u})^{q}\mathcal{L}(q)\}$. Thus, we obtain from Lemma 2.1 that almost every sample path of $x(t)$ is locally but uniformly Hölder-continuous with an exponent ϑ for $\vartheta\in(0,\frac{q-2}{2q})$, and hence almost every sample path of $x(t)$ is uniformly continuous on $t\geq0$. The proof of Lemma 4.1 is complete. □

Theorem 4.1

If $a^{l}>{c^{u}}/{b^{l}}$, then system (2.5) is globally attractive.

Proof

Let $y_{1}(t)$ and $y_{2}(t)$ be, respectively, arbitrary two solutions of system (2.5) with initial values $y_{1}(0)>0$ and $y_{2}(0)>0$. Suppose that $x_{1}(t)$ is a solution of the system (4.7) with $x_{1}(0)=y_{1}(0)$,

$$\begin{aligned} dx(t)={}&x (t) \biggl(r(t)-a(t) \prod _{0< \tau_{k}< t}(1+\lambda_{k})x(t)- \frac{c(t)\prod_{0< \tau_{k}< t}(1+\lambda_{k})x(t)}{b(t) + [\prod_{0< \tau_{k}< t}(1+\lambda_{k})x(t) ]^{2}} \biggr)\,dt \\ &{} +\sigma(t)x(t)\,dB(t) \end{aligned}$$

(4.7)

and $x_{2}(t)$ is a solution of the system (4.8) with $x_{2}(0)=y_{2}(0)$,

$$\begin{aligned} dx(t)={}&x (t) \biggl(r(t)-a(t) \prod _{0< \tau_{k}< t}(1+\lambda_{k})x(t)- \frac{c(t)\prod_{0< \tau_{k}< t}(1+\lambda_{k})x(t)}{b(t) + [\prod_{0< \tau_{k}< t}(1+\lambda_{k})x(t) ]^{2}} \biggr)\,dt \\ &{} +\sigma(t)x(t)\,dB(t). \end{aligned}$$

(4.8)

Thus, we obtain

$$ y_{1}(t)= \prod_{0< \tau_{k}< t}(1+ \lambda_{k})x_{1}(t), \qquad y_{2}(t)= \prod _{0< \tau_{k}< t}(1+\lambda_{k})x_{2}(t). $$

(4.9)

Define

$$ V(t)=\bigl|\ln x_{1}(t)-\ln x_{2}(t)\bigr|. $$

(4.10)

Applying Itô’s formula, and calculating the right differential $D^{+}V(t)$ of $V(t)$, we have

$$\begin{aligned} D^{+}V(t)={}&\operatorname{sgn}\bigl(x_{1}(t)-x_{2}(t) \bigr)\,d\bigl(\ln x_{1}(t)-\ln x_{2}(t)\bigr) \\ ={}&\operatorname{sgn}\bigl(x_{1}(t)-x_{2}(t)\bigr) \biggl\{ \biggl[ \frac {dx_{1}(t)}{x_{1}(t)}-\frac{(dx_{1}(t))^{2}}{2x^{2}_{1}(t)} \biggr] - \biggl[ \frac{dx_{2}(t)}{x_{2}(t)}-\frac {(dx_{2}(t))^{2}}{2x^{2}_{2}(t)} \biggr] \biggr\} \\ ={}&\operatorname{sgn}\bigl(x_{1}(t)-x_{2}(t)\bigr) \biggl\{ - \prod_{0< \tau _{k}< t}(1+\lambda_{k})a(t) \bigl(x_{1}(t)-x_{2}(t)\bigr) \\ &{}+ \frac{c(t) \prod_{0< \tau_{k}< t}(1+\lambda_{k})(x_{1}(t)- x_{2}(t)) ([\prod_{0< \tau_{k}< t}(1+\lambda _{k})]^{2}x_{1}(t)x_{2}(t)-b(t) )}{ (b(t)+[ \prod_{0< \tau_{k}< t}(1+\lambda _{k})x_{1}(t)]^{2} ) (b(t)+[ \prod_{0< \tau_{k}< t}(1+\lambda_{k})x_{2}(t)]^{2} )} \biggr\} \,dt \\ ={}& \biggl\{ - \prod_{0< \tau_{k}< t}(1+\lambda _{k})a(t)\bigl|x_{1}(t)-x_{2}(t)\bigr| \\ &{}+ \frac{c(t) \prod_{0< \tau_{k}< t}(1+\lambda_{k})|x_{1}(t)- x_{2}(t)| ([\prod_{0< \tau_{k}< t}(1+\lambda _{k})]^{2}x_{1}(t)x_{2}(t)-b(t) )}{ (b(t)+[ \prod_{0< \tau_{k}< t}(1+\lambda _{k})x_{1}(t)]^{2} ) (b(t)+[ \prod_{0< \tau_{k}< t}(1+\lambda_{k})x_{2}(t)]^{2} )} \biggr\} \,dt. \end{aligned}$$

(4.11)

Let

$$\Theta= \frac{c(t) \prod_{0< \tau_{k}< t}(1+\lambda _{k})|x_{1}(t)- x_{2}(t)| ([\prod_{0< \tau_{k}< t}(1+\lambda_{k})]^{2}x_{1}(t)x_{2}(t)-b(t) )}{ (b(t)+[ \prod_{0< \tau_{k}< t}(1+\lambda_{k})x_{1}(t)]^{2} ) (b(t)+[ \prod_{0< \tau_{k}< t}(1+\lambda_{k})x_{2}(t)]^{2} )}. $$

Next, we focus on the estimation of Θ. It follows from (4.9) that $x_{1}>0$ and $x_{2}>0$. Without loss of generality, assume that $x_{1}< x_{2}$, then

$$\begin{aligned} \Theta&\leq \frac{c(t) \prod_{0< \tau _{k}< t}(1+\lambda_{k})|x_{1}(t)- x_{2}(t)|[\prod_{0< \tau_{k}< t}(1+\lambda_{k})]^{2}x_{2}^{2}(t)}{b(t)[ \prod_{0< \tau_{k}< t}(1+\lambda_{k})x_{2}(t)]^{2}} \\ &= \frac{c(t) \prod_{0< \tau_{k}< t}(1+\lambda _{k})|x_{1}(t)- x_{2}(t)|}{b(t)}, \end{aligned}$$

which, together with (4.11) and the assumption (S), leads to

$$D^{V}(t)+\leq- \prod_{0< \tau_{k}< t}(1+ \lambda_{k})\biggl\{ a(t)-\frac {c(t)}{b(t)}\biggr\} \bigl|x_{1}(t)- x_{2}(t)\bigr|\,dt\leq-m\biggl(a^{l}-\frac{c^{u}}{b^{l}} \biggr)\bigl|x_{1}(t)-x_{2}(t)\bigr|\,dt, $$

and, moreover, integrating on both sides yields

$$ V(t)\leq V(0)-m \biggl(a^{l}- \frac{c^{u}}{b^{l}} \biggr)\int _{0}^{t}\bigl|x_{1}(s)-x_{2}(s)\bigr|\,ds. $$

(4.12)

Namely

$$ V(t)+m \biggl(a^{l}- \frac{c^{u}}{b^{l}} \biggr)\int _{0}^{t}\bigl|x_{1}(s)-x_{2}(s)\bigr|\,ds \leq V(0)< +\infty. $$

(4.13)

Notice that $V(t)\geq0$, then $|x_{1}(t)-x_{2}(t)|\in L^{1}[0, +\infty)$. It follows from Lemmas 4.1 and 2.3 that $\lim_{t\rightarrow+\infty}|x_{1}(t)-x_{2}(t)|=0$ a.s. Thus one obtains from (4.9), (4.10), and the assumption (S) that

$$\lim_{t\rightarrow+\infty}\bigl|y_{1}(t)-y_{2}(t)\bigr|=\lim _{t\rightarrow+\infty} \prod_{0< \tau_{k}< t}(1+ \lambda_{k})\bigl|x_{1}(t)-x_{2}(t)\bigr|\leq M\lim _{t\rightarrow+\infty}|x_{1}(t)-x_{2}(t)|=0 \quad\mbox{a.s.} $$

The proof of Theorem 4.1 is complete. □

5 Numerical simulation

In the present paper, a nonautonomous single-species model with impulsive effects and stochastic perturbations is proposed and sufficient conditions for the extinction, stochastic permanence and global attractivity of system (2.5) are established, respectively. To illustrate the above analytical results, we consider the following three specific numerical examples.

Example 1

(Extinction)

Consider the following system:

$$ \left \{ \textstyle\begin{array}{@{}l} dy(t)=y(t) (0.5+0.1\sin t-(0.75+0.05\sin t)y(t)- \frac{(0.13+0.03\sin t)y(t)}{0.22+0.02\sin t+y^{2}(t)} )\,dt\\ \hphantom{dy(t)=}{}+(\sqrt{0.4}+0.1\sin t)y(t)\,dB(t),\quad t\neq\tau_{k},\\ y(\tau_{k}^{+})=(1+\lambda_{k})y(\tau_{k}),\quad t=\tau_{k}, k\in\mathbb{N}. \end{array}\displaystyle \right . $$

(5.1)

Let $y(0)=0.3$, $\tau_{k}=k$, $\lambda_{k}=e^{\frac{(-1)^{k+1}}{k}}-1$, then $1<\prod_{k=1}^{+\infty}(1+\lambda_{k})<2$. Notice that $\varphi(t)=0.5+0.1\sin t-0.5(\sqrt{0.4}+0.1\sin t)^{2}$ and

$$\limsup_{t\rightarrow+\infty}t^{-1} \biggl(\sum _{0< \tau_{k}< t}\ln(1+\lambda _{k})+\int_{0}^{t} \varphi(s)\,ds \biggr)= -0.0525< 0. $$

It follows from Theorem 3.1 that system (5.1) is extinct (see Figure 1).

Figure 1

System ( 5.1 ) is extinct.

Example 2

(Stochastic permanence)

Consider the following system:

$$ \left \{ \textstyle\begin{array}{@{}l} dy(t)=y(t) (0.75+0.05\sin t-(0.5+0.1\sin t)y(t)- \frac{(0.15+0.05\sin t)y(t)}{1.2+0.2\sin t+y^{2}(t)} )\,dt\\ \hphantom{dy(t)=}{}+(\sqrt{0.3}+0.1\sin t)y(t)\,dB(t),\quad t\neq\tau_{k},\\ y(\tau_{k}^{+})=(1+\lambda_{k})y(\tau_{k}),\quad t=\tau_{k}, k\in\mathbb{N}. \end{array}\displaystyle \right . $$

(5.2)

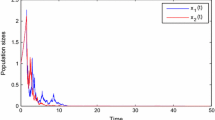
Let $y(0)=0.3$, $\tau_{k}=k$, $\lambda_{k}=e^{\frac{(-1)^{k+1}}{k^{2}}}-1$, then $1<\prod_{k=1}^{+\infty}(1+\lambda_{k})<e$. Obviously, $\varphi(t)=0.75+0.05\sin t-0.5(\sqrt{0.3}+0.1\sin t)^{2}$, and $\varphi^{l}=0.4902>0$, so by Theorem 3.2 we know that system (5.2) is stochastically permanent (see Figure 2).

Figure 2

System ( 5.2 ) is stochastically permanent.

Example 3

(Global attractivity)

Consider the following system:

$$ \left \{ \textstyle\begin{array}{@{}l} dy(t)=y(t) (0.71+0.01\sin t-(0.5+0.1\sin t)y(t)- \frac{(0.25+0.05\sin t)y(t)}{1.2+0.2\sin t+y^{2}(t)} )\,dt\\ \hphantom{dy(t)=}{} +(\sqrt{0.5}+0.1\sin t)y(t)\,dB(t),\quad t\neq\tau_{k},\\ y(\tau_{k}^{+})=(1+\lambda_{k})y(\tau_{k}),\quad t=\tau_{k}, k\in\mathbb{N}. \end{array}\displaystyle \right . $$

(5.3)

Let $y_{1}(0)=1.2$, $y_{2}(0)=0.3$, $\tau_{k}=k$, $\lambda_{k}=e^{\frac{(-1)^{k+1}}{k^{2}}}-1$, then $1<\prod_{k=1}^{+\infty}(1+\lambda_{k})<e$, $a^{l}=0.4>c^{u}/b^{l}=0.3$. Thus, it follows from Theorem 4.1 that system (5.3) is globally attractive (see Figure 3).

Figure 3

System ( 5.3 ) is global attractive.