1 Introduction

Differential equations and difference equations are widely applied in epidemiological modeling. They are two typical mathematical approaches for modeling infectious diseases. Since the theory and method for dynamical studies of differential equations have developed much more completely than those for difference equations, there are relatively few difference equations in epidemiological modeling compared with differential equations. In recent years, there were increasing interest and research results on discrete epidemic models [1–8]. The fact that the epidemiological data are usually collected in discrete time units, such as days, weeks or months, makes the discrete model a natural choice to describe a disease transmission. The straightforward recurrence relationship of the difference equation models is easier to understand, which is also a prominent advantage over the differential equation models. The direct comparison of the model results with the actual data provides us a fast and simple way to validate the model structure and parameter estimation. The fact that the discrete models exhibit a richer dynamical behavior than the continuous models brings about more challenging problems for researches, and more interesting results can be obtained. For example, the simple logistic model, \(x_{n+1}=rx_{n}(1-x_{n}/K)\), the Ricker model \(x_{n+1}=x_{n}e^{r-x_{n}/K}\) [9–11], and the Hassell model, \(x_{n+1}=\lambda x_{n}(1+a x_{n})^{-b}\) [12] exhibit a rich dynamical behavior.

There have been increasing interest and more studies on the discrete time epidemic models recently. Various discrete epidemic models have been successfully applied to describe the infectious disease transmission, such as SARS, tuberculosis, HIV/AIDS [13–18]. The theoretical study of discrete epidemic models focuses on the computation of the basic reproduction number [19–21], the existence and the global stability of the disease-free equilibrium [4, 5, 14–16], the existence and the local stability of the endemic equilibrium [22, 23], and the persistence of the disease [14, 15]. Attention has also be paid to various bifurcations of the discrete epidemic models, the equilibrium bifurcation [3, 21, 24–26], the transcritical bifurcation, the flip bifurcation, the saddle-node bifurcation, the Hopf bifurcation, and the bifurcation to chaos [3–5].

There also have been many researches studying mathematical models of the transmission dynamics of TB in human populations. Those researches include slow and fast progression, a variable latent period, MDR TB, multiple strains, exogenous reinfection, generalized households, co-infection with HIV, and the control strategy for TB [27–35]. However, there are a few papers using discrete mathematical models to study the treatment of latent TB as a TB control strategy [3, 36, 37]. The treatment of latent tuberculosis infection is essential to controlling and eliminating TB, because it substantially reduces the risk from latent TB to active TB cases. In this paper, we use the discrete models with direct progression and treatment of latently infected individuals to analyze the impact of the treatment of latently infected individuals on TB transmission.

Our discrete model with treatment of latent TB individuals is presented in the next section. The positivity of solutions is also discussed. The global stability of the disease-free equilibrium and the persistence of the system is discussed in Section 3. The stability of endemic equilibrium is proved in Section 4. The effect of two treatment strategies is studied in Section 5. Numerical simulations are done on the basis of the TB infection data in China to show the effect of treatment strategies. The last section includes concluding remarks and discussions.

2 The discrete TB model

TB is an airborne infectious disease transmitting from person to person via droplets with TB bacilli. After being infected, most people become latently infectious, with the bacteria being alive in the body but inactive. Latently infectious individuals do not have symptoms and cannot spread the infection to others. Most people are able to fight the infection with their immune system, but those people with latent infection are at risk of developing the active disease. Based on these characteristics, there have been many continuous models to be used to describe TB transmission. Here, we will build the discrete mathematical model for TB transmission which considers the direct progression, chemoprophylaxis for the latent individuals, and treatment of the infectious individuals.

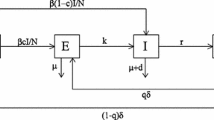
The total population is epidemiologically divided into susceptible, latent, and infectious classes. Let \(S(t)\) be the number of susceptible individuals at time t, \(L(t)\) be the number of latent individuals, and \(I(t)\) be the number of infectious individuals. \(N(t)=S(t)+L(t)+I(t)\) is the total population size. We assume that individuals recovered by successful treatment do not acquire immunity, and they will become member of the susceptible compartment. Hence our model is of SLIS type.

Susceptible individuals may get infected and enter the latent compartment. The surviving latent individuals will experience one of the two mutually exclusive events to leave the latent compartment, naturally progressing into infectious class, or receiving the treatment. These two events happen randomly. The probabilities for receiving the treatment is m, and \(1-m\) is the probabilities for natural progression. Our model framework takes the following form:

$$\begin{aligned}& S(t+1)=\Lambda+p\biggl(1-\frac{\beta I(t)}{N(t)}\biggr)S(t)+pkmL(t)+p \gamma I(t), \\& L(t+1)=q\frac{p\beta S(t)I(t)}{N(t)}+p(1-\alpha) (1-m)L(t)+p(1-k)mL(t), \\& I(t+1)=(1-q)\frac{p\beta S(t)I(t)}{N(t)}+p\alpha(1-m)L(t)+p(1-\gamma)I(t), \end{aligned}$$
(1)

where Λ is the recruitment rate into the population, p the survival probability; k is the conditional probability that a latent individual is treated successfully given that the individual receives the treatment, and it should rely on the capability of finding latent individuals and budgetary issues. α is the probability that a latent individual becomes an infectious individual that the natural progression happens; γ the probability that an infectious individual recovers successfully; \(1-\frac{\beta I(t)}{N(t)}\) is for the probability of not becoming infected, where β characterizes the disease transmission probability, satisfying \(0<\beta<1\); q is the probability that the infected ones enter the latent compartment, accordingly, \(1-q\) is the probability that the infected ones enter the infectious compartment by the fast development; all parameters are positive and less than one.

Based on biological considerations, system (1) will be studied in the following region:

$$\Omega=\biggl\{ (S, L, I)\in R^{3}_{+}\Bigm|S\geq0, L\geq0, I\geq0, S+L+I \leq\frac {\Lambda}{1-p}\biggr\} . $$

In the following, we first discuss the positivity and boundedness of solutions for system (1). The following theorem holds.

Theorem 2.1

The solutions \(S(t)\), \(L(t)\), and \(I(t)\) of system (1) with initial value \(S(0)=S_{0}\geq0\), \(L(0)=L_{0}\geq0\), and \(I(0)=I_{0}\geq0\), respectively, are non-negative for all \(t\geq0\), \(t\in N\). For the system (1), the region Ω is positively invariant and all solutions starting in the Ω approach, enter, or stay in Ω.

Proof

Let \(S(0)=S_{0}\geq0\), \(L(0)=L_{0}\geq0\), and \(I(0)=I_{0}\geq0\), by using (1), we have

$$\begin{aligned}& S(1)=\Lambda+p\biggl(1-\frac{\beta I_{0}}{N_{0}}\biggr)S_{0}+pkmL_{0}+p \gamma I_{0}, \\& L(1)=q\frac{p\beta S_{0}I_{0}}{N_{0}}+p(1-\alpha) (1-m)L_{0}+p(1-k)mL_{0}, \\& I(1)=(1-q)\frac{p\beta S_{0}I_{0}}{N_{0}}+p\alpha(1-m)L_{0}+p(1- \gamma)I_{0}. \end{aligned}$$

Because of \(0\leq I(t)\leq N(t)\) for any \(t\geq0\), \(t\in N\), \(0\leq\beta \leq1\), we know that \(1-\frac{\beta I_{0}}{N_{0}}\geq0\). It implies that \(S(1)>0\). In addition, \(0<\alpha<1\), \(0< k<1\), and \(0< m<1\) illustrate \(L(1)\geq0\). Furthermore, \(0<\gamma<1\) implies that \(I(1)\geq0\) holds. The recurrent procedure implies that \(S(t)>0\), \(L(t)\geq0\), \(I(t)\geq0\) for all \(t\geq0\), \(t\in N\). The solutions of (1) are non-negative.

By using \(N(t)=S(t)+L(t)+I(t)\), we know \(N(t)\) satisfies

$$ N(t+1)=\Lambda+pN(t) \quad \mbox{or}\quad N(t)= \frac{\Lambda(1-p^{t})}{1-p}+p^{t}N(0). $$
(2)

The fact \(0< p<1\) and the last equation in (2) implies that \(N^{*}=\frac{\Lambda}{1-p}\) is the unique equilibrium of (2), and \(N^{*}\) is globally asymptotically stable, i.e., for any solution \(N(t)\) of (2) with positive initial value \(N(0)\), \(\lim_{t\rightarrow\infty}N(t)=N^{*}\) holds. It implies that \(N(t)\) is bounded and all solutions starting in the region Ω approach, enter or stay in Ω. □

Using the limiting equations and \(S(t)=N^{*}-L(t)-I(t)\), we reduce the three dimensional system (1) into two dimensional ones:

$$ \begin{aligned} &L(t+1)=q\frac{p\beta(N^{*}-L(t)-I(t))I(t)}{N^{*}}+p(1-\alpha ) (1-m)L(t)+p(1-k)mL(t), \\ &I(t+1)=(1-q)\frac{p\beta(N^{*}-L(t)-I(t))I(t)}{N^{*}}+p\alpha (1-m)L(t)+p(1-\gamma)I(t). \end{aligned} $$
(3)

In the following, we will study the dynamical behavior of model (3) since model (3) exhibits the same qualitative dynamics as those of system (1) [38]. It is clear that the positively invariant of system (3) is

$$\Omega_{1}=\biggl\{ (L, I)\in R^{2}_{+}\Bigm|L\geq0, I\geq0, L+I< \frac{\Lambda}{1-p}\biggr\} . $$

Applying the approach in [39] to our model, we can obtain the basic reproductive number of model (3):

$$R_{0}=\frac{(1-m)p\alpha\times qp\beta}{ (1-p(1-km)+p\alpha(1-m) ) (1-p(1-\gamma) )}+\frac{(1-q)p\beta}{1-p(1-\gamma)}. $$

The basic reproductive number \(R_{0}\) is defined mathematically as the spectral radius of the next generation matrix in [39]; in fact, each term in \(R_{0}\) has a clear epidemiological interpretation. \(1/ (1-p(1-\gamma) )\) is the average infection period. \((1-m)p\alpha/ (1-p(1-km)+p\alpha(1-m) )\) is the proportion of latent individuals that become infectious by natural progression. \(p\beta/ (1-p(1-\gamma) )\) is the average of new cases generated by a typical infectious member in the entire infection period, where \(qp\beta/ (1-p(1-\gamma) )\) is the average of new cases generated by a typical infectious member who enters the infectious compartment by natural progression in the entire infection period, \((1-q)p\beta/ (1-p(1-\gamma) )\) is the average of new cases generated by a typical infectious member who enters the infectious compartment by direct progression in the entire infection period.

3 The extinction and persistence for the disease

By directly calculating model (3), we know there exists the disease-free equilibrium \(P_{0}^{*}=(L_{0}^{*},I_{0}^{*})=(0,0)\) when \(R_{0}<1\), and there is an endemic equilibrium \(P_{1}^{*}=(L_{1}^{*},I_{1}^{*})\) when \(R_{0}>1\), where

$$L_{1}^{*}=\frac{qp\beta I^{*}_{1}}{R_{0} (1-p(1-km)+p\alpha(1-m) )}, \qquad I_{1}^{*}= \frac{N^{*}(R_{0}-1)}{R_{0}+\frac{qp\beta}{1-p(1-km)+p\alpha(1-m)}}. $$

In the following, we will use the linearization matrix to discuss the local stability of equilibrium. The Jacobian matrix of model (3) at equilibrium \(P^{*}\) is

$$J\bigl(P^{*}\bigr)=\left ( \begin{array}{@{}c@{\quad}c@{}} -\frac{qp\beta}{N^{*}}I^{*}+p(1-\alpha)(1-m)+p(1-k)m & \frac{qp\beta }{N^{*}}(N^{*}-L^{*}-2I^{*}) \\ -\frac{(1-q)p\beta}{N^{*}}I^{*}+p\alpha(1-m) & \frac{(1-q)p\beta }{N^{*}}(N^{*}-L^{*}-2I^{*})+p(1-\gamma) \end{array} \right ). $$

3.1 The extinction for the disease

Theorem 3.1

If \(R_{0}<1\), then the disease-free equilibrium \(P_{0}^{*}\) of model (3) is globally asymptotically stable; if \(R_{0}>1\), then \(P_{0}^{*}\) is unstable.

Proof

When \(R_{0}<1\), we have \(P^{*}=P_{0}^{*}\), and

$$J\bigl(P^{*}_{0}\bigr)=\left ( \begin{array}{@{}c@{\quad}c@{}} p(1-\alpha)(1-m)+p(1-k)m & qp\beta\\ p\alpha(1-m) & (1-q)p\beta+p(1-\gamma) \end{array} \right ). $$

We denote

$$\begin{aligned} f(\lambda) =&\lambda^{2}- \bigl(p(1-\alpha) (1-m)+p(1-k)m+p(1-\gamma )+(1-q)p\beta \bigr)\lambda \\ &{}+ \bigl(p(1-\alpha) (1-m)+p(1-k)m \bigr) \bigl((1-q)p\beta+p(1-\gamma ) \bigr)-qp\beta p\alpha(1-m). \end{aligned}$$

It is clear that

$$\begin{aligned}& f(1)= \bigl(1-p(1-km)+p\alpha(1-m) \bigr) \bigl(1-p(1-\gamma) \bigr) (1-R_{0})>0, \\& f(-1)=1+p(1-\alpha) (1-m)+p(1-k)m+p(1-\gamma)+(1-q)p\beta \\& \hphantom{f(-1)=}{}+ \bigl(p(1-\alpha ) (1-m)+p(1-k)m \bigr) \bigl((1-q)p\beta+p(1- \gamma) \bigr)-qp\beta p\alpha(1-m), \\& f(0)= \bigl(p(1-\alpha) (1-m)+p(1-k)m \bigr) \bigl((1-q)p\beta+p(1-\gamma) \bigr)-qp\beta p\alpha(1-m). \end{aligned}$$

Since \(R_{0}<1\), we have \(\frac{(1-m)p\alpha\times qp\beta}{ (1-p(1-km)+p\alpha(1-m) ) (1-p(1-\gamma) )}<1\). Furthermore, we obtain \((1-m)p\alpha qp\beta< (1-p(1-km)+p\alpha (1-m) ) (1-p(1-\gamma) )\). Therefore,

$$\begin{aligned} f(-1) >&1+p(1-\alpha) (1-m)+p(1-k)m+p(1-\gamma)+(1-q)p\beta \\ &{}+ \bigl(p(1-\alpha) (1-m)+p(1-k)m \bigr) \bigl((1-q)p\beta +p(1-\gamma) \bigr) \\ &{}- \bigl(1-p(1-km)+p\alpha(1-m) \bigr) \bigl(1-p(1-\gamma) \bigr) \\ =&(1-q)p\beta+ \bigl(p(1-\alpha) (1-m)+p(1-k)m \bigr) (1-q)p\beta \\ &{}+2 \bigl(p(1-\alpha) (1-m)+p(1-k)m \bigr)+2p(1-\gamma)>0. \end{aligned}$$

Similarly, \(R_{0}<1\) implies that \(\frac{(1-q)p\beta}{1-p(1-\gamma)}<1\). We obtain \((1-q)p\beta<1-p(1-\gamma)\). So, we have

$$\begin{aligned} 1-f(0) =&1- \bigl(p(1-\alpha) (1-m)+p(1-k)m \bigr) \bigl((1-q)p\beta+p(1-\gamma ) \bigr) +qp\beta p\alpha(1-m) \\ >&1-p(1-km) \bigl(1-p(1-\gamma) \bigr)+p\alpha(1-m) \bigl(1-p(1-\gamma) \bigr) \\ &{}+p\alpha(1-m) (1-m)p(1-\gamma)-p(1-km)p(1-\gamma)+qp\beta p\alpha(1-m) \\ =&1-p(1-km)+p\alpha(1-m)+qp\beta p\alpha(1-m)>0, \end{aligned}$$

which illustrates that \(f(0)<1\) as \(R_{0}<1\). By using of the Jury criterion, we know the disease-free equilibrium \(P_{0}^{*}\) is of local stability. If \(R_{0}>1\), we have \(f(1)<0\). The Jury criterion implies that the disease-free equilibrium \(P_{0}^{*}\) is unstable. □

In the following, we use the Lyapunov function to prove the globally asymptotically stability of \(P_{0}^{*}\). We define \(F:[0, N^{*}]\times[0, N^{*}]\rightarrow[0, N^{*}]\times[0, N^{*}]\) by

$$\begin{aligned} F(L,I) =&p \biggl(q\frac{\beta(N^{*}-L-I)I}{N^{*}}+(1-\alpha) (1-m)L+(1-k)mL, \\ &(1-q)\frac{\beta(N^{*}-L-I)I}{N^{*}}+\alpha (1-m)L(t)+(1-\gamma)I \biggr). \end{aligned}$$

Obviously, F is the mapping derived by system (3), and \((0, 0)\) is a fixed point of F. The linear function

$$V(L,I)=\frac{(1-m)p\alpha}{ (1-p(1-km)+p\alpha(1-m) ) (1-p(1-\gamma) )}L+\frac{1}{1-p(1-\gamma)}I $$

on \([0, N^{*}]\times[0, N^{*}]\) is continuous and positive definite with respect to \((0, 0)\). Therefore, V is a Lyapunov function on the domain of F. For any \((L, I)\in[0, N^{*}]\times[0, N^{*}]\),

$$\begin{aligned} \Delta V(L, I) =&\frac{(1-m)p\alpha qp\beta(N^{*}-L-I)I}{ (1-p(1-km)+p\alpha(1-m) ) (1-p(1-\gamma) )N^{*}} \\ &{}+\frac{(1-m)p\alpha p(1-\alpha)(1-m)L}{ (1-p(1-km)+p\alpha(1-m) ) (1-p(1-\gamma) )} \\ &{}+\frac{(1-m)p\alpha p(1-k)mL}{ (1-p(1-km)+p\alpha (1-m) ) (1-p(1-\gamma) )} \\ &{}+\frac{(1-q)p\beta(N^{*}-L-I)I}{ (1-p(1-\gamma) )N^{*}}+\frac{p\alpha (1-m)L}{1-p(1-\gamma)}+\frac{p(1-\gamma)I}{1-p(1-\gamma)} \\ &{} -\frac{p\alpha(1-m)L}{ (1-p(1-km)+p\alpha(1-m) ) (1-p(1-\gamma ) )}-\frac{I}{1-p(1-\gamma)} \\ \leq&\frac{(1-m)p\alpha qp\beta I}{ (1-p(1-km)+p\alpha (1-m) ) (1-p(1-\gamma) )} \\ &{}+\frac{(1-m)p\alpha (p(1-km)-p\alpha(1-m) )L}{ (1-p(1-km)+p\alpha(1-m) ) (1-p(1-\gamma) )}-I+\frac{(1-q)p\beta I}{ (1-p(1-\gamma) )} \\ &{}+\frac {p\alpha(1-m)L}{1-p(1-\gamma)} -\frac{p\alpha(1-m)L}{ (1-p(1-km)+p\alpha(1-m) ) (1-p(1-\gamma ) )} \\ =&\frac{(1-m)p\alpha qp\beta I}{ (1-p(1-km)+p\alpha (1-m) ) (1-p(1-\gamma) )}-\frac{p\alpha(1-m)L}{1-p(1-\gamma)} \\ &{}-I +\frac{(1-q)p\beta I}{ (1-p(1-\gamma) )}+ \frac{p\alpha (1-m)L}{1-p(1-\gamma)} \\ =&\frac{(1-m)p\alpha qp\beta I}{ (1-p(1-km)+p\alpha (1-m) ) (1-p(1-\gamma) )}+\frac{(1-q)p\beta I}{ (1-p(1-\gamma) )}-I \\ =&(R_{0}-1)I. \end{aligned}$$

Hence, if \(R_{0}<1\), then \(\Delta V(L, I)<0\) holds for \((L, I)\in[0, N^{*}]\times[0, N^{*}]\). It follows from Theorem 4.22 in [40] that \(P_{0}^{*}\) is globally asymptotically stable.

We illustrate our theoretical results on disease extinction by numerical simulation. Taking \(\Lambda=10\), \(p=0.994\), \(q=0.95\), \(\beta=0.3\), \(\alpha=0.003\), \(m=0.001\), \(k=0.001\), and \(\gamma=0.2\), we obtain \(R_{0}=0.5298<1\), and the disease-free equilibrium \(P_{0}^{*}=(0, 0)\) is globally asymptotically stable. The solution curves of the latently infected individuals \(L(t)\) and the infectious individuals \(I(t)\) are given in Figure 1(a) and (b), respectively. The initial values at \(t=0\) are \((100, 1)\), \((70, 1.5)\), and \((40, 2)\), respectively. We observe that solutions with positive initial values will converge to the disease-free equilibrium \(P_{0}^{*}\).

Figure 1
figure 1

The global stability of disease-free equilibrium \(\pmb{P_{0}^{*}}\) of model ( 3 ) as \(\pmb{R_{0}<1}\) .

Full size image

3.2 The persistence for the disease

Theorem 3.2

If \(R_{0}>1\), then the disease will have persistence in the population, i.e., there exists a positive ϵ, such that the solution of model (3) with the initial value \(L(0)>0\) and \(I(0)>0\) satisfies

$$\liminf_{t\rightarrow\infty}\bigl\{ L(t), I(t)\bigr\} >\epsilon. $$

Proof

We denote \(\mathcal{X}=\Omega\), \(\mathcal{X}_{0}=\{(L,I)\in\mathcal {X}\mid L>0, I>0\}\), and \(\partial\mathcal{X}_{0}=\mathcal{X}\backslash \mathcal{X}_{0}\). Let \(\Phi: \mathcal{X}\rightarrow\mathcal{X}\), \(\Phi_{t}(x_{0})=\phi (t,x_{0})\) be the solution map of model (3) with \(\phi(0, x_{0})=x_{0}\), and \(x_{0}= (L(0), I(0) )\).

Define \(\mathcal{M}=\{P_{0}^{*}\}\), and

$$M_{\partial}=\bigl\{ (L,I)\in\partial\mathcal{X}_{0}: \phi \bigl(t, (L,I) \bigr)\in \partial\mathcal{X}_{0}, \forall t\geq0\bigr\} . $$

It is clear that \(M_{\partial}=\{(0,0)\}\). Furthermore, there is exactly one fixed point \(P_{0}^{*}=(0,0)\) in \(M_{\partial}\). Because \(N^{*}\) is globally attractive in \(\partial X_{0}\) and due to Lemma 5.9 in [41], we know that no subset of \(\mathcal{M}\) forms a cycle in \(\partial \mathcal{X}_{0}\). The definition of \(M_{\partial}\) implies that \(M_{\partial}\) is the maximum positive invariant set in \(\partial\mathcal{X}_{0}\), that is, \(\Phi_{t}(M_{\partial})\subset M_{\partial}\). Therefore, \(\bigcup_{(L(0),I(0))\in M_{\partial}}=P_{0}^{*}\).

For any solutions \((L(t), I(t))\) of model (3) with initial value \((L(0),I(0) )\in\mathcal{X}_{0}\), we further claim that

$$ \limsup_{t\rightarrow\infty}d \bigl(\Phi_{t} \bigl(L(0), I(0)\bigr), P_{0}^{*} \bigr)>\epsilon. $$
(4)

If it is not true, there exists \(t_{1}>0\), \(t_{1}\in N\), such that \(L(t)\leq \epsilon\), \(I(t)\leq\epsilon\) for all \(t\geq t_{1}\), \(t\in N\). Let \(H(t)=L(t)+I(t)\), then \(H(t)\leq2\epsilon\), \(t\geq t_{1}\), \(t\in N\), and we have

$$H(t+1)=\frac{p\beta(N^{*}-H(t))}{N^{*}}I(t)+pH(t)-pkmL(t)-p\gamma I(t). $$

Furthermore, we have

$$\begin{aligned} H(t+1) =&p\beta I(t)-\frac{p\beta H(t)I(t)}{N^{*}}+pH(t)-pkmL(t)-p\gamma I(t) \\ =&p\beta\bigl(H(t)-L(t)\bigr)-\frac{p\beta H(t)I(t)}{N^{*}}+pH(t)-pkmL(t)-p\gamma I(t) \\ \geq& p\beta H(t)-p\beta L(t)-\frac{p\beta H^{2}(t)}{N^{*}}+p(1-\gamma)H(t)-pkmL(t) \\ =& \biggl(p\beta+p(1-\gamma)-\frac{p\beta H(t)}{N^{*}} \biggr)H(t)-p(\beta+km)\epsilon \\ \geq& \biggl(p\beta+p(1-\gamma)-\frac{p\beta\epsilon}{N^{*}} \biggr)H(t)-p(\beta+km) \epsilon, \quad t\geq t_{1}. \end{aligned}$$

It is clear that the perturbed equation

$$H_{1}(t+1)= \biggl(p\beta+p(1-\gamma)-\frac{p\beta\epsilon}{N^{*}} \biggr)H_{1}(t)-p(\beta+km)\epsilon,\quad t\geq t_{1}, t\in N, $$

or

$$\begin{aligned} H_{1}(t) =& \bigl(-p(\beta+km)\epsilon \bigr)\frac{1- (p\beta +p(1-\gamma) -\frac{p\beta\epsilon}{N^{*}} )^{t-t_{1}}}{1- (p\beta+p(1-\gamma )-\frac{p\beta\epsilon}{N^{*}} )} \\ &{}+ \biggl(p\beta+p(1-\gamma)-\frac{p\beta\epsilon}{N^{*}} \biggr)^{t-t_{1}}H_{1}(t_{1}),\quad t\geq t_{1}, t\in N. \end{aligned}$$

\(R_{0}>1\) implies that \(p\beta+p(1-\gamma)>1\), namely, \(p\beta+p(1-\gamma )-\frac{p\beta\epsilon}{N^{*}}>1\) holds for a small \(\epsilon>0\). Therefore, \(H_{1}(t)\rightarrow\infty\) as \(t\rightarrow\infty\) and \(\epsilon\rightarrow0\). The comparison principle implies that \(H(t)\rightarrow\infty\) as \(t\rightarrow\infty\) and \(\epsilon\rightarrow0\). In fact, \(H(t)\leq2\epsilon\) for all \(t\geq t_{1}\), \(t\in N\), a contradiction. It implies that \(L(t)+I(t)\rightarrow\infty\), for all \(t\geq t_{1}\), \(t\in N\). On the other hand, \(0\leq L(t)\leq\epsilon\), \(0\leq I(t)\leq\epsilon\) for all \(t\geq t_{1}\), \(t\in N\). It implies that \(L(t)\rightarrow\infty\) and \(I(t)\rightarrow\infty\) at least established for all \(t\geq t_{1}\), \(t\in N\). There is a contradiction, that is, the conclusion in (4) holds.

Equation (4) implies that \(P^{*}_{0}\) is isolated in \(\mathcal {X}_{0}\), and \(W^{s}(P^{*}_{0})\cap\mathcal{X}_{0}=\emptyset\). In fact, \(P^{*}_{0}\) is also isolated in \(\partial\mathcal{X}_{0}\) because \(N^{*}\) is globally attractive in \(\partial\mathcal{X}_{0}\). Thus, \(P^{*}_{0}\) is isolated in \(\mathcal{X}\). From Theorem 1.3.1 and Remark 1.3.1 in [42], it follows that Φ is uniformly persistent with respect to \((\mathcal{X}_{0}, \partial\mathcal{X}_{0})\). Furthermore, Theorem 1.3.4 in [42] implies that the solutions of model (3) are uniformly persistent with respect to \((\mathcal{X}_{0}, \partial\mathcal{X}_{0})\) when \(R_{0}>1\). That is, there exists an \(\epsilon>0\), such that

$$\liminf_{t\rightarrow\infty}L(t)>\epsilon>0, \qquad \liminf _{t\rightarrow \infty}I(t)>\epsilon>0. $$

 □

4 The stability of the endemic equilibrium

Theorem 4.1

If \(R_{0}>1\), then the endemic equilibrium \(P_{1}^{*}\) of model (3) is locally asymptotically stable.

Proof

In the case where \(P^{*}=P_{1}^{*}\), we have

$$J\bigl(P^{*}_{1}\bigr)=\left ( \begin{array}{@{}c@{\quad}c@{}} -\frac{qp\beta}{N^{*}}I^{*}_{1}+p(1-\alpha)(1-m)+p(1-k)m & \frac{qp\beta }{N^{*}}(N^{*}-L_{1}^{*}-2I^{*}_{1}) \\ -\frac{(1-q)p\beta}{N^{*}}I^{*}_{1}+p\alpha(1-m) & \frac{(1-q)p\beta }{N^{*}}(N^{*}-L^{*}_{1}-2I^{*}_{1})+p(1-\gamma) \end{array} \right ). $$

We denote

$$\begin{aligned} g(\lambda) =&\lambda^{2}- \biggl(p(1-\alpha) (1-m)+p(1-k)m+p(1- \gamma)-\frac {qp\beta}{N^{*}}I^{*}_{1} \\ &{}+\frac{(1-q)p\beta}{N^{*}}\bigl(N^{*}-L^{*}_{1}-2I^{*}_{1}\bigr) \biggr)\lambda+ \bigl(p(1-\alpha) (1-m)+p(1-k)m \bigr)p(1-\gamma) \\ &{}+ \bigl(p(1-\alpha) (1-m)+p(1-k)m \bigr)\frac{(1-q)p\beta }{N^{*}} \bigl(N^{*}-L^{*}_{1}-2I^{*}_{1}\bigr) \\ &{}-p(1-\gamma)\frac{qp\beta}{N^{*}}I^{*}_{1}-p\alpha\frac{qp\beta }{N^{*}} \bigl(N^{*}-L^{*}_{1}-2I^{*}_{1}\bigr). \end{aligned}$$

By directly calculating, we obtain

$$\begin{aligned}& g(1)= R_{0}\frac{L^{*}_{1}+I^{*}_{1}}{N^{*}} \bigl(1-p(1-\alpha-k) \bigr) \bigl(1-p(1-\gamma) \bigr)>0, \\& g(-1)=2+2 \bigl(p(1-\alpha) (1-m)+p(1-k)m \bigr)-2(1-m)p\alpha\frac {L_{1}^{*}}{I_{1}^{*}} \\& \hphantom{g(-1)=}{}- \bigl(1+ \bigl(p(1-\alpha) (1-m)+p(1-k)m \bigr) (1-q)+p(1- \gamma )q \\& \hphantom{g(-1)=}{}-(1-m)p\alpha q \bigr)\frac{p\beta}{N^{*}}I^{*}_{1}, \\& g(0)=p(1-km)-p\alpha(1-m)- \bigl(p(1-km)-p\alpha(1-m) \bigr)\frac {(1-q)p\beta I^{*}_{1}}{N^{*}} \\& \hphantom{g(0)=}{}-p(1-\gamma)\frac{qp\beta I^{*}_{1}}{N^{*}}-(1-m)p\alpha\frac {L^{*}_{1}}{I^{*}_{1}}+(1-m)p \alpha\frac{qp\beta I^{*}_{1}}{N^{*}}. \end{aligned}$$

Rearranging the expression of \(g(-1)\), we have

$$g(-1)=\frac{a_{2}R^{2}_{0}+a_{1}R_{0}+a_{0}}{R_{0} (1-p(1-km)+p\alpha(1-m) ) (qp\beta+R_{0}(1-p(1-km)+p\alpha(1-m)) )}, $$

where

$$\begin{aligned}& a_{2}=2 \bigl(1+p(1-km)-p\alpha(1-m) \bigr) \bigl(1-p(1-km)+p \alpha(1-m) \bigr)^{2} \\& \hphantom{a_{2}=}{}- \bigl(1-p(1-km)+p\alpha(1-m) \bigr)^{2}p\beta \bigl(1+p\bigl(1-km-\alpha (1-m)\bigr) (1-q) \\& \hphantom{a_{2}=}{}+p(1-\gamma)q-(1-m)p\alpha q \bigr) \\& \hphantom{a_{2}}= \bigl(1-p(1-km)+p\alpha(1-m) \bigr)^{2}\bigl\{ 1-p \beta+1-p(1-\gamma)qp\beta \\& \hphantom{a_{2}=}{}+p \bigl((1-\alpha) (1-m)+(1-k)m \bigr) \bigl(2-(1-q)p\beta \bigr)+(1-m)p\alpha qp\beta\bigr\} >0, \\& a_{1}=2 \bigl(1+p(1-km)-p\alpha(1-m) \bigr) \bigl(1-p(1-km)+p \alpha(1-m) \bigr)qp\beta \\& \hphantom{a_{1}=}{}-2(1-m)p\alpha qp\beta \bigl(1-p(1-km)+p\alpha(1-m) \bigr) \\& \hphantom{a_{1}=}{}+ \bigl(1-p(1-km)+p\alpha(1-m) \bigr)^{2}p\beta \bigl(1+p\bigl(1-km-\alpha (1-m)\bigr) (1-q) \\& \hphantom{a_{1}=}{}+p(1-\gamma)q-(1-m)p\alpha q \bigr), \\& a_{0}=-2(1-m)p\alpha qp\beta\times qp\beta< 0. \end{aligned}$$

\(a_{2}>0\) implies that the quadratic function curve opens upward. \(a_{0}<0\) implies that the quadratic function equation has two real roots, which are positive and negative, respectively. Because of \(a_{2}+a_{1}>0\), we obtain \(-\frac{a_{1}}{2a_{2}}<\frac{1}{2}\), which implies that the axis of symmetry of the quadratic function curve is on the left of \(R_{0}=1\). In addition,

$$\begin{aligned} a_{2}R_{0}^{2}+a_{1}R_{0}+a_{0} =&2 \bigl(1-p(1-km)+p\alpha(1-m)+qp\beta \bigr)\bigl\{ \bigl(1+p(1-km) \\ &{}-p\alpha(1-m) \bigr) \bigl(1-p(1-km)+p\alpha (1-m) \bigr)-(1-m)p\alpha qp \beta\bigr\} \end{aligned}$$

with \(R_{0}=1\). Because of \(1-p(1-km)+p\alpha(1-m)>(1-m)p\alpha qp\beta\), and \(1+p(1-km)-p\alpha(1-m)=1+p(1-\alpha)(1-m)+p(1-k)m>1\), we obtain \(a_{2}R_{0}^{2}+a_{1}R_{0}+a_{0}>0\) as \(R_{0}=1\). Therefore, \(a_{2}R^{2}_{0}+a_{1}R_{0}+a_{0}>0\) as \(R_{0}>1\), that is, \(g(-1)>0\).

Similarly, we have

$$1-g(0)=\frac{b_{2}R^{2}_{0}+b_{1}R_{0}+b_{0}}{R_{0} (1-p(1-km)+p\alpha(1-m) ) (qp\beta+R_{0}(1-p(1-km)+p\alpha(1-m)) )}, $$

where

$$\begin{aligned}& b_{2}= \bigl(1-p(1-km)+p\alpha(1-m) \bigr)^{3}+ \bigl(1-p(1-km)+p\alpha(1-m) \bigr)^{2} \\& \hphantom{b_{2}=}{}\times \bigl(p\bigl(1-km-\alpha(1-m)\bigr) (1-q)+p(1- \gamma)q-(1-m)p\alpha q \bigr)p\beta \\& \hphantom{b_{2}}= \bigl(1-p(1-km)+p\alpha(1-m) \bigr)^{2}\bigl\{ 1-p(1-km) \bigl(1-p\beta(1-q) \bigr) \\& \hphantom{b_{2}=}{}+p\alpha(1-m) (1-p\beta)+p(1-\gamma)qp\beta\bigr\} >0, \\& b_{1}= \bigl(1-p(1-km)+p\alpha(1-m) \bigr)^{2}qp\beta+ \bigl(1-p(1-km)+p\alpha (1-m) \bigr) (1-m)p\alpha qp\beta \\& \hphantom{b_{1}=}{}- \bigl(1-p(1-km)+p\alpha(1-m) \bigr)^{2} \bigl(p \bigl(1-km-\alpha (1-m)\bigr) (1-q)+p(1-\gamma)q \\& \hphantom{b_{1}=}{}-(1-m)p\alpha q \bigr)p\beta, \\& b_{0}=(1-m)p\alpha qp\beta\times qp\beta>0. \end{aligned}$$

\(b_{2}>0\) implies that the quadratic function curve opens upward. \(b_{0}>0\) implies that the quadratic function equation has roots which are of the same sign. Because of \(b_{2}+b_{1}>0\), we obtain \(-\frac{b_{1}}{2b_{2}}<\frac{1}{2}\), which implies that the axis of symmetry of the quadratic function curve is on the left of \(R_{0}=1\). In addition, \(b_{2}R_{0}^{2}+b_{1}R_{0}+b_{0}>0\) as \(R_{0}=1\). Therefore, we obtain \(b_{2}R^{2}_{0}+b_{1}R_{0}+b_{0}>0\) as \(R_{0}>1\), that is, \(g(0)<1\). The Jury criterion implies that the endemic equilibrium \(P_{1}^{*}\) is locally stable as \(R_{0}>1\). □

The global stability of the endemic equilibrium of (3) is very difficult, though Theorems 3.2 and 4.1 established the persistence and local stability as \(R_{0}>1\). We investigate the global stability of the endemic equilibrium by numerical simulations. Taking \(\Lambda=10\), \(p=0.994\), \(q=0.95\), \(\beta=0.7\), \(\alpha=0.003\), \(m=0.001\), \(k=0.001\), and \(\gamma=0.2\), we obtain \(R_{0}=1.2363>1\). In this case, the numerical simulation shows that the endemic equilibrium \(P_{1}^{*}=(313.3017, 5.2621)\) may be globally asymptotically stable. The solution curves of the latently infected individuals \(L(t)\) and the infectious individuals \(I(t)\) are given in Figure 2(a) and (b), respectively. The initial values at \(t=0\) are \((310,5)\), \((313,5.3)\), and \((325,5.5)\), respectively. We observe that solutions with positive initial values will converge to the endemic equilibrium \(P_{1}^{*}\).

Figure 2
figure 2

The global stability of the endemic equilibrium \(\pmb{P_{1}^{*}}\) of ( 3 ) as \(\pmb{R_{0}>1}\) .

Full size image

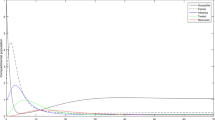
We always assume that the parameter obeys \(0<\beta<1\) in theoretical discussions so as to guarantee the positivity of the solution of (3). In fact, if \(\beta>1\), and β is not large enough, the numerical simulation shows that solutions of (3) are still positive, and the endemic equilibrium \(P_{1}^{*}\) may lose the global stability and there exists chaos as β increases, which can lead to increasing \(R_{0}\) (see Figure 3). In Figure 3, we fix \(\Lambda=10\), \(p=0.994\), \(q=0.01\), \(\alpha=0.001\), \(m=0.01\), \(k=0.1\), \(\gamma=0.8\), and \(\beta\in[0.01, 6.00)\), furthermore, \(0< R_{0}<7.3701\). Figure 3 illustrates that one only has a disease-free equilibrium as \(R_{0}<1\), and an endemic equilibrium exists as \(1< R_{0}<6\). In addition, the endemic equilibrium loses the global stability as \(R_{0}>6\), and exhibits chaotic behavior.

Figure 3
figure 3

The chaos when endemic equilibrium \(\pmb{P_{1}^{*}}\) loses the global stability.

Full size image

5 Effect of control strategies

In our model, we consider the direct progression to active TB once one is infected, and both treatment of latently infected individuals and infectious individuals. By directly calculating, we obtain

$$ \begin{aligned} &\frac{\partial R_{0}}{\partial k}=- \frac{pm\times(1-m)p\alpha\times qp\beta}{ (1-p(1-km)+p\alpha(1-m) )^{2} (1-p(1-\gamma) )}< 0, \\ &\frac{\partial R_{0}}{\partial m}=-\frac{p\alpha\times qp\beta (1-p(1-k) )}{ (1-p(1-km)+p\alpha(1-m) )^{2} (1-p(1-\gamma) )}< 0. \end{aligned} $$
(5)

The two equations of (5) illustrate that the basic reproductive number \(R_{0}\) decreases as the proportion of m and the probability k of successful detection and effective treatment of latently infected individuals. The treatment of latent tuberculosis infection contributes to slowing down TB transmission because it substantially reduces the risk that TB infection will progress to TB disease. Therefore, we consider both treatment of the latently infected individuals and for the infectious individuals. We assume that the word ‘control’ would mean bringing down the number of infectious TB cases.

To see the effect of these interventions, we need to consider the basic reproduction number of the model without treatment of the latent and infectious individuals. This is given by

$$R_{1}=\frac{p\alpha\times qp\beta}{(1-p(1-\alpha))(1-p)}+\frac{(1-q)p\beta}{1-p}. $$

\(R_{1}<1\) implies that TB will die out without any treatment. In fact, \(R_{1}>1\) is the usual case for the current TB epidemic in many countries. Taking China as an example, large scale national sampling surveys of TB epidemiology were carried out in 1979, 1984/85, 2000, and 2010, respectively. The 1979 and 2000 national surveys were more comprehensive and more information was obtained. The tuberculin skin test was done in those two sampling surveys. The result of those two surveys show that PPD (purified protein derivative) positive rates in 1979 and 2000 are 27.9% and 44.5%, respectively [43]. The 2010 national TB epidemiological survey shows that the prevalence of active TB cases in the population 15 years of age and older is 459 cases per 100,000, a little lower than the 466 cases per 100,000 in 2000. The estimated active TB prevalence in the Chinese population in 2010 is 392 cases per 100,000, a little higher than the 367 cases per 100,000 found in 2000 [44]. This information indicates that TB infection remains a serious public health challenge in China.

In China, the population recruitment mainly depends on births. Therefore, we use the average natural death from 2000-2009 as the natural death rate, namely, \(p=0.994\). It is estimated that about 5%-10% of latent TB infection will progress to TB disease [45]. We assume that the lifespan of the population is 75, then the age of the infected individual may be from 1 year old to 75 years old. The individuals may survive 1 year, 2 years, …, or 75 years after becoming TB latent. We choose the average survival time to be \(\frac{75}{2}\approx38\). The estimate of the annual progression rate from latent to infectious is \(\alpha\in[\frac{0.05}{38}, \frac{0.1}{38}]=[0.00132, 0.00263]\). We take \(q=0.99\), and \(\beta\in[0.1, 0.6]\) [46]. The numerical calculation shows that \(R_{1}>1\) (see Figure 4). In short, we always assume that \(R_{1}>1\) in this section.

Figure 4
figure 4

The basic reproductive number \(\pmb{R_{1}}\) .

Full size image

In addition, as \(m\rightarrow0\), the system (3) reduces to a model in which there is no treatment of latent TB individuals. In this case, every TB infected individual leaves the latent compartment only by the natural progression and the reproductive number becomes

$$\lim_{m\rightarrow0}R_{0}=\frac{p\alpha\times qp\beta}{ (1-p(1-\alpha ) )(1-p(1-\gamma))}+ \frac{(1-q)p\beta}{1-p(1-\gamma)}:=R_{2}. $$

We first consider the effect of both treatment of latently infected individuals and for infectious individuals on control TB transmission. The difference between \(R_{1}\) and \(R_{0}\) is

$$\begin{aligned} \Delta_{1} =&R_{1}-R_{0} \\ =&\frac{m (1-p(1-k) )p\alpha qp\beta+p\gamma (1-p(1-km)+p\alpha(1-m) )p\alpha qp\beta}{ (1-p(1-\alpha) )(1-p) (1-p(1-km)+p\alpha(1-m) ) (1-p(1-\gamma) )} \\ &{}+\frac{p\gamma(1-q)p\beta}{(1-p) (1-p(1-\gamma ) )}. \end{aligned}$$

It easy to see that \(\Delta_{1}>0\). It implies that both the treatment of latently infected individuals and for infectious individuals can lead to a decrease of the basic reproductive number. That is, treatment is effective at the population level so as to slow down the spread of TB, while having treatment of the individuals in the latent and the infectious compartment.

5.1 Effect of treatment of the infectious individuals

Because the latently TB infected individuals cannot infect others, one does not take to treatment of latently infected individuals in developing and undeveloped countries so as to save expense. Therefore, we only consider treatment of the TB infectious individuals. We will give the critical value \(\gamma^{*}\) of the probability γ of successful detection and treatment of infectious individuals so that the basic reproductive number of the model is less than one.

When \(m=0\) and \(\gamma>0\) (with only treatment for the infectious individuals), the basic reproductive number is \(R_{2}\). With the application of only treatment of the population in the infectious compartment, we can obtain the difference between \(R_{1}\) and \(R_{2}\):

$$ \Delta_{2}=R_{1}-R_{2}= \frac{p\gamma}{(1-p)(1-p(1-\gamma))} \biggl(\frac{p\alpha \times qp\beta}{1-p(1-\alpha)}+(1-q)p\beta \biggr)>0. $$
(6)

\(\Delta_{2}>0\) implies that the treatment is effective at the population level so as to slow down the spread of TB, while having treatment of the individuals in the infectious compartment.

Using (6), we can calculate the critical values \(\gamma^{*}\) of the disease control parameters γ to have \(R_{2}<1\). Namely,

$$ R_{1}-\frac{p\gamma}{(1-p)(1-p(1-\gamma))} \biggl(\frac{p\alpha\times qp\beta }{1-p(1-\alpha)}+(1-q)p \beta \biggr)< 1. $$
(7)

Rearranging (7), we can obtain

$$ \gamma>\gamma^{*}:=\frac{ (1-p(1-\alpha) )(1-p)^{2}(R_{1}-1)}{p(1-p) (1-p(1-\alpha) )}=\biggl(\frac{1}{p}-1 \biggr) (R_{1}-1). $$
(8)

Equation (8) shows that the basic reproductive number \(R_{2}<1\), while the successful detection and effective treatment probability γ of infectious individuals is more than \(\gamma^{*}\). However, \(\gamma<\gamma^{*}\) will lead to \(R_{2}>1\), which implies that successful detection and effective treatment of infectious individuals is not enough, TB transmission will be in persistence. Therefore, we should strengthen the successful detection and effective treatment of infectious individuals so as to eradicate TB transmission in the population. Taking the same parameter values in Figure 4, the function of the basic reproductive number, \(R_{2}\), is shown in Figure 5 with \(m=0\) and for \(\gamma=0.05\), \(\gamma=0.1\), and \(\gamma=0.2\), respectively.

Figure 5
figure 5

The basic reproductive number \(\pmb{R_{2}}\) .

Full size image

5.2 Effect of treatment of the latent individuals

When the probability γ of successful detection and treatment of infectious individuals does not reach the critical value \(\gamma^{*}\), we also take the treatment of latently TB individuals, and give the critical value \(m^{*}\) of the probability m of the treatment of latently individuals, so that \(R_{0}<1\).

In this case, we assume that \(\gamma<\gamma^{*}\), or \(R_{2}>1\). Similarly, we can obtain the difference between \(R_{2}\) and \(R_{0}\):

$$ \Delta_{3}=R_{2}-R_{0}= \frac{m (1-p(1-k) )p\alpha qp\beta}{ (1-p(1-\alpha) ) (1-p(1-km)+p\alpha(1-m) ) (1-p(1-\gamma ) )}>0. $$
(9)

\(\Delta_{3}>0\) implies that the treatment is effective at the population level so as to slow down the spread of the disease, while having treatment of the individuals in the latent and the infectious compartment.

Using (9), we can calculate the critical values \(m^{*}\) of the disease control parameters m to have \(R_{0}<1\). Namely,

$$ R_{2}-\frac{m (1-p(1-k) )p\alpha qp\beta}{ (1-p(1-\alpha) ) (1-p(1-km)+p\alpha(1-m) ) (1-p(1-\gamma) )}< 1. $$
(10)

Rearranging (10), we can obtain

$$ m>m^{*}:=\frac{p\alpha qp\beta+ (1-p(1-\alpha) ) ((1-q)p\beta -(1-p(1-\gamma)) )}{ p\alpha qp\beta+ (p(1-k)-p(1-\alpha) ) ((1-q)p\beta -(1-p(1-\gamma)) )}. $$
(11)

Because of \(R_{2}>1\), we obtain \(p\alpha qp\beta> (1-p(1-\alpha) ) (1-p(1-\gamma)-(1-q)p\beta )\). It is clear that \((1-p(1-\alpha) ) (1-p(1-\gamma)-(1-q)p\beta )> (p(1-k)-p(1-\alpha) ) ((1-q)p\beta-(1-p(1-\gamma)) )\), which implies \(m^{*}>0\). By (11), we know that if the effective treatment of the individuals in the infectious compartment satisfies \(0<\gamma<\gamma^{*}\), we should strengthen control measures so as to have \(R_{0}<1\). Therefore, we also take the treatment of latent TB individuals, and the probability for receiving the treatment m satisfies \(m>m^{*}\).

Taking the same parameter values in Figure 4, by calculating, we can obtain \(\gamma^{*}=(\frac{1}{p}-1) (R_{1}-1 )\in[0.0127, 0.1798]\), furthermore, we fix \(\gamma=0.01\), satisfying \(0<\gamma<\gamma^{*}\). In addition, taking \(k=0.9\), we use the same parameter values to obtain \(m^{*}\in[0.0015, 0.1391]\). The numerical method shows that \(R_{0}\) with \(\gamma=0.01\) and \(k=0.9\) for \(m=0.001\), \(m=0.01\), \(m=0.1\), and \(m=0.2\), respectively (see Figure 6). Figure 6 shows that, in the case where \(\gamma<\gamma^{*}\), we can control the probability \(m>m^{*}\) of the treatment of latent individuals, so that \(R_{0}<1\).

Figure 6
figure 6

The basic reproductive number \(\pmb{R_{0}}\) with different m .

Full size image

6 Conclusion and discussion

In this paper, we analyze a class of discrete SLIS models with direct progression and chemoprophylaxis for latent TB individuals. The basic reproductive numbers \(R_{0}\) with both treatment of latently infected individuals and infectious individuals are determined. Furthermore, we study the global stability of the disease-free equilibrium as \(R_{0}<1\), the persistence of the system, and the local stability of the endemic equilibrium as \(R_{0}>1\). The numerical simulation shows that when \(\beta>1\), and β is not large enough, the solutions of the model are still positive, and the endemic equilibrium may lose the stability and there exists chaos as β increases, which can lead to \(R_{0}\) increasing. By analyzing \(R_{0}\), we learn that the treatment of latent TB individuals contributes to a decrease of the basic reproductive number, namely, a reduction of the speed of TB transmission.

In addition, the basic reproductive number \(R_{1}\) without treatment, and the basic reproductive number \(R_{2}\) with treatment of infectious individuals are determined, respectively. We also discuss the effect of the treatment of the infectious individuals on TB transmission, and give the critical value \(\gamma^{*}\) of the probability γ of successful detection and treatment of infectious individuals so that the basic reproductive number of the model is \(R_{2}<1\). Once \(R_{2}>1\), that is, \(\gamma<\gamma^{*}\), we need to strengthen control measures so as to slow down the TB transmission. In this situation, we take both the treatment of latently infected individuals and infectious individuals, and give the critical value \(m^{*}\) of probability m of the treatment of latently infected individuals so that the basic reproductive number of the model obeys \(R_{0}<1\).

By using the TB data in China, we compare the effect of these different treatment strategies for the control of TB. The numerical simulations totally support our theoretical results. Moreover, our conclusions show that, if the probability γ of successful detection and treatment of infectious individuals cannot reach the critical value \(\gamma^{*}\), only treatment of infectious individuals cannot effectively control the TB transmission, which implies that we should strengthen control measures so as to slow down the TB transmission. That is, we should take both the treatment of latently infected individuals and of infectious individuals.