$H_{\infty}$ Fuzzy filtering for nonlinear singular systems with time-varying delay

Abstract

This paper considers the $H_{\infty}$ fuzzy filtering problem for continuous-time nonlinear singular systems with time-varying delay through the T-S fuzzy model approach. Firstly, by combining a reciprocally convex combination lemma and the fuzzy Lyapunov-Krasovskii function method, a new bounded real lemma (BRL) is proposed such that the resultant closed-loop systems are admissible and satisfy the prescribed $H_{\infty}$ disturbance attenuation. Then, by using the matrix decoupling technique, we translate the BRL into another form, which separates the coefficient matrices of systems and Lyapunov matrices. On the basis of such a new form of BRL, the fuzzy filter design problem is solved by checking the feasibility of a series of linear matrix inequalities (LMIs), and the filter gains can also be provided explicitly. Numerical examples are presented to show the reduction of the conservativeness compared to some published results in the literature.

1 Introduction

Nowadays, various approaches have been proposed for the filter design, such as Kalman filter design [1, 2], $H_{\infty}$ filter design [3–6] and so on. Kalman filter is based on the assumption that the systems are exactly known and their disturbances are stationary Gaussian noises with known statistics, while $H_{\infty}$ filter can determine an asymptotically stable filter without a certain signal model [7]. Because in practice the statistical information is often incomplete, more and more researchers pay attention to the $H_{\infty}$ filter design problem, and the problem of $H_{\infty}$ filtering has been investigated for a wide range of systems such as time-delay systems [8, 9], uncertain systems [10, 11], fuzzy systems [12, 13] and singular systems [14–16].

It is well known that Takagi-Sugeno (T-S) fuzzy model [17, 18] is an effective way to approximate complex nonlinear systems. For the past two decades, a large number of results on fuzzy systems have been published. For example, a new fuzzy observer-based $H_{\infty}$ controller design scheme was given in [19], and the fuzzy filter design was considered in [4] by using Lyapunov function methods. Besides, since the time-delay phenomenon is always the cause of instability and poor performance, the main methods to study the time-delay systems are the Lyapunov Razumikhin function methods and Lyapunov-Krasovskii functional [20, 21]. As pointed out in [22], the Lyapunov-Razumikhin approach does not impose restrictions on the derivative of the time delay and is a powerful tool for systems, specially when the time-varying delay is nondifferentiable or uncertain. Recently, the study of time-delay systems by the Lyapunov-Razumikhin approach has received much attention [23, 24]. However, the Lyapunov-Razumikhin approach may lead to conservative results [22, 25]; as a result, more and more researchers are devoted to the Lyapunov-Krasovskii approach [26, 27]. Recently, by using the T-S fuzzy model approach, [7] considered the $H_{\infty}$ filter design for nonlinear systems with time-varying delay where the free-weighting matrix method and matrix decoupling method are utilized. On the other hand, singular systems which are also referred to as descriptor systems, generalized state-space systems and differential algebraic systems, can describe physical systems better than normal state-space systems, and they have more extensive applications in electrical circuits, power systems, robots and other areas [28, 29]. Although plentiful results have been reported on the $H_{\infty}$ filter design problems for nonlinear systems with time-varying delay [4, 7, 12], few reports have been published with respect to the $H_{\infty}$ filter design problems for nonlinear singular systems with time-varying delay [30]. As far as we know, the $H_{\infty}$ filter design problems for nonlinear singular systems with time-varying delay have not been investigated sufficiently, which leaves a room for us to improve.

In this paper, the main aim is the fuzzy filter design for the nonlinear singular delayed systems such that the corresponding filter error systems are admissible with the prescribed $H_{\infty}$ attenuation level. Based on a fuzzy Lyapunov-Krasovskii functional (LKF), and by virtue of a reciprocally convex combination lemma, a new BRL is presented for the nonlinear singular delayed systems, and another form of such BRL is derived by using the matrix decoupling technique. With the aid of such a new form of BRL, through selecting the special structure of certain matrices, the fuzzy filter design problems can be tackled by solving a set of LMIs. Finally, two examples are provided to illustrate the effectiveness of the proposed fuzzy filter design method.

This paper is organized as follows. The preliminaries and problem formulation are presented in Section 2. In Section 3, the $H_{\infty}$ filter design method is presented based on the T-S fuzzy model. In Section 4, two numerical examples are presented to show the improvement. Finally, this paper is concluded in Section 5.

The notation used in this paper is standard. The superscript ‘T’ stands for matrix transposition, $\Re^{n}$ denotes the n-dimensional Euclidean space. $L_{2}[0,\infty)$ is the space of square integrable vector-valued function over $[0,\infty)$. The notation $\|\cdot\|$ refers to the Euclidean vector norm. In addition, in symmetric block matrices or long matrix expressions, star ∗ is used as an ellipsis for the terms that are introduced by symmetry and $\operatorname{diag}\{\cdot\}$ stands for a block-diagonal matrix. Matrices, if their dimensions are not explicitly stated, are assumed to be compatible for algebraic operation.

2 Preliminaries and problem formulation

Consider a nonlinear singular system with time-varying delay that could be approximated by a time-delay T-S fuzzy singular model with r plant rules.

Plant rule i: IF $\theta_{1}(x)$ is $M_{i1}$, $\theta_{2}(x)$ is $M_{i2}$ and ⋯ and $\theta_{l}(x)$ is $M_{il}$ THEN

$$ \begin{aligned} &E\dot{x}(t)= A_{i}x(t)+A_{di}x \bigl(t-d(t)\bigr)+B_{i}w(t), \\ &y(t)= C_{i}x(t)+C_{di}x\bigl(t-d(t)\bigr)+D_{i}w(t), \\ &z(t)= F_{i}x(t)+F_{di}x\bigl(t-d(t)\bigr), \\ &x(t)= \phi(t), \quad t\in [-d_{M}, 0 ], \end{aligned} $$

(1)

where $x(t) \in\Re^{n}$, $w(t) \in\Re^{m}$, $y(t) \in\Re^{p}$ and $z(t) \in\Re^{q}$ are respectively the state vector, the disturbance vector which belongs to $L_{2}[0,\infty)$, the measurable output vector and the controlled output vector. E, $A_{i}$, $A_{di}$, $B_{i}$, $C_{i}$, $C_{di}$, $D_{i}$, $F_{i}$ and $F_{di}$ are constant matrices with compatible dimensions, and we assume $\operatorname{rank} E=r_{E}\le n$. $\phi (t)$ is a continuous vector-valued initial function defined on $[-d_{M}, 0 ]$. The time-varying delay $d(t)$ is supposed to be continuously differential and satisfies

$$ d_{m}\le d(t)\le d_{M}, \qquad \dot{d}(t)\le \mu, $$

(2)

where $d_{m}>0$, $d_{M}>0$ and $1>\mu>0$ are scalars.

$\theta_{j}(x)$ and $M_{ij}$ ($i=1,\ldots,r$, $j=1,\ldots,l$) are the premise variables and the fuzzy sets; moreover, for simplicity, the premise variables are supposed to be dependent on state vector only.

By fuzzy blending, the overall fuzzy model is inferred as follows:

$$ \begin{aligned} &E\dot{x}(t)= \sum _{i=1}^{r}h_{i}\bigl(\theta(x)\bigr) \bigl[A_{i}x(t)+A_{di}x\bigl(t-d(t)\bigr)+B_{i}w(t) \bigr], \\ &y(t)= \sum_{i=1}^{r}h_{i}\bigl( \theta(x)\bigr) \bigl[C_{i}x(t)+C_{di}x\bigl(t-d(t) \bigr)+D_{i}w(t) \bigr], \\ &z(t)= \sum_{i=1}^{r}h_{i}\bigl( \theta(x)\bigr) \bigl[F_{i}x(t)+F_{di}x\bigl(t-d(t)\bigr) \bigr], \\ &x(t)= \phi(t), \quad t\in [-d_{M}, 0 ], \end{aligned} $$

(3)

where $\theta(x)=[\theta_{1}(x), \ldots, \theta_{l}(x)]$, $h_{i}(\theta (x))=\omega_{i}(\theta(x))/\sum_{i=1}^{r} \omega_{i}(\theta(x))$, $\omega _{i}(\theta(x))= \prod_{j=1}^{l} M_{ij}(\theta_{j}(x))$, with $M_{ij}(\theta _{j}(x))$ being the grade of membership of $\theta_{j}(x)$ in $M_{ij}$ and $\omega_{i} : \Re^{l}\rightarrow[0,1]$ denoting the membership function corresponding to plant rule i. It is obvious that the fuzzy weighting functions $h_{i}(\theta(x))$ satisfy

$$ h_{i}\bigl(\theta(x)\bigr)\ge0,\quad \sum _{i=1}^{r} h_{i}\bigl(\theta(x)\bigr)=1. $$

(4)

Based on the parallel distributed compensation (PDC), we consider the fuzzy filter in the following form:

$$ \begin{aligned} &E\dot{x}_{f}(t)= \sum _{i=1}^{r}h_{i}\bigl(\theta(x) \bigr) \bigl[A_{fi}x_{f}(t)+B_{fi}y(t) \bigr], \qquad x_{f}(0)= x_{f0}, \\ &z_{f}(t)= \sum_{i=1}^{r}h_{i} \bigl(\theta(x)\bigr)F_{fi}x_{f}(t), \end{aligned} $$

(5)

where $x_{f}(t)\in\Re^{n}$ and $z_{f}(t)\in\Re^{q}$ are the state vector and the controlled output vector of the filter, respectively. $E_{f}$, $A_{fi}$, $B_{fi}$ and $F_{fi}$, $i=1,2,\ldots,r$, are filter parameters to be determined.

Define

$$\eta(t)=\bigl[x^{T}(t), x_{f}^{T}(t) \bigr]^{T},\qquad e(t)=z(t)-z_{f}(t), $$

it follows from system (3) and filter (5) that we can obtain the following filter error system:

$$ \begin{aligned} &\tilde{E}\dot{\eta}(t)= \tilde{A}(h) \eta(t)+\tilde {A}_{d}(h)\eta\bigl(t-d(t)\bigr)+\tilde{B}(h)w(t), \\ &e(t)= \tilde{F}(h)\eta(t)+\tilde{F}_{d}(h)\eta\bigl(t-d(t)\bigr), \end{aligned} $$

(6)

where $\eta(t)=[\phi^{T}(t), x_{f0}^{T}]^{T}$ for $t\in[-d_{M}, 0]$ and

$$\begin{aligned}& \tilde{E}= \begin{bmatrix} E&0\\ 0&E \end{bmatrix}, \\& \begin{aligned}[b] \tilde{A}(h)&=\sum_{i=1}^{r} \sum_{j=1}^{r}h_{i}\bigl(\theta (x)\bigr)h_{j}\bigl(\theta(x)\bigr) \begin{bmatrix} A_{j}&0\\ B_{fi}C_{j}&A_{fi} \end{bmatrix} \\ &=\sum_{i=1}^{r}\sum _{j=1}^{r}h_{i}\bigl(\theta(x) \bigr)h_{j}\bigl(\theta(x)\bigr)\tilde{A}_{ij}= \begin{bmatrix} A(h)&0\\ B_{f}(h)C(h)&A_{f}(h) \end{bmatrix}, \end{aligned} \\& \begin{aligned}[b] \tilde{A}_{d}(h)&=\sum _{i=1}^{r}\sum_{j=1}^{r}h_{i} \bigl(\theta (x)\bigr)h_{j}\bigl(\theta(x)\bigr) \begin{bmatrix} A_{dj}&0\\ B_{fi}C_{dj}&0 \end{bmatrix} \\ &=\sum_{i=1}^{r}\sum _{j=1}^{r}h_{i}\bigl(\theta(x) \bigr)h_{j}\bigl(\theta(x)\bigr)\tilde{A}_{dij}= \begin{bmatrix} A_{d}(h)&0\\ B_{f}(h)C_{d}(h)&0 \end{bmatrix}, \end{aligned} \\& \begin{aligned}[b] \tilde{B}(h)&=\sum_{i=1}^{r} \sum_{j=1}^{r}h_{i}\bigl(\theta (x)\bigr)h_{j}\bigl(\theta(x)\bigr) \begin{bmatrix} B_{j}\\ B_{fi}D_{j} \end{bmatrix} \\ &=\sum_{i=1}^{r}\sum _{j=1}^{r}h_{i}\bigl(\theta(x) \bigr)h_{j}\bigl(\theta(x)\bigr)\tilde{B}_{ij}= \begin{bmatrix} B(h)\\ B_{f}(h)D(h) \end{bmatrix}, \end{aligned} \\& \begin{aligned}[b] \tilde{F}(h)&=\sum_{i=1}^{r} \sum_{j=1}^{r}h_{i}\bigl(\theta (x)\bigr)h_{j}\bigl(\theta(x)\bigr) [ F_{j}\quad {-}F_{fi} ] \\ &=\sum_{i=1}^{r}\sum _{j=1}^{r}h_{i}\bigl(\theta(x) \bigr)h_{j}\bigl(\theta(x)\bigr)\tilde{F}_{ij}= \bigl[ F(h) \quad F_{f}(h) \bigr], \end{aligned} \\& \tilde{F}_{d}(h)=\sum_{j=1}^{r}h_{j} \bigl(\theta(x)\bigr) [ F_{dj}\quad 0 ]=\sum _{i=j}^{r}h_{j}\bigl(\theta(x)\bigr) \tilde{F}_{dj}= \bigl[ F_{d}(h)\quad 0 \bigr]. \end{aligned}$$

The filter design problem to be addressed here can be formulated as follows: for the fuzzy singular system (3) with time-varying delay (2) and a prescribed $H_{\infty}$ bound $\gamma>0$, design a filter in the form of (5) such that the filter error system (6) with $w(t)=0$ is admissible and under the zero initial condition

$$ \int_{0}^{\infty}e^{T}(t)e(t)\,dt< \gamma^{2}\int_{0}^{\infty}w^{T}(t)w(t)\,dt $$

(7)

holds for all $w(t)\neq0$ and $w(t)\in L_{2}[0,\infty)$.

Lemma 1

[31] (Jensen inequality lemma)

For any constant matrix $M\in\Re^{m\times m}$, $M=M^{T}>0$, scalar $\gamma>0$, vector function $\omega : [0, \gamma ]\rightarrow\Re^{m}$ such that the integrations in the following are well defined, then

$$ \gamma\int_{0}^{\gamma}\omega^{T}(t)M \omega(t)\,dt\ge \biggl(\int_{0}^{\gamma}\omega(t)\,dt \biggr)^{T}M \biggl(\int_{0}^{\gamma}\omega(t)\,dt \biggr). $$

(8)

Lemma 2

[32] (Reciprocally convex combination lemma)

Let $f_{1},f_{2},\ldots,f_{N}:\Re^{m}\to\Re$ have positive values in an open subset D of $\Re^{m}$. Then the reciprocally convex combination of $f_{i}$ over D satisfies

$$ \min_{\{\alpha_{i}|\alpha_{i}>0,\sum_{i} a_{i} = 1 \}} \sum_{i} \frac{1}{\alpha_{i}}f_{i}(t)=\sum_{i}f_{i}(t)+ \max_{g_{i,j}(t)}\sum_{i\ne j}g_{i,j}(t) $$

(9)

subject to

$$ \Biggl\{ g_{i,j}:R^{m} \to R, g_{j,i}(t) \equiv g_{i,j}(t), \begin{bmatrix} f_{i}(t)&g_{i,j}(t)\\ g_{i,j}(t)&f_{j}(t) \end{bmatrix} \ge0\Biggr\} . $$

(10)

3 Main results

In this section, initially, we present a novel bounded real lemma for fuzzy singular system (6) with time-varying delay (2), which focuses on tackling the time-varying delay by virtue of the reciprocally convex combination method and fuzzy Lyapunov-Krasovskii function method, then another form of the proposed bounded real lemma is derived by using the matrix decoupling technique. Moreover, based on the equivalent form of the BRL, the filter design problem is solved and the filter parameters are provided.

3.1 Bounded real lemma

Theorem 1

For given scalars $0\le d_{m}< d_{M}$, $\mu<1$, the filter error system (6) is admissible with $H_{\infty}$ performance index γ if there exists a set of positive definite matrices $\tilde{P}$, $\tilde{Q}_{1}(h)$, $\tilde{Q}_{2}(h)$, $\tilde{Q}_{3}(h)$, $\tilde{R}_{1}(h)$, $\tilde{R}_{2}(h)$, matrix $\tilde{Q}$, and matrix $\tilde{S}(h)$ which satisfies $\bigl [ {\scriptsize\begin{matrix}{\tilde{R}_{2}(h)}&{\tilde{S}(h)}\cr {\tilde{S}^{T}(h)}&{\tilde{R}_{2}(h)} \end{matrix}} \bigr ]\ge 0$, such that the following linear matrix inequalities are satisfied:

$$ \Omega(h)= \begin{bmatrix} \Xi(h)&\Gamma_{1}(h)&\Gamma_{2}(h)&\Gamma_{3}(h)\\ {*}&-\tilde{R}_{1}(h)&0&0\\ {*}&*&-\tilde{R}_{2}(h)&0\\ {*}&*&*&-I \end{bmatrix}< 0, $$

(11)

where

$$\begin{aligned}& \Gamma_{1}(h)= \begin{bmatrix} d_{m}\tilde{A}^{T}(h)\tilde{R}_{1}(h)\\ d_{m}\tilde{A}_{d}^{T}(h)\tilde{R}_{1}(h)\\ 0\\ 0\\ d_{m}\tilde{B}_{w}^{T}(h)\tilde {R}_{1}(h) \end{bmatrix},\qquad \Gamma_{2}(h)= \begin{bmatrix} d\tilde{A}^{T}(h)\tilde{R}_{2}(h)\\ d\tilde{A}_{d}^{T}(h)\tilde{R}_{2}(h)\\ 0\\ 0\\ d\tilde{B}_{w}^{T}(h)\tilde {R}_{2}(h) \end{bmatrix}, \\& \Xi(h)= \begin{bmatrix} \Omega_{11}&\Omega_{12}&\Omega_{13}&0&\Omega_{15}\\ {*}&\Omega_{22}&\Omega_{23}&\Omega_{24}&0\\ {*}&*&\Omega_{33}&\Omega_{34}&0\\ {*}&*&*&\Omega_{44}&0\\ {*}&*&*&*&-\gamma^{2}I \end{bmatrix},\qquad \Gamma_{3}(h)= \begin{bmatrix} \tilde{F}^{T}(h)\\ \tilde{F}_{d}^{T}(h)\\ 0\\ 0\\ 0 \end{bmatrix}, \end{aligned}$$

where $d=d_{M}-d_{m}$, full column rank matrix $\tilde{U}$ satisfies $\tilde {E}^{T}\tilde{U}=0$ and

$$\begin{aligned}& \Omega_{11}=\tilde{A}^{T}(h) (\tilde {P}\tilde{E}+\tilde{U} \tilde{Q})+(\tilde{P}\tilde{E}+\tilde{U}\tilde {Q})^{T}\tilde{A}(h)+ \tilde{Q}_{1}(h)+\tilde{Q}_{2}(h)+\tilde{Q}_{3}(h) -\tilde{E}^{T}\tilde{R}_{1}(t)\tilde{E}, \\& \Omega_{12}=(\tilde{P}\tilde{E}+\tilde{U}\tilde{Q})^{T} \tilde {A}_{d}(h), \\& \Omega_{13}=\tilde{E}^{T}\tilde{R}_{1}(h) \tilde{E}, \\& \Omega_{15}=(\tilde{P}\tilde{E}+\tilde{U}\tilde{Q})^{T} \tilde{B}(h), \\& \Omega_{22}=-(1-\mu)\tilde{Q}_{3}(h)-2\tilde {E}^{T}\tilde{R}_{2}(h)\tilde{E}+\tilde{E}^{T} \tilde {S}(h)\tilde{E}+\tilde{E}^{T}\tilde{S}^{T}(h)\tilde{E}, \\& \Omega_{23}=\tilde{E}^{T}\tilde{R}_{2}(h)\tilde {E}-\tilde{E}^{T}\tilde{S}^{T}(h)\tilde{E}, \\& \Omega_{24}=\tilde{E}^{T}\tilde{R}_{2}(h)\tilde {E}-\tilde{E}^{T}\tilde{S}(h)\tilde{E}, \\& \Omega_{33}=-\tilde{Q}_{1}(h)-\tilde{E}^{T}\tilde {R}_{1}(h)\tilde{E}-\tilde{E}^{T}\tilde{R}_{2}(h) \tilde{E}, \\& \Omega_{34}=\tilde{E}^{T}\tilde{S}^{T}(h) \tilde{E}, \\& \Omega_{44}=-\tilde{Q}_{2}(h)-\tilde{E}^{T}\tilde {R}_{2}(h)\tilde{E}. \end{aligned}$$

Proof

The regularity and non-impulsiveness of the filter error system (6) can be proved by a similar way as in [29], thus the details are omitted here.

Next, let us consider the stability of the filter error system (6). Construct the Lyapunov-Krasovskii function as follows:

$$ V\bigl(\eta(t)\bigr)= V_{1}\bigl(\eta(t)\bigr)+ V_{2}\bigl(\eta(t)\bigr)+ V_{3}\bigl(\eta(t)\bigr), $$

(12)

where

$$ \begin{aligned} &V_{1}\bigl(\eta(t)\bigr)= \eta^{T}(t)\tilde{E}^{T}\tilde{P}\tilde{E}\eta(t), \\ &V_{2}\bigl(\eta(t)\bigr)=\int_{t-d_{m}}^{t} \eta^{T}(s)\tilde{Q}_{1}(h)\eta(s)\,ds +\int _{t-d_{M}}^{t} \eta^{T}(s)\tilde{Q}_{2}(h) \eta(s)\,ds \\ &\hphantom{V_{2}(\eta(t))=}{}+\int_{t-d(t)}^{t} \eta^{T}(s)\tilde{Q}_{3}(h)\eta(s)\,ds, \\ &V_{3}\bigl(\eta(t)\bigr)=d_{m}\int_{-d_{m}}^{0} \int_{t+\theta}^{t} \dot{\eta}^{T}(s)\tilde {E}^{T}\tilde{R}_{1}(h)\tilde{E}\dot{\eta}(s)\,ds\,d\theta \\ &\hphantom{V_{3}(\eta(t))=}{}+d\int_{-d_{M}}^{-d_{m}}\int _{t+\theta}^{t} \dot{\eta}^{T}(s) \tilde{E}^{T}\tilde {R}_{2}(h)\tilde{E}\dot{\eta}(s)\,ds\,d\theta \end{aligned} $$

(13)

with

$$\begin{aligned}& \tilde{Q}_{1}(h)=\sum_{i=1}^{r}h_{i} \bigl(\theta(x)\bigr)\tilde {Q}_{1i},\qquad \tilde{Q}_{2}(h)= \sum_{i=1}^{r}h_{i}\bigl(\theta(x) \bigr)\tilde {Q}_{2i} \\& \tilde{Q}_{3}(h)=\sum_{i=1}^{r}h_{i} \bigl(\theta(x)\bigr)\tilde {Q}_{3i},\qquad \tilde{R}_{1}(h)= \sum_{i=1}^{r}h_{i}\bigl(\theta(x) \bigr)\tilde {R}_{1i} \\& \tilde{R}_{2}(h)=\sum_{i=1}^{r}h_{i} \bigl(\theta(x)\bigr)\tilde {R}_{2i},\qquad \tilde{S}(h)=\sum _{i=1}^{r}h_{i}\bigl(\theta(x)\bigr) \tilde{S}_{i}. \end{aligned}$$

The time derivative of (12) along the solutions to (6) can be calculated as

$$\begin{aligned} \dot{V}_{1}\bigl(\eta(t)\bigr)={}&\dot{\eta}^{T}(t) \tilde{E}^{T}\tilde{P}\tilde{E}\eta (t)+\eta^{T}(t) \tilde{E}^{T}\tilde{P}\tilde{E}\dot{\eta}(t) \\ ={}&\dot{\eta}^{T}(t)\tilde{E}^{T}(\tilde{P}\tilde{E}+ \tilde{U}\tilde{Q})\eta (t)+\eta^{T}(t) (\tilde{P}\tilde{E}+\tilde{U} \tilde{Q})^{T}\tilde{E}\dot{\eta }(t) \\ ={}&\bigl(\tilde{A}(h)\eta(t)+\tilde{A}_{d}(t)\eta \bigl(t-d(t)\bigr) \bigr)^{T}(\tilde{P}\tilde{E}+\tilde{U}\tilde{Q})\eta(t) \\ &{}+\eta^{T}(t) (\tilde{P}\tilde{E}+\tilde{U}\tilde{Q})^{T} \bigl(\tilde {A}(h)\eta(t)+\tilde{A}_{d}(h)\eta \bigl(t-d(t)\bigr) \bigr) \\ &{}+w(t)^{T}\tilde{B}_{w}^{T}(h) (\tilde{P} \tilde{E}+\tilde {U}\tilde{Q})\eta(t)+\eta^{T}(t) (\tilde{P}\tilde{E}+ \tilde{U}\tilde {Q})^{T}\tilde{B}_{w}(h)w(t) \\ ={}&\eta^{T}(t) \bigl({\tilde{A}}^{T}(h) (\tilde{P} \tilde{E}+\tilde {U}\tilde{Q})+(\tilde{P}\tilde{E}+\tilde{U}\tilde{Q})^{T} \tilde {A}(h)\bigr)\eta(t) \\ &{}+\eta^{T}\bigl(t-d(t)\bigr)\tilde{A}_{d}^{T}(h) (\tilde{P}\tilde {E}+\tilde{U}\tilde{Q})\eta(t) \\ &{}+\eta^{T}(t) (\tilde{P}\tilde{E}+\tilde{U}\tilde{Q})^{T} \tilde {A}_{d}(h)\eta\bigl(t-d(t)\bigr) \\ &{}+w(t)^{T}\tilde{B}_{w}^{T}(h) (\tilde{P} \tilde{E}+\tilde {U}\tilde{Q})\eta(t)+\eta^{T}(t) (\tilde{P}\tilde{E}+ \tilde{U}\tilde {Q})^{T}\tilde{B}_{w}(h)w(t), \end{aligned}$$

(14)

$$\begin{aligned} \dot{V}_{2}\bigl(\eta(t)\bigr)={}&\eta^{T}(t) \tilde{Q}_{1}(h)\eta (t)-\eta^{T}(t-d_{m}) \tilde{Q}_{1}(h)\eta(t-d_{m}) \\ &{}+\eta ^{T}(t)\tilde{Q}_{2}(h)\eta(t)- \eta^{T}(t-d_{M})\tilde {Q}_{2}(h) \eta(t-d_{M}) \\ &{}+\eta^{T}(t)\tilde{Q}_{3}(h)\eta(t)-\bigl(1-\dot{d}(t) \bigr)\eta ^{T}\bigl(t-d(t)\bigr)\tilde{Q}_{3}(h)\eta \bigl(t-d(t)\bigr) \\ \le{}&\eta^{T}(t) \bigl(\tilde{Q}_{1}(h)+ \tilde{Q}_{2}(h)+\tilde{Q}_{3}(h)\bigr)\eta(t)- \eta^{T}(t-d_{m})\tilde {Q}_{1}(h) \eta(t-d_{m}) \\ &{}-\eta^{T}(t-d_{M})\tilde{Q}_{2}(h) \eta(t-d_{M}) \\ &{}-(1-\mu)\eta^{T}\bigl(t-d(t)\bigr)\tilde{Q}_{3}(h)\eta \bigl(t-d(t)\bigr), \end{aligned}$$

(15)

$$\begin{aligned} \dot{V}_{3}\bigl(\eta(t)\bigr)={}&d_{m}^{2}\dot{ \eta}^{T}(t)\tilde{E}^{T}\tilde {R}_{1}(h)\tilde{E} \dot{\eta}(t)-d_{m}\int_{t-d_{m}}^{t} \dot { \eta}^{T}(s)\tilde{E}^{T}\tilde{R}_{1}(h)\tilde{E} \dot{\eta }(s)\,ds \\ &{}+d^{2}\dot{\eta}^{T}(t)\tilde{E}^{T} \tilde{R}_{2}(h)\tilde {E}\dot{\eta}(t)-d\int_{t-d_{M}}^{t-d_{m}} \dot{\eta}^{T}(s)\tilde{E}^{T}\tilde {R}_{2}(h) \tilde{E}\dot{\eta}(s)\,ds. \end{aligned}$$

(16)

Using Lemma 1, it can be computed that

$$\begin{aligned} &{-}d_{m}\int_{t-d_{m}}^{t}\dot{ \eta}^{T}(s)\tilde{E}^{T}\tilde{R}_{1}(h)\tilde{E} \dot{\eta}(s)\,ds \\ &\quad\le-\bigl[\eta(t)-\eta(t-d_{m})\bigr]^{T} \tilde{E}^{T}\tilde{R}_{1}(h)\tilde{E}\bigl[\eta(t)- \eta(t-d_{m})\bigr] \\ &\quad=-\eta^{T}(t)\tilde{E}^{T}\tilde{R}_{1}(h) \tilde {E}x(t)+\eta^{T}(t)\tilde{E}^{T}\tilde{R}_{1}(h) \tilde{E}\eta (t-d_{m}) \\ &\qquad{}+\eta^{T}(t-d_{m})\tilde{E}^{T} \tilde{R}_{1}(h)\tilde{E}\eta (t)-\eta^{T}(t-d_{m}) \tilde{E}^{T}\tilde{R}_{1}(h)\tilde{E}\eta (t-d_{m}) \\ &\quad= \bigl[ \eta^{T}(t)\quad \eta^{T}(t-d_{m}) \bigr]\mathcal{R}(h) \begin{bmatrix} \eta(t)\\ \eta(t-d_{m}) \end{bmatrix}, \end{aligned}$$

(17)

where

$$\mathcal{R}(h)= \begin{bmatrix} -\tilde{E}^{T}\tilde{R}_{1}(h)\tilde{E}&\tilde{E}^{T}\tilde {R}_{1}(h)\tilde{E}\\ \tilde{E}^{T}\tilde{R}_{1}(h)\tilde{E}&-\tilde{E}^{T}\tilde{R}_{1}(h)\tilde{E} \end{bmatrix}. $$

It is obvious that

$$\begin{aligned} &{-}d\int_{t-d_{M}}^{t-d_{m}}\dot{\eta}^{T}(s) \tilde{E}^{T} \tilde{R}_{2}(h)\tilde{E}\dot{\eta}(s)\,ds \\ &\quad=-d\int_{t-d(t)}^{t-d_{m}}\dot{\eta}^{T}(s) \tilde{E}^{T}\tilde {R}_{2}(h)\tilde{E}\dot{\eta}(s)\,ds-d\int _{t-d_{M}}^{t-d(t)}\dot{\eta}^{T}(s) \tilde{E}^{T}\tilde{R}_{2}(h)\tilde{E}\dot{\eta}(s)\,ds. \end{aligned}$$

(18)

It follows from Lemma 1 that

$$\begin{aligned} &{-}d\int_{t-d(t)}^{t-d_{m}}\dot{\eta}^{T}(s) \tilde{E}^{T} \tilde{R}_{2}(h)\tilde{E}\dot{\eta}(s)\,ds \\ &\quad\le-\frac{d}{d(t)-d_{m}}\bigl[\eta(t-d_{m})-\eta\bigl(t-d(t)\bigr) \bigr]^{T}\tilde{E}^{T}\tilde {R}_{2}(h)\tilde{E} \bigl[\eta(t-d_{m})-\eta\bigl(t-d(t)\bigr)\bigr] \end{aligned}$$

(19)

and

$$\begin{aligned} &{-}d\int_{t-d_{M}}^{t-d(t)}\dot{\eta}^{T}(s) \tilde{E}^{T} \tilde{R}_{2}(h)\tilde{E}\dot{\eta}(s)\,ds \\ &\quad\le-\frac{d}{d_{M}-d(t)}\bigl[\eta\bigl(t-d(t)\bigr)-\eta(t-d_{M}) \bigr]^{T}\tilde{E}^{T}\tilde {R}_{2}(h)\tilde{E} \bigl[\eta\bigl(t-d(t)\bigr)-\eta(t-d_{M})\bigr]. \end{aligned}$$

(20)

On the other hand, applying Lemma 2, we have

$$\begin{aligned} &{-}d\int_{t-d_{M}}^{t-d_{m}}\dot{\eta}^{T}(s) \tilde{E}^{T} \tilde{R}_{2}(h)\tilde{E}\dot{\eta}(s)\,ds \\ &\quad< - \left .\begin{bmatrix} \eta(t-d_{m})-\eta(t-d(t))\\ \eta(t-d(t))-\eta(t-d_{M}) \end{bmatrix} \right .^{T} \mathcal{RS}(h) \begin{bmatrix} \eta(t-d_{m})-\eta(t-d(t))\\ \eta(t-d(t))-\eta(t-d_{M}) \end{bmatrix}, \end{aligned}$$

(21)

where

$$\mathcal{RS}(h)= \begin{bmatrix} \tilde{E}^{T}\tilde{R}_{2}(h)\tilde {E}&\tilde{E}^{T}\tilde{S}(h)\tilde{E}\\ \tilde{E}^{T}\tilde{S}^{T}(h)\tilde{E}&\tilde{E}^{T}\tilde {R}_{2}(h)\tilde{E} \end{bmatrix}. $$

Define $\xi^{T}(t)=[ \eta^{T}(t)\ \eta^{T}(t-d(t))\ \eta^{T}(t-d_{m})\ \eta^{T}(t-d_{M})\ w^{T}(t) ]$. Thus, based on the above computation, we obtain

$$\begin{aligned} \dot{V}\bigl(\eta(t)\bigr)\le{}&\eta^{T}(t) \bigl({ \tilde{A}}^{T}(h) (\tilde {P}\tilde{E}+\tilde{U}\tilde{Q})+(\tilde{P} \tilde{E}+\tilde{U}\tilde {Q})^{T}\tilde{A}(h)\bigr)\eta(t) \\ &{}+\eta^{T}\bigl(t-d(t)\bigr)\tilde{A}_{d}^{T}(h) (\tilde{P}\tilde {E}+\tilde{U}\tilde{Q})\eta(t) \\ &{}+\eta^{T}(t) (\tilde{P}\tilde{E}+\tilde{U}\tilde{Q})^{T} \tilde {A}_{d}(h)\eta\bigl(t-d(t)\bigr) \\ &{}+\eta^{T}(t) \bigl(\tilde{Q}_{1}(h)+ \tilde{Q}_{2}(h)+\tilde{Q}_{3}(h)\bigr)\eta(t)- \eta^{T}(t-d_{m})\tilde {Q}_{1}(h) \eta(t-d_{m}) \\ &{}-\eta^{T}(t-d_{M})\tilde{Q}_{2}(h) \eta(t-d_{M})-(1-\mu)\eta ^{T}\bigl(t-d(t)\bigr) \tilde{Q}_{3}(h)\eta\bigl(t-d(t)\bigr) \\ &{}+d_{m}^{2}\dot{\eta}^{T}(t) \tilde{E}^{T}\tilde{R}_{1}(h)\tilde {E}\dot{ \eta}(t)+d^{2}\dot{\eta}^{T}(t)\tilde{E}^{T} \tilde{R}_{2}(h)\tilde{E}\dot{\eta}(t) \\ &{}+ \bigl[ \eta^{T}(t)\quad \eta^{T}(t-d_{m}) \bigr]\mathcal{R}(h) \begin{bmatrix} \eta(t)\\ \eta(t-d_{m}) \end{bmatrix} \\ &{}- \left .\begin{bmatrix} \eta(t-d_{m})-\eta(t-d(t))\\ \eta(t-d(t))-\eta(t-d_{M}) \end{bmatrix} \right .^{T} \mathcal{RS}(h) \begin{bmatrix} \eta(t-d_{m})-\eta(t-d(t))\\ \eta(t-d(t))-\eta(t-d_{M}) \end{bmatrix} \\ &{}+w(t)^{T}\tilde{B}_{w}^{T}(h) (\tilde{P} \tilde{E}+\tilde {U}\tilde{Q})\eta(t)+\eta^{T}(t) (\tilde{P}\tilde{E}+ \tilde{U}\tilde {Q})^{T}\tilde{B}_{w}(h)w(t) \\ ={}&\xi^{T}(t) \bigl(\Omega^{1}(h) +\Gamma_{1}(h) \tilde{R}_{1}^{-1}(h)\Gamma_{1}^{T}(h) + \Gamma_{2}(h)\tilde{R}_{2}^{-1}(h) \Gamma_{2}^{T}(h) \bigr)\xi(t), \end{aligned}$$

(22)

where

$$ \Omega^{1}(h)= \begin{bmatrix} \Omega_{11}&\Omega_{12}&\Omega_{13}&0&\Omega_{15}\\ {*}&\Omega_{22}&\Omega_{23}&\Omega_{24}&0\\ {*}&*&\Omega_{33}&\Omega_{34}&0\\ {*}&*&*&\Omega_{44}&0\\ {*}&*&*&*&0 \end{bmatrix}. $$

(23)

When the initial states $\eta(0)=0$, it is easy to verify that

$$\begin{aligned} &\int_{0}^{\infty}\bigl(e^{T}(t)e(t)- \gamma^{2}w^{T}(t)w(t) \bigr)\,dt \\ &\quad\le V(\infty)+\int_{0}^{\infty}\bigl(e^{T}(t)e(t)-\gamma^{2}w^{T}(t)w(t) \bigr)\,dt \\ &\quad= \int_{0}^{\infty}\bigl(e^{T}(t)e(t)- \gamma^{2}w^{T}(t)w(t)+\dot{V}(t) \bigr)\,dt \\ &\quad=\xi^{T}(t) \bigl(\Xi(h)+\Gamma_{1}(h) \tilde{R}_{1}^{-1}(h) \Gamma_{1}^{T}(h)+ \Gamma_{2}(h)\tilde{R}_{2}^{-1}(h) \Gamma_{2}^{T}(h)+\Gamma_{3}(h) \Gamma_{3}^{T}(h) \bigr)\xi(t). \end{aligned}$$

(24)

Applying the Schur complement lemma to (11), it follows that

$$\int_{0}^{\infty}\bigl(e^{T}(t)e(t)- \gamma^{2}w^{T}(t)w(t) \bigr)\,dt\le0 $$

under the zero initial conditions.

On the other hand, when $w(t)=0$, choose the Lyapunov-Krasovskii function as in (12), and similar to the above deduction, we can obtain from (11) the time derivative of the Lyapunov-Krasovskii function $\dot{V}(\eta(t))<0$. Thus, according to the stability theory in [29], we can prove the admissibility of nonlinear singular delayed system (6). This completes the proof. □

Remark 1

It is worth mentioning that from the proof of Theorem 1, since the reciprocally convex combination method admits a more tight upper bound than the existing method and the fuzzy Lyapunov-Krasovskii function method is utilized, accordingly, Theorem 1 may be less conservative that others.

With Theorem 1 in hand, we are in a position to propose another form of a bounded real lemma, whose merit is its convenience to design the filter. To this end, we give the result below.

Theorem 2

For given scalars $0\le d_{m}< d_{M}$, $\mu<1$ and δ, the filter error system (6) is admissible with $H_{\infty}$ performance index γ if there exists a set of positive definite matrices $\tilde{P}$, $\tilde{Q}_{1}(h)$, $\tilde{Q}_{2}(h)$, $\tilde{Q}_{3}(h)$, $\tilde{R}_{1}(h)$, $\tilde{R}_{2}(h)$, matrix $\tilde{Q}$, $\tilde{G}$, $\tilde{J}$, matrix $\tilde{S}(h)$ which satisfies $\bigl [ {\scriptsize\begin{matrix}{\tilde{R}_{2}(h)}&{\tilde{S}(h)}\cr {\tilde{S}^{T}(h)}&{\tilde{R}_{2}(h)} \end{matrix}} \bigr ]\ge 0$ such that the following linear matrix inequalities are satisfied:

$$\begin{aligned} {{\Psi(h)= \begin{bmatrix} \Psi_{11}(h)&\Psi _{12}(h)&\Psi_{13}(h)&\Psi _{14}(h)&0&\Psi_{16}(h)&\Psi _{17}(h)&\Psi_{18}(h)&\tilde {F}^{T}(h)\\ {*}&\Psi_{22}(h)&\Psi_{23}(h)&0&0&\Psi _{26}(h)&0&0&0\\ {*}&*&\Psi_{33}(h)&\Psi_{34}(h)&\Psi _{35}(h)&0&\Psi_{37}(h)&\Psi _{38}(h)&\tilde{F}_{d}^{T}(h)\\ {*}&*&*&\Psi_{44}(h)&\Psi_{45}(h)&0&0&0&0\\ {*}&*&*&*&\Psi_{55}(h)&0&0&0&0\\ {*}&*&*&*&*&-\gamma^{2}I&\Psi_{67}(h)&\Psi _{68}(h)&0\\ {*}&*&*&*&*&*&\Psi_{77}(h)&0&0\\ {*}&*&*&*&*&*&*&\Psi_{88}(h)&0\\ {*}&*&*&*&*&*&*&*&-I \end{bmatrix}< 0,}} \end{aligned}$$

(25)

where $d=d_{M}-d_{m}$ and

$$\begin{aligned}& \Psi_{11}(h)=\tilde{A}^{T}(h)\tilde {G}+ \tilde{G}^{T}\tilde{A}(h)+\tilde{Q}_{1}(h) + \tilde{Q}_{2}(h)+\tilde{Q}_{3}(h)-\tilde{E}^{T} \tilde{R}_{1}(h)\tilde{E}, \\& \Psi_{12}(h)=\tilde{A}^{T}(h)\tilde {J}+(\tilde{P}\tilde{E}+ \tilde{U}\tilde{Q})^{T}-\tilde{G}^{T}\,\ \Psi_{13}(h)= \tilde{G}^{T}\tilde{A}_{d}(h), \\& \Psi_{14}(h)=\tilde{E}^{T}\tilde{R}_{1}(h) \tilde{E}, \\& \Psi_{16}(h)=\tilde{G}^{T}\tilde{B}(h), \\& \Psi_{17}(h)=d_{m}\tilde{A}^{T}(h)\tilde {J}, \\& \Psi_{18}(h)=d\tilde{A}^{T}(h)\tilde {J}, \\& \Psi_{22}(h)=-\tilde{J}-\tilde{J}^{T}, \\& \Psi_{23}(h)=\tilde{J}^{T}\tilde{A}_{d}(h), \\& \Psi_{26}(h)=\tilde{J}^{T}\tilde{B}(h), \\& \Psi_{33}(h)=-(1-\mu)\tilde{Q}_{3}(h)-2 \tilde{E}^{T}\tilde{R}_{2}(h)\tilde{E}+\tilde {E}^{T}\tilde{S}(h)\tilde{E}+\tilde{E}^{T}\tilde {S}^{T}(h)\tilde{E}, \\& \Psi_{34}(h)=\tilde{E}^{T}\tilde{R}_{2}(h) \tilde{E}-\tilde{E}^{T}\tilde{S}^{T}(h)\tilde{E}, \\& \Psi_{35}(h)=\tilde{E}^{T}\tilde{R}_{2}(h) \tilde{E}-\tilde{E}^{T}\tilde{S}(h)\tilde{E}, \\& \Psi_{37}(h)=d_{m}\tilde{A}_{d}^{T}(h) \tilde{J}, \\& \Psi_{38}(h)=d\tilde{A}_{d}^{T}(h)\tilde {J}, \\& \Psi_{44}(h)=-\tilde{Q}_{1}(h)-\tilde {E}^{T} \tilde{R}_{1}(h)\tilde{E}-\tilde{E}^{T}\tilde {R}_{2}(h)\tilde{E}, \\& \Psi_{45}(h)=\tilde{E}^{T}\tilde{S}^{T}(h) \tilde{E}, \\& \Psi_{55}(h)=-\tilde{Q}_{2}(h)-\tilde {E}^{T} \tilde{R}_{2}(h)\tilde{E}, \\& \Psi_{67}(h)=d_{m}\tilde{B}^{T}(h)\tilde {J}, \\& \Psi_{68}(h)=d\tilde{B}^{T}(h)\tilde {J}, \\& \Psi_{77}(h)=-\delta\tilde{J}-\delta\tilde{J}^{T}+\delta ^{2}\tilde{R}_{1}(h), \\& \Psi_{88}(h)=-\delta\tilde{J}-\delta\tilde{J}^{T}+\delta ^{2}\tilde{R}_{2}(h) \end{aligned}$$

with full column rank matrix $\tilde{U}$ satisfying $\tilde{E}^{T}\tilde{U}=0$.

Proof

It is evident that for an arbitrary matrix $Y>0$ and constant δ, the following inequality always holds:

$$-X^{T}Y^{-1}X\le-\delta X-\delta X^{T}+{ \delta}^{2}Y. $$

Consequently, we have

$$\begin{aligned}& -\tilde{J}^{T}\tilde{R}_{1}^{-1}(h)\tilde{J}\le- \delta \tilde{J}-\delta\tilde{J}^{T}+\delta^{2} \tilde{R}_{1}(h), \end{aligned}$$

(26)

$$\begin{aligned}& -\tilde{J}^{T}\tilde{R}_{2}^{-1}(h)\tilde{J}\le- \delta \tilde{J}-\delta\tilde{J}^{T}+\delta^{2} \tilde{R}_{2}(h). \end{aligned}$$

(27)

Substitute (26) and (27) into (25), and then pre- and post-multiply (25) by $\operatorname{diag} \{I,I,I,I, I,I,\tilde {R}_{1}(h)\tilde{J}^{-T},\tilde{R}_{2}(h)\tilde{J}^{-T},I\}$ and its transpose, we have

$$\begin{aligned} {{ \begin{bmatrix} \Psi_{11}(h)&\Psi _{12}(h)&\Psi_{13}(h)&\Psi _{14}(h)&0&\Psi_{16}(h)&d_{m}\tilde {A}^{T}(h)\tilde{R}_{1}(h)&d\tilde {A}^{T}(h)\tilde{R}_{2}(h)&\tilde {F}^{T}(h)\\ {*}&\Psi_{22}(h)&\Psi_{23}(h)&0&0&\Psi _{26}(h)&0&0&0\\ {*}&*&\Psi_{33}(h)&\Psi_{34}(h)&\Psi _{35}(h)&0&d_{m}\tilde{A}_{d}^{T}(h)\tilde {R}_{1}(h)&d\tilde{A}_{d}^{T}(h)\tilde {R}_{2}(h)&\tilde{F}_{d}^{T}(h)\\ {*}&*&*&\Psi_{44}(h)&\Psi_{45}(h)&0&0&0&0\\ {*}&*&*&*&\Psi_{55}(h)&0&0&0&0\\ {*}&*&*&*&*&-\gamma^{2}I&d_{m}\tilde{B}^{T}(t) \tilde{R}_{1}(h)&d\tilde{B}^{T}(h)\tilde{R}_{2}(h)&0\\ {*}&*&*&*&*&*&-\tilde{R}_{1}(h)&0&0\\ {*}&*&*&*&*&*&*&-\tilde{R}_{2}(h)&0\\ {*}&*&*&*&*&*&*&*&-I \end{bmatrix}< 0,}} \end{aligned}$$

(28)

where others are the same as in (25).

Pre- and post-multiplying (28) by

$$ \begin{bmatrix} I&A^{T}(h)&0&0&0&0&0&0&0\\ 0&A_{d}^{T}(h)&I&0&0&0&0&0&0\\0&0&0&I&0&0&0&0&0\\ 0&0&0&0&I&0&0&0&0\\ 0&B^{T}(h)&0&0&0&I&0&0&0\\ 0&0&0&0&0&0&I&0&0\\ 0&0&0&0&0&0&0&I&0\\ 0&0&0&0&0&0&0&0&I \end{bmatrix} $$

and its transpose, we can obtain (11); consequently, the filter error system (6) is admissible and satisfies $H_{\infty}$ attenuation level. This completes the proof. □

Remark 2

It should be worth noticing that inequality (11) contains the fuzzy weighting functions $h_{i}(\theta(x))$, we cannot solve these inequalities directly. Fortunately, according to the convexity property (4) of the fuzzy weighting functions $h_{i}(\theta(x))$, a series of suitable conditions which only need the coefficient matrices of each fuzzy subsystem can be obtained.

Thus, in what follows, we give another form which can be handled by LMI toolbox in Matlab effectively.

Lemma 3

For given scalars $0\le d_{m}< d_{M}$, $\mu<1$, and δ, the filter error system (6) is admissible with $H_{\infty}$ performance index γ if there exists a set of positive definite matrices $\tilde{P}$, $\tilde{Q}_{1i}$, $\tilde{Q}_{2i}$, $\tilde{Q}_{3i}$, $\tilde{R}_{1i}$, $\tilde{R}_{2i}$, matrix $\tilde{Q}$, $\tilde{G}$, $\tilde{J}$, matrix $\tilde{S}_{i}$ which satisfies $\bigl [ {\scriptsize\begin{matrix}{\tilde{R}_{2i}}&{\tilde{S}_{i}}\cr {\tilde{S}^{T}_{i}}&{\tilde{R}_{2i}} \end{matrix}} \bigr ]\ge 0$, $i=1,2,\ldots, r$, such that the following linear matrix inequalities are satisfied:

$$ \begin{aligned} & \Psi^{ii}< 0, \quad i=1,2, \ldots, r, \\ &\Psi^{ij}+\Psi^{ji}<0, \quad i<j, \end{aligned} $$

(29)

where

$$\Psi^{ij}= \begin{bmatrix} \Psi_{11}^{ij}&\Psi_{12}^{ij}&\Psi _{13}^{ij}&\Psi_{14}^{ij}&0&\Psi_{16}^{ij}&\Psi_{17}^{ij}&\Psi _{18}^{ij}&\tilde{F}_{ij}^{T}\\{*}&\Psi_{22}^{ij}&\Psi_{23}^{ij}&0&0&\Psi_{26}^{ij}&0&0&0\\{*}&*&\Psi_{33}^{ij}&\Psi_{34}^{ij}&\Psi_{35}^{ij}&0&\Psi_{37}^{ij}&\Psi _{38}^{ij}&\tilde{F}_{dj}^{T}\\{*}&*&*&\Psi_{44}^{ij}&\Psi_{45}^{ij}&0&0&0&0\\{*}&*&*&*&\Psi_{55}^{ij}&0&0&0&0\\{*}&*&*&*&*&-\gamma^{2}I&\Psi_{67}^{ij}&\Psi_{68}^{ij}&0\\{*}&*&*&*&*&*&\Psi_{77}^{ij}&0&0\\{*}&*&*&*&*&*&*&\Psi_{88}^{ij}&0\\{*}&*&*&*&*&*&*&*&-I \end{bmatrix} $$

with

$$\begin{aligned}& \Psi_{11}^{ij}=\tilde{A}_{ij}^{T} \tilde{G}+\tilde{G}^{T}\tilde {A}_{ij}+\tilde{Q}_{1i}+ \tilde{Q}_{2i}+\tilde{Q}_{3i}-\tilde{E}^{T}\tilde {R}_{1}\tilde{E} , \\& \Psi_{12}^{ij}=\tilde{A}_{ij}^{T} \tilde{J}+(\tilde{P}\tilde{E}+\tilde {U}\tilde{Q})^{T}- \tilde{G}^{T}, \\& \Psi_{13}^{ij}=\tilde{G}^{T}\tilde{A}_{dij}, \\& \Psi_{14}^{ij}=\tilde{E}^{T}\tilde{R}_{1i} \tilde{E}, \\& \Psi_{16}^{ij}=\tilde{G}^{T}\tilde{B}_{ij}, \\& \Psi_{17}^{ij}=d_{m}\tilde{A}_{ij}^{T} \tilde{J}, \\& \Psi_{18}^{ij}=d\tilde{A}_{ij}^{T} \tilde{J}, \\& \Psi_{22}^{ij}=-\tilde{J}-\tilde{J}^{T}, \\& \Psi_{23}^{ij}=\tilde{J}^{T}\tilde{A}_{dij}, \\& \Psi_{26}^{ij}=\tilde{J}^{T}\tilde{B}_{ij}, \\& \Psi_{33}^{ij}=-(1-\mu)\tilde{Q}_{3i}-2 \tilde{E}^{T}\tilde {R}_{2i}\tilde{E}+\tilde{E}^{T} \tilde{S}_{i}\tilde{E}+\tilde{E}^{T}\tilde {S}_{i}^{T}\tilde{E}, \\& \Psi_{34}^{ij}=\tilde{E}^{T}\tilde{R}_{2i} \tilde{E}-\tilde{E}^{T}\tilde {S}_{i}^{T}\tilde{E}, \\& \Psi_{35}^{ij}=\tilde{E}^{T}\tilde{R}_{2i} \tilde{E}-\tilde{E}^{T}\tilde {S}_{i}\tilde{E}, \\& \Psi_{37}^{ij}=d_{m}\tilde{A}_{dij}^{T} \tilde{J}, \\& \Psi_{38}^{ij}=d\tilde{A}_{dij}^{T} \tilde{J}, \\& \Psi_{44}^{ij}=-\tilde{Q}_{1i}- \tilde{E}^{T}\tilde{R}_{1i}\tilde {E}-\tilde{E}^{T} \tilde{R}_{2i}\tilde{E}, \\& \Psi_{45}^{ij}=\tilde{E}^{T}\tilde{S}_{i}^{T} \tilde{E}, \\& \Psi_{55}^{ij}=-\tilde{Q}_{2i}- \tilde{E}^{T}\tilde{R}_{2i}\tilde{E}, \\& \Psi_{67}^{ij}=d_{m}\tilde{B}_{ij}^{T} \tilde{J}, \\& \Psi_{68}^{ij}=d\tilde{B}_{ij}^{T} \tilde{J}, \\& \Psi_{77}^{ij}=-\delta\tilde{J}-\delta\tilde{J}^{T}+ \delta^{2}\tilde {R}_{1i}, \\& \Psi_{88}^{ij}=-\delta\tilde{J}-\delta\tilde{J}^{T}+ \delta^{2}\tilde{R}_{2i}. \end{aligned}$$

3.2 Filter design

Based on Lemma 3, by choosing

$$\begin{aligned}& \tilde{G}^{T}= \begin{bmatrix} G_{1}&X\\ G_{2}&X \end{bmatrix},\qquad \tilde{J}^{T}= \begin{bmatrix} J_{1}&X\\ J_{2}&X \end{bmatrix},\qquad \tilde{Q}_{1i}= \begin{bmatrix} Q_{11i}&Q_{12i}\\ Q_{12i}^{T}&Q_{13i} \end{bmatrix}, \\& \tilde{Q}_{2i}= \begin{bmatrix} Q_{21i}&Q_{22i}\\ Q_{22i}^{T}&Q_{23i} \end{bmatrix},\qquad \tilde{Q}_{3i}= \begin{bmatrix} Q_{31i}&Q_{32i}\\ Q_{32i}^{T}&Q_{33i} \end{bmatrix}, \qquad \tilde{R}_{1i}= \begin{bmatrix} R_{11i}&R_{12i}\\ R_{12i}^{T}&R_{13i} \end{bmatrix}, \\& \tilde{R}_{2i}= \begin{bmatrix} R_{21i}&R_{22i}\\ R_{22i}^{T}&R_{23i} \end{bmatrix}, \qquad \tilde{S}_{i}= \begin{bmatrix} S_{1i}&S_{2i}\\ S_{3i}&S_{4i} \end{bmatrix},\qquad \tilde{P}= \begin{bmatrix} P_{1}&P_{2}\\ P_{2}^{T}&P_{3} \end{bmatrix}, \\& \tilde{Q}= \begin{bmatrix} Q_{1}&Q_{2}\\ Q_{3}&Q_{4} \end{bmatrix},\qquad \tilde{U}= \begin{bmatrix} U&0\\ 0&U \end{bmatrix}, \end{aligned}$$

where the full column rank matrix U satisfies $E^{T}U=0$, we can obtain the following result.

Theorem 3

For given scalars $0\le d_{m}< d_{M}$, $\mu<1$, and δ, the filter error system (6) is admissible with $H_{\infty}$ performance index γ if there exists a set of positive definite matrices

$$\begin{aligned}& \tilde{P}= \begin{bmatrix} P_{1}&P_{2}\\ P_{2}^{T}&P_{3} \end{bmatrix},\qquad \tilde{R}_{1i}= \begin{bmatrix} R_{11i}&R_{12i}\\ R_{12i}^{T}&R_{13i} \end{bmatrix},\qquad \tilde{R}_{2i}= \begin{bmatrix} R_{21i}&R_{22i}\\ R_{22i}^{T}&R_{23i} \end{bmatrix}, \\& \tilde{Q}_{1i}= \begin{bmatrix} Q_{11i}&Q_{12i}\\ Q_{12i}^{T}&Q_{13i} \end{bmatrix}, \qquad \tilde{Q}_{2i}= \begin{bmatrix} Q_{21i}&Q_{22i}\\ Q_{22i}^{T}&Q_{23i} \end{bmatrix},\qquad \tilde{Q}_{3i}= \begin{bmatrix} Q_{31i}&Q_{32i}\\ Q_{32i}^{T}&Q_{33i} \end{bmatrix}, \end{aligned}$$

and matrices

$$\begin{aligned}& \tilde{G}^{T}= \begin{bmatrix} G_{1}&X\\ G_{2}&X \end{bmatrix}, \qquad\tilde{J}^{T}= \begin{bmatrix} J_{1}&X\\ J_{2}&X \end{bmatrix},\qquad \tilde{S}_{i}= \begin{bmatrix} S_{1i}&S_{2i}\\ S_{3i}&S_{4i} \end{bmatrix}, \qquad \tilde{Q}= \begin{bmatrix} Q_{1}&Q_{2}\\ Q_{3}&Q_{4} \end{bmatrix} \end{aligned}$$

$i=1,2,\ldots, r$, such that the following linear matrix inequalities are satisfied:

$$\begin{aligned}& \begin{bmatrix} \tilde{R}_{2i}&\tilde{S}_{i}\\ \tilde{S}^{T}_{i}&\tilde{R}_{2i} \end{bmatrix}\ge 0, \end{aligned}$$

(30)

$$\begin{aligned}& \begin{aligned} & \Psi^{ii}< 0, \quad i=1,2,\ldots, r, \\ &\Psi^{ij}+\Psi^{ji}<0, \quad i<j, \end{aligned} \end{aligned}$$

(31)

where

$$ \Psi^{ij}= \begin{bmatrix} \Xi^{ij}&\Gamma_{1}^{ij}&\Gamma_{2}^{ij}&\Gamma_{3}^{ij}\\ {*}&-\delta\tilde{J}-\delta\tilde{J}^{T}+\delta^{2}\tilde{R}_{1i}&0&0\\ {*}&*&-\delta\tilde{J}-\delta\tilde{J}^{T}+\delta^{2}\tilde{R}_{2i}&0\\ {*}&*&*&-I \end{bmatrix}< 0 $$

(32)

with

$$\begin{aligned}& \Gamma_{1}^{ij}= \begin{bmatrix} \Gamma_{11}^{ij}\\ 0\\ \Gamma_{12}^{ij}\\ 0\\ 0\\ \Gamma_{13}^{ij} \end{bmatrix},\qquad \Gamma_{2}^{ij}= \begin{bmatrix} \Gamma_{21}^{ij}\\ 0\\ \Gamma_{22}^{ij}\\ 0\\ 0\\ \Gamma_{23}^{ij} \end{bmatrix},\qquad \Gamma_{3}^{ij}= \begin{bmatrix} \Gamma_{31}^{ij}\\ 0\\ \Gamma_{32}^{ij}\\ 0\\ 0\\ 0 \end{bmatrix}, \\& \Gamma_{11}^{ij}= \begin{bmatrix} d_{m}(A_{j}^{T}J_{1}^{T}+C_{j}^{T}\widehat {B}_{fi}^{T})&d_{m}(A_{j}^{T}J_{2}^{T}+C_{j}^{T}\widehat{B}_{fi}^{T})\\ d_{m}\widehat{A}_{fi}^{T}&d_{m}\widehat{A}_{fi}^{T} \end{bmatrix}, \\& \Gamma_{12}^{ij}= \begin{bmatrix} d_{m}(A_{dj}^{T}J_{1}^{T}+C_{dj}^{T}\widehat {B}_{fi}^{T})&d_{m}(A_{dj}^{T}J_{2}^{T}+C_{dj}^{T}\widehat{B}_{fi}^{T})\\ 0&0 \end{bmatrix}, \\& \Gamma_{13}^{ij}= \bigl[ d_{m}(B_{j}^{T}J_{1}^{T}+D_{j}^{T}\widehat {B}_{fi}^{T})\quad d_{m}(B_{j}^{T}J_{2}^{T}+D_{j}^{T}\widehat{B}_{fi}^{T}) \bigr], \\& \Gamma_{21}^{ij}= \begin{bmatrix} d(A_{j}^{T}J_{1}^{T}+C_{j}^{T}\widehat {B}_{fi}^{T})&d(A_{j}^{T}J_{2}^{T}+C_{j}^{T}\widehat{B}_{fi}^{T})\\ d_{m}\widehat{A}_{fi}^{T}&d_{m}\widehat{A}_{fi}^{T} \end{bmatrix}, \\& \Gamma_{22}^{ij}= \begin{bmatrix} d(A_{dj}^{T}J_{1}^{T}+C_{dj}^{T}\widehat {B}_{fi}^{T})&d(A_{dj}^{T}J_{2}^{T}+C_{dj}^{T}\widehat{B}_{fi}^{T})\\ 0&0 \end{bmatrix}, \\& \Gamma_{23}^{ij}= \bigl[ d(B_{j}^{T}J_{1}^{T}+D_{j}^{T}\widehat {B}_{fi}^{T})\quad d(B_{j}^{T}J_{2}^{T}+D_{j}^{T}\widehat{B}_{fi}^{T}) \bigr], \\& \Gamma_{31}^{ij}= \begin{bmatrix} F_{j}^{T}\\ -\widetilde{F}_{fi}^{T} \end{bmatrix},\qquad \Gamma_{32}^{ij}= \begin{bmatrix} F_{dj}^{T}\\ 0 \end{bmatrix} \end{aligned}$$

(33)

and

$$\begin{aligned}& \Xi^{ij}= \begin{bmatrix} \Psi_{11}^{ij}&\Psi_{12}^{ij}&\Psi_{13}^{ij}&\Psi _{14}^{ij}&0&\Psi_{16}^{ij}\\ {*}&\Psi_{22}^{ij}&\Psi_{23}^{ij}&0&0&\Psi_{26}^{ij}\\ {*}&*&\Psi_{33}^{ij}&\Psi_{34}^{ij}&\Psi_{35}^{ij}&0\\ {*}&*&*&\Psi_{44}^{ij}&\Psi_{45}^{ij}&0\\ {*}&*&*&*&\Psi_{55}^{ij}&0\\ {*}&*&*&*&*&-\gamma^{2}I \end{bmatrix}, \\& \Psi_{11}^{ij}= \begin{bmatrix} \begin{array}{c} He(G_{1}A_{j}+\widehat{B}_{fi}C_{j})+Q_{11i}\\ +Q_{21i}+Q_{31i}-E^{T}R_{11i}E \end{array} & \begin{array}{c} \widehat{A}_{fi}+A_{j}^{T}G_{2}^{T}+C_{j}^{T}\widehat {B}_{fi}^{T}+Q_{12i}\\ +Q_{22i}+Q_{32i}-E^{T}R_{12i}E \end{array} \\ {*} & He(\widehat{A}_{fi})+Q_{13i}+Q_{23i}+Q_{3ei}-E^{T}R_{13i}E \end{bmatrix}, \\& \Psi_{12}^{ij}= \begin{bmatrix} \begin{array}{c} A_{j}^{T}J_{1}^{T}+C_{j}^{T}\widehat{B}_{fi}^{T}+E^{T}P_{1}^{T}\\ +Q_{1}^{T}U^{T}-G_{1} \end{array} & \begin{array}{c} A_{j}^{T}J_{2}^{T}+C_{j}^{T}\widehat{B}_{fi}^{T}+E^{T}P_{2}\\ +Q_{3}^{T}U^{T}-X \end{array}\\ \widehat{A}_{fi}^{T}+E^{T}P_{2}^{T}+Q_{2}^{T}U^{T}-G_{2} &\widehat{A}_{fi}^{T}+E^{T}P_{3}^{T}+Q_{4}^{T}U^{T}-X \end{bmatrix}, \\& \Psi_{13}^{ij}= \begin{bmatrix} G_{1}A_{dj}+\widehat{B}_{fi}C_{dj}&0\\ G_{2}A_{dj}+\widehat{B}_{fi}C_{dj}&0 \end{bmatrix},\qquad \Psi_{14}^{ij}= \begin{bmatrix} E^{T}R_{11i}E&E^{T}R_{12i}E\\ E^{T}R_{12i}^{T}E&E^{T}R_{13i}E \end{bmatrix}, \\& \Psi_{16}^{ij}= \begin{bmatrix} G_{1}B_{j}+\widehat{B}_{fi}D_{j}\\ G_{2}B_{j}+\widehat{B}_{fi}D_{j} \end{bmatrix},\qquad \Psi_{22}^{ij}=- \begin{bmatrix} He(J_{1})&X+J_{2}^{T}\\ {*}&He(X) \end{bmatrix}, \\& \Psi_{23}^{ij}= \begin{bmatrix} J_{1}A_{dj}+\widehat{B}_{fi}C_{dj}&0\\ J_{2}A_{dj}+\widehat{B}_{fi}C_{dj}&0 \end{bmatrix},\qquad \Psi_{26}^{ij}= \begin{bmatrix} J_{1}B_{j}+\widehat{B}_{fi}D_{j}\\ J_{2}B_{j}+\widehat{B}_{fi}D_{j} \end{bmatrix}, \\& \Psi_{33}^{ij}= \begin{bmatrix} \begin{array}{c} (\mu-1)Q_{31i}-2E^{T}R_{21i}E\\ +He(E^{T}S_{1i}E) \end{array} & \begin{array}{c} (\mu-1)Q_{32i}-2E^{T}R_{22i}E\\ +E^{T}S_{2i}E+E^{T}S_{3i}^{T}E \end{array} \\ {*}& \begin{array}{c} (\mu-1)Q_{33i}-2E^{T}R_{23i}E\\ +He(E^{T}S_{4i}E) \end{array} \end{bmatrix}, \\& \Psi_{34}^{ij}= \begin{bmatrix} E^{T}R_{21i}E-E^{T}S_{1i}^{T}E&E^{T}R_{22i}E-E^{T}S_{3i}^{T}E\\ E^{T}R_{22i}^{T}E-E^{T}S_{2i}^{T}E&E^{T}R_{23i}E-E^{T}S_{4i}^{T}E \end{bmatrix}, \\& \Psi_{35}^{ij}= \begin{bmatrix} E^{T}R_{21i}E-E^{T}S_{1i}E&E^{T}R_{22i}E-E^{T}S_{2i}E\\ E^{T}R_{22i}^{T}E-E^{T}S_{3i}E&E^{T}R_{23i}E-E^{T}S_{4i}E \end{bmatrix}, \\& \Psi_{44}^{ij}= \begin{bmatrix} -Q_{11i}-E^{T}R_{11i}E-E^{T}R_{21i}E&-Q_{12i}-E^{T}R_{12i}E-E^{T}R_{22i}E\\ {*}&-Q_{13i}-E^{T}R_{13i}E-E^{T}R_{23i}E \end{bmatrix}, \\& \Psi_{45}^{ij}= \begin{bmatrix} E^{T}S_{1i}^{T}E&E^{T}S_{3i}^{T}E\\ E^{T}S_{2i}^{T}E&E^{T}S_{14i}^{T}E \end{bmatrix},\qquad \Psi_{55}^{ij}= \begin{bmatrix} -Q_{21i}-E^{T}R_{21i}E&-Q_{22i}-E^{T}R_{22i}E\\ {*}&-Q_{23i}-E^{T}R_{23i}E \end{bmatrix}. \end{aligned}$$

(34)

Moreover, if the above LMIs admit solutions, the filter parameters can be expressed as

$$ A_{fi}=X^{-1}\hat{A}_{fi}, \qquad B_{fi}=X^{-1}\hat{B}_{fi},\qquad F_{fi}= \widetilde{F}_{fi}. $$

(35)

Proof

Define

$$\hat{A}_{fi}=XA_{fi}, \qquad\hat{B}_{fi}=XB_{fi}, $$

we have

$$\begin{aligned}& \tilde{G}^{T}\tilde{A}_{ij}= \begin{bmatrix} G_{1}A_{j}+\hat{B}_{fi}C_{j}&\hat{A}_{fi}\\ G_{2}A_{j}+\hat {B}_{fi}C_{j}&\hat{A}_{fi} \end{bmatrix},\qquad \tilde{J}^{T}\tilde{A}_{ij}= \begin{bmatrix} J_{1}A_{j}+\hat{B}_{fi}C_{j}&\hat{A}_{fi}\\ J_{2}A_{j}+\hat {B}_{fi}C_{j}&\hat{A}_{fi} \end{bmatrix}, \\& \tilde{G}^{T}\tilde{A}_{dij}= \begin{bmatrix} G_{1}A_{dj}+\hat{B}_{fi}C_{dj}&0\\ G_{2}A_{dj}+\hat {B}_{fi}C_{dj}&0 \end{bmatrix},\qquad \tilde{J}^{T}\tilde{A}_{dij}= \begin{bmatrix} J_{1}A_{dj}+\hat{B}_{fi}C_{dj}&0\\ J_{2}A_{dj}+\hat {B}_{fi}C_{dj}&0 \end{bmatrix}, \\& \tilde{G}^{T}\tilde{B}_{ij}= \begin{bmatrix} G_{1}B_{j}+\hat{B}_{fi}D_{j}\\ G_{2}B_{j}+\hat{B}_{fi}D_{j} \end{bmatrix},\qquad \tilde{J}^{T}\tilde{B}_{ij}= \begin{bmatrix} J_{1}B_{j}+\hat{B}_{fi}D_{j}\\ J_{2}B_{j}+\hat{B}_{fi}D_{j} \end{bmatrix}. \end{aligned}$$

Then with Lemma 3 in hand, we can obtain Theorem 3 easily. □

Remark 3

It should be noted that by applying Theorem 3, the filter design problems for fuzzy singular system (3) with time-varying delay (2) have been solved. The advantage of Theorem 3 is twofold, one is that both the reciprocally convex combination method and the fuzzy Lyapunov-Krasovskii function method are adopted to bound the reciprocally convex term from the derivative of the Lyapunov-Krasovskii functional tightly, the other is the matrix decoupling method employed in the derivation of theorems proposed in this paper.

4 Illustrative examples

In this section, two examples are presented to illustrate the effectiveness of the filter design method proposed in this paper.

Example 1

Consider the time-delay singular T-S fuzzy system (3) studied in [7] with the following parameters:

$$E= \begin{bmatrix} 1&0\\ 0&1 \end{bmatrix}; $$

Subsystems 1:

$$\begin{aligned}& A_{1}= \begin{bmatrix} -2.1&0.1\\ 1&-2 \end{bmatrix},\qquad A_{d1}= \begin{bmatrix} -1.1&0.1\\ -0.8&-0.9 \end{bmatrix},\qquad B_{1}= \begin{bmatrix} 1\\ -0.2 \end{bmatrix}, \\& C_{1}= [ 1\quad 0 ],\qquad C_{d1}= [ -0.8\quad 0.6 ], \qquad D_{1}=0.3, \\& F_{1}= [ 1\quad {-}0.5 ],\qquad F_{d1}= [ 0.1\quad 0 ]; \end{aligned}$$

Subsystems 2:

$$\begin{aligned}& A_{2}= \begin{bmatrix} -1.9&0\\ -0.2&-1.1 \end{bmatrix},\qquad A_{d2}= \begin{bmatrix} -0.9&0\\ -1.1&-1.2 \end{bmatrix},\qquad B_{2}= \begin{bmatrix} 0.3\\ 0.1 \end{bmatrix}, \\& C_{2}= [ 0.5\quad {-}0.6 ],\qquad C_{d2}= [ -0.2\quad 1 ], \qquad D_{2}=-0.6, \\& F_{2}= [ -0.2\quad 0.3 ],\qquad F_{d2}= [ 0 \quad 0.2 ]. \end{aligned}$$

Since E is nonsingular, thus we choose $U=[ 0\ 0]$. The delay is assumed as $d(t)=0.3+0.2\sin(t)$, then $d_{M}=0.5$, $d_{m}=0$, $\delta=1$ and $\mu=0.2$. By using Theorem 3, the minimum disturbance attenuation level is $\gamma_{\min}=0.3145$ and the filter parameters can be obtained as follows:

$$\begin{aligned}& A_{f1}= \begin{bmatrix} -0.7312&-0.8015\\ 3.7539&-3.7748 \end{bmatrix},\qquad B_{f1}= \begin{bmatrix} -0.8091\\ 0.5341 \end{bmatrix},\qquad F_{f1}= [ -0.6115\quad 0.2997 ] \\& A_{f2}= \begin{bmatrix} -2.1139&0.7056\\ 0.0475&-1.1386 \end{bmatrix},\qquad B_{f2}= \begin{bmatrix} -0.5954\\ 0.6371 \end{bmatrix},\qquad F_{f2}= [ 0.1507\quad {-}0.1931 ]. \end{aligned}$$

Besides, different δ will lead to different γ compared with the result in [7]. By considering several different $d_{M}$, we have Table 1 which shows that our result has less conservatism than the result in [7].

Table 1 Minimum index γ for different δ

Example 2

Consider the singular T-S fuzzy delayed system (3) in [30] with the following parameters:

$$E= \begin{bmatrix} 1&0&0\\ 0&1&0\\ 0&0&0 \end{bmatrix}; $$

Subsystems 1:

$$\begin{aligned}& A_{1}= \begin{bmatrix} -6.3&0.2&0.4\\ 0.3&-3.4&1.2\\ 0.2&0.5&-4.5 \end{bmatrix},\qquad A_{d1}= \begin{bmatrix} 0.2&0&0.2\\ 0.1&0.3&0.1\\ 0.1&0.2&0.1 \end{bmatrix},\qquad B_{1}= \begin{bmatrix} 0.3\\ 0.2\\ 0.5 \end{bmatrix}, \\& C_{1}= \begin{bmatrix} -2.1&0.6&1.3 \end{bmatrix},\qquad C_{d1}= [ 0\quad0 \quad0 ],\qquad D_{1}=0.3, \\& F_{1}= [ 0.7\quad0.8\quad 1.5 ],\qquad F_{d1}= [ 0\quad0 \quad0 ]; \end{aligned}$$

Subsystems 2:

$$\begin{aligned}& A_{2}= \begin{bmatrix} -5.5&0.3&0.6\\ 0.2&-4.6&0.5\\ 0.3&0.8&-3.9 \end{bmatrix},\qquad A_{d2}= \begin{bmatrix} 0.3&0.2&0.1\\ 0&0.1&0.1\\ 0.2&0.1&0.1 \end{bmatrix},\qquad B_{2}= \begin{bmatrix} 1.5\\ 0.6\\ 0.2 \end{bmatrix}, \\& C_{2}= [ 0.6\quad0.3\quad0.7 ],\qquad C_{d2}= [ 0\quad0 \quad0 ],\qquad D_{2}=0.2, \\& F_{2}= [ -0.5\quad0.2\quad0.6 ],\qquad F_{d2}= [ 0\quad0 \quad0 ]. \end{aligned}$$

In this example, we choose $U=[ 0\ 0\ 1]$. The delay is assumed as $d(t)=0.6+0.6\sin(\frac{1}{3}t)$, then $d_{M}=1.2$, $d_{m}=0$, $\delta=1$ and $\mu=0.6$. By using Theorem 3, the minimum disturbance attenuation level is $\gamma_{\min}=0.3486$, which is much better than the level $\gamma=0.9$ in [30], and the filter parameters can be obtained as follows:

$$\begin{aligned}& A_{f1}= \begin{bmatrix} -1.6819&3.8086&-4.4761\\ 0.0425&-1.0829&0.5555\\ 0.0192&-0.1018&-1.6510 \end{bmatrix},\quad B_{f1}= \begin{bmatrix} 0.6973\\ -0.4799\\ -0.5432 \end{bmatrix},\quad F_{f1}= \left .\begin{bmatrix} -0.0026\\ -0.3037\\ -0.2880 \end{bmatrix} \right .^{T}, \\& A_{f2}= \begin{bmatrix} -1.9712&-1.4717&-0.7805\\ 0.0416&-1.3000&0.2990\\ -0.0098&-0.6296&-1.7043 \end{bmatrix},\quad B_{f2}= \begin{bmatrix} -2.4183\\ -1.0940\\ -0.3062 \end{bmatrix},\quad\! F_{f2}= \left .\begin{bmatrix} 0.0072\\ 0.1482\\ -0.0078 \end{bmatrix} \right .^{T}. \end{aligned}$$

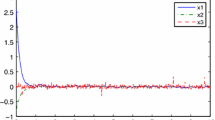
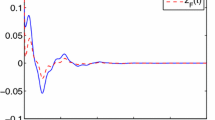
We select the membership function as follows: $h_{1}=\frac{1-\sin(x_{1})}{2}$, $h_{2}=\frac{1+\sin(x_{1})}{2}$. Figure 1 shows the simulation result of the filtering error $e(t) = z(t) - z_{f}(t)$, when $x_{1}(0)=-2$, $x_{2}(0)=3$, $x_{3}(0)=1$, and $\omega(t)=\sin(5t)$. From Figure 1 we can see that the estimation error which is obtained by our filter is below the estimation error obtained by the filter in [30]. Thus, it is obvious that our result is very effective.

Figure 1

Response of filtering error e .

5 Conclusion

In this paper, we have studied the $H_{\infty}$ filtering problem for a class of nonlinear singular systems with time-varying delay through the T-S fuzzy model approach. Based on the fuzzy Lyapunov-Krasovskii functional, combined with a reciprocally convex combination lemma, two types of bounded real lemma, which guarantees the stability and the $H_{\infty}$ attenuation level of the filter error system, are obtained. The filter design problem is also solved by checking the feasibility of a set of LMIs. At last, two numerical examples have been provided to demonstrate the effectiveness of the proposed fuzzy filter design method.