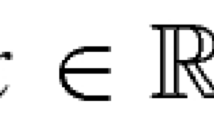Abstract
In this paper, we deal with an attraction–repulsion model with a logistic source as follows:
where \(Q = \Omega \times {\mathbb{R}^{+} }\), \(\Omega \subset {\mathbb{R}^{3}}\) is a bounded domain. We mainly focus on the influence of logistic damping on the global solvability of this model. In dimension 2, q can be equal to 1 (Math. Methods Appl. Sci. 39(2):289–301, 2016). In dimension 3, we derive that the problem admits a global bounded solution when \(q>\frac{8}{7}\). In fact, we transfer the difficulty of estimation to the logistic term through iterative methods, thus, compared to the results in (J. Math. Anal. Appl. 2:448 2017; Z. Angew. Math. Phys. 73(2):1–25 2022) in dimension 3, our results do not require any restrictions on the coefficients.
Similar content being viewed by others
1 Introduction
Chemotaxis refers to the directional movement of cells or organisms towards chemical stimuli along a concentration gradient, which plays an essential role in various biological processes such as wound healing, cancer invasion, and avoidance of predators [4]. The chemotaxis model was first proposed by Keller and Segel in [5] as follows:
which describes the cellular slime mold move towards a higher concentration of a chemical signal. Since it was proposed, it has attracted interest of a large number of scholar’s and they obtained many results about boundedness or blow-up of solutions [6–11]. In a one-dimensional bounded domain, (1.1) admits a global bounded solution [6]. But in dimension two, the solution of (1.1) may blow-up, that is, when \({ \Vert {{u_{0}}} \Vert _{{L^{1}}}} < 4\pi \), the classical solution is global and bounded [7], and when \({ \Vert {{u_{0}}} \Vert _{{L^{1}}}} \ge 4\pi \), \({ \Vert {{u_{0}}} \Vert _{{L^{1}}}} \notin \{ {4k\pi } \vert k \in \mathbb{N}\} \), the blow-up of the solution may occur in finite or infinite time [8, 9]. In dimension N (\(N \ge 3\)), a small critical mass condition alone is not enough to prevent the blow-up of the solution [10, 11].
However, cellular slime mold might experience proliferation or death during the process of directional movement. Since then, Mimura and Tsujikawa [12] introduced a generalized K–S model which considers the proliferation and death of bacteria, that is,
where \(\tau \ge 0\), \(f(u)\) represents the proliferation and death of bacteria, which we call a logistic term. Actually, \(\tau =0\) is a simplified form, which represents the case when chemicals move much faster than bacteria [13]. When \(\tau =0\), we assume that \(f \in {C^{1}}( {[0,\infty )})\), and it satisfies \(f(s) \le c - \mu {s^{2}}\) for all \(s \ge 0\), \(f(s) > 0\) if \(0< s<1\), and \(f(s) < 0\) if \(s > 1\), with some positive constants c, μ. Tello and Winkler [14] derived that the model (1.2) admits a unique global bounded classical solution when either \(N \le 2\) or \(\mu > \frac{{N - 2}}{N}\chi \). When \(\tau >0\), in 2001, Osaki and Yagi [15] proved the model (1.2) admits a global bounded classical solution in \({\mathbb{R}^{1}}\), and then in 2002, they also derived similar results in \({\mathbb{R}^{2}}\) [16, 17]. In 2010, Winkler [18] extended their results to arbitrary space dimensions with the condition \(\mu > {\mu _{0}}\) for some \({\mu _{0}} > 0\). For other results related to (1.2), please refer to [19–22]. In addition, related mathematical models which describe the chemotaxis phenomenon were widely studied, such as the chemotaxis–haptotaxis model [23, 24], chemotaxis–fluid model [25, 26], attraction–repulsion chemotaxis model [27], and so on.
To describe the formation of senile plaques in Alzheimer disease (AD), Luca et al. [28] proposed a attraction–repulsion chemotaxis system in 2003. The interesting aspect of this model is that it includes both chemoattraction and chemorepulsion, and the model read as
where \(Q = \Omega \times {\mathbb{R}^{+} }\), Ω is a bounded domain; \(\frac{\partial }{{\partial {\mathbf{n}}}}\) represent the derivative with respect to the outer normal of ∂Ω; u, v, w represent the concentration of microglia, the concentration of chemoattractant and the concentration of chemorepellent, respectively; χ and ξ are chemotactic coefficients; \(f(u)\) represents the proliferation or death of cells; \({\alpha _{i}},{\beta _{i}}> 0\) (\(i = 1,2\)) are rates of production and decay of the chemicals, respectively. This model attracted a large number of scholars, and they obtained many results of this model. First, we introduce the results if \(f(u) \equiv 0\). In [29], Tao and Wang derived that the model (1.3) admits a global classical solution in higher dimensions if repulsion prevails over attraction \((\xi {\alpha _{2}} - \chi {\alpha _{1}} > 0)\) for the case \({\tau _{1}} = {\tau _{2}} = 0\); they also proved that the model (1.3) admits a global classical solution in \({\mathbb{R}^{2}}\) if repulsion prevails over attraction for the case \({\tau _{1}} = {\tau _{2}} = 1\) which needs the smallness assumption on the initial data \({u_{0}}\). Then Jin [30] removed the smallness assumption on \({u_{0}}\) in [29], and proved that model (1.3) admits a unique nonnegative classical solution when \({\tau _{1}} = {\tau _{2}} = 1\) in \({\mathbb{R}^{2}}\). The global solvability of the model (1.3) for the case \(\xi {\alpha _{2}} - \chi {\alpha _{1}} = 0\) in \({\mathbb{R}^{2}}\) was established in [31]. The results in [32] indicated that even for the case \(\xi {\alpha _{2}} - \chi {\alpha _{1}} < 0\), (1.3) admits a global classical solution in \({\mathbb{R}^{2}}\) for the parabolic–parabolic system.
For the case \(f(u) \ne 0\), there are also many results. When \({\tau _{1}} = {\tau _{2}} = 0\), \(f(u) \le \lambda - \mu {u^{p}}\), Li and Zhao [33] proved that the model (1.3) admits a unique global bounded classical solution if
The results indicated that the model (1.3) admits a global bounded classical solution under the weak logistic damping in the case \(\xi {\beta _{2}} > \chi {\beta _{1}}\), but when \(\xi {\beta _{2}} < \chi {\beta _{1}}\), the logistic damping must be stronger. Xu and Zheng [34] improved the the results in [33] for the case \(\xi {\beta _{2}} = \chi {\beta _{1}}\) by proving that a weaker restriction \(p > \frac{{2N + 2}}{{N + 2}}\) is sufficient to ensure the global boundedness of solutions. When \({\tau _{1}} = {\tau _{2}} = 0\), \(f(u) \le \mu u(1 - u)\), Zhang and Li [35] proved that the model (1.3) admits a unique global bounded classical solution if one of the following assumptions holds:
When \({\tau _{1}} = {\tau _{2}} = 1\), \(f(u) \le \lambda u - \mu {u^{p}}\) with \(p \ge 1\), \(\xi {\beta _{2}} = \chi {\beta _{1}}\), Wang, Zhuang, and Zheng [36] proved that the model (1.3) admits a global bounded classical solution if
In [2], Li et al. proved that when \({\tau _{1}} = {\tau _{2}} = 1\), \(f(u) = u(1 - \mu {u^{p}})\) with \(p\ge 1\), the model (1.3) admits a global bounded classical solution if \({\alpha _{i}}(i = 1,2) \ge \frac{1}{2}\), \(\mu \ge \max \{ {{(\frac{{41}}{2}\chi {\beta _{1}} + 9\xi { \beta _{2}})}^{p}}, (9\chi {\beta _{1}} + \frac{{41}}{2}\xi {\beta _{2}})^{p} \}\) in \({\mathbb{R}^{3}}\). In 2022, Ren and Liu [3] improved their results in [2] by avoiding any restriction on \({\alpha _{i}}\) (\(i = 1,2\)).
In this paper, we consider the following attraction–repulsion model:
where \(Q = \Omega \times {\mathbb{R}^{+} }\), \(\Omega \subset {\mathbb{R}^{3}}\) is a bounded domain. All the coefficients χ, ξ, μ, \({\alpha _{1}}\), \({\alpha _{2}}\), \({\beta _{1}}\), \({\beta _{2}}\) are positive. Actually, the model (1.4) admits a global classical solution when \(q \ge 1\) in \({\mathbb{R}^{2}}\) [1], which requires no restrictions on the coefficients, and the logistic damping is weak. Our results indicate that the model (1.4) admits a global classical solution when \(q > \frac{{8}}{{7}}\) in dimension 3. Compared to the results in [2, 3], our results do not require any restrictions on the coefficients. In fact, we transferred the difficulty of estimation to the logistic term. Our proof is mainly divided into two parts, that is, we consider the case \(q \ge 2\) and \(\frac{8}{7}< q <2\). When \(\frac{8}{7}< q <2\), we use the iterative method to improve the regularity of u.
Then we give the assumptions of this paper:
Our main results read as follows:
Theorem 1.1
Let \(\Omega \subset {\mathbb{R}^{3}}\) be a bounded domain. Assume that (H) holds and \(q > \frac{8}{7}\). Then for any \(\chi ,\xi ,\mu ,{\alpha _{1}},{\alpha _{2}},{\beta _{1}},{\beta _{2}} > 0\), (1.4) admits a unique global bounded classical solution which satisfies
where C is independent of t.
2 Preliminaries
In this paper, for the convenience of writing, we denote \({ \Vert \cdot \Vert _{{L^{p}}}} = { \Vert \cdot \Vert _{{L^{p}}( \Omega )}}\). Since all the estimates of v and w are almost the same except for the coefficients, we show the details for v, and just list the results for w without any proof. Next, we will give some lemmas, which will be used throughout this paper.
Lemma 2.1
([37])
Let \(T>0\), \(\tau \in (0,T)\), \(\delta \ge 0\), \(a>0\), \(b \ge 0\), and suppose that \(f:[0,T) \to [0,\infty )\) is absolutely continuous and satisfies
where \(h \ge 0\), \(h(t) \in L_{\mathrm{loc}}^{1}([0,T))\), and
Then
Lemma 2.2
([38])
Assume \({u_{0}} \in {W^{2,p}}(\Omega )\), and \(f \in L_{\mathrm{loc}}^{p}([0, + \infty );{L^{p}}(\Omega ))\) with
where \(\tau >0\) is a fixed constant. Then the following problem:
admits a unique solution \(u \in L_{\mathrm{loc}}^{p}([0, + \infty );{W^{2,p}}(\Omega ))\), \({u_{t}} \in L_{\mathrm{loc}}^{p}([0, + \infty );{L^{p}}(\Omega ))\) with
where \(C(A,\alpha ,\beta )\) and \(C(\alpha ,\beta )\) are constants independent of τ.
Remark 2.1
In this paper, we fix \(\tau = \min \{ 1,\frac{{{T_{\max }}}}{2}\} \le 1\). Thus, all the constants in this paper are independent of τ. In fact, if \(\tau =1\), it is easy to see that the constants in Lemma 2.2 can be fixed. While if \(\tau <1\), it implies that \({T_{\max }} < 2\), all the \(\int _{t - \tau }^{t} { \Vert \cdot \Vert \,ds} \) can be replaced by \(\int _{0}^{{T_{\max }}} { \Vert \cdot \Vert \,ds} \).
Lemma 2.3
([23])
Assume that Ω is bounded and let \(\omega \in {C^{2}}(\overline{\Omega})\) satisfy \({ {\frac{{\partial \omega}}{{\partial \textbf {n}}}} \vert _{ \partial \Omega }} = 0\), where n is the outward unit normal vector to the boundary ∂Ω. Then we have
where \(\kappa > 0\) is an upper bound for the curvatures of Ω.
3 Main results
Using a fixed point argument similar to that in [39], we obtain the following local existence result of classical solution to (1.4).
Lemma 3.1
Let \(\Omega \subset {\mathbb{R}^{N}}\), \(N \ge 1\) be a bounded domain with a smooth boundary. Assume that \({u_{0}}\), \({v_{0}}\), \({w_{0}}\) satisfy (H). Then there exists \({T_{\max }} \in (0, + \infty ]\) such that the problem (1.4) admits a unique nonnegative classical solution \((u,v,w) \in {C^{0}}(\overline{\Omega}\times [0,{T_{\max }})) \cap {C^{2,1}}( \overline{\Omega}\times (0,{T_{\max }}))\). Moreover, either \({T_{\max }} =\infty \), or
By Lemma 3.1, we see that in order to prove the global existence of a classical solution, we assume that \({T_{\max }} < \infty \), and only need to show the boundedness of \(\Vert {u( \cdot ,t)} \Vert _{{L^{\infty }}(\Omega )} + {{ \Vert {v( \cdot ,t)} \Vert }_{{L^{\infty }}(\Omega )}} + {{ \Vert {w( \cdot ,t)} \Vert }_{{L^{\infty }}(\Omega )}}\) for any \(t \in (0,{T_{\max }})\).
It is not difficult to obtain the following lemma.
Lemma 3.2
Let \((u,v,w)\) be the solution of (1.4), and assume (H) holds. Then we have
where the constants C at most depend on χ, μ, ξ, \({\alpha _{1}}\), \({\alpha _{2}}\), \({\beta _{1}}\), \({\beta _{2}}\), \({u_{0}}\), \({v_{0}}\), \({w_{0}}\), but are independent of \({T_{\max }}\) and τ.
Proof
By a direct integration to the first equation of (1.4), we have
which means
Since Ω is a bounded domain, it is easy to see that \({ ( {\int _{\Omega }{u\,dx} } )^{q + 1}} \le \int _{ \Omega }{{u^{q + 1}}\,dx} \) for any \(q \ge 1\), and then, by Lemma 2.1, we obtain (3.1).
Using (3.1) and Lemma 2.2, we obtain (3.2). Similarly, we obtain (3.3).
Multiplying the second equation of (1.4) by v and \(- \Delta v\), respectively, integrating them over Ω, and using Young’s inequality, we obtain
Combining the above two inequalities yields
and then, by (3.1) and Lemma 2.1, we obtain (3.4). Similarly, we have (3.5). □
Through the above lemma, we have the following results.
Lemma 3.3
Let \((u,v,w)\) be the solution of (1.4), and assume (H) holds. Then for any \(r \ge 2\), \(R>1\), \(p>1\), we have
where C at most depend on χ, μ, ξ, \({\alpha _{1}}\), \({\alpha _{2}}\), \({\beta _{1}}\), \({\beta _{2}}\), \({u_{0}}\), \({v_{0}}\), \({w_{0}}\), but are independent of \({T_{\max }}\) and τ.
Proof
For any \(p>1\), multiplying the first equation of (1.4) by \(p{u^{p - 1}}\), and integrating it over Ω, for any \(q>1\), we have
and then rearranging it we obtain (3.6).
Applying ∇ to the second equation of (1.4), and multiplying the resulting equation by \({ \vert {\nabla v} \vert ^{r - 2}}\nabla v\) (for any \(r \ge 2\)), by a direct calculation, it is easy to see that \({ \vert {\nabla v} \vert ^{r - 2}}\nabla v \cdot \nabla \Delta v = \frac{1}{2}{ \vert {\nabla v} \vert ^{r - 2}}\Delta { \vert { \nabla v} \vert ^{2}} - { \vert {\nabla v} \vert ^{r - 2}}{ \vert {{D^{2}}v} \vert ^{2}}\). Now integrating the result over Ω and combining with Lemma 2.3, we have
Rearranging the above inequality, for any \(R>1\), we have
It is easy to see that for any \(\delta >0\) and \(f \in {L^{{q_{1}}}} \cap {L^{{q_{2}}}}\), we have
where \(1 \le {q_{1}} < {q_{2}}\), \(r' \in [{q_{1}},{q_{2}}]\), \(\alpha = \frac{{{q_{1}}({q_{2}} - r')}}{{r'({q_{2}} - {q_{1}})}}\). Using the boundary trace embedding inequalities [40], (3.4) and (3.10), we obtain
Now taking \(\varepsilon = \frac{{r - 2}}{{{r^{2}}}}\) and combining this inequality with (3.9), we obtain (3.7). □
(I) Estimates for \(q \ge 2\).
Lemma 3.4
Let \((u,v,w)\) be the solution of (1.4), and assume (H) holds. If \(N = 3\), \(q \ge 2\), then for any \(p>1\), we have
where \({C_{p}}\) depends only on p, Ω, \({u_{0}}\), and C depend on Ω, \({u_{0}}\). All of them are independent of τ and \({T_{\max }}\).
Proof
Recalling (3.1), and taking \(\frac{{2R}}{{R - 1}} = q + 1\), \(r = q + 1\) in (3.7) and (3.8), then using Lemma 2.1, we obtain
For any \(p>1\), multiplying by \({u^{p - 1}}\) the first equation of (1.4), and integrating the result over Ω, we have
Now rearranging it, we have
Using (3.1), (3.14), and Gagliardo–Nirenberg interpolation inequality [34], for any \(q>2\), we have
Similarly, we have
Taking \(\varepsilon ,\overline{\varepsilon}= \frac{{p - 1}}{2p}\), and using the above two inequalities in (3.16), we obtain
And then by Lemma 2.1, we obtain (3.11).
Now we consider the case for \(q=2\). Taking \(p=3\) in (3.16), we obtain
By Gagliardo–Nirenberg interpolation inequality and (3.14), we have
Similarly, we get
Now combining these above three inequalities, we have
Using (3.14), (3.15), and Lemma 2.1, we obtain
By Duhamel’s principle, the second equation of (1.4) can be expressed as follows:
where \({\{ {e^{t\Delta }}\} _{t \ge 0}}\) represents the Neumann heat semigroup in Ω; for more details about the theory of Neumann heat semigroups, please refer to [10, 41, 42]. Then for any \(r \in (1, + \infty )\), \(t \in (0,{T_{\max }})\), we have
thus, we obtain
Similarity, we have
and then, using the above two inequalities in (3.16) and taking advantage of Lemma 2.1, we have (3.11).
Similar to the proof above, and by (3.11), for any \(t \in (0,{T_{\max }})\), we also have
and
The estimate of w is similar that of v, so we have (3.13). The proof is complete. □
(II) Estimates for \(q < 2\).
Lemma 3.5
Let \((u,v,w)\) be the solution of (1.4). Assume (H) holds, and \({a_{n}} + q < 5\) with \(q<2\). If
then for any \(r < \frac{{3({a_{n}} + q)}}{{5 - ({a_{n}} + q)}}\), we have
and for any \(p + q < \frac{{5q}}{2} \cdot \frac{{{a_{n}} + q}}{{5 - ({a_{n}} + q)}}\), we have
where \({C_{n}}(r)\), \({C_{n + 1}}(p)\) are independent of τ and \({T_{\max }}\), which only depend on p, r, n, \({u_{0}}\), \({v_{0}}\), and Ω.
Proof
Taking \(r = {a_{n}} + q\), \(R = \frac{{{a_{n}} + q}}{{{a_{n}} + q - 2}}\) in (3.7), where \(\{ {a_{n}}\} \) is positive with \({a_{1}} = 1\), we have
Then by Lemma 2.1, we obtain
Moreover, we select a nonnegative sequence \(\{ {r_{k}}\} \) with \({r_{k + 1}} = 2 + \frac{{5({a_{n}} + q - 2)}}{{3({a_{n}} + q)}}{r_{k}}\). Obviously, \({r_{k}}\) is monotonically increasing. Next, we prove that if
then
By Gagliardo–Nirenberg interpolation inequality, we have
which means
Recalling (3.7) and taking \(\frac{{2R}}{{R - 1}} = {a_{n}} + q\), \(( {r - 2} )R = \frac{{5}}{3}{r_{k}}\), that is, \(R = \frac{{{a_{n}} + q}}{{{a_{n}} + q - 2}}\), \(r = 2 + \frac{{5({a_{n}} + q - 2)}}{{3({a_{n}} + q)}}{r_{k}}\), we then have
Now (3.23) is obtained by Lemma 2.1. Note that \({r_{k + 1}} - \frac{{3({a_{n}} + q)}}{{5 - ({a_{n}} + q)}} = \frac{5}{3} \cdot \frac{{{a_{n}} + q - 2}}{{{a_{n}} + q}} ( {{r_{k}} - \frac{{3({a_{n}} + q)}}{{5 - ({a_{n}} + q)}}} )\), where \(0 < \frac{5}{3} \cdot \frac{{{a_{n}} + q - 2}}{{{a_{n}} + q}} < 1\), which means \(\{ {{r_{k}} - \frac{{3({a_{n}} + q)}}{{5 - ({a_{n}} + q)}}} \}\) is monotonically decreasing, so \({r_{k}}\) goes to \(\frac{{3({a_{n}} + q)}}{{5 - ({a_{n}} + q)}}\), thus (3.18) holds. Recalling (3.8) and taking \(\frac{{2(p + q)}}{q} = \frac{{5}}{3}r\), similarly we can obtain (3.19) through (3.8), and thus (3.20) holds for any \(p + q < \frac{{5q}}{2} \cdot \frac{{{a_{n}} + q}}{{5 - ({a_{n}} + q)}}\). □
Lemma 3.6
Let \((u,v,w)\) be the solution of (1.4), assume (H) holds, and \(\frac{{8}}{{7}} < q < 2\). Then for any \(p \in (1, + \infty )\), we have
where C are independent of τ and \({T_{\max }}\).
Proof
Letting \({A_{n + 1}} + q = \frac{{5q}}{2} \cdot \frac{{{A_{n}} + q}}{{5 - ({A_{n}} + q)}}\) with \({A_{1}} = 1\), we see that
Since \(q > \frac{{8}}{7}\), it indicates that \(\{ {A_{n + 1}} + q\} \) is monotonically increasing. Thus there exists \(M=M(q)\) such that \({A_{M}} + q > 5\). Then by Lemma 3.5, there exists \({p_{M}} + q \ge 5\) such that (3.20) holds. Since \(q<2\), we have
Then similar to the proof in Lemma 3.4 for the case \(q=2\), we have (3.25), (3.26), and (3.27). □
Proof of Theorem 1.1
Combining Lemmas 3.4 and 3.6, we see that for any \(q > \frac{8}{7}\),
Next, we use the standard Moser’s iterative technique to prove the boundedness of \({ \Vert {u( \cdot ,t)} \Vert _{{L^{\infty }}}}\).
Multiplying the first equation of (1.4) by \(p{u^{p - 1}}\) (for any \(p \ge 2\)), and by (3.28), (3.29), we obtain
which means
where C is independent of p. By Gagliardo–Nirenberg interpolation inequality and Young’s inequality, we have
where \({C_{40}}\), \({C_{41}}\), \({C_{42}}\) are independent of p, and \(\frac{1}{2}p(p - 1) > \frac{1}{4}{p^{2}}\) since \(p \ge 2\). Thus, we have
where C is independent of p. Taking \({p_{j}} = 2{p_{j - 1}}\) with \({p_{1}} = 2\), \({Q_{j}} = \max \{ \sup_{t \in (0,{T_{\max }})} \Vert u( \cdot , t) \Vert _{{L^{{p_{j}}}}}, \Vert {{u_{0}}} \Vert _{{L^{\infty }}}\} \), replacing p, \({\frac{p}{2}}\) by \({p_{j}}\), \({p_{j - 1}}\) in (3.31), and by a direct calculation, for any \(j \ge 2\), we obtain
Then for any \(n>2\), we have
Letting \(n \to \infty \), we obtain
It is easy to see that \({\sum_{j = 2}^{\infty }{\frac{1}{{{2^{j}}}}} }\) and \({\sum_{j = 2}^{\infty }{\frac{{5j}}{{{2^{j}}}}} }\) are convergent. Recalling Lemmas 3.4 and 3.6, we have
Combining this with (3.28), (3.29), we complete the proof of Theorem 1.1. □
Data Availability
No datasets were generated or analysed during the current study.
References
Li, X.: Boundedness in a two-dimensional attraction–repulsion system with nonlinear diffusion. Math. Methods Appl. Sci. 39(2), 289–301 (2016)
Li, D., Mu, C., Lin, K., Wang, L.: Large time behavior of solution to an attraction–repulsion Chemotaxis system with logistic source in three dimensions. J. Math. Anal. Appl. 2, 448 (2017)
Ren, G., Liu, B.: Boundedness and stabilization in the 3D minimal attraction–repulsion Chemotaxis model with logistic source. Z. Angew. Math. Phys. 73(2), 1–25 (2022)
Isenbach, M.: Chemotaxis. Imperial College Press, London (2004)
Keller, E.F., Segel, L.A.: Initiation of slime mold aggregation viewed as an instability. J. Theor. Biol. 26(3), 399–415 (1970)
Osaki, K., Yagi, A.: Finite dimensional attractors for one-dimensional Keller–Segel equations. Funkc. Ekvacioj 44, 441–469 (2001)
Nagai, T., Senba, T., Yoshida, K.: Application of the Trudinger–Moser inequality to a parabolic system of Chemotaxis. Funkc. Ekvacioj 40, 411–433 (1997)
Horstmann, D., Wang, G.: Blow-up in a Chemotaxis model without symmetry assumptions. Eur. J. Appl. Math. 12(02), 159–177 (2001)
Senba, T., Suzuki, T.: Parabolic system of Chemotaxis: blowup in a finite and the infinite time. Methods Appl. Anal. 8(2), 349–367 (2001)
Winkler, M.: Aggregation vs. global diffusive behavior in the higher-dimensional Keller–Segel model. J. Differ. Equ. 248(12), 2889–2905 (2010)
Winkler, M.: Finite-time blow-up in the higher-dimensional parabolic–parabolic Keller–Segel system. J. Math. Pures Appl. 100, 748–767 (2013)
Mimura, M., Tsujikawa, T.: Aggregating pattern dynamics in a Chemotaxis model including growth. Phys. A, Stat. Mech. Appl. 230(3–4), 499–543 (1996)
Jäger, W., Luckhaus, S.: On explosions of solutions to a system of partial differential equations modelling Chemotaxis. Trans. Am. Math. Soc. 329(2), 819–824 (1992)
Tello, J., Winkler, M.: A Chemotaxis system with logistic source. Commun. Partial Differ. Equ. 32(6), 849–877 (2007)
Osaki, K., Yagi, A.: Finite dimensional attractor for one-dimensional Keller–Segel equations. Funkc. Ekvacioj 44(3), 441–470 (2001)
Osaki, K.: Global existence for a Chemotaxis–growth system in \(\mathbb{R}^{2}\). Adv. Math. Sci. Appl. 12, 587–606 (2002)
Osaki, K., Tsujikawa, T., Yagi, A., Mimura, M.: Exponential attractor for a Chemotaxis–growth system of equations. Nonlinear Anal. 51(1), 119–144 (2002)
Winkler, M.: Boundedness in the higher-dimensional parabolic–parabolic Chemotaxis system with logistic source. Commun. Partial Differ. Equ. 35(8), 1516–1537 (2010)
Lankeit, J.: Eventual smoothness and asymptotics in a three-dimensional Chemotaxis system with logistic source. J. Differ. Equ. 258(4), 1158–1191 (2015)
Viglialoro, G.: Boundedness properties of very weak solutions to a fully parabolic Chemotaxis-system with logistic source. Nonlinear Anal., Real World Appl. 34, 520–535 (2017)
Viglialoro, G., Woolley, T.E.: Eventual smoothness and asymptotic behaviour of solutions to a Chemotaxis system perturbed by a logistic growth. Discrete Contin. Dyn. Syst. 23(8), 3023–3045 (2018)
Winkler, M.: Finite-time blow-up in low-dimensional Keller–Segel systems with logistic-type superlinear degradation. Z. Angew. Math. Phys. 69, 1–25 (2018)
Zhang, D., Jin, C.: Global solvability to a cancer invasion model with remodeling of ECM and porous medium diffusion. Commun. Math. Sci. 20(6), 1493–1516 (2022)
Zhang, D., Jin, C., Xiang, Y.: Stabilization to a cancer invasion model with remodeling mechanism and slow diffusion. Z. Angew. Math. Phys. 73(5), 201 (2022)
Jin, C.: Global classical solution and stability to a coupled Chemotaxis–fluid model with logistic source. Discrete Contin. Dyn. Syst. 38(7), 3547–3566 (2018)
Jin, C.: Global bounded weak solutions and asymptotic behavior to a Chemotaxis–Stokes model with non-Newtonian filtration slow diffusion. J. Differ. Equ. 287, 148–184 (2021)
Wang, W., Zhuang, M., Zheng, S.: Positive effects of repulsion on boundedness in a fully parabolic attraction–repulsion Chemotaxis system with logistic source. J. Differ. Equ. 264(3), 2011–2027 (2018)
Luca, M., Chavez-Ross, A., Edelstein-Keshet, L., Mogilner, A.: Chemotactic signaling, microglia, and Alzheimer’s disease senile plaques: is there a connection? Bull. Math. Biol. 65(4), 693–730 (2003)
Tao, Y., Wang, Z.: Competing effects of attraction vs. repulsion in Chemotaxis. Math. Models Methods Appl. Sci. 23(01), 1–36 (2013)
Jin, H.: Boundedness of the attraction-repulsion Keller–Segel system. J. Math. Anal. Appl. 422, 1463–1478 (2015)
Lin, K., Mu, C., Wang, L.: Large-time behavior of an attraction–repulsion Chemotaxis system. J. Math. Anal. Appl. 426(1), 105–124 (2015)
Lin, K., Mu, C.: Global existence and convergence to steady states for an attraction–repulsion Chemotaxis system. Nonlinear Anal., Real World Appl. 31, 630–642 (2016)
Li, X., Xiang, Z.: On an attraction-repulsion Chemotaxis system with a logistic source. IMA J. Appl. Math. 81, 165–198 (2016)
Xu, P., Zheng, S.: Global boundedness in an attraction-repulsion Chemotaxis system with logistic source. Appl. Math. Lett. 83, 1–6 (2018)
Zhang, Q., Li, Y.: An attraction–repulsion Chemotaxis system with logistic source. Z. Angew. Math. Mech. 96, 570–584 (2016)
Wang, W., Zhuang, M., Zheng, S.: Positive effects of repulsion on boundedness in a fully parabolic attraction-repulsion Chemotaxis system with logistic source. J. Differ. Equ. 264, 2011–2027 (2018)
Jin, C., Wang, Y., Yin, J.: Global solvability and stability to a nutrient–taxis model with porous medium slow diffusion (2018). arXiv:1804.03964
Jin, C.: Global solvability and stabilization to a cancer invasion model with remodelling of ECM. Nonlinearity 33(10), 5049–5079 (2022)
Horstmann, D., Winkler, M.: Boundedness vs. blow-up in a Chemotaxis system. J. Differ. Equ. 215, 52–107 (2005)
Diaz, J., Véron, L.: Local vanishing properties of solutions of elliptic and parabolic quasilinear equations. Trans. Am. Math. Soc. 290(2) (1985)
Ishida, S., Seki, K., Yokota, T.: Boundedness in quasilinear Keller–Segel systems of parabolic–parabolic type on non-convex bounded domains. J. Differ. Equ. 256(8), 2993–3010 (2014)
Sugiyama, Y.: Time global existence and asymptotic behavior of solutions to degenerate quasi-linear parabolic systems of Chemotaxis. Differ. Integral Equ. 20(2), 133–180 (2007)
Li, D., Mu, C., Lin, K., Wang, L.: Large time behavior of solution to an attraction–repulsion Chemotaxis system with logistic source in three dimensions. J. Math. Anal. Appl. 2, 448 (2017)
Ren, G., Liu, B.: Boundedness and stabilization in the 3D minimal attraction–repulsion Chemotaxis model with logistic source. Z. Angew. Math. Phys. 73(2), 1–25 (2022)
Funding
This article received no funding at all.
Author information
Authors and Affiliations
Contributions
All content of this article was completed by myself.
Corresponding author
Ethics declarations
Ethics approval and consent to participate
Not applicable.
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Zhang, D. Global solvability and boundedness to a attraction–repulsion model with logistic source. Bound Value Probl 2024, 94 (2024). https://doi.org/10.1186/s13661-024-01904-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13661-024-01904-9