Abstract
In this paper, we study the existence, nonexistence, and multiplicity of positive solutions to a nonlinear impulsive Sturm–Liouville boundary value problem with a parameter. By using a variational method, we prove that the problem has at least two positive solutions for the parameter \(\lambda \in (0,\Lambda )\), one positive solution for \(\lambda =\Lambda \), and no positive solution for \(\lambda >\Lambda \), where \(\Lambda >0\) is a constant.
Similar content being viewed by others
1 Introduction
In this paper, we investigate the following nonlinear impulsive Sturm–Liouville boundary value problem:
where \(J=[0,1]\), p is a positive integer, \(0=t_{0}< t_{1}< t_{2}<\cdots<t_{p}<t_{p+1}=1\), \(Lu=(h(t)u'(t))'-q(t)u(t)\), \(R_{1}(u)=\alpha u'(0)-\beta u(0), R_{2}(u)=\gamma u'(1)+\sigma u(1)\), \(\alpha,\beta ,\gamma ,\sigma \in \mathbb{R}\), \(\Delta (h(t_{k})u'(t_{k}))=h(t_{k}^{+})u'(t_{k}^{+})-h(t_{k}^{-})u'(t_{k}^{-})\), \(u'(t_{k}^{+})\) and \(u'(t_{k}^{-})\) represent the right limit and the left limit of \(u'(t)\) at \(t_{k}\), respectively, and λ is a positive parameter.
The following conditions are assumed:
- \((H_{1})\):
-
\(h\in C^{1}(J), q\in C(J), h>0,q>0 \) for all \(t\in J\), \(\alpha ,\beta ,\gamma ,\sigma \geq 0\), \(\alpha ^{2}+\beta ^{2}>0,\gamma ^{2}+\sigma ^{2}>0\), and the linear equation (2.1) has only a trivial solution.
- \((H_{2})\):
-
\(f\in C(J\times \mathbb{R}^{+},\mathbb{R}^{+})\), where \(\mathbb{R}^{+}=(0,+\infty )\). \(f(t,x)=o(x)\) as \(x\rightarrow 0^{+}\) uniformly to \(t\in J\), and there exist constants \(\mu >2\) and \(r>0\) such that for \(x\geq r, t\in J\),
$$ \mu F(t,x)\leq xf(t,x), $$where \(F(t,x)=\int _{0}^{x}f(t,s)\,ds\).
- \((H_{3})\):
-
\(I_{k}\in C([0,+\infty ),[0,+\infty ))\). For any \(k\in \{1,2,\ldots, p\}\), \(I_{k}(x)\rightarrow +\infty \) as \(x\rightarrow +\infty \) or \(\sup_{x>0}I_{k}(x)<\infty \), and there exist \(1\leq K\leq p\), \(0\leq \tau _{0}<1, \kappa >0\) such that \(I_{K}(x)\geq \kappa x^{\tau _{0}}\) for \(x>0\).
It should be noted that impulsive differential equations are important models described by phenomena with abrupt changes in their states. Such models have considerable popularity in physics, population dynamics, ecology, industrial robotics, economics, biotechnology, and so on, see [1–3].
In recent years, boundary value problems of impulsive differential equations have been researched extensively, see for example [4–18] and the references therein. In [19], Tian and Ge studied the special cases of (1.1) without parameters
where \(\mu \in \mathbb{R}\), g and \(s_{k}\) are of superlinear growth or sublinear growth, the authors showed the existence of one or two positive solutions for (1.2). In [20], authors obtained the existence of a sign-changing solution and multiple solutions of
The technical approach makes use of the minimax method.
In [21], by using a three critical point theorem, authors considered the following fourth order impulsive differential equations with two control parameters:
They established the sharp bounds of the parameters λ and μ for which problem (1.4) admits at least three solutions. For the existence and multiplicity results of solutions of impulsive boundary value problems obtained by using variational methods, we refer to [22–31].
To our knowledge, there are few studies on the connection between the number of solutions and the given parameter for impulsive differential equations. The aim of this paper is to show the multiplicity, existence, and nonexistence of positive solutions for various values of the given parameter. Our result shows that the number of positive solutions of (1.1) changes if the parameter crosses a certain threshold.
This paper is organized as follows. In Sect. 2, we recall some preliminary results. In Sect. 3, by using the mountain pass principle, we prove that (1.1) has at least two positive solutions if λ is sufficiently small, and no solution if λ is sufficiently large, see Theorem 3.1. Throughout the paper, the symbols \(C_{1}, C_{2}, \ldots \) denote various positive constants whose exact values are not essential to the analysis of the problem. In addition, without loss of generality, we may assume that \(f(t,x)=0,I_{k}(x)=0(1\leq k\leq p)\) for \(x<0\) as we only consider positive solutions.
2 Basic lemma
Let \(G(t,s)\) be Green’s function of the problem
From [32], \(G(t,s)\) can be written as
Lemma 2.1
The function \(G(t,s)\) defined by (2.2) has the following properties:
\((1)\) \(m\in C^{2}(J,\mathbb{R}) \) is increasing and \(m(t)>0, t\in (0,1]\).
\((2)\) \(n\in C^{2}(J,\mathbb{R}) \) is decreasing and \(n(t)>0, t\in [0,1)\).
\((3)\) \(Lm\equiv 0, m(0)= \alpha , m'(0)= \beta \).
\((4)\) \(Ln\equiv 0, n(1)= \gamma , n'(1)= -\sigma \).
\((5)\) ω is a positive constant and \(p(t)(m'(t)n(t)-m(t)n'(t))\equiv \omega \).
\((6)\) \(G(t,s)\) is continuous and symmetric in \(\{(t,s): 0\leq t \leq s\leq 1\} \times \{(t,s): 0\leq s \leq t\leq 1 \}\).
\((7)\) \(G(t,s)\) has continuous partial derivatives in \(\{(t,s): 0\leq t \leq s\leq 1\}, \{(t,s): 0\leq s \leq t\leq 1 \}\).
\((8)\) For each fixed \(s\in [0,1], G(t,s)\) satisfies \(LG(t,s)=0\) for \(t\neq s, t\in J\) and \(R_{1}(G)=R_{2}(G)=0\).
\((9)\) \(G_{t}'\) has a discontinuous point of the first kind at \(t=s\) and \(G_{t}'(s+0,s)-G_{t}'(s-0,s)=-\frac{1}{h(s)}, s\in (0,1)\).
Let \(P=\{u\in C(J), u\geq 0\}\) and \((Tu)(t)=\int _{0}^{1}G(t,s)u(s)\,ds\), then
By the Krein–Rutman theorem, the spectral radius \(r(T)>0\) is determined by a simple eigenvalue of T having an eigenfunction \(\varphi _{0}(t)\in P\) with \(\varphi _{0}>0, t\in (0,1)\). It is easy to check that \(\lambda ^{*}=r^{-1}(T)\) is the smallest eigenvalue of the eigenvalue problem:
and \(\varphi _{0}\) is eigenfunction corresponding to \(\lambda _{1}\).
Definition 2.1
A function \(u\in \Theta =\{x\in C(J):h x'\in C(J/\{t_{1},\ldots,t_{p}\}),x'(t_{k}^{+}),x'(t_{k}^{-})\) exists and \(x'(t_{k})=x'(t_{k}^{-})\}\) is said to be a solution of (1.1) if u satisfies the equation in (1.1) for \(t\in J/\{t_{1}, t_{2},\ldots,t_{p}\}\) and impulsive conditions, boundary conditions of (1.1). The function u is a positive solution of (1.1) if u is a solution of (1.1) and \(u(t)>0\) for \(t\in (0,1)\).
Let
Define an inner product in H as follows:
This inner product induces the norm
It is easy to check that H with the inner product \((\cdot , \cdot )\) is a Hilbert space, and \(u^{+}=\max \{u,0\}\in H, u^{-}=\max \{-u,0\}\in H \) for \(u\in H \).
Define the functional \(\Phi _{\lambda}\) in H by
Then \(\Phi _{\lambda}\in C^{1}(H,R)\), and
Lemma 2.2
If \(u\in H\), then there is \(C>0\) such that
where \(|u|_{0}=\max_{t\in J}|u(t)|\).
Proof
Let \(\|\cdot \|_{H}\) be the usual norm of \(H^{1}(0,1)\). From the imbedding theorem, we know that there is \(C_{0}>0\) such that
Note that there exists \(C>0\) such that
The claim follows. □
Lemma 2.3
The problem of finding a solution u of (1.1) is equivalent to that of finding a critical point of \(\Phi _{\lambda}\), that is, \(\langle \Phi '_{\lambda}(u),v \rangle =0 \) for all \(v\in H\).
Proof
Assume that \(u\in \Theta \) is a solution of (1.1). It is easy to check that \(u\in H\). For any \(v\in H\),
that is,
Hence, u is a critical point of \(\Phi _{\lambda}\) in H.
Let \(u\in H\) be a critical point of \(\Phi _{\lambda}\), then \(\langle \Phi '_{\lambda}(u),v\rangle =0\) for any \(v\in H\). Without generality, we have
Hence,
So, \(hu'\) has a weak derivative satisfying
From the continuity of \(h,q, f,u\), we see that \((hu')'\) exists for \(t\in (t_{k},t_{k+1})\). Hence u satisfies the equality in (1.1).
Noting that
we get
Next, we show that u satisfies the impulsive conditions in (1.1). If this is not the case, without loss of generality, we may assume that there exists \(i\in \{1,2,\ldots,p\}\) such that
Let \(v=\Pi _{j=0,j\neq i}^{p+1}(t-t_{j})\), then by (2.4),
which contradicts (2.4). So u satisfies the impulsive conditions in (1.1). Similarly, u satisfies the boundary conditions. □
Lemma 2.4
The function \(u\in \Theta \) is a solution of (1.1), then u satisfies
Proof
Let \(g\in C(J), d_{k}\in \mathbb{R}\) \((1\leq k\leq p)\) and consider the equation
We only need to show that the solution u of (2.5) satisfies
It is easy to check that (2.5) has a unique solution. Let
It follows from Theorem 3.1.1 in [32] that \(S_{1}\in C^{2}(J)\) and
Hence,\(-\Delta (h(t_{k})S_{1}'(t_{k}))=0\) for \(1\leq k\leq p\). From \((8)\) and \((9)\) of Lemma 2.1, one easily shows that \(S_{2}\in C(J)\) and
which implies that \((hS_{2})'=qS_{2}\in C(J/\{t_{1},\ldots,t_{p}\})\). Hence, S is the solution of (2.5). □
Corollary 2.1
Let \(g\geq 0\) for \(t\in J\) and \(d_{k}\geq 0\) for \(1\leq k\leq p\), then the solution of (2.5) is positive if \(g\not \equiv 0\) or \(d_{k}\not \equiv 0\).
3 Main result
In this section, we give our main result. Firstly, we need to prove some lemmas.
Lemma 3.1
Let \((H_{1})-(H_{3})\) hold. Then the problem
has a positive solution for sufficiently small \(\tau >0\).
Proof
Let
By the imbedding theorem, \(\widetilde{C}>0, \widehat{C}>0\). From \((H_{2})\), there exist \(a>0,b>0,\sigma >0\) such that
Consider the functional
whose critical point is a solution of (3.1). If \(u\neq 0\) is a solution of (3.1), from Corollary 2.1, u is a positive solution of (3.1).
Taking \(\tau <\frac{\sigma}{8\widehat{C}p}\), for \(\|u\|=8p\tau \), we have
For any \(u^{+}\neq 0\),
as \(t\rightarrow +\infty \) since \(\mu >2\). Hence, there exists \(e\in H\) with \(\|e\|>8p\tau \) such that \(J(e)<0\).
It remains to check that J satisfies the PS condition. Let \(\{u_{n}\}\subset H\) such that \(|J(u_{n})|\leq M\) and \(|J'(u_{n})|\rightarrow \) as \(n\rightarrow \infty \). Then
for some constants \(C_{1}>0\) and \(C_{2}>0\). So, \(\{u_{n}\}\) is bounded in H. Considering a subsequence if necessary, we may assume that \(u_{n}\rightharpoonup u\) in H. Thus,
Noting that \(u_{n}\rightharpoonup u\) in H implies \(u_{n}\rightarrow u\) in \(C(J)\), we have
as \(n\rightarrow \infty \). Hence, \(\|u_{n}-u\|\rightarrow 0\), that is, \(u_{n}\rightarrow u\) in H. Then the mountain pass theorem implies that J has the critical point u with \(J(u)>0\). Clearly, \(u\not \equiv 0\). □
Let \(\Lambda _{1}=\{\lambda >0, \text{(1.1)}\) has positive solution} and \(\Lambda =\sup{\Lambda _{1}}\).
Lemma 3.2
There exists \(\bar{\lambda}>0\) such that (1.1) has at least a positive solution \(u_{\lambda}\) for \(\lambda \in (0,\bar{\lambda})\) and \(u_{\lambda}\) is the local minimum of \(\Phi _{\lambda}\) with \(\Phi _{\lambda}(u_{\lambda})<0\). Moreover, \(u_{\lambda _{1}}\leq u_{\lambda _{2}}\) for \(0<\lambda _{1}\leq \lambda _{2}<\bar{\lambda}\).
Proof
Let \(\tau >0\) be sufficiently small and \(x_{\tau}\) be the positive solution of (3.1) in Lemma 3.1. Consider the equation
where
Obviously, the solution of (3.4) is equivalent to the critical point of \(\phi _{\lambda _{0},T_{x_{\tau}}}\), where
Since \(T_{x_{\tau}}(s),T_{x_{\tau}(t_{k})}(s)\) are bounded, we obtain that for any \(u\in H\),
which imply that \(\phi _{\lambda _{0},T_{x_{\tau}}(u)}\rightarrow +\infty \) as \(\|u\|\rightarrow +\infty \). In addition, \(\phi _{\lambda _{0},T_{x_{\tau}}(u)}\) is sequentially weakly lower semicontinuous. It follows that there exists \(u_{\lambda _{0}}\in H\) such that
Let \(\xi >0\) be sufficiently small such that \(\xi \varphi _{0}(t_{K})\leq x_{\tau}(t_{K})\). We obtain
where we use the fact that
Clearly,
which implies that \(u_{\lambda _{0}}\not \equiv 0\). It is easy to show that \(u_{\lambda _{0}}\geq 0\) and
Choosing \(v=(u_{\lambda _{0}}-x_{\tau})^{+}\in H\) as a test function, we have
Next we show that \(u_{\lambda _{0}}\) is a positive solution of (1.1) with \(\lambda =\lambda _{0}\). Since \(u_{\lambda _{0}}\not \equiv 0\) and \(u_{\lambda _{0}}\geq 0\), we may assume that there exists \(t^{*}\in (0,1)\) such that \(u_{\lambda _{0}}(t^{*})>0\). Because \(u_{\lambda _{0}} \) is continuous, there exists an open interval \(D\subset J\) with \(t^{*}\in D\) such that \(u_{\lambda _{0}}(t)>0 \) for all \(t\in D\). Hence \(f(t,u_{\lambda _{0}}(t))>0\) for \(t\in D\). From Lemma 2.3, we obtain
for \(t\in (0,1)\).
Assume that \(\mu \in (0,\lambda )\) and \(u_{\lambda}\) is a positive solution of (1.1) with the parameter λ. We consider the functional \(\phi _{\mu ,T_{u_{\lambda}}}\). By using a similar reasoning as above, one may obtain that \(\phi _{\mu ,T_{u_{\lambda}}}\) has the critical point \(u_{\mu}\leq u_{\lambda}\), which is a positive solution of (1.1) with μ and the local minimum of \(\Phi _{\mu}\) with \(\Phi _{\mu}(u_{\mu})<0\). □
Lemma 3.3
\(0<\Lambda <+\infty \).
Proof
Clearly, \(\Lambda _{1}\neq \emptyset \). Let \(u_{\lambda}\) be a positive solution of (1.1), then
Note that \(\varphi _{0}\) is the solution of (2.3) with \(\lambda =\lambda ^{*}\), which satisfies
By \((H_{2})\) and (3.3), there exists \(C_{7}>0\) such that
Hence,
In addition, by Lemma 2.3 and \((H_{3})\), we have
which implies that
Hence, \(\Lambda <+\infty \). □
Remark 3.1
Since \(\lambda ^{*}\int _{0}^{1}\varphi _{0}u_{\lambda }\,dt\geq \lambda \sum_{k=1}^{p}I_{k}(u_{\lambda}(t_{k}))\varphi _{0}(t_{k})\), there exists \(M>0\) independent of λ such that \(I_{k}(u_{\lambda}(t_{k}))< M\) for \(\forall 1\leq k\leq p\). By \((H_{3})\), there exists \(\overline{C}>0\) independent of λ such that for any \(1\leq k\leq p\),
Lemma 3.4
\(\Lambda \in \Lambda _{1}\).
Proof
Let \(\{\lambda _{n}\}\in \Lambda _{1}\) be an increasing sequence such that \(\lambda _{n}\rightarrow \Lambda \) as \(n\rightarrow \infty \). For every \(n\geq 1\), one can find \(u_{n}\in H\) such that \(u_{n}\) is a positive solution of (1.1) with \(\lambda =\lambda _{n}\). Since \(f\geq 0,I_{k}\geq 0\) and λ is increasing, if \(m>n\),
Consider the functional \(\phi _{\lambda _{n},T_{u_{m}}}\). Similar to Lemma 3.2, we obtain that \(\phi _{\lambda _{n},T_{u_{m}}}\) has a critical point \(u_{\lambda _{n}}\leq u_{m}\), which is a local minimum of \(\phi _{\lambda _{n}}\) with \(\Phi _{\lambda _{n}}(u_{\lambda _{n}})<0\). Hence, without loss of generality, we may assume that for all \(n\geq 1\),
Hence,
From Remark 3.1 and \((H_{2})\), we have
Hence
which implies that \(\{u_{n}\}\) is bounded in H. Up to a subsequence, we have
It follows that for any \(v\in H\),
Combining with \(\langle \Phi '_{\lambda _{n}}(u_{n}),v\rangle =0\) and \(\lambda _{n}\rightarrow \Lambda \), we have
Hence, û is a solution of (1.1) with \(\lambda =\Lambda \). Finally, we show that \(\hat{u}>0\) for \(t\in (0,1)\). Clearly, \(\hat{u}\geq 0\) since \(u_{n}\geq 0\). In addition,
and therefore, \(\|u_{n}\|\rightarrow \|\hat{u}\|\). Hence,
which implies that \(\hat{u}\not \equiv 0\), which is the positive solution of (1.1) with \(\lambda =\Lambda \). □
Define
where \(u_{\lambda}\) is the local minimum of \(\Phi _{\lambda}\) with \(\Phi _{\lambda}(u_{\lambda})<0\) obtained in Lemma 3.2.
Definition 3.1
Let \(\Xi \subseteq H\) be a closed set and \(\varphi \in C^{1}(H,\mathbb{R})\). We say that a sequence \(\{v_{n}\}\subset H\) is a \((PS)_{\Xi ,c}\) sequence of φ if
as \(n\rightarrow \infty \). φ satisfies the \((PS)_{\Xi ,c}\) condition if every \((PS)_{\Xi ,c}\) sequence of φ has a convergent subsequence.
Lemma 3.5
[33] Let \(\varphi \in C^{1}(H,\mathbb{R})\). Consider the number
where Γ is the set of all continuous paths joining two points u and v in H. Suppose that Ξ is a closed subset of H such that
separates u and v. If φ satisfies the \((PS)_{\Xi ,c}\) condition, then φ has a critical point of level c on Ξ.
Lemma 3.6
Suppose that Ξ is a close subset of H, then \(\Phi _{0}\) satisfies the \((PS)_{\Xi ,c}\) condition for any \(c\in \mathbb{R}\).
Proof
Clearly, \(\Phi _{0}\in C^{1}(H,\mathbb{R})\), and there exist \(C_{14}>0,C_{15}>0 \) such that
Assume that \(\{u_{n}\}\subset H\) is a \((PS)_{\Xi ,c}\) sequence of \(\Phi _{0}\), we have
Similar to (3.8), using (3.7) and (3.16), we have
Let \(\Omega _{n}^{1}=\{t\in J: u_{n}(t)\geq 0\}, \Omega _{n}^{2}=\{t \in J: u_{n}(t)< 0\} \), then if n is sufficiently large,
From (3.12), there exists \(C_{16}>0\) such that
It follows that there exist \(C_{17}>0, C_{18}>0\) such that if n is sufficiently large,
Hence, if n is sufficiently large, we have
This implies that \(\{u_{n}\}\subset H\) is bounded. By a standard argument, one can show that \(\{u_{n}\}\) has a convergent subsequence. □
Remark 3.2
For \(\Phi _{0}\),
Theorem 3.1
There exists \(0<\Lambda <+\infty \) such that (1.1) has at least two positive solutions for all \(\lambda \in (0,\Lambda )\), one positive solution for \(\lambda =\Lambda \), and no positive solutions for \(\lambda >\Lambda \).
Proof
From Lemma 3.2 and Lemma 3.3, (1.1) has no solution for \(\lambda >\Lambda \), at least one positive solution for \(\lambda =\Lambda \) and a positive solution \(u_{\lambda}\) with \(\Phi _{\lambda}(u_{\lambda})<0\) for \(0<\lambda <\Lambda \).
It is easy to show that \(\Phi _{0}(u_{\lambda}+s\varphi _{0})\rightarrow -\infty \) as \(s\rightarrow +\infty \). Noting that
we fix \(s_{0}>0\) such that \(R_{2}=:\|u_{\lambda}+s_{0}\varphi _{0}\|> R_{1}=:\|u_{\lambda}\|\), and
Let \(\Gamma =\{\xi \in C([0,1],H)|\xi (0)=u_{\lambda},\xi (1)=u_{\lambda}+s_{0} \varphi _{0}\}\), and
It follows that \(\rho \geq \Phi _{0}(u_{\lambda})=\Phi _{\lambda}(u_{\lambda})\). If \(\rho =\Phi _{\lambda}(u_{\lambda})\), from (3.21), there exists \(0<\delta <R_{2}-R_{1}\) such that \(\inf \{\Phi _{0}(u)|\|u\|=R\}=\rho \) for all \(R\in (R_{1},R_{1}+\delta )\). Let \(\Xi =H\) if \(\rho > \Phi _{\lambda}(u_{\lambda})\) and \(\Xi =\{u:\|u\|=R_{1}+\delta /2\}\) if \(\rho = \Phi _{\lambda}(u_{\lambda})\). Clearly,
separates \(u_{\lambda}\) and \(u_{\lambda}+s_{0}\varphi _{0}\). Hence, \(\Phi _{0}\) has a critical point \(v_{\lambda}\) such that \(\Phi _{0}(v_{\lambda})=\rho \) and \(v_{\lambda}\in \Xi \). If \(\rho = \Phi _{\lambda}(u_{\lambda}), \|v_{\lambda}\| =R_{1}+ \delta /2>\|u_{\lambda}\|\), if \(\rho >\phi _{\lambda}(u_{\lambda})\), \(\Phi _{0}(v_{\lambda})=\rho >\Phi _{\lambda}(u_{\lambda})=\Phi _{0}(u_{ \lambda})\). Hence, \(v_{\lambda}\not \equiv u_{\lambda}\) and
Choosing \(w=(u_{\lambda}-v_{\lambda})^{+}\), we have
which implies that \(\|(u_{\lambda}-v_{\lambda})^{+}\|=0 \) and \(u_{\lambda}\leq v_{\lambda}\). Hence,
and \(v_{\lambda}\) is the second positive solution of (1.1). □
Remark 3.3
In fact, the function f satisfying \((H_{2})\) is of superlinear growth, and the impulsive function affecting the number of positive solutions is of sublinear growth.
Example 3.1
Consider the differential equation
Clearly, the nonimpulsive differential equation corresponding (3.22) has a positive solution \(x\equiv 1\). The results in [19] cannot be applied to (3.22) since the nonlinear function and impulsive functions in [19] are of superlinear growth or of sublinear growth.
Assume that x is a positive solution of (3.22), then
and
Clearly, \(x\not \equiv 1\). If \(\lambda \ge 1/4\), then we have
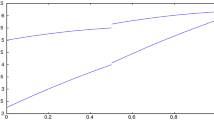
Hence, (3.22) has no positive solution if \(\lambda \ge 1/4\). From Theorem 3.1, (3.22) has two positive solutions for sufficiently small \(\lambda >0\). When \(\lambda =0.0001\), two positive solutions of (3.22) can be found in Fig. 1.
Positive solutions to the equation of Example 3.22
4 Conclusion
In this paper, we discussed the existence, nonexistence, and multiplicity of positive solutions for a class of impulsive Sturm–Liouville boundary value problems with a parameter. Using the mountain pass principle, we show that the number of positive solutions depends on the change of parameters, in which sublinear impulsive perturbation plays an important role. In fact, one can prove that the nonimpulsive case of (1.1), that is, \(I_{k}\equiv 0(1\leq k\leq p)\), has at least a positive solution. How does the combination of impulsive perturbation and parameter affect the behavior of the equation? We will discuss the issue in follow-up research.
References
Bainov, D., Simeonov, P.: Systems with Impulse Effect. Ellis Horwood Series, Mathematics and Its Applications. Chichester (1989)
Benchohra, M., Henderson, J.: Theory of Impulsive Differential Equations. Contemporary Mathematics and Its Applications, vol. 2. Hindawi Publishing Corporation, New York (2006)
Lakshmikantham, V.D., Bainov, D., Simeonov, P.S.: Impulsive Differential Equations and Inclusions. World Scientific, Singapore (1989)
Agarwa, R.P., Franco, D., O’Regan, D.: Singular boundary value problems for first and second order impulsive differential equations. Aequ. Math. 69, 83–96 (2005). https://doi.org/10.1007/s00010-004-2735-9
Ahmad, B., Nieto, J.J.: Existence and approximation of solutions for a class of nonlinear impulsive functional differential equations with anti-periodic boundary conditions. Nonlinear Anal. 10, 3291–3298 (2008). https://doi.org/10.1016/j.na.2007.09.018
Buyukkahraman, M.L.: Existence of periodic solutions to a certain impulsive differential equation with piecewise constant arguments. Eurasian Math. J. 14, 54–60 (2022). https://doi.org/10.32523/2077-9879-2022-13-4-54-60
Chen, J., Tisdell, C.C., Yuan, R.: On the solvability of periodic boundary value problems with impulse. J. Math. Anal. Appl. 331, 902–912 (2007). https://doi.org/10.1016/j.jmaa.2006.09.021
Gasimov, Y.S., Jafari, H., Mardanov, M.J., Sardarova, R.A., Sharifov, Y.A.: Existence and uniqueness of the solutions of the nonlinear impulse differential equations with nonlocal boundary conditions. Quaest. Math. 45, 1399–1412 (2022). https://doi.org/10.2989/16073606.2021.1945702
Li, J.L., Nieto, J.J., Shen, J.H.: Impulsive periodic boundary value problems of first-order differential equations. J. Math. Anal. Appl. 325, 226–236 (2007). https://doi.org/10.1016/j.jmaa.2005.04.005
Liu, Y.J.: Further results on periodic boundary value problems for nonlinear first order impulsive functional differential equations. J. Math. Anal. Appl. 327, 435–452 (2007). https://doi.org/10.1016/j.jmaa.2006.01.027
Li, Q.Y., Zhou, Y.M., Cong, F.Z., Liu, H.: Positive solutions to superlinear attractive singular impulsive differential equation. Appl. Math. Comput. 338, 822–827 (2018). https://doi.org/10.1016/j.amc.2018.07.003
Min, D.D., Chen, F.Q.: Variational methods to the p-Laplacian type nonlinear fractional order impulsive differential equations with Sturm-Liouville boundary-value problem. Fract. Calc. Appl. Anal. 24, 1069–1093 (2021). https://doi.org/10.1515/fca-2021-0046
Nieto, J.J., O’Regan, D.: Variational approach to impulsive differential equations. Nonlinear Anal., Real World Appl. 10, 680–690 (2009). https://doi.org/10.1016/j.nonrwa.2007.10.022
Oz, O., Karaca, I.Y.: Existence and nonexistence of positive solutions for the second-order m-point eigenvalue impulsive boundary value problem. Miskolc Math. Notes 23, 847–866 (2022). https://doi.org/10.18514/MMN.2022.3767
Qian, D.B., Li, X.Y.: Periodic solutions for ordinary differential equations with sublinear impulsive effects. J. Math. Anal. Appl. 303, 288–303 (2005). https://doi.org/10.1016/j.jmaa.2004.08.034
Rachunkova, I., Tomecek, J.: Existence principle for BVPS with state-dependent impulses. Topol. Methods Nonlinear Anal. 44, 349–368 (2014). https://doi.org/10.12775/TMNA.2014.050
Wang, W., Guo, L.: New existence results for periodic boundary value problems with impulsive effects. Adv. Differ. Equ. 2015, Article ID 275 (2015). https://doi.org/10.1186/s13662-015-0601-9
Zhou, Q.S., Jiang, D.Q., Tian, Y.: Multiplicity of positive solutions to periodic boundary value problems for second order impulsive differential equations. J. Mol. Med. 26, 113–124 (2010). https://doi.org/10.1007/s10255-007-7136-0
Tian, Y., Ge, W.G.: Variational methods to Sturm-Liouville boundary value problem for impulsive differential equations. Nonlinear Anal. TMA 72, 277–287 (2010). https://doi.org/10.1016/j.na.2009.06.051
Tian, Y., Ge, W.G.: Multiple solutions of impulsive Sturm-Liouville boundary value problem via lower and upper solutions and variational methods. J. Math. Anal. Appl. 387, 475–489 (2018). https://doi.org/10.1016/j.jmaa.2011.08.042
Afrouzi, G.A., Hadjian, A., Rădukescu, V.D.: Variational approach to fourth-order impulsive differential equations with two control parameters. Results Math. 65, 371–384 (2014). https://doi.org/10.1007/s00025-013-0351-5
Afroui, G.A., Hadjian, A.Z.: A variational approach for boundary value problems for impulsive fractional differential equations. Fract. Calc. Appl. Anal. 21, 1565–1584 (2018). https://doi.org/10.1515/fca-2018-0082
Chen, P., Tang, X.: New existence and multiplicity of solutions for some Dirichlet problems with impulsive effects. Math. Comput. Model. 55, 723–739 (2012). https://doi.org/10.1016/j.mcm.2011.08.046
Heidarkhani, S., Ferrara, M., Salari, A.: Infinitely many periodic solutions for a class of perturbed second-order differential equations with impulses. Acta Appl. Math. 139, 81–94 (2015). https://doi.org/10.1007/s10440-014-9970-4
Sun, J.T., Chen, H., Yang, L.: The existence and multiplicity of solutions for an impulsive differential equation with two parameters via a variational method. Nonlinear Anal. 72, 440–449 (2010). https://doi.org/10.1016/j.na.2010.03.035
Tian, Y., Zhang, M.: Variational method to differential equations with instantaneous and non-instantaneous impulses. J. Mol. Med. 94, 160–165 (2019). https://doi.org/10.1016/j.aml.2019.02.034
Wang, S.H., Tian, Y.: Variational methods to the fourth-order linear and nonlinear differential equations with non-instantaneous impulses. J. Appl. Anal. Comput. 10, 2521–2536 (2020). https://doi.org/10.11948/20190413
Wang, W.B.: Infinitely many solutions for nonlinear periodic boundary value problem with impulses. RACSAM 111, 1093–1103 (2017). https://doi.org/10.1007/s13398-016-0348-5
Wang, W.B., Liu, Y.: Infinitely many solutions for higher order impulsive equations without symmetry. Rocky Mt. J. Math. 52, 1473–1484 (2022). https://doi.org/10.1216/rmj.2022.52.1473
Wang, W.B., Zuo, X.X.: Bifurcation type phenomena for positive solutions of a class of impulsive differential equations. Math. Methods Appl. Sci. 23, 1–14 (2023). https://doi.org/10.1002/mma.9011
Zhang, D., Dai, B.X.: Infinitely many solutions for a class of nonlinear impulsive differential equations with periodic boundary conditions. Comput. Math. Appl. 61, 3153–3160 (2011). https://doi.org/10.1016/j.camwa.2011.04.003
Guo, D., Sun, J., Liu, Z.: Functional Methods in Nonlinear Ordinary Differential Equation. Shandong Science and Technology Press, Jinan (1995)
Youssef, J.: The Mountain Pass Theorem, Variant,Generalizations and Some Applications. Encyclopedia of Mathematics and Its Applications. Cambridge University Press, Britain (2003)
Funding
The third author is supported by Hunan Provincial Natural Science Foundation of China (No 2022JJ30236).
Author information
Authors and Affiliations
Contributions
All authors contributed to the study conception and technical content. The first draft of the manuscript was written by Piao Liu and Weibing Wang, and all authors commented on further versions of the manuscript. All authors have read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Yang, X., Liu, P. & Wang, W. Multiplicity and nonexistence of positive solutions to impulsive Sturm–Liouville boundary value problems. Bound Value Probl 2024, 51 (2024). https://doi.org/10.1186/s13661-024-01840-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13661-024-01840-8