Numerical solution of system of second-order integro-differential equations using nonclassical sinc collocation method

Abstract

In this paper, a nonclassical sinc collocation method is constructed for the numerical solution of systems of second-order integro-differential equations of the Volterra and Fredholm types. The novelty of the approach is based on using the new nonclassical weight function for sinc method instead of the classic ones. The sinc collocation method based on nonclassical weight functions is used to reduce the system of integro-differential equations to a system of algebraic equations. Furthermore, the convergence of the method is proposed theoretically, showing that the method converges exponentially. By solving some examples, including problems with a non-smooth solution, the results are compared with other existing results to demonstrate the efficiency of the new method.

1 Introduction

In the definition of integro-differential equations, the unknown function is under the sign of integration, and its derivatives also appear in the equation. Such a problem can be classified into the Fredholm and Volterra types. The upper bound of an integral part in the Volterra type is variable while it is a constant for the Fredholm type [1, 2].

Many important problems can be modeled by a system of integral or integro-differential equations. So, solving the integro-differential equations has attracted much attention from applied mathematics researchers [3].

Finding the exact solution of the integro-differential systems is quite challenging, so it is often necessary to propose efficient numerical techniques.

Recently, several numerical methods, such as single term walsh series [1], Legendre wavelets operational method [4], Bernstein operation matrix method [5], Chebyshev collocation method [6], Fibonacci polynomials method [7], spectral Legendre-Chebyshev [8], spectral method based on orthogonal polynomials [9], differential transform [10] and Chebyshev quadrature collocation method [11] have been used to approximate the solution of integro-differential equations. In [12–15], the stochastic integro-differential equations have been solved using moving least squares, cubic B-spline, meshless discrete collocation, and orthonormal Bernstein polynomials method. In addition, some good attempts have been made to approximate the solution of integro-differential equations based on hybrid parabolic and block-pulse functions, the truncated Fibonacci series, Bernoulli polynomials, and rationalized Haar functions [14, 16–21].

In this paper, we considered the general form of he second-order linear Fredholm integro-differential system

$$ \sum_{\gamma =0}^{2} \mathbf{A}_{\gamma}\mathbf{Y}^{(\gamma )}(x)= \mathbf{F}(x)+ \int _{0}^{1}\sum_{\gamma =0}^{2} \mathbf{B}_{\gamma} \mathbf{Y}^{(\gamma )}(t)\,dt, $$

(1.1)

and the second-order Volterra integro-differential system

$$ \sum_{\gamma =0}^{2} \mathbf{A}_{\gamma}\mathbf{Y}^{(\gamma )}(x)= \mathbf{F}(x)+ \int _{0}^{x}\sum_{\gamma =0}^{2} \mathbf{B}_{\gamma} \mathbf{Y}^{(\gamma )}(t)\,dt, $$

(1.2)

subjected to the initial conditions

$$ \mathbf{Y}(0)=[\alpha _{1},\ldots ,\alpha _{m}]^{T},\qquad \mathbf{Y}^{ \prime}(0)=[\beta _{1},\ldots ,\beta _{m}]^{T} $$

(1.3)

where

$$\begin{aligned}& \mathbf{A}_{\gamma}=\bigl[p^{(\gamma )}_{i,j}(x) \bigr]_{{m\times m}}, \qquad \mathbf{B}_{\gamma}=\bigl[q^{(\gamma )}_{i,j}(x,t) \bigr]_{{m\times m}}, \quad \gamma =0,1,2,\\& \mathbf{F}(x)=\bigl[f_{1}(x),\ldots ,f_{m}(x) \bigr]^{T}, \end{aligned}$$

and $\mathbf{Y}(x)=[y_{1}(x),\ldots ,y_{m}(x)]^{T}$ are unknown functions to be determined. The functions $f_{i}(x)$ and the coefficients $p^{(\gamma )}_{i,j}(x)$ and $q^{(\gamma )}_{i,j}(x)$ should be continues on $[0,1]$ but do not need to be differentiable on $[0,1]$. It is known that such a model problem can be used to simulate the wind ripple in the desert [22], the fractal model of dropwise condensation [23], the glass-forming composition for bulk metallic glasses [24], and many other phenomena. So, constructing the reliable algorithms for solving the problem is of high importance.

Frank Stenger introduced numerical approximations based on sinc function [25, 26], and then they were expanded for many applications in numerical analysis [27]. The classical sinc basis functions have been widely used to solve the linear Fredholm integro-differential equations [28], the Volterra integral and integro-differential equations [29], and the nonlinear second-order integro-differential equations system with Dirichlet conditions [30].

For the first time, Shizgal extended the nonclassical weight functions to approximate the solution of the Boltzmann equation [31]. Then the method has been used to approximate the eigenvalues and eigenfunction of the Schrödinger equation [32]. Our method consists of reducing the solution of the problems (1.1) or (1.2) with initial conditions (1.3) to a system of algebraic equations. To do this, we will use the nonclassical sinc collocation method. It is known that the classical translated sinc basis functions are not differentiable at zero, so we will try to construct the nonclassical sinc basis functions such that they are differentiable at zero. Also, we will use some proper weight functions that produce more accurate results compared to the classical basis functions to solve the problem above. It will be proved that the nonclassical sinc method converges to the exact solution with exponential rates of convergence. Since the method does not need differentiability of the solution on the boundary, the method is also applicable for problems with the non-smooth solution.

The paper is organized as follows: In Sect. 2, the sinc basis functions are introduced to be used in the subsequent sections. In Sect. 3, the nonclassical sinc collocation method is used to approximate the solution of systems (1.1) and (1.2) along with the initial conditions (1.3). In Sect. 4, we discussed the convergence and error analysis of the proposed method. In Sect. 5, the methods have been used to solve some problems to demonstrate the applicability and accuracy of the methods computationally. Finally, Sect. 6 is devoted to the conclusion of the paper.

2 Sinc function preliminaries

To be used in the next section, we will recall the following results taken from [27, 29, 33–38].

One can define the sinc function for the whole real numbers as follows

$$ \operatorname{sinc}(x)=\textstyle\begin{cases} \frac{\sin(\pi x)}{\pi x}, & x\neq 0, \\ 1, & x=0. \end{cases} $$

Also, the translated sinc functions for $h>0$ can be defined as

$$ S(j,h) (x)=\operatorname{sinc} \biggl(\frac{x-jh}{h} \biggr),\quad j=0, \pm 1,\pm 2, \ldots . $$

The cardinality of the translated sinc basis functions at the interpolating points $x_{k}=kh$ is obvious, i.e.,

$$ S(j,h) (kh)=\delta _{jk}=\textstyle\begin{cases} 1, & j=k, \\ 0, & j\neq k. \end{cases} $$

For the function f defined on real line with $h>0$, the following series

$$ C(f,h) (x)=\sum_{j=-\infty}^{\infty}f(jh)S(j,h) (x) $$

is called the Whittaker cardinal expansion of f if this series converges. It is clear that the cardinal function is an interpolant for f at the points $\{jh\}_{j=-\infty}^{\infty}$ in the infinite strip

$$ D_{s}\equiv \bigl\{ w=u+iv: \vert v \vert < d\leq \pi /2\bigr\} , $$

which is a subset of the complex plane. To use the sinc basis functions on the finite interval $(0,1)$, we can apply the conformal map

$$ \phi (z)=\ln \biggl(\frac{z}{1-z} \biggr), $$

with the eye-shaped domain

$$ D_{E}= \biggl\{ z=x+iy: \biggl\vert \arg \biggl( \frac{z}{1-z} \biggr) \biggr\vert < d \leq \pi /2 \biggr\} , $$

and the range $D_{s}$.

We will combine the translated sinc functions with the conformal mapping ϕ to obtain the basis functions

$$ S_{j}(z)=S(j,h)o\phi (z)=\operatorname{sinc} \biggl(\frac{\phi (z)-jh}{h} \biggr), \quad z\in D_{E}. $$

(2.1)

The inverse mapping of $w=\phi (z)$ is as follows

$$ z=\phi ^{-1}(w)=\frac{e^{w}}{1+e^{w}}. $$

For the evenly spaced knots $\{kh\}_{k=-\infty}^{\infty}$ on the real line, their corresponding images $x_{k}\in (0,1)$, which are real in $D_{E}$, are

$$ x_{k}=\phi ^{-1}(kh)= \frac{e^{kh}}{1+e^{kh}},\quad k=0,\pm 1,\pm 2, \ldots . $$

(2.2)

Let $D_{E}$ be a simply connected domain in the complex plane with boundary points $a\neq b$ and ϕ be a conformal map from $D_{E}$ onto $D_{s}$ with $\phi (a)=-\infty$ and $\phi (b)=\infty$. Also, let us denote by ψ the inverse map of ϕ and define

$$ \Gamma =\bigl\{ z\in \mathbb{C}:z=\psi (u),u\in \mathbb{R}\bigr\} $$

and

$$ z_{j}=\psi (jh),\quad j=0,\pm 1,\pm 2,\ldots . $$

Definition 1

Let $B(D_{E})$ be the class of functions f, which are analytic in $D_{E}$, and

$$ \int _{\psi (L+u)} \bigl\vert f(z)\,dz \bigr\vert \rightarrow 0, \quad u\rightarrow \pm \infty , $$

where $L=\{iv:|v|< d\}$ and on the boundary of $D_{E}$ (denoted by $\partial D_{E}$)

$$ N(f,D_{E})\equiv \int _{\partial D_{E}} \bigl\vert f(z)\,dz \bigr\vert < \infty . $$

Theorem 2

Let $f\in B(D_{E})$, and let n be a positive integer then

$$ \sup_{-\infty < x< \infty} \Biggl\vert f(x)-\sum _{j=-n}^{n}f(x_{j})S(k,h)o \phi (x) \Biggr\vert \leq k_{1}n^{\frac{1}{2}}e^{-\sqrt{\pi d \alpha n}}, $$

for some constant $c>0$ in which the mesh-size h is chosen as:

$$ h=\sqrt{\frac{\pi d}{\alpha n}}. $$

(2.3)

Proof

See [33]. □

Theorem 3

Let for $f\in B(D_{E})$ and some positive constants α, β, and C we have

$$ \biggl\vert \frac{f(x)}{\phi ^{\prime}(x)} \biggr\vert \leq c\textstyle\begin{cases} e^{-\alpha \vert \phi (x) \vert }, & x\in \Gamma _{a}, \\ e^{-\beta \vert \phi (x) \vert }, & x\in \Gamma _{b}, \end{cases} $$

with

$$ \Gamma _{a}=\bigl\{ x\in \Gamma :\phi (x)\in (- \infty ,0)\bigr\} , $$

(2.4)

and

$$ \Gamma _{b}=\bigl\{ x\in \Gamma :\phi (x)\in [0, \infty )\bigr\} . $$

(2.5)

If h is selected as (2.3), then for all $x\in \Gamma$,

$$ \Biggl\vert \int _{0}^{1} f(t)\,dt-h\sum _{j=-n}^{n} \frac{f(x_{j})}{\phi '(x_{j})} \Biggr\vert \leq k_{2}e^{-\sqrt{\pi\,d \alpha n}}, $$

(2.6)

Proof

See [34]. □

If we suppose that $\frac{q^{(0)}_{i,j}(x,.)}{\phi '}$, $\frac{q^{(1)}_{i,j}(x,.)}{\phi '}$, $\frac{q^{(2)}_{i,j}(x,.)}{\phi '}\in B(D_{E})$, then using (2.6) on the right-hand side of (1.1), we have

$$\begin{aligned}& \int _{0}^{1} \bigl(q^{(0)}_{i,j}(x,t)y_{1}(t)+q^{(1)}_{i,j}(x,t)y_{j}'(t)+q^{(2)}_{i,j}(x,t)y_{j}''(t) \bigr)\,dt \\& \quad =h\sum_{g=-n}^{n} \biggl(\frac{q^{(0)}_{i,j}(x,t_{g})}{\phi '(t_{g})}y_{j}(t_{g})+ \frac{q^{(1)}_{i,j}(x,t_{g})}{\phi '(t_{g})}y_{j}'(t_{g})+ \frac{q^{(2)}_{i,j}(x,t_{g})}{\phi '(t_{g})}y_{j}''(t_{g}) \biggr). \end{aligned}$$

(2.7)

Theorem 4

Let for $f\in B(D_{E})$ and the positive constants α, β, and C we have

$$ \biggl\vert \frac{f(x)}{\phi ^{\prime}(x)} \biggr\vert \leq c\textstyle\begin{cases} e^{-\alpha \vert \phi (x) \vert }, & x\in \Gamma _{a}, \\ e^{-\beta \vert \phi (x) \vert }, & x\in \Gamma _{b}, \end{cases} $$

where $\Gamma _{a}$ and $\Gamma _{b}$ are defined in (2.4) and (2.5). If h is selected as (2.3), then for all $x\in \Gamma$, we have

$$ \Biggl\vert \int _{0}^{x_{l}}f(t)\,dt-h\sum _{j=-n}^{n}\delta _{lj}^{(-1)} \frac{f(x_{j})}{\phi ^{\prime}(x_{j})} \Biggr\vert \leq k_{3}e^{-\sqrt{ \pi\,d\alpha n}}, $$

(2.8)

where

$$ \delta _{lj}^{(-1)}=\frac{1}{2}+ \int _{0}^{l-j} \frac{\sin (\pi t)}{\pi t}\,dt. $$

(2.9)

Proof

See [29, 35]. □

Also, if we suppose that $\frac{q^{(0)}_{i,j}(x,.)}{\phi ^{\prime}}$, $\frac{q^{(1)}_{i,j}(x,.)}{\phi ^{\prime}}$, $\frac{q^{(2)}_{i,j}(x,.)}{\phi ^{\prime}}\in B(D_{E})$, then using (2.8) on the right-hand side of (1.2), we obtain

$$\begin{aligned} & \int _{0}^{x_{l}} \bigl(q^{(0)}_{i,j}(x,t)y_{1}(t)+q^{(1)}_{i,j}(x,t)y_{j}^{ \prime}(t)+q^{(2)}_{i,j}(x,t)y_{j}^{\prime \prime}(t) \bigr)\,dt \\ & \quad= h\sum_{g=-n}^{n}\delta _{\lg}^{(-1)} \biggl( \frac{q^{(0)}_{i,j}(x,t_{g})}{\phi ^{\prime}(t_{g})}y_{j}(t_{g})+ \frac{q^{(1)}_{i,j}(x,t_{g})}{\phi ^{\prime}(t_{g})}y_{j}^{\prime}(t_{g})+ \frac{q^{(2)}_{i,j}(x,t_{g})}{\phi ^{\prime}(t_{g})}y_{j}^{\prime \prime}(t_{g}) \biggr) \end{aligned}$$

(2.10)

Lemma 5

For the simply connected domains $D_{E}$ and $D_{s}$ and the one-to-one conformal mapping $\phi :D_{E}\rightarrow D_{s}$, we have

$$\begin{aligned}& \delta _{j,k}^{(0)}=\bigl[S(j,h)o\phi (x) \bigr]|_{x=x_{k}}=\textstyle\begin{cases} 1, & j=k, \\ 0, & j\neq k, \end{cases}\displaystyle \end{aligned}$$

(2.11)

$$\begin{aligned}& \delta _{j,k}^{(1)}=h \frac{d}{d\phi}\bigl[S(j,h)o\phi (x)\bigr]|_{x=x_{k}}= \textstyle\begin{cases} 0, & j=k, \\ \frac{(-1)^{k-j}}{k-j}, & j\neq k, \end{cases}\displaystyle \end{aligned}$$

(2.12)

$$\begin{aligned}& \delta _{j,k}^{(2)}=h^{2} \frac{d^{2}}{d\phi ^{2}}\bigl[S(j,h)o\phi (x)\bigr] |_{x=x_{k}}=\textstyle\begin{cases} \frac{-\pi ^{2}}{3}, & j=k, \\ \frac{-2(-1)^{k-j}}{(k-j)^{2}}, & j\neq k. \end{cases}\displaystyle \end{aligned}$$

(2.13)

Proof

See [36]. □

Using the nonclassical sinc basis functions, $f(x)$ can be approximated on the whole real line as follows [37]

$$ f(x)\simeq \hat{f}(x)=\sum_{j=-\infty}^{\infty} \frac{W(x)}{W(jh)}f(jh)\operatorname{sinc} \biggl(\frac{x-jh}{h} \biggr), $$

(2.14)

where $W(x)$ is a positive weight function. Obviously, for the points $x_{k}=kh$, the interpolation conditions

$$ \hat{f}(kh)=f(kh),\quad k=0,\pm 1,\pm 2,\ldots , $$

hold.

Theorem 6

Let ${\phi ^{\prime}}^{2}f\in B(D_{E})$, and for some constant $c_{1}$, the weight function W satisfies $\frac{W(x)}{W(x_{j})}< c_{1}$. Also, let for some positive constants α, β, and c we have

$$ \bigl\vert \bigl(\phi ^{\prime} f\bigr) (x) \bigr\vert \leq c\textstyle\begin{cases} e^{-\alpha \vert \phi (x) \vert }, & x\in \Gamma _{a}, \\ e^{-\beta \vert \phi (x) \vert }, & x\in \Gamma _{b}, \end{cases} $$

where $\Gamma _{a}$ and $\Gamma _{b}$ are defined in (2.4) and (2.5). If h is satisfied in (2.3), then for all $x\in \Gamma$, we have, [37]

$$ \Biggl\vert f(x)-\sum_{j=-n}^{n} \phi ^{\prime}(x_{j}) f(x_{j}) \frac{W(x)}{W(x_{j})} \frac{\operatorname{sinc} (\frac{\phi (x)-jh}{h} )}{\phi ^{\prime}(x)} \Biggr\vert \leq c_{1}k_{4}n^{1/2}e^{-\sqrt{\pi\,d\alpha n}}. $$

(2.15)

Proof

See [37]. □

3 The nonclassical sinc collocation method

Consider the Fredholm integro-differential system (1.1) as well as the Volterra integro-differential system (1.2) connected with initial conditions (1.3). Let $\mathbf{Y}= [y_{1}(x),\cdot ,y_{j}(x),\ldots , y_{m}(x) ]^{T} \in B(D_{E})$ be the exact solution of (1.1)-(1.3) or (1.2)-(1.3). The translated sinc functions $S_{k}(x)$ are not differentiable at zero, so we define the new functions

$$ \biggl\{ \frac{S_{k}(x)}{\phi ^{\prime}(x)} \biggr\} _{k=-n}^{n} $$

(3.1)

and call them the modified sinc basis functions. The new basis functions are satisfied in the relations

$$ \lim_{x\rightarrow 0}\frac{S_{k}(x)}{\phi ^{\prime}(x)}=0, \qquad \lim _{x\rightarrow 0} \biggl(\frac{S_{k}(x)}{\phi ^{\prime}(x)} \biggr)^{\prime}=0, $$

so they are well defined and differentiable at zero now. Using the new basis (3.1), we define $u_{j,n}(x)$ as

$$ u_{j,n}(x)=\sum_{k=-n}^{n}c_{j,k} \frac{w_{j}(x)}{w_{j}(x_{k})} \frac{S_{k}(x)}{\phi ^{\prime}(x)},\quad j=1,\ldots , m $$

(3.2)

to approximate the exact solution $y_{j}(x)$, where $c_{j,k}$ are unknown constants to be determined. Since the basis functions are zero at the initial point, and the initial conditions of the problem are not homogenous, we need to add the polynomials

$$\begin{aligned} v_{j}(x)={}&(2\alpha _{j}+\beta _{j})x^{3}-(3\alpha _{j}+2\beta _{j})x^{2}+ \beta _{j}x+\alpha _{j} \\ &{}+A_{j}\bigl(3x^{2}-2x^{3} \bigr)+B_{j}\bigl(x^{3}-x^{2}\bigr),\quad j=1,\ldots m, \end{aligned}$$

(3.3)

to the approximate solution (3.2), to be satisfied in the initial conditions (1.3). So, the new approximate solution can be defined as

$$ \mathbf{Y}_{n}(x)= \bigl[y_{1,n}(x), \ldots ,y_{m,n}(x) \bigr]^{T} $$

(3.4)

where

$$ y_{j,n}(x)=u_{j,n}(x)+v_{j}(x), \quad j=1,\ldots ,m $$

(3.5)

It should be noted that the approximate solution $\mathbf{Y}_{n}(x)$ now satisfies the initial conditions (1.3), i.e.,

$$\begin{aligned}& y_{j,n}(0)=\alpha _{j},\quad j=1,\ldots , m,\\& y_{j,n}^{\prime}(0)=\beta _{j},\quad j=1,\ldots ,m. \end{aligned}$$

3.1 Fredholm integro-differential system

Substituting $\mathbf{Y}_{n}(x)$ into (1.1) and multiplying both sides by $\frac{h^{2}}{\phi ^{\prime}}$, we have a relation that can be discretized at the sinc grid points $x_{l}$, $l=-n,\ldots ,n$, to obtain

$$\begin{aligned} & h^{2}\sum_{k=-n}^{n} \biggl(\mathbf{A}_{2}\mathbf{T}^{(2)}_{k}(x_{l})+ \frac{1}{\phi ^{\prime}(x_{l})}\mathbf{A}_{1}\mathbf{T}^{(1)}_{k}(x_{l})+ \frac{1}{\phi ^{{\prime}^{2}}(x_{l})}\mathbf{A}_{0}\mathbf{T}^{(0)}_{k}(x_{l}) \biggr)\mathbf{c}_{k} \\ &\quad{}+\frac{h^{2}}{\phi ^{\prime}(x_{l})} \bigl(\mathbf{A}_{2} \mathbf{v}^{ \prime \prime}(x_{l})+\mathbf{A}_{1} \mathbf{v}^{\prime}(x_{l})+ \mathbf{A}_{0} \mathbf{v}(x_{l}) \bigr) \\ &\quad{}- \frac{h^{2}}{\phi ^{\prime}(x_{l})} \int _{0}^{1} \sum_{k=-n}^{n} \biggl(\phi ^{\prime}(t)\mathbf{B}_{2}\mathbf{T}^{(2)}_{k}(t)+ \mathbf{B}_{1}\mathbf{T}^{(1)}_{k}(t)+ \frac{1}{\phi ^{\prime}(t)} \mathbf{B}_{0}\mathbf{T}^{(0)}_{k}(t) \biggr)\mathbf{c}_{k}\,dt \\ &\quad{}-\frac{h^{2}}{\phi ^{\prime}(x_{l})} \int _{0}^{1} \bigl(\mathbf{B}_{2} \mathbf{v}^{\prime \prime}(t)+\mathbf{B}_{1} \mathbf{v}^{\prime}(t)+ \mathbf{B}_{0} \mathbf{v}(t) \bigr)\,dt= \frac{h^{2}}{\phi ^{\prime}(x_{k})} \mathbf{f}(x_{l}), \end{aligned}$$

(3.6)

where

$$ \mathbf{c}_{k}=[c_{1,k},\ldots , c_{m,k}], \quad \mathbf{T}^{(\gamma )}_{k}= \bigl[T^{(\gamma )}_{1,k},\ldots , T^{(\gamma )}_{m,k} \bigr], $$

(3.7)

with

$$\begin{aligned} &T^{(0)}_{j,k}(x)=\frac{W_{j}(x)}{W_{j}(x_{k})}S_{j}(x), \\ & T^{(\gamma )}_{j,k}(x)= \frac{1}{ (\phi '(x) )^{\gamma -1}} \frac{d^{\gamma}}{dx^{\gamma}} \biggl( \frac{W_{j}(x) S_{j}(x)}{W_{j}(x_{k})\phi '(x)} \biggr), \quad \gamma =1,2. \end{aligned}$$

(3.8)

Simplifying (3.6), we obtain the following system of linear equations

$$\begin{aligned} &\sum_{j=1}^{m}\sum _{k=-n}^{n} \biggl[ \biggl(p^{(2)}_{i,j}(x_{l}) \frac{W_{j}(x_{l})}{W_{j}(x_{k})} \biggr)\delta _{kl}^{(2)}+h \biggl( \frac{W_{j}(x_{l})}{W_{j}(x_{k})} \biggl(p^{(1)}_{i,j}(x_{l}) \frac{1}{\phi ^{\prime}(x_{l})}-p^{(2)}_{i,j}(x_{l}) \frac{\phi ^{\prime \prime}(x_{l})}{\phi ^{{\prime}^{2}}(x_{l})} \biggr) \\ &\qquad{}+\frac{W_{j}^{\prime}(x_{l})}{W_{j}(x_{k})} \biggl(2p^{(2)}_{i,j}(x_{l}) \frac{1}{\phi ^{\prime}(x_{l})} \biggr) \biggr)\delta _{kl}^{(1)}+h^{2} \biggl(\frac{W_{j}(x_{l})}{W_{j}(x_{k})} \biggl(p^{(0)}_{i,j}(x_{l}) \frac{1}{\phi ^{{\prime}^{2}}(x_{l})}-p^{(1)}_{i,j}(x_{l}) \frac{\phi ^{\prime \prime}(x_{l})}{\phi ^{{\prime}^{3}}(x_{l})} \\ &\qquad{}+p^{(2)}_{i,j}(x_{l}) \biggl( \frac{2\phi ^{{\prime \prime}^{2}}(x_{l})-\phi ^{\prime \prime \prime}(x_{l})\phi ^{\prime}(x_{l})}{\phi ^{{\prime}^{4}}(x_{l})} \biggr) \biggr) +\frac{W_{j}^{\prime}(x_{l})}{W_{j}(x_{k})} \biggl(p^{(1)}_{i,j}(x_{l}) \frac{1}{\phi ^{{\prime}^{2}}(x_{l})}-2 \frac{\phi ^{\prime \prime}(x_{l})}{\phi ^{{\prime}^{2}}(x_{l})} \biggr) \\ &\qquad{}+\frac{W_{j}^{\prime \prime}(x_{l})}{W_{j}(x_{k})} \frac{1}{\phi ^{{\prime}^{2}}(x_{l})} \biggr)\delta _{kl}^{(0)} \biggr]c_{j,k}+ \sum_{j=1}^{m} \frac{h^{2}}{\phi ^{\prime}(x_{l})} \bigl(p^{(0)}_{i,j}(x_{l})v_{j}(x_{l})+p^{(1)}_{i,j}(x_{l})v_{j}^{ \prime}(x_{l}) \\ &\qquad{}+p^{(2)}_{i,j}(x_{l})v_{j}^{\prime \prime}(x_{l}) \bigr)- \frac{h^{3}}{\phi ^{\prime}(x_{l})}\sum_{g=-n}^{n} \frac{1}{\phi ^{\prime}(t_{g})} \Biggl[\sum_{j=1}^{m} \sum_{k=-n}^{n} \frac{1}{h^{2}} \biggl(q^{(2)}_{i,j}(x_{l},t_{g}) \phi ^{\prime}(t_{g}) \frac{W_{j}(t_{g})}{W_{j}(x_{k})} \biggr)\delta _{kg}^{(2)} \\ &\qquad{}+\frac{1}{h} \biggl(\frac{W_{j}(t_{g})}{W_{j}(x_{k})} \biggl(q^{(1)}_{i,j}(x_{l},t_{g})-q^{(2)}_{i,j}(x_{l},t_{g}) \biggl(\frac{\phi ^{\prime \prime}(t_{g})}{\phi ^{\prime}(t_{g})} \biggr) \biggr)+\frac{W_{j}^{\prime}(t_{g})}{W_{j}(x_{k})} \bigl(2q^{(2)}_{i,j}(x_{l},t_{g}) \bigr) \biggr)\delta _{kg}^{(1)} \\ &\qquad{}+\biggl(\frac{W_{j}(t_{g})}{W_{j}(x_{k})} \biggl(q^{(0)}_{i,j}(x_{l},t_{g}) \frac{1}{\phi ^{\prime}(t_{g})}-q^{(1)}_{i,j}(x_{l},t_{g}) \frac{\phi ^{\prime \prime}(t_{g})}{\phi ^{\prime}(t_{g})} \\ &\qquad{}+q^{(2)}_{i,j}(x_{l},t_{g}) \biggl( \frac{2\phi ^{\prime \prime}(t_{g})-\phi ^{\prime \prime \prime}(t_{g})\phi ^{\prime}(t_{g})}{\phi ^{{\prime}^{3}}(t_{g})} \biggr) \biggr) \\ &\qquad{}+\frac{W_{j}^{\prime}(t_{g})}{W_{j}(x_{k})} \biggl(q^{(1)}_{i,j}(x_{l},t_{g}) \frac{1}{\phi ^{\prime}(t_{g})}-2q^{(2)}_{i,j}(x_{l},t_{g}) \frac{\phi ^{\prime \prime}(t_{g})}{\phi ^{{\prime}^{2}}(t_{g})} \biggr) \\ &\qquad{}+\frac{W_{j}^{\prime \prime \prime}(t_{g})}{W_{j}(x_{k})} \frac{1}{\phi ^{\prime}(t_{g})} \biggr)\delta _{kg}^{(0)} )c_{j,k} \Biggr]-\frac{h^{3}}{\phi ^{\prime}(x_{l})}\sum_{j=1}^{m} \sum_{g=-n}^{n} \frac{1}{\phi ^{\prime}(x_{k})} \bigl(q^{(2)}_{i,j}(x_{l},t_{g})v_{j}^{ \prime \prime}(t_{g}) \\ &\qquad{}+q^{(1)}_{i,j}(x_{l},t_{g})v_{j}^{\prime}(t_{g})+q^{(0)}_{i,j}(x_{l},t_{g})v_{j}(t_{g}) \bigr)=\frac{h^{2}}{\phi ^{\prime}(x_{l})}f_{i}(x_{l}), \\ & \quad l=-n, \ldots , n,\quad i=1, \ldots , m, \end{aligned}$$

(3.9)

where we used $c_{j,-n}=c_{j,n}=0$, $j=1,\ldots , m$. Now, the unknowns $c_{j,k}$, $A_{j}$, $B_{j}$ and thus the approximate solutions $y_{j,n}(x)$, $j=1,\ldots , m$ can be determined via the solution of the linear system (3.9).

3.2 Volterra integro-differential system

In a similar manner, substituting $\mathbf{Y}_{n}(x)$ from (3.4) into (1.2) and multiplying both sides by $\frac{h^{2}}{\phi ^{\prime}}$, we have a relation for which after discretizing at the sinc grid points $x_{l}$, $l=-n,\ldots ,n$, can be written as

$$\begin{aligned} & h^{2}\sum_{k=-n}^{n} \biggl(\mathbf{A}_{2}\mathbf{T}^{(2)}_{k}(x_{l})+ \frac{1}{\phi ^{\prime}(x_{l})}\mathbf{A}_{1}\mathbf{T}^{(1)}_{k}(x_{l})+ \frac{1}{\phi ^{{\prime}^{2}}(x_{l})}\mathbf{A}_{0}\mathbf{T}^{(0)}_{k}(x_{l}) \biggr)\mathbf{c}_{k} \\ &\quad{}+\frac{h^{2}}{\phi ^{\prime}(x_{l})} \bigl(\mathbf{A}_{2} \mathbf{v}^{ \prime \prime}(x_{l})+\mathbf{A}_{1} \mathbf{v}^{\prime}(x_{l})+ \mathbf{A}_{0} \mathbf{v}(x_{l}) \bigr) \\ &\quad{}-\frac{h^{2}}{\phi ^{\prime}(x_{l})} \int _{0}^{x_{l}} \sum _{k=-n}^{n} \biggl(\phi ^{\prime}(t) \mathbf{B}_{2}\mathbf{T}^{(2)}_{k}(t)+ \mathbf{B}_{1}\mathbf{T}^{(1)}_{k}(t)+ \frac{1}{\phi ^{\prime}(t)} \mathbf{B}_{0}\mathbf{T}^{(0)}_{k}(t) \biggr)\mathbf{c}_{k}\,dt \\ &\quad{}-\frac{h^{2}}{\phi ^{\prime}(x_{l})} \int _{0}^{1} \bigl(\mathbf{B}_{2} \mathbf{v}^{\prime \prime}(t)+\mathbf{B}_{1} \mathbf{v}^{\prime}(t)+ \mathbf{B}_{0} \mathbf{v}(t) \bigr)\,dt= \frac{h^{2}}{\phi ^{\prime}(x_{k})} \mathbf{f}(x_{l}), \end{aligned}$$

(3.10)

where $\mathbf{c}_{k}$ ant $\mathbf{T}^{(\gamma )}_{k}$ were already defined in (3.7).

Simplifying (3.10), we obtain the following system of linear equations with the unknowns $c_{j,k}, k=-n,\ldots ,n$,

$$\begin{aligned} &\sum_{j=1}^{m}\sum _{k=-n}^{n} \biggl[ \biggl(p^{(2)}_{i,j}(x_{l}) \frac{W_{j}(x_{l})}{W_{j}(x_{k})} \biggr)\delta _{kl}^{(2)}+h \biggl( \frac{W_{j}(x_{l})}{W_{j}(x_{k})} \biggl(p^{(1)}_{i,j}(x_{l}) \frac{1}{\phi ^{\prime}(x_{l})}-p^{(2)}_{i,j}(x_{l}) \frac{\phi ^{\prime \prime}(x_{l})}{\phi ^{{\prime}^{2}}(x_{l})} \biggr) \\ &\qquad{}+\frac{W_{j}^{\prime}(x_{l})}{W_{j}(x_{k})} \biggl(2p^{(2)}_{i,j}(x_{l}) \frac{1}{\phi ^{\prime}(x_{l})} \biggr) \biggr)\delta _{kl}^{(1)}+h^{2} \biggl(\frac{W_{j}(x_{l})}{W_{j}(x_{k})} \biggl(p^{(0)}_{i,j}(x_{l}) \frac{1}{\phi ^{{\prime}^{2}}(x_{l})}-p^{(1)}_{i,j}(x_{l}) \frac{\phi ^{\prime \prime}(x_{l})}{\phi ^{{\prime}^{3}}(x_{l})} \\ &\qquad{}+p^{(2)}_{i,j}(x_{l}) \biggl( \frac{2\phi ^{{\prime \prime}^{2}}(x_{l})-\phi ^{\prime \prime \prime}(x_{l})\phi ^{\prime}(x_{l})}{\phi ^{{\prime}^{4}}(x_{l})} \biggr) \biggr)+\frac{W_{j}^{\prime}(x_{l})}{W_{j}(x_{k})} \biggl(p^{(1)}_{i,j}(x_{l}) \frac{1}{\phi ^{{\prime}^{2}}(x_{l})}-2 \frac{\phi ^{\prime \prime}(x_{l})}{\phi ^{{\prime}^{2}}(x_{l})} \biggr) \\ &\qquad{}+\frac{W_{j}^{\prime \prime}(x_{l})}{W_{j}(x_{k})} \frac{1}{\phi ^{{\prime}^{2}}(x_{l})} \biggr)\delta _{kl}^{(0)} \biggr]c_{j,k}+ \sum_{j=1}^{m} \frac{h^{2}}{\phi ^{\prime}(x_{l})} (p^{(0)}_{i,j}(x_{l})v_{j}(x_{l})+p^{(1)}_{i,j}(x_{l})v_{j}^{ \prime}(x_{l}) ) \\ &\qquad{}+p^{(2)}_{i,j}(x_{l})v_{j}^{\prime \prime}(x_{l})- \frac{h^{3}}{\phi ^{\prime}(x_{l})}\sum_{g=-n}^{n} \delta _{\lg}^{(-1)} \frac{1}{\phi ^{\prime}(t_{g})} \Biggl[\sum _{j=1}^{m}\sum _{k=-n}^{n} \frac{1}{h^{2}} \biggl(q^{(2)}_{i,j}(x_{l},t_{g}) \phi ^{\prime}(t_{g}) \frac{W_{j}(t_{g})}{W_{j}(x_{k})} \biggr)\delta _{kg}^{(2)} \\ &\qquad{}+\frac{1}{h} \biggl( \frac{W_{j}(t_{g})}{W_{j}(x_{k})} \biggl(q^{(1)}_{i,j}(x_{l},t_{g})-q^{(2)}_{i,j}(x_{l},t_{g}) \biggl(\frac{\phi ^{\prime \prime}(t_{g})}{\phi ^{\prime}(t_{g})} \biggr) \biggr)+\frac{W_{j}^{\prime}(t_{g})}{W_{j}(x_{k})} \bigl(2q^{(2)}_{i,j}(x_{l},t_{g})\delta _{kg}^{(1)} \bigr) \biggr) \\ &\qquad{}+ \biggl(\frac{W_{j}(t_{g})}{W_{j}(x_{k})} \biggl(q^{(0)}_{i,j}(x_{l},t_{g}) \frac{1}{\phi ^{\prime}(t_{g})}-q^{(1)}_{i,j}(x_{l},t_{g}) \frac{\phi ^{\prime \prime}(t_{g})}{\phi ^{\prime}(t_{g})}+q^{(2)}_{i,j}(x_{l},t_{g}) \\ &\qquad{}\times \biggl( \frac{2\phi ^{\prime \prime}(t_{g})-\phi ^{\prime \prime \prime}(t_{g})\phi ^{\prime}(t_{g})}{\phi ^{{\prime}^{3}}(t_{g})} \biggr) \biggr)+\frac{W_{j}^{\prime}(t_{g})}{W_{j}(x_{k})} \biggl(q^{(1)}_{i,j}(x_{l},t_{g}) \frac{1}{\phi ^{\prime}(t_{g})}-2q^{(2)}_{i,j}(x_{l},t_{g}) \frac{\phi ^{\prime \prime}(t_{g})}{\phi ^{{\prime}^{2}}(t_{g})} \biggr) \\ &\qquad{}+\frac{W_{j}^{\prime \prime \prime}(t_{g})}{W_{j}(x_{k})} \frac{1}{\phi ^{\prime}(t_{g})} \biggr)\delta _{kg}^{(0)} )c_{j,k} \Biggr] -\frac{h^{3}}{\phi ^{\prime}(x_{l})}\sum _{j=1}^{m}\sum_{g=-n}^{n} \delta _{\lg}^{(-1)}\frac{1}{\phi ^{\prime}(x_{k})} \bigl(q^{(2)}_{i,j}(x_{l},t_{g})v_{j}^{ \prime \prime}(t_{g}) \\ &\qquad{}+q^{(1)}_{i,j}(x_{l},t_{g})v_{j}^{\prime}(t_{g})+q^{(0)}_{i,j}(x_{l},t_{g})v_{j}(t_{g}) \bigr)=\frac{h^{2}}{\phi ^{\prime}(x_{l})}f_{i}(x_{l}), \\ & \quad l=-n,\ldots ,n, i=1,\ldots ,m, \end{aligned}$$

(3.11)

where we used $c_{j,-n}=c_{j,n}=0 j=1,\ldots , m$. Solving the system of linear equations (3.11), the unknowns $c_{j,k}$, $A_{j}$, $B_{j}$ and therefore the approximate solution $y_{j,n}(x)$ for $j=1,\ldots ,m$ can be obtained.

4 Error analysis

To be used in the following, let us define $I^{(s)}=[\delta _{kl}^{(s)}]$ for $s=0,1,2$, where $\delta _{kl}^{s}=(-1)^{s}\delta _{lk}^{s}$, based on (2.11)-(2.13). Also, from (3.3), we get

$$ A_{j}=y_{j}(0),\qquad B_{j}=y_{j}^{\prime}(0), \quad j=1,\ldots , m, $$

and

$$\begin{aligned} v_{j}(x)={}&(2\alpha _{j}+\beta _{j})x^{3}-(3 \alpha _{j}+2\beta _{j})x^{2}+ \beta _{j}x+\alpha _{j} \\ &{}+y_{j}(0) \bigl(3x^{2}-2x^{3} \bigr)+y_{j}^{\prime}(0) \bigl(x^{3}-x^{2} \bigr),\quad j=1, \ldots , m. \end{aligned}$$

First, we will establish the error analysis for the case of Fredholm-type problems, and it will be almost similar to the Volterra type.

4.1 Fredholm integro-differential system

With the above notations, the system of equations (3.9) can be rewritten in the following matrix form

$$ \mathbf{A}\mathbf{c}=\mathbf{q}, $$

(4.1)

where

$$\begin{aligned}& \mathbf{c}=[0,c_{1,-n+1},\ldots , c_{1,n-1},0,\ldots , 0,c_{m,-n+1}, \ldots , c_{m,n-1},0]^{T},\\& \mathbf{q}=[q_{1,-n},\ldots , q_{1,n},\ldots , q_{m,-n}, \ldots , q_{m,n}]^{T}, \end{aligned}$$

with

$$\begin{aligned} q_{i,l}={}&{-}\sum_{j=1}^{m} \frac{h^{2}}{\phi ^{\prime}(x_{l})} \bigl(p^{(0)}_{i,j}(x_{l})v_{j}(x_{l})+p^{(1)}_{i,j}(x_{l})v_{j}^{ \prime}(x_{l})+p^{(2)}_{i,j}(x_{l})v_{j}^{\prime \prime}(x_{l}) \bigr) \\ & {}+ \frac{h^{3}}{\phi ^{\prime}(x_{l})}\sum_{j=1}^{m} \sum_{g=-n}^{n} \frac{1}{\phi ^{\prime}(x_{k})} \bigl(q^{(0)}_{i,j}(x_{l},t_{g})v_{j}(t_{g})+ q^{(1)}_{i,j}(x_{l},t_{g})v_{j}^{\prime}(t_{g}) \\ & {}+ q^{(2)}_{i,j}(x_{l},t_{g})v_{j}^{\prime \prime}(t_{g}) \bigr)+ \frac{h^{2}}{\phi ^{\prime}(x_{l})}f_{i}(x_{l}), \end{aligned}$$

and A is the $m\times m$ block matrix

$$ \mathbf{A}= \begin{bmatrix} A_{11}&A_{12}&\ldots &A_{1m} \\ A_{21}&A_{22}&\ldots &A_{2m} \\ \vdots & \vdots &\ddots &\vdots \\ A_{m1}& A_{m2}& \ldots &A_{mm} \end{bmatrix} $$

where $A_{ij}=[a_{i,j}^{(l,k)}]_{{(2n+1)\times (2n+1)}}$ are the square matrices with

$$\begin{aligned}& \begin{aligned} a_{i,j}^{(l,k)}={}& \biggl(p^{(2)}_{i,j}(x_{l}) \frac{W_{j}(x_{l})}{W_{j}(x_{k})} \biggr)I^{(2)}-h \biggl( \frac{W_{j}(x_{l})}{W_{j}(x_{k})} \biggl(p^{(1)}_{i,j}(x_{l}) \frac{1}{\phi ^{\prime}(x_{l})}- p^{(2)}_{i,j}(x_{l}) \frac{\phi ^{\prime \prime}(x_{l})}{\phi ^{{\prime}^{2}}(x_{l})} \biggr) \\ & {}+\frac{W_{j}^{\prime}(x_{l})}{W_{j}(x_{k})} \biggl(2p^{(2)}_{i,j}(x_{l}) \frac{1}{\phi ^{\prime}(x_{l})} \biggr) \biggr)I^{(1)} \\ & {}+ h^{2} \biggl( \frac{W_{j}(x_{l})}{W_{j}(x_{k})} \biggl(p^{(0)}_{i,j}(x_{l}) \frac{1}{\phi ^{{\prime}^{2}}(x_{l})}-p^{(1)}_{i,j}(x_{l}) \frac{\phi ^{\prime \prime}(x_{l})}{\phi ^{{\prime}^{3}}(x_{l})} \\ & {} +p^{(2)}_{i,j}(x_{l}) \biggl( \frac{2\phi ^{{\prime \prime}^{2}}(x_{l})-\phi ^{\prime \prime \prime}(x_{l})\phi ^{\prime}(x_{l})}{\phi ^{{\prime}^{4}}(x_{l})} \biggr) \biggr) \\ & {}+ \frac{W_{j}^{\prime}(x_{l})}{W_{j}(x_{k})} \biggl(p^{(1)}_{i,j}(x_{l}) \frac{1}{\phi ^{{\prime}^{2}}(x_{l})}-2 \frac{\phi ^{\prime \prime}(x_{l})}{\phi ^{{\prime}^{2}}(x_{l})} \biggr) +\frac{W_{j}^{\prime \prime}(x_{l})}{W_{j}(x_{k})} \frac{1}{\phi ^{{\prime}^{2}}(x_{l})} \biggr)I^{(0)} \\ & {}- \frac{h^{3}}{\phi ^{\prime}(x_{l})}\sum_{g=-n}^{n}\frac{1}{\phi ^{\prime}(t_{g})} \biggl[\frac{1}{h^{2}} \biggl(q^{(2)}_{i,j}(x_{l},t_{g}) \phi ^{\prime}(t_{g}) \frac{W_{j}(t_{g})}{W_{j}(x_{k})} \biggr)I^{(2)} \\ & {}- \frac{1}{h} \biggl( \frac{W_{j}(t_{g})}{W_{j}(x_{k})}\biggl(q^{(1)}_{i,j}(x_{l},t_{g})-q^{(2)}_{i,j}(x_{l},t_{g}) \biggl( \frac{\phi ^{\prime \prime}(t_{g})}{\phi ^{\prime}(t_{g})} \biggr) \biggr)+\frac{W_{j}^{\prime}(t_{g})}{W_{j}(x_{k})} \bigl(2q^{(2)}_{i,j}(x_{l},t_{g}) \bigr) \biggr)I^{(1)} \\ & {}+ \biggl(\frac{W_{j}(t_{g})}{W_{j}(x_{k})}\biggl(q^{(0)}_{i,j}(x_{l},t_{g}) \frac{1}{\phi ^{\prime}(t_{g})}-q^{(1)}_{i,j}(x_{l},t_{g}) \frac{\phi ^{\prime \prime}(t_{g})}{\phi ^{\prime}(t_{g})} \\ & {}+q^{(2)}_{i,j}(x_{l},t_{g}) \biggl( \frac{2\phi ^{\prime \prime}(t_{g})-\phi ^{\prime \prime \prime}(t_{g})\phi ^{\prime}(t_{g})}{\phi ^{{\prime}^{3}}(t_{g})} \biggr) \biggr) \\ & {}+ \frac{W_{j}^{\prime}(t_{g})}{W_{j}(x_{k})} \biggl(q^{(1)}_{i,j}(x_{l},t_{g}) \frac{1}{\phi ^{\prime}(t_{g})}-2q^{(2)}_{i,j}(x_{l},t_{g}) \frac{\phi ^{\prime \prime}(t_{g})}{\phi ^{{\prime}^{2}}(t_{g})} \biggr)+\frac{W_{j}^{\prime \prime \prime}(t_{g})}{W_{j}(x_{k})} \frac{1}{\phi ^{\prime}(t_{g})} \biggr)I^{(0)} ) \biggr], \end{aligned} \\& \quad k,l=-n, \ldots , n. \end{aligned}$$

To be able to find a bound on the error $\vert \mathbf{Y}(x)-\mathbf{Y}_{n}(x) \vert$, we need to obtain a bound on $\|\mathbf{A}\hat{\mathbf{Y}^{*}}-\mathbf{q}\|$ where

$$ \hat{\mathbf{Y}^{*}}=\bigl[\hat{y^{*}}_{1,-n}, \ldots ,\hat{y^{*}}_{1,n}, \ldots , \hat{y^{*}}_{m,-n}, \ldots ,\hat{y^{*}}_{m,n}\bigr]^{T} $$

and

$$ \hat{y^{*}}_{j,n}=\bigl(\phi ^{\prime}y_{j}^{*} \bigr) (x_{n})=\phi ^{\prime}(x_{n}) (y_{j}-v_{j}) (x_{n}), \quad j=1,\ldots ,m. $$

Lemma 7

Let $\phi ^{{\prime}^{2}}y_{j}^{*}\in B(D_{E})$ for $j=1,\ldots ,m$, and for positive constants α, β, and c, we have

$$ \bigl\vert \bigl(\phi ^{\prime} y_{j}^{*} \bigr) (x) \bigr\vert = \bigl\vert \bigl(\phi ^{ \prime} (y_{j}-v_{j}) \bigr) (x) \bigr\vert \leq c\textstyle\begin{cases} e^{-\alpha \vert \phi (x) \vert }, & x\in \Gamma _{a}, \\ e^{-\beta \vert \phi (x) \vert }, & x\in \Gamma _{b}, \end{cases} $$

(4.2)

Let h be selected as (2.3), and the weight functions $W_{j},j=1,\ldots , m$ are defined such that $\frac{W_{j}(x)}{W_{j}(x_{k})}< c_{1}$, $\frac{W_{j}^{\prime}(x)}{W_{j}(x_{k})}< c_{1}$ and $\frac{W_{j}^{\prime \prime}(x)}{W_{j}(x_{k})}< c_{1}$, then we have

$$ \bigl\Vert \mathbf{A}\hat{\mathbf{Y}^{*}}- \mathbf{q} \bigr\Vert \leq k_{8}n^{\frac{1}{2}}e^{- \sqrt{\pi\,d \alpha n}} $$

(4.3)

with the previously defended A, $\hat{\mathbf{Y}^{*}}$, and q.

Proof

Assume that the kernels $k_{j,\gamma},j=1,\ldots , m$, $\gamma =0,1,2$, defined as

$$ k_{j,\gamma}(x,z)=\frac{1}{2\pi i (\phi ^{\prime}(x))^{\gamma -1}} \frac{\partial ^{\gamma}}{\partial x^{\gamma}} \biggl( \frac{\sin (\frac{\pi \phi (x)}{h} ) W_{j}(x)}{\phi ^{\prime}(x) (\phi (z)-\phi (x) )W_{j}(z)} \biggr) $$

(4.4)

are associated with the modified nonclassical sinc functions. We can expand $\hat{y_{j}^{*}}(x)=y_{j}^{*}(x)\phi ^{\prime}(x)$ as follows

$$ y_{j}^{*}(x)-\sum _{k=-\infty}^{\infty}\hat{y_{j}^{*}}(x_{k}) \frac{T^{(0)}_{j,k}(x)}{\phi ^{\prime}(x)}= \int _{\partial D} \frac{k_{j,0}(x,z)}{\phi ^{\prime}(x)\sin (\frac{\pi \phi (z)}{h} )} \phi ^{\prime}(z) \hat{y_{j}^{*}}(z)\,dz, $$

where $T^{(0)}_{j,k}(x)$ are defined by (3.8). Thus, we have

$$\begin{aligned}& \frac{d^{\gamma}}{dx^{\gamma}}y_{j}^{*}(x)-\sum _{k=-\infty}^{\infty}\bigl( \phi ^{\prime}(x) \bigr)^{\gamma -1}T^{(\gamma )}_{j,k}(x)\hat{y_{j}^{*}}(x_{k}) \quad \\& \quad = \int _{\partial D} \frac{(\phi ^{\prime}(x))^{\gamma -1}k_{j,\gamma}(x,z)}{\sin (\frac{\pi \phi (z)}{h} )} \phi ^{\prime}(z) \hat{y_{j}^{*}}(z)\,dz,\quad \gamma =0,1,2. \end{aligned}$$

Let us define the form of the residual vector $\mathbf{r}=\mathbf{A}\hat{\mathbf{Y}^{*}}-\mathbf{q}$ by

$$ \mathbf{r}=[r_{1,-n},\ldots ,r_{1,n},\ldots ,r_{m,-n},\ldots ,r_{m,n}]^{T}, $$

then, by replacing $c_{j,k}$ with $\hat{y_{j}^{*}}(x_{k})$ in (3.9), we have

$$\begin{aligned} r_{i,l}={}&\bigl\{ \mathbf{A}\hat{ \mathbf{Y}^{*}}-\mathbf{q}\bigr\} _{i,l} \\ ={}&h^{2}\sum_{j=1}^{m}\sum _{k=-n}^{n} \biggl(p^{(2)}_{i,j}(x_{l})T^{(2)}_{j,k}(x_{l})+ \frac{q^{(1)}_{i,j}(x_{l})}{\phi ^{\prime}(x_{l})}T^{(1)}_{j,k}(x_{l})+ \frac{p^{(0)}_{i,j}(x_{l})}{\phi ^{{\prime}^{2}}(x_{l})}T^{(0)}_{j,k}(x_{l}) \biggr)\hat{y_{j}^{*}}(x_{k}) \\ &\qquad{}+\sum_{j=1}^{m}\frac{h^{2}}{\phi ^{\prime}(x_{l})} \bigl(p^{(2)}_{i,j}(x_{l})v_{j}^{ \prime \prime}(x_{l})+p^{(1)}_{i,j}(x_{l})v_{j}^{\prime}(x_{l})+ p^{(0)}_{i,j}(x_{l})v_{j}(x_{l}) \bigr) \\ &\qquad{}-\frac{h^{2}}{\phi ^{\prime}(x_{l})} \int _{0}^{1} \sum_{j=1}^{m} \sum_{k=-n}^{n} \biggl(q^{(2)}_{i,j}(x_{l},t) \phi ^{\prime}(t)T^{(2)}_{j,k}(t)+q^{(1)}_{i,j}(x_{l},t)T^{(1)}_{j,k}(t) \\ &\qquad{}+\frac{q^{(0)}_{i,j}(x_{l},t)}{\phi ^{\prime}(t)}T^{(0)}_{j,k}(t) \biggr) \hat{y_{j}^{*}}(x_{k})\,dt - \frac{h^{2}}{\phi ^{\prime}(x_{l})} \int _{0}^{1}\sum_{j=1}^{m} \bigl(q^{(2)}_{i,j}(x_{l},t)v_{j}^{\prime \prime}(t) \\ &\qquad{}+q^{(1)}_{i,j}(x_{l},t)v_{j}^{\prime}(t)+q^{(0)}_{i,j}(x_{l},t)v_{j}(t) \bigr)\,dt-\frac{h^{2}}{\phi ^{\prime}(x_{k})}f_{i}(x_{l}). \end{aligned}$$

(4.5)

Since $\frac{h^{2}}{\phi ^{\prime}}(Ly_{j}-f_{i})=0$, by subtracting this relation from (4.5), we have

$$\begin{aligned} r_{i,l}&= \bigl\{ \mathbf{A}\hat{\mathbf{Y}^{*}}- \mathbf{q} \bigr\} _{i,l}- \frac{h^{2}}{\phi ^{\prime}(x_{l})}(Ly_{j}-f_{i}) (x_{l}) \\ &=h^{2}\sum_{j=1}^{m}\sum _{k=-n}^{n} \biggl(p^{(2)}_{i,j}(x_{l})T^{(2)}_{j,k}(x_{l})+ \frac{p^{(1)}_{i,j}(x_{l})}{\phi ^{\prime}(x_{l})}T^{(1)}_{j,k}(x_{l})+ \frac{p^{(0)}_{i,j}(x_{l})}{\phi ^{{\prime}^{2}}(x_{l})}T^{(0)}_{j,k}(x_{l}) \biggr)\hat{y_{j}^{*}}(x_{k}) \\ &+\sum_{j=1}^{m}\frac{h^{2}}{\phi ^{\prime}(x_{l})} \bigl(p^{(2)}_{i,j}(x_{l})v_{j}^{ \prime \prime}(x_{l})+p^{(1)}_{i,j}(x_{l})v_{j}^{\prime}(x_{l})+p^{(0)}_{i,j}(x_{l})v_{j}(x_{l}) \bigr)- \frac{h^{2}}{\phi ^{\prime}(x_{l})} \\ & \int _{0}^{1} \sum_{j=1}^{m} \sum_{k=-n}^{n} \biggl(q^{(2)}_{i,j}(x_{l},t) \phi ^{\prime}(t)T^{(2)}_{j,k}(t)+q^{(1)}_{i,j}(x_{l},t)T^{(1)}_{j,k}(t)+ \frac{q^{(0)}_{i,j}(x_{l},t)}{\phi ^{\prime}(t)}T^{(0)}_{j,k}(t) \biggr) \\ &\hat{y_{j}^{*}}(x_{k})\,dt- \frac{h^{2}}{\phi ^{\prime}(x_{l})} \int _{0}^{1} \sum_{j=1}^{m} \bigl(q^{(2)}_{i,j}(x_{l},t)v_{j}^{\prime \prime}(t)+q^{(1)}_{i,j}(x_{l},t)v_{j}^{ \prime}(t)+q^{(0)}_{i,j}(x_{l},t)v_{j}(t) \bigr)\,dt \\ -&\frac{h^{2}}{\phi ^{\prime}(x_{l})}f_{i}(x_{l})- \frac{h^{2}}{\phi ^{\prime}(x_{l})}\sum_{j=1}^{m} \bigl(p^{(2)}_{i,j}(x_{l})y_{j}^{ \prime \prime}(x_{l})+p^{(2)}_{i,j}(x_{l})y_{j}^{\prime}(x_{l})+p^{(0)}_{i,j}(x_{l})y_{j}(x_{l}) \bigr) \\ +&\frac{h^{2}}{\phi ^{\prime}(x_{l})} \int _{0}^{1}\sum_{j=1}^{m} \bigl(q^{(2)}_{i,j}(x_{l},t)y_{j}^{\prime \prime}(t)+q^{(1)}_{i,j}(x_{l},t)y_{j}^{ \prime}(t)+q^{(0)}_{i,j}(x_{l},t)y_{j}(t) \bigr)\,dt+ \frac{h^{2}}{\phi ^{\prime}(x_{k})}f_{i}(x_{l}) \\ =&r_{i,l}^{(1)}+r_{i,l}^{(2)}+r_{i,l}^{(3)} +r_{i,l}^{(4)}, \end{aligned}$$

where

$$\begin{aligned}& r_{i,l}^{(1)}=-\frac{h^{2}}{\phi ^{\prime}(x_{l})}\sum _{j=1}^{m} \bigl(p^{(2)}_{i,j}(x_{l})y_{j}^{\prime \prime}(x_{l})+p^{(1)}_{i,j}(x_{l})y_{j}^{ \prime}(x_{l})+p^{(0)}_{i,j}(x_{l})y_{j}(x_{l}) \bigr) \\& \hphantom{r_{i,l}^{(1)}=} {}+ \sum_{j=1}^{m}\frac{h^{2}}{\phi ^{\prime}(x_{l})} \bigl(p^{(2)}_{i,j}(x_{l})v_{j}^{ \prime \prime}(x_{l})+p^{(1)}_{i,j}(x_{l})v_{j}^{\prime}(x_{l})+p^{(0)}_{i,j}(x_{l})v_{j}(x_{l}) \bigr) \\& \hphantom{r_{i,l}^{(1)}=} {}+ h^{2}\sum_{j=1}^{m}\sum _{k=-\infty}^{\infty} \biggl(p^{(2)}_{i,j}(x_{l})T^{(2)}_{j,k}(x_{l})+ \frac{p^{(1)}_{i,j}(x_{l})}{\phi ^{\prime}(x_{l})}T^{(1)}_{j,k}(x_{l})+ \frac{p^{(0)}_{i,j}(x_{l})}{\phi ^{{\prime}^{2}}(x_{l})}T^{(0)}_{j,k}(x_{l}) \biggr)\hat{y_{j}^{*}}(x_{k}) \\& \hphantom{r_{i,l}^{(1)}}=- \frac{h^{2}}{\phi ^{\prime}(x_{l})} \Biggl(\sum_{j=1}^{m} \bigl(p^{(2)}_{i,j}(x_{l})y_{j}^{*^{ \prime \prime}}(x_{l})+p^{(1)}_{i,j}(x_{l})y_{j}^{*^{\prime}}(x_{l})+p^{(0)}_{i,j}(x_{l})y_{j}^{*}(x_{l}) \bigr) \Biggr) \\& \hphantom{r_{i,l}^{(1)}=} {}+ h^{2}\sum_{j=1}^{m}\sum _{k=-\infty}^{\infty} \biggl(p^{(2)}_{i,j}(x_{l})T^{(2)}_{j,k}(x_{l})+ \frac{p^{(1)}_{i,j}(x_{l})}{\phi ^{\prime}(x_{l})}T^{(1)}_{j,k}(x_{l})+ \frac{p^{(0)}_{i,j}(x_{l})}{\phi ^{{\prime}^{2}}(x_{l})}T^{(0)}_{j,k}(x_{l}) \biggr)\hat{y_{j}^{*}}(x_{k}) \\& \hphantom{r_{i,l}^{(1)}}=- h^{2}\sum_{j=1}^{m} \int _{\partial D_{E}} \biggl[p^{(2)}_{i,j}(x_{l})k_{2,j}(x_{l},z)+ \frac{p^{(1)}_{i,j}(x_{l})}{\phi ^{\prime}(x_{l})}k_{1,j}(x_{l},z) \\& \hphantom{r_{i,l}^{(1)}=} {}+ \frac{p^{(0)}_{i,j}(x_{l})}{\phi ^{{\prime}^{2}}(x_{l})}k_{0,j}(x_{l},z) \biggr] \frac{\phi ^{\prime}(z)\hat{y_{j}^{*}}(z)}{\sin (\frac{\pi \phi (z)}{h} )}\,dz, \\& \begin{aligned} r_{i,l}^{(2)} ={}&{-}h^{2}\sum_{j=1}^{m}\sum _{k=-\infty}^{-n-1} \biggl(p^{(2)}_{i,j}(x_{l})T^{(2)}_{j,k}(x_{l})+ \frac{p^{(1)}_{i,j}(x_{l})}{\phi ^{\prime}(x_{l})}T^{(1)}_{j,k}(x_{l})+ \frac{p^{(0)}_{i,j}(x_{l})}{\phi ^{{\prime}^{2}}(x_{l})}T^{(0)}_{j,k}(x_{l}) \biggr)\hat{y_{j}^{*}}(x_{k}) \\ &{}- h^{2}\sum_{j=1}^{m}\sum _{k=n+1}^{\infty} \biggl(p^{(2)}_{i,j}(x_{l})T^{(2)}_{j,k}(x_{l})+ \frac{p^{(1)}_{i,j}(x_{l})}{\phi ^{\prime}(x_{l})}T^{(1)}_{j,k}(x_{l})+ \frac{p^{(0)}_{i,j}(x_{l})}{\phi ^{{\prime}^{2}}(x_{l})}T^{(0)}_{j,k}(x_{l}) \biggr)\hat{y_{j}^{*}}(x_{k}), \end{aligned} \\& r_{i,l}^{(3)}=\frac{h^{2}}{\phi ^{\prime}(x_{l})} \bigl(f_{i}(x_{l})-f_{i}(x_{l}) \bigr)=0, \\& \begin{aligned} r_{i,l}^{(4)}={}&\frac{h^{2}}{\phi ^{\prime}(x_{l})} \int _{0}^{1} \sum_{j=1}^{m} \sum_{k=-n}^{n} \biggl(q^{(2)}_{i,j}(x_{l},t) \phi ^{\prime}(t)T^{(2)}_{j,k}(t) \quad \\ & {}+ q^{(1)}_{i,j}(x_{l},t)T^{(1)}_{j,k}(t)+ \frac{q^{(0)}_{i,j}(x_{l},t)}{\phi ^{\prime}(t)}T^{(0)}_{j,k}(t) \biggr) \hat{y_{j}^{*}}(x_{k})\,dt \\ & {}+ \frac{h^{2}}{\phi ^{\prime}(x_{l})} \int _{0}^{1}\sum_{j=1}^{m} \bigl(q^{(2)}_{i,j}(x_{l},t)y_{j}^{\prime \prime}(t)+q^{(1)}_{i,j}(x_{l},t)y_{j}^{ \prime}(t)+q^{(0)}_{i,j}(x_{l},t)y_{j}(t) \bigr)\,dt \\ & {}- \frac{h^{2}}{\phi ^{\prime}(x_{l})} \int _{0}^{1}\sum_{j=1}^{m} \bigl(q^{(2)}_{i,j}(x_{l},t)v_{j}^{\prime \prime}(t)+q^{(1)}_{i,j}(x_{l},t)v_{j}^{ \prime}(t)+q^{(0)}_{i,j}(x_{l},t)v_{j}(t) \bigr)\,dt \\ ={}&\frac{h^{2}}{\phi ^{\prime}(x_{l})} \int _{0}^{1}\sum_{j=1}^{m} \bigl(q^{(2)}_{i,j}(x_{l},t)y_{j}^{*^{\prime \prime}}(t)+q^{(1)}_{i,j}(x_{l},t)y_{j}^{*^{ \prime}}(t)+q^{(0)}_{i,j}(x_{l},t)y_{j}^{*}(t) \bigr)\,dt \\ & {}- \frac{h^{3}}{\phi ^{\prime}(x_{l})}\sum_{g=-n}^{n} \sum_{j=1}^{m} \sum _{k=-n}^{n} \biggl(q^{(2)}_{i,j}(x_{l},t_{g})T^{(2)}_{j,k}(t_{g})+ \frac{q^{(1)}_{i,j}(x_{l},t_{g})}{\phi ^{\prime}(t_{g})}T^{(1)}_{j,k}(t_{g}) \\ & {}+ \frac{q^{(0)}_{i,j}(x_{l},t_{g})}{\phi ^{{\prime}^{2}}(t_{g})}T^{(0)}_{j,k}(t_{g}) \biggr)\hat{y_{j}^{*}}(x_{k}). \end{aligned} \end{aligned}$$

From (4.4), we deduce that

$$\begin{aligned}& k_{j,0}(x_{l},z)=0, \quad \\& k_{j,1}(x_{l},z)= \frac{(-1)^{l}W_{j}(x_{l})}{2ih(\phi (z)-lh)W_{j}(z)}, \\& k_{j,2}(x_{l},z)=\frac{(-1)^{l}}{2ih(\phi (z)-lh)^{2}} \biggl(2+\bigl( \phi (z)-lh\bigr) \biggl(\frac{1}{\phi ^{\prime}} \biggr)^{\prime}(x_{l}) \biggr)\frac{W_{j}(x_{l})}{W_{j}(z)} \\& \hphantom{k_{j,2}(x_{l},z)=}{}\times \frac{(-1)^{l}W_{j}^{\prime}(x_{l})}{2ih(\phi (z)-lh)W_{j}(z)} \biggl(\frac{2}{\phi ^{\prime}} \biggr) (x_{l}). \end{aligned}$$

Also, for the mapping $\phi (x)$, we have the following bounds

$$ \begin{gathered} \biggl\vert \frac{1}{\phi ^{\prime}(x)} \biggr\vert \leq \frac{1}{4},\qquad \biggl\vert \biggl(\frac{1}{\phi ^{\prime}(x)} \biggr)^{\prime} \biggr\vert \leq 1,\\ \biggl\vert \biggl( \frac{1}{\phi ^{\prime}(x)} \biggr)^{ \prime \prime} \biggr\vert \leq 2,\qquad \biggl\vert \biggl( \frac{1}{\phi ^{\prime}} \biggr) \biggl(\frac{1}{\phi ^{\prime}} \biggr)^{\prime \prime} \biggr\vert \leq \frac{1}{2}, \end{gathered} $$

(4.6)

Note that on $\partial D_{E}$, we have $|I\phi (z)|=d$, thus by defining $u(z)=R\phi (z)$ and using the bounds in (4.6) and lemmas assumptions on $W_{j}$, we have

$$ \bigl\vert k_{j,1}(x_{l},z) \bigr\vert \leq \frac{c_{1}c_{1}^{\prime}h^{-1}}{ ((u(z)-lh)^{2}+d^{2} )^{\frac{1}{2}}}, \qquad \bigl\vert k_{j,2}(x_{l},z) \bigr\vert \leq \frac{c_{1}c_{2}^{\prime}h^{-1}}{ ((u(z)-lh)^{2}+d^{2} )^{\frac{1}{2}}}, $$

which results in

$$ h^{2} \biggl\vert p^{(2)}_{i,j}(x_{l}) k_{j,2}(x_{l},z)+ \frac{p^{(1)}_{i,j}(x_{l})}{\phi ^{\prime}(x_{l})}k_{j,1}(x_{l},z) \biggr\vert \leq \frac{c_{1}c_{2}h}{ ((u(z)-lh)^{2}+d^{2} )^{\frac{1}{2}}}, $$

(4.7)

where the constant $c_{2}$ is depending on h, d, and the on bounds in (4.6). Thus, we have

$$\begin{aligned} \bigl\Vert \mathbf{A}\hat{\mathbf{Y}^{*}}- \mathbf{q} \bigr\Vert ={}& \Biggl( \sum_{i=1}^{m} \sum_{l=-n}^{n} \vert r_{i,l} \vert ^{2} \Biggr)^{\frac{1}{2}} \\ \leq{}& \Biggl(\sum_{i=1}^{m}\sum _{l=-n}^{n} \bigl\vert r_{i,l}^{(1)} \bigr\vert ^{2} \Biggr)^{\frac{1}{2}} + \Biggl(\sum _{i=1}^{m}\sum_{l=-n}^{n} \bigl\vert r_{i,l}^{(2)} \bigr\vert ^{2} \Biggr)^{\frac{1}{2}} \\ &{}+ \Biggl(\sum_{i=1}^{m}\sum _{l=-n}^{n} \bigl\vert r_{i,l}^{(3)} \bigr\vert ^{2} \Biggr)^{ \frac{1}{2}}+ \Biggl(\sum _{i=1}^{m}\sum_{l=-n}^{n} \bigl\vert r_{i,l}^{(4)} \bigr\vert ^{2} \Biggr)^{\frac{1}{2}}. \end{aligned}$$

(4.8)

For the first term on right-hand side, we have

$$\begin{aligned} \Biggl(\sum_{i=1}^{m} \sum_{l=-n}^{n} \bigl\vert r_{i,l}^{(1)} \bigr\vert ^{2} \Biggr)^{ \frac{1}{2}}& \leq \Biggl(\sum_{i=1}^{m} \sum_{l=-n}^{n}\sum _{j=1}^{m} \biggl\vert \int _{\partial D_{E}} \frac{c_{1}c_{2}h}{ ((u(z)-kh)^{2}+d^{2} )^{\frac{1}{2}}} \frac{|\phi ^{\prime}(z)\hat{y_{j}^{*}}(z)}{ \vert \sin (\frac{\pi \phi (z)}{h} ) \vert } \biggr\vert \,dz \vert \vert ^{2} \Biggr)^{\frac{1}{2}} \\ & \leq \frac{k_{5}c_{1}}{ (\sinh (\frac{\pi d}{h} ) )}, \end{aligned}$$

(4.9)

which the last inequality is obtained using (4.7), the bound $\sinh (\frac{\pi d}{h} )\leq \sin ( \frac{\pi \phi (z)}{h} )$ on $\partial D_{E}$ and the integrability of $|\phi ^{\prime}\hat{y_{j}^{*}}|$.

Now for the second term on the right-hand side of (4.8), we can use relations (4.2) and (4.6) as follows

$$\begin{aligned} \Biggl(\sum_{i=1}^{m} \sum_{l=-n}^{n} \bigl\vert r_{i,l}^{(2)} \bigr\vert ^{2} \Biggr)^{\frac{1}{2}} ={}& \Biggl(\sum_{i=1}^{m} \sum_{l=-n}^{n} \Biggl\vert \sum _{j=1}^{m}\sum _{k< -n,k>n} \biggl[ \biggl(p^{(2)}_{i,j}(x_{l}) \frac{W_{j}(x_{l})}{W_{j}(x_{k})} \biggr)\delta _{kl}^{(2)} \\ & {}+ h \biggl(\frac{W_{j}(x_{l})}{W_{j}(x_{k})} \biggl(p^{(1)}_{i,j}(x_{l}) \frac{1}{\phi ^{\prime}(x_{l})}-p^{(2)}_{i,j}(x_{l}) \frac{\phi ^{\prime \prime}(x_{l})}{\phi ^{{\prime}^{2}}(x_{l})} \biggr) \\ & {}+ \frac{W_{j}^{\prime}(x_{l})}{W_{j}(x_{k})} \biggl(2p^{(2)}_{i,j}(x_{l}) \frac{1}{\phi ^{\prime}(x_{l})} \biggr) \biggr)\delta _{kl}^{(1)}+ \\ & {}+ h^{2} \biggl(\frac{W_{j}(x_{l})}{W_{j}(x_{k})} \biggl(p^{(0)}_{i,j}(x_{l}) \frac{1}{\phi ^{\prime}(x_{l})} -p^{(1)}_{i,j}(x_{l}) \frac{\phi ^{\prime \prime}(x_{l})}{\phi ^{{\prime}^{3}}(x_{l})} \\ & {}+ p^{(2)}_{i,j}(x_{l}) \biggl( \frac{2\phi ^{{\prime \prime}^{2}}(x_{l})-\phi ^{\prime \prime \prime}(x_{l})\phi ^{\prime}(x_{l})}{\phi ^{{\prime}^{4}}(x_{l})} \biggr) \biggr) \\ & {}+ \frac{W_{j}^{\prime}(x_{l})}{W_{j}(x_{k})} \biggl(p^{(1)}_{i,j}(x_{l}) \frac{1}{\phi ^{{\prime}^{2}}(x_{l})}-2 \frac{\phi ^{\prime \prime}(x_{l})}{\phi ^{{\prime}^{2}}(x_{l})} \biggr) \\ & {}+ \frac{W_{j}^{\prime \prime }(x_{l})}{W_{j}(x_{k})} \frac{1}{\phi ^{{\prime}^{2}}(x_{l})} \biggr)\delta _{kl}^{(0)} \biggr] \hat{y_{j}^{*}}(x_{k}) \Biggr\vert ^{2} \Biggr) \\ \leq{} & \Biggl( c_{1}^{2}c_{3}^{\prime} \sum_{i=1}^{m}\sum _{l=-n}^{n} \Biggl(\sum _{k< -n,k>n}\gamma _{kl}^{2}\sum _{j=1}^{m}\sum_{k< -n,k>n} \bigl\vert \hat{y_{j}^{*}}(x_{k}) \bigr\vert ^{2} \Biggr) \Biggr)^{\frac{1}{2}} \\ \leq {}& \frac{c_{1}k_{6}}{h}e^{-\alpha nh}, \end{aligned}$$

(4.10)

where $\gamma _{kl}$ is defined by

$$ \gamma _{kl}=\max \bigl\{ \bigl\vert \delta _{kl}^{(0)} \bigr\vert , \bigl\vert \delta _{kl}^{(1)} \bigr\vert , \bigl\vert \delta _{kl}^{(2)} \bigr\vert \bigr\} . $$

Also, for the third term on the right-hand side of (4.8), we have

$$ \Biggl(\sum_{i=1}^{m} \sum_{l=-n}^{n} \bigl\vert r_{i,l}^{(3)} \bigr\vert ^{2} \Biggr)^{ \frac{1}{2}}=0. $$

(4.11)

Finally, the fourth term on the right-hand side of (4.8) can be bounded using (2.6) as follows

$$\begin{aligned} \Biggl(\sum_{i=1}^{m} \sum_{l=-n}^{n} \bigl\vert r_{i,l}^{(4)} \bigr\vert ^{2} \Biggr)^{ \frac{1}{2}}={}& \Biggl(\sum_{i=1}^{m} \sum_{l=-n}^{n} \Biggl\vert \frac{h^{2}}{\phi ^{\prime}(x_{l})} \int _{0}^{1}\sum_{j=1}^{m} \bigl(q^{(2)}_{i,j}(x_{l},t)y_{j}^{*^{ \prime \prime}}(t) \\ &+{}q^{(1)}_{i,j}(x_{l},t)y_{j}^{*^{\prime}}(t)+q^{(0)}_{i,j}(x_{l},t)y_{j}^{*}(t) \bigr)\,dt \\ &{}-\frac{h^{3}}{\phi ^{\prime}(x_{l})}\sum_{i=1}^{m} \sum_{g=-n}^{n} \sum _{j=1}^{m} \sum_{k=-n}^{n} \biggl(q^{(2)}_{i,j}(x_{l},t_{g})T^{(2)}_{j,k}(t_{g}) \\ &{}+\frac{q^{(1)}_{i,j}(x_{l},t_{g})}{\phi ^{\prime}(t_{g})}T^{(1)}_{j,k}(t_{g})+ \frac{q^{(0)}_{i,j}(x_{l},t_{g})}{\phi ^{{\prime}^{2}}(t_{g})}T^{(0)}_{j,k}(t_{g}) \biggr)\hat{y_{j}^{*}}(x_{k}) \Biggr\vert ^{2} \Biggr)^{\frac{1}{2}} \\ \leq{} &k_{7}n^{\frac{1}{2}}e^{-\sqrt{\pi\,d \alpha n}}. \end{aligned}$$

(4.12)

Now using (4.9)-(4.12), we obtain the result

$$ \bigl\Vert \mathbf{A}\hat{\mathbf{Y}^{*}}-\mathbf{q} \bigr\Vert \leq k_{8}n^{\frac{1}{2}}e^{-\sqrt{\pi\,d \alpha n}}. $$

 □

Theorem 8

Let $\mathbf{Y}(x)$ and $\mathbf{Y}_{n}(x)$ be the exact and the sinc-approximate solutions of (1.1)-(1.3), respectively. If all assumptions of lemma 7are holds, then we have the following bound

$$ \bigl\vert \mathbf{Y}(x)-\mathbf{Y}_{n}(x) \bigr\vert \leq c_{1}\biggl(k_{4}+ \frac{1}{4}\rho k_{8}\biggr) n^{\frac{1}{2}}e^{-\sqrt{\pi\,d \alpha n}}, \quad x\in \Gamma . $$

Proof

Let $\eta (x)=[\eta _{1,n}(x),\ldots , \eta _{m,n}(x)]^{T}$, where functions $\eta _{j,n}((x))$ are

$$ \eta _{j,n}(x)=\frac{1}{\phi ^{\prime}(x)}\sum _{k=-n}^{n} \frac{W_{j}(x)}{W_{j}(x_{k})}y_{j}^{*}(x_{k}) \phi ^{\prime}(x_{k})S_{k}(x)= \frac{1}{\phi ^{\prime}(x)}\sum_{k=-n}^{n} \frac{W_{j}(x)}{W_{j}(x_{k})}\hat{y_{j}^{*}}(x_{k})S_{k}(x). $$

From (3.5), we have

$$\begin{aligned} \mathbf{Y}(x)-\mathbf{Y}_{n}(x)&=\mathbf{Y}(x)- \mathbf{Y}_{n}(x)+\eta _{n}(x)- \eta _{n}(x) \\ &=\mathbf{Y}(x)-\mathbf{u}_{n}(x)-\mathbf{v}(x)+\eta _{n}(x)-\eta _{n}(x), \end{aligned}$$

where $\mathbf{u}_{n}(x)$ and $\mathbf{v}(x)$ are the vectors defined before. Since $\mathbf{Y}^{*}(x)=\mathbf{Y}(x)-\mathbf{v}(x)$, we obtain

$$ \mathbf{Y}(x)-\mathbf{Y}_{n}(x)= \bigl(\mathbf{Y}^{*}(x)- \eta _{n}(x) \bigr)+ \bigl(\eta _{n}(x)- \mathbf{u}_{n}(x) \bigr). $$

Now we can use the triangular inequality on the relation above to obtain

$$ \bigl\vert \mathbf{Y}(x)-\mathbf{Y}_{n}(x) \bigr\vert \leq \bigl\vert \mathbf{Y}^{*}(x)- \eta _{n}(x) \bigr\vert + \bigl\vert \eta _{n}(x)- \mathbf{u}_{n}(x) \bigr\vert . $$

(4.13)

By theorem 6 and the results in [39], we get

$$ \sup_{x\in \Gamma} \bigl\vert \mathbf{Y}^{*}(x)-\eta _{n}(x) \bigr\vert \leq c_{1}k_{4}n^{ \frac{1}{2}}e^{-\sqrt{\pi\,d \alpha n}}. $$

(4.14)

To find a bound on

$$ \bigl\vert \eta _{n}(x)-\mathbf{u}_{n}(x) \bigr\vert = \Biggl\vert \frac{1}{\phi ^{\prime}(x)}\sum_{k=-n}^{n} \frac{\mathbf{W}(x)}{\mathbf{W}(x_{k})} \bigl(\hat{\mathbf{Y}^{*}}(x_{k})- \mathbf{c}_{k} \bigr)S_{k}(x) \Biggr\vert , $$

we can use the Cauchy–Schwartz inequality to obtain

$$\begin{aligned} \bigl\vert \eta _{n}(x)-\mathbf{u}_{n}(x) \bigr\vert &\leq \Biggl(\sum_{k=-n}^{n} \bigl\vert \hat{\mathbf{Y}^{*}}(x_{k})- \mathbf{c}_{k} \bigr\vert ^{2} \Biggr)^{ \frac{1}{2}} \Biggl(\sum_{k=-n}^{n} \biggl\vert \frac{\mathbf{W}(x)}{\mathbf{W}(x_{k})} \frac{S_{k}(x)}{\phi ^{\prime}} \biggr\vert ^{2} \Biggr)^{\frac{1}{2}} \\ & \leq \frac{c_{1}}{4} \Biggl(\sum_{k=-n}^{n} \bigl\vert \hat{\mathbf{Y}^{*}}(x_{k})- \mathbf{c}_{k} \bigr\vert ^{2} \Biggr)^{ \frac{1}{2}}= \frac{c_{1}}{4} \bigl\Vert \hat{\mathbf{Y}^{*}}-\mathbf{c} \bigr\Vert , \end{aligned}$$

(4.15)

where the boundedness of $\frac{1}{\phi ^{\prime}(x)}$ and $\frac{\mathbf{W}(x)}{\mathbf{W}(x_{k})}< c_{1}$ are used to obtain the last relation. Now, from (4.3), we have

$$\begin{aligned} \bigl\Vert \hat{\mathbf{Y}^{*}}-\mathbf{c} \bigr\Vert = \bigl\Vert \mathbf{A}^{-1}\bigl(\mathbf{A} \hat{ \mathbf{Y}^{*}}-\mathbf{q}\bigr) \bigr\Vert \leq \Vert A \Vert ^{-1} \bigl\Vert \mathbf{A} \hat{\mathbf{Y}^{*}}- \mathbf{q} \bigr\Vert \leq \rho k_{8}n^{\frac{1}{2}}e^{- \sqrt{\pi\,d \alpha n}}. \end{aligned}$$

(4.16)

where $\rho =\|A\|^{-1}$. Finally, combining the results (4.13)-(4.16), we deduce that

$$ \bigl\vert \mathbf{Y}(x)-\mathbf{Y}_{n}(x) \bigr\vert \leq c_{1}\biggl(k_{4}+ \frac{1}{4}\rho k_{8}\biggr) n^{\frac{1}{2}}e^{-\sqrt{\pi\,d \alpha n}}. $$

 □

4.2 Volterra integro-differential system

The error analysis procedure for the Volterra case can be done similarly, except that in this case, the matrices $A_{ij}$ are defined by $A_{ij}=[a_{i,j}^{(l,k)}]_{{(2n+1)\times (2n+1)}}$, where

$$\begin{aligned} &\begin{aligned} a_{i,j}^{(l,k)}={}& \biggl(p^{(2)}_{i,j}(x_{l}) \frac{W_{j}(x_{l})}{W_{j}(x_{k})} \biggr)I^{(2)}-h \biggl( \frac{W_{j}(x_{l})}{W_{j}(x_{k})} \biggl(p^{(1)}_{i,j}(x_{l}) \frac{1}{\phi ^{\prime}(x_{l})} \\ & {}- p^{(2)}_{i,j}(x_{l}) \frac{\phi ^{\prime \prime}(x_{l})}{\phi ^{{\prime}^{2}}(x_{l})} \biggr)+\frac{W_{j}^{\prime}(x_{l})}{W_{j}(x_{k})} \biggl(2p^{(2)}_{i,j}(x_{l}) \frac{1}{\phi ^{\prime}(x_{l})} \biggr) \biggr)I^{(1)} \\ & {}+ h^{2} \biggl( \frac{W_{j}(x_{l})}{W_{j}(x_{k})}\biggl(p^{(0)}_{i,j}(x_{l}) \frac{1}{\phi ^{{\prime}^{2}}(x_{l})}-p^{(1)}_{i,j}(x_{l}) \frac{\phi ^{\prime \prime}(x_{l})}{\phi ^{{\prime}^{3}}(x_{l})} \\ & {} +p^{(2)}_{i,j}(x_{l}) \biggl( \frac{2\phi ^{{\prime \prime}^{2}}(x_{l})-\phi ^{\prime \prime \prime}(x_{l})\phi ^{\prime}(x_{l})}{\phi ^{{\prime}^{4}}(x_{l})} \biggr) \biggr) \\ & {}+ \frac{W_{j}^{\prime}(x_{l})}{W_{j}(x_{k})} \biggl(p^{(1)}_{i,j}(x_{l}) \frac{1}{\phi ^{{\prime}^{2}}(x_{l})}-2 \frac{\phi ^{\prime \prime}(x_{l})}{\phi ^{{\prime}^{2}}(x_{l})} \biggr) +\frac{W_{j}^{\prime \prime}(x_{l})}{W_{j}(x_{k})} \frac{1}{\phi ^{{\prime}^{2}}(x_{l})} \biggr)I^{(0)} \\ & {}- \frac{h^{3}}{\phi ^{\prime}(x_{l})}\sum_{g=-n}^{n} \delta _{\lg}^{(-1)} \frac{1}{\phi ^{\prime}(t_{g})} \biggl[ \frac{1}{h^{2}} \biggl(q^{(2)}_{i,j}(x_{l},t_{g}) \phi ^{\prime}(t_{g})\frac{W_{j}(t_{g})}{W_{j}(x_{k})} \biggr)I^{(2)} \\ & {}- \frac{1}{h} \biggl(\frac{W_{j}(t_{g})}{W_{j}(x_{k})} \biggl(q^{(1)}_{i,j}(x_{l},t_{g})-q^{(2)}_{i,j}(x_{l},t_{g}) \biggl( \frac{\phi ^{\prime \prime}(t_{g})}{\phi ^{\prime}(t_{g})} \biggr) \biggr)+\frac{W_{j}^{\prime}(t_{g})}{W_{j}(x_{k})} \bigl(2q^{(2)}_{i,j}(x_{l},t_{g}) \bigr) \biggr)I^{(1)} \\ & {}+ \biggl(\frac{W_{j}(t_{g})}{W_{j}(x_{k})}\biggl(p^{(0)}_{i,j}(x_{l},t_{g}) \frac{1}{\phi ^{\prime}(t_{g})}-q^{(1)}_{i,j}(x_{l},t_{g}) \frac{\phi ^{\prime \prime}(t_{g})}{\phi ^{\prime}(t_{g})} \\ & {}+q^{(2)}_{i,j}(x_{l},t_{g}) \biggl( \frac{2\phi ^{\prime \prime}(t_{g})-\phi ^{\prime \prime \prime}(t_{g})\phi ^{\prime}(t_{g})}{\phi ^{{\prime}^{3}}(t_{g})} \biggr) \biggr) \\ & {}+ \frac{W_{j}^{\prime}(t_{g})}{W_{j}(x_{k})} \biggl(q^{(1)}_{i,j}(x_{l},t_{g}) \frac{1}{\phi ^{\prime}(t_{g})}-2q^{(2)}_{i,j}(x_{l},t_{g}) \frac{\phi ^{\prime \prime}(t_{g})}{\phi ^{{\prime}^{2}}(t_{g})} \biggr)+\frac{W_{j}^{\prime \prime \prime}(t_{g})}{W_{j}(x_{k})} \frac{1}{\phi ^{\prime}(t_{g})} \biggr)I^{(0)} ) \biggr], \end{aligned} \\ & \quad k,l=-n, \ldots , n. \end{aligned}$$

5 Numerical experiments

In this section, some problems will be tested using the nonclassical sinc collocation method, and the results will be compared with other existing methods. We choose $\alpha =\frac{1}{2}$ and $d=\frac{\pi}{2}$ to solve the examples.

To be able to compare the results with other existing methods, we obtain maximum absolute errors at equally spaced points

$$ \Delta \equiv \{kj, ~ j=0,\ldots ,100, k=0.01\}. $$

in the following form

$$ E_{i}=\max_{0\leq j\leq 100} \bigl\vert y_{i,n}(kj)-y_{i}(kj) \bigr\vert , \quad 1\leq i \leq m $$

where $y_{i}(x)$ and $y_{i,n}(x)$ are the exact and approximate solutions, respectively. All programs are written in Maple 2020, on a system with Intel Core i3 CPU and 4 GB of RAM.

Example 1

Consider the following problem

$$ \textstyle\begin{cases} y_{1}^{\prime \prime}(x)-xy_{2}^{\prime}(x)-y_{1}(x)=f_{1}(x)+\int _{0}^{1} (x\cos (t)y_{1}(t)-x\sin (t)y_{2}(t) )\,dt, \\ y_{2}^{\prime \prime}(x)-2xy_{1}^{\prime}(x)+y_{2}(x)=f_{2}(x)+\int _{0}^{1} (\sin (x)\cos (t)y_{1}(t)-\sin (x)\sin (t)y_{2}(t) )\,dt, \end{cases} $$

along with the initial conditions

$$ y_{1}(0)=0, \qquad y_{2}(0)=1, \qquad y_{1}^{\prime}(0)=1, \qquad y_{2}^{\prime}(0)=0. $$

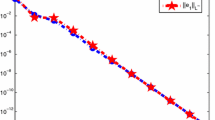
The exact solution is $y_{1}(x)=\sin (x)$, $y_{2}(x)=\cos (x)$. We solved this problem for various values of n with different kinds of weight functions and tabulated the maximum absolute errors at the equidistant points in Table 1. The errors have been compared with those in [5] based on a Laguerre approach. We solved the problem with $n=10$ with different kinds of weight functions and tabulated the numerical approximations at equidistant points in Table 2. Table 3 shows the numerical results obtained by the Laguerre approach [5] with $m=5$ to be compared with our results. The log-plot of the errors are plotted in Figs. 1 and 2 for different types of weight functions $w_{1}$ and $w_{2}$ to show the exponential rates of convergence.

Figure 1

The log-plot of errors for Example 1 with $w_{1}=w_{2}=1$

Figure 2

The log-plot of errors for Example 1 with $w_{1}=1+x$, $w_{2}=0.1+\sin (\pi x)$

Table 1 The maximum absolute errors at the equidistant point for Example 1

Table 2 Approximate solutions with $n=10$ using the presented method for Example 1

Table 3 Approximate solutions with $m=5$ in [5] for Example 1

Example 2

Consider the following problem

$$ \textstyle\begin{cases} 4xy_{1}^{\prime \prime}(x)+y_{2}^{\prime \prime}(x)+y_{3}^{\prime}(x)=f_{1}(x)+ \int _{0}^{x} (ty_{2}^{\prime}(t)+x^{2}y_{3}^{\prime}(t)+xty_{1}(t)+e^{x}y_{2}(t) )\,dt, \\ x^{3}y_{2}^{\prime \prime}(x)+e^{x}y_{3}^{\prime \prime}(x)+y_{2}^{ \prime}(x)=f_{2}(x)+\int _{0}^{x} (y_{1}(t)+y_{2}(t)+4ty_{3}(t) )\,dt, \\ 2y_{1}^{\prime \prime}(x)+xy_{2}^{\prime \prime}(x)+y_{3}^{\prime \prime}(x)=f_{3}(x)+\int _{0}^{x} (y_{3}^{\prime}(t)+2y_{2}(t) )\,dt, \end{cases} $$

connected with initial conditions

$$ y_{1}(0)=1, \qquad y_{2}(0)=0, \qquad y_{3}(0)=0, \qquad y_{1}^{\prime}(0)=-1, \qquad y_{2}^{\prime}(0)=0, \qquad y_{3}^{\prime}(0)=1. $$

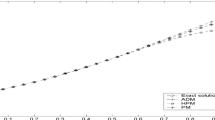
The exact solution is $y_{1}(x)=e^{-x}$, $y_{2}(x)=x^{2}e^{x}$, $y_{3}(x)=x$. By defining $w_{1}(x)=1+x$, $w_{2}(x)=0.1+\sin (\pi x)$, $w_{3}(x)=1+x$, we solved this problem with $n=20$ and tabulated the approximate and exact solutions at equidistant points in Table 4. Table 5 contains the results obtained in [1] and [40] based on a single term Walsh series technique and spectral method at equidistant points. Comparing the results in Tables 4 and 5, we observe that our method is much more efficient. Finally, in Table 6, we tabulated the errors obtained by our method for different weight functions with $n=20$ at equidistant points.

Table 4 Approximate solutions using the presented method with $n=20$ for Example 2

Table 5 Numerical results in references for Example 2

Table 6 Absolute errors of the presented method with $n=20$ for Example 2

Example 3

Consider the following problem

$$ \textstyle\begin{cases} y_{1}^{\prime \prime}(x)+2y_{2}^{\prime}(x)+5y_{2}(x)-y_{1}(x)=f_{1}(x)+ \int _{0}^{1} (-ty_{1}(t)+y_{2}(t) )\,dt, \\ y_{2}^{\prime \prime}(x)+3y_{1}^{\prime}(x)+7y_{2}(x)-9y_{1}(x)=f_{2}(x)+ \int _{0}^{1} (-t^{2}y_{1}(t)+4y_{2}(t) )\,dt, \end{cases} $$

along with the initial conditions

$$ y_{1}(0)=0, \qquad y_{2}(0)=0, \qquad y_{1}^{\prime}(0)=0, \qquad y_{2}^{\prime}(0)=0. $$

The exact solution is $y_{1}(x)=\sqrt[3]{x^{4}}$, $y_{2}(x)=\sqrt{x^{3}}$. It is obvious that the exact solution $y_{1}$ is not differentiable at zero, indeed $y_{1}\in C[0,1]$ only. So, many of the existing methods will get into trouble while trying to approximate the solution. The new sinc method based on nonclassical basis functions does not need the exact solution to be differentiable at the boundaries. Thus, it is expected to obtain good accuracy using the presented method for this problem. We approximated the solution with $n=30$ using various kinds of weight functions, $w_{1}=1$, $w_{2}=1$ and $w_{1}=1+\sin (x)$, $w_{2}=1+x$, and tabulated the absolute errors at equidistant points in Table 7.

Table 7 Absolute errors of the presented method with $n=30$ for Example 3

6 Conclusion

A method based on the nonclassical sinc collocation was used to solve the system of second-order linear integro-differential equations of both Volterra and Fredholm types. The classic sinc basis functions are not differentiable at zero, so we define the new nonclassical basis functions that are differentiable with zero derivative at zero. The new basis functions have been used to approximate the solution. Based on a theoretical analysis, it was shown that the new method achieves exponential convergence. It could be proved that, if accuracy is desired in the solution of a differential or integral equation, the complexity of solving a differential equation problem via a finite difference or finite element method is usually far larger than the corresponding complexity for sinc methods [41]. Also, it is proved that, while the h–p finite element method also enabled sinc-like exponential convergence, these methods do not converge as fast as sinc methods (see [42]). Some numerical examples with various kinds of basis functions have been solved and compared with existing methods confirming the theory in a good manner. It should be noted that the method could be easily extended to solve the fractional integro-differential equations based on the approach introduced in our previous papers [43, 44], and it is the subject of our future research.