1 Introduction

It is known that the difference equations involving quantum calculus play an important role in modeling many problems in engineering, physics, and mathematics, for further information the reader can address the following works [1–3]. In recent years, differential equations with fractional quantum calculus have been extensively studied by several scientific researchers, see for instance [4–7]. In this sense, several interesting topics concerning research for differential equations involving fractional quantum calculus have been devoted to the existence and the Ulam–Hyers stability of the solutions. Recently, many interesting results concerning the existence and Ulam-type stability of solutions for differential equations with fractional q-calculus have been obtained, see [8–11] and the references therein. In [12, 13], the existence and uniqueness of solutions were investigated for sequential differential equations with q-fractional calculus.

In the 1960s, British Railways wanted to make the electric locomotive faster and to develop a new type of electric locomotive. The goal was to make the trains faster. An important component for the new high-speed electric locomotive was the pantograph. The purpose of the pantograph is to collect current from an overhead wire, which is necessary for the locomotive to be able to move; see Fig. 1.

Figure 1
figure 1

Physical application: Collection pantograph system

Full size image

To make sure that the electric locomotive can move smoothly with high speed, it is necessary that there are no interruptions in the current-collection system. Therefore, the pantograph should stay in contact with the overhead wire for the whole time, particularly when the pantograph passes the supports of the overhead wire, which is a critical passage. Therefore, Ockendon and Tayler studied the motion of the pantograph head on an electric locomotive in [14] and developed a special delay differential equation of the form

$$ \upvarphi^{\prime } ( \rho )= \gamma _{1} \upvarphi ( \rho )+ \gamma _{2} \upvarphi ( \lambda \rho ), $$

for \(\rho >0\), where \(\gamma _{i}\) is a real constant and \(0< \lambda <1\) for \(\lambda \in \mathbb{R}\). In [15] the authors described different classes of exact solutions to nonlinear pantograph-type reaction–diffusion equations of the form

$$ \upvarphi_{\rho} ( y, \rho ) = \bigl[\hslash (\upvarphi) \upvarphi_{y}\bigr]_{y} + \mathfrak{g} ( \upvarphi, \acute{\upvarphi} ), $$

where \(\upvarphi = \upvarphi ( y, \rho )\) and \(\acute{\upvarphi}= \upvarphi ( py, q \rho )\), \(p,q >0\) such that p and q cannot be equal to 1 at the same time.

The authors in [16] considered the following initial value problem for the fractional pantograph equation in quantum form

$$ \textstyle\begin{cases} {}^{C }\mathcal{D}_{ q}^{\theta} \upvarphi ( \rho )= \mathfrak{g} ( \rho, \upvarphi (\rho ), \upvarphi ( \lambda \rho ) ), & \rho \in (0,1), \\ \upvarphi^{ (i ) } ( 0 ) = \upvarphi_{0},& \end{cases} $$

where \(\theta , \lambda \in (0,1)\), \(\mathfrak{g}: [ 0,\delta ] \times \mathbb{R} \times \mathbb{R} \to \mathbb{R} \) is a continuous function. Abdo et al. in [17] investigated two AB-Caputo-type implicit fractional differential equations with nonlinear integral conditions described by

$$ \textstyle\begin{cases} {}^{ABC }\mathcal{D}_{ a^{+}}^{\theta} \upvarphi ( \rho ) = \mathfrak{g} ( \rho, \upvarphi (\rho ), {}^{ABC }\mathcal{D}_{ a^{+}}^{\theta} ), & \theta \in (0,1], \\ \upvarphi ( a ) - \upvarphi^{\prime } ( a ) = \int _{a}^{\top } \mathfrak{u}(\eta , \upvarphi(\eta )) \,\mathrm{d}\eta ,& \end{cases} $$

and

$$ \textstyle\begin{cases} {}^{ABC }\mathcal{D}_{ a^{+}}^{\theta} \upvarphi ( \rho ) = \mathfrak{g} ( \rho, \upvarphi (\rho ), {}^{ABC }\mathcal{D}_{ a^{+}}^{\theta} ),& \theta \in (1,2], \\ \upvarphi ( a )=0, \qquad \upvarphi ( \top ) = \int _{a}^{\top } \mathfrak{u}(\eta , \upvarphi(\eta )) \,\mathrm{d}\eta , & \end{cases} $$

for \(\rho \in [a,\top ]\), where \({}^{ABC }\mathcal{D}_{ a^{+}}^{\theta}\) is the AB-Caputo-type fractional differential of order θ, while \(\mathfrak{g} \in C([a,\top ] \times \mathbb{R}^{2}) \) and \(\mathfrak{u} \in C([a,\top ] \times \mathbb{R})\). In 2021, Ali et al. studied the given class of fractional order of pantograph differential equations under multipoint boundary conditions

$$ \textstyle\begin{cases} \mathcal{D}_{ 0^{+}}^{\theta} \upvarphi ( \rho )= \mathfrak{g} ( \rho, \upvarphi (\rho ), \upvarphi ( \lambda \rho ) ), & \rho \in {}[ 0,1 ] , \\ \upvarphi^{ (i ) } ( 0 ) =0,& i=0,1,2,\dots , m-2, \\ \upvarphi ( 1 ) = \sum_{i=1}^{k} \upgamma _{0i} \upvarphi ( \upgamma _{1i} ),& \vartheta _{i}>0, \upgamma _{0i} \in \mathbb{R}, \end{cases} $$

where \(\mathcal{D}_{ 0^{+}}^{\theta}\) represents the Riemann–Liouville derivative with arbitrary order \(( m-1, m ]\), \(m \geq 2\) and \(0 < \upgamma _{0i}\), \(\upgamma _{1i} \in < 1\) with \(\sum_{i=1}^{m-2} \upgamma _{0i} \upgamma _{1i} <1\) and \(\mathfrak{g}: [ 0,1 ] \times \mathbb{R} \times \mathbb{R} \to \mathbb{R} \) is a continuous function [18]. Also, Alzabut et al. investigated the following nonlinear discrete fractional pantograph equation

$$ \textstyle\begin{cases} {}^{C }\mathcal{D}_{ q}^{\theta} \upvarphi ( \rho )= \mathfrak{g} ( \rho+\beta , \upvarphi (\rho +\beta ), \upvarphi ( \lambda ( \rho + \beta ) ) ), & \rho \in \mathbb{N}_{1-\beta}, \beta \in (0,1], \\ \upvarphi ( 0 ) =p ( \upvarphi ),& \end{cases} $$

where \({}^{C }\mathcal{D}^{(\cdot)}\) is the Caputo fractional derivative, \(\mathbb{N}_{1-\beta} = \{\rho , \rho +1, \rho +2, \dots \}\), \(\lambda\in ( 0,1 )\), \(p : C( [0, \infty ), \mathbb{C} )\to \mathbb{R}\), and \(\mathfrak{g}: [ 0,\delta ] \times \mathbb{R} \times \mathbb{R} \to \mathbb{R} \) is a Lipschitz continuous function with respect to φ [19]. Derbazi et al. determined the existence criteria of extremal solutions for the following θ-Caputo-type fractional differential equations in a Caputo sense with nonlinear boundary conditions

$$ \textstyle\begin{cases} {}^{C }\mathcal{D}_{ a^{+}}^{\nu , \theta} \upvarphi ( \rho ) = \mathfrak{g} ( \rho, \upvarphi ( \rho ) ), & \rho \in [a, b], \\ \mathfrak{u} ( \upvarphi(a), \upvarphi(b) )=0,& \end{cases} $$

where \({}^{C }\mathcal{D}_{ a^{+}}^{\nu , \theta}\) is the θ-fractional operator of order \(0< \nu \leq 1\) in the Caputo sense and this was investigated and \(\mathfrak{g}\in C([a, b]\times \mathbb{R})\), \(\mathfrak{u}\in C(\mathbb{R}^{2})\) [20]. For more information related to this topics see [21–27].

Motivated by the aforementioned works, we investigated the existence and Ulam-stability analysis for the following class of fractional pantograph q-difference equation \((\mathbb{F}\mathrm{P}q{-}\mathbb{DE})\) with nonlocal boundary conditions

$$ \textstyle\begin{cases} {}^{C }\mathcal{D}_{ q}^{\theta} \upvarphi ( \rho ) = \mathfrak{g} ( \rho, \upvarphi (\rho ), \upvarphi ( \lambda \rho ) ), & \theta \in ( m-1, m ], m \geq 2, \\ \upvarphi^{ (i ) } ( 0 ) =0,& i=0,1,2,\dots , m-2, \\ \upvarphi ( \delta )= \sum_{i=1}^{k} \upgamma _{0i} ( \mathcal{I}_{ q}^{ \vartheta _{i}} \upvarphi ( \upgamma _{1i} ) - \mathcal{I}_{ q}^{\vartheta _{i}} \upvarphi ( \upgamma _{2i} ) ),& \vartheta _{i}>0, \upgamma _{0i} \in \mathbb{R}, \end{cases} $$
(1)

where \({}^{C }\mathcal{D}_{ q}^{(\cdot)}\), \(\mathcal{I}_{ q}^{(\cdot)}\) are the Caputo fractional q-derivative and Riemann–Liouville fractional q-integral, respectively, \(q\in (0,1 )\), \(\rho \in [ 0, \delta ] \), \(m\in \mathbb{N}\), \(\lambda\in ( 0,1 )\),

$$ 0< \upgamma _{2i} < \upgamma _{1i}< \cdots < \upgamma _{2k} < \upgamma _{1k} < \delta ,\quad i=1,2,\dots , k,$$

and \(\mathfrak{g}: [ 0,\delta ] \times \mathbb{R}\times \mathbb{R} \to \mathbb{R} \) is a given continuous function.

In Sect. 2, we recall some essential definitions of fractional quantum calculus. Section 3 contains our main results in this work, while an example is presented to support the validity of our obtained results. An application, together with some needed algorithms for the problems, are given in Sect. 4. In Sect. 5, some conclusions are presented.

2 Preliminary notions

We recall some basic definitions and necessary lemmas related to fractional q-calculus and nonlinear analysis that will be used in the following.

Let \(\Sigma = [ 0,\delta ]\), and consider the Banach spaces \(C ( \Sigma ,\mathbb{R} ) \) and \(L^{1} (\Sigma ,\mathbb{R} ) \) of Lebesgue integrable functions \(\upvarphi : \Sigma \to \mathbb{R}\) with the norm \(\Vert \upvarphi \Vert = \sup \{ \vert \upvarphi ( \rho ) \vert : \rho \in \Sigma \}\), and

$$ \Vert \upvarphi \Vert _{L^{1}} = \int _{\Sigma } \bigl\vert \upvarphi ( \rho ) \bigr\vert \, \mathrm{d} \rho,$$

respectively. Let \(q\in ( 0,1 ) \). Then, the q-number is defined by

$$ [ b ]_{q} = \frac{1-q^{b}}{1-q}, \quad b\in \mathbb{R}.$$

The q-analog of the power \((p-r )^{m}\) is

$$ ( p-r )^{(m)}=\textstyle\begin{cases} 1,& m=0, \\ \prod_{i=0}^{m-1} ( p-rq^{i} ), & m\in \mathbb{N}, p,r\in \mathbb{R}. \end{cases} $$

The q-gamma function is defined by [28]

$$ \Gamma _{q} ( b ) = \frac{ ( 1-q )^{ ( b-1 ) }}{ ( 1-q ) ^{b-1}},\quad b\in \mathbb{R} \backslash \{ 0,-1,-2,\dots \}.$$

Note that the q-gamma function satisfies \(\Gamma _{q} ( 1+b ) = [ b ]_{q} \Gamma _{q} ( b ) \). The 1st-q-derivative of a function \(\upvarphi :\mathrm{J} \to \mathbb{R}\) is given by

$$ ( \mathcal{D}_{ q}\upvarphi ) ( \rho ) = \frac{\upvarphi ( \rho ) - \upvarphi ( q \rho ) }{ ( 1-q ) \rho }, \quad \rho \neq 0, \qquad ( \mathcal{D}_{ q} \upvarphi ) ( 0 ) =\lim _{ t \to 0} ( \mathcal{D}_{ q}\upvarphi ) ( \rho ),$$

and for the higher orders, it becomes \(\mathcal{D}_{ q}^{0}\upvarphi ( \rho ) = \upvarphi ( \rho )\), \(\mathcal{D}_{ q}^{m} \upvarphi ( \rho ) = \mathcal{D}_{ q} \mathcal{D}_{ q}^{m-1} \upvarphi ( \rho ) \), for \(\text{ }\rho \in \Sigma \), \(\text{ } m\in \{ 1,2,\dots \}\). Set \(\Sigma _{\rho }:= \{ \rho q^{m}:n\in \mathbb{N} \} \cup \{ 0 \} \) [28]. The 1st-q-integral of a function \(\upvarphi : \Sigma _{\rho} \to \mathbb{R} \) is defined by

$$ ( \mathcal{I}_{ q}\upvarphi ) ( \rho ) = \int _{0}^{\rho } \upvarphi ( \varpi ) \, \mathrm{d}_{q} \varpi = \sum_{n=0}^{ \infty } \rho ( 1- q ) q^{n} \upvarphi \bigl( \rho q^{n} \bigr) ,$$

provided that the series absolutely converges [28]. We note that \(( \mathcal{D}_{ q} \mathcal{I}_{ q} \upvarphi ) ( \rho ) = \upvarphi ( \rho )\), while φ is continuous at 0, then \(( \mathcal{I}_{ q} \mathcal{D}_{ q} \upvarphi ) ( \rho ) =\upvarphi ( \rho ) -\upvarphi ( 0 )\). The ϑth Riemann–Liouville fractional q-integral of a function \(\upvarphi: \Sigma \to \mathbb{R}\) is defined by [29], \(( \mathcal{I}_{ q}^{0} \upvarphi ) ( \rho ) =\upvarphi ( \rho )\) and

$$ \mathcal{I}_{ q}^{\vartheta}\upvarphi ( \rho ) = \int _{0}^{\rho } \frac{ ( \rho -q\varpi )^{ ( \vartheta - 1 ) }}{ \Gamma _{q} ( \vartheta )} \upvarphi ( \varpi ) \,\mathrm{d}_{q}\varpi , \quad \rho \in [ 0,\infty ).$$

The θth Caputo fractional q-derivative of a function \(\upvarphi: \Sigma \to \mathbb{R}\) is given by [30],

$$ \bigl( {}^{C }\mathcal{D}_{ q}^{0} \upvarphi \bigr) ( \rho ) =\upvarphi ( \rho ) \quad \& \quad {}^{C } \mathcal{D}_{ q}^{\theta _{1}} \upvarphi ( \rho ) = \mathcal{I}_{ q}^{ [\theta ] - \theta} \mathcal{D}_{ q}^{ [ \theta ] } \upvarphi ( \rho ), \quad \text{ }\rho \in \Sigma .$$

For more details about the fractional q-operators, see [22].

Lemma 2.1

([22, 28])

Let \(\theta _{1}, \theta _{2} \geq 0\). Then, we have the following relations

  1. (i)

    \(\mathcal{I}_{ q}^{\theta _{1}} \mathcal{I}_{ q}^{\theta _{2}} \upvarphi ( \rho ) = \mathcal{I}_{ q}^{\theta _{1}+ \theta _{2}}\upvarphi ( \rho ) \);

  2. (ii)

    \({}^{C }\mathcal{D}_{ q}^{\theta _{1}} \mathcal{I}_{ q}^{\theta _{1}} \upvarphi ( \rho ) =\upvarphi ( \rho )\);

  3. (iii)

    \(\mathcal{I}_{ q}^{\theta _{1}} s^{\rho } = \frac{\Gamma _{q} ( 1+\rho ) }{ \Gamma _{q} ( 1+\rho +\theta ) }s^{ \rho +\theta }\), \(\rho \in ( -1,\infty )\), \(s >0\).

Lemma 2.2

([30])

Let \(\theta \in ( m-1,m ) \). Then, the following equality holds

$$ \mathcal{I}_{ q}^{\theta} {}^{C } \mathcal{D}_{ q}^{\theta} \upvarphi ( \rho ) = \upvarphi ( \rho ) - \sum_{j=0}^{m-1} \frac{\rho ^{j}}{ \Gamma _{q} ( 1+j ) } \mathcal{D}_{ q}^{ \theta} \upvarphi ( 0 ).$$

In view of Lemma 2.2, the general series solution of the following equation \(\mathcal{I}_{ q}^{\theta} {}^{C }\mathcal{D}_{ q}^{\theta} \upvarphi ( \rho ) =0\) is

$$ \upvarphi ( \rho ) = \zeta _{0} +\zeta _{1} \rho + \zeta _{2} \rho ^{2} + \cdots + \zeta _{m-1} \rho ^{m-1}, \quad \zeta _{j}\in \mathbb{R}, \&\, m=[\theta _{1}]+1.$$

Hence, we have

$$ \mathcal{I}_{ q}^{\theta} {}^{C } \mathcal{D}_{ q}^{\theta} \upvarphi ( \rho ) = \upvarphi ( \rho ) + \zeta _{0}+\zeta _{1}\rho +\zeta _{2}\rho ^{2}+\cdots + \zeta _{m-1} \rho ^{m-1}. $$

Theorem 2.3

(Banach fixed-point theorem [31])

Let \(\Omega \neq \emptyset \) be a closed subset of a Banach space \((\mathcal{X}, \Vert \cdot \Vert )\). If \(\mathcal{Z}:\Omega \to \Omega \) is a contraction mapping, then Φ admits a unique fixed point.

Theorem 2.4

(Schaefer fixed-point theorem [31])

Let \(\mathcal{Z} \) be a continuous compact operator of a Banach space \(\mathcal{X}\) into itself, such that the set

$$ \{ \rho \in \mathcal{X} : \rho = \lambda \mathcal{Z} \rho \textit{ for some } 0 \leq \lambda \leq 1 \},$$

is bounded. Then, \(\mathcal{Z}\) has a fixed point.

3 Existence and uniqueness results

In what follows, we apply some fixed-point theorems to demonstrate the existence and uniqueness results for problem (1). To obtain the existence results for problem (1), the following auxiliary lemma is needed.

Lemma 3.1

For any \(\omega \in C(\Sigma , \mathbb{R})\), the \(\mathbb{F}\mathrm{P}q{-}\mathbb{DE}\) with nonlocal boundary conditions

$$ \textstyle\begin{cases} {}^{C }\mathcal{D}_{ q}^{\theta} \upvarphi (\rho )= \omega ( \rho ), & \theta \in ( m-1, m ], m \geq 2, \\ \upvarphi^{ (i ) } ( 0 ) =0,& i=0,1,2,\dots , m-2, \\ \upvarphi ( \delta )= \sum_{i=1}^{k} \upgamma _{0i} ( \mathcal{I}_{ q}^{ \vartheta _{i}} \upvarphi ( \upgamma _{1i} ) - \mathcal{I}_{ q}^{\vartheta _{i}} \upvarphi ( \upgamma _{2i} ) ),& \vartheta _{i}>0, \upgamma _{0i} \in \mathbb{R}, \end{cases} $$
(2)

for \(q\in (0,1 )\), \(\rho \in [ 0,\delta ]\), \(m\in \mathbb{N}\),

$$ 0< \upgamma _{2i} < \upgamma _{1i}< \cdots < \upgamma _{2k} < \upgamma _{1k}< \delta ,\quad i=1,2,\dots , k,$$

has a unique solution given by

$$ \upvarphi ( \rho ) = \mathcal{I}_{ q}^{\theta} \omega ( \rho ) +\frac{\rho ^{m-1}}{\Lambda } \Biggl[ \sum_{i=1}^{k} \upgamma _{0i} \bigl(\mathcal{I}_{ q}^{ \vartheta _{i} + \theta } \omega ( \upgamma _{1i} ) - \mathcal{I}_{ q}^{\vartheta _{i}+\theta} \omega ( \upgamma _{2i} ) \bigr) - \mathcal{I}_{ q}^{\theta} \omega ( \delta ) \Biggr], $$
(3)

where

$$ \Lambda := \sum_{i=1}^{k} \frac{\upgamma _{0i} \Gamma _{q} (m ) }{ \Gamma _{q} ( m + \vartheta _{i} ) } \bigl( \upgamma _{2i}^{\vartheta _{i} + m-1} - \upgamma _{1i}^{ \vartheta _{i} + m-1} \bigr) + \delta ^{ m-1} \neq 0. $$
(4)

Proof

Assume φ satisfies problem (1). First, we write this equation as

$$ \mathcal{I}_{ q}^{\theta} {}^{C } \mathcal{D}_{ q}^{\theta} \upvarphi ( \rho ) = \mathcal{I}_{ q}^{\theta} \omega ( \rho ).$$

In view of Lemma 2.2, we have

$$ \upvarphi ( \rho ) = \mathcal{I}_{ q}^{\theta } \omega ( \rho ) -\zeta _{0} - \zeta _{1} \rho -\zeta _{2} \rho ^{2}- \cdots - \zeta _{m-1}\rho ^{m-1}. $$
(5)

Applying the BCs, we obtain

$$ \zeta _{0} = \zeta _{1}=\zeta _{2}=\cdots =\zeta _{m-2}=0. $$
(6)

By substituting (6) into (5), we obtain

$$ \upvarphi ( \rho ) =\mathcal{I}_{ q}^{\theta} \omega ( \rho ) -\zeta _{m-1}\rho ^{m-1}. $$
(7)

Applying the integrator operator \(\mathcal{I}_{ q}^{ \vartheta _{i}}\) to both sides of equation (7), we obtain

$$ \mathcal{I}_{ q}^{\vartheta _{i}} \upvarphi ( \rho ) = \mathcal{I}_{ q}^{\vartheta _{i}+\theta _{1} } \omega ( \rho ) - \zeta _{m-1} \mathcal{I}_{ q}^{\vartheta _{i}} \rho ^{m-1}.$$

Using the condition

$$ \upvarphi ( \delta ) =\sum_{i=1}^{k} \upgamma _{0i} \bigl( \mathcal{I}_{ q}^{\vartheta _{i}} \upvarphi ( \upgamma _{1i} ) - \mathcal{I}_{ q}^{ \vartheta _{i}} \upvarphi ( \upgamma _{2i} ) \bigr),$$

we have

$$\begin{aligned} \mathcal{I}_{ q}^{\theta _{1}} \omega ( \delta ) - \zeta _{m-1} \delta ^{m-1} & = \sum _{i=1}^{k}\upgamma _{0i} \biggl[ \mathcal{I}_{ q}^{\vartheta _{i} + \theta _{1}} \upvarphi ( \upgamma _{1i} ) - \mathcal{I}_{ q}^{\vartheta _{i}+\theta _{1} }\upvarphi ( \upgamma _{2i} ) \\ &\quad{} + \zeta _{m-1} \frac{\Gamma _{q} ( m ) }{\Gamma _{q} ( m+ \vartheta _{i} ) } \bigl( \xi \upgamma _{2i}^{\vartheta _{i} + m-1} - \upgamma _{1i}^{\vartheta _{i}+m-1} \bigr) \biggr]. \end{aligned}$$
(8)

By solving (8), we find that

$$ \zeta _{m-1} = \frac{1}{\Lambda } \Biggl( \mathcal{I}_{ q}^{\theta} \omega ( \delta ) - \sum _{i=1}^{k} \upgamma _{0i} \bigl[ \mathcal{I}_{ q}^{\vartheta _{i}+\theta } \upvarphi ( \upgamma _{1i} ) - \mathcal{I}_{ q}^{ \vartheta _{i} + \theta}\upvarphi ( \upgamma _{2i} ) \bigr] \Biggr). $$
(9)

By inserting (9) into (7), we obtain (3). □

To obtain our findings, we need the following assumptions.

  1. (As1)

    There is a constant \(l_{\mathfrak{g}}>0\) such that

    $$ \bigl\vert \mathfrak{g} ( \rho , \upvarphi, \upvarphi ) - \mathfrak{g} ( \rho , \tilde{\upvarphi}, \tilde{\upvarphi} ) \bigr\vert \leq l_{\mathfrak{g}} \bigl( \vert \upvarphi-\tilde{\upvarphi} \vert + \vert \upvarphi - \tilde{ \upvarphi} \vert \bigr),$$

    for \(\rho \in \Sigma \) and \(\upvarphi ,\tilde{\upvarphi}\in \mathbb{R}\).

  2. (As2)

    There exist constants \(\mathrm{D}, \mathrm{h}_{\mathfrak{g}}^{ ( 1 )}, \mathrm{h}_{\mathfrak{g}}^{ ( 2 ) }>0\) such that

    $$ \bigl\vert \mathfrak{g} \bigl( \rho , \upvarphi ( \rho ), \upvarphi ( \lambda \rho ) \bigr) \bigr\vert \leq \mathrm{D}+ \mathrm{h}_{\mathfrak{g}}^{ ( 1 ) } \bigl\vert \upvarphi ( \rho ) \bigr\vert + \mathrm{h}_{\mathfrak{g}}^{ (2 ) } \bigl\vert \upvarphi ( \lambda \rho ) \bigr\vert , \quad \forall ( \rho , \upvarphi ) \in \Sigma \times \mathbb{R}. $$

3.1 Existence and uniqueness results via Banach’s fixed-point theorem

Theorem 3.2

Let (As1) be valid, then \(\mathbb{F}\mathrm{P}q{-}\mathbb{DE}\) (1) has a unique mild solution on Σ, whenever

$$ \mathrm{k}^{\ast }l_{\mathfrak{g}}< 1, $$
(10)

where

$$\begin{aligned} \mathrm{k}^{\ast} & = \frac{2 (\delta ^{\theta } + \delta ^{m+ \theta -1} )}{ \Gamma _{q} ( \theta + 1 ) } + \sum _{i=1}^{k} \vert \upgamma _{0i} \vert \frac{4\delta ^{m+ \vartheta _{i}+\theta -1}}{ \vert \Lambda \vert \Gamma _{q} ( \vartheta _{i} + \theta +1 ) }. \end{aligned}$$
(11)

Proof

We switch problem (1) into a fixed-point problem and we consider the operator \(\tilde{\mathcal{Z}} : C(\Sigma , \mathbb{R})\to C(\Sigma , \mathbb{R})\) as

$$\begin{aligned} ( \tilde{\mathcal{Z}} \upvarphi ) ( \rho ) & = \mathcal{I}_{ q}^{\theta} \mathfrak{g} \bigl( \rho , \upvarphi ( \rho ), \upvarphi ( \lambda \rho ) \bigr) \\ & \quad{}+\frac{\rho ^{m-1}}{\Lambda } \Biggl[ \sum_{i=1}^{k} \upgamma _{0i} \bigl( \mathcal{I}_{ q}^{\vartheta _{i} + \theta } \mathfrak{g} \bigl( \upgamma _{1i}, \upvarphi ( \upgamma _{1i} ), \upvarphi ( \lambda \upgamma _{1i} ) \bigr) \\ & \quad{}- \mathcal{I}_{ q}^{\vartheta _{i} + \theta } \mathfrak{g} \bigl( \upgamma _{2i}, \upvarphi ( \upgamma _{2i} ), \upvarphi ( \lambda \upgamma _{2i} ) \bigr) \bigr) \Biggr] \\ &\quad{}- \frac{\rho ^{m-1}}{\Lambda } \mathcal{I}_{ q}^{\theta} \mathfrak{g} \bigl( \delta , \upvarphi ( \delta ),\upvarphi ( \lambda \delta ) \bigr). \end{aligned}$$
(12)

Clearly, the solution of (1) is as a fixed point of the operator \(\tilde{\mathcal{Z}}\). By (As1), for any \(\upvarphi ,\tilde{\upvarphi}\in C(\Sigma , \mathbb{R})\) and \(\rho \in \Sigma \), we obtain

$$\begin{aligned} & \bigl\vert ( \tilde{\mathcal{Z}}\upvarphi ) ( \rho ) - ( \tilde{\mathcal{Z}} \tilde{\upvarphi} ) ( \rho ) \bigr\vert \\ &\quad \leq \mathcal{I}_{ q}^{\theta} \bigl\vert \mathfrak{g} \bigl( \rho , \upvarphi ( \rho ), \upvarphi ( \lambda \rho ) \bigr) - \mathfrak{g} \bigl( \rho, \tilde{ \upvarphi} ( \rho ), \tilde{\upvarphi} ( \lambda \rho ) \bigr) \bigr\vert \\ &\quad \quad{}+ \frac{ \rho^{m-1}}{ \vert \Lambda \vert } \Biggl[ \sum_{i=1}^{k} \vert \upgamma _{0i} \vert \bigl( \mathcal{I}_{ q}^{\vartheta _{i} +\theta } \bigl\vert \mathfrak{g} \bigl( \upgamma _{1i}, \upvarphi ( \upgamma _{1i} ) ,\upvarphi ( \lambda \upgamma _{1i} ) \bigr) \\ &\quad \quad{}- \mathfrak{g} \bigl( \upgamma _{1i}, \tilde{ \upvarphi} ( \upgamma _{1i} ), \tilde{\upvarphi} ( \lambda \upgamma _{1i} ) \bigr) \bigr\vert + \mathcal{I}_{ q}^{\vartheta _{i} + \theta } \bigl\vert \mathfrak{g} \bigl( \upgamma _{2i}, \upvarphi ( \upgamma _{2i} ) , \upvarphi ( \lambda \upgamma _{2i} ) \bigr) \\ &\quad \quad{}- \mathfrak{g} \bigl( \upgamma _{2i}, \tilde{\upvarphi} ( \upgamma _{2i} ), \tilde{\upvarphi} ( \lambda \upgamma _{2i} ) \bigr) \bigr\vert \bigr) \\ &\quad \quad{}+I_{q}^{\theta} \bigl\vert \mathfrak{g} \bigl( \delta , \upvarphi ( \delta ) ,\upvarphi ( \lambda \delta ) \bigr) -\mathfrak{g} \bigl( \delta , \tilde{\upvarphi} ( \delta ) , \tilde{\upvarphi} ( \lambda \delta ) \bigr) \bigr\vert \Biggr] \\ &\quad \leq \frac{\rho ^{\theta} l_{\mathfrak{g}}}{ \Gamma _{q} ( \theta + 1 ) } \bigl( \Vert \upvarphi - \tilde{\upvarphi} \Vert + \Vert \upvarphi - \tilde{\upvarphi} \Vert \bigr) \\ &\quad \quad{}+ \frac{\delta ^{m-1}l_{\mathfrak{g}} ( \Vert \upvarphi -\tilde{\upvarphi} \Vert + \Vert \upvarphi - \tilde{\upvarphi} \Vert ) }{ \vert \Lambda \vert } \\ &\quad \quad{}\times \Biggl[ \sum_{i=1}^{k} \vert \upgamma _{0i} \vert \biggl( \frac{\upgamma _{1i}^{\vartheta _{i} + \theta}}{ \Gamma _{q} ( \vartheta _{i}+\theta + 1 ) }+ \frac{\upgamma _{2i}^{\vartheta _{i} + \theta }}{\Gamma _{q} ( \vartheta _{i} + \theta + 1 ) } \biggr) + \frac{\delta ^{ \theta}}{\Gamma _{q} ( \theta +1 ) } \Biggr] \\ &\quad \leq \Biggl[ \frac{2\delta ^{ \theta}}{\Gamma _{q} ( \theta + 1 ) } + \sum_{i=1}^{k} \vert \upgamma _{0i} \vert \frac{4\delta ^{m+\vartheta _{i} + \theta - 1}}{ \vert \Lambda \vert \Gamma _{q} ( \vartheta _{i} + \theta + 1 ) } \\ &\quad \quad{}+ \frac{2\delta ^{m+\theta -1}}{\Gamma _{q} ( \theta +1 ) } \Biggr] l_{\mathfrak{g}} \Vert \upvarphi - \tilde{\upvarphi} \Vert . \end{aligned}$$

Thus,

$$ \bigl\Vert ( \tilde{\mathcal{Z}} \upvarphi ) - ( \tilde{\mathcal{Z}} \tilde{ \upvarphi} ) \bigr\Vert \leq \mathrm{k }^{\ast } l_{\mathfrak{g}} \Vert \upvarphi - \tilde{\upvarphi} \Vert .$$

From (10), \(\tilde{\mathcal{Z}}\) is a contraction. As an outcome of Banach’s FPT, \(\tilde{\mathcal{Z}}\) has a unique fixed point that is a unique mild solution of (1) on Σ. □

3.2 Existence results via Schaefer’s fixed-point theorem

Theorem 3.3

Suppose that the hypothesis (As2) is satisfied. Then, \(\mathbb{F}\mathrm{P}q{-}\mathbb{DE}\) (1) has at least one solution on Σ, whenever \(\mathrm{N}_{1}<1\), where

$$\begin{aligned} \mathrm{N}_{1}& =\frac{\delta ^{\theta } ( \mathrm{h}_{\mathfrak{g}}^{ ( 1 ) }+\mathrm{h}_{\mathfrak{g}}^{ ( 2 ) } ) }{\Gamma _{q} ( \theta +1 ) }+ \frac{ ( \mathrm{h}_{\mathfrak{g}}^{ ( 1 ) }+ \mathrm{h}_{\mathfrak{g}}^{ ( 2 ) } ) \delta ^{m-1}}{ \vert \Lambda \vert } \sum_{i=1}^{k} \frac{2 \vert \upgamma _{0i} \vert \mathcal{I}_{ q}^{\vartheta _{i} + \theta }}{\Gamma _{q} ( \vartheta _{i} + \theta +1 )} \\ & \quad{}+ \frac{ \delta ^{ m +\theta -1} ( \mathrm{h}_{\mathfrak{g}}^{ ( 1 ) }+\mathrm{h}_{\mathfrak{g}}^{ ( 2 ) } ) }{ \vert \Lambda \vert \Gamma _{q} ( \theta + 1 ) }. \end{aligned}$$
(13)

Proof

We shall use Schaefer’s fixed-point theorem to demonstrate that \(\tilde{\mathcal{Z}}\) defined in (12) has a fixed point. The proof will be given in the following steps.

Step 1. \(\tilde{\mathcal{Z}}\) is continuous. Let a sequence \(\upvarphi _{n} \to \upvarphi \) in \(C(\Sigma , \mathbb{R})\). Since \(\mathfrak{g}\) is continuous, we have

$$ \bigl\vert \mathfrak{g} \bigl( \rho , \upvarphi _{n} ( \rho ), \upvarphi _{n} ( \lambda \rho ) \bigr) - \mathfrak{g} \bigl( \rho , \upvarphi ( \rho ) , \upvarphi ( \lambda \rho ) \bigr) \bigr\vert \rightarrow 0,$$

as \(n\to \infty \). Thus, for any \(\rho\in \Sigma \), we write

$$\begin{aligned} & \bigl\vert ( \tilde{\mathcal{Z}} \upvarphi _{n} ) (\rho ) - ( \tilde{\mathcal{Z}}\upvarphi ) ( \rho ) \bigr\vert \\ &\quad \leq \int _{0}^{\rho } \frac{ (\rho - q \varpi )^{ ( \theta -1 ) }}{\Gamma _{q} ( \theta ) } \bigl\vert \mathfrak{g} \bigl( \varpi , \upvarphi _{n} ( \varpi ), \upvarphi _{n} ( \lambda \varpi ) \bigr) \\ &\quad \quad{}- \mathfrak{g} \bigl( \varpi , \upvarphi ( \varpi ), \upvarphi ( \lambda \varpi ) \bigr) \bigr\vert \,\mathrm{d}_{q} \varpi \\ &\quad \quad{}+ \frac{ \rho ^{m-1}}{ \vert \Lambda \vert } \sum_{i=1}^{k} \vert \upgamma _{0i} \vert \int _{0}^{ \upgamma _{1i}} \frac{ ( \upgamma _{1i} - q \varpi )^{ ( \theta -1 ) }}{\Gamma _{q} ( \theta ) } \bigl\vert \mathfrak{g} \bigl( \varpi, \upvarphi _{n} ( \varpi ), \upvarphi_{n} ( \lambda \varpi ) \bigr) \\ &\quad \quad{}-\mathfrak{g} \bigl(\varpi, \upvarphi ( \varpi ), \upvarphi ( \lambda \varpi ) \bigr) \bigr\vert \,\mathrm{d}_{q} \varpi \\ &\quad \quad{}+ \frac{\rho ^{m-1}}{ \vert \Lambda \vert } \sum_{i=1}^{k} \vert \upgamma _{0i} \vert \int _{0}^{ \upgamma _{1i}} \frac{ ( \upgamma _{2i} - q\varpi )^{ ( \theta _{1}-1 ) }}{\Gamma _{q} ( \theta ) } \bigl\vert \mathfrak{g} \bigl( \varpi , \upvarphi _{n} ( \varpi ), \upvarphi _{n} ( \lambda \varpi ) \bigr) \\ &\quad \quad{}- \mathfrak{g} \bigl( \varpi , \upvarphi ( \varpi ) ,\upvarphi ( \lambda \varpi ) \bigr) \bigr\vert \,\mathrm{d}_{q} \varpi \\ &\quad \quad{}+ \frac{\rho ^{m-1}}{ \vert \Lambda \vert } \int _{0}^{ \delta} \frac{ ( \delta - q\varpi )^{ ( \theta -1 ) }}{\Gamma _{q} ( \theta ) } \bigl\vert \mathfrak{g} \bigl( \varpi , \upvarphi _{n} ( \varpi ) , \upvarphi _{n} ( \lambda \varpi ) \bigr) \\ &\quad \quad{}-\mathfrak{g} \bigl( \varpi ,\upvarphi ( \varpi ) ,\upvarphi ( \lambda \varpi ) \bigr) \bigr\vert \,\mathrm{d}_{q} \varpi. \end{aligned}$$

Hence, we obtain

$$ \bigl\Vert ( \tilde{\mathcal{Z}}\upvarphi _{n} ) - ( \tilde{ \mathcal{Z}}\upvarphi ) \bigr\Vert \rightarrow 0\quad \text{as } n \to \infty .$$

Consequently, \(\tilde{\mathcal{Z}}\) is continuous.

Step 2. The image of a bounded set under \(\tilde{\mathcal{Z}}\) is bounded in \(C(\Sigma , \mathbb{R})\). Indeed, it is enough to show that for any \(\omega >0\), there exists a positive constant ζ such that for each

$$ \upvarphi \in \Omega _{\omega }= \bigl\{ \upvarphi \in C(\Sigma , \mathbb{R}) : \Vert \upvarphi \Vert \leq \omega \bigr\} ,$$

we have \(\Vert \tilde{\mathcal{Z}} \upvarphi \Vert \leq \zeta \). In fact, we have

$$\begin{aligned} \bigl\vert ( \tilde{\mathcal{Z}}\upvarphi ) ( \rho ) \bigr\vert & \leq \mathcal{I}_{ q}^{ \theta } \bigl\vert \mathfrak{g} \bigl( \rho , \upvarphi ( \rho ), \upvarphi ( \lambda \rho ) \bigr) \bigr\vert \\ & \quad{}+ \frac{\rho ^{m-1}}{ \vert \Lambda \vert } \Biggl[ \sum_{i=1}^{k} \vert \upgamma _{0i} \vert \bigl( \mathcal{I}_{ q}^{\vartheta _{i} +\theta} \bigl\vert \mathfrak{g} \bigl( \upgamma _{1i}, \upvarphi ( _{i} ), \upvarphi ( \lambda _{i} ) \bigr) \bigr\vert \\ & \quad{}+\mathcal{I}_{ q}^{\vartheta _{i}+\theta } \bigl\vert \mathfrak{g} \bigl( \upgamma _{2i} , \upvarphi ( \upgamma _{2i} ) , \upvarphi ( \lambda \upgamma _{2i} ) \bigr) \bigr\vert \bigr) \Biggr] \\ &\quad{}+ \frac{\rho ^{m-1}}{ \vert \Lambda \vert } \mathcal{I}_{ q}^{\theta} \bigl\vert \mathfrak{g} \bigl( \delta , \upvarphi ( \delta ) ,\upvarphi ( \lambda \delta ) \bigr) \bigr\vert \\ & \leq \frac{\delta ^{\theta} ( \mathrm{D}+ ( \mathrm{h}_{\mathfrak{g}}^{ ( 1 ) } + \mathrm{h}_{\mathfrak{g}}^{ ( 2 ) } )\omega ) }{ \Gamma _{q} ( \theta + 1 ) } \\ & \quad{}+ \frac{ ( \mathrm{D}+ ( \mathrm{h}_{\mathfrak{g}}^{ ( 1 ) } + \mathrm{h}_{\mathfrak{g}}^{ ( 2 ) } ) \omega ) \delta ^{m-1}}{ \vert \Lambda \vert } \sum_{i=1}^{k} \frac{2 \vert \upgamma _{0i} \vert \delta ^{\vartheta _{i} + \theta }}{\Gamma _{q} ( \vartheta _{i}+\theta + 1 ) } \\ & \quad{}+ \frac{\delta ^{m+\theta _{1}-1} ( \mathrm{D}+ ( \mathrm{h}_{\mathfrak{g}}^{ (1 )}+\mathrm{h}_{\mathfrak{g}}^{ ( 2 ) } ) \omega ) }{ \vert \Lambda \vert \Gamma _{q} ( \theta +1 ) }, \end{aligned}$$

and consequently

$$\begin{aligned} \Vert \tilde{\mathcal{Z}}\upvarphi \Vert & \leq \Biggl( \frac{ \delta ^{\theta } ( \mathrm{D}+\mathrm{h}_{\mathfrak{g}} \omega ) }{\Gamma _{q} ( \theta +1 ) } \\ & \quad{}+ \frac{ ( \mathrm{D}+ ( \mathrm{h}_{\mathfrak{g}}^{ ( 1 ) }+\mathrm{h}_{\mathfrak{g}}^{ ( 2 ) } ) \omega ) \delta ^{m-1}}{ \vert \Lambda \vert } \sum_{i=1}^{k} \frac{2 \vert \upgamma _{0i} \vert \delta ^{\vartheta _{i} + \theta} }{ \Gamma _{q} ( \vartheta _{i}+\theta + 1 ) } \\ &\quad{} + \frac{ \delta ^{m+\theta -1} ( \mathrm{D}+\mathrm{h}_{\mathfrak{g}} \omega ) }{ \vert \Lambda \vert \Gamma _{q} (\theta +1 ) } \Biggr) :=\zeta , \end{aligned}$$

where \(\mathrm{h}_{\mathfrak{g}} = \mathrm{h}_{\mathfrak{g}}^{ ( 1 ) } + \mathrm{h}_{\mathfrak{g}}^{ ( 2 ) }\).

Step 3. \(\tilde{\mathcal{Z}}\) sends bounded sets of \(C(\Sigma , \mathbb{R})\) into equicontinuous sets. For \(\rho_{1}, \rho _{2}\in \Sigma \), \(\rho _{1} < \rho _{2}\) and for \(\upvarphi \in \Omega _{\omega }\), we have

$$\begin{aligned} & \bigl\vert ( \tilde{\mathcal{Z}}\upvarphi ) ( \rho_{2} ) - ( \tilde{\mathcal{Z}}\upvarphi ) ( \rho_{1} ) \bigr\vert \\ &\quad \leq \int _{0}^{\rho_{2}} \frac{ ( \rho _{2} - q\varpi )^{ ( \theta -1 ) }}{\Gamma _{q} ( \theta ) } \bigl\vert \mathfrak{g} \bigl( \varpi ,\upvarphi ( \varpi ) ,\upvarphi ( \lambda \varpi ) \bigr) \bigr\vert \,\mathrm{d}_{q} \varpi \\ &\quad \quad{}- \int _{0}^{\rho_{1}} \frac{ ( \rho _{1} - q\varpi )^{ ( \theta -1 ) }}{\Gamma _{q} ( \theta ) } \bigl\vert \mathfrak{g} \bigl( \varpi ,\upvarphi ( \varpi ) ,\upvarphi ( \lambda \varpi ) \bigr) \bigr\vert \,\mathrm{d}_{q} \varpi \\ &\quad \quad{}+ \biggl\vert \frac{\rho_{2}^{m-1} - \rho_{1}^{m-1}}{ \vert \Lambda \vert } \biggr\vert \\ &\quad \quad{}\times \sum_{i=1}^{k} \vert \upgamma _{0i} \vert \int _{0}^{\upgamma _{1i} } \frac{ ( \upgamma _{1i} - q \varpi )^{ ( \theta - 1 ) }}{\Gamma _{q} ( \theta ) } \bigl\vert \mathfrak{g} \bigl( \varpi , \upvarphi ( \varpi ), \upvarphi ( \lambda \varpi ) \bigr) \bigr\vert \,\mathrm{d}_{q} \varpi \\ &\quad \quad{}+ \biggl\vert \frac{\rho_{2}^{m-1} - \rho_{1}^{m-1}}{ \vert \Lambda \vert } \biggr\vert \int _{0}^{\delta} \frac{ ( \delta - q\varpi ) ^{ ( \theta -1 ) }}{\Gamma _{q} ( \theta ) } \bigl\vert \mathfrak{g} \bigl( \varpi ,\upvarphi ( \varpi ) ,\upvarphi ( \lambda \varpi ) \bigr) \bigr\vert \,\mathrm{d}_{q} \varpi. \end{aligned}$$

As \(\rho_{1} \rightarrow \rho _{2}\), we obtain

$$ \bigl\vert ( \tilde{\mathcal{Z}} \upvarphi ) ( \rho _{2})- ( \tilde{\mathcal{Z}} \upvarphi ) (\rho _{1}) \bigr\vert \to 0.$$

Consequently, \(\tilde{\mathcal{Z}} ( \Omega _{\omega } ) \) is equicontinuous. From the previous steps, together with the Arzelá–Ascoli theorem, we deduce that \(\tilde{\mathcal{Z}}\) is completely continuous.

Step 4. A priori bounds. Now, it remains to prove that the set

$$ \mathcal{U} = \bigl\{ \upvarphi \in C(\Sigma , \mathbb{R}) : \upvarphi = \varrho \tilde{\mathcal{Z}} \upvarphi , \text{for some } \varrho \in (0,1) \bigr\} ,$$

is bounded. Let \(\upvarphi \in \mathcal{U}\) and for each \(\rho \in \Sigma \), we have

$$\begin{aligned} \bigl\vert \upvarphi ( \rho ) \bigr\vert & = \bigl\vert \varrho \tilde{ \mathcal{Z}} \bigl( \upvarphi ( \rho ) \bigr) \bigr\vert \\ &\leq \mathcal{I}_{ q}^{\theta _{1}} \bigl\vert \mathfrak{g} \bigl( \rho , \upvarphi ( \rho ), \upvarphi ( \lambda \rho ) \bigr) \bigr\vert \\ & \quad{}+ \frac{ \rho ^{m-1}}{ \vert \Lambda \vert } \Biggl[ \sum_{i=1}^{k} \vert \upgamma _{0i} \vert \bigl( \mathcal{I}_{ q}^{\vartheta _{i}+ \theta } \bigl\vert \mathfrak{g} \bigl( \upgamma _{1i}, \upvarphi ( \upgamma _{1i} ), \upvarphi ( \lambda \upgamma _{1i} ) \bigr) \bigr\vert \\ & \quad{}+ \mathcal{I}_{ q}^{\vartheta _{i} + \theta} \bigl\vert \mathfrak{g} \bigl( \upgamma _{2i}, \upvarphi ( \upgamma _{2i} ), \upvarphi ( \lambda \upgamma _{2i} ) \bigr) \bigr\vert \bigr) \Biggr] \\ & \quad{}+ \frac{\rho ^{m-1}}{ \vert \Lambda \vert } \mathcal{I}_{ q}^{\theta} \bigl\vert \mathfrak{g} \bigl( \delta , \upvarphi ( \delta ) , \upvarphi ( \lambda \delta ) \bigr) \bigr\vert \\ & \leq \frac{ \delta ^{\theta} ( \mathrm{D}+ ( \mathrm{h}_{\mathfrak{g}}^{ ( 1 ) } + \mathrm{h}_{\mathfrak{g}}^{ ( 2 ) } ) \Vert \upvarphi \Vert ) }{ \Gamma _{q} ( \theta +1 ) } \\ & \quad{}+ \frac{ ( \mathrm{D}+ ( \mathrm{h}_{\mathfrak{g}}^{ ( 1 ) }+\mathrm{h}_{\mathfrak{g}}^{ ( 2 ) } ) \Vert \upvarphi \Vert ) \delta ^{m-1} }{ \vert \Lambda \vert } \sum_{i=1}^{k} \frac{ 2 \vert \gamma _{i} \vert \delta ^{\vartheta _{i} + \theta} }{ \Gamma _{q} ( \vartheta _{i} + \theta + 1 ) } \\ &\quad{}+ \frac{\delta ^{ m + \theta -1} ( \mathrm{D}+ (\mathrm{h}_{\mathfrak{g}}^{ ( 1 ) } + \mathrm{h}_{\mathfrak{g}}^{ ( 2 ) } ) \Vert \upvarphi \Vert ) }{ \vert \Lambda \vert \Gamma _{q} ( \theta + 1 ) } . \end{aligned}$$
(14)

From inequality (14), we obtain \(\Vert \upvarphi \Vert \leq \frac{\mathrm{N}_{2}}{ ( 1- \mathrm{N}_{1} )}\), where

$$\begin{aligned} \mathrm{N}_{2}& =\frac{\delta ^{ \theta} \mathrm{D}}{\Gamma _{q} (\theta + 1 ) } + \frac{\mathrm{D} \delta ^{m-1}}{ \vert \Lambda \vert } \sum_{i=1}^{k} \frac{2 \vert \upgamma _{0i} \vert \delta ^{\vartheta _{i} + \theta }}{\Gamma _{q} ( \vartheta _{i} + \theta +1 ) }+\frac{\delta ^{m + \theta - 1 } \mathrm{D}}{ \vert \Lambda \vert \Gamma _{q} ( \theta + 1 )}. \end{aligned}$$
(15)

This means that the set \(\mathcal{U}\) is bounded. We infer from Schaefer’s fixed-point theorem that \(\tilde{\mathcal{Z}}\) possesses at least one fixed point. Consequently, there is at least one solution to the problem (1). □

4 Ulam–Hyers stability

In this section, we discuss two types of Ulam stability for solutions of problem (1).

Theorem 4.1

Suppose that the hypothesis (As1) and condition (10) are satisfied. Then, the problem (1) is Ulam–Hyers stable. Moreover, it is also generalized Ulam–Hyers stable.

Proof

Let \(\varepsilon >0\). Let \(\hat{\upvarphi}\in C(\Sigma , \mathbb{R})\) be any solution of the inequality

$$ \bigl\vert {}^{C }\mathcal{D}_{ q}^{\theta} \hat{ \upvarphi} ( \rho ) -\mathfrak{g} \bigl( \rho , \hat{\upvarphi} ( \rho ) , \hat{ \upvarphi} ( \lambda \rho ) \bigr) \bigr\vert \leq \varepsilon , \quad \rho \in \Sigma .$$

Then, there exists \(\mathrm{Q}\in C(\Sigma , \mathbb{R})\) such that

$$ {}^{C }\mathcal{D}_{ q}^{\theta} \hat{ \upvarphi} ( \rho ) = \mathfrak{g} \bigl( \rho , \hat{\upvarphi} ( \rho ), \hat{ \upvarphi} ( \lambda \rho ) \bigr) +\mathrm{Q } ( \rho ), \quad \rho \in \Sigma , $$
(16)

and \(\vert \mathrm{Q} ( \rho ) \vert \leq \varepsilon \), \(\rho \in \Sigma \). This gives

$$\begin{aligned} \hat{\upvarphi} ( \rho ) & = \mathcal{I}_{ q}^{\theta} \mathfrak{g} \bigl( \rho , \hat{\upvarphi} ( \rho ), \hat{\upvarphi} ( \lambda \rho ) \bigr) \\ &\quad{}+ \frac{\rho ^{m-1}}{\Lambda } \Biggl[ \sum_{i=1}^{k} \upgamma _{0i} \bigl( \mathcal{I}_{ q}^{\vartheta _{i} + \theta } \mathfrak{g} \bigl( \upgamma _{1i}, \hat{\upvarphi} ( \upgamma _{1i} ), \hat{\upvarphi} ( \lambda \upgamma _{1i} ) \bigr) \\ & \quad{}- \mathcal{I}_{ q}^{\vartheta _{i} + \theta } \mathfrak{g} \bigl( \upgamma _{2i}, \hat{\upvarphi} ( \upgamma _{2i} ) , \hat{ \upvarphi} ( \lambda \upgamma _{2i} ) \bigr) \bigr) \Biggr] \\ & \quad{}- \frac{\rho ^{m-1}}{\Lambda } \mathcal{I}_{ q}^{\theta} \mathfrak{g} \bigl( \delta , \hat{\upvarphi} ( \delta ), \hat{\upvarphi} ( \lambda \delta ) \bigr) + \mathcal{I}_{ q}^{\theta} \mathrm{Q} ( \rho ). \end{aligned}$$
(17)

On the other hand, let \(\upvarphi \in C(\Sigma , \mathbb{R})\) be a unique solution of the \(\mathbb{F}\mathrm{P}q{-}\mathbb{DE}\) (1). From Lemma 3.1, we have

$$\begin{aligned} \upvarphi ( \rho ) & =\mathcal{I}_{ q}^{\theta} \mathfrak{g} \bigl( \rho , \upvarphi ( \rho ), \upvarphi ( \lambda \rho ) \bigr) \\ & \quad{}+ \frac{\rho ^{m-1}}{\Lambda } \Biggl[ \sum_{i=1}^{k} \upgamma _{0i} \bigl( \mathcal{I}_{ q}^{\vartheta _{i} + \theta } \mathfrak{g} \bigl( \upgamma _{1i}, \upvarphi ( \upgamma _{1i} ) , \upvarphi ( \lambda \upgamma _{1i} ) \bigr) \\ & \quad{}- \mathcal{I}_{ q}^{\vartheta _{i}+\theta} \mathfrak{g} \bigl( \upgamma _{2i},\upvarphi ( \upgamma _{2i} ), \upvarphi ( \lambda \upgamma _{2i} ) \bigr) \bigr) \Biggr] \\ & \quad{}- \frac{\rho ^{m-1}}{\Lambda} \mathcal{I}_{ q}^{\theta} \mathfrak{g} \bigl( \delta ,\upvarphi ( \delta ), \upvarphi ( \lambda \delta ) \bigr). \end{aligned}$$
(18)

From (17), (18), and assumption (As1), we obtain

$$\begin{aligned} \bigl\vert \hat{\upvarphi} ( \rho ) - \upvarphi ( \rho ) \bigr\vert & \leq \mathcal{I}_{ q}^{\theta} \bigl\vert \mathrm{Q} ( \rho ) \bigr\vert + \mathcal{I}_{ q}^{\theta} \bigl\vert \mathfrak{g} \bigl( \rho ,\upvarphi ( \rho ) ,\upvarphi ( \lambda \rho ) \bigr) \\ & \quad{}-\mathfrak{g} \bigl( \rho , \hat{\upvarphi} ( \rho ), \hat{\upvarphi} ( \lambda \rho ) \bigr) \bigr\vert \\ & \quad{}+ \frac{\rho ^{m-1}}{ \vert \Lambda \vert } \Biggl[ \sum_{i=1}^{k} \vert \upgamma _{0i} \vert \bigl( \mathcal{I}_{ q}^{\vartheta _{i} + \theta} \bigl\vert \mathfrak{g} \bigl( \upgamma _{1i}, \upvarphi ( \upgamma _{1i} ) , \upvarphi ( \lambda \upgamma _{1i} ) \bigr) \\ & \quad{}-\mathfrak{g} \bigl(\upgamma _{1i}, \hat{\upvarphi} ( \upgamma _{1i} ), \hat{\upvarphi} ( \lambda \upgamma _{1i} ) \bigr) \bigr\vert \\ & \quad{}+\mathcal{I}_{ q}^{\vartheta _{i} + \theta} \bigl\vert \mathfrak{g} \bigl( \upgamma _{2i}, \upvarphi ( \upgamma _{2i} ) , \upvarphi ( \lambda \upgamma _{2i} ) \bigr) \\ & \quad{}-\mathfrak{g} \bigl( \upgamma _{2i}, \hat{\upvarphi} ( \upgamma _{2i} ) , \hat{\upvarphi} ( \lambda \upgamma _{2i} ) \bigr) \bigr\vert \bigr) \\ & \quad{}+\mathcal{I}_{ q}^{\theta} \bigl\vert \mathfrak{g} \bigl( \delta ,\upvarphi ( \delta ) , \upvarphi ( \lambda \delta ) \bigr) - \mathfrak{g} \bigl(\delta , \tilde{\upvarphi} ( \delta ) , \tilde{\upvarphi} ( \lambda \delta ) \bigr) \bigr\vert \Biggr] \\ & \leq \frac{\delta ^{\theta }\varepsilon }{ \Gamma _{q} ( \theta + 1 ) } + \mathrm{k}^{\ast }l_{\mathfrak{g}} \Vert \upvarphi - \hat{\upvarphi} \Vert . \end{aligned}$$

Hence,

$$ \bigl\Vert \hat{\upvarphi} ( \rho ) - \upvarphi ( \rho ) \bigr\Vert \leq \frac{T^{\theta _{1}}\varepsilon }{\Gamma _{q} ( \theta _{1}+1 ) }+ \mathrm{k}^{\ast }l_{f} \Vert \upvarphi - \hat{\upvarphi} \Vert ,$$

where \(\mathrm{k}^{\ast }\) is defined in (11). Consequently,

$$ \bigl\Vert \hat{\upvarphi} ( \rho ) -\upvarphi ( \rho ) \bigr\Vert \leq \frac{\delta ^{\theta}}{\Gamma _{q} ( \theta + 1 ) ( 1-\mathrm{k}^{ \ast} l_{\mathfrak{g}} ) } \varepsilon . $$
(19)

Consequently, the problem (1) is Ulam–Hyers stable. By setting

$$ \phi ( \varepsilon ) = \frac{\delta ^{\theta} }{ \Gamma _{q} ( \theta + 1 ) ( 1-\mathrm{k}^{\ast } l_{\mathfrak{g}} ) } \varepsilon ,$$

we obtain

$$ \bigl\Vert \hat{\upvarphi} ( \rho ) - \upvarphi ( \rho ) \bigr\Vert \leq \phi (\varepsilon ). $$
(20)

Clearly in (20), \(\phi ( \varepsilon ) =0\). Therefore, the problem (1) is also generalized Ulam–Hyers stable. □

5 Illustrative examples with a numerical approach

In this section, we provide two examples to validate the obtained results.

Example 5.1

Consider the following nonlocal boundary value problem of \(\mathbb{F}\mathrm{P}q{-}\mathbb{DE}\) as

$$ \textstyle\begin{cases} {}^{C }\mathcal{D}_{ q}^{7/2} \upvarphi ( \rho ) = \mathfrak{g} ( \rho, \upvarphi (\rho ), \upvarphi ( \frac{1}{2} \rho ) ), \\ \upvarphi ( 0 ) = \upvarphi^{\prime } ( 0 ) = \upvarphi^{ \prime \prime} ( 0 )=0, \\ \upvarphi ( 1 ) = \frac {1}{3} ( \mathcal{I}_{ q}^{ 1/3} \upvarphi ( \frac{1}{2} ) - \mathcal{I}_{ q}^{1/4} \upvarphi ( \frac{1}{6} ) ) \\ \hphantom{ \upvarphi ( 1 ) ={}}{}+ \frac {1}{4} ( \mathcal{I}_{ q}^{ 1/3} \upvarphi ( \frac{1}{4} ) - \mathcal{I}_{ q}^{1/4} \upvarphi ( \frac{1}{8} ) ), \end{cases} $$
(21)

for \(\rho \in \Sigma = [0, 1]\) with \(\delta =1>0\). Here, \(\theta =\frac{7}{2} \in (3, 4]\) with \(m=4 \geq 2\), \(\lambda = \frac{1}{2} \in (0,1)\), \(i=0,1,2\), \(k=2\), \(\upgamma _{01} = \frac{1}{3} \in \mathbb{R}\), \(\upgamma _{02} = \frac{1}{4} \in \mathbb{R}\), \(\vartheta _{1} = \frac{1}{3} >0\), \(\vartheta _{2} = \frac{1}{4}>0\), \(\upgamma _{11} = \frac{1}{2} \in (0,1)\), \(\upgamma _{12} = \frac{1}{4} \in (0,1)\), and \(\upgamma _{21} = \frac{1}{6}\in (0,1)\), \(\upgamma _{22}=\frac{1}{8} \in (0,1)\). We consider three cases

$$ q= \biggl\{ \frac{3}{10}, \frac{1}{2}, \frac{9}{10} \biggr\} ,$$

for the problem. With Eq. (4) and these data we find that

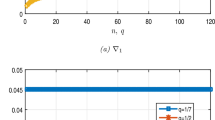
$$\begin{aligned} \Lambda &= \sum_{i=1}^{k} \frac{\upgamma _{0i} \Gamma _{q} ( m ) }{ \Gamma _{q} ( m + \vartheta _{i} ) } \bigl( \upgamma _{2i}^{\vartheta _{i} + m-1} - \upgamma _{1i}^{\vartheta _{i} + m-1} \bigr) + \delta ^{ m-1} \\ (k=2)\quad & = \frac{\upgamma _{01} \Gamma _{q} (4 ) }{ \Gamma _{q} ( 4 + \vartheta _{1} ) } \bigl( \upgamma _{21}^{\vartheta _{1} + 3} - \upgamma _{11}^{\vartheta _{1} + 3} \bigr) \\ & \quad{}+ \frac{\upgamma _{02} \Gamma _{q} (4 ) }{ \Gamma _{q} ( 4 + \vartheta _{2} ) } \bigl( \upgamma _{22}^{\vartheta _{2} + 3} - \upgamma _{12}^{\vartheta _{2} + 3} \bigr)+ \delta ^{ 3} \\ & = \frac{\frac{1}{3} \Gamma _{q} (4 ) }{ \Gamma _{q} ( 4 + \frac{1}{3} ) } \biggl( \biggl(\frac{1}{4} \biggr)^{\frac{1}{3} + 3} - \biggl(\frac{1}{2} \biggr)^{\frac{1}{3} + 3} \biggr) \\ & \quad{}+ \frac{\frac{1}{4} \Gamma _{q} ( 4 ) }{ \Gamma _{q} ( 4 + \frac{1}{4} ) } \biggl( \biggl(\frac{1}{8} \biggr)^{\frac{1}{4} + 3} - \biggl(\frac{1}{6} \biggr)^{\frac{1}{4} + 3} \biggr)+ \delta ^{ 3} \\ & \simeq \left \{\textstyle\begin{array}{l@{\quad}l} 0.9728, & q=\frac{3}{10}, \\ 0.9746, & q=\frac{1}{2}, \\ 0.9777, & q=\frac{9}{10} \end{array}\displaystyle \right \} < 1. \end{aligned}$$
(22)

One can see these results in Table 1 and the graphical representation of Λ for three cases of q in Fig. 2. Consider the function

$$ \mathfrak{g} \biggl( \rho , \upvarphi ( \rho ) , \upvarphi \biggl( \frac{1}{2} \rho \biggr) \biggr) = \frac{\cos ( \rho ) \vert \upvarphi ( \rho ) \vert }{ (\exp ( \rho ^{2} ) + 5 ) ( \vert \upvarphi ( \rho ) \vert +1 ) } + \frac{\exp ( -\sin ( \rho ) ) \upvarphi ( \frac{1}{2}\rho ) }{ ( 6+ \rho ) ( \vert \upvarphi ( \frac{1}{2}\rho ) \vert +1 )}. $$

Now, for every \(\upvarphi , \tilde{\upvarphi} \in \mathbb{R}\) and \(\rho \in \Sigma \), one has

$$\begin{aligned} & \biggl\vert \mathfrak{g} \biggl( \rho , \upvarphi ( \rho ), \upvarphi \biggl( \frac{1}{2} \rho \biggr) \biggr) - \mathfrak{g} \biggl( \rho , \tilde{ \upvarphi} ( \rho ), \tilde{\upvarphi} \biggl( \frac{1}{2}\rho \biggr) \biggr) \biggr\vert \\ &\quad \leq \biggl\vert \frac{\cos ( \rho ) }{ ( \exp ( \rho ^{2} ) +5 ) } \biggl( \frac{ \vert \upvarphi ( \rho ) \vert }{ ( \vert \upvarphi ( \rho ) \vert +1 ) } - \frac{ \vert \tilde{\upvarphi} ( \rho ) \vert }{ ( \vert \tilde{\upvarphi} ( \rho ) \vert +1 ) } \biggr) \biggr\vert \\ &\quad \quad{}+ \biggl\vert \frac{\exp ( -\sin ( \rho ) ) }{ ( 6+\rho ) } \biggl( \frac{\upvarphi ( \frac{1}{2} \rho ) }{ ( \vert \upvarphi ( \frac{1}{2} \rho ) \vert +1 ) } - \frac{\tilde{\upvarphi} (\frac{1}{2}\rho )}{ ( \vert \tilde{\upvarphi} ( \frac{1}{2}\rho ) \vert +1 ) } \biggr) \biggr\vert \\ &\quad \leq \biggl\vert \frac{\cos ( \rho ) }{ ( \exp ( \rho ^{2} ) +5 ) } \biggr\vert \biggl\vert \frac{\upvarphi ( \rho ) -\tilde{\upvarphi} ( \rho ) }{ ( \vert \upvarphi ( \rho ) \vert +1 ) ( \vert \tilde{\upvarphi} ( \rho ) \vert +1 ) } \biggr\vert \\ &\quad \quad{}+ \biggl\vert \frac{\exp ( -\sin ( \rho ) ) }{ ( 6+\rho ) } \biggr\vert \biggl\vert \frac{\upvarphi ( \frac{1}{2}\rho ) - \tilde{\upvarphi} (\frac{1}{2} \rho ) }{ ( \vert \upvarphi ( \frac{1}{2} \rho ) \vert +1 ) ( \vert \tilde{\upvarphi} ( \frac{1}{2}\rho ) \vert + 1 ) } \biggr\vert \\ &\quad \leq \biggl\vert \frac{\cos ( \rho ) }{ ( \exp ( \rho ^{2} ) +5 ) } \biggr\vert \bigl\vert \upvarphi ( \rho ) -\tilde{\upvarphi} (\rho ) \bigr\vert \\ &\quad \quad{}+ \biggl\vert \frac{\exp ( -\sin (\rho ) ) }{ ( 6 + \rho ) } \biggr\vert \biggl\vert \upvarphi \biggl( \frac{1}{2} \rho \biggr) - \tilde{\upvarphi} \biggl( \frac{1}{2}\rho \biggr) \biggr\vert \\ &\quad \leq \frac{1}{6} \biggl( \bigl\vert \upvarphi ( \rho ) -\tilde{ \upvarphi} ( \rho ) \bigr\vert + \biggl\vert \upvarphi \biggl( \frac{1}{2}\rho \biggr) - \tilde{\upvarphi} \biggl( \frac{1}{2}\rho \biggr) \biggr\vert \biggr), \end{aligned}$$

thus, the assumption (As1) is satisfied for \(l_{\mathfrak{g}}=\frac{1}{6}\) and by using Eq. (11) we obtain

$$\begin{aligned} \mathrm{k}^{\ast} l_{\mathfrak{g}} & = \frac{2 (\delta ^{\theta } + \delta ^{m+ \theta -1} )}{ \Gamma _{q} ( \theta + 1 ) } + \sum _{i=1}^{k} \vert \upgamma _{0i} \vert \frac{4\delta ^{m+ \vartheta _{i}+\theta -1}}{ \vert \Lambda \vert \Gamma _{q} ( \vartheta _{i} + \theta +1 ) } \\ (k=2)\quad & = \frac{4}{ \Gamma _{q} ( \frac{7}{2}+ 1 ) } + \biggl\vert \frac{1}{3} \biggr\vert \frac{4}{ \vert \Lambda \vert \Gamma _{q} ( \frac{1}{3} + \frac{7}{2} +1 ) } \\ & \quad{}+ \biggl\vert \frac{1}{4} \biggr\vert \frac{4}{ \vert \Lambda \vert \Gamma _{q} ( \frac{1}{4} + \frac{7}{2}+1 ) } \\ & \simeq \left \{\textstyle\begin{array}{l@{\quad}l} 0.4716, & q=\frac{3}{10}, \\ 0.2558, & q=\frac{1}{2}, \\ 0.0315, & q=\frac{9}{10} \end{array}\displaystyle \right \} < 1. \end{aligned}$$
Figure 2
figure 2

Graphical representation of Λ for \(q \in \{\frac{3}{10} , \frac{1}{2}, \frac{9}{10} \}\) in Example 5.1 according to Eq. (4)

Full size image
Table 1 Numerical results of \(\Gamma _{q}(m)\) and Λ of \(\mathbb{F}\mathrm{D}q-\mathbb{DP}\) (21) with \(q\in \{ \frac{3}{10}, \frac{1}{2}, \frac{9}{10} \}\) in Example 5.1
Full size table

Table 2 shows these results and the graphical representation of \(\mathrm{k}^{\ast}\) for three cases of q can be seen in Fig. 3. Hence, inequality (10) holds. Hence, all hypotheses of Theorem 3.2 hold, and so the problem (21) has at most one solution on Σ. Further, it follows from Theorem 4.1 that the problem (21) is Ulam–Hyers stable and consequently it is also generalized Ulam–Hyers stable.

Figure 3
figure 3

Graphical representation of \(\mathrm{k}^{\ast}\) for \(q \in \{\frac{3}{10} , \frac{1}{2}, \frac{9}{10} \}\) in Example 5.1 according to Eq. (10)

Full size image
Table 2 Numerical results of \(\Gamma _{q}(\theta +1)\) and \(\mathrm{k}^{\ast}\) of \(\mathbb{F}\mathrm{D}q-\mathbb{DP}\) (21) with \(q\in \{ \frac{3}{10}, \frac{1}{2}, \frac{9}{10} \}\) in Example 5.1
Full size table

Example 5.2

Consider problem (21) with the function

$$ \mathfrak{g} \biggl( \rho, \upvarphi ( \rho ) , \upvarphi \biggl( \frac{1}{2} \rho \biggr) \biggr) = 2 +\frac{1}{4}\sqrt{ \bigl\vert \upvarphi ( \rho ) \bigr\vert } + \frac{1}{7}\sqrt{ \biggl\vert \upvarphi \biggl( \frac{1}{2} \rho \biggr) \biggr\vert }.$$

Now, for any \(\upvarphi \in \mathbb{R}\) and \(\rho \in \Sigma \), we have

$$ \biggl\vert \mathfrak{g} \biggl( \rho, \upvarphi ( \rho ), \upvarphi \biggl( \frac{1}{2} \rho \biggr) \biggr) \biggr\vert \leq 2 + \frac{1}{4} \bigl\vert \upvarphi ( \rho ) \bigr\vert + \frac{1}{7} \biggl\vert \upvarphi \biggl( \frac{1}{2} \rho \biggr) \biggr\vert ,$$

thus, the assumption (As2) is satisfied for \(\mathrm{D}=2\), \(\mathrm{h}_{\mathfrak{g}}^{ ( 1 ) }= \frac{1}{4}\) and \(\mathrm{h}_{\mathfrak{g} }^{ ( 2 ) }=\frac{1}{7}\) and

$$\begin{aligned} \mathrm{N}_{1}& =\frac{\delta ^{\theta } ( \mathrm{h}_{\mathfrak{g}}^{ ( 1 ) } + \mathrm{h}_{\mathfrak{g}}^{ ( 2 ) } ) }{\Gamma _{q} ( \theta +1 ) }+\frac{ ( \mathrm{h}_{\mathfrak{g}}^{ ( 1 ) } + \mathrm{h}_{\mathfrak{g}}^{ ( 2 ) } ) \delta ^{m-1}}{ \vert \Lambda \vert } \sum _{i=1}^{k} \frac{2 \vert \gamma \vert \delta ^{\vartheta _{i} + \theta }}{\Gamma _{q} ( \vartheta _{i}+\theta +1 ) } \\ &\quad{}+ \frac{\delta ^{m+\theta -1} ( \mathrm{h}_{\mathfrak{g}}^{ ( 1 ) } + \mathrm{h}_{\mathfrak{g}}^{ ( 2 ) } ) }{ \vert \Lambda \vert \Gamma _{q} ( \theta _{1}+1 ) } \\ & =\frac{\frac{1}{4} + \frac{1}{7} }{\Gamma _{q} ( \frac{7}{2} +1 ) } + \frac{\frac{1}{4} + \frac{1}{7} }{ \vert \Lambda \vert } \biggl[ \frac{2 \vert \frac{1}{3} \vert }{ \Gamma _{q} ( \frac{1}{3} + \frac{7}{2} +1 ) } + \frac{2 \vert \frac{1}{4} \vert }{\Gamma _{q} ( \frac{1}{4} + \frac{1}{4} +1 ) } \biggr] \\ &\quad{}+ \frac{ \frac{1}{4} + \frac{1}{7}}{ \vert \frac{1}{2} \vert \Gamma _{q} ( \frac{7}{2}+1 ) } \\ &\simeq \left \{\textstyle\begin{array}{l@{\quad}l} 0.5609, & q=\frac{3}{10}, \\ 0.3041, & q=\frac{1}{2}, \\ 0.0376, & q=\frac{9}{10} \end{array}\displaystyle \right \} < 1. \end{aligned}$$

Table 3 shows these results and the graphical representation of \(\mathrm{N}_{1}\) for three cases of q can be seen in Fig. 4. Hence, all items of Theorem 3.3 are satisfied. Hence, the problem (21) possesses at least one solution on Σ.

Figure 4
figure 4

Graphical representation of \(\mathrm{N}_{1}\) for \(q \in \{\frac{3}{10} , \frac{1}{2}, \frac{9}{10} \}\) in Example 5.2 according to Eq. (13)

Full size image
Table 3 Numerical results of \(\mathrm{N}_{1}\) of \(\mathbb{F}\mathrm{D}q-\mathbb{DP}\) (21) with \(q\in \{ \frac{3}{10}, \frac{1}{2}, \frac{9}{10} \}\) in Example 5.2
Full size table

6 Conclusion

The \(\mathbb{F}\mathrm{P}q{-}\mathbb{DE}\) has been investigated in this work in detail. The investigation of this particular equation provides us with a powerful tool in modeling most scientific phenomena without the need to remove most parameters that have an essential role in the physical interpretation of the studied phenomena. For the first time, we have described the existence and uniqueness of solutions of various classes of nonlinear pantograph-type \(\mathbb{F}\mathrm{P}q{-}\mathbb{DE}\) (1) on a time scale under some BCs. Also, the two types of Ulam stability of the problem (1) are considered. We presented a few examples of \(\mathbb{F} \mathrm{P}q-\mathbb{DE}\) (1) that describe our outcomes.