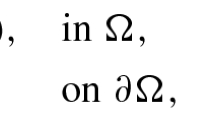Ground state sign-changing solutions for a class of double-phase problem in bounded domains

Abstract

This paper is concerned with the following double-phase problem:

$$ \textstyle\begin{cases} -\operatorname{div}( \vert \nabla u \vert ^{p-2}\nabla u+a(x) \vert \nabla u \vert ^{q-2}\nabla u)=f(x,u)& \text{in }\varOmega, \\ u=0 &\text{on }\partial\varOmega, \end{cases} $$

where $N\geq2$ and $1< p< q< N$. Assuming that the primitive of $f(x,u)$ is asymptotically q-linear as $|u|\rightarrow\infty$ and a weak version of Nehari-type monotonicity condition that the function $u\mapsto\frac{f(x,u)}{|u|^{q-1}}$ is nondecreasing on $(-\infty,0) \cup(0,\infty)$ for a.e. $x\in\varOmega$, we prove the existence of one ground state sign-changing solution via the constraint variational method and quantitative deformation lemma for the equation. Our results improve and generalize some results obtained by Liu and Dai (J. Differ. Equ. 265(9):4311–4334, 2018).

1 Introduction and main results

Differential equations and variational problems with double phase operator are a new and interesting topic. It arises from the nonlinear elasticity theory, strongly anisotropic materials, Lavrentiev’s phenomenon, and so on (see [2–5]). The study on double-phase problems attracts more and more interest in recent years, and many results have been obtained [1, 6–10]. More precisely, the research is related to the energy functional

$$ u\mapsto \int _{\varOmega }\bigl( \vert \nabla u \vert ^{p}+a(x) \vert \nabla u \vert ^{q}\bigr)\,dx, $$

(1)

where the integrand switches between two different elliptic behaviors. In [5], energies of the form (1) are used in the context of homogenization and elasticity, and the function a drives the geometry of a composite of two different materials with hardening powers p and q.

In this paper, we are concerned with the existence of sign-changing solutions of the double-phase problem

where Ω is a smooth bounded domain in $\mathbb{R}^{N}$, $N\geq 2$, $1< p< q< N$, and

$$ \begin{aligned} \frac{q}{p}< 1+ \frac{1}{N},\qquad a:\overline{\varOmega }\mapsto [0,+\infty ) \quad \text{is Lipschitz continuous}, \end{aligned} $$

(2)

and $f:\varOmega \times \mathbb{R}\mapsto \mathbb{R}$ is a Carathéodory function satisfying the following assumptions:

$(h_{1})$:

$f(x,t)=o(|t|^{p-2}t)$ as $t\rightarrow 0$ uniformly in $x\in \varOmega$;

$(h_{2})$:

there exist $q< r< p^{*}$ and some positive constant C such that

$$ \bigl\vert f(x,t) \bigr\vert \leq C\bigl(1 + \vert t \vert ^{r-1}\bigr), $$

where $p^{*} = \frac{Np}{N-p}$ is the critical exponent.

$(h_{3})$:

$\lim_{|t|\rightarrow +\infty } \frac{F(x,t)}{|t|^{q}} = +\infty$ uniformly in $x\in \varOmega$, where $F(x,t)=\int _{0}^{t}f(x,s)\,ds$;

$(h_{4})$:

the function $t\mapsto \frac{f(x,t)}{|t|^{q-1}}$ is nondecreasing on $(-\infty ,0)\cup (0,+\infty )$ for a.e. $x\in \varOmega$.

The solution of (P) is understand in the weak sense, that is, $u\in W_{0}^{1,H}(\varOmega )$ is a solution of (P) if

$$\begin{aligned}& \int _{\varOmega }\bigl( \vert \nabla u \vert ^{p-2} \nabla u\cdot \nabla v+a(x) \vert \nabla u \vert ^{q-2} \nabla u \cdot \nabla v\bigr)\,dx \\& \quad = \int _{\varOmega }f(x,u)v\,dx,\quad \forall v \in W_{0}^{1,H}(\varOmega ), \end{aligned}$$

where $W_{0}^{1,H}(\varOmega )$ will be defined in Sect. 2.

Note that energy functional φ associated with (P) is defined by

$$ \varphi (u)= \int _{\varOmega }\biggl(\frac{1}{p} \vert \nabla u \vert ^{p}+\frac{a(x)}{q} \vert \nabla u \vert ^{q}\biggr)\,dx- \int _{\varOmega }F(x,u)\,dx. $$

It is a well-known consequence of $(h_{1})$ and $(h_{2})$ that $\varphi \in C^{1}(W_{0}^{1,H}(\varOmega ),\mathbb{R})$ and the critical points of φ are weak solutions of (P). Furthermore, if $u\in W_{0}^{1,H}(\varOmega )$ is a solution of (P) and $u^{\pm } \neq 0$, then u is a sign-changing solution of (P), where

$$ u^{+}(x):=\max \bigl\{ u(x),0\bigr\} \quad \text{and}\quad u^{-}(x):=\min \bigl\{ u(x),0\bigr\} . $$

To facilitate the narrative, we set

$$\begin{aligned}& \mathbb{M}_{0}:=\bigl\{ u\in W_{0}^{1,H}( \varOmega ): u^{\pm }\neq 0, \bigl\langle \varphi '(u),u^{+} \bigr\rangle =\bigl\langle \varphi '(u),u^{-}\bigr\rangle =0\bigr\} , \\& \mathbb{N}_{0}:=\bigl\{ u\in W_{0}^{1,H}( \varOmega ): u\neq 0, \bigl\langle \varphi '(u),u\bigr\rangle =0 \bigr\} , \end{aligned}$$

and put

$$ m_{0}:=\inf_{u\in \mathbb{M}_{0}}\varphi (u),\qquad n_{0}:=\inf_{u\in \mathbb{N}_{0}}\varphi (u). $$

Let us recall some previous results that led us to the present research. The first result is due to Perera and Squassina [6], who considered the following form of (P) with the q-superlinear nonlinearity:

Applying the Morse theory, they proved that ($P_{1}$) has a nontrivial solution by assuming that either

$(T_{1})$:

$\lambda \notin \{\lambda _{k}\}_{k=1}^{\infty }$; or

$(T_{2})$:

for some $\delta >0$, $\frac{|t|^{r}}{r}+H(x,t)\leq 0$ for a.e. $x\in \varOmega$ and $|t|\leq \delta$; or

$(T_{3})$:

$\frac{|t|^{r}}{r}+H(x,t)\geq c|t|^{s}$ for a.e. $x\in \varOmega$ and all $t\in \mathbb{R}$ for some $s\in (p,q)$ and $c>0$.

Recently, Liu and Dai [1] investigated the sign-changing ground state solution of (P) under $(h_{1})$, $(h_{2})$, $(h_{3})$, and

$(h_{4})'$:

the function $t\mapsto \frac{f(x,t)}{|t|^{q-1}}$ is strictly increasing on $(-\infty ,0)\cup (0,+\infty )$.

Additionally, Liu and Dai [9] also obtained the existence of at least three ground state solutions of (P) by using the strong maximum principle for the homogeneous double-phase problem.

It is a well-known consequence of $(h_{4})'$ that there is unique $t_{u}>0$ such that $t_{u} u\in \mathbb{N}_{0}$ for every $u\in W_{0} ^{1,H}(\varOmega )\setminus \{0\}$, which implies that φ has at most one minimizer on $\mathbb{M}_{0}$. Moreover, $(h_{4})'$ plays a crucial role in [1]. In fact, condition $(h_{4})'$ implies that every minimizer of φ on $\mathbb{M}_{0}$ is a critical point. However, if $t\mapsto \frac{f(x,t)}{|t|^{q-1}}$ is nonstrictly increasing, then $t_{u}$ and minimizer of φ on $\mathbb{M} _{0}$ may not be unique, and their arguments become invalid.

Motivated by the aforementioned works, in the present paper, our goal is to generalize the results mentioned to (P) under a weaker assumption. Precisely, we obtain following results.

Theorem 1.1

Assume that$(h_{1})$–$(h_{4})$hold. Then problem (P) has a sign-changing solution$u_{0}\in \mathbb{M}_{0}$such that

$$ \varphi (u_{0})=\inf_{u\in \mathbb{M}_{0}}\varphi (u). $$

Furthermore, suppose that

$$ \begin{aligned} \frac{1}{q}f(x,t)t-F(x,t)>0, \quad \forall x\in \varOmega , t\neq 0, \end{aligned} $$

(3)

then$u_{0}$has precisely two nodal domains.

Theorem 1.2

Assume that$(h_{1})$–$(h_{4})$hold. Then$m_{0}\geq 2n_{0}$.

The rest of this paper is organized as follows. In Sect. 2, we present some necessary preliminary knowledge on space $W_{0}^{1,H}(\varOmega )$. In Sect. 3, we give some preliminary lemmas needed for the proofs of our main results. We complete the proofs of Theorems 1.1–1.2 in Sect. 4.

2 Preliminaries

To discuss problem (P), we need some facts on the space $W_{0}^{1,H}( \varOmega )$, which is called the Musielak–Orlicz–Sobolev space. For this reason, we recall some properties involving the Musielak–Orlicz spaces, which can be found in [10–14] and references therein.

Denote by $N(\varOmega )$ the set of all generalized N-functions. For $1 < p < q$ and $0\leq a(\cdot )\in L^{1}(\varOmega )$, we define

$$ H(x,t)=t^{p}+a(x)t^{q}, \quad (x,t)\in \varOmega \times [0,+\infty ). $$

It is clear that $H\in N(\varOmega )$ is locally integrable and

$$ H(x,2t)\leq 2^{q} H(x,t), \quad (x,t)\in \varOmega \times [0,+\infty ), $$

which is called condition $(\triangle _{2})$.

The Musielak–Orlicz space $L^{H}(\varOmega )$ is defined by

$$ L^{H}(\varOmega )= \biggl\{ u:\varOmega \rightarrow \mathbb{R} \text{ measurable } : \int _{\varOmega }H\bigl(x, \vert u \vert \bigr)\,dx< +\infty \biggr\} , $$

endowed with the Luxemburg norm

$$ \vert u \vert _{H}=\mathrm{inf} \biggl\{ \lambda >0: \int _{\varOmega }H\biggl(x, \biggl\vert \frac{u}{ \lambda } \biggr\vert \biggr)\,dx\leq 1 \biggr\} . $$

The Musielak–Orlicz–Sobolev space $W^{1, H}(\varOmega )$ is defined by

$$ W^{1, H}(\varOmega )=\bigl\{ u\in L^{H}(\varOmega ): \vert \nabla u \vert \in L^{H}(\varOmega ) \bigr\} $$

and is equipped with the norm

$$ \begin{aligned} \Vert u \Vert = \vert u \vert _{H}+ \vert \nabla u \vert _{H}. \end{aligned} $$

(4)

We denote by $W_{0}^{1,H}(\varOmega )$ the completion of $C_{0}^{\infty }(\varOmega )$ in $W^{1,H}(\varOmega )$. With these norms, the spaces $L^{H}(\varOmega )$, $W_{0}^{1,H}(\varOmega )$ and $W^{1,H}(\varOmega )$ are separable reflexive Banach spaces; see [10] for the details.

Proposition 2.1

([1, Proposition 2.1])

Set$\rho _{H}(u)=\int _{ \varOmega }(|u|^{p}+a(x)|u|^{q})\,dx$. For$u\in L^{H}(\varOmega )$, we have:

• (i) For$u\neq 0$, $|u|_{H}=\lambda \Leftrightarrow \rho _{H}(\frac{u}{ \lambda })=1$;

• (ii) $|u|_{H}<1(=1; >1)\Leftrightarrow \rho _{H}(u)<1(=1; >1)$;

• (iii) If$|u|_{H}\geq 1$, then$|u|^{p}_{H}\leq \rho _{H}(u)\leq |u|^{q} _{H}$;

• (iv) If$|u|_{H}\leq 1$, then$|u|^{q}_{H}\leq \rho _{H}(u)\leq |u|^{p} _{H}$.

Proposition 2.2

([11, Propositions 2.15 and 2.18])

• (1) If$1\leq \vartheta \leq p^{*}$, then the embedding from$W_{0}^{1,H}(\varOmega )$to$L^{\vartheta }(\varOmega )$is continuous. In particular, if$\vartheta \in [1,p^{*})$, then the embedding$W_{0}^{1,H}(\varOmega )\hookrightarrow L^{\vartheta }(\varOmega )$is compact.

• (2) Assume that (2) holds. Then the Poincaré’s inequality holds, that is, there exists a positive constant$C_{0}$such that

  $$ \vert u \vert _{H}\leq C_{0} \vert \nabla u \vert _{H},\quad u\in W_{0}^{1, H}(\varOmega ). $$

By this lemma there exists $c_{\vartheta }> 0$ such that

$$ \vert u \vert _{\vartheta }\leq c_{\vartheta } \Vert u \Vert , \quad \forall u\in W_{0}^{H}( \varOmega ), $$

where $|u|_{s}$ denotes the usual norm in $L^{\vartheta }(\varOmega )$ for $1\leq \vartheta < p^{*}$. It follows from (2) of Proposition 2.2 that $|\nabla u|_{H}$ is an equivalent norm in $W_{0}^{1, H}(\varOmega )$. We will use the equivalent norm in the following discussion and write $\|u\|=|\nabla u|_{H}$ for simplicity.

To discuss problem (P), we need to define a functional in $W_{0}^{1,H}(\varOmega )$:

$$ \begin{aligned} J(u)= \int _{\varOmega }\biggl(\frac{1}{p} \vert \nabla u \vert ^{p}+\frac{a(x)}{q} \vert \nabla u \vert ^{q}\biggr)\,dx. \end{aligned} $$

We know that (see [15, p. 63, example]) $J\in C^{1}(W_{0}^{1,H}( \varOmega ),\mathbb{R})$ and the double-phase operator $-\operatorname{div}(| \nabla u|^{p-2}\nabla u+a(x)|\nabla u|^{q-2}\nabla u)$ is the derivative operator of J in the weak sense. We denote $L=J': W_{0}^{1,H}( \varOmega )\rightarrow (W_{0}^{1,H}(\varOmega ))^{*}$. Then

$$ \begin{aligned} \bigl\langle L(u), v\bigr\rangle = \int _{\varOmega }\bigl( \vert \nabla u \vert ^{p-2} \nabla u\cdot \nabla v+a(x) \vert \nabla u \vert ^{q-2}\nabla u\cdot \nabla v\bigr)\,dx \end{aligned} $$

for all $u, v\in W_{0}^{1,H}(\varOmega )$. Here $(W_{0}^{1,H}(\varOmega ))^{*}$ denotes the dual space of $W_{0}^{1,H}( \varOmega )$, and $\langle \cdot , \cdot \rangle$ denotes the pairing between $W_{0}^{1,H}(\varOmega )$ and $(W_{0}^{1,H}(\varOmega ))^{*}$. Then we have the following:

Proposition 2.3

([1, Proposition 3.1])

Let$E= W^{1,H}_{0}(\varOmega )$, and letLbe as before. Then

• (1) $L: E\rightarrow E^{*}$a continuous, bounded, and strictly monotone operator.

• (2) $L: E\rightarrow E^{*}$is a mapping of type$(S)_{+}$, that is, if$u_{n}\rightharpoonup u$inEand$\limsup_{n\rightarrow +\infty }\langle L(u_{n})-L(u), u_{n}-u\rangle \leq 0$, then$u_{n}\rightarrow u$inE.

• (3) $L: E\rightarrow E^{*}$is a homeomorphism.

3 Some preliminary lemmas

In this section, we give some preliminary lemmas crucial for proving our results.

Lemma 3.1

If assumptions$(h_{1})$–$(h_{4})$hold, then

$$ \begin{aligned}[b] \varphi (u)\geq{} &\varphi \bigl(su^{+}+tu^{-}\bigr)+\frac{1-s^{q}}{q}\bigl\langle \varphi '(u),u^{+}\bigr\rangle + \frac{1-t^{q}}{q}\bigl\langle \varphi '(u),u ^{-} \bigr\rangle \\ &{}+ \int _{\varOmega }g(s) \bigl\vert \nabla u^{+} \bigr\vert ^{p}\,dx+ \int _{\varOmega }g(t) \bigl\vert \nabla u^{-} \bigr\vert ^{p}\,dx, \\ &{}\forall u=u^{+}+u^{-}\in E, s,t\geq 0, \end{aligned} $$

(5)

where$g(\tau )=\frac{1-\tau ^{p}}{p}-\frac{1-\tau ^{q}}{q}$, $\tau \geq 0$.

Proof

By condition $(h_{4})$ we have

$$ \begin{aligned}[b] &\frac{1-t^{q}}{q}\tau f(x, \tau )+F(x,t\tau )-F(x,\tau ) \\ &\quad = \int _{t} ^{1} f(x,\tau )s^{q-1}\tau \,ds- \int _{t}^{1} f(x,\tau s)\tau \,ds \\ &\quad = \int _{t}^{1} \biggl[\frac{f(x,\tau )}{ \vert \tau \vert ^{q-1}}- \frac{f(x,\tau s)}{ \vert \tau s \vert ^{q-1}} \biggr]s^{q-1} \vert \tau \vert ^{q-1}\tau \,ds \\ &\quad \geq 0,\quad t\geq 0, \tau \in \mathbb{R}\setminus \{0\}. \end{aligned} $$

(6)

Clearly, $g(t)\geq g(1)=0$ for any $t\geq 0$. Hence from (6) it follows that

$$\begin{aligned}& \varphi (u)-\varphi \bigl(su^{+}+tu^{-} \bigr) \\& \quad = \int _{\varOmega }\biggl(\frac{1}{p} \bigl\vert \nabla u^{+} \bigr\vert ^{p}+\frac{a(x)}{q} \bigl\vert \nabla u^{+} \bigr\vert ^{q}\biggr)\,dx- \int _{\varOmega }F\bigl(x,u ^{+}\bigr)\,dx \\& \qquad {}+ \int _{\varOmega }\biggl(\frac{1}{p} \bigl\vert \nabla u^{-} \bigr\vert ^{p}+ \frac{a(x)}{q} \bigl\vert \nabla u^{-} \bigr\vert ^{q}\biggr)\,dx- \int _{\varOmega }F\bigl(x,u^{-}\bigr)\,dx \\& \qquad {}- \int _{\varOmega }\biggl(\frac{s^{p}}{p} \bigl\vert \nabla u^{+} \bigr\vert ^{p}+\frac{a(x)s^{q}}{q} \bigl\vert \nabla u^{+} \bigr\vert ^{q}\biggr)\,dx+ \int _{\varOmega }F\bigl(x,su^{+}\bigr)\,dx \\& \qquad {}- \int _{\varOmega }\biggl(\frac{t ^{p}}{p} \bigl\vert \nabla u^{-} \bigr\vert ^{p}+\frac{a(x)t^{q}}{q} \bigl\vert \nabla u^{-} \bigr\vert ^{q}\biggr)\,dx+ \int _{\varOmega }F\bigl(x,tu^{-}\bigr)\,dx \\& \qquad {}-\frac{1-s^{q}}{q}\bigl\langle \varphi '(u),u ^{+}\bigr\rangle -\frac{1-t^{q}}{q}\bigl\langle \varphi '(u),u^{-}\bigr\rangle \\& \qquad {}+\frac{1-s ^{q}}{q}\bigl\langle \varphi '(u),u^{+} \bigr\rangle +\frac{1-t^{q}}{q}\bigl\langle \varphi '(u),u^{-} \bigr\rangle \\& \quad = \int _{\varOmega }g(s) \bigl\vert \nabla u^{+} \bigr\vert ^{p}\,dx+ \int _{\varOmega }g(t) \bigl\vert \nabla u^{-} \bigr\vert ^{p}\,dx \\& \qquad {}+\frac{1-s^{q}}{q}\bigl\langle \varphi '(u),u^{+} \bigr\rangle +\frac{1-t^{q}}{q}\bigl\langle \varphi '(u),u ^{-}\bigr\rangle \\& \qquad {}+ \int _{\varOmega } \biggl[\frac{1-s^{q}}{q}f\bigl(x,u^{+} \bigr)u^{+}+F\bigl(x,su ^{+}\bigr)-F \bigl(x,u^{+}\bigr) \biggr]\,dx \\& \qquad {}+ \int _{\varOmega } \biggl[\frac{1-t^{q}}{q}f\bigl(x,u ^{-}\bigr)u^{-}+F\bigl(x,tu^{-}\bigr)-F \bigl(x,u^{-}\bigr) \biggr]\,dx \\& \quad \geq \frac{1-s^{q}}{q} \bigl\langle \varphi '(u),u^{+} \bigr\rangle +\frac{1-t^{q}}{q}\bigl\langle \varphi '(u),u ^{-}\bigr\rangle \\& \qquad {}+ \int _{\varOmega }g(s) \bigl\vert \nabla u^{+} \bigr\vert ^{p}\,dx+ \int _{\varOmega }g(t) \bigl\vert \nabla u^{-} \bigr\vert ^{p}\,dx. \end{aligned}$$

The proof is completed. □

From Lemma 3.1 we immediately have the following two corollaries.

Corollary 3.2

Assume that$(h_{1})$–$(h_{4})$hold. If$u=u^{+}+u^{-}\in \mathbb{M}_{0}$, then

$$\begin{aligned}& \varphi (u)=\varphi \bigl(u^{+}+u^{-} \bigr)=\max_{s,t\geq 0}\varphi \bigl(su ^{+}+tu^{-} \bigr). \end{aligned}$$

Corollary 3.3

Assume that$(h_{1})$–$(h_{4})$hold. If$u\in \mathbb{N}_{0}$, then

$$\begin{aligned}& \varphi (u)=\max_{t\geq 0}\varphi (tu). \end{aligned}$$

Lemma 3.4

Assume that$(h_{1})$–$(h_{3})$and$(h_{4})'$hold. If$u\in E$and$u^{\pm }\neq 0$, then there exists a unique pair$(s_{u}, t_{u})$of positive numbers such that

$$ s_{u} u^{+}+t_{u} u^{-}\in \mathbb{M}_{0}. $$

Proof

For any $u\in E$ with $u^{\pm }\neq 0$, we consider the functions $g(s,t), h(s,t): [0,+\infty )\times [0,+\infty )\rightarrow \mathbb{R}$ given by

$$ g(s,t)=\bigl\langle \varphi '\bigl(su^{+}+tu^{-} \bigr),su^{+}\bigr\rangle \quad \text{and}\quad h(s,t)=\bigl\langle \varphi '\bigl(su^{+}+tu^{-} \bigr),tu^{-}\bigr\rangle . $$

We directly compute that

$$ \begin{aligned} g(s,t)={} &\bigl\langle \varphi '\bigl(su^{+}+tu^{-} \bigr),su^{+}\bigr\rangle \\ ={}& \int _{ \varOmega }\bigl(s^{p} \bigl\vert \nabla u^{+} \bigr\vert ^{p}+a(x)s^{q} \bigl\vert \nabla u^{+} \bigr\vert ^{q}\bigr)\,dx- \int _{\varOmega }f\bigl(x,su^{+}\bigr)su^{+} \,dx, \\ h(s,t)={}&\bigl\langle \varphi '\bigl(su^{+}+tu ^{-}\bigr),tu^{-}\bigr\rangle \\ ={}& \int _{\varOmega }\bigl(t^{p} \bigl\vert \nabla u^{-} \bigr\vert ^{p}+a(x)t ^{q} \bigl\vert \nabla u^{-} \bigr\vert ^{q}\bigr)\,dx- \int _{\varOmega }f\bigl(x,tu^{-}\bigr)tu^{-} \,dx. \end{aligned} $$

(7)

Using assumptions $(h_{1})$ and $(h_{2})$, we deduce that, for any $\varepsilon >0$, there is $C_{\varepsilon }>0$ such that, for all $(x,t)\in \varOmega \times \mathbb{R}$,

$$ \begin{aligned} & \bigl\vert f(x,t) \bigr\vert \leq \varepsilon \vert t \vert ^{p-1}+C_{\varepsilon } \vert t \vert ^{r-1}, \\ & \bigl\vert F(x,t) \bigr\vert \leq \varepsilon \vert t \vert ^{p}+C_{\varepsilon } \vert t \vert ^{r}, \end{aligned} $$

(8)

where $r\in [1,p^{*})$ was given in $(h_{2})$.

Thus, for $s>0$ sufficiently small, by (8) and Proposition 2.2(2) we have

$$ \begin{aligned}[b] g(s,t)={} & \int _{\varOmega }\bigl(s^{p} \bigl\vert \nabla u^{+} \bigr\vert ^{p}+a(x)s^{q} \bigl\vert \nabla u ^{+} \bigr\vert ^{q}\bigr)\,dx- \int _{\varOmega }f\bigl(x,su^{+}\bigr)su^{+} \,dx \\ \geq {}&s^{q} \int _{ \varOmega }\bigl( \bigl\vert \nabla u^{+} \bigr\vert ^{p}+ a(x) \bigl\vert \nabla u^{+} \bigr\vert ^{q}\bigr)\,dx \\ &- \int _{ \varOmega } \bigl(\varepsilon s^{p} \bigl\vert u^{+} \bigr\vert ^{p}+C_{\varepsilon }s^{r} \bigl\vert u^{+} \bigr\vert ^{r}\bigr)\,dx \\ \geq {}& \textstyle\begin{cases} s^{q} \Vert u^{+} \Vert ^{q}-\varepsilon c_{p}^{p}s^{p} \Vert u^{+} \Vert ^{p} - C_{ \varepsilon }c_{r}^{r}s^{r} \Vert u^{+} \Vert ^{r}&\text{if } \Vert u^{+} \Vert < 1, \\ s^{q} \Vert u^{+} \Vert ^{p}-\varepsilon c_{p}^{p}s^{p} \Vert u^{+} \Vert ^{p} - C _{\varepsilon }c_{r}^{r}s^{r} \Vert u^{+} \Vert ^{r}&\text{if } \Vert u^{+} \Vert >1, \end{cases}\displaystyle \end{aligned} $$

(9)

and

$$\begin{aligned} h(s,t) = & \int _{\varOmega }\bigl(t^{p} \bigl\vert \nabla u^{-} \bigr\vert ^{p}+a(x)t^{q} \bigl\vert \nabla u ^{-} \bigr\vert ^{q}\bigr)\,dx- \int _{\varOmega }f\bigl(x,tu^{-}\bigr)tu^{-} \,dx \\ \geq &t^{q} \int _{ \varOmega }\bigl( \bigl\vert \nabla u^{-} \bigr\vert ^{p}+ a(x) \bigl\vert \nabla u^{-} \bigr\vert ^{q}\bigr)\,dx \\ &{}- \int _{ \varOmega } \bigl(\varepsilon t^{p} \bigl\vert u^{-} \bigr\vert ^{p}+C_{\varepsilon }t^{r} \bigl\vert u^{-} \bigr\vert ^{r}\bigr)\,dx \\ \geq & \textstyle\begin{cases} t^{q} \Vert u^{-} \Vert ^{q}-\varepsilon c_{p}^{p}t^{p} \Vert u^{-} \Vert ^{p} - C_{ \varepsilon }c_{r}^{r}t^{r} \Vert u^{-} \Vert ^{r}&\text{if } \Vert u^{-} \Vert < 1, \\ t^{q} \Vert u^{-} \Vert ^{p}-\varepsilon c_{p}^{p}t^{p} \Vert u^{-} \Vert ^{p} - C _{\varepsilon }c_{r}^{r}t^{r} \Vert u^{-} \Vert ^{r}&\text{if } \Vert u^{-} \Vert >1. \end{cases}\displaystyle \end{aligned}$$

(10)

By (9), (10), and the arbitrariness of ε, it is easy to prove that $g(s,s)>0$ and $h(s,s)>0$ for $s>0$ small.

Moreover, using (6), we have

$$ \begin{aligned} \frac{1}{q}\tau f(x,\tau )-F(x,\tau )\geq 0,\quad \tau \in \mathbb{R} \setminus \{0\}. \end{aligned} $$

(11)

Hence by (11) and $(h_{3})$ we have that, for $s>1$,

$$ \begin{aligned}[b] g(s,t)&= \int _{\varOmega }\bigl(s^{p} \bigl\vert \nabla u^{+} \bigr\vert ^{p}+a(x)s^{q} \bigl\vert \nabla u ^{+} \bigr\vert ^{q}\bigr)\,dx- \int _{\varOmega }f\bigl(x,su^{+}\bigr)su^{+} \,dx \\ &\leq s^{q} \int _{ \varOmega }\bigl( \bigl\vert \nabla u^{+} \bigr\vert ^{p}+a(x) \bigl\vert \nabla u^{+} \bigr\vert ^{q}\bigr)\,dx-q \int _{\varOmega } F\bigl(x,su^{+}\bigr)\,dx \\ &=s^{q} \int _{\varOmega }\bigl( \bigl\vert \nabla u^{+} \bigr\vert ^{p}+a(x) \bigl\vert \nabla u^{+} \bigr\vert ^{q}\bigr)\,dx-q \int _{\varOmega } \frac{F(x,su^{+})}{ \vert su^{+} \vert ^{q}} \bigl\vert su ^{+} \bigr\vert ^{q}\,dx \\ &=s^{q} \biggl( \int _{\varOmega }\bigl( \bigl\vert \nabla u^{+} \bigr\vert ^{p}+a(x) \bigl\vert \nabla u^{+} \bigr\vert ^{q}\bigr)\,dx-q \int _{u^{+}\neq 0} \frac{F(x,su^{+})}{ \vert su^{+} \vert ^{q}} \bigl\vert u^{+} \bigr\vert ^{q}\,dx \biggr) \end{aligned} $$

(12)

and, for $t>1$,

$$ \begin{aligned}[b] g(s,t)={}& \int _{\varOmega }\bigl(t^{p} \bigl\vert \nabla u^{-} \bigr\vert ^{p}+a(x)t^{q} \bigl\vert \nabla u ^{-} \bigr\vert ^{q}\bigr)\,dx- \int _{\varOmega }f\bigl(x,tu^{-}\bigr)tu^{-} \,dx \\ \leq {}&t^{q} \int _{ \varOmega }\bigl( \bigl\vert \nabla u^{-} \bigr\vert ^{p}+a(x) \bigl\vert \nabla u^{-} \bigr\vert ^{q}\bigr)\,dx-q \int _{\varOmega } F\bigl(x,tu^{+}\bigr)\,dx \\ ={}&t^{q} \int _{\varOmega }\bigl( \bigl\vert \nabla u^{-} \bigr\vert ^{p}+a(x) \bigl\vert \nabla u^{-} \bigr\vert ^{q}\bigr)\,dx-q \int _{\varOmega } \frac{F(x,tu^{-})}{ \vert tu^{-} \vert ^{q}} \bigl\vert tu ^{-} \bigr\vert ^{q}\,dx \\ ={}&t^{q} \biggl( \int _{\varOmega }\bigl( \bigl\vert \nabla u^{-} \bigr\vert ^{p}+a(x) \bigl\vert \nabla u^{-} \bigr\vert ^{q}\bigr)\,dx-q \int _{u^{-}\neq 0} \frac{F(x,tu^{+})}{ \vert tu^{-} \vert ^{q}} \bigl\vert u^{-} \bigr\vert ^{q}\,dx \biggr), \end{aligned} $$

(13)

which yields that $g(t,t)<0$ and $h(t,t)<0$ for $t>0$ large. Thus there are $0< T< R$ such that

$$ \begin{aligned} g(T,T), h(T,T)>0 \quad \text{and}\quad g(R,R), h(R,R)< 0. \end{aligned} $$

(14)

This fact, combined with (7), implies that

$$ g(T,t)=g(T,T)>0,\qquad g(R,t)=g(R,R)< 0,\quad t\in [r,R], $$

and

$$ h(T,t)=h(T,T)>0,\qquad h(R,t)=h(R,R)< 0, \quad t\in [r,R]. $$

So, by the Miranda theorem in [16] we can find $(s_{u},t_{u}) \in (T,R)\times (T,R)$ such that $g(s_{u},t_{u})=h(s_{u},t_{u})=0$. Therefore $s_{u} u^{+}+t_{u} u^{-}\in \mathbb{M}_{0}$.

Next, we prove the uniqueness. Let $(s_{i}, t_{i})$ be such that $s_{i} u^{+}+t_{i} u^{-}\in \mathbb{M}_{0}$, $i=1,2$, that is,

$$ \begin{aligned} g(s_{1},t_{1})=h(s_{1},t_{1})=g(s_{2},t_{2})=h(s_{2},t_{2})=0. \end{aligned} $$

(15)

Then from (5), (7), and (15) it follows that

$$ \begin{aligned}[b] \varphi \bigl(s_{1}u^{+}+t_{1}u^{-} \bigr)\geq{} &\frac{s_{1}^{q}-s_{2}^{q}}{qs _{1}^{q}}\bigl\langle \varphi ' \bigl(s_{1}u^{+}+t_{1}u^{-} \bigr),s_{1}u^{+}\bigr\rangle \\ &{} +\frac{t_{1}^{q}-t_{2}^{q}}{qt_{1}^{q}}\bigl\langle \varphi ' \bigl(s_{1}u ^{+}+t_{1}u^{-} \bigr),t_{1}u^{-}\bigr\rangle \\ &+\varphi \bigl(s_{2}u^{+}+t_{2}u^{-} \bigr) \\ &{}+ \biggl(\frac{s_{1}^{p}-s_{2}^{p}}{p}-\frac{s_{1}^{q}-s_{2}^{q}}{qs _{1}^{q}}s_{1}^{p} \biggr) \int _{\varOmega } \bigl\vert \nabla u^{+} \bigr\vert ^{p}\,dx \\ &{}+ \biggl(\frac{t _{1}^{p}-t_{2}^{p}}{p}-\frac{t_{1}^{q}-t_{2}^{q}}{qt_{1}^{q}}t_{1} ^{p} \biggr) \int _{\varOmega } \bigl\vert \nabla u^{-} \bigr\vert ^{p}\,dx \\ ={}&\varphi \bigl(s_{2}u^{+}+t _{2}u^{-} \bigr) \\ &{}+ \biggl(\frac{s_{1}^{p}-s_{2}^{p}}{p}-\frac{s_{1}^{q}-s _{2}^{q}}{qs_{1}^{q}}s_{1}^{p} \biggr) \int _{\varOmega } \bigl\vert \nabla u^{+} \bigr\vert ^{p}\,dx \\ &{}+ \biggl(\frac{t_{1}^{p}-t_{2}^{p}}{p}-\frac{t_{1}^{q}-t_{2}^{q}}{qt _{1}^{q}}t_{1}^{p} \biggr) \int _{\varOmega } \bigl\vert \nabla u^{-} \bigr\vert ^{p}\,dx \end{aligned} $$

(16)

and

$$ \begin{aligned}[b] \varphi \bigl(s_{2}u^{+}+t_{2}u^{-} \bigr)\geq{} &\frac{s_{2}^{q}-s_{1}^{q}}{qs _{2}^{q}}\bigl\langle \varphi ' \bigl(s_{2}u^{+}+t_{2}u^{-} \bigr),s_{2}u^{+}\bigr\rangle \\ &{} +\frac{t_{2}^{q}-t_{1}^{q}}{qt_{2}^{q}}\bigl\langle \varphi ' \bigl(s_{2}u ^{+}+t_{2}u^{-} \bigr),t_{2}u^{-}\bigr\rangle \\ &{}+\varphi \bigl(s_{1}u^{+}+t_{1}u ^{-}\bigr) \\ &{}+ \biggl(\frac{s_{2}^{p}-s_{1}^{p}}{p}-\frac{s_{2}^{q}-s_{1} ^{q}}{qs_{2}^{q}}s_{2}^{p} \biggr) \int _{\varOmega } \bigl\vert \nabla u^{+} \bigr\vert ^{p}\,dx \\ &{}+ \biggl(\frac{t_{2}^{p}-t_{1}^{p}}{p}-\frac{t_{2}^{q}-t_{1}^{q}}{qt_{2} ^{q}}t_{2}^{p} \biggr) \int _{\varOmega } \bigl\vert \nabla u^{-} \bigr\vert ^{p}\,dx \\ ={}&\varphi \bigl(s _{1}u^{+}+t_{1}u^{-} \bigr) \\ &{}+ \biggl(\frac{s_{2}^{p}-s_{1}^{p}}{p}-\frac{s _{2}^{q}-s_{1}^{q}}{qs_{2}^{q}}s_{2}^{p} \biggr) \int _{\varOmega } \bigl\vert \nabla u ^{+} \bigr\vert ^{p}\,dx \\ &{}+ \biggl(\frac{t_{2}^{p}-t_{1}^{p}}{p}-\frac{t_{2}^{q}-t _{1}^{q}}{qt_{2}^{q}}t_{2}^{p} \biggr) \int _{\varOmega } \bigl\vert \nabla u^{-} \bigr\vert ^{p}\,dx. \end{aligned} $$

(17)

Both (16) and (17) imply that $s_{1}=s_{2}$ and $t_{1}=t_{2}$, which in turn implies that $(s_{u},t_{u})$ is the unique pair of positive numbers such that $s_{u} u^{+}+t_{u} u^{-}\in \mathbb{M}_{0}$. We end the proof. □

Furthermore we have the following:

Lemma 3.5

Assume that$(h_{1})$–$(h_{3})$and$(h_{4})'$hold. Then

$$ m_{0}=\inf_{u\in \mathbb{M}_{0}}\varphi (u)=\inf _{u\in E,u^{\pm }\neq 0}\max_{s,t\geq 0}\varphi \bigl(su^{+}+tu ^{-}\bigr). $$

Proof

By Corollary 3.2 we conclude that

$$ \begin{aligned}[b] \inf_{u\in E,u^{\pm }\neq 0} \max_{s,t\geq 0}\varphi \bigl(su ^{+}+tu^{-} \bigr)\leq{} & \inf_{u\in \mathbb{M}_{0}}\max_{s,t\geq 0}\varphi \bigl(su^{+}+tu^{-}\bigr) \\ ={}&\inf_{u\in \mathbb{M}_{0}}\varphi (u)=m_{0}. \end{aligned} $$

(18)

Moreover, for any $u\in E$ with $u^{\pm }\neq 0$, from Lemma 3.4 we deduce that

$$ \max_{s,t\geq 0}\varphi \bigl(su^{+}+tu^{-} \bigr)\geq \varphi \bigl(s_{u}u ^{+}+t_{u}u^{-} \bigr)\geq \inf_{u\in \mathbb{M}_{0}}\varphi (u)=m _{0}, $$

which implies

$$ \begin{aligned} \inf_{u\in E,u^{\pm }\neq 0}\max _{s,t\geq 0}\varphi \bigl(su ^{+}+tu^{-} \bigr)\geq \inf_{u\in \mathbb{M}_{0}}\varphi (u)=m_{0}. \end{aligned} $$

(19)

Therefore the conclusion directly follows from (18) and (19). □

Lemma 3.6

Assume that$(h_{1})$–$(h_{3})$and$(h_{4})'$hold. Then$m_{0}>0$can be achieved.

Proof

Firstly, we will show that $m_{0}>0$. Indeed, for every $u\in \mathbb{M}_{0}$, we have $u\in \mathbb{N}_{0}$ and $\langle \varphi '(u),u\rangle =0$. Then by $(h_{1})$–$(h_{2})$ and Propositions 2.1 and 2.2 we get

$$\begin{aligned}& \begin{aligned} &\varepsilon c_{p}^{p} \Vert u \Vert ^{p}+C_{\varepsilon }c_{r}^{r} \Vert u \Vert ^{r} \\ &\quad \geq\varepsilon \vert u \vert _{p}^{p}+C_{\varepsilon } \vert u \vert _{r}^{r} \\ &\quad \geq \int _{\varOmega }f(x,u)u\,dx \\ &\quad = \int _{\varOmega }\bigl( \vert \nabla u \vert ^{p}+a(x) \vert \nabla u \vert ^{q}\bigr)\,dx \\ &\quad \geq\textstyle\begin{cases} \Vert u \Vert ^{q}&\text{if } \Vert u \Vert < 1, \\ \Vert u \Vert ^{p}&\text{if } \Vert u \Vert >1. \end{cases}\displaystyle \end{aligned} \end{aligned}$$

Thus, for any $u\in \mathbb{N}_{0}$ with $\|u\|<1$, we have that

$$ \frac{1}{2} \Vert u \Vert ^{q}\leq C_{\varepsilon }c_{r}^{r} \Vert u \Vert ^{r}, $$

which implies that

$$ \Vert u \Vert \geq \biggl(\frac{1}{2C_{\varepsilon }c_{r}^{r}} \biggr)^{ \frac{1}{r-q}}=: \alpha _{0}. $$

Therefore we obtain that $m_{0}=\inf_{u\in \mathbb{M}_{0}} \varphi (u)\geq \alpha _{0}>0$.

It remains to prove that $u_{0}\in \mathbb{M}_{0}$ and $\varphi (u _{0})=m_{0}$. Let $\{u_{n}\}\subset \mathbb{M}_{0}$ be a sequence of functions such that $\varphi (u_{n})\rightarrow m_{0}$ as $n\rightarrow +\infty$. Firstly, we claim that $\{u_{n}\}$ is bounded. Suppose, by contradiction, that $\|u_{n}\|\rightarrow +\infty$ and let $v_{n}=\frac{u_{n}}{\|u_{n}\|}$. Without loss of generality, we may assume that $v_{n}\rightharpoonup v$ in E. By the Sobolev embedding theorem we have

$$ v_{n}\rightarrow v \quad \text{in } L^{\vartheta }( \varOmega ), 1\leq \vartheta < p^{*},\qquad v_{n} \rightarrow v \quad \text{a.e. on } \varOmega . $$

If $v=0$, then $v_{n}\rightarrow 0$ in $L^{\vartheta }( \varOmega )$ for $1\leq \vartheta < p^{*}$. Fix $R>[q(m_{0}+1)]^{ \frac{1}{p}}(>1)$. By $(h_{1})$–$(h_{2})$ there exists $C_{1}>0$ such that

$$ F(x,t)\leq \vert t \vert ^{p}+C_{1} \vert t \vert ^{r},\quad x\in \varOmega , t\in \mathbb{R}. $$

Then we have that

$$ \begin{aligned} \limsup_{n\rightarrow \infty } \int _{\varOmega }F(x,Rv_{n})\,dx \leq R^{p} \lim_{n\rightarrow \infty }\bigl( \vert v_{n} \vert _{p}^{p}+C_{1}R ^{r} \vert v_{n} \vert _{r}^{r}\bigr)=0. \end{aligned} $$

(20)

Let $t_{n}=\frac{R}{\|u_{n}\|}$. Hence by (20) and Corollary 3.3 we get that

$$\begin{aligned}& \begin{aligned} m_{0}+o(1)={} &\varphi (u_{n}) \\ \geq{}& \varphi (t_{n}u_{n}) \\ ={}&\varphi (Rv_{n}) \\ ={}& \int _{\varOmega }\biggl(\frac{1}{p}R^{p} \vert \nabla v_{n} \vert ^{p}+\frac{a(x)}{q}R ^{q} \vert \nabla v_{n} \vert ^{q} \biggr)\,dx- \int _{\varOmega }F(x,Rv_{n})\,dx \\ \geq {}& \frac{1}{q}R^{p}- \int _{\varOmega }F(x,Rv_{n})\,dx \\ \geq {}&\frac{1}{q}R^{p}+o(1) \\ >{}&m_{0}+1+o(1), \end{aligned} \end{aligned}$$

which yields a contradiction. Thus $v\neq 0$.

For $x\in \{y\in \mathbb{R}^{N}: v(y)\neq 0\}$, it is clear that $\lim_{n\rightarrow +\infty }|u_{n}(x)|=+\infty$. By hypotheses $(h_{1})$ and $(h_{2})$ we can find $C_{2}\in \mathbb{R}$ such that

$$ \begin{aligned} F(x,t)\geq C_{2},\quad (x,t)\in \varOmega \times \mathbb{R}. \end{aligned} $$

(21)

Hence by using (21), $(h_{3})$, Proposition 2.1, and Fatou’s lemma we have

$$\begin{aligned} 0 = &\lim_{n\rightarrow +\infty }\frac{m+o(1)}{ \Vert u_{n} \Vert ^{q}}= \lim _{n\rightarrow +\infty }\frac{\varphi (u_{n})}{ \Vert u_{n} \Vert ^{q}} \\ \leq &\lim_{n\rightarrow +\infty } \biggl[\frac{1}{p} \frac{ \int _{\varOmega }( \vert \nabla u_{n} \vert ^{p}+a(x) \vert \nabla u_{n} \vert ^{q})\,dx}{ \Vert u_{n} \Vert ^{q}}- \int _{\varOmega }\frac{F(x,u_{n})}{ \Vert u_{n} \Vert ^{q}}\,dx \biggr] \\ \leq &\frac{1}{p}-\lim_{n\rightarrow +\infty } \int _{\varOmega }\frac{F(x,u _{n})}{ \Vert u_{n} \Vert ^{q}}\,dx \\ =&\frac{1}{p}-\lim_{n\rightarrow +\infty } \int _{\varOmega }\frac{F(x,u_{n})-C_{2}}{ \Vert u_{n} \Vert ^{q}}\,dx \\ \leq &\frac{1}{p}-\liminf_{n\rightarrow +\infty } \int _{\varOmega }\frac{F(x,u_{n})-C_{2}}{ \Vert u_{n} \Vert ^{q}}\,dx \\ =&\frac{1}{p}-\liminf_{n\rightarrow +\infty } \int _{\varOmega }\frac{F(x,u_{n})}{ \Vert u_{n} \Vert ^{q}}\,dx \\ \leq &\frac{1}{p}- \int _{\varOmega }\liminf_{n\rightarrow +\infty } \frac{F(x,u_{n}(x))}{ \vert u _{n}(x) \vert ^{q}} \bigl\vert v_{n}(x) \bigr\vert ^{q}\,dx \\ =&-\infty . \end{aligned}$$

This contradiction shows that $\{u_{n}\}$ is bounded in E. Going if necessary to a subsequence, we can assume that $u_{n}^{\pm }\rightharpoonup u_{0}^{\pm }$ in E. Then $u_{n}^{\pm }\rightarrow u_{0}^{\pm }$ in $L^{\vartheta }(\varOmega )$ for $\vartheta \in [1,p^{*})$ and $u_{n}\rightarrow u_{0}$ a.e. on Ω.

Our next goal is to prove that $u_{0}\in \mathbb{M}_{0}$ and $\varphi (u_{0})=m_{0}$. Firstly, we claim that $\inf_{u\in \mathbb{N}_{0}}\varphi (u)>0$. Indeed, for every $u\in \mathbb{N}_{0}$, we have $\langle \varphi '(u),u\rangle =0$. Then by $(h_{1})$, $(h_{2})$, and Propositions 2.1 and 2.2 we get

$$\begin{aligned}& \varepsilon c_{p}^{p} \Vert u \Vert ^{p}+C_{\varepsilon }c_{r}^{r} \Vert u \Vert ^{r} \\& \quad \geq \varepsilon \vert u \vert _{p}^{p}+C_{\varepsilon } \vert u \vert _{r}^{r} \\& \quad \geq \int _{\varOmega }f(x,u)u\,dx \\& \quad = \int _{\varOmega }\bigl( \vert \nabla u \vert ^{p}+a(x) \vert \nabla u \vert ^{q}\bigr)\,dx \\& \quad \geq \textstyle\begin{cases} \Vert u \Vert ^{q}&\text{if } \Vert u \Vert < 1, \\ \Vert u \Vert ^{p}&\text{if } \Vert u \Vert >1. \end{cases}\displaystyle \end{aligned}$$

Thus, for any $u\in \mathbb{N}_{0}$ with $\|u\|<1$, we have that

$$ \frac{1}{2} \Vert u \Vert ^{q}\leq C_{\varepsilon }c_{r}^{r} \Vert u \Vert ^{r}, $$

which implies that $\|u\|\geq \alpha _{0}$. This implies that $\inf_{u\in \mathbb{N}_{0}}\varphi (u)>0$. Note that $\{u_{n}\}_{n\in N}\subset \mathbb{M}_{0}$. Then it is obvious that $\{u_{n}^{\pm }\}_{n\in N}\subset \mathbb{N}_{0}$, that is,

$$ \begin{aligned} \int _{\varOmega }\bigl( \bigl\vert \nabla u_{n}^{\pm } \bigr\vert ^{p}+a(x) \bigl\vert \nabla u_{n}^{\pm } \bigr\vert ^{q}\bigr)\,dx= \int _{\varOmega }f\bigl(x,u_{n}^{\pm } \bigr)u_{n}^{\pm }\,dx \quad \text{and}\quad \bigl\Vert u_{n} ^{\pm } \bigr\Vert \geq \alpha _{0}. \end{aligned} $$

By $(h_{1})$ and $(h_{2})$, for any $\varepsilon > 0$, there exists $C_{\varepsilon }> 0$ such that

$$ \begin{aligned} \bigl\vert f(x,t) \bigr\vert \leq \varepsilon \vert t \vert ^{p-1}+C_{\varepsilon } \vert t \vert ^{r-1} \end{aligned} $$

(22)

for all $(x,t)\in \varOmega \times \mathbb{R}$, where $r\in [1,p^{*})$ was given in $(h_{2})$. Thus

$$\begin{aligned}& \min \bigl\{ \alpha _{0}^{p}, \alpha _{0}^{q}\bigr\} \\& \quad \leq \min \bigl\{ \bigl\Vert u_{n}^{ \pm } \bigr\Vert ^{p}, \bigl\Vert u_{n}^{\pm } \bigr\Vert ^{q}\bigr\} \\& \quad \leq \int _{\varOmega }\bigl( \bigl\vert \nabla u _{n}^{\pm } \bigr\vert ^{p}+a(x) \bigl\vert \nabla u_{n}^{\pm } \bigr\vert ^{q}\bigr)\,dx \\& \quad = \int _{\varOmega }f\bigl(x,u _{n}^{\pm } \bigr)u_{n}^{\pm }\,dx \\& \quad \leq \varepsilon \int _{\varOmega } \bigl\vert u_{n} ^{\pm } \bigr\vert ^{p}\,dx+C_{\varepsilon } \int _{\varOmega } \bigl\vert u_{n}^{\pm } \bigr\vert ^{r}\,dx. \end{aligned}$$

(23)

Because of the boundedness of $u_{n}$, there is $C_{1}>0$ such that

$$\begin{aligned}& \min \bigl\{ \alpha _{0}^{p},\alpha _{0}^{q}\bigr\} \leq \varepsilon C_{1}+C_{ \varepsilon } \int _{\varOmega } \bigl\vert u_{n}^{\pm } \bigr\vert ^{r}\,dx. \end{aligned}$$

Choosing $\varepsilon =\frac{\min \{\alpha _{0}^{p},\alpha _{0}^{q}\}}{2C _{1}}$, we get

$$\begin{aligned}& \int _{\varOmega } \bigl\vert u_{n}^{\pm } \bigr\vert ^{r}\,dx\geq \frac{\min \{\alpha _{0}^{p}, \alpha _{0}^{q}\}}{2C_{\varepsilon }}. \end{aligned}$$

By the compactness of the embedding $E\hookrightarrow L^{r}(\varOmega )$ for $p< q< r< p^{*}$ we get

$$\begin{aligned}& \int _{\varOmega } \bigl\vert u_{0}^{\pm } \bigr\vert ^{r}\,dx\geq \frac{\min \{\alpha _{0}^{p}, \alpha _{0}^{q}\}}{2C_{\varepsilon }}, \end{aligned}$$

which yields $u_{0}^{\pm }\neq 0$. Moreover, note that $u_{n}^{\pm } \rightarrow u_{0}^{\pm }$ in $L^{\vartheta }(\varOmega )$, $\vartheta \in [1,p^{*})$. By conditions $(h_{1})$ and $(h_{2})$, combined with the Hölder inequality and Lebesgue theorem, we have

$$ \begin{aligned} &\lim_{n\rightarrow +\infty } \int _{\varOmega }f\bigl(x,u_{n}^{\pm }\bigr)u _{n}^{\pm }\,dx= \int _{\varOmega }f\bigl(x,u_{0}^{\pm } \bigr)u_{0}^{\pm }\,dx, \\ & \lim_{n\rightarrow +\infty } \int _{\varOmega }F\bigl(x,u_{n}^{\pm }\bigr) \,dx= \int _{\varOmega }F\bigl(x,u_{0}^{\pm }\bigr) \,dx.\end{aligned} $$

(24)

Hence by the weak lower semicontinuity of the norm we conclude that

$$\begin{aligned} \bigl\langle \varphi '(u_{0}), u_{0}^{\pm }\bigr\rangle = & \int _{\varOmega }\bigl( \bigl\vert \nabla u_{0}^{\pm } \bigr\vert ^{p}+a(x) \bigl\vert \nabla u_{0}^{\pm } \bigr\vert ^{q}\bigr)\,dx- \int _{ \varOmega }f\bigl(x,u_{0}^{\pm } \bigr)u_{0}^{\pm }\,dx \\ \leq &\liminf_{n\rightarrow +\infty } \int _{\varOmega }\bigl( \bigl\vert \nabla u_{n}^{\pm } \bigr\vert ^{p}+a(x) \bigl\vert \nabla u_{n}^{\pm } \bigr\vert ^{q}\bigr)\,dx \\ &{}-\lim_{n\rightarrow +\infty } \int _{\varOmega }f\bigl(x,u_{n}^{\pm } \bigr)u_{n}^{\pm }\,dx \\ =&\liminf_{n\rightarrow +\infty }\bigl\langle \varphi '(u_{n}), u_{n}^{ \pm }\bigr\rangle =0, \end{aligned}$$

(25)

because $u_{n}^{\pm }\in \mathbb{N}_{0}$. Thus by Lemma 3.4 there exist $s_{0}, t_{0}>0$ such that $s_{0}u_{0}^{+}+t_{0}u_{0}^{-} \in \mathbb{M}_{0}$. Consequently, from (24) and Lemma 3.1 we have

$$\begin{aligned} m_{0} = & \lim_{n\rightarrow +\infty } \biggl[\varphi (u_{n})- \frac{1}{q}\bigl\langle \varphi '(u_{n}), u_{n}\bigr\rangle \biggr] \\ =&\lim_{n\rightarrow +\infty } \int _{\varOmega } \biggl(\frac{1}{p}- \frac{1}{q} \biggr) \vert \nabla u_{n} \vert ^{p}\,dx+\lim_{n\rightarrow + \infty } \int _{\varOmega } \biggl[\frac{1}{q}f(x,u_{n})u_{n}-F(x,u_{n}) \biggr]\,dx \\ \geq &\liminf_{n\rightarrow +\infty } \int _{\varOmega } \biggl(\frac{1}{p}-\frac{1}{q} \biggr) \vert \nabla u_{n} \vert ^{p}\,dx+\lim _{n\rightarrow +\infty } \int _{\varOmega } \biggl[\frac{1}{q}f(x,u _{n})u_{n}-F(x,u_{n}) \biggr]\,dx \\ \geq & \int _{\varOmega } \biggl(\frac{1}{p}- \frac{1}{q} \biggr) \vert \nabla u_{0} \vert ^{p}\,dx+ \int _{\varOmega } \biggl[\frac{1}{q}f(x,u _{0})u_{0}-F(x,u_{0}) \biggr]\,dx \\ =&\varphi (u_{0})-\frac{1}{q}\bigl\langle \varphi '(u_{0}), u_{0}\bigr\rangle \\ \geq &\varphi \bigl(s_{0}u_{0}^{+}+t_{0}u _{0}^{-}\bigr)+\frac{1-s_{0}^{q}}{q}\bigl\langle \varphi '(u_{0}),u_{0}^{+} \bigr\rangle +\frac{1-t_{0}^{q}}{q}\bigl\langle \varphi '(u_{0}),u_{0}^{-} \bigr\rangle \\ &{}-\frac{1}{q}\bigl\langle \varphi '(u_{0}), u_{0}\bigr\rangle \\ =& \varphi \bigl(s_{0}u_{0}^{+}+t_{0}u_{0}^{-} \bigr)-\frac{s_{0}^{q}}{q}\bigl\langle \varphi '(u_{0}),u_{0}^{+} \bigr\rangle -\frac{t_{0}^{q}}{q}\bigl\langle \varphi '(u_{0}),u_{0}^{-} \bigr\rangle \\ \geq &m_{0}-\frac{s_{0}^{q}}{q}\bigl\langle \varphi '(u_{0}),u_{0}^{+}\bigr\rangle -\frac{t_{0}^{q}}{q}\bigl\langle \varphi '(u_{0}),u_{0}^{-} \bigr\rangle . \end{aligned}$$

This shows that

$$ \frac{s_{0}^{q}}{q}\bigl\langle \varphi '(u_{0}),u_{0}^{+} \bigr\rangle +\frac{t _{0}^{q}}{q}\bigl\langle \varphi '(u_{0}),u_{0}^{-} \bigr\rangle \geq 0. $$

From this and from (25) we conclude that

$$ \bigl\langle \varphi '(u_{0}),u_{0}^{\pm } \bigr\rangle =0 \quad \text{and}\quad \varphi (u_{0})=m_{0}. $$

 □

Similarly to the proof of [1, Theorem 1.4], we can prove the following lemma.

Lemma 3.7

Assume that$(h_{1})$–$(h_{3})$and$(h_{4})'$hold. If$u_{0}\in \mathbb{M}_{0}$and$\varphi (u_{0})=m_{0}$, then$u_{0}$is a critical point ofφ.

Proof

It is clear that $\langle \varphi '(u_{0}^{\pm }),u _{0}^{\pm }\rangle =0=\langle \varphi '(u_{0}),u_{0}^{\pm }\rangle$. It follows from assumption $(h_{4})'$ that, for $0< s\neq 1$ and $0< t\neq 1$,

$$\begin{aligned} \varphi \bigl(su_{0}^{+}+tu_{0}^{-} \bigr) = &\varphi \bigl(su_{0}^{+}\bigr)+\varphi \bigl(tu_{0} ^{-}\bigr) \\ < &\varphi \bigl(u_{0}^{+}\bigr)+\varphi \bigl(u_{0}^{-}\bigr) \\ =&\varphi (u_{0})= m_{0}. \end{aligned}$$

(26)

If $\varphi '(u_{0})\neq 0$, then there exist $\delta >0$ and $\nu >0$ such that

$$ \Vert v-u_{0} \Vert \leq 3\delta \quad \Rightarrow \quad \bigl\Vert \varphi '(v) \bigr\Vert \geq \nu . $$

Let $D=(\frac{1}{2},\frac{3}{2})\times (\frac{1}{2},\frac{3}{2})$ and $g(s,t)=su_{0}^{+}+tu_{0}^{-}$. By (26) we have

$$ \begin{aligned} \beta =\max_{(s,t)\in \partial D} \varphi \bigl(g(s,t)\bigr)< m_{0}. \end{aligned} $$

(27)

Let $\varepsilon :=\min \{\frac{m_{0}-\beta }{4},\frac{\lambda \delta }{8}\}$ and $B(u,\delta ):=\{v\in E:\|v-u\|\leq \delta \}$. Then [17, Lemma 2.3] yields a deformation η such that

• (a) $\eta (1,v)=v$ if $\varphi (v)< m_{0}-2\varepsilon$ or $\varphi (v)>m _{0}+2\varepsilon$,

• (b) $\eta (1,\varphi ^{m_{0}+\varepsilon }\cap B(u,\delta ))\subset \varphi ^{m_{0}-\varepsilon }$, and

• (c) $\varphi (\eta (1,v))\leq \varphi (v)$ for all $v\in E$,

where $\varphi ^{m_{0}\pm \varepsilon }:=\{v\in E: \varphi (v)\leq m _{0}\pm \varepsilon \}$.

It is easy to see that

$$ \max_{(s,t)\in D}\varphi \bigl(\eta \bigl(1,g(s,t)\bigr) \bigr)< m_{0}. $$

Next, we show that $\eta (1,g(D))\cap \mathbb{M}_{0}\neq \emptyset$, contradicting the definition of $m_{0}$. Let $h(s,t)=\eta (1,g(s,t))$, $\varphi _{0}(s,t)=\langle \varphi '(su_{0}^{+})u_{0}^{+}, \varphi '(su _{0}^{-})u_{0}^{-}\rangle$, and $\varphi _{1}(s,t)=\langle \frac{1}{s}\varphi '(h^{+}(s,t)), \frac{1}{t}\varphi '(h^{-}(s,t)) \rangle$. Note that

$$\begin{aligned}& \bigl\langle \varphi '\bigl(tu_{0}^{\pm } \bigr), u_{0}^{\pm }\bigr\rangle >0 \quad \text{if } 0< t< 1, \\& \bigl\langle \varphi '\bigl(tu_{0}^{\pm } \bigr), u_{0}^{ \pm }\bigr\rangle < 0 \quad \text{if } t>1. \end{aligned}$$

Hence we have that $\deg (\varphi _{0}, D, 0)=1$. On the other hand, using (27) and property (a) of η, we have that $g=h$ on ∂D. Hence $\varphi _{1}=\varphi _{0}$ on ∂D and $\deg (\varphi _{1}, D, 0)=\deg (\varphi _{0}, D, 0)=1$. This show that $\varphi _{1}(s,t)=0$ for some $(s,t)\in D$, and so $\eta (1,g(s,t))=h(s,t) \in \mathbb{M}_{0}$. Therefore $u_{0}$ is a critical point of φ. □

4 Sign-changing solutions

For any $\lambda >0$, let $f_{\lambda }(x,t)=f(x,t)+\lambda r|t|^{r-2}t$ and

$$ \varphi _{\lambda }(u)=\varphi (u)-\lambda \vert u \vert _{r}^{r},\quad u\in E. $$

Similarly, we define

$$\begin{aligned}& \mathbb{M}_{\lambda }:=\bigl\{ u\in E: u^{\pm }\neq 0, \bigl\langle \varphi _{\lambda }'(u),u^{+}\bigr\rangle =\bigl\langle \varphi _{\lambda }'(u),u ^{-}\bigr\rangle =0\bigr\} , \\& \mathbb{N}_{\lambda }:=\bigl\{ u\in E: u\neq 0, \bigl\langle \varphi _{\lambda }'(u),u \bigr\rangle =0\bigr\} , \end{aligned}$$

and

$$ m_{\lambda }:=\inf_{u\in \mathbb{M}_{\lambda }}\varphi _{\lambda }(u), \quad n_{\lambda }:=\inf_{u\in \mathbb{N}_{\lambda }} \varphi _{\lambda }(u). $$

Lemma 4.1

Assume that$(h_{1})$–$(h_{4})$hold. Then there exists a constant$\alpha >0$, which does not depend on$\lambda \in (0,1]$, such that

$$ \varphi _{\lambda }(u)\geq \alpha ,\quad u\in \mathbb{N}_{\lambda }, \lambda \in (0,1]. $$

Proof

For any $\varepsilon >0$, by $(h_{1})$, $(h_{2})$, and Propositions 2.1 and 2.2, for any $\lambda \in (0,1]$ and $u\in \mathbb{N}_{\lambda }$, we have

$$\begin{aligned}& \varepsilon c_{p}^{p} \Vert u \Vert ^{p}+(C_{\varepsilon }+1) c_{r}^{r} \Vert u \Vert ^{r} \\& \quad \geq \varepsilon \vert u \vert _{p}^{p}+(C_{\varepsilon }+1) \vert u \vert _{r}^{r} \\& \quad \geq \int _{\varOmega }f_{\lambda }(x,u)u\,dx \\& \quad = \int _{\varOmega }\bigl( \vert \nabla u \vert ^{p}+a(x) \vert \nabla u \vert ^{q}\bigr)\,dx \\& \quad \geq \textstyle\begin{cases} \Vert u \Vert ^{q}&\text{if } \Vert u \Vert < 1, \\ \Vert u \Vert ^{p}&\text{if } \Vert u \Vert >1. \end{cases}\displaystyle \end{aligned}$$

Thus for any $u\in \mathbb{N}_{\lambda }$ with $\|u\|<1$, we have that

$$ \frac{1}{2} \Vert u \Vert ^{q}\leq (C_{\varepsilon }+1) c_{r}^{r} \Vert u \Vert ^{r}, $$

which implies that

$$ \Vert u \Vert \geq \biggl(\frac{1}{2(C_{\varepsilon }+1) c_{r}^{r}} \biggr)^{ \frac{1}{r-q}}. $$

The proof is completed. □

Now we are ready to prove Theorem 1.1.

Proof of Theorem 1.1

Clearly, for every $\lambda >0$, $f_{\lambda }$ satisfies conditions $(h_{1})$–$(h_{3})$ and $(h_{4})'$, and Lemmas 3.6 and 3.7 imply that there exists $u_{\lambda }\in \mathbb{M}_{\lambda }$ such that

$$ \begin{aligned} \varphi _{\lambda }(u_{\lambda })=m_{\lambda } \quad \text{and}\quad \varphi _{\lambda }'(u_{\lambda })=0. \end{aligned} $$

(28)

Furthermore, under assumptions $(h_{1})$–$(h_{3})$, we easily obtain that $\mathbb{M}_{0}\neq \emptyset$. Let $v_{0}\in \mathbb{M}_{0}$. Then $\varphi (v_{0}):=\kappa >0$ and $\langle \varphi '(v_{0}),v_{0} ^{\pm }\rangle =0$. Therefore by Lemma 3.4 there exist $s_{\lambda }>0$ and $t_{\lambda }>0$ such that $s_{\lambda }v_{0} ^{+}+t_{\lambda }v_{0}^{-}\in \mathbb{M}_{\lambda }$. Then from Corollary 3.2 and Lemma 4.1 we have

$$ \begin{aligned}[b] \kappa &=\varphi (v_{0}) \\ &\geq \varphi \bigl(s_{\lambda }v_{0}^{+}+t_{ \lambda }v_{0}^{-} \bigr) \\ &\geq\varphi _{\lambda }\bigl(s_{\lambda }v_{0}^{+}+t _{\lambda }v_{0}^{-}\bigr) \\ &\geq m_{\lambda }\geq c_{*},\quad \lambda \in (0,1). \end{aligned} $$

(29)

Hence, we can choose a sequence $\{\lambda _{n}\}$ such that $\lambda _{n}\rightarrow 0$ as $n\rightarrow +\infty$ and

$$ \begin{aligned} u_{\lambda _{n}}\in \mathbb{M}_{\lambda _{n}},\qquad \varphi _{\lambda _{n}}(u _{\lambda _{n}})=m_{\lambda _{n}}\rightarrow \overline{m}, \qquad \varphi '_{ \lambda _{n}}(u_{\lambda _{n}})=0. \end{aligned} $$

(30)

Thus we only need to prove the following claims to complete the proof of Theorem 1.1.

Claim 1

$\{u_{\lambda _{n}}\}$is bounded inE.

Arguing by contradiction, suppose that $\|u_{\lambda _{n}}\|\rightarrow +\infty$ as $n\rightarrow +\infty$. We define the sequence $v_{n} =\frac{u_{\lambda _{n}}}{\|u_{\lambda _{n}}\|}$, $n=1,2,\dots$. It is clear that $\{v_{n}\}\subset E$ and $\|v_{n}\|=1$ for any $n\in N$. Therefore, going if necessary to a subsequence, we may assume that

$$ \begin{aligned} & v_{n}\rightharpoonup v \quad \text{in } E, \\ & v_{n}\rightarrow v \quad \text{in } L^{\vartheta }( \varOmega ), 1\leq \vartheta < p^{*}, \\ & v _{n}(x)\rightarrow v(x) \quad \text{a.e. on } \varOmega . \end{aligned} $$

(31)

If $v=0$, then $v_{n}\rightarrow 0$ in $L^{\vartheta }(\varOmega )$ for $1\leq \vartheta < p^{*}$. Fix $R>[q(m_{0}+1)]^{\frac{1}{p}}$. Using conditions $(h_{1})$–$(h_{2})$ and the Lebesgue dominated convergence theorem, we deduce that

$$ \begin{aligned} \limsup_{n\rightarrow \infty } \int _{\varOmega }F(x,Rv_{n})\,dx \leq R^{p} \lim_{n\rightarrow \infty }\bigl( \vert v_{n} \vert _{p}^{p}+C_{3}R ^{r} \vert v_{n} \vert _{r}^{r}\bigr)=0 \end{aligned} $$

(32)

for some constant $C_{3}>0$.

Let $t_{n}=\frac{R}{\|u_{n}\|}$. Then by (32) and Corollary 3.3 we get that

$$\begin{aligned} m_{\lambda _{n}} = &\varphi _{\lambda _{n}}(u_{\lambda _{n}}) \geq \varphi _{\lambda _{n}}(t_{n}u_{\lambda _{n}})=\varphi _{\lambda _{n}}(Rv _{n}) \\ =& \int _{\varOmega }\biggl(\frac{1}{p}R^{p} \vert \nabla v_{n} \vert ^{p}+ \frac{a(x)}{q}R^{q} \vert \nabla v_{n} \vert ^{q}\biggr)\,dx \\ &{}- \int _{\varOmega }\bigl(F(x,Rv_{n})+ \lambda _{n}R^{r} \vert v_{n} \vert ^{r}\bigr)\,dx \\ \geq &\frac{1}{q}R^{p}- \int _{\varOmega }\bigl(F(x,Rv_{n})+\lambda _{n}R^{r} \vert v_{n} \vert ^{r}\bigr)\,dx \\ =&\frac{1}{q}R^{p}+o(1)>m _{0}+1+o(1), \end{aligned}$$

which yields a contradiction. Thus $v\neq 0$.

By $(h_{3})$ we get

$$ \lim_{k\rightarrow +\infty }\frac{F(x,u_{\lambda _{n}}(x))}{ \Vert u _{\lambda _{n}} \Vert ^{q}}=\lim_{k\rightarrow +\infty } \frac{F(x,u _{\lambda _{n}}(x))}{ \vert u_{\lambda _{n}}(x) \vert ^{q}} \bigl\vert v_{n}(x) \bigr\vert ^{q}=+\infty $$

for all $x\in \varOmega _{0}:=\{x\in \varOmega : v(x)\neq 0\}$. Therefore, using (21), (30), and Fatou’s lemma, we have

$$\begin{aligned} 0 \leq &\lim_{n\rightarrow \infty } \frac{\varphi _{\lambda _{n}}(u _{\lambda _{n}})}{ \Vert u_{\lambda _{n}} \Vert ^{q}} \\ \leq &\lim_{n\rightarrow \infty } \biggl[\frac{1}{p} \frac{\int _{\varOmega }( \vert \nabla u_{\lambda _{n}} \vert ^{p}+a(x) \vert \nabla u_{\lambda _{n}} \vert ^{q})\,dx}{ \Vert u _{n} \Vert ^{q}} \\ &{}- \int _{\varOmega }\frac{F(x,u_{\lambda _{n}})+\lambda _{n} \vert u _{\lambda _{n}} \vert ^{r}}{ \Vert u_{\lambda _{n}} \Vert ^{q}}\,dx \biggr] \\ \leq &\lim_{n\rightarrow \infty } \biggl[\frac{1}{p} \frac{\int _{\varOmega }( \vert \nabla u_{\lambda _{n}} \vert ^{p}+a(x) \vert \nabla u_{\lambda _{n}} \vert ^{q})\,dx}{ \Vert u _{\lambda _{n}} \Vert ^{q}}- \int _{\varOmega }\frac{F(x,u_{\lambda _{n}})}{ \Vert u _{\lambda _{n}} \Vert ^{q}}\,dx \biggr] \\ \leq &\frac{1}{p} -\lim_{n\rightarrow \infty } \int _{\varOmega }\frac{F(x,u_{\lambda _{n}})}{ \Vert u _{\lambda _{n}} \Vert ^{q}}\,dx \\ =&\frac{1}{p}-\lim_{n\rightarrow \infty } \int _{\varOmega }\frac{F(x,u_{\lambda _{n}})-C _{2}}{ \Vert u_{\lambda _{n}} \Vert ^{q}}\,dx \\ \leq &\frac{1}{p}-\liminf_{n\rightarrow \infty } \int _{\varOmega _{0}}\frac{F(x,u_{\lambda _{n}})-C_{2}}{ \Vert u_{\lambda _{n}} \Vert ^{q}}\,dx \\ =&\frac{1}{p}-\liminf_{n\rightarrow \infty } \int _{\varOmega _{0}}\frac{F(x,u_{\lambda _{n}}(x))}{ \vert u_{\lambda _{n}}(x) \vert ^{q}} \bigl\vert v_{n}(x) \bigr\vert ^{q}\,dx \\ \rightarrow &- \infty , \end{aligned}$$

(33)

which is contradiction. The proof of Claim 1 is complete. Thus there exist a subsequence of $\{\lambda _{n}\}$, still denoted by $\{\lambda _{n}\}$, and $u_{0}\in E$ such that

$$ u_{\lambda _{n}}\rightharpoonup u_{0} \quad \text{in } E. $$

Claim 2

$\varphi (u_{0})=m_{0}$and$\varphi '(u_{0})=0$.

By the Sobolev embedding theorem, $u_{\lambda _{n}}\rightarrow u_{0}$ in $L^{\vartheta }(\varOmega ), 1\leq \vartheta < p^{*}$, and $u_{\lambda _{n}}(x)\rightarrow u_{0}(x)$ a.e. on Ω. By $(h_{2})$ and the Hölder inequality it is easy to directly compute that

$$\begin{aligned}& \int _{\varOmega } \bigl\vert f(x,u_{\lambda _{n}}) \bigr\vert \vert u_{n}-u_{0} \vert \,dx \\& \quad \leq \int _{\varOmega }C\bigl(1+ \vert u_{\lambda _{n}} \vert ^{r-1}\bigr) \vert u_{n}-u_{0} \vert \,dx \\& \quad \leq C \int _{\varOmega } \vert u_{n} \vert ^{r-1} \vert u_{\lambda _{n}}-u_{0} \vert \,dx+C \int _{\varOmega } \vert u _{n}-u_{0} \vert \,dx \\& \quad \leq C \biggl( \int _{\varOmega } \vert u_{\lambda _{n}} \vert ^{(r-1)r'}\,dx \biggr)^{\frac{1}{r'}} \biggl( \int _{\varOmega } \vert u_{\lambda _{n}}-u_{0} \vert ^{r}\,dx \biggr)^{\frac{1}{r}} \\& \qquad {}+C \int _{\varOmega } \vert u_{\lambda _{n}}-u_{0} \vert \,dx \\& \quad =C \biggl( \int _{\varOmega } \vert u_{\lambda _{n}} \vert ^{r}\,dx \biggr)^{\frac{r-1}{r}} \biggl( \int _{\varOmega } \vert u_{\lambda _{n}}-u_{0} \vert ^{r}\,dx \biggr)^{\frac{1}{r}} +C \int _{\varOmega } \vert u_{\lambda _{n}}-u_{0} \vert \,dx \\& \quad =C \vert u_{\lambda _{n}} \vert _{r} ^{r-1} \vert u_{\lambda _{n}}-u_{0} \vert _{r}+C \vert u_{\lambda _{n}}-u_{0} \vert _{1} \\& \quad \rightarrow 0 \quad \text{as } n\rightarrow \infty , \end{aligned}$$

(34)

where $\frac{1}{r}+\frac{1}{r'}=1$. Then, using (30), (34), and $(h_{2})$, we deduce

$$\begin{aligned} \bigl\langle L(u_{\lambda _{n}})-L(u_{0}), u_{\lambda _{n}}-u_{0}\bigr\rangle =& \bigl\langle \varphi _{\lambda _{n}}'(u_{\lambda _{n}})-\varphi '(u_{0}), u _{\lambda _{n}}-u_{0}\bigr\rangle \\ &{}+ \int _{\varOmega } \bigl[f(x,u_{\lambda _{n}})+ \lambda _{n} r \vert u_{\lambda _{n}} \vert ^{r-2}u_{\lambda _{n}} \bigr](u_{\lambda _{n}}-u_{0})\,dx \\ &{}- \int _{\varOmega }f(x,u_{0}) (u_{\lambda _{n}}-u_{0}) \,dx \\ \rightarrow &0\quad \text{as } n\rightarrow +\infty . \end{aligned}$$

Since L is of type $(S)_{+}$, we see that

$$ u_{\lambda _{n}}\rightarrow u_{0} \quad \text{in } E, $$

(35)

and so $u_{\lambda _{n}}^{\pm }\rightarrow u_{0}^{\pm }$ in E. Thus from (30) it follows that $\varphi (u _{0})=\overline{m}$.

Moreover, by Proposition 2.3, (30), and (35) we get

$$\begin{aligned} \bigl\langle \varphi '(u_{0}), \eta \bigr\rangle =&\bigl\langle L(u_{0}),\eta \bigr\rangle - \int _{\varOmega }f(x,u_{0})\eta \,dx \\ =&\lim_{n\rightarrow + \infty } \biggl(\bigl\langle L(u_{\lambda _{n}}),\eta \bigr\rangle - \int _{\varOmega }\bigl[f(x,u _{\lambda _{n}})+\lambda _{n} r \vert u_{\lambda _{n}} \vert ^{r-2}u_{\lambda _{n}} \bigr] \eta \,dx \biggr) \\ =&\lim_{n\rightarrow +\infty }\bigl\langle \varphi _{\lambda _{n}}'(u_{\lambda _{n}}), \eta \bigr\rangle \\ =&0,\quad \eta \in E. \end{aligned}$$

(36)

This shows that $\varphi '(u_{0})=0$. Again from Lemma 4.1 and (35) we have

$$\begin{aligned}& \int _{\varOmega } \biggl[\frac{1}{q}f\bigl(x,u_{0}^{\pm } \bigr)u_{0}^{\pm }-F\bigl(x,u _{0}^{\pm } \bigr) \biggr]\,dx+ \int _{\varOmega } \biggl(\frac{1}{p}-\frac{1}{q} \biggr) \bigl\vert \nabla u_{0}^{\pm } \bigr\vert ^{p}\,dx \\& \quad =\lim_{n\rightarrow +\infty } \int _{\varOmega } \biggl[\frac{1}{q}f\bigl(x,u_{\lambda _{n}}^{\pm } \bigr)u_{\lambda _{n}}^{\pm }-F\bigl(x,u_{\lambda _{n}}^{\pm } \bigr) \biggr]\,dx \\& \qquad {}+\lim_{n\rightarrow +\infty } \int _{\varOmega } \biggl(\frac{1}{p}- \frac{1}{q} \biggr) \bigl\vert \nabla u_{\lambda _{n}}^{\pm } \bigr\vert ^{p}\,dx+\lim_{n\rightarrow +\infty } \frac{\lambda _{n}(r-q)}{q} \bigl\vert u_{\lambda _{n}}^{\pm } \bigr\vert _{r}^{r} \\& \quad =\lim_{n\rightarrow +\infty } \biggl[ \varphi _{\lambda _{n}} \bigl(u_{\lambda _{n}}^{\pm }\bigr)-\frac{1}{q}\bigl\langle \varphi _{\lambda _{n}}'\bigl(u_{\lambda _{n}}^{\pm } \bigr),u_{n}^{\pm }\bigr\rangle \biggr] \\& \quad =\lim_{n\rightarrow +\infty }\varphi _{\lambda _{n}}\bigl(u _{\lambda _{n}}^{\pm }\bigr) \\& \quad \geq \alpha >0. \end{aligned}$$

(37)

This, together with (6) ($t=0$), shows that $u_{0}^{\pm } \neq 0$. Therefore

$$ \varphi '(u_{0})=0, \quad u_{0}\in \mathbb{M}_{0}, \quad \text{and}\quad \varphi (u _{0})=\overline{m}\geq m_{0}. $$

Next, we will prove that $\varphi (u_{0})= m_{0}$. Let ε be any positive number. Since $m_{0}=\inf_{u\in \mathbb{M}_{0}} \varphi (u)$, there exists $v_{\varepsilon }\in \mathbb{M}_{0}$ such that $\varphi (v_{\varepsilon })< m_{0}+\varepsilon$. Then $(h_{3})$ implies that there exists $M_{\varepsilon }>1$ such that, for $s\geq M_{\varepsilon }$ or $t\geq M_{\varepsilon }$,

$$\begin{aligned} \varphi _{\lambda _{n}}\bigl(sv_{\varepsilon }^{+}+tv_{\varepsilon }^{-} \bigr) = & \int _{\varOmega }\biggl(\frac{s^{p}}{p} \bigl\vert \nabla v_{\varepsilon }^{+} \bigr\vert ^{p}+ \frac{s ^{q}}{q} \bigl\vert \nabla v_{\varepsilon }^{+} \bigr\vert ^{q}\biggr)\,dx- \int _{\varOmega }F\bigl(x,sv_{ \varepsilon }^{+}\bigr) \,dx \\ &{}-\lambda _{n}s^{r} \int _{\varOmega } \bigl\vert v_{\varepsilon }^{+} \bigr\vert ^{r}\,dx \\ &{}+ \int _{\varOmega }\biggl(\frac{t^{p}}{p} \bigl\vert \nabla v_{\varepsilon }^{-} \bigr\vert ^{p}+ \frac{t^{q}}{q} \bigl\vert \nabla v_{\varepsilon }^{-} \bigr\vert ^{q}\biggr)\,dx- \int _{\varOmega }F\bigl(x,tv_{\varepsilon }^{-}\bigr) \,dx \\ &{}-\lambda _{n}t^{r} \int _{\varOmega } \bigl\vert v_{\varepsilon }^{-} \bigr\vert ^{r}\,dx \\ \leq & \int _{\varOmega }\biggl(\frac{s ^{p}}{p} \bigl\vert \nabla v_{\varepsilon }^{+} \bigr\vert ^{p}+ \frac{s^{q}}{q} \bigl\vert \nabla v _{\varepsilon }^{+} \bigr\vert ^{q}\biggr)\,dx- \int _{\varOmega }F\bigl(x,sv_{\varepsilon }^{+}\bigr) \,dx \\ &{}+ \int _{\varOmega }\biggl(\frac{t^{p}}{p} \bigl\vert \nabla v_{\varepsilon }^{-} \bigr\vert ^{p}+ \frac{t ^{q}}{q} \bigl\vert \nabla v_{\varepsilon }^{-} \bigr\vert ^{q}\biggr)\,dx- \int _{\varOmega }F\bigl(x,tv_{ \varepsilon }^{-}\bigr) \,dx \\ < &0. \end{aligned}$$

(38)

In view of Lemma 3.4, there exists a pair $(s_{n},t_{n})$ of positive numbers such that $s_{n}v_{\varepsilon }^{+}+t_{n}v_{\varepsilon }^{-}\in \mathbb{M}_{\lambda _{n}}$, which, together with (38), implies $0< s_{n}$, $t_{n}< M_{\varepsilon }$. Thus from Lemma 3.1 and $\langle \varphi '(v_{\varepsilon }),v_{\varepsilon }^{\pm }\rangle =0$ we have

$$\begin{aligned} m_{0}+\varepsilon > &\varphi (v_{\varepsilon })= \varphi _{\lambda _{n}}(v _{\varepsilon })+\lambda _{n} \vert v_{\varepsilon } \vert _{r}^{r} \\ \geq & \varphi _{\lambda _{n}}\bigl(s_{n}v_{\varepsilon }^{+}+t_{n}v_{\varepsilon } ^{-}\bigr)+\frac{1-s_{n}^{q}}{q}\bigl\langle \varphi _{\lambda _{n}}'(v_{\varepsilon }),v_{\varepsilon }^{+} \bigr\rangle +\frac{1-t_{n}^{q}}{q}\bigl\langle \varphi _{\lambda _{n}}'(v_{\varepsilon }),v_{\varepsilon }^{-} \bigr\rangle \\ &{}+ \int _{\varOmega }g(s_{n}) \bigl\vert \nabla v_{\varepsilon }^{+} \bigr\vert ^{p}\,dx+ \int _{\varOmega }g(t_{n}) \bigl\vert \nabla v_{\varepsilon }^{-} \bigr\vert ^{p}\,dx \\ \geq & m _{\lambda _{n}}-\frac{1+K_{\varepsilon }^{q}}{q} \bigl\vert \bigl\langle \varphi _{\lambda _{n}}'(v_{\varepsilon }),v_{\varepsilon }^{+} \bigr\rangle \bigr\vert -\frac{1+K_{\varepsilon }^{q}}{q} \bigl\vert \bigl\langle \varphi _{\lambda _{n}}'(v _{\varepsilon }),v_{\varepsilon }^{-} \bigr\rangle \bigr\vert \\ =&m_{\lambda _{n}}-\frac{(1+K _{\varepsilon }^{q})r\lambda _{n}}{q} \bigl\vert v_{\varepsilon }^{+} \bigr\vert _{r}^{r}-\frac{(1+K _{\varepsilon }^{q})r\lambda _{n}}{q} \bigl\vert v_{\varepsilon }^{-} \bigr\vert _{r}^{r}, \end{aligned}$$

which yields

$$ \begin{aligned} \overline{m}=\lim _{n\rightarrow +\infty }m_{\lambda _{n}}\leq m _{0}+\varepsilon . \end{aligned} $$

(39)

Since $\varepsilon > 0$ is arbitrary, we have $\overline{m}\leq m_{0}$. Thus $\overline{m}= m_{0}$, that is, $\varphi (u_{0})=m_{0}$.

Now we show that $u_{0}$ has exactly two nodal domains. Let $u_{0}=u_{1}+u_{2}+u_{3}$, where

$$ \begin{aligned} &u_{1}\geq 0,\qquad u_{2}\leq 0, \qquad \varOmega _{1}\cap \varOmega _{2}=\emptyset , \\ &u _{1}|_{\varOmega \backslash (\varOmega _{1}\cup \varOmega _{2})}=u_{2}|_{\varOmega \backslash (\varOmega _{1}\cup \varOmega _{2})}=u_{3}|_{\varOmega _{1}\cup \varOmega _{2}}, \\ & \varOmega _{1}:=\bigl\{ x\in \varOmega | u_{1}(x)>0 \bigr\} ,\qquad \varOmega _{2}:=\bigl\{ x \in \varOmega | u_{1}(x)< 0\bigr\} , \end{aligned} $$

(40)

and $\varOmega _{i}$ ($i=1,2$) are connected open subsets of Ω.

Setting $v=u_{1}+u_{2}$, we see that $v^{+}=u_{1}$ and $v^{-}=u_{2}$, that is, $v^{\pm }\neq 0$. Noting that $\varphi '(u_{0})=0$, by a simple computation we have

$$ \begin{aligned} &\bigl\langle \varphi '(v), v^{+}\bigr\rangle =\bigl\langle \varphi '(v), v^{-} \bigr\rangle =0. \end{aligned} $$

(41)

By Lemma 3.1 and again by (40) and (41) we conclude that

$$\begin{aligned} m_{0} = &\varphi (u_{0})=\varphi (u_{0})-\frac{1}{q}\bigl\langle \varphi '(u _{0}), u_{0}\bigr\rangle \\ =&\varphi (v)+\varphi (u_{3})-\frac{1}{q} \bigl(\bigl\langle \varphi '(v), v\bigr\rangle +\bigl\langle \varphi '(u_{3}), u_{3} \bigr\rangle \bigr) \\ \geq & \sup_{s,t\geq 0} \biggl[\varphi \bigl(sv^{+}+tv ^{-}\bigr)+\frac{1-s^{q}}{q}\bigl\langle \varphi '(v),v^{+}\bigr\rangle +\frac{1-t ^{q}}{q}\bigl\langle \varphi '(v),v^{-}\bigr\rangle \\ &{}+ \int _{\varOmega }g(s) \bigl\vert \nabla v^{+} \bigr\vert ^{p}\,dx+ \int _{\varOmega }g(t) \bigl\vert \nabla v^{-} \bigr\vert ^{p}\,dx \biggr]+ \varphi (u_{3})- \frac{1}{q}\bigl\langle \varphi '(u_{3}), u_{3}\bigr\rangle \\ \geq & \sup_{s,t\geq 0}\varphi \bigl(sv^{+}+tv^{-} \bigr)+\varphi (u_{3})- \frac{1}{q}\bigl\langle \varphi '(u_{3}), u_{3}\bigr\rangle \\ \geq & m_{0}+ \int _{\varOmega } \biggl(\frac{1}{q}f(x,u_{3})u_{3}-F(x,u_{3}) \biggr)\,dx+ \biggl(\frac{1}{p}-\frac{1}{q} \biggr) \int _{\varOmega } \vert \nabla u_{3} \vert ^{p}\,dx \\ \geq & m_{0}+ \int _{\varOmega }\biggl(\frac{1}{q}f(x,u_{3})u_{3}-F(x,u_{3}) \biggr)\,dx, \end{aligned}$$

which, together with (3), shows that $u_{3}=0$. Therefore $u_{0}$ has exactly two nodal domains.  □

Proof of Theorem 1.2

By Theorem 1.1 there exists $u_{0}\in \mathbb{M}_{0}$ such that $\varphi (u_{0})=m_{0}$. Since $u_{0}^{\pm }\in \mathbb{N}_{0}$, we have $m_{0}=\varphi (u_{0})= \varphi (u_{0}^{+})+\varphi (u_{0}^{-})\geq 2n_{0}$. □