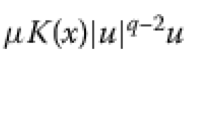1 Introduction

We are concerned with the following p-biharmonic equations:

$$ \Delta _{p}^{2} u+M \biggl( \int _{\mathbb{R}^{N}}\varPhi _{0}(x,\nabla u) \,dx \biggr) \operatorname{div}\bigl(\varphi (x,\nabla u)\bigr)+V(x) \vert u \vert ^{p-2}u=\lambda f(x,u) \quad \text{in } \mathbb{R}^{N}, $$
(P)

where \(2< 2p<N\), \(1< p< p_{*}:=\frac{Np}{N-2p}\), \(\Delta _{p} ^{2}u=\Delta (|\Delta u|^{p-2}\Delta u)\) is a p-biharmonic operator, the function \(\varphi (x,v)\) is of type \(\lvert v \rvert ^{p-2}v\), \(\varphi (x,v)=\frac{d}{dv}\varPhi _{0}(x,v)\), the potential function \(V:\mathbb{R}^{N}\to (0,\infty )\) is continuous, and \(f:\mathbb{R} ^{N}\times \mathbb{R} \to \mathbb{R}\) satisfies the Carathéodory condition.

The fourth-order differential equations arise in the study of deflections of elastic beams on nonlinear elastic foundations. Thus, they become very significant in engineering and physics. Many authors considered this type of equation in recent years, and we refer to [9, 13, 27] and the references therein. For this reason, the existence of solutions of p-biharmonic equations has been studied by several authors; see [6, 8, 12, 15, 21, 24, 30, 31, 34]. To obtain the existence and multiplicity results for the p-Laplace type operators, which generalize the usual p-Laplacian, the authors in [10, 28] considered the following condition:

$$ d \vert v \vert ^{p}\le \varphi (x,v)\cdot v \le p\varPhi _{0}(x,v) $$

for all \(x\in \mathbb{R}^{N}\) and \(v\in \mathbb{R}^{N}\), and for some positive constant d; see also [14]. On the other hand, Kirchhoff in [20] initially proposed the following equation:

$$ \rho \frac{\partial ^{2} u}{\partial t^{2}} - \biggl(\frac{\rho _{0}}{h} + \frac{E}{2L} \int _{0}^{L} \biggl\vert \frac{\partial u}{\partial x} \biggr\vert \,dx \biggr) \frac{\partial ^{2} u}{\partial x^{2}} = 0, $$

which is a generalization of the classical D’Alembert’s wave equation. Also, Woinowsky and Krieger [33] in the 1950s considered a stationary analogue of the evolution equation of Kirchhoff type, namely

$$ u_{tt} +\Delta ^{2}u - M\bigl( \Vert \nabla u \Vert ^{2}\bigr)\Delta u = f (x, u), $$

as a model for the deflection of an extensible beam on nonlinear foundations. Here, u denotes the displacement, f is the force that the foundations exert on the beam, and M models the effects of the small changes in the length of the beam (see, e.g., [3,4,5, 7] for the physics viewpoint model). In view of mathematics, many researchers have extensively studied the existence of weak solutions for the elliptic problem of Kirchhoff type in recent years (see, e.g., [11, 16, 18]). Based on these references, we consider the generalized elliptic equation (P) involving the p-biharmonic and generalized p-Laplacian of Kirchhoff type.

Since the seminal paper of Ambrosetti and Rabinowitz in [2], the existence of solutions for the elliptic problem has been studied by many researchers. A common feature of these works is that the following condition, which is originally due to Ambrosetti and Rabinowitz, is imposed on the nonlinearity f:

  1. (AR)

    There exist positive constants m and ζ such that \(\zeta >p\) and

    $$ 0< \zeta F(x,t)\le f(x,t)t \quad \text{for } x\in \varOmega \text{ and } \lvert t \rvert \ge m, $$

    where \(F(x,t)=\int _{0}^{t}f(x,s) \,ds\), and Ω is a bounded domain in \(\mathbb{R}^{N}\).

The (AR) condition above is somewhat natural and important to guarantee the boundedness of Palais–Smale sequence of Euler–Lagrange functional for an elliptic equation, however, this condition is very restrictive and eliminates many nonlinearities. Thus, many researchers have tried to drop the (AR) condition for elliptic equations associated with the p-Laplacian; see, e.g., [1, 23, 25, 26, 29].

The purpose of this paper is to study the existence of weak solutions for problem (P) without assuming the (AR) condition, but imposing various assumptions for the divergence part φ and nonlinear term f. In particular, as observed by Remark 1.8 in [23], there are many examples which do not fulfill the condition of the nonlinear term f given in [1, 25, 26]. On the other hand, in case of the whole space \(\mathbb{R}^{N}\), the main difficulty of this problem is the lack of compactness for the Sobolev theorem. In that sense, our study is to pursue two goals. First, we show the existence of nontrivial weak solutions for the problem above using the mountain pass theorem. To be precise, we prove the existence of weak solutions for problem (P) under Cerami condition, as a weak version of the Palais–Smale condition. Also, we try to do analysis using the properties of Kirchhoff function M and function φ. Second, we show the multiplicity of weak solutions to problem (P) via the fountain theorem. To the best of our knowledge, there were no such existence results for our problem in this situation.

2 Preliminaries

In this section, we briefly describe the framework for our problem. We assume that the potential \(V\in C(\mathbb{R}^{N})\) is a continuous function with

  1. (V)

    \(\inf_{x\in \mathbb{R}^{N}}V(x)>0\), and \(\operatorname{meas} \{x\in \mathbb{R}^{N}:V(x)\le K \}<+\infty \) for all \(K\in \mathbb{R}\).

Also, we set \(D^{p}(\mathbb{R}^{N}) = \{u\in L^{p_{*}}(\mathbb{R}^{N})| \Delta u \in L^{p}(\mathbb{R}^{N})\}\). Thus, we define the function space as follows:

$$ X= \biggl\{ u \in D^{p}\bigl(\mathbb{R}^{N}\bigr) : \int _{\mathbb{R}^{N}} \bigl( \lvert \Delta u \rvert ^{p}+ \vert \nabla u \vert ^{p} +V(x) \lvert u \rvert ^{p} \bigr) \,dx < + \infty \biggr\} $$

equipped with the norm

$$ \Vert u \Vert _{X}^{p}= \Vert \Delta u \Vert ^{p}_{L^{p}(\mathbb{R}^{N})}+ \Vert \nabla u \Vert ^{p}_{L^{p}(\mathbb{R}^{N})}+ \bigl\Vert V^{1/p}u \bigr\Vert ^{p}_{L^{p}( \mathbb{R}^{N})}. $$

For our problem, we first assume that \(M:\mathbb{R}^{+} \to \mathbb{R}^{+}\) satisfies the following conditions:

  1. (M1)

    \(M\in C(\mathbb{R}^{+})\) satisfies \(\inf_{t\in \mathbb{R}^{+}} M(t) \geq m_{0} > 0\), where \(m_{0}\) is a constant.

  2. (M2)

    There exists \(\theta \in [1,\frac{N}{N-p})\) such that \(\theta \mathcal{M}(t)=\theta \int _{0}^{t} M(\tau )\,d \tau \geq M(t)t \) for any \(t\geq 0\).

A typical example for M is given by \(M(t)=b_{0} +b_{1}t^{n}\) with \(n>0\), \(b_{0}>0\), and \(b_{1}\geq 0\).

Next, we assume that \(\varphi : \mathbb{R}^{N}\times \mathbb{R}^{N} \to \mathbb{R}^{N}\) is a continuous function with the continuous derivative with respect to v of the mapping \(\varPhi _{0}:\mathbb{R}^{N}\times \mathbb{R}^{N} \to \mathbb{R}\), \(\varPhi _{0}=\varPhi _{0}(x,v)\), that is, \(\varphi (x,v)=\frac{d}{dv}\varPhi _{0}(x,v)\). Suppose that φ and \(\varPhi _{0}\) satisfy the following assumptions:

  1. (J1)

    The equality

    $$ \varPhi _{0}(x,\mathbf{0})=0 $$

    holds for almost all \(x\in \mathbb{R}^{N}\).

  2. (J2)

    There are a nonnegative function \(a\in L^{p'}(\mathbb{R} ^{N})\) and a nonnegative constant b such that

    $$ \bigl\vert \varphi (x,v) \bigr\vert \le a(x)+b \vert v \vert ^{p-1} $$

    holds for almost all \(x\in \mathbb{R}^{N}\) and for all \(v\in \mathbb{R}^{N}\). Here, \(p'\) is a conjugate number of p.

  3. (J3)

    The relations

    $$ d \vert v \vert ^{p}\le \varphi (x,v)\cdot v\quad \text{and} \quad d \vert v \vert ^{p}\le p \varPhi _{0}(x,v) $$

    hold for all \(x\in \mathbb{R}^{N}\) and \(v\in \mathbb{R}^{N}\), where d is a positive constant.

  4. (J4)

    \(\varPhi _{0}(x,\cdot )\) is strictly convex in \(\mathbb{R} ^{N}\) for all \(x\in \mathbb{R}^{N}\).

  5. (J5)

    The relation

    $$ p\varPhi _{0}(x,v)-\varphi (x,v)\cdot v \ge 0 $$

    holds for all \(x\in \mathbb{R}^{N}\) and all \(v\in \mathbb{R}^{N}\).

Let us define the functional \(\varPhi : X \to \mathbb{R}\) by

$$ \varPhi (u)=\frac{1}{p} \int _{\mathbb{R}^{N}} \lvert \Delta u \rvert ^{p} \,dx+ \mathcal{M} \biggl( \int _{\mathbb{R}^{N}}\varPhi _{0}(x,\nabla u) \,dx \biggr)+ \frac{1}{p} \int _{\mathbb{R}^{N}}V(x) \lvert u \rvert ^{p} \,dx. $$

It is not difficult to prove that the functional \(\varPhi \in C^{1}(X, \mathbb{R})\), and its Fréchet derivative is given by

$$ \begin{aligned} \bigl\langle \varPhi ^{\prime }(u),v\bigr\rangle &= \int _{\mathbb{R}^{N}} \lvert \Delta u \rvert ^{p-2} \Delta u \Delta v \,dx+M \biggl( \int _{\mathbb{R}^{N}}\varPhi _{0}(x, \nabla u) \,dx \biggr) \int _{\mathbb{R}^{N}}\varphi (x,\nabla u)\cdot \nabla v \,dx\\ &\quad {}+ \int _{\mathbb{R}^{N}}V(x) \lvert u \rvert ^{p-2}uv \,dx. \end{aligned} $$

We give some examples satisfying assumptions (J1)–(J5).

Example 2.1

  1. (1)

    Let us consider the following functions:

    $$ \varphi (x,v)= \lvert v \rvert ^{p-2}v \quad \text{and} \quad \varPhi _{0}(x,v)=\frac{ \lvert v \rvert ^{p}}{p} $$

    for \(v\in \mathbb{R}^{N}\) and \(x\in \mathbb{R}^{N}\). Then it is obvious that assumptions (J1)–(J5) hold.

  2. (2)

    Suppose that \(a\in L^{2p'}(\mathbb{R}^{N})\), and there is a positive constant \(a_{0}\) such that \(a(x)\ge a_{0}\) for almost all \(x\in \mathbb{R}^{N}\). We consider

    $$ \varphi (x,t)= \bigl(a(x)+t^{2} \bigr)^{\frac{p-2}{2}}t \quad \text{and} \quad \varPhi _{0}(x,t)=\frac{1}{p} \bigl[ \bigl(a(x)+t^{2} \bigr)^{\frac{p}{2}}-a(x)^{\frac{p}{2}} \bigr] $$

    for \(t\in \mathbb{R}\), where \(p\geq 2\) for all \(x\in \mathbb{R}^{N}\). Then assumptions (J1)–(J5) hold.

By analogous arguments as in [19, 22], the following lemma is easily checked, and thus we omit the proof. That is, the operator \(\varPhi ^{\prime }\) is a mapping of type \((S_{+})\).

Lemma 2.2

Assume that (V), (M1), (M2), and (J1)–(J4) hold. Then the functional \(\varPhi :X\to \mathbb{R}\) is convex and weakly lower semicontinuous on X. Moreover, the operator \(\varPhi ^{\prime }\) is a mapping of type \((S_{+})\), i.e., if \(u_{n}\rightharpoonup u\) in X and \(\limsup_{n\to \infty } \langle \varPhi ^{\prime }(u_{n})-\varPhi ^{ \prime }(u), u_{n}-u \rangle \le 0\), then \(u_{n}\to u\) in X as \(n\to \infty \).

Denoting \(F(x,t)=\int _{0}^{t}f(x,s) \,ds\), for the number θ given in (M2), we assume that

  1. (F1)

    \(f: \mathbb{R}^{N}\times \mathbb{R} \to \mathbb{R}\) satisfies the Carathéodory condition in the sense that \(f(\cdot ,t)\) is measurable for all \(t\in \mathbb{R}\) and \(f(x,\cdot )\) is continuous for almost all \(x\in \mathbb{R}^{N}\).

  2. (F2)

    There exist nonnegative functions \(\rho \in L^{q^{\prime }}(\mathbb{R}^{N})\cap L^{\infty }(\mathbb{R}^{N})\) and \(\sigma \in L^{ \infty }(\mathbb{R}^{N})\) such that

    $$ \bigl\lvert f(x,t) \bigr\rvert \le \rho (x)+\sigma (x) \lvert t \rvert ^{q-1},\quad q\in (\theta p,p_{*}) $$

    for all \((x,t)\in \mathbb{R}^{N}\times \mathbb{R}\).

  3. (F3)

    There exists \(\delta >0\) such that

    $$ F(x,t)\leq 0 \quad \text{for } x\in \mathbb{R}^{N} \text{ and } \lvert t \rvert < \delta . $$
  4. (F4)

    \(\lim_{ \lvert t \rvert \to \infty }{\frac{F(x,t)}{ \lvert t \rvert ^{\theta p}}}=\infty \) uniformly for almost all \(x\in \mathbb{R}^{N}\).

  5. (F5)

    There exist \(c_{0}\ge 0\), \(r_{0}\ge 0\), and \(\kappa > \frac{N}{p}\) such that

    $$ \bigl\lvert F(x,t) \bigr\rvert ^{\kappa }\le c_{0} \lvert t \rvert ^{\kappa p}{\mathfrak{F}}(x,t) $$

    for all \((x,t)\in \mathbb{R}^{N}\times \mathbb{R}\) and \(\lvert t \rvert \ge r_{0}\), where \({\mathfrak{F}}(x,t)=\frac{1}{\theta p}f(x,t)t-F(x,t) \ge 0\).

  6. (F6)

    There exist \(\mu >\theta p\) and \(\varrho >0\) such that

    $$ \mu F(x,t)\leq tf(x,t)+\varrho t^{p} $$

    for all \((x,t)\in \mathbb{R}^{N} \times \mathbb{R}\).

Next, we give some examples with respect to assumptions (F1)–(F6).

Since assumption (F5) is weaker than the following assumption, namely that

$$ \frac{f(x,t)}{ \lvert t \rvert ^{\theta -2}t} \quad \text{is increasing for $t> 0$ and decreasing for $t< 0$} $$
(2.1)

for any \(x\in \mathbb{R}^{N}\), we check that the following example satisfies assumption (F5) by applying condition (2.1).

Example 2.3

Let us consider

$$ f(x,t)= \lvert t \rvert ^{q-2}t\log { \bigl(1+ \lvert t \rvert \bigr)} $$

for all \(t\in \mathbb{R}\). It is clear that function f satisfies assumptions (F1)–(F4). Since the following ratio, namely

$$ \frac{f(x,t)}{ \lvert t \rvert ^{p-2}t}=\frac{ \lvert t \rvert ^{q-2}t\log { (1+ \lvert t \rvert )}}{ \lvert t \rvert ^{p-2}t}= \lvert t \rvert ^{q-p} \log { \bigl(1+ \lvert t \rvert \bigr)}, $$

is increasing for \(t> 0\) and decreasing for \(t< 0\) if \(q>p=\theta \), it follows that assumption (F5) holds.

The following example can be found in [23] for the case of p-Laplace operator.

Example 2.4

Consider the following function:

$$ f(x,t)= \lvert t \rvert ^{p-2}t\bigl(4 \lvert t \rvert ^{3}+2t \sin t-4 \cos t\bigr). $$

Then this function satisfies conditions (F2), (F6), but not the (AR) condition.

Define the functional \(\varPsi :X\to \mathbb{R}\) by

$$ \varPsi (u)= \int _{\mathbb{R}^{N}}F(x,u) \,dx. $$

Then it is easy to check that \(\varPsi \in C^{1}(X,\mathbb{R})\) and its Fréchet derivative is

$$ \bigl\langle \varPsi ^{\prime }(u),v \bigr\rangle = \int _{\mathbb{R}^{N}}f(x,u)v \,dx $$

for any \(u,v \in X\). Next we define the functional \(I_{\lambda }:X \to \mathbb{R}\) by

$$ I_{\lambda }(u)=\varPhi (u)-\lambda \varPsi (u). $$

Then it follows that the functional \(I_{\lambda }\in C^{1}(X,\mathbb{R})\) and its Fréchet derivative is

$$\begin{aligned} \bigl\langle I_{\lambda }^{\prime }(u),v \bigr\rangle &= \int _{\mathbb{R}^{N}} \lvert \Delta u \rvert ^{p-2} \Delta u \Delta v \,dx+M \biggl( \int _{\mathbb{R}^{N}}\varPhi _{0}(x,\nabla u) \,dx \biggr) \int _{\mathbb{R}^{N}}\varphi (x,\nabla u)\cdot \nabla v \,dx \\ &\quad{}+ \int _{\mathbb{R}^{N}}V(x) \lvert u \rvert ^{p-2}uv \,dx- \lambda \int _{\mathbb{R}^{N}}f(x,u)v \,dx \end{aligned}$$

for any \(u,v\in X\).

In our setting, first of all, we need the following lemma. Using a similar argument as in [17, Lemma 3.2], we can see that the functionals Ψ and \(\varPsi ^{\prime }\) are weakly strongly continuous on X. We give a detailed proof for the convenience of the reader.

Lemma 2.5

Assume that (V) and (F1)–(F2) hold. Then Ψ and \(\varPsi ^{\prime }\) are weakly strongly continuous on X.

Proof

See Appendix. □

3 Existence of weak solutions

Definition 3.1

We say that \(u\in X\) is a weak solution of problem (P) if

$$\begin{aligned} & \int _{\mathbb{R}^{N}} \lvert \Delta u \rvert ^{p-2}\Delta u \cdot \Delta v \,dx+M \biggl( \int _{\mathbb{R}^{N}}\varPhi _{0}(x,\nabla u) \,dx \biggr) \int _{\mathbb{R}^{N}}\varphi (x,\nabla u)\cdot \nabla v \,dx \\ &\quad {}+ \int _{\mathbb{R}^{N}}V(x) \lvert u \rvert ^{p-2}uv \,dx-\lambda \int _{\mathbb{R}^{N}}f(x,u) v \,dx=0 \end{aligned}$$

for any \(v\in X\).

The following result is used to show that the energy functional \(I_{\lambda }\) satisfies the geometric conditions of the mountain pass theorem.

Lemma 3.2

Assume that (V), (M1), (M2), (J1)–(J3), and (F1)–(F4) hold. Then the geometric conditions in the mountain pass theorem hold, i.e.,

  1. (1)

    \(u=0\) is a strict local minimum for \(I_{\lambda }(u)\),

  2. (2)

    \(I_{\lambda }(u)\) is unbounded from below on X.

Proof

By assumption (F3), \(u=0\) is a strict local minimum for \(I_{\lambda }(u)\). Next we claim that condition (2) holds. Assumption (F4) implies that for any \(K_{0}>0\), there exists a constant \(\delta >0\) such that

$$ F(x,t)\ge K_{0} \lvert t \rvert ^{\theta p} $$
(3.1)

for \(\lvert t \rvert >\delta \) and for almost all \(x \in \mathbb{R}^{N}\). Note that for \(t>1\), we can easily check that \(\mathcal{M}(t)\leq \mathcal{M}(1)t\). For any \(v\in X\setminus \{0 \}\), from assumptions (J2), (J3) and relation (3.1), we have

$$\begin{aligned} I_{\lambda }(tv) &=\frac{1}{p} \int _{\mathbb{R}^{N}} \lvert t\Delta v \rvert ^{p} \,dx+ \mathcal{M} \biggl( \int _{\mathbb{R}^{N}}\varPhi _{0}(x,t\nabla v) \,dx \biggr)\\ &\quad {}+ \frac{1}{p} \int _{\mathbb{R}^{N}}V(x) \lvert t \rvert ^{p} \lvert v \rvert ^{p} \,dx-\lambda \int _{\mathbb{R}^{N}}F(x,tv) \,dx \\ &\le \frac{1}{p} \int _{\mathbb{R}^{N}} \lvert t\Delta v \rvert ^{p} \,dx+ \mathcal{M}(1) \biggl( \int _{\mathbb{R}^{N}}\varPhi _{0}(x,t\nabla v) \,dx \biggr)^{\theta }\\ &\quad {}+\frac{1}{p} \int _{\mathbb{R}^{N}}V(x) \lvert t \rvert ^{p} \lvert v \rvert ^{p} \,dx-\lambda \int _{\mathbb{R}^{N}}F(x,tv) \,dx \\ &\le \frac{1}{p} \lvert t \rvert ^{p} \Vert v \Vert _{X}^{p}+ \mathcal{M}(1) \biggl( \int _{\mathbb{R}^{N}}a(x) \lvert t\nabla v \rvert + \frac{b}{p} \lvert t \nabla v \rvert ^{p} \,dx \biggr)^{ \theta }-\lambda \int _{\mathbb{R}^{N}}F(x,tv) \,dx \\ &\le \lvert t \rvert ^{\theta p} \biggl(\frac{1}{p} \Vert v \Vert _{X}^{p}+\mathcal{M}(1) \biggl( \int _{\mathbb{R}^{N}}a(x) \lvert \nabla v \rvert + \frac{b}{p} \lvert \nabla v \rvert ^{p} \,dx \biggr)^{ \theta }-\lambda K_{0} \int _{\mathbb{R}^{N}} \lvert v \rvert ^{\theta p} \,dx \biggr) \end{aligned}$$

for sufficiently large \(t>1\). If \(K_{0}\) is large enough, then we assert that \(I_{\lambda }(tv)\to -\infty \) as \(t \to \infty \). Hence we conclude that the functional \(I_{\lambda }\) is unbounded from below. This completes the proof. □

With the aid of Lemmas 2.2 and 2.5, we prove that the energy functional \(I_{\lambda }\) satisfies the Cerami condition \((C)_{c}\) condition, for short, i.e., for \(c\in \mathbb{R}\), any sequence \(\{u_{n} \}\subset X\) such that

$$ I_{\lambda }(u_{n})\to c \quad \text{and} \quad \bigl\Vert I_{\lambda }^{ \prime }(u_{n}) \bigr\Vert _{X^{*}}\bigl(1+ \Vert u_{n} \Vert _{X} \bigr)\to 0 \quad \text{as } n\to \infty $$

has a convergent subsequence. This plays a key role in obtaining the existence of a nontrivial weak solution for the given problem.

Lemma 3.3

Assume that (V), (M1), (M2), (J1)–(J5), and (F1)–(F5) hold. Then the functional \(I_{\lambda }\) satisfies the \((C)_{c}\) condition for any \(\lambda >0\).

Proof

For \(c\in \mathbb{R}\), let \(\{u_{n}\}\) be a \((C)_{c}\)-sequence in X, that is,

$$ I_{\lambda }(u_{n})\to c \quad \text{and} \quad \bigl\Vert I_{\lambda }^{ \prime }(u_{n}) \bigr\Vert _{X^{*}}\bigl(1+ \Vert u_{n} \Vert _{X}\bigr)\to 0 \quad \text{as } n\to \infty . $$
(3.2)

This says that

$$ c = I_{\lambda }(u_{n})+o(1)\quad \text{and} \quad \bigl\langle I_{ \lambda }^{\prime }(u_{n}), u_{n} \bigr\rangle =o(1), $$
(3.3)

where \(o(1)\to 0\) as \(n\to \infty \). It follows from Lemmas 2.2 and 2.5 that \(\varPhi ^{\prime }\) and \(\varPsi ^{\prime }\) are mappings of type \((S_{+})\). Since \(I_{\lambda }^{\prime }\) is of type \((S_{+})\) and X is reflexive, it suffices to prove that the sequence \(\{u_{n}\}\) is bounded in X. We argue by contradiction. Suppose that the sequence \(\{u_{n} \}\) is unbounded in X. Then we may assume that \(\|u_{n}\|_{X}>1\) and \(\|u_{n}\|_{X}\to \infty \) as \(n\to \infty \). Define a sequence \(\{w_{n} \}\) by \(w_{n}={u_{n}}/{\|u_{n}\|_{X}}\). It is clear that \(\{w_{n} \} \subset X\) and \(\|w_{n}\|_{X}=1\). Hence, up to a subsequence still denoted by \(\{w_{n} \}\), we obtain \(w_{n}\rightharpoonup w\) in X as \(n\to \infty \) and note that

$$ w_{n}(x) \to w(x)\quad \text{a.e. in } \mathbb{R}^{N} \quad \text{and} \quad w_{n} \to w\quad \text{in }L^{s}\bigl(\mathbb{R}^{N}\bigr) \text{ as } n \to \infty $$
(3.4)

for \(1< s<p_{*}\). According to assumptions (M1), (M2), (J3), and relation (3.3), we obtain that

$$\begin{aligned} c &=I_{\lambda }(u_{n})+o(1) \\ &=\frac{1}{p} \int _{\mathbb{R}^{N}} \lvert \Delta u_{n} \rvert ^{p} \,dx+\mathcal{M} \biggl( \int _{\mathbb{R}^{N}}\varPhi _{0}(x,\nabla u_{n}) \,dx \biggr) \\ &\quad {}+\frac{1}{p} \int _{\mathbb{R}^{N}}V(x) \lvert u_{n} \rvert ^{p} \,dx-\lambda \int _{\mathbb{R}^{N}}{F(x,u_{n})} \,dx+o(1) \\ &\geq \frac{1}{p} \int _{\mathbb{R}^{N}} \lvert \Delta u_{n} \rvert ^{p} \,dx+\frac{1}{\theta }M \biggl( \int _{\mathbb{R}^{N}}\varPhi _{0}(x,\nabla u_{n}) \,dx \biggr) \int _{\mathbb{R}^{N}}\varPhi _{0}(x,\nabla u_{n}) \,dx \\ & \quad{}+ \frac{1}{p} \int _{\mathbb{R}^{N}}V(x) \lvert u_{n} \rvert ^{p} \,dx-\lambda \int _{\mathbb{R}^{N}}{F(x,u_{n})} \,dx+o(1) \\ &\geq \frac{1}{p} \int _{\mathbb{R}^{N}} \lvert \Delta u_{n} \rvert ^{p} \,dx+\frac{dm_{0}}{\theta p} \int _{\mathbb{R}^{N}} \lvert \nabla u_{n} \rvert ^{p} \,dx \\ &\quad {}+\frac{1}{p} \int _{\mathbb{R}^{N}}V(x) \lvert u _{n} \rvert ^{p} \,dx-\lambda \int _{\mathbb{R}^{N}}{F(x,u_{n})} \,dx+o(1) \\ &\geq \frac{\min \{1,dm_{0}\}}{\theta p} \Vert u_{n} \Vert _{X}^{p}-\lambda \int _{\mathbb{R}^{N}}{F(x,u_{n})} \,dx+o(1). \end{aligned}$$
(3.5)

Since \(\|u_{n}\|_{X}\to \infty \) as \(n\to \infty \), we have

$$ \int _{\mathbb{R}^{N}}{F(x,u_{n})} \,dx\geq \frac{\min \{1,dm_{0}\}}{ \theta p\lambda } \Vert u_{n} \Vert _{X}^{p}- \frac{c}{\lambda }+\frac{o(1)}{ \lambda } \to \infty \quad \text{as } n\to \infty . $$
(3.6)

In addition, we assert that

$$\begin{aligned} I_{\lambda }(u_{n}) &=\frac{1}{p} \int _{\mathbb{R}^{N}} \lvert \Delta u_{n} \rvert ^{p} \,dx+\mathcal{M} \biggl( \int _{\mathbb{R}^{N}}\varPhi _{0}(x,\nabla u_{n}) \,dx \biggr)\\ &\quad {}+\frac{1}{p} \int _{\mathbb{R}^{N}}V(x) \lvert u_{n} \rvert ^{p} \,dx-\lambda \int _{\mathbb{R}^{N}} {F(x,u_{n})} \,dx \\ &\le \frac{1}{p} \Vert u_{n} \Vert _{X}^{p}+\mathcal{M} \biggl( \int _{\mathbb{R} ^{N}}\varPhi _{0}(x,\nabla u_{n}) \,dx \biggr)-\lambda \int _{\mathbb{R}^{N}} {F(x,u_{n})} \,dx. \end{aligned}$$

Combining this with relation (3.3), we obtain that

$$ \frac{1}{p} \Vert u_{n} \Vert _{X}^{p}+\mathcal{M} \biggl( \int _{\mathbb{R}^{N}} \varPhi _{0}(x,\nabla u_{n}) \,dx \biggr)\ge \lambda \int _{\mathbb{R}^{N}} {F(x,u_{n})} \,dx+c-o(1) $$

for sufficiently large n. Assumption (F4) implies that there exists \(t_{0}>1\) such that \({F(x,t)}>{ \lvert t \rvert ^{\theta p}}\) for all \(x\in \mathbb{R}^{N}\) and \(\lvert t \rvert >t _{0}\). From assumptions (F1) and (F2), there exists \(\mathcal{C}>0\) such that \(\lvert F(x,t) \rvert \leq \mathcal{C}\) for all \((x,t)\in \mathbb{R}^{N} \times [-t_{0},t_{0}]\). Therefore we can choose a real number \(\mathcal{C}_{0}\) such that \(F(x,t)\geq \mathcal{C}_{0}\) for all \((x,t)\in \mathbb{R}^{N}\times \mathbb{R}\), and thus

$$ \frac{F(x,u_{n})-\mathcal{C}_{0}}{\frac{1}{p } \Vert u_{n} \Vert _{X}^{p}+ \mathcal{M} (\int _{\mathbb{R}^{N}}\varPhi _{0}(x,\nabla u_{n}) \,dx )} \geq 0, $$
(3.7)

for all \(x\in \mathbb{R}^{N}\) and for all \(n\in \mathbb{N}\). Set \(\varOmega _{1}= \{ x\in \mathbb{R}^{N} : w(x)\neq0 \}\). By the convergence in (3.4), we know that

$$ \bigl\lvert u_{n}(x) \bigr\rvert = \bigl\lvert w_{n}(x) \bigr\rvert \Vert u_{n} \Vert _{X}\to \infty \quad \text{as } n\to \infty $$

for all \(x\in \varOmega _{1}\). So then, it follows from assumptions (M2), (J2), (F4), and Hölder’s inequality that, for all \(x\in \varOmega _{1}\), we have

$$\begin{aligned} &\lim_{n\to \infty }{\frac{F(x,u_{n})}{\frac{1}{p } \Vert u_{n} \Vert _{X} ^{p}+\mathcal{M} (\int _{\mathbb{R}^{N}}\varPhi _{0}(x,\nabla u_{n}) \,dx )}} \\ &\quad \geq \lim_{n\to \infty }{\frac{F(x,u_{n})}{\frac{1}{p } \Vert u_{n} \Vert _{X} ^{p}+\mathcal{M}(1) (1+ (\int _{\mathbb{R}^{N}}\varPhi _{0}(x, \nabla u_{n}) \,dx )^{\theta } )}} \\ &\quad \geq \lim_{n\to \infty }{\frac{F(x,u_{n})}{\frac{1}{p } \Vert u_{n} \Vert _{X} ^{p}+\mathcal{M}(1) (1+ (\int _{\mathbb{R}^{N}}a(x) \lvert \nabla u _{n} \rvert +\frac{b}{p} \lvert \nabla u_{n} \rvert ^{p} \,dx )^{\theta } )}} \\ &\quad \geq \lim_{n\to \infty }{\frac{F(x,u_{n})}{\frac{1}{p } \Vert u_{n} \Vert _{X} ^{p}+\mathcal{M}(1) (1+ ( \Vert a \Vert _{L^{p'}(\mathbb{R}^{N})} \Vert \nabla u_{n} \Vert _{L^{p}(\mathbb{R}^{N})}+\frac{b}{p} \Vert \nabla u_{n} \Vert _{L ^{p}(\mathbb{R}^{N})}^{p} )^{\theta } )}} \\ &\quad \geq \lim_{n\to \infty }{\frac{F(x,u_{n})}{ (\frac{1}{p }+ \mathcal{M}(1) (1+ ( \Vert a \Vert _{L^{p'}(\mathbb{R}^{N})}+ \frac{b}{p} )^{\theta } ) ) \Vert u_{n} \Vert _{X}^{ \theta p}}} \\ &\quad = \lim_{n\to \infty }{\frac{F(x,u_{n})}{ (\frac{1}{p }+ \mathcal{M}(1) (1+ ( \Vert a \Vert _{L^{p'}(\mathbb{R}^{N})}+ \frac{b}{p} )^{\theta } ) ) \lvert u_{n}(x) \rvert ^{\theta p}} \bigl\lvert w_{n}(x) \bigr\rvert ^{\theta p}} \\ &\quad = \infty , \end{aligned}$$
(3.8)

where we have used the inequality \(\mathcal{M} (t)\leq \mathcal{M}(1) (1+{t}^{\theta } )\) for all \(t\in \mathbb{R}^{+}\), since if \(0\le t<1\), then \(\mathcal{M} (t)=\int _{0}^{t} M(\tau ) \,d\tau \leq \mathcal{M}(1)\) and if \(t>1\), then \(\mathcal{M} (t)\leq \mathcal{M}(1)t ^{\theta }\). Hence we get that \(\operatorname{meas}(\varOmega _{1})=0\). Indeed, if \(\operatorname{meas}(\varOmega _{1})\neq0\), according to (3.6)–(3.8) and Fatou’s lemma, we would obtain

$$\begin{aligned} \frac{1}{\lambda } &={\liminf_{n\to \infty }{ \frac{ {\int _{\mathbb{R}^{N}}{F(x,u_{n})} \,dx}}{ \lambda \int _{\mathbb{R}^{N}}{F(x,u_{n})} \,dx+c-o(1)}}} \\ &\geq {\liminf_{n\to \infty } \int _{\mathbb{R}^{N}}{\frac{F(x,u_{n})}{ \frac{1}{p } \Vert u_{n} \Vert _{X}^{p}+\mathcal{M} (\int _{\mathbb{R}^{N}} \varPhi _{0}(x,\nabla u_{n}) \,dx )}}} \,dx \\ &\geq {\liminf_{n\to \infty } \int _{\varOmega _{1}}{\frac{F(x,u_{n})}{ \frac{1}{p } \Vert u_{n} \Vert _{X}^{p}+\mathcal{M} (\int _{\mathbb{R}^{N}} \varPhi _{0}(x,\nabla u_{n}) \,dx )}}} \,dx \\ &\quad {}- \limsup _{n\to \infty } { \int _{\varOmega _{1}}{\frac{\mathcal{C}_{0}}{\frac{1}{p } \Vert u_{n} \Vert _{X} ^{p}+\mathcal{M} (\int _{\mathbb{R}^{N}}\varPhi _{0}(x,\nabla u_{n}) \,dx )}} \,dx} \\ &= \liminf_{n\to \infty }{ \int _{\varOmega _{1}}{\frac{F(x,u_{n})- \mathcal{C}_{0}}{\frac{1}{p } \Vert u_{n} \Vert _{X}^{p}+\mathcal{M} (\int _{\mathbb{R}^{N}}\varPhi _{0}(x,\nabla u_{n}) \,dx )}} \,dx} \\ &\ge \int _{\varOmega _{1}}{\liminf_{n\to \infty }{ \frac{F(x,u_{n})- \mathcal{C}_{0}}{\frac{1}{p } \Vert u_{n} \Vert _{X}^{p}+\mathcal{M} (\int _{\mathbb{R}^{N}}\varPhi _{0}(x,\nabla u_{n}) \,dx )}}} \,dx \\ &\ge \int _{\varOmega _{1}}{\liminf_{n\to \infty }{ \frac{F(x,u_{n})}{ \frac{1}{p } \Vert u_{n} \Vert _{X}^{p}+\mathcal{M} (\int _{\mathbb{R}^{N}} \varPhi _{0}(x,\nabla u_{n}) \,dx )}}} \,dx \\ &\quad {}-{ \int _{\varOmega _{1}} \limsup_{n\to \infty }{ \frac{\mathcal{C}_{0}}{\frac{1}{p } \Vert u_{n} \Vert _{X}^{p}+\mathcal{M} (\int _{\mathbb{R}^{N}}\varPhi _{0}(x,\nabla u _{n}) \,dx )}} \,dx} \\ &=\infty , \end{aligned}$$
(3.9)

which is a contradiction. Thus \(w(x)=0\) for almost all \(x\in \mathbb{R} ^{N}\). Using assumptions (M1)–(M2) and (J5), we get

$$\begin{aligned} c+1 &\ge I_{\lambda }(u_{n})-\frac{1}{\theta p} \bigl\langle I_{ \lambda }^{\prime }(u_{n}),u_{n} \bigr\rangle \\ &=\frac{1}{p} \int _{\mathbb{R}^{N}} \lvert \Delta u_{n} \rvert ^{p} \,dx+\mathcal{M} \biggl( \int _{\mathbb{R}^{N}}\varPhi _{0}(x,\nabla u_{n}) \,dx \biggr) \\ &\quad {}+\frac{1}{p} \int _{\mathbb{R}^{N}}V(x) \lvert u_{n} \rvert ^{p} \,dx-\lambda \int _{\mathbb{R}^{N}}{F(x,u_{n})} \,dx \\ & \quad -\frac{1}{\theta p} \int _{\mathbb{R}^{N}} \lvert \Delta u_{n} \rvert ^{p} \,dx-\frac{1}{\theta p}M \biggl( \int _{\mathbb{R}^{N}}\varPhi _{0}(x, \nabla u_{n}) \,dx \biggr) \int _{\mathbb{R}^{N}}\varphi (x,\nabla u_{n}) \cdot \nabla u_{n} \,dx \\ & \quad -\frac{1}{\theta p} \int _{\mathbb{R}^{N}}V(x) \lvert u_{n} \rvert ^{p} \,dx +\frac{1}{\theta p}\lambda \int _{\mathbb{R}^{N}}f(x,u_{n})u_{n} \,dx \\ &\ge \frac{1}{\theta }M \biggl( \int _{\mathbb{R}^{N}}\varPhi _{0}(x,\nabla u _{n}) \,dx \biggr) \int _{\mathbb{R}^{N}}\varPhi _{0}(x,\nabla u_{n}) \,dx- \lambda \int _{\mathbb{R}^{N}}{F(x,u_{n})} \,dx \\ & \quad -\frac{1}{\theta p}M \biggl( \int _{\mathbb{R}^{N}}\varPhi _{0}(x,\nabla u_{n}) \,dx \biggr) \int _{\mathbb{R}^{N}}\varphi (x,\nabla u_{n})\cdot \nabla u_{n} \,dx+\frac{1}{\theta p}\lambda \int _{\mathbb{R}^{N}}f(x,u _{n})u_{n} \,dx \\ & = \frac{1}{\theta }M \biggl( \int _{\mathbb{R}^{N}}\varPhi _{0}(x,\nabla u_{n}) \,dx \biggr) \biggl( \int _{\mathbb{R}^{N}}\varPhi _{0}(x,\nabla u_{n}) \,dx- \frac{1}{p} \int _{\mathbb{R}^{N}}\varphi (x,\nabla u_{n})\cdot \nabla u _{n} \,dx \biggr) \\ &\quad{}+\lambda \int _{\mathbb{R}^{N}}{\mathfrak{F}}(x,u_{n}) \,dx \\ &\ge \lambda \int _{\mathbb{R}^{N}}{\mathfrak{F}}(x,u_{n}) \,dx \end{aligned}$$
(3.10)

for n large enough. Let us define \(\varOmega _{n}(a,b):=\{ x\in \mathbb{R} ^{N} : a \le \lvert u_{n}(x) \rvert < b \}\) for \(a \geq 0\). The convergence in (3.4) means that

$$ w_{n}\to 0 \quad \text{in } L^{r}\bigl(\mathbb{R}^{N}\bigr)\quad \text{and} \quad w_{n}(x)\to 0 \quad \text{a.e. in } \mathbb{R}^{N} \text{ as } n\to \infty $$
(3.11)

for \(1 < r < p_{*}\). Hence by using (3.5) we get

$$ 0< \frac{\min \{1,dm_{0}\}}{\lambda \theta p} \le \limsup_{n\to \infty } \int _{\mathbb{R}^{N}}{\frac{ \lvert F(x,u_{n}) \rvert }{ \Vert u _{n} \Vert _{X}^{p}}} \,dx. $$
(3.12)

On the other hand, from assumption (F2) and relation (3.11), it follows that

$$\begin{aligned} &\int _{\varOmega _{n}(0,r_{0})}{\frac{F(x,u_{n})}{ \Vert u_{n} \Vert _{X}^{p}}} \,dx \\ &\quad \le \int _{\varOmega _{n}(0,r_{0})}\frac{\rho (x) \lvert u_{n}(x) \rvert + \frac{ \sigma (x)}{q} \lvert u_{n}(x) \rvert ^{q}}{ \Vert u_{n} \Vert _{X} ^{p}} \,dx \\ &\quad \le \frac{C_{1}}{ \Vert u_{n} \Vert _{X}^{p}} \Vert \rho \Vert _{L^{q^{\prime }}(\mathbb{R}^{N})} \Vert u_{n} \Vert _{L^{q}(\mathbb{R}^{N})} \\ &\qquad {} + \frac{ \Vert \sigma \Vert _{L^{\infty }(\mathbb{R}^{N})}}{q} \int _{\varOmega _{n}(0,r_{0})} \bigl\lvert u _{n}(x) \bigr\rvert ^{q-p} \bigl\lvert w_{n}(x) \bigr\rvert ^{p} \,dx \\ &\quad \le \frac{C_{1}}{ \Vert u_{n} \Vert _{X}^{p}} \Vert \rho \Vert _{L^{q^{\prime }}(\mathbb{R}^{N})} \Vert u_{n} \Vert _{L^{q}(\mathbb{R}^{N})} + \frac{ \Vert \sigma \Vert _{L^{\infty }(\mathbb{R}^{N})}}{q}r_{0}^{q-p} \int _{\mathbb{R}^{N}} \bigl\lvert w _{n}(x) \bigr\rvert ^{p} \,dx \\ &\quad \le \frac{C_{2}}{ \Vert u_{n} \Vert _{X}^{p}} \Vert \rho \Vert _{L^{q^{\prime }}(\mathbb{R}^{N})} \Vert u_{n} \Vert _{X} + \frac{ \Vert \sigma \Vert _{L^{\infty }(\mathbb{R}^{N})}}{q}r_{0}^{q-p} \int _{\mathbb{R}^{N}} \bigl\lvert w_{n}(x) \bigr\rvert ^{p} \,dx \\ &\quad \le \frac{C_{3}}{ \Vert u_{n} \Vert _{X}^{p-1}} + \frac{ \Vert \sigma \Vert _{L ^{\infty }(\mathbb{R}^{N})}}{q}r_{0}^{q-p} \int _{\mathbb{R}^{N}} \bigl\lvert w _{n}(x) \bigr\rvert ^{p} \,dx \to 0 \quad \text{as } n\to \infty \end{aligned}$$
(3.13)

for some positive constants \(C_{i}\) \((i=1,2,3)\). Set \(\kappa ^{\prime }=\kappa / (\kappa -1)\). Since \(\kappa > N / p\), we get \(1 < \kappa ^{\prime } p < p_{*}\). Hence, it follows from (F5), (3.10), and (3.11) that

$$\begin{aligned} \int _{\varOmega _{n}(r_{0},\infty )}{\frac{ \lvert F(x,u_{n}) \rvert }{ \Vert u_{n} \Vert _{X}^{p}}} \,dx &\leq \int _{\varOmega _{n}(r_{0},\infty )}{\frac{ \lvert F(x,u_{n}) \rvert }{ \lvert u_{n}(x) \rvert ^{p}} \bigl\lvert w_{n}(x) \bigr\rvert ^{p}} \,dx \\ &\le \biggl\{ \int _{\varOmega _{n}(r_{0},\infty )} \biggl(\frac{ \lvert F(x,u _{n}) \rvert }{ \lvert u_{n}(x) \rvert ^{p}} \biggr) ^{\kappa } \,dx \biggr\} ^{\frac{1}{\kappa }} \biggl\{ \int _{\varOmega (r_{0},\infty )} \bigl\lvert w_{n}(x) \bigr\rvert ^{ \kappa ^{\prime } p} \biggr\} ^{\frac{1}{\kappa ^{\prime }}} \\ &\le c_{0}^{\frac{1}{\kappa }} \biggl\{ \int _{\varOmega _{n}(r_{0},\infty )}{\mathfrak{F}}(x,u_{n}) \,dx \biggr\} ^{\frac{1}{\kappa }} \biggl\{ \int _{\mathbb{R}^{N}} \bigl\lvert w_{n}(x) \bigr\rvert ^{\kappa ^{\prime }p} \biggr\} ^{\frac{1}{\kappa ^{\prime }}} \\ &\le c_{0}^{\frac{1}{\kappa }} \biggl(\frac{c+1}{\lambda } \biggr) ^{\frac{1}{\kappa }} \biggl\{ \int _{\mathbb{R}^{N}} \bigl\lvert w_{n}(x) \bigr\rvert ^{\kappa ^{\prime }p} \biggr\} ^{\frac{1}{\kappa ^{\prime }}} \to 0 \quad \text{as } n\to \infty . \end{aligned}$$
(3.14)

Combining the estimates in (3.13) with (3.14), we have

$$ \int _{\mathbb{R}^{N}}{\frac{ \lvert F(x,u_{n}) \rvert }{ \Vert u _{n} \Vert _{X}^{p}}} \,dx = \int _{\varOmega _{n}(0,r_{0})}{\frac{ \lvert F(x,u _{n}) \rvert }{ \Vert u_{n} \Vert _{X}^{p}}} \,dx+ \int _{\varOmega _{n}(r_{0},\infty )}{\frac{ \lvert F(x,u_{n}) \rvert }{ \Vert u_{n} \Vert _{X}^{p}}} \,dx \to 0 \quad \text{as } n \to \infty , $$

which contradicts (3.12). This completes the proof. □

Using Lemma 3.3, we prove the existence of a nontrivial weak solution for our problem under the considered assumptions.

Theorem 3.4

Assume that (V), (M1), (M2), (J1)–(J5), and (F1)–(F5) hold. Then problem (P) has a nontrivial weak solution for all \(\lambda >0\).

Proof

Note that \(I_{\lambda }(0)=0\). In view of Lemma 3.2, the geometric conditions in the mountain pass theorem are fulfilled. And also \(I_{\lambda }\) satisfies the \((C)_{c}\) condition for any \(\lambda >0\) by Lemma 3.3. Hence, problem (P) has a nontrivial weak solution for all \(\lambda >0\). This completes the proof. □

Next, under assumption (F6) instead of (F5), we show that \(I_{\lambda }\) satisfies the Cerami condition.

Lemma 3.5

Assume that (V), (M1), (M2), (J1)–(J5), (F1)–(F4), and (F6) hold. Then the functional \(I_{\lambda }\) satisfies the \((C)_{c}\) condition for any \(\lambda >0\).

Proof

For \(c\in \mathbb{R}\), let \(\{u_{n}\}\) be a \((C)_{c}\)-sequence in X satisfying (3.2). Following the proof of Lemma 3.3, we only prove that \(\{u_{n}\}\) is bounded in X. To this end, arguing by contradiction, suppose that \(\|u_{n}\|_{X}\rightarrow \infty \) as \(n\to \infty \). Let \(v_{n}=u_{n}/\|u_{n}\|_{X}\). Then \(\|v_{n}\|_{X}=1\). Passing to a subsequence, we may assume that \(v_{n}\rightharpoonup v\) as \(n\to \infty \) in X. Thus by an embedding theorem, for \(1< s< p_{*}\), we have

$$ v_{n} \rightarrow v \quad \text{in } L^{s}\bigl( \mathbb{R}^{N}\bigr)\quad \text{and} \quad v_{n}(x) \rightarrow v(x) \quad \text{a.e. in } \mathbb{R}^{N} \text{ as } n\to \infty . $$

From (M1), (M2), (J5), and (F6), it follows that

$$\begin{aligned} c+1 &\ge I_{\lambda }(u_{n})-\frac{1}{\mu } \bigl\langle I_{\lambda } ^{\prime }(u_{n}),u_{n} \bigr\rangle \\ &=\frac{1}{p} \int _{\mathbb{R}^{N}} \lvert \Delta u_{n} \rvert ^{p} \,dx+\mathcal{M} \biggl( \int _{\mathbb{R}^{N}}\varPhi _{0}(x,\nabla u_{n}) \,dx \biggr) \\ &\quad {}+\frac{1}{p} \int _{\mathbb{R}^{N}}V(x) \lvert u_{n} \rvert ^{p} \,dx- \lambda \int _{\mathbb{R}^{N}}{F(x,u_{n})} \,dx \\ &\quad{}-\frac{1}{\mu } \int _{\mathbb{R}^{N}} \lvert \Delta u_{n} \rvert ^{p} \,dx-\frac{1}{\mu }M \biggl( \int _{\mathbb{R}^{N}}\varPhi _{0}(x,\nabla u_{n}) \,dx \biggr) \int _{\mathbb{R}^{N}}\varphi (x,\nabla u_{n})\cdot \nabla u_{n} \,dx \\ & \quad{}- \frac{1}{\mu } \int _{\mathbb{R}^{N}}V(x) \lvert u_{n} \rvert ^{p} \,dx+ \frac{\lambda }{\mu } \int _{\mathbb{R}^{N}}{f(x,u_{n})u_{n}} \,dx \\ &\geq \biggl(\frac{1}{p}-\frac{1}{\mu } \biggr) \int _{\mathbb{R}^{N}} \lvert \Delta u _{n} \rvert ^{p} \,dx+m_{0} \biggl(\frac{1}{\theta p}- \frac{1}{ \mu } \biggr) \int _{\mathbb{R}^{N}}\varphi (x,\nabla u_{n})\cdot \nabla u _{n} \,dx \\ & \quad{}+ \biggl(\frac{1}{p}-\frac{1}{\mu } \biggr) \int _{\mathbb{R}^{N}}V(x) \lvert u_{n} \rvert ^{p} \,dx-\frac{\lambda \varrho }{ \mu } \int _{\mathbb{R}^{N}} \lvert u_{n} \rvert ^{p} \,dx \\ &\geq \min \{dm_{0},1\} \biggl(\frac{1}{\theta p}- \frac{1}{\mu } \biggr) \biggl( \int _{\mathbb{R}^{N}} \lvert \Delta u_{n} \rvert ^{p} \,dx+ \int _{\mathbb{R}^{N}} \lvert \nabla u_{n} \rvert ^{p} \,dx + \int _{\mathbb{R}^{N}}V(x) \lvert u_{n} \rvert ^{p} \,dx \biggr) \\ &\quad {}-\frac{ \lambda \varrho }{\mu } \int _{\mathbb{R}^{N}} \lvert u_{n} \rvert ^{p} \,dx \\ &\geq \min \{dm_{0},1\} \biggl(\frac{1}{\theta p}- \frac{1}{\mu } \biggr) \Vert u_{n} \Vert _{X}^{p}-\frac{\lambda \varrho }{\mu } \int _{\mathbb{R}^{N}} \lvert u_{n} \rvert ^{p} \,dx \quad \text{for large } n \in \mathbb{N}. \end{aligned}$$

This implies

$$ 1\leq \frac{\lambda \varrho \theta p}{\min \{dm_{0},1\}(\mu -\theta p)} \limsup_{n\rightarrow \infty } \Vert v_{n} \Vert _{L^{p}(\mathbb{R}^{N})}^{p}= \frac{ \lambda \varrho \theta p}{\min \{dm_{0},1\}(\mu -\theta p)} \Vert v \Vert _{L ^{p}(\mathbb{R}^{N})}^{p}. $$
(3.15)

Hence, due to (3.15), we see that \(v\neq 0\). From the same argument as in Lemma 3.3, we can show that the relations (3.6), (3.7), and (3.8) hold, and hence we conclude that relation (3.9) is true. Therefore we get a contradiction. Thus \(\{u_{n}\}\) is bounded in X. This completes the proof. □

Next, applying the fountain theorem in [32, Theorem 3.6] with the oddity of f, we demonstrate infinitely many weak solutions for problem (P). To do this, let W be a reflexive and separable Banach space. Then there are \(\{e_{n}\}\subseteq W\) and \(\{f_{n}^{*} \}\subseteq W^{*}\) such that

$$ W=\overline{\mathrm{span}\{e_{n}:n=1,2,\dots \}}, \qquad W^{*}=\overline{\mathrm{span}\bigl\{ f_{n}^{*}:n=1,2, \dots \bigr\} }, $$

and

$$\begin{aligned} \bigl\langle f^{*}_{i},e_{j} \bigr\rangle =\textstyle\begin{cases} 1 &\text{if } i=j, \\ 0 &\text{if } i\ne j. \end{cases}\displaystyle \end{aligned}$$

Let us denote \(W_{n}=\operatorname{span}\{e_{n}\}\), \(Y_{k}=\bigoplus_{n=1} ^{k}W_{n}\), and \(Z_{k}= \overline{\bigoplus_{n=k}^{\infty }W_{n}}\). In order to establish the existence result, we use the following Fountain theorem.

Lemma 3.6

([1, 32])

Let X be a real reflexive Banach space, \(I \in C^{1}(X,\mathbb{R})\) satisfies the \({(C)_{c}}\) condition for any \(c>0\) and I is even. If for each sufficiently large \(k \in \mathbb{N}\), there exist \(\rho _{k}> \delta _{k}>0\) such that the following conditions hold:

  1. (1)

    \(b_{k}:=\inf \{ I(u):u\in Z_{k}, \|u\|_{X}= \delta _{k}\}\to \infty\) as \(k\to \infty \);

  2. (2)

    \(a_{k}:=\max \{ I(u):u\in Y_{k}, \|u\|_{X}=\rho _{k}\} \le 0\).

Then the functional I has an unbounded sequence of critical values, i.e., there exists a sequence \(\{u_{n}\}\subset X\) such that \(I^{\prime }(u_{n})=0\) and \(I(u_{n})\to +\infty \) as \(n\to +\infty \).

Theorem 3.7

Assume that (V), (M1), (M2), (J1)–(J5), and (F1)–(F5) hold. If \(\varPhi _{0}(x,-v)=\varPhi _{0}(x,v)\) holds for all \((x,v)\in \mathbb{R}^{N}\times \mathbb{R}^{N}\) and \(f(x,-t)=-f(x,t)\) holds for all \((x,t)\in \mathbb{R}^{N} \times \mathbb{R}\), then for any \(\lambda >0\), problem (P) possesses an unbounded sequence of nontrivial weak solutions \(\{u_{n}\}\) in X such that \(I_{\lambda }( u_{n})\to \infty \) as \(n\to \infty \).

Proof

It is obvious that \(I_{\lambda }\) is an even functional and satisfies the \((C)_{c}\) condition. It suffices to show that there exist \(\rho _{k}> \delta _{k}>0\) such that

  1. (1)

    \(b_{k}:=\inf \{I_{\lambda }(u):u\in Z_{k}, \|u\|_{X}= \delta _{k}\}\to \infty \quad \text{as } n\to \infty \);

  2. (2)

    \(a_{k}:=\max \{I_{\lambda }(u):u\in Y_{k}, \|u\|_{X}= \rho _{k}\}\le 0\),

for k large enough. Denote

$$ \alpha _{k}:=\sup_{u \in Z_{k}, \Vert u \Vert _{X}=1} \Vert u \Vert _{L^{q}( \mathbb{R}^{N})}. $$

Then we have \(\alpha _{k} \to 0\) as \(k \to \infty \). In fact, assume to the contrary that there exist \(\varepsilon _{0}>0\) and a sequence \(\{u_{k}\}\) in \(Z_{k}\) such that

$$ \Vert u_{k} \Vert _{X}=1 \quad \text{and} \quad \Vert u_{k} \Vert _{L^{q}( \mathbb{R}^{N})} \ge \varepsilon _{0} $$

for all \(k \ge k_{0}\). By the boundedness of the sequence \(\{u_{k}\}\) in X, we can find an element \(u \in X\) such that \(u_{k} \rightharpoonup u\) in X as \(n\to \infty \) and

$$ \bigl\langle {f_{j}^{*},u}\bigr\rangle =\lim _{k \to \infty }{\bigl\langle {f_{j}^{*},u _{k}}\bigr\rangle }=0 $$

for \(j=1,2,\dots \). Thus we deduce \(u=0\). However, we see that

$$ \varepsilon _{0} \le \lim_{k \to \infty }{ \Vert u_{k} \Vert _{L^{q}(\mathbb{R} ^{N})}}= \Vert u \Vert _{L^{q}(\mathbb{R}^{N})}=0, $$

which is a contradiction.

For any \(u \in Z_{k}\), we may suppose that \(\|u\|_{X}>1\). According to assumptions (M1), (M2), (J3), and (F2), we obtain that

$$\begin{aligned} I_{\lambda }(u) &=\frac{1}{p} \int _{\mathbb{R}^{N}} \lvert \Delta u \rvert ^{p} \,dx+ \mathcal{M} \biggl( \int _{\mathbb{R}^{N}}\varPhi _{0}(x,\nabla u) \,dx \biggr) \\ &\quad {}+ \frac{1}{p} \int _{\mathbb{R}^{N}}V(x) \lvert u \rvert ^{p} \,dx- \lambda \int _{\mathbb{R}^{N}}{F(x,u)} \,dx \\ &\ge \frac{1}{p} \int _{\mathbb{R}^{N}} \lvert \Delta u \rvert ^{p} \,dx+ \frac{1}{\theta }M \biggl( \int _{\mathbb{R}^{N}}\varPhi _{0}(x,\nabla u) \,dx \biggr) \int _{\mathbb{R}^{N}}\varPhi _{0}(x,\nabla u) \,dx \\ &\quad {}+ \frac{1}{p} \int _{\mathbb{R}^{N}}V(x) \lvert u \rvert ^{p} \,dx -\lambda \int _{\mathbb{R}^{N}} \bigl\lvert \rho (x) \bigr\rvert \lvert u \rvert \,dx-\lambda \int _{\mathbb{R}^{N}}\frac{ \lvert \sigma (x) \rvert }{q} \lvert u \rvert ^{q} \,dx \\ &\ge \frac{\min \{1,dm_{0}\}}{\theta p} \biggl( \int _{\mathbb{R}^{N}} \lvert \Delta u \rvert ^{p} \,dx+ \int _{\mathbb{R}^{N}} \lvert \nabla u \rvert ^{p} \,dx + \int _{\mathbb{R}^{N}}V(x) \lvert u \rvert ^{p} \,dx \biggr) \\ &\quad{}-\lambda \int _{\mathbb{R}^{N}} \bigl\lvert \rho (x) \bigr\rvert \lvert u \rvert \,dx-\lambda \int _{\mathbb{R}^{N}}\frac{ \lvert \sigma (x) \rvert }{q} \lvert u \rvert ^{q} \,dx \\ &\ge \frac{\min \{1,dm_{0}\}}{\theta p} \Vert u \Vert ^{p}_{X} -2\lambda \Vert \rho \Vert _{L^{q^{\prime }}(\mathbb{R}^{N})} \Vert u \Vert _{L^{q}(\mathbb{R} ^{N})} -\frac{2\lambda }{q} \Vert \sigma \Vert _{L^{\infty }(\mathbb{R}^{N})} \int _{\mathbb{R}^{N}} \lvert u \rvert ^{q} \,dx \\ &\ge \frac{\min \{1,dm_{0}\}}{\theta p} \Vert u \Vert ^{p}_{X}-2 \lambda C _{4} \Vert u \Vert _{X} - \frac{2\lambda }{q} \alpha _{k}^{q}C_{5} \Vert u \Vert ^{q} _{X}, \end{aligned}$$

where \(C_{4}\) and \(C_{5}\) are positive constants. If we take

$$ \delta _{k}= \biggl(\frac{{2\lambda }C_{5}\alpha _{k}^{q}}{\min \{1,dm _{0} \}} \biggr)^{{1}/ (p-q )}, $$

then \(\delta _{k}\to \infty \) as \(k\to \infty \) because \(\theta p< q\) and \(\alpha _{k}\to 0\) as \(k\to \infty \). Hence, if \(u \in Z_{k}\) and \(\|u\|_{X}=\delta _{k}\), then we conclude that

$$ I_{\lambda }(u)\ge {\min \{1,dm_{0} \}} \biggl( \frac{1}{ \theta p}-\frac{1}{q} \biggr)\delta _{k}^{p}-2 \lambda C_{4} \delta _{k} \to \infty \quad \text{as } k \to \infty . $$

This implies that condition (1) holds.

The proof of condition (2) proceeds analogously as in the proof of [1, Theorem 1.3]. For the reader’s convenience, we give the proof. Assume that condition (2) is not true. Then for some k there exists a sequence \(\{u_{n}\}\) in \(Y_{k}\) such that

$$ \Vert u_{n} \Vert _{X}\to \infty \quad \text{as } n\to \infty \quad \text{and}\quad I_{\lambda }(u_{n}) \ge 0. $$
(3.16)

Set \(w_{n}=u_{n}/\|u_{n}\|_{X}\). Note that \(\|w_{n}\|_{X}=1\). Since \(\dim {Y_{k}}<\infty \), there exists \(w\in Y_{k}\setminus \{0\}\) such that, up to a subsequence,

$$ \Vert w_{n}-w \Vert _{X}\to 0 \quad \text{and} \quad w_{n}(x)\to w(x) $$

for almost all \(x\in \mathbb{R}^{N}\) as \(n\to \infty \). If \(w(x)\neq 0\), then \(\lvert u_{n}(x) \rvert \to \infty \) for all \(x\in \mathbb{R}^{N}\) as \(n\to \infty \). Hence we obtain by assumption (F4) that

$$ \lim_{n\to \infty }{\frac{F(x,u_{n}(x))}{ \Vert u_{n} \Vert _{X}^{\theta p}}} = \lim _{n\to \infty }{\frac{F(x,u_{n}(x))}{ \lvert u_{n}(x) \rvert ^{\theta p}} \bigl\lvert w_{n}(x) \bigr\rvert ^{\theta p} } = \infty $$

for all \(x\in \varOmega _{2}:= \{ x\in \mathbb{R}^{N} : w(x)\neq0 \}\). As in the proof of Lemma 3.3, we have

$$ \int _{\varOmega _{2}}{\frac{F(x,u_{n}(x))}{ \Vert u_{n} \Vert _{X}^{\theta p}}} \,dx\to \infty \quad \text{as }n\to \infty . $$

Therefore, we conclude that

$$\begin{aligned} I_{\lambda }(u_{n}) &\le \frac{1}{p} \Vert u_{n} \Vert _{X}^{p}+\mathcal{M} \biggl( \int _{\mathbb{R}^{N}}\varPhi _{0}(x,\nabla u_{n}) \,dx \biggr)-\lambda \int _{\mathbb{R}^{N}}{F(x,u_{n})} \,dx \\ &\leq \frac{1}{p} \Vert u_{n} \Vert _{X}^{\theta p}+\mathcal{M}(1) \biggl(1+ \biggl( \Vert a \Vert _{L^{p'}(\mathbb{R}^{N})}+\frac{b}{p} \biggr)^{\theta } \biggr) \Vert u_{n} \Vert _{X}^{\theta p}-\lambda \int _{\mathbb{R}^{N}}{F(x,u_{n})} \,dx \\ &\leq \Vert u_{n} \Vert _{X}^{\theta p} \biggl(\frac{1}{p}+\mathcal{M}(1) \biggl(1+ \biggl( \Vert a \Vert _{L^{p'}(\mathbb{R}^{N})}+\frac{b}{p} \biggr) ^{\theta } \biggr)-\lambda \int _{\varOmega _{2}}{\frac{F(x,u_{n}(x))}{ \Vert u_{n} \Vert _{X}^{p}}} \,dx \biggr)\\ &\to -\infty \quad \text{as }n\to \infty , \end{aligned}$$

which contradicts (3.16). This completes the proof. □

Remark 3.8

Although we replace (F5) with (F6) in the assumptions of Theorem 3.7, we can show that problem (P) possesses an unbounded sequence of nontrivial weak solutions \(\{u_{n}\}\) in X such that \(I_{\lambda }( u_{n})\to \infty \) as \(n\to \infty \).