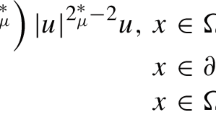1 Introduction

In this paper, we consider the Neumann problem to the following parabolic equation:

$$ \textstyle\begin{cases} u_{t}-\Delta u=u\log \vert u \vert - \fint_{\Omega } u\log \vert u \vert \,dx, & x\in \Omega, t>0, \\ \frac{\partial u}{\partial n}=0, & x\in \partial \Omega, t>0, \\ u(x,0)=u_{0}(x), & x\in \Omega, \end{cases} $$
(1.1)

where \(\Omega \subset {\bf {R}}^{n}\) is a bounded domain with smooth boundary, \(\fint_{\Omega }u_{0}\,dx=\frac{1}{|\Omega |}\int_{\Omega }u _{0}\,dx=0\) with \(u_{0}\not \equiv 0\). It is easy to check that the solution u of (1.1) is \(L^{1}\)-conservative and hence

$$\begin{aligned} \int_{\Omega }u\,dx= \int_{\Omega } u_{0}\,dx=0. \end{aligned}$$
(1.2)

In fact, problem (1.1) has been studied by many other authors in a more general form:

$$\begin{aligned} \textstyle\begin{cases} u_{t}-\Delta u=f(u)-\fint_{\Omega } f(u)\,dx,& x\in \Omega, t>0, \\ \frac{\partial u}{\partial n}=0,& x\in \partial \Omega, t>0, \\ u(x,0)=u_{0}(x),& x\in \Omega. \end{cases}\displaystyle \end{aligned}$$
(1.3)

Here, Ω is a bounded smooth domain in \({\bf R}^{n}\) (\(n\geq 1\)) with \(| \Omega | \) denoting its Lebesgue measure, n is the outer normal vector of ∂Ω, and the function \(f(u)\) is usually taken to be a power of u. Problem (1.3) is also interesting in its own right, due to the fact that the comparison principle does not always hold for it. So it is often necessary to introduce some new techniques. The negative solutions of (1.3) with \(f(u)=|u|^{p}\) are studied in [1]. When \(f(u)=u|u|^{p}\) and \(\int_{\Omega }u\,dx>0\) are studied in [2], the non-global existence result is discussed by using a convexity argument and under the energy condition

$$ E(u_{0})= \int_{\Omega } \biggl[ \frac{1}{2} \vert \nabla u_{0} \vert ^{2}- \frac{1}{p+1} \vert u_{0} \vert ^{p+1} \biggr]\,dx\leq -C. $$

When \(\int_{\Omega }u\,dx=0\), their conclusion can be found in [3, 4].

Further, the nonlocal p-Laplace equation

$$\begin{aligned} \textstyle\begin{cases} u_{t}-\operatorname{div}( \vert \nabla u \vert ^{p-2}\nabla u)=u^{q}-\fint_{\Omega } u ^{q}\,dx,& x\in \Omega, t>0, \\ \frac{\partial u}{\partial n}=0,& x\in \partial \Omega, t>0, \\ u(x,0)=u_{0}(x),& x\in \Omega, \end{cases}\displaystyle \end{aligned}$$
(1.4)

is given in [5, 6], where a critical blow-up solution is determined by q and the sign of the initial energy. In particular, the conditions under which the changing sign solutions vanish in finite time are obtained. At the same time, a thin-film has also received much attention, and it reads as follows:

$$\begin{aligned} \textstyle\begin{cases} u_{t}+u_{xxxx}= \vert u \vert ^{p-1}u-\fint_{\Omega } u^{p-1}u\,dx, & x\in \Omega, t>0, \\ u_{x}=u_{xxx}=0, & x\in \partial \Omega, t>0, \\ u(x,0)=u_{0}(x), & x\in \Omega. \end{cases}\displaystyle \end{aligned}$$
(1.5)

We can find it in [7, 8], where the threshold results of global existence and non-existence for the sign-changing weak solutions are given by the potential well method. Further, the conditions under which the global solutions become extinct in finite time are obtained and the asymptotic behavior of non-extinct solutions is studied.

To our knowledge, there have been few works concerned with the blow-up and extinction for the nonlocal parabolic equation with logarithmic nonlinearity. It is a remarkable fact that a nonlocal parabolic equation with logarithmic nonlinearity does not admit the usual maximum principle and the comparison principle. Because of this main difficulty, some most effective methods, such as the method of upper and lower solutions, are not valid here anymore. Inspired by the ideas in [9–18], the threshold results for the global existence and blow-up of the weak solutions are given by the potential well method, the classical Galerkin method, and the logarithmic Sobolev inequality. Further we discuss the non-extinction properties and the asymptotic behavior of the global solutions.

On the other hand, to handle logarithmic nonlinear term, we need the following logarithmic Sobolev inequality, which was introduced by [10, 19, 20].

Proposition 1.1

([10, 19, 20])

Let u be any function in \(H^{1}({\bf R}^{n})\) and \(a>0\) be any number. Then

$$\begin{aligned} 2 \int_{R^{n}} \bigl\vert u(x) \bigr\vert ^{2}\log \biggl( \frac{ \vert u(x) \vert }{ \Vert u \Vert _{L^{2}(R^{n})}} \biggr)\,dx +n(1+\log a) \Vert u \Vert _{L^{2}(R^{n})}^{2}\leq \frac{a^{2}}{\pi } \int_{R ^{n}} \bigl\vert \nabla u(x) \bigr\vert ^{2} \,dx. \end{aligned}$$
(1.6)

For \(u\in H_{0}^{1}(\Omega)\), we can define \(u(x)=0\) for \(x\in {\bf R}^{n}\setminus \Omega \). Then \(u\in H^{1}({\bf R}^{n})\), that is to say, for a general domain Ω, we have the following logarithmic Sobolev inequality:

$$\begin{aligned} 2 \int_{\Omega } \bigl\vert u(x) \bigr\vert ^{2}\log \biggl( \frac{ \vert u(x) \vert }{ \Vert u \Vert _{L^{2}(\Omega)}} \biggr)\,dx +n(1+\log a) \Vert u \Vert _{L^{2}(\Omega)}^{2}\leq \frac{a^{2}}{ \pi } \int_{\Omega } \bigl\vert \nabla u(x) \bigr\vert ^{2} \,dx, \end{aligned}$$
(1.7)

where u is any function in \(H^{1}(\Omega)\), \(a>0\) is any number.

To state our main results, we need the following definitions.

Definition 1.1

(Weak solution)

A function \(u(x,t)\) is called a weak solution of (1.1), if \(u\in L^{\infty }(0,T;H^{2}(\Omega))\), \(u_{t}\in L^{2}(0,T;L^{2}(\Omega))\), and satisfies (1.1) in the distribution sense, i.e.,

$$\begin{aligned} (u_{t}, \varphi)_{2}+(\nabla u, \varphi)_{2}= \bigl(u\log \vert u \vert , \varphi\bigr)_{2}- \biggl( \fint_{\Omega } u\log \vert u \vert , \varphi \biggr) _{2} \end{aligned}$$
(1.8)

for any \(\varphi \in H_{0}^{1}(\Omega)\), \(t\in (0,T)\), where \(u(0,x)=u_{0}(x)\in H_{0}^{1}(\Omega)\), and \((\cdot, \cdot)_{2}\) means the inner product \((\cdot, \cdot)_{L^{2}(\Omega)}\).

Definition 1.2

(Finite time blow-up)

Let \(u(x,t)\) be a weak solution of (1.1). We call \(u(x,t)\) blow-up in finite time if the maximal existence time T is finite and

$$ \lim_{t\rightarrow T^{-}} \bigl\Vert u(\cdot, t) \bigr\Vert _{L^{2}(\Omega)}=+\infty. $$

Definition 1.3

(Blow-up at +∞)

Let \(u(x,t)\) be a weak solution of (1.1). We call \(u(x,t)\) blow-up at +∞ if the maximal existence time \(T=+\infty \) and

$$ \lim_{t\rightarrow +\infty } \bigl\Vert u(\cdot, t) \bigr\Vert _{L^{2}(\Omega)}=+\infty. $$

For convenience, we introduce some notations here. Denote by \(\|\cdot \|_{p}\) the \(L^{p}(\Omega)\) norm for \(1\leq p\leq \infty \) and define

$$\begin{aligned}& \begin{aligned} &J(u)=\frac{1}{2} \Vert \nabla u \Vert _{{2}}^{2}-\frac{1}{2} \int_{\Omega }u^{2} \log \vert u \vert \,dx+ \frac{1}{4} \int_{\Omega }u^{2}\,dx, \\ &I(u)= \Vert \nabla u \Vert _{{2}}^{2}- \int_{\Omega }u^{2}\log \vert u \vert \,dx. \end{aligned} \end{aligned}$$
(1.9)

Then it is obvious that

$$\begin{aligned}& \begin{aligned}&J(u)=\frac{1}{2}I(u)+\frac{1}{4} \Vert u \Vert _{2}^{2}, \\ &\Phi =\bigl\{ u\in H^{2}_{0}(\Omega);I(u)=0, \Vert u \Vert ^{2}_{2}\neq 0\bigr\} , \\ &d=\inf_{u\in \Phi }J(u), \\ &M=\frac{1}{4}(2\pi)^{\frac{n}{2}}e^{n}. \end{aligned} \end{aligned}$$
(1.10)

From [10], we know \(d\geq M\).

$$ W=\bigl\{ u\in H_{0}^{1};I(u)>0, J(u)< d\bigr\} \cup \{0\}, \qquad V=\bigl\{ u\in H_{0}^{1};I(u)< 0,J(u)< d \bigr\} , $$

and for \(\delta >0\), we define

$$\begin{aligned}& \begin{aligned} &I_{\delta }(u)=\delta \Vert \nabla u \Vert _{{2}}^{2}- \int_{\Omega }u^{2} \log \vert u \vert \,dx, \\ &N_{\delta }=\bigl\{ u\in H^{2}_{0}(\Omega); I_{\delta }(u)=0, \Vert u \Vert ^{2}_{2} \neq 0\bigr\} , \\ &d_{\delta }=\inf_{u\in N_{\delta }}J(u), \\ &W_{\delta }=\bigl\{ u\in H_{0}^{1}; I_{\delta }(u)>0, J(u)< d(\delta)\bigr\} \cup \{0\}, \\ & V_{\delta }=\bigl\{ u\in H_{0}^{1}; I_{\delta }(u)< 0,J(u)< d( \delta)\bigr\} . \end{aligned} \end{aligned}$$
(1.11)

The local existence of the weak solutions can be obtained via the standard parabolic theory. It is easy to obtain the following equality:

$$\begin{aligned} \int_{0}^{t} \Vert u_{\tau } \Vert _{2}^{2}\,d\tau =J(u_{0})-J(u),\quad 0< t< T. \end{aligned}$$
(1.12)

Theorem 1.1

If \(u_{0}\in H_{0}^{1}\), \(0< J(u_{0})< M\), and \(I(u_{0})>0\). Then problem (1.1) has a unique global weak solution, which does not blow up in finite time. Moreover,

$$ \Vert u \Vert _{2}^{2}\leq 2e^{e^{t}}\log \frac{1}{2} \Vert u_{0} \Vert _{2}^{2}. $$

Theorem 1.2

Assume \(J(u_{0})<0\), then the solution \(u(x,t)\) of problem (1.1) is blow-up at +∞. Moreover, if \(\|u_{0}\|_{2} ^{2}\leq -2J(u_{0})\), the lower bound for blow-up rate can be estimated by

$$\begin{aligned} \Vert u \Vert _{2}^{2}\geq 2 \Vert u_{0} \Vert _{2}^{2}, \end{aligned}$$
(1.13)

which is independent of t.

Theorem 1.3

Assume \(0< J(u_{0})< M\), then the solution \(u(x,t)\) of problem (1.1) is non-extinct in finite time; moreover, \(\|u\|_{2}^{2}\) can be estimated by

$$\begin{aligned} \Vert u \Vert _{2}^{2}\geq \Vert u_{0} \Vert _{2}^{2}e^{-bt},\quad b=n(1+\log \sqrt{2\pi }). \end{aligned}$$
(1.14)

\(\|\cdot,\cdot \|_{2}\) means \(\|\cdot,\cdot \|_{L^{2}(\Omega)}\).

Remark 1.1

For a nonlocal parabolic equation, [5–8, 21] get the results under appropriate conditions on blow-up in finite time. However, if \(f(u)\) is the logarithmic nonlinear term \(u\log |u|\) in (1.3), then Theorem 1.2 tells us that the weak solution is blow-up at +∞.

Our paper is organized as follows. In Sect. 2, we establish new lemmas relative to the logarithmic nonlinear term. Next, in Sect. 3, we prove Theorem 1.1 (global existence and decay estimate). Finally, we give the proof of Theorems 1.2 (blow-up at +∞ and the lower bound for blow-up rate) and 1.3 (non-extinction and estimate).

2 Preliminaries

In this section, we briefly collect some important properties of the functions and sets defined in the Introduction.

Lemma 2.1

([9])

Suppose that \(\theta >0\), \(\alpha >0\), \(\beta >0\) and \(h(t)\) is a nonnegative and absolutely continuous function satisfying \(h'(t)+\alpha h^{\theta }(t)\geq \beta \), then for \(0< t<\infty \), it holds

$$ h(t)\geq \min \biggl\{ h(0), \biggl( \frac{\beta }{\alpha } \biggr) ^{\frac{1}{ \theta }} \biggr\} . $$

Lemma 2.2

If \(0< J(u_{0})< E_{1}=\frac{1}{4}e^{b}\), where \(b=n(1+\log \sqrt{2\pi })\), then there exists a positive constant \(\alpha_{2}>\alpha_{1}\) such that

$$\begin{aligned} \Vert u \Vert _{2}\geq \alpha_{2}. \end{aligned}$$
(2.1)

Proof

Using the logarithmic Sobolev inequality in Proposition 1.1, for any \(a>0\), we have

$$\begin{aligned} J(u) =&\frac{1}{2} \Vert \nabla u \Vert _{2}^{2}-\frac{1}{2} \int_{\Omega }u^{2} \biggl( \log \frac{ \vert u \vert }{ \Vert u \Vert _{2}}+\log \Vert u \Vert _{2} \biggr)\,dx+\frac{1}{4} \Vert u \Vert _{2}^{2}, \\ \geq & \biggl( \frac{1}{2}-\frac{a^{2}}{4\pi } \biggr) \Vert \nabla u \Vert _{2} ^{2}+\frac{1}{4}n(1+\log a) \Vert u \Vert _{2}^{2}-\frac{1}{2}\log \Vert u \Vert _{2} \Vert u \Vert _{2}^{2}+\frac{1}{4} \Vert u \Vert _{2}^{2}. \end{aligned}$$
(2.2)

Let \(a=\sqrt{2\pi }\) in (2.2), we have

$$\begin{aligned} J(u)\geq \biggl( \frac{1}{4}n(1+\log a)-\frac{1}{2} \log \Vert u \Vert _{2}+ \frac{1}{4} \biggr) \Vert u \Vert _{2}^{2}. \end{aligned}$$
(2.3)

Denote \(\alpha =\|u\|_{2}\), \(b=n(1+\log \sqrt{2\pi })\), we have

$$\begin{aligned} h(\alpha)=\biggl(\frac{b}{4}-\frac{\log \alpha }{2}+ \frac{1}{4}\biggr)\alpha^{2}. \end{aligned}$$
(2.4)

Let

$$ h'(\alpha_{1})=0, \qquad E_{1}=h( \alpha_{1}). $$

Furthermore, we get \(h(\alpha)\) is increasing in \((0,\alpha_{1})\) and decreasing in \((\alpha_{1},\infty)\). Since \(J(u_{0})< E_{1}\), there exists a positive constant \(\alpha_{2}>\alpha_{1}\) such that \(J(u_{0})=h(\alpha_{2})\). Let \(\alpha_{0}=\|u_{0}\|_{2}\), from (2.3) and (2.4), we have

$$ h(\alpha_{0})\leq J(u_{0}). $$

Since \(\alpha_{0},\alpha_{2} \geq \alpha_{1}\), we get \(\alpha_{0} \geq \alpha_{2}\), so (2.1) holds for \(t=0\).

To prove (2.1) for \(t>0\), we assume the contrary that \(\|u( \cdot,t)\|_{2}<\alpha_{2}\) for some \(t_{0}>0\). By the continuity of \(\|u(\cdot,t)\|_{2}\) and \(\alpha_{1}<\alpha_{2}\), we may choose \(t_{0}\) such that \(\|u(\cdot,t_{0})\|_{2}>\alpha_{1}\), then it follows from (2.3)

$$ J(u_{0})=h(\alpha_{2})< h\bigl( \bigl\Vert u( \cdot,t_{0}) \bigr\Vert _{2}\bigr)\leq J(u) (t_{0}), $$

which contradicts the fact that \(J(u)\) is nonincreasing in t by (1.12), so (2.1) is true. □

Lemma 2.3

Let \(H(u)=E_{1}-J(u)\), \(J(u_{0})< E_{1}\), then \(H(u)\) satisfies the following estimates:

$$ 0< H(u_{0})\leq H(u). $$

Proof

It is obvious that \(H(u)\) is nondecreasing in t, by (1.12), then it follows from \(J(u_{0})< E_{1}\) that

$$ H(u)\geq H(u_{0})=E_{1}-J(u_{0})>0. $$

 □

Remark 2.1

From Lemma 2.4 in [10], M can be obtained by the definition of d, but in this paper, \(E_{1}=h(\alpha_{1})\), \(\alpha_{1}=e^{\frac{b}{2}}\), so we can get from (2.4)

$$ E_{1}=\frac{1}{4}e^{b}=M. $$

3 Proofs of Theorem 1.1

Proof of Theorem 1.1

We choose \(w_{j}(x)\) to be the orthogonal basis of \(H_{0}^{1}\) and construct the following approximate solution \(u_{m}(x,t)\) of problem (1.1):

$$ u_{m}(x,t)=\sum_{j=1}^{m}g_{i}(t)w_{j}(x), \quad \mbox{for } m=1,2,\ldots, $$

which satisfies

$$\begin{aligned}& (u_{mt}, w_{s})_{2}+(\nabla u_{m}, \nabla w_{s})_{2}=\bigl(u_{m}\log \vert u _{m} \vert , w_{s}\bigr)_{2}-\biggl( \fint_{\Omega } u_{m}\log \vert u_{m} \vert , w_{s}\biggr)_{2} \end{aligned}$$
(3.1)
$$\begin{aligned}& u_{m}(x,0)=\sum_{j=1}^{m}a_{j}w_{j}(x) \rightarrow u_{0} \end{aligned}$$
(3.2)

and \((\cdot,\cdot)_{2}\) means the inner product \((\cdot,\cdot)_{L ^{2}(\Omega)}\).

Next we need some a priori estimates on the approximate solutions \(u_{m}\), multiplying by \(g_{s}(t)\) and summing for s, for sufficiently large m. From (1.11), we obtain

$$\begin{aligned} \int_{0}^{t} \Vert u_{m\tau } \Vert _{2}^{2}\,d\tau +J\bigl(u_{m}(t)\bigr)=J \bigl(u_{m}(0)\bigr)< M \leq d, \quad 0\leq t< \infty. \end{aligned}$$
(3.3)

From the proof of Theorem 1.1 in [10], we have

$$\begin{aligned}& \Vert u_{m} \Vert _{2}^{2}< 4M, \\& \Vert \nabla u_{m} \Vert _{2}^{2}< C_{M}, \\& \int_{\Omega }\bigl(u_{m}\log \vert u_{m} \vert \bigr)^{2}\,dx\leq e^{-2} \vert \Omega \vert + \biggl( \frac{n-2}{2} \biggr) ^{2}S^{2\ast } \Vert \nabla u_{m} \Vert _{2}^{2\ast }\leq C^{\prime}M, \end{aligned}$$

where S is the best constant of the Sobolev embedding \(H_{0}^{1}( \Omega)\hookrightarrow L^{\frac{2n}{n-2}}(\Omega)\).

Denote \(\rightarrow (w^{*})\) as the weakly star convergence. Therefore, we obtain a subsequence of \(u_{m}\), which is still denoted by itself, our sending \(m\rightarrow \infty \),

$$\begin{aligned}& u_{m}\rightarrow u \bigl(w^{*}\bigr) \quad \text{in } L^{\infty }\bigl(0,\infty; H _{0}^{1}(\Omega)\bigr) \text{ in } \Omega \times [0,+\infty), \\& u_{mt}\rightarrow u_{t} \bigl(w^{*}\bigr) \quad \text{in } L^{2}\bigl(0,\infty;L ^{2}(\Omega)\bigr), \\& u_{m}\log \vert u_{m} \vert \rightarrow u\log \vert u \vert \bigl(w^{*}\bigr) \quad \text{in } L^{ \infty }\bigl(0, \infty;L^{2}(\Omega)\bigr), \\& \fint_{\Omega }u_{m}\log \vert u_{m} \vert \rightarrow \fint_{\Omega }u\log \vert u \vert \bigl(w^{*}\bigr) \quad \text{in } L^{\infty }\bigl(0,\infty;L^{2}(\Omega)\bigr). \end{aligned}$$

Hence, we have

$$\begin{aligned} (u_{t}, w_{s})_{2}+(\nabla u, \nabla w_{s})_{2}=\bigl(u\log \vert u \vert , w _{s} \bigr)_{2}- \biggl( \fint_{\Omega } u\log \vert u \vert , w_{s} \biggr) _{2}. \end{aligned}$$
(3.4)

Next, we prove the uniqueness of the weak solution. Suppose that problem (1.1) admits two weak solutions \(u_{1}\) and \(u_{2}\), set \(w=u_{1}-u_{2}\), and w solves

$$\begin{aligned} \textstyle\begin{cases} w_{t}-\Delta w=f(u_{1})-f(u_{2}),\quad (x,t)\in \Omega \times (0.T), \\ \frac{\partial w}{\partial n}=0, \quad (x,t)\in \Omega \times (0.T), \\ w(x,0)=0, \quad x\in \Omega, \end{cases}\displaystyle \end{aligned}$$
(3.5)

where \(f(u)=u\log |u|-\fint_{\Omega } u\log |u|\). Multiplying both sides of the first equation of (3.5) by w and integrating the result over \(\Omega \times (0,t)\), we have

$$\begin{aligned} & \int_{0}^{t} \int_{\Omega }\bigl(w_{t}w+ \vert \nabla w \vert ^{2}\bigr)\,dx\,ds \\ &\quad = \int_{0}^{t} \int_{\Omega } \bigl( u_{1}\log \vert u_{1} \vert -u_{2}\log \vert u_{2} \vert \bigr) w\,dx\,ds \\ &\qquad {} - \int_{0}^{t} \int_{\Omega } \biggl( \fint_{\Omega }u_{1}\log \vert u_{1} \vert -u _{2}\log \vert u_{2} \vert \biggr) w\,dx\,ds \\ &\quad = \int_{0}^{t} \int_{\Omega } \bigl( u_{1}\log \vert u_{1} \vert -u_{2}\log \vert u_{2} \vert \bigr) w\,dx\,ds \\ &\quad \leq C \int_{0}^{t} \int_{\Omega }w^{2}\,dx\,ds, \end{aligned}$$

where C is a positive constant.

Noticing that \(w(x,0)=0\), we have

$$ \int_{\Omega }w^{2}(x,t)\,dx\leq C \int_{0}^{t} \int_{\Omega }w^{2}(x,t)\,dx\,dt. $$

Using Gronwall’s inequality, we get that

$$ \int_{\Omega }w^{2}(x,t)\,dx=0. $$

Thus \(w=0\) a.e. in \(\Omega \times (0,T)\).

We define \(M(t)=\frac{1}{2}\|u\|_{2}^{2}\), then

$$\begin{aligned} M'(t)=(u_{t},u)_{2}= \biggl( \bigl(u\log \vert u \vert ,u\bigr)_{2}- \biggl( \fint_{\Omega }u \log \vert u \vert \,dx,u \biggr) _{2}+ \Vert \nabla u \Vert _{2}^{2} \biggr) =-I(u). \end{aligned}$$
(3.6)

By using (1.9) and Proposition 1.1, we know

$$\begin{aligned} I(u)\geq \biggl( \frac{n(2+\log (2\pi)}{4}-\log \Vert u \Vert _{2}^{2} \biggr) \Vert u \Vert _{2}^{2}, \end{aligned}$$
(3.7)

where \(a=\sqrt{2\pi }\).

From (3.6) and (3.7)

$$ M(t)\log M(t)-M'(t)\geq \biggl( \frac{n(2+\log (2\pi)}{4}-\log \Vert u \Vert _{2}^{2} \biggr) \Vert u \Vert _{2}^{2}\geq 0, $$

we have

$$ \bigl( \log M(t) \bigr) ^{\prime}\leq \log M(t). $$

This means

$$ M(t)\leq e^{e^{t}}\log \frac{1}{2} \Vert u_{0} \Vert _{2}^{2}, $$

then

$$ \Vert u \Vert _{2}^{2}\leq 2e^{e^{t}}\log \frac{1}{2} \Vert u_{0} \Vert _{2}^{2} \quad \text{for all } t\geq 0, $$

which implies that \(u(x,t)\) does not blow up in finite time. □

4 Proofs of Theorems 1.2 and 1.3

Proof of Theorem 1.2

By the definition of \(J(u),J(u_{0})<0\) and (1.12), \(M(t)\) satisfies

$$\begin{aligned} M '(t) =& \int_{\Omega }u\cdot u_{t}\,dx \\ =& \int_{\Omega }u\biggl(\Delta u+u \log \vert u \vert - \fint_{\Omega } u\log \vert u \vert \biggr)\,dx \\ =& \int_{\Omega }\bigl(- \vert \nabla u \vert ^{2}+u^{2} \log \vert u \vert \bigr)\,dx \\ \geq &-2J(u) \\ \geq &2 \int_{0}^{t} \Vert u_{\tau } \Vert _{2}^{2}\,d\tau. \end{aligned}$$
(4.1)

And by the definition of weak solution, we know that \(u\in L^{\infty }(0,T;H^{2}(\Omega))\). For any \(t_{0}>0\), we claim that

$$\begin{aligned} \int_{0}^{t_{0}} \Vert u_{\tau } \Vert _{2}^{2}\,d\tau >0. \end{aligned}$$
(4.2)

Otherwise, there exists \(t_{0}>0\) such that \(\int_{0}^{t_{0}}\|u_{ \tau }\|_{2}^{2}\,d\tau =0\), and hence \(u_{t}=0\) for a.e. \((x,t)\in \Omega \times (0,t_{0})\). Then it follows from (4.1) that

$$ - \vert \nabla u \vert ^{2}+u^{2}\log \vert u \vert =0 $$

for a.e. \(t\in (0,t_{0})\), and then we get from (1.9)

$$ J(u)= \int_{\Omega }\frac{1}{4}u^{2}\,dx. $$

Combining it with \(J(u)\leq J(u_{0})\leq 0\), we obtain \(\|u\|_{2}=0\) for all \(t\in [0,t_{0}]\), which contradicts the definition of u. Then (4.2) follows.

Fix \(t_{0}>0\) and let \(\delta =\int_{0}^{t}\|u_{\tau }\|_{2}^{2}\,d\tau \), then we know that δ is a positive constant. Integrating (4.1) over \((t_{0},t)\), we obtain

$$\begin{aligned} M(t) \geq &M(t_{0})+ \int_{t_{0}}^{t} \int_{0}^{s} \Vert u_{\tau } \Vert _{2}^{2}\,d\tau \,ds \geq \delta (t-t_{0}). \end{aligned}$$
(4.3)

Hence,

$$\begin{aligned} \lim_{t\rightarrow \infty }H'(t)=\lim_{t\rightarrow \infty }M(t)= \infty. \end{aligned}$$
(4.4)

And from (4.1), we know

$$\begin{aligned} M'(t) =& \int_{\Omega }u\cdot u_{t}\,dx \\ =& \int_{\Omega }u\biggl(\Delta u+u \log \vert u \vert - \fint_{\Omega } u\log \vert u \vert \biggr)\,dx \\ =& \int_{\Omega }\bigl(- \vert \nabla u \vert ^{2}+u^{2} \log \vert u \vert \bigr)\,dx \\ =&-2J(u)+\frac{1}{2} \Vert u \Vert _{2}^{2} \\ \geq &-\frac{1}{2} \Vert u \Vert _{2}^{2}-2J(u_{0}). \end{aligned}$$
(4.5)

By using Lemma 2.1, \(J(u_{0})<0\), and \(\|u_{0}\|_{2}^{2}\leq -2J(u _{0})\), we have

$$\begin{aligned} M(t) \geq & \min \bigl\{ \Vert u_{0} \Vert _{2}^{2},-2J(u_{0}) \bigr\} \\ \geq & \Vert u_{0} \Vert _{2}^{2}, \end{aligned}$$

which means (1.13) is true. □

Proof of Theorem 1.3

We define \(\beta =\frac{\alpha_{2}}{\alpha _{1}}>1\), \(M(t)=\frac{1}{2}\|u\|_{2}^{2}\). Then, by the definitions of \(J(u)\), \(M(t)\), and Lemma 2.3, we have

$$\begin{aligned} M'(t) =& \int_{\Omega }u\cdot u_{t}\,dx \\ =& \int_{\Omega }u\biggl(\Delta u+u \log \vert u \vert - \fint_{\Omega } u\log \vert u \vert \biggr)\,dx \\ =& \int_{\Omega }\bigl(- \vert \nabla u \vert ^{2}+u^{2} \log \vert u \vert \bigr)\,dx \\ =&-2J(u)+\frac{1}{2} \int_{\Omega }u^{2}\,dx \\ =&-2E_{1}+H(u)+\frac{1}{2} \int_{\Omega }u^{2}\,dx. \end{aligned}$$
(4.6)

By using (2.1) and (2.2) in Lemma 2.2, we get

$$\begin{aligned} E_{1} =&\biggl(\frac{1}{4}b- \frac{1}{2}\log \frac{\alpha_{2}}{\beta }+ \frac{1}{4}\biggr) \frac{\alpha_{2}^{2}}{\beta^{2}} \\ \leq & \biggl( \frac{1}{4}b+\frac{1}{4} \biggr) \frac{\alpha_{2}^{2}}{ \beta^{2}} \\ \leq & \biggl( \frac{1}{4}b+\frac{1}{4} \biggr) \Vert u \Vert _{2}^{2}. \end{aligned}$$
(4.7)

Then it follows from (4.6), (4.7), and Lemma 2.3 that

$$\begin{aligned} M'(t) \geq &-2E_{1}+\frac{1}{2} \Vert u \Vert _{2}^{2} \\ \geq &-\frac{1}{2}b \Vert u \Vert _{2}^{2} \\ \geq &-bM(t), \end{aligned}$$
(4.8)

which means (1.14) is true. □