Abstract
In this work, we implement the mortar spectral element method for the biharmonic problem with a homogeneous boundary condition. We consider a polygonal domain with corners which relies on the mortar decomposition domain technique. We propose the Strang and Fix algorithm, which permits to enlarge the discrete space of the solution by the first singular function. The interest of this algorithm is the approximation of the solution and the leading singular coefficient which has a physical significance in the propagation of cracks. We give some numerical results which confirm the optimality of the order of the error.
Similar content being viewed by others
1 Introduction
Consider the fourth order problem with homogeneous boundary conditions called the biharmonic homogeneous problem
where Ω is a polygonal domain of \(\mathbb {R}^{d}, d=2,3\) and ∂Ω is a Lipschitz-continuous boundary of Ω [1].
This type of problem is involved in many problems in the mechanics of a continuous medium for both fluids and solids. Other applications such as some models in control theory involve fourth order operators. The solution φ of this type of problem is composed of regular and singular parts [2–4]. To weaken the effect of the geometric singularity, we apply the method of domain decomposition without overlapping. This method is associated with the mortar method [5] with variational spectral elements discretization. Since the discrete solution (polynomial) is regular on each sub-domain of the decomposition, then the non-conformity results in the imposition of an integral matching condition on the solution and its normal derivative. This matching condition type is weak. It allows great geometric flexibility and is perfectly suited to parallel computing. The approximation of a singular part of the solution using the finite element method is presented in [6, 7]. In [8], the authors prove an optimal approximation by polynomials using the spectral method. In this work we will use these results to implement the mortar spectral elements method for the Strang and Fix algorithm [9] in the case of the biharmonic problem. It consists in enlarging the discrete space by the first singular function. The polynomial basis of the new discrete space permits us to approximate the solution and the leading singularity coefficient. This coefficient has a physical signification in the crack propagation [10–13]. We begin by writing the matrix system, then we use the conjugate gradient algorithm to solve it. We illustrate the good convergence of the presented method through numerical error curves. This work is an extension of the work presented in [14] for the case of domain with geometric singularity.
An outline of this paper is as follows. In Sect. 2, we present the geometry of the domain and a continuous problem, we give singular functions and some regularity results. In Sect. 3, we present a discrete problem. The error result obtained from the discretization of the biharmonic problem by the mortar spectral method is showed in Sect. 4. Section 5 is devoted to the implementation of the mortar spectral element method. We describe the matrix system and its resolution algorithm. Finally, we present some numerical results which confirm the interest in the method.
2 Continuous problem
We decompose the domain Ω into K rectangles \(\Omega_{k}\), \(1 \le k \le K\), such that
We designate by \(\overline{\Gamma}^{k,j}\), \(1 \le j \le4\), the sides of the sub-domain \(\overline{\Omega}_{k}\), \(1 \le k \le K\), and
the interface of the decomposition.
The skeleton of the decomposition is defined as follows:
We denote by \(\mathcal {V}\) the set of vertices of the sub-domain for our decomposition. Let \(\Gamma^{k(m),j(m)}\) be an open set of segments disjoint two by two for an integer m in a set \(\mathcal {M}\). Then
We called mortars the segments \(\Gamma^{k(m),j(m)}, m\in\mathcal {M}\). The intersection of a sub-domain \(\Omega_{k}\), \(1 \le k \le K\), with the boundary ∂Ω is reduced to an element of \(\mathcal {V}\).
We suppose that the singular angles are \(\frac{\pi}{2}\), \(\frac{3\pi }{2}\), or 2π. For its importance in the fluid mechanics and in mechanic (cracks propagation), we will handle specially the cases \(\frac {3\pi}{2}\) and 2π. Since the treatment of singularities is local, we reduce our study to a single geometric vertex v and ω the associated angle. We suppose that the sides of sub-domains are parallel to the scale axis of origin v. We consider \((r,\theta )\) the polar coordinates with r the distance from a point to the vertex v and the line \(\theta=0\) contains a side of ∂Ω.
We need the following conformity hypothesis for our analysis later.
Assumption 1
Let Δ be the union of sub-domains which contain the vertex \({\bf v}\). We suppose that the decomposition of the domain Δ is geometric conforming (for \(\Omega_{k}\) and \(\Omega_{l}\) included in Δ, \(\bar{\Omega}_{k} \cap\bar{\Omega}_{l}={\Gamma}^{kl}, k\neq l\), \({\Gamma }^{kl}\) is an edge of both \(\Omega_{k}\) and \(\Omega_{l}\)).
Problem (1) is equivalent to the following variational formulation:
For \(f\in H^{-2}(\Omega)\), find \(\varphi\in H_{0}^{2}(\Omega)\) for all \(\psi\in H_{0}^{2}(\Omega)\)
where \(a(\varphi,\psi)=\int_{\Omega}\Delta\varphi: \Delta\psi \,dx\,dy\) and \(\langle\cdot,\cdot\rangle\) is the duality product between \(H^{-2}(\Omega)\) and \(H_{0}^{2}(\Omega)\).
According to the Lax–Milgram theorem, problem (2) has a unique solution, since the bilinear form \(a(\cdot,\cdot)\) is continuous in \(H_{0}^{2}(\Omega)\times H_{0}^{2}(\Omega)\) and coercive in \(H_{0}^{2}(\Omega )\). We consider the following stability condition:
where C is a positive constant which is dependent just on Ω [15, 16].
For handling the singularities, we consider the bi-Laplacian characteristic equation
The solution of problem (1) is decomposed into the form \(\varphi=\varphi_{R}+\lambda S_{1}\) such that \(\varphi_{R}\in H^{s+2}(\Omega ), s< 1+\eta(\omega)\) and
where C is a positive constant, \(\lambda_{1}\) is the first singular coefficient and
• If \(\omega=\frac{3\pi}{2}\), we have \(\eta(\omega)=0.54484\), \(s < 1.544\), and \(\phi(\theta)=2.093 (\cos(0.459 \theta)-\cos (1.544 \theta) )+1.093 (2.193\sin(0.459 \theta)-\sin (1.544 \theta) )\).
However, if \(f \in H^{s-2}(\Omega)\) with \(s<2.908\), we can still push the decomposition of the solution of problem (1) as
The regular part of the solution \({\tilde{\varphi}}_{R}\) is in the space \(H^{s+2}(\Omega)\) such that
where C is a positive constant and \(\lambda_{2}\) is the second singular coefficient. The second singularity function is defined as
where \(\eta_{1}(\omega)\) is the second real solution of equation (3) in the band \(0 < \text{Real}(z) < 1 (\eta_{1}(\frac{3\pi }{2})\simeq0.908529)\) and \(\varsigma(\theta)=4.302 (\cos(0.092 \theta)-\cos(1.908 \theta) )-1.815 (10.869\sin(0.092 \theta )- 0.524\sin(1.908 \theta) )\).
• If \(\omega=2\pi\), we have \(\eta(\omega)=0.5\), \(s <1.5\), and
Since f belongs to \(H^{s-2}(\Omega)\), then \(\tilde{\varphi}_{R}\) belongs to \(H^{s+2}(\Omega)\) for \(s<2,5\) such that
where C is a positive constant.
3 Discrete problem
We introduce the discretization parameter \(\delta=(N_{k})_{1\le k \le K}\), where \(\mathbb {P}_{N_{k}}(\Omega_{k})\), \({1\le k \le K}\), are the approximation polynomials with degrees less or equal to \(N_{k}\) in each sub-domain \(\Omega_{k}\).
We define the mortars functions space
where \(\psi_{\delta}\) is a test function.
The Galerkin method with numerical integration is used for spatial discretization. To take into account boundary conditions of the fourth order studied problem, we choose a quadrature formula presented in the following lemma.
Lemma 3.1
There exist \(\xi_{j}\), \(1\le j \le N-1\) (\(N\ge2\)), a set of unique points \(\rho_{j}\), \(1\le j \le N-1\), a set of unique positive reals \(\rho _{+}\), \(\rho_{-}\) such that \(\forall\varrho\in\mathbb {P}_{2N-1}(]{-}1,1[)\)
Proof
See [17] for the calculation of \(\rho_{j}\), \(\xi_{j}\); \(1\le j \le N-1\) (the zeros of the derivative of the Legendre polynomial \(L_{N}\)) and the proof of (7). □
Definition 3.2
For φ, ψ two continuous functions on \(\bar{\hat{\Omega }}=[-1,1]\times[-1,1]\) such that \(\varphi=\psi=0\) on ∂Ω, we define
-
$$(\varphi,\psi)_{N}=\sum_{i=1}^{N-1} \sum_{j=1}^{N-1}\varphi(\xi_{i}, \xi_{j}) \psi(\xi_{i},\xi_{j}) \rho_{i} \rho_{j} $$
the discrete scalar product.
-
$$(\varphi,\psi)_{N_{k}}=\frac{ \vert \Omega_{k} \vert }{4}\sum _{i=1}^{N_{k}-1}\sum_{j=1}^{N_{k}-1} \bigl(\varphi\circ B^{k} \bigr) (\xi_{i},\xi_{j}) \bigl(\psi\circ B^{k} \bigr) (\xi_{i},\xi _{j}) \rho_{i} \rho_{j}, $$
where \(B^{k}\) is the bijection from Ω̂ to \(\Omega_{k}\).
-
\(X_{\delta}\) is the space of functions \(\psi_{\delta}\) such that
-
\(\psi_{\delta}^{k}=\psi_{\delta}/_{\Omega_{k}}\in\mathbb {P}_{N_{k}}(\Omega_{k})\), \(1\le k \le K\),
-
\(\psi_{\delta}= \frac{\partial\psi_{\delta }}{\partial n}=0 \text{ on } \partial\Omega\),
-
there exist , \(1 \le j \le4\), \(\int_{\Gamma ^{k,j}}(\psi_{\delta}-\varrho_{0})(\tau) \mu(\tau) \,d \tau=0\) and \(\int_{\Gamma^{k,j}}(\frac{\partial\psi_{\delta }}{\partial n}-\varrho_{1})(\tau) \mu(\tau) \,d \tau=0\) \(\forall\mu\in \mathbb {P}_{N_{k}-4}(\Gamma^{k,j})\).
-
The discrete problem of continuous problem (1) is as follows.
For \(f\in\mathcal {C}(\overline{\Omega})\), find \(\varphi_{\delta}\in X_{\delta}\) such that
where \(a_{\delta}(\varphi_{\delta},\psi_{\delta})= \sum_{k=1}^{K}(\Delta\varphi_{\delta}^{k},\Delta\psi_{\delta}^{k})_{N_{k}}\) and \((f,\psi_{\delta})_{\delta}= \sum_{k=1}^{K}(f,\psi_{\delta }^{k})_{N_{k}}\).
We proceed now to the enlargement of the discrete space \(X_{\delta}\) to the space
using the Strang and Fix algorithm [9], where \(S_{1}\) is the first singular function.
We obtain then for \(\varphi_{\delta}^{*}=\varphi_{\delta}+\alpha S_{1}\) and \(\psi_{\delta}^{*}=\psi_{\delta}+\beta S_{1}\) in \(X_{\delta}^{*}\)
We refer to the appendix of [10] for the algorithm which permits to compute the singular integral \(\int_{\Omega_{k}}\Delta\psi_{\delta}^{k} \Delta S_{1} \,dx\).
We consider the following discrete problem:
Find \(\varphi_{\delta}^{*}\in X_{\delta}^{*}\) such that
where .
We define two norms on the space \(X_{\delta}^{*}\)
and
Proposition 3.3
For \(f\in L^{2}(\Omega)\), the discrete problem (8) has a unique solution \(\varphi_{\delta}^{*}\) in \(X_{\delta}^{*}\) and
Proof
To study problem (8), we begin by giving the properties of the bilinear form \(a_{\delta}^{*}(\cdot,\cdot)\) (see [18], Prop. 5.2, for the proof).
There exist two positive functions \(C_{1}\) and \(C_{2}\) independent of δ such that for all \(\varphi_{\delta}^{*}\), \(\psi_{\delta}^{*}\) in \(X_{\delta}^{*}\)
and
Using the fact that \(\Vert \cdot \Vert _{*1}\) and \(\Vert \cdot \Vert _{*2}\) are equivalent with a constant depending on the parameter δ ([18] Prop 5.1), an inf-sup condition will be showed for the bilinear form \(a_{\delta }^{*}(\cdot,\cdot)\) using the norm \(\Vert \Vert _{*1}\) (see [18], Prop. 5.5, for the proof). □
4 Error estimate
Proposition 4.1
Let f in \(H^{s-2}(\Omega)\) for \(s>0\), then, for all \(\epsilon> 0\),
where \(\sigma_{k}\), \(1\le k \le K\), verifies
and \(N= {\inf_{1\leq k\leq K}}N_{k}\).
Proof
By inf-sup condition on the bilinear form \(a_{\delta}^{*}(\cdot,\cdot)\), there exists a constant ν such that
Using (12) and the Strang lemma, we obtain
n is the outside normal and \([\omega]\) is the jump of ω on the interfaces.
We will estimate the terms of inequality (13) to obtain the order of convergence. Using the fact that the singular function \(S_{1}\) is regular in the neighborhood of v, the jump terms \((\omega_{\delta k}^{*}-\omega _{\delta l}^{*})\) (respectively \((\frac{\partial\omega_{\delta k}^{*}}{\partial n}-\frac{\partial\omega_{\delta l}^{*}}{\partial n} )\)) are reduced through each interface \(\gamma_{kl}\) to \((\omega _{\delta k}-\omega_{\delta l})\) (respectively \((\frac{\partial \omega_{\delta k}}{\partial n}-\frac{\partial\omega_{\delta l}}{\partial n} )\)). Furthermore, using the hypothesis of conformity on Δ, these obtained quantities vanish. Moreover, \(\varphi=\varphi_{R}\) on \(\Omega/\overline{\Delta}\); we obtain then
where \(\varrho_{0}\) (respectively \(\varrho_{1}\)) is the mortar function associated with \(\omega_{\delta}\) (respectively \(\frac{\partial\omega _{\delta}}{\partial n}\)).
We then obtain the following [19]:
We have by definition of \(X_{\delta}^{*}\)
where
Choosing \(\psi_{\delta}^{*}=\psi_{\delta}\in X_{\delta}^{-}\) and by the exactness of the quadrature formula (7)
Finally, by doing the sum of these results, we have
If \(f \in H^{s-2}(\Omega)\) for \(\eta(\omega)< s<\eta(\omega)+2\), then \(\varphi_{R}\in H^{s+2}(\Omega)\) and the trace (respectively the normal derivative trace) of \(\varphi_{R} \in H^{s-\frac{1}{2}}(\partial\Omega _{k})\) (respectively \(\in H^{s-\frac{3}{2}}(\partial\Omega_{k})\)); \(1\le k \le K\). Choosing \(\mu_{kj}\) and \(\chi_{kj}\), the orthogonal projections on \(\mathbb {P}_{N_{k} -4}(\Gamma^{kj})\), we deduce
and
Moreover, we obtain
If f in \(H^{s-2}(\Omega), s<2+\eta_{1}(\omega)\), where \(\eta _{1}(\omega)\) is the second real solution of (3), in the band \(0<\text{Real}(z)<s\), then using (5) and Assumption 1, we show that
We indicate that
Using the results of the singular functions approximation through polynomials (see [8]), we obtain
Then
therefore
Using these results, we obtain, for \(f\in H^{s-2}(\Omega)\), \(s>0\), and \(\varepsilon>0\),
where \(\sigma_{k}\) is given by (11).
By the Aubin–Nische duality, we obtain the desired estimation with the \(L^{2}\) norm. □
Remark 4.2
We denote that in the case of the crack (respectively \(\omega={3\pi\over 2}\)) the convergence order is \(N^{\epsilon-2}\) (respectively \(N^{\epsilon-{8\over 3}}\)). This demonstrates that the method is highly accurate.
5 Numerical implementation and results
In this section we are interested in the implementation of the mortar method for the Strang and Fix algorithm in the case of a fourth order problem. The implementation is performed using the spectral elements method with a global algorithm for the resolution. In the spectral discretization the algorithmic aspect is mainly identical despite the diversity of the problems to be solved. The main ideas behind this algorithm are inspired by the works of Anagnostou [20] and Belhachmi and Bernardi [21].
The program is written in Matlab, which permits a good memory optimization and provides a data structure depending on the initial geometry. The program has three modules corresponding to the three phases of the problem resolution. The first module is about the geometric aspect. The second module is related to the discretization of the problem which leads to the linear system. Finally, the last module is the resolution of the linear system and the exploitation of the results. This three components are programmed in a relatively general way and as much as possible are independent.
5.1 Choice of the basis
To describe algebraically the discrete problem (8), it is necessary to choose a basis of the space \(X_{\delta}^{*}\). This basis is defined naturally through local basis (on each sub-domain) and therefore relative to the discretization.
For the quadrature formula, the number of equations is greater than the number of unknowns. We neglect the first \(i=1\) and the last \(i=N-1\) in dimension 1. The basic polynomials for the Gauss–Lobatto quadrature formula are the Hermit interpolation polynomials that are defined on the interval \(]{-}1,1[\) by
We verify that these polynomials are represented by the formula
where the constants \(c_{i}\) are given by
with \(a=\frac{A}{2}(1+p^{\prime}(-1)-\frac{L_{N}^{\prime}(-1)}{L_{N}(-1)})\) and \(b=A+a\), where \(p(x)=(x-\xi_{1})(x-\xi_{N-1})\) and \(A=\frac{p(-1)}{4 L_{N}^{\prime}(-1)}\). In a similar way, we have
with \(c=\frac{B}{2}(-1+p^{\prime}(-1)+\frac{L_{N}^{\prime}(1)}{L_{N}(1)})\) and \(d=B-a\), where \(B=\frac{p(1)}{4 L_{N}^{\prime}(1)}\). Finally,
with
and
with
It follows that for \(\varphi_{\delta}^{*}=\varphi_{\delta}+ \lambda_{1\delta } {S_{1}}\) in the space \(X^{*}_{\delta}\), where \(\lambda_{1\delta}\) is the approximate value of the leading singular coefficient \(\lambda_{1}\),
with \({\varphi_{\delta}}_{ij}={\varphi_{\delta}}(\xi_{i}^{k},\xi_{j}^{k})\); \(2\le i,j\le N-2\), \(h_{i}^{N_{k}}= h_{i}\circ{B^{k}}^{-1}\) and \((\xi_{i}^{k},\xi _{j}^{k})=B^{k}(\xi_{i},\xi_{j})\). The boundary values are as follows: \({\varphi _{\delta}}_{\pm1j}={\varphi_{\delta}}(\pm1,\xi_{j}^{k})\) for \(1\le j\le N-1\) respectively \({\varphi_{\delta}}_{i\pm1}={\varphi_{\delta}}(\xi_{i}^{k},\pm1)\) for \(1\le i\le N-1\) and
and finally \({\varphi_{\delta}}_{00}=\frac{\partial^{2} \tilde{{\varphi _{\delta}}}}{\partial x\partial y}(-1,-1)\); \({\varphi_{\delta}}_{0N}=\frac {\partial^{2} \tilde{{\varphi_{\delta}}}}{\partial x\partial y}(-1,1)\) and likewise \({\varphi_{\delta}}_{N0}=\frac{\partial^{2} \tilde{{\varphi_{\delta}}}}{\partial x\partial y}(1,-1)\); \({\varphi_{\delta}}_{NN}=\frac{\partial ^{2} \tilde{{\varphi_{\delta}}}}{\partial x\partial y}(1,1)\) with \({\varphi _{\delta}}=\tilde{{\varphi_{\delta}}} \circ{B^{k}}^{-1}\).
5.2 The matching matrix Q
Let the following two integral matching conditions hold: there exist , \(1 \le j \le4\),
and
The conversion of the above conditions in matrix form represents an important step in solving the discrete problem (8). It is the matrix Q, more precisely its transpose, which purges the vector of the unknowns from the false degrees of freedom. The calculation of this matrix is completely local. It is done for each pair side and mortar associated. In our case, two elementary matrices intervene: one resulting from the condition on the trace \(Q_{1}\), the other from the condition on the trace of normal derivative \(Q_{2}\). In order to simplify the formulas, we will take the same degree of polynomials in each sub-domain. We write
and
where \(\gamma^{m}\) is the mortar associated with the side \(\Gamma ^{k,l}\).
On the other hand, to make the explicit calculation, we need to choose a basis of the space of the polynomials \(\mathbb {P}_{N-4}(\Gamma ^{k,l})\). As we have \((N-1)\) interior points and we must neglect two, we obtain
with
Finally, if \(\Phi=(\varrho_{0},\varrho_{1})\) the integral matching conditions (16) and (17) are written in matrix form
The matrix Q is defined by \(Q=B^{-1}P\). Remark that the matrix B is quasi-tridiagonal, its inversion is fast and at lower cost. Note that in the case of problem of fourth order, the mortar is in fact doubled in order to take into account the values of the solution and its normal derivative. From the algebraic point of view, \(Q_{1}\) and \(Q_{2}\) are local matrices and Q is a global matching matrix obtained by the following representation:
where \(\varphi^{*}_{\delta}\) is the vector of admissible unknowns and \(\tilde{\varphi}^{*}_{\delta}\) is the vector of degrees of freedom.
5.3 The discrete equation
To put the variational problem (8) in the form of a linear system, we will evaluate the two members of the equation. It is assumed for simplicity that the sub-domain \(\Omega_{k}\) is sent on the reference square \(\hat{\Omega}=\mathopen{]}{-}1,1[^{2}\) by the homothety \({B^{k}}^{-1}\), then
where
and J is the Jacobian of the transformation
Then we obtain
and
where
with
5.4 The linear system and algorithm of resolution
The discrete equation leads to the following linear system:
The matrix A is obtained by assembling the bi-Laplacian matrices \(A^{k}=(\Delta(h_{i} h_{j}); \Delta(h_{p} h_{q} ) )_{N_{k}}, 1\leq k\leq K\), in the sub-domains. It takes the form
Naturally this matrix is not explicitly assembled in the effective resolution. Ψ denotes the vector of the admissible unknowns formed by the values of the solution in all the collocation points of the sub-domains and their respective boundaries. Finally, F is the second member given by
We denote that the matrix A is diagonal by block, symmetric, and positive definite. This permits us to solve the problem using the gradient conjugate algorithm method. However, it is not system (18) that we solve since it includes false degrees of freedom. The latter are eliminated by the action of the matrix \(Q^{T}\). The global system that we solve is
where Ψ̃ is the vector formed by the unknowns to internal collocation points and the values of the mortar functions on the skeleton of the decomposition. The matrix \(\tilde{A} = Q^{T} A Q\) is symmetric and positive definite. The following conjugate gradient algorithm explains how to solve system (19).
For this, let \(\tilde{\Psi}_{0}\) be arbitrary, \(R_{0}=Q^{T}F-\widetilde{A} \tilde{\Psi}_{0}\), \(T_{0}=R_{0}\), and
It is clear that all calculations (vector matrix product that is the most expensive, of order \(O(N^{3})\) for each element, as well as projections by Q and \(Q^{T}\)) are made at the local level (on each sub-domain). Consequently, the code can be parallelized.
5.5 Numerical results
We present in this section some numerical tests to confirm the obtained theoretical results. The error between the continuous and discrete solutions is studied. We consider the convergence in the case of both analytical and singular solutions for two domains where \(\omega=2\pi\) and \(\omega={{3\pi}\over 2}\) (Fig. 1).
The polynomial degree in the domain \(\bar{\Omega}_{k}, 1 \leq k\leq K\), containing the singular point v is denoted by N. In the other rectangular sub-domains, the degree of the polynomial is fixed less than N.
We begin by showing the efficiency of using the Strang and Fix algorithm with the method of domain decomposition.
For the two studied domains, we consider the first singular function as a given solution
-
for \(\omega=\frac{3\pi}{2}\),
$$\begin{aligned} \varphi^{*}_{\delta}(r,\theta)={}&S_{1}(r, \theta)=r^{1.54484}\phi(\theta) \\ ={}&r^{1.54484} \bigl[2.093 \bigl(\cos(0.459 \theta)-\cos(1.544 \theta ) \bigr) \\ &{} +1.093 \bigl(2.193\sin(0.459 \theta )-\sin(1.544 \theta) \bigr) \bigr], \end{aligned}$$(20) -
if \(\omega={2\pi}\),
$$ \varphi^{*}_{\delta}(r,\theta)=S_{1}(r, \theta)=r^{{3\over 2}} \biggl( \biggl(\sin {3\over 2}\theta-3\sin {\theta\over 2} \biggr) + \biggl(\cos{3\over 2}\theta-\cos {\theta\over 2} \biggr) \biggr). $$(21)
We present in Figs. 2 and 3 the obtained curves of the error respectively for the obtained solution from (20) and (21). The logarithm of the error with respect on one hand to N and on the other hand to the logarithm of N to obtain the slope is given. The obtained figures show that the Strang and Fix algorithm improves the results.
Error curves for the solution defined from (20)
Error curves for the solution defined from (21)
In the second example we choose the stream function
as an analytic function. In this case, the obtained error curves are presented in Fig. 4 for the two studied domains. We remark that the error is approximately the same. This shows the non-utility of the use of the Strang and Fix algorithm in the case where the solution is regular.
Error curves for the solution from (22), for \(\omega=\frac {3\pi}{2}\) and \(\omega=2\pi\)
We consider now the second singular function as a given solution which is obtained for each domain:
(i) for \(\omega=\frac{3\pi}{2}\),
(ii) for \(\omega=2\pi\),
The error convergence curves corresponding to these solutions are presented in Fig. 5. This shows that the convergence is not good with or without the Strang and Fix algorithm. This is due to the fact that we have to add the second singular function to the discrete space \(X^{*}_{\delta}\) (difficult to numerically implement) in order to improve the convergence.
We study now two examples of the numerical calculation of the discrete leading singularity coefficient \(\lambda_{1\delta}\) with respect to N.
Example 1
\(\varphi_{\delta}^{*}(x,y)=\sin^{2}\pi x^{2}\sin^{2}\pi y^{2}\) and \(\omega={3\pi \over 2}\).
N | 15 | 20 | 25 | 30 | 35 | 40 | 50 |
|---|---|---|---|---|---|---|---|
\(\lambda_{1\delta}\) | 7.0 10−1 | 4.453 10−3 | −0.951 10−9 | −3.041 10−12 | 1.382 10−13 | 6.221 10−14 | 0.329 10−14 |
Example 2
\(\varphi_{\delta}^{*}(r,\theta)=S_{1}(r,\theta )=r^{1.5}(\sin(1.5\theta)-3\sin(0.5\theta) + \cos(1.5\theta)-\cos (0.5\theta))\), and \(\omega={2\pi}\).
N | 15 | 20 | 30 | 40 | 45 | 50 | 60 |
|---|---|---|---|---|---|---|---|
\(\lambda_{1\delta}\) | 0.6976 | 0.8019 | 0.9054 | 0.9893 | 0.9993 | 1 | 1 |
Figure 6 shows the error curves in a logarithmic scale of the numerical solution of the discrete problem (8) (respectively the leading singularity coefficient) with respect to \(\log(N)\) in the case of \(\omega= {2\pi}\). Using this figure, the convergence order for the leading singularity coefficient is equal to 1.9986 and is equal to that of the solution. In our precedent work [22], the optimal order of convergence (3.9986) was obtained by the dual method.
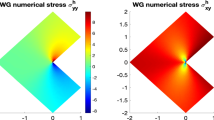
Finally, in Fig. 7 we present an application test corresponding to the discrete solution of the two biharmonic problems:
-
problem (25) for \(\omega=\frac{3\pi}{2}\),
-
the singular stream function in the cavity domain (see Fig. 8) for \(\omega=2 \pi\).
where \(\Gamma_{0}=\{(r,\theta) \text{ such that } \theta=0 \text{ and } \theta=\omega\}\).
The isovalues of solution for the cavity problem (left) and problem (25) (right)
6 Conclusion
In this paper we were interested in the numerical implementation of the mortar spectral method. We considered the biharmonic problem with a homogeneous boundary condition. The Strang and Fix algorithm was implemented. It consists in enlarging the space of the discrete solution by the first singular function. The obtained errors confirm that the used method permits us to improve the order of convergence. The present work shows the importance of the Strang and Fix algorithm coupled with the mortar spectral element method in solving a singular problem in the domain with corner. The mathematical analysis presented in this work can be adapted to other partial differential equations.
References
Baraket, S., Rădulescu, V.: Combined effects of concave-convex nonlinearities in a fourth-order problem with variable exponent. Adv. Nonlinear Anal. 16(3), 409–419 (2016)
Grisvard, P.: Elliptic Problems in Nonsmooth Domains. Pitman, Marshfield (1985)
Grisvard, P.: Singularities in Boundary Value Problems. Springer, Amsterdam (1982)
Kondratiev, V.A.: Boundary value problems for elliptic equations in domain with conical or angular points. Trans. Mosc. Math. Soc. 16, 227–313 (1967)
Bernardi, C., Maday, Y., Patera, A.T.: A new nonconforming approach to domain decomposition: the mortar element method. In: Brézis, H., Lions, J.L. (eds.) Nonlinear Partial Differential Equations and Their Applications, pp. 16–27 (1991) Collège de France Seminar
Babuška, I., Rosenzweig, M.B.: A finite element scheme for domains with corners. Numer. Math. 20, 1–21 (1972)
Babuška, I., Suri, M.: The optimal convergence rate of the p-version of the finite element method. SIAM J. Numer. Anal. 24, 750–776 (1987)
Bernardi, C., Maday, Y.: Polynomial approximation of some singular functions. Appl. Anal. 42, 1–32 (1991)
Strang, G., Fix, G.J.: An Analysis of the Finite Element Method. Prentice-Hall, New Jersey (1973)
Amara, M., Bernardi, C., Moussaoui, M.A.: Handling corner singularities by mortar elements method. Appl. Anal. 46, 25–44 (1992)
Amara, M., Moussaou, M.A.: Approximation de coefficients de singularité. C. R. Acad. Sci. Paris, Sér. I 313, 335–338 (1991)
Amara, M., Moussaou, M.A.: Approximation of solution and singularity coefficients for an elliptic equation in a plane polygonal domain. Preprint, E.N.S. Lyon (1989)
Kumar, K., Kumar, D., Singh, J.: Fractional modelling arising in unidirectional propagation of long waves in dispersive media. Adv. Nonlinear Stud. 5(4), 383–394 (2016)
Belhachmi, Z.: Méthode d’éléments spectraux avec joints pour la résolution de problèmes d’ordre quatre. Ph.D. thesis, Université Pierre et Marie Curie (1994)
Rădulescu, V., Repovš, D.: Partial Differential Equations with Variable Exponents: Variational Methods and Qualitative Analysis. Taylor and Francis Group, Boca Raton (2015)
Rădulescu, V.: Nonlinear elliptic equations with variable exponent: old and new. Nonlinear Anal., Theory Methods Appl. 121, 336–369 (2015)
Bernardi, C., Maday, Y.: Approximations Spectrales de Problèmes aux Limites Elliptiques. Collection Mathématiques et Applications. Springer, Paris (1996)
Abdelwahed, M., Chorfi, N., Rădulescu, V.: Handling geometric singularity by mortar spectral elements method for a fourth order problem. Electron. J. Differ. Equ. 2017, 82 (2017)
Belhachmi, Z.: Nonconforming mortar element methods for the spectral discretization of two-dimensional fourth-order problems. SIAM J. Numer. Anal. 34, 1545–1573 (1997)
Anagnostou, G.: Non conforming sliding spectral element methods for unsteady incompressible Navier–Stokes equation. Ph.D. thesis, Maassachusets Institute of Technology, Cambridge (1991)
Belhachmi, Z., Bernardi, C.: Resolution of fourth-order problems by the mortar element method. Comput. Methods Appl. Mech. Eng. 116, 53–58 (1994)
Abdelwahed, M., Chorfi, N., Rădulescu, V.: Approximation of the leading singular coefficient of an elliptic fourth-order equation. Electron. J. Differ. Equ. 2017, 305 (2017)
Acknowledgements
The authors would like to extend their sincere appreciation to the Deanship of Scientific Research at King Saud University for funding this Research group No (RG-1435-026).
Availability of data and materials
Not Applicable.
Funding
Not applicable.
Author information
Authors and Affiliations
Contributions
The authors declare that the study was realized in collaboration with equal responsibility. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Abdelwahed, M., Al Salam, A. & Chorfi, N. Solving the singular two-dimensional fourth order problem by the mortar spectral element method. Bound Value Probl 2018, 39 (2018). https://doi.org/10.1186/s13661-018-0960-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13661-018-0960-8