1 Introduction

We consider a nonlinear Schrödinger equation (NLS) with Dirac distribution defect [1–4]

$$ i u_{t}+\frac{1}{2} u_{xx}+q\delta_{a} u+g \bigl( \vert u \vert ^{2} \bigr) u=0 \quad\mbox{in } \boldsymbol {\Omega}\times \mathbb{R}_{+}, $$
(1)

where \(\boldsymbol {\Omega}\subset\mathbb{R}\), \(u=u(x,t)\) is the unknown solution maps \(\boldsymbol {\Omega}\times\mathbb{R}_{+}\) into \(\mathbb{C}\), \(\delta_{a}\) is the Dirac distribution at the point \(a\in \boldsymbol {\Omega }\), namely, \(\langle \delta_{a},v\rangle = v(a) \) for \(v \in \mathbf {H}^{1}(\boldsymbol {\Omega})\), and \(q \in\mathbb{R}\) represents its intensity parameter. Such distribution is introduced in order to model physically the defect at the point \(x=a\) (see [3–6]). The function g represents a generalization of the classical nonlinear Schrödinger equation (see for example [7–9]).

This specific model (1) is of recent research from a physical point of view in nonlinear optics plasma physics, water wave, quantum mechanics, hydrodynamics; see for example [10–15].

In nonlinear optics, equation (1) models a soliton propagating in a medium with a point defect [4, 16] or a wide soliton with a much narrower one in a bimodal fiber [17]. In the case when \(a=0\) and \(g(s)=s\), this model coincides with the Gross–Pitaevskii equation; see, for instance [1, 2, 4, 18, 19] and the references therein. See also [6, 20, 21] for some recent results dealing with NLS models.

The well-posedness of the solutions of the NLS equation (1) has been studied in the literature. In the case when \(q=0\) and \(\boldsymbol {\Omega}=\mathbb{R}\), the global existence in \(\mathbf {H}^{1}(\mathbb {R})\) and in \(\mathbf {L}^{2}(\mathbb{R})\) were proved in [22–24]. For bounded \(\boldsymbol {\Omega}\subset \mathbb{R}\) and with the standard boundary conditions (Dirichlet, Neumann and periodic), NLS equation (1) possesses a unique global solution in \(\mathbf {H}^{1}(\boldsymbol {\Omega})\), as was proved in [7]. In the last case \(q\neq0\) and \(g(s)=s\), in [4] the well-posedness in \(\mathbf {H}^{1}(\mathbb{R})\) of the solution of NLS equation (1) was proved.

The aim of this paper is to investigate the NLS equation (1) with Dirac interaction defect (\(q\neq0\)) in the case of a half-line in \(\mathbb{R}\). We consider for example \(\boldsymbol {\Omega}=\mathopen{]}-\infty,0[\) (the same calculations remain true for a positive half-line choice of Ω). The equation is endowed with a non-standard boundary condition at the point 0 in order to avoid the perturbations of the solutions caused by the boundary \(\{0\}\). The condition is actually necessary to achieve numerical solutions of the equation, as was demonstrated in [25–27]. The initial data is then supposed of a compact support in Ω. Our main results that have been proved entail that the NLS equation (1) has a unique solution in \(\mathbf {H}^{1}(\boldsymbol {\Omega})\). The demonstration is based on the Galerkin method. The continuous dependence of the solutions with regard to the initial data is also looked into.

The remainder of this paper is organized as follows. In Section 2, we provide some problem formulation and necessary technical results. In Section 3, we demonstrate the global well-posedness of the NLS equation in \(\mathbf {H}^{1}(\boldsymbol {\Omega})\). A few concluding remarks are given in Section 4.

2 Problem formulation and preliminaries

We discuss the nonlinear Schrödinger equation (NLS)

$$ i u_{t}+\frac{1}{2} u_{xx}+q\delta_{a} u +g \bigl( \vert u \vert ^{2} \bigr) u=0 \quad\mbox{in } \boldsymbol {\Omega }\times \mathbb{R}_{+}, $$
(2)

where \(\boldsymbol {\Omega}=\mathopen{]}-\infty,0[\), \(a<0\) and \(\delta_{a}\) is a Dirac interaction defect at point a. The smooth functional \(g\in \mathcal{C}^{1} ([0,+\infty[,\mathbb{R} )\) verifies the following conditions: There exist constants \(C\geq0\), \(\alpha_{1} > 0\), \(\alpha_{2} > 0\) and \(\theta\in[0,2[\) such that

$$ { \textstyle\begin{cases} g(r)\leq\alpha_{1} (1+r^{\theta} )\quad \mbox{for } r\geq0, \\ G(r)=\int_{0}^{r} g(s) \,ds\quad \mbox{and} \quad \vert G(r) \vert \leq\alpha_{2} r (1+r^{\theta} ) \quad\mbox{for } r\geq0, \\ \vert g'(r) \vert \leq C \quad\mbox{for } r\geq0. \end{cases}\displaystyle } $$
(3)

We associate with equation (2) a non-standard boundary condition at the point \(x=0\),

$$ \partial_{n} u(0,t)+\sqrt{2}e^{-i\pi/4}e^{i\mathbb{V}(0,t)} \partial_{t}^{1/2} \bigl(e^{-i\mathbb{V}(0,t)}u(0,t) \bigr)=0 \quad\mbox{for } t\in\mathbb{R}_{+}, $$
(4)

where the operator \(\partial_{n}\) is the normal derivative, the phase function \(\mathbb{V}\) defined by \(\mathbb{V}(x,t)= {\int _{0}^{t}g ( \vert u(x,s) \vert ^{2} ) \,ds}\) and operator \(\partial_{t}^{1/2}\) represent a \(\frac{1}{2}\) order Riemann–Liouville fractional derivative defined by

$$ \partial_{t}^{1/2}\bigl(h(t)\bigr)=\frac{1}{\sqrt{\pi}} \partial_{t} \biggl( \int _{0}^{t}\frac{h(s)}{\sqrt{t-s}}\,ds \biggr). $$
(5)

This result (4) is obtained by [25–27] with an initial data that has compact support in Ω, it represents an artificial boundary condition on \(x=0\) to the NLS equation (2) with \(q=0\). This condition is added in order to avoid the perturbation effect on the solutions resulting from the reflection at the limit point \(\{0\}\).

We consider \(u_{0} \in \mathbf {H}^{1}(\boldsymbol {\Omega})\) to be an initial data, such that its support is compact in Ω (see [25–27])

$$ u(x,0)=u_{0}(x) \quad\mbox{for } x\in \boldsymbol {\Omega}. $$
(6)

Next, using the method applied in [28], we obtain our first technical result.

Lemma 1

Consider the initial value problem in \(\mathbb{C}^{m}\)

$$ \textstyle\begin{cases} H^{\prime}(t) =\mathbf{M} \partial_{t}^{1/2} H(t) + \mathbf {P}(H(t)), \\ H(0)=H_{0}, \end{cases} $$
(7)

where M is a square matrix of order m, P represents a polynomial function of \(\mathbb{C}^{m}\), \(H_{0} \in\mathbb{C}^{m}\) is a constant vector. Then the problem (7) has a unique local solution \(H\in L^{\infty}(0,T;\mathbb{C}^{m})\).

Proof

We integrate (7) between 0 and t, to get

$$ H(t)=H_{0} +\frac{1}{\sqrt{\pi}} \mathbf{M} \int_{0}^{t}\frac {H(\tau)}{\sqrt{t-\tau}}\,d\tau-\mathbf{M} \bigl[I^{1/2}_{t} H(t)\bigr]_{t=0}+ \int_{0}^{t} \mathbf{P}\bigl(H(s)\bigr)\,ds, $$
(8)

where \(I_{t}^{1/2}\) represents the Riemann–Liouville fractional integral operator of \(\frac{1}{2}\) order defined by

$$ I_{t}^{1/2}\bigl(h(t)\bigr)=\frac{1}{\sqrt{\pi}} \int_{0}^{t}\frac {h(s)}{\sqrt{t-s}}\,ds. $$

Since \(H\in L^{\infty}(0,T;\mathbb{C}^{m})\) we have \([I^{1/2}_{t} H(t)]_{t=0}=0\). Then equation (8) becomes

$$ H(t)=H_{0} +\frac{1}{\sqrt{\pi}} \mathbf{M} \int_{0}^{t}\frac {H(\tau)}{\sqrt{t-\tau}}\,d\tau+ \int_{0}^{t} \mathbf{P}\bigl(H(s)\bigr)\,ds. $$
(9)

We show that there exists a unique function H verifying equation (9) by applying the Banach fixed-point theorem. Let \(T>0\), we denote

$$ X_{T}=L^{\infty}\bigl(0,T,\mathbb{C}^{m}\bigr) \quad\mbox{and} \quad \Vert H \Vert _{X_{T}} =\sup_{t\in[0,T]} \bigl\Vert H(t) \bigr\Vert _{2}, $$

where \(\Vert \cdot \Vert _{2}\) is the Euclidean norm in \(\mathbb{C}^{m}\). We are looking for a fixed point of the functional

$$ \Phi\bigl(H(t)\bigr)=H_{0} +\frac{1}{\sqrt{\pi}} \mathbf{M} \int_{0}^{t}\frac {H(\tau)}{\sqrt{t-\tau}}\,d\tau+ \int_{0}^{t} \mathbf{P}\bigl(H(s)\bigr)\,ds. $$
(10)

Φ sends the closed ball \(B_{X_{T}} (0, R)\) into itself. Let \(R= 2 \Vert H_{0} \Vert _{2} \) and let \(H\in X_{T} \) such that \(\Vert H \Vert _{X_{T}}\leq R\). Using (9), there exists a constant \(C_{1}(R)>0\) such that

$$\begin{aligned} \bigl\Vert \Phi(H) \bigr\Vert _{2} &\leq \Vert H_{0} \Vert _{2} + \frac{2}{\sqrt {\pi}} \Vert \mathbf{M} \Vert _{2} \sqrt{T} R + C_{1}(R) T \\ &\leq\frac{R}{2} + \biggl(\frac{2 \Vert \mathbf{M} \Vert _{2} \sqrt {T}}{\sqrt{\pi}} + \frac{C_{1}(R)T}{R} \biggr) R, \end{aligned}$$

where \(\Vert \mathbf{M} \Vert _{2} = \sup_{ \Vert Y \Vert _{2} =1 } \Vert \mathbf{M} Y \Vert _{2}\). If you choose T such that \((\frac{2 \Vert \mathbf{M} \Vert _{2} \sqrt{T}}{\sqrt{\pi}} + \frac{C_{1}(R)T}{R} )\leq\frac{1}{2}\) we see that the functional Φ sends the closed ball \(B_{X_{T}} (0, R)\) into itself.

Φ is a contraction mapping in \(B_{X_{T}} (0, R)\). Let \(H, L \in B_{X_{T}} (0, R)\) such that \(\Vert H \Vert _{X_{T}}\leq R\) and \(\Vert L \Vert _{X_{T}}\leq R\). Let \(t< T\) where T satisfies \((\frac{2 \Vert \mathbf{M} \Vert _{2} \sqrt{T}}{\sqrt{\pi}} + \frac {C_{1}(R)T}{R} )\leq\frac{1}{2}\). We have

$$\begin{aligned} \bigl\Vert \Phi(H)-\Phi(L) \bigr\Vert _{2} \leq\frac{2 \Vert \mathbf{M} \Vert _{2} \sqrt{T}}{\sqrt{\pi}} \Vert H-L \Vert _{X_{T}} + \int_{0}^{t} \bigl\vert \mathbf{P} \bigl(H(s) \bigr)-\mathbf{P}\bigl(L(s)\bigr) \bigr\vert \,ds. \end{aligned}$$

Since P is a polynomial function and \(B_{X_{T}} (0, R)\) is bounded, P has Lipschitz continuity in \(B_{X_{T}} (0, R)\). This shows that there exists a constant \(C_{2}(R)>0\) such that

$$\begin{aligned} \bigl\Vert \Phi(H)-\Phi(L) \bigr\Vert _{2} &\leq \frac{2 \Vert \mathbf{M} \Vert _{2} \sqrt{T}}{\sqrt{\pi}} \Vert H-L \Vert _{X_{T}} + C_{2}(R) T \Vert H-L \Vert _{X_{T}} \\ &\leq \biggl(\frac{2 \Vert \mathbf{M} \Vert _{2} \sqrt{T}}{\sqrt{\pi}} + C_{2}(R) T \biggr) \Vert H-L \Vert _{X_{T}}. \end{aligned}$$

By choosing \(C(R)=\min ( \frac{C_{1}(R)}{R}, C_{2}(R) )\), there exists \(T>0\) such that \((\frac{2 \Vert \mathbf{M} \Vert _{2} \sqrt{T}}{\sqrt{\pi}} + \frac{C_{1}(R)T}{R} )\leq\frac{1}{2}\) and \((\frac{2 \Vert \mathbf{M} \Vert _{2} \sqrt{T}}{\sqrt{\pi}} + C_{2}(R) T )\leq \frac{1}{2}<1\). This shows that the functional Φ is a contraction mapping in \(B_{X_{T}} (0, R)\). By applying the Banach fixed-point theorem, there exists a unique function H verifying equation (9). □

The following lemma was proved in [9, 29].

Lemma 2

Let \(\phi\in \mathbf {H}^{1/4}(0,\mathbf {T})\) and \(\psi\in \mathbf {H}^{3/4}(0,\mathbf {T})\), such that \(\psi(0)=0\), be two functions extended by zero outside \([0,T]\). Then we have the following inequalities:

$$\begin{aligned} &\mathrm{(i)}\quad \operatorname{\mathcal{R}e} \biggl(e^{i\pi/4} \int_{0}^{+\infty}\overline{\phi} \partial_{t}^{1/2} \phi \,dt \biggr)\geq0; \\ &\mathrm{(ii)}\quad \operatorname{\mathcal{R}e} \biggl(e^{-i\pi/4} \int_{0}^{+\infty}\overline{\psi_{t}} \partial_{t}^{1/2}\psi \,dt \biggr)\geq0. \end{aligned}$$

Remark 1

Let \(\phi\in \mathbf {H}^{1/4}(t_{1},t_{2})\) be a function extended by zero outside \([t_{1},t_{2}]\); we have

$$ \operatorname{\mathcal{R}e} \biggl(e^{ i\pi/4} \int_{t_{1}}^{t_{2}}\overline{\phi} \partial_{t}^{1/2} \phi \,dt \biggr)\geq0. $$

We state that the following lemma proved in [9].

Lemma 3

Let the complex function \(w\in \mathbf {H}^{1}(\boldsymbol {\Omega})\) be defined in \(\boldsymbol {\Omega}=\mathopen{]}-\infty,0[\). Then we have

$$ \bigl\vert w(0) \bigr\vert ^{2} \leq2 \Vert w \Vert _{L^{2}(\Omega)} \Vert w_{x} \Vert _{L^{2}(\Omega)}. $$

We introduce our technical result.

Lemma 4

Let \(\boldsymbol {\Omega}=\mathopen{]}-\infty,0[\), we assume that the sequence \((\lambda_{m} )_{m}\) of \(\mathbf {H}^{1}(\boldsymbol {\Omega})\) is such that \(\Vert \lambda_{m} \Vert _{H^{1}(\Omega)}\leq C\) and \(\lambda_{m} \longrightarrow 0\) in \(\mathbf {L}^{2}(\boldsymbol {\Omega})\) when \(m\longrightarrow+\infty\). Then \(\lambda_{m}(0)\longrightarrow0\) when \(m\longrightarrow+\infty\).

Proof

Since \(\lambda_{m} \in \mathbf {H}^{1}(\boldsymbol {\Omega})\), by using Lemma 3, we have

$$\begin{aligned} \bigl\vert \lambda_{m}(0) \bigr\vert ^{2} &\leq2 \Vert \lambda_{mx} \Vert _{L^{2}(\Omega)} \Vert \lambda_{m} \Vert _{L^{2}(\Omega)} \\ &\leq2 C \Vert \lambda_{m} \Vert _{L^{2}(\Omega)}. \end{aligned}$$

Hence the result. □

Finally, we state the last lemma, which has been proved in [30].

Lemma 5

Let \(K\times]0,T[\) be an open bounded subset of \(\mathbb{R}_{x} \times \mathbb{R}_{t}\), \(g_{\mu}\) and g are functions in \(L^{q}(K\times ]0,T[)\), \(1< q<\infty\), such that

$$ \Vert g_{\mu} \Vert _{L^{q}(K\times]0,T[)}\leq C\quad \textit{and}\quad g_{\mu }\longrightarrow g \quad\textit{a.e in } K\times]0,T[. $$

Then \(g_{\mu}\rightharpoonup g\) in the weak topology of \(L^{q}(K\times]0,T[)\).

3 Well-posedness of NLS equation

In this section, we are able to announce and prove our main result.

Theorem 1

Let \(u_{0}\in \mathbf {H}^{1}(\boldsymbol {\Omega})\) be an initial data with compact support in Ω. Then there exists a unique function \(u\in \mathcal{C}^{0}([0,+\infty[;\mathbf {H}^{1}(\boldsymbol {\Omega}))\cap \mathcal{C}^{1}([0,+\infty[;[\mathbf {H}^{1}(\boldsymbol {\Omega})]^{\prime})\) solution to the NLS equation (2)–(4)–(6), where \(\mathcal{C}^{k}(\mathbf {I};\mathbf {E})\) represents the space of k times continuously differentiable functions on I in E, \([\mathbf {H}^{1}(\boldsymbol {\Omega} )]'\) is the dual of \(\mathbf {H}^{1}(\boldsymbol {\Omega})\).

Remark 2

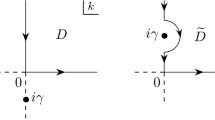
If u is a solution of the NLS equation (2)–(4)–(6), then \(\tilde{u}: (x,t)\longmapsto u(-x,t) \) is also a solution of the following NLS equation:

$$ \textstyle\begin{cases} i \tilde{u}_{t}+\frac{1}{2} \tilde{u}_{xx}+q\delta_{-a} \tilde{u} +g ( \vert \tilde{u} \vert ^{2} ) \tilde{u}=0\quad \mbox{in }\tilde{\boldsymbol {\Omega}}\times\mathbb{R}_{+} \\ \partial_{n} \tilde{u}(0,t)+\sqrt{2}e^{-i\pi/4}e^{i\tilde {\mathbb{V}}(0,t)} \partial_{t}^{1/2} (e^{-i\tilde{\mathbb{V}}(0,t)}\tilde {u}(0,t) )=0,\quad t\in\mathbb{R}_{+},\\ \tilde{u}(x,0)=u_{0}(-x), \quad x\in\Omega, \end{cases} $$
(11)

where \(\tilde{\boldsymbol {\Omega}}=\mathopen{]}0,+\infty[\) and \(\tilde{\mathbb{V}}(x,t)=\int_{0}^{t}g ( \vert \tilde{u}(x,s) \vert ^{2} ) \,ds \).

The remainder of this section contains the proof of Theorem 1.

For the sake of simplicity, we make a change of the unknown solution to the nonlinear equation (2)–(4)–(6),

$$ v(x,t)=\exp\bigl(-i \mathbb{V}(0,t)\bigr)u(x,t). $$
(12)

Therefore, the NLS equation (2)–(4)–(6) is rewritten in the form

$$ \textstyle\begin{cases} i v_{t}+\frac{1}{2} v_{xx}+q\delta_{a} v + ( g ( \vert v(x,t) \vert ^{2} )-g ( \vert v(0,t) \vert ^{2} ) ) v=0 \quad\mbox{in } \boldsymbol {\Omega}\times\mathbb {R}_{+}, \\ \partial_{n} v(0,t)+\sqrt{2}e^{-i\pi/4} \partial_{t}^{1/2} (v(0,t) )=0,\quad t\in\mathbb{R}_{+},\\ v(x,0)=u_{0}(x),\quad x\in\Omega. \end{cases} $$
(13)

Remark 3

From (12), we have the following properties:

  1. (i)

    \({ \vert v(x,t) \vert = \vert u(x,t) \vert }\),

  2. (ii)

    \({u(x,t)=\exp (i \int_{0}^{t}g ( \vert v(0,s) \vert ^{2} ) \,ds ) v(x,t)}\),

  3. (iii)

    \({ \Vert v(t) \Vert _{H^{m}(\Omega)}= \Vert u(t) \Vert _{H^{m}(\Omega)}}\) for all \(m\geq0\).

We use the Galerkin method to show that there exists a solution \(v\in \mathcal{C}^{0}([0,+\infty[;\mathbf {H}^{1}(\boldsymbol {\Omega}))\cap \mathcal{C}^{1}([0,+\infty[;[\mathbf {H}^{1}(\boldsymbol {\Omega})]^{\prime})\) of the NLS equation (13). This method is divided into three steps as shown below. Also, we prove the uniqueness of this solution in the last subsection. As a result, by Remark 3 there exists a unique function \(u\in \mathcal{C}^{0}([0,+\infty[;\mathbf {H}^{1}(\boldsymbol {\Omega}))\cap \mathbf {\mathcal{C}}^{1}([0,+\infty[;[\mathbf {H}^{1}(\boldsymbol {\Omega})]^{\prime})\), a solution of (2)–(4)–(6).

3.1 First step: approximate problem

Let \((\varphi_{k})_{k}\) be an orthonormal basis of functions in \(\mathbf {H}^{1}(\boldsymbol {\Omega})\). For \(m\geq1\), we set \(\mathcal{H}_{m} = \operatorname{Span}(\varphi _{1},\ldots, \varphi_{m})\) and we define the orthogonal projection operator \(P_{m}\) by

$$ \begin{aligned} &P_{m}: H^{1}(\Omega) \to \mathcal{H}_{m} \\ &\phantom{P_{m}:} v \mapsto P_{m}(v)=\sum_{k=1}^{m} \langle v,\varphi_{k} \rangle _{H^{1}(\Omega)} \varphi_{k}, \end{aligned} $$
(14)

where \(\langle\cdot,\cdot\rangle_{H^{1}(\Omega)}\) is the scalar product in \(\mathbf {H}^{1}(\boldsymbol {\Omega})\). For \(m\geq1\), we shall approximate v in (13) by

$$ v_{m}(t)=\sum_{k=1}^{m} h_{km}(t)\varphi_{k}, $$
(15)

which satisfies, for all \(k \in\{1,2,\ldots,m \}\),

$$ \textstyle\begin{cases} \frac{d}{dt} \langle i v_{m}, \varphi_{k} \rangle_{L^{2}(\Omega ),L^{2}(\Omega)}-\frac{1}{2}\langle v_{mx},\varphi_{kx}\rangle _{L^{2}(\Omega),L^{2}(\Omega)} \\ \quad{}-\frac{\sqrt{2}e^{-i\pi/4}}{2}\partial_{t}^{1/2} (v_{m}(0,t) )\overline{\varphi_{k}(0)} +q \langle\delta_{a} v_{m},\varphi_{k} \rangle_{[H^{1}(\Omega )]',H^{1}(\Omega)} \\ \quad{}+\langle g ( \vert v_{m} \vert ^{2} ) v_{m},\varphi_{k} \rangle _{L^{2}(\Omega),L^{2}(\Omega)} -g ( \vert v_{m}(0,t) \vert ^{2} )\langle v_{m},\varphi_{k} \rangle_{L^{2}(\Omega),L^{2}(\Omega)}=0, \\ v_{m}(0) = P_{m}(u_{0}). \end{cases} $$
(16)

We get the system

$$ i \mathbf{A} H'_{m}(t) - \frac{\sqrt{2}e^{-i\pi/4}}{2} \mathbf{B} \partial_{t}^{1/2} H_{m}(t) = \mathbf{F} \bigl(H_{m}(t)\bigr), $$
(17)

where F is a polynomial function, A and B are square matrices of order m defined by

$$ \mathbf{A}= \bigl( \langle\varphi_{j}, \varphi_{k} \rangle_{L^{2}(\Omega),L^{2}(\Omega)} \bigr)_{k,j}, \qquad \mathbf{B}= \bigl( \varphi_{j}(0)\overline{\varphi_{k}(0)} \bigr)_{k,j} $$

and

$$ H_{m}(t)= \begin{pmatrix} h_{1m}(t) \\ \cdot \\ \cdot \\ \cdot\\ h_{mm}(t) \end{pmatrix} \in\mathbb{C}^{m}, $$

such that at \(t=0\) the components of \(H_{m}(0)\) are

$$ h_{mk}(0)=k\mbox{{th} element of } u_{m0}. $$
(18)

The matrix A is Hermitian and positive-definite, then it is invertible. Therefore

$$ H'_{m}(t) + \frac{\sqrt{2}e^{i\pi/4}}{2} \mathbf{A}^{-1} \mathbf{B} \partial_{t}^{1/2} H_{m}(t) = -i \mathbf{A}^{-1}\mathbf{F}\bigl(H_{m}(t)\bigr). $$
(19)

We set

$$ \mathbf{M}=-\frac{\sqrt{2}e^{i\pi/4}}{2} \mathbf{A}^{-1}\mathbf{B} $$

and

$$ \mathbf{P}\bigl(H_{m}(t)\bigr)=-i \mathbf{A}^{-1}\mathbf{F} \bigl(H_{m}(t)\bigr). $$

The system (19) becomes

$$ \textstyle\begin{cases} H'_{m}(t) =\mathbf{M} \partial_{t}^{1/2} H_{m}(t) + \mathbf{P}(H_{m}(t)), \\ H_{m}(0)=H_{m0}, \end{cases} $$
(20)

where P is a polynomial function of \(\mathbb{C}^{m}\). By using Lemma 1, we see that the system (20) has a unique local solution. Then we obtain a unique function \(H_{m} = (h_{1m},\ldots,h_{mm})\) in \([0, T_{m}]\), a solution of (17) with the initial condition (18). As a result, the approximate problem (16) has a unique solution \(v_{m}\) such that \(v_{m}: [0,T_{m}]\rightarrow\mathcal{H}_{m} \). The existence of a maximal solution \(v_{m}\) (defined on \([0, T_{\mathrm{max}}[\)) is obtained by iterating m, where \(T_{\mathrm{max}}\) is the maximum time of the existence such that \(v_{m}: [0,T_{\mathrm{max}}[\rightarrow\mathcal{H}_{m} \). Then we have \(T_{\mathrm{max}}<+\infty\) and \(\lim_{t \to T_{\mathrm{max}}} \vert v_{m} \vert =+\infty\), or \(T_{\mathrm{max}}=+\infty\).

3.2 Second step: a priori estimates

3.2.1 Estimate in \(\mathbf {L}^{2}(\boldsymbol {\Omega})\)

We multiply (13) by \(-i\overline{v}\) and we integrate in space domain Ω. We then integrate by parts the second term and consider the real part, to get

$$ \frac{d}{dt} \bigl\Vert v(t) \bigr\Vert _{L^{2}(\Omega)}^{2} =\operatorname{\mathcal{R}e} \bigl(i \overline{v(0,t)} \partial_{n} v(0,t) \bigr). $$
(21)

We integrate this equality between 0 and t with \(t\in[0,+\infty [\), to get

$$ \bigl\Vert v(t) \bigr\Vert _{L^{2}(\Omega)}^{2} - \Vert u_{0} \Vert _{L^{2}(\Omega)}^{2}= \int_{0}^{t}\operatorname{\mathcal{R}e} \bigl(i \overline{v(0,s)} \partial_{n} v(0,s) \bigr)\,ds. $$

By using the boundary condition for (13) and Lemma 2, we show that \(\int_{0}^{t}\operatorname{\mathcal{R}e} (i \overline {v(0,s)} \partial_{n} v(0, s) )\,ds \leq0\). Hence

$$ \mbox{For } t\geq0, \quad\bigl\Vert v(t) \bigr\Vert _{L^{2}(\Omega)}^{2} \leq \Vert u_{0} \Vert _{L^{2}(\Omega)}^{2}. $$

This gives the a priori estimate in \(\mathbf {L}^{2}(\boldsymbol {\Omega})\)

$$ \sup_{m} \sup_{ t \in[0,+\infty[} \bigl\Vert v_{m} (t) \bigr\Vert _{L^{2}(\Omega )}\leq \Vert u_{0} \Vert _{L^{2}(\Omega)}=K_{0}. $$
(22)

3.2.2 Estimate in \(\mathbf {H}^{1}(\boldsymbol {\Omega})\)

We multiply the first equality of (13) by \(\overline{v_{t}}\) and we integrate in Ω. By considering the real part, we obtain

$$ \frac{d}{dt}\Psi\bigl(v(t)\bigr)=2\operatorname{\mathcal{R}e} \bigl(\overline {v_{t}(0,t)}\partial_{n} v(0,t) \bigr)-2g \bigl( \bigl\vert v(0,t) \bigr\vert ^{2} \bigr)\frac{d}{dt} \Vert v \Vert ^{2}_{L^{2}(\Omega)}, $$
(23)

where

$$ \Psi\bigl(v(t)\bigr)= \Vert v_{x} \Vert ^{2}_{L^{2}(\Omega)}-2q \bigl\vert v(a,t) \bigr\vert ^{2}-2 \int_{\Omega}G \bigl( \vert v \vert ^{2} \bigr)\,dx, $$
(24)

with G is defined by (3).

From the following, we set that K can be any positive constant depending only on q, \(\alpha_{1}\), \(\alpha_{2}\), θ and \(K_{0}\).

We have

$$\begin{aligned} \biggl\vert -g \bigl( \bigl\vert v(0,t) \bigr\vert ^{2} \bigr) \frac{d}{dt} \Vert v \Vert ^{2}_{L^{2}(\Omega)} \biggr\vert &= \bigl\vert g \bigl( \bigl\vert v(0,t) \bigr\vert ^{2} \bigr) \bigr\vert \frac{d}{dt} \bigl( \lambda(t) \Vert v \Vert ^{2}_{L^{2}(\Omega)} \bigr), \end{aligned}$$
(25)

where \(\lambda(t)=\operatorname{sign} (\frac{d}{dt} \Vert v \Vert ^{2}_{L^{2}(\Omega)} )\). By using (3), (25) and equality (23), we obtain

$$ \frac{d}{dt}\Psi\bigl(v(t)\bigr)\leq2\operatorname{\mathcal{R}e} \bigl(\overline {v_{t}(0,t)}\partial_{n} v(0,t) \bigr)+2\alpha_{1} \bigl(1+ \bigl\vert v(0,t) \bigr\vert ^{2\theta} \bigr) \frac{d}{dt} \bigl(\lambda(t) \Vert v \Vert ^{2}_{L^{2}(\Omega)} \bigr). $$

Therefore

$$\begin{aligned} \frac{d}{dt} \bigl(\Psi\bigl(v(t)\bigr) -2\alpha_{1} \lambda(t) \Vert v \Vert ^{2}_{L^{2}(\Omega)} \bigr)\leq{}&2\operatorname{\mathcal{R}e} \bigl( \overline {v_{t}(0,t)}\partial_{n} v(0,t) \bigr) \\ &{}+2\alpha_{1} \bigl\vert v(0,t) \bigr\vert ^{2\theta} \frac{d}{dt} \bigl(\lambda (t) \Vert v \Vert ^{2}_{L^{2}(\Omega)} \bigr). \end{aligned}$$
(26)

We use Lemma 3 and (22), to get

$$\begin{aligned} &\frac{d}{dt} \bigl(\Psi\bigl(v(t)\bigr) -2\alpha_{1} \lambda(t) \Vert v \Vert ^{2}_{L^{2}(\Omega)} \bigr) \\ &\quad\leq2\operatorname{\mathcal{R}e} \bigl(\overline{v_{t}(0,t)}\partial_{n} v(0,t) \bigr)+K \bigl\Vert v_{x}(t) \bigr\Vert _{L^{2}(\Omega)}^{\theta}\frac {d}{dt} \bigl(\lambda(t) \Vert v \Vert ^{2}_{L^{2}(\Omega)} \bigr) \\ &\quad \leq 2\operatorname{\mathcal{R}e} \bigl(\overline{v_{t}(0,t)}\partial_{n} v(0,t) \bigr)+K \sup_{s\in[0,T_{\mathrm{max}}[} \bigl( \bigl\Vert v_{x}(s) \bigr\Vert _{L^{2}(\Omega)}^{\theta} \bigr) \frac{d}{dt} \bigl(\lambda(t) \Vert v \Vert ^{2}_{L^{2}(\Omega)} \bigr), \end{aligned}$$

where \(T_{\mathrm{max}}>0\) is the maximum time of existence of \((v_{m})_{m}\), which gives

$$\begin{aligned} &\frac{d}{dt} \Bigl(\Psi\bigl(v(t)\bigr) -2\alpha_{1} \lambda(t) \Vert v \Vert ^{2}_{L^{2}(\Omega)} - K \sup_{s\in[0,T]} \bigl( \bigl\Vert v_{x}(s) \bigr\Vert _{L^{2}(\Omega)}^{\theta} \bigr) \lambda(t) \bigl\Vert v(t) \bigr\Vert ^{2}_{L^{2}(\Omega)} \Bigr) \\ &\quad \leq2\operatorname{\mathcal{R}e} \bigl(\overline{v_{t}(0,t)}\partial_{n} v(0,t) \bigr). \end{aligned}$$
(27)

Integrating the equality (27) between 0 and t, we get

$$\begin{aligned} &\Psi\bigl(v(t)\bigr) -2\alpha_{1} \lambda(t) \Vert v \Vert ^{2}_{L^{2}(\Omega)} - K \sup_{s\in[0,T]} \bigl( \bigl\Vert v_{x}(s) \bigr\Vert _{L^{2}(\Omega)}^{\theta } \bigr) \lambda(t) \bigl\Vert v(t) \bigr\Vert ^{2}_{L^{2}(\Omega)} \\ &\quad \leq\Psi(u_{0}) +2\alpha_{1} \Vert u_{0} \Vert ^{2}_{L^{2}(\Omega)} +K \Vert u_{0} \Vert ^{2}_{L^{2}(\Omega)}\sup_{s\in[0,T_{\mathrm{max}}[} \bigl( \bigl\Vert v_{x}(s) \bigr\Vert _{L^{2}(\Omega)}^{\theta} \bigr) \\ & \qquad{}- 2\sqrt{2}\operatorname{\mathcal{R}e} \biggl(e^{-i\pi/4} \int_{0}^{t} \overline {v_{t}(0,t)} \partial_{t}^{1/2} v(0,t) \biggr). \end{aligned}$$

Using Lemma 2, we obtain

$$ \Psi\bigl(v(t)\bigr)\leq\Psi(u_{0}) +K + K \sup_{s\in[0,T_{\mathrm{max}}[} \bigl( \bigl\Vert v_{x}(s) \bigr\Vert _{L^{2}(\Omega)}^{\theta} \bigr). $$

Using equation (24) of \(\Psi(v(t))\), we have

$$\begin{aligned} \bigl\Vert v_{x}(t) \bigr\Vert ^{2}_{L^{2}(\Omega)} \leq{}& K \sup_{s\in[0,T_{\mathrm{max}}[} \bigl( \bigl\Vert v_{x}(s) \bigr\Vert _{L^{2}(\Omega )}^{\theta} \bigr)+2q \bigl\vert v(a,t) \bigr\vert ^{2} \\ & {}+2 \int_{\Omega}G \bigl( \vert v \vert ^{2} \bigr)\,dx+ \Psi(u_{0}) +K. \end{aligned}$$
(28)

We will majorize the second member of (28).

By using the Young inequality, we get

$$ K \sup_{s\in[0,T_{\mathrm{max}}[} \bigl( \bigl\Vert v_{x}(s) \bigr\Vert _{L^{2}(\Omega )}^{\theta} \bigr)\leq\frac{1}{4}\sup _{s\in[0,T_{\mathrm{max}}[} \bigl\Vert v_{x}(s) \bigr\Vert _{L^{2}(\Omega)}^{2}+ K. $$
(29)

We apply the Agmon and Young inequalities using (22), and we have

$$ 2q \bigl\vert v(a,t) \bigr\vert ^{2}\leq2 \vert q \vert \Vert v \Vert _{L^{2}(\Omega )} \Vert v_{x} \Vert _{L^{2}(\Omega)} \leq2 \vert q \vert K_{0} \Vert v_{x} \Vert _{L^{2}(\Omega)}\leq\frac{1}{4} \Vert v_{x} \Vert _{L^{2}(\Omega)}^{2}+ K. $$
(30)

By considering (3) and by using the Gagliardo–Nirenberg and the Young inequalities, we have

$$\begin{aligned} 2 \int_{\Omega} G\bigl( \bigl\vert v(x,t) \bigr\vert ^{2}\bigr) \,dx &\leq2\alpha_{2} \bigl\Vert v(t) \bigr\Vert _{L^{2}(\Omega)}+2\alpha_{2} \int_{\Omega} \bigl\vert v(x,t) \bigr\vert ^{2(\theta+1)} \,dx \\ & \leq2 \alpha_{2} K_{0}^{2} + 2 \alpha_{2} C \bigl\Vert v(t) \bigr\Vert _{L^{2}(\Omega )}^{2+\theta} \bigl\Vert v_{x}(t) \bigr\Vert _{L^{2}(\Omega)}^{\theta} \\ & \leq K+K \bigl\Vert v_{x}(t) \bigr\Vert _{L^{2}(\Omega)}^{\theta} \\ & \leq\frac{1}{4} \bigl\Vert v_{x}(t) \bigr\Vert _{L^{2}(\Omega)}^{2}+ K. \end{aligned}$$
(31)

Then, by using (28), (29), (30) and (31), we obtain

$$ \frac{1}{2} \bigl\Vert v_{x}(t) \bigr\Vert _{L^{2}(\Omega)}^{2}\leq\frac {1}{4}\sup_{s\in[0,T_{\mathrm{max}}[} \bigl\Vert v_{x}(s) \bigr\Vert _{L^{2}(\Omega)}^{2} + K+ \Psi(u_{0}). $$

By taking the supremum on the left side of this inequality, we obtain

$$ \sup_{t\in[0,T_{\mathrm{max}}[} \bigl\Vert v_{x}(t) \bigr\Vert _{L^{2}(\Omega)}^{2}\leq K+4\Psi(u_{0}). $$

Then \(T_{\mathrm{max}}=+\infty\) and the sequence \((v_{m})_{m}\) remains bounded in \(\mathcal{C}_{b}([0,+\infty[; \mathbf {H}^{1}(\boldsymbol {\Omega}))\). Hence, there exists \(K_{1} > 0\), which is dependent on the equation data, such that

$$ \sup_{m} \sup_{t\in[0,+\infty[} \bigl\Vert v_{m}(t) \bigr\Vert _{H^{1}(\Omega )}\leq K_{1}. $$
(32)

We now specify the space where \((v'_{m})_{m}\) remains bounded. By (16), we see that

$$ i v'_{m}=P_{m}^{*} \biggl( - \frac{1}{2}v_{mxx}-q\delta_{a}v_{m} -g\bigl( \vert v_{m} \vert ^{2}\bigr) v_{m}+g\bigl( \bigl\vert v_{m}(0,t) \bigr\vert ^{2}\bigr) v_{m} \biggr), $$

where \(P_{m}^{*}\) is the operator of \([\mathbf {H}^{1}(\boldsymbol {\Omega})]^{\prime}\) in \(\mathcal{H}_{m}\) defined by \(\forall\eta\in[\mathbf {H}^{1}(\boldsymbol {\Omega})]^{\prime}\), \(\forall\omega\in \mathbf {H}^{1}(\boldsymbol {\Omega})\), \(\langle P_{m}^{*}\eta,\omega\rangle _{H^{1}(\Omega),[H^{1}(\Omega)]'}=\langle\eta,P_{m}\omega\rangle _{[H^{1}(\Omega)]',H^{1}(\Omega)} \). We see that \(P_{m}^{*}\) is a bounded operator on \([\mathbf {H}^{1}(\boldsymbol {\Omega} )]^{\prime}\). The operator \(\partial_{x}^{2}: \mathbf {H}^{1}(\boldsymbol {\Omega})\longrightarrow[\mathbf {H}^{1}(\boldsymbol {\Omega} )]^{\prime}\) is continuous, then \((P_{m}^{*}(v_{mxx}))_{m}\) is a bounded sequence in \([\mathbf {H}^{1}(\boldsymbol {\Omega})]^{\prime}\). On the other hand, the sequence \((\delta_{a} v_{m})_{m}\) remains bounded in \([\mathbf {H}^{\frac{3}{4}}(\boldsymbol {\Omega} )]'\) and the sequences \(P_{m}^{*}(g( \vert v_{m} \vert ^{2} ) v_{m})_{m}\) and \(P_{m}^{*}(g( \vert v_{m}(0,t) \vert ^{2} ) v_{m})_{m}\) remain bounded in \(\mathbf {H}^{1}(\boldsymbol {\Omega})\). Hence, we see that \((v^{\prime}_{m})_{m}\) remains bounded in \(\mathcal{C}_{b} ([0,+\infty[; [\mathbf {H}^{1}(\Omega)]^{\prime})\).

3.2.3 Estimate of \(x v(t)\) in \(\mathbf {L}^{2}(\boldsymbol {\Omega})\)

In order to pass to the limit in the nonlinear term, we require the inclusion of the approximated solution \(v_{m}\) in \(\mathbf {H}^{1}(\boldsymbol {\Omega})\cap \mathbf {L}^{2} (\boldsymbol {\Omega}; (1+x^{2})\,dx )\). The reason behind this necessity is the well-known compact injection: \(\mathbf {H}^{1}(\boldsymbol {\Omega})\cap \mathbf {L}^{2} (\boldsymbol {\Omega}; (1+x^{2})\,dx )\) in \(\mathbf {L}^{2}(\boldsymbol {\Omega})\). We have already proved the estimate of \(v_{m}\) in \(\mathbf {H}^{1}(\boldsymbol {\Omega})\) and so this section shows the estimate of \(v_{m}\) in \(\mathbf {L}^{2} (\boldsymbol {\Omega}; (1+x^{2})\,dx )\).

We multiply (13) by \(-i x^{2} \overline{v}\) and we integrate in Ω. By using integration by parts and by considering the real part, we get

$$\begin{aligned} \frac{1}{2}\frac{d}{dt} \bigl\Vert x v(t) \bigr\Vert _{L^{2}(\Omega)}^{2}= -\frac {1}{2} \operatorname{\mathcal{R}e} \bigl[i x^{2} v_{x}(x,t)\overline{v(x,t)} \bigr]_{-\infty}^{0} -\operatorname{\mathcal{R}e} \biggl( i \int_{\Omega} x v_{x}\overline{v} \,dx \biggr). \end{aligned}$$

Since \(v\in \mathbf {H}^{1}(\boldsymbol {\Omega})\) we have \(\frac{1}{2} \operatorname{\mathcal{R}e} [i x^{2} v_{x}(x,t)\overline{v(x,t)} ]_{-\infty}^{0}=0 \). Then, by using the Cauchy–Schwarz inequality and (32), we have

$$\begin{aligned} \frac{d}{dt} \bigl\Vert x v(t) \bigr\Vert _{L^{2}(\Omega)}^{2} &= -2\operatorname{\mathcal{R}e} \biggl( i \int_{\Omega} x v_{x}\overline{v} \,dx \biggr) \\ &\leq2 \bigl\Vert v_{x}(t) \bigr\Vert _{L^{2}(\Omega)} \bigl\Vert x v(t) \bigr\Vert _{L^{2}(\Omega)} \\ &\leq2 K_{1} \bigl\Vert x v(t) \bigr\Vert _{L^{2}(\Omega)}. \end{aligned}$$

By applying the Young inequality, we get

$$ \frac{d}{dt} \bigl\Vert x v(t) \bigr\Vert _{L^{2}(\Omega)}^{2} -\epsilon \bigl\Vert x v(t) \bigr\Vert _{L^{2}(\Omega)}^{2} \leq K, $$

with \(\epsilon>0\). By applying the Gronwall lemma, for all \(T\in \mathopen{]}0,+\infty[\) we have

$$ \forall t\in[0,T]\quad \bigl\Vert x v(t) \bigr\Vert _{L^{2}(\Omega)}^{2} \leq e^{\epsilon T} \Vert x u_{0} \Vert _{L^{2}(\Omega)}^{2}+ \frac{K}{\epsilon} \bigl(e^{\epsilon T} -1 \bigr). $$

Since \(u_{0}\) is with compact support in Ω, we have \(\Vert x u_{0} \Vert _{L^{2}(\Omega)}^{2} \leq K\).

Hence, there exists a constant \(K(T)>0\) such that

$$ \forall t\in[0,T] \quad\bigl\Vert x v(t) \bigr\Vert _{L^{2}(\Omega)}^{2} \leq K(T). $$

This gives the sequence

$$ (v_{m})_{m} \mbox{ remains bounded in } \mathcal{C}_{b}\bigl([0,T]; \mathbf {H}^{1}(\boldsymbol {\Omega})\cap \mathbf {L}^{2} \bigl(\Omega; \bigl(1+x^{2}\bigr)\,dx \bigr) \bigr). $$
(33)

3.3 Third step: passing to the limit

Since the sequence \((v_{m})_{m}\) remains bounded in \(\mathcal {C}_{b}([0,+\infty[; \mathbf {H}^{1}(\boldsymbol {\Omega}))\), for \(\forall T>0\), \((v_{m})_{m}\) is bounded in \(\mathbf {L}^{\infty}(0,\mathbf {T};\mathbf {H}^{1}(\boldsymbol {\Omega}))\). By the Banach–Alaoglu theorem, we deduce that \((v_{m})_{m}\) admits a subsequence still denoted \((v_{m})_{m}\) such that

$$ v_{m}\rightharpoonup v \mbox{ weakly } \star\mbox{ in } \mathbf {L}^{\infty }\bigl(0,\mathbf {T};\mathbf {H}^{1}(\boldsymbol {\Omega})\bigr). $$
(34)

By using (33) and since the embedding \(\mathbf {H}^{1}(\boldsymbol {\Omega})\cap \mathbf {L}^{2} (\boldsymbol {\Omega}; (1+x^{2})\,dx ) \hookrightarrow \mathbf {L}^{2}(\boldsymbol {\Omega})\) is compact, we have

$$ \forall t\in[0,T] \quad v_{m}(t) \longrightarrow v(t)\quad \mbox{strongly in } \mathbf {L}^{2}(\boldsymbol {\Omega}). $$
(35)

On the other hand, the sequence \((\frac{d v_{m}}{dt})_{m}\) is bounded in \(\mathbf {L}^{\infty}(0,\mathbf {T};[\mathbf {H}^{1}(\boldsymbol {\Omega})]')\). Then it admits a subsequence which converges weakly ⋆ to \(h\in \mathbf {L}^{\infty}(0,\mathbf {T};[\mathbf {H}^{1}(\boldsymbol {\Omega})]')\). We have \(h=\frac{d v}{dt}\). Indeed, we have \(\frac{d v_{m}}{dt}\longrightarrow h \) in \(\mathcal{D}'((0,T)\times \boldsymbol {\Omega}) \). Otherwise, using (34) we obtain \(\frac{d v_{m}}{dt}\longrightarrow\frac{d v}{dt}\) in \(\mathcal {D}'((0,T)\times\Omega) \). By the uniqueness of the limit in \(\mathcal{D}'((0,T)\times \boldsymbol {\Omega})\), we obtain \(h=\frac{d u}{dt}\). This implies that

$$ \frac{d v_{m}}{dt}\rightharpoonup\frac{d v}{dt} \mbox{ weakly }\star \mbox{ in } \mathbf {L}^{\infty}\bigl(0,\mathbf {T};\bigl[\mathbf {H}^{1}(\boldsymbol {\Omega}) \bigr]'\bigr). $$
(36)

Now, we consider \(\omega\in\mathcal{D}([0, T ])\) such that \(\omega (T) = 0\). We pass to the limit in each term in the equation

$$ \int_{0}^{T} \biggl\langle i v'_{m}+ \frac{1}{2}v_{mxx}+q \delta_{a} v_{m}+ \bigl[ g \bigl( \vert v_{m} \vert ^{2} \bigr)- g \bigl( \bigl\vert v_{m}(0,t) \bigr\vert ^{2} \bigr) \bigr] v_{m},\omega(t)\varphi_{k} \biggr\rangle \,dt = 0, $$
(37)

where \(\langle\cdot,\cdot\rangle= \langle\cdot,\cdot\rangle _{[H^{1}(\Omega)]',H^{1}(\Omega)}\).

Passing to the limit for the term \(I_{m} = \int_{0}^{T} \langle i v'_{m},\omega(t)\varphi_{k} \rangle_{[H^{1}(\Omega )]',H^{1}(\Omega)} \,dt\): By integration by parts with respect to time, we get

$$\begin{aligned} I_{m} = -\bigl\langle i v_{m}(0),\omega(0) \varphi_{k}\bigr\rangle _{L^{2}(\Omega ),L^{2}(\Omega)}- \int_{0}^{T} \bigl\langle i v_{m}, \omega'(t)\varphi _{k} \bigr\rangle _{H^{1}(\Omega),[H^{1}(\Omega)]'} \,dt. \end{aligned}$$

By using (34), we obtain

$$ \lim_{m \to+\infty} I_{m} =-\bigl\langle i u_{0}, \omega(0)\varphi_{k}\bigr\rangle _{L^{2}(\Omega),L^{2}(\Omega)}- \int_{0}^{T} \bigl\langle i v,\omega '(t)\varphi_{k} \bigr\rangle _{H^{1}(\Omega),[H^{1}(\Omega)]'} \,dt. $$
(38)

Passing to the limit for the term \(J_{m}=\int_{0}^{T} \langle v_{mxx},\omega(t)\varphi_{k} \rangle_{[H^{1}(\Omega )]',H^{1}(\Omega)} \,dt\): Applying the Green formula, we have

$$ J_{m} = \int_{0}^{T} \partial_{n} v_{m}(0,t)\overline{\varphi_{k}(0)}\omega (t)\,dt - \int_{0}^{T}\bigl\langle v_{mx},\omega(t) \varphi_{kx}\bigr\rangle _{L^{2}(\Omega),L^{2}(\Omega)} \,dt. $$

By using (34) we have

$$\begin{aligned} &\lim_{m \to+\infty} \int_{0}^{T}\bigl\langle v_{mx},\omega(t) \varphi _{kx}\bigr\rangle _{L^{2}(\Omega),L^{2}(\Omega)} \,dt \\ &\quad= \int_{0}^{T}\bigl\langle v_{x}, \omega(t)\varphi_{kx}\bigr\rangle _{L^{2}(\Omega),L^{2}(\Omega)} \,dt. \end{aligned}$$

It remains to demonstrate

$$\begin{aligned} &\lim_{m \to+\infty} \int_{0}^{T} \partial_{n} v_{m}(0,t)\overline {\varphi_{k}(0)}\omega(t)\,dt \\ &\quad= \int_{0}^{T} \partial_{n} v(0,t) \overline {\varphi_{k}(0)}\omega(t)\,dt. \end{aligned}$$
(39)

Indeed,

$$\begin{aligned} & \int_{0}^{T} \partial_{n} \bigl( v_{m}(0,t)-v(0,t) \bigr)\overline {\varphi_{k}(0)} \omega(t)\,dt \\ &\quad =-\sqrt{2}e^{-i\pi/4} \overline{\varphi_{k}(0)} \int_{0}^{T} \partial_{t}^{1/2} \bigl(v_{m}(0,t)-v(0,t) \bigr)\omega(t)\,dt \\ &\quad= -\frac{\sqrt{2}e^{-i\pi/4} \overline{\varphi_{k}(0)}}{\sqrt{\pi }} \int_{0}^{T} \partial_{t} \biggl( \int_{0}^{t} \frac {v_{m}(0,s)-v(0,s)}{\sqrt{t-s}}\,ds \biggr) \omega(t)\,dt \\ &\quad= \frac{\sqrt{2}e^{-i\pi/4} \overline{\varphi_{k}(0)}}{\sqrt{\pi }} \int_{0}^{T} \omega'(t) \biggl( \int_{0}^{t} \frac {v_{m}(0,s)-v(0,s)}{\sqrt{t-s}}\,ds \biggr)\,dt. \end{aligned}$$

By using (35) and by applying Lemma 4, we then obtain (39). This gives

$$\begin{aligned} \lim_{m \to+\infty} J_{m} &= \int_{0}^{T} \partial_{n} v(0,t) \overline {\varphi_{k}(0)}\omega(t)\,dt - \int_{0}^{T}\bigl\langle v_{x},\omega (t)\varphi_{kx}\bigr\rangle _{L^{2}(\Omega),L^{2}(\Omega)} \,dt \\ &= \int_{0}^{T} \bigl\langle v_{xx}, \omega(t)\varphi_{k} \bigr\rangle _{[H^{1}(\Omega)]',H^{1}(\Omega)} \,dt. \end{aligned}$$
(40)

Passing to the limit for the term \(L_{m}=\int_{0}^{T} \langle g ( \vert v_{m} \vert ^{2} ) v_{m},\omega(t)\varphi _{k} \rangle_{[H^{1}(\Omega)]',H^{1}(\Omega)} \,dt\): By using (34), (35) and (36), we have \(v_{m} \longrightarrow v\) strongly in \(\mathcal {C}^{0}([0,T];\mathbf {L}^{2}(\boldsymbol {\Omega}))\). Let K be a compact of Ω, since \(v_{m} g( \vert v_{m} \vert ^{2})\) belongs to a bounded set of \(\mathbf {L}^{\infty}(0,\mathbf {T},\mathbf {L}^{2}(\mathbf {K}))\) we extract a subsequence of \((v_{m} )_{m}\) (noted again \((v_{m} )_{m}\)) such that \(v_{m} g( \vert v_{m} \vert ^{2})\rightharpoonup w \) weakly ⋆ in \(\mathbf {L}^{\infty}(0,\mathbf {T},\mathbf {L}^{2}(\mathbf {K}))\). By using Lemma 5, we have \(g( \vert v_{m} \vert ^{2}) v_{m} \longrightarrow g ( \vert v \vert ^{2} ) v\) strongly in \(\mathcal{C}^{0}([0,T];\mathbf {L}^{2}(\boldsymbol {\Omega}))\). Hence

$$ \lim_{m \to+\infty} L_{m} = \int_{0}^{T} \bigl\langle g \bigl( \vert v \vert ^{2} \bigr) v,\omega(t)\varphi_{k} \bigr\rangle _{[H^{1}(\Omega )]',H^{1}(\Omega)} \,dt. $$
(41)

Passing to the limit for the term \(K_{m}=\int_{0}^{T} g ( \vert v_{m}(0,t) \vert ^{2} ) \langle v_{m},\omega(t)\varphi _{k} \rangle_{[H^{1}(\Omega)]',H^{1}(\Omega)} \,dt\): We have

$$\begin{aligned} & \int_{0}^{T} \bigl\langle g \bigl( \bigl\vert v_{m}(0,t) \bigr\vert ^{2} \bigr) v_{m}-g \bigl( \bigl\vert v(0,t) \bigr\vert ^{2} \bigr) v,\omega(t) \varphi_{k} \bigr\rangle _{[H^{1}(\Omega)]',H^{1}(\Omega)} \,dt \\ &\quad= \int_{0}^{T} \bigl[ g \bigl( \bigl\vert v_{m}(0,t) \bigr\vert ^{2} \bigr)- g \bigl( \bigl\vert v(0,t) \bigr\vert ^{2} \bigr) \bigr] \bigl\langle v_{m}, \omega (t)\varphi_{k} \bigr\rangle _{[H^{1}(\Omega)]',H^{1}(\Omega)} \,dt \\ &\qquad{}+ \int_{0}^{T} \bigl\langle v_{m} -v,g \bigl( \bigl\vert v(0,t) \bigr\vert ^{2} \bigr)\omega(t) \varphi_{k} \bigr\rangle _{[H^{1}(\Omega )]',H^{1}(\Omega)} \,dt. \end{aligned}$$

Since g is continuous and by using Lemma 4, we have

$$ \lim_{m \to+\infty} g \bigl( \bigl\vert v_{m}(0,t) \bigr\vert ^{2} \bigr)=g \bigl( \bigl\vert v(0,t) \bigr\vert ^{2} \bigr). $$

By using the fact that \((v_{m})_{m}\) is bounded in \(\mathcal{C}_{b} ([0,\mathbf {T}];\mathbf {H}^{1}(\boldsymbol {\Omega}))\), we get

$$ \lim_{m \to+\infty} \int_{0}^{T} \bigl[ g \bigl( \bigl\vert v_{m}(0,t) \bigr\vert ^{2} \bigr)- g \bigl( \bigl\vert v(0,t) \bigr\vert ^{2} \bigr) \bigr] \bigl\langle v_{m}, \omega(t)\varphi_{k} \bigr\rangle _{[H^{1}(\Omega )]',H^{1}(\Omega)} \,dt =0. $$

Using the weak convergence ⋆ of \((v_{m})_{m}\) to v in \(\mathbf {L}^{\infty}(0,\mathbf {T};\mathbf {H}^{1}(\boldsymbol {\Omega}))\) and \(g ( \vert v(0,\cdot) \vert ^{2} )\in \mathbf {L}^{\infty}(0,\mathbf {T})\), we obtain

$$ \lim_{m \to+\infty} \int_{0}^{T} \bigl\langle v_{m} -v,g \bigl( \bigl\vert v(0,t) \bigr\vert ^{2} \bigr)\omega(t) \varphi_{k} \bigr\rangle _{[H^{1}(\Omega )]',H^{1}(\Omega)} \,dt =0. $$

This gives

$$ \lim_{m \to+\infty} K_{m} = \int_{0}^{T} \bigl\langle g \bigl( \bigl\vert v(0,t) \bigr\vert ^{2} \bigr) v,\omega(t)\varphi_{k} \bigr\rangle _{[H^{1}(\Omega)]',H^{1}(\Omega)} \,dt. $$
(42)

Passing to the limit for the term \(D_{m}=\int_{0}^{T} \langle\delta_{a} v_{m},\omega(t)\varphi_{k} \rangle _{[H^{1}(\Omega)]',H^{1}(\Omega)} \,dt\): For all \(\varepsilon>0\), we have \(\delta_{a}\in[\mathbf {H}^{\frac {1}{2}+\varepsilon}(\boldsymbol {\Omega})]'\). Then the sequence \((\delta_{a} v_{m}(t))_{m}\) is bounded in \([\mathbf {H}^{\frac {1}{2}+\varepsilon}(\boldsymbol {\Omega})]'\); in particular in \([\mathbf {H}^{\frac{3}{4}}(\boldsymbol {\Omega})]'\). Indeed,

$$\begin{aligned} \Vert \delta_{a} v_{m} \Vert _{[H^{\frac{3}{4}}(\Omega)]'} &=\sup _{ \Vert \varphi \Vert _{H^{\frac{3}{4}}(\Omega)}=1} \bigl\vert v_{m} (a)\varphi(a) \bigr\vert \\ &= \bigl\vert v_{m} (a) \bigr\vert \sup_{ \Vert \varphi \Vert _{H^{\frac {3}{4}}(\Omega)}=1} \bigl\vert \varphi(a) \bigr\vert \\ &= \bigl\vert v_{m}(a) \bigr\vert \Vert \delta_{a} \Vert _{[H^{\frac{3}{4}}(\Omega)]'}. \end{aligned}$$

By using Agmon’s inequality, we have

$$\begin{aligned} \Vert \delta_{a} v_{m} \Vert _{[H^{\frac{3}{4}}(\Omega)]'} &\leq \Vert \delta_{a} \Vert _{[H^{\frac{3}{4}}(\Omega)]'} \Vert v_{m} \Vert _{L^{2}(\Omega)}^{1/2} \Vert v_{mx} \Vert _{L^{2}(\Omega)}^{1/2} \\ &\leq \Vert \delta_{a} \Vert _{[H^{\frac{3}{4}}(\Omega)]'} \Vert v_{m} \Vert _{H^{1}(\Omega)}. \end{aligned}$$
(43)

We use the Banach–Alaoglu theorem to obtain

$$ \delta_{a} v_{m} \rightharpoonup\xi \mbox{ weakly } \star \mbox{ in } \mathbf {L}^{\infty}\bigl(0,\mathbf {T};\bigl[\mathbf {H}^{\frac{3}{4}}(\boldsymbol {\Omega}) \bigr]'\bigr). $$

Therefore \(\forall\psi\in \mathbf {L}^{1}(0,\mathbf {T};\mathbf {H}^{3/4}(\boldsymbol {\Omega}))\) we have

$$ \lim_{m \to+\infty} \int_{0}^{T} \langle\delta_{a} v_{m},\psi \rangle_{[H^{3/4}(\Omega)]',H^{3/4}(\Omega)} \,dt = \int _{0}^{T} \langle\xi,\psi \rangle_{[H^{3/4}(\Omega )]',H^{3/4}(\Omega)} \,dt. $$

In particular \(\forall\psi\in \mathbf {L}^{1}(0,\mathbf {T};\mathbf {H}^{1}(\boldsymbol {\Omega}))\) we have

$$ \lim_{m \to+\infty} \int_{0}^{T} \langle\delta_{a} v_{m},\psi \rangle_{[H^{1}(\Omega)]',H^{1}(\Omega)} \,dt = \int _{0}^{T} \langle\xi,\psi \rangle_{[H^{1}(\Omega )]',H^{1}(\Omega)} \,dt. $$

We just justify that \(\xi=\delta_{a} v\). Note that \(\delta_{a} v \in [\mathbf {H}^{\frac{3}{4}}(\boldsymbol {\Omega})]'\). Using (43) we have

$$ \Vert \delta_{a} v_{m} -\delta_{a} v \Vert _{[H^{\frac{3}{4}}(\Omega )]'}\leq \Vert \delta_{a} \Vert _{[H^{\frac{3}{4}}(\Omega)]'} \Vert v_{m} -v \Vert _{L^{2}(\Omega)}^{1/2} \Vert v_{mx} - v_{x} \Vert _{L^{2}(\Omega)}^{1/2}. $$

We know that \(v_{m} \longrightarrow v \mbox{ strongly in }\mathcal{C} ([0,\mathbf {T}];\mathbf {L}_{\mathrm{loc}}^{2}(\boldsymbol {\Omega}) ) \) and \((v_{m})_{m}\) is bounded in \(\mathcal{C}^{0}([0,\mathbf {T}]; \mathbf {H}^{1}(\boldsymbol {\Omega} ))\). Then, for all K compact on Ω, we have

$$ \delta_{a} v_{m} \longrightarrow\delta_{a} v \mbox{ strongly in }\mathcal{C}^{0} \bigl([0,\mathbf {T}]; \bigl[\mathbf {H}^{\frac{3}{4}}(\mathbf {K})\bigr]' \bigr). $$

Otherwise, we have

$$ \delta_{a} v_{m} \longrightarrow\xi \quad \mbox{in } \mathcal{D}' \bigl((0,\mathbf {T})\times \boldsymbol {\Omega} \bigr). $$

By using the uniqueness of the limit in \(\mathcal{D}'\), we get \(\xi=\delta_{a} u\). This implies that

$$ \lim_{m \to+\infty} D_{m}= \int_{0}^{T} \bigl\langle \delta_{a} v, \omega(t)\varphi_{k} \bigr\rangle _{[H^{1}(\Omega)]',H^{1}(\Omega)} \,dt. $$
(44)

Passing to the limit for equation ( 37 ): By using (37), (38), (40), (41), (42) and (44), we deduce that, for all \(\varphi\in \mathbf {H}^{1}(\boldsymbol {\Omega})\),

$$\begin{aligned} &{-}\bigl\langle i u_{0},\omega(0)\varphi\bigr\rangle _{L^{2}(\Omega),L^{2}(\Omega )}- \int_{0}^{T}\bigl\langle i v,\omega'(t) \varphi\bigr\rangle _{H^{1}(\Omega ),[H^{1}(\Omega)]'} \,dt \\ &\quad{}+ \frac{1}{2} \int_{0}^{T}\bigl\langle v_{xx},\omega(t) \varphi\bigr\rangle _{[H^{1}(\Omega)]',H^{1}(\Omega)} \,dt +q \int_{0}^{T}\bigl\langle \delta_{a} v, \omega(t)\varphi\bigr\rangle _{[H^{1}(\Omega)]',H^{1}(\Omega)} \,dt \\ &\quad{} + \int_{0}^{T}\bigl\langle \bigl[ g\bigl( \vert v \vert ^{2} \bigr)-g\bigl( \bigl\vert v(0,t) \bigr\vert ^{2} \bigr)\bigr] v,\omega(t)\varphi\bigr\rangle _{[H^{1}(\Omega)]',H^{1}(\Omega)} \,dt =0. \end{aligned}$$
(45)

For \(\omega\in\mathcal{D}(0, \mathbf {T})\), we see that v obeys

$$ \int_{0}^{T} \biggl\langle i v'+ \frac{1}{2}v_{xx}+q\delta_{a} v +\bigl[g\bigl( \vert v \vert ^{2}\bigr)-g\bigl( \bigl\vert v(0,t) \bigr\vert ^{2}\bigr)\bigr] v,\varphi \biggr\rangle _{{[H^{1}(\Omega)]',H^{1}(\Omega)}}\omega(t)\,dt=0. $$

We just justify that for all \(\varphi\in \mathbf {H}^{1}(\boldsymbol {\Omega})\) we have

$$ \biggl\langle i v'+\frac{1}{2}v_{xx}+q \delta_{a} v +\bigl[g\bigl( \vert v \vert ^{2}\bigr)-g \bigl( \bigl\vert v(0,t) \bigr\vert ^{2}\bigr)\bigr] v,\varphi \biggr\rangle _{[H^{1}(\Omega )]',H^{1}(\Omega)}=0. $$
(46)

Then v satisfies the initial condition \(v(0)=u_{0}\). We consider \(\omega\in\mathcal{D}([0,T])\); \(\omega(T)=0\), and multiply equation (46) by \(\omega(t)\). We integrate between 0 and T to obtain

$$\begin{aligned} &{-}\bigl\langle i v(0),\omega(0)\varphi\bigr\rangle _{L^{2}(\Omega ),L^{2}(\Omega)} - \int_{0}^{T}\bigl\langle i v,\omega'(t) \varphi\bigr\rangle _{H^{1}(\Omega ),[H^{1}(\Omega)]'} \,dt \\ &\quad{} + \frac{1}{2} \int_{0}^{T} \bigl\langle v_{xx}, \omega(t)\varphi \bigr\rangle _{[H^{1}(\Omega)]',H^{1}(\Omega)} \,dt +q \int_{0}^{T} \bigl\langle \delta_{a} v, \omega(t)\varphi \bigr\rangle _{[H^{1}(\Omega)]',H^{1}(\Omega)} \,dt \\ &\quad{} + \int_{0}^{T} \bigl\langle \bigl[g\bigl( \vert v \vert ^{2}\bigr)-g\bigl( \bigl\vert v(0,t) \bigr\vert ^{2}\bigr)\bigr] v,\omega(t)\varphi \bigr\rangle _{[H^{1}(\Omega)]',H^{1}(\Omega )} \,dt=0. \end{aligned}$$
(47)

Combining (45) and (47), we get

$$ \forall\varphi\in H^{1}(\Omega), \quad \bigl\langle i u_{0}, \omega(0)\varphi \bigr\rangle _{L^{2}(\Omega),L^{2}(\Omega)} = \bigl\langle i v(0),\omega(0) \varphi \bigr\rangle _{L^{2}(\Omega ),L^{2}(\Omega)}. $$

By choosing \(\omega(0)=1\), we deduce that \(v(0)=u_{0}\). We then justify that

$$ v\in\mathcal{C}^{0}\bigl([0,+\infty[;\mathbf {H}^{1}(\boldsymbol {\Omega}) \bigr)\cap\mathcal {C}^{1} \bigl([0,+\infty[;\bigl[\mathbf {H}^{1}( \boldsymbol {\Omega})\bigr]' \bigr), $$

and this satisfies the problem (13).

3.4 Uniqueness and continuous dependence of the solutions

Let \(v(t)\) and \(\widehat{v}(t)\) be two solutions satisfying the problem (13) which follow, respectively, from the initial data \(u_{0}\) and \(\widehat{u}_{0}\). We set \(w(t)=v(t)-\widehat{v}(t)\) with the initial condition \(w(0)=u_{0}-\widehat{u}_{0}\). Then we obtain

$$ i w_{t}+\frac{1}{2} w_{xx}+q \delta_{a} w+g \bigl( \vert v \vert ^{2}\bigr) u-g\bigl( \vert \widehat{v} \vert ^{2}\bigr) \widehat{v}- g\bigl( \bigl\vert v(0,t) \bigr\vert ^{2}\bigr) u+g\bigl( \bigl\vert \widehat{v}(0,t) \bigr\vert ^{2}\bigr) \widehat{v}=0, $$
(48)

with the boundary condition

$$ \partial_{n} w(0,t)+\sqrt{2}e^{-i\pi/4} \partial_{t}^{1/2} \bigl(w(0,t) \bigr)=0,\quad t\in\mathbb{R}_{+}. $$
(49)

We multiply (48) by w̅ and we take the imaginary part, to obtain

$$\begin{aligned} \frac{1}{2}\frac{d}{dt} \Vert w \Vert _{L^{2}(\Omega)}={}&- \operatorname{\mathcal{I}m} \bigl( \partial_{n} w(0,t) \overline{w}(0,t) \bigr)- \operatorname{\mathcal{I}m} \biggl( \int_{\Omega} \bigl(g\bigl( \vert v \vert ^{2}\bigr) v- g\bigl( \vert \widehat {v} \vert ^{2}\bigr) \widehat{v} \bigr) \overline{w}\,dx \biggr) \\ &{}+\operatorname{\mathcal{I}m} \biggl( \int_{\Omega} \bigl(g\bigl( \bigl\vert v(0,t) \bigr\vert ^{2}\bigr) u- g\bigl( \bigl\vert \widehat{v}(0,t) \bigr\vert ^{2}\bigr) \widehat{v} \bigr)\overline {w}\,dx \biggr). \end{aligned}$$
(50)

By using (49), we have

$$\begin{aligned} -\operatorname{\mathcal{I}m} \bigl( \partial_{n} w(0,t) \overline{w}(0,t) \bigr) &= \operatorname{\mathcal{R}e} \bigl( i \partial_{n} w(0,t) \overline{w}(0,t) \bigr) \\ &= -\sqrt{2} \operatorname{\mathcal{R}e} \bigl(e^{i\pi/4} \overline{w}(0,t) \partial_{t}^{1/2} \bigl(w(0,t) \bigr) \bigr). \end{aligned}$$

The other right terms of (50) are shown to be bounded by applying the Cauchy–Schwarz inequality and the fact that the injection of \(\mathbf {H}^{1}(\boldsymbol {\Omega})\) in \(\mathbf {L}^{\infty}(\boldsymbol {\Omega})\) is continuous, and by using (3), we have

$$ -\operatorname{\mathcal{I}m} \biggl( \int_{\Omega} \bigl(g\bigl( \vert v \vert ^{2}\bigr) v- g\bigl( \vert \widehat{v} \vert ^{2}\bigr) \widehat{v} \bigr) \overline{w}\,dx \biggr) \leq K \bigl\Vert w(t) \bigr\Vert _{L^{2}(\Omega)}^{2}, $$

and by applying Lemma 3, we have

$$ \operatorname{\mathcal{I}m} \biggl( \int_{\Omega} \bigl(g\bigl( \bigl\vert v(0,t) \bigr\vert ^{2}\bigr) u- g\bigl( \bigl\vert \widehat{v}(0,t) \bigr\vert ^{2}\bigr) \widehat{v} \bigr)\overline {w}\,dx \biggr)\leq K \bigl\Vert w(t) \bigr\Vert _{L^{2}(\Omega)}^{2}. $$

From the above inequalities, we obtain

$$ \frac{d}{dt} \bigl\Vert w(t) \bigr\Vert _{L^{2}(\Omega)}^{2} \leq K \bigl\Vert w(t) \bigr\Vert _{L^{2}(\Omega)}^{2}-\sqrt{2} \operatorname{\mathcal{R}e} \bigl(e^{i\pi/4} \overline {w}(0,t) \partial_{t}^{1/2} \bigl(w(0,t) \bigr) \bigr). $$

We apply Gronwall’s lemma and Lemma 2, to obtain

$$ \bigl\Vert w(t) \bigr\Vert _{L^{2}(\Omega)}^{2}\leq e^{K t} \bigl\Vert w(0) \bigr\Vert _{L^{2}(\Omega)}^{2}\leq e^{K t} \Vert u_{0}-\widehat{u}_{0} \Vert _{L^{2}(\Omega)}^{2}. $$
(51)

Therefore the uniqueness of the solution of (13) follows immediately.

Finally, from Remark 3, there exists a unique function \(u\in\mathcal{C}^{0}([0,+\infty[;\mathbf {H}^{1}(\boldsymbol {\Omega}))\cap \mathcal {C}^{1}([0,+\infty[;[\mathbf {H}^{1}(\boldsymbol {\Omega})]')\) solution of the NLS equation (2)–(4)–(6) such that

$$ u(x,t)=\exp \biggl(i \int_{0}^{t}g \bigl( \bigl\vert v(0,s) \bigr\vert \bigr) \,ds \biggr) v(x,t). $$

Moreover, the following proposition shows that the continuous dependence of the solutions of the NLS equation (2)–(4)–(6).

Proposition 1

The map

$$ \begin{aligned}& \mathbf {H}^{1} (\boldsymbol {\Omega}) \longrightarrow \mathbf {H}^{1}(\boldsymbol {\Omega} ) \\ &u_{0} \mapsto u(t), \end{aligned} $$
(52)

is continuous on bounded subsets of \(\mathbf {H}^{1}(\boldsymbol {\Omega})\) for the strong topology of \(\mathbf {L}^{2}(\boldsymbol {\Omega})\).

Proof

Let \(u(t)\) and \(\widehat{u}(t)\) be two solutions of NLS equation (2)–(4)–(6) which are issued, respectively, from the initial data \(u_{0}\) and \(\widehat{u}_{0}\). By using Remark 3, we have

$$\begin{aligned} u(t)-\widehat{u}(t)=\exp \biggl(i \int_{0}^{t}g \bigl( \bigl\vert v(0,s) \bigr\vert ^{2} \bigr) \,ds \biggr) v(x,t) -\exp \biggl(i \int_{0}^{t}g \bigl( \bigl\vert \widehat{v}(0,s) \bigr\vert ^{2} \bigr) \,ds \biggr) \widehat{v}(x,t). \end{aligned}$$

Then we have

$$\begin{aligned} \bigl\Vert u(t)-\widehat{u}(t) \bigr\Vert _{L^{2}(\Omega)} \leq \bigl\Vert v(t)-\widehat{v}(t) \bigr\Vert _{L^{2}(\Omega)}+ \bigl\Vert \widehat{v}(t) \bigr\Vert _{L^{2}(\Omega)} \int_{0}^{t} \bigl\vert g \bigl( \bigl\vert v(0,s) \bigr\vert ^{2} \bigr)-g \bigl( \bigl\vert \widehat{v}(0,s) \bigr\vert ^{2} \bigr) \bigr\vert \,ds. \end{aligned}$$

By applying the mean value theorem and (3) and by using Lemma 3, we get

$$\begin{aligned} \bigl\Vert u(t)-\widehat{u}(t) \bigr\Vert _{L^{2}(\Omega)}\leq \sup _{t\in[0,T]} \bigl[ \bigl\Vert w(t) \bigr\Vert _{L^{2}(\Omega)}+K \bigl\Vert w(t) \bigr\Vert _{L^{2}(\Omega )}^{\frac{1}{2}} \bigr]\leq K\sup _{t\in[0,T]} \bigl[ \bigl\Vert w(t) \bigr\Vert _{L^{2}(\Omega)}^{\frac{1}{2}} \bigr], \end{aligned}$$

where \(T>0\). Finally, by taking the supremum on the left side of the last inequality and by applying (51), we get

$$\begin{aligned} \sup_{t\in[0,T]} \bigl[ \bigl\Vert u(t)-\widehat{u}(t) \bigr\Vert _{L^{2}(\Omega )} \bigr]\leq K \sup_{t\in[0,T]} \bigl[ e^{\frac{K-\gamma}{4} t} \bigr] \Vert u_{0}-\widehat{u}_{0} \Vert _{L^{2}(\Omega)}^{\frac{1}{2}}, \end{aligned}$$

which gives the result. □

Remark 4

The choice of the negative half-line Ω does not affect the well-posedness of the NLS equation. In fact, according to Remark 2, we deduce that if \(\Omega=\mathopen{]}0,+\infty[\), \(a>0\) and \(u_{0}\) has a compact support in Ω, then the NLS equation

$$ \textstyle\begin{cases} i u_{t}+\frac{1}{2} u_{xx}+q\delta_{a} u +g ( \vert u \vert ^{2} ) u=0 \quad \mbox{in }\boldsymbol {\Omega}\times\mathbb {R}_{+} \\ \partial_{n} u(0,t)+\sqrt{2}e^{-i\pi/4}e^{i\mathbb{V}(0,t)} \partial_{t}^{1/2} (e^{-i\mathbb{V}(0,t)}u(0,t) )=0, \quad t\in \mathbb{R}_{+},\\ u(x,0)=u_{0}(x), \quad x\in\Omega \end{cases} $$

has a unique solution \(u\in\mathcal{C}^{0}([0,+\infty[;\mathbf {H}^{1}(\boldsymbol {\Omega} ))\cap\mathcal{C}^{1}([0,+\infty[;[\mathbf {H}^{1}(\boldsymbol {\Omega})]')\). Moreover, the map \(u_{0} \mapsto u(t)\) is continuous on bounded subsets of \(\mathbf {H}^{1}(\boldsymbol {\Omega})\) for the strong topology of \(\mathbf {L}^{2}(\boldsymbol {\Omega})\).

4 Conclusion

In this paper, we have studied a nonlinear Schrödinger equation with Dirac distribution in a half-line domain of \(\mathbb{R}\). For this purpose, a non-standard boundary condition was considered in order to demonstrate the well-posedness of the solution. Then, by using the Galerkin method, we have shown that this equation can have a unique solution in \(\mathbf {H}^{1}(\boldsymbol {\Omega})\).

The remaining question is to investigate the nonlinear Schrödinger equation with the Dirac distribution on a bounded domain of \(\mathbb {R}\) or \(\mathbb{R}^{2}\) with non-standard boundary conditions. This is a delicate issue which needs future research.