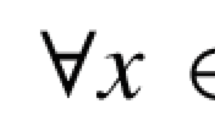1 Introduction

This paper concerns the initial value problems for the nonlinear fourth-order Schrödinger equations

$$\begin{aligned} \left \{ \textstyle\begin{array}{@{}l} i\partial_{t}u+\Delta^{2}u=|u|^{p}u,\\ u(0, x)=u_{0}(x),\quad x\in\mathbb{R}^{n}, \end{array}\displaystyle \right . \end{aligned}$$
(1.1)

where \(0< p<\frac{8}{(n-4)^{+}}\) (we use the convention: \(\frac {8}{(n-4)^{+}}=+\infty\) when \(2\leq n\leq4\); \(\frac{8}{(n-4)^{+}}=\frac {8}{n-4}\) when \(n\geq5\)), \(u(t,x):\mathbb{R}\times\mathbb {R}^{n}\rightarrow\mathbb{C}\), \(n\geq2\), is the unknown function and Δ is the Laplace operator, \(t\in[0,+\infty)\).

Problem (1.1) was first introduced by Karpman [1]. Karpman and Shagalov [2] considered the conditions for existence and stability of solutions about the fourth-order Schrödinger equation

$$\begin{aligned} i\partial_{t}\Psi+\frac{1}{2}\Delta\Psi+ \frac{1}{2}\gamma\Delta^{2}\Psi +|\Psi|^{2p}\Psi=0, \end{aligned}$$
(1.2)

where p is an integer and

$$\begin{aligned} p\geq1, \quad \Delta=\nabla_{\alpha}\nabla_{\alpha}, \quad \alpha=1, \ldots,n, n=1,2,3. \end{aligned}$$

Pausader [3] established the global well-posedness for the energy critical fourth-order Schrödinger equation

$$\begin{aligned} i\partial_{t} u+\Delta^{2}u+\varepsilon\Delta u+f\bigl(|u|^{2}\bigr)u=0 \end{aligned}$$
(1.3)

in the radial case by Strichartz-type estimates, while a specific nonlinear fourth-order Schrödinger equation as above (1.3) had been recently discussed by Fibich et al. [4]. They described various properties of the equation in the subcritical regime.

Moreover, for \(f(|u|^{2})u=|u|^{p-1}u\) one could also consider the focusing equation

$$\begin{aligned} i\partial_{t} u+\Delta^{2}u-\varepsilon\Delta u-|u|^{p-1}u=0 \end{aligned}$$

and proved that the solutions blow up in finite time for large data [5, 6].

Motivated by the above works, Pausader and Xia [7] proved the scattering theory for the defocusing fourth-order Schrödinger equation

$$\begin{aligned} \left \{ \textstyle\begin{array}{@{}l} i\partial_{t}u+\Delta^{2}u-\varepsilon\Delta u+|u|^{p-1}u=0, \\ u(0)=u_{0}\in H^{2}_{x}(\mathbb{R}^{n}), \end{array}\displaystyle \right . \end{aligned}$$

in low spatial dimensions (\(1\leq n \leq4\)) by a virial-type estimate and Morawetz-type estimate.

Recently, Wang [8] proved the small data scattering and large data local well-posedness for the fourth-order nonlinear problem

$$\begin{aligned} \left \{ \textstyle\begin{array}{@{}l} i\partial_{t}u+\Delta^{2}u=\mu|u|^{p}u, \\ u(0, x)=u_{0}(x), \end{array}\displaystyle \right . \end{aligned}$$
(1.4)

where \(\mu=\pm1\), in critical \(H^{s_{c}}\) space and in particular, for some \(s_{c} \leq0\) by Fourier restriction theory and Strichartz-type estimates, but the sharp conditions of the global existence and blow up for the problem by potential well theory is still not considered for \(\mu=1\). In this paper we try to solve this problem by a concavity method and potential well theory. Recently, the concavity method and potential well theory were applied by Shen et al. [9] to study the initial boundary value problem for fourth-order wave equations with nonlinear strain and source terms at high energy level. For other related results, we refer the reader to [10–18].

The plan of this paper is as follows. In the second section, we state some propositions, lemmas, and definitions and prove some invariant sets. In the third section, we state the sharp condition for the global existence and nonexistence of problem (1.1).

Throughout this paper, the \(H^{2}(\mathbb{R}^{n})\)-norm will be designated by \(\|\cdot\|_{H^{2}}\), also, the \(L^{p}(\mathbb{R}^{n})\)-norm will be denoted by \(\|\cdot\|_{L^{p}}\) (if \(p=2\), \(\|\cdot\|_{L^{2}}\) is denoted \(\|\cdot\|\)). For simplicity, hereafter, \(\int_{\mathbb {R}^{n}}\cdot\,dx\) is denoted ∫⋅.

2 Preliminaries

For problem (1.1), we define the energy space in the course of nature by

$$\begin{aligned} H= \biggl\{ u\in H^{2}\bigl(\mathbb{R}^{n}\bigr) \Big| \int|x|^{2}|u|^{2}< \infty \biggr\} . \end{aligned}$$
(2.1)

Proposition 2.1

([19, 20])

Let \(u_{0}\in H\). Then there exists a unique solution u of the Cauchy problem (1.1) in \(C([0, T]; H)\) for some \(T\in(0,\infty]\) (maximal existence time). Furthermore, we can get alternatives: \(T =\infty\) or \(T<\infty\) and

$$\lim_{t\rightarrow T}\|u\|_{H^{2}}=\infty. $$

Moreover, u satisfies

$$\begin{aligned}& \int|u|^{2}= \int|u_{0}|^{2}, \end{aligned}$$
(2.2)
$$\begin{aligned}& E(t)=\frac{1}{2} \int \biggl(|\Delta u|^{2}-\frac{2}{p+2}|u|^{p+2} \biggr)\equiv E(0). \end{aligned}$$
(2.3)

From [19, 20], we can get the following lemma.

Lemma 2.2

Suppose \(u_{0}\in H\), \(u\in C([0,T); H)\) be a solution to problem (1.1). Let \(J(t)=\int|x|^{2}|u|^{2}\), then

$$\begin{aligned} J^{''}(t)=8 \int \biggl(|\Delta u|^{2}-\frac{np}{2(p+2)}|u|^{p+2} \biggr). \end{aligned}$$
(2.4)

Furthermore, we consider the following steady-state equation:

$$\begin{aligned} -\Delta^{2}\varphi+\varphi+\varphi|\varphi|^{p}=0, \quad \varphi\in H. \end{aligned}$$
(2.5)

For any solution of (2.5), we define the following functionals:

$$\begin{aligned} &P(\varphi)=\frac{1}{2} \int \biggl(|\Delta\varphi|^{2}-|\varphi|^{2}- \frac {2}{p+2}|\varphi|^{p+2} \biggr), \end{aligned}$$
(2.6)
$$\begin{aligned} &I(\varphi)= \int \bigl(|\Delta\varphi|^{2}-|\varphi|^{2}-| \varphi|^{p+2} \bigr). \end{aligned}$$
(2.7)

When \(\varphi_{0}\in H\) and φ are a solution of problem (1.1) in \(C([0,T]; H)\), we have

$$\begin{aligned} P(\varphi)\equiv P(\varphi_{0}), \end{aligned}$$
(2.8)

and we define the set

$$M=\bigl\{ \varphi\in H\setminus\{0\}|I(\varphi)=0\bigr\} . $$

Now, we study the following constrained variational problem:

$$\begin{aligned} d=\inf_{\varphi\in M}P(\varphi). \end{aligned}$$
(2.9)

By a similar argument to [21], we get the following lemmas.

Lemma 2.3

Solution of (2.5) belongs to M.

Proof

Let \(\varphi(x)\) be a solution of steady-state equation (2.5). Then we get

$$\begin{aligned} \int\bigl(|\Delta\varphi|^{2}-|\varphi|^{2}-| \varphi|^{p+2}\bigr)=0, \end{aligned}$$
(2.10)

from which

$$I(\varphi)=0. $$

Hence \(\varphi\in M\). □

Lemma 2.4

When \(\varphi(x)\in M\), we have \(d>0\).

Proof

By (2.6) and (2.7), on M we get

$$\begin{aligned} P(\varphi)=\frac{p}{2(p+2)} \int|\varphi|^{p+2}. \end{aligned}$$
(2.11)

Combined with (2.9), we obtain the conclusion. □

Lemma 2.5

Let \(\varphi\in H \), \(\lambda>0\), and \(\varphi_{\lambda}(x)=\lambda \varphi(x)\). Then there exists a unique \(\lambda^{*}>0\) (depending on φ) such that \(I(\varphi_{\lambda^{*}})=0\) and \(I(\varphi _{\lambda})>0\), for \(\lambda\in(0, \mu)\); \(I(\varphi_{\lambda})<0\), for \(\lambda>\lambda^{*}\). Furthermore, \(P(\varphi_{\lambda^{*}})\geq P(\varphi_{\lambda})\), for any \(\lambda>0\).

Proof

From \(\varphi_{\lambda}=\lambda\varphi\), (2.6) and (2.7), we have

$$\begin{aligned} I(\varphi_{\lambda})=\lambda^{2} \int \bigl(|\Delta\varphi|^{2}-|\varphi |^{2}- \lambda^{p}|\varphi|^{p+2} \bigr) \end{aligned}$$
(2.12)

and

$$\begin{aligned} P(\varphi_{\lambda})=\frac{\lambda^{2}}{2} \int \bigl(|\Delta\varphi |^{2}-|\varphi|^{2} \bigr)- \frac{\lambda^{p+2}}{p+2} \int|\varphi |^{p+2}. \end{aligned}$$
(2.13)

Furthermore, there exists a unique positive constant \(\lambda^{*}>0\) (depending on φ) such that \(I(\varphi_{\lambda^{*}}) = 0\) and we can easily see that

$$\begin{aligned} I(\varphi_{\lambda})>0 \quad\mbox{for } \lambda\in\bigl(0, \lambda^{*}\bigr) \end{aligned}$$

and

$$\begin{aligned} I(\varphi_{\lambda})< 0 \quad\mbox{for } \lambda>\lambda^{*}. \end{aligned}$$

Combining

$$\begin{aligned} \frac{d}{d\lambda}P(\varphi_{\lambda})=\lambda^{-1}I( \varphi_{\lambda}) \end{aligned}$$

with

$$\begin{aligned} I(\varphi_{\lambda^{*}})=0, \end{aligned}$$

we obtain

$$\begin{aligned} P(\varphi_{\lambda^{*}})\geq P(\varphi_{\lambda}), \quad\mbox{for any } \lambda>0. \end{aligned}$$

This completes the proof of the lemma. □

Now we discuss the invariant sets of solution for problem (1.1).

Theorem 2.6

Let

$$\begin{aligned} V=\bigl\{ \varphi\in H\setminus\{0\} |P(\varphi)< d,I(\varphi)< 0 \bigr\} . \end{aligned}$$
(2.14)

If \(u_{0}\in V\), then the solution \(u(x,t)\) of problem (1.1) also belongs to V for any t in the interval \([0, T)\).

Notice that on the basis of Theorem 2.6 one says that V is an invariant set of problem (1.1).

Proof

Let \(u_{0}\in V\). By Proposition 2.1 there exists a unique \(u(x, t)\in C([0, T); H)\) with \(T<\infty\) such that \(u(x, t)\) is a solution of problem (1.1). As (2.8) shows,

$$\begin{aligned} P(u) = P(u_{0}), \quad t \in[0, T). \end{aligned}$$

It means that \(P(u_{0})< d\) is equivalent to \(P(u)< d\) for any \(t\in[0, T)\).

If \(u_{0}\in V\), then we have \(u\in V\) for \(t\in[0,T)\). Indeed, if it was false, there exists a first time \(t_{1}\in(0,T)\) such that \(I(u(x, t_{1})) = 0\). By (2.6), (2.7), and

$$\begin{aligned} P \bigl(u (x, t_{1} ) \bigr)>0, \end{aligned}$$

we have \(u(x, t_{1}) \neq0\). Otherwise \(P(u(x, t_{1})) = 0\), which contradicts \(P(u(x, t_{1}))> 0\). From (2.9), it follows that \(P(u(x, t_{1}))\geq d\). This contradicts \(P(u(x, t)) < d\) for any \(t\in[0, T)\), since \(I(u(x, t)) < 0\). In other words, \(u(x, t) \in V\) for any \(t\in[0, T)\). So, V is an invariant manifold of (1.1). □

By a proof similar to that of Theorem 2.6, we can obtain the following theorem.

Theorem 2.7

Define

$$\begin{aligned} W=\bigl\{ \varphi\in H\setminus\{0\} |P(\varphi)< d,I(\varphi)>0 \bigr\} \cup\{0\}, \end{aligned}$$
(2.15)

Then W is an invariant set of problem (1.1).

3 The conditions for global well-posedness

Theorem 3.1

(Global existence)

Let \(u_{0}\in W\), then the existence time of solution \(u(x,t)\) for problem (1.1) is infinite.

Proof

If \(u_{0}\in W\), from Theorem 2.7, we know that \(u(x, t)\in W\) for \(t\in[0, T)\). For fixed \(t\in[0, T)\), we denote \(u(x, t) = u\). Then we have \(P(u) < d\), \(I(u) > 0\). It follows from (2.6) and (2.7) that

$$\begin{aligned} & \biggl(\frac{1}{2}-\frac{1}{p+2} \biggr) \int \bigl(|\Delta u|^{2}-|u|^{2} \bigr) \\ &\quad< \frac{1}{2} \int \biggl(|\Delta u|^{2}-|u|^{2}- \frac{2}{p+2}|u|^{p+2} \biggr) < d, \end{aligned}$$

which indicates

$$\begin{aligned} \int\bigl(|\Delta u|^{2}-|u|^{2}\bigr)< \frac{2(p+2)}{p}d. \end{aligned}$$
(3.1)

From Proposition 2.1 and (3.1), we know that u globally exists on \(t \in[0,\infty)\).

Let \(u_{0} = 0\). From (2.2), we have \(u = 0\), which shows that u is a trivial solution of problem (1.1). □

Lemma 3.2

Assume that \(\varphi\in H\) and \(\lambda^{*}>0\) satisfy \(I(\varphi _{\lambda^{*}}) = 0\). Suppose \(\lambda^{*}<1\), then it follows that

$$\begin{aligned} P(\varphi)-P(\varphi_{\lambda^{*}})\geq\frac{1}{2}I( \varphi). \end{aligned}$$
(3.2)

Proof

From the proof of Lemma 2.5 we know

$$\begin{aligned} &I(\varphi_{\lambda})=a\lambda^{2}-b \lambda^{p+2}, \end{aligned}$$
(3.3)
$$\begin{aligned} &P(\varphi_{\lambda})=a\frac{\lambda^{2}}{2}-b\frac{\lambda ^{p+2}}{p+2}, \end{aligned}$$
(3.4)

where \(a=\int(|\Delta\varphi|^{2}+|\varphi|^{2})\), \(b=\int|\varphi|^{p+2}\).

Notice that \(I(\varphi_{\lambda^{*}}) = 0\) requires

$$\begin{aligned} a{\lambda^{*}}^{2}=b{\lambda^{*}}^{p+2}. \end{aligned}$$
(3.5)

Observe that \(\varphi= \varphi_{\lambda^{*}=1}\) and \(I(\varphi) = a -b\), using (3.5), we get

$$\begin{aligned} P(\varphi)-P(\varphi_{\lambda^{*}})=\frac{1}{2}I(\varphi)+ \frac {bp}{2(p+2)}\bigl(1-{\lambda^{*}}^{p+2}\bigr), \end{aligned}$$
(3.6)

and the result of Lemma 3.2 is obtained from (3.6) since \(\lambda^{*}<1\) and \(0< p<\frac {8}{n-4} \). Lemma 3.2 is proved. □

Theorem 3.3

(Blow up in finite time)

Let \(p>1\), \(n>\frac{2(p+2)}{p}\), \(u_{0}\in V\), \(E(0)< d\), then any solution \(u(x, t)\) to problem (1.1) blows up in finite time.

Proof

Since \(u_{0}\in V\), for \(t\in[0,T)\), from Theorem 2.6 we have \(u(x,t)\in V\), i.e., \(I(u)<0\). Then we obtain

$$\begin{aligned} I(u)< 0, \qquad P(u)< d, \quad t\in[0,T). \end{aligned}$$
(3.7)

Since \(u_{0}\in L^{2}(\mathbb{R}^{n})\), \(u\in L^{2}(\mathbb{R}^{n})\), by Lemma 2.2 it follows that

$$\begin{aligned} \frac{d^{2}}{dt^{2}} \int|x|^{2}|u|^{2}\leq8 \biggl(I(u)+ \int|u_{0}|^{2} \biggr). \end{aligned}$$
(3.8)

For fixed \(t\in[0,T)\), \(u=u(t)\). Let \(\lambda^{*}>0\) be such that

$$\begin{aligned} I(u_{\lambda^{*}})=0. \end{aligned}$$

Since \(I(u)<0\), we know from Lemma 2.5 that \(\lambda^{*}<1\). Because

$$\begin{aligned} P\bigl(u_{\lambda}^{*}\bigr)\geq d, \qquad P(u)=P(u_{0}). \end{aligned}$$

By Lemma 3.2, we get

$$\begin{aligned} I(u)\leq2\bigl(P(u_{0})-d\bigr)< 0. \end{aligned}$$
(3.9)

By (2.8), (2.9), and \(E(0)< d\), it follows that

$$\begin{aligned} J''(t)&=\frac{d^{2}}{dt^{2}} \int|x|^{2}|u|^{2} \\ &\leq8 \biggl(2\bigl(P(u_{0})-d\bigr)+ \int|u_{0}|^{2} \biggr) \\ &=-16d+8 \int \biggl(|\Delta u_{0}|^{2}-|u_{0}|^{2}- \frac{2}{p+2}|u_{0}|^{p+2} \biggr)+8 \int|u_{0}|^{2} \\ &=-16d+16E(0) \\ &=-c_{0},\quad 0\leq t< T, \end{aligned}$$
(3.10)

where \(c_{0}\) is a positive constant. Furthermore, we can get

$$J'(t)\leq-c_{0}t+J'(0), \quad 0\leq t< T. $$

Hence there exists a \(t_{0}\geq0\), such that \(J'(t)< J'(0)<0\) for \(t>t_{0}\) and

$$\begin{aligned} J(t)< J'(t_{0}) (t-t_{0})+J(t_{0}), \quad t_{0} < t< T, \end{aligned}$$
(3.11)

since \(J(0)>0\) (by \(I(u_{0})<0\)). From (3.11), we know that there exists a \(T_{1}>0\) such that \(J(t)>0\) for \(t\in[0,T_{1})\),

$$\begin{aligned} \lim_{t\rightarrow T_{1}}J(t)=0. \end{aligned}$$
(3.12)

From (3.12), the Hölder inequality, and the Hardy inequality, we have

$$\begin{aligned} \|u_{0}\|^{2}=\|u\|^{2}&= \int\frac{|u|}{|x|}|x||u| \\ &\geq \biggl( \int\frac{|u|^{2}}{|x|^{2}} \biggr)^{\frac{1}{2}} \biggl( \int |x|^{2}|u|^{2} \biggr)^{\frac{1}{2}} \\ &\geq C\|\nabla u\|J^{\frac{1}{2}}{t}, \end{aligned}$$

and it follows that

$$\lim_{t\rightarrow T}\bigl\| \nabla u(t)\bigr\| =\infty, $$

which contradicts \(T= +\infty\). Finally, we can get

$$\lim_{t\rightarrow T}\bigl\| u(t)\bigr\| _{H^{2}}=+\infty. $$

i.e. the solution of problem (1.1) blows up in finite time. □