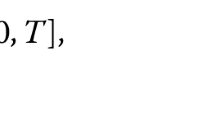Global and blowup solutions of semilinear heat equation involving the square root of the Laplacian

Abstract

In this paper, we consider nonlinear parabolic equations involving a nonlocal operator: the square root of the Laplacian in a bounded domain with zero Dirichlet boundary condition. We use the method on harmonic extension to study the existence and asymptotic estimates of global solutions, as well as the blowup of the parabolic equation.

1 Introduction

This paper is concerned with the study of global and blowup solutions of semilinear heat equation involving a nonlocal positive operator: the square root of the Laplacian in a bounded domain with zero Dirichlet boundary conditions. We consider the semilinear heat equation of the following form:

$$ \left \{ \textstyle\begin{array}{l@{\quad}l} u_{t}+(-\Delta)^{1/2}u=u^{p}, & (x,t)\in\Omega\times(0,T); \\ u(x,t)=0, & (x,t)\in\partial\Omega\times(0,T); \\ u(x,0)=u_{0}(x), &u_{0}(x)\geq0, u_{0}(x) \not\equiv0, \end{array}\displaystyle \right . $$

(1.1)

where Ω is a smooth boundary domain of $\mathbb{R}^{n}$ ($n\geq 2$) and $(-\Delta)^{1/2}$ stands for the square root of the Laplacian operator −Δ in Ω with zero Dirichlet boundary values on ∂Ω, and $p=2^{\#}-1=\frac{n+1}{n-1}$, $2^{\#}=\frac{2n}{n-1}$ is the critical Sobolev exponent.

Nonlinear evolution problems involving fractional Laplacian describing the anomalous diffusion were extensively studied in the mathematical and physical literature (see [1–7] for references). This equation is

$$ u_{t}+(-\Delta)^{\alpha/2}u=u^{p}, \quad \mbox{in } R^{n}\times (0,T), $$

(1.2)

where $0<\alpha< 2$.

However, the parabolic equation in a bounded domain, i.e. the equation

$$ \left \{ \textstyle\begin{array}{l@{\quad}l} u_{t}+(-\Delta)^{\alpha/2}u=u^{p}, & (x,t)\in\Omega\times (0,T); \\ u(x,0)=u_{0}(x), & u_{0}(x)\geq0, u_{0}(x) \not\equiv0, \end{array}\displaystyle \right . $$

(1.3)

is seldom researched. The main difficulty is that the fractional operator, such as $(-\Delta)^{1/2}$, is nonlocal and nonlinear so that this problem may not possess some geometry structures, for example, the mountain pass structure, the Poincaré inequality structure, etc. In order to overcome this difficulty, we turn to another method, which was introduced by Caffarelli and Silvestre in [8] and since then has been widely used in [9–11]. They used this idea to consider the state equation of (1.3): elliptic problems involving a nonlocal operator. In this paper, we shall employ a similar method to [9] or [8] to study the parabolic equation (1.1) involving the square root of the Laplacian.

Firstly, we define lower (high)-energy initial value.

Associated to problem (1.1), the corresponding energy functional $I:H_{0}^{1/2}(\Omega )\rightarrow \mathbb{R}$ is defined as follows:

$$I(u)=\frac{1}{2}\int_{\Omega}\bigl\vert (- \Delta)^{1/4}u\bigr\vert ^{2}\, dx-\frac{1}{2^{\# }}\int _{\Omega}|u|^{2^{\#}}\, dx. $$

Definition 1.1

We say that a function $u_{0}(x)$ possesses lower-energy if $u_{0}(x)$ satisfies $E(u_{0}(x))< \frac{1}{2n}S^{n}$.

Otherwise, we say that $u_{0}(x)$ possesses high-energy, where S denotes the best Sobolev constant.

We shall see the existence of global solutions with lower-energy and the difference of asymptotic behavior of blowing-up solutions with lower-energy and those with high-energy in the following results.

Remark 1.1

Lions [12] showed that

$$S=\inf\biggl\{ \frac{\int_{R_{+}^{n+1}}|\nabla w(x,y)|^{2}\,dx\,dy}{(\int_{R^{n}}|w(x,0)|^{2^{\#}}\,dx)^{2/2^{\#}}}\Big| w\in D^{1,2}\bigl(R_{+}^{n+1} \bigr)\biggr\} . $$

Escobar [13] proved that the extremal functions all have the form

$$U_{\varepsilon}(x,y)=\frac{\varepsilon ^{(n-1)/2}}{|(x-x_{0},y+\varepsilon)|^{n-1}}, $$

where $x_{0}\in R^{n}$ and $\varepsilon>0$ are arbitrary. In addition, the best constant is

$$S=\frac{(n-1)\sigma_{n}^{1/n}}{2}, $$

where $\sigma_{n}$ denotes the volume of n-dimensional sphere $R^{n}\subset R^{n+1}$.

In this paper, we consider the following weak solution.

Definition 1.2

We say that a function u is a solution of (1.1) in $\Omega\times (0,T)$ if

$$\begin{aligned}& u\in L^{\infty}\bigl(0,T; H^{1/2}_{0}(\Omega)\bigr), \\& u_{t}\in L^{2}\bigl(0,T;L^{2}(\Omega)\bigr), \end{aligned}$$

and satisfies (1.1) in the distribution sense.

Remark 1.2

The analogous problem to (1.1) for the Laplacian has been investigated widely in the last decades. This is the problem

$$ \left \{ \textstyle\begin{array}{l@{\quad}l} u_{t}-\Delta u=u^{p}, & (x,t)\in\Omega\times(0,T); \\ u(x,t)=0, & (x,t)\in\partial\Omega\times(0,T); \\ u(x,0)=u_{0}(x), & u_{0}(x)\geq0, u_{0}(x) \not\equiv0, \end{array}\displaystyle \right . $$

(1.4)

see [14] and references therein. In [14], Tan first introduced the energy method to study the existence and asymptotic estimates of global solution of (1.4) in $R^{n}$ ($n\geq 3$), and gave the sufficient conditions of finite time blowup of local solution by the classical concave method. Finally, he considered the asymptotic behavior of any global solution.

For the square root $(-\Delta)^{1/2}$ of the Laplacian, we derive the following results.

Theorem 1.1

Let $u_{0}(x)$ be a lower-energy initial value and $E(u_{0}(x))\leq 0$. Then $u(x,y,t;u_{0})$ blows up in finite time.

Theorem 1.2

Let $u_{0}(x)$ (≢0) be a lower-energy initial value with $E(u_{0}(x))> 0$.

(1^∘):

If $\int_{\Omega}|u_{0}|^{2^{\#}}\,dx< S^{n}$, then (1.1) has a global solution $u(x,t;u_{0})$.

Moreover, there exist $K_{1}>0$ and $K_{2}>0$ such that

$$\begin{aligned}& \|u\|_{H_{0}^{1/2}}=O\bigl(e^{-K_{1}t}\bigr),\quad t\rightarrow\infty, \end{aligned}$$

(1.5)

$$\begin{aligned}& \|u\|_{L^{2}}=O\bigl(e^{-K_{2}t}\bigr),\quad t\rightarrow\infty. \end{aligned}$$

(1.6)

(2^∘):

If $\int_{\Omega}|u_{0}|^{2^{\#}}\,dx> S^{n}$, then the local solution blows up in finite time.

As $(-\Delta)^{1/2}$ is nonlocal and nonlinear, we realize problem (1.1) through a local problem in one more dimension by a Dirichlet to Neumann map. Here the Sobolev trace embedding comes into play, and its critical exponent $2^{\#}=\frac{2n}{n-1}$, $n\geq2$, is the power in Theorem 1.2.

2 Preliminaries

In this section we collect preliminary facts for future reference.

Let $\{\lambda_{k},\varphi_{k}\}_{k=1}^{\infty}$ be the eigenvalues and corresponding eigenfunctions of the Laplacian operator −Δ in Ω with zero Dirichlet boundary values on ∂Ω, such that $\|\varphi_{k}\|_{L^{2}(\Omega)}=1$. Let

$$H_{0}^{1/2}(\Omega)=\Biggl\{ u= \sum _{k=0}^{\infty}a_{k}\varphi _{k}\in L^{2}:\|u\|_{H_{0}^{1/2}(\Omega)}=\Biggl( \sum_{k=0}^{\infty}a_{k}^{2} \lambda_{k}^{1/2}\Biggr)^{1/2}< \infty\Biggr\} . $$

Denote by $H_{0}^{-1/2}(\Omega)$ the dual space of $H_{0}^{1/2}(\Omega)$. $(-\Delta)^{1/2}$ is given by

$$ (-\Delta)^{1/2} u= \sum_{k=1}^{\infty} \alpha_{k}\lambda _{k}^{1/2}\varphi_{k} $$

(2.1)

for $u= \sum_{k=1}^{\infty}\alpha_{k}\varphi_{k}\in L^{2}(\Omega)$.

Regarding (1.1) as elliptic with respect to x variables, we have, from [9],

$$ \left \{ \textstyle\begin{array}{l@{\quad}l} -\Delta v=0, & (x,y)\in C; \\ v=0, & (x,y)\in\partial_{L} C; \\ \frac{\partial v}{\partial n}=-v_{t}+v^{p}, & (x,y)\in \Omega\times\{0\}; \\ v(x,0,0)=v_{0}(x,0)=u_{0}(x), & u_{0}(x)\geq0, u_{0}(x) \not\equiv0. \end{array}\displaystyle \right . $$

(2.2)

That is, we will study the following mixed boundary value problem in a half cylinder:

$$ \left \{ \textstyle\begin{array}{l@{\quad}l} -\Delta v=0, & (x,y,t)\in C\times(0,T); \\ v=0, & (x,y,t)\in\partial_{L} C\times(0,T); \\ v_{t}+\frac{\partial v}{\partial n}=v^{p}, & (x,y,t)\in \Omega\times\{0\}\times (0,T); \\ v(x,0,0)=v_{0}(x,0)=u_{0}(x), & u_{0}(x)\geq0, u_{0}(x) \not\equiv0, \end{array}\displaystyle \right . $$

(2.3)

where n is the unit outer normal to $\Omega\times\{0\}\times (0,T)$, $C=\Omega\times(0, \infty)$ and its lateral boundary is denoted by

$$\partial_{L}C=\partial\Omega\times[0, \infty). $$

If v satisfies (2.3), then the trace u on $\Omega\times\{0\}\times (0,T)$ of the function v will be a solution of problem (1.1). We consider the Sobolev space of a function in $H^{1}(\mathcal{C})$ whose traces vanish on $\partial_{L}\mathcal{C}$,

$$ H_{0,L}^{1}(\mathcal{C})=\bigl\{ v\in H^{1}( \mathcal{C})|v=0 \mbox{ a.e. on } \partial_{L}\mathcal{C}\bigr\} , $$

(2.4)

equipped with the norm

$$ \|v\|=\biggl(\int_{\mathcal{C}}|\nabla v|^{2}\,dx\,dy \biggr)^{1/2}. $$

(2.5)

Denote by $\mathcal{V}_{0}(\Omega)$ the space of traces on $\Omega\times\{0\}$ of functions in $H_{0,L}^{1}(\mathcal{C})$:

$$\mathcal{V}_{0}(\Omega)=\bigl\{ u=\operatorname{tr}_{\Omega}v|v \in H_{0,L}^{1}(\mathcal{C})\bigr\} . $$

It is easy to see that for every $\eta\in C^{\infty}(\overline{\mathcal{C}})\cap H^{1}(\mathcal{C})$ and $\eta\equiv0$ on $\partial_{L}\mathcal{C}$,

$$\int_{\mathcal{C}}\nabla v \nabla\eta \,dx\,dy=\int _{\Omega}\frac{\partial v}{\partial n}\eta \,dx. $$

Since the harmonic extension operator is bijective from $\mathcal {V}_{0}(\Omega)$ to $H_{0,L}^{1}(\mathcal{C})$, by using the trace theorem we can deduce the following definition.

Definition 2.1

Assume v is the harmonic extension of u (in the weak sense) to $\mathcal{C}$ and vanishing on $\partial_{L}\mathcal{C}$. Let us define the operator $(-\Delta)^{1/2}:\mathcal{V}_{0}(\Omega)\rightarrow \mathcal{V}_{0}^{*}(\Omega)$ by

$${\biggl.(-\Delta)^{1/2}u=\frac{\partial v}{\partial n}\biggr|_{\Omega\times\{0\}}}, $$

where $\mathcal{V}_{0}^{*}(\Omega)$ is the dual space of $\mathcal{V}_{0}(\Omega)$.

Equation (2.3) corresponds formally to the $L^{2}$ gradient flow associated to the energy functional

$$E(v)=\frac{1}{2}\int_{\mathcal{C}}|\nabla v|^{2}\,dx \,dy-\frac{1}{2^{\# }}\int_{\Omega\times\{0\}}|v|^{2^{\#}}\,dx. $$

One formally sees at once that $E(v)$ is decreasing in time along the trajectory for

$$\frac{d}{dt}E\bigl(v(x,y,t)\bigr)=-\int_{\Omega\times\{0\}}v_{t}^{2}(x,y,t) \,dx, $$

i.e. $E(v)$ is a Lyapunov functional for this flow.

In the following, we give some properties of the space $H_{0,L}^{1}(\mathcal{C})$. Denote by $D^{1,2}(R^{n+1}_{+})$ the closure of the set of smooth functions compactly supported in $\overline{R}_{+}^{n+1}$ with respect to the norm of $\|w\|_{D^{1,2}(R^{n+1}_{+})}=(\int_{R^{n+1}_{+}}|\nabla w|^{2}\,dx\,dy)^{1/2}$.

We recall the well-known Sobolev inequality. For $w\in D^{1,2}(R^{n+1}_{+})$, we have

$$ \biggl(\int_{R^{n}}\bigl\vert w(x,0)\bigr\vert ^{2n/(n-1)}\,dx\biggr)^{(n-1)/2n}\leq C\biggl(\int_{R^{n+1}_{+}} \bigl\vert \nabla w(x,y)\bigr\vert ^{2}\,dx\,dy\biggr)^{1/2}, $$

(2.6)

where C depends only on n.

The Sobolev trace inequality leads directly to the next three lemmas. For $v\in H_{0,L}^{1}(\mathcal{C})$, its extension by zero in $R_{+}^{n+1}\backslash\mathcal{C}$ can be approximated by functions compactly supported in $R_{+}^{n+1}$. Thus the Sobolev trace inequality (2.6) leads to the following.

Lemma 2.1

[9]

Let $n\geq2$ and $2^{\#}=\frac{2n}{n-1}$. Then there exists a constant C, depending only n, such that, for all $v\in H_{0, L}^{1}(\mathcal{C})$,

$$ \biggl(\int_{\Omega}\bigl\vert v(x,0)\bigr\vert ^{2^{\#}}\,dx\biggr)^{1/2^{\#}}\leq C\biggl(\int_{\mathcal {C}} \bigl\vert \nabla v(x,y)\bigr\vert ^{2}\,dx\,dy\biggr)^{1/2}. $$

(2.7)

By Hölder’s inequality, since Ω is bounded, the above lemma leads to the following.

Lemma 2.2

[9]

• (i) Let $1\leq q\leq2^{\#}$ for $n\geq2$. Then we have, for all $v\in H_{0,L}^{1}(\mathcal{C})$,

  $$ \biggl(\int_{\Omega}\bigl\vert v(x,0)\bigr\vert ^{q}\,dx\biggr)^{1/q}\leq C\biggl(\int_{\mathcal{C}} \bigl\vert \nabla v(x,y)\bigr\vert ^{2}\,dx\,dy\biggr)^{1/2}, $$

  (2.8)

  where C depends only on n, q, and the measure of Ω. Moreover, (2.5) also holds for $1\leq q< \infty$ if $n=1$.

• (ii) Let $1\leq q< 2^{\#}=\frac{2n}{n-1}$ for $n\geq2$ and $1\leq q< \infty$ for $n=1$. Then $\operatorname{tr}_{\Omega}(H_{0,L}^{1}(\mathcal{C}))$ is compactly embedded in $L^{q}(\mathcal{C})$.

Lemma 2.3

[15]

$$ \bigl\Vert (-\Delta)^{1/2}u\bigr\Vert _{H_{0}^{-1/2}(\Omega)}=\|u \|_{H_{0}^{1/2}(\Omega )}=\|v\|_{H^{1/2}_{0,L}(C)}. $$

(2.9)

3 Proof of Theorem 1.1

In fact, we can prove a more general result. If there exists some $t_{0}$ such that $E(v(t_{0}))\leq0$, then $v(x,y,t;u_{0})$ blows up in finite time. We shall employ the classical concavity method (see [14, 16, 17]). Suppose that $t_{\mathrm{max}}=\infty$ and denote $f(t)=\frac{1}{2}\int_{t_{0}}^{t}\int_{\Omega\times \{0\}}|v|^{2}\,dx\,ds$.

We perform standard manipulations:

$$\begin{aligned}& \int_{t_{0}}^{t}\int_{\Omega\times \{0\}}v_{s}^{2} \,dx\,ds+\frac{1}{2}\int_{\mathcal{C}}|\nabla v|^{2} \,dx\,dy-\frac{1}{2^{\#}}\int_{\Omega\times\{0\}}|v|^{2^{\#}}\,dx =E \bigl(v(t_{0})\bigr), \end{aligned}$$

(3.1)

$$\begin{aligned}& f'(t)=\frac{1}{2}\int_{\Omega\times\{0\}}|v_{0}|^{2} \,dx+\int_{t_{0}}^{t}\biggl[-\int_{\mathcal{C}}| \nabla v|^{2}\,dx\,dy+\int_{\Omega\times\{ 0\}}|v|^{2^{\#}} \,dx\biggr]\,ds, \end{aligned}$$

(3.2)

$$\begin{aligned}& f''(t)=-\int_{\mathcal{C}}|\nabla v|^{2}\,dx\,dy+\int_{\Omega\times\{0\} }|v|^{2^{\#}} \,dx. \end{aligned}$$

(3.3)

By (3.1), (3.3), we have

$$ f''(t)=\biggl(\frac{2^{\#}}{2}-1\biggr)\int _{\mathcal{C}}|\nabla v|^{2}\,dx\,dy-2^{\# }E \bigl(v(t_{0})\bigr)+2^{\#}\int_{t_{0}}^{t} \int_{\Omega\times\{0\} }v_{s}^{2}\,dx\,ds. $$

(3.4)

From the assumption, $E(v(t_{0}))\leq0$ such that

$$ \biggl(\frac{2^{\#}}{2}-1\biggr)\int_{\mathcal{C}}|\nabla v|^{2}\,dx\,dy-2^{\# }E\bigl(v(t_{0})\bigr)> 0 $$

(3.5)

for all $t\geq t_{0}$. If we had $t_{\mathrm{max}}=\infty$, this inequality would yield

$$\begin{aligned}& \lim_{t\rightarrow\infty}f'(t)=\infty, \\& \lim_{t\rightarrow\infty}f(t)= \lim_{t\rightarrow\infty} \biggl(f(t_{0})+\int_{t_{0}}^{t}f'(s) \,ds\biggr)= \lim_{t\rightarrow\infty}\int_{t_{0}}^{t}f'(s) \,ds=\infty, \\& f''(t)\geq2^{\#}\int_{t_{0}}^{t} \int_{\Omega\times\{0\} }v_{s}^{2}\,dx\,ds \end{aligned}$$

and

$$\begin{aligned} f(t)f''(t) \geq& \frac{2^{\#}}{2}\biggl(\int _{t_{0}}^{t}\int_{\Omega\times\{0\} }\bigl\vert v(s)\bigr\vert ^{2}\,dx\,ds\biggr) \biggl(\int_{t_{0}}^{t} \int_{\Omega\times\{0\} }\bigl\vert v_{s}(s)\bigr\vert ^{2}\,dx\,ds\biggr) \\ \geq& \frac{2^{\#}}{2}\biggl(\int_{t_{0}}^{t}\int _{\Omega\times \{0\}}vv_{s}\,dx\,ds\biggr)^{2} = \frac{2^{\#}}{2}\bigl(f'(t)-f'(0)\bigr)^{2}, \end{aligned}$$

and as $t\rightarrow\infty$ we have, for some $\alpha> 0$ and $\forall t\geq t_{0}$,

$$f(t)f''(t)\geq (1+\alpha) \bigl(f'(t) \bigr)^{2}. $$

Hence $f^{-\alpha}(t)$ is concave on $[t_{0},\infty]$, $f^{-\alpha}(t)> 0$, and $\lim_{t\rightarrow\infty}f^{-\alpha}(t)=0$. This contradiction proves that $t_{\mathrm{max}}< \infty$, which completes the proof of Theorem 1.1.

4 Proof of Theorem 1.2

We divide the proof into several steps.

Step 1: Proof of existence.

(i) As regards a priori estimates and local existence, assume $v_{n_{0}}\in H_{0,L}^{1}(\mathcal{C})$ such that

$$v_{n_{0}}\rightarrow v_{0},\quad \mbox{strongly in } H_{0,L}^{1}(\mathcal{C}) $$

and

$$E(v_{n_{0}})< \frac{1}{2n}S^{n}, \qquad \int _{\Omega\times \{0\}}|v_{n_{0}}|^{2^{\#}}\,dx< S^{n}. $$

On the other hand, multiplying (2.3) by $v_{nt}$ and integrating, we have

$$ \int_{0}^{t}\int_{\Omega\times \{0\}}v_{ns}^{2} \,dx\,ds+\frac{1}{2}\int_{\mathcal{C}}|\nabla v_{n}|^{2}\,dx\,dy-\frac{1}{2^{\#}}\int _{\Omega\times \{0\}}|v_{n}|^{2^{\#}}\,dx\leq E(v_{n_{0}}). $$

(4.1)

For the sake of convenience, define

$$\Sigma=\biggl\{ v\Big|v\in H^{1}_{0,L}(\mathcal{C}), v\geq0, v \not\equiv0, E(v)< \frac{1}{2n}S^{n}, \int_{\Omega\times\{0\}}|v|^{2^{\#}} \,dx< S^{n}\biggr\} . $$

Now, we show that $v_{n}(t)\in\Sigma$, for any $t\geq0$. Suppose that it does not hold and let $t^{*}$ be the smallest time for which $v_{n}(t^{*})\notin\Sigma$. Then in virtue of the continuity of $v_{n}(t)$, we see that $v_{n}(t^{*})\in\partial\Sigma$. Hence

$$E\bigl(v_{n}\bigl(t^{*}\bigr)\bigr)=\frac{1}{2n}S^{n} \quad \mbox{or} \quad \int_{\mathcal{C}}|\nabla v_{n}|^{2} \,dx\,dy=\int_{\Omega\times\{0\}}|v_{n}|^{2^{\#}}\,dx, $$

which contradicts (4.1). Then from (4.1) and noting that if

$$\int_{\Omega\times\{0\}}|v_{n}|^{2^{\#}} \,dx< S^{n}, $$

then

$$\int_{\mathcal{C}}|\nabla v_{n}|^{2}\,dx\,dy> \int_{\Omega\times\{0\}}|v_{n}|^{2^{\#}}\,dx, $$

we have

$$ \int_{0}^{t}\int_{\Omega\times\{0\}}\bigl\vert v_{n}'(s)\bigr\vert ^{2}\,dx\,ds+ \frac {1}{2n}\int_{\mathcal{C}}|\nabla v_{n}|^{2} \,dx\,dy\leq E(v_{0})< \frac{1}{2n}S^{n}. $$

(4.2)

Thus, we obtain

$$\begin{aligned}& \int_{0}^{t}\int_{\Omega\times\{0\}}|v_{ns}|^{2} \,dx\,ds< \frac {1}{2n}S^{n}, \end{aligned}$$

(4.3)

$$\begin{aligned}& \int_{\mathcal{C}}|\nabla v_{n}|^{2}\,dx\,dy< S^{n}. \end{aligned}$$

(4.4)

From (4.4), we have

$$ \int_{0}^{t}\int_{\mathcal{C}}|\nabla v_{n}|^{2}\, dx\, dy\, ds\leq C(T), $$

(4.5)

where $C(T)$ is the constant independent of n.

Using the trace theorem, we see, from the prior estimates (4.3) and (4.4), that there exist a subsequence (not relabeled) and a function v such that

$$\begin{aligned}& v_{n}\rightarrow v,\quad \mbox{a.e. on } \mathcal{C}\times(0,T), \\& v_{n}\rightharpoonup v ,\quad \mbox{weakly in } H_{0,L}^{1}( \mathcal{C}), \\& v_{n}(x,0,t)\rightarrow v(x,0,t) ,\quad \mbox{strongly in } L^{q}\bigl(\Omega \times(0,T)\bigr), 2\leq q< 2^{\#}, \\& v_{nt}\rightharpoonup v_{t}, \quad \mbox{weakly in } L^{2}\bigl(\Omega\times\{0\} \times(0,T)\bigr). \end{aligned}$$

In particular, for every $\varphi\in H_{0, L}^{1}(\mathcal{C})$, we obtain, from Lemma 2.2, that, as $n\rightarrow\infty$,

$$\begin{aligned}& \int_{\Omega\times\{0\}}v_{nt}\varphi+\int_{\mathcal{C}} \nabla v_{n}\nabla\varphi-\int_{\Omega\times\{0\}}|v_{n}|^{2^{\# }-2}v_{n} \varphi \,dx=0 \\& \quad \Rightarrow\quad \int_{\Omega\times\{0\}}v_{t}\varphi+\int _{\mathcal {C}}\nabla v\nabla\varphi-\int_{\Omega\times\{0\}}|v|^{2^{\# }-2}v \varphi \,dx=0, \end{aligned}$$

which implies that the function v is a desired local solution of (2.3) and $v\in H_{0, L}^{1}(\mathcal{C})$.

(ii) As regards global existence, multiplying (2.3) by $v_{t}$ and integrating, we obtain

$$\int_{0}^{t}\int_{\Omega\times\{0\}}\bigl\vert v'(s)\bigr\vert ^{2}\,dx\,ds + E\bigl(v(x,0,t) \bigr)= E(u_{0})< \frac{1}{2n}S^{n}. $$

Thus,

$$ E\bigl(v(x,0,t)\bigr)< \frac{1}{2n}S^{n} $$

(4.6)

for any $t> 0$.

Note if

$$\int_{\Omega\times \{0\}}|v|^{2{\#}}\,dx< S^{n}, $$

then

$$\int_{\mathcal{C}}|\nabla v|^{2}\,dx\,dy>\int _{\Omega\times \{0\}}|v|^{2{\#}}\,dx. $$

Now we prove that $v(x,0,t)\in\partial\Sigma$ for any $t> 0$, then we have

$$E\bigl(v(x,0,t)\bigr)\geq\frac{1}{2n}S^{n}, $$

which is a contradiction. Hence

$$\int_{\mathcal{C}}|\nabla v|^{2}\,dx\,dy>\int _{\Omega\times\{0\}}|v|^{2{\#}}\,dx $$

for any $t>0$. Therefore,

$$\int_{0}^{t}\int_{\Omega\times\{0\}}\bigl\vert v'(s)\bigr\vert ^{2}\,dx\,ds +\frac {1}{2n} \int_{\mathcal{C}}|\nabla v|^{2}\,dx\,dy \leq E(u_{0})< \frac{1}{2n}S^{n}, $$

which implies

$$\begin{aligned}& \int_{\mathcal{C}}|\nabla v|^{2}\,dx\,dy< S^{n}, \end{aligned}$$

(4.7)

$$\begin{aligned}& \bigl\Vert v'(t)\bigr\Vert _{L^{2}(0,T;L^{2}(\mathcal{C}))}^{2}< \frac{1}{2n}S^{n} \end{aligned}$$

(4.8)

for any $T> 0$. Thus, $v(x,y,t)$ is a global solution of (2.3).

Step 2: Proof of (1.5).

We apply the same argument as in [18], and for the sake of completeness, we give the proof. Let

$$h\bigl(v(t)\bigr)=\int_{\mathcal{C}}|\nabla v|^{2}\,dx\,dy- \int_{\Omega\times\{0\}}|v|^{2^{\#}}\,dx, $$

then by Step 1, we have $h(v(t))> 0$, for all $t\geq0$.

As for the Sobolev trace inequality, we have

$$\int_{\Omega\times\{0\}}\bigl\vert v(x,0,t)\bigr\vert ^{2^{\#}} \,dx\leq\frac{1}{S^{\frac {2^{\#}}{2}}} \biggl(\int_{\mathcal{C}}|\nabla v|^{2}\,dx\,dy\biggr)^{\frac{2^{\#}}{2}} $$

and the inequality

$$E(u_{0})> \frac{1}{2n}\int_{\mathcal{C}}|\nabla v|^{2}\,dx\,dy $$

implies

$$ \int_{\Omega\times\{0\}}\bigl\vert v(x,0,t)\bigr\vert ^{2^{\#}} \,dx< \frac{1}{S^{\frac{2^{\# }}{2}}}\bigl(2nE(u_{0})\bigr)^{\frac{2^{\#}}{2}-1}\int _{\mathcal{C}}|\nabla v|^{2}\,dx\,dy. $$

(4.9)

For simplicity, denote $\frac{1}{S^{\frac{2^{\#}}{2}}}(2n E(v_{0}))^{\frac{2^{\#}}{2}-1}$ by δ ($0<\delta< 1$). Letting $\gamma=1-\delta$, we have

$$ \int_{\Omega\times\{0\}}\bigl\vert v(x,0,t)\bigr\vert ^{2^{\#}} \,dx\leq (1-\gamma)\int_{\mathcal{C}}|\nabla v|^{2}\,dx \,dy. $$

(4.10)

Let $T> t_{0}$ be a fixed number, then

$$\frac{1}{2}\frac{d}{dt}\int_{\Omega\times\{0\}}\bigl\vert v(x,0,t)\bigr\vert ^{2}\,dx=-h\bigl(v(t)\bigr). $$

Using Lemma 2.2, there exists a positive constant $C_{1}$ such that

$$\begin{aligned} \int_{t}^{T}h\bigl(v(s)\bigr)\,ds =&\frac{1}{2}\int_{\Omega\times \{0\}}\bigl\vert v(x,0,t)\bigr\vert ^{2}\,dx-\int_{\Omega\times\{0\}}\bigl\vert v(x,0,T)\bigr\vert ^{2}\,dx \\ \leq& \frac{1}{2}\int_{\Omega\times\{0\}}\bigl\vert v(x,0,t)\bigr\vert ^{2}\,dx\leq C_{1}\int_{\mathcal{C}}| \nabla v|^{2}\,dx\,dy. \end{aligned}$$

(4.11)

Furthermore, inequality (4.10) implies

$$\begin{aligned} E\bigl(v(t)\bigr) =& \frac{1}{2}\int_{\mathcal{C}}| \nabla v|^{2}\,dx\,dy-\frac{1}{2^{\#}}\int_{\Omega\times \{0\}} \bigl\vert v(x,0,t)\bigr\vert ^{2^{\#}}\,dx \\ =& \frac{1}{2}\int_{\mathcal{C}}|\nabla v|^{2}\,dx \,dy+\frac{1}{2^{\#}}\biggl[h\bigl(v(t)\bigr)-\int_{\mathcal{C}}| \nabla v|^{2}\,dx\,dy\biggr] \\ =&\frac{1}{2n}\int_{\mathcal{C}}|\nabla v|^{2}\,dx \,dy+\frac{1}{2^{\# }}h\bigl(v(t)\bigr) \\ \geq& \frac{1}{2n}\int_{\mathcal{C}}|\nabla v|^{2} \,dx\,dy, \end{aligned}$$

(4.12)

on $[t_{0}, \infty)$.

Therefore, by inequalities (4.11) and (4.12), we obtain

$$ \int_{t}^{T}h\bigl(v(s)\bigr)\,ds\leq C_{1}E\bigl(v(t)\bigr), $$

(4.13)

on $[t_{0},T]$. On the other hand, inequality (4.10) implies

$$ \gamma\int_{\mathcal{C}}|\nabla v|^{2}\,dx\,dy\leq h \bigl(v(t)\bigr), $$

(4.14)

on $[t_{0}, \infty)$.

By inequalities (4.12) and (4.14), we have

$$ E\bigl(v(t)\bigr)\leq\biggl(\frac{1}{2n\gamma}+\frac{1}{2^{\#}}\biggr)h \bigl(v(t)\bigr). $$

(4.15)

Furthermore, (4.13) and (4.15) give

$$C_{1}\int_{t}^{T}E\bigl(v(s)\bigr) \,ds\leq E\bigl(v(t)\bigr), $$

on $[t_{0},T]$.

Then, from the arbitrariness of $T>t_{0}$, we have

$$C_{1}\int_{t}^{\infty}E\bigl(v(s)\bigr) \,ds\leq E\bigl(v(t)\bigr). $$

Let $T_{0}>t_{0}$ be sufficiently large such that $C_{1}^{-1}\leq T_{0}$, it follows that

$$ \int_{t}^{\infty}E\bigl(v(s)\bigr)\,ds\leq T_{0}E\bigl(v(t)\bigr), $$

(4.16)

on $[t_{0}, \infty)$.

Setting $y(t)=\int_{t}^{\infty} E(v(s))\,ds$, it follows from (4.16) that

$$TE\bigl(v(T_{0}+t)\bigr)\leq\int_{t}^{T_{0}+t}E \bigl(v(s)\bigr)\,ds\leq\int_{t}^{\infty }E\bigl(v(s) \bigr)\,ds\leq C_{2}e^{-\frac{t}{T_{0}}}. $$

By (4.12), we have

$$\frac{1}{2n}\int_{\mathcal{C}}\bigl|\nabla v(T_{0}+t)\bigr|^{2} \,dx\,dy\leq C_{3}e^{-\frac{t}{T_{0}}} $$

for some constant $C_{3}$ for large $t>T_{0}$. Hence

$$\int_{\mathcal{C}}|\nabla v|^{2}\,dx\,dy=O \bigl(e^{-K_{1}t}\bigr), \quad \mbox{as } t\rightarrow\infty. $$

From Lemma 2.3, we have

$$\|u\|_{H^{1/2}_{0}(\Omega)}=\int_{\mathcal{C}}|\nabla v|^{2}\,dx \,dy=O\bigl(e^{-K_{1}t}\bigr), \quad \mbox{as } t\rightarrow\infty. $$

Step 3: Proof of (1.6).

Obviously

$$\int_{\Omega\times\{0\}}\bigl\vert \nabla v(x,0,t;v_{0})\bigr\vert ^{2}\,dx< S^{n} $$

and

$$ \frac{d}{dt}\int_{\Omega\times\{0\}}\bigl\vert v(t)\bigr\vert ^{2}\,dx+\int_{\mathcal {C}}|\nabla v|^{2}\,dx\,dy \leq\int_{\Omega\times \{0\}}|v|^{2^{\#}}\,dx $$

(4.17)

for all $t>0$. By the same argument as Step 2, we have

$$\frac{d}{dt}\int_{\Omega\times\{0\}}\bigl\vert v(t)\bigr\vert ^{2}\,dx< -(1-\delta)\int_{\mathcal{C}}|\nabla v|^{2}\,dx\,dy\leq- C_{4}\int_{\Omega\times\{0\}}\bigl\vert v(x,0,t)\bigr\vert ^{2}\,dx. $$

We see that the estimate

$$\int_{\Omega\times\{0\}}\bigl\vert v(x,0,t)\bigr\vert ^{2} \,dx=O\bigl(e^{-K_{2}t}\bigr), \quad \mbox{as } t\rightarrow\infty, $$

holds. That is,

$$\|u\|_{L^{2}(\Omega)}=\int_{\Omega\times\{0\} }\bigl\vert v(x,0,t)\bigr\vert ^{2}\,dx=O\bigl(e^{-K_{2}t}\bigr), \quad \mbox{as } t \rightarrow\infty. $$

Step 4: Proof that if $\int_{\Omega}|u_{0}|^{2^{\#}}\,dx> S^{n}$, then the local solution blows up in finite time.

We divide the proof into two steps.

(i) First of all, we define a set which consists of the functions that satisfy the following conditions:

$$\begin{aligned}& E\bigl(v_{0}(x,0)\bigr)< \frac{1}{2n}S^{n}, \end{aligned}$$

(4.18)

$$\begin{aligned}& \int_{\Omega\times\{0\}}\bigl\vert v_{0}(x,0)\bigr\vert ^{2^{\#}}\,dx=S^{n}. \end{aligned}$$

(4.19)

We claim that the set is an empty set.

Indeed, let $v_{0}$ belong to the set. If $v_{0}$ satisfies

$$\int_{\mathcal{C}}\bigl\vert \nabla v_{0}(x,y)\bigr\vert ^{2}\,dx\,dy< \int_{\Omega\times \{0\}}\bigl\vert v_{0}(x,0)\bigr\vert ^{2^{\#}}\,dx, $$

then

$$\begin{aligned} S^{n} &\geq \int_{\Omega\times\{0\}}\bigl\vert v_{0}(x,0)\bigr\vert ^{2^{\#}}\,dx\geq \int _{\mathcal{C}}\bigl\vert \nabla v_{0}(x,y)\bigr\vert ^{2}\,dx\,dy \\ &\geq S\biggl(\int_{\Omega\times \{0\}}\bigl\vert v_{0}(x,0)\bigr\vert ^{2^{\#}}\,dx\biggr)^{\frac{2}{2^{\#}}}=S^{n}, \end{aligned}$$

and hence

$$\begin{aligned}& \int_{\mathcal{C}}\bigl\vert \nabla v_{0}(x,y)\bigr\vert ^{2}\,dx\,dy=\int_{\Omega\times \{0\}}\bigl\vert v_{0}(x,0)\bigr\vert ^{2^{\#}}\,dx=S^{n}, \\& E\bigl(v_{0}(x,0)\bigr)=\frac{1}{2}\int_{\mathcal{C}} \bigl\vert \nabla v_{0}(x,y)\bigr\vert ^{2}\,dx\,dy- \frac{1}{2^{\#}}\int_{\Omega\times \{0\}}\bigl\vert v_{0}(x,0) \bigr\vert ^{2^{\#}}\,dx=\frac{1}{2n}S^{n}, \end{aligned}$$

which is contradictory to condition (4.18).

If $v_{0}$ satisfies $\int_{\mathcal{C}}|\nabla v_{0}(x,y)|^{2}\,dx\,dy> \int_{\Omega\times \{0\}}|v_{0}(x,0)|^{2^{\#}}\,dx$, then from inequality (4.18), we see that

$$\begin{aligned} \frac{1}{2n}S^{n}&> E\bigl(v_{0}(x,0)\bigr)= \frac{1}{2}\int_{\mathcal{C}}\bigl\vert \nabla v_{0}(x,y)\bigr\vert ^{2}\,dx\,dy-\frac{1}{2^{\#}}\int _{\Omega\times \{0\}}\bigl\vert v_{0}(x,0)\bigr\vert ^{2^{\#}}\,dx \\ &> \frac{1}{2n}\int_{\Omega\times \{0\}}\bigl\vert v_{0}(x,0)\bigr\vert ^{2^{\#}}\,dx. \end{aligned}$$

It implies $\int_{\Omega\times \{0\}}|v_{0}(x,0)|^{2^{\#}}\,dx< S^{n}$ which is a contradiction because of condition (4.19). Therefore, that set is an empty set.

(ii) Thus, we consider only the following case:

$$ E\bigl(v_{0}(x,0)\bigr)< \frac{1}{2n}S^{n},\qquad \int _{\Omega\times\{0\}}\bigl\vert v_{0}(x,0)\bigr\vert ^{2^{\#}}\,dx> S^{n}. $$

(4.20)

Obviously, in this case we have $S^{n}< \int_{\mathcal{C}}|\nabla v_{0}(x,y)|^{2}\,dx\,dy< \int_{\Omega\times \{0\}}|v_{0}(x,0)|^{2^{\#}}\,dx$. If $v(x,y,t)$ is a global solution, then we can deduce that $v(x,y,t)$ does not converge strongly to 0 in $H_{0,L}^{1}(\mathcal{C})$. Otherwise, there will exist a $t^{*}$ ($t^{*}> 0$) such that

$$E\bigl(v\bigl(t^{*}\bigr)\bigr)< \frac{1}{2n}S^{n}, \qquad \int_{\Omega\times\{0\}}\bigl\vert v\bigl(x,0,t^{*}\bigr) \bigr\vert ^{2^{\#}}\,dx= S^{n}, $$

which contradicts part (i).

To complete the proof of Theorem 1.2(2^∘), we first prove the following.

Claim

$v_{0}$ satisfies (4.20) and $v(x,y,t;v_{0})$ is a global solution. For $\forall t\in[0,T]$ the following inequalities hold:

$$ S^{n}< \int_{\mathcal{C}}\bigl\vert \nabla v(x,y,t)\bigr\vert ^{2}\,dx\,dy< \int_{\Omega\times \{0\}}\bigl\vert v(x,0,t) \bigr\vert ^{2^{\#}}\,dx. $$

(4.21)

Indeed, if there exists a $t^{*}\in[0,T_{\mathrm{max}}]$ such that

$$\int_{\mathcal{C}}\bigl\vert \nabla v\bigl(x,y,t^{*} \bigr)\bigr\vert ^{2}\,dx\,dy= \int_{\Omega\times \{0\}}\bigl\vert v\bigl(x,0,t^{*}\bigr)\bigr\vert ^{2^{\#}}\,dx, $$

then we have

$$\int_{\mathcal{C}}\bigl\vert \nabla v\bigl(x,y,t^{*} \bigr)\bigr\vert ^{2}\,dx\,dy= \int_{\Omega\times \{0\}}\bigl\vert v\bigl(x,0,t^{*}\bigr)\bigr\vert ^{2^{\#}}\,dx\geq S^{n}. $$

But

$$\frac{1}{2n}S^{n}> E\bigl(v\bigl(t^{*}\bigr)\bigr)= \frac{1}{2n}\int_{\mathcal{C}}\bigl\vert \nabla v \bigl(x,y,t^{*}\bigr)\bigr\vert ^{2}\,dx\,dy, $$

which is a contradiction. Therefore there exists a constant $\eta>0$ sufficiently small and independent of t, rely on $v_{0}$ such that

$$ \int_{\Omega\times \{0\}}\bigl\vert v\bigl(x,0,t^{*}\bigr)\bigr\vert ^{2^{\#}}\,dx\geq (1+\eta)\int_{\mathcal{C}}\bigl\vert \nabla v\bigl(x,y,t^{*}\bigr)\bigr\vert ^{2}\,dx \,dy $$

(4.22)

for any $t\in[0,\infty]$, which completes the proof of the claim.

Now we can complete the proof of Theorem 1.2(2^∘). We shall employ the same argument as the proof of Theorem 1.1. Suppose that $T_{\mathrm{max}}=\infty$ and denote $f(t)=\frac{1}{2}\int_{t_{0}}^{t}\int_{\Omega\times \{0\}}|v|^{2}\,dx\,ds$. We obtain (3.1), (3.3), and from (3.3) and (4.22) we have

$$\begin{aligned} f''(t)&=-\int_{\mathcal{C}}\bigl\vert \nabla v\bigl(x,y,t^{*}\bigr)\bigr\vert ^{2}\,dx\,dy+ (1+ \eta)\int_{\mathcal{C}}\bigl\vert \nabla v\bigl(x,y,t^{*} \bigr)\bigr\vert ^{2}\,dx\,dy \\ &=\eta\int_{\mathcal{C}}\bigl\vert \nabla v\bigl(x,y,t^{*}\bigr)\bigr\vert ^{2}\,dx \,dy. \end{aligned}$$

If we have $T_{\mathrm{max}}=\infty$, then this inequality would yield

$$\lim_{t\rightarrow \infty}f(t)= \lim_{t\rightarrow \infty}f'(t)= \infty. $$

By (3.2) and (3.3) we have

$$f''(t)=\biggl(\frac{2^{\#}}{2}-1\biggr)\int _{\mathcal{C}}\bigl\vert \nabla v\bigl(x,y,t^{*}\bigr) \bigr\vert ^{2}\,dx\,dy-2^{\#}E\bigl(v(t_{0}) \bigr)+2^{\#}\int_{t_{0}}^{t}\int _{\Omega\times \{0\}}v_{s}^{2}\,dx\,ds, $$

and by (4.20), we have

$$\biggl(\frac{2^{\#}}{2}-1\biggr)\int_{\mathcal{C}}\bigl\vert \nabla v\bigl(x,y,t^{*}\bigr)\bigr\vert ^{2}\,dx \,dy-2^{\#}E\bigl(v(t_{0})\bigr)\geq0, $$

which implies

$$f''(t) \geq 2^{\#}\int_{t_{0}}^{t} \int_{\Omega\times\{0\}}v_{s}^{2}\,dx\,ds $$

and

$$f(t)f''(t)\geq \frac{2^{*}}{2}\bigl(f'(t)-f'(0) \bigr)^{2}. $$

By the argument of the proof of Theorem 1.1, we obtain a contradiction, which completes the proof of Theorem 1.2(2^∘).