1 Introduction

The subject of waves on a fluid of variable depth has involved wide attention in a renewed way with the increased interest of researchers studying extreme waves, like tsunami, particularly to improve the related knowledge in an attempt to reduce the gap between theory and application [1–6]. In this article we deal with a two-dimensional problem of surface waves generated by a time dependent sea-bottom upheaval on a beach with uniform slope. Although we are not dealing with tsunami waves as such, at the outset it is sensible to note that tsunami waves in the mid ocean are, in fact, small amplitude waves moving with tremendous velocity. In the last ten to fifteen years, we have seen many works but probably not many theoretical works which analyse asymptotically waves on beaches with respect to space-time parameters; the most illuminating analytical works are those of Ehrenmark [7] and Constantin [8], the latter of which deals with non-linear governing equations in a Lagrangian approach. We are not here to discuss wave-current interaction on variable bed, but it is also another important aspect in which questions are many and answers are inadequate [9–11]. The scarcity of analytical solutions in this type of motion is perhaps due to the complex hydrodynamics involved, and even if we have the formal solution, the analysis of wave integrals is difficult, to say the least. Needless to say that numerical computation of wave integrals has its own demerits as a serious error may creep in due to the oscillatory nature of the integrals. In this paper we have resorted to asymptotic analysis of waves in the unsteady state generated by a ground motion perfectly arbitrary except for the periodicity. Suppose the ocean to be initially at rest and free from any underlying current. We assume that waves are excited only by the action of a time-dependent deformation of sea-bottom at time \(t = 0\), without any initial distribution of surface displacement and velocity. The governing equations and conditions used for the problem are usual linearised equations and conditions for small amplitude waves. Additional conditions such as boundedness conditions at infinity in the horizontal direction, usually required, are imposed. There is, of course, no a priori method of selecting mathematical solution best representing the physical phenomena but the approach to the solution here runs as follows: with a slight change of notation, we have used complex potential, and extensive application of integral transform is made. The main hurdle to a formal solution, as will be evident from the discussion in the subsequent sections, lies in the solution of a Fredholm integral equation of the first kind. For this we demonstrate that the solution is obtained for a 45∘ beach angle; for other beach angles, the present problem still remains unsolved.

Assuming an arbitrarily distributed ground motion oscillatory in time, the formal solution to the problem is subjected to an asymptotic analysis by Van der Waerden’s method [12] which provides uniform asymptotic estimate of the wave height in an unsteady motion even in the vicinity of the critical line. For an exponentially distributed ground motion, we show that it is possible to extract the exact course of variation of wave height at the origin (that is, at the shore line) with time t. In a concluding section some interesting features of the wave motion are discussed with interpretations and illustrations of the analytical and asymptotic results found.

The linear theory of generation of small amplitude waves in a potential problem is justified if the length scales in horizontal and vertical directions are comparable. Linear theory of wave generation and propagation is realistic even with tsunami waves as we find many tsunami source regions are elliptical, with a major axis beyond hundreds of kilometres corresponding to the active part of the fault. The fact that most of the tsunami energy is transmitted at right angles to the major axis allows researchers to regard in this context the propagation of the tsunami in the open sea as being two-dimensional [13]. By this we surmise that mathematical analysis of similar nature may be adopted while analysing wave integrals for the tsunami wave propagation at the open sea where the wave amplitudes are small. Last but not the least, for understanding and analysing ocean waves, some books and articles in dynamical oceanography remain authoritative even with the passing of time and should be mentioned [14–17].

2 The problem

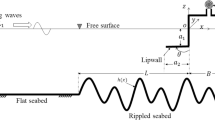
A heavy and homogeneous inviscid liquid lies between two half-planes, namely the free surface \(y =0\) (\(x \ge0\)) and a rigid sloping beach \(y = - x\), in its state of rest at time \(t = 0\) (see Figure 1). Surface waves are generated by a time-dependent deformation of sea-bottom. Considering a two-dimensional problem, we have, for a small amplitude wave motion, the following linearised equations along with the boundary conditions and initial conditions:

$$\begin{aligned}& \nabla^{2} \varphi\equiv\frac{\partial^{2} \varphi}{ \partial x^{2}}+ \frac{\partial^{2} \varphi}{ \partial y^{2}}=0, \end{aligned}$$
(2.1)
$$\begin{aligned}& \left . \begin{aligned} &\frac{\partial^{2} \varphi}{ \partial t^{2}}+ g \frac{\partial\varphi}{\partial y}=0, \\ &\frac{\partial\varphi}{\partial n}= g \eta \end{aligned} \right \}\quad \mbox{on } y=0, \end{aligned}$$
(2.2)
$$\begin{aligned}& \frac{\partial\varphi}{\partial n}= F(x,t)\quad \mbox{on } y=-x, \end{aligned}$$
(2.3)
$$\begin{aligned}& \varphi(x,0;0)=0, \qquad \eta(x;0)=0. \end{aligned}$$
(2.4)

Here \(\varphi(x, y; t)\) is the velocity potential, \(\eta(x; t)\) is the free surface elevation, g is the acceleration due to gravity and \(\vec{n}\) is unit outward drawn normal to the beach. The function \(F(x, t)\) representing the bottom disturbance is assumed to satisfy certain conditions which are stated in Section 4 below.

Figure 1
figure 1

Schematic diagram of the problem.

Full size image

3 The solution of the problem

To solve the system of equations (2.1)-(2.4), we write φ in the form

$$ \varphi(x, y; t)=\int_{0}^{\infty} \bigl( A(m,t) \overline{\varphi}(x,y;m) + B(m,t) \overline{\varphi} _{1}(x,y;m) \bigr)\, dm, $$
(3.1)

where \(\overline{\varphi}(x, y; m)\) is the well-known solution (see [18]) of the following equations subject to the above conditions of boundedness at the origin and infinity:

$$\left \{ \begin{array}{l@{\quad}l} \overline{\varphi}_{xx} + \overline{\varphi }_{yy}=0 & \mbox{throughout the fluid}, \\ \overline{\varphi}_{x} + \overline{\varphi}_{y}=0 & \mbox{on } y = -x , x \ge0, \\ \overline{\varphi}_{y}= m \overline{\varphi} & \mbox{on } y = 0 , x \ge0. \end{array} \right . $$

Also if

$$\overline{\varphi}(x, y; m)= \operatorname{Re} w(x+ iy;m), $$

where w is the complex potential, we take

$$\overline{\varphi}_{1}(x, y; m)=\operatorname{Re} w(x- iy;m). $$

The explicit expressions of \(\overline{\varphi}(x, y; m)\) and \(\overline{\varphi}_{1}(x, y; m)\) are

$$\begin{aligned}& \overline{\varphi}(x, y; m)=e^{my} \cos \biggl(mx+ \frac{\pi }{4} \biggr) + e^{-mx} \cos \biggl(my-\frac{\pi}{4} \biggr) , \end{aligned}$$
(3.2)
$$\begin{aligned}& \overline{\varphi}_{1}(x, y; m)=e^{-my} \cos \biggl(mx+\frac{\pi }{4} \biggr) + e^{-mx} \cos \biggl(my+ \frac{\pi}{4} \biggr) . \end{aligned}$$
(3.3)

Equation (2.3) then leads to the following integral equation of the first kind for the determination of \(B(m, t)\):

$$ F(x,t)= -2 \sqrt{2} \int_{0}^{\infty}m B(m,t) \cosh mx \cos mx \, dm. $$
(3.4)

Multiplying both sides of (3.4) by \(e^{\frac{-x^{2}}{ 4\gamma}}\), we integrate the results with respect to x from 0 to ∞, and make a change of order of integration in the repeated integral. In the latter, use of a known result [19] for the integral with respect to x transforms equation (3.4) to

$$ -2 ( 2\pi\gamma)^{\frac{1}{2}} \int_{0}^{\infty}m B(m,t) \cos\bigl(2\gamma m^{2}\bigr) \, dm = \int_{0}^{\infty} e^{\frac{-x^{2}}{ 4\gamma}} F(x,t) \, dx. $$
(3.5)

The integral equation (3.5) may now be solved by the application of the inversion theorem on Fourier cosine transforms. This yields

$$ B(m,t) = -2 \bigl( 2\pi^{3}\bigr)^{\frac{1}{2}} \int _{0}^{\infty}\gamma^{-\frac{1}{2}} \cos\bigl(2\gamma m^{2}\bigr)\, d\gamma\int_{0}^{\infty} e^{\frac{-x^{2}}{ 4\gamma}} F(x,t)\, dx. $$
(3.6)

Evaluating the first integral with respect to γ in (3.6), we finally get

$$ B(m,t) = -\frac{2}{\pi m} \int_{0}^{\infty} e^{-mx} \cos \biggl(mx+\frac{\pi}{4} \biggr) F(x,t) \, dx. $$
(3.7)

By (2.2) and (3.1),

$$A_{tt} + gm A = -B_{tt} + gm B. $$

The general solution of this equation is

$$\begin{aligned} A(m,t) =& {\biggl.A_{1}(m)\cos\sigma t + B_{1}(m) \sin\sigma t + \sigma^{-1} \sin\sigma t \frac{\partial B(m,s)}{\partial t}\biggr|_{s=0}} \\ &{} + B(m,0) \cos\sigma t -B(m,t) +2 \int_{0}^{t} \sigma B(m,s) \sin\sigma(t-s) \, ds, \end{aligned}$$
(3.8)

where \(\sigma^{2}=g m\).

Conditions (2.4) show that

$$A_{1}(m)=-B(m,0) $$

and

$$B_{1}(m)=-\sigma^{-1}B(m,0). $$

Therefore

$$ A(m,t) = 2 \int_{0}^{t} \sigma B(m,s) \sin\sigma (t-s) \, ds- B(m,t). $$
(3.9)

Hence

$$\begin{aligned} \varphi(x, y; t) =& \int_{0}^{\infty } \biggl(B(m,t) \bigl(\overline{\varphi}_{1}(x, y; m)-\overline{\varphi}(x, y; m) \bigr) \\ &{}+ 2 \sigma\overline{\varphi}(x, y; m)\int_{0}^{\infty}B(m,s) \sin\sigma(t-s) \, ds \biggr) \, dm. \end{aligned}$$

With the help of (3.2) and (3.3) we get

$$\begin{aligned} \varphi(x, y; t) =& \int_{0}^{\infty} \biggl[-e^{-m(x+y)}B(m,t) \biggl(e^{mx} \bigl(e^{2my}-1 \bigr) \cos \biggl(mx+\frac{\pi}{4} \biggr) \\ &{}+ \sqrt{2} e^{my}\sin(my) \biggr) + \int_{0}^{\infty}B(m,s) \sin\sigma(t-s) \, ds\biggr] \, dm. \end{aligned}$$
(3.10)

Equation (2.2) then gives

$$\begin{aligned} \eta(x; t) =& -\frac{2^{\frac{3}{2}}}{\pi} \int_{0}^{\infty} \frac{\sin(t \sqrt{gm})}{\sqrt{gm}} \biggl[ e^{-mx}+\sqrt{2} \cos \biggl(mx+ \frac{\pi}{4} \biggr) \biggr] \\ &{}\times \biggl( \int_{0}^{\infty}e^{-m\alpha} \sqrt{2} \cos \biggl(m\alpha+\frac{\pi}{4} \biggr) F(\alpha,s)\, d\alpha \biggr)\, dm. \end{aligned}$$
(3.11)

Clearly, it is sufficient for the above procedure to hold that the function

$$\gamma^{-1/2} \int_{0}^{\infty}e^{-\frac {x^{2}}{4\gamma}} F(x,t)\, dx $$

should

  1. (i)

    exist for \(\gamma>0\),

  2. (ii)

    admit of a Fourier cosine transform with the parameter \(2m^{2}\ge0\), and

  3. (iii)

    this transform, when used for \(B(m, t)\) in (3.4), makes the integral uniformly convergent in \(x\ge0\).

The above expression (3.11) is evidently the exact integral solution of the problem as formulated in (2.1)-(2.4).

4 Detailed asymptotic analysis of η for a time-periodic ground motion

We assume

$$F(x, t) = f (x) \exp(i \omega t), \quad t > 0, $$

where \(f(x)\) is non-zero on an interval \(a \le x \le b\) and zero outside \([a, b]\) with ω being the forcing frequency.

For now, (3.11) is the following:

$$\begin{aligned} \eta(x; t) =& -\frac{2^{\frac{3}{2}}}{\pi} \int_{a}^{b}f( \alpha) \biggl( \int_{0}^{\infty} \biggl[e^{-mx}+ \sqrt{2} \cos \biggl(mx+\frac{\pi}{4} \biggr) \biggr]e^{-m\alpha}\cos \biggl(m\alpha+\frac{\pi}{4} \biggr) \\ &{}\times \biggl( \int_{0}^{t}e^{i\omega s} \cos\sigma (t-s)\, ds \biggr)\, dm\biggr)\, d\alpha. \end{aligned}$$
(4.1)

Evaluating the time integral, we rearrange the integrand to write η as follows:

$$ \eta= \frac{2 i }{\pi} \bigl((1+i) (I_{11}+I_{12})+(1-i) (I_{21}+I_{22})+2\bigl(I'_{11}+I'_{12} \bigr) \bigr) , $$
(4.2)

where, for \(k,j=1,2 \),

$$I_{jk}(x,t)= \int_{0}^{\infty} \bigl( \omega-(-1)^{k} \sigma \bigr)^{-1} \bigl( e^{i\omega t} - e^{(-1)^{k+1}i\sigma t} \bigr) F_{1}(m) e^{(-1)^{j+1}imx}\, dm $$

and

$$I'_{1k}(x,t)= \int_{0}^{\infty} \bigl( \omega -(-1)^{k+1} \sigma \bigr)^{-1} \bigl( e^{i\omega t} - e^{(-1)^{k+1}i\sigma t} \bigr) F_{1}(m) e^{-mx}\, dm, $$

with

$$ F_{1}(m)= \int_{a}^{b} f(\alpha) \cos \biggl(m\alpha +\frac{\pi}{4} \biggr) e^{-m\alpha}\, d \alpha. $$
(4.3)

When suitable restrictions are placed on \(F_{1}(m)\), the integrals \(I_{jk}\) and \(I'_{1k}\), \(j,k=1,2\), are all proper integrals. It is possible to write

$$\begin{aligned}& I_{j1}(x,t)= e^{i\omega t} \, \mathrm{p.v.} \int_{0}^{\infty} ( \omega- \sigma )^{-1}F_{1}(m) e^{(-1)^{j+1}i m x} \, dm \\& \hphantom{I_{j1}(x,t)=}{} - \mathrm{p.v.} \int_{0}^{\infty} ( \omega- \sigma )^{-1}F_{1}(m) e^{(-1)^{j+1}i (m x+(-1)^{j+1}\sigma t)}\, dm, \\& I_{j2}(x,t)= e^{i\omega t} \int_{0}^{\infty} ( \omega+ \sigma )^{-1}F_{1}(m) e^{(-1)^{j+1}i m x} \, dm \\& \hphantom{I_{j2}(x,t)=} - \int_{0}^{\infty} ( \omega+ \sigma )^{-1}F_{1}(m) e^{(-1)^{j+1}i (m x+(-1)^{j}\sigma t)}\, dm, \\& I'_{11}(x,t)= e^{i\omega t} \, \mathrm{p.v.} \int _{0}^{\infty} ( \omega- \sigma )^{-1}F_{1}(m) e^{- m x} \, dm \\& \hphantom{I'_{11}(x,t)=}{} - \mathrm{p.v.} \int_{0}^{\infty} ( \omega- \sigma )^{-1}F_{1}(m) e^{i\sigma t}e^{ -m x } \, dm, \\& I'_{12}(x,t)= e^{i\omega t} \int_{0}^{\infty} ( \omega- \sigma )^{-1}F_{1}(m) e^{- m x}\, dm \\& \hphantom{I'_{12}(x,t)= }{} - \int_{0}^{\infty} ( \omega- \sigma )^{-1}F_{1}(m) e^{-i\sigma t}e^{ -m x }\, dm. \end{aligned}$$

This is because the principal values (for \(k = 1\)) or ordinary values (for \(k =2\)) of the integrals on the right-hand side clearly exist. At \(\sigma=\omega\), the integrand in each term on the right-hand side is either continuous without a saddle point or has a pole (\(k = 1\)), while in the second term of \(I_{jk}\), there is a saddle point of combination \(mx - \sigma t\) only when \(|k-j|=1\). In the first three cases (that is, in \(I'_{12}\), \(I_{22}\), first part of \(I_{12}\)), the asymptotic contribution for large x and t may be determined by the method of integration by parts.

The contribution of a lone pole (in \(I_{11}\), \(I'_{11}\), first part of \(I_{21}\)) may be determined with the help of a formula due to Lighthill [20], Theorem 19, p.42, for finding asymptotic estimate of the Fourier transform of a generalised function: ‘if \(f(k)\) has a simple pole at \(k = \alpha\), then as \(|x|\to\infty\),

$$ \int_{a}^{b} f(k) e^{i k t} \, dk \sim\pi i \operatorname {sgn}(x)\, \bigl[\mbox{residue of } f(k)e^{i k t} \mbox{ at } k=\alpha \bigr]+ O\bigl( |x|^{-1} \bigr) $$
(4.4)

when \(a<\alpha<b\).’

The contribution of the lone saddle point (second part of \(I_{12}\)) is given by the corresponding formula. Thus the integrals \(I_{11}\), \(I_{22}\), \(I'_{11}\) and \(I'_{12}\) are each of order \(O( x^{-1})\) or \(O(t^{-1})\) as \(x\to\infty\) or \(t\to\infty\), and

$$ I_{12}=- \biggl(\frac{\pi gt^{2}}{x^{3}} \biggr)^{1/2} \biggl(\frac{gt}{2x}+\omega \biggr)^{-1}F_{1} \biggl(\frac{ gt^{2}}{4x^{2}} \biggr) \exp \biggl(-i \biggl( \frac{ gt^{2}}{4x}- \frac{ \pi}{4} \biggr) \biggr)+ O\bigl( x^{-1}\bigr) $$
(4.5)

for \(\frac{ gt^{2}}{4x}\gg1\), \(\frac {x}{b}\gg1\).

The first part of \(I_{21}\) is asymptotically equal to

$$ \frac{2\pi i g}{\omega} F_{1} \biggl(\frac{ \omega ^{2}}{g} \biggr) \exp \biggl(i \biggl( \omega t- \frac{ \omega ^{2}x}{g} \biggr) \biggr) $$
(4.6)

for \(\frac{ \omega^{2}x}{g}\gg1\).

For the second part of the integral \(I_{21}\), the integrand has both a pole and a saddle point at \(s = gt / 2x\), which coincide with \(x = gt / 2\sigma\). We use a method essentially due to Van der Waerden for finding out the asymptotic contribution of this part which remains uniformly valid even in the neighbourhood of the strip \(x = gt / 2\sigma\).

The second part of the integral \(I_{21}\) is written as

$$ \frac{2}{g}\, \mathrm{p.v.} \int_{0}^{\infty} \sigma ( \sigma-\omega )^{-1} \exp \biggl(i \sigma t - \frac{ i \sigma^{2}x}{g} \biggr) F_{1} \biggl(\frac{ \sigma^{2}}{g} \biggr)\, d \sigma, $$
(4.7)

where the path of integration passes below/above the point \(\sigma= \omega\) accordingly as \(w > \frac{gt}{2x}\) or \(w < \frac{gt}{2x}\).

We introduce a new variable \(u = \frac{\sigma}{\omega }- \frac{gt}{2 \omega x}\) in (4.7), which then becomes

$$ \frac{2}{g}\, \mathrm{p.v.} \int_{0}^{\infty} \biggl[ \sigma ( \sigma-\omega )^{-1} \frac{d\sigma}{du} F_{1} \biggl(\frac {\sigma^{2}}{g} \biggr) \biggr]_{(u)} \exp \biggl(i \biggl( \frac{ gt^{2} }{4x}-\frac{u^{2}\omega^{2}x}{g} \biggr) \biggr)\, du. $$
(4.8)

Writing the expression within the braces equals

$$ P(u-u_{0})^{-1} + \sum _{k=0}^{n} \alpha_{k} u^{k}, $$
(4.9)

where \(u_{0}=(u)_{\sigma=\omega}= 1-\frac{ gt }{2\omega x}\), with P and \(\alpha_{0}\) are found to be

$$ \begin{aligned} &P= \frac{2\omega}{g} F_{1} \biggl(\frac{\omega ^{2}}{g} \biggr), \\ &\alpha_{0}=\omega \biggl(\frac{gt}{2x}-\omega \biggr)^{-1} \biggl(\frac{t}{x}F_{1} \biggl( \frac{gt^{2}}{4x^{2}} \biggr)- \frac {2\omega}{g} F_{1} \biggl( \frac{\omega^{2}}{g} \biggr) \biggr). \end{aligned} $$
(4.10)

For \(\frac{\omega^{2} x}{g} \gg1\), Watson’s lemma [21] (and also [22]) is applied to (4.8) after (4.9) is substituted for the terms within the braces in it. Expression (4.7) is thus asymptotically equal to

$$\begin{aligned}& P \exp{ \biggl(\frac{igt^{2} }{4x} \biggr)}\, \mathrm {p.v.} \int _{-\infty}^{\infty} (u-u_{0})^{-1} \exp{ \biggl(-i \frac{u^{2}\omega^{2}x}{g} \biggr)}\, du \\& \quad {}+ \alpha_{0} \exp{ \biggl(i \frac{gt^{2}}{4x} \biggr)} \int _{-\infty}^{\infty} \exp{ \biggl(-i \frac{u^{2}\omega^{2}x}{g} \biggr)}\, du. \end{aligned}$$
(4.11)

On simplification, expression (4.11) (that is, the asymptotic part of \(I_{21}\)) becomes

$$\begin{aligned}& -\pi\sqrt{2} P \exp{ \biggl( i \biggl(\omega t - \frac {\omega^{2} x}{g}+\frac{\pi}{4} \biggr) \biggr)} G \biggl( \frac {\omega^{2} xu^{2}_{0}}{g} \biggr) \operatorname{sgn}(u_{0}) \\& \quad {}+ \alpha_{0} \biggl(\frac{\pi g}{\omega^{2}x} \biggr)^{1/2} \exp{ \biggl( i \biggl( \frac{gt^{2}}{4x}+\frac{\pi}{4} \biggr) \biggr)}, \end{aligned}$$
(4.12)

where \(G(z) = C(z) + i S(z)\), \(C(z)\) and \(S(z)\) denote the Fresnel integrals.

Collecting the results from (4.5), (4.6), (4.10) and (4.12), we obtain finally the following asymptotic expansion for \(\frac{g t^{2}}{4x} \gg1\), \(\frac{x}{b} \gg1\):

$$\begin{aligned} g\eta \sim& 2^{5/2}i \omega \biggl( \exp{ \biggl( i \frac{\pi}{4} \biggr)} -\sqrt{2} \operatorname{sgn}(u_{0}) G \biggl( \frac {\omega^{2} xu_{0}^{2}}{g} \biggr) \biggr) F_{1} \biggl( \frac{\omega^{2}}{g} \biggr) \exp{ \biggl( i \biggl(\omega t -\frac{\omega^{2} x}{g} \biggr) \biggr)} \\ &{}+ \biggl( \frac{8 g^{3} t^{2}}{\pi x^{3}} \biggr)^{1/2} \biggl( \frac{ g t}{2x}+\omega \biggr)^{-1} F_{1} \biggl( \frac{g t^{2}}{4x^{2}} \biggr) \exp{ \biggl( -i \frac{gt^{2}}{4x} \biggr)} \\ &{}+ \biggl( \frac{8 g^{3}}{\pi x} \biggr)^{1/2} \biggl( \frac{g t}{2x}-\omega \biggr)^{-1} \biggl( \frac{t}{x}F_{1} \biggl( \frac{g t^{2}}{4x^{2}} \biggr)- \frac{2\omega}{g}F_{1} \biggl( \frac {\omega^{2}}{g} \biggr) \biggr) \exp{ \biggl( i \frac{gt^{2}}{4x} \biggr)} \\ &{}+ O \bigl(x^{-1} \bigr). \end{aligned}$$
(4.13)

It is clear that expansion (4.13) is uniformly valid even when \(\frac{2\omega x}{gt}\) is near unity; in fact, it holds in a wider region where it joins up with the asymptotic expansions of the Fresnel integrals. Thus if \(2\omega x \ll gt\), equation (4.13) reduces to

$$ \eta \sim 8 \sqrt{2} \frac{\omega}{g} F_{1} \biggl( \frac {\omega^{2}}{g} \biggr) \exp{ \biggl( i \biggl(\omega t -\frac{\omega ^{2} x}{g}- \frac{\pi}{4} \biggr) \biggr)}. $$
(4.14)

When \(2\omega x \gg gt\), from equation (4.13) we have

$$ \eta \sim - \biggl( \frac{32 g t^{2}}{\pi\omega^{2}x^{3}} \biggr)^{1/2} F_{1}(0) \biggl( i \sin\frac{gt^{2}}{4x} + \frac{g t}{2\omega x} \cos \frac{gt^{2}}{4x} \biggr). $$
(4.15)

We will try to explore the physical conclusion from these results (4.13)-(4.15) in the latter section.

5 Displacement at the origin

We consider the disturbance model given by

$$ F_{1}(x,t) = k P_{1} e^{-kx} \sin( \omega t),\quad 0\le x< \infty , t\ge0, $$
(5.1)

where k and \(P_{1}\) are real constants and ω is the frequency.

By (4.1), the displacement at the origin may be expressed as

$$\begin{aligned} \eta_{0} = & -2^{\frac{5}{2}}k P_{1} \pi^{-1} \int_{0}^{\infty} \biggl( \int _{0}^{\infty} e^{-(m+k)\alpha} \cos \biggl(m\alpha+ \frac{\pi}{4} \biggr) \\ &{}\times \biggl( \int_{0}^{t} \sin(\omega s) \cos\bigl(\sigma(t-s)\bigr)\, ds \biggr) \, d\alpha \biggr)\, dm \\ =& 2 i k \omega P_{1}(\pi g)^{-1} \bigl(H(m_{1})-H(m_{2}) \bigr), \end{aligned}$$
(5.2)

where

$$H(m_{j})= \int_{0}^{\infty} (m+m_{j})^{-1} \biggl(m-\frac {\omega^{2}}{g} \biggr)^{-1}(\cos\sigma t-\cos\omega t) \, dm $$

with \(m_{j}=2^{-1/2}k \exp{(-1)^{j} \frac{i\pi}{4}}\).

Using two well-known results on Stieltjes transforms [23], p.22, Section 14.1, Equation (4) and Section 14.2, Equation (54), we evaluate the above integrals and obtain finally

$$ \frac{\pi g}{4 \omega P_{1}} \eta_{0} =\eta'_{01}+ \eta'_{02}, $$
(5.3)

where

$$\begin{aligned}& \eta'_{01}= - \frac{4(\cos a \operatorname{ci} a+\sin a \operatorname{si} a)+2\pi\sin a- (\frac{\pi(b+1)}{2}+\log\frac {b^{2}}{2} )\cos a }{1+(1+b)^{2}}, \end{aligned}$$
(5.4)
$$\begin{aligned}& \eta'_{02}= 2 \operatorname{Re} \bigl[ \bigl(1+i(1+b)\bigr)^{-1}\bigl( \exp\bigl(-\sqrt{gt^{2}m_{1}} \bigr) \overline{E}i \bigl(\sqrt {gt^{2}m_{1}}\bigr) \\& \hphantom{\eta'_{02}=}{}+ \exp\bigl(\sqrt{gt^{2}m_{1}}\bigr) Ei \bigl(- \sqrt{gt^{2}m_{1}}\bigr) \bigr) \bigr], \end{aligned}$$
(5.5)

where \(a = \omega t\) and \(b = \frac{2\omega^{2}}{gk}\), and (six, cix, \(Ei(x)\), \(\overline{E}i (x)\)) ≡ (sine, cosine, exponential) integrals.

6 Physical interpretation of the results obtained in Sections 4 and 5 with numerical illustrations

The results obtained in (4.13)-(4.15) and (5.3)-(5.5) are particularly of interest. Asymptotic analysis done in (4.14) and (4.15) is obviously for different ranges of values for x, and we have considered the disturbance model as prescribed in (5.1).

Figure 2 shows the graph of the wave elevation corresponding to result (4.14) at some value of x (here it is \(x = 10\)) and after a comparatively long time with respect to the space variable, and the next figure (Figure 3) is the graph of the same but corresponding to result (4.15) at some large value of x (here it is \(x = 1\text{,}000\)), where variation is again depicted with respect to time, but keeping in view the restrictions on x and t, the range of t is small compared to the space variable x.

Figure 2
figure 2

\(\pmb{2\omega x \ll gt}\) .

Full size image
Figure 3
figure 3

\(\pmb{2\omega x \gg gt}\) .

Full size image

These two plots cannot be depicted on the same time scale due to the obvious restrictions on them while attaining corresponding asymptotic results, but qualitatively the wave structure in both cases is visible. Far more interesting would perhaps be the illustration of η following result (4.13) from where these two results (4.14) and (4.15) are derived. The Fresnel integrals have come into expression (4.13) from the asymptotic evaluation of the second part of the integral \(I_{21}\) when pole and saddle points coalesce under the influence of the parameters. The contribution of Fresnel integrals is quite evident as the whole expression in its asymptotic behaviour joins hands with Fresnel integrals with both the large values of x and t and all other restrictions leading up to expression (4.13). In Figures 4 and 5, which are drawn at the same scale, it is clearly demonstrated how gradually the whole asymptotic expression of underlying current tends towards the asymptotic value of Fresnel integral function with increasing value of t. We have seen the repetition of the same phenomenon with the space variable also, i.e., if t remains fixed and if the value of x starts increasing. Since too many parameters are involved here so the wave characteristics will only be depicted when further restrictions, viz. \(2\omega x \ll gt\) or \(2\omega x \gg gt\), would be imposed upon them (see Figures 2 and 3).

Figure 4
figure 4

Asymptotic expression of η valid uniformly when \(\pmb{2\omega x\sim gt}\) .

Full size image
Figure 5
figure 5

Comparison of asymptotic behaviour of η and the Fresnel integral function.

Full size image

We have illustrated the wave height \(\eta_{0}\) (Figure 6) at the shoreline along with its predominantly large component \(\eta'_{01}\) (Figure 7). The relative smallness of \(\eta '_{02}\) in comparison to \(\eta'_{01}\) is perhaps due to the scale of t adopted.

Figure 6
figure 6

Wave height \(\pmb{\eta_{0}}\) at the shoreline.

Full size image
Figure 7
figure 7

Wave height component \(\pmb{\eta_{01}'}\) .

Full size image

The numerical computations done here are all with a hypothetical disturbance as mentioned in (5.1) at the sea-bed with values of the parameters being \(a = 0\), \(b = \sqrt {2}\), \(g=10\), \(\omega= 0.5\), \(k = 0.005\).

Mathematica software is used for the relevant programming to compute and illustrate the graphs.

7 Conclusion

The problem that we have examined here is a potential problem on a beach where waves are generated by a disturbance at the sea-bed with very little restrictions on the nature of the disturbance except for the oscillation. The solution and asymptotic analysis of waves are discussed at length. The beach angle here is 45∘, which is a severe restriction in regard to a real life situation. The first author has found the solution for a similar type of problem for other beach angles too and also with a non-uniformly sloping beach of the form \(y = - qx^{r}\) but with the shallow water regime [6]. But with the potential problem the solution in the unsteady state for any arbitrary beach angle is not known to have been realised. Extracting wave form from a wave integral is always difficult in a mathematical context. The analysis presented here has addressed two basic issues. Firstly, it has shown the way to reach an exact solution when two decisive points, say one saddle point and a pole or two saddle points in a wave integral are in proximity. This situation is very common in the asymptotic analysis of wave integrals. Our results show quite categorically the nature of waves at large times and long distances in such a situation. From mathematical point of view, this is quite interesting. Secondly, in an oceanographic context these results may be used for all such similar cases of wave generation due to bottom disturbances where, under the influence of many parameters, an identical situation crops up and analytical solution fails to analyse the situation. For example, extreme waves like tsunami are essentially small amplitude waves at the deep sea so their analysis may be helpful in tsunami wave analysis more so as tsunamis are influenced by many oceanographic parameters. For the second point though we place one caveat that we have not dealt here with tsunami waves as such.