On the solutions and conservation laws of the coupled Drinfeld-Sokolov-Satsuma-Hirota system

Abstract

In this paper we study the coupled Drinfeld-Sokolov-Satsuma-Hirota system, which was developed as one example of nonlinear equations possessing Lax pairs of a special form. Also this system was found as a special case of the four-reduction of the Kadomtsev-Petviashivilli hierarchy. We obtain exact solutions of the system by using Lie symmetry analysis along with the simplest equation and Jacobi elliptic equation methods. Also, symmetry reductions are obtained based on the optimal system of one-dimensional subalgebras. In addition, the conservation laws are derived using two approaches: the new conservation theorem due to Ibragimov and the multiplier method.

1 Introduction

In recent years many nonlinear evolution equations (NLEEs) have been used to model many real world problems in various fields of science and engineering. Thus, finding exact explicit solutions of NLEEs is a very important endeavor. It is also true that finding solutions of NLEEs is a difficult task, and only in few special cases one can write down the explicit solutions. However, despite of this fact, various methods of solving NLEEs have been proposed in the literature recently. Some of the most important methods found in the literature include the ansatz method [1], [2], the Weierstrass elliptic function expansion method [3], the Darboux transformation [4], Hirota’s bilinear method [5], the $(G^{\prime }/G)$-expansion method [6], the Jacobi elliptic function expansion method [7], [8], the inverse scattering transform method [9], the homogeneous balance method [10], the Bäcklund transformation [11], the F-expansion method [12], the exp-function method [13], the multiple exp-function method [14], the variable separation approach [15], the sine-cosine method [16], the tri-function method [17], [18], and the Lie symmetry method [19]–[25].

In this paper we study the coupled Drinfeld-Sokolov-Satsuma-Hirota (DSSH) system

$$\begin{array}{r}{u}_t-6u{u}_x+u_{xxx}-6v_x=0,\\ v_t-2v_{xxx}+6u{v}_x=0.\end{array}$$

(1)

This system was introduced independently by Drinfeld and Sokolov [26], and by Satsuma and Hirota [27]. The coupled DSSH system [26] was given as one of numerous examples of nonlinear equations possessing Lax pairs of a special form. Also, the coupled DSSH system [27] was found as a special case of the four-reduction of the KP hierarchy, and its explicit one-soliton solution was constructed. Gürses and Karasu [28] found a recursion operator and a bi-Hamiltonian structure for (1). Wazwaz [29] used three distinct methods, namely the Cole-Hopf transformation, Hirota’s bilinear and the exp-function methods, and obtained solitons, multiple soliton solutions, multiple singular soliton solutions, and plane periodic solutions. Zheng [30] used the $(G^{\prime }/G)$-expansion method and obtained traveling wave solutions of (1).

In this paper we firstly perform symmetry reductions of (1) using Lie group analysis [19]–[24], which are based on the optimal systems of one-dimensional subalgebras. The simplest equation method [31] and the Jacobi elliptic function method [32] are later employed to obtain some exact solutions of (1). In addition to this, conservation laws are derived for (1) using the new conservation theorem [33] and the multiplier method [34].

It is well known that the conservation laws play a very important role in the solution process of differential equations. Also, one can safely say that the existence of a large number of conservation laws of a system of partial differential equations is a strong indication of its integrability [19]. Recently, conservation laws have been used to find exact solutions of certain partial differential equations [35], [36].

2 Symmetry analysis of (1)

The symmetry group of the coupled DSSH system (1) will be generated by the vector field of the form

$$X={\xi }^1(t,x,u,v)\frac{\partial }{\partial t}+{\xi }^2(t,x,u,v)\frac{\partial }{\partial x}+{\eta }^1(t,x,u,v)\frac{\partial }{\partial u}+{\eta }^2(t,x,u,v)\frac{\partial }{\partial v}.$$

The application of the third prolongation ${pr}^{(3)}X$ to (1) results in an overdetermined system of linear partial differential equations. The general solution of these equations with the aid of Maple is given by

$$\begin{array}{c}{\xi }^1(t,x,u,v)=C_1+3t{C}_4,\hfill \\ {\xi }^2(t,x,u,v)=C_2+x{C}_4,\hfill \\ {\eta }^1(t,x,u,v)=-2C_{4}u,\hfill \\ {\eta }^2(t,x,u,v)=C_3-4v{C}_4,\hfill \end{array}$$

where $C_i$, $i=1,\dots ,4$, are arbitrary constants. The above general solution contains four arbitrary constants, and hence the infinitesimal symmetries of (1) form the four-dimensional Lie algebra spanned by the following linearly independent operators:

$$X_1=\frac{\partial }{\partial t},X_2=\frac{\partial }{\partial x},X_3=\frac{\partial }{\partial v},X_4=3t\frac{\partial }{\partial t}+x\frac{\partial }{\partial x}-2u\frac{\partial }{\partial u}-4v\frac{\partial }{\partial v}.$$

2.1 Optimal system of one-dimensional subalgebras

In this subsection we present the optimal system of one-dimensional subalgebras for equation (1) to obtain the optimal system of group-invariant solutions. The method which we use here for obtaining the optimal system of one-dimensional subalgebras is given in [20]. The adjoint transformations are given by

$$Ad(exp(\epsilon X_i))X_j=X_j-\epsilon [X_i,X_j]+\frac{1}{2}{\epsilon }^2[X_i,[X_i,X_j]]-\cdots .$$

The commutator table of the Lie point symmetries of equation (1) and the adjoint representations of the symmetry group of (1) on its Lie algebra are given in Table 1 and Table 2, respectively. Table 1 and Table 2 are then used to construct the optimal system of one-dimensional subalgebras for equation (1).

Table 1 Commutator table of the Lie algebra of equation ( 1 )

Table 2 Adjoint table of the Lie algebra of equation ( 1 )

From Tables 1 and 2 and following [20], one can obtain an optimal system of one-dimensional subalgebras given by $\{X_4,b{X}_1+c{X}_2+d{X}_3\}$, where $b,c,d=0,\pm 1$.

2.2 Symmetry reductions of (1)

In this subsection we use the optimal system of one-dimensional subalgebras calculated above to obtain symmetry reductions.

Case 1. $X_4$

The operator $X_4$ gives rise to the group-invariant solution

$$u=t^{-\frac{2}{3}}F(z),v=t^{-\frac{4}{3}}G(z),$$

(2)

where $z=x{t}^{-1/3}$ is an invariant of the symmetry $X_4$. Substitution of (2) into (1) results in the system of ordinary differential equations (ODEs), where F and G satisfy

$$\begin{array}{c}4G(z)+6G^{{}^{‴}}(z)-18F(z)G^{\prime }(z)+z{G}^{\prime }(z)=0,\hfill \\ 2F(z)-3F^{‴}(z)+zF(z)+18F(z)F^{\prime }(z)+18G(z)=0.\hfill \end{array}$$

Case 2. $b{X}_1+c{X}_2+d{X}_3$; $b,c,d=0,\pm 1$

The symmetry $b{X}_1+c{X}_2+d{X}_3$ gives rise to the group-invariant solution

$$u=F(z),v=G(z)+td/b,$$

(3)

where $z=(bx-ct)/b$ is an invariant of the symmetry $b{X}_1+c{X}_2+d{X}_3$. The insertion of (3) into (1) results in the system of ODEs

$$\begin{array}{c}6bF(z)F^{\prime }(z)+c{F}^{\prime }(z)-b{F}^{‴}(z)+6b{G}^{\prime }(z)=0,\hfill \\ c{G}^{\prime }(z)-6bF(z)G^{\prime }(z)+2b{G}^{‴}(z)-d=0.\hfill \end{array}$$

3 Exact solutions of (1) using the simplest equation method

Taking the linear combination of the translation symmetries, viz.$X_1+\lambda X_2$, and solving the corresponding Lagrange system for the symmetry $X_1+\lambda X_2$, one obtains an invariant $z=x-\lambda t$ and the group-invariant solution of the form

$$u=F(z),v=G(z),$$

(4)

where the functions F and G satisfy

$$F^{‴}(z)-\lambda F^{\prime }(z)-6F(z)F^{\prime }(z)-6G^{\prime }(z)=0,$$

(5a)

$$6F(z)G^{\prime }(z)-2G^{‴}(z)-\lambda G^{\prime }(z)=0.$$

(5b)

Now we use the simplest equation method [25], [31] to solve system (5a)-(5b); and as a result, we obtain the exact solutions of our coupled DSSH system (1). Bernoulli and Riccati equations will be used as the simplest equations.

Let us consider the solutions of (5a)-(5b) in the form

$$F(z)=\sum _{i=0}^M{\mathcal{A}}_i{(H(z))}^i,G(z)=\sum _{i=0}^N{\mathcal{B}}_i{(H(z))}^i,$$

(6)

where $H(z)$ satisfies the Bernoulli or Riccati equation, M and N are positive integers that can be determined by a balancing procedure and ${\mathcal{A}}_i$’s and ${\mathcal{B}}_i$’s are parameters to be determined.

3.1 Solutions of (1) using the Bernoulli equation as the simplest equation

The balancing procedure gives $M=2$ and $N=4$, and hence the solutions of (5a)-(5b) are of the form

$$F(z)={\mathcal{A}}_0+{\mathcal{A}}_{1}H+{\mathcal{A}}_2{H}^2,$$

(7a)

$$G(z)={\mathcal{B}}_0+{\mathcal{B}}_{1}H+{\mathcal{B}}_2{H}^2+{\mathcal{B}}_3{H}^3+{\mathcal{B}}_4{H}^4.$$

(7b)

Substituting (7a)-(7b) into (5a)-(5b) and making use of the Bernoulli equation [25] and then equating the coefficients of the functions $H^i$ to zero, we obtain an algebraic system of equations in terms of ${\mathcal{A}}_i$ ($i=0,1,2$) and ${\mathcal{B}}_i$ ($i=0,1,2,3,4$). Solving the resultant system of algebraic equations with the aid of Maple, one possible set of values of ${\mathcal{A}}_i$ and ${\mathcal{B}}_i$ is as follows:

$$\begin{array}{c}\lambda =\frac{7}{2}{a}^2,{\mathcal{A}}_0=\frac{11}{12}{a}^2,{\mathcal{A}}_1=10ab,{\mathcal{A}}_2=10b^2,\hfill \\ {\mathcal{B}}_1=-\frac{40}{3}{a}^{3}b,{\mathcal{B}}_2=-\frac{160}{3}{a}^2{b}^2,{\mathcal{B}}_3=-80b^{3}a,{\mathcal{B}}_4=-40b^4.\hfill \end{array}$$

As a result, a solution of (1) is

$$\begin{array}{rl}u(t,x)=& {\mathcal{A}}_0+{\mathcal{A}}_{1}a\left\{\frac{cosh[a(z+C)]+sinh[a(z+C)]}{1-bcosh[a(z+C)]-bsinh[a(z+C)]}\right\}\\ +{\mathcal{A}}_2{a}^2{\left\{\frac{cosh[a(z+C)]+sinh[a(z+C)]}{1-bcosh[a(z+C)]-bsinh[a(z+C)]}\right\}}^2,\end{array}$$

(8a)

$$\begin{array}{rl}v(t,x)=& {\mathcal{B}}_0+{\mathcal{B}}_{1}a\left\{\frac{cosh[a(z+C)]+sinh[a(z+C)]}{1-bcosh[a(z+C)]-bsinh[a(z+C)]}\right\}\\ +{\mathcal{B}}_2{a}^2{\left\{\frac{cosh[a(z+C)]+sinh[a(z+C)]}{1-bcosh[a(z+C)]-bsinh[a(z+C)]}\right\}}^2\\ +{\mathcal{B}}_3{a}^3{\left\{\frac{cosh[a(z+C)]+sinh[a(z+C)]}{1-bcosh[a(z+C)]-bsinh[a(z+C)]}\right\}}^3\\ +{\mathcal{B}}_4{a}^4{\left\{\frac{cosh[a(z+C)]+sinh[a(z+C)]}{1-bcosh[a(z+C)]-bsinh[a(z+C)]}\right\}}^4,\end{array}$$

(8b)

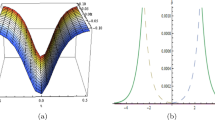
where $z=x-\lambda t$. The profile of solution (8a)-(8b) is given in Figure 1.

Figure 1

Profile of ( 8a )-( 8b ).

3.2 Solutions of (1) using the Riccati equation as the simplest equation

In this case the balancing procedure also gives the same values of M and N, i.e., $M=2$ and $N=4$. Thus the solutions of (5a)-(5b) are of the form

$$F(z)={\mathcal{A}}_0+{\mathcal{A}}_{1}H+{\mathcal{A}}_2{H}^2,$$

(9a)

$$G(z)={\mathcal{B}}_0+{\mathcal{B}}_{1}H+{\mathcal{B}}_2{H}^2+{\mathcal{B}}_3{H}^3+{\mathcal{B}}_4{H}^4.$$

(9b)

Substituting (9a)-(9b) into (5a)-(5b) and making use of the Riccati equation [25], we obtain an algebraic system of equations in terms of ${\mathcal{A}}_i$ and ${\mathcal{B}}_i$. Solving the resultant system, one possible set of values is as follows:

$$\begin{array}{c}\lambda =-\frac{7}{200}\left(\frac{400a^{3}c-A_1^2}{a^2}\right),{\mathcal{A}}_0=\frac{7,600a^{3}c+11A_1^2}{1,200a^2},\hfill \\ {\mathcal{A}}_1=10ab,{\mathcal{A}}_2=10a^2,\hfill \\ {\mathcal{B}}_1=-\frac{A_1(200a^{3}c+A_1^2)}{75a^2},{\mathcal{B}}_2=-\frac{8}{15}{A}_1^2-\frac{80}{3}{a}^{3}c,\hfill \\ {\mathcal{B}}_3=-8a^2{A}_1,{\mathcal{B}}_4=-40a^4.\hfill \end{array}$$

Hence solutions of (1) are

$$\begin{array}{rl}u(t,x)=& {\mathcal{A}}_0+{\mathcal{A}}_1\{-\frac{b}{2a}-\frac{\theta }{2a}tanh[\frac{1}{2}\theta (z+C)]\}\\ +{\mathcal{A}}_2{\{-\frac{b}{2a}-\frac{\theta }{2a}tanh[\frac{1}{2}\theta (z+C)]\}}^2,\end{array}$$

(10a)

$$\begin{array}{rl}v(t,x)=& {\mathcal{B}}_0+{\mathcal{B}}_1\{-\frac{b}{2a}-\frac{\theta }{2a}tanh[\frac{1}{2}\theta (z+C)]\}\\ +{\mathcal{B}}_2{\{-\frac{b}{2a}-\frac{\theta }{2a}tanh[\frac{1}{2}\theta (z+C)]\}}^2\\ +{\mathcal{B}}_3{\{-\frac{b}{2a}-\frac{\theta }{2a}tanh[\frac{1}{2}\theta (z+C)]\}}^3\\ +{\mathcal{B}}_4{\{-\frac{b}{2a}-\frac{\theta }{2a}tanh[\frac{1}{2}\theta (z+C)]\}}^4\end{array}$$

(10b)

and

$$\begin{array}{rl}u(t,x)=& {\mathcal{A}}_0+{\mathcal{A}}_1\{-\frac{b}{2a}-\frac{\theta }{2a}tanh\left(\frac{1}{2}\theta z\right)+\frac{sech(\frac{\theta z}{2})}{Ccosh(\frac{\theta z}{2})-\frac{2a}{\theta }sinh(\frac{\theta z}{2})}\}\\ +{\mathcal{A}}_2{\{-\frac{b}{2a}-\frac{\theta }{2a}tanh\left(\frac{1}{2}\theta z\right)+\frac{sech(\frac{\theta z}{2})}{Ccosh(\frac{\theta z}{2})-\frac{2a}{\theta }sinh(\frac{\theta z}{2})}\}}^2,\end{array}$$

(11a)

$$\begin{array}{rl}v(t,x)=& {\mathcal{B}}_0+{\mathcal{B}}_1\{-\frac{b}{2a}-\frac{\theta }{2a}tanh\left(\frac{1}{2}\theta z\right)+\frac{sech(\frac{\theta z}{2})}{Ccosh(\frac{\theta z}{2})-\frac{2a}{\theta }sinh(\frac{\theta z}{2})}\}\\ +{\mathcal{B}}_2{\{-\frac{b}{2a}-\frac{\theta }{2a}tanh\left(\frac{1}{2}\theta z\right)+\frac{sech(\frac{\theta z}{2})}{Ccosh(\frac{\theta z}{2})-\frac{2a}{\theta }sinh(\frac{\theta z}{2})}\}}^2\\ +{\mathcal{B}}_3{\{-\frac{b}{2a}-\frac{\theta }{2a}tanh\left(\frac{1}{2}\theta z\right)+\frac{sech(\frac{\theta z}{2})}{Ccosh(\frac{\theta z}{2})-\frac{2a}{\theta }sinh(\frac{\theta z}{2})}\}}^3\\ +{\mathcal{B}}_4{\{-\frac{b}{2a}-\frac{\theta }{2a}tanh\left(\frac{1}{2}\theta z\right)+\frac{sech(\frac{\theta z}{2})}{Ccosh(\frac{\theta z}{2})-\frac{2a}{\theta }sinh(\frac{\theta z}{2})}\}}^4,\end{array}$$

(11b)

where $z=x-\lambda t$.

3.3 Solutions of (1) in terms of Jacobi elliptic functions

We now present exact solutions of the coupled DSSH system (1) that are expressed in Jacobi elliptic functions. The cosine-amplitude function $cn(z|\omega )$ and the sine-amplitude function $sn(z|\omega )$ satisfy the first-order differential equations

$$H^{\prime }(z)=-{\left\{(1-H^2(z))(1-\omega +\omega H^2(z))\right\}}^{\frac{1}{2}}$$

(12)

and

$$H^{\prime }(z)={\left\{(1-H^2(z))(1-\omega H^2(z))\right\}}^{\frac{1}{2}},$$

(13)

respectively [32], [37].

Treating the above first-order ODEs as our simplest equations and then proceeding as before, we obtain the cnoidal and snoidal wave solutions that are given by

$$u(t,x)=A_0+A_{1}cn(z|\omega )+A_2{cn}^2(z|\omega ),$$

(14a)

$$v(t,x)=B_0+B_{1}cn(z|\omega )+B_2{cn}^2(z|\omega )+B_3{cn}^3(z|\omega )+B_4{cn}^4(z|\omega ),$$

(14b)

where

$$\begin{array}{c}\lambda =42k-280\omega +140,A_0=k,A_1=-10\omega ,A_2=0,\hfill \\ B_1=0,B_2=80k\omega -480{\omega }^2+240\omega ,B_3=0,B_4=-40{\omega }^2,\hfill \\ k\text{ is any root of }3k^2+(-40\omega +20)k+133{\omega }^2-133\omega +33\omega =0\hfill \end{array}$$

and

$$\begin{array}{c}u(t,x)=A_0+A_{1}sn(z|\omega )+A_2{sn}^2(z|\omega ),\hfill \\ v(t,x)=B_0+B_{1}sn(z|\omega )+B_2{sn}^2(z|\omega )+B_3{sn}^3(z|\omega )+B_4{sn}^4(z|\omega ),\hfill \end{array}$$

where

$$\begin{array}{c}\lambda =42k+140\omega +140,A_0=k(\nu +4\omega +4),A_1=0,A_2=10\omega ,\hfill \\ B_1=0,B_2=-80k\omega -240{\omega }^2-240\omega ,B_3=0,B_4=-40{\omega }^2,\hfill \\ k\text{ is any root of }3k^2+(20\omega +20)k+33{\omega }^2+67\omega +33=0,\hfill \end{array}$$

and $z=x-\nu t$. The profile of solution (14a)-(14b) is given in Figure 2.

Figure 2

Profile of cniodal waves ( 14a )-( 14b ).

4 Conservation laws

In this section we construct conservation laws for the coupled Drinfeld-Sokolov-Satsuma-Hirota system (1). The new conservation theorem due to Ibragimov [33] and the multiplier method [34] will be used. For the notations used in this section, the reader is referred to [33].

4.1 Construction of conservation laws using the new conservation theorem

In this subsection we construct conservation laws for (1) by applying the new conservation theorem [33].

The coupled DSSH system together with its adjoint equation is given by

$$\begin{array}{r}{E}_{{\alpha }_1}\equiv u_t-6u{u}_x+u_{xxx}-6v_x=0,\\ E_{{\alpha }_2}\equiv v_t-2v_{xxx}+6u{v}_x=0,\end{array}$$

(15)

$$\begin{array}{r}{E}_{{\alpha }_1}^{\ast }\equiv -p_t+6u{p}_x-p_{xxx}+6q{v}_x=0,\\ E_{{\alpha }_2}^{\ast }\equiv -q_t-6u{q}_x+2q_{xxx}+6p_x-6q{u}_x=0.\end{array}$$

(16)

One can easily verify that the third-order Lagrangian for the system of equations (15) and (16) is given by

$$L=p(u_t-6u{u}_x+u_{xxx}-6v_x)+q(v_t-2v_{xxx}+6u{v}_x).$$

(17)

We recall that the coupled DSSH system admits the following four Lie point symmetries:

$$X_1=\frac{\partial }{\partial t},X_2=\frac{\partial }{\partial x},X_3=\frac{\partial }{\partial v},X_4=3t\frac{\partial }{\partial t}+x\frac{\partial }{\partial x}-2u\frac{\partial }{\partial u}-4v\frac{\partial }{\partial v}.$$

Thus we have the following four cases:

• (i) For the Lie point symmetry $X_1={\partial }_t$, the corresponding Lie characteristic functions are $W^1=-u_t$ and $W^2=-v_t$. Thus, by using Ibragimov’s theorem [33], the components of the conserved vector are given by

  $$\begin{array}{c}{T}_1^t=-6p{u}_{x}u+p{u}_{xxx}-6p{v}_x+6qu{v}_x-2q{v}_{xxx},\hfill \\ T_1^x=6pu{u}_t-p{u}_{txx}+6p{v}_t-6qu{v}_t+2q{v}_{txx}-u_t{p}_{xx}+p_x{u}_{tx}+2v_t{q}_{xx}-2q_x{v}_{tx}.\hfill \end{array}$$

• (ii) The Lie point symmetry $X_2={\partial }_x$ has the Lie characteristic functions that are given by $W^1=-u_x$ and $W^2=-v_x$. Hence, by the application of Ibragimov’s theorem [33], the conserved vector $(T_2^t,T_2^x)$ is given by

  $$\begin{array}{c}{T}_2^t=-p{u}_x-q{v}_x,\hfill \\ T_2^x=p{u}_t+q{v}_t-u_x{p}_{xx}+p_x{u}_{xx}+2v_x{q}_{xx}-2q_x{v}_{xx}.\hfill \end{array}$$

• (iii) The symmetry generator $X_3={\partial }_v$ has the Lie characteristic functions given by $W^1=0$ and $W^2=1$, and hence in this case one can obtain the conserved vector whose components are

  $$\begin{array}{c}{T}_3^t=q,\hfill \\ T_3^x=-6p+6uq-2q_{xx}.\hfill \end{array}$$

• (iv) Finally, we consider the symmetry generator $X_4=-3t{\partial }_t-x{\partial }_x+2u{\partial }_u+4v{\partial }_v$, which has the Lie characteristic functions $W^1=2u+3t{u}_t+x{u}_x$ and $W^2=4v+3t{v}_t+x{v}_x$. By invoking Ibragimov’s theorem [33], the components of the conserved vector are given by

  $$\begin{array}{c}{T}_4^t=18tpu{u}_x+xp{u}_x-3tp{u}_{xxx}+18tp{v}_x-18tqu{v}_x+xq{v}_x+6tq{v}_{xxx}+2pu+4qv,\hfill \\ \begin{array}{rl}{T}_4^x=& 2u{p}_{xx}-18tpu{u}_t+4p{u}_{xx}-xp{u}_t+3tp{u}_{txx}-18tp{v}_t+18tqu{v}_t-8v{q}_{xx}-12q{v}_{xx}\\ -xq{v}_t-6tq{v}_{txx}-12u^{2}p-24pv+24quv+3t{u}_t{p}_{xx}-3t{p}_x{u}_{tx}-3p_x{u}_x+x{u}_x{p}_{xx}\\ -x{p}_x{u}_{xx}-6t{v}_t{q}_{xx}+6t{q}_x{v}_{tx}+10q_x{v}_x-2x{v}_x{q}_{xx}+2x{q}_x{v}_{xx}.\end{array}\hfill \end{array}$$

4.2 Construction of conservation laws using the multiplier method

Here we use the multiplier method [34] to construct conservation laws for the coupled DSSH system (1). The second-order multipliers ${\mathrm{\Lambda }}_1={\mathrm{\Lambda }}_1(t,x,u,v,u_x,v_x,u_{xx},v_{xx})$ and ${\mathrm{\Lambda }}_2={\mathrm{\Lambda }}_2(t,x,u,v,u_x,v_x,u_{xx},v_{xx})$ are given by

$$\begin{array}{c}{\mathrm{\Lambda }}_1=\frac{1}{2}(3u^2-u_{xx}+2v)C_2+C_{1}tu+C_{3}u+\frac{1}{6}{C}_{1}x,\hfill \\ {\mathrm{\Lambda }}_2=C_{2}u+C_{1}t+C_3,\hfill \end{array}$$

where $C_i$, $i=1,\dots ,3$, are arbitrary constants. Corresponding to the above multipliers, we obtain the following three local conserved vectors of (1):

$$\begin{array}{c}{T}_1^t=\frac{1}{6}\{3t{u}^2+xu+6tv\},\hfill \\ T_1^x=\frac{1}{6}\{6t{u}_{xx}u-12t{u}^3-3x{u}^2-6xv-3t{u}_x^2-12t{v}_{xx}-u_x+x{u}_{xx}\};\hfill \\ T_2^t=\frac{1}{4}\{-u_{xx}u+4uv+2u^3\},\hfill \\ T_2^x=\frac{1}{4}\{-8v_{xx}u+4u_{xx}v+6u_{xx}{u}^2+u{u}_{tx}-12u^{2}v-9u^4-12v^2-u_t{u}_x+8u_x{v}_x-u_{xx}^2\};\hfill \end{array}$$

and

$$\begin{array}{c}{T}_3^t=\frac{1}{2}\{u^2+2v\},\hfill \\ T_3^x=\frac{1}{2}\{2u_{xx}u-4u^3-u_x^2-4v_{xx}\}.\hfill \end{array}$$

Remark

It should be noted that higher-order conservation laws of (1) can be computed by increasing the order of the multipliers.

5 Concluding remarks

In this paper firstly we obtained the solutions of the Drinfeld-Sokolov-Satsuma-Hirota equation by employing Lie group analysis together with the simplest and Jacobi elliptic equation methods. Also symmetry reductions were obtained based on the optimal systems of one-dimensional subalgebras. The exact solutions obtained were traveling wave solutions, cnoidal and snoidal wave solutions. Furthermore, the conservation laws for the underlying equation were derived by using two different approaches, namely the new conservation theorem and the multiplier method. The importance of the conservation laws was explained in the introduction.