General decay synchronization stability on the nonautonomous BAM recurrent neural networks with delays

Abstract

This paper studies the general decay synchronization (GDS) of a class of nonautonomous bidirectional associative memory recurrent neural networks (BAMRNNs) with mixed time delays. By employing the Lyapunov method and useful inequality techniques, some sufficient conditions on the general decay synchronization for BAMRNNs are derived. In addition, an example with numerical simulations is presented to illustrate the obtained theoretical results.

1 Introduction

It is well known that the bidirectional associative memory (BAM) neural networks were first proposed in 1987 by Kosko [1], which extend the unidirectional autoassociation of Hopfield [2]. At present, the bidirectional associative memory (BAM) neural-network models have been accepted by many scientists and have been widely used in signal processing, automatic control engineering, associative memory, parallel computing, combinatorial optimization, pattern recognition, and so on [3–16].

It is worth noting that synchronization is a typical dynamical property of neural networks and presents major concerns when we investigate the dynamical behaviors of chaotic neural networks. Recently, the research on the synchronization of neural networks (NNs) model has attracted a lot of attention [8–27] as there are many benefits of having synchronization in some engineering applications such as language emergence and development, harmonic oscillation generation, secure communication, and information science. Moreover, synchronization, as a typical collective behavior, has been observed in biological systems such as synchronous fireflies, flocking of birds, and swarming of fish. Therefore, it is important to investigate the synchronization behaviors of the bidirectional associative memory neural-network (BAMNNs) systems.

Moreover, recently in [18, 19], a new concept of synchronization, namely general decay synchronization (GDS), was introduced for a class of chaotic NNs. Up to now, there have been many studies related to the study of GDS problems for various kinds of neural networks with time delays and the references cited therein [18–27]. For example, the study of general decay synchronization for time-varying delayed and mixed time delayed recurrent neural networks [18–21], time-varying delayed and mixed time delayed BAM neural networks [22, 23], delayed memristor-based Cohen–Grossberg neural networks [24], time-varying delayed fuzzy cellular neural networks [25], discrete time delayed competitive neural networks [26], and time-varying delayed complex multilink dynamic networks [27], are considered.

On the other hand, everything in the real world often changes with time. However, the intrinsic parameters of autonomous NNs [3–27] will not change with time, thus, we have some limitations in mathematical modeling of neural-network systems. Therefore, a nonautonomous scenario is necessary for NNs models, making it worthy to study the NNs models in a nonautonomous environment. Moreover, hitherto, most of the published works are devoted to the autonomous NNs [1–27], and there are few papers considered nonautonomous NNs [28, 29]. For example, in [28, 29], the authors considered the following nonautonomous cellular neural networks (CNNs) with time-variable delays and infinite delays

$$ \begin{aligned}[b] \dot{z}_{i}(t)={}&-a_{i}(t)z_{i}(t)+ \sum_{j=1}^{n}b_{ij}(t)l_{j} \bigl(z_{j} \bigl(t- \gamma _{ij}(t) \bigr) \bigr) \\ &{}+\sum_{j=1}^{n}c_{ij}(t) \int ^{\infty}_{0}\Gamma _{ij}(s)h_{j} \bigl(z_{j}(t-s) \bigr)\,ds+ \Upsilon _{i}(t), \end{aligned} $$

(1)

where $i,j=1,2,\ldots ,n$, $t\in R$, n corresponds to the number of units in a neural network, $z_{i}(t)$ denotes the state vector of the ith unit at the time t, $a_{i}(t)>0$ denotes the rate with which the ith unit will reset its potential to the resting state in isolation when disconnected from the network and external inputs at the time t, $b_{ij}(t)$ and $c_{ij}(t)$ represent the connection weights at the time $t,\gamma _{ij}(t)\geq 0$ denotes the transmission delay of the ith unit along the axon of the jth unit at the time t, $\Upsilon _{i}(t)$ denotes the external bias on the ith unit at the time t, $l_{j}$ and $h_{j}$ are activation functions of signal transmission, and $\Gamma _{ij}(u)$ corresponds to the transmission-delay kernel. The authors obtained some sufficient conditions on the exponential convergence for system (1) by using the differential inequality strategies. To the best of our knowledge, no study has been conducted to date for general decay synchronization on the nonautonomous BAM recurrent neural networks with distributed time delays and continuous time delays. Therefore, in light of the above analysis and as an extension of previously known works [3–29], this paper will address the following nonautonomous BAM recurrent neural networks with delays

$$ \textstyle\begin{cases} \dot{x}_{i}(t)= -c_{i}(t)x_{i}(t)+\sum_{j=1}^{n}r_{ji}(t)f_{j}(y_{j}(t))+ \sum_{j=1}^{n}a_{ji}(t)f_{j}(y_{j}(t-\tau _{ij}(t))) \\ \hphantom{\dot{x}_{i}(t)=}{} +\sum_{j=1}^{n}b_{ji}(t)\int ^{0}_{-\theta _{ij}}K_{ij}(s)g_{j}(y_{j}(t+s))\,ds+I_{i}(t), \\ \dot{y}_{j}(t)= -d_{j}(t)y_{j}(t)+\sum_{i=1}^{m}o_{ij}(t)h_{i}(x_{i}(t))+ \sum_{i=1}^{m}p_{ij}(t)h_{i}(x_{i}(t-\sigma _{ij}(t))) \\ \hphantom{\dot{y}_{j}(t)=}{} +\sum_{i=1}^{m}q_{ij}(t)\int ^{0}_{-\gamma _{ij}}H_{ij}(s)l_{i}(x_{i}(t+s))\,ds+J_{j}(t), \end{cases} $$

(2)

where $i \in \mathcal{I} \triangleq \{1,2,\ldots ,m\}$ and $j \in \mathcal{J} \triangleq \{1,2,\ldots ,n\}$; $m\geq 2$ and $n\geq 2$ correspond to the number of neurons in the neural fields $X_{U}$ and $Y_{U}$, respectively; $x_{i}(t)$ and $y_{j}(t)$ denote the state variable of the ith neurons from the neural fields $X_{U}$ and jth neurons from the neural fields $Y_{U}$, respectively; $c_{i}(t)>0$, $d_{j}(t)>0$ are the passive decay rates to the state of ith, jth neurons at the time t; $r_{ji}(t)$, $a_{ji}(t)$, $b_{ji}(t)$ and $o_{ij}(t)$, $p_{ij}(t)$, $q_{ij}(t)$ represent the connection strengths and the time delay connection strengths at the time t, respectively; $f_{j}(\cdot )$, $g_{j}(\cdot )$, $h_{i}(\cdot )$, and $l_{i}(\cdot )$ are the neuron feedback functions; $\tau _{ij}(t)$, $\theta _{ij}$, $\gamma _{ij}$, and $\sigma _{ij}(t)$ denote the time delay along the axon of the jth neuron from the ith neuron and satisfy $0\leq \tau _{ij}(t)\leq \tau _{ij}$, $0\leq \sigma _{ij}(t)\leq \sigma _{ij}$, $\theta _{ij}>0$, $\gamma _{ij}>0$; $I_{i}(t)$, and $J_{j}(t)$ correspond to the external bias on the ith neurons from the neural fields $X_{U}$ and the jth neurons from the neural fields $Y_{U}$ at the time t, respectively. $K_{ij}(s)$, $H_{ij}(s)$ correspond to the transmission delay kernels and satisfy $\int _{-\theta _{ij}}^{0}K_{ij}(s)\,ds=1$, $\int _{-\gamma _{ij}}^{0}H_{ij}(s)\,ds=1$.

The main purpose of this paper is by constructing suitable Lyapunov–Krasovskii functionals and applying the method given in [18, 19] to establish some new sufficient conditions on the general decay synchronization for system (2).

2 Preliminaries

In this paper, the initial conditions for system (2) are given by

$$ \begin{aligned} x_{i}(\theta )=\varphi ^{x}_{i}(\theta ), \quad \theta \in [-\tau ,0], \\ y_{j}(\theta )=\varphi ^{y}_{j}(\theta ), \quad \theta \in [-\sigma ,0], \end{aligned} $$

where $\tau =\max_{i,j} \{ \tau _{ij},\theta _{ij}\}$, $\sigma =\max_{i,j} \{ \sigma _{ij},\gamma _{ij}\}$, $\varphi ^{x}=(\varphi ^{x}_{1}( \theta ),\varphi ^{x}_{2}(\theta ), \ldots ,\varphi ^{x}_{m}(\theta )) \in C([-\tau ,0],R^{m})$, $\varphi ^{y}=(\varphi ^{y}_{1}(\theta ), \varphi ^{y}_{2}(\theta ),\ldots ,\varphi ^{y}_{n}(\theta ))\in C([- \sigma ,0],R^{n})$, which denotes the Banach space of all continuous functions mapping $(-\infty ,0]$ into $R^{n}$ with norm defined by

$$ \bigl\Vert \varphi ^{x} \bigr\Vert =\sum ^{m}_{i=1}\sup_{s\in [-\tau ,0]} \bigl\vert \varphi ^{x}_{i}(s) \bigr\vert \quad \text{and} \quad \bigl\Vert \varphi ^{y} \bigr\Vert =\sum ^{n}_{j=1}\sup_{s\in [-\sigma ,0]} \bigl\vert \varphi ^{y}_{j}(s) \bigr\vert . $$

In the paper, we consider system (2) as the drive system, the response system is given as follows

$$ \textstyle\begin{cases} \dot{u}_{i}(t)= -c_{i}(t)u_{i}(t)+\sum_{j=1}^{n}r_{ji}(t)f_{j}(v_{j}(t))+ \sum_{j=1}^{n}a_{ji}(t)f_{j}(v_{j}(t-\tau _{ij}(t))) \\ \hphantom{\dot{u}_{i}(t)=}{} +\sum_{j=1}^{n}b_{ji}(t)\int ^{0}_{-\theta _{ij}}K_{ij}(s)g_{j}(v_{j}(t+s))\,ds+I_{i}(t)+p_{i}(t), \\ \dot{v}_{j}(t)=-d_{j}(t)v_{j}(t)+\sum_{i=1}^{m}o_{ij}(t)h_{i}(u_{i}(t))+ \sum_{i=1}^{m}p_{ij}(t)h_{i}(u_{i}(t-\sigma _{ij}(t))) \\ \hphantom{\dot{v}_{j}(t)=}{} +\sum_{i=1}^{m}q_{ij}(t)\int ^{0}_{-\gamma _{ij}}H_{ij}(s)l_{i}(u_{i}(t+s))\,ds+J_{j}(t)+q_{j}(t), \end{cases} $$

(3)

where $p_{i}(t)$, $q_{j}(t)$ are the controllers to be designed. Let $e_{i}(t)=u_{i}(t)-x_{i}(t)$ and $z_{j}(t)=v_{j}(t)-y_{j}(t)$, then the corresponding error system between drive system (2) and response system (3) can be written as

$$ \textstyle\begin{cases} \dot{e}_{i}(t)= -c_{i}(t)e_{i}(t)+\sum_{j=1}^{n}r_{ji}(t) \tilde{f}_{j}(z_{j}(t))+\sum_{j=1}^{n}a_{ji}(t)\tilde{f}_{j}(z_{j}(t- \tau _{ij}(t))) \\ \hphantom{\dot{e}_{i}(t)=}{} +\sum_{j=1}^{n}b_{ji}(t)\int ^{0}_{-\theta _{ij}}K_{ij}(s) \tilde{g}_{j}(z_{j}(t+s))\,ds+p_{i}(t), \\ \dot{z}_{j}(t)= -d_{j}(t)z_{j}(t)+\sum_{i=1}^{m}o_{ij}(t) \tilde{h}_{i}(e_{i}(t))+\sum_{i=1}^{m}p_{ij}(t)\tilde{h}_{i}(e_{i}(t- \sigma _{ij}(t))) \\ \hphantom{\dot{z}_{j}(t)=}{} +\sum_{i=1}^{m}q_{ij}(t)\int ^{0}_{-\gamma _{ij}}H_{ij}(s) \tilde{l}_{i}(e_{i}(t+s))\,ds+q_{j}(t), \end{cases} $$

(4)

where $\tilde{f}_{j}(z_{j}(t))=f_{j}(v_{j}(t))-f_{j}(y_{j}(t))$, $\tilde{f}_{j}(z_{j}(t- \tau _{ij}(t)))=f_{j}(v_{j}(t-\tau _{ij}(t))) -f_{j}(y_{j}(t-\tau _{ij}(t)))$, $\tilde{g}_{j}(z_{j}(t+s))=g_{j}(v_{j}(t+s)) -g_{j}(y_{i}(t+s))$, and $\tilde{h}_{i}(e_{i}(t))=h_{i}(u_{i}(t))-h_{i}(x_{i}(t))$, $\tilde{h}_{i}(e_{i}(t-\sigma _{ij}(t)))=h_{i}(u_{i}(t-\sigma _{ij}(t)))-h_{i}(x_{i}(t- \sigma _{ij}(t)))$, $\tilde{l}_{i}(e_{i}(t+s))=l_{i}(u_{i}(t+s)) -l_{i}(x_{i}(t+s))$.

Throughout this paper, we assume that the following assumptions are satisfied:

$\mathbf{H}_{1}$: Neuron feedback functions $f_{j}(u)$, $g_{j}(u)$, $h_{i}(u)$, and $l_{i}(u)$ are continuous and there exist nonnegative constants $M^{f}_{j}>0$, $M^{g}_{j}>0$, $M^{h}_{i}>0$, $M^{l}_{i}>0$, and $L^{f}_{j}>0$, $L^{g}_{j}>0$, $L^{h}_{i}>0$, $L^{l}_{i}>0$, such that for any $v_{1},v_{2}\in R$

$$ \begin{aligned} & \bigl\vert f_{j}(v_{1})-f_{j}(v_{2}) \bigr\vert \leq L^{f}_{j} \vert v_{1}-v_{2} \vert +M^{f}_{j}, \bigl\vert g_{j}(v_{1})-g_{j}(v_{2}) \bigr\vert \leq L^{g}_{j} \vert v_{1}-v_{2} \vert +M^{g}_{j},\quad \forall \ v_{1},v_{2} \in R, \\ & \bigl\vert h_{i}(v_{1})-h_{i}(v_{2}) \bigr\vert \leq L^{h}_{i} \vert v_{1}-v_{2} \vert +M^{h}_{i}, \bigl\vert l_{i}(v_{1})-l_{i}(v_{2}) \bigr\vert \leq L^{l}_{i} \vert v_{1}-v_{2} \vert +M^{l}_{i}, \quad \forall \ v_{1},v_{2}\in R. \ \end{aligned} $$

$\mathbf{H}_{2}$: Time-varying delays $\tau _{ij}(t)$, $\sigma _{ij}(t)$ are differentiable, and there exist real numbers $0\leq {\mu}^{f}_{ij}$, ${\mu}^{h}_{ij}< 1$ such that

$$ 0\leq \dot{\tau}_{ij}(t)\leq \mu ^{f}_{ij}, \quad 0\leq \dot{\sigma}_{ij}(t) \leq \mu ^{g}_{ij}. $$

Now, we will give the definitions of a ψ-type function and GDS.

Definition 1

([18, 19])

A function $\psi :R^{+}\rightarrow [1,+\infty )$ is said to be a ψ-type function if it satisfies the following conditions:

1) $\psi (t)$ is differentiable and nondecreasing $t\in R^{+}$;

2) $\psi (0)=1$ and $\psi (+\infty )=+\infty$;

3) $\tilde{\psi}(t)=\dot{\psi}(t)/\psi (t)$ is nondecreasing for $t\in R^{+}$ and $\psi ^{*}=\sup_{t\geq 0}\tilde{\psi}(t)<+\infty$, where $\dot{\psi}(t)$ is the time derivative of ${\psi}(t)$;

4) For any $t, s \geq 0$, $\psi (t+s)\leq \psi (t) \psi (s)$.

It is easy to check that functions $\psi (t)=e^{\alpha t}$, $\psi (t)=(1+t)^{\alpha}$ and $\psi (t) = 1 + \alpha \log (1+t)$ for any $\alpha > 0$ satisfy the above four conditions, and thus can be seen as ψ-type functions.

Definition 2

([18, 19])

The drive–response systems (2) and (3) are said to be general decay synchronized if there exist a constant $\varepsilon >0$ and a ψ-type function ψ such that

$$ \lim_{t\rightarrow +\infty} \sup \frac{\log ( \Vert e(t) \Vert + \Vert z(t) \Vert )}{\log \psi (t)}\leq - \varepsilon , $$

where $e(t)=(e_{1}(t),e_{2}(t),\ldots ,e_{m}(t))^{T}$, $z(t)=(z_{1}(t),z_{2}(t), \ldots ,z_{n}(t))^{T}$, then $\varepsilon >0$ can be seen as the convergence rate as the synchronization error approaches zero.

$\mathbf{H}_{3}$: For functions $\psi (t)$, $\tilde{\psi}(t)$ given in Definition 1, there exist a function $\varrho (t)\in C(R,R^{+})$ and a constant $\delta >0$ such that for any $t\geq 0$

$$ \tilde{\psi}(t)\leq 1,\quad \sup_{t\in [0,+\infty )} \int _{0}^{t} \psi ^{\delta} (s)\varrho (s)\,ds< +\infty . $$

For a continuous function $f(t)$ defined on R, we define $f^{L}=\inf_{t\in R}\{f(t)\}$ and $f^{M}=\sup_{t\in R}\{f(t)\}$.

Now, we present a useful lemma.

Lemma 1

([23])

Under assumption $\mathbf{H}_{3}$, assume that the synchronization errors $e(t)$ and $z(t)$ between the drive–response systems (2) and (3) satisfied the differential equations $\dot{e}(t)={F}(t,e(t),z(t))$ and $\dot{z}(t)={G}(t,e(t),z(t))$, respectively, where the functions ${F}(t,e(t),z(t))$ and ${G}(t,e(t),z(t))$ are locally bounded. If there exist a Lyapunov functional $V(t,e(t), z(t)):R^{+}\times R^{m}\times R^{n} \rightarrow R^{+}$, and positive constants $\lambda _{1}$, $\lambda _{2}$ such that for any $(t,e(t),z(t))\in R^{+}\times R^{m}\times R^{n}$,

$$\begin{aligned}& \lambda _{1} \bigl( \bigl\Vert e(t) \bigr\Vert ^{2}+ \bigl\Vert z(t) \bigr\Vert ^{2} \bigr)\leq V \bigl(t,e(t),z(t) \bigr),\\& \frac{d V(t,e(t),z(t))}{dt}|_{(3)}\leq -\delta V \bigl(t,e(t),z(t) \bigr) + \lambda _{2} \varrho (t), \end{aligned}$$

where ε and $\varrho (t)$ are defined in $\mathbf{H}_{3}$. Then, the drive–response systems (2) and (3) will realize GDS in the sense of Definition 2, and the convergence rate of GDS is δ.

3 Main results

In this section, we will obtain some sufficient conditions to insure the GDS of systems (2) and (3). First, under assumption $\mathbf{H}_{3}$ we design the controllers $p_{i}(t)$ and $q_{j}(t)$ of response system (3) as follows

$$ \begin{gathered} p_{i}(t)=-\alpha ^{p}_{i}(t) \operatorname{sign} \bigl(e_{i}(t) \bigr) - \frac{\eta _{i}(t) \Vert e(t) \Vert e_{i}(t)}{e_{i}(t)+\varrho _{1}(t)}, \quad i \in \mathcal{I}, \\ q_{j}(t)= -\alpha ^{q}_{j}(t) \operatorname{sign} \bigl(z_{j}(t) \bigr) - \frac{\beta _{j}(t) \Vert z(t) \Vert z_{j}(t)}{z_{j}(t)+\varrho _{2}(t)}, \quad j\in \mathcal{J}, \end{gathered} $$

(5)

where $\eta _{i}(t)$, $\alpha ^{p}_{i}(t)$ for $i\in \mathcal{I}$ and $\beta _{j}(t)$, $\alpha ^{q}_{j}(t)$ for $j\in \mathcal{J}$ are positive control gains satisfying

$$ \textstyle\begin{cases} c^{L}_{i}+\eta _{i}^{L}-\sum_{j=1}^{n} ( \frac{A^{h}_{ji}}{1-{\mu}^{g}_{ji}}+A^{l}_{ji} ) -\sum_{j=1}^{n}C^{f}_{ij}=:E^{f}_{i}>0, \\ \alpha ^{pL}_{i}-\sum_{j=1}^{n} \vert a_{ji} \vert M^{f}_{j}- \sum_{j=1}^{n} \vert b^{M}_{ji} \vert M^{g}_{j}>0, \\ d^{L}_{j}+\beta _{j}^{L}-\sum_{i=1}^{m} ( \frac{A^{f}_{ji}}{1-\mu ^{f}_{ji}}+A^{g}_{ji} ) -\sum_{i=1}^{m}C^{h}_{ij}=:E^{h}_{j}>0, \\ \alpha ^{qL}_{j}-\sum_{i=1}^{m} \vert p_{ij}^{M} \vert M^{g}_{i} - \sum_{i=1}^{m} \vert q_{ij}^{M} \vert M_{i}^{l}>0, \end{cases} $$

(6)

where ${A}^{r}_{ij}=|r_{ji}^{M}|L^{f}_{j}$, ${A}^{f}_{ij}=|a_{ji}^{M}|L^{f}_{j}$, ${A}^{g}_{ij}=|b_{ji}^{M}|L^{g}_{j}$, ${A}^{o}_{ij}=|o_{ij}^{M}|L^{h}_{i}$, ${A}^{h}_{ij}=|p_{ij}^{M}|L^{h}_{i}$, ${A}^{l}_{ij}=|q_{ij}^{M}|L^{l}_{i}$, ${C}^{f}_{ij}=B^{f}_{ij}\theta _{ij}$, ${C}^{h}_{ij}=B^{h}_{ij}\sigma _{ij}$.

Then, from nonlinear feedback controller (7), we have the following theorem.

Theorem 1

Suppose $\mathbf{H}_{1}$–$\mathbf{H}_{3}$ hold and the control gains $\eta _{i}(t)$, $\alpha ^{p}_{i}(t)$ and $\beta _{j}(t)$, $\alpha ^{q}_{j}(t)$ satisfy the inequality (7), then the response network (3) can be general decay synchronized with the drive network (2) under the nonlinear controller (5).

Proof

First, we construct the following Lyapunov–Krasovskii functionals:

$$\begin{aligned}& \begin{aligned} V_{11}(t)={}& \sum _{i=1}^{m} \bigl\vert {e}_{i}(t) \bigr\vert + \sum_{i=1}^{m} \sum _{j=1}^{n}A^{f}_{ij} \int _{t-\tau _{ij}(t)}^{t} \frac{ \vert z_{j}(s) \vert }{1-\mu ^{f}_{ij}}\,ds \\ &{}+\sum_{i=1}^{m} \sum _{j=1}^{n}A^{g}_{ij} \int _{- \theta _{ij}}^{0}K_{ij}(s) \int _{t+s}^{t} \bigl\vert z_{j}( \varsigma ) \bigr\vert \,d \varsigma \,ds, \end{aligned} \\& \begin{aligned} V_{21}(t)={}& \sum _{j=1}^{n} \bigl\vert z_{j}(t) \bigr\vert + \sum_{j=1}^{n} \sum _{i=1}^{m}A^{h}_{ij} \int _{t-\sigma _{ij}(t)}^{t} \frac{ \vert e_{i}(s) \vert }{1-{\mu}^{g}_{ij}}\,ds \\ &{} + \sum_{j=1}^{n}\sum _{i=1}^{m}A^{l}_{ij} \int _{- \gamma _{ij}}^{0}H_{ij}(s) \int _{t+s}^{t} \bigl\vert e_{i}( \varsigma ) \bigr\vert \,d \varsigma \,ds. \end{aligned} \end{aligned}$$

Calculating the derivative of $V_{11}(t)+V_{21}(t)$ along system (4), we obtain

$$\begin{aligned} \dot{V}_{11}(t)+\dot{V}_{21}(t) =& \sum _{i=1}^{m} \Biggl\{ \operatorname{sign} \bigl(e_{i}(t) \bigr) \Biggl[ -c_{i}(t)e_{i}(t)+ \sum_{j=1}^{n}r_{ji}(t) \tilde{f}_{j} \bigl(z_{j}(t) \bigr) \ \\ & {}+ \sum_{j=1}^{n}a_{ji}(t) \tilde{f}_{j} \bigl(z_{j} \bigl(t- \tau _{ij}(t) \bigr) \bigr) +\sum_{j=1}^{n}b_{ji}(t) \int ^{0}_{-\theta _{ij}}K_{ij}(s) \tilde{g}_{j} \bigl(z_{j}(t+s) \bigr)\,ds \\ & {}- \alpha ^{p}_{i}(t)\operatorname{sign} \bigl(e_{i}(t) \bigr)- \frac{\eta _{i}(t) \Vert e(t) \Vert e_{i}(t)}{e_{i}(t)+\varrho _{1}(t)} \Biggr] \\ & {}+ \sum_{j=1}^{n} A^{f}_{ij} \biggl( \frac{1}{1-\mu ^{f}_{ij}} \bigl\vert z_{j}(t) \bigr\vert - \frac{ (1-\dot{\tau}_{ij}(t))}{1-\mu ^{f}_{ij}} \bigl\vert z_{j} \bigl(t-\tau _{ij}(t) \bigr) \bigr\vert \biggr) \\ & {}+ \sum_{j=1}^{n}A^{g}_{ij} \int ^{0}_{-\theta _{ij}}K_{ij}(s) \bigl( \bigl\vert z_{j}(t) \bigr\vert - \bigl\vert z_{j}(t+s) \bigr\vert \bigr)\,ds \Biggr\} \\ & {}+ \sum_{j=1}^{n} \Biggl\{ \operatorname{sign} \bigl(z_{j}(t) \bigr) \Biggl[ -d_{j}(t)z_{j}(t)+ \sum_{i=1}^{m}o_{ij}(t) \tilde{h}_{i} \bigl(e_{i}(t) \bigr) \\ & {}+ \sum_{i=1}^{m}p_{ij}(t) \tilde{h}_{i} \bigl(e_{i} \bigl(t- \sigma _{ij}(t) \bigr) \bigr) +\sum_{i=1}^{m}q_{ij}(t) \int ^{0}_{-\gamma _{ij}}H_{ij}(s) \tilde{l}_{i} \bigl(e_{i}(t+s) \bigr)\,ds \\ & {}- \alpha ^{q}_{j}(t)\operatorname{sign} \bigl(z_{j}(t) \bigr)- \frac{\beta _{j}(t) \Vert z(t) \Vert z_{j}(t)}{z_{j}(t)+\varrho _{2}(t)} \Biggr] \\ & {}+ \sum_{i=1}^{m} A^{h}_{ij} \biggl( \frac{1}{1-{\mu}^{g}_{ij}} \bigl\vert e_{i}(t) \bigr\vert - \frac{ (1-\dot{\sigma}_{ij}(t))}{1-{\mu}^{g}_{ij}} \bigl\vert e_{i} \bigl(t-\sigma _{ij}(t) \bigr) \bigr\vert \biggr) \\ & {}+ \sum_{i=1}^{m}A^{l}_{ij} \int ^{0}_{-\gamma _{ij}}H_{ij}(s) \bigl( \bigl\vert e_{i}(t) \bigr\vert - \bigl\vert e_{i}(t+s) \bigr\vert \bigr)\,ds \Biggr\} \\ \leq & \sum_{i=1}^{m} \Biggl\{ -c_{i}^{L} \bigl\vert e_{i}(t) \bigr\vert +\sum_{j=1}^{n} \bigl\vert r_{ji}^{M} \bigr\vert \bigl\vert \tilde{f}_{j} \bigl(z_{j}(t) \bigr) \bigr\vert +\sum _{j=1}^{n} \bigl\vert a_{ji}^{M} \bigr\vert \bigl\vert \tilde{f}_{j} \bigl(z_{j} \bigl(t-\tau _{ij}(t) \bigr) \bigr) \bigr\vert \\ & {}+ \sum_{j=1}^{n} \bigl\vert b_{ji}^{M} \bigr\vert \int ^{0}_{-\theta _{ij}}K_{ij}(s) \tilde{g}_{j} \bigl(z_{j}(t+s) \bigr)\,ds - \bigl\vert \alpha ^{pL}_{i} \bigr\vert - \frac{\eta _{i}^{L} \Vert e(t) \Vert \vert e_{i}(t) \vert }{ \vert e_{i}(t) \vert +\varrho _{1}(t)} \\ & {}+ \sum_{j=1}^{n} \biggl( \frac{A^{f}_{ij}}{1-\mu ^{f}_{ij}}+A^{g}_{ij} \biggr) \bigl\vert z_{j}(t) \bigr\vert -\sum_{j=1}^{n}A^{f}_{ij} \bigl\vert z_{j} \bigl(t- \tau _{ij}(t) \bigr) \bigr\vert \\ & {}- \sum_{j=1}^{n}A^{g}_{ij} \int ^{0}_{-\theta _{ij}}K_{ij}(s) \bigl\vert z_{j}(t+s) \bigr\vert \,ds \Biggr\} + \sum _{j=1}^{n} \Biggl\{ \sum _{i=1}^{m} \bigl\vert o^{M}_{ij} \bigr\vert \bigl\vert \tilde{h}_{i} \bigl(e_{i}(t) \bigr) \bigr\vert \\ & {}+ \sum_{i=1}^{m} \bigl\vert p^{M}_{ij} \bigr\vert \bigl\vert \tilde{h}_{i} \bigl(e_{i} \bigl(t- \sigma _{ij}(t) \bigr) \bigr) \bigr\vert +\sum _{i=1}^{m} \bigl\vert q_{ij}^{M} \bigr\vert \int ^{0}_{- \gamma _{ij}}H_{ij}(s) \bigl\vert \tilde{l}_{i} \bigl(e_{i}(t+s) \bigr) \bigr\vert \,ds \\ & {}- \alpha ^{qL}_{j}- \frac{\beta ^{L}_{j} \Vert z(t) \Vert \vert z_{j}(t) \vert }{ \vert z_{j}(t) \vert +\varrho _{2}(t)} + \sum _{i=1}^{m} \biggl(\frac{A^{h}_{ij}}{1-{\mu}^{g}_{ij}}+A^{l}_{ij} \biggr) \bigl\vert e_{i}(t) \bigr\vert - \bigl\vert d_{j}^{L} \bigr\vert \bigl\vert z_{j}(t) \bigr\vert \\ & {}- \sum_{i=1}^{m}A^{h}_{ij} \bigl\vert e_{i} \bigl(t-\sigma _{ij}(t) \bigr) \bigr\vert - \sum_{i=1}^{m}A^{l}_{ij} \int ^{0}_{-\gamma _{ij}}H_{ij}(s) \bigl\vert e_{i}(t+s) \bigr\vert \,ds \Biggr\} . \end{aligned}$$

(7)

Now, using $\mathbf{H}_{1}$, we have

$$\begin{aligned}& \sum_{i=1}^{m}\sum _{j=1}^{n} \bigl\vert r_{ji}^{M} \bigr\vert \bigl\vert \tilde{f}_{j} \bigl(z_{j}(t) \bigr) \bigr\vert \leq \sum_{i=1}^{m} \sum_{j=1}^{n}A^{r}_{ij} \bigl\vert z_{j}(t) \bigr\vert +\sum _{i=1}^{m} \sum_{j=1}^{n} \bigl\vert r_{ji}^{M} \bigr\vert M^{f}_{j}, \end{aligned}$$

(8)

$$\begin{aligned}& \sum_{i=1}^{m}\sum _{j=1}^{n} \bigl\vert a_{ji}^{M} \bigr\vert \bigl\vert \tilde{f}_{j} \bigl(z_{j} \bigl(t- \tau _{ij}(t) \bigr) \bigr) \bigr\vert \leq \sum _{i=1}^{m}\sum_{j=1}^{n}A^{f}_{ij} \bigl\vert z_{j} \bigl(t- \tau _{ij}(t) \bigr) \bigr\vert +\sum_{i=1}^{m}\sum _{j=1}^{n} \bigl\vert a_{ji}^{M} \bigr\vert M^{f}_{j}, \end{aligned}$$

(9)

$$\begin{aligned}& \sum_{j=1}^{n}\sum _{i=1}^{m} \bigl\vert o_{ij}^{M} \bigr\vert \bigl\vert \tilde{h}_{i} \bigl(e_{i}(t) \bigr) \bigr\vert \leq \sum_{j=1}^{n} \sum_{i=1}^{m}A^{o}_{ij} \bigl\vert e_{i}(t) \bigr\vert +\sum _{j=1}^{n} \sum_{i=1}^{m} \bigl\vert o_{ij}^{M} \bigr\vert M^{h}_{i}, \end{aligned}$$

(10)

$$\begin{aligned}& \sum_{j=1}^{n}\sum _{i=1}^{m} \bigl\vert p_{ij}^{M} \bigr\vert \bigl\vert \tilde{h}_{i} \bigl(e_{i} \bigl(t- \sigma _{ij}(t) \bigr) \bigr) \bigr\vert \leq \sum _{j=1}^{n}\sum_{i=1}^{m}A^{h}_{ij} \bigl\vert e_{i} \bigl(t- \sigma _{ij}(t) \bigr) \bigr\vert +\sum_{j=1}^{n}\sum _{i=1}^{m} \bigl\vert p_{ij}^{M} \bigr\vert M^{h}_{i}, \end{aligned}$$

(11)

$$\begin{aligned}& \begin{aligned}[b] \sum_{i=1}^{m}\sum _{j=1}^{n} \bigl\vert b_{ji}^{M} \bigr\vert \int ^{0}_{- \theta _{ij}}K_{ij}(s) \bigl\vert \widetilde{g}_{j} \bigl(z_{j}(t+s) \bigr) \bigr\vert \,ds\leq{}& \sum_{i=1}^{m}\sum _{j=1}^{n}A^{g}_{ij} \int ^{0}_{- \theta _{ij}}K_{ij}(s) \bigl\vert z_{j}(t+s) \bigr\vert \,ds \\ &{} +\sum_{i=1}^{m}\sum _{j=1}^{n} \bigl\vert b_{ji}^{M} \bigr\vert M^{g}_{j}, \end{aligned} \end{aligned}$$

(12)

$$\begin{aligned}& \begin{aligned}[b] \sum_{j=1}^{n} \sum_{i=1}^{m} \bigl\vert q_{ij}^{M} \bigr\vert \int ^{0}_{- \gamma _{ij}}H_{ij}(s) \bigl\vert \widetilde{l}_{i} \bigl(e_{i}(t+s) \bigr) \bigr\vert \,ds\leq {}& \sum_{j=1}^{n}\sum _{i=1}^{m}A^{l}_{ij} \int ^{0}_{- \gamma _{ij}}H_{ij}(s) \bigl\vert e_{i}(t+s) \bigr\vert \,ds \\ &{} +\sum_{j=1}^{n}\sum _{i=1}^{m} \bigl\vert q_{ij}^{M} \bigr\vert M^{l}_{i}. \end{aligned} \end{aligned}$$

(13)

Using $\mathbf{H}_{2}$ and from the above inequalities (7)–(13), we have

$$\begin{aligned} \dot{V}_{11}(t)+\dot{V}_{21}(t) \leq {}& \sum _{i=1}^{m} \Biggl\{ -c_{i}^{L} \bigl\vert e_{i}(t) \bigr\vert +\sum _{j=1}^{n} \bigl\vert r_{ji}^{M} \bigr\vert M^{f}_{j}+ \sum _{j=1}^{n} \bigl\vert a_{ji}^{M} \bigr\vert M^{f}_{j}+\sum _{j=1}^{n} \bigl\vert b^{M}_{ji} \bigr\vert M^{g}_{j} -\alpha ^{pL}_{i} \\ &{} - \frac{\eta _{i}^{L} \Vert e(t) \Vert \vert e_{i}(t) \vert }{ \vert e_{i}(t) \vert +\varrho _{1}(t)} + \sum_{j=1}^{n} \biggl(\frac{A^{f}_{ij}}{1-\mu ^{f}_{ij}}+A^{r}_{ij}+A^{g}_{ij} \biggr) \bigl\vert z_{j}(t) \bigr\vert \Biggr\} \\ & {} + \sum_{j=1}^{n} \Biggl\{ -d^{L}_{j} \bigl\vert z_{j}(t) \bigr\vert +\sum_{i=1}^{m} \bigl\vert o_{ij}^{M} \bigr\vert M^{g}_{i}+ \sum_{i=1}^{m} \bigl\vert p_{ij}^{M} \bigr\vert M^{g}_{i} +\sum_{i=1}^{m} \bigl\vert q_{ij}^{M} \bigr\vert M_{i}^{l} \\ & {}-\alpha ^{qL}_{j}- \frac{\beta _{j}^{L} \Vert z(t) \Vert \vert z_{j}(t) \vert }{ \vert z_{j}(t) \vert +\varrho _{2}(t)} + \sum _{i=1}^{m} \biggl(\frac{A^{h}_{ij}}{1-{\mu}^{g}_{ij}}+A^{o}_{ij}+A^{l}_{ij} \biggr) \bigl\vert e_{i}(t) \bigr\vert \Biggr\} . \end{aligned}$$

(14)

Next, we construct the following Lyapunov–Krasovskii functionals:

$$\begin{aligned}& V_{12}(t)=\sum_{i=1}^{m} \sum_{j=1}^{n}B^{f}_{ij} \int _{-\tau _{ij}}^{0} \int _{t+s}^{t} \bigl\vert e_{i}( \epsilon ) \bigr\vert \,d\epsilon \,ds+ \sum_{i=1}^{m} \sum_{j=1}^{n}B^{g}_{ij} \int _{-\theta _{ij}}^{0}K_{ij}(s) \int ^{0}_{s} \int _{t+\varsigma}^{t} \bigl\vert e_{i}( \epsilon ) \bigr\vert \,d\epsilon\,d \varsigma \,ds, \\& V_{22}(t)=\sum_{j=1}^{n} \sum_{i=1}^{m}B^{h}_{ij} \int _{-\sigma _{ij}}^{0} \int _{t+s}^{t} \bigl\vert z_{j}( \epsilon ) \bigr\vert \,d\epsilon \,ds+ \sum_{j=1}^{n} \sum_{i=1}^{m}B^{l}_{ij} \int _{-\gamma _{ij}}^{0}H_{ij}(s) \int ^{0}_{s} \int _{t+\varsigma}^{t} \bigl\vert z_{j}( \epsilon ) \bigr\vert \,d\epsilon\,d \varsigma \,ds, \end{aligned}$$

where $B^{f}_{ij}>0$, $B^{g}_{ij}>0$, $B^{h}_{ij}>0$, $B^{l}_{ij}>0$ are constants. Calculating the derivative of $V_{12}(t)$, we obtain

$$\begin{aligned} \dot{V}_{12}(t) ={}& \sum_{i=1}^{m} \sum_{j=1}^{n} \biggl[B^{f}_{ij} \biggl(\tau _{ij} \bigl\vert e_{i}(t) \bigr\vert - \int _{t-\tau _{ij}}^{t} \bigl\vert e_{i}(s) \bigr\vert \,ds \biggr) \\ &{} +B^{g}_{ij} \int _{-\theta _{ij}}^{0}K_{ij}(s) \int ^{0}_{s} \bigl( \bigl\vert e_{i}(t) \bigr\vert - \bigl\vert e_{i}(t+\varsigma ) \bigr\vert \bigr)\,d\varsigma \,ds \biggr] \\ \leq {}& \sum_{i=1}^{m}\sum _{j=1}^{n}{C}^{f}_{ij} \bigl\vert e_{i}(t) \bigr\vert -D_{1}, \end{aligned}$$

(15)

where

$$ D_{1}=\sum_{i=1}^{m}\sum _{j=1}^{n} \biggl[B^{f}_{ij} \int ^{t}_{t- \tau _{ij}} \bigl\vert e_{i}(s) \bigr\vert \,ds+B^{g}_{ij} \int _{-\theta _{ij}}^{0} \int ^{t}_{t+s} \bigl\vert e_{i}( \omega ) \bigr\vert \,d\omega \,ds \biggr]. $$

Similarly, we have

$$ \dot{V}_{22}(t) \leq \sum_{j=1}^{n} \sum_{i=1}^{m}{C}^{h}_{ij} \bigl\vert z_{j}(t) \bigr\vert -D_{2}, $$

(16)

where

$$ D_{2}=\sum_{j=1}^{n}\sum _{i=1}^{m} \biggl[B^{h}_{ij} \int ^{t}_{t- \sigma _{ij}} \bigl\vert z_{j}(s) \bigr\vert \,ds+B^{l}_{ij} \int _{-\gamma _{ij}}^{0} \int ^{t}_{t+s} \bigl\vert z_{j}( \omega ) \bigr\vert \,d\omega \,ds \biggr]. $$

Then, there exist positive scalars $\chi _{1}> 1$ and $\chi _{2}> 1$ such that

$$ \begin{gathered} \sum_{i=1}^{m} \bigl\vert e_{i}(t) \bigr\vert \leq V_{1}(t) \leq \chi _{1} \sum_{i=1}^{m} \bigl\vert e_{i}(t) \bigr\vert + \frac{\chi _{1}}{E_{1}}D_{1}, \\ \sum_{j=1}^{n} \bigl\vert z_{j}(t) \bigr\vert \leq V_{2}(t) \leq \chi _{2} \sum_{j=1}^{n} \bigl\vert z_{j}(t) \bigr\vert + \frac{\chi _{2}}{E_{2}}D_{2}, \end{gathered} $$

(17)

where $V_{1}(t)=V_{11}(t)+V_{12}(t)$, $V_{2}(t)=V_{21}(t)+V_{22}(t)$, $E_{1}=\min_{i\in \mathcal{I}}\{E^{f}_{i} \}$, $E_{2}=\min_{j\in \mathcal{J}}\{E^{h}_{j} \}$. Finally, we construct the following Lyapunov–Krasovskii functional:

$$ V(t)=V_{1}(t)+V_{2}(t). $$

Calculating the derivative of $V(t)$ and from (14)–(16), we obtain

$$\begin{aligned} \dot{V}(t) \leq{} & \sum_{i=1}^{m} \Biggl\{ - \Biggl[c^{L}_{i}-\sum _{j=1}^{n} \biggl( \frac{A^{h}_{ji}}{1-{\mu}^{g}_{ji}}+A^{o}_{ji}+A^{l}_{ji} \biggr) -\sum_{j=1}^{n}C^{f}_{ij} \Biggr] \bigl\vert e_{i}(t) \bigr\vert - \Biggl[\alpha ^{pL}_{i} \\ & {}- \sum_{j=1}^{n} \vert r_{ji} \vert M^{f}_{j}-\sum _{j=1}^{n} \vert a_{ji} \vert M^{f}_{j}- \sum_{j=1}^{n} \bigl\vert b^{M}_{ji} \bigr\vert M^{g}_{j} \Biggr] - \frac{\eta _{i}^{L} \Vert e(t) \Vert \vert e_{i}(t) \vert }{ \Vert e(t) \Vert +\varrho _{1}(t)} \Biggr\} \\ & {}- D_{1}+\sum_{j=1}^{n} \Biggl\{ - \Biggl[d^{L}_{j}-\sum _{i=1}^{m} \biggl(\frac{A^{f}_{ji}}{1-\mu ^{f}_{ji}}+A^{r}_{ji}+A^{g}_{ji} \biggr) - \sum_{i=1}^{m}C^{h}_{ij} \Biggr] \bigl\vert z_{j}(t) \bigr\vert - \Biggl[\alpha ^{qL}_{j} \\ & {}- \sum_{i=1}^{m} \bigl\vert o_{ij}^{M} \bigr\vert M^{g}_{i}- \sum_{i=1}^{m} \bigl\vert p_{ij}^{M} \bigr\vert M^{g}_{i} -\sum_{i=1}^{m} \bigl\vert q_{ij}^{M} \bigr\vert M_{i}^{l} \Biggr] - \frac{\beta _{j}^{L} \Vert z(t) \Vert \vert z_{j}(t) \vert }{ \Vert z_{j}(t) \Vert +\varrho _{2}(t)} \Biggr\} -D_{2} \\ \leq {}& \sum_{i=1}^{m} \Biggl\{ - \Biggl[c^{L}_{i}+\eta _{i}^{L}- \sum_{j=1}^{n} \biggl( \frac{A^{h}_{ji}}{1-{\mu}^{g}_{ji}}+A^{o}_{ji}+A^{l}_{ji} \biggr) -\sum_{j=1}^{n}C^{f}_{ij} \Biggr] \bigl\vert e_{i}(t) \bigr\vert \\ & {}- \Biggl[\alpha ^{pL}_{i}-\sum _{j=1}^{n} \vert r_{ji} \vert M^{f}_{j}- \sum_{j=1}^{n} \vert a_{ji} \vert M^{f}_{j}-\sum _{j=1}^{n} \bigl\vert b^{M}_{ji} \bigr\vert M^{g}_{j} \Biggr] \\ & {}+ \eta _{i} \bigl\vert e_{i}(t) \bigr\vert - \frac{\eta _{i}^{L} \Vert e(t) \Vert \vert e_{i}(t) \vert }{ \Vert e(t) \Vert +\varrho _{1}(t)} \Biggr\} -D_{1} +\sum _{j=1}^{n} \Biggl\{ - \Biggl[d^{L}_{j}+ \beta _{j}^{L} \\ & {}- \sum_{i=1}^{m} \biggl( \frac{A^{f}_{ji}}{1-\mu ^{f}_{ji}}+A^{r}_{ji}+A^{g}_{ji} \biggr) -\sum_{i=1}^{m}C^{h}_{ij} \Biggr] \bigl\vert z_{j}(t) \bigr\vert - \Biggl[\alpha ^{qL}_{j}-\sum_{i=1}^{m} \bigl\vert o_{ij}^{M} \bigr\vert M^{g}_{i} \\ & {}- \sum_{i=1}^{m} \bigl\vert p_{ij}^{M} \bigr\vert M^{g}_{i} -\sum_{i=1}^{m} \bigl\vert q_{ij}^{M} \bigr\vert M_{i}^{l} \Biggr] +\beta _{j} \bigl\vert z_{j}(t) \bigr\vert - \frac{\beta _{j}^{L} \Vert z(t) \Vert \vert z_{j}(t) \vert }{ \Vert z_{j}(t) \Vert +\varrho _{2}(t)} \Biggr\} -D_{2} \\ \leq{} & {}- \sum_{i=1}^{m}E^{f}_{i} \bigl\vert e_{i}(t) \bigr\vert -\sum _{j=1}^{n}E^{h}_{i} \bigl\vert z_{j}(t) \bigr\vert +\frac{\eta \Vert e(t) \Vert \varrho _{1}(t)}{ \Vert e(t) \Vert +\varrho _{1}(t)}+ \frac{\beta \Vert z(t) \Vert \varrho _{2}(t)}{ \Vert z_{j}(t) \Vert +\varrho _{2}(t)} \\ & {}- D_{1}-D_{2}, \end{aligned}$$

(18)

where ${\eta}=\max_{i\in \mathcal{I}}\{\eta _{i}^{L}\}>0$, ${\beta}=\max_{j \in \mathcal{J}}\{\beta _{j}^{L}\}>0$. By using the inequality $0 \leq ab/(a + b) \leq a$ for any $a > 0$, $b> 0$, we have

$$ \dot{V}(t) \leq -\sum_{i=1}^{m}E^{f}_{i} \bigl\vert e_{i}(t) \bigr\vert - \sum _{j=1}^{n}E^{h}_{i} \bigl\vert z_{j}(t) \bigr\vert + \eta \varrho _{1}(t)+\beta \varrho _{2}(t)-D_{1}-D_{2}. $$

(19)

Now, taking a small enough δ such that $\delta \chi _{1}< E_{1}$ and $\delta \chi _{2}< E_{2}$, then from the inequalities (17) and (19), we obtain

$$\begin{aligned} \frac{d}{dt}V(t) + \delta V(t) \leq {}& - \sum _{i=1}^{m}E^{f}_{i} \bigl\vert e_{i}(t) \bigr\vert + \eta \varrho _{1}(t)-D_{1} + \delta \Biggl(\chi _{1} \sum_{i=1}^{m} \bigl\vert e_{i}(t) \bigr\vert + \frac{\chi _{1}}{E_{1}}D_{1} \Biggr) \\ &{}-\sum_{j=1}^{n}E^{h}_{j} \bigl\vert z_{j}(t) \bigr\vert + \beta \varrho _{2}(t)-D_{2} + \delta \Biggl(\chi _{2} \sum_{j=1}^{n} \bigl\vert z_{j}(t) \bigr\vert + \frac{\chi _{2}}{E_{2}}D_{2} \Biggr) \\ \leq{} & (\delta \chi _{1}-E_{1})\sum _{i=1}^{m} \bigl\vert e_{i}(t) \bigr\vert + \biggl( \frac{\delta \chi _{1}}{E_{1}}-1 \biggr)D_{1} +\eta \varrho _{1}(t)-(\delta \chi _{2}-E_{2}) \sum_{j=1}^{n} \bigl\vert z_{j}(t) \bigr\vert \\ &{}+ \biggl( \frac{\delta \chi _{2}}{E_{2}}-1 \biggr)D_{2} +\beta \varrho _{2}(t) \\ \leq{} & \gamma \varrho (t), \end{aligned}$$

where $\gamma =\max \{\eta ,\beta \}$ and $\varrho (t)=\varrho _{1}(t)+\varrho _{2}(t)$. Thus, we have

$$ \dot{V}(t)\leq -\delta V(t)+\gamma \varrho (t). $$

Then, from Lemma 1, the drive–response systems (2) and (3) achieve GDS under the adaptive nonlinear controller (5). The convergence rate of $e(t)$ and $z(t)$ approaching zero is δ. □

Remark 1

In this paper, compared with previous studies, both distributed time delays and continuous time delays with nonautonomous bidirectional associative memory recurrent neural networks (BAMRNNs) are considered. As the coefficients of autonomous RNNs models in [20, 21] will not change with time, there are some limitations in mathematical modeling of neural-network systems. Hence, system (2) and the results obtained in this study can be seen as the extensions and supplements of previously known studies [18–27].

If, in $\mathbf{H}_{1}$ we assume that the neuron feedback functions $f_{j}(u)$, $g_{j}(u)$, $h_{i}(u)$, $l_{i}(u)$ are globally Lipschitz, i.e., the constants $M^{f}_{j}=M^{g}_{j}=0$, $M^{h}_{i}=M^{l}_{i}=0$, then the $\mathbf{H}_{1}$ turns to:

$\bar{\mathbf{H}}_{1}$: $f_{j}(u)$, $g_{j}(u)$, $h_{i}(u)$, $l_{i}(u)$ are globally Lipschitz continuous, i.e., there exist constants $L_{j}^{f}>0$, $L^{g}_{j}>0$, $L^{h}_{i}>0$, $L^{l}_{i}>0$, such that

$$\begin{aligned}& \bigl\vert f_{j}(v_{1})-f_{j}(v_{2}) \bigr\vert \leq L^{f}_{j} \vert v_{1}-v_{2} \vert ,\qquad \bigl\vert g_{j}(v_{1})-g_{j}(v_{2}) \bigr\vert \leq L^{g}_{j} \vert v_{1}-v_{2} \vert ,\\& \bigl\vert h_{i}(v_{1})-h_{i}(v_{2}) \bigr\vert \leq L^{h}_{i} \vert v_{1}-v_{2} \vert ,\qquad \bigl\vert l_{i}(v_{1})-l_{i}(v_{2}) \bigr\vert \leq L^{l}_{i} \vert v_{1}-v_{2} \vert . \end{aligned}$$

In addition, the controller (6) and inequality (5) in system (2) becomes

$$ \begin{gathered} p_{i}(t)= - \frac{\eta _{i}(t) \Vert e(t) \Vert e_{i}(t)}{e_{i}(t)+\varrho _{1}(t)}, \quad i\in \mathcal{I}, \\ q_{j}(t)= - \frac{\beta _{j}(t) \Vert z(t) \Vert z_{j}(t)}{z_{j}(t)+\varrho _{2}(t)},\quad j\in \mathcal{J}, \end{gathered} $$

(20)

and

$$ \textstyle\begin{cases} c^{L}_{i}+\eta _{i}^{L}-\sum_{j=1}^{n} ( \frac{A^{h}_{ji}}{1-{\mu}^{g}_{ji}}+A^{o}_{ji}+A^{l}_{ji} ) -\sum_{j=1}^{n}C^{f}_{ij}=:E^{f}_{i}>0, \\ d^{L}_{j}+\beta _{j}^{L}-\sum_{i=1}^{m} ( \frac{A^{f}_{ji}}{1-\mu ^{f}_{ji}}+A^{r}_{ji}+A^{g}_{ji} ) -\sum_{i=1}^{m}C^{h}_{ij}=:E^{h}_{j}>0. \end{cases} $$

(21)

Then, from Theorem 1, we have the following corollary.

Corollary 1

Suppose $\bar{\mathbf{H}}_{1}$, $\mathbf{H}_{2}$, $\mathbf{H}_{3}$ hold and the control gains $\eta _{i}$, $\beta _{j}$ satisfy the inequality (21), then the response network (2) can be general decay synchronized with the drive network (1) under the nonlinear controller (20).

4 Numerical simulations

In this section, one example is given to illustrate the effectiveness of our results obtained in this paper.

Example 1

For $n=2$, $m=2$, consider the following two-dimensional BAMRNNs system with mixed time delays

$$ \textstyle\begin{cases} \dot{x}_{i}(t)= -c_{i}(t)x_{i}(t)+\sum_{j=1}^{2}r_{ji}(t)f_{j}(y_{j}(t))+ \sum_{j=1}^{2}a_{ji}(t)f_{j}(y_{j}(t-\tau _{ij}(t))) \\ \hphantom{\dot{x}_{i}(t)=}{} +\sum_{j=1}^{2}b_{ji}(t)\int ^{0}_{-\theta _{ij}}K_{ij}(s)g_{j}(y_{j}(t+s))\,ds+I_{i}(t), \\ \dot{y}_{j}(t)= -d_{j}(t)y_{j}(t)+\sum_{i=1}^{2}o_{ij}(t)h_{i}(x_{i}(t))+ \sum_{i=1}^{2}p_{ij}(t)h_{i}(x_{i}(t-\sigma _{ij}(t))) \\ \hphantom{\dot{y}_{j}(t)=}{} +\sum_{i=1}^{2}q_{ij}(t)\int ^{0}_{-\gamma _{ij}}H_{ij}(s)l_{i}(x_{i}(t+s))\,ds+J_{j}(t). \end{cases} $$

(22)

The corresponding response system of system (22) is given as

$$ \textstyle\begin{cases} \dot{u}_{i}(t)= -c_{i}(t)u_{i}(t)+\sum_{j=1}^{2}r_{ji}(t)f_{j}(v_{j}(t))+ \sum_{j=1}^{2}a_{ji}(t)f_{j}(v_{j}(t-\tau _{ij}(t))) \\ \hphantom{\dot{u}_{i}(t)= }{} +\sum_{j=1}^{2}b_{ji}(t)\int ^{0}_{-\theta _{ij}}K_{ij}(s)g_{j}(v_{j}(t+s))\,ds+I_{i}(t)+p_{i}(t), \\ \dot{v}_{j}(t)= -d_{j}(t)v_{j}(t)+\sum_{i=1}^{2}o_{ij}(t)h_{i}(u_{i}(t))+ \sum_{i=1}^{2}p_{ij}(t)h_{i}(u_{i}(t-\sigma _{ij}(t))) \\ \hphantom{\dot{v}_{j}(t)=}{} +\sum_{i=1}^{2}q_{ij}(t)\int ^{0}_{-\gamma _{ij}}H_{ij}(s)l_{i}(u_{i}(t+s))\,ds+J_{j}(t)+q_{j}(t), \end{cases} $$

(23)

where $f_{1}(u)=f_{2}(u)=1.11\tanh (u)$, $g_{1}(u)=g_{2}(u)=1.12\tanh (u)$, $h_{1}(u)=h_{2}(u)=1.4\tanh (u)$, $g_{1}(u)=g_{2}(u)=1.15\tanh (u)$, and the other parameters of systems (22) and (23) are chosen such that $c_{1}=1.11+0.15|\sin (t)|$, $c_{2}=1.12+0.15|\sin (t)|$, $d_{1}=1.13+0.15|\cos (t)|$, $d_{2}=1.14+0.15|\cot (t)|$, $r_{11}=1.75+0.15|\sin (t)|$, $r_{12}=-2.45+0.15|\sin (t)|$, $r_{21}=-0.11+0.2|\sin (t)|$, $r_{22}=3.1+0.2|\sin (t)|$, $a_{11}=-1.55+0.15| \sin (t)|$, $a_{12}=-0.17+0.15|\sin (t)|$, $a_{21}=-0.12+0.2|\sin (t)|$, $a_{22}=-2.35+2|\sin (t)|$, $b_{11}=0.2+0.15|\cot (t)|$, $b_{12}=-0.2+0.15| \cot (t)|$, $b_{21}=0$, $b_{22}=0.14+2|\cot (t)|$, $o_{11}=2+0.15|\cot (t)|$, $o_{12}=-0.15+0.15|\cot (t)|$, $o_{21}=-2.5+0.2| \cot (t)|$, $o_{22}=3.4+0.2|\cot (t)|$, $p_{11}=-1.55+0.15|\cot (t)|$, $\ p_{12}=-0.11+0.15|\cot (t)|$, $p_{21}=-0.15+0.2|\cot (t)|$, $p_{22}=-2.4+0.2| \cot (t)|$, $q_{11}=0.2+0.14|\cot (t)|$, $q_{12}=0$, $q_{21}=-0.18+0.2| \cot (t)|$, $q_{22}=0.15+0.2|\cot (t)|$, $\tau _{ij}(t)={e^{t}}/{(2+e^{t})}$, $\sigma _{ij}(t)=e^{t}/(3+e^{t})$, $\theta _{ij}=2/(1+i)$, $\gamma _{ij}=1/(2+j)$, and $I_{i}=\frac{1+|\sin(t)|}{10000}$, $J_{j}=\frac{1+|\cos(t)|}{1000}$ for $i,j=1,2$.

The nonlinear feedback controllers $p_{i}(t)$, $q_{j}(t)$ are given as follows:

$$ \begin{gathered} p_{i}(t)=-\alpha ^{p}_{i}(t) \operatorname{sign} \bigl(e_{i}(t) \bigr) - \frac{\eta _{i}(t) \Vert e(t) \Vert e_{i}(t)}{e_{i}(t)+\varrho _{1}(t)}, \quad i \in \mathcal{I}, \\ q_{j}(t)= -\alpha ^{q}_{j}(t) \operatorname{sign} \bigl(z_{j}(t) \bigr) - \frac{\beta _{j}(t) \Vert z(t) \Vert z_{j}(t)}{z_{j}(t)+\varrho _{2}(t)}, \quad j\in \mathcal{J}, \end{gathered} $$

(24)

where $e_{i}(t)=u_{i}(t)-x_{i}(t)$, $z_{j}(t)=v_{j}(t)-y_{j}(t)$ for $i=1,2$, $j=1,2$.

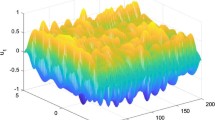
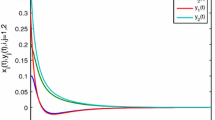
By choosing $L^{f}_{j}>=L^{g}_{j}=L^{h}_{i}=L^{l}_{i}=1(i,j=1,2)$, $M^{f}_{j}=0.01$, $M^{g}_{j}=0.02$, $M^{h}_{i}=0.024$, $M^{l}_{i}=0.03(i,j=1,2)$, and $\sigma _{ij}=\tau _{ij}=1$, we know that assumptions $\mathbf{H}_{1}$ and $\mathbf{H}_{2}$ are satisfied. Further, letting $\varrho _{1}(t)=e^{-1.11t}$, $\varrho _{2}(t)=e^{-1.12t}$, $\psi (t)=e^{1.5t}$, and choosing $\alpha ^{p}_{1}(t)=\alpha ^{p}_{2}(t)=1.25+0.2|\sin (t)|$, $\alpha ^{q}_{1}(t)= \alpha ^{q}_{2}(t)=1.3+0.15|\cot (t)|$, $\eta _{1}(t)=7.5+0.15|\cot (t)|$, $\eta _{2}(t)=5.5+0.15|\cot (t)|$, $\beta _{1}(t)=7+0.2|\sin (t)|$, $\beta _{2}(t)=6+0.2|\sin (t)|$, then, the assumption $\mathbf{H}_{3}$ and inequality (6) of Theorem 1 also hold. Therefore, from Theorem 1, the drive–response systems (22) and (23) can achieve GDS under the controller (24). The time evolution of synchronization errors and the synchronization curves with nonlinear feedback controller (24) between drive–response systems (22) and (23) are shown in Figs. 1(a) and (b), and Figs. 2(a)–(d), where the initial values of drive system (22) are chosen as $x_{1}(\theta )=0.3$, $x_{2}(\theta )=0.6$, $y_{2}(\theta )=4$, and $y_{2}(\theta )=-4$ and $\theta \in [0,1]$. Also, the initial values of response system (23) are chosen as $u_{1}(\theta )=-0.9$, $u_{2}(\theta )=0.9$, $v_{2}(\theta )=-0.7$ and $v_{2}(\theta )=-0.8$, and $\theta \in [-1,1]$.

Figure 1

The evaluation of synchronization error ${e}_{1}(t)$, ${e}_{2}(t)$ and ${z}_{1}(t)$, ${z}_{2}(t)$

Figure 2

Synchronization curves of $x_{1}(t)$, $u_{1}(t)$, $x_{2}(t)$, $u_{2}(t)$ and $y_{1}(t)$, $\upsilon _{1}(t)$, $y_{2}(t)$, $\upsilon _{2}(t)$

Remark 2

It is noteworthy that the convergence rate of the system is not easy to obtain in many practical cases. For example, consider the following equation [20]

$$ \dot{z}(t)=-\frac{1}{2}t^{3}, \quad t\geq 0. $$

Although, we can find that the above equation is asymptotically stable, we are not in a position to estimate the convergent rate of the solution of it. However, the GDS can overcome the above-mentioned problem. For example, in the above example, if we choose $\delta =0.2$, then the convergence rate of synchronization between drive–response systems (22) and (23) is 0.2.

5 Conclusion

In the present paper, we have studied a class of nonautonomous bidirectional associative memory recurrent neural networks (BAMRNNs) with mixed time delays, and by using the Lyapunov stability theory, employing useful inequality techniques, and applying the method given in [18, 19], we obtained some new sufficient conditions on the general decay synchronization of the drive–response systems (2) and (3). Finally, one example with numerical simulations is provided to demonstrate the effectiveness and feasibility of the obtained results. In comparison to previous studies, we extend the systems in [20, 21, 28, 29] to the mixed time-delayed nonautonomous bidirectional associative memory recurrent neural-network (BAMRNNs) system, and we also obtained some sufficient conditions on the above-mentioned results for the considered system (2). Moreover, the GDS contains logarithmic synchronization, exponential synchronization, polynomial synchronization, and other synchronization as its special cases, and also the GDS of NNs have some applications, such as in image processing, combinatorial optimization, pattern recognition, signal processing, associative memory, and other areas. Hence, system (2) and the results of this paper are general, and they also complement and extend some previous results [18–28].

Recently, the dynamic analysis and applications of fractional-order networks systems with delays has been significantly developed [29–33]. Hence, we have interesting future work such as the GDS on the fractional-order neural networks with delays.