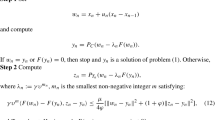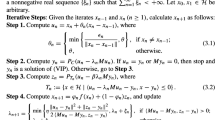Self-adaptive subgradient extragradient-type methods for solving variational inequalities

Abstract

In this paper, we introduce two subgradient extragradient-type algorithms for solving variational inequality problems in the real Hilbert space. The first one can be applied when the mapping f is strongly pseudomonotone (not monotone) and Lipschitz continuous. The first algorithm only needs two projections, where the first projection onto closed convex set C and the second projection onto a half-space $C_{k}$. The strong convergence theorem is also established. The second algorithm is relaxed and self-adaptive; that is, at each iteration, calculating two projections onto some half-spaces and the step size can be selected in some adaptive ways. Under the assumption that f is monotone and Lipschitz continuous, a weak convergence theorem is provided. Finally, we provide numerical experiments to show the efficiency and advantage of the proposed algorithms.

1 Introduction

Let H be a real Hilbert space with the inner product $\langle \cdot , \cdot \rangle$. The classic variational inequality problems for f on C are to find a point $x^{*} \in C$ such that

$$ \bigl\langle f\bigl(x^{*}\bigr),x-x^{*} \bigr\rangle \geq 0, \quad \forall x\in C, $$

(1.1)

where C is a nonempty closed convex subset of H, and f is a mapping from H to H. The problem and its solution set will be denoted by $VI(C,f)$ and $\operatorname{SOL}(C,f)$. This class of variational inequality problems arises in many fields such as optimal control, optimization, partial differential equations, and some other nonlinear problems; see [1] and the references therein. Nowadays, variational inequality problems with uncertain data are a very interesting topic, and the robust optimization has recently emerged as a powerful approach to deal with mathematical programming problems with data uncertainty. For more details, we refer the readers to [18, 29, 30].

In order to solve variational inequality problems, many solution methods have been introduced [7, 12, 14, 16, 17, 31]. Among these methods, subgradient extragrdeint method has attracted much attention. This method has the following form:

$$\begin{aligned}& y^{k}=P_{C}\bigl(x^{k}-\tau f\bigl(x^{k}\bigr)\bigr), \end{aligned}$$

(1.2)

$$\begin{aligned}& x^{k+1}=P_{T_{k}}\bigl(x^{k}-\tau f\bigl(y^{k}\bigr)\bigr), \end{aligned}$$

(1.3)

where $T_{k}:=\{w\in H| \langle x^{k}-\tau f(x^{k})-y^{k}, w-y^{k}\rangle \leq 0 \}$ is a half-space and $\tau >0$ is a constant. Under the assumption that f is monotone and L-Lipschitz continuous, the method (1.2)-(1.3) weakly converges to a solution to $VI(C,f)$.

The subgradient extragradient method has received a great deal of attention and many authors modified and improved it in various ways, see [9, 10, 25, 35]. To the best of our knowledge, almost subgradient extragradient-type algorithms about variational inequality problems need to assume f is monotone Lipschitz continuous and need one projection on C. These observations lead us to the following concerns:

Question 1

Can we propose a new subgradient extragradient-type algorithm for solving strongly pseudomonotone (not monotone) variational inequality problems?

Question 2

Can we propose a new subgradient extragradient-type projection algorithm such that the projection on C can be replaced by half-space?

In this paper, the main purpose is to solve the two questions. We first introduce a subgradient extragradient-type algorithm for solving Question 1. Under the assumptions that f is strongly pseudomonotone(not monotone) and Lipschitz continuous, we establish the strong convergence theorem. The first algorithm has the following form:

$$\begin{aligned}& y^{k}=P_{C}\bigl(x^{k}- \lambda _{k} f\bigl(x^{k}\bigr)\bigr), \end{aligned}$$

(1.4)

$$\begin{aligned}& x^{k+1}=P_{C_{k}}\bigl(y^{k}- \lambda _{k}\bigl( f\bigl(y^{k}\bigr)-f \bigl(x^{k}\bigr)\bigr)\bigr), \end{aligned}$$

(1.5)

where $C_{k}$ is a half-space (a precise definition will be given in Sect. 3 (3.2)). The main feature of the new algorithm is that: it only requires the strong pseudomonotonicity (not monotone) and Lipschitz continuity (there is no need to know or estimate the Lipschitz constant of f) of the involving mapping instead of the monotonicity and L-Lipschitz continuity conditions as in [4]. Moreover, in the new algorithm, the step sizes $\lambda _{k}$ do not necessarily converge to zero, and we get the strong convergence theorem.

Note that, in the algorithms (1.2)-(1.3) and (1.4)-(1.5), one still needs to execute one projection onto the closed convex set C at each iteration. If C has a simple structure (e.g., half-space, a ball, or a subspace), the projection $P_{C}$ can be computed easily. But, if C is a general closed convex set, one has to solve the minimal distance problem to compute the projection onto C, which is complicated in general.

To overcome this flaw, we present the second algorithm, named two-subgradient extragradient algorithm, for solving monotone and Lipschitz continuous variational inequality problems defined on a level set of a convex function. The two-subgradient extragradient algorithm has the following form:

$$\begin{aligned}& y^{k}=P_{C_{k}}\bigl(x^{k}- \lambda _{k} f\bigl(x^{k}\bigr)\bigr), \end{aligned}$$

(1.6)

$$\begin{aligned}& x^{k+1}=P_{C_{k}}\bigl(y^{k}- \lambda _{k}\bigl( f\bigl(y^{k}\bigr)-f \bigl(x^{k}\bigr)\bigr)\bigr), \end{aligned}$$

(1.7)

where $C_{k}$ is a half-space (a precise definition will be given in Sect. 4). It is well known that the projection onto half-space can be calculated directly. Clearly, the two-subgradient extragradient algorithm is easy to implement. We prove that the sequence generated by the algorithm (1.6)-(1.7) weakly converges to a solution to $VI(C,f)$ for the case where the closed convex set C can be represented as a lower level set of a continuously differentiable convex function. Moreover, the step size $\lambda _{k}$ in this algorithm can be selected in some adaptive way; that is, we have no need to know or to estimate any information as regards the Lipschitz constant of f.

Our paper is organized as follows: In Sect. 2, we collect some basic definitions and preliminary results. In Sect. 3, we propose an extragradient-type algorithm and analyze its convergence and convergence rate. In Sect. 4, we consider the two-subgradient extragradient algorithm and analyze its convergence and convergence rate. Numerical results are reported in Sect. 5.

2 Preliminaries

In this section, we recall some definitions and results for further use. For the given nonempty closed convex set C in H, the orthogonal projection from H to C is defined by

$$ P_{C}(x)= {\mathrm{argmin}} \bigl\{ \Vert y-x \Vert \mid y\in C \bigr\} , \quad x\in H. $$

(2.1)

We write $x^{k}\rightarrow x$ and $x^{k} \rightharpoonup x$ to indicate that the sequence $\{x^{k}\}$ converges strongly and weakly to x, respectively.

Definition 2.1

Let $f: H\rightarrow H$ be a mapping. f is called Lipschitz continuous with constant $L>0$, if

$$ \bigl\Vert f(x)-f(y) \bigr\Vert \leq L \Vert x-y \Vert , \quad \forall x,y\in H .$$

Definition 2.2

Let $f: C\rightarrow H$ be a mapping. f is called

• (a) monotone on C, if

  $$ \bigl\langle f(y)-f(x), y-x\bigr\rangle \geq 0, \quad \forall x,y\in C;$$

• (b) σ-strongly pseudomonotone on C, if there exists $\sigma >0$ such that

  $$ \bigl\langle f(x),y-x\bigr\rangle \geq 0 \quad \Rightarrow\quad \bigl\langle f(y),y-x\bigr\rangle \geq \sigma \Vert x-y \Vert ^{2}, \quad \forall x,y\in C.$$

Remark 2.1

We claim that property (b) guarantees that $VI(C,f)$ have one solution at most. Indeed, if $u,v\in \operatorname{SOL}(C,f)$ and if (b) is satisfied, then $\langle f(v),u-v\rangle \geq 0$ and $\langle f(v),v-u\rangle \geq \sigma \|v-u\|^{2}$. Adding these two inequalities yields $\sigma \|v-u\|^{2} \leq 0$, which implies $u=v$. Note also that property (b) and the continuity of f guarantee that $VI(C,f)$ has a unique solution [19].

In the following, we introduce an example to illustrate that f is strongly pseudomonotone but is not monotone in general.

Example 2.1

Let $H=l_{2}$ be a real Hilbert space whose elements are square-summable sequences of real scalars, i.e.,

$$ H=\Biggl\{ u=(u_{1},u_{2},\ldots , u_{n}, \ldots ): \sum_{n=1}^{\infty} \vert u_{n} \vert ^{2}< \infty \Biggr\} .$$

The inner product and the induced norm on H are given by

$$ \langle u,v\rangle =\sum_{n=1}^{\infty}u_{n}v_{n} \quad \text{and} \quad \Vert u \Vert =\sqrt{\langle u,u \rangle}$$

for any $u=(u_{1},u_{2},\ldots , u_{n},\ldots )$, $v=(v_{1},v_{2},\ldots , v_{n},\ldots )\in H$.

Let α and β be two positive real numbers such that $\beta <\alpha$ and $1-\alpha \beta <0$. Let us set

$$ C=\bigl\{ u\in H: \Vert u \Vert \leq \alpha \bigr\} ,\quad f(u)= \frac{u}{1+ \Vert u \Vert ^{2}}.$$

We now show that f is strongly pseudomonotone. Indeed, let $u,v\in C$ be such that $\langle f(u),v-u\rangle \geq 0$. This implies that $\langle u,v-u\rangle \geq 0$. Consequently,

$$\begin{aligned} \bigl\langle f(v),v-u\bigr\rangle = & \frac{1}{1+ \Vert v \Vert ^{2}} \langle v,v-u \rangle \\ \geq & \frac{1}{1+ \Vert v \Vert ^{2}} \bigl( \langle v,v-u\rangle - \langle u,v-u \rangle \bigr) \\ \geq & \frac{1}{1+\alpha ^{2}} \Vert u-v \Vert ^{2} \\ = & \gamma \Vert u-v \Vert ^{2}, \end{aligned}$$

where $\gamma :=\frac{1}{1+\alpha ^{2}}>0$. Taking $u=(\alpha ,0,\ldots ,0,\ldots )$, $v=(\beta ,0,\ldots ,0,\ldots )\in C$, we find

$$ \bigl\langle f(u)-f(v),u-v\bigr\rangle =\bigl(\alpha ^{2}-\beta ^{2}\bigr)\biggl[ \frac{1-\alpha \beta}{(1+\alpha ^{2})(1+\beta ^{2})}\biggr]< 0.$$

This means f is not monotone on C.

Definition 2.3

Let $f: H\rightarrow (-\infty , +\infty ]$, and $x\in H$. Then f is weakly sequential lower semicontinuous at x if for every sequence $\{x^{k}\}$ in H,

$$ x^{k}\rightharpoonup x \quad \Rightarrow\quad f(x) \leq \lim _{k \rightarrow {\infty}} {\mathrm{inf}} f\bigl(x^{k} \bigr).$$

Definition 2.4

A mapping $c: H \rightarrow R$, is said to be Gâteaux differentiable at a point $x\in H$, if there exists an element, denoted by $c^{\prime }(x) \in H$, such that

$$ \lim_{t \rightarrow 0} \frac{c(x+t\theta )-c(x))}{t}= \bigl\langle c^{\prime }(x), \theta \bigr\rangle , \quad \forall \theta \in H, $$

(2.2)

where $c^{\prime }(x)$ is called the Gâteaux differential of c at x.

Definition 2.5

For a convex function $c: H\rightarrow R$, c is said to be subdifferentiable at a point $x\in H$ if the set

$$ \partial c(x) \triangleq \bigl\{ v\in H \mid c(y) \geq c(x)+ \langle v, y-x \rangle , \forall y\in H \bigr\} $$

(2.3)

is not empty. Each element in $\partial c(x)$ is called a subgradient of c at x. c is said to be subdifferentiable on H if c is subdifferentiable at each $x\in H$.

Note that if $c(x)$ is Gâteaux differentiable at x, then $\partial c(x)=\{c'(x)\}$.

Definition 2.6

Suppose that a sequence $\{x^{k}\}$ in H converges in norm to $x^{*} \in H$. We say that

• (a) $\{x^{k}\}$ converges to $x^{*}$ with R-linear convergence rate if

  $$ \lim_{k \rightarrow {\infty}} \sup \bigl\Vert x^{k}-x^{*} \bigr\Vert ^{1/k}< 1. $$

• (b) $\{x^{k}\}$ converges to $x^{*}$ with Q-linear convergence rate if there exists $\mu \in (0,1)$ such that

  $$ \bigl\Vert x^{k+1}-x^{*} \bigr\Vert \leq \mu \bigl\Vert x^{k}-x^{*} \bigr\Vert . $$

  for all sufficiently large k.

Note that Q-linear convergence rate implies R-linear convergence rate; see [[23], Sect. 9.3]. We remark here that R-linear convergence does not imply Q-linear convergence in general. We consider one simple example, which is derived from [15].

Example 2.2

Let $\{x^{k}\}\in \mathbb{R}$ be the sequence of real numbers defined by

$$\begin{aligned} x^{k}= \textstyle\begin{cases} 2^{-k}, &~ k~ \text{is}~ \text{even}, \\ 3^{-k}, &~ k ~\text{is}~ \text{odd}. \end{cases}\displaystyle \end{aligned}$$

Since

$$ \lim_{k \rightarrow {\infty}} \sup \bigl\Vert x^{k}-0 \bigr\Vert ^{1/k} = \frac{1}{2}, $$

$\{x^{k}\}$ converges to 0 with an R-linear convergence rate. Note that

$$ \lim_{k \rightarrow {\infty}} \sup \frac{ \Vert x^{k+1}-0 \Vert }{ \Vert x^{k}-0 \Vert }=+\infty , $$

this implies $\{x^{k}\}$ does not converge to 0 with the Q-linear convergence rate.

The following well-known properties of the projection operator will be used in this paper.

Lemma 2.1

Let $P_{C}(\cdot )$ be the projection onto C. Then

• (a) $\langle x-P_{C}(x), y- P_{C}(x)\rangle \leq 0$, $\forall x\in H$, $y\in C$;

• (b) $\|x-y\|^{2}\geq \|x-P_{C}(x)\|^{2}+\|y-P_{C}(x)\|^{2}$, $\forall x\in H$, $y\in C$;

• (c) $\|P_{C}(y)-P_{C}(x)\| \leq \langle P_{C}(y)-P_{C}(x),y-x \rangle$, $\forall x,y\in H$;

• (d) $\|P_{C}(y)-P_{C}(x)\| \leq \|y-x\|$, $\forall x,y\in H$.

Lemma 2.2

([2])

Let $f:H\rightarrow (-\infty , +\infty ]$ be convex. Then the following are equivalent:

• (a) f is weakly sequential lower semicontinuous;

• (b) f is lower semicontinuous.

Lemma 2.3

([22](Opial))

Assume that C is a nonempty subset of H, and $\{x^{k}\}$ is a sequence in H such that the following two conditions hold:

• (i) $\forall x\in C$, $\lim_{k \rightarrow {\infty}}\|x^{k}-x\|$ exists;

• (ii) every sequential weak cluster point of $\{x^{k}\}$ belongs to C.

Then $\{x^{k}\}$ converges weakly to a point in C.

Lemma 2.4

([13])

Assume that the solution set $\operatorname{SOL}(C,f)$ of $VI(C,f)$ is nonempty. Given $x^{*}\in C$ and C is defined in (3.1), where C is a Gâteaux differentiable convex function. Then $x^{*}\in \operatorname{SOL}(C,f)$ if and only if we have either

• (i) $f(x^{*})=0$, or

• (ii) $x^{*}\in \partial C$ and there exists a positive constant η such that $f(x^{*})=-\eta c'(x^{*})$.

Remark 2.2

According to Sect. 5: Application in [13], we remark here that determining η is an easy and/or feasible task.

Lemma 2.5

([5])

Consider the problem $VI(C,f)$ with C being a nonempty, closed, convex subset of a real Hilbert space H and $f:C\rightarrow H$ being pseudo-monotone and continuous. Then, $x^{*}$ is a solution to $VI(C,f)$ if and only if

$$ \bigl\langle f(x), x-x^{*}\bigr\rangle \geq 0, \quad \forall x\in C.$$

3 Convergence of subgradient extragradient-type algorithm

In this section, we introduce a self-adaptive subgradient extragradient-type method for solving variational inequality problems. The nonempty closed convex set C will be given as follows:

$$ C=\bigl\{ x\in H\mid c(x) \leq 0\bigr\} , $$

(3.1)

where $c:H \rightarrow R$ is a convex function.

We define the half-space as

$$ C_{k}=\bigl\{ x\in H \mid c\bigl(x^{k} \bigr)+ \bigl\langle \zeta ^{k}, x-x^{k} \bigr\rangle \leq 0 \bigr\} , $$

(3.2)

with $\zeta ^{k} \in \partial c(x^{k})$, where $\partial c(x^{k})$ is the subdifferential of c at $x^{k}$. It is clear that $C \subset C_{k}$ for any $k\geq 0$.

In order to prove our theorem, we assume that the following conditions are satisfied:

C1::

The mapping $f: H \rightarrow H$ is σ-strongly pseudomonotone and Lipschitz continuous (but we have no need to know or estimate the Lipschitz constant of f).

Note that strong pseudomonotonicity and the continuity of f guarantee that $VI(C,f)$ has a unique solution denoted by $x^{*}$.

Now we propose our Algorithm 1.

Algorithm 1

Subgradient extragradient-type algorithm

The following lemma gives an explicit formula of $P_{C_{k}}$.

Lemma 3.1

([24])

For any $y\in H$,

$$ P_{C_{k}}(y)= \textstyle\begin{cases} y-\frac{c(x^{k})+\langle u, y-x^{k}\rangle}{ \Vert u \Vert ^{2}}u, & c(x^{k})+ \langle u, y-x^{k}\rangle >0 , \\ y, &c(x^{k})+\langle u, y-x^{k}\rangle \leq 0, \end{cases} $$

where $u \in \partial c(x^{k})$.

Lemma 3.2

The sequence $\{\lambda _{k}\}$ is nonincreasing and is bounded away from zero. Moreover, there exists a number $m>0$ such that

• (1) $\lambda _{k+1}=\lambda _{k}$ and $\lambda _{k}\|f(x^{k})-f(y^{k})\|\leq \rho \|x^{k}-y^{k}\|$ for all $k\geq m$.

• (2) $\lambda _{k} \geq \lambda _{-1}\delta ^{m+1}$ for any $k\geq 0$.

Proof

Since $\delta \in (0,1)$, it is easy to see the sequence $\{\lambda _{k}\}$ is nonincreasing. We claim this sequence is bounded away from zero. Suppose, on the contrary, that $\lambda _{k}\rightarrow 0$. Then, there exists a subsequence $\{\lambda _{k_{i}}\}\subset \{\lambda _{k} \}$ such that

$$ \lambda _{k_{i}-1} \bigl\Vert f\bigl(x^{k_{i}-1}\bigr)-f \bigl(y^{k_{i}-1}\bigr) \bigr\Vert > \rho \bigl\Vert x^{k_{i}-1}-y^{k_{i}-1} \bigr\Vert .$$

Let L be the Lipschitz constant of f, we have

$$ \lambda _{k_{i}-1}> \rho \frac{ \Vert x^{k_{i}-1}-y^{k_{i}-1} \Vert }{ \Vert f(x^{k_{i}-1})-f(y^{k_{i}-1}) \Vert } \geq \frac{\rho}{L}.$$

Obviously, this inequality contradicts the fact $\lambda _{k}\rightarrow 0$. Therefore, there exists a number $m>0$ such that

$$ \lambda _{k+1}=\lambda _{k} \quad \text{and} \quad \lambda _{k} \bigl\Vert f \bigl(x^{k}\bigr)-f\bigl(y^{k}\bigr) \bigr\Vert \leq \rho \bigl\Vert x^{k}-y^{k} \bigr\Vert $$

(3.3)

for all $k\geq m$. Since the sequence $\{\lambda _{k}\}$ is nonincreasing, the preceding relation (3.3) implies $\lambda _{k} \geq \lambda _{m} \geq \lambda _{-1} \delta ^{m+1}$ for all k. □

The following lemma plays a key role in our convergence analysis.

Lemma 3.3

For $x^{*} \in SOL(C,f)$, let the sequences $\{x^{k}\}$ and $\{y^{k}\}$ be generated by Algorithm 1. There exists a number $m>0$ such that

$$\begin{aligned} \bigl\Vert x^{k+1}-x^{*} \bigr\Vert ^{2} \leq \bigl\Vert x^{k}-x^{*} \bigr\Vert ^{2}-\bigl(1-\rho ^{2}\bigr) \bigl\Vert x^{k}-y^{k} \bigr\Vert ^{2}-2\sigma \lambda _{k} \bigl\Vert y^{k}-x^{*} \bigr\Vert ^{2} \end{aligned}$$

for all $k\geq m$.

Proof

For $x^{*} \in \operatorname{SOL}(C,f)$, $x^{*} \in C_{k}$ due to $\operatorname{SOL}(C,f)\subset C\subset C_{k}$ for all $k \geq 0$. Using Lemma 2.1, we have

$$\begin{aligned} \bigl\Vert x^{k+1}-x^{*} \bigr\Vert ^{2} =& \|P_{C_{k}}(y^{k}-\lambda _{k}\bigl(f\bigl(y^{k}\bigr)- f\bigl(x^{k} \bigr)\bigr)-x^{*} \|^{2} \\ =&\|P_{C_{k}}(y^{k}-\lambda _{k}\bigl(f \bigl(y^{k}\bigr)- f\bigl(x^{k}\bigr)\bigr)-P_{C_{k}} \bigl(x^{*}\bigr) \|^{2} \\ \leq & \bigl\Vert y^{k}-\lambda _{k}\bigl(f \bigl(y^{k}\bigr)- f\bigl(x^{k}\bigr)\bigr)-x^{*} \bigr\Vert ^{2} \\ =& \bigl\Vert y^{k}-x^{*} \bigr\Vert ^{2}+\lambda _{k}^{2} \bigl\Vert f \bigl(y^{k}\bigr)- f\bigl(x^{k}\bigr) \bigr\Vert ^{2} -2 \lambda _{k}\bigl\langle f\bigl(y^{k} \bigr)-f\bigl(x^{k}\bigr),y^{k}-x^{*}\bigr\rangle \\ =& \bigl\Vert x^{k}-x^{*} \bigr\Vert ^{2}+ \bigl\Vert x^{k}-y^{k} \bigr\Vert ^{2}+2\bigl\langle y^{k}-x^{k}, x^{k}-x^{*} \bigr\rangle \\ &{} +\lambda _{k}^{2} \bigl\Vert f\bigl(y^{k} \bigr)- f\bigl(x^{k}\bigr) \bigr\Vert ^{2}-2\lambda _{k}\bigl\langle f\bigl(y^{k}\bigr)-f \bigl(x^{k}\bigr),y^{k}-x^{*} \bigr\rangle \\ =& \bigl\Vert x^{k}-x^{*} \bigr\Vert ^{2}+ \bigl\Vert x^{k}-y^{k} \bigr\Vert ^{2}-2\bigl\langle y^{k}-x^{k}, y^{k}-x^{k} \bigr\rangle +2\bigl\langle y^{k}-x^{k}, y^{k}-x^{*} \bigr\rangle \\ &{} +\lambda _{k}^{2} \bigl\Vert f \bigl(y^{k}\bigr)- f\bigl(x^{k}\bigr) \bigr\Vert ^{2}-2\lambda _{k}\bigl\langle f\bigl(y^{k}\bigr)-f \bigl(x^{k}\bigr),y^{k}-x^{*}\bigr\rangle . \end{aligned}$$

(3.4)

Noting that $y^{k}=P_{C} (x^{k}-\lambda _{k} f(x^{k},v^{k}))$, this implies that

$$ \bigl\langle y^{k}-x^{k}+\lambda _{k} f \bigl(x^{k}\bigr), y^{k}-x^{*}\bigr\rangle \leq 0, $$

(3.5)

or equivalently

$$ \bigl\langle y^{k}-x^{k}, y^{k}-x^{*} \bigr\rangle \leq -\lambda _{k} \bigl\langle f\bigl(x^{k} \bigr),y^{k}-x^{*} \bigr\rangle . $$

(3.6)

By (3.4), (3.6), and Lemma 3.2, $\forall k \geq m$, we get

$$\begin{aligned} \bigl\Vert x^{k+1}-x^{*} \bigr\Vert ^{2} \leq & \bigl\Vert x^{k}-x^{*} \bigr\Vert ^{2}- \bigl\Vert x^{k}-y^{k} \bigr\Vert ^{2}-2 \lambda _{k}\bigl\langle f \bigl(x^{k}\bigr),y^{k}-x^{*}\bigr\rangle \\ &{}+\lambda _{k}^{2} \bigl\Vert f\bigl(y^{k} \bigr)-f\bigl(x^{k}\bigr) \bigr\Vert ^{2}-2\lambda _{k}\bigl\langle f\bigl(y^{k}\bigr)-f \bigl(x^{k}\bigr),y^{k}-x^{*} \bigr\rangle \\ =& \bigl\Vert x^{k}-x^{*} \bigr\Vert ^{2}- \bigl\Vert x^{k}-y^{k} \bigr\Vert ^{2}+\lambda _{k}^{2} \bigl\Vert f \bigl(y^{k}\bigr)-f\bigl(x^{k}\bigr) \bigr\Vert ^{2} -2\lambda _{k} \bigl\langle f\bigl(y^{k} \bigr),y^{k}-x^{*}\bigr\rangle \\ \leq & \bigl\Vert x^{k}-x^{*} \bigr\Vert ^{2}-\bigl(1-\rho ^{2}\bigr) \bigl\Vert x^{k}-y^{k} \bigr\Vert ^{2}-2 \sigma \lambda _{k} \bigl\Vert y^{k}-x^{*} \bigr\Vert ^{2}, \end{aligned}$$

(3.7)

where the third term in the right-hand side of (3.7) is estimated by the strong pseudomonotonicity of f. □

Theorem 3.1

Suppose that condition C1 is satisfied. Then the sequences $\{x^{k}\}$ and $\{y^{k}\}$ generated by Algorithm 1 strongly converge to a unique solution to $VI(C,f)$.

Proof

Let $x^{*} \in \operatorname{SOL}(C,f)$. Using Lemma 3.3, there exists a number $m>0$ such that for all $k\geq m$,

$$ \bigl\Vert x^{k+1}-x^{*} \bigr\Vert ^{2} \leq \bigl\Vert x^{k}-x^{*} \bigr\Vert ^{2}-\bigl(1-\rho ^{2}\bigr) \bigl\Vert x^{k}-y^{k} \bigr\Vert ^{2}-2 \sigma \lambda _{k} \bigl\Vert y^{k}-x^{*} \bigr\Vert ^{2}, $$

(3.8)

or equivalently

$$ \bigl(1-\rho ^{2}\bigr) \bigl\Vert x^{k}-y^{k} \bigr\Vert ^{2}+2 \sigma \lambda _{k} \bigl\Vert y^{k}-x^{*} \bigr\Vert ^{2} \leq \bigl\Vert x^{k}-x^{*} \bigr\Vert ^{2}- \bigl\Vert x^{k+1}-x^{*} \bigr\Vert ^{2}. $$

(3.9)

Continuing, we get for all integers $n \geq 0$,

$$ \sum_{k=0}^{n}\bigl(1-\rho ^{2}\bigr) \bigl\Vert x^{k}-y^{k} \bigr\Vert ^{2}+ \sum_{k=0}^{n} 2 \sigma \lambda _{k} \bigl\Vert y^{k}-x^{*} \bigr\Vert ^{2} \leq \bigl\Vert x^{0}-x^{*} \bigr\Vert ^{2}. $$

(3.10)

Since the sequence $\{\sum_{k=0}^{n}(1-\rho ^{2})\|x^{k}-y^{k}\|^{2}+ \sum_{k=0}^{n} 2 \sigma \lambda _{k} \|y^{k}-x^{*}\|^{2}\}$ is monotonically increasing and bounded, we obtain

$$ \sum_{k=0}^{\infty}\bigl(1-\rho ^{2}\bigr) \bigl\Vert x^{k}-y^{k} \bigr\Vert ^{2}+ \sum_{k=0}^{\infty}2 \sigma \lambda _{k} \bigl\Vert y^{k}-x^{*} \bigr\Vert ^{2} \leq \bigl\Vert x^{0}-x^{*} \bigr\Vert ^{2}. $$

(3.11)

By Lemma 3.2, $\{\lambda _{k}\}$ is bounded away from zero. Hence, we have

$$ \lim_{k \rightarrow {\infty}} \bigl\Vert y^{k}-x^{*} \bigr\Vert ^{2} =0 \quad \text{and} \quad \lim _{k \rightarrow {\infty}} \bigl\Vert x^{k}-y^{k} \bigr\Vert ^{2}=0. $$

(3.12)

That is, $x^{k} \rightarrow x^{*}$ and $y^{k} \rightarrow x^{*}$. This completes the proof. □

We note that Algorithm 1 can give convergence when f is strongly pseudomonotone and Lipschitz continuous without $P_{C_{k}}$ in Step 3. We now give a convergence result via the following new method.

Theorem 3.2

Assume that condition C1 is satisfied. Let $\rho , \delta \in [a,b] \subset (0,1)$; $\lambda _{-1}\in (0,\infty )$. Choose $x^{-1}, x^{0}, y^{-1} \in H$. Let $p_{k-1}=x^{k-1}-y^{k-1}$.

$$\begin{aligned} \lambda _{k}= \textstyle\begin{cases} \lambda _{k-1}, &~ \lambda _{k-1} \Vert f(x^{k-1})-f(y^{k-1}) \Vert \leq \rho \Vert p_{k-1} \Vert , \\ \lambda _{k-1}\delta , &\textit{otherwise}. \end{cases}\displaystyle \end{aligned}$$

(3.13)

Suppose $\{x^{k}\}$ is generated by

$$\begin{aligned} \textstyle\begin{cases} y^{k}=P_{C}(x^{k}-\lambda _{k} f(x^{k})) \\ x^{k+1}=y^{k}-\lambda _{k}( f(y^{k})-f(x^{k})). \end{cases}\displaystyle \end{aligned}$$

(3.14)

Then the sequences $\{x^{k}\}$ and $\{y^{k}\}$ generated by (3.14) strongly converge to a unique solution to $VI(C,f)$.

Proof

Similar to the proof of Theorem 3.1, it is not difficult to get a conclusion. We omit the proof here. □

Remark 3.1

• (a) Suppose f is monotone and L-Lipschitz continuous. Let $\lambda _{k}=\lambda \in (0,1/L)$. Then the new method (3.13)-(3.14) reduces to the algorithm proposed by Tseng in [34].

• (b) Tseng’s algorithm [34] has been studied extensively by many authors; see [3, 26, 27, 32, 33, 36] and the references therein. We notice that many modified Tseng’s algorithms require that the operator f is monotone and Lipschitz continuous operator. Recently, weak convergence has been obtained in several papers [3, 26, 27], even when the cost operator is pseudomonotone.

• (c) We obtain strong convergence under the assumptions that f is strongly pseudomonotone and Lipschitz continuous. That is to say, the new method (3.13)-(3.14) is different from the methods suggested in [3, 26, 27, 32–34, 36].

Before ending this section, we provide a result on the linear convergence rate of the iterative sequence generated by Algorithm 1.

Theorem 3.3

Let $f:C\rightarrow H$ be strongly pseudomonotone and L-Lipschitz continuous mapping. Then the sequence generated by Algorithm 1 converges in norm to the unique solution $x^{*}$ of $VI(C,f)$ with a Q-linear convergence rate.

Proof

It follows from Lemma 3.3 that

$$\begin{aligned} \bigl\Vert x^{k+1}-x^{*} \bigr\Vert ^{2} \leq \bigl\Vert x^{k}-x^{*} \bigr\Vert ^{2}-\bigl(1-\rho ^{2}\bigr) \bigl\Vert x^{k}-y^{k} \bigr\Vert ^{2}-2\sigma \lambda _{k} \bigl\Vert y^{k}-x^{*} \bigr\Vert ^{2}. \end{aligned}$$

Put

$$ \beta :=\frac{1}{2} {\mathrm{min}}\bigl\{ 1-b^{2}, 2\sigma \lambda _{-1}\delta ^{m+1} \bigr\} . $$

By Lemma 3.2$(2)$, we have

$$ 2\sigma \lambda _{k} \geq 2\sigma \lambda _{-1}\delta ^{m+1}\geq 2 \beta . $$

Note that

$$ 1-\rho ^{2} \geq 1-b^{2} \geq 2\beta . $$

Thus, we get

$$\begin{aligned} \bigl\Vert x^{k+1}-x^{*} \bigr\Vert ^{2} \leq & \bigl\Vert x^{k}-x^{*} \bigr\Vert ^{2}-2\beta \bigl( \bigl\Vert x^{k}-y^{k} \bigr\Vert ^{2}+ \bigl\Vert y^{k}-x^{*} \bigr\Vert ^{2}\bigr) \\ \leq & \bigl\Vert x^{k}-x^{*} \bigr\Vert ^{2}-\beta \bigl( \bigl\Vert x^{k}-y^{k} \bigr\Vert + \bigl\Vert y^{k}-x^{*} \bigr\Vert \bigr)^{2} \\ \leq & \bigl\Vert x^{k}-x^{*} \bigr\Vert ^{2}-\beta \bigl\Vert \bigl(x^{k}-y^{k} \bigr)+ \bigl(y^{k}-x^{*}\bigr) \bigr\Vert ^{2} \\ =&(1-\beta ) \bigl\Vert x^{k}-x^{*} \bigr\Vert ^{2}. \end{aligned}$$

Hence,

$$\begin{aligned} \bigl\Vert x^{k+1}-x^{*} \bigr\Vert \leq \mu \bigl\Vert x^{k}-x^{*} \bigr\Vert , \end{aligned}$$

(3.15)

where $\mu :=\sqrt{1-\beta}\in (0,1)$. The inequality (3.15) shows that $\{x^{k}\}$ converges in norm to $x^{*}$ with a Q-linear convergence rate. □

4 Convergence of two-subgradient extragradient algorithm

In this section, we introduce an algorithm named two-subgradient extragradient algorithm, which replaces the first projection in Algorithm 1 onto closed convex set C with a projection onto a specific constructible half-space $C_{k}$. We assume that C is the same form given in (3.1). In order to prove our theorem, we assume the following conditions are satisfied:

A1::

$\operatorname{SOL}(C,f)\neq 0$.

A2::

The mapping $f: H \rightarrow H$ is monotone and Lipschitz continuous (but we do not need to know or estimate the Lipschitz constant of f).

A3::

• (a) The feasible set $C=\{x\in H\mid c(x) \leq 0\}$ is continuously Gâteaux differentiable convex function.

• (b) Gâteaux differential of c at x, denoted by $c'(x)$, is K-Lipschitz continuous.

The following lemma plays an important role in our convergence analysis.

Lemma 4.1

For any $x^{*} \in \operatorname{SOL}(X,F)$ and let the sequences $\{x^{k}\}$ and $\{y^{k}\}$ be generated by Algorithm 2. Then we have

$$\begin{aligned} \bigl\Vert x^{k+1}-x^{*} \bigr\Vert ^{2} \leq \bigl\Vert x^{k}-x^{*} \bigr\Vert ^{2}-\bigl(1-\rho ^{2}-2\lambda _{k} \eta K \bigr) \bigl\Vert x^{k}-y^{k} \bigr\Vert ^{2}. \end{aligned}$$

for all $k\geq m$.

Algorithm 2

Two-subgradient extragradient algorithm

Proof

By an argument very similar to the proof of Lemma 3.3, it is not difficult to get the following inequality:

$$\begin{aligned} \bigl\Vert x^{k+1}-x^{*} \bigr\Vert ^{2} \leq & \bigl\Vert x^{k}-x^{*} \bigr\Vert ^{2}-\bigl(1-\rho ^{2}\bigr) \bigl\Vert x^{k}-y^{k} \bigr\Vert ^{2}-2\lambda _{k} \bigl\langle f\bigl(x^{*}\bigr),y^{k}-x^{*} \bigr\rangle , \end{aligned}$$

(4.1)

where the second inequality follows by the monotonicity of f.

The subsequent proof is divided into the following two cases:

Case 1::

$f(x^{*})=0$, then Lemma 4.1 holds immediately in view of (4.1).

Case 2::

$f(x^{*})\neq 0$.

By Lemma 2.4, we have $x^{*}\in \partial C$ and there exists $\eta >0$ such that $f(x^{*}) =-\eta c'(x^{*})$. Because $c(\cdot )$ is differentiable convex function, it follows

$$ c\bigl(x^{*}\bigr)+ \bigl\langle c' \bigl(x^{*}\bigr),y^{k}-x^{*}\bigr\rangle \leq c\bigl(y^{k}\bigr).$$

Note that $c(x^{*})=0$ due to $x^{*} \in \partial C$, we have

$$ \bigl\langle f\bigl(x^{*}\bigr), x^{*}-y^{k}\bigr\rangle \leq \eta c\bigl(y^{k} \bigr). $$

(4.2)

Since $y^{k}\in C_{k}$ and by the definition of $C_{k}$ in step 3, we have

$$ c\bigl(x^{k}\bigr)+\bigl\langle c' \bigl(x^{k}\bigr), y^{k}-x^{k}\bigr\rangle \leq 0. $$

By the convexity of $c(\cdot )$, we have

$$ c\bigl(y^{k}\bigr)+ \bigl\langle c' \bigl(y^{k}\bigr), x^{k}-y^{k}\bigr\rangle \leq c\bigl(x^{k}\bigr). $$

Adding the two above inequalities, we get

$$ c\bigl(y^{k}\bigr)\leq \bigl\langle c'\bigl(y^{k}\bigr)-c' \bigl(x^{k}\bigr), y^{k}-x^{k}\bigr\rangle \leq K \bigl\Vert y^{k}-x^{k} \bigr\Vert ^{2}, $$

(4.3)

where the second inequality follows from the Lipschitz continuity of $c'(\cdot )$. Thus, combining (4.1), (4.2), and (4.3), we get

$$ \bigl\Vert x^{k+1}-x^{*} \bigr\Vert ^{2} \leq \bigl\Vert x^{k}-x^{*} \bigr\Vert ^{2}-\bigl(1-\rho ^{2}-2\lambda _{k} \eta K \bigr) \bigl\Vert x^{k}-y^{k} \bigr\Vert ^{2}. $$

 □

Theorem 4.1

Suppose that conditions A1-A3 are satisfied. Let $0<\lambda _{-1} \leq \frac{1-\rho ^{2}}{2\eta K}$. Then the sequence $\{x^{k}\}$ generated by Algorithm 2 weakly converges to a solution to $VI(C,f)$.

Proof

Let $x^{*} \in \operatorname{SOL}(C,f)$. Using Lemma 4.1, there exists a number $m>0$ such that

$$ \bigl\Vert x^{k+1}-x^{*} \bigr\Vert ^{2} \leq \bigl\Vert x^{k}-x^{*} \bigr\Vert ^{2}-\bigl(1-\rho ^{2}-2\lambda _{k} \eta K \bigr) \bigl\Vert x^{k}-y^{k} \bigr\Vert ^{2} $$

(4.4)

for all $k\geq m$. By Remark 2.2, determining η is an easy and/or feasible task. So, find a number $\lambda _{-1} \leq \frac{1-\rho ^{2}}{2\eta K}$ is a feasible task. Since $\{ \lambda _{k} \}$ is nonincreasing, we get $\lambda _{k} \leq \frac{1-\rho ^{2}}{2\eta K}$ for all $k \geq 0$. Thus, we have $1-\rho ^{2}-2\lambda _{k} \eta K \geq 0$, which implies that $\lim_{k \rightarrow {\infty}} \|x^{k}-x^{*}\|$ exists and $\lim_{k \rightarrow {\infty}} \|x^{k}-y^{k}\|=0$. Thus, the sequence $\{x^{k}\}$ is bounded. Consequently, $\{y^{k}\}$ is also bounded. Let $\hat{x}\in H$ be a sequential weak cluster of $\{x^{k}\}$, then there exists a subsequence $\{x^{k_{i}}\}$ of $\{x^{k}\}$ such that $\lim_{i \rightarrow {\infty}} x^{k_{i}}=\hat{x}$. Since $\|x^{k}-y^{k}\| \rightarrow 0$, we also have $\lim_{i \rightarrow {\infty}} y^{k_{i}}=\hat{x}$. Due to $y^{k_{i}} \in C_{k_{i}}$ and the definition of $C_{k_{i}}$,

$$ c\bigl(x^{k_{i}}\bigr)- \bigl\langle c' \bigl(x^{k_{i}}\bigr),x^{k_{i}}-y^{k_{i}} \bigr\rangle \leq 0, $$

we can get

$$ c\bigl(x^{k_{i}}\bigr)\leq \bigl\Vert c'\bigl(x^{k_{i}}\bigr) \bigr\Vert \bigl\Vert x^{k_{i}}-y^{k_{i}} \bigr\Vert . $$

Since $c'(\cdot )$ is Lipschitz continuous and $\{x^{k_{i}}\}$ is bounded, we deduce that $c'(x^{k_{i}})$ is bounded on any bounded sets of H. This fact means that there exists a constant $M>0$ such that

$$ c\bigl(x^{k_{i}}\bigr)\leq M \bigl\Vert x^{k_{i}}-y^{k_{i}} \bigr\Vert \rightarrow 0. $$

(4.5)

Because $c(\cdot )$ is convex and lower semicontinuous, using Lemma 2.2, we get $c(\cdot )$ is weak sequential lower semicontinuous. Thus, by combining (4.5) and Definition 2.3, we obtain

$$ c(\hat{x}) \leq \lim_{i \rightarrow {\infty}} {\mathrm{inf}} c \bigl(x^{k_{i}}\bigr) \leq 0, $$

(4.6)

which means $\hat{x}\in C$.

Now we turn to show $\hat{x} \in \operatorname{SOL}(C,f)$.

Note that $C\subset C_{k}$ for all $k \geq 0$. From $y^{k_{i}}=P_{C_{k_{i}}}(x^{k_{i}}-\lambda _{k_{i}}f(x^{k_{i}}))$ and f is monotone, $\forall x\in C \subset C_{k_{i}}$, we get

$$\begin{aligned} 0 \leq & \bigl\langle y^{k_{i}}-x^{k_{i}}+ \lambda _{k_{i}}f\bigl(x^{k_{i}}\bigr),x-y^{k_{i}} \bigr\rangle \\ =& \bigl\langle y^{k_{i}}-x^{k_{i}},x-y^{k_{i}}\bigr\rangle +\lambda _{k_{i}} \bigl\langle f\bigl(x^{k_{i}}\bigr), x-y^{k_{i}}\bigr\rangle \\ =& \bigl\langle y^{k_{i}}-x^{k_{i}},x-y^{k_{i}}\bigr\rangle +\lambda _{k_{i}} \bigl\langle f\bigl(x^{k_{i}}\bigr), x^{k_{i}}-y^{k_{i}}\bigr\rangle + \lambda _{k_{i}} \bigl\langle f\bigl(x^{k_{i}}\bigr), x-x^{k_{i}})\bigr\rangle \\ \leq & \bigl\langle y^{k_{i}}-x^{k_{i}},x-y^{k_{i}} \bigr\rangle +\lambda _{k_{i}} \bigl\langle f\bigl(x^{k_{i}} \bigr), x^{k_{i}}-y^{k_{i}}\bigr\rangle + \lambda _{k_{i}} \bigl\langle f(x), x-x^{k_{i}}\bigr\rangle . \end{aligned}$$

(4.7)

By Lemma 3.2, we get $\lambda _{k}>0$ is bounded away from zero. Passing to the limit in (4.7), we have

$$ \bigl\langle f(x),x-\hat{x} \bigr\rangle \geq 0, \quad \forall x \in C. $$

By Lemma 2.5, we have $\hat{x} \in \operatorname{SOL}(C,f)$. Therefore, we proved that

• (1) $\lim_{k \rightarrow {\infty}} \|x^{k}-x^{*}\|$ exists;

• (2) If $x^{k_{i}}\rightharpoonup \hat{x}$ then $\hat{x}\in \operatorname{SOL}(C,f)$.

It follows from Lemma 2.3 that the sequence $\{x^{k}\}$ converges weakly to a solution to $VI(C,f)$. □

Before ending this section, we prove the convergence rate of the iterative sequence generated by Algorithm 2 in the ergodic sense. The base of the complexity proof ([8]) is

$$ \operatorname{SOL}(C,f)=\bigcap_{u\in C} \bigl\{ z\in C |\bigl\langle f(u), u-z \bigr\rangle \geq 0 \bigr\} . $$

In order to prove the convergence rate, the following key inequality is needed. Indeed, by an argument very similar to the proof of Lemma 4.1, it is not difficult to get the following result.

Lemma 4.2

Let $\{x^{k}\}$ and $\{y^{k}\}$ be two sequences generated by Algorithm 2, and let $\lambda _{k}$ be selected as Step 1 in Algorithm 2. Suppose conditions A1-A3 are satisfied. Then for any $u \in C$, we get

$$ \bigl\Vert x^{k+1}-u \bigr\Vert ^{2} \leq \bigl\Vert x^{k}-u \bigr\Vert -(1-\rho ) \bigl\Vert x^{k}-u \bigr\Vert ^{2}-2\lambda _{k} \bigl\langle f(u), y^{k}-u\bigr\rangle . $$

Theorem 4.2

For any integer $n>0$, there exists a sequence $\{z^{n}\}$ satisfying $z^{n}\rightharpoonup x^{*}\in \operatorname{SOL}(C,f)$ and

$$ \bigl\langle f(u), z^{n}-u\bigr\rangle \leq \frac{ \Vert x^{0}-u \Vert ^{2}}{T_{k}},\quad \forall u \in C, $$

where

$$ z^{n}=\frac{\sum_{k=0}^{n} 2\lambda _{k}y^{k}}{T_{n}} \quad \textit{and} \quad T_{n}=\sum_{k=0}^{n} 2\lambda _{k}. $$

(4.8)

Proof

By Lemma 4.2, we have

$$ 2\lambda _{k} \bigl\langle f(u), y^{k}-u\bigr\rangle \leq \bigl\Vert x^{k}-u \bigr\Vert ^{2}- \bigl\Vert x^{k+1}-u \bigr\Vert ^{2}. $$

(4.9)

Summing (4.9) over $k=0,1,\ldots ,n$, we have

$$ \Biggl\langle f(u), \sum_{k=0}^{n} 2\lambda _{k}y^{k}- \sum_{k=0}^{n}2 \lambda _{k}u\Biggr\rangle \leq \bigl\Vert x^{0}-u \bigr\Vert ^{2}, \quad\forall u\in C. $$

(4.10)

Combining (4.8) and (4.10), we derive

$$ \bigl\langle f(u), z^{n}-u\bigr\rangle \leq \frac{ \Vert x^{0}-u \Vert ^{2}}{T_{n}} , \quad \forall u\in C. $$

(4.11)

Note that from the fact that $y^{k}\rightharpoonup x^{*}\in \operatorname{SOL}(C,f)$ and $z^{n}$ is a convex combination of $y^{0}, y^{1},\ldots ,y^{k}$, we get $z^{n}\rightharpoonup x^{*} \in \operatorname{SOL}(C,f)$. This completes the proof. □

Denote $\alpha :=\lambda _{-1}\delta ^{m+1}$. From Lemma 3.2(2), $\lambda _{k} \geq \alpha$ holds for all $k\geq 0$. This fact together with the relation (4.8) yields

$$ T_{n}\geq 2(n+1)\alpha . $$

The preceding inequality implies Algorithm 2 has $O(\frac{1}{n})$ convergence rate. For a given accuracy $\epsilon >0$ and any bounded subset $X\subset C$, Algorithm 2 achieves

$$ \bigl\langle f(u), z^{n}-u\bigr\rangle \leq \epsilon $$

in at most $\lceil \frac{r}{2\alpha \epsilon} \rceil$ iterations, where $r=\sup\{\|x^{0}-u\|^{2} |u\in X\}$.

5 Numerical experiments

In order to evaluate the performance of the proposed algorithms, we present numerical examples relative to the variational inequalities. In this section, we provide some numerical experiments to demonstrate the convergence of our algorithms and compare the algorithms we proposed with the existing algorithms in [11, 21, 28]. The MATLAB codes are run on a PC (with Intel(R) Core(TM) i7-6700HQ CPU@2.60 GHz, 2.59 GHZ, RAM 16.0 GB) under MATLAB Version 9.2.0.538062 (R2017a) Service Pack 1, which contains Global optimization Toolbox version 3.4.2.

Example 5.1

We consider $VI(C,f)$ with the constraint set $C =\{x\in \mathbb{R}^{20}: \|x\|-5\leq 0\}$. Define $f: \mathbb{R}^{20}\rightarrow \mathbb{R}^{20}$ by

$$ f(x)=\biggl(2-\frac{1}{1+ \Vert x \Vert }\biggr)x.$$

In this case, we can verify that $x^{*}=0$ is the solution to $VI(C,f)$. We note that f is 1-strongly pseudomonotone and 4-Lipschitz continuous on $\mathbb{R}^{n}$ (See Example 3.3 [20]) and is not (strongly) monotone. It means that when the methods in [11, 28] are applied to solve Example 5.1, its iteration point sequence may not converge to the solution point.

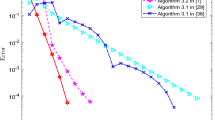
In the implementation of Algorithm 1, we take $\rho =0.5$, $\delta =0.1$, $\lambda _{-1}=0.5$. In the implementation of Algorithm 3.1 in [21], we set $\lambda =0.05$, $\delta =0.025$ and $\gamma =0.49$. Moreover, we choose $x^{0}=\frac{x^{T}}{\|x^{T}\|}$, $x^{-1}=\frac{x^{T}}{\|x^{T}\|}$ and $y^{-1}=0$ as the staring point for Algorithm 1, where $x^{T}=(1,1,\ldots ,1)^{T}$. We choose $x^{0}=\frac{x^{T}}{\|x^{T}\|}$, $x^{1}=\frac{x^{T}}{\|x^{T}\|}$ as the staring point for Algorithm 3.1 in [21]. The numerical results of Example 5.1 are shown in Fig. 1, which illustrate the sequence generated by Algorithm 1 is more efficient in comparison with Algorithm 3.1 in [21].

Figure 1

Comparison of the number of iterations of Algorithm 1 with algorithm in [21] for Example 5.1

Example 5.2

Consider variational inequality problems $VI(C,f)$. The constraint set $C=\{(x_{1},x_{2})\in \mathbb{R}^{2} : x_{1}^{2}+x_{2}^{2} \leq 100 \}$. Let $f: C\rightarrow \mathbb{R}^{2}$ be defined by $f(x)=(2x_{1}+2x_{2}+\sin(x_{1}),-2x_{1}+2x_{2}+\sin(x_{2}))^{T}$, $\forall x=(x_{1},x_{2})^{T}\in C$.

For Example 5.2, the following conclusions can be obtained from [6]:

• (1) F is 1-strongly monotone and $\sqrt{26}$-Lipschitz continuous mapping.

• (2) $x^{*}=(0,0)^{T}\in C$ is the unique solution to $VI(C,f)$.

In this example, we take $\rho =0.5$, $\delta =0.1$, $\lambda _{-1}=0.5$ for Algorithm 1,2; $\gamma =0.4$, $\delta =0.2$, $\lambda =0.05$ for Algorithm 3.1 in [21]; set $\lambda =\frac{1}{20}$, $\gamma =1$ and $\alpha _{k}=\frac{1}{k+1}$ for Algorithm 4.1 in [11]; set $\theta =0.25$, $\sigma =0.7$, $\gamma =0.6$ and $\alpha _{k}=\frac{1}{k+1}$ for Algorithm 3.3 in [28]. For Example 5.2, we choose $x^{0}=(-10,-12)^{T}$, $x^{-1}=(0,0)^{T}$, $y^{-1}=(-1,5)^{T}$ as the initial points for Algorithm 1 and Algorithm 2; $x^{1}=(-10,-12)^{T}$, $x^{0}=(0,0)^{T}$ as the initial points for [21, 28]; $x^{0}=(-10,-12)^{T}$ as the initial point for [11]. The numerical results of Example 5.2 are shown in Fig. 2 and have suggested that our algorithms are more efficient in comparison with existing algorithms such as the methods in [11, 21, 28].

Figure 2

Comparison of the number of iterations of Algorithm 1 and Algorithm 2 with algorithms in [11, 21, 28] for Example 5.2

Example 5.3

Consider $VI(C,f)$ with constraint set $C=\{x\in R^{m}: \|x\|^{2} -100\leq 0\}$. Define $f(x):\mathbb{R}^{m}\rightarrow \mathbb{R}^{m}$ by $f(x)=x+q$, where $q\in \mathbb{R}^{m}$.

It is easy to verify that f is 1-Lipschitz continuous and 1-strongly monotone mapping. Therefore, the variational inequality (1.1) has a unique solution. For $q = 0$, the solution set $\operatorname{SOL}(C, f) = \{0\}$. In our experiment, we take $m=100$.

In this example, we select the parameters $\rho =0.5$, $\delta =0.1$, $\lambda _{-1}=0.5$ for Algorithm 1 and Algorithm 2; $\gamma =0.49$, $\delta =0.2$, $\lambda =0.05$ for Algorithm 3.1 in [21]; $\lambda =1$, $\gamma =1$ and $\alpha _{k}=\frac{1}{k+1}$ for Algorithm 4.1 [11]; $\theta =0.25$, $\sigma =0.7$, $\gamma =0.6$ and $\alpha _{k}=\frac{1}{k+1}$ for Algorithm 3.3 [28]. We choose $x^{0}=x^{T}$, $x^{-1}=\frac{x^{T}}{\|x^{T}\|}$, $y^{-1}=(0,0,\ldots ,0)^{T}$ as the initial points for Algorithm 1 and Algorithm 2; $x^{1}=x^{T}$, $x^{0}=\frac{x^{T}}{\|x^{T}\|}$ as the initial points for [21, 28]; $x^{0}=x^{T}$ as the initial point for [11], where $x^{T}=(1,1,\ldots ,1)^{T}$. The numerical results of Example 5.3 are shown in Fig. 3, where it can be seen that the behavior of Algorithm 1 and Algorithm 2 is better than the algorithms in [11, 21, 28].

Figure 3

Comparison of the number of iterations of Algorithm 1 and Algorithm 2 with algorithms in [11, 21, 28] for Example 5.3