1 Introduction

In recent times, the fractional calculus has been extensively studied. There are many definitions for the fractional derivative operator. The Riemann–Liouville fractional derivative and the Caputo fractional derivative are two of the most often used definitions of the fractional derivatives. Recently, in the case the kernel has no singularities, Caputo and Fabrizio have introduced a new definition of the fractional derivatives [1]. Fractional calculus is a subject with a long history and has gained great interest in different fields of applied science, and many authors considered this topic [2–12]. For example, Alrefai and Abdeljawad in [13] studied the analysis for fractional diffusion equations with fractional derivative with non-singular kernel.

In this work, we restore the space source term problem for a fractional diffusion equation with a Caputo–Fabrizio derivative. The fractional diffusion equation is discussed in this paper as follows:

$$\begin{aligned} \textstyle\begin{cases} {}_{0}^{CF}\mathbb{D}_{t}^{\alpha } u + \mathscr{B} u = \mathcal{F}( \mathrm{x} ,t ), & \text{in } {\Omega } \times (0, T), \\ u(\mathrm{x},t) = 0, & \text{on } \partial {\Omega } \times (0,T), \\ u(\mathrm{x},0) = \mathrm{g}(\mathrm{x}), & \text{in } {\Omega } , \end{cases}\displaystyle \end{aligned}$$
(1.1)

where \(0< \alpha < 1\), \(T >0\) is a fixed value and \({\Omega } \in \mathbb{R}^{d}\) is a bounded domain with sufficient smooth boundary ∂Ω. \({}_{0}^{CF}\mathbb{D}_{t}^{\alpha } \) is the Caputo–Fabrizio operator for fractional derivatives of order α. From [14], we have the following formula:

$$\begin{aligned} {}_{0}^{CF}\mathbb{D}_{t}^{\alpha } v(t) = \frac{\mathcal{A}(\alpha )}{1- \alpha } \bigl( v^{(1)} \ast \widetilde{f} \bigr) (t), \qquad \widetilde{f}(t)= \exp \biggl( - \frac{\alpha }{1- \alpha } t \biggr), \quad t \in (0, \infty ), \end{aligned}$$

with ∗ defines the convolution and \(\mathcal{A}(\alpha )\) is a normalization function such that \(\mathcal{A}(0 ) = \mathcal{A}(1 ) = 1\).

For the spatial-fractional and temporal-fractional derivatives, there are a lot of new definitions to be presented. In [15–18], we can see more properties and applications of this new fractional derivative. In [19], the authors proved uniqueness of the solution to an initial value problem for linear fractional differential equation with \(1 < \alpha \le 2\).

The problem (1.1) is associated to anomalous diffusion phenomenon in physical motivations. In the case \(0 < \alpha < 1\), the model (1.1) is used for the super-diffusive model in heterogeneous media. Some physical background is found. For example, as regards the physical application of fractional calculus, the authors in [20] have shown that the fractional calculus is effective to account for the damping controllers which are compared to the classical derivative. The authors in [21] considered the separation and stability of solutions to nonlinear systems involving Caputo–Fabrizio derivatives.

Our purpose in this paper is to find an inversion source problem for (1.1). Assume that the source term \(\mathcal{F}(\mathrm{x} ,t )\) of the problem (1.1) is a forward problem, which can be split into \(\mathscr{F} (\mathrm{x}) Q(t)\) where \(Q(t)\) is known in advance. Hence, we want to identify the space source term \(\mathscr{F} (\mathrm{x} )\) by using the value of the final time T as follows:

$$\begin{aligned} \mathrm{u} (\mathrm{x}, T) = H (\mathrm{x}), \quad \mathrm{x} \in { \Omega }. \end{aligned}$$
(1.2)

In fact, the measurements are noised, instead of receiving the exact data H, we have the approximation data \(H ^{\varepsilon }\) that satisfies

$$\begin{aligned} \bigl\Vert H ^{\varepsilon } - H \bigr\Vert _{L^{2}(\Omega ) } \le \varepsilon , \end{aligned}$$
(1.3)

where \(\varepsilon > 0\) is the noise level. A small error between the given observation \(H^{\varepsilon }\) and the exact data \(H^{\varepsilon }\) leads to a large error in the solution in output data. This is a reason why we propose some regularization methods in order to recover stable approximations for the unknown space source function.

In this paper, we apply the fractional Landweber method and modified quasi-boundary value method to restore the unknown space source function \(\mathscr{F} \). The idea of the modified quasi-boundary value method mainly comes from Denche and Bessila’s paper [22], where they solved the following backward heat conduction problem. For references to this method, the reader can see [23–25]. In [26], Klann and Ramlau introduced the fractional Landweber method for a linear ill-posed problem. We give an a posteriori choice of the regularization parameter based on an a priori bound of the exact solution that cannot be known exactly in practice. Here, the regularization parameter by the a priori rule is easier than an a posteriori rule. For references to this method, the reader can see [27]. According to this work, we can compare which method is the more optimal for the space source term problem for the fractional diffusion equation with the Caputo–Fabrizio derivative.

The paper is organized as follows. In Sect. 2, we recall some preliminary results. The exact solution, the ill-posedness of the inverse problem and the conditional stability are also discussed in Sect. 2. In Sects. 3 and 4, we present a modified quasi-boundary value method and the fractional Landweber regularization method. The convergence estimate under an a priori assumption for the exact solution and the a posteriori regularization parameter choice rule are considered in here. In Sect. 5, we show a numerical example to illustrate the proposed method.

2 The solution and some notations

2.1 Some basic results

In this section, we recall some useful results. Let us consider the operator \(\mathscr{B} \) on the domain \(\mathcal{D}(-\mathscr{B} ):= \mathcal{H}_{0}^{1}(\Omega )\cap \mathcal{H}^{2}(\Omega )\). We assume that \(-\mathscr{B} \) has eigenvalues \(\lambda _{k} \) with the corresponding eigenfunction \(w_{k} \in \mathcal{D}(-\mathscr{B} ) \).

Note \(0 < \lambda _{1} \le \lambda _{2} \le \lambda _{3} \le \cdots \le \lambda _{k} \le \cdots \) and \(\lambda _{k} \to \infty \) as \(k \to \infty \). The negative Laplacian operator −Δ on \(\mathbb{X}\) is the most popular case of \(\mathscr{B} \). We have

$$ \textstyle\begin{cases} \mathscr{B} w_{k}(\mathrm{x}) = - \lambda _{k} w_{k}(\mathrm{x}) , & \mathtt{x} \in \Omega , \\ w_{k}(\mathtt{x} ) = 0, & \mathtt{x} \in \partial \Omega . \end{cases} $$

From [28], we see that \(\mathrm{a}_{k} \ge C k ^{\frac{2}{d}}\) for C is a constant and \(k \in \mathbb{N}\).

For all \(p \geq 0\), let us define the Hilbert scale spaces and fractional powers of \(\mathscr{B}\) as follows:

$$\begin{aligned}& \mathscr{B} ^{p} v := \textstyle\begin{cases} \sum_{k=1}^{\infty }\mathrm{a}_{k} ^{p} \langle v,w_{k}\rangle w_{k},& \text{if } p \neq 0 , \\ \sum_{k=1}^{\infty }\langle v,w_{k}\rangle w_{k}, & \text{if } p = 0, \end{cases}\displaystyle \end{aligned}$$
(2.1)
$$\begin{aligned}& \text{and} \quad v \in \mathcal{D}\bigl((-\mathscr{B} )^{p} \bigr): = \Biggl\{ v \in L^{2}(\Omega ) : \sum_{k=1}^{\infty }\mathrm{a}_{k} ^{2p} \bigl\vert \langle v, w_{k}\rangle \bigr\vert ^{2} < \infty \Biggr\} . \end{aligned}$$
(2.2)

And we have the following norm in the Banach space \(\mathcal{D}((-\mathscr{B} )^{p} )\):

$$ \Vert z \Vert _{\mathcal{D}((-\mathscr{B} )^{p} )} := \Biggl( \sum_{k=1}^{\infty } \mathrm{a}_{k} ^{2p} \bigl\vert \langle z,w_{k} \rangle \bigr\vert ^{2} \Biggr) ^{\frac{1}{2}},\quad z \in \mathcal{D}\bigl((- \mathscr{B} )^{p} \bigr). $$

It is easy to see that \(\| v \|_{\mathcal{D}((-\mathscr{B} )^{p} ) } = \| (-\mathscr{B} )^{p} v \|_{\mathcal{L}^{2}(\Omega ) }\). Its domain is a Hilbert space endowed \(\mathcal{D}((-\mathscr{B} )^{-p})\) with the dual inner product \(\langle \cdot,\cdot\rangle _{-p,p}\) taken between \(\mathcal{D}((-\mathscr{B} )^{-p})\) and \(\mathcal{D}((-\mathscr{B} )^{p})\). This generates the norm \(\| v \|_{\mathcal{D}((-\mathscr{B} )^{-p})}= ( \sum_{k=1}^{\infty }\mathrm{a}_{k} ^{-2p} \vert \langle v,w_{k} \rangle _{-p,p} \vert ^{2} ) ^{\frac{1}{2}} \). Now, we begin with the following two lemmas.

Lemma 2.1

([29, 30])

For \(0 < \mathtt{k} < 1\), \(\mathrm {q} > 0 \) and \(\mathtt{m} \in \mathbb{N}\), we obtain

$$\begin{aligned} (1 - \mathtt{k})^{\mathtt{m}} \mathtt{k} ^{\mathrm {q}} \le \mathrm {q}^{\mathrm {q}} (\mathtt{m} + 1) ^{-\mathrm {q}} < \mathrm {q}^{ \mathrm {q}} \mathtt{m} ^{-\mathrm {q}}. \end{aligned}$$

Lemma 2.2

For p, γ, \(\lambda _{1}\) be positive constant. Let G be a function defined by

$$\begin{aligned} G(z) = \frac{\gamma z^{2-p}}{\gamma z^{2} + \beta } ,\quad z>0, \end{aligned}$$
(2.3)

in which \({Z}_{1} = {Z}_{1}(p,\beta )\) and \({Z}_{2} = Z_{2}(p,\beta ,\lambda _{1} )\). Then we have the estimate

$$\begin{aligned} G(z) \le \textstyle\begin{cases} Z_{1}\gamma ^{\frac{p}{2}},& \textit{if } 0 < p < 2, \\ {Z}_{2} \gamma ,& \textit{if } p \ge 2, z \ge \lambda _{1}. \end{cases}\displaystyle \end{aligned}$$
(2.4)

Proof

See [23], Lemma 2.7. □

By taking the inner product of the main equation of (1.1) with \(w_{k}(x)\), we get the following equality:

$$\begin{aligned} {}_{0}^{CF}\mathbb{D}_{t}^{\alpha } u_{k} (t) - \lambda _{k} u_{k} (t) = \mathcal{F}_{k} (t), \qquad u_{k}(0) = \mathrm{g}_{k} = \langle \mathrm{g} , w_{k} \rangle , \qquad H_{k} = \langle H , w_{k} \rangle , \end{aligned}$$
(2.5)

where \(u_{k} (t) = \langle u(\cdot , t) , w_{k}(\cdot ) \rangle \), \(\mathcal{F}_{k} (t) = \langle \mathcal{F} (\cdot , t) , w_{k}( \cdot ) \rangle = Q (\tau ) \langle \mathscr{F} , w_{k} \rangle \) stand for its Fourier coefficient.

Thanks to [1], the Laplace transform of the Caputo–Fabrizio derivative has the following expression:

$$\begin{aligned} \mathcal{L} \bigl[ {}_{0}^{CF}\mathbb{D}_{t}^{\alpha } u(t) \bigr] = \frac{ h \mathcal{L} [u] (h) - u(0) }{h + \alpha (1-h)}, \quad h >0. \end{aligned}$$
(2.6)

We thus get \(\frac{ h \mathcal{L} [u_{k}] (h) - u_{k}(0) }{h + \alpha (1-h)} = \lambda _{k} \mathcal{L} [u_{k}] (h) + \mathcal{L} [\mathcal{F}_{k} ] (h) \). By \(\lambda _{k} > 0\) and \(\alpha \in (0,1)\), we obtain

$$ \mathcal{L} [u_{k}] (h) = \frac{1}{1 + \lambda _{k} (1- \alpha )} \biggl[ \frac{1}{h + \frac{ \lambda _{k} \alpha }{1 + \lambda _{k} (1- \alpha )} } \mathrm{g}_{k} + \frac{ \lambda _{k} \alpha }{1 + \lambda _{k} (1- \alpha )} \mathcal{L} [ \mathcal{F}_{k} ] (h) \biggr]. $$

Thanks to [31], we get

$$\begin{aligned} u_{k} (t) &= \frac{1}{1 + \lambda _{k} (1- \alpha )} \exp \biggl( - \frac{ \alpha \lambda _{k} t }{1 + \lambda _{k} (1- \alpha )} \biggr) \mathrm{g}_{k} \\ &\quad{}+ \frac{1}{1 + \lambda _{k} (1- \alpha )} \exp \biggl(- \frac{ \alpha \lambda _{k} t }{1 + \lambda _{k} (1- \alpha )} \biggr) \mathcal{F}_{k} (t). \end{aligned}$$
(2.7)

This implies that the solution of Problem (1.1) is given by the Fourier series

$$\begin{aligned} u(x,t) &= \sum_{k=1}^{\infty } \biggl[ \frac{1}{1 + \lambda _{k} (1- \alpha )} \exp \biggl( - \frac{\alpha \lambda _{k} t }{1 + \lambda _{k} (1- \alpha )} \biggr) \mathrm{g}_{k} \\ &\quad{}+ \frac{1}{1 + \lambda _{k} (1- \alpha )} \int _{0}^{t} \exp \biggl( - \frac{\alpha \lambda _{k} (t-s) }{1 + \lambda _{k} (1- \alpha )} \biggr) \mathcal{F}_{k} (s) \,\mathrm{d} s \biggr] w_{k}( \mathrm{x}) . \end{aligned}$$
(2.8)

By \(t= T\) in (2.7) and we get

$$\begin{aligned} H_{k} &= \frac{1}{1 + \lambda _{k} (1- \alpha )} \exp \biggl( - \frac{ \alpha \lambda _{k} t }{1 + \lambda _{k} (1- \alpha )} \biggr) \mathrm{g}_{k} \\ &\quad{}+ \frac{\mathscr{F}_{k}}{1 + \lambda _{k} (1- \alpha )} \int _{0}^{T} \exp \biggl( - \frac{ \alpha \lambda _{k} (t-s) }{1 + \lambda _{k} (1- \alpha )} \biggr) Q(s) \,\mathrm{d} s, \end{aligned}$$
(2.9)

where \(H_{k}= \langle H,w_{k}\rangle \), with \(k \in \mathbb{N}\).

Lemma 2.3

Let \(Q_{1} > 0\), and let \(Q\in C( [0,T ]; \mathbb{R} ) \) be a positive continuous function satisfy \(\inf_{t \in [0, T ]} | Q (t) |= Q_{1}\). Suppose that \(\| Q \|_{\infty } = \sup_{t \in [0,T ]}| Q (t)|\), then we have

$$\begin{aligned} K_{2, \alpha } (T, \lambda _{1}) \frac{Q_{1}}{ \lambda _{k}} &\le \frac{1}{1 + \lambda _{k} (1- \alpha )} \int _{0}^{T} \exp \biggl( - \frac{ \alpha \lambda _{k} (T-s) }{1 + \lambda _{k} (1- \alpha )} \biggr) Q (s) \,\mathrm{d} s \\ & \le K_{1, \alpha } (T) \frac{ \Vert Q \Vert _{\infty } }{\lambda _{k} }, \end{aligned}$$
(2.10)

for all \(k \in \mathbb{N}\).

Proof

First, we obtain

$$\begin{aligned} \frac{1}{1 + \lambda _{k} (1- \alpha )} \int _{0}^{T} \exp \biggl( - \frac{ \alpha \lambda _{k} (T-s) }{1 + \lambda _{k} (1- \alpha )} \biggr) Q (s) \,\mathrm{d} s \le K_{1, \alpha } (T) \frac{ \Vert Q \Vert _{\infty } }{\lambda _{k} }, \end{aligned}$$
(2.11)

where we noted that \(\exp ( - \frac{ \alpha \lambda _{k} (T-s) }{1 + \lambda _{k} (1- \alpha )} ) \le 1\) for \(\forall t \ge 0\), and \(K_{1, \alpha } (T) = \frac{T}{1 - \alpha }\). Otherwise, we also get

$$\begin{aligned} & \frac{1}{1 + \lambda _{k} (1- \alpha )} \int _{0}^{T} \exp \biggl( - \frac{ \alpha \lambda _{k} (T-s) }{1 + \lambda _{k} (1- \alpha )} \biggr) Q (s) \,\mathrm{d} s \\ &\quad = \frac{1}{1 + \lambda _{k} (1- \alpha )} \exp \biggl( - \frac{ \alpha \lambda _{k} T }{1 + \lambda _{k} (1- \alpha )} \biggr) \int _{0}^{T} \exp \biggl( \frac{ \alpha \lambda _{k} s }{1 + \lambda _{k} (1- \alpha )} \biggr) Q (s) \,\mathrm{d} s \\ &\quad \ge \frac{Q_{1}}{\alpha \lambda _{l}} \exp \biggl( - \frac{ \alpha \lambda _{k} T }{1 + \lambda _{k} (1- \alpha )} \biggr) \biggl( \exp \biggl( \frac{ \alpha \lambda _{k} T }{1 + \lambda _{l} (1- \alpha )} \biggr) - 1 \biggr). \end{aligned}$$

This implies that

$$\begin{aligned} & \frac{1}{1 + \lambda _{k} (1- \alpha )} \int _{0}^{T} \exp \biggl( - \frac{ \alpha \lambda _{k} (T-s) }{1 + \lambda _{k} (1- \alpha )} \biggr) Q (s) \,\mathrm{d} s \\ &\quad \ge \frac{Q_{1}}{\alpha \lambda _{k}} \biggl( 1- \exp \biggl( - \frac{ \alpha \lambda _{k} T }{1 + \lambda _{k} (1- \alpha )} \biggr) \biggr) \\ &\quad \ge K_{2, \alpha } (T, \lambda _{1}) \frac{Q_{1}}{ \lambda _{k}}, \end{aligned}$$

where \(K_{2, \alpha } (T, \lambda _{1}) = \frac{1}{\alpha } ( 1- \exp ( -\frac{ \alpha \lambda _{1} T }{1 + \lambda _{1} (1- \alpha )} ) ) \). □

2.2 Ill-posedness and stability estimates

For any \(v \in L^{2}(\Omega ) \), let \(R : L^{2}(\Omega ) \rightarrow L^{2}(\Omega ) \) be the following operator:

$$\begin{aligned} (R v) (\mathrm{x}) &:= \int _{\Omega } \kappa (\mathrm{y}, \mathrm{x}) v (\mathrm{y}) \,d \mathrm{y} \\ &= \sum_{k=1}^{\infty } \frac{1}{1 + \lambda _{k} (1- \alpha )} \int _{0}^{T} \exp \biggl( - \frac{ \alpha \lambda _{k} (T-s) }{1 + \lambda _{k} (1- \alpha )} \biggr) Q (s) \,\mathrm{d} s \bigl\langle v , w_{k}(\cdot ) \bigr\rangle w_{k}( \mathrm{x}), \end{aligned}$$

where the kernel \(\kappa (\cdot ,\cdot )\) satisfies

$$ \kappa (\mathrm{y}, \mathrm{x}) := \sum_{k=1}^{\infty } \frac{1}{1 + \lambda _{k} (1- \alpha )} \int _{0}^{T} \exp \biggl( - \frac{ \alpha \lambda _{k} (T-s) }{1 + \lambda _{k} (1- \alpha )} \biggr) Q (s) \,\mathrm{d} s w_{k}(\mathrm{y}) w_{k}( \mathrm{x}). $$

Since our problem is of finding \(\mathscr{F}\) which can be transform into \(R \mathscr{F} = P \) where \(P = \sum_{k=1}^{\infty } P_{k} w_{k}\), with \(P_{k} := H_{k} - \frac{1}{1 + \lambda _{k} (1- \alpha )} \exp ( - \frac{ \alpha \lambda _{k} t }{1 + \lambda _{k} (1- \alpha )} ) \mathrm{g}_{k}\), we write

$$\begin{aligned} \mathscr{F}_{k} = \frac{P_{k}}{\frac{1}{1 + \lambda _{k} (1- \alpha )} \int _{0}^{T} \exp ( - \frac{ \alpha \lambda _{k} (T-s) }{1 + \lambda _{k} (1- \alpha )} ) Q (s) \,\mathrm{d} s}. \end{aligned}$$
(2.12)

It is easy to see that \(R : L^{2}(\Omega ) \to L^{2}(\Omega ) \) is compact operator. It leads to the Problem (1.1) to be ill-posed. To show the ill-posedness of this problem, we propose an illustrative example. Assume that \(\mathrm{g} = 0\), we choose the final data \(H^{m} (\mathrm{x} ) = \frac{w_{m} (\mathrm{x} )}{\sqrt{\lambda _{m}}}\) then the corresponding source terms are

$$\begin{aligned} \mathscr{F}^{m} &= \sum_{k=1}^{\infty } \frac{P_{k} w_{k}(\mathrm{x})}{\frac{1}{1 + \lambda _{k} (1- \alpha )} \int _{0}^{T} \exp ( - \frac{ \alpha \lambda _{k} (T-s) }{1 + \lambda _{k} (1- \alpha )} ) Q (s) \,\mathrm{d} s} \\ &= \frac{1}{\frac{\sqrt{\lambda _{m}}}{1 + \lambda _{m} (1- \alpha )} \int _{0}^{T} \exp ( - \frac{ \alpha \lambda _{m} (T-s) }{1 + \lambda _{m} (1- \alpha )} ) Q (s) \,\mathrm{d} s} . \end{aligned}$$

Hence, we get \(\mathscr{F}^{m} \ge \frac{ \sqrt{\lambda _{m}} }{ \| Q \|_{\infty } K_{1, \alpha } (T)} \). This implies that \(\lim_{m \to \infty }\| \mathscr{F}^{m} (\mathrm{\cdot } ) \|_{L^{2}( \Omega ) } \to \infty \). But \(\| H^{m} \|_{L^{2}(\Omega )} = \frac{1}{\sqrt{\lambda _{m} }} \), or \(\lim_{m \to \infty }\| H ^{m} (\cdot ) \|_{L^{2}(\Omega ) } \to 0\). Therefore, the problem (1.1) satisfying (1.2) is ill-posed in the sense of Hadamard.

3 Modified quasi-boundary value method

In this section, we present a regularization method to solve our problem. Now, we study a quasi-boundary value method to solve problem (1.1) and give two convergence estimates under an a priori parameter choice rule, respectively. Applying the modified quasi-boundary value method given by [23], we propose the following regularized solution with exact data P:

$$\begin{aligned} \mathscr{F}_{\mathrm{n}(\varepsilon )} (\mathrm{x} ) = \sum _{k=1}^{ \infty } \frac{\langle P, w_{k} \rangle w_{k} }{ \lambda _{k}[\mathrm{n}(\varepsilon )] + \frac{1}{1 + \lambda _{k} (1- \alpha )} \int _{0}^{T} \exp ( - \frac{ \alpha \lambda _{k} (T-s) }{1 + \lambda _{k} (1- \alpha )} ) Q (s) \,\mathrm{d} s } \cdot \end{aligned}$$
(3.1)

We have the solution with the observation data \(H ^{\varepsilon } \),

$$\begin{aligned} \mathscr{F}_{\mathrm{n}(\varepsilon )}^{\varepsilon } (\mathrm{x} ) = \sum _{k=1}^{\infty } \frac{\langle P^{\varepsilon }, w_{k} \rangle w_{k} }{ \lambda _{k}[\mathrm{n}(\varepsilon )] + \frac{1}{1 + \lambda _{k} (1- \alpha )} \int _{0}^{T} \exp ( - \frac{ \alpha \lambda _{k} (T-s) }{1 + \lambda _{k} (1- \alpha )} ) Q (s) \,\mathrm{d} s }, \end{aligned}$$
(3.2)

here \(P^{\varepsilon } := H^{\varepsilon } - \sum_{k=1}^{\infty } ( \frac{1}{1 + \lambda _{k} (1- \alpha )} \exp ( - \frac{ \alpha \lambda _{k} T }{1 + \lambda _{k} (1- \alpha )} ) \mathrm{g}_{k} ) w_{k}(\mathrm{x} )\) and

$$\begin{aligned} \mathscr{F}(\mathrm{x} ) = \sum_{k=1}^{\infty } \frac{\langle P, w_{k} \rangle w_{k}}{\frac{1}{1 + \lambda _{k} (1- \alpha )} \int _{0}^{T} \exp ( - \frac{ \alpha \lambda _{k} (T-s) }{1 + \lambda _{k} (1- \alpha )} ) Q (s) \,ds} \cdot \end{aligned}$$
(3.3)

Afterwards, we will give an error estimation for \(\|\mathscr{F}(\cdot )-\mathscr{F}_{n(\varepsilon )}^{\varepsilon }( \cdot ) \|_{L^{2}({ \Omega })}\) and show the convergence rate under a suitable choice for the regularization parameter.

Theorem 3.1

Let \(H \in L^{2}(\Omega ) \) and \(Q: [0,T ] \to \mathbb{R}\) for all \(t \in [0,T ]\). Assume that the a priori bound condition \(\| \mathscr{F} \|_{\mathcal{D}((-\mathscr{B} )^{p} ) } \le \mathcal{M}\) and the assumption (1.3) holds.

If we choose the regularization parameter

$$\mathrm{n}(\varepsilon ) = \textstyle\begin{cases} \lfloor ( \frac{\varepsilon }{\mathcal{M}} )^{ \frac{2}{p+1}} \rfloor , &0 < p < 2, \\ \lfloor (\frac{\varepsilon }{\mathcal{M}} )^{\frac{2}{3}} \rfloor , &p \ge 2, \end{cases} $$

then we get

$$\begin{aligned} & \bigl\Vert \mathscr{F}_{\mathrm{n}(\varepsilon )} ^{\varepsilon } ( \cdot ) - \mathscr{F} ( \cdot ) \bigr\Vert _{L^{2}(\Omega ) } \\ &\quad \le \textstyle\begin{cases} ( ( 2^{-1} [ K_{2, \alpha } (T, \lambda _{1})Q_{1} ]^{- \frac{1}{2}} ) + Z_{1} ) \mathcal{M}^{\frac{1}{p+1}} \varepsilon ^{\frac{p}{p+1}},& \textit{if } 0 < p < 2, \\ ( ( 2^{-1} [ K_{2,\alpha } (T, \lambda _{1})Q_{1} ]^{- \frac{1}{2}} ) + Z_{2} ) \mathcal{M}^{\frac{1}{3}} \varepsilon ^{\frac{2}{3}},& \textit{if } p \ge 2. \end{cases}\displaystyle \end{aligned}$$

Proof

Using the triangle inequality, we get

$$\begin{aligned} \bigl\Vert \mathscr{F}_{\mathrm{n}(\varepsilon )} ^{\varepsilon } ( \cdot ) - \mathscr{F} ( \cdot ) \bigr\Vert _{L^{2}(\Omega ) } \le \bigl\Vert \mathscr{F}_{ \mathrm{n}(\varepsilon )}^{\varepsilon } ( \cdot ) - \mathscr{F}_{ \mathrm{n}(\varepsilon )} ( \cdot ) \bigr\Vert _{L^{2}(\Omega ) } + \bigl\Vert \mathscr{F}_{\mathrm{n}(\varepsilon )} ( \cdot ) - \mathscr{F} ( \cdot ) \bigr\Vert _{L^{2}(\Omega ) }. \end{aligned}$$
(3.4)

First, we give an estimate for the first term \(\| \mathscr{F}_{\mathrm{n}(\varepsilon )} ^{\varepsilon } ( \cdot ) - \mathscr{F}_{\mathrm{n}(\varepsilon )} ( \cdot ) \|_{L^{2}( \Omega ) }\), then we get

$$\begin{aligned} &\bigl\Vert \mathscr{F}_{\mathrm{n}(\varepsilon )}^{\varepsilon } ( \cdot ) - \mathscr{F}_{\mathrm{n}(\varepsilon )} ( \cdot ) \bigr\Vert ^{2}_{L^{2}( \Omega ) } \\ &\quad = \sum_{k=1}^{\infty } \frac{ \vert \langle P^{\varepsilon } - P, w_{k} \rangle \vert ^{2} }{ ( \lambda _{k}[\mathrm{n}(\varepsilon )] + \frac{1}{1 + \lambda _{k} (1- \alpha )} \int _{0}^{T} \exp ( - \frac{ \alpha \lambda _{k} (T-s) }{1 + \lambda _{k} (1- \alpha )} ) Q (s) \,\mathrm{d} s )^{2}} \\ &\quad \le \sup_{k \geq 1} \biggl( \frac{1}{ \lambda _{k} \mathrm{n}(\varepsilon ) + K_{2, \alpha } (T, \lambda _{1}) \frac{Q_{1}}{ \lambda _{k}} } \biggr)^{2} \bigl\Vert P^{\varepsilon } - P \bigr\Vert ^{2}_{L^{2}(\Omega ) } \le \sup_{k \geq 1 } \bigl( \mathscr{A}^{2}_{k} \bigr) \varepsilon ^{2}. \end{aligned}$$
(3.5)

From (3.5), applying Lemma 2.3 and the inequality \((a + b) \geq 2 \sqrt{ab}\), \(\forall a,b \geq 0\), then we obtain

$$\begin{aligned} \mathscr{A}^{2}_{k} = \biggl( \frac{1}{ \lambda _{k} \mathrm{n}(\varepsilon ) + K_{2, \alpha } (T, \lambda _{1}) \frac{Q_{1}}{ \lambda _{k}} } \biggr)^{2} \leq \frac{1}{4 \mathrm{n}(\varepsilon ) K_{2, \alpha } (T, \lambda _{1})Q_{1} } \cdot \end{aligned}$$
(3.6)

Substituting (3.6) into (3.5), we have

$$\begin{aligned} \bigl\Vert \mathscr{F}_{\mathrm{n}(\varepsilon )}^{\varepsilon } & ( \cdot ) - \mathscr{F}_{\mathrm{n}(\varepsilon )} ( \cdot ) \bigr\Vert _{L^{2}( \Omega ) } \leq \frac{\varepsilon }{\sqrt{\mathrm{n}(\varepsilon )}} \bigl( 2^{-1} \bigl[ K_{2, \alpha } (T, \lambda _{1})Q_{1} \bigr]^{-\frac{1}{2}} \bigr). \end{aligned}$$
(3.7)

On the other hand, we estimate the second term \(\| \mathscr{F}_{\mathrm{n}(\varepsilon )} ( \cdot ) - \mathscr{F} ( \cdot ) \|_{L^{2}(\Omega ) }\), for brevity, we put \(\mathscr{V}_{k,\alpha }(Q,T,s) = \frac{1}{1 + \lambda _{k} (1- \alpha )} \int _{0}^{T} \exp ( - \frac{ \alpha \lambda _{k} (T-s) }{1 + \lambda _{k} (1- \alpha )} ) Q (s) \,\mathrm{d} s\). From (3.3) and (3.1), we obtain

$$\begin{aligned} \mathscr{F}_{\mathrm{n}(\varepsilon )} (x) - \mathscr{F} (x) = \sum _{k=1}^{ \infty } \biggl( \frac{\lambda _{k} \mathrm{n}(\varepsilon ) }{ \mathscr{V}_{k,\alpha }(Q,T,s) (\lambda _{k} \mathrm{n}(\varepsilon ) + \mathscr{V}_{k,\alpha }(Q,T,s) )} \biggr) \langle P, w_{k} \rangle w_{k} \cdot \end{aligned}$$
(3.8)

Using the a priori bound condition \(\| \mathscr{F} \|_{\mathcal{D}((-\mathscr{B} )^{p} ) } \le \mathcal{M,}\) from (3.8), we show that

$$\begin{aligned} \bigl\Vert \mathscr{F}_{\mathrm{n}(\varepsilon )} (\cdot ) - \mathscr{F} ( \cdot ) \bigr\Vert ^{2}_{L^{2}(\Omega ) } &= \sum _{k=1}^{ \infty } \biggl( \frac{ \vert < P, w_{k} > \vert }{\mathscr{V}_{k,\alpha }(Q,T,s)} \biggr)^{2} \lambda _{k}^{2p} \biggl( \frac{\lambda _{k}\mathrm{n}(\varepsilon )}{\lambda _{k} \mathrm{n}(\varepsilon ) + \mathscr{V}_{k,\alpha }(Q,T,s)} \biggr)^{2} \lambda _{k}^{-2p} \\ &\leq \mathcal{M} \sup_{k \geq 1} (\mathcal{B}_{k} )^{2}, \end{aligned}$$
(3.9)

in which

$$\begin{aligned} \mathcal{B}_{k} = \frac{\lambda _{k}^{1-p}\mathrm{n}(\varepsilon )}{\lambda _{k} \mathrm{n}(\varepsilon ) + \mathscr{V}_{k,\alpha }(Q,T,s)} \leq \frac{n(\varepsilon ) \lambda _{k}^{2-p} }{ n(\varepsilon ) \lambda _{k}^{2} + K_{2,\alpha }(T,\lambda _{1}) Q_{1} }. \end{aligned}$$
(3.10)

From (3.10), applying the Lemma 2.2, by replacing \(\beta = K_{2, \alpha } (T, \lambda _{1})Q_{1} \) and \(\gamma = \mathrm{n}(\varepsilon )\), we can find that

$$\begin{aligned} \sup_{k \in \mathbb{N}}\mathcal{B}_{k} \leq \textstyle\begin{cases} Z_{1} [n(\varepsilon ) ]^{\frac{p}{2}}, & \text{if } 0 < p < 2, \\ Z_{2} [\mathrm{n}(\varepsilon ) ],& \text{if } p \ge 2. \end{cases}\displaystyle \end{aligned}$$
(3.11)

Combining (3.4) to (3.11), it gives

$$\begin{aligned} & \bigl\Vert \mathscr{F}_{\mathrm{n}(\varepsilon )} ^{\varepsilon } ( \cdot ) - \mathscr{F} ( \cdot ) \bigr\Vert _{L^{2}(\Omega ) } \\ &\quad \leq \frac{\varepsilon }{\sqrt{\mathrm{n}(\varepsilon )}} \bigl( 2^{-1} \bigl[ K_{2, \alpha } (T, \lambda _{1})Q_{1} \bigr]^{-\frac{1}{2}} \bigr) + \textstyle\begin{cases} Z_{1} [n(\varepsilon ) ]^{\frac{p}{2}},& \text{if } 0 < p < 2, \\ Z_{2} [\mathrm{n}(\varepsilon ) ],& \text{if } p \ge 2. \end{cases}\displaystyle \end{aligned}$$
(3.12)

By choosing the regularization parameter \(\mathrm{n}(\varepsilon )\) as follows:

$$\begin{aligned} \mathrm{n}(\varepsilon ) = \textstyle\begin{cases} (\frac{\varepsilon }{\mathcal{M}} )^{\frac{2}{p+1}}, & \text{if } 0 < p < 2, \\ (\frac{\varepsilon }{\mathcal{M}} )^{\frac{2}{3}},& \text{if } p \ge 2, \end{cases}\displaystyle \end{aligned}$$
(3.13)

we conclude that

$$\begin{aligned} & \bigl\Vert \mathscr{F}_{\mathrm{n}(\varepsilon )} ^{\varepsilon } ( \cdot ) - \mathscr{F} ( \cdot ) \bigr\Vert _{L^{2}(\Omega ) } \\ &\quad \leq \textstyle\begin{cases} ( ( 2^{-1} [ K_{2, \alpha } (T, \lambda _{1})Q_{1} ]^{- \frac{1}{2}} ) + Z_{1} ) \mathcal{M}^{\frac{1}{p+1}} \varepsilon ^{\frac{p}{p+1}}, & \text{if } 0 < p < 2, \\ ( ( 2^{-1} [ K_{2,\alpha } (T, \lambda _{1})Q_{1} ]^{- \frac{1}{2}} ) + Z_{2} ) \mathcal{M}^{\frac{1}{3}} \varepsilon ^{\frac{2}{3}},& \text{if } p \ge 2. \end{cases}\displaystyle \end{aligned}$$
(3.14)

The proof is finished. □

4 Fractional Landweber regularization method and convergence rate

In this section, we propose a fractional Landweber regularization method to solve the ill-posed problem (1.1) satisfying (1.2). The convergence rates for the regularized solution under two parameter choice rules are also considered.

From [32], \(R \mathscr{F} = P \) is equivalent to

$$\begin{aligned} \mathscr{F} = \bigl( I - \mathrm{c} R^{*}R \bigr) \mathscr{F} + \mathrm{c} R^{*} P , \quad \text{for any } \mathrm{c} > 0, \end{aligned}$$
(4.1)

where \(0 < \mathrm{c} < \Vert R \Vert ^{-2}\) and \(R^{*}\) is the adjoint operator of R.

Applying the fractional Landweber method given by [26], we propose the regularized solution with exact data H as follows:

$$\begin{aligned} &\mathscr{F}_{\mathrm{n} ,\chi } (\mathrm{x}) \\ &\quad = \sum_{k=1}^{\infty } \frac{ [ 1 - ( 1 - \mathrm{c} [ \frac{1}{1 + \lambda _{k} (1- \alpha )} \int _{0}^{T} \exp ( - \frac{ \alpha \lambda _{k} (T-s) }{1 + \lambda _{k} (1- \alpha )} ) Q (s) \,\mathrm{d} s ]^{2} )^{\mathrm{n}} ] ^{ \chi }}{\frac{1}{1 + \lambda _{k} (1- \alpha )} \int _{0}^{T} \exp ( - \frac{ \alpha \lambda _{k} (T-s) }{1 + \lambda _{k} (1- \alpha )} ) Q (s) \,\mathrm{d} s } \langle P, w_{k} \rangle w_{k}. \end{aligned}$$

We have the solution with the observation data noised \(H ^{\varepsilon } \) as follows:

$$\begin{aligned} &\mathscr{F}_{\mathrm{n} ,\chi } ^{\varepsilon } (\mathrm{x}) \\ &\quad = \sum_{k=1}^{\infty } \frac{ [ 1 - ( 1 - \mathrm{c} [ \frac{1}{1 + \lambda _{k} (1- \alpha )} \int _{0}^{T} \exp ( - \frac{ \alpha \lambda _{k} (T-s) }{1 + \lambda _{k} (1- \alpha )} ) Q (s) \,\mathrm{d} s ]^{2} )^{\mathrm{n}} ] ^{ \chi }}{\frac{1}{1 + \lambda _{k} (1- \alpha )} \int _{0}^{T} \exp ( - \frac{ \alpha \lambda _{k} (T-s) }{1 + \lambda _{k} (1- \alpha )} ) Q (s) \,\mathrm{d} s } \bigl\langle P^{\varepsilon }, w_{k} \bigr\rangle w_{k}, \end{aligned}$$

here \(P^{\varepsilon } := H^{\varepsilon } - \sum_{k=1}^{\infty } ( \frac{1}{1 + \lambda _{k} (1- \alpha )} \exp ( - \frac{ \alpha \lambda _{k} T }{1 + \lambda _{k} (1- \alpha )} ) \mathrm{g}_{k} ) w_{k}(\mathrm{x} )\), \(\chi \in ( \frac{1}{2}, 1 ] \) is the fractional order, and \(\mathrm{n} > 0 \) is the iterative step and is a regularization parameter. Here, we note that when \(\chi = 1\), the fractional Landweber method becomes a standard Landweber regularization.

Lemma 4.1

Let \(\lambda _{k} >0 \), \(\chi \in (\frac{1}{2},1]\), \(\mathrm{n} > 0\) and \(0 < \mathrm{c} [ \frac{1}{1 + \lambda _{k} (1- \alpha )} \int _{0}^{T} \exp ( - \frac{ \alpha \lambda _{k} (T-s) }{1 + \lambda _{k} (1- \alpha )} ) Q (s) \,\mathrm{d} s ]^{2} < 1\), we obtain

$$\begin{aligned} \sup_{k \geq 1} \frac{ [ 1 - ( 1 - \mathrm{c} [ \frac{1}{1 + \lambda _{k} (1- \alpha )} \int _{0}^{T} \exp ( - \frac{ \alpha \lambda _{k} (T-s) }{1 + \lambda _{k} (1- \alpha )} ) Q (s) \,\mathrm{d} s ]^{2} )^{\mathrm{n}} ] ^{ \chi }}{\frac{1}{1 + \lambda _{k} (1- \alpha )} \int _{0}^{T} \exp ( - \frac{ \alpha \lambda _{k} (T-s) }{1 + \lambda _{k} (1- \alpha )} ) Q (s) \,\mathrm{d} s } \le \mathrm{c} ^{\frac{1}{2}} \mathrm{n} ^{\frac{1}{2}} . \end{aligned}$$
(4.2)

Proof

First, we define \(\vartheta (z) := z^{-2} [ 1 - ( 1 - z^{2})^{\mathrm{n} } ]^{2 \chi } \), where

$$ z^{2} := \mathrm{c} \biggl[ \frac{1}{1 + \lambda _{k} (1- \alpha )} \int _{0}^{T} \exp \biggl( - \frac{ \alpha \lambda _{k} (T-s) }{1 + \lambda _{k} (1- \alpha )} \biggr) Q (s) \,\mathrm{d} s \biggr]^{2}. $$

It is easy to see that the function \(\vartheta (z)\) is continuous in \([0, + \infty )\) when \(z \in (0,1)\) and

$$\begin{aligned} \frac{ [ 1 - ( 1 - \mathrm{c} [ \frac{1}{1 + \lambda _{k} (1- \alpha )} \int _{0}^{T} \exp ( - \frac{ \alpha \lambda _{k} (T-s) }{1 + \lambda _{k} (1- \alpha )} ) Q (s) \,\mathrm{d} s ]^{2} )^{\mathrm{n}} ] ^{ \chi }}{\frac{1}{1 + \lambda _{k} (1- \alpha )} \int _{0}^{T} \exp ( - \frac{ \alpha \lambda _{k} (T-s) }{1 + \lambda _{k} (1- \alpha )} ) Q (s) \,\mathrm{d} s } = \mathrm{c} ^{\frac{1}{2}} \vartheta ^{2} (z). \end{aligned}$$

For \(\chi \in (\frac{1}{2},1]\) and \(z \in (0,1)\), applying Lemma 3.3 of [26] we get \(\vartheta (z) \le \mathrm{n} \). That infers the inequality (4.2) is correct. □

4.1 A priori parameter choice rule and convergence estimate

Let us choose \(\mathrm{n} := \mathrm{n} (\varepsilon )\) such that \(\| \mathscr{F}_{\mathrm{n} ,\chi } ^{\varepsilon } ( \cdot ) - \mathscr{F} ( \cdot ) \|_{L^{2}(\Omega ) } \to 0\) as \(\varepsilon \to 0\). Using an a priori regularization parameter choice rule, we propose the convergent rate for the fractional Landweber regularized solution \(\mathscr{F}_{\mathrm{n} ,\chi } ^{\varepsilon } \) to the exact solution \(\mathscr{F} \). In order to give an error estimate, we assume that \(\| \mathscr{F} \|_{\mathcal{D}((-\mathscr{B} )^{p} ) } \le \mathcal{M}\). Our result holds for any \(p \ge 0\), where \(\mathcal{M}\) is a positive constant and \(\mathscr{F}\) is recalled in (2.12).

Theorem 4.2

Let \(H \in L^{2}(\Omega ) \) and \(Q: [0,T ] \to \mathbb{R}\) for all \(t \in [0,T ]\). Assume that the a priori bound condition \(\| \mathscr{F} \|_{\mathcal{D}((-\mathscr{B} )^{p} ) } \le \mathcal{M}\) and the assumption (1.3) holds.

If we choose the regularization parameter

$$\mathrm{n} = \textstyle\begin{cases} \lfloor ( \frac{\mathcal{M}}{\varepsilon } )^{ \frac{2}{p + 1 }} \rfloor , &0 < p < 2, \\ \lfloor (\frac{\mathcal{M}}{\varepsilon } )^{\frac{2}{3}} \rfloor , &p \ge 2, \end{cases} $$

then we get

$$\begin{aligned} & \bigl\Vert \mathscr{F}_{\mathrm{n} ,\chi } ^{\varepsilon } ( \cdot ) - \mathscr{F} ( \cdot ) \bigr\Vert _{L^{2}(\Omega ) } \\ &\quad \le \textstyle\begin{cases} ( \mathrm{c} + ( \mathrm{c} [ K_{2, \alpha } (T, \lambda _{1}) Q_{1} ]^{2} )^{-\frac{p}{2}} ( \frac{p}{2} )^{ \frac{p}{2}} ) \mathcal{M}^{\frac{1}{p + 1 }} \varepsilon ^{ \frac{p}{p + 1 }}, &0 < p < 2, \\ ( \mathrm{c} + \mathrm{c} [ K_{2, \alpha } (T, \lambda _{1}) Q_{1} ]^{2} ) \mathcal{M}^{\frac{1}{3 }} \varepsilon ^{\frac{2}{3 }} , &p \ge 2. \end{cases}\displaystyle \end{aligned}$$

Proof

From the triangle inequality, we obtain

$$\begin{aligned} \bigl\Vert \mathscr{F}_{\mathrm{n} ,\chi } ^{\varepsilon } ( \cdot ) - \mathscr{F} ( \cdot ) \bigr\Vert _{L^{2}(\Omega ) } \le \bigl\Vert \mathscr{F}_{ \mathrm{n} ,\chi } ^{\varepsilon } ( \cdot ) - \mathscr{F}_{ \mathrm{n} ,\chi } ( \cdot ) \bigr\Vert _{L^{2}(\Omega ) } + \bigl\Vert \mathscr{F}_{\mathrm{n}, \chi } ( \cdot ) - \mathscr{F} ( \cdot ) \bigr\Vert _{L^{2}( \Omega ) }. \end{aligned}$$
(4.3)

Firstly, we give an estimate for the first term \(\| \mathscr{F}_{\mathrm{n} ,\chi } ^{\varepsilon } ( \cdot ) - \mathscr{F}_{\mathrm{n} ,\chi } ( \cdot ) \|_{L^{2}(\Omega ) }\). Applying Lemma 4.1, then we get

$$\begin{aligned} & \bigl\Vert \mathscr{F}_{\mathrm{n} ,\chi } ^{\varepsilon } ( \cdot ) - \mathscr{F}_{\mathrm{n} ,\chi } ( \cdot ) \bigr\Vert _{L^{2}(\Omega ) } \\ &\quad = \Biggl( \sum_{k=1}^{\infty } \frac{ [ 1 - ( 1 - \mathrm{c} [ \frac{1}{1 + \lambda _{k} (1- \alpha )} \int _{0}^{T} \exp ( - \frac{ \alpha \lambda _{k} (T-s) }{1 + \lambda _{k} (1- \alpha )} ) Q (s) \,\mathrm{d} s ]^{2} )^{\mathrm{n}} ] ^{ 2\chi }}{ ( \frac{1}{1 + \lambda _{k} (1- \alpha )} \int _{0}^{T} \exp ( - \frac{ \alpha \lambda _{k} (T-s) }{1 + \lambda _{k} (1- \alpha )} ) Q (s) \,\mathrm{d} s )^{2} } \bigl\vert \bigl\langle P^{\varepsilon } - P, w_{k} \bigr\rangle \bigr\vert \Biggr)^{\frac{1}{2}} \\ &\quad \le \sup_{k \ge 1 } \frac{ [ 1 - ( 1 - \mathrm{c} [ \frac{1}{1 + \lambda _{k} (1- \alpha )} \int _{0}^{T} \exp ( - \frac{ \alpha \lambda _{k} (T-s) }{1 + \lambda _{k} (1- \alpha )} ) Q (s) \,\mathrm{d} s ]^{2} )^{\mathrm{n}} ] ^{ \chi }}{\frac{1}{1 + \lambda _{k} (1- \alpha )} \int _{0}^{T} \exp ( - \frac{ \alpha \lambda _{k} (T-s) }{1 + \lambda _{k} (1- \alpha )} ) Q (s) \,\mathrm{d} s } \bigl\Vert P^{\varepsilon } - P \bigr\Vert _{L^{2}(\Omega ) } \\ &\quad \le \mathrm{c} ^{ \frac{1}{2}} \mathrm{n} ^{\frac{1}{2}} \varepsilon . \end{aligned}$$
(4.4)

Next, we estimate the second term,

$$\begin{aligned} & \bigl\Vert \mathscr{F}_{\mathrm{n}, \chi } ( \cdot )- \mathscr{F} ( \cdot ) \bigr\Vert _{L^{2}(\Omega ) } \\ &\quad = \Biggl\Vert \sum_{k=1}^{\infty } \frac{ 1 - [ 1 - ( 1 - \mathrm{c} [ \frac{1}{1 + \lambda _{k} (1- \alpha )} \int _{0}^{T} \exp ( - \frac{ \alpha \lambda _{k} (T-s) }{1 + \lambda _{k} (1- \alpha )} ) Q (s) \,\mathrm{d} s ]^{2} )^{\mathrm{n}} ] ^{ \chi }}{\frac{1}{1 + \lambda _{k} (1- \alpha )} \int _{0}^{T} \exp ( - \frac{ \alpha \lambda _{k} (T-s) }{1 + \lambda _{k} (1- \alpha )} ) Q (s) \,\mathrm{d} s } \langle P, w_{k} \rangle w_{k} \Biggr\Vert _{L^{2}(\Omega ) } . \end{aligned}$$
(4.5)

Because \(\chi \in ( \frac{1}{2}, 1 ] \), we thus get

$$\begin{aligned} & \bigl\Vert \mathscr{F}_{\mathrm{n}, \chi } ( \cdot ) - \mathscr{F} ( \cdot ) \bigr\Vert _{L^{2}(\Omega ) } \\ &\quad \le \Biggl\Vert \sum_{k=1}^{\infty } \biggl( 1 - \mathrm{c} \biggl[ \frac{1}{1 + \lambda _{k} (1- \alpha )} \int _{0}^{T} \exp \biggl( - \frac{ \alpha \lambda _{k} (T-s) }{1 + \lambda _{k} (1- \alpha )} \biggr) Q (s) \,\mathrm{d} s \biggr]^{2} \biggr)^{\mathrm{n}} \langle \mathscr{F}, w_{k} \rangle w_{k} \Biggr\Vert _{L^{2}(\Omega ) }. \end{aligned}$$

Lemma 2.3 now shows that

$$\begin{aligned} \bigl\Vert \mathscr{F}_{\mathrm{n}, \chi } ( \cdot ) - \mathscr{F} ( \cdot ) \bigr\Vert _{L^{2}(\Omega ) } &\le \Biggl\Vert \sum_{k=1}^{\infty } \biggl( 1 - \mathrm{c} \biggl[ K_{2, \alpha } (T, \lambda _{1}) \frac{Q_{1}}{ \lambda _{k}} \biggr]^{2} \biggr)^{\mathrm{n}} \langle \mathscr{F}, w_{k} \rangle w_{k} \Biggr\Vert _{L^{2}(\Omega ) } \\ &\le \Biggl( \sum_{k=1}^{\infty } \biggl( 1 - \mathrm{c} \biggl[ K_{2, \alpha } (T, \lambda _{1}) \frac{Q_{1}}{ \lambda _{k}} \biggr]^{2} \biggr)^{2\mathrm{n}} \lambda _{k}^{2p} \lambda _{k}^{-2p} \bigl\vert \langle \mathscr{F}, w_{k} \rangle \bigr\vert ^{2} \Biggr)^{\frac{1}{2}} \\ &\le \sup_{ k \ge 1 } \biggl( \biggl( 1 - \mathrm{c} \biggl[ K_{2, \alpha } (T, \lambda _{1}) \frac{Q_{1}}{ \lambda _{k}} \biggr]^{2} \biggr)^{ \mathrm{n}} \lambda _{k}^{-p} \biggr) \Biggl( \sum_{k=1}^{\infty } \lambda _{k}^{2p} \bigl\vert \langle \mathscr{F}, w_{k} \rangle \bigr\vert ^{2} \Biggr)^{ \frac{1}{2}} . \end{aligned}$$

Hence, we see that

$$\begin{aligned} \bigl\Vert \mathscr{F}_{\mathrm{n} ,\chi } ^{\varepsilon } ( \cdot ) - \mathscr{F} ( \cdot ) \bigr\Vert _{L^{2}(\Omega ) } \le \mathrm{c} ^{ \frac{1}{2}} \mathrm{n} ^{\frac{1}{2}} \varepsilon + \bigl( \mathrm{c} \bigl[ K_{2, \alpha } (T, \lambda _{1}) Q_{1} \bigr]^{2} \bigr)^{-\frac{p}{2}} \biggl( \frac{p}{2} \biggr)^{\frac{p}{2}} \mathrm{n}^{-\frac{p}{2}} \mathcal{M}. \end{aligned}$$

Choose the regularization parameter

$$\mathrm{n} = \textstyle\begin{cases} \lfloor ( \frac{\mathcal{M}}{\varepsilon } )^{ \frac{2}{p + 1 }} \rfloor , &0 < p < 2, \\ \lfloor (\frac{\mathcal{M}}{\varepsilon } )^{\frac{2}{3}} \rfloor , &p \ge 2, \end{cases} $$

then we get

$$\begin{aligned} & \bigl\Vert \mathscr{F}_{\mathrm{n} ,\chi } ^{\varepsilon } ( \cdot ) - \mathscr{F} ( \cdot ) \bigr\Vert _{L^{2}(\Omega ) } \\ &\quad \le \textstyle\begin{cases} ( \mathrm{c} + ( \mathrm{c} [ K_{2, \alpha } (T, \lambda _{1}) Q_{1} ]^{2} )^{-\frac{p}{2}} ( \frac{p}{2} )^{ \frac{p}{2}} ) \mathcal{M}^{\frac{1}{p + 1 }} \varepsilon ^{ \frac{p}{p + 1 }}, &0 < p < 2, \\ ( \mathrm{c} + \mathrm{c} [ K_{2, \alpha } (T, \lambda _{1}) Q_{1} ]^{2} ) \mathcal{M}^{\frac{1}{3 }} \varepsilon ^{\frac{2}{3 }} , &p \ge 2. \end{cases}\displaystyle \end{aligned}$$

This ends the proof. □

4.2 A posteriori parameter choice rule and convergence estimate

Now, based on Morozov’s discrepancy principle [33], we consider the choice of the a posterior regularization. Let us choose the regularization parameter n such that

$$\begin{aligned} \bigl\Vert R \mathscr{F}_{\mathrm{n} ,\chi } ^{\varepsilon } - P ^{ \varepsilon } \bigr\Vert _{L^{2}(\Omega ) } \le \mu \varepsilon \le \bigl\Vert R \mathscr{F}_{\mathrm{n}-1 ,\chi } ^{\varepsilon } - P ^{ \varepsilon } \bigr\Vert _{L^{2}(\Omega ) }, \end{aligned}$$
(4.6)

where \(\| P^{\varepsilon } \|_{L^{2}(\Omega ) } \ge \mu \varepsilon >0 \). Choosing \(\mu > 1\) and the bound for n is given and depends on ε and \(\mathcal{M}\).

Theorem 4.3

If n satisfies (4.6), we can get the following inequality:

$$\begin{aligned} \mathrm{n} \le \frac{p +1}{2 \mathrm{c} K_{2, \alpha }^{2} (T, \lambda _{1}) Q_{1}^{2} } \biggl( \frac{ \mathcal{M} K_{1, \alpha } (T) \Vert Q \Vert _{\infty }}{ ( \mu - 1) \varepsilon } \biggr)^{\frac{2}{p+1}}. \end{aligned}$$
(4.7)

Then we have the following estimations

• If \(0 < p < 1\) then

$$\begin{aligned} \bigl\Vert \mathscr{F}_{\mathrm{n} ,\chi } ^{\varepsilon } ( \cdot ) - \mathscr{F} ( \cdot ) \bigr\Vert _{L^{2}(\Omega ) } &\le \biggl[ \biggl( \frac{p +1}{2 K_{2, \alpha }^{2} (T, \lambda _{1}) Q_{1}^{2} } \biggr)^{ \frac{1}{2}} \biggl( \frac{ K_{1, \alpha } (T) \Vert Q \Vert _{\infty }}{ ( \mu - 1) } \biggr)^{ \frac{1}{p+1}} \\ &\quad{}+ \biggl( \frac{1+ \mu }{ Q_{1} K_{2, \alpha } (T, \lambda _{1}) } \biggr) ^{\frac{p}{p+1}} \biggr] \mathcal{M} ^{\frac{1}{p+1}} \varepsilon ^{\frac{p}{p+1}}. \end{aligned}$$
(4.8)

• If \(p\ge 1\) then

$$\begin{aligned} & \bigl\Vert \mathscr{F}_{\mathrm{n} ,\chi } ^{\varepsilon } ( \cdot ) - \mathscr{F} ( \cdot ) \bigr\Vert _{L^{2}(\Omega ) } \\ &\quad \le \biggl[ \biggl( \frac{ (p +1) K_{1, \alpha } (T) \Vert Q \Vert _{\infty }}{ 2 ( \mu - 1) K_{2, \alpha }^{2} (T, \lambda _{1}) Q_{1}^{2}} \mathcal{M} \varepsilon \biggr)^{\frac{1}{2}} + \biggl( \frac{1+ \mu }{ Q_{1} K_{2, \alpha } (T, \lambda _{1}) } \biggr) ^{ \frac{1}{2}} \biggr] \mathcal{M} ^{\frac{1}{2}} \varepsilon ^{ \frac{1}{2}}. \end{aligned}$$
(4.9)

Proof

From (4.6), we have

$$\begin{aligned} \mu \varepsilon &\le \bigl\Vert \mathcal{K} \mathscr{F}_{\mathrm{n} - 1 , \chi } ^{\varepsilon } - P ^{\varepsilon } \bigr\Vert _{L^{2}(\Omega ) } \\ & = \Biggl\Vert \sum_{k=1}^{\infty } \biggl( \biggl[ 1 - \biggl( 1 - \mathrm{c} \biggl[ \frac{1}{1 + \lambda _{k} (1- \alpha )} \\ &\quad{}\times \int _{0}^{T} \exp \biggl( - \frac{ \alpha \lambda _{k} (T-s) }{1 + \lambda _{k} (1- \alpha )} \biggr) Q (s) \,\mathrm{d} s \biggr]^{2} \biggr)^{\mathrm{n}-1} \biggr] ^{ \chi } - 1 \biggr) \bigl\langle P^{\varepsilon }, w_{k} \bigr\rangle w_{k} \Biggr\Vert _{L^{2}(\Omega ) }. \end{aligned}$$

By \(\chi \in (\frac{1}{2};1]\) and \(0 < \mathrm{c} [ \frac{1}{1 + \lambda _{k} (1- \alpha )} \int _{0}^{T} \exp ( - \frac{ \alpha \lambda _{k} (T-s) }{1 + \lambda _{k} (1- \alpha )} ) Q (s) \,\mathrm{d} s ]^{2} < 1\), we obtain

$$\begin{aligned} \mu \varepsilon \le \bigl\Vert \mathcal{K} \mathscr{F}_{\mathrm{n} - 1 , \chi } ^{\varepsilon } - P ^{\varepsilon } \bigr\Vert _{L^{2}(\Omega ) } = \bigl\Vert P ^{\varepsilon } - P \bigr\Vert _{L^{2}(\Omega ) } + \mathcal{O}, \end{aligned}$$

whereby

$$\begin{aligned} \mathcal{O} &= \Biggl\Vert \sum_{k=1}^{\infty } \biggl( 1 - \mathrm{c} \biggl[ \frac{1}{1 + \lambda _{k} (1- \alpha )} \int _{0}^{T} \exp \biggl( - \frac{ \alpha \lambda _{k} (T-s) }{1 + \lambda _{k} (1- \alpha )} \biggr) Q (s) \,\mathrm{d} s \biggr]^{2} \biggr)^{\mathrm{n}-1}\\ &\quad {}\times \bigl\langle P^{ \varepsilon }, w_{k} \bigr\rangle w_{k} \Biggr\Vert _{L^{2}(\Omega )}. \end{aligned}$$

In view of Lemma 2.3 and (2.12), we get

$$\begin{aligned} \mathcal{O} &\le \Biggl\Vert \sum_{k=1}^{\infty } \biggl( 1 - \mathrm{c} \biggl[ K_{2, \alpha } (T, \lambda _{1}) \frac{Q_{1}}{ \lambda _{k}} \biggr]^{2} \biggr)^{\mathrm{n}-1} \bigl\langle P^{\varepsilon }, w_{k} \bigr\rangle w_{k} \Biggr\Vert _{L^{2}(\Omega ) } \\ &\le \Biggl\Vert \sum_{k=1}^{\infty } \biggl( 1 - \mathrm{c} \biggl[ K_{2, \alpha } (T, \lambda _{1}) \frac{Q_{1}}{ \lambda _{k}} \biggr]^{2} \biggr)^{\mathrm{n}-1} \bigl\langle P^{\varepsilon }, w_{k} \bigr\rangle w_{k} \Biggr\Vert _{L^{2}(\Omega ) } \\ &\le \Biggl( \sum_{k=1}^{\infty } \biggl( 1 - \mathrm{c} \biggl[ K_{2, \alpha } (T, \lambda _{1}) \frac{Q_{1}}{ \lambda _{k}} \biggr]^{2} \biggr)^{2(\mathrm{n}-1)} \lambda _{k}^{2p} \lambda _{k}^{-2p} \bigl\vert \bigl\langle P^{\varepsilon }, w_{k} \bigr\rangle \bigr\vert ^{2} \Biggr) ^{\frac{1}{2}} \\ &\le \sup_{k \geq 1} \biggl( \biggl( 1 - \mathrm{c} \biggl[ K_{2, \alpha } (T, \lambda _{1}) \frac{Q_{1}}{ \lambda _{k}} \biggr]^{2} \biggr)^{ \mathrm{n} - 1} \lambda _{k}^{-p - 1} K_{1, \alpha } (T) \Vert Q \Vert _{ \infty } \biggr) \Biggl( \sum _{k=1}^{\infty } \lambda _{k}^{2p} \bigl\vert \langle \mathscr{F}, w_{k} \rangle \bigr\vert ^{2} \Biggr)^{\frac{1}{2}} . \end{aligned}$$

By Lemma 2.1, we conclude that

$$\begin{aligned} \mathcal{O} &\le \sup_{k \geq 1 } \biggl( \biggl( 1 - \mathrm{c} \biggl[ K_{2, \alpha } (T, \lambda _{1}) \frac{Q_{1}}{ \lambda _{k}} \biggr]^{2} \biggr)^{\mathrm{n} - 1} \lambda _{k}^{-p - 1} K_{1, \alpha } (T) \Vert Q \Vert _{\infty } \biggr) \Biggl( \sum _{k=1}^{\infty } \lambda _{k}^{2p} \bigl\vert \langle \mathscr{F}, w_{k} \rangle \bigr\vert ^{2} \Biggr)^{\frac{1}{2}} \\ &\le \frac{K_{1, \alpha } (T) \Vert Q \Vert _{\infty }}{ (\mathrm{c}^{\frac{1}{2}} K_{2, \alpha } (T, \lambda _{1}) Q_{1})^{p +1 } } \biggl( \frac{p +1}{2} \biggr)^{\frac{p +1}{2}} \frac{ \mathcal{M}}{\mathrm{n}^{\frac{p +1}{2}}}. \end{aligned}$$

We have \(( \mu - 1) \varepsilon \le \frac{K_{1, \alpha } (T) \| Q \|_{\infty }}{ (\mathrm{c}^{\frac{1}{2}} K_{2, \alpha } (T, \lambda _{1}) Q_{1})^{p +1 } } ( \frac{p +1}{2} )^{\frac{p +1}{2}} \frac{ \mathcal{M}}{\mathrm{n}^{\frac{p +1}{2}}} \). This implies that

$$\begin{aligned} \mathrm{n} \le \textstyle\begin{cases} \frac{p +1}{2 \mathrm{c} K_{2, \alpha }^{2} (T, \lambda _{1}) Q_{1}^{2} } ( \frac{ \mathcal{M} K_{1, \alpha } (T) \Vert Q \Vert _{\infty }}{ ( \mu - 1) \varepsilon } )^{\frac{2}{p+1}}, & 0 < p < 1, \\ \frac{ \mathcal{M} (p +1) K_{1, \alpha } (T) \Vert Q \Vert _{\infty }}{ 2 \varepsilon \mathrm{c}( \mu - 1) K_{2, \alpha }^{2} (T, \lambda _{1}) Q_{1}^{2}} , & p \ge 1. \end{cases}\displaystyle \end{aligned}$$
(4.10)

In view of (4.4) and (4.10), we get

$$\begin{aligned} & \bigl\Vert \mathscr{F}_{\mathrm{n} ,\chi } ^{\varepsilon } ( \cdot ) - \mathscr{F}_{\mathrm{n} ,\chi } ( \cdot ) \bigr\Vert _{L^{2}(\Omega ) } \\ &\quad \le \textstyle\begin{cases} ( \frac{p +1}{2 K_{2, \alpha }^{2} (T, \lambda _{1}) Q_{1}^{2} } )^{\frac{1}{2}} ( \frac{ K_{1, \alpha } (T) \Vert Q \Vert _{\infty }}{ ( \mu - 1) } )^{ \frac{1}{p+1}} \mathcal{M} ^{\frac{1}{p+1}} \varepsilon ^{ \frac{p}{p+1}}, & 0 < p < 1, \\ ( \frac{ (p +1) K_{1, \alpha } (T) \Vert Q \Vert _{\infty }}{ 2 ( \mu - 1) K_{2, \alpha }^{2} (T, \lambda _{1}) Q_{1}^{2}} \mathcal{M} \varepsilon )^{\frac{1}{2}} , &p \ge 1. \end{cases}\displaystyle \end{aligned}$$
(4.11)

From (4.5) and applying Hölder’s inequality, we deduce that

$$\begin{aligned} & \bigl\Vert \mathscr{F}_{\mathrm{n}, \chi } ( \cdot ) - \mathscr{F} ( \cdot ) \bigr\Vert _{L^{2}(\Omega ) } \\ &\quad = \mathcal{P} \Biggl\Vert \sum_{k=1}^{\infty } \frac{ 1 - [ 1 - ( 1 - \mathrm{c} [ \frac{1}{1 + \lambda _{k} (1- \alpha )} \int _{0}^{T} \exp ( - \frac{ \alpha \lambda _{k} (T-s) }{1 + \lambda _{k} (1- \alpha )} ) Q (s) \,d s ]^{2} )^{\mathrm{n}} ] ^{ \chi }}{\frac{1}{1 + \lambda _{k} (1- \alpha )} \int _{0}^{T} \exp ( - \frac{ \alpha \lambda _{k} (T-s) }{1 + \lambda _{k} (1- \alpha )} ) Q (s) \,\mathrm{d} s } \langle P, w_{k} \rangle w_{k} \Biggr\Vert _{L^{2}(\Omega ) } ^{ \frac{p}{p+1}}. \end{aligned}$$
(4.12)

Here

$$\begin{aligned} \mathcal{P} &= \Biggl\Vert \sum_{k=1}^{\infty } \frac{ 1 - [ 1 - ( 1 - \mathrm{c} [ \frac{1}{1 + \lambda _{k} (1- \alpha )} \int _{0}^{T} \exp ( - \frac{ \alpha \lambda _{k} (T-s) }{1 + \lambda _{k} (1- \alpha )} ) Q (s) \,d s ]^{2} )^{\mathrm{n}} ] ^{ \chi }}{\frac{1}{1 + \lambda _{k} (1- \alpha )} \int _{0}^{T} \exp ( - \frac{ \alpha \lambda _{k} (T-s) }{1 + \lambda _{k} (1- \alpha )} ) Q (s) \,\mathrm{d} s } \langle P, w_{k} \rangle w_{k} \Biggr\Vert _{L^{2}(\Omega ) } ^{ \frac{1}{p+1}} \\ &\le \Biggl\Vert \sum_{k=1}^{\infty } \langle \mathscr{F}, w_{k} \rangle w_{k} \Biggr\Vert _{L^{2}(\Omega ) } ^{\frac{1}{p+1}} \le \sup_{k \geq 1 } \biggl( \frac{1}{\lambda _{k}} \biggr)^{\frac{p}{p+1}} \Vert \mathscr{F} \Vert _{\mathcal{D}((-\mathscr{B} )^{p} ) }^{\frac{1}{p+1}}, \end{aligned}$$
(4.13)

where we note that \(\chi \in (\frac{1}{2},1]\) and

$$ 0 < \mathrm{c} \biggl[ \frac{1}{1 + \lambda _{k} (1- \alpha )} \int _{0}^{T} \exp \biggl( - \frac{ \alpha \lambda _{k} (T-s) }{1 + \lambda _{k} (1- \alpha )} \biggr) Q (s) \,d s \biggr]^{2} < 1. $$

Hence, we obtain

$$\begin{aligned} & \bigl\Vert \mathscr{F}_{\mathrm{n}, \chi } ( \cdot ) - \mathscr{F} ( \cdot ) \bigr\Vert _{L^{2}(\Omega ) } \\ &\quad \le \sup_{k \geq 1} \biggl( \frac{1}{ \frac{\lambda _{k} }{1 + \lambda _{k} (1- \alpha )} \int _{0}^{T} \exp ( - \frac{ \alpha \lambda _{k} (T-s) }{1 + \lambda _{k} (1- \alpha )} ) Q (s) \,\mathrm{d} s} \biggr)^{\frac{p}{p+1}} \\ &\qquad{} \times \mathcal{M} ^{\frac{1}{p+1}} \Biggl( \Biggl\Vert \sum _{k=1}^{ \infty } \bigl\langle P - P^{\varepsilon }, w_{k} \bigr\rangle w_{k} \Biggr\Vert _{L^{2}( \Omega ) } \\ &\qquad{}+ \Biggl\Vert \sum_{k=1}^{\infty } \biggl( 1 - \biggl[ 1 - \biggl( 1 - \mathrm{c} \biggl[ \frac{1}{1 + \lambda _{k} (1- \alpha )} \\ &\qquad{} \times \int _{0}^{T} \exp \biggl( - \frac{ \alpha \lambda _{k} (T-s) }{1 + \lambda _{k} (1- \alpha )} \biggr) Q (s) \,d s \biggr]^{2} \biggr)^{\mathrm{n}} \biggr] ^{ \chi } \biggr) \bigl\langle P^{\varepsilon }, w_{k} \bigr\rangle w_{k} \Biggr\Vert _{L^{2}( \Omega ) } \Biggr) ^{\frac{p}{p+1}}. \end{aligned}$$

In view of (4.6), \(\| \mathscr{F}_{\mathrm{n}, \chi } ( \cdot ) - \mathscr{F} ( \cdot ) \|_{L^{2}(\Omega ) } \le ( \frac{1+ \mu }{ Q_{1} K_{2, \alpha } (T, \lambda _{1}) } ) ^{ \frac{p}{p+1}} \mathcal{M} ^{\frac{1}{p+1}} \varepsilon ^{ \frac{p}{p+1}} \). This implies the following.

• If \(0 < p < 1\) then

$$\begin{aligned} \bigl\Vert \mathscr{F}_{\mathrm{n} ,\chi } ^{\varepsilon } ( \cdot ) - \mathscr{F} ( \cdot ) \bigr\Vert _{L^{2}(\Omega ) } &\le \biggl[ \biggl( \frac{p +1}{2 K_{2, \alpha }^{2} (T, \lambda _{1}) Q_{1}^{2} } \biggr)^{ \frac{1}{2}} \biggl( \frac{ K_{1, \alpha } (T) \Vert Q \Vert _{\infty }}{ ( \mu - 1) } \biggr)^{ \frac{1}{p+1}} \\ &\quad{}+ \biggl( \frac{1+ \mu }{ Q_{1} K_{2, \alpha } (T, \lambda _{1}) } \biggr) ^{\frac{p}{p+1}} \biggr] \mathcal{M} ^{\frac{1}{p+1}} \varepsilon ^{\frac{p}{p+1}}. \end{aligned}$$
(4.14)

• If \(p\ge 1\) then

$$\begin{aligned} & \bigl\Vert \mathscr{F}_{\mathrm{n} ,\chi } ^{\varepsilon } ( \cdot ) - \mathscr{F} ( \cdot ) \bigr\Vert _{L^{2}(\Omega ) } \\ & \quad \le \biggl[ \biggl( \frac{ (p +1) K_{1, \alpha } (T) \Vert Q \Vert _{\infty }}{ 2 ( \mu - 1) K_{2, \alpha }^{2} (T, \lambda _{1}) Q_{1}^{2}} \mathcal{M} \varepsilon \biggr)^{\frac{1}{2}} + \biggl( \frac{1+ \mu }{ Q_{1} K_{2, \alpha } (T, \lambda _{1}) } \biggr) ^{ \frac{1}{2}} \biggr] \mathcal{M} ^{\frac{1}{2}} \varepsilon ^{ \frac{1}{2}}. \end{aligned}$$
(4.15)

 □

5 Numerical test

In this section, we show a numerical example to illustrate the proposed method. The numerical test is constructed in the following way: Firstly, we set up some computations which support this example as follows: Let \(\alpha \in (0,1)\), \(T =1\) be a fixed value and \((\mathrm{x},t) \in (0,\pi ) \times (0,1)\). Then we have the eigenvalues \(\lambda _{k} = k^{2}\), \(k = 1,2,\ldots\) , with corresponding eigenfunction \(w_{k}(\mathrm{x}) = \sqrt{\frac{2}{\pi }}\sin (k\mathrm{x})\) and the inner product \(\langle \cdot , \cdot \rangle _{L^{2}(0,\pi )}\) is given by

$$\begin{aligned} \langle a, b \rangle _{L^{2}(0,\pi )} = \int _{0}^{\pi } ab \,\mathrm{d}\mathrm{x}. \end{aligned}$$
(5.1)

In Mathlab software, to compute a integral, we use the code which made by Juan Camilo Medina; see Juan Camilo Medina, Simpson’s Rule Integration, MATLAB Central File Exchange. Retrieved March 19, 2020.

Secondly, we choose the exact data function \(\mathrm{g}(\mathrm{x})\) and \(F(\mathrm{x},t)\) as follows:

$$\begin{aligned} \mathrm{g}(\mathrm{x}) = \sqrt{\frac{2}{\pi }} \sin (\mathrm{x}), \qquad F( \mathrm{x},t) = \sqrt{\frac{2}{\pi }}t^{2}\sin (2\mathrm{x}). \end{aligned}$$
(5.2)

A uniform Cartesian grid can be generated as follows (see Fig. 1 as an illustration):

$$\begin{aligned} &\mathrm{x}_{i} = (i-1)h_{\mathrm{x}}, \quad i = 1,2,\ldots,M+1, h_{ \mathrm{x}} = \frac{\pi }{M}, \\ &t_{j} = (j-1)h_{t}, \quad j = 1,2,\ldots,N+1, h_{t} = \frac{1}{N}. \end{aligned}$$

Then we have the following exact solution:

$$\begin{aligned} &u(\mathrm{x},t) \\ &\quad = \sum_{k=1}^{\infty } \biggl[ \frac{1}{1 + k^{2} (1- \alpha )} \exp \biggl( - \frac{\alpha k^{2} t }{1 + k^{2} (1- \alpha )} \biggr) \int _{0}^{ \pi } \mathrm{g}(\mathrm{x})\sqrt{ \frac{2}{\pi }} \sin (k\mathrm{x}) \,\mathrm{d}\mathrm{x} \\ &\qquad{}+ \frac{1}{1 + k^{2} (1- \alpha )} \int _{0}^{t} \exp \biggl( - \frac{\alpha k^{2} (t-s) }{1 + k^{2} (1- \alpha )} \biggr) \int _{0}^{ \pi } F(\mathrm{x},s)\sqrt{ \frac{2}{\pi }} \sin (k\mathrm{x}) \,\mathrm{d} \mathrm{x} \,\mathrm{d} s \biggr] \\ &\qquad {}\times \sqrt{\frac{2}{\pi }} \sin (k\mathrm{x}). \end{aligned}$$
(5.3)
Figure 1
figure 1

A uniform Cartesian grid on \((\mathrm{x},t) \in (0,\pi ) \times (0,1)\)

Full size image

We can see the graph of \(u(\mathrm{x},t)\) on \((\mathrm{x},t) \in (0,\pi ) \times (0,1)\) in Fig. 2.

Figure 2
figure 2

The solution \(u(\mathrm{x},t)\) on \((\mathrm{x},t) \in (0,\pi ) \times (0,1)\)

Full size image

From (5.3), we have the value of the final time as follows:

$$\begin{aligned} H (\mathrm{x} ) &= \frac{\sqrt{2\pi } \exp (\frac{\alpha }{\alpha -2} )}{\pi (2-\alpha )} \sin (x) + \frac{\sqrt{2\pi } \exp (\frac{4\alpha }{4\alpha -5} )}{32\pi } \\ &\quad {} \times \biggl[ \bigl(16\alpha ^{2}-24\alpha +13\bigr)\exp \biggl( \frac{4}{5- 4\alpha } \biggr) + (5-4\alpha )^{2} \biggr] \sin (2 \mathrm{x}). \end{aligned}$$
(5.4)

Thirdly, we consider the noise model satisfies

$$\begin{aligned} H ^{\varepsilon } =H + \varepsilon \operatorname{randn}(\cdot ), \end{aligned}$$
(5.5)

where the noise level \(\varepsilon \longrightarrow 0^{+}\) and the function \(\operatorname{randn}(\cdot )\) generates arrays of random numbers whose elements are normally distributed with mean 0, variance \(\sigma ^{2}=1\); see Fig. 3.

Figure 3
figure 3

The graph of functions H and \(H^{\varepsilon }\)

Full size image

Next, the source function with the exact data H as follows:

$$\begin{aligned} &\mathscr{F}_{\mathrm{n} ,\theta } (\mathrm{x} ) \\ &\quad = \sum_{k=1}^{\infty } \frac{ [ 1 - ( 1 - \mathrm{c} [ \frac{1}{1 + k^{2} (1- \alpha )} \int _{0}^{1} \exp ( - \frac{ \alpha k^{2} (1-s) }{1 + k^{2} (1- \alpha )} ) {Q} (s) \,\mathrm{d} s ]^{2} )^{\mathrm{n}} ] ^{ \chi }}{\frac{1}{1 + k^{2} (1- \alpha )} \int _{0}^{1} \exp ( - \frac{ \alpha k^{2} (1-s) }{1 + k^{2} (1- \alpha )} ) {Q} (s) \,\mathrm{d} s } \langle \mathscr{P}, w_{k} \rangle w_{k}, \end{aligned}$$

where \(\mathscr{P }_{k} := {H}_{k} - \frac{1}{1 + k^{2} (1- \alpha )} \exp ( - \frac{ \alpha k^{2} }{1 + k^{2} (1- \alpha )} ) \mathrm{g}_{k} \).

According to the fractional Landweber regularization method, we have the source function with noise data \(H ^{\varepsilon }\) as follows:

$$\begin{aligned} &\mathscr{F}_{\mathrm{n} ,\chi } ^{\varepsilon } (\mathrm{x} ) \\ &\quad = \sum_{k=1}^{\infty } \frac{ [ 1 - ( 1 - \mathrm{c} [ \frac{1}{1 + k^{2} (1- \alpha )} \int _{0}^{1} \exp ( - \frac{ \alpha k^{2} (1-s) }{1 + k^{2} (1- \alpha )} ) Q (s) \,\mathrm{d} s ]^{2} )^{\mathrm{n}} ] ^{ \chi }}{\frac{1}{1 + k^{2} (1- \alpha )} \int _{0}^{1} \exp ( - \frac{ \alpha k^{2} (1-s) }{1 + k^{2} (1- \alpha )} ) Q(s)\,\mathrm{d} s } \bigl\langle \mathscr{P}^{\varepsilon }, w_{k} \bigr\rangle w_{k}. \end{aligned}$$

Here \(\mathscr{P}^{\varepsilon } := H^{\varepsilon } - \sum_{k=1}^{ \infty } ( \frac{1}{1 + k^{2} (1- \alpha )} \exp ( - \frac{ \alpha k^{2} }{1 + k^{2} (1- \alpha )} ) \mathrm{g}_{k} ) w_{k}(\mathrm{x} )\), \(\chi \in ( \frac{1}{2}, 1 ] \) is the fractional order, and \(\mathrm{n} > 0 \) is a regularization parameter.

The absolute error estimation \({E}^{\epsilon }_{\alpha }\) between the exact source function \(\mathscr{F}_{\mathrm{n} ,\theta } \) and the regularized source function \(\mathscr{F}_{\mathrm{n} ,\chi } ^{\varepsilon } \) is as follows:

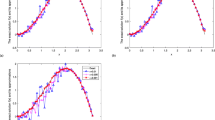
$$\begin{aligned} {E}^{\epsilon }_{\alpha }&= \Biggl(\frac{1}{{M+1}} \sum _{i=1}^{M+1} \bigl\vert \mathscr{F}_{\mathrm{n} ,\theta } (\mathrm{x}_{i} ) - \mathscr{F}_{\mathrm{n} ,\chi } ^{\varepsilon } ( \mathrm{x}_{i} ) \bigr\vert ^{2} \Biggr)^{1/2}. \end{aligned}$$
(5.6)

The results of this example are shown in Table 1. In Fig. 4, we present the graph of the exact and regularized source functions. From the error table and the figures above, we can see that the smaller the ε, the better the computed approximation. In particular, the regularized source function will gradually approach the exact source function as ε tends to zero.

Figure 4
figure 4

The exact source function \(\mathscr{F}_{\mathrm{n} ,\theta } \) and the regularized source function \(\mathscr{F}_{\mathrm{n} ,\chi } ^{\varepsilon } \) for \(\mathrm{x} \in (0,\pi )\)

Full size image
Table 1 The error estimation between the exact and regularized source functions for \(\alpha \in \{0.1, 0.3, 0.5, 0.7, 0.9\}\) and \(\mathrm{x} \in (0,\pi )\)
Full size table

6 Conclusions

In this paper, we study the source function for the Caputo–Fabrizio time fractional diffusion equation with the new kernel. We show that the backward problem for this equation is ill-posed (in the sense of Hadamard). Then the fractional Landweber and the modified quasi-boundary value methods are used to deal with this inverse problem and the regularized solution is also obtained. We also give the convergence estimates between the regularized solution and the exact solution by using the a priori regularization parameter choice rule and the a posteriori parameter choice rule. Finally, we give a numerical example to illustrate the proposed method.